Abstract
Actor Networks are a modeling framework for cyber-physical system protocols based on Latour’s actor-network theory that addresses the way we now create and exploit the power of computational networks. We advance a logic for modeling and reasoning about such actor networks, which is obtained through a two-stage constrained hybridization process. The first stage results in a logic that captures the structure of actor networks and the way knowledge flows across them; the second addresses the dynamic aspects of actor networks, that is the way they can evolve as a result of the interactions that occur within them. For each of these stages, we develop a sound and complete proof system.
Access provided by CONRICYT-eBooks. Download conference paper PDF
Similar content being viewed by others
1 Introduction
Over the past few years, there has been a renewed interest in modal logics for computer science through the family of the so-called hybrid logics (see [1] for a comprehensive overview). The development of hybrid logics originated in Arthur Prior’s work in the 1960s [2]. In their most basic form, these are logics obtained by enriching ordinary modal logics with nominals—symbols that name individual states (possible worlds) in Kripke models—and dedicated satisfaction operators \(@_{a}\) that enable a change of perspective from the current state to the one that corresponds to the nominal a. A significant body of research exists around this class of logics, among which [3,4,5,6] are recent publications.
In this paper, we are specifically interested in the present-day applications of hybrid logics to the specification and verification of reconfigurable systems [7]. In a nutshell, the idea is that system configurations (and the functionalities associated with them) can be regarded as local models of a Kripke structure, and that they can change simply by switching from one mode of operation to another via an accessibility relation. The key advancement here lies in the fact that the characteristic features of hybrid logic can be developed, through a process known as hybridization [8], on top of an arbitrary logic used for expressing configuration-specific requirements. This means that, depending on the base logic, configurations can be captured, for example, as algebras, relational structures or, when the hybridization process is iterated, even as Kripke models.
Actor Networks. Our interest in this area results from a new modeling framework for cyber-physical system protocols proposed in [9] around the concept of Actor Network (or ant), which addresses networks whose components are no longer limited to programs but can also include humans or physical artifacts as actors. ants should therefore be understood in the wider sense of Latour’s actor-network theory [10]: actors are cyber-physical entities that have shared agency—from people, to objects, and to locations; they interact through so-called channels that account, for example, for observations that an actor may make of another, of control that an actor may exert on another, or of movement of an actor inside another (say, a person to a location). Interaction, rather than computation, has become the critical source of complexity, thus giving rise to new challenges in ensuring the reliability of the systems that are now operating in cyberspace.
Contributions. The ordinary hybridization process yields logical systems that are suitable for dealing with either the static/structural aspects or with the dynamic aspects of actor networks. From a static perspective, hybrid logics can be naturally used, for example, to give faithful descriptions of the shapes of networks, of the (states of the) actors involved, or of the channels through which interactions can take place. However, accommodating at the same time both the structure and the behaviour of ants raises some difficulties because these two aspects require distinct, and possibly conflicting, interpretations of the hybrid features. For example, from a structural point of view, modalities denote channels, whereas from a behavioural point of view they stand for graphs of interactions between actors. That is, the challenge raised by ants lies precisely in capturing the way in which the structure of such networks evolves. This leads us to propose a two-layered hybridization process, where the first level corresponds to the structure, and the second to the dynamics of actor networks.
The paper consists of two main technical sections. In Sect. 2 we introduce the underlying model theory of actor networks. We start by formalizing the main static concepts: actors, interaction channels, the knowledge that actors may have and the way it may be acquired across certain channels, and the placement of some actors relative to other actors. Then, we formalize the key notion of interaction and the way an interaction can change the state of a network.
Section 3 is devoted to the logics through which we can specify and reason about the states of an actor network and about the state transitions associated with interactions. These logics are obtained through a sequence of two processes of constrained hybridization, meaning that (a) the models of the hybrid logics implicitly satisfy additional semantic constraints, and (b) we actually operate across three logical levels—each level captures a different aspect of actor networks (knowledge, structure, or dynamics), and each is defined as an exogenous enrichment (with new hybrid features) of the previous level.
Notational Conventions. Most of the structures we deal with in this paper are presented as tuples—whose components, in turn, may also be tuple-based structures—that satisfy certain cohesion properties. To keep the notations as simple as possible, and avoid spelling out all the components of a given structure, we make use of subscripts. For example, we may denote the set \(\mathcal {N}\) of nodes of a graph \(\mathcal {G}\) by \(\mathcal {N}_{\mathcal {G}}\), the underlying graph \(\mathcal {G}\) of an ant schema \(\mathcal {A}\) by \(\mathcal {G}_{\mathcal {A}}\), and the domain \(\mathcal {D}\) of an actor network \(\nu \) by \(\mathcal {D}_{\nu }\). When there is no risk of confusion, we overload this notation in order to refer to the hereditary components of a structure. That is, we may denote, for example, the set \(\mathcal {N}\) of nodes of the underlying graph of an ant schema \(\mathcal {A}\) by \(\mathcal {N}_{\mathcal {A}}\)—even if \(\mathcal {N}\) is not a direct component of \(\mathcal {A}\).
2 Actor Networks
2.1 Schemas
Definition 1
(Schema). An  \(\mathcal {A}\) consists of:
\(\mathcal {A}\) consists of:
-
a finite directed graph \(\mathcal {G}= \langle \mathcal {N}, \mathcal {C}, \delta , \rho \rangle \), where \(\mathcal {N}\) is a non-empty set (of nodes, called actors), \(\mathcal {C}\) is a set (of edges, called channels), and \(\delta \) and \(\rho \) are maps \(\mathcal {C}\rightarrow \mathcal {N}\) that give the domain (origin) and codomain (target) of every channel;
-
a partially ordered set \(\mathcal {T}\) (of channel types, with a subtype relationship);
-
a function \(\tau :\mathcal {C}\rightarrow 2^{\mathcal {T}}\) that assigns a non-empty upper setFootnote 1 of channel types to every channel, such that for every \(n, n' \in \mathcal {N}\) and \(\kappa \in \mathcal {T}\) there is at most one channel \(c \in \mathcal {C}\) such that \(\delta (c) = n\), \(\rho (c) = n'\), and \(\kappa \in \tau (c)\); and
-
a set \(\mathcal {P}\) (of propositional symbols).
The nodes of an ant schema represent actors executing a given protocol and edges represent channels that link together those actors. Channels are typed in order to account for different modes of relationship between actors. The propositional symbols are used to represent knowledge that is held by the different actors, including data. Pieces of data (or knowledge) have by themselves no agency in the context of the protocol, otherwise they would be actors; for example, in a given protocol, money could be data but, in another protocol, bank notes could be actors, in the sense that they can change hands, be lost, and so on. Knowledge/data can be transmitted across channels as appropriate.
Example 2
Consider the ant schema \(\textsf {Elevator}\) whose graph and typing function are depicted in Fig. 1. The nodes \(\textit{F0}\) and \(\textit{F1}\) correspond to the ground and first floor of a building, and \(\textit{E}\) to the elevator proper, which we often refer to as \(\textsf {Elevator}\) unless it is ambiguous. The node \(\textit{C}\) corresponds to the elevator cabin, which we often refer to as Cabin, and \(\textit{P0}\) and \(\textit{P1}\) correspond to the two platforms where the cabin can be—\(\textit{P0}\) for the ground floor and \(\textit{P1}\) for the first floor. The node \(\textit{A}\) represents a user of the elevator, which we refer to as Alice.
\(\textsf {Elevator}\) has a number of channels of different types:
-
The channel type \( mov \) captures the movement of one actor inside another. The two channels of type \( mov \) that connect \(\textit{P0}\) and \(\textit{P1}\) allow the cabin to move between the two platforms (up or down).
-
The type \( door \) is a subtype of \( mov \). The two channels of type \( door \) connect \(\textit{F0}\) and \(\textit{F1}\) to \(\textit{C}\) in order to allow users to enter or exit the cabin from or to the floor. Although these two channels are also of type \( mov \), for readability we tend to depict only the minimal types when representing ant schemas.
-
The channel type \( obs \) captures observations that an actor may make of another. The channels of type \( obs \) that connect \(\textit{E}\) to \(\textit{F0}\) and \(\textit{F1}\) account for observations of the state of \(\textsf {Elevator}\) at either floor, while those that connect \(\textit{F0}\) and \(\textit{F1}\) to \(\textit{A}\) account for observations that Alice makes of either floor.
-
The channel type \( ctr \) captures forms of control that one actor may exert on another. The two channels of type \( ctr \) that connect \(\textit{F0}\) to \(\textit{E}\) and \(\textit{F1}\) to \(\textit{E}\) are for transmitting requests from floors to \(\textsf {Elevator}\), and the channel that connects \(\textit{C}\) to \(\textit{E}\) is for transmitting requests from Cabin to \(\textsf {Elevator}\).
-
The channel subtype \( btn \) of \( ctr \) captures the special case of control achieved through a button. The three channels of type \( btn \) that connect \(\textit{A}\) to \(\textit{F0}\), \(\textit{F1}\), and \(\textit{C}\) account for the buttons that Alice can press at either floor or at Cabin.
Last but not least, the ant schema \(\textsf {Elevator}\) has two propositional symbols,  and
and  . These are used to capture knowledge of where Cabin is.
. These are used to capture knowledge of where Cabin is.
2.2 States
A structure for an ant schema \(\mathcal {A}\) consists of a subgraph of \(\mathcal {G}_{\mathcal {A}}\) together with a forest (or placement graph, as in [11]) over its nodes that captures ‘location’.
Definition 3
(Structure). A structure for a schema \(\mathcal {A}\) is a pair \(\langle \mathcal {H}, \mathcal {F}\rangle \) where:
-
\(\mathcal {H}\) is a subgraph of \(\mathcal {G}_{\mathcal {A}}\), and
-
\(\mathcal {F}\) is a forest over \(\mathcal {N}_{\mathcal {H}}\), meaning that every node n has either none or a unique parent, denoted \(\mathcal {F}(n)\). Nodes without a parent are called roots.
We say that \(\langle \mathcal {H}_{1}, \mathcal {F}_{1} \rangle \) is a substructure of (or is included in) \(\langle \mathcal {H}_{2}, \mathcal {F}_{2} \rangle \) if:
-
\(\mathcal {H}_{1}\) is a subgraph of \(\mathcal {H}_{2}\), and
-
for every \(n \in \mathcal {N}_{\mathcal {H}_{1}}\) such that \(\mathcal {F}_{1}(n)\) is defined, \(\mathcal {F}_{2}(n)\) is also defined and equal to \(\mathcal {F}_{1}(n)\)—that is, the hierarchy is strictly preserved.
The notion of substructure defines a partial order, which we denote by \(\preceq \).
Example 4
An ant structure for \(\textsf {Elevator}\) is depicted in Fig. 2. The forest, on the right, places the two platforms inside \(\textsf {Elevator}\), the Cabin inside the platform of the first floor, and Alice at the ground floor; both floors are outside \(\textsf {Elevator}\).
The graph, on the left, indicates the channels that are available: for example, the channel that corresponds to the button that Alice can press to call the elevator, and the one that connects \(\textit{F0}\) to \(\textit{E}\) and allows the floor to transmit requests to \(\textsf {Elevator}\). Notice that, for readability, we always include the channel types in figures, even though they are not formally part of ant structures.
To better visualize ant structures, we combine the graph and the forest components through the nesting of nodes in the graph. This can be seen in Fig. 3, where three ant structures are presented.
A state is an ant structure together with a valuation of the propositional symbols, which assigns to each node and propositional symbol the truth value of the propositional symbol at that node. We work with a three-valued Łukasiewicz logic, i.e., propositions may have values  (true),
(true),  (false), or
(false), or  (undefined).
(undefined).
Definition 5
(State). A state of an ant schema \(\mathcal {A}\) consists of a structure \(\mathcal {S}\) for \(\mathcal {A}\) such that \(\mathcal {N}_{\mathcal {S}} = \mathcal {N}_{\mathcal {A}}\) (i.e., the structure has all the nodes of the schema) together with, for each node n, a valuation  .
.
We denote the set of states of an ant schema \(\mathcal {A}\) by \(\mathbb {S}_{\mathcal {A}}\) and, following our notational convention, the structure underlying a state \(\sigma \) by \(\mathcal {S}_{\sigma }\).
Example 6
As an example, we define the state \(\textsf {elevator}_{0}\) whose underlying structure is shown in the top-left part of Fig. 4 and whose valuation is given by:

That is, the actors/nodes \(\textit{E}\), \(\textit{F0}\), \(\textit{F1}\) and \(\textit{A}\) all know that Cabin is at the platform \(\textit{P1}\) (and that it is not at \(\textit{P0}\)); no other node knows where Cabin is.
2.3 Interactions
Channels provide the means for actors to interact with each other. The interactions through which actors change protocol states can be more complex (in the sense that they can involve many actors and channels) and are therefore defined as ant structures: given an interaction, its nodes are the actors of the ant schema that are involved in the interaction, and its channels are those through which those actors interact with each other.
Definition 7
(Interaction). An interaction in the context of an ant schema \(\mathcal {A}\) is a structure for \(\mathcal {A}\). We denote by \(\mathbb {I}_{\mathcal {A}}\) the set of all interactions of \(\mathcal {A}\).
Example 8
Figure 3 depicts three interactions for the ant schema \(\textsf {Elevator}\):
-
(a)
callElevator0: Alice is at the ground floor and presses the button to call the elevator; the request is transmitted to \(\textsf {Elevator}\) through a \( ctr \) channel.
-
(b)
moveCabin0: Cabin is at the first floor and the channel through which it can move to the ground floor is available.
-
(c)
enterCabin0: Alice is at the ground floor and observes the position of the cabin through the two channels of type \( obs \); the channel of type \( door \) that connects \(\textit{F0}\) to \(\textit{C}\) is available for Alice to enter the cabin.
2.4 Networks
Protocols are formalized as actor networks. An actor network consists of (a) an ant schema, which contains all the actors and the channels that connect them; (b) a set of possible worlds—each being associated with a so-called admissible state—including a subset of designated initial worlds; (c) a set of all possible interactions through which the actor network can evolve; and (d) for every such interaction, a transition relation on the set of worlds. Formally,
Definition 9
(Actor network). An actor network \(\nu \) consists of:
-
an ant schema \(\mathcal {A}\),
-
a domain (set of worlds) \(\mathcal {D}\) together with a labeling function \(\varsigma :\mathcal {D}\rightarrow \mathbb {S}_{\mathcal {A}}\),
-
a non-empty subset \(\mathcal {D}_{0} \subseteq \mathcal {D}\) of initial worlds (whose labels are initial states),
-
a set \(\mathcal {I}\subseteq \mathbb {I}_{\mathcal {A}}\) of interactions for \(\mathcal {A}\),
-
a transition relation
 such that, for each interaction \(\iota \in \mathcal {I}\),
such that, for each interaction \(\iota \in \mathcal {I}\),  implies \(\iota \preceq \mathcal {S}_{\varsigma (w)}\) (interactions are substructures of the source states).
implies \(\iota \preceq \mathcal {S}_{\varsigma (w)}\) (interactions are substructures of the source states).
We say that a state of \(\mathcal {A}\) is admissible for \(\nu \) if it corresponds to one of its worlds; we denote by \(\mathbb {S}_{\nu }\) the image of \(\mathcal {D}\) under \(\varsigma \) (i.e., the set of admissible states of \(\nu \)).
Therefore, an actor network can be regarded as a labeled transition system over a set of states of the schema, transitions being labeled with interactions.
Example 10
An actor network \(\nu _\textsf {Elevator}\) with \(\textsf {Elevator}\) as its schema could have, for example, \(\textsf {elevator}_{0}\) (labeled with the state defined in Example 4) as one of its initial worlds, and the worlds and transitions presented in Fig. 4, among others. Note that the valuations are not included in these diagrams; an axiomatic presentation of the valuations is discussed in Sect. 3.
The ‘horizontal’ transitions in Fig. 4 are performed by the interaction callElevator0 (cf. Fig. 3(a)). The one at the top starts at \(\textsf {elevator}_{0}\). Although several actors and channels are present in \(\textsf {elevator}_{0}\), the interaction callElevator0 indicates that the actors that are active in the transition are Alice, \(\textsf {Elevator}\) and \(\textit{F0}\) (the ground floor), and that the active channels are those that connect \(\textit{A}\) to \(\textit{F0}\) and \(\textit{F0}\) to \(\textit{E}\). That is to say, Alice presses the button at \(\textit{F0}\) and the request is transmitted to \(\textsf {Elevator}\). The transition to \(\textsf {elevator}_{1}\) activates the channel of type \( mov \) that connects \(\textit{P1}\) to \(\textit{P0}\) through which \(\textsf {Elevator}\) can respond to the request (i.e., move the cabin), and closes the channel of type \( btn \) from \(\textit{A}\) to \(\textit{F0}\), i.e., Alice is no longer able to call the elevator.
The other transition (at the bottom) performed by callElevator0 starts in a different world, \(\textsf {elevator}_{0}'\), where Cabin is in \(\textit{P0}\). It opens the two channels of type \( door \) between \(\textit{F0}\) and \(\textit{C}\) that allow users to enter or exit the cabin.
The ‘vertical’ transition from \(\textsf {elevator}_{1}\) to \(\textsf {elevator}_{2}\) is performed by the interaction moveCabin0 (cf. Fig. 3(b)). As indicated by the interaction, this computation is local to \(\textit{P0}\), \(\textit{P1}\), \(\textit{F0}\), \(\textit{F1}\), \(\textit{E}\), and \(\textit{C}\). The transition moves the cabin from \(\textit{P1}\) to \(\textit{P0}\), closes the channel of type \( mov \) that connects the two platforms and—just like the transition between \(\textsf {elevator}_{0}'\) and \(\textsf {elevator}_{2}\)—opens the two channels of type \( door \) that allow users to enter or exit the cabin.
3 Logics for ANts
3.1 The Base Logic
The logics through which we can specify and reason about actor networks are obtained through an iterated process of constrained hybridization. At the base of this construction is the three-valued propositional Łukasiewicz logic, which we recall below. A signature for the Łukasiewicz logic is given by a set \(\mathcal {P}\) of atomic propositions (the propositional symbols defined by an ant schema).
Definition 11
(Syntax). The set \(\textsf {\L {}}(\mathcal {P})\) of sentences of the base logic is the least set that includes \(\mathcal {P}\) and is closed under negation (\(\overline{p}\)) and implication (\(p \mathrel {\supset }q\)).
Definition 12
(Semantics). Base-logic sentences are interpreted over functions  as follows: The negation maps
as follows: The negation maps  to
to  and vice versa, and leaves
and vice versa, and leaves  unchanged. The implication \(p \mathrel {\supset }q\) evaluates to
unchanged. The implication \(p \mathrel {\supset }q\) evaluates to  if
if  and
and  , to
, to  if
if  and
and  or
or  and
and  , and to
, and to  in all other cases. We say that a proposition p is valid if
in all other cases. We say that a proposition p is valid if  for all valuations \([\![{\_}]\!]\).
for all valuations \([\![{\_}]\!]\).
The following modalities, which return Boolean values, are useful:

3.2 The State Logic
The logic through which we can specify and reason about the states of an ant is a constrained hybridization of \(\textsf {\L {}}(\mathcal {P})\). Therefore, there are two main ingredients to consider here. Firstly, an  signature, denoted \(\varSigma \) in what follows, which consists of a set \(\mathcal {P}\) of propositional symbols (i.e., a signature of the base Łukasiewicz logic), a countably infinite set \(\mathcal {N}\! om \) of nominals that includes a set \(\mathcal {N}\) of actor names, and a set \(\mathcal {T}\) of channel types (regarded as modalities). Secondly, a partial order on \(\mathcal {T}\) and an edge-labeled directed finite graph \(\mathcal {G}\) with components \(\mathcal {N}\), \(\mathcal {C}\), \(\delta \), \(\rho \), and \(\tau \) as in Definition 1. These provide the constraints that we impose on the models of the hybrid logic.
signature, denoted \(\varSigma \) in what follows, which consists of a set \(\mathcal {P}\) of propositional symbols (i.e., a signature of the base Łukasiewicz logic), a countably infinite set \(\mathcal {N}\! om \) of nominals that includes a set \(\mathcal {N}\) of actor names, and a set \(\mathcal {T}\) of channel types (regarded as modalities). Secondly, a partial order on \(\mathcal {T}\) and an edge-labeled directed finite graph \(\mathcal {G}\) with components \(\mathcal {N}\), \(\mathcal {C}\), \(\delta \), \(\rho \), and \(\tau \) as in Definition 1. These provide the constraints that we impose on the models of the hybrid logic.
Definition 13
(Syntax). The syntax of the state logic is given by the grammar

where \(p \in \textsf {\L {}}(\mathcal {P})\), \(a \in \mathcal {N}\! om \), \(b \in \mathcal {N}\! om \setminus \mathcal {N}\), \(\kappa \in \mathcal {T}\), and \(\pi \) is a distinguished and new parent modality. We denote this set of sentences by \(\textsf {State}(\varSigma )\).
In the most general setting, hybrid sentences are evaluated over unconstrained Kripke models, that is over triples \(\langle W, R, V \rangle \), where W is a set of nodes or possible worlds, R is a family of accessibility relations \(R_{\lambda } \subseteq W \times W\), indexed by modalities \(\lambda \), and V is a family of interpretations of the symbols from \(\mathcal {P}\) indexed by possible worlds. The semantics of hybrid logics often includes additional constraints; for example, in the S4 variant of hybrid propositional logic, the accessibility relations are reflexive and transitive, and in the S5 variant they are reflexive and Euclidean. The constraints that we consider for the state logic follow from the underlying graph structure of the ant schema used:
-
There is a one-to-one correspondence between actors and possible worlds. For notational convenience, we do not distinguish possible worlds from actors.
-
The accessibility relations conform to the channels and the channel types of the schema: for each channel type \(\kappa \), \(R_{\kappa }\) consists of those pairs of nodes \((n, n')\) that are connected through a channel of type \(\kappa \).
-
The interpretation of the parent modality \(\pi \) is functional and acyclic.
In other words, the constrained models of the hybridization of \(\textsf {\L {}}(\mathcal {P})\) that we consider here are states of the actor-network schema \(\mathcal {A}= \langle \mathcal {G}, \mathcal {T}, \tau , \mathcal {P}\rangle \).
Definition 14
(Semantics). Given a state \(\sigma = \langle \mathcal {S}, \mathcal {V}\rangle \) of \(\mathcal {A}\), an assignment is a map \(\alpha :\mathcal {N}\! om \rightarrow \mathcal {N}_{\mathcal {S}}\) whose restriction to the set \(\mathcal {N}\) of actor names is the identity.Footnote 2 The satisfaction relation between ant states and state-logic sentences is parameterized by assignments \(\alpha \) and by actors n (i.e., by nodes of \(\mathcal {S}\)):
-
\(\sigma , \alpha , n \vDash a\) iff \(\alpha (a) = n\);
-
\(\sigma , \alpha , n \vDash p\) iff
 where \([\![{\_}]\!]_{n}\) is the valuation defined by \(\mathcal {V}_{n}\) over \(\mathcal {P}\);
where \([\![{\_}]\!]_{n}\) is the valuation defined by \(\mathcal {V}_{n}\) over \(\mathcal {P}\); -
\(\sigma , \alpha , n \vDash \lnot \,\phi \) iff \(\sigma , \alpha , n \not \vDash \phi \);
-
\(\sigma , \alpha , n \vDash \phi _{1} \mathrel {\rightarrow }\phi _{2}\) iff \(\sigma , \alpha , n \vDash \phi _{1}\) implies \(\sigma , \alpha , n \vDash \phi _{2}\);
-
\(\sigma , \alpha , n \vDash \langle \kappa \rangle {\phi }\) iff there is \(c \in \mathcal {C}\) such that \(\delta (c) = n\), \(\kappa \in \tau (c)\), and \(\sigma , \alpha , \rho (c) \vDash \phi \);
-
\(\sigma , \alpha , n \vDash \langle \pi \rangle {\phi }\) iff \(\mathcal {F}(n)\) is defined and \(\sigma , \alpha , \mathcal {F}(n) \vDash \phi \);
-
\(\sigma , \alpha , n \vDash @_{a}\,\phi \) iff \(\sigma , \alpha , \alpha (a) \vDash \phi \);
-
\(\sigma , \alpha , n \vDash \exists b\,\phi \) iff \(\sigma , \alpha ', n \vDash \phi \) for some \(\alpha '\) that agrees with \(\alpha \) on \(\mathcal {N}\! om \setminus \{b\}\).
We also define validity of a sentence at a state to mean that it is satisfied for every assignment at every node, validity of a sentence at an ant structure to mean that it is satisfied at every state for it, and absolute validity of a sentence (at a schema) to mean that it is valid at every state of the schema:
-
 for all assignments \(\alpha :\mathcal {N}\! om \rightarrow \mathcal {N}\) and all \(n \in \mathcal {N}\);
for all assignments \(\alpha :\mathcal {N}\! om \rightarrow \mathcal {N}\) and all \(n \in \mathcal {N}\); -
\(\mathcal {S}\vDash \phi \) iff \(\sigma \vDash \phi \) for all states \(\sigma \) such that \(\mathcal {S}\preceq \mathcal {S}_{\sigma }\);
-
\(\mathcal {A}\vDash \phi \), or simply \(\vDash \phi \), iff \(\sigma \vDash \phi \) for all \(\sigma \in \mathbb {S}_{\mathcal {A}}\).
The validity relations extend to sets of sentences to mean that every sentence in the set is valid. Given a set \(\varPhi \) of sentences, we denote by \(\mathbb {S}_{\varPhi }\) the set of states over which all the sentences in \(\varPhi \) are valid.
We use the usual propositional connectives for conjunction (\(\wedge \)) and disjunction (\(\vee \)), as well as the dual modal operators (\([\_]\,\!\)) and quantifier (\(\forall \,\!\)) given by:
-
\([\kappa ]\,\phi \triangleq \lnot \,\langle \kappa \rangle {\lnot \,\phi }\)
That is, \(\sigma , \alpha , n \vDash [\kappa ]\,\phi \) iff \(\sigma , \alpha , \rho (c) \vDash \phi \) for all \(c \in \mathcal {C}\) with \(\delta (c) = n\) & \(\kappa \in \tau (c)\).
-
\([\pi ]\,\phi \triangleq \lnot \,\langle \pi \rangle {\lnot \,\phi }\)
That is, \(\sigma , \alpha , n \vDash [\pi ]\,\phi \) iff \(\sigma , \alpha , \mathcal {F}(n) \vDash \phi \) if \(\mathcal {F}(n)\) is defined.
-
\(\forall b\,\phi \triangleq \lnot \,\exists b\,\lnot \,\phi \)
That is, \(\sigma , \alpha , n \vDash \forall b\,\phi \) iff \(\sigma , \alpha ', n \vDash \phi \) for all \(\alpha '\) that agree with \(\alpha \) on \(\mathcal {N}\! om \setminus \{b\}\).
Notice that the symbols used for the negation  and implication (\(\mathrel {\supset }\)) in the base logic are different from those of the state logic (\(\lnot \,\!\) and \(\mathrel {\rightarrow }\), respectively) to mark the difference between the two levels.
and implication (\(\mathrel {\supset }\)) in the base logic are different from those of the state logic (\(\lnot \,\!\) and \(\mathrel {\rightarrow }\), respectively) to mark the difference between the two levels.
Example 15
The sentences presented below are properties of (valid at) the state \(\textsf {elevator}_{0}\) from Example 6, of its underlying structure \(\mathcal {S}_{\textsf {elevator}_{0}}\), or of the ant schema itself. Naturally, any property of \(\mathcal {S}_{\textsf {elevator}_{0}}\) is also a property of \(\textsf {elevator}_{0}\), and any property of \(\textsf {Elevator}\) is also a property of \(\mathcal {S}_{\textsf {elevator}_{0}}\). Notice, however, that the converse does not hold for the following sentences:
- \({ S1}\) :
-

The actors \(\textit{E}\), \(\textit{F0}\), \(\textit{F1}\), and \(\textit{A}\) know that the cabin is at the first platform.
- \({ S2}\) :
-
\(\mathcal {S}_{\textsf {elevator}_{0}} \vDash @_{\textit{A}}\,[ btn ]\,\langle ctr \rangle {\textit{E}}\)
Whenever Alice calls the elevator, the request is transmitted to the \(\textsf {Elevator}\).
- \({ S3}\) :
-
\(\textsf {Elevator}\vDash \bigl ( (\textit{F0} \vee \textit{F1}) \mathrel {\rightarrow }[ obs ]\,\textit{A} \bigr ) \wedge \bigl ( \langle obs \rangle {\textit{A}} \mathrel {\rightarrow }(\textit{F0} \vee \textit{F1}) \bigr )\)
The floors can only be observed by Alice, and that is all Alice can observe.
Definition 16
(State specification). A state specification for an ant schema \(\mathcal {A}\) consists of a signature \(\varSigma \) for \(\mathcal {A}\) (i.e., with the same actor names, channel types, and propositional symbols as the schema) and a set of sentences in \(\textsf {State}(\varSigma )\).
The sentences of a state specification of an ant schema are used to restrict the set of admissible states of the actor networks defined over that schema.
Example 17
A state specification of \(\textsf {Elevator}\) could consist of the instances of the following sentence schemas, which we denote by \(\varPhi _{\textsf {Elevator}}\):
- \({ E1}\) :
-
 for \(i \in \{0, 1\}\)
for \(i \in \{0, 1\}\)
The cabin is at platform i if and only if the elevator knows it.
- \({ E2}\) :
-
\(p \mathrel {\rightarrow }[ obs ]\,p\) for every \(p \in \textsf {\L {}}(\mathcal {P})\)
Knowledge is propagated through observation channels.
That is, this specification of \(\textsf {Elevator}\) determines what knowledge nodes have about the whereabouts of Cabin: the elevator proper always knows where Cabin is and the other nodes can acquire that information through observation channels.
The state logic is useful for deriving properties of states, ant structures, and of ant schemas and their specifications.
Definition 18
(Entailment). Given a finite set \(\varPhi \) of sentences and a sentence \(\phi \) (defined over the same signature as \(\varPhi \)), we say that \(\phi \) is a semantic consequence of \(\varPhi \), or that \(\varPhi \) entails \(\phi \), and write \(\varPhi \vDash \phi \), if \(\sigma \vDash \phi \) for all \(\sigma \in \mathbb {S}_{\varPhi }\).
The following two propositions allow us to redefine the three kinds validity of a state sentence in terms of entailment. They provide a syntactic characterization (as a set of sentences) \(\varPhi _{\sigma }\)/\(\varPhi _{\mathcal {S}}\) for every state \(\sigma \) or structure \(\mathcal {S}\). A sentence \(\phi \) is valid at a state \(\sigma \) if and only if \(\varPhi _{\sigma } \vDash \phi \), and is valid at an ant structure \(\mathcal {S}\) if and only if \(\varPhi _{\mathcal {S}} \vDash \phi \); obviously, \(\phi \) is absolutely valid if and only if \(\emptyset \vDash \phi \).
Proposition 19
Let \(\varPhi _{\mathcal {S}}\) be the (finite) set of all sentences of the form \(@_{a}\,\langle \lambda \rangle {b}\) that are valid at a structure \(\mathcal {S}\), where a and b are actor names and \(\lambda \) is a modality (i.e., a channel type or the parent modality \(\pi \)). Then \(\mathbb {S}_{\varPhi _{\mathcal {S}}} = \{ \sigma \in \mathbb {S}_{\mathcal {A}} \mid \mathcal {S}\preceq \mathcal {S}_{\sigma } \}\).
Proposition 20
For every state \(\sigma \), let \(\varPhi _{\sigma }\) be the (finite) set that extends \(\varPhi _{\mathcal {S}_{\sigma }}\) with all state sentences of the form \(\lnot \,@_{a}\,\langle \kappa \rangle {b}\), \(@_{a}\,[\pi ]\,\) false,  ,
,  , or
, or  that are valid at \(\sigma \), where a and b are actor names, \(\kappa \) is a type that labels one of the channels between a and b in the ant schema, and p is a propositional symbol. Then \(\sigma \) is the only state that satisfies \(\varPhi _{\sigma }\).
that are valid at \(\sigma \), where a and b are actor names, \(\kappa \) is a type that labels one of the channels between a and b in the ant schema, and p is a propositional symbol. Then \(\sigma \) is the only state that satisfies \(\varPhi _{\sigma }\).
Entailment can be derived syntactically through the use of a proof system. The Hilbert-style axiomatization of the basic, unconstrained hybrid logic in Fig. 5 is both a simplification (because we do not consider the binder \(\downarrow \)) and an extension (due to the multi-modality setting and the different base logic) of the axiom system given in [3, Chap. 2].
Proposition 21
([3, Chap. 2]). The axiom schemata and inference rules presented in Fig. 5 are sound and complete with respect to the unconstrained Kripke-frame semantics of basic hybrid logic.
Unlike the models of the basic hybrid logic, the models of the state logic are subject to the constraints defined by the ant schema. Because of this, the axiom schemata and inference rules from Fig. 5 are no longer complete—though, obviously, they remain sound—with respect to the constrained Kripke semantics of the state logic. There are two main categories of new tautologies: those that arise from the ant schema used, and those that are innate to the state logic. The former category contains, for instance, when considering the ant schema \(\textsf {Elevator}\) from Example 2, sentences like \(\lnot \,@_{A}\,\langle ctr \rangle {E}\) (Alice cannot control the elevator directly.), while the latter contains sentences like \(\lnot \,@_{a}\,b\), where a and b are distinct actor names, or \(\langle \pi \rangle {\phi } \mathrel {\rightarrow }[\pi ]\,\phi \).
In order to regain completeness, we introduce new axioms that reflect the semantic constraints of the state logic. The axiom schemata  and
and  from Fig. 6 ensure that all possible worlds correspond to actor names, and that no two distinct names are interpreted in the same way. The axiom schema
from Fig. 6 ensure that all possible worlds correspond to actor names, and that no two distinct names are interpreted in the same way. The axiom schema  rules out those channels that are not defined in the ant schema, while
rules out those channels that are not defined in the ant schema, while  captures the channel subtyping relation. Lastly, \(\pi \)
1 and \(\pi \)
2 specify that the interpretations of the distinguished parent modality are functional and acyclic, respectively.
captures the channel subtyping relation. Lastly, \(\pi \)
1 and \(\pi \)
2 specify that the interpretations of the distinguished parent modality are functional and acyclic, respectively.
Definition 22
Under the notations and assumptions of Definition 18, we say that \(\phi \) is provable from \(\varPhi \), and write \(\varPhi \vdash \phi \), if and only if \(\phi \) can be derived from \(\varPhi \) using the axiom schemata and inference rules from Figs. 5 and 6.
The soundness and completeness of the proof system for the state logic follow from Proposition 21 and the lemma below.
Lemma 23
For any ant schema \(\mathcal {A}\), the states in \(\mathbb {S}_{\mathcal {A}}\) are given precisely by those Kripke structures that satisfy the axioms in Fig. 6.
Proposition 24
The extension of the proof system for hybrid logic with the axiom schemata in Fig. 6 yields a sound and complete axiomatization of the state logic.
Example 25
The properties  and
and  can be derived for \(\mathcal {S}_{\textsf {elevator}_{0}}\) under the specification \(\varPhi _{\textsf {Elevator}}\) from Example 17. In symbols,
can be derived for \(\mathcal {S}_{\textsf {elevator}_{0}}\) under the specification \(\varPhi _{\textsf {Elevator}}\) from Example 17. In symbols,

This example shows that valuations can sometimes be fully determined by the ant structure and the axioms associated with the ant schema. In this particular case, the valuation of the atomic proposition  at the nodes \(\textit{F0}\) and \(\textit{A}\) can be derived from the structural properties of the ant structure and from the axiomatization of the way in which knowledge is propagated (see Example 17).
at the nodes \(\textit{F0}\) and \(\textit{A}\) can be derived from the structural properties of the ant structure and from the axiomatization of the way in which knowledge is propagated (see Example 17).
There are other general properties of \(\textsf {Elevator}\) that we might want to prove. For example, \(@_{\textit{C}}\,\langle \pi \rangle {(\textit{P0} \vee \textit{P1})}\)—the cabin is either at \(\textit{P0}\) or at \(\textit{P1}\). Because such properties are not structural, in the sense that they do not hold at every state of \(\textsf {Elevator}\), they should be proved instead at the level of actor networks, which define the way states can evolve through repeated interactions. The corresponding logic for this kind of proofs is defined in the next sub-section.
3.3 The ant Logic
The logic through which we can reason about the actor networks of an ant schema \(\mathcal {A}\) requires a further level of hybridization. In this case, a higher-level actor-network signature \(\varOmega \) consists of a signature \(\varSigma \) of the state logic (now playing the role of the base logic), a countably infinite set \(\mathcal {N}\! om \) of nominals together with a non-empty subset \( Init \subseteq \mathcal {N}\! om \) of names of initial states, and a set \(\mathcal {I}\) of interactions for \(\mathcal {A}\) (regarded as modalities).
Definition 26
(Syntax). The syntax of the ant logic is given by the grammar

where \(\phi \in \textsf {State}(\varSigma )\), \(i \in \mathcal {N}\! om \), \(j \in \mathcal {N}\! om \setminus Init \), and \(\iota \in \mathcal {I}\). We denote by \(\textsf {{\small AN}t}(\varOmega )\) the set of ant-logic sentences defined over the signature \(\varOmega \).
Notice that we use double symbols for the connectives of the ant logic, and that the satisfaction operators are denoted using a colon. We extend the use of the double-symbol notation to the dual modal operators (\([\![\_]\!]\,\!\)) and to the universal quantifier ( ), which are defined as in Sect. 3.2.
), which are defined as in Sect. 3.2.
Example 27
We can now write sentences about the dynamics of \(\textsf {Elevator}\) like

meaning that at the state \(\textsf {elevator}_{0}\) (which, by Proposition 20, is characterized by the sentences in \(\varPhi _{\textsf {elevator}_{0}}\)) there is a transition to the state \(\textsf {elevator}_{1}\) performed by the interaction callElevator0. Note that, by Proposition 20, the sets of sentences \(\varPhi _{\textsf {elevator}_{0}}\) and \(\varPhi _{\textsf {elevator}_{1}}\) are finite, hence the conjunctions in the antecedent and consequent of the implication above are well formed.
The semantics of the ant logic is defined once more by means of constrained Kripke models. This time, we restrict only the interpretations of the modalities: all interactions \(\iota \in \mathcal {I}\) are substructures of the underlying structures of the states on which (the relational interpretations of) \(\iota \) are defined (see Definition 9). That is, the models of the ant logic are actor networks.
Definition 28
(Semantics). The satisfaction relation for the ant logic is defined for an actor network \(\nu \) with interactions according to \(\varOmega \), an assignment \(\alpha :\mathcal {N}\! om \rightarrow \mathcal {D}_{\nu }\) (which, in this case, is just a function), and a world \(w \in \mathcal {D}_{\nu }\):
-
 iff \(\alpha (i) = w\);
iff \(\alpha (i) = w\); -
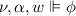 iff \(\varsigma _{\nu }(w) \vDash \phi \);
iff \(\varsigma _{\nu }(w) \vDash \phi \); -
 iff
iff  ;
; -
 iff
iff  implies
implies  ;
; -
 iff there is a transition
iff there is a transition  in \(\nu \) such that
in \(\nu \) such that  ;
; -
 iff
iff  ;
; -
 iff
iff  for some \(\alpha '\) that agrees with \(\alpha \) on \(\mathcal {N}\! om \setminus \{j\}\).
for some \(\alpha '\) that agrees with \(\alpha \) on \(\mathcal {N}\! om \setminus \{j\}\).
Similarly to the first level of hybridization, we say that an ant-logic sentence \(\psi \) defined over \(\varOmega \) is valid in an actor network if it is satisfied, for every assignment, at every world of the network, and that a sentence \(\psi \) is absolutely valid if it is valid in every actor network:
-
 iff
iff  for all assignments \(\alpha :\mathcal {N}\! om \rightarrow \mathcal {D}_{\nu }\) and all \(w \in \mathcal {D}_{\nu }\);
for all assignments \(\alpha :\mathcal {N}\! om \rightarrow \mathcal {D}_{\nu }\) and all \(w \in \mathcal {D}_{\nu }\); -
 iff
iff  for all actor networks \(\nu \) over \(\varOmega \).
for all actor networks \(\nu \) over \(\varOmega \).
Given a set \(\varPsi \) of ant sentences, we denote by \(\mathbb {N}_{\varPsi }\) the set of actor networks over which all the sentences in \(\varPsi \) are valid; and, given another sentence \(\psi \), we say that \(\varPsi \) entails \(\psi \), which we denote  , if
, if  for all \(\nu \in \mathbb {N}_{\varPsi }\).
for all \(\nu \in \mathbb {N}_{\varPsi }\).
The proof theory for the ant logic builds once again on the proof theory for the basic hybrid logic. To that end, we use the same axiom schemata and inference rules from Fig. 5, only that in this case the tautologies of the Łukasiewicz logic are replaced by those of the state logic, and the Boolean and hybrid connectives of the state logic are replaced by those of the ant logic. In addition, through the axiom schema Inter from Fig. 7, we introduce new axioms that reflect the semantic constraints of the models of the ant logic: state properties of interactions hold in the states where the transitions occur.
Definition 29
An ant sentence \(\psi \) is provable from a set \(\varPsi \) of sentences (of the same signature as \(\psi \)), denoted \(\varPsi \Vdash \psi \), if \(\psi \) can be derived from \(\varPsi \) using the axiom system for hybrid logic and the additional axiom schema defined in Fig. 7.
Example 30
Consider the following axiomatization of the transitions of an actor network for the ant schema \(\textsf {Elevator}\). Most of the sentences below are of the form \(\phi _{1} \mathrel {\Rightarrow }[\![\iota ]\!]\,\phi _{2}\). They generalize Hoare triples and express properties of the transitions performed by interactions: intuitively, the sentence \(\phi _{1}\) is a precondition under which the interaction \(\iota \) ensures the postcondition \(\phi _{2}\).
- \({ T1}\) :
-
\(@_{\textit{C}}\,\langle \pi \rangle {\textit{P1}} \mathrel {\Rightarrow }[\![\textsf {callElevator0}]\!]\,@_{\textit{P1}}\,\langle mov \rangle {\textit{P0}}\)
When the elevator is called (at the ground floor) and the cabin is at the first platform, a request to move the cabin to the ground platform is issued.
- \({ T2}\) :
-
\(@_{\textit{C}}\,\langle \pi \rangle {\textit{P0}} \mathrel {\Rightarrow }[\![\textsf {callElevator0}]\!]\,@_{\textit{F0}}\,\langle door \rangle {(\textit{C} \wedge \langle door \rangle {\textit{F0}})}\)
If the cabin is already at the ground platform, then the doors are opened.
- \({ T3}\) :
-
\([\![\textsf {moveCabin0}]\!]\,@_{\textit{F0}}\,\langle door \rangle {(\textit{C} \wedge \langle door \rangle {\textit{F0}})}\)
The doors are opened whenever the cabin moves to the (ground) platform.
- \({ T4}\) :
-

If Alice is at \(\textit{F0}\) and the doors are open, then she can enter the cabin.
- \({ T5}\) :
-
\(@_{a}\,\langle \pi \rangle {s} \mathrel {\Rightarrow }[\![\iota ]\!]\,@_{a}\,\langle \pi \rangle {t}\) for interactions \(\iota \) such that \(\iota \vDash @_{s}\,\langle mov \rangle {t}\)
Any interaction that involves a channel of type \( mov \) between actors s and t (regarded as locations) determines the movement to t of any actor in s.
- \({ T6}\) :
-
\(@_{a}\,\langle \pi \rangle {s} \mathrel {\Rightarrow }[\![\iota ]\!]\,@_{a}\,\langle \pi \rangle {s}\) for interactions \(\iota \) such that \(\iota \not \vDash @_{s}\,\langle mov \rangle \textsf {true}\)
But if the interaction does not involve a \( mov \) channel starting as s, then the actors in s maintain their location.
Then we can derive complex actor-network sentences such as:

That is, provided that we start at a world where Cabin is at one of the platforms, if the elevator is called, then Alice either knows immediately that the cabin is at the ground platform, or she discovers this as soon as the cabin is moved.
Proposition 31
The extension of the hybrid-logic proof system with the axiom schema in Fig. 7 yields a sound and complete axiomatization of the ant logic.

4 Concluding Remarks
In this paper, we have shown how a suite of logics can be developed through a two-stage constrained-hybridization process, providing in this way support for the specification and verification of cyber-physical system protocols modeled as actor networks (ants) in the sense of [9]. The first stage of the hybridization process results in a logic that captures the structure of actor networks and the way knowledge flows across such networks; the second addresses the dynamic aspects of actor networks, that is the way their structure can evolve as a result of the interactions that occur within them.
One of the main novelties of our approach is that we rely on unconventional semantic constraints, derived from the structural characteristics of actor-network states, or from the general properties of the state transitions. This results in faithful representations, at a logical level, of the way computation is performed in actor networks. That is, constrained models capture the relationship between the higher-level reconfigurations of networks and the lower-level interactions between actors that trigger them. Besides expressivity, a key property of these constraints is that they can be axiomatized within hybrid logic. This enables the use of conventional (sound and complete) proof systems for hybrid logic as a tool through which we can formally verify properties of actor networks.
Two main research directions are ongoing. The first aims to use the expressive power of our formalism to reason about security protocols in cyber-physical systems, in particular the existence of covert channels. The second aims to extend the logic to support the modeling of the transition system defined by interactions through graph transformations.
Notes
- 1.
We recall that an upper set of \(\mathcal {T}\) is an upward closed subset U of \(\mathcal {T}\). That is, U contains all channel types \(\kappa ' \in \mathcal {T}\) for which there exists \(\kappa \in U\) such that \(\kappa \le \kappa '\).
- 2.
Recall that, by Definition 5, \(\mathcal {N}_{\mathcal {S}} = \mathcal {N}\).
References
Blackburn, P.: Representation, reasoning, and relational structures: a hybrid logic manifesto. Logic J. IGPL 8(3), 339–365 (2000)
Prior, A.: Past, Present and Future. Oxford University Press, Oxford (1967)
Braüner, T.: Hybrid Logic and its Proof-Theory. Applied Logic Series, vol. 37. Springer, Dordrecht (2011). https://doi.org/10.1007/978-94-007-0002-4
Neves, R., Madeira, A., Martins, M.A., Barbosa, L.S.: Proof theory for hybrid(ised) logics. Sci. Comput. Program. 126, 73–93 (2016)
Diaconescu, R.: Quasi-varieties and initial semantics for hybridized institutions. J. Logic Comput. 26(3), 855–891 (2016)
Găină, D.: Birkhoff style calculi for hybrid logics. Formal Aspects Comput. 29(5), 805–832 (2017)
Madeira, A., Neves, R., Barbosa, L.S., Martins, M.A.: A method for rigorous design of reconfigurable systems. Sci. Comput. Program. 132, 50–76 (2016)
Martins, M.A., Madeira, A., Diaconescu, R., Barbosa, L.S.: Hybridization of institutions. In: Corradini, A., Klin, B., Cîrstea, C. (eds.) CALCO 2011. LNCS, vol. 6859, pp. 283–297. Springer, Heidelberg (2011). https://doi.org/10.1007/978-3-642-22944-2_20
Pavlovic, D., Meadows, C.: Actor-network procedures (extended abstract). In: Ramanujam, R., Ramaswamy, S. (eds.) ICDCIT 2012. LNCS, vol. 7154, pp. 7–26. Springer, Heidelberg (2012). https://doi.org/10.1007/978-3-642-28073-3_2
Latour, B.: Reassembling the Social: An Introduction to Actor-Network Theory. Oxford University Press, Oxford (2005)
Milner, R.: The space and motion of communicating agents. CUP (2009)
Malinowski, G.: Many-Valued Logics. Oxford Logic Guides. Clarendon Press, Oxford (1993)
Acknowledgment
The work of D. Pavlovic was partially supported by NSF. J. Fiadeiro and A. Lopes received support from AFOSR for research visits to the University of Hawaii.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2018 Springer International Publishing AG
About this paper
Cite this paper
Fiadeiro, J., Ţuţu, I., Lopes, A., Pavlovic, D. (2018). Logics for Actor Networks: A Case Study in Constrained Hybridization. In: Madeira, A., Benevides, M. (eds) Dynamic Logic. New Trends and Applications. DALI 2017. Lecture Notes in Computer Science(), vol 10669. Springer, Cham. https://doi.org/10.1007/978-3-319-73579-5_7
Download citation
DOI: https://doi.org/10.1007/978-3-319-73579-5_7
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-319-73578-8
Online ISBN: 978-3-319-73579-5
eBook Packages: Computer ScienceComputer Science (R0)









 such that, for each interaction
such that, for each interaction  implies
implies  where
where  for all assignments
for all assignments 
 for
for 

 iff
iff 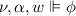 iff
iff  iff
iff  ;
; iff
iff  implies
implies  ;
; iff there is a transition
iff there is a transition  in
in  ;
; iff
iff  ;
; iff
iff  for some
for some  iff
iff  for all assignments
for all assignments  iff
iff  for all actor networks
for all actor networks 
