Abstract
Actor-based programming has become an important technique for the development of concurrent and distributed systems. This paper presents a new automaton model for actor systems and demonstrates how the model can be used for compositional verification. The model allows expressing the detailed behavior of actor components where components are built from actors and other components. It abstracts from internal and environment behavior, supports encapsulation of actors, and captures the dynamic aspects of actor creation and exposure of actor names to the component environment, which are crucial for verification. We handle these changes at the component interface by specializing dynamic I/O automata. The model can be used as a foundation of different verification techniques. We illustrate this by combining weakest precondition techniques on the actor level with simulation proofs on the component level.
Access provided by Autonomous University of Puebla. Download conference paper PDF
Similar content being viewed by others
Keywords
These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.
1 Introduction
Actors [2] are a well studied programming model that gets more and more attention for developing concurrent and distributed systems (e.g., actors in Scala [19]). At runtime, an actor-based system consists of a dynamically changing set of actors. Actors are similar to objects: They have a unique name and a local state; they can create new actors and send messages to other actors addressing them by their name. As the sender does not wait for a reply, i.e., messages are passed asynchronously, message sending naturally leads to concurrent behavior of sender and receiver.
Our overall goal is the compositional verification of actor systems. More precisely, we want to verify the behavior of actor components independently of their environment and use component specifications to verify larger components. This goal entails the following requirements:
-
A hierarchical component concept is needed that goes beyond single actors and allows to develop components by encapsulating other components.
-
Components have to be handled in an open way, i.e., without knowing their environment (cf. [20]).
-
Dynamic actor creation and the passing of actor names has to be captured.
The combination of these requirements is surprisingly challenging. In particular, a component consisting of several actors might expose some of its actors to the environment, thereby enabling the environment to interact with these actors. Exposing actors to the environment dynamically changes the component interface (as demonstrated in Sect. 2). Thus, it is important to precisely keep track of the exposed actors to capture the component behavior.
We use automaton models as they allow constructive specification techniques [27]. They can incorporate both notions of states and actions, making them flexible to integrate with various verification techniques. In particular, they are often compositional which allows for compositional reasoning. The challenge is to capture the dynamic behavior at the component interfaces. In our approach, we follow the ideas of the dynamic I/O automaton (DIOA) model [6, 7]. As the high degree of dynamicity provided by DIOA is larger than needed for our purposes and as it would further complicate verification, we adapt DIOA to actor systems. In summary, the paper makes the following contributions:
-
It formally develops an automaton model that faithfully captures the dynamic semantics of actors and components (Sect. 3).
-
It combines a verification technique for actor programs and a simulation-based proof technique to a two-tier verification approach for actor components (Sect. 4).
The paper closes with a discussion on related work and a conclusion.
Notation. We use abstract data structures sequence, set, multiset and map. The sequence data structure is represented by \( Seq \langle T \rangle \), with T denoting the type of the sequence elements. An empty sequence is denoted by \([] \) and a sequence concatenation is simply juxtaposition. The set data structure \( Set \langle T \rangle \) is a container of values of type T while a multiset is denoted by \(\mathcal {M}\langle T \rangle \). Standard notations for sets are used. The map data structure \( Map \langle S, T \rangle \) is an associative container that maps unique keys of type S to values of type T. An empty map is denoted by \(\{\} \). If m is a map, \(m[x \mapsto y]\) represents the insertion or update of the key x with value y to m. The value y of key x is represented by m(x). If x is not associated to any value, then \(m(x) = \mathsf {undef}\). The predicate \( diffOn (m_1, m_2, X)\) for a set of keys X is true if \(m_1\) may differ from \(m_2\) with respect to the values of keys in X and other keys are mapped to the same value.
2 Class-Based Actor Programming
Our techniques have been developed for the verification of ABS programs [23]. ABS is a class-based actor language with futures, subtyping and recursive data types. In this paper, we only consider a core fragment of ABS, called \(\alpha \textsf {ABS}\). As illustrated in Listing 1.1, the syntax of \(\alpha \textsf {ABS}\) is similar to Java. Actor creation is like object creation using the new expression. The state of an actor consists of creation parameters and attributes (e.g., a  -actor has the creation parameter c and an attribute w). A class defines the messages that are understood by its actors. The body of a message definition is a statement that is executed when the message is processed. Messages may have parameters, but do not have a return value. Syntactically, sending a message is similar to calling a method in Java. Semantically, a send is executed by adding the message to the buffer of the receiver actor. Actors retrieve messages from the buffer one by one and execute them until completionFootnote 1.
-actor has the creation parameter c and an attribute w). A class defines the messages that are understood by its actors. The body of a message definition is a statement that is executed when the message is processed. Messages may have parameters, but do not have a return value. Syntactically, sending a message is similar to calling a method in Java. Semantically, a send is executed by adding the message to the buffer of the receiver actor. Actors retrieve messages from the buffer one by one and execute them until completionFootnote 1.

The program in Listing 1.1 realizes a tiny server. Clients can request sessions from the server and then use the session actors to perform a query. The session actors internally use workers to execute the query and to send the response to the client. The domain of queries and results are represented by the data types  and
and  , respectively. Details of these types and of how queries are computed are not of interest here. The example is not meant to be realistic; rather it is designed to illustrate three important aspects:
, respectively. Details of these types and of how queries are computed are not of interest here. The example is not meant to be realistic; rather it is designed to illustrate three important aspects:
-
The server component is used in an unknown environment. The only information about the environment is that there are clients and that these clients accept the messages
 and
and  . In particular, we do not known what the clients do with the session actors.
. In particular, we do not known what the clients do with the session actors. -
At runtime, the server consists of a server actor, a set of session actors, and sets of workers. The session actors are dynamically created and exposed to the environment. Thus, they are part of the behavioral interface of the server. The worker actors are encapsulated and can never be accessed from the environment. They all use the server’s database that can only be accessed via the session interface.
-
The sessions run concurrentlyFootnote 2.
Inspired by component frameworks like OSGi [35], a component consists of a set of classes \(\mathbf {C}\) with a designated activator class \(C_0 \in \mathbf {C}\) [26]. The idea is that a component instance is created by creating an actor of class \(C_0\). All actors transitively created by this activator belong to the component instance. Consequently, we require \(\mathbf {C}\) to contain all classes of actors that might transitively be created by actors of class \(C_0\). In the example, the  class is the activator for a component consisting of
class is the activator for a component consisting of  . A subcomponent contains less classes and a different activator class; e.g.,
. A subcomponent contains less classes and a different activator class; e.g.,  with activator class
with activator class  is a subcomponent of the server component. Based on this notion, we can verify the
is a subcomponent of the server component. Based on this notion, we can verify the  properties from the properties of the
properties from the properties of the  component in a hierarchical way.
component in a hierarchical way.
A safety property of the server is that its sessions correctly respond to the queries. In the following sections, we show how to accurately represent such systems using the DIOA model and verify that the implementation satisfies the desired behavior.
3 Automaton Model
The DIOA model [7] is a two-tier automaton model based on signature automata (SA)Footnote 3, formalized in Definition 1. On top of the standard elements of transition systems: the set of (initial) states and the labeled transition relation, SA also have state signatures: a description of its input, output and internal actions parameterized by the state. The state-based classification of actions (of the universe \(\mathbf {Act}\)) not only allows us to explicitly distinguish the externally observable behavior represented by the automata, but also to have the interaction possibilities dependent on the states. The two-tier aspect and the state signatures are what are extended from I/O automata (IOA) [29]. SA retain an important property of IOA: they are input-enabled.
Definition 1
(Signature Automata). A signature automaton \(\mathcal {A}= \langle states (\mathcal {A}), start (\mathcal {A}), sig (\mathcal {A}), steps (\mathcal {A}) \rangle \) is a 4-tuple where
-
\( states (\mathcal {A})\) is a set of states,
-
\( start (\mathcal {A}) \subseteq states (\mathcal {A})\) is a non-empty set of initial states,
-
\( sig (\mathcal {A})\) is a signature mapping where for each \(s \in states (\mathcal {A})\), \( sig (\mathcal {A})(s) = \langle in (\mathcal {A})(s), out (\mathcal {A})(s), int (\mathcal {A})(s) \rangle \) where \( in (\mathcal {A})(s), out (\mathcal {A})(s), int (\mathcal {A})(s) \subseteq \mathbf {Act}\) such that \( in (\mathcal {A})(s) \cap out (\mathcal {A})(s) = in (\mathcal {A})(s) \cap int (\mathcal {A})(s) = out (\mathcal {A})(s) \cap int (\mathcal {A})(s) = \emptyset \),
-
\( steps (\mathcal {A}) \subseteq states (\mathcal {A}) \times acts (\mathcal {A}) \times states (\mathcal {A})\) is a transition relation, such that
-
\(\forall (s, l, s') \in steps (\mathcal {A}): l \in \widehat{ sig }(\mathcal {A})(s)\),
-
\(\forall s \in states (\mathcal {A}): \forall l \in in (\mathcal {A})(s): \exists s' \in states (\mathcal {A}): s \xrightarrow {l} s'\), and
-
 ,
,
where the \(\widehat{\ }\)-operator represents the union of sets of the signature tuple.
-
Behavior can be represented by an SA in terms of executions and traces. An execution is a sequence of alternating sequence \(s_0 l_1 s_1 \ldots \) of states and actions such that \(s_0\) is an initial state and \(s_{i-1} \xrightarrow {l_i} s_i\) is a transition in SA. A trace is the observable variant of an execution, i.e., the projection of the execution to the sequence of its actions. The overall behavior of an entity represented by an SA is captured by a set of executions (traces). We further define an external trace to be a trace derived from an execution where each action \(l_i\) is either an input or output action at state \(s_{i-1}\). The external traces describe the observable interaction between the entity and its environment.
The state signatures of SA are very flexible, such that an action may be an input action in one state and output in another, for example. This flexibility is excessive for representing actor systems, so we define in the following how to restrict them.
3.1 First Tier Model
The first tier of a DIOA model for actors is populated by actor automata (AA): SA that are enriched with the characteristics of (groups of) actors. This means:
-
An actor can only send messages to other actors and pass these actors’ names as parameters when they have been exposed to that actor.
-
An actor must be able to accept any possible message sent by its environment.
-
A newly created actor always has a fresh name.
-
An actor processes one incoming message to completion at a time.
Before we show how to enrich SA to represent these characteristics, we first introduce several elementary building blocks. We shortly define a notion of components based on the creation dependency between classes. This notion allows for a definition of AA that covers both actors and component instances.
The universes of actor(name)s, classes, messages, and data values are represented by \(a, b \in \mathbf {A}\), \(C \in \mathbf {C}\mathbf {L}\), \(m \in \mathbf {M}\), and \(d \in \mathbf {D}\), respectively. We say “actor a” to refer to an actor of some unique name a. The behavior of each actor is represented by a class C. A class also determines what kind of messages an actor of that class can process, represented by \( aMsg (C) \subseteq \mathbf {M}\). This function states which messages are allowed to be sent to the actor and which messages the actor can send to other actors. We overload this function with an extra parameter \( type \in \{ in , out , int \}\) to distinguish respectively which messages are part of the input interface of the class, which messages can be sent by the actor to another actor, and which messages the actor can send to itself, e.g., to trigger internal computations. The function \( class (a)\) represents the class of actor a and the parameterized universe \(\mathbf {A}(C)\) defines the set of actors of class C. The component with activator class C is denoted by \([C]\).
A message m can be an actor creation message  or a message send \( mtd (\overline{p})\). A parameter can either be a data value d or an actor name. As with actors, the universe of a data type D can be represented by \(\mathbf {D}(D)\).
or a message send \( mtd (\overline{p})\). A parameter can either be a data value d or an actor name. As with actors, the universe of a data type D can be represented by \(\mathbf {D}(D)\).
From these universes we build the set of events \(\mathbf {E}\) which replaces the domain of actions \(\mathbf {Act}\) for AA. An event \(e \in \mathbf {E}\) represents the occurrence of a message \(m = msg (e)\) being sent from the sender actor \(a = sender (e)\) to the target actor \(b = target (e)\) or being reacted to by b. If m is a creation message, b will be the name of the newly created actor while a is its creator. The actor creation event is written as  . We assume that actors are named hierarchically, so that we can say whether b is transitively created by a by checking that a is an ancestor of b (written \(a \in ancestors (b)\)). For message sends, we distinguish between the emittance of the message (\(a \rightarrow b: mtd (\overline{p})\)) and its reaction (\(a \twoheadrightarrow b: mtd (\overline{p})\)). The function \( param (e)\) extracts the parameters of the message \( msg (e)\), while the function \( acq (e)\), short for acquaintance, extracts the actors exposed in e.
. We assume that actors are named hierarchically, so that we can say whether b is transitively created by a by checking that a is an ancestor of b (written \(a \in ancestors (b)\)). For message sends, we distinguish between the emittance of the message (\(a \rightarrow b: mtd (\overline{p})\)) and its reaction (\(a \twoheadrightarrow b: mtd (\overline{p})\)). The function \( param (e)\) extracts the parameters of the message \( msg (e)\), while the function \( acq (e)\), short for acquaintance, extracts the actors exposed in e.
Adapting SA to represent actors and component instances (together we call them entities) based on the context described above requires two ingredients: enriched states and some constraints placed on the initial states, the state signatures and the transition relation. Definition 2 describes the states and constraints utilizing the function \( isLocal \) that identifies whether an actor is represented by the AA:
Definition 2
(Actor Automata). A parameterized SA \(\mathcal {A}( this , kind ) = \langle states (\mathcal {A}), start (\mathcal {A}), sig (\mathcal {A}), steps (\mathcal {A}) \rangle \) with the following description:
-
1.
\( states (\mathcal {A})\) is a map with a fixed domain \(V \subseteq \mathbf {V}\) denoting the variables stored by the entity. V includes the following variables: \( buf \), \( known \), \( expActors \), \( ready \), \( nameGen \), and \( t_{gen} \), representing an event bag (of type \(\mathcal {M}\langle \mathbf {E} \rangle \)), the set of known actors (\(2^\mathbf {A}\)), the set of exposed actors (\(2^\mathbf {A}\)), whether the entity is at a ready point (\(\mathbf {B}\)), the actor name generator (\(2^\mathbf {A}\)), and the traces generated by the entity (\( Seq \langle \mathbf {E} \rangle \)), respectively. The read-only class parameters are stored under the variable \( params \). Other variables are internal and grouped together under \( ints \).
-
2.
A non-empty set of initial states \( start (\mathcal {A}) \subseteq states (\mathcal {A})\).
-
3.
A signature mapping \( sig (\mathcal {A})\) where for each state \(s \in states (\mathcal {A})\), \( sig (\mathcal {A})(s) = \langle in (\mathcal {A})(s), out (\mathcal {A})(s), int (\mathcal {A})(s) \rangle \), where \( in (\mathcal {A})(s), out (\mathcal {A})(s), int (\mathcal {A})(s) \subseteq \mathbf {E}\).
-
4.
A transition relation \( steps (\mathcal {A}) \subseteq states (\mathcal {A}) \times acts (\mathcal {A}) \times states (\mathcal {A})\).
is an actor automaton representing an entity (with the initial actor) of kind “actor” (\( TAct \)) or “component instance” (\( TComp \)) of name \( this \) of class/component D when it satisfies the following constraints:
-
A1.
\(\forall s \in start (\mathcal {A}): s( buf ) = s( nameGen ) = \emptyset \wedge this \in s( known ) \wedge s( ready )\)
\(\wedge ~s( expActors ) = \{ this \} \wedge s( t_{gen} ) = []\).
-
A2.
\(\forall s \in states (\mathcal {A}): in (\mathcal {A})(s) =\)
\(\left\{ e \left| \begin{array}{l} isEmit (e) \wedge msg (e) \in aMsg (D, in )\\ \wedge ~ isLocal ( target (e), this , kind ) \wedge \lnot isLocal ( sender (e), this , kind ) \end{array} \right. \right\} \).
-
A3.
\(\forall s \in states (\mathcal {A}): out (\mathcal {A})(s) =\)
\(\left\{ e \left| \begin{array}{l} isEmit (e) \wedge acq (e) \subseteq s( known )\wedge msg (e) \in aMsg (D, out )\\ \wedge ~( isSend (e) \implies isLocal ( sender (e), this , kind ) \\ {i} {i}\qquad \qquad \qquad \qquad \wedge ~\lnot isLocal ( target (e), this , kind ))\\ \wedge ~( isCreate (e) \implies target (e) \notin s( nameGen ) \wedge sender (e) = this ) \end{array}\right. \right\} \).
-
A4.
\(\forall s \in states (\mathcal {A}): int (\mathcal {A})(s) =\) \(\left\{ e \left| \begin{array}{l} ( isReact (e) \implies emitOf (e) \in s( buf )) \\ \wedge ~( isEmit (e) \implies isSend (e) \wedge acq (e) \subseteq s( known ) \\ \qquad \qquad \qquad \qquad \qquad \wedge isLocal ( sender (e), this , kind ) \wedge isLocal ( target (e), this , kind )) \end{array} \right. \right\} \).
-
A5.
\(\forall (s, e, s') \in steps (\mathcal {A}): e \in in (\mathcal {A})(s) \implies s' = s[ buf \mapsto s( buf ) \cup \{ e \}]\).
-
A6.
\(\forall (s, e, s') \in steps (\mathcal {A}): isReact (e) \implies s( ready )\)
\(\wedge ~ diffOn (s, s', \{ buf , known , ready , t_{gen} , ints \}) \wedge s'( t_{gen} ) = s( t_{gen} ) \ e\)
\(\wedge ~s'( buf ) = s( buf ) - \{ emitOf (e) \} \wedge s'( known ) = s( known ) \cup acq (e) \).
-
A7.
\(\forall (s, e, s') \in steps (\mathcal {A}): isEmit (e) \wedge e \in out (\mathcal {A})(s) \cup int (\mathcal {A})(s) \implies \)
\(\wedge ~ diffOn (s, s'', \{ expActors , ready , t_{gen} , ints \}) \wedge s'( t_{gen} ) = s( t_{gen} ) \ e\)
\(\wedge ~( isCreate (e) \implies s'( known ) = s''( known ) \cup \{ target (e) \}~\)
\(\wedge ~s'( nameGen ) = s''( nameGen ) \cup \{ target (e) \})\)
\(\wedge ~(e \in int (\mathcal {A})(s) \implies s'( buf ) = s''( buf ) \cup \{ e \})\).
Definition 2 describes how SA are transformed to AA. AA are parameterized with the (initial) actor (of the component instance) \( this \), mimicking how classes are behavior templates of actors, and \( kind \), the kind of the entity. The events used in a particular AA are parameterized accordingly by \( this \). The states consist of predefined variables governing the local event buffer, the exposure knowledge of non-local and local actors from and to the environment, whether the actor is ready to process the next incoming message or whether the component instance is ready to execute the next message, the actor name generator, and the trace the entity has generated. These variables allow the construction of Constraints A1 to A7 that regulate over the state signatures and the transition relation to represent the actor characteristics.
Constraint A1 defines the initial states, where the buffer is still empty, the entity knowledge is still at its minimum, the entity is ready to process an incoming message and no actor has been generated yet. For a component instance, the last aspect means that no locally created actor is exposed to the environment.
Constraints A2 to A4 describe how the state signatures are derived from the state. The input and output state signatures are restricted by the allowed messages of the class/component and message direction. Only emittance events are part of these signatures. The internal state signatures are either reaction events to events stored in the buffer or emittance events where both sender and target actors are local.
Constraints A5 to A7 describe the effect of all transitions on the state variables. All incoming messages are put into the buffer without otherwise changing the state. The entity can only react to a message when it is ready to do so. Executing a reaction event causes the corresponding emittance event to be removed from the buffer and the set of known actors is updated by the newly received acquaintance. When an output or internal event can be emitted, we allow the set of exposed actors, the values of the ready flag and the internal variables to be changed. If the event is an actor creation event, the entity knows the created actor. To ensure fresh names, the name generator keeps the name of the created actor. If it is an internal event, then the event is directly added to the entity’s buffer.
We drop the parameters \( this \) and \( kind \) from an AA when they are irrelevant to the discussion. The name(s) of the (set of) actor(s) is retrieved by the function \( names \):
For AA representing component instances, the function returns an over-approximation of the set of actors that are local to the instance.
More specific behavior of an AA that goes beyond the constraints is expressed by so-called AA specifications. We illustrate such specifications by an example.
Example 1
The behavior of an AA representing the server component (i.e., the system) can be specified in three parts: the provided and required interfaces, which form the set of allowed messages, the internal state, and the actions taken by a server component instance. As a component, the server’s provided interface consists not only of the server actor’s own interface (where it provides the  method), but also of the interface of the associated session actors (where they provide the
method), but also of the interface of the associated session actors (where they provide the  method). The required interface consists of the
method). The required interface consists of the  and
and  methods. The component’s specification does not include the internal communication, because they are not observable by the environment.
methods. The component’s specification does not include the internal communication, because they are not observable by the environment.
The internal states of the server component need to capture the created sessions, to which client each session is mapped to, and the queries the component instance is currently processing. The states of this component are populated when the component instance reacts to a message of the provided interface. This reaction is marked by the execution of an event  or
or  . In response, the server component sends back a fresh session
. In response, the server component sends back a fresh session  or the computed query
or the computed query  , respectively.
, respectively.
The specifications for AA that represent classes can be further optimized because each actor processes one incoming message at a time. The actions executed by the  class can be represented by the AA using the following event sequence:
class can be represented by the AA using the following event sequence:

The AA definition allows this event sequence to be portrayed accurately.
Important to note is that AA does not utilize the full flexibility of SA with regards to the state signature. An input event will always be an input event, and similarly to output and internal event. The lemma formalizes this fact.
Lemma 1
Let \(\mathcal {A}\) be an AA. We define \( in (\mathcal {A})\) to be \({\bigcup }_{s \in states (\mathcal {A})} in (\mathcal {A})(s)\), and similarly for \( out (\mathcal {A})\) and \( int (\mathcal {A})\). Then \( in (\mathcal {A}) \cap out (\mathcal {A}) = in (\mathcal {A}) \cap int (\mathcal {A}) = out (\mathcal {A}) \cap int (\mathcal {A}) = \emptyset \).
Proof
Follows from Constraints A2 to A4.
This lemma implies that AA are essentially more flexible IOA and verification procedures for IOA are reusable. This lemma is also carried over to the second tier which handles the dynamic creation aspect.
3.2 Second Tier Model
Missing from the first tier is the effect of creating an actor or a component instance. Attie and Lynch [7] model this effect by defining configuration automata (CA). CA are based on the notion of configurations: the set of \(\mathbb {A}\) of alive SA and a mapping \(\mathbb {S}\) that maps each SA in \(\mathbb {A}\) to a particular state. The configuration information allow CA, the main semantic model, to represent open systems that feature dynamic creation. Here we present the tweaked CA for actor systems.
For an actor system, on top of the set of alive AA and the state information, a configuration needs to store the information of actors that have been exposed to the environment \(\mathbb {E}\). We set some sanity conditions on the alive AA such that they are pairwise representing distinct entities and it is impossible for AA to create entities that are already alive. Definition 3 formalizes this requirement using the \( names \) function and the output state signature of each AA in the configuration.
Definition 3
(Configurations). A configuration \(\mathbb {C}\) is a triple \(\langle \mathbb {A}, \mathbb {S}, \mathbb {E} \rangle \) where \(\mathbb {A}\) is a set of AA, \(\mathbb {S}\) maps each AA \(\mathcal {A}\in \mathbb {A}\) to a state \(s \in states (\mathcal {A})\), and \(\mathbb {E}\subseteq names (\mathbb {C})\) is the set of actor(name)s that have been exposed to the environment such that
The \( names \) function is lifted to configurations:  .
.
Important to CA is that they are derived from configurations. That is, the signatures and the available transitions in a CA are fully dictated by the AA present in the configurations and their state mapping. The following definition precisely provides how to derive the signature of a configuration. It is based on the observation that an event is always observable by at most two actors: the sender and the target.
Definition 4
(Signatures of a Configuration). Let \(\mathbb {C}= \langle \mathbb {A}, \mathbb {S}, \mathbb {E} \rangle \) be a configuration. Let \( commonEv \) be the set of common events between actors represented within the configuration: \( commonEv = \left\{ \right. e \left| \right. sender (e), target (e) \in names (\mathbb {C}) \left. \right\} \). Let \( envEv \) be the set of bogus events generated by the environment:
Then, the signature of \(\mathbb {C}\) is \( sig (\mathbb {C}) = \langle in (\mathbb {C}), out (\mathbb {C}), int (\mathbb {C}) \rangle \), where
-
 ,
, -
 ,
, -
 ,
,
The signature of a configuration is the aggregation of the state signatures of each AA in the configuration. All events sent by and to actors in the configuration are clumped together as internal events. These common events from each actor’s perspective are external events, but from the system’s perspective they occur within the system. A special attention is needed for the input events, where due to the lack of information of the system on the AA stage, each AA is modeled as open as possible. This openness, however, include events that can never be generated by the environment (and the system at the current configuration): messages coming from an actor not represented by an AA in the configuration whose parameters include actors of the configuration that are not yet exposed. To retain input-enabledness, they must be removed from the configuration’s input signature.
For each event in the signature of a configuration, we can derive the effect of executing that event from the involved AA. This transition from the pre-configuration to the post-configuration can be seen as an aggregate of the transitions of the participating AA. If the event creates another entity, the AA representing that entity is added to the configuration, such that the AA is mapped to some initial state. All AA that can participate in executing that event must perform the corresponding transition. The post-state of each transition is recorded in the post-configuration. The post-configuration also takes note of which actors become exposed to the environment after executing the event. Definition 5 formalizes this description.
Definition 5
(Intrinsic Transitions). Let \(\mathbb {C}= \langle \mathbb {A}, \mathbb {S}, \mathbb {E} \rangle \), \(\mathbb {C}' = \langle \mathbb {A}', \mathbb {S}', \mathbb {E}' \rangle \) be configurations and e an event. Let \(\mathcal {A}'( target (e))\) be an AA of class \( class (e)\) or component \([ class (e)]\), if e is a creation event (i.e., \( isCreate (e)\)). There is an intrinsic transition from \(\mathbb {C}\) to \(\mathbb {C}'\) labeled by e, written  , iff
, iff
-
1.
\(e \in \widehat{ sig }(\mathbb {C})\),
-
2.
\(\mathbb {A}' = \mathbb {A}\cup \{ \mathcal {A}'( target (e)) \mid isCreate (e) \}\),
-
3.
for all \(\mathcal {A}\in \mathbb {A}' - \mathbb {A}: \mathbb {S}'(\mathcal {A}) \in start (\mathcal {A}) \wedge \mathbb {S}'(\mathcal {A})( params ) = param (e)\),
-
4.
for all \(\mathcal {A}\in \mathbb {A}:\) if \(e \in \widehat{ sig }(\mathcal {A})(\mathbb {S}(\mathcal {A})) \wedge \mathbb {S}(\mathcal {A}) \xrightarrow {e}_\mathcal {A}s\), then \(\mathbb {S}'(\mathcal {A}) = s\), otherwise \(\mathbb {S}'(\mathcal {A}) = \mathbb {S}(\mathcal {A})\), and
-
5.
\(\mathbb {E}' = \mathbb {E}\cup \left\{ a \left| \begin{array}{l} isSend (e) \wedge target (e) \notin names (\mathbb {C})\\ \wedge ~a \in acq (e) - \{ a \mid ancestors (a) \cap names (\mathbb {C}) = \emptyset \} \end{array} \right. \right\} \).
The following definition assembles the configurations, signatures, and transitions into a CA. More precisely, all configurations are taken from AA that are deemed alive (Definition 3), whose signatures and possible transitions are exactly as stated in Definitions 4 and 5, respectively. For simplicity, we restrict ourselves to CA where initially only one entity is present in the configuration. Initial configurations that contain more than one entity can be simulated by having a main actor that creates the other entities and sends a start message to them in a non-deterministic order.
Definition 6
(Configuration Automata). A configuration automaton \(\mathcal {C}\) is a pair \(\langle sa (\mathcal {C}), config (\mathcal {C}) \rangle \) where
-
\( sa (\mathcal {C})\) is an SA; (the parts of this SA are abbreviated to \( states (\mathcal {C}) = states ( sa (\mathcal {C}))\), \( start (\mathcal {C}) = start ( sa (\mathcal {C}))\), etc. for brevity)
-
a configuration mapping \( config (\mathcal {C})\) with domain \( states (\mathcal {C})\) such that for all \(x \in states (\mathcal {C})\), \( config (\mathcal {C})(x)\) is a configuration;
such that the following constraints are satisfied:
-
1.
If \(x \in start (\mathcal {C})\) and \((\mathcal {A}, s) \in config (\mathcal {C})(x)\), then \(s \in start (\mathcal {A})\).
Additionally, \(\forall x \in start (\mathcal {C}): \langle \mathbb {A}, \mathbb {S}, \mathbb {E} \rangle = config (\mathcal {C})(x) \wedge |\mathbb {A}| = 1 \wedge \mathbb {E}\subseteq names (\mathbb {A})\).
-
2.
If \((x, e, x') \in steps (\mathcal {C})\) then
 .
. -
3.
If \(x \in states (\mathcal {C})\) and
 for some event e and a configuration \(\mathbb {C}\), then \(\exists x' \in states (\mathcal {C})\) such that \( config (\mathcal {C})(x') = \mathbb {C}\) and \((x, e, x') \in steps (\mathcal {C})\).
for some event e and a configuration \(\mathbb {C}\), then \(\exists x' \in states (\mathcal {C})\) such that \( config (\mathcal {C})(x') = \mathbb {C}\) and \((x, e, x') \in steps (\mathcal {C})\). -
4.
\(\forall x \in states (\mathcal {C}): in (\mathcal {C})(x) = in ( config (\mathcal {C})(x))\)
\(\wedge out (\mathcal {C})(x) = out ( config (\mathcal {C})(x)) \wedge int (\mathcal {C})(x) = int ( config (\mathcal {C})(x))\).
4 Verification
The automaton model can be used for verifying the correctness of an implementation of an actor system. We follow a two-tier approach proposed by, e.g., Misra and Chandy [30] to perform this task. The first tier is verifying that the class implementation satisfies the class specification, represented by an AA. In this tier, we follow an approach by Dovland et al. [15], where the class implementations are checked against desired trace-based class invariants. First, a trace-based class invariant is extracted from the AA. Then, the class implementation is translated into a simple sequential language in the spirit of the transformational approach by Olderog and Apt [34]. The verification takes place by, e.g., taking the weakest-liberal precondition of the translated implementation and deducing that the weakest-liberal precondition holds. This technique allows the verification of safety properties. The second tier is done by constructing a simulation relation from the CA representing the implementation of the component to the CA representing the component specification. This relation checks whether the component specification is fulfilled by the activator class and subcomponent specifications. We use a specialized simulation relation called the possibility map [29, 33], which synchronizes only on external events. This tier allows the verification of liveness properties on top of the safety properties.
In the following subsections, we sketch how verification on each tier works. More details including a soundness proof for a more complex setting and the model’s congruence to an actor-based language are available [24]. The reference also contains an application of the verification technique to components with recursive unbounded actor creation of a single chain.
4.1 Class Verification
Verifying the class implementation is done in two parts. First, we encode the AA representing the class specification as a class invariant. The class invariant reflects what needs to remain true at an actor before and after executing a method in response of an incoming message. Furthermore, it also ensures whenever an actor is in the middle of a computation, that computation is part of a response of the actor to an incoming message. To support the verification effort on this tier, we include a user-defined relation \(\rho (\overline{f}, s)\) which links the class parameters used in the implementation and the state variables used in the AA. It is typically given during the verification process as the implementation is available and only the internal variables of the specification are compared to the class parameters.
Definition 7
(Class Invariants). Let \(\mathcal {A}\) be an AA. Given a predicate \(\rho (\overline{f}, s)\) over the class parameters \(\overline{f}\) and a state s of the \(\mathcal {A}\), the class invariant  of \(\mathcal {A}\) over \(\overline{f}\) and the trace \(\mathsf {t}\) is defined as follows:
of \(\mathcal {A}\) over \(\overline{f}\) and the trace \(\mathsf {t}\) is defined as follows:

Following the idea of Dovland et al. [15], we encode the class implementation into a simple sequential language SEQ with non-deterministic assignments [5]. This language consists of the typical sequential statement constructs, such as conditional, skip and sequential composition, enriched with a non-deterministic assignment, an  statement, and a procedure construct. The non-deterministic assignment is used to assign the names of newly created actors, while the
statement, and a procedure construct. The non-deterministic assignment is used to assign the names of newly created actors, while the  statement is used to establish that the invariant holds before and after the method execution, respectively. The procedure construct is used to represent the methods of a class.
statement is used to establish that the invariant holds before and after the method execution, respectively. The procedure construct is used to represent the methods of a class.
Encoding the implementation in SEQ has the advantage of using well-established semantics such as the weakest liberal precondition semantics. This means we can introduce the following verification condition of class C with the invariant  :
:

where  maintains the well-formedness of trace \(\mathsf {t}\), \(m(\overline{x})~ body _m\) is a method definition in C populated by parameters \(\overline{x}\), and \( wlp (s, Q)\) is the weakest liberal precondition that ensures that postcondition Q holds after executing statement s.
maintains the well-formedness of trace \(\mathsf {t}\), \(m(\overline{x})~ body _m\) is a method definition in C populated by parameters \(\overline{x}\), and \( wlp (s, Q)\) is the weakest liberal precondition that ensures that postcondition Q holds after executing statement s.
Example 2
The class invariant of the  class is derived from its AA \(\mathcal {A}\) (Example 1) by setting the predicate \(\rho \) as \( true \):
class is derived from its AA \(\mathcal {A}\) (Example 1) by setting the predicate \(\rho \) as \( true \):  . Assuming
. Assuming  ,
,  and
and  , the verification condition for the implementation in Listing 1.1 is
, the verification condition for the implementation in Listing 1.1 is

The verification proceeds by first-order logic deduction rules.
4.2 Component Verification
The second tier deals with verifying components and ultimately the whole system. The main verification method is the possibility map [29, 33], a specialized simulation relation that allows an implementation to synchronize with its specification only on external events. That is, an implementation may conduct an arbitrary number of internal transitions to fulfill its desired observable behavior.
Definition 8
(Possibility Maps). Let \(\mathcal {C}_1, \mathcal {C}_2\) be CA and \( E _{ ext } \subseteq Act (\mathcal {C}_1)\) a set of events. A map \(r = Map \langle states (\mathcal {C}_1), states (\mathcal {C}_2) \rangle \) is a possibility map from \(\mathcal {C}_1\) to \(\mathcal {C}_2\) with respect to \( E _{ ext }\) if the following conditions hold.
-
1.
If \(x \in start (\mathcal {C}_1)\) then \(r(x) \ne \mathsf {undef}\) and \(r(x) \in start (\mathcal {C}_2)\).
-
2.
If
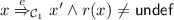 then \(r(x') \ne \mathsf {undef}\) and either \(e \notin E _{ ext } \wedge r(x) = r(x')\) or
then \(r(x') \ne \mathsf {undef}\) and either \(e \notin E _{ ext } \wedge r(x) = r(x')\) or  .
.
This verification method is defined for IOA and in general does not work for DIOA due to the dynamic state signatures. Actor systems have the advantage that the set of external events can be over-approximated (Lemma 1). This set is defined by the following function given the initial actor of the component instance:
In addition to the external events, the component specification utilizes the reaction events of the input events which are captured by the following function.
If we can find a possibility map with respect to \(E_{ cmp }\) between the CA containing the AA of the component specification and the CA containing the AA of the class specification, then the component specification is satisfied by its implementation.
Theorem 1
Let \(\mathcal {C}_{[C]}\) be a CA whose initial configurations consist of a component instance of component \([C]\) and \(\mathcal {C}_{C}\) a CA whose initial configurations consist of an actor \( this \) of class C. Let \(r = Map \langle states (\mathcal {C}_C), states (\mathcal {C}_{[C]}) \rangle \) be a possibility map from \(\mathcal {C}_C\) to \(\mathcal {C}_{[C]}\) with respect to \( E _{ cmp }( this )\). Given the set of external traces \( xtraces (\mathcal {C})\) of CA \(\mathcal {C}\), then,
Proof
Follows from [33] for IOA and Lemma 1.
Example 3
Assume we have a verified specification of the  component, where it represents the
component, where it represents the  and the
and the  of each query from the environment. The internal state of the
of each query from the environment. The internal state of the  component is the set of queries the component instance is currently processing. Using the specifications of the
component is the set of queries the component instance is currently processing. Using the specifications of the  component and the
component and the  class (Example 1), we can construct a possibility map between them and the AA of the
class (Example 1), we can construct a possibility map between them and the AA of the  component by:
component by:
-
equating the event bag of the
 component instance to the event bags of the
component instance to the event bags of the  component instances and the
component instances and the  actor,
actor, -
equating the queries of the
 component instance to the queries of the
component instance to the queries of the  component instance, and
component instance, and -
mapping the correct
 component instance to each client, as stored in the internal state of the
component instance to each client, as stored in the internal state of the  component instance.
component instance.
5 Related Work
There are several automaton models for representing actors, but they either do not consider actor creation or all actors are assumed to be present in the system from the start. Belonging to the former approach are the translation of actor programs to constraint automata [37] and the modeling of timing aspects of actor programs by timed automata [22]. An example of the latter is the work by Leo [28] where actor systems are modeled by the composition of an infinite number of IOA, each of which has a flag indicating whether the represented actor has been created.
Automaton models that accurately capture dynamic creation need to store the created names. History-dependent automata [31, 32] provide a generalized means to encode systems with dynamic creation, but without a separation of concerns between the behavior of the system’s individual entities and the collective, instantiated behavior. Similar to DIOA [6, 7], dynamic communicating automata (DCA) [8, 9] and dynamic register automata [1] provide this separation, where a template automaton is used to describe the generic behavior of each process in the system. Instantiations of the template automaton (i.e., the processes) is collected in a configuration (for DCA, message sequence charts [21]). These models need a composition operator to avoid packing the behavior of every system component into one template automaton. Callable timed automata [10] represent behavioral templates for calls and the (timed) systems are represented using timed transition systems. An adaptation for actor systems is not straightforward, as the semantics are based on the calls instead of entities such as actors. Dynamic reactive modules [17] model process classes as transition systems that use logical formulas to describe the transition relations. This framework is more suitable for systems whose entities share variables.
Logics can be used to model actor systems. Some models based on temporal logic have been pursued [11, 16, 36], but they carry the drawback that the implementation has to be encoded in full together with the specification’s formula. A promising approach is the use of trace-based dynamic logic [4, 12, 13], which can handle actor systems with more complex features such as futures. The modularity of the verification of this approach is up to the method level, with the integration of a (static) component notion as defined in this paper is still to be investigated. We have investigated a generalized Hoare logic based on the splitting of traces into input and output traces [25]. Implementation verification using this approach is an open challenge.
Models based on process algebra [3, 18] require the construction of a (bi)simulation relation to compare the implementation and the specification, unless abstractions are applied [14, 40] which allow automatic model checking at the loss of some precision. A translation from the expressive Specification Diagram for actor systems [38] to process algebra has been worked out [39].
6 Conclusion
In this paper we presented an automaton model based on DIOA for representing actor systems. The automaton model provides an explicit support for dynamic creation and dynamic topology. It enables accurate representation of the complete observable behavior of the actor systems, while allowing abstractions to be built based on a simple hierarchical component notion. The integration with the component notion enables a hierarchical end-to-end verification approach. We illustrate it using a transformational approach to a sequential language to verify the implementation and a simulation relation to verify the components.
We envision several directions of further research. First, a full support for futures in the model is still not yet established. One way to support this is by introducing a special kind of SA that only represent futures. An interesting question is how the futures generated by the environment can be handled by the model. Another direction is to investigate other verification techniques applicable to this model. Some preliminary work on adapting temporal logic for DIOA exists, but the logical rules and their soundness are not yet fully investigated.
Notes
- 1.
\(\alpha \textsf {ABS}\) does not support suspension of tasks or wait statements.
- 2.
For simplicity, we have only one worker per session. It is easy to extend the example to support pools of workers.
- 3.
We use abbreviations for automata to also represent “a single automaton”. The usage is apparent from the context.
References
Abdulla, P.A., Atig, M.F., Kara, A., Rezine, O.: Verification of dynamic register automata. In: FSTTCS, pp. 653–665 (2014)
Agha, G.: Actors: A Model of Concurrent Computation in Distributed Systems. MIT Press, Cambridge (1986)
Agha, G., Thati, P.: An algebraic theory of actors and its application to a simple object-based language. In: Owe, O., Krogdahl, S., Lyche, T. (eds.) From Object-Orientation to Formal Methods. LNCS, vol. 2635, pp. 26–57. Springer, Heidelberg (2004)
Ahrendt, W., Dylla, M.: A system for compositional verification of asynchronous objects. Sci. Comput. Program. 77(12), 1289–1309 (2012)
Apt, K.R.: Ten years of Hoare’s logic: a survey part II: nondeterminism. Theor. Comput. Sci. 28, 83–109 (1984)
Attie, P.C., Lynch, N.A.: Dynamic Input/Output automata: a formal model for dynamic systems. In: Larsen, K.G., Nielsen, M. (eds.) CONCUR 2001. LNCS, vol. 2154, pp. 137–151. Springer, Heidelberg (2001)
Attie, P.C., Lynch, N.: Dynamic Input/Output automata: a formal and compositional model for dynamic systems. Inf. Comput. (2015) (To appear)
Bollig, B., Cyriac, A., Hélouët, L., Kara, A., Schwentick, T.: Dynamic communicating automata and branching high-level MSCs. In: Dediu, A.-H., Martín-Vide, C., Truthe, B. (eds.) LATA 2013. LNCS, vol. 7810, pp. 177–189. Springer, Heidelberg (2013)
Bollig, B., Hélouët, L.: Realizability of dynamic MSC languages. In: Ablayev, F., Mayr, E.W. (eds.) CSR 2010. LNCS, vol. 6072, pp. 48–59. Springer, Heidelberg (2010)
Boudjadar, A., Vaandrager, F., Bodeveix, J.-P., Filali, M.: Extending UPPAAL for the modeling and verification of dynamic real-time systems. In: Arbab, F., Sirjani, M. (eds.) FSEN 2013. LNCS, vol. 8161, pp. 111–132. Springer, Heidelberg (2013)
Dam, M., Fredlund, L., Gurov, D.: Toward parametric verification of open distributed systems. In: de Roever, W.-P., Langmaack, H., Pnueli, A. (eds.) COMPOS 1997. LNCS, vol. 1536, pp. 150–185. Springer, Heidelberg (1998)
Din, C.C., Dovland, J., Johnsen, E.B., Owe, O.: Observable behavior of distributed systems: component reasoning for concurrent objects. J. Log. Algebr. Program. 81(3), 227–256 (2012)
Din, C.C., Owe, O.: Compositional and sound reasoning about active objects with shared futures. Research report 437 (2014)
D’Osualdo, E., Kochems, J., Ong, C.-H.L.: Automatic verification of erlang-style concurrency. In: Logozzo, F., Fähndrich, M. (eds.) Static Analysis. LNCS, vol. 7935, pp. 454–476. Springer, Heidelberg (2013)
Dovland, J., Johnsen, E.B., Owe, O.: Verification of concurrent objects with asynchronous method calls. In: SwSTE, pp. 141–150 (2005)
Duarte, C.H.C.: Proof-theoretic foundations for the design of actor systems. Math. Struct. Comput. Sci. 9(3), 227–252 (1999)
Fisher, J., Henzinger, T.A., Nickovic, D., Piterman, N., Singh, A.V., Vardi, M.Y.: Dynamic reactive modules. In: Katoen, J.-P., König, B. (eds.) CONCUR 2011. LNCS, vol. 6901, pp. 404–418. Springer, Heidelberg (2011)
Gaspari, M., Zavattaro, G.: An algebra of actors. In: Ciancarini, P., Fantechi, A., Gorrieri, R. (eds.) FMOODS. Springer, New York (1999)
Haller, P., Odersky, M.: Scala actors: unifying thread-based and event-based programming. Theor. Comput. Sci. 410(2–3), 202–220 (2009)
International Telecommunication Union - Telecommunication Standardization. Open distributed processing - reference models parts 1–4. Technical report, ISO/IEC (1995)
International Telecommunication Union - Telecommunication Standardization. Recommendation Z.120: Message Sequence Chart (MSC). Technical report, ISO/IEC (2011)
Jaghoori, M.M., Chothia, T.: Timed automata semantics for analyzing Creol. In: FOCLASA, pp. 108–122 (2010)
Johnsen, E.B., Hähnle, R., Schäfer, J., Schlatte, R., Steffen, M.: ABS: a core language for abstract behavioral specification. In: Aichernig, B.K., de Boer, F.S., Bonsangue, M.M. (eds.) Formal Methods for Components and Objects. LNCS, vol. 6957, pp. 142–164. Springer, Heidelberg (2011)
Kurnia, I.W.: An automata-theoretic approach to open actor system verification. Ph.D. thesis, University of Kaiserslautern, January 2015
Kurnia, I.W., Poetzsch-Heffter, A.: A relational trace logic for simple hierarchical actor-based component systems. In: AGERE! 2012, pp. 47–58. ACM (2012)
Kurnia, I.W., Poetzsch-Heffter, A.: Verification of open concurrent object systems. In: Giachino, E., Hähnle, R., de Boer, F.S., Bonsangue, M.M. (eds.) Formal Methods for Components and Objects. LNCS, vol. 7866, pp. 83–118. Springer, Heidelberg (2013)
Lamport, L.: What good is temporal logic? In: IFIP Congress, pp. 657–668 (1983)
Leo, J.: Dynamic process creation in a static model. Master’s thesis, MIT (1990)
Lynch, N., Tuttle, M.R.: Hierarchical correctness proofs for distributed algorithms. In: PODC, pp. 137–151 (1987)
Misra, J., Mani Chandy, K.: Proofs of networks of processes. IEEE Trans. Software Eng. 7(4), 417–426 (1981)
Montanari, U., Pistore, M.: Ugo Montanari and Marco Pistore. ENTCS 10, 170–188 (1997)
Montanari, U., Pistore, M.: History-dependent automata: an introduction. In: Bernardo, M., Bogliolo, A. (eds.) SFM-Moby 2005. LNCS, vol. 3465, pp. 1–28. Springer, Heidelberg (2005)
Nipkow, T., Slind, K.: I/O automata in Isabelle/HOL. In: Dybjer, P., Nordström, B., Smith, J. (eds.) TYPES. LNCS, vol. 996, pp. 101–119. Springer, Heidelberg (1994)
Olderog, E.-R., Apt, K.R.: Fairness in parallel programs: the transformational approach. ACM TOPLAS 10(3), 420–455 (1988)
OSGi core release 5 (2012). http://www.osgi.org
Schacht, S.: Formal reasoning about actor programs using temporal logic. In: Agha, G., De Cindio, F., Rozenberg, G. (eds.) APN 2001. LNCS, vol. 2001, pp. 445–460. Springer, Heidelberg (2001)
Sirjani, M., Jaghoori, M.M., Baier, C., Arbab, F.: Compositional semantics of an actor-based language using constraint automata. In: Ciancarini, P., Wiklicky, H. (eds.) COORDINATION 2006. LNCS, vol. 4038, pp. 281–297. Springer, Heidelberg (2006)
Smith, S., Talcott, C.L.: Specification diagrams for actor systems. High.-Order Symb. Comput. 15(4), 301–348 (2002)
Thati, P., Talcott, C., Agha, G.: Techniques for executing and reasoning about specification diagrams. In: Rattray, C., Maharaj, S., Shankland, C. (eds.) AMAST 2004. LNCS, vol. 3116, pp. 521–536. Springer, Heidelberg (2004)
Zufferey, D., Wies, T., Henzinger, T.A.: Ideal abstractions for well-structured transition systems. In: Kuncak, V., Rybalchenko, A. (eds.) VMCAI 2012. LNCS, vol. 7148, pp. 445–460. Springer, Heidelberg (2012)
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2016 Springer International Publishing Switzerland
About this paper
Cite this paper
Kurnia, I.W., Poetzsch-Heffter, A. (2016). Modeling Actor Systems Using Dynamic I/O Automata. In: Mazzara, M., Voronkov, A. (eds) Perspectives of System Informatics. PSI 2015. Lecture Notes in Computer Science(), vol 9609. Springer, Cham. https://doi.org/10.1007/978-3-319-41579-6_15
Download citation
DOI: https://doi.org/10.1007/978-3-319-41579-6_15
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-319-41578-9
Online ISBN: 978-3-319-41579-6
eBook Packages: Computer ScienceComputer Science (R0)




 and
and  . In particular, we do not known what the clients do with the session actors.
. In particular, we do not known what the clients do with the session actors. ,
, ,
, ,
, ,
, .
. for some event e and a configuration
for some event e and a configuration 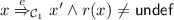 then
then  .
. component instance to the event bags of the
component instance to the event bags of the  component instances and the
component instances and the  actor,
actor, component instance to the queries of the
component instance to the queries of the  component instance, and
component instance, and component instance to each client, as stored in the internal state of the
component instance to each client, as stored in the internal state of the  component instance.
component instance.