Metric Geometries in an Axiomatic Perspective

Abstract

In his 1854 Habilitationsvortrag Riemann presented a new concept of space endowed with a metric of great generality, which, through specification of the metric, gave rise to the spaces of constant curvature. In a different vein, yet with a similar aim, J. Hjelmslev, A. Schmidt, and F. Bachmann, introduced axiomatically a very general notion of plane geometry, which provides the foundation for the elementary versions of the geometries of spaces of constant curvature. We present a survey of these absolute geometric structures and their first-order axiomatizations, as well as of higher-dimensional variants thereof. In the 2-dimensional case, these structures were called metric planes by F. Bachmann, and they can be seen as the common substratum for the classical plane geometries: Euclidean, hyperbolic, and elliptic. They are endowed with a very general notion of orthogonality or reflection that can be specialized into that of the classical geometries by means of additional axioms. By looking at all the possible ways in which orthogonality can be introduced in terms of polarities, defined on (the intervals of a chain of subspaces of) projective spaces, one obtains a further generalization: the Cayley-Klein geometries. We present a survey of projective spaces endowed with an orthogonality and the associated Cayley-Klein geometries.

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

1 Introduction

With his Habilitationsvortrag of 1854, Riemann opened up a great number of vistas. Its first paragraph indicates Riemann’s disagreement with the conventional, Euclidean approach to the foundations of geometry:

Bekanntlich setzt die Geometrie sowohl den Begriff des Raumes, als die ersten Grundbegriffe für die Constructionen im Raume als etwas Gegebenes voraus. Sie giebt von ihnen nur Nominaldefinitionen, während die wesentlichen Bestimmungen in Form von Axiomen auftreten. Das Verhältniss dieser Voraussetzungen bleibt dabei in Dunkeln; man sieht weder ein, ob und in wie weit ihre Verbindung nothwendig, noch a priori, ob sie möglich ist.¹

Here we find, for the first time (as noticed by Ferreirós [21, p. 69]), a statement of the requirement that the consistency of an axiom system be proved (“ob ihre Verbindung [die Verbindung der Voraussetzungen] möglich ist” (“whether their [the assumptions’] association is possible”). Expressed in a modern language unavailable in his time, Riemann would ask, given axioms $\alpha _1, \ldots , \alpha _n$, for a proof that their Verbindung (“association”) $\alpha _1\wedge \ldots \wedge \alpha _n$ is satisfiable. There is a requirement of the independence of the axioms implicit in the phrase “ob [...] ihre Verbindung nothwendig ist” (“whether [...] their association is necessary”), as well as one asking for the structure of the models of independence of an axiom, implicit in the request to find out “in wie weit ihre Verbindung nothwendig [ist]” [“to what extent their association is necessary”].

It will become apparent during this survey that Riemann’s critique no longer applies to the modern axiomatization of geometry, that the “assumptions” have been weakened, producing a very general notion of “geometry,” and that the “relations between” these “assumptions” are no longer “obscure.”

The great breakthroughs the Habilitationsvortrag contains, pertaining to the concept of a differentiable manifold and to that of Riemannian geometry, have been analyzed in detail in [11,12,13,14, 21, 54, 82,83,84], and will not be referred to in the sequel.

There is no doubt in our minds regarding the visionary value of the Habilitationsvortrag or of its importance for the foundations of geometry. Our goal is to indicate how the aims Riemann had in mind when he provided a solid foundation for geometry, leading to spaces of constant curvature, can be reached from a different point of view, using advances in abstract algebra, logic, and our understanding of the structure of the Universe, none of which were present in any usable form in 1854.

Riemann’s overall aim can be read from his critique of past attempts, and from his own proposal. What he dislikes in the old axiomatic approach is the fact that one lonely geometry appears at the end of a list of axioms, making it very hard, if not impossible, to judge the contribution of the individual axioms. Nor is there a fundamental concept of space available, which allows, by adding new axioms, (hypotheses as Riemann would say, to emphasize their arbitrary nature, as opposed to axioms, which were thought to be true), to obtain a wide variety of geometries. It wasn’t quite true that this did not exist at all in 1854, but it is apparent that Riemann had no knowledge of it, since he cites only Euclid and Legendre as precursors in the foundations of geometry. In §15 of his Appendix of 1832, J. Bolyai had defined absolute geometry, a geometry worthy of being considered a scientiam spatii, that did allow the addition of further hypotheses to reach more specific geometries. Riemann’s aim, of starting with an n-dimensional manifold, and then adding a metric, is certainly much more bold, and offers a far more general notion of space. However, that approach, although very general from one point of view, is extraordinarily restrictive from another point of view. It stipulates that space be continuous, and be modeled by the real numbers. Riemann is very well aware that this is a hyothesis, i.e., that it is not a self-evident truth. He writes:

Die Frage über die Gültigkeit der Voraussetzungen der Geometrie im Unendlichkleinen hängt zusammen mit der Frage nach dem innern Grunde der Massverhältnisse des Raumes. Bei dieser Frage, welche wohl noch zur Lehre vom Raume gerechnet werden darf, kommt die obige Bemerkung zur Anwendung, dass bei einer discreten Mannigfaltigkeit das Princip der Massverhältnisse schon in dem Begriffe dieser Mannigfaltigkeit enthalten ist, bei einer stetigen aber anders woher hinzukommen muss. Es muss also entweder das dem Raume zu Grunde liegende Wirkliche eine discrete Mannigfaltigkeit bilden, oder der Grund der Massverhältnisse ausserhalb, in darauf wirkenden bindenen Kräften, gesucht werden.²

This concern with the discrete in the context of “metric relations” is highly unusual for the prevailing zeitgeist. Riemann very likely expressed it due to the acknowledged influence the philosopher Johann Friedrich Herbart (1776–1841) had on his own philosophical outlook (the only other acknowledged influence being that of Gauß).³ Among the five ideas from Herbart’s works that “gave rise to many of Riemann’s epoch-making speculations,” ([77, p. 63]) Bertrand Russell lists Herbart’s “general preference for the discrete above the continuous.” ([77, pp. 62–63]).

Riemann was interested in the connection between geometry and physics, in particular the spatial structure of the Universe. The recent realization that space very likely exhibits a granular structure (see [76] for a contemporary point of view, and [35, p. 705] for the same realization a century ago, in Hilbert’s words “ein homogenes Kontinuum, das die fortgesetzte Teilbarkeit zuliesse und somit das Unendlich-Kleine realiseren würde, [wird] in der Wirklichkeit nirgends angetroffen. Die unendliche Teilbarkeit eines Kontinuums ist nur eine in Gedanken vorhandene Operation, nur eine Idee, die durch unsere Beobachtungen der Natur und die Erfahrungen der Physik und Chemie widerlegt wird.”⁴) makes a search for a foundation of geometry that would not be completely dependent on the real numbers desirable from this point of view as well.

Most mathematicians, in Riemann’s time and at present, work inside well-established theories and objects, inside a social consensus of what is acceptable and what not. A very small minority, among whose ranks one could, in his own time, consider J. Bolyai and N. I. Lobachevsky to belong, develop a firm belief in the validity of a well-reasoned vision that does not yet have a place in the world of socially accepted mathematical practice. An idealist strain is at work here, one for which what is born of exact thought is primordial, one for which “in the beginning was the word.” This approach looks at mathematics as the art of producing new insights from a few basic principles, that have been singled out as “hypotheses,” central to the envisioned realm of discourse. The idealist approach originates with the ancient Greeks, and it is no wonder that some of its early practitioners in modern times, in particular Russell and Hilbert, were under their spell.

As the author of the Habilitationsvortrag, Riemann is an accomplished idealist. He emphasizes the hypothetical character of the assumptions, finds it necessary to justify at length the choice of continuous rather than discrete scales, and—much like Lobachevsky and Bolyai before him—has no problem believing in the truth of his “Riemannian manifolds” more than 100 years before they were shown to exist globally in the sense concrete mathematical practice would deem convincing, namely as submanifolds of a Euclidean space with the induced metric. That was the way 2-dimensional manifolds had been first considered by Gauß  and the representation of a part of the hyperbolic plane in that manner by Beltrami in 1868 was the turning point eventually leading to the social acceptance of hyperbolic geometry.

Few abstractly existing entities, without a concrete model, had been put forward before (such as complex numbers), and certainly none of that level of complexity.

Approaches that were not accessible in 1854 were those involving groups, whose abstract concept had only appeared that same year, in Cayley’s papers. Nor was there any awareness of the complexities involved in providing a foundation ex nihilo for the real numbers. With our current knowledge, we know that the real numbers, if they are to receive a foundation from the ground up, in the idealist manner, require the language of set theory and its axioms. As Skolem had emphasized since 1923, and as has become commonly accepted (see [18]) for the past 70 years or so, in the words of J. Ferreirós,“if we are interested in producing an axiomatic system, we can only use first-order logic.” [20, p. 472]) And within first-order logic, the real numbers cannot be axiomatized on the basis of addition, multiplication, some constants, and the order relation. They do require all of set theory, which means the foundation for all of mathematics.

Riemann had no reason to doubt the fundamental nature of the real numbers, as their only competition in the world of Grössenbegriffe, which Riemann mentions when referring to discrete or continuous Bestimmungsweisen, were the natural numbers. In that foundationally innocent time before 1854, the notion of a field was non-existent, nor was there any doubt that Archimedeanity is a fundamental attribute of any Grössenbegriff.

We should mention from the start of our alternative approach—one that bears no direct relation to Riemann’s Habilitationsvortrag—that no elementary account of the foundations of geometry (i.e., no first-order axiomatization) can ever hope to provide a foundation for the bewildering variety of Riemannian manifolds, i.e., to have all of them among its models. What we can do inside our elementary approach is to do justice to Riemann’s desire of starting with a very general notion of space that allows, through a step by step process (often referred to as a Stufenaufbau in German), for the foundation of the essentially geometric scaffolding of spaces of constant curvature (the differential geometric story of which has been told elsewhere, see [114]).

Despite the apparent differences in these two approaches, there are historical connections inexorably leading from Riemann to Hilbert, and then to Hjelmslev, to Hilbert’s student Arnold Schmidt, and finally to Bachmann. In the fourth appendix to his Grundlagen der Geometrie, Hilbert starts with “the studies of Riemann and Helmholtz on the foundations of geometry”,⁵ which have led (“veranlaßten”) Lie to approach the problem by using the concept of a group. He then proposes his own version of what we call today the Riemann-Helmholtz-Lie space problem in both topological and group-theoretical terms. On the last page of that appendix, Hilbert points out that the difference between the approach mixing topology with group theory and that of the “main part” (“Hauptteil”) of the book lies in the place occupied by the axiom of continuity in the scaffolding of the axiom system. In the fourth appendix Über die Grundlagen der Geometrie, continuity is assumed from the start, so comes first, whereas in the axiom system of the Grundlagen der Geometrie it comes last, to allow for a continuity-independent development of elementary geometry. Bachmann’s approach, which will be followed closely in this survey, can be seen as combining the group-theoretical aspect present in Hilbert’s fourth appendix, and originating in the Riemann-Helmholtz-Lie space problem, with the continuity-independent approach found in the elementary foundation of geometry—along ancient Greek lines going back to Aristotle’s Posterior Analytics—in the “main part” of the Grundlagen der Geometrie. It was precisely the Aristotelian approach that had been completely forgotten, and was nowhere present in the mathematics of the first half of the 19th century. Up until the modern axiomatization of arithmetic and geometry, the zeitgeist was one of the belief in the unity of all mathematics, in the spirit of Plato (see [46]). There was no sense to be made out of Aristotle’s Posterior Analytics, A 7, 75a38-b20, the first half of which reads (in the translation of Theophilos Kouremenos):

It follows that it is impossible to prove something by passing to it from another kind, e. g. to prove a geometrical truth with arithmetic. For there are three elements in demonstration: what is proved, the conclusion (which is an attribute belonging to a kind in itself); the axioms (which are premises of the proof); third, the underlying kind whose attributes and properties that hold of it in itself are revealed by the demonstration. The axioms, which are premises of demonstration, may be identical in two or more sciences: in the case of two different kinds such as arithmetic and geometry, however, you cannot fit arithmetical demonstration to the attributes of magnitudes, unless the magnitudes in question are numbers; how this is possible in certain cases I will explain later. Arithmetical proof always has its own kind, and so do the proofs in the other sciences. Thus, if a proof is to cross from one science to another, the kind must be the same absolutely or to some extent. Otherwise crossing is evidently impossible since the extreme and the middle terms must come from the same kind; for, if they do not hold in themselves, they hold incidentally.

At the start of the modern axiomatic approach we have Pasch, who in 1882 provided a modern axiomatic foundation for ordered geometry (see [67] for details on their possible axiomatizations). These can be considered, in a certain sense, the elementary version of differentiable manifolds, given that there is only a topology present (the one induced by the order relation), but no metric, i.e., no notion of orthogonality or congruence. In dimensions ${\ge }3$, these spaces are, however, much more rigidly structured than manifolds, given that they have to be Desarguesian, i.e., that they can be embedded in projective spaces over ordered skew fields. In trying to mimic Riemann’s approach, one could start with ordered spaces and then add a notion of orthogonality or congruence to obtain elementary versions of spaces of constant curvature. This would roughly correspond to the approach present in Hilbert’s Grundlagen der Geometrie of 1899. There the axioms are divided into groups. The first group consists of incidence axioms, the second group of order axioms, the third group of congruence axioms. Taken together, the three groups axiomatize an elementary (i.e., first-order) version of J. Bolyai’s absolute geometry .

We will follow instead a different Stufenaufbau, that starts with a bare bones orthogonality structure, in which there is neither order nor the various forms of free mobility that Riemann asks of his geometry, nor the possibility of embedding the structures in Euclidean spaces over the real numbers. This originates, to a certain extent, in Hilbert’s work (see also [68]), for he states, in the conclusion of his Grundlagen der Geometrie, that he was led throughout by the fundamental principle (Grundsatz):

eine jede sich darbietende Frage in der Weise zu erörtern, daß  wir zugleich prüften, ob ihre Beantwortung auf einem verschiedenen Wege mit gewissen eingeschränkten Hilfsmitteln möglich ist.⁶

This purely metric⁷ treatment of geometry started with the 2-dimensional case, and is due, in large measure, to J. Hjelmslev. It was he who, in [36], had the deep insight that line-reflections have certain properties that are independent of any assumption regarding parallels, and thus absolute. Line-reflections—and with them the crucial three-reflection theorem, stating that the composition of three reflections in lines which have a common perpendicular or a common point must be a line-reflection—had been the subject of earlier studies, such as [31, 33, 89, 113]. However, in these works, line-reflections were treated inside the particular geometry at hand (Euclidean, hyperbolic, or elliptic), and not independently of it, as they were by Hjelmslev, who carried on this line of research in [37]. Many more geometers—whose contributions are chronicled in [7, 38]—have helped build up geometry in terms of line-reflections. Their work helped remove order or free mobility assumptions. What is left after the removal work was done consists of the three-reflections theorem, beside very basic axioms stating that there are at least two points, that there is exactly one line incident with two distinct points, that perpendicular lines intersect, and that through every point there is a perpendicular to any line, which is unique if the point and the line are incident. The final touch in carving this austere axiom system came from Bachmann [4], who showed that two axioms from the axiom system of Hilbert’s student Schmidt [80] are superfluous.

Later, several of Bachmann’s students and other geometers extended the reflection-geometric axiomatization to higher-dimensional and to dimension-free geometries. It is these geometries that we consider to be the elementary (first-order) counterpart of Riemannian manifolds. They share the following characteristics: (i) they are both defined as abstract structures, which can be shown—with great effort—to be embeddable in some Euclidean space (in the case of Riemannian manifolds) or in some projective-metric space (in the case of reflection geometries); (ii) they both allow the definition of a notion of orthogonality (in the case of Riemannian manifolds on the tangent space of each point), defined by a bilinear symmetric map (which is given a priori in the Riemannian case, while it is discovered through the hard work of a representation theorem in the case of reflection geometries). Since the symmetric bilinear map is left unspecified, except for the restriction that the radical (orthogonal complement) of the quadratic space it determines be ${\le }1$, in the case of reflection geometries, the notion of space thus created is one of wide generality.

Much like in the case of Riemannian manifolds, some of which were known in the 2-dimensional case as surfaces in 3-dimensional Euclidean space, variants of the reflection-geometrically defined geometries had been studied earlier as inhabitants of projective-metric spaces. Understanding a metric geometry inside a projective space originated in the discovery of Cayley [15] and Klein [42] that projective geometry allows the introduction of metric concepts. By distinguishing an absolute figure (the absolute) in a real projective manifold, they were able to introduce a projective measure (Maßbestimmung). Metrical properties became properties of the relation of a figure to the absolute and the projective Maßbestimmung “blazed a convenient road through [the] jungle undergrowth of Lobachevsky’s computations.”⁸

In the Euclidean case the absolute is a degenerate imaginary conic, consisting of a couple of complex points, called “the circular points at infinity” (see [92, II §8] or [42]). If the two complex circular points are replaced by a real non-degenerate conic then the associated geometry is the geometry of Bolyai and Lobachevsky, commonly referred to, following Klein, as hyperbolic. If the absolute non-degenerate conic is imaginary, then the associated geometry is, again following Kleinian terminology, elliptic. Elliptic geometry is the spherical geometry of Riemann if antipodal points are identified, so that any two points have a unique joining line. The incidence structure of an elliptic plane, i.e., an elliptic plane in which one “forgets” the metric structure, is a projective plane. Elliptic lines are unbounded⁹ but of finite length—a distinction which Riemann emphasized in section III.2 of his Habilitationsvortrag with the words:

Bei der Ausdehnung der Raumconstructionen in’s Unmessbargrosse ist Unbegrenztheit und Unendlichkeit zu scheiden; jene gehört zu den Ausdehnungsverhältnissen, diese zu den Massverhältnissen.¹⁰

Klein made a systematic analysis to determine all projective measures of a projective space and described the associated Euclidean and non-Euclidean geometries which are nowadays commonly referred to as Cayley-Klein geometries. He himself was initially reluctant to refer to them as geometries, for although they have “from a logical point of view equal rights beside Euclidean geometry”,¹¹ “they are in part not usable for measurements in the outside world”,¹² so he preferred to refer to them as Maßbestimmungen. With the advent of relativity theory, he changed his mind and pointed out that all the geometries underlying the newly proposed models of “space”, be they Minkowski space or de Sitter space, were among the “geometries” for which he had reserved the more modest term “projective measure”.

Cayley and Klein showed that both Euclidean and hyperbolic geometry are subordinate to projective geometry, and that the only difference—from a projective point of view—is in the choice of the absolute. Moreover, all Cayley-Klein geometries are independent entities in their own right, in the sense that they do not need to be considered as geometries embedded in projective geometry. The fact that, even if the Cayley-Klein geometries are abstractly defined, they end up being embeddable in a projective space with a projective metric, is a remarkable result, referred to as the Begründung (grounding) of a geometry. It is worth mentioning that such a Begründung cannot proceed by constructing a model in Euclidean space, such as a sphere model of elliptic geometry, for such constructions presuppose Euclidean geometry rather than happen inside the neutrality of the projective setting.

This Cayley-Klein approach was not without its critics from an epistemological point of view. Its fundamental problem, as pointed out by Russell in his Foundations of Geometry [77, p. 31], was one of circularity (see also [26, Chaps. 1–3]):

But what are projective coordinates, and how are they introduced? This question was not touched upon in Cayley’s Memoir, and it seemed, therefore, as if a logical error were involved in using coordinates to define distance. For coordinates, in all previous systems, had been deduced from distance; to use any existing coordinate system in defining distance was, accordingly, to incur a vicious circle.¹³

This criticism asks one to justify in a purely geometrical manner the introduction of coordinates in geometry to validate the Cayley-Klein approach. This problem had been left unanswered for a very long time after Descartes showed that geometry can be practised inside a coordinate structure without providing reasons why synthetically given geometry can be coordinatized. In other words, the problems was to indicate how numbers or magnitudes show up in a realm like that of synthetic geometry, in which they do not belong to the vocabulary of its axiom system. This question was first answered by Schur [89, 90], and made widely known for Euclidean geometry by Hilbert in the Grundlagen der Geometrie with his arithmetic of line segments (Streckenrechnung). It is also addressed in [42, Kap. V] for the projective case to ensure that the construction of non-Euclidean geometries does not depend upon the specifically Euclidean coordinatization process. For absolute geometry, where the task is significantly more complex, it was Hjelmslev and Bachmann who provided the coordinatization of an abstractly presented geometry by means of their calculus of reflections. This method turns out to be applicable to all Cayley-Klein geometries.

Our aim is to survey results of what can be considered the modern axiomatic foundation of geometry. This will bring to light the little known fact that this is a field of research with its own challenging problems, rather than one of largely historical interest.

Given the axiomatic nature of our undertaking, one needs a language in which to write the axioms, and a logic by means of which to deduce consequences from those axioms. Based on the work of Skolem, Hilbert and Ackermann, Gödel, and Tarski, a consensus had been reached by the end of the first half of the 20th century that, as Skolem had emphasized since 1923, “if we are interested in producing an axiomatic system, we can only use first-order logic” (cp. [20, p. 472]).

Given that symbolic logic is not within the comfort zone of a majority of present-day mathematicians, each axiom that is phrased in formal logic is followed by a plain English description of what it says. This allows the reader to skip the formal part of an axiom without losing the thread of the story.

We will proceed by first presenting the theory of metric planes in its group-theoretical axiomatization in Sect. 2.1, followed by a more traditional, synthetic geometric, axiomatization in Sect. 2.2, and a partial algebraic characterization of the models in Sect. 2.3. Next come the introduction of order and free mobility in Sects. 2.4 and 2.5, turning metric planes into Hilbert planes (planes satisfying the axioms for absolute geometry presented by Hilbert in [34]), as well as Pejas’s algebraic characterization of Hilbert planes. We next pause to reflect in Sect. 2.6 on the methodological advantages of this approach, and mention the generalizations of metric planes proposed in the literature in Sect. 2.7. Sections 3 and 4 are devoted to n-dimensional and dimension-free generalizations of metric planes. Given that the orthogonality relation of metric planes or of higher-dimensional metric spaces is induced by a polarity defined on a subspace of a projective plane or space, we turn in Sect. 5 to the study of all possible orthogonality relations that are induced by polarities. The 2-dimensional case is treated in Sect. 5.1, the finite-dimensional case in Sect. 5.2. While the 2-dimensional case has a venerable history, going back to Cayley [15] and Klein [42], the higher-dimensional case has been systematically dealt with only recently in [106, 108], and offers a better understanding of the manner in which Cayley-Klein geometries, which are dealt with in Sect. 6, come into existence. The 2-dimensional case of Cayley-Klein geometries is treated in greater detail in Sect. 6.1, with a novel reflection-geometric axiomatization presented in Sect. 6.3. Remarks concerning finite plane Cayley-Klein geometries and on the connection between Cayley-Klein spaces and differential geometry can be found in Sects. 6.2 and 6.4. We append a reasonably comprehensive list of references.

2 Metric Planes

2.1 2.1   The Group-Theoretical Approach

We now present metric planes as they appear in [7]. There, however, they are presented as structures living inside groups generated by a set of involutions. This is not a first-order axiomatization (a fact Bachmann knew all too well, having written his thesis and done research in formal logic), but rather a convenient language in which the theory should be presented to a wider audience. That the theory could be phrased in first-order logic he no doubt knew. We choose to present the theory of metric planes in formal logic just to show that it can be done, that it is an elementary theory, far removed from the concept of set.¹⁴ Our language will be a one-sorted one, with variables to be interpreted as “rigid motions,” containing a unary predicate symbol G, with G(x) to be interpreted as “x is a line-reflection,” a constant symbol 1, to be interpreted as “the identity,” and a binary operation $\circ$, with $\circ (a, b)$, which we shall write as $a\circ b$, to be interpreted as “the composition of a with b.”

To improve the readability of the axioms, we introduce the following abbreviations:

$$\begin{aligned} a^2&= a\circ a,\\ \iota (g)&:\Leftrightarrow g\ne 1 \wedge g^2=1, \\ a \! \mid \! b&:\Leftrightarrow G(a)\wedge G(b)\wedge \iota (a\circ b),\\ J(abc)&:\Leftrightarrow \iota ((a\circ b)\circ c),\\ pq \! \mid \! a&:\Leftrightarrow p \! \mid \! q \wedge G(a) \wedge J(pqa). \end{aligned}$$

Thus $\iota (g)$ stands for “g is an involutory element;” $a \! \mid \! b$ for “a and b are orthogonal lines;” J(abc) stands for “a, b, and c lie in a pencil;” $pq \! \mid \! a$ stands for “the line a and the orthogonal lines p and q lie in a pencil.” The axioms are (we omit universal quantifiers whenever the axioms are universal sentences):

M 1 :

$(a\circ b)\circ c = a\circ (b\circ c)$

M 2 :

$(\forall a)(\exists b)\, b\circ a = 1$

M 3 :

$1\circ a = a$

M 4 :

$G(a)\rightarrow \iota (a)$

M 5 :

$G(a)\wedge G(b)\rightarrow G(a\circ (b\circ a))$

M 6 :

$(\forall abcd)(\exists g)\, a \! \mid \! b \wedge c \! \mid \! d \rightarrow G(g)\wedge J(abg)\wedge J(cdg)$

M 7 :

$ab \! \mid \! g \wedge cd \! \mid \! g \wedge ab \! \mid \! h \wedge cd \! \mid \! h \rightarrow (g=h \vee a\circ b = c\circ d)$

M 8 :

$\bigwedge _{i=1}^3 pq \! \mid \! a_i \rightarrow G(a_1\circ (a_2\circ a_3))$

M 9 :

$\bigwedge _{i=1}^3 g \! \mid \! a_i \rightarrow G(a_1\circ (a_2\circ a_3))$

M 10 :

$(\exists ghj)\, g \! \mid \! h \wedge G(j)\wedge \lnot j \! \mid \! g \wedge \lnot j \! \mid \! h \wedge \lnot J(jgh)$

M 11 :

$(\forall x)(\exists ghj)\, G(g)\wedge G(h)\wedge G(j)\wedge (x=g\circ h \vee x= g\circ (h\circ j))$

Since $a\circ b$ with $a\!\mid \! b$ represents a point-reflection, we may think of an unordered pair (a, b) with $a\! \mid \! b$ as a point, an element a with G(a) as a line, two lines a and b for which $a\! \mid \! b$ as a pair of perpendicular lines, and say that a point (p, q) is incident with the line a if $pq \!\mid \! a$. With these figures of speech in mind, the above axioms make the following statements: M1, M2, and M3 are the group axioms for the operation $\circ$; M4 states that line-reflections are involutions; M5 states the invariance of the set of line-reflections, M6 states that any two points can be joined by a line, which is unique according to M7; M8 and M9 state that the composition of three reflections in lines that have a common point or a common perpendicular is a line-reflection; M10 states that there are three lines g, h, and j, such that g and h are perpendicular, j is perpendicular to neither g nor h, nor does j go through the intersection point of g and h; M11 states that every motion is the composition of two or three line-reflections. It is this fact, that every element of the group generated by line-reflections can be written as the product of at most three line-reflections, that made the first-order axiomatization of the group of motions of a metric plane possible. Notice that, in the presence of M11, M4, M1, and M3, the statement regarding the existence of the inverse, M2, becomes superfluous. We have listed it nevertheless, given that M1–M3 will be used in axiom systems that appear later. We will denote by ${\mathcal M}$ the axiom system $\{$ M1–M11 $\}$ for metric planes.

From here on, there are two options, according to the answer the question “Is it possible for a product of an odd number of line-reflections to be the identity?” receives. If the answer is yes, which means—given that any product of an odd number of line-reflections can be reduced to a product of three line-reflections—that

El 1 :

$(\exists abc)\, G(a)\wedge G(b)\wedge G(c)\wedge a\circ (b\circ c)=1$

then we have an axiom system for elliptic planes (the geometry first mentioned by Riemann in his Habilitationsvortrag as a geometry with positive constant curvature). El1 states that the composition of three line-reflections can be the identity.

If the answer is no, meaning that $\lnot$ El1 holds, then we have a non-elliptic metric plane. The presence of $\lnot$ El1 ensures that the perpendicular from a point not on a line to that line is unique.

Within the theory of metric planes we can separate the hypotheses regarding the nature of the metric (Euclidean or non-Euclidean (hyperbolic, elliptic)) from those regarding free mobility (with subdivisions into the free mobility of points (every point-pair has a midpoint) and the free mobility of lines (every pair of intersecting lines has an angle bisector)), and from those regarding the order of the plane. These three requirements are almost completely distinct, in the sense that a metric plane may satisfy, within limits, a variety of combinations of them. The two cases in which one hypothesis leads to another are the case in which the metric is hyperbolic, in which the order comes for free, and the case of a Euclidean metric, in which the free mobility of points, i. e., the universal existence of midpoints, is ensured.

2.1.1 2.1.1   The Elliptic Case

There are simpler axiom systems for elliptic planes than ${\mathcal M}\cup \{$ El1 $\}$. The first in-depth study of an axiomatization in terms of reflections for elliptic planes goes back to Baer [10]. After proving that one of Baer’s axioms is superfluous and re-writing Baer’s axiom system, Heimbeck [28] showed that $\{$ M1–M3, El2, El3, El4 $\}$ is an axiom system for elliptic planes in a one-sorted language with one binary operation symbol $\circ$. The specifically elliptic axioms are:

El2 :

$(\forall g)(\exists i)(\forall x)\, g\ne 1\rightarrow ( \iota (i) \wedge (\iota (x)\rightarrow (\iota (x\circ g) \leftrightarrow \iota (x\circ i)))$

El3 :

$(\forall g)(\exists h)\, \iota (g)\rightarrow g\circ h\ne h\circ g$

El4 :

$(\exists g)\, g\ne 1$

El2 states that, for all elements $g\ne 1$ of the group, there is an involution i of that group, such that the set of all involutions x for which $x\circ g$ is an involution coincides with the set of all involutions x for which $x\circ i$ is an involution. El3 states that no involution commutes with all elements of the group, and El4 that the group is not trivial.

2.1.2 2.1.2   The Hyperbolic Case

Two lines a and b are called non-connectable, to be denoted by $\omega (a,b)$ if a and b neither intersect nor have a common perpendicular, i.e.,

$$ \omega (a,b)\Leftrightarrow (\forall gh)\, \lnot (gh \! \mid \! a\wedge gh \! \mid \! b)\wedge \lnot (g \! \mid \! a\wedge g \! \mid \! b). $$

To obtain an axiom system for hyperbolic planes from metric planes, one just needs to add two axioms to $\{$ M1–M11 $\}$, namely (addition in the indices being modulo 3)

H 1 :

$(\exists ab)\, \omega (a,b)$

H 2 :

$(\forall a_1a_2a_3mng)\, (\bigwedge _{i=1}^3mn \! \mid \! a_i \wedge \omega (a_i,g))\rightarrow (\bigvee _{i=1}^3 a_i=a_{i+3})$

H1 states that there are two lines that are non-connectable. H2 states that through a given point (m, n) there can be at most two lines $a_i$ that are non-connectable with a given line g. The theory axiomatized by ${\mathcal M}\cup \{$ H1, H2 $\}$ was studied by Klingenberg [43], who showed that all of its models are isomorphic to Beltrami-Cayley-Klein unit disk models of hyperbolic geometry built over arbitrary ordered fields. To get to the elementary version of plane hyperbolic geometry, first axiomatized by Hilbert [33], one needs to add to ${\mathcal M}\cup \{$ H2 $\}$ an axiom stronger than H1, namely one that states that from a point $(p_1, p_2)$ to a line g not through $(p_1, p_2)$ there are two distinct lines non-connectable with g, i.e.,

H 3 :

$(\forall p_1p_2g)(\exists a_1a_2)\, p_1 \! \mid \! p_2\wedge \lnot (p_1p_2\! \mid \! g) \rightarrow a_1\ne a_2\wedge \bigwedge _{i=1}^2 (p_1p_2 \! \mid \! a_i\wedge \omega (a_i,g))$

It forces the arbitrary ordered coordinate field of the models of ${\mathcal M}\cup \{$ H1, H2 $\}$ to be Euclidean, i.e., one in which all positive elements must have square roots. As shown in [43, 4.5], one can replace H3 with the requirement that every point-pair has a midpoint

H 4 :

$(\forall a_1a_2b_1b_2)(\exists c_1c_2)\, a_1 \! \mid \! a_2\wedge b_1 \! \mid \! b_2$

      $\rightarrow c_1 \! \mid \! c_2\wedge ((c_1\circ c_2)\circ (a_1\circ a_2))\circ (c_1\circ c_2)= b_1\circ b_2$

to get another axiom system, ${\mathcal M}\cup \{$ H1, H2, H4 $\}$, for Hilbert’s plane elementary hyperbolic geometry. Another, simpler axiom system in terms of line-reflections and their composition can be found in [9, Satz 7].

2.1.3 2.1.3   The Euclidean Case

There are two particular behaviors that may be deemed as Euclidean. One is purely metric and can be expressed by either requiring the existence of a rectangle, i.e.,

E 1 :

$(\exists abcd)\, a \! \mid \! c\wedge b \! \mid \! c\wedge a \! \mid \! d \wedge b \! \mid \! d\wedge a\ne b \wedge c\ne d$

or by asking that a quadrilateral with three right angles is a rectangle,

E 2 :

$a \! \mid \! c\wedge b \! \mid \! c\wedge a \! \mid \! d \rightarrow b \! \mid \! d$

It turns out that, in the presence of ${\mathcal M}$, E1 and E2 are equivalent (see [7, p. 306]).

Alternatively, one may think of the behavior of parallels as being quintessentially Euclidean and ask that two distinct lines either intersect or have a common perpendicular, i.e.,

E3 :

$(\forall ab)(\exists mn)\, a\ne b\rightarrow (mn \! \mid \! a\wedge mn \! \mid \! b)\vee (m \! \mid \! a\wedge m \! \mid \! b)$

That E1 (or E2) describe a phenomenon different from that E3 postulates became apparent only after Dehn’s [16] investigation, at Hilbert’s suggestion, of the matter. Dehn found out that, even if both order and free mobility were present, E1 and E2 do not imply E3. On the either hand, neither is the reverse implication E3 $\rightarrow$ E1 valid in the presence of ${\mathcal M}$ (see [7, p. 124]).

Put differently, a metric plane satisfies both E1 and E3 if and only if Playfair’s form of the Euclidean parallel postulate—“There is exactly one line through P that does not intersect l, whenever P is a point not on the line l”—holds in it.

2.2 2.2   The Synthetic Approach

The axiom system ${\mathcal M}$ we have presented for metric planes appears to be one for its group of motions, not for the geometry itself. It turns out, however, that the information contained in the group of motions of a metric plane, in which we know which of the involutory elements are to be considered as line-reflections, contains enough information to enable the recovery of the underlying geometry. That underlying geometry can be axiomatized, as shown in [7, §2,3], in a more traditional, synthetic, manner, in which the individual variables are the usual points and lines, and the primitive notions are incidence, line orthogonality, and reflections in lines. Technically speaking, the axiom system is one inside a bi-sorted logic, given that there are two distinct kinds of variables, with points and lines to be denoted by upper-case, respectively lower-case letters of the Latin alphabet. Point-line incidence, a binary relation with point variables in the first place and line variables in the second, will be denoted by I, and we will write $P\,$ I $\, l$ instead of I $\, (P,l)$. Line orthogonality, a binary relation among lines, will be denoted by $\perp$, and we will write $g\perp h$ instead of $\perp (g,h)$. Reflections in lines are binary operations—the first argument of which are line variables, whereas the second argument and its value are of the same sort (that is, both line variables or both point variables)—are denoted by $\sigma$.

An axiom system logically equivalent to ${\mathcal M}$ thus is (addition in the indices being modulo 3):

O 1 :

$(\exists AB)\, A\ne B$

O 2 :

$(\forall g)(\exists A_1A_2A_3)\, \bigwedge _{i=1}^3A_i\ne A_{i+1}\wedge \bigwedge _{i=1}^3 A_i\,$ I $\, g$

O 3 :

$(\forall AB)(\exists ^{=1} g)\, A\ne B\rightarrow A\,$ I $\, g\wedge B\,$ I $\, g$

O 4 :

$(\forall ab)\, a\perp b\rightarrow b\perp a$

O 5 :

$(\forall ab)(\exists P)\, a\perp b\rightarrow P\,$ I $\, a\wedge P\,$ I $\, b$

O 6 :

$(\forall Pg)(\exists h)\, P\,$ I $\,h\wedge h\perp g$

O 7 :

$P\,$ I $\,g\wedge P\,$ I $\,m\wedge g\perp m\wedge P\,$ I $\,n\wedge g\perp n\rightarrow m=n$

O 8 :

$\sigma (g,\sigma (g,h))=h\wedge \sigma (g,\sigma (g,P))=P$

O 9 :

$(P\,$ I $\,h\rightarrow \sigma (g,P)\,$ I $\,\sigma (g,h))\wedge (m\perp n\rightarrow \sigma (g,m)\perp \sigma (g,n))$

O 10 :

$(\forall Pga_1a_2a_3)(\exists b)(\forall Xx)\, [(\bigwedge _{i=1}^3P\,$ I $\,a_i)\vee (\bigwedge _{i=1}^3 g\perp a_i)]$

   $\rightarrow \sigma (a_1,\sigma (a_2, \sigma (a_3, x))=\sigma (b,x)\wedge \sigma (a_1,\sigma (a_2, \sigma (a_3, X))=\sigma (b,X)$

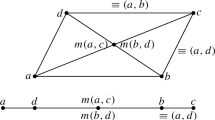
Here O1 states that there are two distinct points; O2 that every line has at least three points on it; O3 that any two distinct points are incident with a unique line; O4 that line-orthogonality is a symmetric relation; O5 that orthogonal lines intersect; O6 and O7 that there is, through any given point P a perpendicular h to any given line g, which is unique if P is on g; O8 states that, for each line g, the mapping $\alpha _g(\cdot )$, defined by $\alpha _g(\cdot ):=\alpha (g, \cdot )$ is an involution (and thus a bijection) on the set of points and lines; O9 states that, for any line g, $\sigma _g$ preserves both incidence and orthogonality; O10 is the three-reflection theorem, stating that the composition of reflections in three lines with a common point or a common perpendicular is a line reflection.

There is also, as shown in [64], an axiom system for metric planes that can be expressed, in terms of $\forall \exists$-axioms (axioms in which all universal quantifiers precede all existential quantifiers) stated in a language with points and the single ternary relation of orthogonality—with $\perp (abc)$ to be read as abc is a right triangle with right angle at a—as primitive notions.

Another synthetic axiomatization, as well as one in terms of groups operating on sets (all in first-order logic) have been proposed for non-elliptic metric planes in [61] and in [52], and their logical equivalence to the group theoretic axiomatization ${\mathcal M}\cup \{\lnot$ El1 was spelled out in [63].

2.3 2.3   Algebraic Characterization

Metric planes, being embeddable in projective planes satisfying the Pappus axiom, can be, to a certain degree, characterized algebraically. To do so we recall a few notions from analytic projective geometry.

By a projective-metric coordinate plane $\mathfrak {P} (K, \mathfrak {f})$ over a field K of characteristic ${\ne }2$, with $\mathfrak {f}$ a symmetric bilinear form, which may be chosen to be defined by

$$\begin{aligned} {\mathfrak f}(\mathbf{x}, \mathbf{y})= \lambda x_1y_1 +\mu x_2y_2+\nu x_3y_3, \end{aligned}$$

(1)

with $\lambda \mu \ne 0$, for $\mathbf{x}, \mathbf{y}\in K^3$ (where $\mathbf{u}$ always denotes the triple $(u_1, u_2, u_3)$, line or point, according to context), we understand a set of points and lines—the former to be denoted by (x, y, z) the latter by [u, v, w] (determined up to multiplication by a non-zero scalar, not all coordinates being allowed to be 0)—endowed with a notion of incidence—point (x, y, z) being incident with line [u, v, w] if and only if $xu+yv+zw=0$—and an orthogonality of lines defined by $\mathfrak {f}$, under which lines $\mathbf{g}$ and $\mathbf{g}'$ are orthogonal if and only if $\mathfrak {f}$ $(\mathbf{g}, \mathbf{g}')=0$.

The reflection of a line $\mathbf{u}=[u_1,u_2,u_3]$ in a line $\mathbf{v}=[v_1,v_2,v_3]$ is the line

$$ 2\mathbf{v}\frac{{\mathfrak f}(\mathbf{v}, \mathbf{u})}{{\mathfrak f}(\mathbf{v}, \mathbf{v})}-\mathbf{u}. $$

Every model of a metric plane (i.e., of ${\mathcal M}$) can be represented as a locally-complete subplane (i.e., one containing with every point all the lines of the projective-metric plane that are incident with it) that contains the point (0, 0, 1) of a projective-metric coordinate plane $\mathfrak {P}$ $(K,\mathfrak {f})$, from which it inherits the collinearity and orthogonality relations.

The problem of conveniently describing algebraically the possible point-sets of metric planes inside projective-metric planes, also known as the Umkehrproblem, is hopeless in this generality.¹⁵ For several classes of metric planes satisfying additional axioms, however, the Umkehrproblem was solved.

If the metric plane satisfies E1 and E3 (in which case it is called a Euclidean plane), then the point-set is precisely the affine plane over some field K of characteristic ${\ne }2$ (i.e., the projective plane mentioned above, from which the line [0, 0, 1] has been removed), and in (1) we have $\nu =0$ and ${\mathfrak f}(\mathbf{x}, \mathbf{x})\ne 0$ for $\mathbf{x}\ne \mathbf{0}$. The models can be described more conveniently in terms of a constant k, with $-k$ not a square in K, as having the point and line set of the affine plane over K, i.e., points are pairs (x, y) of elements from K, lines are triples [u, v, w], point-line incidence is given by $ux+vy+w=0$, whereas the orthogonality of the lines [u, v, w] and $[u',v',w']$ is given by

$$\begin{aligned} kuu'+vv'=0. \end{aligned}$$

(2)

If a metric plane satisfies only E1 (in which case it is called a metric-Euclidean plane), then it can be embedded in a Euclidean plane. There is a large literature providing alternative axiomatization of Euclidean planes [27, 57, 60, 81] and of metric-Euclidean planes [3, 7, 59], as well as a detailed description of their models.

In a metric plane which satisfies El1, we have $\lambda \mu \nu \ne 0$ and ${\mathfrak f}(\mathbf{x}, \mathbf{x})=0$ holds only for $\mathbf{x}=\mathbf{0}$ in (1).

In a metric plane which satisfies H1, we have that K is an ordered field, $\lambda \mu \nu \ne 0$, there is $\mathbf{x}\ne \mathbf{0}$ such that ${\mathfrak f}(\mathbf{x}, \mathbf{x})=0$ in (1). The points of the metric plane are all the points inside the absolute (which is the set of solutions of ${\mathfrak f}(\mathbf{x}, \mathbf{x})=0$).

2.3.1 2.3.1   Free Mobility

A metric plane is said to possess free mobility if any two intersecting lines g and h have an angle bisector w (i.e., if $(w\circ g) \circ w = h$ holds), and any two points $(a_1,a_2)$ and $(b_1, b_2)$ (recall that points are pairs of orthogonal lines) have a midpoint $(c_1, c_2)$ (i.e., if $((c_1\circ c_2)\circ (a_1\circ a_2))\circ (c_1\circ c_2)= b_1\circ b_2$ holds). The rather intricate algebraic structure of these metric planes has been described in [17].

2.4 2.4   Order

To introduce order in metric planes, we need an additional predicate, a ternary one, Z, among points, with Z(ABC) standing for “B lies between A and C.” To simplify the statement of the axioms, it is useful to have a name for the collinearity predicate, so we introduce the following abbreviation

$$ L(ABC)\Leftrightarrow (\exists g)\, A\, \text{ I }\, g\wedge B\,\text{ I }\, g\wedge C\,\text{ I }\, g, $$

with L(ABC) to be read as “A, B, and C are collinear points.”

Z 1 :

If A, B, and C are three different collinear points, then Z(ABC)

or Z(BCA) or Z(BCA).

Z 2 :

If Z(ABC), then A, B,  and C are collinear points.

Z 3 :

If Z(ABC), then Z(CBA).

Z 4 :

If Z(ABC), then Z(ACB) does not hold.

Z 5 :

If Z(ACB) and Z(ABD), then Z(CBD).

Z 6 :

If Z(CAB) and Z(ABD), then Z(CBD).

Z 7 :

If $C\ne D$, Z(ABC), and Z(ABD), then Z(BCD) or Z(BDC)).

Z 8 :

For all $A\ne B$ there exists a point C such that Z(ABC).

Z 9 :

If A, B, and C are three non-collinear points and D and E are two points

such that Z(ADC), E is such that it is neither collinear with A and C

nor with D and B, then there exists a point F collinear with E and D,

such that Z(AFB) or Z(BFC).

Z1 ensures that any three points on any line are in some order; Z2 that only collinear points are ordered, Z3–Z7 are linear order axioms, Z8 states that the order is unending. Z9 is the Pasch axiom, stating that the line determined by D and E, which intersects the side AC of triangle ABC, must intersect one of the sides AB or BC as well. Ordered metric planes, i.e., the models of $\{$ O1–O10, Z1–Z9 $\}$, are well-understood in case the metric is Euclidean, that is, whenever the plane satisfies E1. There is an algebraic characterization of ordered metric planes with a non-Euclidean metric, due to Pejas [72], which is, however, not very helpful in establishing the validity of a given statement.

2.5 2.5   Order and Free Mobility

Metric planes endowed with both order and free mobility are, historically speaking, at the origin of the term absolute, coined by J. Bolyai. They are the models of the plane axioms of the groups I, II, and III (of incidence, order, and congruence) in the second and in all later editions of Hilbert’s Grundlagen der Geometrie. One of the greatest achievements of the reflection-geometric foundation of geometry has been the algebraic characterization of the models of these planes, also called Hilbert planes . It happens to be a very useful characterization, in the sense that one can often accomplish much more and much easier with the algebraic description than with synthetic geometry.

Let K be again a field of characteristic ${\ne }2$, and k an element of K, to be referred to as the orthogonality constant (or the metric constant). By the affine-metric plane $\mathfrak {A} (K, k)$ (cf. [32, p. 215]) we mean the projective plane $\mathfrak {P}$(K) over the field K from which the line [0, 0, 1], as well as all the points on it have been removed (and we write $\mathfrak {A}(K)$ for the structure with the remaining point-set, the corresponding line-set, with their incidence and orthogonality relations), for whose points of the form (x, y, 1) we shall write (x, y) (which is incident with a line [u, v, w] if and only if $xu+yv+w=0$), together with a notion of orthogonality, the lines [u, v, w] and $[u', v', w']$ being orthogonal if and only if

$$\begin{aligned} uu' + vv' + kww' = 0. \end{aligned}$$

(3)

If K is an ordered field, then one can order $\mathfrak {A}(K)$ in the usual way.

The algebraic characterization of the Hilbert planes consists in specifying a point-set E of an affine-metric plane $\mathfrak {A}(K, k)$, which is the universe of the Hilbert plane. The Hilbert plane will thus inherit the order relation Z from $\mathfrak {A}(K)$. We can also define a notion of congruence of two segments $\mathbf{ab}$ and $\mathbf{cd}$, which will be given, in case $E \subset \mathfrak {A}(K, 0)$, by the usual Euclidean formula

$$ (a_{1} - b_{1})^{2} + (a_{2} - b_{2})^{2} = (c_{1} - d_{1})^{2} + (c_{2} - d_{2})^{2} $$

and, in case $E \subset \mathfrak {A}$(K, k) with $k\ne 0$, by

$$\begin{aligned} \frac{F(\mathbf{a},\mathbf{b})^{2}}{Q(\mathbf{a})Q(\mathbf{b})} = \frac{F(\mathbf{c},\mathbf{d})^{2}}{Q(\mathbf{c})Q(\mathbf{d})}, \end{aligned}$$

(4)

where

$$ F(\mathbf{x},\mathbf{y}) = k(x_{1}y_{1} + x_{2}y_{2}) + 1, Q(\mathbf{x}) = F(\mathbf{x},\mathbf{x}), \text{ and } \mathbf{x} = (x_{1}, x_{2}), \mathbf{y} = (y_{1}, y_{2}). $$

Let now K be an ordered Pythagorean field, R the ring of finite elements, i.e., $R = \{ x \in K \, :\, (\exists n \in \mathbf{N})\, |x| < n \}$ and P the ideal of infinitely small elements of K, i.e., $P = \{ 0 \} \cup \{ x \in K \, :\, x^{-1} \not \in R \}$. All Hilbert planes are isomorphic to a plane of the following three types:

Type 1 :

$E = \{ (a,b)\, :\, a, b \in M\} \subset \mathfrak {A} (K, 0)$, where M is an R-module $\ne (0)$;

Type 2 :

$E = \{ (a,b)\, :\, a, b \in M\} \subset \mathfrak {A}$(K, k) with $k \ne 0$, where M is an R-module $\ne (0)$ included in $\{ a \in K \mid ka^{2} \in P\}$, that satisfies the condition

$$ a \in M \Rightarrow ka^{2} + 1 \in K^{2}; $$

Type 3 :

$E = \{\mathbf{x} \, :\, Q(\mathbf{x}) > 0, Q(\mathbf{x}) \not \in J \} \subset \mathfrak {A} (K, k)$ with $k < 0$, where $J \subseteq P$ is a prime ideal of R that satisfies the condition

$$ ka^2 +1 > 0, ka^2 +1 \not \in J \Rightarrow ka^2 +1 \in K^2, $$

with K satisfying

$$ \{a \in K \, :\, ka^2 \in R \setminus P \} \ne \emptyset . $$

The meaning of k in this context can be best described by mentioning that its sign is the same as that of $\alpha +\beta +\gamma -\pi$, where $\alpha$, $\beta$, and $\gamma$ are the measures of the three angles of a triangle.

Thus, a Hilbert plane is either (i) a part of an ordered Euclidean plane with free mobility (Type 1), thus a plane of Dehn-type, as these were first described in [16], or (ii) an infinitely small neighborhood of the origin in a plane with an arbitrary orthogonality constant, or (iii) a generalized Beltrami-Cayley-Klein model, consisting of the interior of a circle, with, possibly, an infinitely small collar around its circumference removed.

This characterization, due to Pejas [71], may be considered to be one of the most impressive early applications of the reflection-geometric approach. It may look strange that a first-order theory (the geometry of Hilbert planes) has models that require second-order notions (such as R and P which occur in the representation theorem) for their description. These models can, indeed, be expressed completely inside first-order logic, but we chose the original expression of Pejas for its intuitive character.

2.6 2.6   Methodological Reflections

One may, at this point, ask what is gained by this approach, other than Pejas’s representation theorem, which answered an existing open question. Do metric planes, in themselves, have an interesting geometry, the way Riemannian manifolds have?

There are, indeed, a wide variety of universal statements $\sigma$, expressed solely in terms of incidence, orthogonality, and segment congruence, that are commonly encountered as theorems in Euclidean geometry, and which turn out to be either true in all metric planes or else logically equivalent to E1 (i.e. we have either ${\mathcal M}\vdash \sigma$ or ${\mathcal M}\vdash \sigma \leftrightarrow \mathbf{E1}$). In the first category we have the theorem stating the concurrence of the altitudes of a triangle (a concurrence re-interpreted to mean that the composition of the reflections in the three altitudes is a line-reflection¹⁶)— in fact, less is needed for that theorem, as shown in [6]—and the one stating that the medians of a triangle lie in a pencil. In the same category is the theorem stating that a triangle with two congruent medians is isosceles (see [69]). These theorems are significantly harder to prove inside the theory of metric planes than inside Euclidean geometry. However, their proofs reveal the true reasons for the validity of these theorems, which their better-known proofs in an affine setting obscure.

In the second category, that of statements equivalent to E1, we have, as shown in [66], the statement that, in a non-isosceles triangle ABC, with $AB\not \equiv AC$, with M, N and P the midpoints of AB, AC, and BC respectively, and R the midpoint of MN, the points A, R, and P are collinear. In the “not yet decided” category is a theorem that raised Hilbert’s interest (see [68]), called Three Chord Theorem. It states that, if three circles pairwise intersect in two points, then the three lines joining those two points (to be referred in the sequel as “chords”) lie in a pencil. It probably belongs to the first category, theorems true in ${\mathcal M}$. What is important, though, is the profoundly changed nature of the questions asked. Whereas previously the question was whether a statement $\sigma$ holds in Euclidean geometry, or, more generally holds in ${\mathcal M}\cup \{\text{ E1 }\}$, the question is now whether that statement is one of metric geometry or whether its validity is characterizing the Euclidean nature of the metric of the metric plane. There is no theorem stating that a purely metric universal statement $\sigma$, true in Euclidean geometry, must be in one of the two categories. It just so happens that this is the case for all known instances in which the question has been answered.

If we are presented with a universal statement $\sigma$, true in Euclidean geometry, but involving order, then there are more options. One of them is that the statement holds without additional assumptions regarding the nature of the metric. In that case, an additional question arises, namely whether the statement is true in all ordered metric planes, or whether it holds only inside all standard ordered metric planes, which are those in which the foot of the altitude to the hypotenuse of a right triangle always lies between the endpoints of the hypotenuse. While the number of universal statements involving both order and metric notions known to be true in Hilbert planes is large, there are very few known to hold in all ordered metric planes. A version of the Steiner-Lehmus theorem holds in all standard metric planes, as shown in [69]. It is very likely that all universal statements that hold in all Hilbert planes are true in all standard ordered metric planes, but no such theorem has been proved. Candidates for sentences that are likely true in all ordered metric planes are: (i) Urquhart’s theorem, usually referred to as “the most ‘elementary’ theorem of Euclidean geometry” (see [70, 110]), when stated as a universal sentence; (ii) Gergonne’s theorem, stating that the lines joining the vertices of a triangle with the points of tangency of the inscribed circle are concurrent; (iii) the Steiner-Lehmus theorem. A candidate for a universal statement which, given the theory of ordered metric planes, is equivalent to E1, is Morley’s trisector theorem.

Another option is that $\sigma$ holds in some Hilbert planes and not in others. For example, its validity may depend on the sign of the orthogonality constant k, as is the case of the Erdős-Mordell inequality, whose validity is equivalent to the statement that $k\le 0$ (as shown in [65]). Or it may hold only in planes of Type 1 and 2, as is the case with the universal statement equivalent to Bachmann’s Lotschnittaxiom (“A quadrangle with three right angles closes,” see [5]), stated in [58]. Yet the change in perspective is the same as in the case of metric planes without order. Instead of asking for the truth of a certain statement, we are asking for its relative strength vis-à-vis the theory of ordered metric planes, for its strength as a hypothesis, in case it is not a theorem holding in all ordered metric planes.

2.7 2.7   Generalizations of Metric Planes

There are even more general notions than that of a metric plane, in which the above questions can be asked. The weakest is that of a generalized metric plane, whose properties are analyzed in [7, §2,4–5], and which can be considered as axiomatized by the axioms O1–O9 (so no form of the three reflections axiom is assumed). Hardly any theorem of interest holds in them, although it is not easy to prove that a certain theorem does not hold in generalized metric planes, given that there is no useful description of their models. The theorem stating that the altitudes of a triangle lie in a pencil is known not to hold in them, as it is equivalent to the validity of the three reflections theorem for lines with a common perpendicular, as shown in [6]. Generalized metric planes that do satisfy the three reflections theorem for lines with a common perpendicular, referred to in [9] as semi-absolute planes, are the next stage in the hierarchy of generalizations of metric planes. It is not easy to determine which particular theorems that hold in metric planes already do so in semi-absolute planes.

Another generalization is that of the Hjelmslev planes, in which both the existence and the uniqueness of the line joining two points may be omitted. Their properties have been studied in [8] and they are reasonably well understood. Closely related are the plane Cayley-Klein geometries, that we will turn to in Sect. 6. A further generalization, to pre-Hjelmslev groups, can be found in [78] (see also [45]).

An independent level of generalization is that of the S-planes, introduced by Lingenberg, which are based on a certain relaxation of the three reflections axiom. Their properties were presented in monograph form in [48], and most theorems valid in metric planes, sometimes with slight modifications, hold in S-planes as well.

3 Higher-Dimensional Metric Spaces

The question regarding higher-dimensional analogues of metric planes was first raised for the 3-dimensional case. The first reflection-geometric axiom system, in the style of ${\mathcal M}$, was put forward in [1]. One in the style of the O-axioms in Sect. 2.2, in terms of points, planes, point-plane incidence, plane orthogonality, and reflections in planes, logically equivalent to that in [1], was put forward in [79].

Ahrens’s [1] axiom system has been extended by Kinder [40] to one for n-dimensional metric spaces, for any $n\ge 2$. In analogy to the 2-dimensional case, their models can be embedded in projective-metric n-dimensional spaces, where the metric is given, again, by a symmetric bilinear form. We will no longer write its axioms in symbolic language, as it is by now plain how the English of the axiom systems expressed inside group theory with a distinguished set of generators can be translated into first-order logic, provided that every element of the group can be written as the composition of an a priori bounded number of generators.

The fundamental assumption of n-dimensional metric geometry thus on (G, S) is that G is a group (written multiplicatively) and that S is a set of involutory elements of S which generates G, and such that $bab\in S$, for all $a,b\in S$. The elements of S will be denoted by lowercase Latin letters and will be called reflections in hyperplanes (also referred to simply as hyperplanes). As before, we will write, for any two involutory elements of G, $\alpha$ and $\beta$, $\alpha \! \mid \! \beta$ whenever $\alpha \beta$ is involutory. We also write $\alpha _{11}, \ldots \alpha _{1n_1} \! \mid \! \alpha _{21},\ldots , \alpha _{2n_2}\! \mid \!\ldots \! \mid \! \alpha _{m1}, \ldots \alpha _{mn_m}$ to mean that, for all $i<k$, we have $\alpha _{ij}\! \mid \! \alpha _{kl}$. An involutory product $a_1a_2\ldots a_n$, with $a_1\! \mid \!a_2\! \mid \!\ldots \! \mid \!a_n$ will be referred to as a point reflection (or simply as a point), and will be denoted by uppercase Latin letters. In addition to the fundamental assumption, Kinder postulates the following:

K 1 :

Given $a_1,\ldots a_{n-1}, A$, there is an a such that $a\! \mid \! a_1,\ldots , a_{n-1}, A$.

K 2 :

Given $a_1,\ldots a_{n-2}, A, B$, with $a_1\! \mid \! \ldots \! \mid \! a_{n-2}\! \mid \! A, B$ there is an a such that

      $a\! \mid \! a_1,\ldots , a_{n-2}, A, B$.

K 3 :

If $a_1\! \mid \!\ldots \! \mid \! a_{n-2} \! \mid \! a, b \! \mid \! A, B$, then $a=b$ or $A=B$.

K 4 :

Given $a_1,\ldots a_{n-2}, A, a,b,c$, with $a_1\! \mid \! \ldots \! \mid \! a_{n-2}, A \! \mid \! a,b,c$ and $a_{n-2}\ne A$,

      there is a d with $ab=dc$.

K 5 :

Given $a_1,\ldots a_{n-1}, a,b,c$, with $a_1\! \mid \!\ldots \! \mid \! a_{n-1} \! \mid \! a,b,c$, there is a d with

      $ab=dc$.

K 6 :

There are n hyperplane reflections $a_1,\ldots a_{n}$ with $a_1\! \mid \!\ldots \! \mid \! a_{n}$.

K 7 :

Given $a_1,\ldots a_{n}$, with $a_1\! \mid \!\ldots \! \mid \! a_{n}$, there is an a with $a\! \mid \! a_1,\ldots , a_{n-1}$,

   as well as $a\ne a_n$ and $a\!\not \mid \!a_n$.

For $n=2$ this axiom system is equivalent to ${\mathcal M}$, and for $n=3$ to the axiom system of Ahrens.

As in the 2-dimensional case, one can add additional axioms to specify the nature of the metric (i.e., the nature of the symmetric bilinear form). Thus two hyperplanes a and b will be called non-connectable if there is neither a point A with $A \! \mid \! a,b$, nor a line $\varGamma$ with $\varGamma \! \mid \! a,b$. Here a line is a product $a_1\ldots a_{n-1}$ of $n-1$ many hyperplanes, with $a_1\! \mid \! \ldots \! \mid \! a_{n-1}$.

Among the additional axioms we have

$\mathbf{P}_n$ :

(Existence of a polar simplex) There are $a_1,\ldots a_{n+1}$, with $a_1 \! \mid \! \ldots \! \mid \! a_{n+1}$.

$\mathbf{E}_n$ :

(Existence of a rectangle) There are $a_1,\ldots a_{n-2}, a,b,c,d$, with

   $a_1\! \mid \! \ldots \! \mid \! a_{n-2}\! \mid \! a,b \! \mid \! c,d$.

$\mathbf{H}_n$ :

(The hyperbolic metric axiom) There are non-connectable hyperplanes.

$\mathbf{C}_n$ :

(The completeness axiom) If $a_1 \! \mid \! \ldots \! \mid \! a_{n-2} \! \mid \! a, b_1,b_2, b_3, P$, as well as

$b_1, b_2, b_3 \! \mid \! P$, and, for $i=1,2,3$, the hyperplanes a and $b_i$ are

non-connectable, then one of $b_1= b_2$, $b_2=b_3, b_3=b_1$ must hold.

In the presence of the fundamental assumption, of K1–K7 (the models of which will be referred to as n-dimensional metric spaces) and of $\mathbf{C}_n$: (i) adding $\mathbf{E}_n$ we get n-dimensional Euclidean geometry¹⁷; (2) adding $\mathbf{H}_n$ we get n-dimensional hyperbolic geometry; (3) adding $\mathbf{P}_n$ we get n-dimensional elliptic geometry (which has received an alternative axiomatization in [41]). These names are meant to express the fact that these are the n-dimensional generalizations of the 2-dimensional cases presented in Sects. 2.1.1–2.1.3 (the hyperbolic case being the n-dimensional generalization of Klingenberg’s generalized hyperbolic geometry, in which, just like in the 2-dimensional case, the coordinate fields needs only be ordered). More on these geometries and those obtained in the absence of $\mathbf{C}_n$, as well as models of n-dimensional Euclidean geometries, are found in [39].

As in the 2-dimensional case, these metric spaces can be seen as subspaces of projective-metric spaces, but, just like in the 2-dimensional case (if not more so), the question of describing algebraically the possible point-sets of metric spaces within the projective-metric space is hopeless.

In the important special case in which we add free mobility axioms, the order axioms Z1–Z8, as well as Peano’s form of the Pasch axiom (which asks that a line l that intersects the extension of side AB of a triangle ABC in D, with Z(ABD), and side BC in E, must also intersect side AC in a point F) to the axiom system for metric spaces, the models are, as shown by Klopsch [44], similar to the models in Pejas’s [71] characterization of models of Hilbert planes. A more in-depth analysis of the Umkehrproblem for metric spaces can be found in [30].

The question we raised in the 2-dimensional case, regarding the revolutionary nature of this approach, the complete change of perspective, is best illustrated with two examples.

The first looks at the following theorem of 3-dimensional Euclidean geometry: “The points of tangency of a skew quadrilateral, whose sides are tangent to a sphere, are co-planar.” This statement is, as can be easily seen, one of the 3-dimensional metric space axiomatized by Ahrens and Scherf (and the $n=3$ case of Kinder’s axiom presented above). It is likely that it holds in all 3-dimensional metric spaces.

The second example looks at a problem requiring order besides metric notions for its statement. The problem of the thirteen spheres in Euclidean three-space, going back, as a conjecture, to Newton (and a disagreeing Gregory), states that the largest number of non-overlapping unit spheres that can be arranged such that they each touch another given unit sphere is 12. This is also called the kissing number in dimension 3. It was proved in [91] (see also [49]). There are two statements the problem makes: (i) that there are 12 non-overlapping unit spheres that can be arranged such that they each touch another given unit sphere, and (ii) that no 13 non-overlapping unit spheres can be arranged such that they each touch another given unit sphere. A similar question, known as the kissing number problem, can be asked in any finite dimension, and the precise values are known only for $n=4, 8, 24$. This problem can, in any dimension, be stated inside the theory of ordered metric spaces, raising the question: “In which 3-dimensional metric spaces is the kissing number 12?” Similarly for higher dimensions. It is very likely that (ii) does not hold in the hyperbolic case. One can see this by reasoning along the following lines: in three-dimensional hyperbolic space over the real numbers, (ii) is certainly false, as can be seen from the Pizzetti-Toponogov triangle comparison theorem, which states that if O is the center of the original unit sphere ${\mathfrak U}$ and A and B two points of tangency of outside spheres with ${\mathfrak U}$, and $A'$ and $B'$ the reflections of O in A and B respectively, then the distance between $A'$ and $B'$ is greater in hyperbolic space than in Euclidean space, and the difference can be made very large by choosing a large “unit.” One expects this kind of behavior to be present in the much more austere world of ordered metric spaces satisfying $\mathbf{H}_3$. So, the question would become: “what is part (ii) of the thirteen sphere problem equivalent to?” Is it $\lnot \mathbf{H}_3$? Does part (i) hold in all ordered metric spaces? This is by no means trivial, as the “sphere” in our 3-dimensional metric spaces may have far fewer points on its “surface” than in the real Euclidean case.

A generalization of n-dimensional metric spaces along the lines of Lingenberg’s generalization of metric planes was carried out for $n=3$ in [55] and for all $n\ge 2$ in [56].

There are generalizations of metric spaces, in which, just like in the 2-dimensional case, one asks only for basic orthogonality axioms and for the existence of reflections, but no three-reflections theorem. They can be obtained in the 3-dimensional case by dropping the three-reflections axiom in Scherf’s axiom system. In the dimension-free case, to which we turn, they were considered in [95].

4 The Dimension-Free Case

What if we do not want to specify the dimension of the space, but just know that it is at least 2?

This question was first raised and answered by Smith [93, 94], in the synthetic tradition—with point, lines, planes, incidence, line-orthogonality, reflections in points and in lines as primitive notions—by extending the work of Lenz [47] on incidence and orthogonality. Later, Smith [97], provided another synthetic axiom system for the non-elliptic case in terms of points, orthocomplemented hyperplanes, incidence and orthogonality as primitive notions.

The reflection-geometric approach was provided by Ewald’s [19] axiom system for the groups of motions of such spaces, in terms of point-reflections and line-reflections. He showed that those geometries can be embedded in projective-metric spaces. Alternative embeddings were provided in [22, 23]. Ewald’s axiom system was simplified by Heimbeck [29], and it is that axiom system that we present here.

The fundamental assumption is this time that ${\mathfrak G}$ is a group with invariant complexes ${\mathfrak P}$ and ${\mathfrak L}$ of involutions, which together generate ${\mathfrak G}$.

Here, by “invariant” we mean that, for all $g\in {\mathfrak G}$, $p\in {\mathfrak P}$, $l\in {\mathfrak L}$, we have $g^{-1}pg\in {\mathfrak P}$ and $g^{-1}lg\in {\mathfrak L}$. The elements of ${\mathfrak P}$ are called “points” (or “point-reflections”), those of ${\mathfrak L}$ “lines” (or “line-reflections”), the former to be denoted by upper-case Latin letters, the latter by lower-case Latin letters. The sign $\mid$ has the same meaning as before, and we say that line g connects the distinct points P and Q if and only if $P,Q \! \mid \! g$ and $X\! \mid \!P,Q \Rightarrow g^{-1}Xg=X$. We say that P is incident with g (and write $P\,$ I $\,g$) if and only if g connects P with a point $Q\ne P$. We say that line g is “orthogonal” to line h (and write $g\perp h$) if and only if $g \!\mid \, h$ and there is a point P incident with both g and h. We say that the lines g, h, and k lie in a pencil if and only if ghk is a line and there is a point P incident with each of g, h, k, and ghk. We denote by $\langle P, g\rangle$ the set of points X for which $X=P$ or else g connects P and X. We denote by $\langle Pg\rangle$ the set of points X for which $X \! \mid \! Pg$. The axioms are:

E-H 1 :

Any two distinct points P and Q have a unique line (P, Q) connecting them.

E-H 2 :

If P, Q, R, and S are four different points, and if (P, Q), (P, R), (P, S)

lie in a pencil, then so do (R, Q), (R, P), (R, S).

E-H 3 :

For all Q with $Q\not \in \langle P,g\rangle$ there is a point $R\in \langle P, g\rangle$, with $(Q,R)\perp g$.

E-H 4 :

If Q and R belong to $\langle P,g\rangle$, then PQR is a point.

E-H 5 :

If $P\,$ I $\,g$, then $\langle P,g\rangle \cap \langle Pg\rangle =\{P\}$.

E-H 6 :

There are three different lines. There are three different points incident

with every line.

One gets an axiom system for elliptic geometry by stipulating that

Ell :

There are different points P and Q with $PQ=QP$.

To get an axiom system equivalent to that of Ewald one needs an additional axiom,

E-H 7 :

If $P\,$ I $\,g$, $P'\,$ I $\,g'$, $\langle Pg\rangle =\langle P'g'\rangle$, then $Pg=P'g'$.

If these geometries satisfy an additional, quite technical axiom, stated in [25], whose intuitive meaning is very simple, namely that all the points should not lie in a finite-dimensional subspace of the entire space, then ${\mathfrak G}$ is isomorphic to a subgroup of a projective-metric space. In the absence of that axiom, the same can be said only about a factor group of ${\mathfrak G}$.

In the dimension-free elliptic case, a mixed synthetic and reflection-theoretic axiom system can be found in [96], and another reflection-theoretic one in [24].

Axiom systems for the dimension-free Euclidean case can be found in [85, 86].

A broad generalization of the concept of (dimension-free) metric geometry has been proposed by E. M. Schröder in [87, 88].

5 Projective-Metric Geometry

5.1 5.1   Projective-Metric Planes

A projective plane is a triple $(\mathcal {P}, \mathcal {L}, \mathrm {I})$, consisting of a set $\mathcal {P}$ of points, a set $\mathcal {L}$ of lines, and a (symmetric) incidence relation I, with the property that any two distinct points are incident with a unique line and any two distinct lines are incident with a unique point. The only existence assumption it must satisfy is that it contains a quadrangle and a quadrilateral.

Plane projective geometry enjoys the property referred to as the principle of duality: Every definition remains valid and every theorem remains true if we consistently interchange the words “point” and “line” (the incidence relation being symmetric, it is self-dual, and thus need no change).

Central problems of the foundations of geometry, such as the introduction of numbers and the role of three-dimensional space for plane geometry, find conclusive answers in the projective setting. A projective plane can be coordinatized by a skew field (resp. a commutative field) of characteristic ${\ne }2$ if and only if the configuration theorem of Desargues (resp. Pappus) and the Fano axiom hold. A projective plane is embeddable in a projective space (of dimension ${\ge }3$) if and only if the theorem of Desargues holds.

Introduction of a metric.

In a projective plane $(\mathcal {P}, \mathcal {L}, \mathrm {I})$ a metric can be introduced by an orthogonality relation on the set of lines (which we denote by a, b, ...) and on the set of points (which we denote by A, B, ...). Let $\perp$ be a binary relation on $\mathcal {L}$ with $a \perp b$ to be read as “a and b are orthogonal lines” and let $\top$ be a relation on $\mathcal {P}$ with $A \top B$ to be read as “A and B are orthogonal (or polar) points.”

A point A is a pole of a line a if every line through A is orthogonal to a. Dually, a line b is a polar of a point B if every point on b is polar to B.

Following Struve and Struve [104], we call $(\mathcal {P}, \mathcal {L}, \mathrm {I}, \perp , \top )$ a projective-metric plane if the following axioms and the dual ones (which we do not explicitly state) hold:

PM1. :

Every line a has a pole A.

PM2. :

Every triangle has altitudes which intersect in a common point.

PM3. :

A point A is the pole of a line a if and only if a is the polar of A.

PM4. :

There are lines a, b with $a \not \perp b$ and points A, B with $A \not \!\!\top B$.

To get the dual axioms, just interchange the words point and line and the relations $\perp$ and $\top$. Notice that the axioms PM3 and PM4 are self-dual.

Given that the axiom system is self-dual (i.e., it contains the dual of each of its axioms), the principle of duality can be extended to projective-metric geometry: every definition remains valid, and every theorem remains true, if we consistently interchange the words “point” and “line” and the relations $\perp$ and $\top$.

There are seven types of projective-metric planes. They can be classified based on the properties of the following sets: (i) the set $\mathcal {L}_{r}$ of radical lines (which are orthogonal to every line), (ii) the set $\mathcal {L}_{i}$ of isotropic lines (which are orthogonal to themselves), (iii) the set $\mathcal {P}_{r}$ of radical points (which are polar to every point), and (iv) the set $\mathcal {P}_{i}$ of isotropic points (which are polar to themselves):

(1):

planes with an elliptic metric: $\mid \!\! \mathcal {L}_{r}\!\!\mid = 0$ and $\mathcal {L}_{i} = \mathcal {L}_{r}$;

(2):

planes with a hyperbolic metric: $\mid \!\! \mathcal {L}_{r}\!\!\mid = 0$ and $\mathcal {L}_{i} \ne \mathcal {L}_{r}$;

(3):

planes with an Euclidean metric: $\mid \!\! \mathcal {L}_{r}\!\!\mid = 1$ and $\mathcal {L}_{i} = \mathcal {L}_{r}$;

(4):

planes with a Minkowskian metric: $\mid \!\! \mathcal {L}_{r}\!\!\mid = 1$ and $\mathcal {L}_{i} \ne \mathcal {L}_{r}$;

(5):

planes with a co-Euclidean metric: $\mid \!\! \mathcal {L}_{r}\!\!\mid \ge 2$ and $\mathcal {P}_{r}\!\!\mid \le 1$ and $\mathcal {P}_{i} = \mathcal {P}_{r}$;

(6):

planes with a co-Minkowskian metric: $\mid \!\! \mathcal {L}_{r}\!\!\mid \ge 2$ and $\mathcal {P}_{r}\!\!\mid \le 1$ and $\mathcal {P}_{i} \ne \mathcal {P}_{r}$;

(7):

planes with a Galilean metric: $\mid \!\! \mathcal {L}_{r}\!\!\mid \ge 2$ and $\mathcal {P}_{r}\!\!\mid \ge 2$.

Algebraic models.

Every projective-metric plane can be represented as a projective-metric coordinate plane $\mathfrak {P}(K,\mathfrak {f})$ over a field K of characteristic ${\ne }2$ and a (non-trivial) symmetric bilinear form f. If V is a three-dimensional vector space over K and f a non-null symmetric bilinear form on V, then elements $\textit{x}$ and $\textit{y}$ of V are called orthogonal if $f(\textit{x}, \textit{y}) = 0$. If T is a subspace of V, then $T^{\perp } = \{\textit{x} \in V: f(\textit{x}, \textit{y}) = 0$ for all $\textit{y} \in T\}$ is a subspace of V; subspaces $T_{1}$ and $T_{2}$ are called orthogonal, which we denote by $T_1\vdash T_2$, if $T_{1} \cap T_{2}^{\perp } \ne \{\textit{o}\}$ and $T_{1}^{\perp } \cap T_{2} \ne \{\textit{o}\}$, where $\textit{o}$ stands for be the null vector.

$(\mathcal {P}, \mathcal {L}, \mathrm {I}, \perp , \top )$ is a projective-metric coordinate plane if

• $\mathcal {P}$ is the set of all i-dimensional subspaces of V with $i \in \{1, 2\}$;

• $\mathcal {L}$ is the set of all j-dimensional subspaces of V with $j \in \{1, 2\}$ and $j \ne i$;

• $\mathrm {I}$ is the set-theoretic inclusion restricted to $(\mathcal {P} \times \mathcal {L}) \cup (\mathcal {L} \times \mathcal {P})$;

• $\perp$ is the relation $\vdash$ restricted to $\mathcal {L} \times \mathcal {L}$;

• $\top$ is the relation $\vdash$ restricted to $\mathcal {P} \times \mathcal {P}$.

The seven types of projective-metric planes correspond to different dimensions of the radical and of the Witt index of the vector space V.

5.2 5.2   Projective-Metric Spaces of Arbitrary Finite Dimension

There are various ways to axiomatize projective geometry of higher dimensions. Veblen’s classical axiomatization [112] is based on the terms of “point” and “line” and a binary relation of incidence. Inside that setting, higher dimensional subspaces are defined as sets of points.

We will follow Menger [50, 51], who noticed that projective geometry can be considered as a theory about joins and meets of linear subspaces (Geometrie des Verbindens und Schneidens). He axiomatized projective spaces in a first-order language with one sort of individual variables, to be referred to as “subspaces” or “flats” and denoted by lowercase Greek letters, two binary operations $\vee$ and $\wedge$, called “join” and “meet”, and two constant symbols $\textsf {0}$ and $\textsf {1}$, which are called “element zero” and “element one”.

The axioms are simple postulates about the joining and intersecting of geometric subspaces. They state that the operations $\vee$ and $\wedge$ are commutative and associative with neutral elements 0 and 1, and that the absorption laws hold. The models of this axiom system, $\mathcal {L} = (\textsf {L}, \vee , \wedge , \textsc {0}, \textsc {1})$, are lattices with $\textsf {0}$ and $\textsf {1}$.

To characterize projective spaces of dimension $n \ge 3$, one needs to add to the above-mentioned axioms the requirements that the lattice $\mathcal {L}$ be complemented and irreducible and that the maximal length of a chain of $\mathcal {L}$ be $n + 1$. In an algebraic language this can be summarized by the statement that $\mathcal {L}$ is an irreducible projective lattice.

The dual of each axiom holds, so the principle of duality holds in projective-metric geometry of arbitrary finite dimension.

The notion of a “point”, which is the basic concept of analytic geometry and particularly of Riemannian geometry, is not even mentioned in the axiom system. The complete elimination of the notion of point from geometry was one of the ideas of von Neumann’s continuous geometries.

In complete harmony with Euclid’s first words in the Elements, “A point is that which has no part”, the elements $\alpha$ of $\mathcal {L}$ for which $\varepsilon \le \alpha \rightarrow \varepsilon =\textsc {0}$ are called “points” of a projective space (i.e., the points are precisely the atoms of the projective lattice).

Since points and lines are no longer distinguished from subspaces of other dimensions, the sentences of projective geometry are statements about finite sets of elements of the basic class of subspaces, without any need for either a multi-sorted language or of set-theoretical definitions of subspaces. Unlike the first modern axiomatizations of geometry, by Pasch, Peano, Pieri, and Hilbert, which were expressed in languages which contained only relation symbols, but no operation symbol, the above axiomatization, with two operation symbols and no relation symbol, is much closer in spirit to those of arithmetic or of algebraic theories.

Algebraic models.

Every projective space of dimension $n \ge 3$ can be represented as the lattice of subspaces of a finite dimensional vector space over a skew field (division ring) with the set-theoretic inclusion $\subseteq$ as $\le$-relation of the associated partially ordered set of subspaces.

Introduction of a metric.

Much like in the 2-dimensional case, in a projective space of dimension $n \ge 3$ a metric can be introduced by an orthogonality relation. The metric is called singular if there are radical subspaces and ordinary otherwise.

In the ordinary case, the orthogonality relation is a binary relation, which is defined on the set of hyperplanes (subspaces of dimension $n-1$) and on the set of points, and which satisfies mutatis mutandis the axioms for projective-metric planes noted in Sect. 5.1. The orthogonality relation can be described algebraically by a non-degenerate symmetric bilinear form which is a hyperbolic polarity if there are self-polar points, an elliptic polarity otherwise.

The classical example of a projective space with a singular metric is the projective closure of a Euclidean space. The orthogonality relation of Euclidean subspaces induces on the hyperplane $\varepsilon$ at infinity an elliptic metric (in the sense of Sect. 5.1).

In the general case, the hyperplane at infinity may as well be endowed with a hyperbolic metric (as in Minkowskian geometry) or with a Euclidean metric (as in a Galilean geometry)—to mention only two alternatives—and the subspace at infinity need not be a hyperplane but may be a subspace of arbitrary dimension.

This general situation is captured in the following definition which is formulated in an algebraical setting (an axiomatic definition can be given along the lines of Sect. 5.1). A metric in a projective space is given by a flag $0< \varepsilon _1< \ldots< \varepsilon _{r} < 1$ of subspaces and a (hyperbolic or elliptic) polarity on each of the associated intervals $[0,\varepsilon _1], ..., [\varepsilon _{r},1]$.

$(\mathcal {L}, ((\varepsilon _1, \pi _1),..., (\varepsilon _r, \pi _{r}), (1, \pi _{r+1})))$ with $r \ge 0$ is a projective space with Cayley-Klein metric (or Cayley-Klein space  for short) of dimension $n \ge 0$ if the following assumptions hold:

• (1) $\mathcal {L}$ is a projective lattice of finite dimension n.

• (2) $\varepsilon _1, ... , \varepsilon _{r}$ are subspaces of $\mathcal {L}$ with $0< \varepsilon _1< \ldots< \varepsilon _{r} < 1$.

• (3) $\pi _k$ is a hyperbolic or elliptic polarity on the interval $[\varepsilon _{k-1},\varepsilon _k]$ with $1 \le k \le r+1$ and $\varepsilon _0 = 0$ and $\varepsilon _{r+1} = 1$.

For notational convenience we denote a Cayley-Klein space by $\mathcal {CK}(\varepsilon _0, ..., \varepsilon _{r+1})$, if the underlying polarities $\pi _k$ are of no special concern. If $\mathcal {CK}(\varepsilon _0, ..., \varepsilon _{r+1})$ is a Cayley-Klein space, then the Cayley-Klein space $\mathcal {CK}(\varepsilon _i, ..., \varepsilon _k)$ (for $0 \le i < k \le r+1$) is called ordinary if $k = i + 1$ and singular otherwise.

That the principle of duality can be extended from projective geometry to projective-metric geometry (Cayley-Klein spaces) can be seen by noticing that the dual of an interval [$\varepsilon _{k-1}, \varepsilon _k$] of a projective lattice $\mathcal {L}$ is an interval of the dual projective lattice $\mathcal {L}^*$, and that the dual of a polarity (on an interval of $\mathcal {L}$) is a polarity (on an interval of $\mathcal {L}^*$).

Of special interest are Cayley-Klein spaces which are self-dual, i.e., isomorphic to their dual structures. $\mathcal {CK}(\varepsilon _0, ..., \varepsilon _{r+1})$ is self-dual if and only if $\mathcal {CK}(\varepsilon _k, \varepsilon _{k+1})$ and $\mathcal {CK}(\varepsilon _{r-k}, \varepsilon _{r+1-k})$ are isomorphic (for $0 \le k \le r$).

Every ordinary Cayley-Klein space is self-dual. Further examples are the projective closure of a Galilean plane over a field of characteristic ${\ne }2$ and the projective closure of the Desargues configuration which can be embedded in the projective plane with an elliptic metric over the field of order 5.

As mentioned in Sect. 5.1, there are seven Cayley-Klein spaces of dimension 2. There are eighteen Cayley-Klein spaces of dimension 3. For a detailed classification see Struve and Struve [106].

Metric concepts like the pole-polar-theory of quadratic spaces can be extended to Cayley-Klein spaces. A subspace $\beta$ is a polar of a subspace $\alpha$ if the projections of $\alpha$ and $\beta$ into the intervals $[\varepsilon _k, \varepsilon _{k+1}]$ ¹⁸ map $\alpha$ and $\beta$ onto polar elements of the ordinary Cayley-Klein spaces $\mathcal {CK}(\varepsilon _k, \varepsilon _{k+1})$.

If $\beta$ is a polar of $\alpha$, then $\alpha$ is a polar of $\beta$. In an n-dimensional Cayley-Klein space, the sum of the dimensions of a subspace and of its polar is equal to $n - 1$, a formula which is well known for projective spaces with an elliptic or a hyperbolic metric. Every subspace of a Cayley-Klein space has at least one polar. A subspace $\alpha$ with a unique polar is called regular. This is equivalent to the existence of an integer k with $\alpha \wedge \varepsilon _{k} = 0$ and $\alpha \vee \varepsilon _{k+1} = 1$.

Subspaces $\alpha$ and $\beta$ are orthogonal if there are subspaces $\alpha ^{*}$ and $\beta ^{*}$ which are polar to $\alpha$ respectively $\beta$ and satisfy $\alpha \le \beta ^{*}$ and $\beta \le \alpha ^{*}$.

Let $\beta$ be a polar of $\alpha$ with $\alpha \wedge \beta = 0$ (i.e., let $\alpha$ and $\beta$ be complements). The harmonic homology $\sigma _{\alpha \beta }$ with $\alpha$ and $\beta$ as center and axis leaves the subspaces $\varepsilon _{k}$ invariant and induces an automorphism on $\mathcal {CK}(\varepsilon _k, \varepsilon _{k+1})$. Hence $\sigma _{\alpha \beta }$ is an involution of the group of automorphism of the Cayley-Klein space which we call a (projective) reflection in $\alpha$ respectively $\beta$. The group which is generated by all reflections $\sigma _{\alpha \beta }$ is called the group of motions.

This highlights the special role of reflections in projective geometry: They can be used to single out motions within the group of all projective collineations.

Bachmann (see [7, §20,11]) carried this idea a step further. He showed that projective-metric geometry can be formulated in the group of motions of a projective-metric space (a quadratic space). Geometric relations like incidence and orthogonality correspond to group-theoretical relations between elements of the group of motions (e.g., projective subspaces are orthogonal respectively incident if the product of the associated reflections is involutory). This correspondence allows not only the proof of geometric theorems by group-theoretical calculations but also group-theoretical characterizations of orthogonal groups (see Bachmann [7, §20,8 and §20,11]).

The full group $\mathcal {G}$ of projective automorphisms of a Cayley-Klein space has been analyzed in Struve and Struve [107]. In the ordinary case, $\mathcal {G}$ can be represented as the orthogonal group of the associated quadratic space.

In the singular case, an element $\varphi$ of $\mathcal {G}$ is called a dilatation ¹⁹ if $\varphi$ is the identity on the ordinary Cayley-Klein spaces $\mathcal {CK}(\varepsilon _k, \varepsilon _{k+1})$ with $0 \le k \le r$. The group of dilatations is a normal subgroup of $\mathcal {G}$.

Every element of $\mathcal {G}$ is up to a dilatation uniquely determined by its operation on the ordinary Cayley-Klein spaces $\mathcal {CK}(\varepsilon _k, \varepsilon _{k+1})$, and conversely every automorphism of a Cayley-Klein space $\mathcal {CK}(\varepsilon _k, \varepsilon _{k+1})$ can be extended to an element of $\mathcal {G}$ (in a trivial way). Hence the group $\mathcal {G}$ is the semi-direct product of the (normal) group of dilatations and the subgroup of $\mathcal {G}$ which is generated by the (extensions) of the automorphisms of the Cayley-Klein spaces $\mathcal {CK}(\varepsilon _k, \varepsilon _{k+1})$.

This representation theorem of $\mathcal {G}$ generalizes theorems which are well-known in metric affine geometry (i.e., in Euclidean, Minkowskian, and Galilean geometry).

6 Cayley-Klein Geometries

In the approach of Cayley and Klein non-Euclidean geometries are introduced as geometries living inside of a projective space which is endowed with a projective metric.

Following this approach we consider in this section real projective spaces, which are endowed with a Cayley-Klein metric, and single out substructures which define Cayley-Klein geometries.

Following Klein, these substructures are called Eigentlichkeitsbereiche ²⁰ and the associated points, lines, planes etc. “proper subspaces”. Geometric relations such as incidence and orthogonality are inherited from the associated Cayley-Klein space.

There are different ways to distinguish substructures of a projective-metric space. Klein’s famous model of hyperbolic geometry, for example, is defined as a substructure of the real projective plane $\mathbf {P}^{\mathbf {2}}$, where a projective metric is given by a hyperbolic polarity $\pi$. Points of the hyperbolic plane $\mathbf {H}^{\mathbf {2}}$ are the points of $\mathbf {P}^{\mathbf {2}}$ which are interior to the “absolute conic” of self-conjugate points of $\pi$. Lines of $\mathbf {H}^{\mathbf {2}}$ are the lines of $\mathbf {P}^{\mathbf {2}}$ which are incident with at least one interior point. The projective reflections in points and in lines of $\mathbf {H}^{\mathbf {2}}$ generate the group of motions of $\mathbf {H}^{\mathbf {2}}$ (which is in fact isomorphic to the full group of automorphisms of $\mathbf {P}^{\mathbf {2}}$).

The set of points of $\mathbf {P}^{\mathbf {2}}$ which are exterior to the “absolute conic” of the polarity $\pi$ (any two of these points have according to Klein a real positive distance) are the set of points of the co-hyperbolic geometry (see Sect. 6.1).

This shows that to a given Cayley-Klein space there may exist several substructures which are Cayley-Klein geometries. Necessary conditions for a substructure to be an n-dimensional Cayley-Klein geometry are:

• (1) Subspaces with the same dimension are “of the same kind”.

• (2) The substructure contains with a subspace all subspaces which have the same dimension and which are of the same kind.

• (3) There is a flag which contains subspaces of dimension 0, 1, 2, ..., n.

A classification of subspaces of a Cayley-Klein space into elements “of the same kind” can be done in various ways. For example, in a projective space with a hyperbolic polarity—as in Klein’s model of a hyperbolic plane—the set of points is the union of the set of isotropic points (which form a conic $\kappa$) and the set of points which are internal resp. external with respect to $\kappa$. A point which is not incident with a tangent to $\kappa$ is an internal point. A point which is not an internal point and not on $\kappa$ is an external point. The geometric classification into internal and external points corresponds on the algebraic side to the distinction between points with signature 0 or 1 (signature²¹ of a point with respect to the bilinear form which describes $\kappa$).

Similarly, the set of lines is the union of the set of isotropic lines (tangents to $\kappa$) and the sets of lines which are incident with two resp. none of the points of $\kappa$ (secants and non-secants), a classification which corresponds on the algebraic side to the distinction between lines with signature 1 or 2.

Condition (2) ensures that a Cayley-Klein geometry is maximal with respect to the property which defines the classification of subspaces of equal dimension. So, in Klein’s model of a hyperbolic plane, every interior point of the absolute conic $\kappa$ is a point of the model.

According to condition (3), there is a chain of subspaces which contains elements of every dimension of the projective space. This ensures that the dimension of the Cayley-Klein geometry is n.

These considerations lead to the following model-theoretic definition of (real) ordinary Cayley-Klein geometries:

If $0< \alpha _{1}< ...< \alpha _{n} < 1$ is a maximal flag of subspaces of an ordinary Cayley-Klein space, then the set of subspaces $\beta$ which have the same dimension and signature as one of the elements $\alpha _{k}$ is the set of subspaces of a Cayley-Klein geometry.

The general (not necessarily ordinary) case can be reduced to the ordinary one since a Cayley-Klein space $\mathcal {CK}(\varepsilon _0, ..., \varepsilon _{r+1})$ is build up from the ordinary Cayley-Klein spaces $\mathcal {CK}(\varepsilon _k, \varepsilon _{k+1})$. This leads to the following general model-theoretic definition of (real) Cayley-Klein geometries :

If $0< \alpha _{1}< ...< \alpha _{n} < 1$ is a maximal flag of subspaces of a Cayley-Klein space $\mathcal {CK}(\varepsilon _0, ..., \varepsilon _{r+1})$ which contains $\varepsilon _0, ..., \varepsilon _{r+1}$ as subspaces, then the set of subspaces $\beta$ which have a polar with the same dimension and signature as one of the elements $\alpha _{k}$ is the set of subspaces of a Cayley-Klein geometry.

The dual structure of a Cayley-Klein geometry is a Cayley-Klein geometry, i.e., the principle of duality can be extended to metric geometry. So, for example, the dual geometry of n-dimensional hyperbolic geometry is co-hyperbolic geometry. Elliptic geometry is self-dual.

The number of real Cayley-Klein geometries of dimension n is $3^{n}$ (with $n \ge 1$). For a more detailed discussion of plane Cayley-Klein geometries we refer to Sect. 4. The number of real ordinary Cayley-Klein geometries of dimension n is $2^{n}$.

Cayley-Klein geometries have properties which are well known from Euclidean, hyperbolic and elliptic geometry: Every subspace $\alpha$ of a Cayley-Klein geometry is regular. There exists one and only one projective reflection $\sigma _{\alpha }$ in $\alpha$. The set of reflections $\sigma _{\alpha }$ generates the group of motions and the calculus of reflections allows the axiomatization and the coordinatization of a Cayley-Klein geometry.

Remark

This definition of a Cayley-Klein geometry is based on the algebraic notion of the signature of a subspace. This corresponds, as we indicated above, to geometric properties which are more complex (like a classification in interior and exterior points or in secants and non-secants) and which may depend on properties of the underlying field of coordinates. The algebraic notion of signature of a subspace allows, on the other hand, a simple definition, which only assumes that the field of coordinates allows the introduction of a half-order (i.e., of a homomorphism from the multiplicative group of K into the cyclic group $(\{1, -1\}, \cdot )$ of order two; see [108]). This is satisfied in particular by all fields which are orderable or of finite order. The concept of a Cayley-Klein geometry is hence not restricted to the real or complex case.

6.1 6.1   Plane Cayley-Klein Geometries

Let $\mathbf {P}_{3}(\mathbb {R})$ be the 3-dimensional projective space over the field of real numbers and $\mathcal {Q}$ a non-degenerate quadric of $\mathbf {P}_{3}(\mathbb {R})$, i.e., a quadric with the property that there exists a plane section which is a non-degenerate conic.

As is well known, up to projective equivalence, there are three quadrics of this kind, namely, the sphere, which has no generators (there are no lines lying entirely in the quadric), the cone, where every point (with the exception of the vertex) is incident with exactly one generator, and the ruled surface, where every point is incident with exactly two generators. The vertex of a cone is incident with all generators and is called a singular point.

We call a line g a secant (or secant line) of $\mathcal {Q}$ if g is incident with exactly two points of $\mathcal {Q}$. The line g is called a tangent (or a tangent line) of $\mathcal {Q}$ if g and $\mathcal {Q}$ have one and only one non-singular point of intersection.

A plane $\varepsilon$ is called a secant plane of $\mathcal {Q}$ if the points of intersection of $\varepsilon$ and $\mathcal {Q}$ are the points of a non-degenerate conic. The secant planes through a point A of the projective space can be divided into three classes, depending on whether they contain one, two or no tangent line to $\mathcal {Q}$.

In every secant plane $\varepsilon$ of $\mathcal {Q}$ there is a projective reflection, i.e., an involutory projective collineation leaving $\mathcal {Q}$ invariant, and $\varepsilon$ and the pole of $\varepsilon$ (with respect to $\mathcal {Q}$) pointwise fixed. In every secant line g of $\mathcal {Q}$ there is a projective reflection, i.e., an involutory projective collineation leaving $\mathcal {Q}$ invariant, and g and the polar of g (with respect to $\mathcal {Q}$) pointwise fixed.

With these concepts in mind we now give a model-theoretic characterization of all nine plane Cayley-Klein geometries.

$(\mathcal {P}, \mathcal {L}, \textit{G})$ is called a plane Cayley-Klein geometry if there is a point A and a non-degenerate quadric $\mathcal {Q}$ of $\mathbf {P}_{3}(\mathbb {R})$ and a number $n \in \{0, 1, 2\}$ such that

• $\mathcal {P}$ is the set of secant lines through A.

• $\mathcal {L}$ is the set of secant planes through A which contain n tangents to $\mathcal {Q}$.

• $\textit{G}$ is the group of projective collineations generated by reflections in the elements of $\mathcal {P}$ and $\mathcal {L}$ (restricted to $\mathcal {P} \cup \mathcal {L}$).

The elements of $\mathcal {P}$ are the points and the elements of $\mathcal {L}$ are the lines of the plane Cayley-Klein geometry. The incidence relation between points and lines is inherited from the projective space.

The elements of G are called motions. In each point A and in each line g of the plane Cayley-Klein geometry there exists a unique reflection, which is the restriction of the associated projective reflection in A (resp. g) to $\mathcal {P} \cup \mathcal {L}$.

Metric concepts can be defined in the following way: Two pairs (B, C) and (D, E) of points (which can be thought of as segments) are called congruent if there is a motion $\alpha$ with $B^{\alpha } = D$ and $C^{\alpha } = E$. Dually, two pairs (b, c) and (d, e) of lines (which can be thought of as angles) are called congruent if there is a motion $\alpha$ with $b^{\alpha } = d$ and $c^{\alpha } = e$.

The type of a plane Cayley-Klein geometry is a pair of natural numbers (m, n) with $m, n \in \{0, 1, 2\}$ where m denotes the number of generators through a non-singular point of the quadric $\mathcal {Q}$ and n the number of lines of the elements of $\mathcal {L}$ which are incident with A and tangent to $\mathcal {Q}$.

The value of m is 0, 1 or 2 depending on whether $\mathcal {Q}$ is a sphere, a cone, or a ruled surface. If A is a point of $\mathcal {Q}$ then $n = 1$. If A is an interior point of $\mathcal {Q}$ then $n = 0$ and if A is an exterior point then $n = 2$.

According to Struve and Struve [102] there are nine real plane Cayley-Klein geometries which are presented (name and type) in the following table.

$$ \begin{array}{c|c|c} elliptic &{} Euclidean &{} hyperbolic \\ (0, 0) &{} (0, 1) &{} (0, 2) \\ \hline co-Euclidean &{} Galilean &{} co-Minkowskian \\ (1, 0) &{} (1, 1) &{} (1, 2) \\ \hline co-hyperbolic &{} Minkowskian &{} doubly\, hyperbolic \\ (2, 0) &{} (2, 1) &{} (2, 2) \\ \end{array}$$

The points and lines of a plane Cayley-Klein geometry $(\mathcal {P}, \mathcal {L}, \textit{G})$ are lines and planes through a point A of a projective space $\mathbf {P}$. Hence $(\mathcal {P}, \mathcal {L}, \textit{G})$ can be extended to a projective ideal plane: ideal points are the lines through A, ideal lines are the planes through A, and the incidence relation is inherited from $\mathbf {P}$. The motions of a plane Cayley-Klein geometry (which are induced by collineations of $\mathbf {P}$, which have A as a fixed point) can be extended to collineations of the projective ideal plane.

To represent the points and lines of $(\mathcal {P}, \mathcal {L}, \textit{G})$ by points and lines of $\mathbf P$ we consider the intersection of the elements of $\mathcal {P}$ and $\mathcal {L}$ with a secant plane of $\mathcal {Q}$ which is not incident with A. In this way one gets Klein models of the Cayley-Klein geometries.

• 1. The Klein model of an elliptic plane is a projective plane.

• 2. The Klein model of a Euclidean plane is an affine plane.

• 3. The Klein model of a hyperbolic plane contains the interior points of a non-degenerate conic $\kappa$ and the lines which are incident with at least one interior point of $\kappa$.

• 4. The Klein model of a co-Euclidean plane is obtained from a projective plane by the removal of a point A and of all lines which are incident with A.

• 5. The Klein model of a Galilean plane is obtained from an affine plane by the removal of a pencil of parallel lines.

• 6. The Klein model of a co-Minkowskian plane contains exactly all points of an affine plane which lie between two parallel lines a and b as well as all lines which are not parallel to a or b.

• 7. The Klein model of a co-hyperbolic plane contains exactly the exterior points of a non-degenerate conic $\kappa$ and the lines which have no common point with $\kappa$.

• 8. The Klein model of a Minkowskian plane is obtained from an affine plane by the removal of two pencils of parallel lines.

• 9. The Klein model of a doubly hyperbolic plane contains exactly the exterior points of a non-degenerate conic $\kappa$ and the lines which are incident with at least one interior point of $\kappa$.

As mentioned above, in each point A and in each line g of a plane Cayley-Klein geometry there exists a unique reflection, which is the restriction of the associated projective reflection in A (resp. g) to $\mathcal {P} \cup \mathcal {L}$. This shows that metric geometry in the sense of Cayley and Klein can be formulated in the group of motions. For an axiomatization and coordinatization of plane Cayley-Klein geometries over fields of characteristic ${\ne }2$ we refer to Sect. 6.3.

The geometry of plane sections of a quadric $\mathcal {Q}$ is the circle geometry of Möbius, Laguerre or Minkowski depending on whether $\mathcal {Q}$ is a sphere, a cone, or a ruled surface. The points of the circle geometries are the non-singular points of $\mathcal {Q}$ and the circles are the plane sections of $\mathcal {Q}$. The points and lines of a plane Cayley-Klein geometry can be represented as point-pairs and circles of the above-mentioned circle geometries. The group of motions of a Cayley-Klein geometry is isomorphic to a group of circle transformations. In this way one gets Poincar $\acute{e}$ models of the Cayley-Klein geometries.

6.2 6.2   Finite Cayley-Klein Geometries

The model-theoretic characterization of plane Cayley-Klein geometry, given in Sect. 6.1, allows the transfer of Riemann’s idea of an elliptic plane to the realm of finite geometries.

In the 3-dimensional projective space over the finite field $\mathbf {GF(n)}$ of order n there exist three non-degenerate quadrics $\mathcal {Q}$ (i.e., quadrics with the property that there exists a plane section which is a non-degenerate conic): the sphere without generators, the cone with one generator through every point distinct from the vertex, and the ruled surface with two generators through every point of the quadric.

Let A be an arbitrary point of the projective space. The set of secant lines through A and the set of secant planes through A with n tangents to $\mathcal {Q}$ for a number $n \in \{0, 1, 2\}$ are the set $\mathcal {P}$ of points and the set $\mathcal {L}$ of lines of a plane Cayley-Klein geometry (if both sets are non-empty). The group of projective collineations generated by reflections in the elements of $\mathcal {P}$ and $\mathcal {L}$ (restricted to $\mathcal {P} \cup \mathcal {L}$) is the group of motions of the Cayley-Klein geometry.

As in the real case, there are nine plane Cayley-Klein geometries over any finite field of characteristic ${\ne }2$. Among these finite geometries there are well-known configurations: The configurations of Desargues, Pappus, and Petersen (with their groups of automorphisms) can be represented by the elliptic plane over $\mathbf {GF(5)}$, the Galilean plane over $\mathbf {GF(3)}$, and the hyperbolic plane over $\mathbf {GF(5)}$. This is in stark contrast to the theory of metric planes, presented in Sect. 2.1, for which there are finite models only in the case of the Euclidean metric, i.e., only if $\mathbf{E1}$ holds (see [7, §6,12]).

Every finite plane Cayley-Klein geometry can be represented as a Klein model and as a Poincaré model. For the number of points and lines of a finite Cayley-Klein geometry and a uniform representation of the groups of motions we refer to Struve and Struve [103].

6.3 6.3   Cayley-Klein Geometries and Reflection Geometry

According to the table (in Sect. 6.1) there are nine types of plane Cayley-Klein geometries. Elliptic, Euclidean, and hyperbolic planes are metric planes in the sense of Bachmann, which were characterized in Sect. 2.1.

For a characterization of all types of plane Cayley-Klein geometries, several aspects of Bachmann’s notion of a metric plane have to be broadened. The most important aspect is the principle of duality: the dual of a Cayley-Klein geometry is also a Cayley-Klein geometry.

Thus the set S of line reflections will no longer play a distinguished role in the group of motions G. S no longer needs to be a set of generators of G, and the set P of point reflections can no longer be defined as the set of involutions of $S^{2} = \{ab: a, b \in S\}$.

This corresponds to new geometric phenomena which are unknown in the setting of classical plane absolute geometry. In a Cayley-Klein geometry there may be motions which are involutions without being point or line reflections. A rotation which is not the identity (the product of the reflections in lines a and b with a unique point of intersection) may have several fixed points, and the product of the reflections in three lines a, b, c which are the sides of a non-degenerate triangle may be a line reflection.

On the other hand, well known axioms of classical plane absolute geometry, such as the uniqueness of a joining line, the existence of a perpendicular (in a self-dual form), and the three reflections theorems (in a dual form), continue to hold.

We generalize the axiom system for metric planes based on the following principles:

• The axiom system is satisfied by the metric planes of Sect. 2.1.

• The axiom system is satisfied by all types of plane Cayley-Klein geometries (for reasons of simplicity with the exception of the doubly hyperbolic case).

• The axiom system allows a formulation in a first-order language.

• The axioms are statements about points and lines with a direct geometric interpretation and without any non-geometric assumptions about the type or structure of the underlying group G (such as $Z(G) = 1$).

• The axiom system contains with each axiom the dual one.

(G, S, P) is called a Cayley-Klein group ²² if the following Basic Assumption and axioms hold (see [109])²³:

Basic Assumption Let G be a group and S and P invariant subsets of involutions of G such that

N 1 :

If $a \! \mid \! b$ then $ab \in P$.

N 2 :

If $A \! \mid \! B$ then $AB \in S$.

N 3 :

For every pair (A, b) there exists (a, B) with $a \! \mid \! A$ and $B \! \mid \! b$ and $Aa = bB$

and if $A \ne b$ then (a, B) is unique.

N 4 :

If $A, B \! \mid \! c, d$ then $A = B$ or $c = d$.

N 5 :

If $A, B, C \! \mid \! d$ then $ABC \in P$.

N 6 :

If $a, b, c \! \mid \! D$ then $abc \in S$.

N 7 :

If $A \! \mid \! a$ and $B \! \mid \! b$ and $C \! \mid \! c$ and $Aa = Bb = Cc$ then $ABC \! \in \! P$ and $abc \! \in \! S$.

N 8 :

There exists a quadrangle.

According to axiom $\mathbf N1$, orthogonal lines a, b intersect in the point ab. $\mathbf N2$ is the dual axiom which states that polar points A, B are incident with the line AB. Axiom $\mathbf N3$ states that, if A is a point and b a line, then there exists a line a through A and a point B on b with $Aa = bB$ (a “perpendicular” from A to b with foot B) and that (a, B) is unique if A is not the pole of b. According to N4, two different points have at most one joining line and two different lines have at most one common point. N5 states that, if A, B, C are collinear points, then ABC is a point (the fourth reflection point). $\mathbf N6$ is the dual axiom, which states that, if a, b, c are copunctual lines, then abc is a line, the fourth reflection line. N7 is a self-dual axiom which is a special generalization of the theorem of three reflections. According to N8, there exists at least a quadrilateral (the assumption of the existence of a triangle—cp. axiom M10 in Sect. 2.1—does not hold in every Cayley-Klein geometry, e. g., in the Minkowskian plane over $\mathbf {GF(3)}$).

The metric planes of Sect. 2 are exactly those plane Cayley-Klein geometries which satisfy the axiom of the existence of a joining line (as Euclidean, hyperbolic and elliptic planes). The Galilean, co-Minkowskian, and co-Euclidean planes satisfy the dual parallel axiom.

If A is not incident with b, then there is a unique point on b which has no joining line with A.

By dualization one gets the following two statements: The elliptic, co-Euclidean and co-hyperbolic planes are dual metric planes, i.e., plane Cayley-Klein geometries with the property that any two lines have a point of intersection. The Euclidean, Galilean and Minkowskian planes satisfy the parallel postulate

If A is not incident with b, then there is a unique line through A which has no point of intersection with b.

A plane Cayley-Klein geometry which satisfies the parallel axiom is singular, i.e., the set of translations forms a group (or equivalently, in any quadrilateral with three right angles the fourth angle is a right one).

The hyperbolic and co-Minkowskian planes satisfy the hyperbolic parallel axiom which states that through a given point A there are at most two lines a and b that have neither a common point nor a common line with a given line g (cp. axiom H2 in Sect. 2.1.2). The co-hyperbolic and Minkowskian planes satisfy the dual hyperbolic parallel axiom.

For axiomatizations of Cayley-Klein geometries in terms of reflections we refer for Minkowskian planes to Wolff [115], for Galilean planes to Struve [100], for co-Minkowskian and co-Euclidean planes to Struve and Struve [101, 105] (cp. Bachmann [8]), and for metric planes to the references in Sect. 2.1.

Methodological reflections.

In the axiomatic approach to geometry, a Begründung has the important function of providing a convenient means of ensuring the consistency of that geometry’s axiom system. The latter can be reduced by means of an embedding in a projective-metric space (with respect to both the incidence and the metric structure) to the consistency of the algebraic structure that coordinatizes that projective-metric space. Those algebraic structures are fields with some additional properties. Since the axiom systems of those fields can be extended to that of the theory of real-closed fields, which we know to be consistent (see [62, p. 68]), any fragment thereof must be consistent as well.

Begründungen in this sense were provided first by Hilbert in his Grundlagen der Geometrie [34] and then in Neue Begründung der Bolyai-Lobatschefskyschen Geometrie [33], then by Hjelmslev in Neue Begründung der ebenen Geometrie [36], by Podehl and Reidemeister in Eine Begründung der elliptischen Geometrie [73], by Bachmann in Eine Begründung der absoluten Geometrie in der Ebene [2] and by many other geometers who worked in the foundations of geometry.

It is worth emphasizing that a geometry’s Begründung (i.e., its embedding in a projective-metric space) not only ensures its “existence” from a logical point of view in Hilbert’s sense, but also its authenticity from a projective-geometric point of view championed by Klein, as a geometry in its own right, in no way inferior or subservient to the Euclidean one.

6.4 6.4   Cayley-Klein Spaces and Differential Geometry

Cayley-Klein manifolds.

There are many natural connections between Riemannian manifolds and Cayley-Klein spaces. The tangent space of an n-dimensional Riemannian manifold is an n-dimensional vector space endowed with a (positive definite) quadratic form, which corresponds—from a geometric point of view—to an $(n-1)$-dimensional Cayley-Klein space with an elliptic metric. The elements of the Cayley-Klein space can be represented by the set of Euclidean subspaces through the point of contact of the tangent space (if the manifold is embedded in a Euclidean space). If the quadratic form of a manifold is not positive definite, then the metric of the associated Cayley-Klein space is hyperbolic and the manifold is called pseudo-Riemannian.

The second connection we want to point to is that a Riemannian manifold which is embedded in a Euclidean space is also embeddable in the projective closure of that Euclidean space. This means that the concept of a Riemannian manifold can be generalized by considering manifolds which are embedded in arbitrary Cayley-Klein spaces (and whose tangent spaces can be Cayley-Klein spaces of any type). Such manifolds are called by Rosenfeld [75] quasi-Riemannian or quasipseudo-Riemannian (see also [116]). Perhaps a more appropriate name would be Cayley-Klein manifold. The groups of motions of Cayley-Klein spaces are examples for Cayley-Klein manifolds.