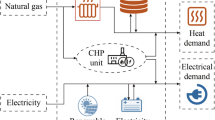
Abstract
The electric power system consists of units for electricity production, devices that make use of the electricity, and a power grid that connects them. The aim of the power grid utilities is to enable the reliable transportation of electrical energy from the production to the consumption, while satisfying system constraints, and all these for the lowest possible price. Conventional power system is facing the problems of gradual depletion of fossil fuel resources, poor energy efficiency, and negative environmental effects. These problems have persuaded system utilities to a new trend of power generation. The new trend incorporates power production at distribution voltage level by using non-conventional or renewable energy sources such as natural gas, biogas, wind power, solar photovoltaic cells, fuel cells, combined heat and power (CHP) systems, and micro turbines. Microgrids (MGs) are accounted as the building blocks of the future power systems known as smart girds. This chapter presents the power flow constrained short-term hourly scheduling of DG units. In the most of the MG scheduling literature, the physical constraints of electric power transmission, known as power flow constraints, has not been taken into account. This simplification may result in a solution that is not technically acceptable. In this study, a MG incorporating cogeneration facilities, conventional power units, and heat-only units are considered. The optimal scheduling determines the performance of units in order to supply whole electrical and thermal demand of the MG as well as determining the amount of exchanging power between main and microgrid. In addition, the heat–power dual dependency characteristic in different types of CHP units are considered, and all technical constraints of generation units have been satisfied as well. A mixed-integer linear formulation has been employed to model the non-convex feasible operation region of CHP unit. In this study, a heat buffer tank, with the ability of heat storage, has been incorporated in the proposed framework. Moreover, in order to consider realistic model of the problem, network operation constraints such as voltage magnitude of buses and line flow limits are taken into account.
Access provided by CONRICYT-eBooks. Download chapter PDF
Similar content being viewed by others
Keywords
1 Introduction
In recent years, the rapid escalation in implementation of fossil fuel, poor energy efficiency, and environmental issues have been a significant concern for many utilities, modern societies, and researchers [1, 2]. Effectively use of distributed energy resources (DER), (e.g., wind, biomass, solar, and hydro), combined heat and power (CHP) systems and energy storage technologies may result in a more flexibility, low cost, environmentally, friendly and reliable energy [3, 4]. Aggregation of various DERs, storage devices, and loads, at medium and low voltage distribution systems, forms small power systems called microgrids (MGs). The MGs can be utilized either interconnected or isolated from the main distribution grid as a controlled entity [1, 5].
Recently, incorporating CHP units in MGs have drawn more attention [6]. Utilizing the CHP systems for simultaneous supply of electrical and thermal energy is the primary motivation. In addition, conversion of primary fossil fuels, even by the most modern combined cycle plants, could only achieve efficiencies between 50% and 60%. However, during electricity generation process of CHP units employing waste heat to provide thermal energy will result in fuel conversion efficiencies of the order of 90% [7]. It should be mentioned that the heat and power outputs of CHP units are non-separable and dependent to each other. In other words, in a CHP system, the power generation limitations depend on the heat generation of system, and the heat generation borders depend upon the power generation of the system. In [8, 9], the CHP economic dispatch (CHPED) problem is handled envisaging heat–power dependency feature.
In deregulation and restructured power system, the MG owner tries to supply the MG electrical and heat demand at minimum cost. In this regard, the MG owner would use various resources such as self-generating facilities and highly competitive electricity markets. Due to MGs major technological and regulatory innovation of small-scale on-site CHP-based DERs, MG has become empowering to compete with traditional centralized electricity plant [10]. However, the CHP-based MG owner should consider network operation constraints as well as all technical constraints of generation units in the scheduling problem.
Most researchers concentrate on the management and scheduling of MGs [11,12,13,14]. In [11], an intelligent MG energy management with aim of emission and operation cost minimization has been investigated. In [12], a model to make energy trading decisions has been proposed. The proposed model in [12] determines scheduling of units envisaging systems constraints.
The scheduling problem of a MG with islanding constraints is studied in [13]. The objective of [13] is to minimize the MG total operation cost. The problem is decomposed into a grid-connected operation master problem and an islanded operation subproblem. A stochastic framework for operation management of MGs has been proposed in [14]. This paper considers the grid-connected mode, which includes photovoltaic panel (PV), wind turbine (WT), micro-turbine, fuel cell, and energy storage devices.
Operation of CHP units in terms of satisfying both thermal and electrical demand has been investigated in many works [9, 15, 16]. In these works, the hourly scheduling of industrial and commercial customers with cogeneration facilities has been studied, taking the feasible operation region of CHP units into account. In [17], operation of a micro-CHP-based residential MG has been investigated. Thermal load has been studied in [17] in terms of the required hot water and desired building temperature. A mathematical framework for operation of micro-CHPs in a MG has been addressed in [18]. In this work, the grid-connected mode is considered for MG, in which, the MG is able to interchange the electrical energy with the main grid. The objective of the proposed model in [18] is to minimize total costs while meeting heat demand of the grid. In [19], a stochastic programming framework for optimal 24-h scheduling of CHP-based MGs has been proposed. The authors of [19] aim at finding the optimal set points of energy resources for profit maximization, considering uncertainties and demand response programs.
Considering the physical constraints of electric power transmission in the MG scheduling is very vital, especially in the presence of multiple demands. Operational challenges of a MG associated with renewable energy resources (RES) and controllable loads have been addressed in [20]. The power flow (PF) constraints have been taken into account in [20]. Power flow constraints in MG scheduling problem with multiple demands have not been taken into account in all above mentioned works.
In the current chapter, 24-h PF-constrained scheduling of CHP-based MG is conducted. The purpose of the work is to take advantage of the opportunity, to sell any excess electricity to the market in order to maximize the revenue regarding to the prices in the day-ahead market. The unit’s operating costs as well as start-up and shutdown costs and cost of power purchases from the power market have been taken into account while satisfying the heat and power demand of the MG. Moreover, network operation constraints such as voltage magnitude of buses and line flow limits have been considered to simulate more realistic model of the problem.
This chapter assumes that the MG possesses a power-only unit, a boiler unit, and two cogeneration facilities. In addition, a heat buffer tank, with the ability of heat storage, has been incorporated in the proposed model. The solution of the scheduling problem meets the terms of technical constraints of all facilities, comprising of minimum up/down time of the facilities, minimum and maximum capacity of units, and dual dependencies of heat and power generation in the CHP systems. The detailed descriptions of proposed model are provided in the following sections.
2 Problem Statement and Mathematical Formulation
The optimal load flow constrained scheduling problem is formulated as a mixed-integer nonlinear programming optimization problem. The objective of the optimal operational scheduling of the CHP-based MG is minimizing the cost of power and heat procurement over a day-ahead period of time, in the presence of several constraints.
2.1 Objective Function
The objective function of the scheduling problem is to minimize the total cost. The facilities’ operation cost is of importance in the MG scheduling problem. Owing to severe problems of frequent turning on and off [18], the diminishing of units’ start-ups and shutdowns is indispensable. Hence, against the most existing works, the all units’ start-ups and shutdowns are incorporated in the objective function. It is noteworthy to say that it is assumed that the MG is utilized in grid-connected mode that can buy/sell the electricity from/to the main grid regarding to the market prices.
It is assumed that the CHP-based MG is equipped with conventional power and heat-only units, CHP units, and the heat buffer tank. Therefore, the objective function in the load flow constrained self-scheduling problem of MG to be minimized encompasses the units’ start-up and shutdown costs, units’ operational cost, expense of procuring energy from the utility as well as taking advantage of selling power to the market:
where k, \(l\) and m represent the indices for cogeneration units, power-only units and boiler units, respectively. \(P_{t}^{\text{grid}}\) is the amount of electricity sold to the main network, and \(\lambda_{t}\) indicates the forecasted market price at time t. Also, \({\text{CSU}}_{h,t} /{\text{CSD}}_{h,t}\) stand for the start-up/shutdown cost and \({\text{SU}}_{h,t} /{\text{SD}}_{h,t}\) show the binary variables representing the start-up/shutdown status of hth system at time interval t. \(C_{ht}\) is the total operation cost of generation facilities, which will be described in the following section.
The total operation cost of a CHP unit [21], conventional power-only, \(C_{l,t}^{P}\), and heat-only, \(C_{m,\,t}^{B}\), units, respectively can be defined as:
The binary variables \({\text{SU}}_{h,t}\) and \({\text{SD}}_{h,t}\) are used to model the start-up and shutdown status of the facilities, as follows:
where, \(U_{h,\,t}\) is binary variable, which is equal to 1 if the hth generation unit is selected at time interval t; otherwise it would be zero. \(a_{k} ,\,b_{k} ,\,c_{k} ,\,d_{k} ,\,e_{k}\) and \(f_{k}\) represent cost coefficient of cogeneration facility, \(\psi_{l}\) and \(\psi_{m}\) indicate the linear cost coefficient of power-only and heat-only facilities, respectively.
2.2 Constraints
The objective function is restricted by equality and inequality constraints, which are as follows.
2.2.1 Load Flow Equations
This chapter considers PF equations in the CHP-based MG scheduling problem in order to simulate more realistic framework of the problem. The following equations characterize the flow of power throughout the system, which are determined by Kirchhoff’s laws:
which are the active and reactive power flow equations, respectively. N bus is number of buses of the MG. Also, \(P_{i,t}^{g}\) and \(Q_{i,t}^{g}\) are active and reactive power flow of DERs located on bus i, respectively. \(P_{t}^{\text{grid}}\) and \(Q_{t}^{\text{grid}}\) stand for active and reactive power bought from the utility through the bus which is connected to the main grid at time t, respectively. \(V_{i,t}\) is the voltage of bus i at time interval t. \(Y_{ij}\) and \(\theta_{ij,t}\) are magnitude and phase angle of feeder’s admittance. \(P_{i,t}^{l}\) and \(Q_{i,t}^{l}\) are active and reactive load of bus i at time t, respectively.
-
(a)
Voltage limits
Voltage limits refer to the requirement for the system bus voltages magnitude, \(V_{i,t}\), to be kept at permissible range. Moreover, the voltage magnitude for substation buses, \(V_{s}\), should be maintained at the nominal value \(V_{s}^{n}\):
-
(b)
Exchangeable power limit
Exchangeable apparent power with the main grid has to be in a limited bound in order to have the stable operation [22].
-
(c)
Apparent power Flow limits for branches
It is essential to keep the apparent power flowing from each branch, \(S_{{{\text{br}},t}}\) of MG in its admissible range:
2.2.2 Generation Units Constrains
The operating constraints of generation units contain the minimum up/down time limits, ramping rate constrains, and the generation capacity of facilities. The time duration for which the generation units are on/off at time t, \(X_{h,t}^{\text{on}} ,X_{h,t}^{\text{off}}\), could be expressed as follows:
where, \(U_{h,t}\) is a binary variable defining on/ off status of the hth generation unit. Minimum up/down time (\({\text{UT}}/{\text{DT}}\)) limits are imposed by:
The following equations formulate the ramping up/down rate limits (\(R^{\text{up}} /R^{\text{down}}\)) of power generation and CHP systems:
-
(a)
CHP units
It is noteworthy to say that the power and heat productions of the CHP units are mutually dependent and could not be organized separately. Two types of feasible operating region (FOR) can be defined for CHP systems [23]. The first and second types FOR of a CHP unit are exposed in Fig. 1. The first type FOR may be characterized utilizing linear formulation and Eqs. (19)–(23) model this FOR in the CHP-based MG scheduling problem [24].
where M is a sufficiently large number, and indices A, B, C, and D represent four bordering points of the FOR in the first type of CHP system. Equation (19) expresses the area under the curve AB. The area upper the curve BC and CD are modeled implementing Eqs. (20) and (21), respectively. Referring to the Eqs. (20)–(21), the output power for a decommitted unit (\(U_{K,t} = 0\)) would be zero. Moreover, the heat and power generations for a decommitted unit have to be set to zero, which would be executed by Eqs. (22) and (23), respectively.
As can be seen from Fig. 1, the FOR related to type two is non-convex which may be divided into two-convex subregions, namely subregion I and subregion II, as shown in Fig. 1. The type 2 FOR is surrounded by the boundary curve ABCDEFG. Along the boundary curve BC, the power capacity decreases as the heat generation of system increases, while the power capacity declines along the curve CD. In this case, by employing the customary formulation, similar to the first FOR type representation, the colored region (FEG) could not be developed. Therefore, this non-convex area is handled by employing binary variables \(X_{1}\) and \(X_{2}\) [23]. Hence, the non-convex region should be divided into two-convex subregions I and II. The subsequent equations model the FOR of CHP unit in the MG scheduling problem, [24]:
In the second type, again indexes A, B, C, D, E, and F represent the connection points of the FOR relevant to Fig. 1b. Equations (24) and (25) describe the region under the curve BC and upper the curve CD, respectively. The upper area of the curves EF and DE are described using (26) and (27), respectively. In Eqs. (26–29), CHP unit operation in the first (second) convex subdivision of FOR could be modeled by using \(X_{1t} = 1\) (\(X_{2t} = 1\)). Referring to Eq. (30), the operation region of CHP unit type 2 can be either I or II as the unit status is ON and none of them whenever the unit turns OFF. Furthermore, for a decommited unit, Eqs. (31) and (32) will fix the heat and power production to zero.
-
(b)
Power-only and heat-only units’ constraints
The capacity restrictions of power and heat-only units can be stated as below:
2.2.3 Heat Buffer Tank
The heat buffer tank has been developed from the model presented in [18]. The heat buffer tank is subjected to the boiler and CHP units. In the proposed system, the heat storing is also possible. The total produced heat, \(\overline{H}_{t}\), could be calculated as:
As the heat exposed to the heat buffer tank is, respectively, effected by the loss (\(\beta_{\text{loss}}\)) and extra heat generation (\(\beta_{\text{gain}}\)) during shutdown and start-up periods, the real heat, \(H_{t}\), that the buffer tank would be supplied could be presented as follows [18]:
Hence, the existent heat in the heat buffer tank, \(B_{t}\), could be stated as:
where \(\eta\) and \(H_{t}^{\text{D}}\) are heat loss rate and heat demand at time interval t (MWth). In addition, the capacity of heat storage is constrained as:
In this chapter, the practical state of heat storage system is simulated by envisaging the ramping up/down rates as below:
3 Simulation Studies
In this section, at first the structure of the considered MG is introduced, and afterward the simulation results of optimal PF-constrained scheduling are presented.
3.1 Microgrid Structure
To investigate the validity and outperformance of the proposed scheduling model, a six-bus meshed MG has been implemented as the test bed here. The single line diagram of this system is depicted in Fig. 2. In the studied case, bus 1 is connected to the main grid, and the MG is able to procure the power from the grid according to the pool market prices. Referring to Fig. 2, the studied MG comprises a power-only unit and a boiler unit, two cogeneration units with different FORs, and a heat buffer tank along with the electrical and thermal loads. The location of all units is illustrated in Fig. 2. The fundamental network data including the active and reactive loads for all buses and impedance of branches are presented in Fig. 3 and Table 1, respectively [19, 25]. The admissible range for the voltage magnitudes of all buses has been determined to be between 0.95 and 1.05 p.u, respectively. The heat demand of MG is developed from [19, 25] and provided in Table 2. In addition, Table 2 presents the hourly market price in $/kW. The FOR of cogeneration units is portrayed in Fig. 4. Characteristics of the heat buffer tank are provided in Table 3. The start-up and shutdown cost of units are presented in Table 4. Table 5 provides the cost function coefficients of CHP systems. The cost functions of power-only and heat-only are supposed to be linear and stated in Eqs. (41)–(42), respectively. The proposed optimization problem is a mixed-integer nonlinear programming (MINLP) that considers the load flow constraint. Hence, the problem can be classified as an optimal power flow problem, focusing on the energy resource management in the MG. Mathematical modeling of the load flow constrained CHP-based MG scheduling problem is solved by using SBB/CONOPT solver [26] under General Algebraic Modeling System (GAMS) environment [27]. The SBB is a GAMS solver for MINLP models. It is based on a combination of the standard Branch and Bound method known as mixed-integer linear programming (MILP) and the standard nonlinear programming (NLP) solvers, which are already supported by GAMS.
In this chapter, two case studies have been investigated:
-
Case 1: CHP-based MG scheduling neglecting PF constraints.
-
Case 2: CHP-based MG scheduling considering PF constraints.
3.2 Simulation Results
3.2.1 Case Study 1
CHP-based MG scheduling
In this case, the MG scheduling problem has been solved using proposed framework. All technical and economic constraints excluding PF constraints have been envisaged. Table 6 and Fig. 5 summarize the results of case 1. Regarding Table 6, the cost of MG energy supply would be $339.298. In addition, the MG revenue from the electricity market participation over 24-h time horizon would be $237.014. According to Fig. 5, CHP units 1 and 2 will produce about 62 and 26% of total produced power, respectively. Moreover, power-only unit produces only 12% of total generated power. This fact is due to the less operation cost of CHP units, in comparison with power-only unit and also CHP units’ heat-power dependency.
Figure 6 illustrates the produced power of all units at the scheduling horizon. As can be seen from Table 6 and Fig. 6, the MG would not purchase power from the market. Due to low operation cost of CHP units, the MG prefers to sell the power to the macrogrid regarding the market prices. It should be mentioned that the amount of exchangeable power with grid has not been limited in this case. Hence, the CHP unit 1 produces power in its maximum capacity at all time intervals, taking into account its ramp up rate constraint in order to take advantages of market participation. The CHP unit 1 does not produce heat at any intervals. Therefore, CHP unit 2 would provide all heat demand of the MG. According to simulation results, the boiler would not participate in supplying heat demand, due to its higher operation cost in comparison with CHP units.
3.2.2 Case Study 2
In the second case, the effect of PF constraints in the CHP-based MG scheduling problem is scrutinized. The MG scheduling problem is solved, considering all technical and economic constraints as well as PF constraints. The results regarding case 2 are provided in Table 6. According to Table 6, the MG revenue from the market participation would be $155.652. This revenue comes from selling the excess electrical energy to the market as it is operating in the grid-connected mode. The revenue has been decreased about 34.3% in comparison with the case study 1. In addition, the generation cost is decreased to $288.951. This fact is due to PF constraints which will limit the apparent power flowing from each branch of MG. Moreover, according to Fig. 7, about 7% of produced power will be lost in the branches of network.
Figure 8 presents the voltage magnitude of all buses. According to this figure, the voltage magnitude of all buses is limited between 0.95 and 1.05 p.u. The generated power of units has been depicted in Fig. 9. In this case, again, power-only unit provides power, only in few hours of the day. Referring to Fig. 9 and market prices in Table 2, the MG sells power to the market according to the pool market prices, namely the MG would sell more power in high market price time intervals and less in low price hours to take the most advantages of grid-connected mode and market participation. The heat production of units is portrayed in Fig. 10. As can be seen from Fig. 10, the CHP units produce heat according to their generated power and FOR. The boiler unit does not produce heat at all, due to its high operation cost. Moreover, the buffer tank will be discharged completely till hour eight, considering its ramp down rate. After hour eight, the produced heat of CHP unit 1 meets the hourly heat demand of MG. Hence, there is no need to store heat in the buffer tank.
4 Conclusions
This chapter presented a power flow constrained programing framework for optimal hourly scheduling of a CHP-based MG, including two conventional power and heat generation units, two types of cogeneration units, and a heat buffer tank. In the optimal scheduling problem of the MG, the objective is to minimize thermal and electrical energy supply cost of MG, as well as taking advantage of market participation to sell excess power in high market price hours and purchase it in low price time intervals. In this chapter, the CHP systems with heat–power dual dependency characteristic are modeled using mixed-integer linear programming formulation. This chapter discussed two case studies in order to scrutinize the impact of PF constraints in the optimal hourly scheduling of CHP-based MGs. According to the simulation results, the proposed model can cover the total thermal and electrical demands with respect to economic criteria as well as physical constraints of the network. The results show that by applying PF constraints the value of objective function has been increased about 30% from $102.284 to $133.299. In addition, total amount of sold power to the pool market has been decreased comparing to the base case (case without PF constraint). This fact is due to PF constraints which will impose apparent power flowing from each branch of MG limitation and power losses in the network.
References
H. Jiayi, J. Chuanwen, and X. Rong, “A review on distributed energy resources and MicroGrid,” Renewable and Sustainable Energy Reviews, vol. 12, pp. 2472–2483, 2008.
A. Zangeneh, S. Jadid, and A. Rahimi-Kian, “Promotion strategy of clean technologies in distributed generation expansion planning,” Renewable Energy, vol. 34, pp. 2765–2773, 2009.
P. M. Costa, M. A. Matos, and J. P. Lopes, “Regulation of microgeneration and microgrids,” Energy Policy, vol. 36, pp. 3893–3904, 2008.
P. Dondi, D. Bayoumi, C. Haederli, D. Julian, and M. Suter, “Network integration of distributed power generation,” Journal of Power Sources, vol. 106, pp. 1–9, 2002.
A. Soroudi, M. Ehsan, and H. Zareipour, “A practical eco-environmental distribution network planning model including fuel cells and non-renewable distributed energy resources,” Renewable Energy, vol. 36, pp. 179–188, 2011.
M. Motevasel, A. R. Seifi, and T. Niknam, “Multi-objective energy management of CHP (combined heat and power)-based micro-grid,” Energy, vol. 51, pp. 123–136, 2013.
A. Vasebi, M. Fesanghary, and S. Bathaee, “Combined heat and power economic dispatch by harmony search algorithm,” International Journal of Electrical Power & Energy Systems, vol. 29, pp. 713–719, 2007.
M. T. Hagh, S. Teimourzadeh, M. Alipour, and P. Aliasghary, “Improved group search optimization method for solving CHPED in large scale power systems,” Energy Conversion and Management, vol. 80, pp. 446–456, 2014.
M. Alipour, K. Zare, and B. Mohammadi-Ivatloo, “Short-term scheduling of combined heat and power generation units in the presence of demand response programs,” Energy, vol. 71, pp. 289–301, 2014.
A. K. Basu, A. Bhattacharya, S. Chowdhury, and S. Chowdhury, “Planned scheduling for economic power sharing in a CHP-based micro-grid,” Power Systems, IEEE Transactions on, vol. 27, pp. 30–38, 2012.
A. Chaouachi, R. M. Kamel, R. Andoulsi, and K. Nagasaka, “Multiobjective intelligent energy management for a microgrid,” Industrial Electronics, IEEE Transactions on, vol. 60, pp. 1688–1699, 2013.
C. Changsong, D. Shanxu, C. Tao, L. Bangyin, and Y. Jinjun, “Energy trading model for optimal microgrid scheduling based on genetic algorithm,” in Power Electronics and Motion Control Conference, 2009. IPEMC’09. IEEE 6th International, 2009, pp. 2136–2139.
A. Khodaei, “Microgrid optimal scheduling with multi-period islanding constraints,” Power Systems, IEEE Transactions on, vol. 29, pp. 1383–1392, 2014.
S. Mohammadi, S. Soleymani, and B. Mozafari, “Scenario-based stochastic operation management of microgrid including wind, photovoltaic, micro-turbine, fuel cell and energy storage devices,” International Journal of Electrical Power & Energy Systems, vol. 54, pp. 525–535, 2014.
M. Alipour, B. Mohammadi-Ivatloo, and K. Zare, “Stochastic risk-constrained short-term scheduling of industrial cogeneration systems in the presence of demand response programs,” Applied Energy, vol. 136, pp. 393–404, 2014.
M. Alipour, K. Zare, and B. Mohammadi-Ivatloo, “Optimal risk-constrained participation of industrial cogeneration systems in the day-ahead energy markets,” Renewable and Sustainable Energy Reviews, vol. 60, pp. 421–432, 2016.
M. Tasdighi, H. Ghasemi, and A. Rahimi-Kian, “Residential microgrid scheduling based on smart meters data and temperature dependent thermal load modeling,” Smart Grid, IEEE Transactions on, vol. 5, pp. 349–357, 2014.
G. M. Kopanos, M. C. Georgiadis, and E. N. Pistikopoulos, “Energy production planning of a network of micro combined heat and power generators,” Applied Energy, vol. 102, pp. 1522–1534, 2013.
M. Alipour, B. Mohammadi-Ivatloo, and K. Zare, “Stochastic Scheduling of Renewable and CHP-Based Microgrids,” Industrial Informatics, IEEE Transactions on, vol. 11, pp. 1049–1058, 2015.
W. Su, J. Wang, and J. Roh, “Stochastic energy scheduling in microgrids with intermittent renewable energy resources,” Smart Grid, IEEE Transactions on, vol. 5, pp. 1876–1883, 2014.
G. Piperagkas, A. Anastasiadis, and N. Hatziargyriou, “Stochastic PSO-based heat and power dispatch under environmental constraints incorporating CHP and wind power units,” Electric Power Systems Research, vol. 81, pp. 209–218, 2011.
J. Aghaei and M.-I. Alizadeh, “Multi-objective self-scheduling of CHP (combined heat and power)-based microgrids considering demand response programs and ESSs (energy storage systems),” Energy, vol. 55, pp. 1044–1054, 2013.
Z. W. Geem and Y.-H. Cho, “Handling non-convex heat-power feasible region in combined heat and power economic dispatch,” International Journal of Electrical Power & Energy Systems, vol. 34, pp. 171–173, 2012.
M. Moradi-Dalvand, B. Mohammadi-Ivatloo, and M. A. Fotouhi Ghazvini, “Short-Term Scheduling of Microgrid with Renewable sources and Combined Heat and Power,” in Smart microgrids, new advances, Challenges and Opportunities in the actual Power systems, ed.
A. K. Basu, S. Chowdhury, and S. Chowdhury, “Impact of strategic deployment of CHP-based DERs on microgrid reliability,” Power Delivery, IEEE Transactions on, vol. 25, pp. 1697–1705, 2010.
”The gams software website,” Available: http://www.gams.com/dd/docs/solvers/conopt.pdf, 2012 [Online]
D. K. A. Brooke, and A. Meeraus. “Gams users guide”, Available: http://www.gams.com/docs/ gams/GAMSUsersGuide.pdf [Online].
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2017 Springer International Publishing AG
About this chapter
Cite this chapter
Alipour, M., Zare, K., Seyedi, H. (2017). Power Flow Constrained Short-Term Scheduling of CHP Units. In: Azzopardi, B. (eds) Sustainable Development in Energy Systems. Springer, Cham. https://doi.org/10.1007/978-3-319-54808-1_8
Download citation
DOI: https://doi.org/10.1007/978-3-319-54808-1_8
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-319-54806-7
Online ISBN: 978-3-319-54808-1
eBook Packages: EnergyEnergy (R0)