Abstract
In order to integrate renewable and non-renewable energy resources like combined heat and power (CHP) systems, microgrid seems to be a good idea. This paper has developed an optimization framework for economic dispatch of microgrids including CHP plants, boiler units, conventional power generators, photovoltaic units, wind turbines and battery storage system in a 10-bus test system. The main goal of proposed paper is to optimally dispatch the studied microgrid in the mentioned test system considering impacts of heat buffer tank and battery energy storage. It should be noted that the studied test system is composed of several zones in which microgrid system can be operated in connected/islanded mode. Optimal economic dispatch problem of microgrid is studied within a 24-h time horizon, and the obtained results are analyzed for comparison.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Microgrid is a novel concept that has been innovated through integrating several types of energy resources including renewable and non-renewable ones like photovoltaic (PV) cells, wind turbines (WT), distributed energy sources and cogeneration systems (Alipour et al. 2015; Abu-Sharkh et al. 2006). Renewable units used in these systems can reduce total emission of power system (Barklund et al. 2008; Kanchev et al. 2011). Furthermore, microgrids can exchange power with the upstream network to gain economic profit (Nazari-Heris et al. 2017). Generating electrical and thermal energy at the same time, combined heat and power systems increase total system efficiency (Alipour et al. 2014). Since economic dispatch of CHP units is a non-convex nonlinear problem, integration of these units with other generation systems can be challenging (Nazari-Heris et al. 2017). In order to solve such a non-convex problem, various methods including benders decomposition approach (Abdolmohammadi and Ahad 2013), Lagrangian relaxation method (Sashirekha et al. 2013) and branch and bound technique (Rong and Lahdelma 2007) can be used. Economic dispatch problem of microgrid energy systems has been studied in some researches as follows: uncertainty-based economic dispatch of microgrid under different optimization goals, planning methods and reliability indices have been studied in Wu et al. (2014). Monte Carlo simulation approach along with particle swarm optimization method has been used to model power flow of microgrid in both grid-connected and islanded modes. Microgrid energy system has been optimally allocated and scheduled using improved adaptive genetic algorithm in Wu et al. (2016) in which management costs, investment costs, the rate of extra energy of microgrid and cost of emission have been taken into account. Particle swarm optimization method and two-point estimate approaches have been used to manage energy consumption of microgrid in Baziar and Kavousi-Fard (2013). Chaotic local search and fuzzy self-adaptive techniques have been employed to solve economic dispatch problem of microgrid with considering environmental issues in Moghaddam et al. (2011). In order to minimize total operation cost and emission of microgrid, epsilon-constraint approach and hybrid augmented-weighted technique have been employed in Rezvani et al. (2015). Uncertainty-based operation of microgrid has been studied considering uncertainty of real-time market price in Liu et al. (2016). Controlling operation of a DC microgrid has been studied in the presence of electric vehicles in Kai-Wei and Liaw (2016) in which wind permanent magnet synchronous generator capable of exchanging power with the upstream network has been used. Controlling strategies of a hybrid PV-diesel-battery microgrid containing on/off control and monitoring have been studied in Kusakana (2015). Modified adaptive firefly algorithm has been employed to minimize total operation cost of microgrid in Talari et al. (2015). Microgrid energy system has been optimally planned using a mixed-integer linear programming in Jaramillo and Weidlich (2016) to minimize total operation cost and emission of microgrid. Uncertainty-based operation of microgrid under uncertainty of renewable energy resources has been studied in Sobu and Guohong (2012). Uncertainty-based operation CHP-based microgrid has been studied with subject to uncertainty of wind generation in Dolatabadi and Behnam (2017) in which conditional value-at-risk (CVaR) measure has been used to evaluate the risks.
In this paper, a new optimization framework has been presented for optimal dispatch of a CHP-based microgrid in a 10-bus test system. The studied model is composed of conventional thermal plants, two CHP systems, boiler units, heat buffer tanks, wind generation system, PV system and electrical storage. Effects of dual dependency of generated heat and power by CHP unit as well as start-up and shutdown costs of generation systems have been taken into account in the proposed paper. A mixed-integer linear programming has been used to formulate optimal operation of CHP system with non-convex feasible operating zones. Studied test system is divided into several zones, each one with its own generation units and demands. Each zone can be operated in grid-connected or islanded mode to supply its local energy demand. The main goal of proposed paper is to optimize operation of microgrid in a way that both electrical and thermal demands are supplied while total operation cost of system is minimized.
Proposed paper is categorized as follows: Economic dispatch problem is formulated in Sect. 2. Case studies are presented in Sect. 3, and the results are reported in Sect. 4. Finally, the conclusions are provided in Sect. 5.
2 Problem Formulation
Studied model in this paper is composed of CHP systems, boiler, conventional power generators, heat tank, PV systems, wind units and electrical storage system.
As the objective function, total operation cost of CHP-based microgrid including cost of power procurement from upstream network, cost of generation of heat and power by CHP units, cost of conventional power generators, cost of boilers, cost of storage system and start-up and shutdown costs of local generation units should be minimized as follows:
In this formulation, \(N_{\text{Bus}}\) is the number of buses of studied test system. \(h\) is time period. \(P_{\text{k,t,n}}^{\text{CHP}}\) and \(H_{\text{k,t,n}}^{\text{CHP}}\) are the power and heat production of CHP system. Power and heat production of conventional power generators and boilers are expressed by \(P_{\text{l,t,n}}^{\text{G}}\) and \(H_{\text{m,t,n}}^{\text{b}}\). \(P_{\text{t,n}}^{\text{buy}}\) is the purchased power from upstream network. Price of upstream network is expressed by \(\lambda_{\text{t}}\), and \(C_{\text{k,t,n}}^{\text{CHP}}\), \(C_{\text{l,t,n}}^{\text{G}}\) and \(C_{\text{m,t,n}}^{\text{B}}\) are power and heat generation of CHP systems, conventional power generators and boilers, respectively. \({\text{SU}}_{\text{i,t,n}}\) and \({\text{SD}}_{\text{i,t,n}}\) are start-up and shutdown states of local generation units. \({\text{CSU}}_{\text{i,t,n}}\) and \({\text{CSD}}_{\text{i,t,n}}\) are start-up and shutdown costs of local generation units.
2.1 CHP Units
Cost of operation of CHP systems is presented as follows:
In this formulation, \(a_{\text{k}}\), \(b_{\text{k}}\), \(c_{\text{k}}\), \(d_{\text{k}}\), \(e_{\text{k}}\) and \(f_{\text{k}}\) are coefficients of operation cost function of CHP system. \(P_{\text{k,t,n}}^{\text{CHP}}\) is the generated power by CHP systems and \(H_{\text{k,t,n}}^{\text{CHP}}\) is generated heat by these systems.
The relationships between the heat and power generation of CHP systems are expressed in Fig. 1.
Feasible region for operation of CHP systems
Feasible operational region of CHP system 1 is expressed in Fig. 1 (a) which can be modeled linearly as follows:
In these formulations, M is a great number. A, B, C and D are FOR marginal points of CHP system type-1. The area below AB is modeled by (3). The area above the curve BC is modeled by (4). Also, Eq. (5) is used to model the area above curve CD. \({\text{V}}_{{1,{\text{t}},{\text{n}}}}\) is binary variable to express the commitment or decommitment of CHP system which is used in Eqs. (6) and (7).
Non-convex FOR of CHP system type-2 is expressed in Fig. 2b. Mentioned FOR can be separated into two convex regions utilizing binary variables X1 and X2. Linear form of FOR of CHP system type-2 is expressed as follows:
In these formulations, A, B, C, D, E and F are FOR marginal points of CHP system type-2. The area under BC is modeled by (8), and the area above CD is modeled by (9). Equation (10) is used to model the area above EF. Also, the area above curve DE is modeled by (11). \(X_{{1,{\text{t}}}}\) is the binary variable representing first convex region of FOR of CHP system type-2, and \(X_{{2,{\text{t}}}}\) is the binary variable representing first convex region of FOR of CHP system type-1. It should be noted that \(V_{{i,{\text{t}},{\text{n}}}}\) is binary variable expressing the commitment or decommitment of CHP system.
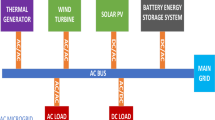
Studied test system (Malakar et al. 2014)
2.2 Conventional Power Generators
Operation cost of conventional power generators can be expressed as follows:
In this formulation, \(\psi_{\text{l}}\) is coefficient of operation cost of conventional power generator. \(P_{{{\text{l}},{\text{t}},{\text{n}}}}^{G}\) is the generated power by these units. It should be noted that the limitation of generation by these units is expressed as follows:
In this equation, \(P_{\text{l}}^{{{\text{G}},{ \rm{min} }}}\) and \(P_{\text{l}}^{{{\text{G}},{ \rm{max} }}}\) are the minimum and the maximum possible generation of conventional power generators.
2.3 Boiler Units
Operation cost of boilers can be expressed as follows:
In this formulation, \(\psi_{\text{m}}\) is coefficient of operation cost of boilers and \(H_{{{\text{m}},{\text{t}},{\text{n}}}}^{B}\) is the generated heat by these units. It should be noted that the limitation of generation by these units is expressed as follows:
In this equation, \(H_{\text{m}}^{{{\text{B}},{ \rm{min} }}}\) and \(H_{\text{m}}^{{{\text{B}},{ \rm{max} }}}\) are the least and the most heat generation of boilers.
Start-up and shutdown conditions of CHP systems, conventional generation system and boilers can be expressed as follows:
2.4 Wind Turbines
Generation of wind turbine is presented as:
In this formulation, \(V_{\text{u,t,n}}^{\text{W}}\) is the wind speed. \(P_{\text{u,t,n}}^{{\prime {\text{W}}}}\) is available generated power by wind turbine. \(V_{\text{u,t,n}}^{\text{CI}}\), \(V_{\text{u,t,n}}^{\text{CO}}\) and \(V_{\text{u,t,n}}^{\text{R}}\) are cut-in, cut-out and rated wind speeds. \(P_{\text{u,t,n}}^{ \rm{max} }\) is the maximum capacity of wind system. It should be noted that scheduled power of wind turbine cannot exceed available generated power by wind turbine which is expressed by (24):
2.5 Photovoltaic Units
Generation of PV system is presented as:
In this formulation, \(P_{{{\text{f}},{\text{t}},{\text{n}}}}^{\text{PV}}\) is produced power by PV system. \(A\) is installation area of PV system.\(P_{\text{PV}}^{\text{rated}}\) is the rated capacity of PV unit per 1 m2 and \(\eta_{\text{PV}}^{\text{t}}\) is the efficiency of PV system. It should be noted that scheduled power of PV system cannot exceed available generated power by PV system which is expressed by (26).
2.6 Battery Storage System
Available energy in the battery storage is expressed as follows (Alipour et al. 2015):
In this formulation, \(E_{{{\text{r}},{\text{t}},{\text{n}}}}^{\text{B}}\) is the available energy in the battery storage. \(\eta_{{{\text{r}},{\text{t}},{\text{n}}}}^{\text{charge}}\) and \(\eta_{{{\text{r}},{\text{t}},{\text{n}}}}^{\text{discharge}}\) are the efficiencies of charge and discharge of battery storage system. The constraint of available energy in the battery storage is as follows:
In this formulation, \(E_{{{\text{r}},{\text{t}},{\text{n}}}}^{\rm{min} }\) and \(E_{{{\text{r}},{\text{t}},{\text{n}}}}^{\rm{max} }\) are the minimum and the maximum available energy in the battery. Limitations of charge and discharge of battery storage are expressed as follows:
In order to separate charge and discharge conditions of battery from each other, Eq. (31) is used.
2.7 Power Flow Constraint
Power balance limitation of studied model including CHP systems, boiler units, conventional power generators, PV systems, wind turbines and battery storage system is expressed as follows:
In this equation, \(V_{\text{t}}^{\text{n}}\) is voltage of bus n and \(V_{\text{t}}^{\text{u}}\) is voltage of bus u. \(\theta_{\text{t}}^{\text{n}}\) is the voltage angle of bus n and \(\theta_{\text{t}}^{\text{u}}\) is the voltage angle of bus u. \(Y_{\text{line}}^{\text{un}}\) is line admittance between buses n and u.
Limitation of line connecting different buses to each other is expressed as follows:
where \(P_{\text{L}}^{\text{un}}\) is maximum capacity of the line connecting different buses to each other.
2.8 Heat Buffer Tank
Utilized model for heat buffer tank is taken from (Shahverdi and Moghaddas-Tafreshi 2008). Total generated heat by microgrid is equal to the heat generation of CHP system and boiler units which is expressed as follows:
Generated heat by buffer tank while considering loss and extra heat production during shutdown and start-up condition is expressed as follows:
In this formulation, \(\beta_{\text{loss}}\) and \(\beta_{\text{gain}}\) are losses during shutdown condition and extra heat production during start-up condition. So, available heat of heat buffer tank can be expressed as follows:
In this formulation, \(\eta\) is the heat loss rate of the heat buffer tank. It should be noted that available heat of heat buffer tank is constrained as follows:
In this equation, \(B_{ \rm{min} }\) and \(B_{ \rm{max} }\) are the minimum and maximum rate of capacities of heat buffer tank. The limitations related to the ramp up and down rates of heat buffer tank are expressed as follows:
It should be noted that \(B_{ \rm{max} }^{\text{charge}}\) and \(B_{ \rm{max} }^{\text{discharge}}\) are the maximum limitations of charge and discharge of heat buffer tank.
3 Case Study
Studied model in this paper is a 10-bus test system including CHP systems, boiler units, conventional power generators, PV system, wind turbine and battery storage. The studied model is captured in Fig. 2. In the studied system, boiler units and heat buffer tank are connected to buses 1, 3 and 7 and battery storage is placed at bus 5. Furthermore, CHP system type-1 is placed at bus 7 and CHP system type-2 is placed at bus 5. PV system is placed at bus 7. Wind units are placed at buses 1 and 3. Furthermore, conventional thermal units are placed at buses 1, 3 and 10. It should be noticed that upstream network is connected to buses 1 and 3.
Info of utilized CHP systems is presented in Table 1.
The cost coefficients related to thermal units and boilers are 100 $/MW and 23.4 $/MWth, respectively (Alipour et al. 2015). Minimum and maximum values of capacity of conventional thermal units are presented in Table 2.
Info of utilized battery storage is presented in Table 3.
Data of utilized heat buffer tank are provided in Table 4.
Start-up and shutdown costs of CHP units, boilers and conventional thermal systems are presented in Table 5.
Output power of PV system is illustrated in Fig. 3.
Output power of PV system
Wind speed profile is taken from (Malakar et al. 2014) which is captured in Fig. 4. According to this figure, rated, cut-in and cut-out wind speeds of wind turbine are 13, 3 and 25 m/s. The maximum wind speed is 10.55 m/s. The maximum generation of wind turbine at buses 9 and 14 is 0.5 MW and 0.4 MW.
Wind speed
Electrical demand and heating demand of CHP-based microgrid are depicted in Figs. 5 and 6, respectively. It is noteworthy that the exchanged power between the buses in microgrid should be lower than rated value which is 0.4 MWh.
Electrical demand of microgrid
Heat demand of microgrid
Each bus of studied model has its own share from electrical and heat demands of network which is illustrated in Fig. 7.
Share of each bus from electrical and heating demands
Finally, price of upstream network is captured in Fig. 8 (Nazari-Heris et al. 2017).
Price of upstream network
4 Simulation Results
In this section, simulation results related to the economic dispatch of CHP-based microgrid in a 10-bus test system have been presented. Studied test system is divided into several zones, and local generation units in each zone can be operated either in grid-connected mode or islanded mode. Zone 1 covers buses 1, 2 and 6. Zone 2 includes buses 3, 4 and 5, and zone 3 includes buses 7, 8, 9 and 10. So, two case studies are investigated, namely operation of CHP-based microgrid in grid-connected mode which is case 1 and operation of CHP-based microgrid in islanded mode which is case 2.
In order to solve the proposed model, DICOPT solver of General Algebraic Modeling System (GAMS) has been used (Brooke and Meeraus 1990). DICOPT is a well-known solver of the GAMS, which is able to solve models of the form:
In which, continuous and discrete variables of the optimization problem are indicated by x and y, respectively. The symbol \(\sim\) is utilized in the optimization problem to define relational operators of \(\{ \le , = , \ge \}\). It can be mentioned that the constraints of the optimization problem can be either linear or nonlinear ones. Bounds l and u on the variables are dealt with directly. To define the smallest integer, greater than or equal to x, \(\left\lceil x \right\rceil\) is used. Similar to such indication, \(\left\lfloor x \right\rfloor\) is utilized to define the largest integer, less than or equal to x. It is notable that the discrete variables can be either binary or integer variables. Accordingly, the DICOPT solver is implemented in this study to solve the presented model for solving the economic dispatch problem of multi-zone microgrids containing the CHP plants, boilers, power generators, PV units, WT and battery storage under limitations of electrical networks. Here, \(f(x, \, y)\) in (40) is the operation cost of the problem mentioned by (1), (2), (17) and (19). The constraints \(g(x, \, y) \sim b\) in (40) are the constraints of the problem (3)–(5), (8)–(14), (21)–(27), (31)–(36), (38) and (39). Additionally, the variables limitation of \(l_{x} \le x \le u_{x}\) in (40) is the variables limitation of the problem mentioned in (6), (7), (15), (16), (18), (20), (28)–(30) and (37).
The results obtained from simulations are presented in the following.
4.1 Results
Case (1) Operation of CHP-based microgrid in grid-connected mode: In this mode, in addition to the local generation units available in the microgrid such as PV system, wind turbines, power generators, CHP units and electrical energy storage system in each zone, provided power by the upstream network which is injected to the buses 1 and 3 can be used to supply energy demand. Total operation cost of CHP-based microgrid in this mode is $3805.634 which includes $1584.706 cost of purchased power from upstream network, $ 309.514 cost of generated power by PO units, $1105.378 cost of CHP units and $ 806.036 cost of HO units. In this case, injected power by the upstream network to the substations 1 and 3 is used to supply some energy demand. The provided power by the upstream network is depicted in Fig. 9. Total generated power by renewable units including PV and wind units is captured in Fig. 10. Furthermore, generated power by power generators or so-called power-only (PO) units at buses 1, 3 and 10 as well as generated heat by boiler units or so-called heat-only (HO) units at buses 3, 5 and 7 are illustrated in Figs. 11 and 12, respectively.
Purchased power from upstream network in grid-connected mode
Produced power by renewable units in grid-connected mode
Produced power by PO units in grid-connected mode
Produced heat by HO units in grid-connected mode
Case (2) Operation of CHP-based microgrid in islanded mode: In this mode, local generation units of microgrid in each zone are the only resources to supply energy demands of microgrid. So, total operation cost of microgrid in this mode is $ 3513.902 which includes $ 1105.378 cost of CHP units, $ 1602.488 cost of PO units and $ 806.036 cost of HO units. According to the obtained results, total operation cost of microgrid in the islanded mode is reduced 7.66% in comparison with grid-connected mode. This reduction is mainly because in islanded mode, renewable units have been operated more to generate more power to supply energy demand in comparison with grid-connected mode. Also, distributed power-only units have generated more power to make up the energy deficiency caused by the absence of power of upstream network. It can be understood from these results that by integrating distributed energy units in microgrids, energy demands can be supplied without considering upstream network which can lead to better economic results. The produced power by renewable units and well-generated power and heat by PO and HO units are illustrated in Figs. 13, 14 and 15.
Produced power by renewable units in islanded mode
Produced power by PO units in islanded mode
Produced heat by HO units in islanded mode
As it can be seen from Figs. 9, 10, 11 and 12, in gird-connected mode, most of the active electrical demand has been satisfied through the imported power from power market. In fact, imported power from power market seems to be more economic for the operator of system. In other words, from economic viewpoints, purchased power from power market with various hourly prices has been preferred to the generated power by local generation units operated with fixed operation cost.
On the other hand, when microgrid has been operated in islanded mode, responsibility of local generation units has been increased to supply electrical demand. As depicted in Figs. 13, 14 and 15, generation of power generators located in buses 1 and 3 has been increased to supply electrical demand. In detail, since power market power is injected to buses 1 and 3 in grid-connected mode, when the injected power to the mentioned buses has been ignored in the islanded mode, total generated power by power generators located in buses 1 and 3 has been increased. For more comparison, total generated power by power generators located in buses 1, 3 and 10 is illustrated in grid-connected and islanded operation modes in Figs. 16, 17 and 18.
Produced heat by PO unit located in bus 1 in different cases
Produced heat by PO unit located in bus 3 in different cases
Produced heat by PO unit located in bus 10 in different cases
4.2 Comparison
The proposed methodology in this paper aims at minimizing total operation cost of renewable-based microgrid by considering power flow constraints. The proposed mathematical-based model is studied in islanded and grid-connected modes. In comparison with other researches that have investigated the similar problem, the results obtained in this paper seem to be more realistic. In other words, there have been some papers that have dealt with economic scheduling of CHP-based microgrid energy system. For instance, Alipour et al. (2015) have studied optimal scheduling of CHP-based microgrids in which feasible regions of CHP units have been linearly modeled. However, power flow limitations have not been considered in the mentioned paper. In this paper, similar problem has been studied in a 10-bus test system with considering power flow limitations. Considering power flow constraints can lead to accurate simulations so that supplied power by the generation sections can be calculated more accurately. In this paper, the main goal of proposing optimization model for microgrid energy systems is to assess optimal scheduling of CHP-based microgrid energy systems in realistic condition to reach practical results.
A comprehensive comparison of the literature with the present study is provided in Table 6, which includes different viewpoints. The main objective of each study as well as time horizon of each work has been reported. In addition, the system components of studied systems have been introduced including CHP, thermal generator, boiler, wind, PV, fuel cell and battery. Moreover, the consideration of multi-zone structure and implementation of the frameworks on multi-bus system are determined. Finally, the solution method of each introduced model is investigated, which contains GAMS optimization solvers, Lagrangian relaxation method, branch and bound technique and heuristic optimization method. It can be observed that the presented model in this paper can be defined as a comprehensive model in terms of consideration of multi-zone structure and multi-bus system in integrated heat and power microgrids taking into account the limitation of electrical energy network. Thus, the presented model is superior to other works in the literature by solving the optimal scheduling of integrated heat and power energy systems in realistic condition since both multi-zone structure and multi-bus system as well as CHP units, energy storage technologies and renewable energy sources are taken into account in the present study.
5 Simulation Results
Economic dispatch of CHP-based microgrid in a 10-bus test system is studied under power flow constraints in this paper. Studied test system is divided into several zones, and each zone can operate either in grid-connected mode or islanded mode. The studied test system includes local generation units including renewable and non-renewable ones such as conventional thermal plants, CHP units, WT units, PV system, battery storage systems, boiler units and heat buffer tank. Mixed-integer linear programming is used to model the feasible operating regions of CHP units. The simulation results revealed that total operation cost of CHP-based microgrid in islanded mode is reduced 7.66% in comparison with grid-connected mode. In fact, in the islanded mode, by integrating renewable and non-renewable distributed generation units, energy demand is supplied through local units, which has led to better economic operation of microgrid. In other words, increase in portion of renewable units in supplying energy demand has reduced total cost of operating system. So, it can be concluded that optimal operation of CHP-based microgrid can be obtained in islanded mode.
Abbreviations
- \({\text{t}}\) :
-
Index of scheduling time
- \({\text{n}}\), \({\text{u}}\) :
-
Index of buses
- \({\text{k}}\) :
-
Index of CHP generation units
- \({\text{l}}\) :
-
Index of power generation units
- \({\text{m}}\) :
-
Index of boiler units
- \({\text{i}}\) :
-
Index of local generation units
- \(\lambda_{\text{t}}\) :
-
Price of power market
- \(\psi_{\text{m}}\) :
-
Coefficient used for modeling cost function of boilers
- \(\psi_{\text{l}}\) :
-
Coefficient used for modeling cost function of power generation units
- \(\beta_{\text{loss}}\) :
-
Amount of loss within shutdown condition
- \(\beta_{\text{gain}}\) :
-
Excess generated heat within start-up condition
- \(\eta\) :
-
Rate of loss of heat in heat buffer tank
- \(\eta_{{{\text{r}},{\text{n}}}}^{\text{charge}}\) :
-
Charge efficiency of battery
- \(\eta_{{{\text{r}},{\text{n}}}}^{\text{discharge}}\) :
-
Discharge efficiency of battery
- \(\eta_{\text{PV}}^{\text{t}}\) :
-
Efficiency of PV system
- \(A\) :
-
Installation area of PV system
- \(a_{\text{k}}\) :
-
Coefficient related to cost function of CHP units
- \(b_{\text{k}}\) :
-
Coefficient related to cost function of CHP units
- \(c_{\text{k}}\) :
-
Coefficient related to cost function of CHP units
- \(d_{\text{k}}\) :
-
Coefficient related to cost function of CHP units
- \(e_{\text{k}}\) :
-
Coefficient related to cost function of CHP units
- \(f_{\text{k}}\) :
-
Coefficient related to cost function of CHP units
- \(B_{\rm{min} }\) :
-
Minimum heat of heat buffer tank
- \(B_{\rm{max} }\) :
-
Maximum heat of heat buffer tank
- \(B_{\rm{max} }^{\text{charge}}\) :
-
Maximum charge rate of buffer tank
- \(B_{\rm{max} }^{\text{discharge}}\) :
-
Maximum discharge rate of buffer tank
- \({\text{CSU}}_{{{\text{i}},{\text{t}},{\text{n}}}}\) :
-
Start-up cost of local generation units
- \({\text{CSD}}_{\text{i,t,n}}\) :
-
Shutdown cost of local generation units
- \(E_{{{\text{r}},{\text{t}},{\text{n}}}}^{\rm{min} }\) :
-
Minimum energy of battery
- \(E_{\text{r,t,n}}^{ \rm{max} }\) :
-
Maximum energy of battery
- \(H_{\text{m}}^{\text{B,min}}\) :
-
Minimum heat production of boiler
- \(H_{\text{m}}^{\text{B,max}}\) :
-
Maximum heat production of boiler
- \(\overline{{H_{\text{t,n}} }}\) :
-
Total produced heat by boilers and CHP units
- \(H\) :
-
Number of time periods
- \(N_{\text{CHP}}\) :
-
Number of CHP generation units
- \(N_{\text{G}}\) :
-
Number of power generators
- \(N_{\text{B}}\) :
-
Number of boiler units
- \(N_{\text{bus}}\) :
-
Number of buses
- \(M\) :
-
A great number
- \(P_{\text{PV}}^{\text{rated}}\) :
-
Rated capacity of PV unit per 1 m2
- \(P_{\text{r,t,n}}^{\text{demand}}\) :
-
Base value of active electrical load
- \(P_{\text{l}}^{\text{G,max}}\) :
-
Maximum power production capacity of conventional power generators
- \(P_{\text{l}}^{\text{G,min}}\) :
-
Minimum power production capacity of conventional power generators
- \(P_{\text{u,t,n}}^{ \rm{max} }\) :
-
Maximum power of wind generation unit
- \(P_{\text{L}}^{\text{un}}\) :
-
Limitation of capacity of line in microgrid
- \(P_{\text{r,t,n}}^{\text{charge,min}}\) :
-
Minimum charge constraint of battery
- \(P_{\text{r,t,n}}^{\text{charge,max}}\) :
-
Maximum charge constraint of battery
- \(P_{\text{r,t,n}}^{\text{discharge,min}}\) :
-
Minimum discharge rate of battery
- \(P_{\text{r,t,n}}^{\text{discharge,max}}\) :
-
Maximum discharge rate of battery
- \(V_{\text{u,t,n}}^{\text{CI}}\) :
-
Cut-in wind speed of wind unit
- \(V_{\text{u,t,n}}^{\text{R}}\) :
-
Rated wind speed of wind unit
- \(V_{\text{u,t,n}}^{\text{CO}}\) :
-
Cut-out wind speed of wind unit
- \(Y_{\text{line}}^{\text{mn}}\) :
-
Admittance of line
- \(\alpha_{\text{r,t,n}}^{\text{charge}}\) :
-
Binary variable for charging condition of battery
- \(\beta_{\text{r,t,n}}^{\text{discharge}}\) :
-
Binary variable for discharging condition of battery
- \(B_{\text{t,n}}\) :
-
Available heat of heat buffer unit
- \(C_{\text{k,t,n}}^{\text{CHP}}\) :
-
Cost of energy generation of CHP units
- \(C_{\text{l,t,n}}^{\text{G}}\) :
-
Cost of generated power by power generators
- \(C_{\text{m,t,n}}^{\text{B}}\) :
-
Cost of heat generation of boiler units
- \(E_{\text{r,t,n}}^{\text{B}}\) :
-
Energy of battery
- \(H_{\text{k,t,n}}^{\text{CHP}}\) :
-
Produced heat by CHP generation units
- \(H_{\text{m,t,n}}^{\text{b}}\) :
-
Produced heat by boilers
- \(H_{\text{t,n}}^{\text{D}}\) :
-
Output heat of heat buffer tank
- \(H_{\text{t,n}}\) :
-
Provided heat by heat buffer
- \(P_{\text{t,n}}^{\text{buy}}\) :
-
Imported power from power market
- \(P_{\text{k,t,n}}^{\text{CHP}}\) :
-
Generated power by CHP generation units
- \(P_{\text{l,t,n}}^{\text{G}}\) :
-
Generated power by power generators
- \(P_{\text{u,t,n}}^{{\prime {\text{W}}}}\) :
-
Produced power by wind generation units
- \(P_{\text{u,t,n}}^{\text{W}}\) :
-
Scheduled power of wind turbine
- \(P_{{{\text{f}},{\text{t}},{\text{n}}}}^{{\prime {\text{PV}}}}\) :
-
Generated power by PV system
- \(P_{{f,{\text{t}},{\text{n}}}}^{\text{PV}}\) :
-
Produced power by PV system
- \(P_{\text{r,t,n}}^{\text{discharge}}\) :
-
Discharging power of battery
- \(P_{\text{r,t,n}}^{\text{charge}}\) :
-
Charging power of battery
- \({\text{SU}}_{\text{i,t,n}}\) :
-
Start-up condition of electrical units
- \({\text{SD}}_{\text{i,t,n}}\) :
-
Shutdown condition of electrical units
- \({\text{SU}}_{\text{h,t,n}}\) :
-
Start-up condition of thermal energy units
- \({\text{SD}}_{\text{h,t,n}}\) :
-
Shutdown condition of thermal energy units
- \(V_{\text{u,t,n}}^{\text{W}}\) :
-
Hourly speed of wind
- \(V_{{ 1 , {\text{t,n}}}}\) :
-
Binary variable expressing ON/OFF condition of CHP type-1
- \(V_{{ 2 , {\text{t,n}}}}\) :
-
Binary variable expressing ON/OFF condition of CHP type-2
- \(V_{\text{m,t,n}}\) :
-
Binary variable expressing ON/OFF condition of boilers
- \(V_{\text{t}}^{\text{n}}\) :
-
Voltage magnitude at bus n
- \(V_{\text{t}}^{\text{u}}\) :
-
Voltage magnitude at bus u
- \(X_{{1,{\text{t}},{\text{n}}}}\) :
-
Binary variable used for modeling first convex region of FOR of CHP type-2
- \(X_{{ 2 , {\text{t,n}}}}\) :
-
Binary variable used for modeling second convex region of FOR of CHP type-2
- \(\theta_{\text{t}}^{\text{n}}\) :
-
Voltage angle at bus n
- \(\theta_{\text{t}}^{\text{u}}\) :
-
Voltage angle at bus u
References
Abdolmohammadi HR, Ahad K (2013) A Benders decomposition approach for a combined heat and power economic dispatch. Energy Convers Manag 71:21–31
Abu-Sharkh S et al (2006) Can microgrids make a major contribution to UK energy supply? Renew Sustain Energy Rev 10(2):78–127
Alipour M, Zare K, Mohammadi-Ivatloo B (2014) Short-term scheduling of combined heat and power generation units in the presence of demand response programs. Energy 71:289–301
Alipour M, Mohammadi-Ivatloo B, Zare K (2015) Stochastic scheduling of renewable and CHP-based microgrids. IEEE Trans Ind Inf 11(5):1049–1058
Barklund E et al (2008) Energy management in autonomous microgrid using stability-constrained droop control of inverters. IEEE Trans Power Electron 23(5):2346–2352
Baziar A, Kavousi-Fard A (2013) Considering uncertainty in the optimal energy management of renewable micro-grids including storage devices. Renewable Energy 59:158–166
Brooke DKA, Meeraus A (1990) Gams User’s Guide, O. A. http://www.gams.com/docs/gams/GAMSUsers, and Guide.pdf
Dolatabadi A, Behnam MI (2017) Stochastic risk-constrained scheduling of smart energy hub in the presence of wind power and demand response. Appl Therm Eng 123:40–49
Haghrah A, Nazari-Heris M, Mohammadi-Ivatloo B (2016) Solving combined heat and power economic dispatch problem using real coded genetic algorithm with improved Mühlenbein mutation. Appl Therm Eng 99:465–475
Jaramillo LB, Weidlich A (2016) Optimal microgrid scheduling with peak load reduction involving an electrolyzer and flexible loads. Appl Energy 169:857–865
Kai-Wei H, Liaw C-M (2016) Incorporated operation control of DC microgrid and electric vehicle. IEEE Trans on Industrial Electronics 63(1):202–215
Kanchev H et al (2011) Energy management and operational planning of a microgrid with a PV-based active generator for smart grid applications. IEEE Trans Ind Electron 58(10):4583–4592
Kusakana K (2015) Optimal scheduled power flow for distributed photovoltaic/wind/diesel generators with battery storage system. IET Renew Power Gener 9(8):916–924
Liu G, Xu Y, Tomsovic K (2016) Bidding strategy for microgrid in day-ahead market based on hybrid stochastic/robust optimization. IEEE Trans on Smart Grid 7(1):227–237
Malakar T, Goswami SK, Sinha AK (2014) Optimum scheduling of micro grid connected wind-pumped storage hydro plant in a frequency based pricing environment. Int J Electr Power Energy Syst 1(54):341–351
Moghaddam AA et al (2011) Multi-objective operation management of a renewable MG (micro-grid) with back-up micro-turbine/fuel cell/battery hybrid power source. Energy 36(11):6490–6507
Nazari-Heris M, Abapour S, Mohammadi-Ivatloo B (2017a) Optimal economic dispatch of FC-CHP based heat and power micro-grids. Appl Therm Eng 114:756–769
Nazari-Heris M, Mehdinejad M, Mohammadi-Ivatloo B, Babamalek-Gharehpetian G (2017b) Combined heat and power economic dispatch problem solution by implementation of whale optimization method. Neural Comput Appl 31:1–16
Nazari-Heris M, Mohammadi-Ivatloo B, Gharehpetian GB (2018a) A comprehensive review of heuristic optimization algorithms for optimal combined heat and power dispatch from economic and environmental perspectives. Renew Sustain Energy Rev 81:2128–2143
Nazari-Heris M, Mohammadi-Ivatloo B, Gharehpetian GB, Shahidehpour M (2018b) Robust short-term scheduling of integrated heat and power microgrids. IEEE Syst J 99:1–9
Rezvani A et al (2015) Environmental/economic scheduling of a micro-grid with renewable energy resources. J Clean Prod 87:216–226
Rong A, Lahdelma R (2007) An efficient envelope-based Branch and Bound algorithm for non-convex combined heat and power production planning. Eur J Oper Res 183(1):412–431
Sashirekha A, Pasupuleti J, Moin NH, Tan CS (2013) Combined heat and power (CHP) economic dispatch solved using Lagrangian relaxation with surrogate subgradient multiplier updates. Int J Electr Power Energy Syst 44(1):421–430
Shahverdi M, Moghaddas-Tafreshi SM (2008) Operation optimization of fuel cell power plant with new method in thermal recovery using particle swarm algorithm. In: 3rd International conference on electric utility deregulation and restructuring and power technologies, DRPT 2008. IEEE
Sobu A, Guohong W (2012) Optimal operation planning method for isolated micro grid considering uncertainties of renewable power generations and load demand. In: Innovative Smart Grid Technologies-Asia (ISGT Asia), 2012 IEEE
Talari S, Yazdaninejad M, Haghifam MR (2015) Stochastic-based scheduling of the microgrid operation including wind turbines, photovoltaic cells, energy storages and responsive loads. IET Gener Transm Distrib 9(12):1498–1509
Wu H, Liu X, Ding M (2014) Dynamic economic dispatch of a microgrid: mathematical models and solution algorithm. Int J Electr Power Energy Syst 63:336–346
Wu H et al (2016) Optimal allocation of microgrid considering economic dispatch based on hybrid weighted bilevel planning method and algorithm improvement. Int J Electr Power Energy Syst 75:28–37
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Nazari-Heris, F., Mohammadi-Ivatloo, B. & Nazarpour, D. Economic Dispatch of Renewable Energy and CHP-Based Multi-zone Microgrids Under Limitations of Electrical Network. Iran J Sci Technol Trans Electr Eng 44, 155–168 (2020). https://doi.org/10.1007/s40998-019-00208-4
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s40998-019-00208-4