Keywords

1 Introduction

Currently, the demand for electric energy is growing rapidly. On the other hand, the conventional energy sources are depleting fast, their costs are going up, and they are causing the environment contamination. To meet these challenges, the attention has focused to renewable and clean energy sources, like wind, solar, fuel cell, etc. [6, 39].

Wind energy is an important renewable green energy resource. Indeed, it is omnipresent, environmentally friendly, and freely available [8]. Further, it is characterized by its high reliability and cost effectiveness. Thanks to all these features, the wind power generation capacity has been growing rapidly, with an average annual growth around 30 %, in the world, over the last decade.

Fig. 1
figure 1

Cage induction generator-based fixed speed wind turbine

Full size image

Electric energy is generated from wind using a wind turbine and an electric generator. It can be used either for standalone loads or fed into the electric network through a suitable power electronic converters.

A wind turbine operates either at a fixed or variable speed.

  • A fixed-speed wind turbine generator generally uses a squirrel-cage induction generator to convert the mechanical energy from the wind turbine into electrical energy (Fig. 1). The generator is connected directly to the electric network. The system operates almost at constant speed even if the wind speed varies. This topology is simple, less expensive and effective. But, it suffers from the low energy capture, mechanical stress and mediocre power quality [8, 20, 21, 25].

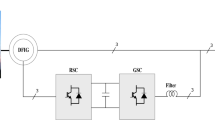
  • Variable-speed wind turbine generator provides high efficiency in capturing the energy from wind over a wider range of wind speeds, along with better power quality. Also this scheme is capable to regulate the power factor, by either consuming or producing reactive power, and ensure lower mechanical stress. The power electronic converters are incorporated between the electrical machine and the power system as shown in Fig. 2 [22, 24, 33].

Most of the major wind turbine manufacturers are developing new megawatt scale wind turbines based on variable-speed operation with pitch control.

Fig. 2
figure 2

Variable speed wind turbine connected to a grid

Full size image

1.1 Wind Turbine Generators Technologies

Different types of electric machines are used for the generation of electric energy from wind:

  • Permanent Magnets Synchronous Generator (PMSG): The PM generators can be divided into radial-flux and axial-flux generators. The advantages of a PMSG configuration are gearless construction, the elimination of a dc excitation system, full controllability of the system for maximum wind power extraction and grid interface; and straightforward in accomplishing fault-ride through and grid support [7, 20, 21]. However, the major drawback of the PMSG is the high cost of the PM material and power converter [28].

  • Doubly-Fed Induction Generator (DFIG)—wounded rotor: With this topology, the stator is connected directly to the grid whereas the rotor is linked to the grid via a bidirectional converter [27, 32]. The main characteristics of the DFIG are (i) limited operating speed range (ii) small scale power electronic converter (iii) reduced power losses and cost (vi) complete control of active and reactive power exchanged with the grid. However the most important disadvantages are necessity of gear and use of slip-rings which involve maintenance.

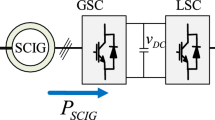
  • Squirrel Cage Induction Generator (SCIG): Induction generators were used for a long time for constant speed wind turbines. In this operating mode, the pitch control or active stall control are imposed for power limitation and protection. Currently, it is used for variable-speed wind energy systems which guarantee superior wind power extraction and better efficiency. In comparison with the DFIG, this configuration offers extended speed operating range, and complete decoupling between the generator and the network (Fig. 2), which results in higher power extraction at different wind speeds and improved capability to realize the low-voltage ride-through. Indeed, SCIG provides some advantages when compared with the PMSG and DFIG such as light weight, small size, high reliability, maintenance less, high efficiency, low cost and operational simplicity [19, 36].

1.2 Control Technique Strategies of WECS

Wind generator and its control is a very complex electromechanical system. Linear controllers have been widely used in the engineering field for their reliability and simplicity. However, their parameters are usually tuned with the approximately linearized model. Consequently, the dynamic control performance may not be guaranteed during the transients of the wind turbine with WECS. To overcome these disadvantages, many methods for the design of controllers for the WECS have been investigated in order to ensure better control performance in terms of transient stability and robustness to parameter uncertainties or disturbances. These methods are summarized as follow:

  • Field Oriented Control (FOC). Common control of grid-connected WECS is based on FOC [1, 5]. The scheme decouples the stator current into active and reactive components in the synchronous reference frame. In this technique, the control of the system is accomplished by regulating the decoupled stator currents, using proportional-integral controllers [3]. However, the major disadvantage for this linear control scheme is that the performance may demean in the case of deviation of the machine parameters, such as stator and rotor inductances and resistances, from values used in the control system.

  • Feedback linearization. The control based on this technique has been the subject of several investigations [14]. The aim of this method is to make the model of the system to be controlled exactly linearized by coordinate transformation using differential geometry theory. The obtained linearized system allows the synthesis of the control laws based on the linear optimal control principles. However, these control designs require precise models and often cancel some useful nonlinearities. Therefore, it does not guarantee the robustness in the presence of parameter uncertainties or disturbances. To overcome this drawback, numerous adaptive versions of the feedback linearizing techniques are then proposed [15, 38]. References [26, 41] present an application of this approach.

  • Backstepping technique. This method offers an efficient tool for controller synthesis through building step by step the Lyapunov functions which can guarantee the asymptotic stability of the overall closed-loop system [17]. Indeed, the backstepping is less restrictive compared to the feedback linearization control which cancels the nonlinearities that might be useful. Unlike the adaptive controllers, based on certain equivalence, which separate the design of the controller and the terms of adaptation, adaptive backstepping has emerged as an alternative. This technique has been successfully applied for control of power system and wind power generator system in [3, 29, 30].

  • Direct Torque Control (DTC). In contrast to vector control with linear controllers (PI), DTC technique presents advantages such as simple structure and insensitivity to the parameters disturbances. The DTC technique directly controls machine torque and flux by selecting voltage vectors from a look-up-table using the stator flux and torque information. The problems with the DTC method is that (i) performances are very mediocre during starting and low-speed operation; (ii) converter switching frequency variation complicates the power circuit design; (iii) ripples in flux and torque [34]. This is due to the use of predefined switching table and hysteresis regulator. To deal with those drawbacks modified DTC strategies, incorporating space vector modulation, have been used to obtain constant switching frequency [16]. Nevertheless, further drawbacks were introduced, such as additional PI controller parameters, and sensitivity to system parameter variations [13, 18].

  • Direct Power Control (DPC). More recently, direct power control was developed based on the principles of DTC strategy. In [42], it was demonstrated that the control system is less complicated and robust against parameters machine variation. Nevertheless, switching frequency varies significantly with active and reactive power variations, rotor slip, and hysteresis bandwidth of power controllers. References [12, 34, 42] present an application of this technique.

  • Sliding-Mode Control (SMC). It is the most robust control techniques for systems with uncertainties and parameter variations. It dates back to the 70 s with the work of Utkin [40]. SMC features simple implementation, disturbance rejection, strong robustness, and fast responses. Nevertheless, the problems of chattering inherent in this type of discontinuous control appear quickly and may excite the highfrequency dynamics neglected sometimes leading to instability. Methods to tackle this phenomenon have been developed [35]. More recently, This technique has been successfully applied for wind power system in [10, 11, 23, 37].

In this study, a SMC strategy, for a variable speed wind turbine equipped with SCIG connected to the grid through power converters is developed:

  • The prime control objective of the WECS is to capture the maximum wind power through MPPT control strategy. To this end, the turbine tip-speed ratio should be kept at its optimum value despite wind variations.

  • The second objective consists of maintaining the DC bus voltage constant and to achieve the grid-side Unity Power Factor (UPF).

In the sections that follow, the chapter first introduces the mathematical model of different components of wind energy conversion system in Sect. 2. Then, Sect. 3 presents the synthesis of the control laws of the SCIG in order to maximize the wind energy conversion efficiency. Control design, of active and reactive power injected into the grid, is developed in Sect. 4. Section 5 presents the simulation results to demonstrate the performance of the proposed SMC strategy. Finally, the conclusions are made in Sect. 6.

2 Mathematical Model of Wind Energy Conversion System

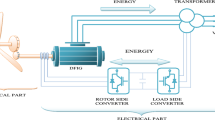
The complete wind energy conversion system consists mainly of three parts: a wind turbine drive train, a SCIG, and two back-to back Voltage Source Converters (VSC). The system considered is shown in Fig. 3.

Fig. 3
figure 3

Control scheme of wind turbine based-SCIG connected to a grid

Full size image

2.1 Model of Wind Turbine

The wind turbine basic principle is to convert the linear action of the wind into rotational energy. The converted energy is used to drive an electrical generator. Hence, the kinetic energy of the wind is transformed to electric power.

The wind power acting on the swept area of the blade A is a function of the air density (\(1.225 \,\mathrm{kg}/\mathrm{m}^{2}\)) and the wind speed \(V_{w}\) (m/s). The transmitted power Pw (w) is generally deduced from the wind power using the power coefficient \(C_{p}\) as [9]

$$\begin{aligned} P_w =\frac{1}{2}.C_p (\lambda ,\beta )\cdot \rho \cdot A \cdot V_w^3 \end{aligned}$$
(1)

The power coefficient is a nonlinear function of the tip speed-ratio \(\lambda \), which depends on the wind velocity and the rotation speed of the shaft \(\omega _{t}\).

$$\begin{aligned} \lambda =\frac{R\cdot \omega _m }{V_w } \end{aligned}$$
(2)

where R is the blade radius (m). The coefficient of power is expressed as

$$\begin{aligned} C_p (\lambda ,\beta )&=C_1 \left( {\frac{C_2 }{\lambda _i }-C_3 \cdot \beta -C_4 } \right) \cdot \exp \left( {\frac{-C_5 }{\lambda _i }-C_6 \cdot \lambda } \right) \nonumber \\ \displaystyle \quad \,\,\, \frac{1}{\lambda _i }&=\frac{1}{\lambda +0.08\cdot \beta }-\frac{0.035}{\beta ^{3}+1} \end{aligned}$$
(3)

The parameters of coefficient of power are defined in Table 1.

Table 1 Parameters of the coefficient of power
Full size table

Then, the input torque in the transmission mechanical system is given as

$$\begin{aligned} T_w =\frac{P_w }{\omega _t }=\frac{C_p (\lambda ,\beta )\cdot \rho \cdot A\cdot V_w^3 }{2\omega _t } \end{aligned}$$
(4)

The maximum value of \(C_{p}\) (\(\lambda ,\beta \)) is \(C_{pmax} = \textit{0.47}\) and obtained for \(\lambda _{opt} = \textit{8.1}\) and for \(\beta = 0^{\circ }\). If the parameters are in pet unit, \(\lambda _{pu}\) and \(C_{p\_pu}\) can be computed as

$$\begin{aligned} \left. \begin{array}{ll} &{}\displaystyle \,\lambda _{pu} =\frac{\lambda }{\lambda _{opt} }\\ &{}\displaystyle C_{p\_pu} =\frac{C_p }{C_{p-opt} } \end{array}\right. \end{aligned}$$
(5)

Both mechanical shafts are linked by the gearbox. The equation is expressed as [2]

$$\begin{aligned} 2H\frac{d\omega _m }{dt}=T_m -T_e -F\omega _m \end{aligned}$$
(6)

where \(H=H_{b}+H_{h}+H_{g}\) is the inertia constant of the single rotating mass (which includes the blades, hub and generator rotor), \(\omega _{m}\) is the rotor speed and F is the damping coefficient of a single mass.

2.2 Model of the Induction Generator

The generator, converting mechanical energy into electrical energy, is a SCIG with its stator windings connected to the grid through a frequency converter. The induction generator is described by 5th nonlinear mathematical model, in the space vector by the following state-space form [3, 20, 21]

$$\begin{aligned} \frac{1}{\omega _b }\frac{di_{sd} }{dt}=-\partial _1 i_{sd} +\omega _s i_{sq} -\partial _2 \phi _{rd} -\frac{V_{sd} }{\sigma L_s } \end{aligned}$$
(7)
$$\begin{aligned} \frac{1}{\omega _b }\frac{di_{sq} }{dt}=-\partial _1 i_{sq} -\omega _s i_{sd} +\partial _3 \phi _{rd} -\frac{V_{sq} }{\sigma L_s }\end{aligned}$$
(8)
$$\begin{aligned} \frac{1}{\omega _b }\frac{d\phi _{rd} }{dt}=-\frac{R_r \phi _{rd} }{L_r }-\frac{R_r L_m }{L_r }i_{sd} \end{aligned}$$
(9)
$$\begin{aligned} \frac{1}{\omega _b }\frac{d\phi _{rq} }{dt}=-\frac{R_r L_m }{L_r }i_{sq} -\left( {\omega _s -\omega _m } \right) \phi _{rd} \end{aligned}$$
(10)
$$\begin{aligned} 2H\frac{d\omega _m }{dt}=-\frac{L_m }{L_r }\phi _{rd} i_{sq} +T_m -F\omega _m \end{aligned}$$
(11)

where

$$\begin{aligned} \partial _1 =\frac{R_s L_r^2 +R_r L_m^2 }{\sigma L_s L_r^2 }, \partial _2 =\frac{R_r L_m }{\sigma L_s L_r^2 }, \partial _3 =\frac{L_m \omega _m }{\sigma L_s L_r }, \,\, L_r =L_{\sigma r} +L_m \quad \mathrm{and}\quad L_s =L_{\sigma s} +L_m \end{aligned}$$

\(L_{\sigma r}\) and \(L_{\sigma r}\) are the leakage inductances of stator and rotor, \(L_{m}\) is the mutual inductance. \(\omega _{b} =2\pi f\) is the system base frequency, \(\omega _{s}\) is the synchronous electrical speed, \(\omega _{m}\) is the rotor speed of the SCIG.

Remark

The nonlinear control is applied to orient rotor flux on d-axis of the rotating reference frame, therefore, \(\varPhi _{rq}=0\) and \(\varPhi _{rd} = \varPhi _{ref}\).

2.3 Model of the Converters

The frequency converter is built by two current-regulated voltage-source pulse width modulation (PWM) converters: a Machine Side Converter (MSC) and a Grid Side Converter (GSC), with a dc voltage link in between.

The modeling of the converters is made by using the concept of instantaneous average value. The converter is equivalent to a matrix topology as given in (12).

$$\begin{aligned} \left[ {\begin{array}{c} V_{sa} \\ V_{sb} \\ V_{sc} \end{array}} \right] =\frac{V_{dc} }{3}\left[ {{\begin{array}{ccc} 2&{} {-1}&{} {-1} \\ {-1}&{} 2&{} {-1} \\ {-1}&{} {-1}&{} 2 \end{array}}} \right] \left[ {\begin{array}{c} S_a \\ S_b \\ S_c \end{array}} \right] \end{aligned}$$
(12)

\(S_{a}\), \(S_{b}\), \(S_{c}\) are variables which represent the switching status and take the value 1 when the switch is closed (on) and 0 when it is opened (off).

The model of DC link voltage is given as [4]

$$\begin{aligned} Cv_{dc} \frac{dv_{dc} }{dt}=P_{ge} -P_{gr} \end{aligned}$$
(13)

where C is the capacitance, \(P_{ge}\) is the active power of generator and \(P_{gr}\) is the active power injected into AC network.

2.4 The Model of the Filter

The SCIG is connected to the grid through a filter. The model of the filter is given by [20, 21]

$$\begin{aligned} v_{fd} =L_f \frac{di_{fd} }{dt}+R_f i_{fd} -L_f \omega _e i_{fq} +e_d \end{aligned}$$
(14)
$$\begin{aligned} v_{fq} =L_f \frac{di_{fq} }{dt}+R_f i_{fq} +L_f \omega _e i_{fd} +e_q \end{aligned}$$
(15)

where \(L_{f}\) and \(R_{f}\) are the filter inductance and filter resistance respectively; \(v_{fd}\) and \(v_{fq}\) are the filter voltage components of d-axis and q-axis respectively, \(e_{d}\) and \(e_{q}\) are the grid voltage components of d-axis and q-axis respectively, \(i_{fd}\) and \(i_{fq}\) are the values of the current of d axis and q-axis respectively, and \(\omega _{e}=2\pi f\) where f is the grid frequency.

3 Nonlinear Control of SCIG

A generator side converter connected to the stator of the SCIG effectively decouples the generator from the grid. Hence, the generator rotor speed depends only on the wind conditions.

The first control objective is to track the optimum generator speed \(\omega _{m\_opt}\) and to orient the rotor flux on the d-axis.

3.1 Control of Generator Speed

The optimum generator speed \(\omega _{m\_opt}\) is generated by a MPPT technique to determine the stabilizing function. The tracking error between speed and its reference is given as

$$\begin{aligned} e_1 =\omega _{m\_opt} -\omega _m \end{aligned}$$
(16)

The sliding surface is chosen as follow

$$\begin{aligned} S_1 (t)=K_1 e_1 (t) \end{aligned}$$
(17)

where \(K_1\) is a positive constant feedback gain.

In order to satisfy the sliding mode existence law, the control input is chosen to have the following structure

$$\begin{aligned} u(t)=u_{eq} (t)+u_n (t) \end{aligned}$$
(18)

where \(u_{eq}(t)\) is an equivalent control-input that determines the system’s behavior on the sliding surface and \(u_{n}(t)\) is a non-linear switching input, which drives the state to the sliding surface and maintains the state on the sliding surface in the presence of the parameter variations and disturbances [31, 40]. The equivalent control-input is obtained from the invariance condition and is given by the following condition \(S_1 =0\) and \(\frac{dS}{dt}=0\Rightarrow u(t)=u_{eq} (t)\).

Hence the derivative of the sliding surface (17) is given as

$$\begin{aligned} \left. \begin{array}{ll} \frac{dS_1 (t)}{dt}&{}=K_1 \left( {\frac{d\omega _{m\_opt} }{dt}-\frac{d\omega _m }{dt}} \right) \\ &{}=K_1 \frac{d\omega _{m\_opt} }{dt}+\frac{K_1 }{2H}\left( {\frac{L_m \phi _{ref} }{L_r }i_{sq} -T_m +F\omega _m } \right) \end{array}\right. \end{aligned}$$
(19)

The \(i_{sq}\) can be viewed as a virtual control in the above equation. It is derived to ensure the SCIG speed convergence to the optimum speed. To ensure the Lyapunov stability criteria i.e. \(\frac{dS_1 }{dt}S_1 \prec 0\), the nonlinear control input \(i_{sq\_eq}\) is defined as

$$\begin{aligned} i_{sq\_eq} =\left( {-2H\frac{d\omega _{m\_opt} }{dt}+T_m -F\omega _m } \right) \frac{L_r }{L_m \varphi _{ref} } \end{aligned}$$
(20)

The nonlinear switching input \(i_{sq-n}\) can be chosen as follows

$$\begin{aligned} i_{sq-n} =-\alpha _1 \frac{2HL_r }{L_m \varphi _{ref} }\,\mathrm{sgn}\left( {e_1 } \right) \end{aligned}$$
(21)

where \(\alpha _{1}\) is a positive constant and the sign function is defined to reduce the phenomenon of charting as

$$\begin{aligned} \mathrm{sgn}\left( {S(t)} \right) =\frac{S(t)}{\left. {\left| {S(t)} \right. } \right| +\varepsilon } \end{aligned}$$
(22)

where \(\varepsilon \) is a small positive number. Then, the reference of q-axis current is expressed as

$$\begin{aligned} i_{sq\_ref} =\left( {-2H\frac{d\omega _{m\_opt} }{dt}+T_m -F\omega _m -2H\alpha _1 \,\mathrm{sgn}\left( {e_1 } \right) } \right) \frac{L_r }{L_m \phi _{ref} } \end{aligned}$$
(23)

Substituting (23) in (19), the q-axis current sliding surface dynamics becomes

$$\begin{aligned} \frac{dS_1 (t)}{dt}=-K_1 \alpha _1 \,\mathrm{sgn}\left( {e_1 } \right) \end{aligned}$$
(24)

3.2 Control of d-Axes Rotor Flux

The d-axis rotor flux \(\varPhi _{rd}\) can be estimated from Eq. (9) as

$$\begin{aligned} \phi _{rd-estim} =-\frac{L_m }{1+T_r \cdot s}i_{sd} \end{aligned}$$
(25)

where \(T_r =\frac{\omega _b L_r }{R_r }\) is the time constant.

The stabilizing error between \(\phi _{rd} \) and its desired trajectory \(\phi _{ref}\) is defined as

$$\begin{aligned} e_2 (t)=\phi _{ref} -\phi _{rd} \end{aligned}$$
(26)

To stabilize the d-axis rotor flux \(\varPhi _{rd}\), the new sliding surface is selected as

$$\begin{aligned} S_2 (t)=K_2 e_2 (t) \end{aligned}$$
(27)

where \(K_2\) is a positive constant. The derivative of \(S_2 (t)\) using (9) and (27) is given as

$$\begin{aligned} \frac{dS_2 (t)}{dt}=K_2 \frac{d\phi _{ref} }{dt}+K_2 \omega _b \frac{R_r }{L_r }\left[ {\phi _{rd} +L_m i_{sd} } \right] \end{aligned}$$
(28)

Then, the equivalent control \(i_{sd\_eq}\) (29) is obtained as the solution of the equation \(\frac{dS_2 (t)}{dt}=0\).

$$\begin{aligned} i_{sd\_eq} =-\frac{L_r }{\omega _b L_m R_r }\frac{d\phi _{ref} }{dt}-\frac{1}{L_m }\phi _{rd} \end{aligned}$$
(29)

As a result, the stabilizing function of the control current is defined as

$$\begin{aligned} i_{sd\_ref} =-\frac{L_r }{\omega _b L_m R_r }\frac{d\phi _{ref} }{dt}-\frac{1}{L_m }\phi _{rd} -\frac{L_r }{\omega _b L_m R_r }\alpha _2 \,\mathrm{sgn}\left( {e_2 } \right) \end{aligned}$$
(30)

where \(\alpha _{2}\) is a positive constant. Using (30), the d-axis current sliding surface dynamics (28) becomes

$$\begin{aligned} \frac{dS_2 (t)}{dt}=-K_2 \alpha _2 \,\mathrm{sgn}\left( {e_2 } \right) \end{aligned}$$
(31)

Since the d-axis current and the q-axis current are not our control inputs, the stabilizing errors between \(i_{sd\_ref}\) and \(i_{sq\_ref}\) and their desired trajectories, respectively, are defined as

$$\begin{aligned} e_3 (t)=i_{sd\_ref} (t)-i_{sd} (t) \end{aligned}$$
(32)
$$\begin{aligned} e_4 (t)=i_{sq\_ref} (t)-i_{sq} (t) \end{aligned}$$
(33)

To stabilize \(i_{sd}(t)\) and \(i_{sq}(t)\), the new sliding surfaces are selected as

$$\begin{aligned} \left\{ {\begin{array}{l} S_3 (t)=K_3 e_3 (t) \\ S_4 (t)=K_4 e_4 (t) \\ \end{array}} \right. \end{aligned}$$
(34)

where \(K_3\) and \(K_4\) are a positive constants. Then, the derivative of sliding surfaces are defined as

$$\begin{aligned} \frac{dS_3 (t)}{dt}=K_3 \left( {\frac{di_{sd\_ref} }{dt}-\frac{di_{sd} }{dt}} \right) \end{aligned}$$
(35)
$$\begin{aligned} \frac{dS_4 (t)}{dt}=K_{_4 } \left( {\frac{di_{sq\_ref} }{dt}-\frac{di_{sq} }{dt}} \right) \end{aligned}$$
(36)

when replacing (7) in (35) and (8) in (36), then track the same steps used to obtain the control currents, the control voltage laws are obtained as

$$\begin{aligned} V_{sd\_ref} =\sigma L_s \left( {-\frac{1}{\omega _b }\frac{di_{sd\_ref} }{dt}-\partial _1 i_{sd} +\omega _s i_{sq} -\partial _2 \phi _{rd} -\frac{\alpha _3 }{\omega _b }\,\mathrm{sgn}\left( {e_3 (t)} \right) } \right) \end{aligned}$$
(37)
$$\begin{aligned} V_{sq\_ref} =\sigma L_s \left( {-\frac{1}{\omega _b }\frac{di_{sq\_ref} }{dt}-\partial _1 i_{sq} -\omega _s i_{sd} +\partial _3 \phi _{rd} -\frac{\alpha _4 }{\omega _b }\,\mathrm{sgn}\left( {e_4 (t)} \right) } \right) \end{aligned}$$
(38)

3.3 Stability Analysis

Theorem 1

The dynamic sliding mode control laws (37) and (38) with stabilizing functions (23) and (30) when applied to the SCIG side converter, guarantee the asymptotic convergence of the generator speed \(\omega _{m}\) and the d-axis rotor flux \(\varPhi _{rd}\) to their desired values \(\omega _{m\_opt}\) and \(\phi _{ref}\), respectively.

Proof

Consider the following positive definite Lyapunov function

$$\begin{aligned} V_1 =\frac{1}{2}S_1^2 +\frac{1}{2}S_2^2 +\frac{1}{2}S_3^2 +\frac{1}{2}S_4^2 \end{aligned}$$
(39)

By considering (24), (31), (35) and (36), the derivative of (39) can be derived as follows

$$\begin{aligned} \frac{dV_1 }{dt}&=\frac{dS_1 }{dt}S_1 +\frac{dS_2 }{dt}S_2 +\frac{dS_3 }{dt}S_3 +\frac{dS_4 }{dt}S_4 \nonumber \\&=-K_1^2 \alpha _1 e_1 \,\mathrm{sgn}\left( {e_1 } \right) -K_2^2 \alpha _2 e_2 \,\mathrm{sgn}\left( {e_2 } \right) \\&\quad +K_3^2 e_3 \left( {\frac{di_{sd\_ref} }{dt}-\frac{di_{sd} }{dt}} \right) \hbox {+}K_4^2 e_4 \left( {\frac{di_{sq\_ref} }{dt}-\frac{di_{sq} }{dt}} \right) \nonumber \end{aligned}$$
(40)

Substituting the control laws (37) and (38) in (40) gives

$$\begin{aligned} \frac{dV_1 }{dt}&=-K_1^2 \alpha _1 e_1 \,\mathrm{sgn}\left( {e_1 (t)} \right) -K_2^2 \alpha _2 e_2 \,\mathrm{sgn}\left( {e_2 (t)} \right) \nonumber \\&\quad -K_3^2 \alpha _3 e_3 \,\mathrm{sgn}\left( {e_3 (t)} \right) -K_4^2 \alpha _4 e_4 \,\mathrm{sgn}\left( {e_4 (t)} \right) \\&=-\sum _{i=1}^4 {\alpha _i K_i^2 \left| {e_i } \right| } <0 \nonumber \end{aligned}$$
(41)

From the above analysis, it is evident that the reaching condition of sliding mode is guaranteed.

4 Sliding Mode Control of Grid Side Converter

The aim of the grid side converter control is to maintain the dc link voltage constant, thereby ensuring that the active power generated by the SCIG is fed to the grid. Also this control must be able to provide perfect tracking performance of the reactive power fed to the network to its reference trajectory.

4.1 Control Laws of Reactive and Active Powers

By orienting the grid voltage space vector on the d axis, we obtain

$$\begin{aligned} \left. \begin{array}{ll} &{} e_d=V \\ &{} e_q=0 \end{array}\right. \end{aligned}$$
(42)

Substituting (42) in (14) and (15) gives the following equations of the filter

$$\begin{aligned} \frac{di_{fd} }{dt}=\frac{1}{L_f }\left( {v_{fd} -R_f i_{fd} +L_f \omega _e i_{fq} -V} \right) \end{aligned}$$
(43)
$$\begin{aligned} \frac{di_{fq} }{dt}=\frac{1}{L_f }\left( {v_{fq} -R_f i_{fq} -L_f \omega _e i_{fd} } \right) \end{aligned}$$
(44)

The reactive power and active power of grid can be expressed as

$$\begin{aligned} P_{gr} =i_{fd} V \end{aligned}$$
(45)
$$\begin{aligned} Q_{gr} =i_{fq} V \end{aligned}$$
(46)

From (45) and (46), it can be seen that the active and reactive power of grid can be controlled by the direct and quadrature components current, respectively. Then, let’s define

$$\begin{aligned} e_5 (t)=i_{fd\_ref} -i_{fd} \end{aligned}$$
(47)
$$\begin{aligned} e_6 (t)=i_{fq\_ref} -i_{fq} \end{aligned}$$
(48)

where \(i_{fd\_ref}\) and \(i_{fq\_ref}\) are the desired values of the \(i_{fd}\) and \(i_{fq}\). The current \(i_{fd\_ref}\) is derived directly from the control loop of the DC bus voltage, while \(i_{fq\_ref}\) is computed by (48). \(Q_{gr}\) is set to zero in order to ensure unit power factor \(i_{fq\_ref} =0\). The sliding surface for \(i_{fd}\) and \(i_{fq}\) can be expressed as

$$\begin{aligned} S_5 (t)=K_5 e_5 (t) \end{aligned}$$
(49)
$$\begin{aligned} S_6 (t)=K_6 e_6 (t) \end{aligned}$$
(50)

The DC bus voltage is regulated by using the proportional integral (PI) regulator. The derivative of (49) and (50) using (43) and (44) gives

$$\begin{aligned} \frac{dS_5 (t)}{dt}=K_5 \left( {\frac{di_{fd\_ref} }{dt}-\frac{1}{L_f }\left( {v_{fd} -R_f i_{fd} +L_f \omega _e i_{fq} -V} \right) } \right) \end{aligned}$$
(51)
$$\begin{aligned} \frac{dS_6 (t)}{dt}=K_6 \left( {\frac{di_{fq\_ref} }{dt}-\frac{1}{L_f }\left( {v_{fq} -R_f i_{fq} -L_f \omega _e i_{fd} } \right) } \right) \end{aligned}$$
(52)

To ensure the reaching condition \(\frac{dS_5 }{dt}S_5 \prec 0\), the equivalent control \(v_{fd-eq}(t)\) is obtained as

$$\begin{aligned} v_{fd-eq} =L_f \frac{di_{fd\_ref} }{dt}+R_f i_{fd} -L_f \omega .i_{fq} +V \end{aligned}$$
(53)

Subsequently, the control law is written as follows

$$\begin{aligned} v_{fd} =L_f \frac{di_{fd\_ref} }{dt}+R_f i_{fd} -L_f \omega .i_{fq} +V+\alpha _5\, \mathrm{sgn}\left( {e_5 (t)} \right) \end{aligned}$$
(54)

In the same way, the control voltage law for the reactive power tracking is given as

$$\begin{aligned} v_{fq} =L_f \frac{di_{fq\_ref} }{dt}+R_f i_{fq} +L_f \omega .i_{fd} +L_f \alpha _6 \,\mathrm{sgn}(e_6 (t)) \end{aligned}$$
(55)

4.2 Stability Analysis

Theorem 2

The dynamic sliding mode control laws (54) and (55) when applied to the grid side converter, guarantee the asymptotic convergence of the reactive and active powers to their reference trajectories \(P_{gr}\) and \(Q_{gr} =0\), respectively.

Proof

Consider the following positive definite Lyapunov function

$$\begin{aligned} V_2 =\frac{1}{2}S_5^2 +\frac{1}{2}S_6^2 \end{aligned}$$
(56)

By considering (51) and (52) the derivative of (56) can be derived as follows

$$\begin{aligned} \frac{dV_2 }{dt}&=\frac{dS_5 }{dt}S_5 +\frac{dS_6 }{dt}S_6\nonumber \\&=K_5^2 e_5 \left( {\frac{di_{fd\_ref} }{dt}-\frac{1}{L_f }\left( {v_{fd} -R_f i_{fd} +L_f \omega _e i_{fq} -V} \right) } \right) \nonumber \\&\quad +K_6^2 e_6 \left( {\frac{di_{fq\_ref} }{dt}-\frac{1}{L_f }\left( {v_{fq} -R_f i_{fq} -L_f \omega _e i_{fd} } \right) } \right) \end{aligned}$$
(57)

Substituting the control laws (54) and (55) in (57) gives

$$\begin{aligned} \frac{dV_2 }{dt}&=-\alpha _5 K_5^2 e_5 \,\mathrm{sgn}\left( {e_5 (t)} \right) -\alpha _6 K_6^2 e_6 \,\mathrm{sgn}(e_6 (t)) \nonumber \\&=-\alpha _5 K_5^2 \left| {e_5 } \right| -\alpha _6 K_6^2 \left| {e_6 } \right| \nonumber \\&\le 0 \end{aligned}$$
(58)

Therefore the condition of sliding mode of the system is guaranteed.

5 Simulation Results and Discussion

A 3 MW, 690 V SCIG wind turbine system is simulated in the MATLAB/Simulink software environment to demonstrate the effectiveness of the proposed control scheme. The SCIG wind turbine is modeled by 5th nonlinear mathematical model. The MSC and the GSC are represented by a switch-level model in which the operation of each individual switch is fully represented. Figure 4 shows the scheme of the implemented system. The parameters of the SCIG wind turbine are given in the Table 2.

Fig. 4
figure 4

Schematic diagram of the proposed control of SCIG wind turbine

Full size image
Table 2 Parameters of the wind turbine SCIG
Full size table
Fig. 5
figure 5

Simulation results of MPPT control of SCIG wind turbine

Full size image

The power reference is generated by a maximum power point tracking (MPPT) algorithm that searches for the peak power on the power–speed curve.

5.1 Responses of MPPT Control

To extract maximum power corresponding to a specified wind velocity, the frequency at the terminals of the SCIG is adjusted in such a way that the machine rotates at a speed corresponding to the MPP. The objective of this case is to show the overall performance of the proposed controller under varied conditions of operation. With this purpose, the simulation was carried out considering the wind speed profile and rated wind speed presented in Fig. 5.

Fig. 6
figure 6

Illustration of tracking performance of DC link voltage

Full size image
Fig. 7
figure 7

Performance tracking of power and wave forms of grid voltage and current

Full size image

In this figure, it’s also represented the pitch angle, the tip speed ratio, the coefficient of power conversion, the aerodynamic power, the generator speed and the optimum speed. It is shown that the pitch angle value is set at \(0^{\circ }\), the tip speed ratio is equal to 8.1, and the power coefficient Cp is around of 0.47 when the wind speed is lower than 11 m/s. Once the rated speed is greater than 11m/s, the rated power 1 p.u (3 MW) is obtained.

Fig. 8
figure 8

Performance of the system under \({+}50\,\%\) change in inductance values

Full size image
Fig. 9
figure 9

Performance of the system under \({+}50\,\%\) change in resistances of stator and rotor

Full size image

5.2 Tracking Performance of DC Link Voltage and Powers

The Fig. 6 depicts the response of the DC bus voltage. It is noticeable that is regulated at 1380 V. Figure 7 presents the simulation results concerning the grid side: the voltage, the current, the reactive and active powers, respectively. It can be seen that the measured active power tracks very well the reference. Also, the reactive power is equal to its reference which is set to 0. Consequently, the unity power factor is achieved, since the current and the voltage of the grid are in phase.

5.3 Robustness to Parameter Disturbances

In this section, simulation results of the wind turbine SCIG under parameter variation is considered, in order to confirm the robustness of the proposed control. While the variations of the stator and rotor leakage inductances during operation are insignificant, mutual inductance variation should be taking into account due to possible variation of the magnetic permeability of the stator and rotor cores under different operating conditions. Figure 8 shows the simulation results with inductances used in the controller with increase of \({+}50\,\%\) from their original values. Besides, variations of stator and rotor resistances should also be considered. Simulation results with change of resistances of stator and rotor (with the range of \({+}50\,\%\)) are shown in Fig. 9. As a result, it can be seen that the proposed scheme can still provide consistent performance even if system parameters have changed.

6 Conclusion

Compared to other types of renewable energy, wind energy system has become a fast increasing energy source in the world; mainly as a consequence of its environmentally friendly, high reliability and cost effectiveness.

WECS based on SCIG is one of promising topology to reduce maintenance costs and to increase mechanical robustness and versatility. Further, it guarantees superior wind power extraction, better efficiency in variable-speed of the wind and improved quality of the energy feed to the grid.

In this context, two simultaneous control objectives have been investigated:

  • the maximization of the energy conversion efficiency based SCIG wind turbine

  • the regulation of the active and reactive power injected into the grid, to ensure UPF,

To this end, a sliding-mode control strategy, which presents attractive features such as robustness to parametric uncertainties of the different components of the system, has been adopted. The globally and exponentially stability of the derived control laws has been proven by applying Lyapunov stability analysis.

Simulation results have been performed to illustrate successful mathematical analysis and prove the effectiveness of the proposed nonlinear control laws. It can be observed from the simulation study that proposed controllers guarantee good performance in terms of (i) tracking of maximum power, (ii) reactive power regulation to guarantee unity power factor and (iii) robust feedback control solution despite parameter uncertainties and disturbances.