1 Introduction

In recent years, renewable energy based on wind and solar resources stood as the main alternative to fossil fuel, especially for electricity production (Şeker et al. 2016; Katir et al. 2020). As a matter of fact, wind energy is available much wider, unlike solar energy which is not equally available worldwide. It is now highly admitted that wind energy conversion systems are key means to get clean and cheap energy (Li et al. 2019; Goudarzi and Zhu 2013). In large-scale electrical power generation based on wind turbines, two electric generators outperform over all variable speed machines which are Synchronous Generators (SGs) and DFIGs (Cheng and Zhu 2014). Compared to other machines including SGs, DFIGs offer a number of advantages, e.g., robustness, inexpensiveness, lightweight, the ability to operate at variable speed and the necessity of smaller power converters. In addition, DFIGs allow the control of all the power exchanged with the grid. Finally, DFIGs enable the control of the active power independently from the control of the reactive power (Bektache and Boukhezzar 2018).

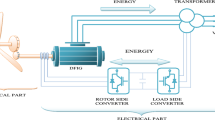
In this study, the DFIG-based wind generation system illustrated in Fig. 1 is considered. The stator windings are directly connected to the grid, whereas the rotor windings are coupled to the grid via the rotor side converter (RSC), DC-link capacitor and the grid side converter (GSC) (Kaloi et al. 2016). A number of control techniques have been proposed in literature to get full benefits from the DFIG machine, despite its nonlinearity and model uncertainty. A review of the control strategies for wind energy conversion systems involving DFIG generators is presented in (Mohd Zin et al. 2013). In (Noussi et al. 2019; Aguilar et al. 2020; Ko et al. 2008), a classical proportional integral (PI) controller is suggested. Due to its linearity and fixed parameters, a PI controller cannot ensure satisfactory performances over wide range operation conditions. A fuzzy tracking controller is dealt with in Zamzoum et al. (2018); Naik et al. (2020), with some interesting trajectory tracking. Model-based controllers, that account for the nonlinearity of DFIG machine, have been proposed using different design techniques. In Noussi et al. (2020b), a sensorless backstepping controller has been designed to ensure maximum power extraction. A passivity-based control scheme involving parameter estimation was suggested in López-García et al. (2016). A number of controllers, developed using the sliding mode control technique, have been proposed for the control of wind turbine systems. However, these research papers tackle only the control of either the generator connected to RSC or the grid linked to GSC (Beltran et al. 2012; Hu et al. 2011; Yang et al. 2018; Golnary and Moradi 2019; Noussi et al. 2020a). Dealing with the control of the entire DFIG-based energy chain has been subject of some works. As a matter of fact, the power transfer of DFIG-based wind energy systems is ensured by the stator-grid association and the rotor connected to the back-to-back converter-grid association. Since there is an interaction between the different parts of the discussed system, it is crucial to consider the control problem of the whole topology to ensure a smooth power transfer from the wind turbine to the grid (Merabet et al. 2018; Noussi et al. 2021). Authors, in Martinez et al. (2012); Saad et al. (2015), discussed the control of the whole system using the sliding mode technique, including a PI controller that was implemented to regulate the DC-link voltage which does not reject disturbances and cannot handle parametric variations.

Designing adaptive sliding mode controllers for DFIG-based wind energy conversion systems has been dealt with in Barambones et al. (2018); Patnaik and Dash (2015); Sun et al. (2017). Nevertheless, only few research works tackled the adaptive sliding mode control of the whole system depicted in Fig. 1. In Patnaik et al. (2016), authors developed an adaptive sliding mode controller for the complete structure, but they used a linear classical PI controller for the DC-link voltage regulation which is sensitive to parameters’ variations. The present paper addresses the control problem considering the complete chain of grid-connected DFIG wind turbine (Fig. 1), using the adaptive sliding mode control technique. The controlled system is able to cope with extra difficulties, including disturbances, unmodeled quantities and parameters’ variations caused by temperature, saturation and skin effect. The control design is based on the whole system model that is obtained by applying electrical and physical laws. The resulting adaptive controller turns out to be constituted of several components, including: (i) an MPPT algorithm that determines online the optimal turbine power value in the sense of maximum energy transfer from the wind to the grid; (ii) a stator powers regulator that makes the DFIG stator active power tracks the optimal value and maintains the stator reactive power at a desired reference; (iii) a DC-link voltage regulator to make energy transfer possible. Then, a theoretical stability analysis is developed proving formally that the adaptive controller actually meets its objectives. The theoretical results are confirmed by several numerical simulations, that also illustrate extra robustness features of the controller.

The paper is organized as follows: In Sect. 2, the mathematical model of DFIG-WECS is developed; Sect. 3 is devoted to the adaptive sliding mode controller design; the stability analysis of the whole closed-loop system is presented in Sect. 4. The performances and robustness of the proposed controller are illustrated by numerical simulation in Sect. 5. Some concluding remarks end the paper.

Fig. 1
figure 1

Simplified scheme of DFIG wind turbine

Full size image

2 System Description and Modeling

The DFIG-based wind generation system under study is depicted in Fig. 1. Accordingly, the wind turbine is connected to the doubly fed induction generator via the gear box system. The back-to-back voltage source converter is used to ensure the maximum power extraction and guarantee the injection of the active and reactive power into the grid.

2.1 Wind Turbine Model

The mechanical power extracted via the wind turbine is given by Mousa et al. (2019):

$$\begin{aligned} {{P}_{t}}=\dfrac{1}{2} \rho \pi {{R}^{2}}{{v}^{3}}{{C}_{p}}\left( \lambda ,\beta \right) \end{aligned}$$
(1)

where \(\rho \), R, v, \(C_{p}\) are the air density, the rotor radius, the wind speed and the power coefficient, respectively.

Moreover, the tip speed ratio can be expressed as:

$$\begin{aligned} \lambda =\dfrac{{{\Omega }_{t}}R}{v} \end{aligned}$$
(2)

where \({{\Omega }_{t}}\) is the wind turbine rotor mechanical speed.

The power coefficient \({{C}_{p}}\) is given as a function of the pitch angle \(\beta \) and the tip speed ratio \(\lambda \):

$$\begin{aligned} {{C}_{p}}\left( \lambda ,\beta \right) ={{C}_{1}}\left( \dfrac{{{C}_{2}}}{{{\lambda }_{i}}}-{{C}_{3}}\beta -{{C}_{4}}{{\beta }^{{{C}_{5}}}}-{{C}_{6}} \right) {{e}^{\dfrac{-{{C}_{7}}}{{{\lambda }_{i}}}}} \end{aligned}$$
(3)

with

$$\begin{aligned} \lambda _{i}^{-1}={{\left( \lambda +0.02\beta \right) }^{-1}}-0.003{{\left( {{\beta }^{3}}+1 \right) }^{-1}} \end{aligned}$$
(4)

where the coefficients \({{C}_{i}}\), \((i= 1,2,\ldots , 7)\), have the values: \({{C}_{1}}=0.73\), \({{C}_{2}}=151\), \({{C}_{3}}=0.58\), \({{C}_{4}}=0.02\), \({{C}_{5}}=2.14\), \({{C}_{6}}=13.2\), \({{C}_{7}}=18.4\).

2.2 DFIG Dynamic Model

The DFIG voltages in the synchronously rotating reference frame can be expressed as follows (Morawiec et al. 2019; Eshkaftaki et al. 2019; Huang et al. 2019):

$$\begin{aligned}&\left( \begin{matrix} {{v}_{sd}} \\ {{v}_{sq}} \\ \end{matrix} \right) ={{R}_{s}}\left( \begin{matrix} {{i}_{sd}} \\ {{i}_{sq}} \\ \end{matrix} \right) +\frac{\mathrm{d}}{\mathrm{d}t}\left( \begin{matrix} {{\phi }_{sd}} \\ {{\phi }_{sq}} \\ \end{matrix} \right) +{{\omega }_{s}}\left( \begin{matrix} 0 &{} -1 \\ 1 &{} 0 \\ \end{matrix} \right) \left( \begin{matrix} {{\phi }_{sd}} \\ {{\phi }_{sq}} \\ \end{matrix} \right) \end{aligned}$$
(5)
$$\begin{aligned}&\left( \begin{matrix} {{v}_{rd}} \\ {{v}_{rq}} \\ \end{matrix} \right) ={{R}_{r}}\left( \begin{matrix} {{i}_{rd}} \\ {{i}_{rq}} \\ \end{matrix} \right) +\frac{\mathrm{d}}{\mathrm{d}t}\left( \begin{matrix} {{\phi }_{rd}} \\ {{\phi }_{rq}} \\ \end{matrix} \right) +{{\omega }_{r}}\left( \begin{matrix} 0 &{} -1 \\ 1 &{} 0 \\ \end{matrix} \right) \left( \begin{matrix} {{\phi }_{rd}} \\ {{\phi }_{rq}} \\ \end{matrix} \right) \nonumber \\ \end{aligned}$$
(6)

where \({v}_{sdq}\), \({v}_{rdq}\), \({i}_{sdq}\), \({i}_{rdq}\), \({\phi }_{sdq}\) and \({\phi }_{rdq}\), denote the mean values, over a switching period, of the real signals of the stator and rotor voltages, currents, fluxes in the d–q reference frame, respectively; \(R_s\) and \(R_r\) are the stator and the rotor resistances; \(\omega _s\) and \(\omega _r\) are the synchronous speed of stator flux and the rotor angular frequency, respectively.

The stator and the rotor fluxes expressions in the d–q reference frame are given by:

$$\begin{aligned} \left( \begin{array}{l} {{\phi }_{sd}} \\ {{\phi }_{sq}} \\ {{\phi }_{rd}} \\ {{\phi }_{rq}} \\ \end{array} \right) =\left( \begin{array}{llll} {{L}_{s}} &{} 0 &{} M &{} 0 \\ 0 &{} {{L}_{s}} &{} 0 &{} M \\ M &{} 0 &{} {{L}_{r}} &{} 0 \\ 0 &{} M &{} 0 &{} {{L}_{r}} \end{array} \right) \left( \begin{array}{l} {{i}_{sd}} \\ {{i}_{sq}} \\ {{i}_{rd}} \\ {{i}_{rq}} \\ \end{array} \right) \end{aligned}$$
(7)

where \(L_s\), \(L_r\) and M denote the stator, rotor and mutual inductances, respectively. On the other hand, the stator and the rotor active and reactive powers are given by:

$$\begin{aligned}&{{P}_{s}}=\frac{3}{2}\left( {{v}_{sd}}{{i}_{sd}} +{{v}_{sq}}{{i}_{sq}} \right) \end{aligned}$$
(8a)
$$\begin{aligned}&{{Q}_{s}}=\frac{3}{2}\left( {{v}_{sq}}{{i}_{sd}}-{{v}_{sd}}{{i}_{sq}} \right) \end{aligned}$$
(8b)
$$\begin{aligned}&{{P}_{r}}=\frac{3}{2}\left( {{v}_{rd}}{{i}_{rd}} +{{v}_{rq}}{{i}_{rq}} \right) \end{aligned}$$
(9a)
$$\begin{aligned}&{{Q}_{r}}=\frac{3}{2}\left( {{v}_{rq}}{{i}_{rd}}-{{v}_{rd}}{{i}_{rq}} \right) . \end{aligned}$$
(9b)

The expression of the generator speed dynamics is written as:

$$\begin{aligned} J\frac{\mathrm{d}{{\Omega }_{m}}}{\mathrm{d}t}={{C}_{g}}-{{C}_{em}}-F{{\Omega }_{m}} \end{aligned}$$
(10)

where \({{\Omega }_{m}}=N{{\Omega }_{t}}\), \(C_g\), \(C_t=NC_g\), N, J and F denote the generator speed, high-speed shaft mechanical torque, low-speed shaft mechanical torque, the gear box gain, rotor inertia and the friction coefficient, respectively.

The equation of the electromagnetic torque is defined by:

$$\begin{aligned} {{C}_{em}}=pM\left( {{i}_{rd}}{{i}_{sq}}-{{i}_{sd}}{{i}_{rq}} \right) . \end{aligned}$$
(11)

2.3 Grid Side Dynamic Model

Applying Kirchhoff’s current law, the current through the DC-link capacitor is given by:

$$\begin{aligned} {i}_{c}={i}_{rdc}-{i}_{gdc}. \end{aligned}$$
(12)

The powers transferred from the DC-link to the grid side converter are expressed as follows:

$$\begin{aligned}&{{P}_{g}}=\frac{3}{2}\left( {{v}_{sd}}{{i}_{gd}}+{{v}_{sq}}{{i}_{gq}} \right) \end{aligned}$$
(13a)
$$\begin{aligned}&{{Q}_{g}}=\frac{3}{2}\left( {{v}_{sq}}{{i}_{gd}}-{{v}_{sd}}{{i}_{gq}} \right) \end{aligned}$$
(13b)

where \({{i}_{gdq}}\) and \({{v}_{dc}}\) are the mean values, over a switching period, of the grid side filter currents in the synchronous reference frame and the DC-link voltage, respectively.

Assuming that the GSC losses are negligible, the DC-link voltage dynamics are described by the equation (Kim et al. 2016):

$$\begin{aligned} {{C}_{dc}}{{v}_{dc}}\frac{\mathrm{d}{{v}_{dc}}}{\mathrm{d}t}={{v}_{dc}}{{i}_{rdc}}-{{P}_{g}}. \end{aligned}$$
(14)

The grid side converter voltages in the synchronously rotating reference are expressed as follows:

$$\begin{aligned} \left( \begin{matrix} {{v}_{nd}} \\ {{v}_{nq}} \\ \end{matrix} \right)&={{R}_{g}}\left( \begin{matrix} {{i}_{gd}} \\ {{i}_{gq}} \\ \end{matrix} \right) +{{L}_{g}}\frac{\mathrm{d}}{\mathrm{d}t}\left( \begin{matrix} {{i}_{gd}} \\ {{i}_{gq}} \\ \end{matrix} \right) +\left( \begin{matrix} {{v}_{sd}} \\ {{v}_{sq}} \\ \end{matrix} \right) \nonumber \\&\quad \,\,+{{L}_{g}}{{\omega }_{s}}\left( \begin{matrix} 0 &{} -1 \\ 1 &{} 0 \\ \end{matrix} \right) \left( \begin{matrix} {{i}_{gd}} \\ {{i}_{gq}} \\ \end{matrix} \right) \end{aligned}$$
(15)

where \({R}_{g}\) and \({L}_{g}\) are the grid side resistance and inductance, respectively.

Fig. 2
figure 2

Wind energy conversion system operating zones

Full size image
Fig. 3
figure 3

Power coefficient as a function of tip speed ratio

Full size image

3 Controller Design

3.1 MPPT Algorithm

It is crucial to include an MPPT loop in the wind system to maximize the available power delivered by the wind turbine (Yang et al. 2016; Falehi and Rafiee 2018; Rezaei 2018). To this end, the present paper addresses the control problem when the wind turbine operates in zone II, see Fig. 2. In this zone, the pitch angle is maintained constant where the controller of the WECS implements the MPPT algorithm to extract the maximum available power during the variations of the wind speed. As this latter increases, the rotor speed increases. When the wind speed becomes more important and the rotor speed reaches its maximum, the wind turbine operates in zone III. In this zone, the aim is to limit the extracted mechanical power. In this case, the mechanical torque should be kept at its nominal value and the pitch angle must be adjusted, thus guaranteeing that the wind turbine operates at the maximum speed and rated power.

The optimal extracted power when the turbine is operating in the maximum power region can be found at optimal values of \({{C}_{p}}\), \(\lambda \) and \(\beta \). Using Eqs. (1) and (2) and Fig. 3, the optimal power is given by 16 and represented in Fig. 4 (Zamzoum et al. 2018):

$$\begin{aligned} {{P}_{t-opt}}=\frac{1}{2}\rho \pi \frac{{{R}^{5}}}{\lambda _{opt}^{3}}{{C}_{pmax }}\Omega _{t}^{3}. \end{aligned}$$
(16)

The reference of the stator active power control loop, illustrated in Fig. 5, is retrieved from the difference between the rotor active power (9a) and the output of the MPPT block (16).

Fig. 4
figure 4

Mechanical power representation as a function of the rotor speed and wind speed

Full size image
Fig. 5
figure 5

MPPT Algorithm

Full size image

3.2 Field Oriented Technique

DFIGs are quite suitable solutions for high power generation requirements, as the generation of electrical power can be fully achieved only from the association of the stator windings and the electrical grid. This entails size reduction of the power converter, as only 20–30% of the rating powers pass through the back-to-back converter. The global extracted power is the sum of the grid side powers and stator powers. In order to simplify the system and power computations, oriented d–q reference frame is applied by adjusting the stator flux so that the quadratic component is null \(\big ( {{\phi }_{sd}}=\frac{{{V}_{s}}}{{{\omega }_{s}}}\), \({{\phi }_{sq}}=0 \big )\) (Golnary and Moradi 2019; Mechter et al. 2016; Xiong et al. 2020). Doing so, the stator voltages equations in (5) get simpler, which together with Eqs. (6) to (8) yields to the following stator powers expressions and the equations of the rotor currents dynamics:

$$\begin{aligned}&{{P}_{s}}=-\frac{3}{2}\frac{M{{V}_{s}}}{{{L}_{s}}}{{i}_{rq}} \end{aligned}$$
(17a)
$$\begin{aligned}&{{Q}_{s}}=-\frac{3}{2}\frac{M{{V}_{s}}}{{{L}_{s}}}\left( {{i}_{rd}}-\frac{{{V}_{s}}}{{{\omega }_{s}}M} \right) \end{aligned}$$
(17b)
$$\begin{aligned}&\frac{\mathrm{d}{{i}_{rq}}}{\mathrm{d}t}=\frac{1}{\sigma {{L}_{r}}}\left( \frac{{{v}_{dc}}}{2}{{u}_{q}} -{{R}_{r}}{{i}_{rq}}-{{\omega }_{r}}\sigma {{L}_{r}}{{i}_{rd}} -{{\omega }_{r}}\frac{M{{\phi }_{sd}}}{{{L}_{s}}} \right) \end{aligned}$$
(18a)
$$\begin{aligned}&\frac{\mathrm{d}{{i}_{rd}}}{\mathrm{d}t}=\frac{1}{\sigma {{L}_{r}}}\left( \frac{{{v}_{dc}}}{2}{{u}_{d}}-{{R}_{r}}{{i}_{rd}}+{{\omega }_{r}}\sigma {{L}_{r}}{{i}_{rq}} \right) . \end{aligned}$$
(18b)

Similarly, the orientation of the d–q frame simplifies the equations of the grid side powers and the filter current dynamics. Therefore, Eqs. (14) and (15) are rewritten as follows:

$$\begin{aligned}&\frac{\mathrm{d}{{v}_{dc}}}{\mathrm{d}t}=\frac{1}{{{C}_{dc}}}\left( {{i}_{rdc}}-\frac{3}{2}\frac{{{V}_{s}}}{{{v}_{dc}}}{{i}_{gd}} \right) \end{aligned}$$
(19a)
$$\begin{aligned}&\frac{\mathrm{d}{{i}_{gq}}}{\mathrm{d}t}=\frac{1}{{{L}_{g}}}\left( \frac{{{v}_{dc}}}{2}{{v}_{q}} -{{R}_{g}}{{i}_{gq}}-{{V}_{s}}-{{\omega }_{s}}{{L}_{g}}{{i}_{gd}} \right) \end{aligned}$$
(19b)
$$\begin{aligned}&\frac{\mathrm{d}{{i}_{gd}}}{\mathrm{d}t}=\frac{1}{{{L}_{g}}}\left( \frac{{{v}_{dc}}}{2}{{v}_{d}}-{{R}_{g}}{{i}_{gd}}+{{\omega }_{s}}{{L}_{g}}{{i}_{gq}} \right) . \end{aligned}$$
(19c)

3.3 Control Objectives

An adaptive sliding mode controller will now be designed for a wind energy conversion system based on DFIG, in order to maximize the produced power and inject it into the grid. There are three main objectives to be simultaneously realized:

  • Active power control: ensure that the active power tracks the optimal reference power provided by the MPPT block.

  • Reactive power control: maintain the stator and grid side reactive powers equal to zero to guarantee the power factor requirement.

  • DC-link regulation: keep the DC-link voltage at a fixed given value.

To meet these objectives, we propose a control scheme consisting of four control loops. A pair of control loops have been used to control the rotor side converter to directly regulate the stator powers, and a pair of control loops have been used to control the grid side converter; one aims at regulating the reactive power by acting on the d-axis current, while the other aims at regulating the DC-link voltage via the q-axis current.

3.4 Rotor Side Controller Design

It is seen in the rotor side reduced model (17) that the stator active power \({{P}_{s}}\) is acted on by the quadrature rotor current \(i_{rq}\), and through the direct current \(i_{rd}\), one can control the stator reactive power \({{Q}_{s}}\).

Using Eqs. (17) and (18), the derivatives, with powers quantities, yield:

$$\begin{aligned} \left( \begin{array}{l} {{{{\dot{P}}}}_{s}} \\ {{{{\dot{Q}}}}_{s}} \\ \end{array} \right) =&\overbrace{\left( \begin{array}{l} \dfrac{-{{R}_{r}}}{\sigma {{L}_{r}}}{{P}_{s}}-{{\omega }_{r}}{{Q}_{s}}+{\dfrac{3{{\omega }_{r}}{{V}_{s}}{{\phi }_{sd}}}{2{{{L}_{s}}}}\left( 1+\dfrac{{{M}^{2}}}{\sigma {{L}_{s}}{{L}_{r}}}\; \right) }\; \\ \dfrac{-{{R}_{r}}}{\sigma {{L}_{r}}}{{Q}_{s}}+{{\omega }_{r}}{{P}_{s}}+\dfrac{3}{2}\dfrac{{{R}_{r}}{{V}_{s}}{{\phi }_{sd}}}{\sigma {{L}_{s}}{{L}_{r}}}\; \\ \end{array} \right) }^{{{f}_{r}}({{P}_{s}},{{Q}_{s}})}\nonumber \\&\quad \quad \underbrace{-\frac{3}{2}\frac{{{V}_{s}}M}{\sigma {{L}_{s}}{{L}_{r}}} \frac{{{v}_{dc}}}{2}\left( \begin{array}{ll} 0 &{} 1 \\ 1 &{} 0 \\ \end{array} \right) }_{D_r}\left( \begin{array}{l} {{u}_{d}} \\ {{u}_{q}} \\ \end{array} \right) \end{aligned}$$
(20)

where the more compact form:

$$\begin{aligned} \left( \begin{matrix} {{{{\dot{P}}}}_{s}} \\ {{{{\dot{Q}}}}_{s}} \\ \end{matrix} \right) ={{f}_{r}}({{P}_{s}},{{Q}_{s}})+{{D}_{r}}{{u}_{dq}} \end{aligned}$$
(21)

\({{u}_{dq}}={{\left( \begin{matrix} {{u}_{d}} &{} {{u}_{q}} \\ \end{matrix} \right) }^{T}}\) is the control vector of the subsystem (21).

The point is that, in practice, the system can face external disturbances (affecting its signals) and parameter uncertainties (affecting its components). Extra unmodeled effects may come into action. Presently, we take in consideration all mentioned modeling errors, by adding uncertainty terms to the two model functions \(f_r\) and \(D_r\). Specifically, the latter are rewritten in the form:

$$\begin{aligned} {{f}_{r}}&={{f}_{r0}}+\Delta {{f}_{r}} \end{aligned}$$
(22)
$$\begin{aligned} {{D}_{r}}&={{D}_{r0}}+\Delta {{D}_{r}} \end{aligned}$$
(23)

where the modeling errors \(\Delta {{f}_{r}}\) and \(\Delta {{D}_{r}}\) are assumed to be bounded and \({{f}_{r0}}\) and \({{D}_{r0}}\) are identical to \({{f}_{r}}\) and \(D_r\), respectively. For convenience, the latter are rewritten:

$$\begin{aligned}&{{f}_{r0}}\left( {{P}_{s}},{{Q}_{s}} \right) =\left( \begin{array}{l} {{f}_{ps}}\left( {{P}_{s}},{{Q}_{s}} \right) \\ {{f}_{qs}}\left( {{P}_{s}},{{Q}_{s}} \right) \\ \end{array} \right) \nonumber \\&\quad =\left( \begin{array}{l} \dfrac{-{{R}_{r}}}{\sigma {{L}_{r}}}{{P}_{s}}-{{\omega }_{r}}{{Q}_{s}} +{\dfrac{3{{\omega }_{r}}{{V}_{s}}{{\phi }_{sd}}}{2{{{L}_{s}}}} \left( 1+\dfrac{{{M}^{2}}}{\sigma {{L}_{s}}{{L}_{r}}}\; \right) }\; \\ \dfrac{-{{R}_{r}}}{\sigma {{L}_{r}}}{{Q}_{s}}+{{\omega }_{r}}{{P}_{s}} +\dfrac{3}{2}\dfrac{{{R}_{r}}{{V}_{s}}{{\phi }_{sd}}}{\sigma {{L}_{s}}{{L}_{r}}}\; \\ \end{array} \right) \end{aligned}$$
(24)

\( {{D}_{r0}}=\left( \begin{array}{ll} 0 &{} {{d}_{ps}}\left( {{v}_{dc}} \right) \\ {{d}_{qs}}\left( {{v}_{dc}} \right) &{} 0 \\ \end{array} \right) \)

\( {{d}_{ps}}\left( {{v}_{dc}} \right) ={{d}_{qs}}\left( {{v}_{dc}} \right) =-\dfrac{3{{V}_{s}}M{{v}_{dc}}}{4\sigma {{L}_{s}}{{L}_{r}}} \).

Taking into consideration the uncertainty terms, then the expression of the stator powers is rewritten as follows:

$$\begin{aligned} \left( \begin{matrix} {{{{\dot{P}}}}_{s}} \\ {{{{\dot{Q}}}}_{s}} \\ \end{matrix} \right) ={{f}_{r0}}({{P}_{s}},{{Q}_{s}})+{{D}_{r0}} \left( {{v}_{dc}} \right) {{u}_{dq}}+{{\Delta }_{r}} \end{aligned}$$
(25)

where \({{\Delta }_{r}}={{\left( \begin{matrix} {{\Delta }_{P_s}} &{} {{\Delta }_{Q_s}} \\ \end{matrix} \right) }^{T}}\) depends on \(\Delta {{f}_{r}}\) and \(\Delta {{D}_{r}}\) of Eqs. (22) and (23).

To enforce the powers \(P_s\) and \(Q_s\) to match their references, denoted \({P}_{s}^{*}\) and \({Q}_{s}^{*}\), we will now design a control law, that generates the control vector \(u_{dq}\), using the sliding mode technique. To this end, we consider the following sliding surfaces:

$$\begin{aligned} {{S}_{r}}=\left( \begin{matrix} {{S}_{{{P}_{s}}}} \\ {{S}_{{{Q}_{s}}}} \\ \end{matrix} \right) =\left( \begin{matrix} {{e}_{{{P}_{s}}}}+{{k }_{1}}\int \limits _{0}^{t}{{{e}_{{{P}_{s}}}} \left( \tau \right) d\tau } \\ {{e}_{{{Q}_{s}}}}+{{k}_{2}}\int \limits _{0}^{t}{{{e}_{{{Q}_{s}}}} \left( \tau \right) d\tau } \\ \end{matrix} \right) \end{aligned}$$
(26)

where

$$\begin{aligned} \left( \begin{matrix} {{e}_{{{P}_{s}}}} \\ {{e}_{{{Q}_{s}}}} \\ \end{matrix} \right) =\left( \begin{matrix} {{P}_{s}}-P_{s}^{*} \\ {{Q}_{s}}-Q_{s}^{*} \\ \end{matrix} \right) \end{aligned}$$
(27)

and \(k_1\), \(k_2\) are positive real design parameters .

The additional integral terms on the right side of (26) are introduced to ensure zero steady-state errors.

The dynamics of the chosen sliding surfaces are expressed as:

$$\begin{aligned} {{{\dot{S}}}_{r}}=\left( \begin{array}{l} {{{{\dot{S}}}}_{{{P}_{s}}}} \\ {{{{\dot{S}}}}_{{{Q}_{s}}}} \\ \end{array} \right) =\left( \begin{array}{l} {{{{\dot{e}}}}_{{{P}_{s}}}}+{{k}_{1}}{{e}_{{{P}_{s}}}} \\ {{{{\dot{e}}}}_{{{Q}_{s}}}}+{{k}_{2}}{{e}_{{{Q}_{s}}}} \\ \end{array} \right) . \end{aligned}$$
(28)

Using (25)–(27), the time derivative of the sliding surfaces is given by:

$$\begin{aligned} {{{\dot{S}}}_{r}}=\left( \begin{matrix} {{k}_{1}}\,{{e}_{{{P}_{s}}}}-{\dot{P}}_{s}^{*} \\ {{k}_{2}}\,{{e}_{{{Q}_{s}}}}-{\dot{Q}}_{s}^{*} \\ \end{matrix} \right) +{{f}_{r0}}({{P}_{s}},{{Q}_{s}})+{{D}_{r0}}{{u}_{dq}} +{{\Delta }_{r}}. \end{aligned}$$
(29)

According to the sliding mode control principle (Barambones et al. 2018), the control signal is described as \({{u}_{dq}}=u_{dq}^{a0}+u_{dq}^{as}\), where \(u_{dq}^{a0}\) denotes the nominal control law, which keeps the system on the sliding surface, and \(u_{dq}^{as}\) is the adaptive switching control law, which contains both a discontinuous component that is responsible for inducing sliding motion on the surface and an adaptive gain that compensates the lumped uncertainty terms.

Thus, the sliding mode vector control law for stator powers can be obtained as follows:

$$\begin{aligned}&{{u}_{dq}}= -D_{r0}^{-1}\Bigg [ \overbrace{\left( \begin{matrix} {{k}_{1}}\,{{e}_{{{P}_{s}}}}-{\dot{P}}_{s}^{*} \\ {{k}_{2}}\,{{e}_{{{Q}_{s}}}}-{\dot{Q}}_{s}^{*} \\ \end{matrix} \right) +{{f}_{r0}}({{P}_{s}},{{Q}_{s}})}^{u_{dq}^{a0}}\nonumber \\&\quad + \underbrace{\left( \begin{matrix} {{{{\hat{\zeta }}}}_{1}}\,sgn\left( {{S}_{{{P}_{s}}}} \right) \\ {{{{\hat{\zeta }}}}_{2}}\,sgn\left( {{S}_{{{Q}_{s}}}} \right) \\ \end{matrix} \right) }_{u_{dq}^{as}} \Bigg ]. \end{aligned}$$
(30)

Accordingly, the dynamics of the estimated switching gains can be suggested as :

$$\begin{aligned} {{\dot{\hat{\zeta }}}_{1}}=\frac{1}{{{\gamma }_{1}}}\left| {{S}_{{{P}_{s}}}} \right| \end{aligned}$$
(31)
$$\begin{aligned} {{\dot{{\hat{\zeta }}}}_{2}}=\frac{1}{{{\gamma }_{2}}}\left| {{S}_{{{Q}_{s}}}} \right| \end{aligned}$$
(32)

where \({{\gamma }_{i}}\) are positive real gains, and \({\hat{\zeta }_{i}}\) denote the estimated adaptation gains which act as adjustable values of the adaptive switching control law gains, \(({i=1,2})\). The adaptation speed of \({{{\hat{\zeta }}}}_{i}\) can be tuned by \({{\gamma }_{i}}\,\), \(({i=1,2})\). The estimation error is defined by Katir et al. (2021):

$$\begin{aligned} {{{\tilde{\zeta }}}_{i}}={{{{\hat{\zeta }}}}_{i}}-{{\zeta }_{i}}. \end{aligned}$$
(33)

3.5 Grid Side Controller Design

The controller of the grid side converter is expected to achieve two main objectives: (i) ensuring a tight regulation of the DC-link voltage (this guarantees a suitable transmission of the power flowing through the rotor of the generator); (ii) controlling the reactive power exchanged with the grid. The controller we are proposing consists of two loops; the first loop aims at regulating the DC bus voltage based on the q-axis filter current, the second loop aims at controlling the grid side reactive power through the d-axis filter current.

The tracking error of the DC-link voltage and the d-axis current can be defined as follows:

$$\begin{aligned} \left( \begin{array}{l} {{e}_{{{i}_{d}}}} \\ {{e}_{v}} \\ \end{array} \right) =\left( \begin{array}{l} {{i}_{gd}}-i_{gd}^{*} \\ {{v}_{dc}}-v_{dc}^{*} \\ \end{array} \right) . \end{aligned}$$
(34)

Using (19), the time derivative of equation (34) yields:

$$\begin{aligned} \left( \begin{array}{l} {{{{\dot{e}}}}_{{{i}_{d}}}} \\ {{{{\dot{e}}}}_{v}} \\ \end{array} \right) =\left( \begin{array}{l} \dfrac{1}{{{L}_{g}}}\left( \dfrac{{{v}_{dc}}}{2}{{v}_{d}}-{{R}_{g}}{{i}_{gd}} +{{\omega }_{s}}{{L}_{g}}{{i}_{gq}} \right) -{\dot{i}}_{gd}^{*} \\ \dfrac{1}{{{C}_{dc}}}\left( {{i}_{rdc}}-\dfrac{3}{2}\dfrac{{{V}_{s}}}{{{v}_{dc}}} {{i}_{gq}} \right) -{\dot{v}}_{dc}^{*} \\ \end{array} \right) .\nonumber \\ \end{aligned}$$
(35)

We define the sliding surfaces as:

$$\begin{aligned} {{S}_{g}}=\left( \begin{matrix} {{S}_{{{i}_{d}}}} \\ {{S}_{v}} \\ \end{matrix} \right) =\left( \begin{matrix} {{e}_{{{i}_{d}}}}+{{k}_{3}}\int \limits _{0}^{t}{{{e}_{{{i}_{d}}}}\left( \tau \right) d\tau } \\ {{{{\dot{e}}}}_{v}}+\varsigma _0\,{{e}_{v}}+{{k}_{4}}\int \limits _{0}^{t}{{{e}_{v}} \left( \tau \right) d\tau } \\ \end{matrix} \right) \end{aligned}$$
(36)

\(k_3\) and \(k_4\) are positive real design parameters.

The choice of the sliding surface \(S_v\) is motivated by the fact that the relative degree of the system is \(n=2\), where the general form is written as:

$$\begin{aligned} {{S}_{x}}={{\left( \frac{\mathrm{d}}{\mathrm{d}t}+\varsigma _0 \right) }^{n-1}}{{e}_{x}}. \end{aligned}$$
(37)

The time derivative of the sliding surfaces is given by:

$$\begin{aligned} {{{\dot{S}}}_{g}}=\left( \begin{matrix} {{{{\dot{S}}}}_{{{i}_{d}}}} \\ {{{{\dot{S}}}}_{v}} \\ \end{matrix} \right) =\left( \begin{matrix} {{{{\dot{e}}}}_{{{i}_{d}}}}+{{k}_{3}}{{e}_{{{i}_{d}}}} \\ {{{\ddot{e}}}_{v}}+\varsigma _{0} {{{{\dot{e}}}}_{v}}+{{k}_{4}}{{e}_{v}} \\ \end{matrix} \right) . \end{aligned}$$
(38)

Using (35), the time derivative of (36) is written as:

$$\begin{aligned} {{{\dot{S}}}_{g}}=\left( \begin{matrix} {{k}_{3}}\,{{e}_{{{i}_{d}}}}-{\dot{i}}_{gd}^{*} \\ {{k}_{4}}\,{{e}_{v}}-\varsigma _0 {\dot{v}}_{dc}^{*}-\ddot{v}_{dc}^{*} \\ \end{matrix} \right)&+{{f}_{g0}} \left( {{v}_{dc}},{{i}_{gd}},{{i}_{gq}} \right) \nonumber \\&\quad +{{D}_{g0}}.{{v}_{dq}}+{{\Delta }_{g}} \end{aligned}$$
(39)

with

$$\begin{aligned} {{\Delta }_{g}}=\left( \begin{matrix} {{\Delta }_{i_d}} \\ {{\Delta }_{v}} \\ \end{matrix} \right) =\left( \begin{matrix} \Delta {{f}_{id}}+\Delta {{d}_{id}}.{{v}_{d}} \\ \Delta {{f}_{v}}+\Delta {{d}_{v}}.{{v}_{q}}+\dfrac{1}{{{C}_{dc}}}{{{{\dot{i}}}}_{rdc}} +\dfrac{ \varsigma _0 }{{{C}_{dc}}}{{i}_{rdc}} \\ \end{matrix} \right) . \end{aligned}$$
(40)

Note that all uncertain terms are gathered in \({{\Delta }_{g}}\), including the current \({{i}_{rdc}}\) which is considered as an external disturbance. The remaining quantities on the right side of (39) are defined as follows:

$$\begin{aligned} {{f}_{g0}}\left( {{v}_{dc}},{{i}_{gd}},{{i}_{gq}} \right)&=\left( \begin{matrix} {{f}_{id}}\left( {{v}_{dc}},{{i}_{gd}},{{i}_{gq}} \right) \\ {{f}_{v}}\left( {{v}_{dc}},{{i}_{gd}},{{i}_{gq}} \right) \\ \end{matrix} \right) \nonumber \\&=\left( \begin{matrix} -{{R}_{g}}{{i}_{gd}}+{{\omega }_{s}}{{L}_{g}}{{i}_{gq}} \\ \dfrac{3}{2}\dfrac{{{V}_{s}}}{{{C}_{dc}}{{v}_{dc}}{{L}_{g}}} \left( {{R}_{g}}{{i}_{gq}}+{{\omega }_{s}}{{L}_{g}}{{i}_{gd}}+{{V}_{s}} \right) \\ \end{matrix} \right) \end{aligned}$$
(41)
$$\begin{aligned} D_{g0}&=\left( \begin{array}{ll} \dfrac{{{v}_{dc}}}{2{{L}_{g}}}\; &{} 0 \\ 0 &{} \dfrac{-3{{V}_{s}}}{4{{C}_{dc}}{{L}_{g}}}\; \\ \end{array} \right) \end{aligned}$$
(42)
$$\begin{aligned} {{v}_{dq}}&={{\left( \begin{array}{ll} {{v}_{d}} &{} {{v}_{q}} \\ \end{array} \right) }^{T}}. \end{aligned}$$
(43)

It can be seen from (39) that the nominal control law appears in the first derivative of the sliding surface. Thus, \(v_{dq}^{a0}={{v}_{dq}}\) is obtained from the invariance of the surface \({{S}_{g}}={{{\dot{S}}}_{g}}=0\). As in the previous subsection, an adaptive switching control law is proposed. Then, the global adaptive control law can be written as follows:

$$\begin{aligned} {{v}_{dq}}&=-D_{g0}^{-1}\Bigg [ \overbrace{\left( \begin{matrix} {{k}_{3}}\,{{e}_{{{i}_{q}}}}-{\dot{i}}_{gd}^{*} \\ {{k}_{4}}\,{{e}_{v}}-\varsigma _0 {\dot{v}}_{dc}^{*}-\ddot{v}_{dc}^{*} \\ \end{matrix} \right) +{{f}_{g0}}\left( {{v}_{dc}},{{i}_{gd}},{{i}_{gq}} \right) }^{v_{dq}^{a0}} \nonumber \\&\quad +\underbrace{\left( \begin{matrix} {{{{\hat{\zeta }}}}_{3}}\,sgn\left( {{S}_{{{i}_{d}}}} \right) \\ {{{{\hat{\zeta }}}}_{4}}\,sgn\left( {{S}_{v}} \right) \\ \end{matrix} \right) }_{v_{dq}^{as}} \Bigg ] \end{aligned}$$
(44)

where the dynamics of the estimated switching gains can be expressed as follows:

$$\begin{aligned} {{\dot{{\hat{\zeta }}}}_{3}}=\dfrac{1}{{{\gamma }_{3}}}\left| {{S}_{{{i}_{d}}}} \right| \end{aligned}$$
(45)
$$\begin{aligned} {{\dot{{\hat{\zeta }}}}_{4}}=\dfrac{1}{{{\gamma }_{4}}}\left| {{S}_{v}} \right| \end{aligned}$$
(46)

where \({{\gamma }_{3}}\) and \({{\gamma }_{4}}\) are positive real gains.

Finally, the complete controller design for stator powers, DC-link voltage and grid side reactive power is established. For convenience, the whole established controller is summarized in Table 1.

Table 1 Recapitulation of the whole proposed adaptive controller
Full size table

4 System Stability Analysis

The stability analysis plays a crucial role in the control theory (Aourir et al. 2020). In this section, the Lyapunov stability approach will be used in the proof of the next theorem to investigate the stability of the whole closed-loop system.

The following two assumptions will be needed for the trajectory tracking:

  1. A1)

    The uncertainties of the system are bounded, i.e., \(\left| {{\Delta }_{x}} \right| \le {{\Delta }_{x\max }}\), \(\quad x\in \lbrace {P_s, Q_s, i_d, v}\rbrace \), where \({{\Delta }_{x}}\) refers to the lumped uncertainties in \({{\Delta }_{r}}\) and \({{\Delta }_{g}}\).

  2. A2)

    It is required that the switching gains verify \({{\zeta }_{i}}\ge {{\Delta }_{xmax }}\) with \(x \in \lbrace {P_s, Q_s, i_d, v}\rbrace \) and \((i=1,2,3,4)\).

Theorem 1

Consider the global control system illustrated in Fig. 6 and composed of: (i) the wind turbine model (1)–(4), DFIG-AC/DC association model (5)–(8) and grid side system model (5)–(15) which are subject to assumption A1; (ii) the rotor side and grid side controllers of Table 1 that are subject to assumption A2, where the design parameters (\({{k}_{1}}\), \({{k}_{2}}\), \({{k}_{3}}\), \({{k}_{4}}\), \({{\gamma }_{1}}\), \({{\gamma }_{2}}\), \({{\gamma }_{3}}\), \({{\gamma }_{4}}\)) are positive real constants. Then, the resulting closed-loop system with state variables (\({{S}_{r}}\),\({{{\tilde{\zeta }}}_{1}}\), \({{{\tilde{\zeta }}}_{2}}\), \({{S}_{g}}\), \({{{\tilde{\zeta }}}_{3}}\), \({{{\tilde{\zeta }}}_{4}}\)) is finite time stable and \(S_r\) and \(S_g\) converge to zero.

Proof

For convenience, the time derivatives of the sliding surfaces of the controllers on both sides can be represented using the following compact form:

$$\begin{aligned} {{{\dot{S}}}_{x}}=-{{{{\hat{\zeta }}}}_{i}} {sgn} \left( {{S}_{x}} \right) +{{\Delta }_{x}} \qquad with \qquad x\in&\lbrace P_s, Q_s, i_d, v \rbrace \nonumber \\&and \quad (i=1,2,3,4). \end{aligned}$$
(47)

Consider the Lyapunov function candidate

$$\begin{aligned} {{V}_{c}}=\frac{1}{2}S_{P_s}^{2}+\frac{1}{2}S_{Q_s}^{2}+\frac{1}{2}S_{i_d}^{2} +\frac{1}{2}S_{v}^{2}+\frac{1}{2}\sum \limits _{i=1}^{4}{{{\gamma }_{i}}{\tilde{\zeta }}_{i}^{2}}. \end{aligned}$$
(48)

Using (47), the time derivative of (48) results to be:

$$\begin{aligned} {{{\dot{V}}}_{c}}=&-{{{\hat{\zeta }}}_{1}}\left| {{S}_{P_s}} \right| -{{{\hat{\zeta }}}_{2}}\left| {{S}_{Q_s}} \right| -{{{\hat{\zeta }}}_{3}}\left| {{S}_{i_d}} \right| -{{\hat{\zeta }}_{4}}\left| {{S}_{v}} \right| \nonumber \\&+{{\Delta }_{P_s}}{{S}_{P_s}}+{{\Delta }_{Q_s}}{{S}_{Q_s}}+{{\Delta }_{i_d}}{{S}_{i_d}}+{{\Delta }_{v}}{{S}_{v}}+\sum \limits _{i=1}^{4}{{{\gamma }_{i}}{{{\tilde{\zeta }}}_{i}}{{{\dot{{\tilde{\zeta }}}}}_{i}}}. \end{aligned}$$
(49)

Taking into account that \(\dot{\tilde{\zeta _i }}=-\dot{\hat{\zeta _i }}\), \((i=1, 2, 3, 4)\), and substituting the dynamics of the adaptive gains of (31), (32), (45) and (46) into (49), we obtain :

$$\begin{aligned} {{{\dot{V}}}_{c}}=&-{{\zeta }_{1}}\left| {{S}_{P_s}} \right| -{{\zeta }_{2}}\left| {{S}_{Q_s}} \right| -{{\zeta }_{3}}\left| {{S}_{i_d}} \right| -{{\zeta }_{4}}\left| {{S}_{v}} \right| \nonumber \\&+{{\Delta }_{P_s}}{{S}_{P_s}}+{{\Delta }_{Q_s}}{{S}_{Q_s}}+{{\Delta }_{i_d}}{{S}_{i_d}}+{{\Delta }_{v}}{{S}_{v}}. \end{aligned}$$
(50)

According to assumption A1, the following inequality applies

$$\begin{aligned} {{{\dot{V}}}_{c}}\le \left( -{{\zeta }_{m}}+4{{\Delta }_{M}} \right) \left( \left| {{S}_{P_s}} \right| +\left| {{S}_{Q_s}} \right| +\left| {{S}_{i_d}} \right| +\left| {{S}_{v}} \right| \right) \end{aligned}$$
(51)

where

\({{\zeta }_{m}}=\min ({{\zeta }_{1}},{{\zeta }_{2}},{{\zeta }_{3}},{{\zeta }_{4}})\),

\({{\Delta }_{M}}=\max (\left| {{\Delta }_{P_smax}}\right| , \left| {{\Delta }_{Q_smax}}\right| , \left| {{\Delta }_{i_dmax}}\right| , \left| {{\Delta }_{vmax}}\right| )\).

Using the next inequality, for \(0<\alpha <2\)

$$\begin{aligned} \sum \limits _{i=1}^{n}{{{\left| {{\vartheta }_{i}} \right| }^{\alpha }}}\ge {{\left( \sum \limits _{i=1}^{n}{\vartheta _{i}^{2}} \right) }^{\frac{\alpha }{2}}}. \end{aligned}$$
(52)

Equation (51) becomes:

$$\begin{aligned} {{{\dot{V}}}_{c}}\le -{{\partial }_{0}}{{V}_{c}} \end{aligned}$$
(53)

where \({{\partial }_{0}}=\sqrt{2}( {{\zeta }_{m}}-4{{\Delta }_{M}} )\).

Finally, the integral of (53) over the time interval \(0 \le \tau \le t\), yields:

$$\begin{aligned} \sqrt{{{V}_{c}}}\le -\frac{1}{2}{{\partial }_{0}}t+\sqrt{{{V}_{c}}( {{t}_{0}} )}. \end{aligned}$$
(54)

In view of assumption A2, it follows that \({{\partial }_{0}} \ge 0\). Therefore, the system with state variables \((S_x, \tilde{\zeta }_{i})\) is stable and \(S_x\) converge to zero in finite time. The convergence time of the closed-loop system is calculated as \(T( {{t}_{0}} )\le \frac{2}{{{\partial }_{0}}}\sqrt{{{V}_{c}}( {{t}_{0}})}\). This end the proof. \(\square \)

Remark 1

In order to reduce the chattering effect produced by the signum function \({sgn}( \cdot )\), a sigmoid \({tanh} ( \cdot )\) function is used instead of \({sgn}( \cdot )\) as suggested in Abouloifa et al. (2018).

Fig. 6
figure 6

Overall control scheme of DFIG wind turbine

Full size image
Table 2 Wind turbine parameters
Full size table
Table 3 Controller parameters
Full size table
Fig. 7
figure 7

Obtained results under fixed wind speed changes (solid line: regulated signals; dotted line: their reference trajectories)

Full size image
Fig. 8
figure 8

Obtained results under variable wind speed changes ( solid line: regulated signals; dotted line: their reference trajectories)

Full size image

5 Simulation Results and Interpretations

Fig. 9
figure 9

Controller robustness under DFIG parameters’ uncertainty (solid line: regulated signals; dotted line: their reference trajectories)

Full size image
Fig. 10
figure 10

Controller robustness under voltage dips (solid line: regulated signals; dotted line: their reference trajectories)

Full size image

The simulation of the studied 2MW DFIG-based wind generation system of Fig. 6 is carried out using MATLAB/ Simulink/ SimPowerSystems environment. Numerical simulation is resorted not only to check the theoretical results of Theorem 1, but also to emphasize extra robustness features of the controller. The simulation study is performed by successively considering the following operating conditions:

  1. (1)

    Fixed wind speed changes

  2. (2)

    Variable wind speed changes

  3. (3)

    Robustness under DFIG parameters uncertainties

  4. (4)

    Robustness under voltage dips

The DFIG-based wind generation parameters are shown in Table 2. The controller parameters shown in Table 3 have proved to be appropriate based on trial-and-error search.

5.1 Fixed Wind Speed

The simulation protocol is such that the wind velocity takes four different values (6.5, 8.5, 10.5, 9)m/s. These velocity values hold successively on the intervals [0, 3[s, [3, 5.5[s, [5.5, 8[s and [8, 10]s, see Fig. 7a.

Figure 7b shows that the stator active power delivered by the wind power conversion system tracks exactly the optimal reference delivered by the MPPT block. Fig. 7c confirms that the stator reactive power rapidly vanishes which guarantees the achievement of the unitary power factor objective, see also Fig. 7g. The tight regulation of the DC-link voltage to a constant value is shown in Fig. 7d. The d-axis filter current, stator currents and the rotor currents are depicted in Fig. 7e, h and i, respectively.

5.2 Variable Wind Speed

To check the ability of the adaptive SMC controller to regulate the powers, under realistic wind speed fluctuations, a random wind speed is chosen as depicted in Fig. 8a with an average speed of 8 m/s. From Fig. 8b–i, it is seen that the proposed adaptive controller performs well despite the changes of the wind. As seen in Fig. 8b, the active power tracks precisely the suggested reference value. Also, Fig. 8c shows that the reactive power converges to zero. On the other hand, the DC-link voltage and direct axis current track their respective references despite the severe wind variations, see Fig.  8d–e. Stator and rotor currents are depicted in Fig. 8h–i, respectively.

5.3 Robustness Tests

To check the robustness of the proposed adaptive controller, two interesting tests are considered: parameters’ uncertainties and grid fault.

5.3.1 Robustness Under DFIG Parameters Uncertainties

In this case study, the rotor resistances and the mutual inductance are subject to variations, reflecting, e.g., the skin effect phenomenon and magnetic saturation problem. These variations are detailed in Table 4 and illustrated in Fig. 10a.

Figure 10b–e shows a satisfactory robustness of the proposed adaptive SMC controller. Actually, the output reference tracking objectives are still satisfactorily achieved despite the parameters \(R_r\) and M uncertainties. Figure 10b shows that the stator active power tracks well its reference signal despite the DFIG parameters’ changes. These latter cause a slight overshooting as it can be seen in the curve of the stator reactive power displayed in Fig. 10c. Figure 10d shows that the DC-link voltage is maintained at the desired value despite the made variations.

Table 4 Parameters variation
Full size table

5.3.2 Robustness Under Voltage Dips

Fig. 9a shows a voltage dips of 90%. Figure 9b–e illustrates the capability of the proposed controller to face grid faults and maintain satisfactory tracking performances.

6 Conclusion

We have considered the problem of controlling the powers of a wind turbine system based on DFIG (Fig. 1). The problem has been addressed using the adaptive sliding mode control technique leading to the design of an adaptive regulator (Table 1). The controlled system has been analyzed in Theorem 1 using Lyapunov stability tools. The theoretical results have been confirmed by numerical simulations which also emphasized extra robustness properties.