An Evaluation of Edge Modification Techniques for Privacy-Preserving on Graphs

Abstract

Noise is added by privacy-preserving methods or anonymization processes to prevent adversaries from re-identifying users in anonymous networks. The noise introduced by the anonymization steps may also affect the data, reducing its utility for subsequent data mining processes. Graph modification approaches are one of the most used and well-known methods to protect the privacy of the data. These methods converts the data by edges or vertices modifications before releasing the perturbed data. In this paper we want to analyse the edge modification techniques found in the literature covering this topic, and then empirically evaluate the information loss introduced by each of these methods. We want to point out how these methods affect the main properties and characteristics of the network, since it will help us to choose the best one to achieve a desired privacy level while preserving data utility.

1 Introduction

In recent years, a huge amount of social and human interaction networks have been made publicly available. Embedded within this data there is user’s private information which must be preserved before releasing this data to third parties and researchers. The study of Ferri et al. [13] reveals that up to 90 % of user groups are concerned by data owners sharing data about them. Backstrom et al. [2] point out that the simple technique of anonymizing graphs by removing the identities of the vertices before publishing the actual graph does not always guarantee privacy. They show that an adversary can infer the identity of the vertices by solving a set of restricted graph isomorphism problems.

Therefore, anonymization processes become an important concern in this scenario. These methods add noise into the original data to hinder re-identification processes. Nevertheless, the noise introduced by the anonymization steps may also affect the data, reducing its utility for subsequent data mining processes. Usually, the larger the data modification, the harder the re-identification but also the less the data utility. Thus, it is necessary to preserve the integrity of the data to ensure that the data mining step is not altered by the anonymization step. The analysis performed on the obfuscated data should produce results as close as possible to the ones the original data would have led to.

Several methods appeared recently to preserve the privacy of the data contained in a graph. One of the most used and well-known approaches is based on “graph modification”. These methods first transform the data by edges or vertices modifications (adding and/or deleting) and then release the perturbed data. The data is thus made available for unconstrained analysis. There are two main approaches in the privacy-preserving literature [23]: (a) random perturbation of the graph structure by randomly adding/removing/switching edges and often referred to as edge randomization [4, 6, 16, 17, 24, 25]; and (b) constrained perturbation of the graph structure via sequential edge modifications in order to fulfil some desired constraints – for example k-anonymity-based approaches that modify the graph so that every node is in the end indistinguishable from $k-1$ other nodes (in terms of node degree for instance) [7, 10, 18–20, 28, 29].

All aforementioned algorithms use edge modification techniques, i.e. add, remove and/or switch edges to achieve a desired privacy level. Nevertheless, it is inevitable to introduce noise in the data, producing a certain amount of information loss, and consequently, deteriorating the utility of the anonymous data. Some authors claim that only adding edges better preserves the data utility, since none true relationship is removed. On the contrary, some other authors claim that removing an edge affects the structure of the graph to a smaller degree than adding an edge [5].

In this paper we want to analyse the edge modification techniques found in the literature covering this topic, and then empirically evaluate the information loss introduced by each of these methods during the perturbation process. We want to understand how these edge modifications affect the main properties and characteristics of the network. This will help us to choose the best edge modification technique to achieve a desired privacy level while keeping data utility and reducing information loss.

1.1 Our Contributions

In this paper we present an empirical evaluation of the basic edge modification techniques, which can help us to increase data utility in anonymous networks. We focus on simple, undirected and unlabelled graphs. Since these graphs have no attributes or labels in the edges, information is only in the structure of the graph itself and, due to this, evaluating edge modification techniques is an critical way to reduce information loss. We offer the following results:

• We analyse the most used and well-known edge modification techniques found in the graph privacy literature.

• We conduct an empirical evaluation of these techniques on several synthetic and real graphs, comparing information loss based on different graph’s properties.

• We demonstrate that graph’s structure must be considered in order to select the best edge modification technique, and it conducts the process to reduce the information loss and increase the data utility.

1.2 Notation

Let $G=(V,E)$ be a simple, undirected and unlabelled graph, where V is the set of vertices and E the set of edges in G. We define $n=\vert V \vert$ to denote the number of vertices and $m=\vert E \vert$ to denote the number of edges. We use $\{i,j\}$ to define an undirected edge from vertex $v_i$ to $v_j$ and $deg(v_i)$ to denote the degree of vertex $v_i$. Finally, we designate $G=(V,E)$ and $\widetilde{G}=(\widetilde{V},\widetilde{E})$ to refer the original and the perturbed graphs, respectively. Note that in this work we use the terms graph and network indistinguishably.

1.3 Roadmap

This paper is organized as follows. In Sect. 2, we review the basic edge modification techniques for privacy-preserving on graphs. Section 3 introduces our experimental framework to analyse and compare the edge modification techniques on both synthetic and real networks. Then, in Sect. 4, we discuss the results in terms of information loss and data utility. Lastly, in Sect. 5, we present the conclusions of this work and some future remarks.

2 Edge Modification Techniques

We define four basic edge modification processes to change the network’s structure by adding, removing or switching edges. These methods are the most basic ones, and they can be combined in order to create complex combinations. We are interested in them since they allow us to model, in a general and conceptual way, most of the privacy-preserving methods based on edge-modification processes. In the following lines we will introduce these basic methods, also called perturbation methods, due to the fact that they can model the perturbation introduced in anonymous data during the anonymization process.

Fig. 1.

Basic operations for edge modification.

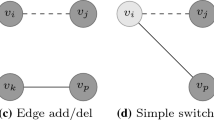
There are four basic edge modifications illustrated in Fig. 1. Dashed lines represent existing edges which will be deleted and solid lines constitute the edges which will be added. Node color indicates whether a node changes its degree (dark grey) or not (light grey) after the edge modification has been carried out. These are:

• Edge add simply consists on adding a new edge $\{v_i, v_j\} \not \in E$. Figure 1a illustrates this operation. The number of the edges will increase ($\widetilde{m} > m$) when anonymization percentage increases. True relationships will be preserved in perturbed data.

• Edge del removes an existing edge $\{v_i, v_j\} \in E$, as depicted in Fig. 1b. Contrary to the previous method, the number of edges decreases $\widetilde{m} < m$ and no fake relationships are included in the anonymous data, but several true relations are deleted from original data.

• Edge add/del is a combination of the previous pair methods. It simply consists of deleting an existing edge $\{v_i, v_j\} \in E$ and adding a new one $\{v_k, v_p\} \not \in E$. Figure 1c illustrates this operation. In this case some true relations are deleted and some fake ones are created, but the total number of edges is preserved ($\widetilde{m} = m$). All vertices involved in this operation change their degree.

• Edge switch occurs between three nodes $v_i, v_j, v_p \in V$ such that $\{v_i, v_j\} \in E$ and $\{v_i, v_p\} \not \in E$. It is defined as deleting edge $\{v_i, v_j\}$ and creating a new edge $\{v_i, v_p\}$ as shown in Fig. 1d. As in the previous case, some true relations are removed, some fake ones are created and the number of edges is also preserved ($\widetilde{m} = m$). However, two vertices change their degree ($v_j$ and $v_p$) while the third one ($v_i$) does not.

For all perturbation methods, the number of vertices remains the same but the degree distribution changes. As previously stated, most of the anonymization methods rely on one (or more) of these basic edge modification operations. We believe that this covers the basic behavior of edge-modification-based methods for graph anonymization, even though some of them do not apply edge modification to the entire edge set.

As aforementioned, some algorithms are based on Edge add [10, 19, 21, 28], since their authors usually claim that this edge modification technique better retain data utility. A similar situation occurs with Edge del [4, 5]. Several random-based anonymization methods are based on the concept of Edge add/del [17, 24, 25] and most k-anonymity methods can be also modelled through the this concept [18, 22, 28, 29]. Lastly, Edge switch is also used in many algorithms, such as [7, 16, 20, 25]. Other methods consider to alter the vertex set to achieve anonymity. This concept is known as noise node addition [9, 11, 26]. We do not consider this algorithms in this paper due to space constraints and we propose it for future work.

3 Evaluating Framework

In this section we will post the experimental framework we have used to analyse and compare the information loss induced by our four edge modification techniques. Our experimental framework considers 10 independent executions of the edge modification methods with a perturbation parameter p in range between 0 % (original graph) and 25 % of total number of edges, i.e., $0 \le p \le 25$.

The process is the following: Firstly, we generate 10 independent sets of perturbed networks (from 0 % to 25 %) using each one of our edge modification techniques (also called perturbation methods). Secondly, we compute the error between the original (G) and each perturbed network ($\widetilde{G}$) using several measures (defined in Sect. 3.2). Thirdly, we compute the average error over the 10 independent sets. We repeat the same process for all our tested networks (detailed in Sect. 3.1). This framework is depicted in Fig. 2.

Fig. 2.

Framework for evaluating information loss induced by edge modification techniques.

3.1 Tested Networks

We use both synthetic and real networks in our experiments. We use software igraph ¹ to generate two kinds of random graphs.

• Erdös-Rényi Model [12] is a classical random graph model. It defines a random graph as n vertices connected by m edges that are chosen randomly from the $n(n-1)/2$ possible edges. In our experiments, we set n=1,000 and m=5,000. This dataset is denoted as “ER-1000”.

• Barabási-Albert Model [3], also called scale-free model, is a network whose degree distribution follows a power-law. That is, for degree d, its probability density function is $P(k) = d^{-\gamma }$. In our experiments, we set the number of vertices to be 1,000 and $\gamma$=1, i.e. linear preferential attachment. This dataset is denoted as “BA-1000”.

Additionally, four different real networks are used in our experiments. Although all these sets are unlabelled, we have selected these datasets because they have different graph’s properties. Table 1 shows a summary of their main features. They are the following ones:

• Zachary’s Karate Club [27] is a network widely used in literature. The graph shows the relationships among 34 members of a karate club.

• Jazz musicians [14] is a collaboration graph of jazz musicians and their relationship.

• URV email [15] is the email communication network at the University Rovira i Virgili in Tarragona (Spain). Nodes are users and each edge represents that at least one email has been sent.

• Political blogosphere data (polblogs) [1] compiles the data on the links among US political blogs.

Table 1. Network’ properties. For each dataset we present the number of vertices (n), number of edges (m), average degree ($\overline{deg}$), average distance ($\overline{dist}$) and diameter (D).

3.2 Information Loss Measures

According to the authors in [8], we use some structural and spectral measures which are strongly or moderately correlated to clustering specific processes. We claim that choosing these measures our results will be applicable not only to graph’s properties, but also to clustering and community detection processes. The first graph structural measure is average distance ($\overline{dist}$), which is defined as the average of the distances between each pair of vertices in the graph. Transitivity (T) is one type of clustering coefficient, which measures and characterizes the presence of local loops near a vertex. It measures the paths’ percentage of length 2 which are also triangles. The above measures evaluate the entire graph as a unique score. We compute the error on these graph metrics as follows:

$$\begin{aligned} \epsilon _{m}(G,\widetilde{G}) = \vert m(G) - m(\widetilde{G}_p) \vert \end{aligned}$$

(1)

where m is one of the graph characteristic metrics, G is the original graph and $\widetilde{G}_p$ is the p-percent perturbed graph, where $0 \le p \le 25$.

The following metrics evaluate specific structural properties for each vertex of the graph: the first one is betweenness centrality ($C_B$), which measures the fraction of the shortest paths that go through each vertex. This measure indicates the centrality of a vertex based on the flow between other vertices in the graph. A vertex with a high value indicates that this vertex is part of many of the shortest paths in the graph, which will be a key vertex in the graph structure. The second one is closeness centrality ($C_C$) and is defined as the inverse of the average distance to all accessible vertices. Finally, the third one is degree centrality ($C_D$), which evaluates the centrality of each vertex associated with its degree, i.e. the fraction of vertices connected to it. We compute the error on vertex metrics by:

$$\begin{aligned} \epsilon _{m}(G,\widetilde{G}) = \sqrt{\frac{1}{n} ((g_{1} - \widetilde{g}_{1})^{2} + \ldots + (g_{n} - \widetilde{g}_{n})^{2})} \end{aligned}$$

(2)

where $g_{i}$ is the value of the metric m for the vertex $v_i$ of G and $\widetilde{g}_{i}$ is the value of the metric m for the vertex $v_i$ of $\widetilde{G}$.

Moreover, one spectral measure which is closely related to many graph characteristics [25] is used. The largest eigenvalue of the adjacency matrix A ($\lambda _{1}$) where $\lambda _{i}$ are the eigenvalues of A and $\lambda _{1} \ge \lambda _{2} \ge \ldots \ge \lambda _{n}$. The eigenvalues of A encode information about the cycles of a graph as well as its diameter.

Fig. 3.

Degree distribution on our synthetic networks. Horizontal axis represent the whole vertex set and vertical axis their degree values.

4 Experimental Results

In this section we will discuss the results of our four edge modification techniques. Results are presented in Table 2. Each cell indicates the error value for the corresponding measure and method computed by Eqs. 1 and 2. Values are averaged from 10 independent executions. The lower the value, the better the method. Although deviation is undesirable, it is inevitable due to the graph’s alteration process.

Table 2. Results for Edge add (Add), Edge Del (Del), Edge add/del (Add/del) and Edge Switch (Switch) methods. For each dataset and method, we compare the results obtained on $\overline{dist}$, T, $C_B$, $C_C$, $C_D$ and $\lambda _{1}$. Last column corresponds to the cumulative normalized error ($\varepsilon$) for each method on all evaluated metrics.

The first two tested networks are the synthetic ones. As we have commented previously, ER-1000 has been created using Erdös-Rényi model. Its degree histogram does not follow de power-law, as it can be seen in Fig. 3a. Most of the vertices have degree values between 7 and 13, while few have degree values lower than 7 or higher than 13. Edge add/del and Edge switch present the best values on almost all metrics used on our experiments, as we can see in Table 2. Last column corresponds to the cumulative normalized error ($\varepsilon$), which points out that Edge switch achieves the lowest information loss, closely followed by Edge add/del. Both Edge add and Edge del get worse results. On the contrary, the second network, BA-1000, has been constructed by applying scale-free model and its degree distribution follows a power-law. Figure 3b points out clearly a large number of vertices with small degree value and few vertices with very high degree value. It is important to underline the scale difference between this figure and the previous one. In this case, Edge add and Edge switch reach results with the lowest information loss. As in the previous case, the difference between these two methods and the other ones (Edge del and Edge add/del) is considerable.

The first tested real network is Zachary’s Karate Club. Although Edge switch achieves the best values, Edge add and Edge add/del get values close to theirs. For instance, we can deepen on behaviour of $\lambda _1$ error in Fig. 4a. The $p=0$ value (x-axis) represents the value of this metric on the original graph. Thus, values close to this point indicate low noise on perturbed data. As we can see, Edge switch remains closer to the original value than the other methods.

Jazz musicians is our second tested real network. The differences among our four methods are smaller using this dataset than the aforementioned experiments. Edge del reaches better results than previous cases and the method which introduces the most information loss is Edge add/del. However, Edge add and Edge switch get slightly lower information loss. For example, we analyse average distance in depth, which usually increases when applying Edge del and decreases when applying Edge add. It is obvious, since removing edges increases paths between vertices and adding new edges decreases paths. Nevertheless, it is interesting to see that perturbation introduced by removing edges is lower than others in this case, as can be seen in Fig. 4b.

Fig. 4.

Examples of the error evolution computed on our experimental framework. Perturbation parameter p varies along the horizontal axis from 0 % (original graph) to 25 %.

Lastly, URV email and Polblogs represent the largest real networks in our experiments. Their structure is similar to BA-1000, since they are both scale-free networks but with parameter $\gamma \approx 0.5$. Results on URV email are similar to ones on BA-1000; Edge add achieves the best results, followed by Edge switch, and again Edge del and Edge add/del get the worst results. We can observe this behaviour in Fig. 4c, where Edge add obtains the lowest error on closeness centrality. The difference is quite important compared to Edge add/del and Edge switch, but even larger compared to Edge del. Similar behaviour can be observed on Polblogs dataset. Edge add achieves the best values, but Edge del and Edge switch also get also good values, close to the ones obtained by Edge add.

Figure 4d depicts transitivity, where all edge modification methods decrease values obtained on original network. As shown, Edge add gets values closer to the original ones on all perturbation percentage. Edge del and Edge switch obtain similar cumulative normalized error on this dataset, suggesting that both introduce similar noise on tested metrics.

As conclusions, we note that Edge switch gets lower information loss when it is applied to networks which do not fulfil the scale-free model, i.e. ER-1000 and Jazz musicians. On the other side, Edge add obtains the lowest information loss when dealing with scale-free networks, such as BA-1000, URV email and Polblogs. Edge switch also achieves good results on scale-free networks. That is not surprising, since Edge switch preserves the degree distribution keeping some related measures close to the original values. On the contrary, Edge del and Edge add/del introduce more perturbation on almost all analysed networks, except Polblogs where Edge del scores the second position and ER-1000 where Edge add/del also succeed to obtain the second position.

5 Conclusions

In this paper we have evaluated the basic edge modification techniques, which are commonly used on privacy-preserving algorithms. We have presented four basic types of edge modification methods, and a framework to assess the behaviour of some graph’s properties during perturbation processes induced by these four edge modification methods. Our framework includes some experimental results both on synthetic and real-world networks.

As we have demonstrated, Edge switch better preserves graph’s properties on networks with a degree distribution which does not follow the power-law. On the contrary, Edge add is the best method to keep graph’s properties when perturbing scale-free networks. Edge del and Edge add/del introduce more noise during perturbation processes on both type of networks.

Many interesting directions for future research have been uncovered by this work. It would be interesting to also consider methods based on noise node addition [11] and information loss measures based on real graph-mining processes, such as clustering or community detection. It would be also very interesting to extend this analysis to other graph’s types (directed or labelled graphs, for instance).