A survey of graph-modification techniques for privacy-preserving on networks

Abstract

Recently, a huge amount of social networks have been made publicly available. In parallel, several definitions and methods have been proposed to protect users’ privacy when publicly releasing these data. Some of them were picked out from relational dataset anonymization techniques, which are riper than network anonymization techniques. In this paper we summarize privacy-preserving techniques, focusing on graph-modification methods which alter graph’s structure and release the entire anonymous network. These methods allow researchers and third-parties to apply all graph-mining processes on anonymous data, from local to global knowledge extraction.

1 Introduction

In recent years, an explosive increase of social networks has been made publicly available. Embedded within this data there is private information about users who appear in it. Therefore, data owners must respect the privacy of users before releasing datasets to third parties. In this scenario, anonymization processes become an important concern. Among others, the study of Ferri et al. (2011) reveals that up to 90 % of user groups are concerned by data owners sharing data about them. Backstrom et al. (2007) point out that the simple technique of anonymizing graphs by removing the identities of the vertices before publishing the actual graph does not always guarantee privacy. They show that there exist adversaries that can infer the identity of the vertices by solving a set of restricted graph isomorphism problems. Some approaches and methods have been imported from anonymization on structured data, but the peculiarities of graph-formatted data avoid these methods to work directly on it. In addition, divide-and-conquer methods do not apply to anonymization of graph data due to the fact that registers are not separable, since removing or adding vertices and edges may affect other vertices and edges as well as the properties of the graph (Zhou and Pei 2008).

1.1 Contributions

In this paper we present the most important categories related to the privacy-preserving (or anonymization) problem, but we will focus our attention on graph-modification methods, since they allow data owners to alter graph’s structure and release the entire network. Consequently, anonymous data can be used to answer all graph-mining tasks, from local to global techniques.

Some other surveys on graph anonymization can be found, but no one else is dedicated to in-depth analysis of graph-modification techniques for privacy-preserving on networks, presenting a wide range of all techniques referring graph-modification operations. In this survey we include not only the most recent methods and algorithms for graph anonymization but also new techniques to preserve the user’s privacy in data publishing processes, such as uncertain graphs. Some other surveys were made some years ago and new definitions and methods have appeared since then (Zhou et al. 2008; Wu et al. 2010b; Hay et al. 2011); others are focused on relational data (De Capitani di Vimercati et al. 2012; Torra 2010); and finally some others are only focused on some specific methods (such as k-anonymity or generalization) (Nagle 2013).

We will review the most important methods of graph-modification techniques for privacy-preserving on networks, i.e. random perturbation, constrained perturbation, uncertain graphs and generalization. Main advantages and drawbacks will be discussed, though sometimes it is hard to compare algorithms due to the lack of common frameworks, datasets and measures.

Firstly, we will pose random perturbation techniques, which are generally the simplest and present the lowest complexity. Thus, they are able to deal with large networks, though they do not offer privacy guarantees, but a probabilistic re-identification model. Due to its simplicity these methods can be adapted to deal with big or streaming data, but none has been specifically developed for this purpose up to now.

Next, we will focus in constrained perturbation methods. Several methods have been propounded in this category, such as k-anonymity. These methods provide privacy guarantees, but its privacy may strongly depend on the adversary’s knowledge. The most basic adversary’s knowledge is based on vertex degree. Several works have been developed to fulfil k-degree anonymity, being able to anonymize large networks based on the vertex degree adversary’s knowledge. We will review the most important methods in this category, discussing the most suitable ones. Additionally, we will consider more complex models, such as k-neighbourhood and k-automorphism, though the complexity arises when dealing with them. Preserving strategies for edge and vertex labelled networks will be also discussed, as so for bipartite graphs.

We will also introduce recently proposed methods based on uncertain graphs. The main problem of these approaches is the nature of uncertain graphs; several graph-mining tasks, such as clustering and community detection algorithms, cannot be applied straightforwardly to uncertain graphs since they are developed to deal with binary-edge graphs. Nonetheless, interesting approaches have been presented and it seems that it will be an active field in the upcoming years.

Finally, generalization methods (also know as clustering approaches) will be introduced. Although they provide suitable privacy levels, the analysis of local measures and metrics from the resulting graphs is not straightforward. Nevertheless, they demonstrated to be able to deal with vertex-labelled networks, offering anonymity in terms of attribute and identity.

1.2 Notation

Let $G=(V,E)$ be a simple, undirected and unlabelled graph, where V is the set of vertices and E the set of edges in G. We define $n=\vert V \vert$ to denote the number of vertices and $m=\vert E \vert$ to denote the number of edges. We use $\{i,j\}$ to define an undirected edge from vertex $v_i$ to $v_j$, $deg(v_i)$ to denote the degree of vertex $v_i$ and the set of 1-neighbourhood of vertex $v_i$ as $\Gamma (v_i)=\{v_j : \{i,j\} \in E \}$. We use d(G) to define the degree sequence of G, where d(G) is a vector of length n such that $d(G)=\{ deg(v_1), deg(v_2), \ldots , deg(v_n) \}$. Finally, we designate $G=(V,E)$ and $\widetilde{G}=(\widetilde{V},\widetilde{E})$ to refer the original and the perturbed graphs, respectively.

1.3 Roadmap

The paper is organized as follows. We introduce the privacy-preserving scenario and problem definition on networks in Sect. 2. Next, in Sect. 3 we present the basic classification for graph-modification techniques. Then we review the state of the art of edge and vertex modification methods in Sect. 4, uncertain graphs in Sect. 5 and generalized graphs in Sect. 6. Lastly, we finish the paper in Sect. 7 discussing the conclusions and commenting the open problems in Sect. 8.

2 Problem definition

Currently, large amounts of data are being collected on social and other kinds of networks, which often contain personal and private information of users and individuals. Although basic processes are performed on data anonymization, such as removing names or other key identifiers, remaining information can still be sensitive, and useful for an attacker to re-identify users and individuals. To solve this problem, methods which introduce noise to the original data have been developed in order to hinder the subsequent processes of re-identification. A natural strategy for protecting sensitive information is to replace identifying attributes with synthetic identifiers. We refer to this procedure as simple or naïve anonymization. This common practice attempts to protect sensitive information by breaking the association between the real-world identity and the sensitive data.

Fig. 1

Naïve anonymization of a toy network, where G (a) is the original graph, $\widetilde{G}$ (b) is the naïve anonymous version and $\widetilde{G}_{Dan}$ (c) is Dan’s 1-neighbourhood

Figure 1a shows a toy example of a social network, where each vertex represents an individual and each edge indicates the friendship relation between them. Figure 1b presents the same graph after a naïve anonymization process, where vertex identifiers have been removed and the graph structure remains the same. One can think users’ privacy is secure, but an attacker can break the privacy and re-identify a user on the anonymous graph. For instance, if an attacker knows that Dan has four friends and two of them are friends themselves, then he can construct the 1-neighbourhood of Dan, depicted in Fig. 1c. From this sub-graph, the attacker can uniquely re-identify user Dan on anonymous graph. Consequently, user’s privacy has been broken by the attacker.

Zhou and Pei (2008) noticed that to define the problem of privacy preservation in publishing social network data, we need to formulate the following issues: firstly, we need to identify information to be preserved. Secondly, we need to model the background knowledge that an adversary may use to attack the privacy. And thirdly, we need to specify the usage of the published social network data so that an anonymization method can try to retain the utility as much as possible while the privacy information is fully preserved.

Regarding the privacy information to be preserved in social networks, three main categories of privacy threats have been identified:

• 1. Identity disclosure occurs when the identity of an individual who is associated with a vertex is revealed. It includes sub-categories such as vertex existence, vertex properties and graph metrics (Zhou et al. 2008).

• 2. Attribute disclosure which seeks not necessarily to identify a vertex, but to reveal sensitive labels of the vertex. The sensitive data associated with each vertex is compromised.

• 3. Link disclosure occurs when the sensitive relationship between two individuals is disclosed. Depending on network’s type, we can refine this category as link relationships, link weight and sensitive edge labels.

Identity disclosure and link disclosure apply on all types of networks. However, attribute disclosure only applies on vertex-labelled networks. In addition, link disclosure can be considered a special type of attribute disclosure, since edges can be seen as a vertex attributes. Identity disclosure often leads to attribute disclosure due to the fact that identity disclosure occurs when an individual is identified within a dataset, whereas attribute disclosure occurs when sensitive information that an individual wished to keep private is identified.

Determining the knowledge of the adversary is a challenging problem. A variety of adversaries’ knowledge have been proposed in conjunction with their attack and a protection method. In cryptanalysis, the authors distinguish between two basic types of attacks, and it may be also an interesting basic classification for network social attacks, although it is also valid for other types of networks: (1) active attacks, where an adversary tries to compromise privacy by strategically creating new user accounts and links before the anonymized network is released, so that these new vertices and edges will then be present in the anonymized version. And (2) passive attacks are carried out by individuals who try to learn the identities of vertices only after the anonymized network has been released.

Two attacks were proposed in Backstrom et al. (2007), where the authors showed that identity disclosure would occur when it is possible to identify a sub-graph in the released naïvely-anonymized graph. The walk-based attack is an active attack in which an adversary creates k accounts and links them randomly, then he creates a particular pattern of links to a set of m other users that he is interested in. The goal is to learn whether two of the monitored vertices have links between them. When the data is released, the adversary can efficiently identify the sub-graph of vertices corresponding to his k accounts with high probability. With as few a $k = \mathcal {O}(log(n))$ accounts, an adversary can recover the links between as many as $m = \mathcal {O}(log^2(n))$ vertices in an arbitrary graph of size n. In the cut-based attack users of the system do not create any new vertices or edges, they simply try to find themselves in the released network, and from this to discover the existence of edges among users to whom they are linked. Therefore, it is a passive attack. In a network with 4.4 million of vertices, the authors find that for the vast majority of users, it is possible for them to exchange structural information with a small coalition of their friends, and subsequently uniquely identify the sub-graph on this coalition in the ambient network. Using this, the coalition can then compromise the privacy of edges among pairs of neighbouring nodes.

Hay et al. (2007, (2008) proposed structural queries Q which represents complete or partial structural information of a target individual that may be available to adversaries. Let Q(v) be a structural query on individual v, then the candidate set is defined as $Cand_Q(v)=\{u \in V : Q(u) = Q(v)\}$. If $\vert Cand_Q(v) \vert$ is small, v can be re-identified with high probability. Vertex refinement queries are used to model the knowledge of the adversary and also to analyse the network in terms of k-anonymity. However, the main problem of this approach is that it can not consider adversary’s partial information. That is, using this approach an adversary with partial knowledge of the adjacent vertices to a target vertex can not be modelled. Sub-graph knowledge queries have been developed to overcome this limitation.

Ying and Wu (2009a) designed an attack based on the probability of an edge exists and the similitude between pairs of vertices on anonymous graph. The attack is modelled using matrix operations: $\widetilde{A}=A+E$ where $\widetilde{A}$ and A are the adjacency matrix of anonymous and original graphs, and E is the perturbation matrix. In structured or relation data, some methods allow an attacker to reconstruct the original matrix (A) from the anonymized matrix ($\widetilde{A}$) and some a priori knowledge about the perturbation method applied. Nevertheless, up to now the results have not been good enough. Ying and Wu also investigated how well the edge randomization approach via addition/deletion can protect privacy of sensitive links. They have conducted theoretical analysis and empirical evaluations to show that vertex proximity measures can be exploited by attackers to enhance the posterior belief and prediction accuracy of the existence of sensitive links among vertices with high similarity values. Same authors proposed to exploit graph space to breach link privacy in Ying and Wu (2009b). Wu et al. (2010a) studied a reconstruction method from randomized graphs by a low rank approximation approach, using the eigen-decomposition of randomized graph to lead the process. Lastly, Vuokko and Terzi (2010) tried to reconstruct randomized vertex-labelled networks using the assumption that vertices which are connected in G are likely to have similar feature vectors F and vice versa. Their method finds, in polynomial time, G and F such that $Pr(G, F \vert \widetilde{G}, \widetilde{F})$ is maximized.

An attack by combining multiple graphs was presented in Narayanan and Shmatikov (2009), where the authors assumed that adversaries have an auxiliary graph whose members overlap with anonymous network and detailed information about a few target nodes. Under these premises, the following attack is considered: First, the adversaries will try to re-identify the seeds in the anonymous network, and second they will try to re-identify more vertices by comparing the neighbourhood on both auxiliary and anonymous networks. Gulyás and Imre (2013, (2015) proposed a technique based on identity separation to avoid this attack that needs cooperative participation of several users. So, in general, this solution may not be applicable. Sharad and Danezis (2014) presented an automated approach to re-identifying nodes in anonymized social networks which uses machine learning (decision forests) to matching pairs of nodes in disparate anonymized sub-graphs.

Other attacks on naively anonymized network data have been developed, which can re-identify vertices, disclose edges between vertices, or expose properties of vertices (e.g., vertex features). These attacks include: matching attacks, which use external knowledge of vertex features (Liu and Terzi 2008; Zou et al. 2009; Zhou and Pei 2008); injection attacks, which alter the network prior to publication (Backstrom et al. 2007); and auxiliary network attacks, which use publicly available networks as an external information source (Narayanan and Shmatikov 2009). To solve these problems, methods which introduce noise to the original data have been developed in order to hinder the subsequent processes of re-identification.

3 Graph-modification techniques

From a high level view, there are three general families of graph-modification techniques to mitigate network data privacy:

• Edge and vertex modification approaches first transform the data by edges or vertices modifications (adding and/or deleting) and then release the perturbed data. The data is thus made available for unconstrained analysis.

• Uncertain graphs are approaches based on adding or removing edges “partially” by assigning a probability to each edge in anonymous network. Instead of creating or deleting edges, the set of all possible edges is considered and a probability is assigned to each edge.

• Generalization or clustering-based approaches, which can be essentially regarded as grouping vertices and edges into partitions called super-vertices and super-edges. The details about individuals can be hidden properly, but the graph may be shrunk considerably after anonymization, which may not be desirable for analysing local structures.

All aforementioned methods first transform the data by different types of graph’s modifications and then release the perturbed data. The data is thus made available for unconstrained analysis. On the contrary, there are “privacy-aware computation” methods, which do not release data, but only the output of an analysis computation. The released output is such that it is very difficult to infer from it any information about an individual input datum. For instance, differential privacy (Dwork 2006) is a well-known privacy-aware computation approach. We do not consider these methods in this survey, since they do not allow us to release the entire network, which provides the widest range of applications for data mining and knowledge extraction.

4 Edge and vertex modification approaches

Edge and vertex modification approaches anonymize a graph by modifying (adding and/or deleting) edges or vertices in the graph. These modifications can be made at random, and we will refer to them as randomization, random perturbation or obfuscation methods. However, modification can be performed in order to fulfil some desired constraints, and in that cases we will call them constrained perturbation methods.

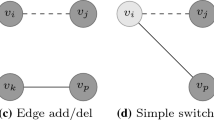
We define three basic edge modification processes to change the network’s structure by adding and/or removing edges. These methods are the most basic ones, and they can be combined in order to create complex combinations. We are interested in them since they allow us to model, in a general and conceptual way, most of the privacy-preserving methods. In the following lines we will introduce these basic methods, which are illustrated in Fig. 2. Dashed lines represent existing edges which will be deleted and solid lines constitute the edges which will be added. Node color indicates whether a node changes its degree (dark grey) or not (light grey) after the edge modification has been carried out. These are:

• Edge add/del is the most generic edge modification. It simply consists of deleting an existing edge $\{v_i, v_j\} \in E$ and adding a new one $\{v_k, v_p\} \not \in E$. Figure 2a illustrates this operation.

• Edge rotation occurs between three nodes $v_i, v_j, v_p \in V$ such that $\{v_i, v_j\} \in E$ and $\{v_i, v_p\} \not \in E$. It is defined as deleting edge $\{v_i, v_j\}$ and creating a new edge $\{v_i, v_p\}$ as Fig. 2b illustrates. Note that edge switch would have been more appropriate but it had already been defined in the relevant literature in the context of a “double switch”.

• Edge switch occurs between four nodes $v_i, v_j, v_k, v_p \in V$ where $\{v_i, v_j\},\{v_k, v_p\} \in E$ and $\{v_i, v_p\},\{v_k, v_j\} \not \in E$. It is defined as deleting edges $\{v_i, v_j\}$ and $\{v_k, v_p\}$ and adding new edges $\{v_i, v_p\}$ and $\{v_k, v_j\}$ as Fig. 2c illustrates.

Fig. 2

Basic operations for edge modification. a Edge add/del, b edge rotation, c edge switch

For all three presented edge modification techniques, the number of nodes and edges remain the same but the degree distribution changes for Edge add/del and Edge rotation while not for Edge switch. Clearly, Edge add/del is the most general concept and all other perturbations can be modelled as a particular case of it: Edge rotation is a sub case of Edge add/del and Edge switch a sub case of Edge rotation.

Most of the methods outlined in this survey are based on one (or a combination of more than one) edge modification techniques previously presented. Several random-based anonymization methods are based on the concept of Edge add/del. For example, the Random Perturbation algorithm (Hay et al. 2007), Spctr Add/Del (Ying and Wu 2008) and Rand Add/Del-B (Ying et al. 2009) use this concept to anonymize graphs. Most k-anonymity methods can be also modelled through the Edge add/del concept (Hay et al. 2008; Zhou and Pei 2008; Zou et al. 2009). Edge rotation is a specification of Edge add/del and a generalization of Edge switch: at every edge rotation, one node keeps its degree and the others change theirs. The UMGA algorithm (Casas-Roma et al. 2013, 2016) applies this concept to anonymize the graph according to the k-degree anonymity concept. Other methods are related to Edge switch: for instance, Rand Switch and Spctr Switch (Ying and Wu 2008) apply this concept to anonymize a graph. Additionally, Liu and Terzi (2008) also apply this concept to the graph’s reconstruction step of their algorithm for k-degree anonymity.

4.1 Random perturbation

These methods are based on adding random noise in original data. They have been well investigated for structured or relational data. Naturally, edge randomization can also be considered as an additive-noise perturbation. Notice that the randomization approaches protect against re-identification in a probabilistic manner. Specifically, methods based on Edge add/del or Edge rotation preserve against identity disclosure, when presuming an adversary’s knowledge based on degree or neighbourhood information, and also against link disclosure. Methods based on Edge switch do not protect against identity disclosure when an adversary has knowledge about vertices’ degree since using this edge modification technique the degree distribution remains the same.

Naturally, graph randomization techniques can be defined in terms of removing some true edges and/or adding some fake ones. Two natural edge-based graph perturbation strategies are:

• Rand add/del applies Edge add/del at random considering the entire edge set, without restrictions or constraints. This strategy preserves the number of edges in the original graph.

• Rand switch randomly switches a pair of existing edges following Edge switch description. This strategy preserves the degree of each vertex and the number of edges.

Fig. 3

Random perturbation example, where G (a) is the original graph, $\widetilde{G}_{ra}$ (b) and $\widetilde{G}_{sw}$ (c) are perturbed versions of the network by Rand add/del and Rand switch, respectively

Example 1

An example of random perturbation process is presented in Fig. 3. The original network is depicted in Fig. 3a. Next, Fig. 3b shows a perturbed version of the same network by Rand add/del. During the anonymization process, two edges have been removed ($\{1,5\}$ and $\{2,3\}$) and two new ones have been created ($\{6,7\}$ and $\{8,9\}$). An alternatively perturbed version of the same network by Rand switch is presented in Fig. 3c, where edges $\{1,2\}$ and $\{4,5\}$ were switched to $\{1,4\}$ and $\{2,5\}$. Both methods preserve the number of vertices and edges. Additionally, Rand switch also preserves the degree sequence, i.e. $d(G) = d(\widetilde{G}_{sw}) = \{3,2,4,4,2,4,2,2,1\}$ while Rand add/del does not, i.e. $d(\widetilde{G}_{ra}) = \{2,1,3,4,1,5,3,3,2\}$.

Hay et al. (2007) proposed a method, called Random perturbation, to anonymize unlabelled graphs using Rand add/del strategy, i.e. randomly removing p edges and then randomly adding p fake edges. The set of vertices does not change and the number of edges is preserved in the anonymous graph. The main advantages of this method are its simplicity but also its low complexity. On the contrary, hubs are not well-protected and can be re-identified. Ying and Wu (2008) studied how different randomization methods (based on Rand add/del and Rand switch) affect the privacy of the relationship between vertices. The authors also developed two algorithms specifically designed to preserve spectral characteristics of the original graph, called Spctr Add/Del and Spctr Switch. The same authors proposed a method to preserve any graph feature within a small range using Markov Chain in Ying and Wu (2009b). Stokes and Torra (2011) stated that an appropriate selection of the eigenvalues in the spectral method can perturbate the graph while keeping its most significative edges. The authors in Casas-Roma (2014) presented an strategy which aims to preserve the most important edges in the network, trying to maximize data utility while achieving a desired privacy level. Generally, methods based on spectral properties of the network achieve lower information loss, but at a cost of increasing complexity.

An interesting comparison between a randomization and a constrained-based method, in terms of identity and link disclosure, was presented by Ying et al. (2009). In addition, the authors developed a variation of Random perturbation method, called Blockwise Random Add/Delete strategy (or simply Rand Add/Del-B). This method divides the graph into blocks according to the degree sequence and implements edge modifications on the vertices at high risk of re-identification, not at random over the entire set of vertices. Blockwise Random Add/Delete strategy achieves better results than the previous ones when dealing with scale-free networks, since it focuses on hubs and other vertices at high risk of re-identification.

More recently, Bonchi et al. (2011, (2014) offered a new information-theoretic perspective on the level of anonymity obtained by random methods. The authors proposed an entropy-based quantification of the anonymity level that is provided by the perturbed graph. They stated that the anonymity level quantified by means of entropy is always greater than or equal to the one based on a-posteriori belief probabilities. They also introduced a new random-based method, called Sparsification, which randomly removes edges without adding new ones. The extended version of the work (Bonchi et al. 2014) also studied the resilience of obfuscation by random sparsification to adversarial attacks that are based on link prediction.

Other approaches are based on generating new random graphs that share some desired properties with the original ones, and releasing one of this new synthetic graphs. For instance, these methods consider the degree sequence of the vertices or other structural graph characteristics like transitivity or average distance between pairs of vertices as important features which the anonymization process must keep as equal as possible on anonymous graphs. Usually, these methods define $\mathcal {G}_{d,S}$ as the space of networks which: (1) keep the degree sequence d and (2) preserve some properties S within a limited range. Therefore, $\mathcal {G}_{d,S}$ contains all graphs which satisfy both properties. For example, an algorithm was proposed for generating synthetic graphs in $\mathcal {G}_{d,S}$ with equal probability in Ying and Wu (2009b) and a method that generates a graph with high probability to keep properties close to the original ones in Hanhijärvi et al. (2009).

4.2 Constrained perturbation

Another widely adopted strategy of edge and vertex modification approaches use edge addition and deletion to meet some desired constraints. Probably, the k-anonymity model is the most well-known in this group even though other models and extensions have been developed.

4.2.1 k-Anonymity

The k-anonymity model was introduced in Samarati (2001) and Sweeney (2002) for privacy preservation on structured or relational data. The k-anonymity model indicates that an attacker can not distinguish between different k records although he manages to find a group of quasi-identifiers. Therefore, the attacker can not re-identify an individual with a probability greater than $\frac{1}{k}$.

Fig. 4

Constrained perturbation example, where G (a) is the original graph, $\widetilde{G}_{em}$ (b) and $\widetilde{G}_{va}$ (c) are 2-degree anonymous versions of the network by edge modifications and by vertex and edge addition, respectively

Some concepts can be used as quasi-identifiers to apply k-anonymity on graph formatted data. A widely applied option is to use the vertex degree as a quasi-identifier. Accordingly, we assume that the attacker knows the degree of some target vertices. If the attacker identifies a single vertex with the same degree in the anonymous graph, then he has re-identified this vertex. That is, $deg(v_{i}) \ne deg(v_{j}) ~ \forall j \ne i$. This model is called k-degree anonymity (Liu and Terzi 2008) and these methods are based on modifying the graph structure (by edge modifications) to ensure that all vertices satisfy k-anonymity for their degree. In other words, the main objective is that all vertices have at least $k-1$ other vertices sharing the same degree. A network $G=(V,E)$ is k-degree anonymous if its degree sequence is k-anonymous, i.e. every distinct value $d_i$ appears at least k times in d(G). Furthermore, Liu and Terzi (2008) developed a method based on integer linear programming and Edge switch in order to construct a new anonymous graph which is k-degree anonymous, $V=\widetilde{V}$ and $E \cap \widetilde{E} \approx E$. Notice that this model protects data from identity disclosure and also from link disclosure but in a probabilistic manner. Hartung et al. (2015) studied the complexity of k-degree anonymity. They showed that k-degree anonymity has a polynomial-size problem kernel when parameterized by the maximum vertex degree $\delta$ of the input graph, and also proved that k-degree anonymity becomes NP-hard on graphs with H-index three.

Example 2

A k-degree anonymity example is illustrated in Fig. 4. The original network G, depicted in Fig. 4a, is $k=1$ degree anonymous since its degree sequence is $d(G)=\{2,4,2,1,3,2,2,2,2\}$. An example of a $k=2$ degree anonymous network is presented in Fig. 4b. Edge modification is used to fulfil the k-degree anonymity model. Thus, the number of vertices is the same, i.e. $\widetilde{n} = n$, and the perturbation is achieved by adding and removing edges. Its degree sequence is $d(\widetilde{G}_{em})= \{2,3,2,2,3,2,2,2,2\}$. Accordingly, it is a 2-degree anonymous sequence due to the fact that each vertex degree value appears at least two times in the degree sequence.

Liu and Terzi’s work inspired many other authors who improved such seminal work both in terms of speed and scalability (allowing to tackle larger datasets) by dealing with different kinds of heuristics. Lu et al. (2012) proposed a greedy algorithm, called Fast k -degree anonymization (FKDA), that anonymizes the original graph by simultaneously adding edges to the original graph while anonymizing its degree sequence. Their algorithm is based on Liu and Terzi’s work and it tries to avoid testing the realizability of the degree sequence, which is a time consuming operation. Hartung et al. (2014) also proposed an enhancement of Liu and Terzi’s heuristic, including new algorithms for each phase which improve theoretical and practical running times. Related to this work, Nagle et al. (2012) proposed a local anonymization algorithm based on k-degree anonymity that focuses on obscuring structurally important vertices that are not well anonymized, thereby reducing the cost of the overall anonymization procedure. However, results are similar to Liu and Terzi’s algorithm in terms of information loss. Furthermore, no analysis of large networks is provided. In Casas-Roma et al. (2013, (2016), the authors also presented a k-degree anonymous algorithm which is based on univariate micro-aggregation and it is able to anonymize large networks of thousands or millions of vertices and edges.

Chester et al. (2011, (2013a) permit modifications to the vertex set, rather than only to the edge set, and this offers some differences with respect to the utility of the released anonymous graph. The authors only created new edges between fake and real vertices or between fakes vertices. They studied k-degree anonymity on both vertex-labelled and unlabelled graphs. Under the constraint of minimum vertex additions, they show that on vertex-labelled graphs, the problem is NP-complete. For unlabelled graphs, they give a near-linear $\mathcal {O}(nk)$ algorithm. Nonetheless, results showed that information loss increases using vertex and edge addition. Following the same path, Bredereck et al. (2014) studied the problem of making an undirected graph k-degree anonymous by adding vertices (together with incident edges). The authors explored three variants of vertex addition and studied their computational complexity. Ma et al. (2015) also presented a k-degree anonymity based on vertex and edge modification. As the previous algorithms, it is a two-step method which firstly finds the optimal target degree of each vertex, and secondly it decides the candidates to increase the vertex degree and adds the edges between vertices to satisfy the requirement.

Example 3

Regarding our previous example presented in Fig. 4, a $k=2$ degree anonymous network by vertex and edge addition is depicted in Fig. 4c. As shown, the original structure remains the same, but a new vertex is added (dark grey) and also two edges $\{a,4\}$ and $\{a,5\}$ are created to fulfil the 2-degree anonymity. Its degree sequence is $d(\widetilde{G}_{va}) = \{2,4,2,2,4,2,2,2,2,2\}$. Using this model, the number of vertices is increased by 1 ($\widetilde{n} = n+1$) and the number of edges by 2 ($\widetilde{m} = m+2$).

Instead of using a vertex degree, Zhou and Pei (2008) considered the 1-neighbourhood sub-graph of the objective vertices as a quasi-identifier. For a vertex $v_i \in V$, $v_i$ is k-anonymous in G if there are at least $k-1$ other vertices $v_1, \ldots , v_{k-1} \in V$ such that $\Gamma (v_i), \Gamma (v_1), \ldots , \Gamma (v_{k-1})$ are isomorphic. Then, G is called k -neighbourhood anonymous if every vertex is k-anonymous considering the 1-neighbourhood. They proposed a greedy method to generalize vertices labels and add fake edges to achieve k-neighbourhood anonymity. The authors consider the network as a vertex-labelled graph $G=(V,E,L,\mathcal {L})$, where V is the vertex set, $E \subseteq V \times V$ is the edge set, L is the label set and $\mathcal {L}$ is the labelling function $\mathcal {L} : V \rightarrow L$ which assigns labels to vertices. The main objective is to create an anonymous network $\widetilde{G}$ which is k-anonymous, $V = \widetilde{V}$, $E = E \cup \widetilde{E}$, and $\widetilde{G}$ can be used to accurately answer aggregate network queries. In addition to identity and link disclosure, the authors also considered attribute disclosure. More recently, an extended and revised version of the paper was presented in Zhou and Pei (2011), demonstrating that the neighbourhood anonymity for vertex-labelled graphs is NP-hard. However, Tripathy and Panda (2010) noted that their algorithm could not handle the situations in which an adversary has knowledge about vertices in the second or higher hops of a vertex, in addition to its immediate neighbours. To handle this problem, they proposed a modification of the algorithm to handle such situations. He et al. (2009) utilized a similar anonymization method that partitions the network in a manner that tries to preserve as much of the structure of the original social network as possible. They do this by anonymizing the local structures of individual nodes such that all generalizations reflect actual structures of the original graph. The privacy level achieved by the aforementioned methods is higher than those obtained by preserving only a k-degree anonymity. However, the complexity of such proposals is too high and these methods cannot be applied efficiently to large networks.

Other authors modelled more complex adversary’s knowledge and used them as quasi-identifiers. For instance, Hay et al. (2008) proposed a method named k -candidate anonymity. In this method, a vertex $v_i$ is k-candidate anonymous with respect to question Q if there are at least $k-1$ other vertices in the graph with the same answer. Formally, $\vert cand_{Q}(v_i) \vert \ge k$ where $cand_{Q}(v_i) = \{ v_j \in V : Q(v_i) = Q(v_j) \}$. A graph is k-candidate anonymous with respect to question Q if all of its vertices are k-candidate with respect to question Q. Zou et al. (2009) consider all structural information about a target vertex as quasi-identifier and propose a new model called k -automorphism to anonymize a network and ensure privacy against this attack. They define a k-automorphic graph as follows: (a) if there exist $k-1$ automorphic functions $F_{a} (a=1, \ldots ,k-1)$ in G, and (b) for each vertex $v_i$ in G, $F_{a_1}(v_i) \ne F_{a_2} (1 \le a_1 \ne a_2 \le k-1)$, then G is called a k-automorphic graph. The key point is determining the automorphic functions. In their work, the authors proposed three methods to develop these functions: graph partitioning, block alignment and edge copy. K-Match algorithm (KM) was developed from these three methods and allows us to generate k-automorphic graphs from the original network. Identity disclosure was protected when considering an adversary’s knowledge based on question Q and automorphic functions, respectively. Since both methods used edge modifications, link disclosure was also protected in a probabilistic manner. Likewise the previous methods, these ones also achieve high privacy levels, but the complexity rises again. Thus, they are not able to deal with large networks in reasonable time.

Tai et al. (2011) identified a new type of attack called a friendship attack, where an adversary utilizes the degrees of two vertices connected by an edge to re-identify related victims in a published network. The concept of $k^2$-degree anonymity was introduced to protect against such attacks, where for every vertex with an incident edge of degree pair $(d_1,d_2)$, there exist at least $k-1$ other vertices sharing the same degree pair. The authors proposed an integer programming formulation to find optimal solution which is not scalable for large networks, but they also presented an heuristic approach for anonymizing medium or large-scale networks.

Assam et al. (2014) introduced the k-core attack, which relies on the concept of coreness (or k-core) and aims to uniquely re-identify vertices or infer the linkage of edges in anonymous graphs by exploiting the degree and coreness of a vertex or the structure of a sub-graph $G_s \subseteq G$ together with the degree and coreness of the vertices in Gs. The authors propounded an structural anonymization technique called (k, $\delta$)-Core anonymity, which uses k-core property to structurally anonymize vertices and edges of a published network and prevent the k-core attack. This method is based on vertex and edge addition, and it seems scalable to large networks of millions of vertices and edges.

Regarding to the theoretical complexity of the problems focused by the aforementioned methods, Kapron et al. (2011) analysed privacy issues for arbitrary and bipartite graphs. For arbitrary graphs, they show NP-hardness and use this result to prove NP-hardness for neighbourhood anonymity, i-hop anonymity, and k-symmetry anonymity. Following the same path, Chester et al. (2013b) studied the complexity of anonymizing different kind of networks (labelled, unlabelled and bipartite) and stated that edge-labelled graphs, label sequence subset anonymization (and thus table graph anonymization, k-neighbourhood anonymity, i-hop anonymity, and k-symmetry) are NP-complete for $k \ge 3$.

The methods we have outlined above work with simple and undirected graphs, but other types of graph are also considered in the literature. Bipartite graphs allow us to represent rich interactions between users on a social network. A rich-interaction graph is defined as $G=(V,I,E)$ where V is the set of users, I is the set of interactions and $E \subseteq V \times I$. All vertices adjacent to specific $i_s \in I$ shares an interaction, i.e, for $v_j \in V : (v_j,i_s) \in E$ all vertices interact on the same $i_s$. Lan et al. (2010) presented an algorithm to meet k-anonymity through automorphism on bipartite networks, called BKM (Bigraph k-automorphism match). They discussed information loss, of both descriptive and structural data, through quasi-identifier generalisations using two measures for both data, namely Normalised Generalised Information Loss (NGIL) and Normalised Structure Information Loss (NSIL) respectively. Hongwei et al. (2013) considered the problem of sensitive edges identification attacks in social networks, which are expressed using bipartite graphs. Three principles against sensitive edge identification based on security-grouping theory (Sihag 2012) were presented: positive one-way ($c_1$, $c_2$)-security algorithm, negative one-way ($c_1$, $c_2$)-security algorithm and two-way ($c_1$, $c_2$)-security algorithm. Based on these principles, a clustering bipartite algorithm divides the simple anonymous bipartite graph into n blocks, and then clusters the blocks into m groups which includes at least k blocks, creating an anonymous version of the graph with an objective function of the minimum anonymous cost (computed by the difference between original an anonymous vertices and edges). However, all aforementioned methods were tested using small and medium networks. Kapron et al. (2011) analysed privacy issues and concluded that k-degree anonymity of unlabelled bipartite graphs is in P for all $k \ge 2$. Additionally, Chester et al. (2013b) stated that for bipartite, unlabelled graphs, degree-based subset anonymization is in P for all values of k.

Cormode et al. (2010) also studied the anonymization problem on bipartite networks, nevertheless they focused on link disclosure instead of identity disclosure. Their scenario is based on the typical pharmacy example, i.e. customers buy products. The association between two nodes (who bought what products) is considered to be private and needs to be protected while properties of some entities (product or customer information) are public. Their anonymization method preserves the graph structure exactly by masking the mapping from entities to vertices rather than masking or altering the graph’s structure. The graph is defined as $G=(V,W,E)$, where V and W are the vertex sets and $E \subseteq V \times W$ is the edge set. The method, called (k,$\ell$)-grouping, splits V into size k groups and W into size $\ell$ groups. In addition, they defined the safe grouping introducing the $\ell$-diversity condition to grouping function and proved that finding a safe, strict 3-grouping is NP-hard.

Edge-labelled networks present specific challenges in terms of privacy and risk disclosure. The following methods understand that the edge information is private and it have to be preserved, so they focus on link disclosure. Kapron et al. (2011) used edge addition to achieve anonymization on social networks modelled as edge-labelled graphs, where the aim is to make a pre-specified subset of vertices k -label sequence anonymous with the minimum number of edge additions. Here, the label sequence of a vertex is the sequence of labels of edges incident to it. Moreover, the authors showed that k -label sequence anonymity is in P for $k = 2$ but it is NP-hard for $k \ge 3$ for labelled bipartite graphs. Additionally, Chester et al. (2013b) stated that for bipartite, edge-labelled graphs, label sequence subset anonymization is in P for $k = 2$ and is NP-complete for $k \ge 3$. Alternatively, Das et al. (2010) considered edge weight anonymization in social graphs. Their approach builds a linear programming model which preserves properties of the graph that are expressible as linear functions of the edge weights. Such properties are related to many graph-theoretic properties such as shortest paths, k-nearest neighbours and minimum spanning tree. The k-anonymity model is applied to edge weight, so an adversary can not identify an edge with a probability greater than $\frac{1}{k}$ based on edge weight knowledge.

Zheleva and Getoor (2007) focused on the problem of preserving the privacy of sensitive relationships in graph data. They considered a database describing a multi-graph $G = (V, E^1, \ldots , E^k,E^s)$, composed of a set of vertices V and sets of edges $E^1, \ldots , E^k, E^s$. Each vertex $v_i$ represents an entity of interest. An edge $e^{1}_{i,j}$ represents a relationship of type $E^1$ between two vertices $v_i$ and $v_j$. The $E^1, \ldots , E^k$ are the observed relationships, and $E^s$ is the sensitive relationship, meaning that it is undesirable to disclose the $e^s$ edges to the adversary. The authors proposed five possible anonymization approaches, ranging from one which removes the least amount of information to a very restrictive one, which removes the greatest amount of relational data.

Even fulfilling some privacy models, an attacker can succeed on acquiring private information. For instance, a privacy leakage can occur on a k-degree anonymous network and user’s privacy information can be revealed to an attacker. For example, we suppose an adversary who wants to know if there is a relation (edge) between users (vertices) $v_1$ and $v_2$. The k-degree anonymity model does not allow an attacker to uniquely re-identify each vertex. Instead, he will obtain two sets $V_{G1}$ where $v_{i} \in V_{G1} \Leftrightarrow deg(v_{i}) = deg(v_{1})$ and $V_{G2}$ where $v_{i} \in V_{G2} \Leftrightarrow deg(v_{i}) = deg(v_{2})$. If there are edges between each vertex on $V_{G1}$ and each vertex on $V_{G2}$, an adversary can infer, with absolutely confidence, that a relation exists between vertices $v_1$ and $v_2$, although he is not able to re-identify each user in group $V_{G1}$ and $V_{G2}$. So, even fulfilling the k-degree anonymity model a link disclosure can occur.

4.2.2 Extending k-anonymity

Aforementioned methods apply k-anonymity model using a variety of concepts as quasi-identifiers. However, some other models appeared trying to extend the k-anonymity model to overcome some specific drawbacks.

Feder et al. (2008) called a graph $(k,\ell )$-anonymous if for every vertex in the graph there exist at least k other vertices that share at least $\ell$ of its neighbours. Given k and $\ell$ they defined two variants of the graph-anonymization problem that ask for the minimum number of edge additions to be made so that the resulting graph is $(k,\ell )$-anonymous. The authors showed that for certain values of k and $\ell$ the problem is polynomial-time solvable, while for others it is NP-hard. Their algorithm solves optimally the weak (2, 1)-anonymization problem in linear time and the strong (2, 1)-anonymization problem can be solved in polynomial time. The complexity of minimally obtaining weak and strong (k, 1)-anonymous graphs remains open for $k=3,4,5,6$ while is NP-hard when $k > 6$.

Severe weaknesses on previous work were found by Stokes and Torra (2012). They state that for any pair $(k, \ell )$ with $k \le \ell$ it is possible to find a graph that is $(k, \ell )$-anonymous, but in which re-identification is possible for a large proportion of the vertices using only two of their neighbour vertices. The authors proposed an alternative definition for k-anonymity, in which G is k-anonymous if for any vertex $v_1\in V$, there are at least k distinct vertices $\{ v_i \}_{i=1}^{k} \in V : \Gamma (v_i) = \Gamma (v_1)$ for all $i \in [1,k]$. Due to the fact that this definition can be quite restrictive, they proposed a relaxation of this definition, which is also a correction of previous definition by Feder et al. According to the authors, a graph is $(k, \ell )$-anonymous if it is k-anonymous with respect to any subset of cardinality at most $\ell$ of the neighbour sets of the vertices of the graph.

Some users cannot be concerned by data owners sharing data about them, such as celebrities. Additionally, these users are hubs-like in network’s structure; outliers considering vertex degree property. Generally, these users are quite hard to anonymize and the perturbation induced in the network is high. To overcome this issue, some authors proposed to anonymize only a subset of vertices, instead of all vertex set. The model is called k-subset anonymity and the goal is to anonymize a given subset of nodes, while adding the fewest possible number of edges. Formally, the k-degree-subset anonymity problem is defined as given an input graph $G=(V,E)$ and an anonymizing subset $X \subseteq V$, produce an output graph $\widetilde{G}=(V,E \cup \widetilde{E})$ such that X is k-degree-anonymous and $\vert \widetilde{E} \vert$ is minimized. Obviously, if $X = V$ then this model is equal to k-anonymity. Chester et al. (2012) introduced the concept of k-subset-degree anonymity as a generalization of the notion of k-degree-anonymity. Additionally, they presented an algorithm for k-subset-degree anonymity which is based on using the degree constrained sub-graph satisfaction problem. The output of the algorithm is an anonymous version of G where enough edges have been added to ensure that all the vertices in X have the same degree as at least $k-1$ others.

4.2.3 Beyond k-anonymity

New privacy challenges appear when dealing with vertex-labelled networks, which are defined as $G=(V, E, L, \mathcal {L})$, where $E = V \times V$, L is the set of labels and $\mathcal {L} : V \rightarrow L$ assigns a label to each vertex. Information contained on vertex attributes is considered confidential, and therefore it must be preserved. Thus, the following methods deal with attribute disclosure and identity disclosure, since as we have previously stated, identity disclosure often leads to attribute disclosure.

Machanavajjhala et al. (2007) introduced the notion of $\ell$-diversity for tabular data, wherein each k-anonymous equivalence class requires $\ell$ different values for each sensitive attribute. In this way, $\ell$-diversity looks to not only protect identity disclosure, but was also to protect against attribute disclosure. Zhou and Pei (2011) adapted the definition of $\ell$-diversity for graphs and proposed a method to achieve k-anonymity and $\ell$-diversity on vertex-labelled networks. Additionally, they showed that the problem of computing optimal k-anonymous and $\ell$-diverse social networks is NP-hard. Alternatively, Yuan et al. (2013) proposed another method to achieve k-degree-$\ell$-diversity anonymity on vertex-labelled networks. This method adds fake vertices and edges, trying to preserve the average path length on anonymous graph. Firstly, it computes the target degree for each vertex, and then this method changes each vertex’s degree to its target degree by adding noise edges and vertices. Average path length is used as a measure to lead the process to a better data utility and lower information loss.

However, even $\ell$-diversity can experience privacy breaches under the skewness attack or similarity attack (Li et al. 2007). To address the shortcomings of $\ell$-diversity, Li et al. (2007) introduced t-closeness model, which requires that the distribution of attribute values within each k-anonymous equivalence class needs to be close to that of the attributes’ distribution throughout the entire set. More recently, Chester and Srivastava (2011) argued that t-closeness cannot be clearly applied to social networks. They proposed a notion of data anonymization called $\alpha$-proximity that protects against attribute disclosure attacks, and provide an algorithm that modifies a vertex-labelled graph by adding new fake edges, so as to ensure it is $\alpha$-proximal. Chester et al. (2013b) demonstrated that for general, vertex-labelled graphs, the vertex label sequence-based anonymization, and consequently t-closeness, is NP-complete.

5 Uncertain graphs

Rather than anonymizing social graphs by generalizing them or adding/removing edges to satisfy given privacy parameters, recent methods have exploited the semantics of uncertain graphs to achieve privacy protection. Considering $G = (V,E)$ as a simple graph, we denote $V_2$ as the set of all $\left( {\begin{array}{c}n\\ 2\end{array}}\right)$ unordered pairs of vertices from V, i.e. $V_2 = \{ (v_i, v_j) : 1 \le i < j \le n \}$. An uncertain graph is a pair $\widetilde{G} = (V,p)$, where $p : V_2 \rightarrow [0, 1]$ is a function that assigns existing probabilities to all possible edges. These techniques anonymize a deterministic graph by converting it into an uncertain form.

Fig. 5

Uncertain graph perturbation example, where G is the original graph. The uncertain version is $G^*$, where some edges have probability equal to 1 (black lines) and others have probability equal to 0 (gray dashed lines). $\widetilde{G}$ is a possible uncertain graph after anonymization process, i.e. injecting uncertainty. a G, b $G^*$, c $\widetilde{G}$

Example 4

Figure 5 shows the anonymization process under the uncertain graph model. The original graph G is depicted in Fig. 5a, and the uncertain version of the same graph is shown in Fig. 5b. As it can be seen, there are all possible edges, i.e. $\left( {\begin{array}{c}6\\ 2\end{array}}\right)$, and each one is assigned to probability equal to 1 (black lines) or 0 (gray dashed lines). Thus, $G^*$ is the representation of G under uncertain graph model, but it is not perturbed or anonymized. The anonymized version is presented in Fig. 5c, where the probability of each edge is set in range [0,1]. Edges with probability equal to 0 are not depicted in $\widetilde{G}$ to preserve a clear visualization of the perturbed uncertain graph.

The first approach was proposed by Boldi et al. (2012) and it is based on injecting uncertainty in social graphs and publishing the resulting uncertain graphs. The authors noticed that from a probabilistic perspective, adding a non-existing edge $\{v_i,v_j\}$ corresponds to changing its probability $p(\{v_i,v_j\})$ from 0 to 1, while removing an existing edge corresponds to changing its probability from 1 to 0. In their method, instead of considering only binary edge probabilities, they allow probabilities to take any value in range [0,1]. Therefore, each edge is associated to an specific probability in the uncertain graph. However, they proposed to inject uncertainty only to a small candidate subset of pairs of vertices $E_c$, and assuming that other pairs of vertices do not exist, i.e. $p(v_i, v_j) = 0 ~ \forall (v_i, v_j) \not \in E_c$. An uncertain graph is $(k,\epsilon )$-obfuscation with respect to property P if the entropy of the distribution $Y_{P(v)}$ over at least $(1 - \epsilon )n$ vertices of $\widetilde{G}$ is greater than or equal to $log_2(k)$, i.e. $H(Y_{P(v)}) \ge log_{2}(k)$.

Nguyen et al. (2015) proposed a generalized obfuscation model based on uncertain adjacency matrices that keep expected node degrees equal to those in the original graph, and a generic framework for privacy and utility quantification of anonymization methods. The same authors presented a second approach (Nguyen et al. 2014) based on maximum variance to achieve better trade-off between privacy and data utility. They also described a quantifying framework for graph anonymization by assessing privacy and utility scores of typical schemes in a unified space.

It is important to underline that statistics and metrics must be defined (or re-defined) to be applied on this kind of graphs, since almost all of them were designed to work with binary-edge graphs and cannot be applied directly on uncertain graphs. In this direction, computation of statistics based on degree, such as number of edges, average degree, maximal degree and degree variance were propounded in Boldi et al. (2012). The same authors also proposed to compute statistics based on the shortest-path distance and clustering coefficient by sampling some graphs in the space of possible edge-binary graphs induced by an specific uncertain graph.

6 Generalization approaches

Generalization approaches (also known as clustering-based approaches) can be essentially regarded as grouping vertices and edges into partitions called super-vertices and super-edges. The details about individuals can be hidden properly, but the graph may be shrunk considerably after anonymization, which may not be desirable for analysing local structures. The generalized graph, which contains the link structures among partitions as well as the aggregate description of each partition, can still be used to study macro-properties of the original graph. Even if it holds the properties of the original graph, it does not have the same granularity. More so than with other anonymization algorithms, the generalization method decreases the utility of the anonymous graph in many cases, while increasing anonymity.

These methods reduce the size of the graph, both the number of vertices and edges, from the original graph. They produce a summary of the original network, which can be also useful to reduce the computation time in subsequent graph mining processes. However, all methods developed heretofore need the whole graph to be applied to. Consequently, they are not able to deal with big or streaming data. Even so, new methods can be developed using this model to generate anonymous and generalized data from very large or streaming datasets.

As all aforementioned methods, generalization approaches also protect against identity disclosure. Moreover, it is interesting to underline that generalization approaches also preserve against attribute and link disclosure, since two vertices from any cluster are indistinguishable based on either their relationships or their attributes.

Fig. 6

Generalization example, where G is the original graph. A vertex set sample partition is presented and used to create a generalized graph $\widetilde{G}$. a G, b vertex set partition, c $\widetilde{G}$

Example 5

A generalization approach is described in Fig. 6, where G is the original network. Firstly, these methods compute a partition of the whole vertex set. A sample partition is presented in Fig. 6b. This is the most important process, since grouping vertices with similar characteristics lead the generalization process to better results, in terms of data utility and information loss. Secondly, once partitions are created, these methods group all vertices in the same partition into a super-vertex and create super-edges between them. A generalized version of G is depicted in Fig. 6c. As shown, each super-vertex contains information about the number of vertices and intra-edges between them. Generally, each super-edge is labelled according to the number of inter-edges between vertices in each super-vertex.

Hay et al. (2008) applied structural generalization approaches using the size of a partition to ensure node anonymity. Their method obtains a vertex k-anonymous super-graph by clustering nodes into super-vertices and edges into super-edges. Each super-vertex represents at least k nodes and each super-edge represents all the edges between nodes in two super-vertices. Only the edge density is published for each partition, so it will be hard to distinguish between individuals in a partition. The authors evaluated the effectiveness of structural queries on real networks from various domains and random graphs. Their results showed that networks are diverse in their resistance to attacks: social and communication networks tend to be more resistant than some random graph models would suggest, and hubs cannot be used to re-identify many of their neighbours.

Campan and Truta (2008, (2009) worked on undirected networks with labelled-vertices and unlabelled-edges. Vertices attributes contains identifiers, quasi-identifiers and sensitive attributes. The k-anonymity model is applied to quasi-identifiers in order to achieve indistinguishable vertices from their attributes or relationships between attributes. The authors developed a new method, called SaNGreeA, designed to anonymize structural information. It clusters vertices into multiple groups and then, a label for each partition is assigned with summary information (such as the number of nodes in the partition). Then, Ford et al. (2009) introduced an extension to k-anonymity model that adds the ability to protect against attribute disclosure. There are two related aspects in anonymizing a vertex-labelled social network: the data associated to the social network’s vertices (identifier, quasi-identifier and sensitive attributes) and the structural information the network carries about the nodes’ relationships have to be properly masked. The resulting masked network data has to protect the nodes against identity disclosure (i.e, determining who exactly is the individual owning the node) and attribute disclosure (i.e, finding out sensitive data about an individual, but without identity disclosure). They also presented a new algorithm, based on the work of Campan and Truta, to enforce p-sensitive k-anonymity on social network data based on a greedy clustering approach. Campan et al. (2015) compared SaNGreeA to a k-degree anonymous algorithm (Lu et al. 2012) in terms of the community preservation between the initial network and its anonymized version. The results show that the k-degree anonymous algorithm better preserves the communities on the released graphs, though the privacy level is also lower.

Bhagat et al. (2009) assumed that adversaries know part of the links and vertices in the graph. They presented two types of anonymization techniques based on the idea of grouping nodes into several classes. The authors pointed out that merely grouping nodes into several classes cannot guarantee the privacy. For instance, one can considers the case where the nodes within one class form a complete graph via a certain interaction. Then, once the adversary knows the target is in the class, he can be sure that the target must participate in the interaction. The authors provided a safety condition, called class safety to ensure that the pattern of links between classes does not leak information: each node cannot have interactions with two (or more) nodes from the same group. Note that the released graph contains the full topological structure of the original graph, and therefore some structural attacks such as the active attack and passive attack (Backstrom et al. 2007) can be applied. To prevent identity disclosure, the authors further proposed a solution, called partitioning approach, which groups edges in the anonymous graph and only releases the number of interactions between two groups.

More recently, Singh and Schramm (2010) took the generalization concept further and create a generalized trie structure that contains information about network sub-graphs and neighbourhoods. This information can be used to answer questions about network centrality characteristics without revealing sensitive information. Stokes and Torra (2011) presented two methods for graph partitioning using the Manhattan distance and the 2-path similarity as measures to create the clusters which group vertices into partitions of k or more elements.

Finally, Sihag (2012) presented a method for k-anonymization via generalization on undirected and unlabelled graphs. In this method, vertices are clustered together into super-vertices of size at least k. The author chose genetic algorithms to optimize this NP-hard problem. The author compared his algorithm with SaNGreeA on small networks (from 10 up to 300 vertices), achieving better results in terms of information loss. Unfortunately, this method does not seems scalable for medium or large networks.

7 Conclusions

In this paper we have presented a survey of recent work on graph modification methods concerning privacy in social networks. We have reviewed the three main categories of graph-modification methods, which are edge and vertex modification, uncertain graphs and generalization approaches.

Obviously, each method has its own advantages and drawbacks. It is important to consider three main aspects before choosing the best method to anonyimize a dataset, which are the specific properties of the network and the data contained in it, the knowledge of the adversary and the utility of the released data.

Table 1 Summary of graph modification techniques and main methods

Edge and vertex modification approaches offer a wide range of graph mining and knowledge extraction from anonymous data. Anonymous data can be used to answer wide range of queries, from local to global data extraction.

Random perturbation techniques are usually the simplest and lowest complexity methods. Due to this, they are able to deal with large networks. Additionally, methods based on random perturbation can be designed to specifically work with streaming or big data. Contrary, they do not offer privacy guarantees, but a probabilistic re-identification model. We underline some methods in Table 1. Hay et al. (2007) proposed the simplest method, which involves very low complexity though privacy was not secure, specially for hub-like vertices. The method in Ying and Wu (2008) reduced information loss during anonymization process, but still no guarantees were presented. Finally, recent method in Bonchi et al. (2014) performed a deep privacy analysis of random sparsification, offering interesting privacy results.

Research privacy attention has been recently focused on constrained perturbation methods. Several proposals have appeared since the k-anonymity work in Liu and Terzi (2008). These methods provide privacy guarantees, but its privacy may strongly depend on the adversary’s knowledge defined by the quasi-identifiers in k-anonymity models. The k-degree anonymity considers basic adversary’s knowledge based on vertex degree. For that reason, methods based on this model are able to anonymize large networks, as demonstrated by works in Lu et al. (2012); Casas-Roma et al. (2013, (2016). Chester et al. (2013a) proposed an interesting alternative based on vertex and edge addition to fulfil k-degree anonymity, though information loss increased and data utility decreased in their experimental framework. Recently, Assam et al. (2014) proposed to protect not only the vertex degree but also the coreness. As aforementioned methods, theirs is able to anonymize large networks. Nonetheless, k-degree anonymity has been criticized to consider too simple adversary’s knowledge. More complex models, such as k-neighbourhood and k-automorphism, appeared to overcome its shortcomings. The main problem of these methods relies on its complexity. Some of them are based on sub-graph isomorphism, which implies high complexity and prevents them from working on large networks efficiently. Finally, as previously commented methods work with simple and undirected networks. However, real networks usually present labels on vertices and edges, multiple types of edges or particular graph structures, such as bipartite networks. Although some works have been done in this direction, for instance Das et al. (2010) in edge-labelled networks or Cormode et al. (2010) in bipartite graphs, it is still a young research field and there exist several open problems.

Methods based on uncertain graphs are more recent than other approaches and they can offer interesting proposals. However, the main problem is the nature of these graphs themselves, which is difficult to apply on several graph-mining tasks, such as clustering and community detection algorithms. Vast majority of graph-mining tasks have been developed to binary-edge graphs and it is not straightforward to redefine them to work on uncertain graphs. In spite of this, works in Boldi et al. (2012); Nguyen et al. (2015) propounded, not only stimulating approaches, but also methods to anonymize real and large networks.

Lastly, generalization approaches provide good privacy levels, though they complicate the analysis of local measures and metrics. Nevertheless, they demonstrated to be able to deal with vertex-labelled networks, offering anonymity in terms of attribute and identity. Due to the fact that they cluster some vertices in the same partition, they hide identity and attribute data of some vertices in the same partition. Campan and Truta (2008, (2009) developed the most well-known generalization method, but the approach in Ford et al. (2009) achieved similar results in terms of information loss and data utility.

8 Open problems

There are several open problems in privacy-preserving data publishing on graphs or social networks. First of all, it is important to underline that some anonymity issues discussed in this paper are NP problems. Consequently, several methods do not achieve the optimal solution but only an approximation. This problem becomes harder when data size increases, as it is happening with currently tremendous explosion of social and interaction networks. Additionally, all methods we have presented, except those based on random perturbation, need to analyse the whole dataset to compute the proposed solution. It makes them unusable to work with big or streaming data, where the whole dataset is not available.

Another problem can be spotted when focusing on other types of networks. For instance, constrained perturbation methods cannot deal with directed networks straightforward. They have to consider in- and out-degree sequences in order to anonymize the network and the problem becomes even more challenging. Moreover, anonymity in rich-interaction graphs will be an interesting research topic in the near future. For example, ensuring k-anonymity in time-varying graphs, i.e. graphs with a structure that changes over time, is quite challenging. Similar problems appear when dealing with multi-layer graphs, i.e. graphs with multiple types of links.

Anonymizing big data is even harder due to the amount and variety of data. The following aspects of anonymization are specific to big data and need to be deeply analysed (D’Acquisto et al. 2015): (1) methods that prevent re-identification and attribute disclosure while allowing some linkability are of interest since big data anonymization should be compatible with linking data from several (anonymized) sources (controlled linkability). (2) Composability is very important for big data, where datasets are formed by merging data from several sources. A privacy model is composable if its privacy guarantees hold for a dataset constructed by linking together several datasets for each of which the privacy guarantee of the model holds. (3) Anonymization of dynamic or streaming data where continuous data streams are considered instead of static datasets, such as the readings of sensors. (4) Computability for large data volumes is challenging in big data. Even static data sets may be challenging to anonymize due to their sheer volume. Hence, computational efficiency may be a critical issue when choosing a privacy model or an anonymization method. (5) Under decentralized anonymization paradigm, the data subject anonymizes one’s data at the source, using one’s personal computing device, before releasing those data to the data controller.

Without being specific to any particular analysis, linkability is key to obtain information from the fusion of data collected by several sources. In big data, information about an individual is often gathered from several independent sources. Hence, the ability to link records that belong to the same individual is crucial in big data creation. The amount of linkability compatible with an anonymization technique or with an anonymization privacy model determines whether and how an analyst can link data independently anonymized that correspond to the same individual. While linkability is desirable from the utility point of view, it is also a privacy threat: the accuracy of linkages should be significantly less in anonymized datasets than in original ones.

Governments and other public institutions all around the world are pressed to publish data to fulfil transparency and to share information with the community. However, releasing more and richer information to researchers and the public comes at the cost of potentially exposing private and sensitive user information. Thus, privacy-preserving will be a key actor in the new era of big, open and linked data.