Keywords

Introduction

Dynamic Geometry Environments (DGE) give rise to a phenomenological domain where leaner manipulated movement and variation together with visual and sensory-motor feedback can guide discernment of geometrical knowledge. DGE are modelled after theoretical systems like Euclidean Geometry and the dynamism that characterizes DGE phenomena gives a new perspective for geometry and geometry education (see for example, Laborde 2000; Strässer 2001; Laborde et al. 2006; Lopez-Real and Leung 2006). In particular, the drag-mode in DGE has been studied in pedagogical settings and gradually understood as a pedagogical tool that is conducive to mathematical reasoning, especially in the process of conjecture formation in geometry (see for example, Arzarello et al. 2002; Baccaglini-Frank 2010; Baccagalini-Frank and Mariotti 2010). The epistemic potential of the drag-mode in DGE lies in its relationship with the discernment of invariants. In this lecture, I will discuss means of discernment and reasoning for DGE based on a combined perspective that puts together elements from the lens of variation in DGE (Leung 2008), the Maintaining Dragging Scheme (Baccaglini-Frank 2010) and abduction in DGE (Baccaglini-Frank 2011), and how they contribute to reasoning in DGE.

Invariant, Discernment and DGE

Resnick (1997) advocated that mathematics is a “science of patterns”. I interpret mathematical pattern is an emerging invariant structure when a phenomenon that concerns number and/or shape is undergoing changes or variation and mathematical experience as “the discernment of invariant pattern concerning numbers and/or shapes and the re-production or representation of that pattern.” (Leung 2010) Variation is about what changes, what stays constant and what the underlying rule is. In phenomenology, one of the hermeneutic rules is to “seek out structural or invariant features of the phenomena” (Ihde 1986, pp. 39–40). Dienes (1963) attributed the abstraction and the generalization processes in mathematical thinking by what he called the perceptual variability principle and the mathematical variability principle:

The perceptual variability principle stated that to abstract a mathematical structure effectively, one must meet it in a number of different situations to perceive its purely structural properties. The mathematical variability principle stated that as every mathematical concept involved essential variables, all these mathematical variables need to be varied if the full generality of the mathematical concept is to be achieved.” (Dienes 1963, p. 158)

Discernment, variation and simultaneity are central concepts in Marton’s Theory of Variation (Marton and Booth 1997; Marton et al. 2004). In particular, discernment of critical features occurs under systematic interaction between learners and the thing to be learnt, and variation is an agent that generates such interaction. Variation in different aspects of a phenomenon unveils the invariant structure of the whole phenomenon. Thus invariants are critical features that define or generalize a phenomenon. This matches what doing mathematics is about, for a major aim of mathematical activity is to separate out invariant patterns while different mathematical entities are varying, and subsequently to generalize, classify, categorize, symbolize, axiomatize and operationalize these patterns (see for example, Mason et al. 2009).

A key feature of DGE is its ability to visually represent geometrical invariants amidst simultaneous variations induced by dragging activities. The variations of the moving image are perceived in contrast to what simultaneously remains invariant. The movement and the identification of invariants are what lies at the heart of activities that aim at exploiting the epistemic potential of DGE (for example, Laborde and Laborde 1995; Hölzl 1996; Healy 2000; Arzarello et al. 2002; Olivero 2002; Leung 2008; Baccaglini-Frank and Mariotti 2010). Hölzl (2001) considered dragging as “a tool to find different representations of one and the same figure in continuous transition. Because dragging acts on a drawing with the effect being determined by the figure, a mediating function emerges.” (Hölzl 2001), and Lopez-Real and Leung (2006) suggested if dragging in DGE is accepted as a tool that can bring about invariant structures and patterns, then “…we have new ‘rules of the game’, or even a new game, for experiencing geometry.” (op cit, p. 676) Furthermore, interaction with dynamic figures through dragging in DGE

could induce a special type of reasoning (or explaining) in DGE in which a signified object in DGE could have a diachronic nature. That is, one has to conceptualize a draggable object in DGE as it varies (over time) under dragging. Hence, a whole object in DGE should be understood as a (continuous) sequence of the “same” object under variation. (Leung and Or, 2007)

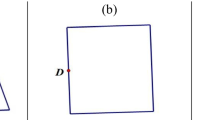
“Sameness” of a sequence of figures recognized as one is given by the perception of invariants that characterize each figure of the sequence. In general, invariants are determined both by the geometrical relations defined by the commands used to construct the dynamic-figure, and by the relationship of dependence between the original relations of the construction and those that are derived as a consequence within the theory of Euclidean Geometry (Baccaglini-Frank et al. 2009; Laborde and Strässer 1990). To illustrate, let us consider the following construction (see Mariotti and Baccaglini-Frank 2011):

ABCD is a quadrilateral in which D is chosen on the parallel line to AB through C, and the perpendicular bisectors of AB and CD, r and s respectively, are constructed.

Figure 1 shows a dynamic figure derived from such construction in Cabri (a DGE). It has a set of constructed invariants (the parallelism between AB and DC, the perpendicularity of s to DC and of r to AB, and the passing of s and r through the midpoints of DC and AB respectively), and consequently all the invariants derived from these (for example the parallelism between r and s) which are all conserved simultaneously during dragging. In particular, in this Cabri construction, A, B, C are free base-points which can be moved by dragging them directly, D is restricted to move along a line parallel to AB through C, r and s are dependent objects which can’t be moved by dragging them directly but can be moved indirectly as a consequence of the movement of other base-points.Footnote 1 Hence as they appear simultaneously during dragging, different invariants may have different status according to the type of control allowed by the DGE (in this Cabri case, direct or indirect). In a constructed figure there is a relationship of dependency between the constructed invariants and any that are derived from these according to Euclidean Geometry. It may happen that a relationship between invariants is an invariant itself, and such a relationship can be discerned through dragging. In our example there is an invariant relationship between invariants that can be expressed by the following statement.

Fig. 1
figure 1

A dynamic trapezium with free vertices A, B, C and perpendicular bisectors r, s. D is on the line parallel to AB that goes through C

Full size image

If two lines are respectively perpendicular to two parallel lines, then the first two lines are parallel.

Discerning invariants and discerning invariant properties between invariants are cognitively quite tasks. I introduce the following terminology:

  • Level-1 invariants: aspects of a dynamic figure, potentially corresponding to geometrical properties that are perceived as constant during variation of the figure through dragging. For example, “AB parallel to CD” and “s parallel to r” are level-1 invariants of the dynamic figure constructed in Fig. 1.

  • Level-2 invariants: invariant relationships between level-1 invariants. For example, “AB parallel to CD causes (or implies) s parallel to r”.

Different dragging modalities can be employed to formulate strategies to unveil these two levels of invariant. Making sense of the sensory-motor feedback under the drag-mode is entirely up to the learner who will need to interpret the “construction steps” as invariant geometrical properties, relate them to other invariants, discover new ones, and eventually through reasoning, logically link the perceived geometrical properties and relationships to one another. In the literature, there are two broad categories of dragging modality (and examples of them) that are in line with Hölzl’s (2001) description of two principle drag modes.

Dragging for testing consists in dragging to check the presence of desired (known) properties in a dynamic figure. It “presupposes an expectation as to the reaction of the construction when it is being dragged” (ibid, p. 83). The movements on the screen can meet that expectation or not. The learner movement will be used to induce on the figure to find the invariants that are being sought after. Examples are: the dragging test (Arzarello et al. 2002, p. 67); the soft dragging (conjecture) test (Baccaglini-Frank and Mariotti 2010); the robust dragging test (or an adaptation of linked dragging or bound dragging (Arzarello et al. 2002; Olivero 2002).

Dragging for searching/discovering consists in dragging to look for new properties of the figure. In other words, “the changing appearance of the drawing must be evaluated under aspects which are still unknown” (ibid, p. 83). These may be possible configurations it might assume, invariants, and/or relationships between them. If, for example, the task is to formulate conjectures on the figure, this type of dragging will be used to discover new properties through the perception of invariants and relationships between them. Examples are: wandering dragging (Arzarello et al. 2002; Olivero 2002); guided dragging (Arzarello et al. 2002; Olivero 2002) and dragging to fit (Lopez-Real and Leung, 2006); lieu muet dragging (Arzarello et al. 2002; Olivero 2002) or maintaining dragging (Baccaglini-Frank and Mariotti 2010; Baccaglini-Frank 2010).

Discernment Through Variation Interactions

As mentioned above, discernment, variation and simultaneity are the central concepts in Marton’s Theory of Variation (Marton et al. 2004; Marton and Booth 2007). Discernment of critical features occurs under systematic interaction between a learner and the thing to be learnt, and variation is the agent that generates such interaction. Local variation in different aspects of a phenomenon unveils the invariant structure of the whole phenomenon. Invariants are critical features that define or generalize a phenomenon. Four basic patterns of variation were proposed by Marton: contrast, generalization, separation and fusion. They form the kernel for discernment under variation in the Theory of Variation. These patterns of variation have the potential to be used to organize a variation experience and generate interactions between learners and the “thing” to be learnt.

In the context of DGE, I consider them as possible types of variation interaction under the drag-mode while a learner is exploring for geometrical invariants.

A variation interaction in DGE is a strategic use of variation to interact with DGE objects in order to bring about discernment of geometrical invariant.

Drag to contrast is the strategy to discern whether a DGE object satisfies a certain condition or not, that is, it seeks to differentiate different DGE phenomena.

Drag to separate is the strategy to bring about awareness of critical geometrical features that may become invariants. It is an awareness of part-whole relationship realized by constraint dragging strategy that purposely varies or not varies certain aspects aiming to separate out invariant features in the whole.

Drag to generalize is the strategy to explore whether after contrast and separation, an observed geometrical feature can occur in a varied situation. It is a conjecture-making activity checking the general validity of a geometrical feature.

Drag to fuse is the strategy to integrate geometrical critical features under simultaneous co-variation. By fusing the separated-out critical geometrical features together, a whole invariant concept may appear. By contrasting critical features, fusion reveals how parts of a whole vary in interconnected ways.

These four types of variation interaction under the drag mode act together in a concerted way to bring about discernment of geometrical properties. I will use the following DGE exploration as an illustrative example (cf. Leung 2003):

(E): Explore how many circles can be constructed through any two given points and explain the construction.

In Fig. 2, a circle is constructed that passes through a free base-point (hence arbitrary) A with a draggable base-point C as its centre, B is another draggable base-point. C is dragged (while not moving A and B) to make the circle visually passing or not passing through B with direct control over C.

Fig. 2
figure 2

Contrast via simultaneous focus: circle centred at C through B or not through B

Full size image

Thus drag to contrast based on simultaneous focus on the varying position of C (hence a sequence of circles) and B allows the learner to discern that many circles can pass through two given points.

In Fig. 3, Trace (a DGE function) is activated for C and C is dragged while keeping point B visually on the circle (A, B are not dragged, hence are the aspects that are being kept constant). It results in a visual path appearing on the screen. This path can be interpreted as a visualization of simultaneous focus because it is a unique simultaneous representation of a time sequence (different appearances in time) of positions that visually satisfied the desired condition. That is, as long as point C varies along this path with A and B kept fixed, the corresponding circles seem to pass through points A and B.

Fig. 3
figure 3

Separation via awareness of critical features: a path is traced while maintaining a circle that passes through A and B

Full size image

The path separated out in Fig. 3 can be “re-generated” for different positions of A and B (Fig. 4). Focussing on the re-appearance of different paths for different positions of A and B through contrast and simultaneous focus allows the discernment of an invariant property of all these paths leading to the generality of such invariant, which may be described geometrically: C seems to lie on a path that is the perpendicular bisector of AB. In this way, a level-1 invariant is being discerned.

Fig. 4
figure 4

Generalization: the repeated appearance of an invariant (path) for different positions of A and B

Full size image

The above variation interactions under the drag-mode bring about fusion (a simultaneous awareness) of two inter-relating critical features: (1) a family of circles where A lies on with C as centre passing through B, and (2) C belongs to a path. Under generalization, the invariant property of all the paths discerned can be interpreted geometrically as “the perpendicular bisector of AB”. This integration and interrelation discerned through fusion can be expressed through the following conjecture:

Given two free points A and B, if a point C moves along the perpendicular bisector of AB, then the circle with C as a centre passes through A and B (Fig. 5).

Fig. 5
figure 5

Fusion: the perpendicular bisector of AB as an invariant relationship between two critical features

Full size image

Thus in this case fusion brings about the awareness of an invariant relationship between two level-1 invariants (the two critical features); that is, a level-2 invariant. The transition from a traced path to a geometrical path (a perpendicular bisector) holds the key to the formation of a conjecture.

In this discernment process, drag to contrast and drag to generalize interact in a mutually enhancing way (to differentiate, to test validity) driven by a drag to separate strategy in order to pin down an invariant property. The drag to separate strategy is a maintaining dragging modality (see a full discussion in the next section) with the Trace turns on. When different critical features (for example, the traced path, perpendicular bisector, isosceles triangle) are discerned, a co-varying drag to fuse strategy can be used to test their correlation. For example, robust or soft dragging tests are types of drag to fuse strategy that focus on simultaneous variation of different geometrical properties testing the validity of a geometrical conjecture. Furthermore, drag to fuse is an underlying variation interaction that permeates all dragging interactions as simultaneous attention on different varying and invariant aspects are fundamental in discernment. Different dragging modalities (for example, those mentioned in the previous section) can be employed to furnish the four variation interactions under the drag-mode.

Discernment Through the Maintaining Dragging Scheme

I discussed how the development of potential awareness of direct and indirect control over level-1 invariants can occur through sensory-motor experience accompanied by reasoning and how variation interactions can be used as a means to discern invariants. The form this reasoning might take on is dependent on the context it is developed in, and in particular, on the learner’s goal (or task) and therefore on the chosen dragging modality. The “reasoning” can take on the form of what has been referred to as scheme or utilization scheme within the instrumental approach (Artigue 2002; Rabardel 1995). This approach puts an artefact in relation to a task and a learner. The learner develops a utilization scheme in order to accomplish the task using the artefact. The combination of the artefact and the developed utilization scheme is the instrument. If dragging in a DGE is considered from an instrumental perspective, particular dragging modalities can be seen as artefacts supporting the task of conjecture-generation. Together with a utilization scheme developed by a learner during a process of instrumental genesis, a particular way of dragging may become an instrument. These utilization schemes developed by the learner are referred to as “dragging schemes”, and they constitute the “reasoning” that accompanies particular uses of dragging (see for example, Leung et al. 2006).

The complexity in a dragging scheme is constituted by becoming aware of the hierarchy induced not only on the elements of a DGE figure but on their properties (that is relationships between elements) by the steps of the construction, and of the fact that such a hierarchy corresponds to logical relationships between the properties of the “geometric figure.” Thus not only can the learner experience different types of control over elements, direct and indirect control, depending on the type of DGE used (cf. footnote 1), may also be purposely exercised over invariants. A fundamental means of discernment is awareness of these types of control, in particular, in the context of inducing new invariants on a dynamic figure. For the example depicted in Fig. 1, it is possible to try to induce a new invariant like “coinciding perpendicular bisectors”. This is often called a soft property (Healy 2000; Laborde 2005). A learner can try to maintain such interesting property by dragging a base point. This type of dragging modality is referred to as maintaining dragging. To illustrate, let’s choose point B as the base point. Figure 6 shows how such property can become a soft invariant as a base point is dragged.

Fig. 6
figure 6

The figure shows a learner trying to maintain the coincidence between the perpendicular bisectors, by dragging point B

Full size image

The movement of B is controlled by the learner and is not random. This control exercised over the movement of B is intentionally direct while that over the invariance of the desired property (r and s coincide) is consequentially indirect. Such awareness developed through sensory-motor experience accompanied by reasoning becomes fundamental when maintaining dragging is used as a means of exploration (Baccaglini-Frank 2010; Mariotti and Baccaglini-Frank2011). Inducing soft invariants on a dynamic figure can be done through the maintaining dragging modality. When this modality is used to search for new conjectures, that is relationships between possible invariants (level-2 invariants), it is referred to as the MD scheme (Baccaglini-Frank 2010; Baccaglini-Frank and Mariotti 2010). This scheme is described through a set of (possibly implicit) tasks the learner addresses in the quest to formulate conjecture:

  • Task 1: Conceive a configuration to be explored by dragging intentionally to maintain the appearance of the desired configuration, thus inducing it as a soft invariant. This conceived configuration is called an intentionally induced invariant.

  • Task 2: Look for a condition that makes the intentionally induced invariant visually verified through maintaining dragging. This can occur either through

    • a geometric interpretation of the movement of the dragged base-point or,

    • a geometric interpretation of the trace mark (path) of the dragged base-point.

    Propose a geometric description of the movement or the path observed.

  • Task 3: Verify the conditional link through the dragging test. A conditional link is a relationship of logical dependency between geometrical properties. This requires the accomplishment of at least some of the following subtasks:

    • representing the invariant observed during dragging through a construction of the proposed geometric description of the path;

    • performing soft dragging test by dragging the base-point along the constructed geometric description of the path;

    • performing a robust dragging test by providing (and constructing) a geometric description of the path that is not dependent upon the dragged-base-point and redefine the base-point on it in order to have a robust invariant, then perform the dragging test.

A key requirement for conceiving a conditional link is the learner’s experience of simultaneity together with direct control; that is, control over the direct movement induced by dragging a base point along the path. In fact, after discovering the invariant observed during dragging, the learner can directly act on the base point to maintain the invariant observed during dragging, and as a consequence simultaneously feel and observe the maintaining of the intentionally induced invariant indirectly. Thus it suggests that a bridge between the experiential field (in dynamic geometry) and the formal world of Euclidean geometry is provided by the following interpretation:

As learners induce invariants in a DGE, the types of control that learners experience over these invariants enable discernment of a-symmetric status among them in spite of the fact that they appear simultaneously. This may lead the learners to interpret the dynamic relationship between invariants as a conditional relationship (If … then…) between geometric properties.

This discernment hypothesis is summarized as follows:

$$ \begin{aligned} {\text{Simultaneity }} + \, & {\text{Direct control via Maintaining Dragging over a soft invariant}} \\ & \quad \quad \quad \quad \quad \to {\text{Premise of a possible conjecture }}\left( {\text{IF}} \right) \\ {\text{Simultaneity }} + \, & {\text{Indirect control via Maintaining Dragging over a soft invariant}} \\ & \quad \quad \quad \quad \quad \to {\text{Conclusion of a possible conjecture }}\left( {\text{THEN}} \right) \\ \end{aligned} $$

When developing such scheme the role of the path is crucial. The notion of path was introduced by Baccaglini-Frank and Mariotti (2009) and is consistent with Leung and Lopez-Real’s (2002) notion of locus of validity. A path can be conceived as a visual record of a controlled variation, but at the same time it may be a record of simultaneous invariance: of the maintained invariant and of a new invariant causing it. A path is a trajectory such that when a base point of a configuration is being dragged along it, the configuration will satisfy a certain prescribed condition. In particular, in the discernment of level-2 invariants a critical role can be played by the conception of a path. As the exploration proceeds the representation of the path (both mental and within DGE) passes through a sequence of steps that capture an evolution process that is representative of the means of discernment that were discussed above. Firstly the path is envisaged (envisaged path), then a path is roughly traced (traced path), then a path is constructed and along such path a base point can be dragged (drag-along path), finally, if possible, a generalized robust path is constructed (generalized robust path).

Discernment Through Path

Continue with the dynamic figure depicted in Fig. 1, I now use it to illustrate how the MD (Maintaining Dragging) Scheme can be applied together with variation interactions utilizing a sequence of paths to formulate a possible conjecture. The exploration problem is:

Explore the possible positions of B such that the perpendicular bisectors r and s coincide

Envisaged Path (Task 1 in MD Scheme)

Wandering dragging B to drag for contrast, for different fixed positions of A, C and D find the possible positions of B that makes the perpendicular bisections r and s coincide (intentionally induced invariant), and the perception of a possible path is forming in the dragging process (Fig. 7).

Fig. 7
figure 7

Envisaged path

Full size image

Traced Path (I) (Task 2 in MD Scheme)

Use the maintaining dragging modality on B with the Trace turned on (lieu muet dragging, drag-to-fit) to drag for separation. A path is traced out while keeping r and s coincide. The path roughly takes the form of a circular arc and the perception of a soft invariant (invariant observed during dragging) is forming in the dragging process (Fig. 8).

Fig. 8
figure 8

Traced path

Full size image

Traced Path (II) (Task 2 in MD Scheme)

Perceptually asserting that the traced path is part of a circle, the next task is to locate the centre of the circle. As the coincided r and s appears to “lie in the middle” of ABCD and ABCD looks like a symmetric trapezium, a reasonable guess would be that the centre may be the intersection of the two diagonals AC and DB. Indeed, simultaneous focus on AC, DB and the coincided r, s with direct control on B via maintaining dragging over a soft invariant (drag to fuse) reveals that the centre of the circle that causes the r, s coincidence (geometric interpretation of the traced path) does seem to lie on the intersection of AC, DB and the coincided r, s (Fig. 9).

Fig. 9
figure 9

Exploring the geometrical interpretation of the traced path

Full size image

Drag-Along Path (Task 3 in MD Scheme)

Construct a circle with the intersection of AC and BD as centre using A as the terminus of a radius. Drag B along the constructed circle (soft dragging) to test the validity of the perceived geometric interpretation of the traced path (drag to generalize). That is, direct control on an invariant observed during dragging causes an indirect control on an intentionally induced invariant. This drag-along path will become the soft invariant that forms the premise of a possible conjecture (Fig. 10).

Fig. 10
figure 10

Soft dragging on the geometrically interpreted path

Full size image

Generalized Robust Path (Task 3 in MD Scheme)

Construct a robust circle using the critical features discerned in Trace Path (II) to confirm the conclusion of a possible conjecture and to perform a robust dragging test (drag to generalize and drag to fuse) on the final construction (Fig. 11).

Fig. 11
figure 11

Generalized robust path

Full size image

  • A Possible Discerned Conjecture

  • Let O be the intersection of the diagonals AC and BD.

  • IF B lies on the circle centred at O with OA as radius

  • THEN the perpendicular bisectors of AB and CD coincide.

This dragging exploration illustration shows how discernment through variation interactions and discernment through the MD Scheme can be merged together under the perception of different types of path resulting in a possible conjecture. Notice that this conjecture is stated in a DGE context where dragging, variation and invariants are implicit.

Reasoning Through Instrumented Abduction

Abduction describes a particular form of reasoning that leads to discernment of experiential phenomena through the generation of explanatory hypotheses. During explorations in DGE and the learner focuses on relating invariants, that is discerning level-2 invariants, the generation of explanatory hypotheses can be a key. In Magnani’s terms (2001) abduction is:

the process of inferring certain facts and/or laws and hypotheses that render some sentences plausible, that explain or discover some (eventually new) phenomenon or observation; it is the process of reasoning in which explanatory hypotheses are formed and evaluated.” (pp. 17–18)

Research studies suggest that when certain utilization schemes have been appropriated during exploration in DGE, associated to dragging modalities, such explanatory hypotheses may be generated through a particular form of abduction. Baccaglini-Frank and Mariotti have described such form of abduction supported by an instrument (in their case the instrument of maintaining dragging), as instrumented abduction (see Baccaglini-Frank 2011). Two characteristics used to define instrumented abduction are: (1) that it occurs at a meta-level through a meta-rule developed during a process of instrumental genesis, and (2) that it is encapsulated in the use of the artefact in the task it is used for.

When using MD to elaborate a conjecture, that is to define a level-2 invariant, the learner perceives invariants and tries to logically link two (or more) of such invariants in a conditional statement. Such a statement (a level-2 invariant) constitutes an “explanatory hypothesis” for the observed phenomenon. With respect to the illustration in the previous section, dragging B to induce the property “r and s coinciding”, the two invariants can be described as: r and s coinciding (III: intentionally induced invariant), and B lies on the circle centred at O with OA as radius (IOD: invariant observed during dragging). The instrumented abduction performed by the learner can be illustrated as

The learner observed and experienced simultaneous phenomenal facts in a DGE while exercising direct and indirect MD controls over them under variation interactions. This learner-centered experience transcends to a meta-level where the learner elaborates a MD discernment meta-rule through a process of turning MD into a conjecture-generation instrument. Then this meta-rule becomes an explanatory hypothesis (in Magnani’s interpretation of abduction) or a conditional link. Thus the rule in an instrumented abduction evolves from the learner’s meta-level reflection on her/his MD experience of simultaneity and variation.

The data analyzed in the study by Baccaglini-Frank and Mariotti (Baccaglini-Frank 2010) suggested that once the MD scheme has been appropriated, the process of conjecture-generation as described by the MD-conjecturing model seems to become “automatic”, and the learner proceeds through steps that lead smoothly to the discovery of invariants and to the generation of a conjecture, with no apparent abductive ruptures in the process. The abduction seems to be concealed within the MD-instrument. This can now be explained through the meta-rule developed during the process of instrumental genesis of the tool (in this case MD) that allows the learner to interpret the phenomenon in her/his experience in dynamic geometry in terms of logical dependence between invariants, and therefore to produce a conditional statement of the type: “if property A (the second invariant perceived) then property B (the first invariant induced)”. Such conditional statement is the product of the learner’s exploration, an explanatory hypothesis, but that becomes “automatic” once the process of instrumental genesis is complete (i.e. the MD scheme has been appropriated). In this sense the abduction seems to be of the type: it occurs at a meta-level through a meta-rule developed during a process of instrumental genesis, and is encapsulated in the use of the MD-artefact in the task of conjecture-generation.

Geometry with a Dragging Principle

DGE are software environments designed to embody Euclidean Geometry in a dynamic and interactive way. Basically they are computer programs that can induce all the properties that are Euclidean consequences of the properties of construction, but not as consequences of the Euclidean axioms. Lopez-Real and Leung (2006) suggested that if dragging in DGE is accepted as a tool that can bring about structures and patterns, then “…we have new ‘rules of the game’, or even a new game, for experiencing geometry.” (op cit, p. 676)

A discernment and reasoning model has been developed in the above discussion where explorations within DGE can lead a learner to transform acting and perceiving to conceptual counterparts and to the fundamental theoretical aspects of the exploration, thus gives us a means to access Euclidean Geometry through the drag-mode. Hence exploring by dragging is a powerful tool supporting geometrical reasoning. This can be expressed as the following Dragging Exploration Principle:

During dragging, a figure maintains all the properties according to which it was constructed and all the consequences that the construction entails in Euclidean Geometry.

This principle implicitly embraces variation, invariants (soft and robust) and sensory-motor perception. Furthermore, it is embedded with a time factor that can be associated to a figure since the possibility of dragging implies variation, which is a temporal phenomenon. A learner has control over a DGE figure through dragging its base points, and can add and take away properties, for example, by freely inducing or relaxing soft invariants. In this way a learner travels back and forth thus imposing a controllable time frame on the dynamic figure, time of a dynamic figure (tf), with respect to a real time sequence tp of a dragging experience. tf can be thought of as reversible and stoppable (with respect to tp) time travelling back and forth with respect to the III and the IOD in which it is possible to modify the figure. These two time-related aspects are direct consequence of the Dragging Exploration Principle. The principle makes possible the appearance of a tp phenomenon and serves as a rule to allow further tf exploration to look for a cause for (or explanation of) the tp phenomenon. In particular, the principle is behind the maintaining dragging modality that drives the path sequence discussed in the previous section which converges to a conditional link (a conjecture) between an III and an IOD.

The Dragging Exploration Principle imbues DGE with an epistemic quality that is process-oriented and user-centred. In particular, the idea of time of a figure opens up a type of geometrical reasoning that could be distinct from deduction and induction, and possibly suggests a different type of pedagogical process. Equipped with this principle, learners can search, via dragging, for reasonable explanations that are consistent with the Euclidean axioms. Fishbien (1993) proposed the notion of figural concept which stated that in geometrical reasoning, geometric figures are mental entities that simultaneously possess both conceptual properties (consistent with Euclidean theory) and figural properties (consistent with sensorial perception such as shape, position and magnitude). This notion is particularly fitting with the Dragging Exploration Principle as a DGE figure is a dynamic geometric entity that is simultaneously Euclidean and sensorial. Under dragging, this simultaneity (with respect to both time frames tp and tf) between abstraction and perception fosters a type of figural reasoning which I call DGE figural reasoning. It is roughly a type of abductive reasoning instrumented by the drag-mode seeking to harmonize between perceived dynamic DGE phenomena and corresponding Euclidean concepts. Variation interactions and the MD Scheme are discernment means that could instrument the drag-mode to bring about such reasoning process. This lecture serves as a starting point for an investigation to pin down the logic behind DGE figural reasoning.