1 Introduction

What makes a Dynamic Geometry Environment (DGE) a powerful mathematical knowledge acquisition microworld is its ability to visually make explicit the implicit dynamism of “thinking about” mathematical (in particular geometrical) concepts. By implicit dynamism I mean that when engaging in mathematical activities or reasoning, we often try to comprehend abstract concepts by some kind of “mental animation”; that is, mentally visualizing variations of conceptual objects in the hope of “seeing” patterns of variation or invariant properties. The success of perceiving such patterns or properties often helps to bring about understanding of the underlying abstract mathematical concept. However, this is mostly a pure-thought process (sometimes with the aid of pencil-and–paper) with usually metaphorical representations of physical reality. In geometry, DGE provides a quasi-reality (Euclidean in nature) embedded in computational technology in which such a cognitive dynamism can be given a visual manifestation.

“It suggests an almost organic allure to dynamic geometry activity – to interacting with mathematics at a level that is simultaneously palpably virtual and virtually palpable.” (Jackiw 2006, p. 147).

In particular, one of DGE’s powers is to equip us during a mathematical thinking episode with the ability to retain (keep fixed) the background of a geometrical configuration while we can selectively bring to the fore dynamically (for example, via drag-mode, hide/show) those parts of the whole configuration that interest us.

Dragging in DGE is a much studied theme in expounding epistemic and pedagogical values of DGE. It provides the user with an interactive means to express his/her geometrical thoughts in visual-dynamic ways that could contribute to the formation of abstract knowledge and the bringing about of learning. Dragging empowers the user to objectify a personal continuum in which s/he could realize his/her geometrical intuition in a dynamically real-time fashion. Hence DGE can be regarded as a potential of geometrical phenomena for the construal of geometrical meanings rather than just a platform for illustrating established rigid geometrical knowledge. Ample research has been carried out to study how dragging in DGE can be instrumental in helping students to solve construction problems, explore geometrical situations, formulate conjectures and even proofs (see for examples, Educational Studies in Mathematics 44:1–161, 2000; International Journal of Computers for Mathematical Learning 6:229–333, 2001; Math ZDM 34(3), 2002). Different dragging strategies or modalities have been investigated attempting to discover the roles that dragging can play in different DGE experiences (see for examples, Hölzl 1996; Schattschneider and King 1997; Leung and Lopez-Real 2002; Laborde 2005). In particular, Arzarello et al. (2002) identified seven dragging modalities (wandering, guided, bound, dummy locus, line, linked, drag test) while trying to analyse conjecture making episodes by students working on a geometrical problem. In that study, these modalities structured a situated hierarchical scheme that seemed to be conducive to the formation of a specific geometrical conjecture. In another vein, Hedegus (2005) pursues the idea that the draggable part (hot spot) of a robust construction constitutes an infrastructure of DGE hence dragging it allows semiotic mediation (see for example, Mariotti 2002), or co-action, between the user and the DGE that the constructed object is embedded in. Hence drag mode is a cognitive tool in DGE that has the potential to become a semiotic system (sign producing process) that construes mathematical meaning. Furthermore, dragging can be studied under the instrumentation approach (Vérillon and Rabardel 1995) where the Drag tool is scrutinized under the instrumental genesis framework (Leung et al. 2006). However, analysing dragging from a tool-use perspective is quite different from seeing how the drag mode works directly in terms of mathematical actions.

Dragging modalities, semiotic mediation and instrumentation should be intrinsically related to each other. A common feature that threads through all of them is variation. Variation is the epistemic essence of the drag mode in DGE. In particular, a key purpose in most DGE dragging strategies is to discover invariant properties in the midst of varying components of a geometrical configuration. Looking for invariance is a mathematical habit-of-mind. These dragging strategies often involve other functionalities in DGE like measurement, hide/show and trace to accentuate the different patterns of variation that can bring about the emergence of geometrical patterns. Therefore, an understanding of how variation contributes to discernment of knowledge might provide an interpretative framework to study the pedagogical and epistemological significances of the drag mode in DGE.

The aim of this paper is to investigate how patterns of variation can be used to frame the Drag tool in discovering mathematical knowledge. In Sect. 2, I will start with a brief discussion on the role of variation as kernel in experiencing phenomena and subsequently introduce Marton’s framework of discernment and awareness that involves specific functions of variation (Marton et al. 2004). These functions will form the basis for the rest of the discussion in the paper. In Sect. 3, I will illustrate how these functions of variation, interacting with Arzarello et al’s dragging modalities, can be used as a meta-tool to organize dragging strategies and to shape geometrical knowledge in DGE in the context of a specific exploration task, thus re-interpreting Arzarello et al. in a potentially more mathematically-relevant way. This will be followed by the introduction of an innovative spectral dragging strategy where one can literally see mathematics in colour pictures. As the exploration evolves, the idea of DGE Theorem and Davis’ Visual Theorem (Davis 1993) will be discussed. In Sect. 4, I will make a speculation on a generic discernment nest structure of dragging experience in terms of the functions of variation. This discernment nest is an attempt to map out the structure of awareness (in particular, from soft DGE construction to robust DGE construction) in experiencing dragging with respect to the functions of variation. On the one hand, the nest can serve as a lens to “re-construe” a dragging experience or as a meta-language to frame different approaches to analyse dragging, while on the other hand; it can be used as a meta-tool to organize pedagogical dragging experiences.

2 Variation

Conceptualization of invariant structures amidst changing phenomena is often regarded as a key sign of knowledge acquisition. In phenomenology, one of the hermeneutic rules is “seek out structural or invariant features of the phenomena”. Furthermore,

“The probing activity of investigation is called variational method… Variations “possibilize” phenomena. Variations thus are devices that seek the invariants in variants and also seek to determine the limits of a phenomenon.” (Ihde 1986, pp. 39–40).

Verillon and Rabardel (1995) in their seminal paper in which they introduced the concept of instrumental genesis, begin the paper with

“Epistemology, notably genetic epistemology, has shown that only a controlled transformation of reality enables the intellect to elaborate its invariant and variational properties. In the real world, persons perform transformations in a variety of contexts and in view of different goals. Consequently, the resulting generation of knowledge occurs in different situations and through different processes.” (pp. 77–78).

This controlled transformation (for example, tool usage) implies “acting” on the environment. Actions bring about changes, changes bring about patterns of variation, and patterns of variation could stabilize possible epistemic states (Gärdenfors 1988), or situated invariant knowledge/belief. Gärdenfors in his treatise Knowledge in Flux (1988) expounded a theory of rational changes of states of belief (a model on the dynamic of epistemic states). A basic element of his approach was the idea of epistemic input.

“On this approach all changes of a state of belief must be accounted for by some “external forces”. These external forces can be described as the “deliverance of experience” by linguistic or nonlinguistic means, and they are called epistemic inputs here.” (Gärdenfors 1988, p. 13; italics in original).

Therefore, an epistemic input delivered by some form of experience transforms an old local invariant belief to a new local invariant belief. Though Gärdenfors was not interested in the concrete forms of the epistemic inputs (his theory was about the effect of epistemic input), the nature of the epistemic input could be deterministic in shaping new epistemic states (knowledge). In the DGE context, these “external forces” (epistemic inputs) that deliver transformational experiences could be the instrumental process of a tool like the drag-mode that mediates knowledge construction.

What constitutes a rational change of states of belief can be scrutinized under the lens of variation. Marton advocated, in his work on learning and awareness (Marton and Booth 1997), that variation and simultaneity play a fundamental role in discernment. His ideas can be captured in a nutshell by the following:

“As we always act in relation to situations as we see them, effective actions spring from effective ways of seeing. Seeing a situation in a certain way amounts to discerning those aspects which are critical for engaging in effective action and taking all of them into consideration (focusing on them) at the same time. In order to discern a certain aspect, one must have experienced variation in those aspects. There is no discernment without variation. The only way we can prepare for the un-definable variation in the future is by experiencing variation in the present and by having experienced variation in the past.” (The abstract of a seminar given by Ference Marton at The University of Hong Kong, 21 Nov 2006).

2.1 Functions of Variation

To sort out the epistemic function of variation in his framework of variation, Marton (Marton et al. 2004) proposed four inter-related functions (or patterns) of variation. They are described as follows:

Contrast: “… in order to experience something, a person must experience something else to compare it with.”

Generalisation: “… in order to fully understand what “three” is, we must also experience varying appearances of “three”,…”

Separation: “In order to experience a certain aspect of something, and in order to separate this aspect from other aspects, it must vary while other aspects remain invariant.”

Fusion: “If there are several critical aspects that the learner has to take into consideration at the same time, they must all be experienced simultaneously.”

(Marton et al. 2004, p. 16).

These four functions act as guiding posts (not exhaustively though) to deconstruct a variational experience (an epistemic input) in probing how such experience can bring about changes in epistemic states.

2.2 Simultaneity

A key concept in understanding how these functions of variation can bring about discernment and awareness is the idea of simultaneity. That is, experiencing different temporal or spatial “instances” of a phenomenon at the same time. Two types of simultaneity are defined by the following descriptions in Marton et al. (2004):

Synchronic Simultaneity (spatial type)

“[…] a way of seeing something as the discernment of various critical features of an instance simultaneously […] [This] is the experience of different co-existing aspects of the same thing at the same time.” (pp. 17–18).

Diachronic Simultaneity (temporal type)

“In order to experience variation in certain respect, we have to experience the different instances that vary in that respect simultaneously, i.e., we have to experience instances that we have encountered at different points in time, at the same time.” (p. 17, italics in original).

Simultaneity therefore steers the functions of variation in shaping an experience (or to realize the intentionality of the observer) to bring about understanding. This framework of variation forms an interpretative lens to “see inside” a phenomenon and acts as a catalytic agent to bring about change in epistemic states.

In the following section, I will describe and discuss, by using a specific geometrical scenario, how the drag mode in DGE can be experienced in the context of variation and in particular, how the functions of variation can structure a DGE dragging exploration. This work is a continuation of my previous work on variation and DGE (Leung 2003; Leung and Chan 2006; Leung et al. 2006).

3 Dragging seen Through the Lens of Variation

I use the word “lens” here to mean a way of seeing a DGE experience. The purpose of this section is to try to let the readers experience a vision of DGE under variation. The four functions contrast, separation, generalization and fusion will be expounded consecutively in sequence under an exploration on a geometrical problem employing known dragging modalities. The exposition sequence will inspire the discernment nest structure to be suggested in Sect. 4. In the last part of this section I will introduce a new dragging strategy indigenous to the Sketchpad™ (Jackiw 2001) environment that allows one to literally see the drag mode in action in a chromatic fashion.

3.1 Drag for Contrast

Contrast is about seeing differences, comparing between what is and what is not, hence anticipating (conjecturing) what can be and cannot be.

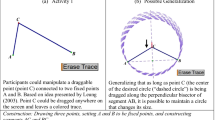
Wandering dragging is a primitive dragging strategy that illustrates well the drag for contrast function. In what follows, I will describe in detail a DGE dragging experience I had using Sketchpad attempting to solve a geometry problem. In the description, I will interpret what I did using the framework of variation (Fig. 1).

Fig. 1
figure 1

The Problem. Determine all possible configurations of A, B, C and D such that the condition ∠ABC = 2∠ADC holds

Full size image

The exploration begins by measuring ∠ABC and ∠ADC to see whether these two numerical values satisfy the desired condition. If so, a valid position is located. If not, drag (either A, B, C or D) in a wandering fashion while simultaneously observing the varying numerical values (synchronic simultaneity) until a valid position is reached. This is searching by contrast. There are four dimensions of variation (i.e. A, B, C and D) in the configuration. Wandering dragging them randomly might not yield a discernable pattern. A refined wandering dragging strategy is needed. It seems sensible to focus on one vertex at a time and see whether wandering dragging it would suggest a possible pattern. At this juncture, my decision on which vertex to use depends on my wandering dragging experience so far. I need to compare and contrast the similarities and differences among the dragging experiences of the four dimensions of variation and make a personal preference (diachronic simultaneity). The given configuration reminds me of a familiar circle theorem: angle at the centre is twice the angle at the circumference. Even though the given situation is more general in nature (length AB is not necessarily equal to length BC), this reminder suggests to me that focusing on D or B might be fruitful, since in these situations I can always specialize to the case where length AB length BC. With this background, starting with wandering dragging D or B could become more strategic.

Suppose D is chosen. To narrow the search, D can be dragged in a bounded, still wandering, fashion such that the ratio ∠ABC/∠ADC is between, say, 1.7 and 2.3 to start with (the numerical choice is arbitrary). This is a kind of guided dragging; in this case, I am guided not by geometrical shape, but by numerical measurement. Turning on the Trace function for D, this dragging strategy paints a partial annulus region R in which the ratio falls into the acceptable range (Fig. 2).

Fig. 2
figure 2

The middle snapshoot shows a partial annulus R as D is being wandering traced between the guided values 1.7 and 2.3

Full size image

I can guess visually that as I narrow the numerical range, the width of the annulus will become smaller and smaller until it becomes part of a circular arc when the ratio ∠ABC/∠ADC is equal to 2. This is a kind of refining wandering dragging strategy under which a sequence of progressively “finer” regions are being compared and contrasted, ever focusing on the possible convergence to a recognizable pattern.

3.2 Drag for Separation

Separating out hidden geometrical patterns and invariant properties is a key objective in any dragging exploration in DGE. During a dragging episode, it is critical to decide what is to be focused on (foreground) and what is to be temporally laid aside (background), or kept fixed, in order for meaningful dragging activities to take place. When a dimension of variation (an aspect) of an object of exploration is being dragged while other dimensions are being kept constant, a potential invariant pattern or property (image) might emerge. The separated-out invariant pattern or property could then become a critical feature in the formation of a conjecture. Guided dragging and dummy locus dragging are two dragging modalities that could strategize separation. In particular, locus of validity (Leung and Lopez-Real 2002) for certain geometrical phenomena can sometime be discerned under these two dragging modalities. A locus of validity is a path on which a certain geometrical condition is satisfied.

The refining wandering dragging strategy illustrated in the previous discussion can be regarded as a separation process (A, B and C are being kept constant while D is varying). To visually separate-out and pin down my guess that the locus of validity is indeed a circular arc, a transition in dragging modalities is needed. I first start with dummy locus dragging. That is, turn the Trace function on for D and drag D while keeping the ratio as close to 2 as possible (Fig. 3).

Fig. 3
figure 3

By dragging D to keep the ratio ∠ABC/∠ADC as close to 2 as possible, a rough recognizable path (dummy locus) of D is being traced

Full size image

The traced-out path would be a close approximation to the desired “final object” (a locus of validity). A preliminary visual guess is being separated-out relative to the fixed positions of A, B and C. The traced locus is an arc-like curve and the next task is to determine the kind of curve that this arc belongs to. I achieve this by dragging D to a position such that the ratio is equal to 2 and plot this location as a fixed point. Repeat this construction exercise until “enough valid points” are plotted (see Fig. 4). A “broken” circular path appears invoking a speculation that the locus of validity is a circle.

Fig. 4
figure 4

A broken circular locus for D

Full size image

Drag D along this imaginary circle (guided dragging) to check that the ratio is indeed closely equal to 2. The desired condition seems to hold except when D lies on the minor arc AC in which case further investigation is needed. Next, I construct this imaginary circle. Pick any three points U, V and W on the broken circular path and construct a circle C 1 passing through them. Observe that all the plotted points appear to lie on C 1 (Fig. 5).

Fig. 5
figure 5

A circle C1 is constructed through U, V and W and it appears to pass through all plotted points

Full size image

Notice that vertices A and C also appear to lie on C 1! This is a critical discovery as it provides a hint on how to construct the desired circle. That is, given the configuration A, B, C and D as in Fig. 1, drag D to a position such that the desired ratio is equal to 2; construct the circle C 2 passing through D, A and C (Fig. 6).

Fig. 6
figure 6

Circle C2 is constructed using A, C and a “valid” D

Full size image

By fixing the positions of A, B, C and employing different dragging strategies and performing intermediate constructions, four progressively refined layers of a locus of validity have been separated-out (Figs. 3, 4, 5, 6). Reviewing how C 2 was separated out, C 2 should be unique as long as A, B and C are kept fixed.

The separation described above is about experiencing the construction of C 2 (the locus of a varying D) relative to a set of fixed A, B and C. It is not hard to see that for different positions of A, B and C, there will be different C 2’s (this will be discussed in detail in the next section). Let us summarize what has been discovered so far and I will state it as a DGE conjecture (the italicized phrases have a DGE situated connotation):

Conjecture Given a quadrilateral as shown in Figure 1 where A, B and C are fixed and D is draggable, then there exists a unique circle passing through A and C such that when D lies on this circle, the condition ∠ABC = 2∠ADC holds.

3.3 Drag for Generalization

A “properly” constructed (robust) figure in DGE is not just a static diagram; rather it is a variable figure that can carry conceptual ideas. A robust square ABCD in DGE is a square constructed in a way such that the invariant or defining properties of a square are preserved under dragging. In terms of dragging strategy, it passes the drag test. Hence, varying appearances of a “square” can be experienced via dragging and the meaning of a square is being manifested in a visual dynamic way. Thus, a robust square is a generalized square exactly in the sense of the generalization function in variation. The drag test is a dragging strategy that can facilitate generalization since its purpose is to let a DGE user discern or verify invariants under varying appearances of the object of exploration.

How does the construction that led to the formulation of the Conjecture above react to the drag test? Since circle C 2 was constructed using vertex D at special positions, it is immediately obvious that C 2 will vary and cease to be a locus of validity when D varies, hence the configuration cannot be robust. In order to experience varying appearances of the required condition aside from the configuration depicted in Fig. 6, A, B, C and D can be dragged to other positions where corresponding loci of validity can be constructed using the same procedure as above. However, the figure ABCD that resulted from this construction strategy is not a generalized figure that always satisfies the desired condition. A generalized figure with respect to a given condition is a figure that satisfies the given condition and passes the dragging test. A robust construction is a generalized figure. To further explore the situation in the hope of constructing a generalized figure, other dimensions of variation (vertices A, B, C) can be activated. I have a choice as to which vertex, other than D, I would like to focus on. Since B lies inside C 2 for different positions of D so far, there might be a hidden structure underlying the positions of B. Suppose B varies while keeping A, C and D fixed (a separation activity). The following set of snapshots (Fig. 7) is taken from a sequence of exploration episodes similar to the drag for separation discussion with D as the dimension of variation in the previous discussion:

Fig. 7
figure 7

Snapshots from an exploration sequence with B as the dimension of variation

Full size image

In Fig. 7, Fig. 6 is put in the background with O as the centre of C 2. It acts as a reference for the new exploration. This would facilitate interpretation of discernment obtained in this exploration under what has been learnt so far (diachronic simultaneity). Episodes 1 and 2 are separation activities using dummy locus dragging and guided dragging respectively. In Episode 3, circle C 3 is constructed passing through E, B and B′. Similar to the previous discovery, C 3 passes through vertices A and C. A locus of validity C 4 is constructed using A, B and C as depicted in Episode 4. Furthermore, a new and important critical feature appears, that is, C 4 seems to pass through the centre O of C 2. This phenomenon generates a new insight! Instead of constructing a “soft” C 2 out of dependency from fixed vertices A, C and a varying D, a robust C 2 can be constructed from fixed vertices A, B and C which will result in a generalized figure. The construction/dragging procedure would go like this (Fig. 8):

Fig. 8
figure 8

Construction of a robust locus of validity

Full size image
  1. (1)

    Construct circle C 4 passing through vertices A, B and C. This will eventually be a locus of validity for B.

  2. (2)

    Join A and C.

  3. (3)

    Construct the perpendicular bisector of AC. Label the point of intersection with C 4 (on the same side as B) as O.

  4. (4)

    Construct circle C 2 with O as the centre and OA (or OC) as radius (Fig. 8a).

  5. (5)

    Merge (a function in Sketchpad) D to the circle C 2 and check that as D is being dragged along C 2, the ratio value 2 remains invariant (Fig. 8b).

  6. (6)

    Check that as A, B and C are being wandering dragged, the ratio value 2 remains invariant.

The dragging modality in Step (5) is link dragging. It is a useful dragging strategy to produce a generalized (robust) figure. The above procedure gives a configuration that passes the drag test. Contrasting to the procedure in Conjecture One, D is no longer an independent point; its movement is confined on C 2 due to the merging action. This is expected for a generalized figure since a figure passing the drag test should be laden with constraints on its components that constitute its invariance. Instead of using A, B, C as the independent points to construct C 4 followed by C 2, it is not difficult to see that one can also use A, C and D as the independent points to construct C 2 followed by C 4 with B confined on C 4 via merging. Furthermore, when D is dragged to positions on C 2 that are below the chord AC (see Fig. 9), the condition still holds if the reflex ∠ABC is used instead.

Fig. 9
figure 9

An interpretation of the robustness of the construction when D is “below” the chord AC

Full size image

Thus, this finding can be considered as a DGE theorem that goes something like this:

Theorem Given the configuration ABCD as shown in Figure 1, there exists a circle that passes through A and C such that when D is linked to it, the condition ∠ABC = 2∠ADC holds. Furthermore, this circle and the circle that passes through A, B and C are generalized loci of validity for the condition.

By generalized loci of validity, in this case generalized circles, it means that these circles vary in size and position as A, B, C (note that D is a dependent point) are being dragged while the condition ∠ABC = 2∠ADC remains invariant (seeing different appearance of the same thing). A “DGE proof” of the theorem is the construction procedure described above which implicitly assumed a “DGE axiom”: Independent or semi-independent point is draggable.

3.4 Drag for Fusion

Fusion is about simultaneity, that is, it is about experiencing different critical features of a phenomenon at the same time. Different parts of an object of exploration in DGE can be varied continuously via different dragging strategies in real time. This brings about a simultaneous awareness of how different critical aspects of a geometrical situation behave, hence creating a potential space for seeing geometrical structure and meaning.

I will illustrate fusion by revisiting Episode 4 in Fig. 7 after the locus of validity C4 was constructed. At that instance, four critical features were present simultaneously on the screen: two loci of validity C 2 (for D) and C 4 (for B), the centre O of C 2, lying on C 4, and the two numerical ratios satisfying the desired condition. When any one of the vertices A, B, C or D is being dragged, one can experience how these four critical features react to it simultaneously (Fig. 10).

Fig. 10
figure 10

Episode 4 in Fig. 7 is a fusion of critical features: C 2, C 4, the centre O and ratio values. One can see that if A, B, C, D (clockwise from upper left) are being dragged to different positions, then O might no longer lie on C 4 and the numerical ratio might no longer be equal to 2

Full size image

By using a drag-to-fit strategy, when one of the vertices A, B, C or D is being dragged, I observed that

C2 and C4 remain as loci of validity for D and B respectively if and only if the centre of C2 lies on C4.

Thus a fusion experience brought about a critical insight that enabled me to construct a generalized C 2 (refer to Fig. 8), resulting in the Theorem in Sect. 3.3.

3.5 Spectral Dragging

In Geometer’s Sketchpad, the intriguing functionality Parametric Color can actually reveal variation visually. For a Sketchpad object, if a draggable component (e.g., a point) is associated with a variable numerical value, then that component can be traced under dragging with an assigned range of colour corresponding to a preset numerical range. I will use this spectral dragging strategy to investigate the above problem and see if there is a different way of seeing the mathematics behind it.

Figure 11 shows the interface of setting up the colour parameter. The variable numerical value is the calculated difference between ∠ABC and 2∠ADC. The significant colour range (Parameter Domain) for the vertex D is set between −2 and 2 in which there is spectral continuum varying from purple to red (−2 to 2) with green corresponding to a colour range roughly between −1 and 1. That is, where D traces a green colour, those are the positions that are sufficiently close to the desired locus of validity (value 0) of D. Hence a locus of validity can be thought of as the kernel of a mapping. Values less than −2 will all become purple and values bigger than 2 will all become red.

Fig. 11
figure 11

Parametric Color interface in Sketchpad

Full size image

3.5.1 Contrast and Separation

Putting the Trace function on for D and dragging it randomly to “scratch out” (the mouse motion is actually a scratching motion) the “underlying colour motif” (bias with a preset interpretation) for this particular geometrical configuration results in a (partial) picture depicted in Fig. 12. I shall call this spectral dragging strategy spectral scratching.

Fig. 12
figure 12

A partial scratch-out picture for D showing a colour pattern for the desired geometrical condition

Full size image

It is visually clear that there is a narrow green circular band containing a circular major arc AC. Hence, if D lies inside this green band then |∠ABC − 2∠ADC| < 1°. In this case, contrast and separation are integrated into one dynamic chromatic experience. Colour differentiation gives rise to contrast and the green circular band (with A, B, C being fixed) gives rise to a visually separated out geometrical pattern.

When fixing A, D and C and applying the same spectral scratching strategy on B, there is another narrow green circular band containing a different circular major arc AC (Fig. 13).

Fig. 13
figure 13

A partial scratch-out picture for B showing a colour pattern for the desired geometrical condition

Full size image

These two green bands in Figs. 12 and 13 are two neighbourhoods of the two generalized circles (C 2 and C 4) in the DGE Theorem stated in Sect. 3.3. However, spectral dragging does not seem to give immediate insight on how to construct the generalized circles for the DGE Theorem, rather, the focus is on the green arcs and the different colour regions. There is a natural tendency in spectral dragging to scratch out the “whole hidden picture”. Figure 14 shows that after scratching below AC, a symmetrical pattern with AC as the axis of symmetry emerges. This is a consequence of the fact that in Sketchpad, all angle measurements are for acute angles only. Thus the “natural” colour pattern in Sketchpad for this exploration is the symmetrical pattern depicted in the Fig. 14 rather than the recognition of the generalized circle C 2 in the DGE Theorem.

Fig. 14
figure 14

A global double circular symmetrical picture for D

Full size image

Similarly, one can fix any three vertices and scratch out the pattern for the remaining vertex. Figure 15 shows a complete scratch-out picture for each vertex while keeping the remaining vertices fixed. (It takes a bit of technical skill to produce the pictures; specifically, a colour-parameterized locus is being dragged). I shall call each picture a variation plane and each colour region a basin of variation (inspired by the term basin of attraction in the theory of dynamical systems). For example, the top left diagram in Fig. 15 shows the variation plane for D with respect to a specific fixed configuration of A, B and C.

Fig. 15
figure 15

Clockwise from top left are the variation planes for D, B, C and A

Full size image

Basins of variation in a variation plane are colour separations according to prescribed numerical ranges. They produce a synchronic simultaneous contrast and weave together a boundary pattern (for example, the double circular shaped boundary pattern in the top left of Fig. 15). The four diagrams in Fig. 15 depict a variation plane each for A, B, C and D.

3.5.2 Generalization

A family of variation planes with the same varying dimension of variation (for example, vertex D) and different fixed configurations of other dimensions of variation (for example, vertices A, B and C) can produce a diachronic simultaneity of variation planes (time-sequenced pictures) which together could reveal a stable boundary structure. This is a generalization. Figures 15(top left) and 16(left) show two variation planes of D with A, B and C in two different configurations. The same double circular shaped boundary pattern with AC as the axis of symmetry appears in both variation planes. (See also Figs. 15(top right) and 16(right) for two variation planes of B).

Fig. 16
figure 16

From left to right are variation planes for D and B with different fixed positions for the other three points as compared to those in Fig. 15 (top left) and (top right)

Full size image

The existence of such a generalized boundary pattern seems to satisfy the description of what Davis (1993) called a Visual Theorem.

“Briefly, a visual theorem is the graphical or visual output from a computer program – usually one of a family of such outputs – which the eye organizes into a coherent, identifiable whole and which is able to inspire mathematical questions of a traditional nature or which contributes in some way to our understanding or enrichment of some mathematical or real world situation.” (Davis 1993, p. 333).

Thus, under spectral dragging in Sketchpad, I can write down a visual theorem like this:

Given a configuration ABCD as in Fig. 1, with respect to the condition ∠ABC = 2∠ADC, the variation plane of D produced by spectral dragging contains a generalized boundary pattern consisting of a symmetrical double-circular boundary pattern with the line passing through A, C as the axis of symmetry.

A similar visual theorem can be written down for the variation plane of B. In contrast to the more traditional feel of the DGE Theorem in Sect. 3.3, this visual theorem provides an alternative experience for the condition ∠ABC = 2∠ADC. Furthermore, the interesting self-crossing boundary patterns for the variation planes of A and C in Fig. 15 (bottom left and right) could lead us into other mathematical insights which I’ll leave the readers to explore. It seems to be more aesthetically satisfying in this spectral dragging strategy to visually manifest a generalized boundary pattern than to construct a generalized robust figure. The latter can of course be done by resorting to the previously discussed exploration techniques, say to construct the robust double circular symmetrical locus of validity (see an example in Fig. 17).

Fig. 17
figure 17

A constructed robust double circular locus of validity for D

Full size image

3.5.3 Fusion

In a variational plane each colour region (basin of variation), in particular its size and shape, is a critical feature of the problem. Thus experiencing the full spectrum of colour regions in a variational plane is a fusion experience. For example, Fig. 18 depicts four variational planes for D with different positions of B relative to A and C.

Fig. 18
figure 18

Four variational planes (two of them are partial) for D with different positions of B relative to A and C

Full size image

By experiencing the shapes and sizes of different colour regions all at once in various variational planes for D, I can observe readily that the radius and size of the green circular-arc band depends on the position of B relative to A and C. If I can further experience a pattern of this dependency, then I might be able to characterize the variational plane for D in a more insightful fashion. Since my purpose here is just to illustrate a possible fusion experience in spectral dragging, I leave the exploration to the readers.

3.5.4 Remark

In the above sections, I attempted to illustrate the epistemological potential of Parametric Color functionality in Sketchpad. In particular, this is a DGE means to experience geometrical phenomena that is not yet explored in mathematics education literature and it might open up a new dimension in developing a DGE visual reasoning framework. The spectral scratching strategy is a dragging modality whose nature is different from that of the Arzarello et al. modalities. Its power is more in the chromatics feedback than in the strategic ways in moving the mouse. In fact, the four functions of variation act more as a lens filtering the chromatics feedback during spectral scratching than as a meta-tool to organize a strategic dragging exploration.

4 Discussion

I have used a discernment framework based on functions of variation to interpret dragging strategies in DGE and discussed how such a framework can mediate geometrical knowledge, even concoct DGE-type theorems. In particular, two dragging experiences for the same exploration problem were studied. One experience employed known dragging strategies seen through the functions of variation that led to a cognitive sequence of conjecturing, constructing and theorizing. The other experience utilized a specific functionality in Sketchpad (Parametric Color) to produce chromatic pictures of a geometrical condition via spectral dragging techniques. It visually revealed the geometry behind the exploration and led to the possibility of talking about the idea of a visual theorem, as proposed by Davis (1993). Furthermore, a variation plane resulting from spectral dragging can provide a vivid picture of the patterns of variation. Hence, using variation as a lens to interpret dragging strategies can produce meaningful mathematics through an organized use of the Dragging tool.

4.1 Discernment Nest

Inspired from the dragging experiences discussed in Sect. 3 and discussions from previous work (Lopez-Real and Leung 2006; Leung and Chan 2006, Leung, Chan and Lopez-Real 2006), I propose a way to experience DGE dragging exploration structured by functions of variation that consists of a nesting of three discernment modes (Fig. 19). The nesting of the three modes in this structure represents a progression of awareness.

Fig. 19
figure 19

A nest structure of three discernment modes for dragging in DGE based on the functions of variation. The inner most rectangular box is mode I that consists of a convolution of mode IA Drag for Contrast and mode IB Drag for Separation that might result in recognition of critical features contributing to separating out a locus of validity or a boundary pattern. The second rectangle is mode II Drag for Generalization that re-enacts the convolution in mode I with different dimensions of variation in the hope of further separating out possible global critical features. The outermost rectangle is mode III Drag for Fusion where simultaneous awareness of all the critical features is the main cognitive activity to interpret the variation in modes I and II anticipating the emergence of a robust construction or concept. The arrows indicate transitions between modes

Full size image

To illustrate the dynamic behind this nest structure or dragging in DGE, I will describe it with reference to the Figures in Sect. 3. Any DGE task that utilizes the Dragging tool can start with discernment mode I in which two variation processes convolute. Mode IA is drag for contrast which often employs the wandering and guided dragging modalities. A goal for this process is to determine different dimensions of variation for the situation at hand and to observe any emerging pattern that could lead to discernment mode IB. Mode IB is drag for separation in which a dimension of variation is chosen to be the variant while other dimensions are being kept fixed. Dummy locus dragging and guided dragging modalities can act on the variant dimension in anticipation to separate out the shape of a possible locus of validity. Further interplay between IA and IB (bottom layer of the circular arrows in Fig. 19) may result in the construction of a locus of validity for the chosen dimension of variation and the formation of a preliminary conjecture. This activity transits (indicated by arrows in Fig. 19) naturally to discernment mode II (in which discernment mode I is embedded) whose purpose is to look for generalization on what was discovered in mode I by re-enacting mode I on different dimensions of variation (top layer of the circular arrows in the overlap in Fig. 19) in the hope of separating out global critical features of the situation at hand (Fig. 7). The drag test modality can be used to check the robustness of the “idea” (Fig. 6, a preliminary soft construction) constructed in mode I. When this is achieved, discernment mode III (integrating all previous modes) is reached where critical features can be simultaneously observed through some dragging activities (fusion), possibly resulting in the construction of a robust figure (Figs. 8 and 10) or the formulation of a robust concept (for example, the DGE Theorem in Sect. 3.3).

In the spectral dragging experience, discernment mode I would be the construction (via spectral dragging) of the variation plane for a dimension of variation where the basins of variation and the boundary patterns literally visualize contrast and separation. The variation plane is a convolution of modes IA and IB. Investigation into the behaviour of the variation planes for different dimensions of variation is discernment mode II seeking for generalizable patterns that might stabilize what was previously discerned (for example, the double circular arc). In discernment mode III, dragging is performed with a simultaneous awareness of all the perceived critical features (for example, boundary behaviours between the regions) of the variation planes, possibly resulting in the conceptualization of some visual theorems or mathematical meanings.

4.2 Transient Sign

DGE objects constructed under different dragging strategies in the Discernment Nest undergo an evolution in meanings and in relation to each other. They can be regarded as “dynamic signs” in the process of concept formation. Indeed, the Dragging tool in DGE has been thought of as a sign (Falcade et al. 2007) that “points to” (a function of signs) certain situated mathematical knowledge via its dynamicity. It is interesting to ask what the “dragging sign” points to.

“…if we accept dragging in DGE as a conceptual tool (or a tool that can bring about structures and patterns) … by including a ‘pointer’ (a proto object that allows dragging) as a fundamental geometrical concept (like that of point, circle), we have new ‘rules of the game’, or even a new game, for experiencing geometry.” (Lopez-Real and Leung 2006, p.676).

In this vein of thought, the nature of the Dragging tool in DGE makes possible the construction of transient signs that are not intrinsically stable but can point to critical features of the phenomenon at hand (for example, a soft construction like Fig. 6 that can respond “properly” to a drag-to-fit strategy). In each mode and sub-mode of the Discernment Nest there were construction activities instrumented by dragging modalities and structured by functions of variation resulting in DGE objects that can be thought of as “dragging signs” for the mode they were in. These dragging signs evolved from one mode to the next as the awareness of critical features deepened. Figure 20 illustrates a “semiotic chain” of dragging signs progressing from mode I to mode III in the Discernment Nest. The first three are transient signs while the last one can be regarded as the “signified object” in this linear sequence of signification.

Fig. 20
figure 20

A semiotic chain of dragging signs progressing from mode I to mode III in the Discernment Nest

Full size image

It is interesting to ask further in what ways do the functions of variation contribute to the semantics (if any) of the “dragging sign”. I hope this will motivate further discussion in this direction. The readers can refer to Presmeg (2006) on the idea of a nested model of semiotic chaining which actually inspired the above discussion.

4.3 Implications

The Discernment Nest structure of variation can act as a generic meta-tool either to shape the Dragging tool into a strategic Dragging instrument, as a lens to interpret the functioning of the drag mode, or as a meta-language to relate different dragging analyses. Pedagogically it can serve as a cognitive frame to design and organize dragging explorations in the context of teaching and learning. It is an interesting question to ask whether this variation discernment structure would arise naturally (and to what degree) in DGE dragging explorations and whether this should be taught to students engaging in DGE exploration. Furthermore, though this paper focuses on dragging mainly, it is natural to extend the discussion (or experiment) to other functionalities in DGE like Trace, Measurement or Hide/Show and see how stable this Nest is relative to them, in particular during actual pedagogical situations. At the back of the mind of any DGE researcher there usually is a lingering epistemological question asking whether DGEs really provide a new kind of geometry. We have seen that the epistemic functions of variation together with the drag mode inspired a DGE situated conjecture and theorem, even a proof of the theorem by DGE construction. Furthermore, the variational plane with respect to spectral dragging appears to open up a new dimension of understanding (at least a colourful representation with underlying structure) for Euclidean type problems. Is this a new kind of geometry? Unlike classical axiomatic deductive Euclidean geometry, geometry realized in DGE is “variable”, in particular due to the drag mode. If the drag mode can be regarded as axiomatic (in the sense of dragging as a self-evident fact in DGE), then it might be possible to envisage an axiomatic system in which “Independent point is draggable” can be treated as an axiom. This might result in a possibly different type of geometrical reasoning from the formal axiomatic Euclidean geometry (see the discussion in Lopez-Real and Leung 2006).

5 Conclusion

I proposed in this paper that variation is a lens that focuses very strongly on mathematical aspects of dragging in DGE and, via two explorations on a geometrical problem; I supported it with the modelling of such a lens, that is, a Discernment Nest structured by functions of variation. The intention of this paper is not to declare that this lens of variation is the lens to interpret dynamic geometry environments, rather, it showed a dimension of variation (keeping in the spirit of variation) in the multifarious facets of the dynamic geometry experience. My hope is that variation could serve as a meta-language to talk about the diverse DGE pedagogical and epistemological practices. The beauty of dynamic geometry is in seeking, rather than in stating, as has been wonderfully expressed by the following quote on the magic in the psychology of dynamic geometry which I will use to end the paper.

“Here, one’s actions are inquisitive and usually tentative: one is seeking, rather than stating. As key components are dragged, the responding motions of one’s figure always appear as improvisational choreography – a single possible performance drawn from the limitless configuration space of the mathematics spread across the mode….There is a tidal movement between the modality of the certain, the expository and the declamatory on the one hand and that of the tentative and conjectural on the other, occasionally even the sudden startled or the frankly surprised.” (Jackiw 2006, p.156).