Keywords

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

1 Introduction

Adolescent idiopathic scoliosis (AIS) refers to a complex deformation in three dimensions (3D) of the spine. Classification of the rich and complex variability of spinal deformities is critical for comparisons between treatments and for long-term patient follow-ups. AIS characterization and treatment recommendations currently rely on the Lenke classification system [10] because of its simplicity and its high inter- and intra-observer reliability compared with previous classification systems [8]. However, these schemes are restricted to a two-dimensional (2D) assessment of scoliosis from radiographs of the spine in the coronal and sagittal planes. Misinterpretations could arise because two different scoliosis deformities may have similar 2D parameters. Therefore, improvements in the scoliosis classification system are necessary to ensure a better understanding and description of the curve morphology.

Computational methods open up new paths to go beyond the Lenke classification. Recent studies seek new groups in the population of AIS using cluster analysis [4, 5, 15, 17] with ISOData, K-Means or fuzzy C-Means algorithms. Their common aspect is founded upon the clustering of expert-based features, which are extracted from 3D spine reconstructions (Cobb angles, kyphosis and planes of maximal deformity). This methodology stems from the fact that clustering algorithms are very sensitive to the curse of dimensionality. Still, these parameters might not be enough to tap all the rich and complex variability in the data. Computational methods should be able to capture the intrinsic dimensionality that explains as much as possible the highly dimensional data into a manifold of much lower dimensionality [2, 11]. Hence, another paradigm for spine classification is to let the algorithm learn its own features to discriminate between different pathological groups. This implies directly analyzing the 3D spine models instead of expert-based features as it has been experimented previously. To our knowledge, only one study tried to learn a manifold from the 3D spine model [7] using Local Linear Embeddings (LLE). In this study, we propose to use stacked auto-encoders—a deep learning algorithm—to reduce the high-dimensionality of 3D spine models in order to identify particular classes within Lenke Type-1 curves. This algorithm was able to outperform principal component analysis (PCA) and LLE [6, 11].

Recent breakthroughs in computer vision and speech processing using deep learning algorithms suggest that artificial neural networks might be better suited to learn representations of highly non-linear data [2]. Training a deep neural network has been a challenging task in many applications. Nowadays, this issue is tackled by leveraging more computation power (i.e. parallelizing tasks), more data and by a better initialization of the multilayer neural network [6]. Deep neural networks promote the learning of more abstract representations that result in improved generalization. Network depth actually helps to become invariant to most local changes in the data and to disentangle the main factor of variations in the data [2].

We propose a computational method for the classification of highly dimensional 3D spine models obtained from a group of patients with AIS. The core of the methodology, detailed in Sect. 2, builds a low-dimensional representation of the 3D spine model based on stacked auto-encoders that capture the main variabilities in the shape of the spine. The low-dimensional codes learnt by the stacked auto-encoders are then clustered using the K-Means++ algorithm. Finally, a statistical analysis assesses the relevance of the clusters identified by the framework based on clinical geometrical indices of the spine. Experiments conducted with this methodology are shown and discussed in Sect. 3, while Sect. 4 concludes this paper.

2 Methods

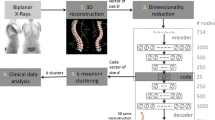
The proposed method consists of four main steps: (1) reconstruction of a 3D spine model from biplanar X-rays for each patient; (2) dimensionality reduction of each high-dimensional model to a low-dimensional space; (3) clustering of the low-dimensional space; (4) analysis of the clusters obtained with the clinical data.

2.1 3D Spine Reconstruction

A 3D model for each patient’s spine was generated from anatomical landmarks with a semi-supervised statistical image-based technique built in a custom software in C++ [13]. Seventeen 3D anatomical landmarks were extracted per vertebra (12 thoracic, 5 lumbar): center, left, right, anterior and posterior of superior and inferior vertebral endplates (10 landmarks); left and right transverse process (2 landmarks); spinous process (1 landmark); and tips of both pedicles (4 landmarks). All 3D spine models were normalized with regards to their height and rigidly translated to a common referential at the L5 vertebra. Hence, each observation contains 867 features, which corresponds to the concatenation of the 3D coordinates of all the landmarks into an observation vector.

2.2 Stacked Auto-encoders for Dimensionality Reduction

An auto-encoder is a neural network that learns a hidden representation to reconstruct its input. Consider a one hidden layer auto-encoder network. First, the input vector \(\mathbf {x}\) of dimension \(d\), representing the 3D coordinates of a spine model, is mapped by an encoder function \(f\) into the hidden layer \(\mathbf {h}\), often called a code layer in the case of auto-encoders:

$$\begin{aligned} \mathbf {h} = f(\mathbf {x}) = s(-\mathbf {W}^{(1)}\mathbf {x}+\mathbf {b}^{(1)})\ \end{aligned}$$
(1)

where \(\mathbf {W}^{(1)}\) is the encoding weight matrix, \(\mathbf {b}^{(1)}\) the bias vector and \(s(\cdot )\) the activation function. Note that this one hidden layer auto-encoder network corresponds to a principal component analysis if the activation function is linear. Then, the code representation is mapped back by a decoder function \(g\) into a reconstruction \(\mathbf {z}\):

$$\begin{aligned} \mathbf {z} = g(f(\mathbf {x})) = s(-\mathbf {W}^{(2)}\mathbf {h}+\mathbf {b}^{(2)})\ \end{aligned}$$
(2)

where \(\mathbf {W}^{(2)}\) is the decoding weight matrix. Tying the weights (\(\mathbf {W}^{(2)}=\mathbf {W}^{(1)^{T}}\)) has several advantages. It acts as a regularizer by preventing tiny gradients and it reduces the number of parameters to optimize [2]. Finally, the parameters \(\theta =\{\mathbf {W}^{(1)}, \mathbf {b}^{(1)}, \mathbf {b}^{(2)}\}\) are optimized in order to minimize the squared reconstruction error:

$$\begin{aligned} L_2(\mathbf {x}, \mathbf {z})=\Vert \mathbf {x} - \mathbf {z} \Vert ^{2}\ . \end{aligned}$$
(3)

In the case of dimensionality reduction, the code layer \(\mathbf {h}\) has a smaller dimension than the input \(\mathbf {x}\). One major drawback comes from the gradient descent algorithm for the training procedure that is very sensitive to the initial weights. If they are far from a good solution, training a deep non-linear auto-encoder network is very hard [6]. A pre-training algorithm is thus required to learn more robust features before fine-tuning the whole model.

The idea for initialization is to build a model that reconstructs the input based on a corrupted version of itself. This can either be done by Restricted Boltzmann Machines (RBMs) [6] or denoising auto-encoders [18] (used in this study). The denoising auto-encoder is considered as a stochastic version of the auto-encoder [18]. The difference lies in the stochastic corruption process that sets randomly some of the inputs to zero. This corrupted version \(\tilde{\mathbf {x}}\) of the input \(\mathbf {x}\) is obtained by a stochastic mapping \(\tilde{\mathbf {x}} \sim q_{D}(\tilde{\mathbf {x}}|\mathbf {x})\) with a proportion of corruption \(v\). The denoising auto-encoder is then trained to reconstruct the uncorrupted version of the input from the corrupted version, which means that the loss function in Eq. 3 remains the same. Therefore, the learning process tries to cancel the stochastic corruption process by capturing the statistical dependencies between the inputs [2]. Once all the layers are pre-trained, the auto-encoder proceeds to a fine-tuning of the parameters \(\theta \) (i.e. without the corruption process).

2.3 K-Means++ Clustering Algorithm

Once the fine-tuning of the stacked auto-encoder has learnt the parameters \(\theta \), low-dimensional codes from the code layer can be extracted for each patient’s spine. Clusters in the codes were obtained using the K-Means++ algorithm [1], which is a variant of the traditional K-Means clustering algorithm but with a selective seeding process. First, a cluster centroid is initialized among a random code layer \(\mathbf h \) of the dataset \(\chi \) following a uniform distribution. Afterwards, a probability is assigned to the rest of the observations for choosing the next centroid:

$$\begin{aligned} p(\mathbf {h})=\frac{D(\mathbf {h})^2}{\sum _{h \in \chi }D(\mathbf {h})^2} \end{aligned}$$
(4)

where \(D(\mathbf {h})^2\) corresponds to the shortest distance from a point \(\mathbf h \) to its closest cluster centroid. After the initialization of the cluster centroids, the K-Means++ algorithm proceeds to the regular Lloyd’s optimization method.

The selection of the right number of clusters \(k\) is based on the validity ratio [14], which minimizes the intra-cluster distance and maximizes the inter-cluster distance. The ratio is defined as \({ validity}={ intra/inter}\). The intra-cluster distance is the average of all the distances between a point and its cluster centroid:

$$\begin{aligned} \text{ intra } = \frac{1}{N}\sum ^{k}_{i=1}\sum _{\mathbf {x} \in C_{i}} \Vert \mathbf {h} - \mathbf {c}_{i} \Vert ^{2}. \end{aligned}$$
(5)

where \(N\) is the number of observations in \(\chi \) and \(\mathbf {c}_i\) the centroid of cluster \(i\). The inter-cluster distance is the minimum distance between cluster centroids.

$$\begin{aligned} \text{ inter } = \min (\Vert \mathbf {c}_{i} - \mathbf {c}_{j} \Vert ^{2}) \end{aligned}$$
(6)

where \(i = 1, 2,\ldots , k-1\) and \(j = i+1,\ldots , k\).

2.4 Clinical Data Analysis

Once clusters were created from the low-dimensional representation of the dataset, we analyzed the clustered data points with 3D geometric indices in the main thoracic (MT) and thoracolumbar/lumbar (TLL) regions for each patient’s spine. One-way ANOVA tested differences between the cluster groups with a significance level \(\alpha =0.05\). The p-values were adjusted with the Bonferroni correction. For all cases, the following 3D spinal indices were computed: the orientation of the plane of maximum curvature (PMC) in each regional curve, which corresponds to the plane orientation where the projected Cobb angle is maximal; the kyphotic angle, measured between T2 and T12 on the sagittal plane; the lumbar lordosis angle, defined between L1 and S1 on the sagittal plane; the Cobb angles in the MT and TLL segments; and the axial orientation of the apical vertebra in the MT region, measured by the Stokes method [16].

3 Clinical Experiments

3.1 Clinical Data

A cohort of 155 AIS patients was recruited for this preliminary study at our institution. A total of 277 reconstructions of the spine was obtained in 3D. From this group, 60 patients had repeat measurements from multiple clinic visits (mean \(=\) 3 visits). The mean thoracic Cobb angle was \(53.2\pm 18.3^{\circ }\) (range \(=11.2\)–\(100.2^{\circ }\)). All patients were diagnosed with a right thoracic deformation and classified as Lenke Type-1 deformity. A lumbar spine modifier (A, B, C) was also assigned to each observation, using the biplanar X-Ray scans available for each patient. The dataset included 277 observations divided in 204 Lenke Type-1A, 43 Lenke Type-1B and 30 Lenke Type-1C deformities. The training set included 235 observations, while the validation set included 42 observations (15 % of the whole dataset). Observations were randomly assigned in each set.

Fig. 1
figure 1

Illustration of the stacked auto-encoders architecture to learn the 3D spine model by minimizing the loss function. The middle layer represents a low-dimensional representation of the data, called the code layer. An optimal layer architecture of 867-900-400-200-50 was found after a coarse grid search of the hyper-parameters

Full size image

3.2 Hyper-Parameters of the Stacked Auto-Encoders

The neural network hyper-parameters were chosen by an exhaustive grid search. The architecture yielding to the lowest validation mean squared error (MSE) is described in Fig. 1. We used an encoder with layers of size 867-900-400-200-50 and a decoder with tied weights to map the high-dimensional patient’s spine models into low-dimensional codes. All units in the network were activated by a sigmoidal function \(s(a)=1/(1+e^{-a})\), except for the 50 units in the code layer that remain linear \(s(a)=a\).

Fig. 2
figure 2

Evolution of the mean squared error (MSE) with respect to the number of epochs to determine the optimal model described in Fig. 1

Full size image

3.3 Training and Testing the Stacked Auto-encoders

Auto-encoder layers were pre-trained and fine-tuned with the stochastic gradient descent method using a GPU implementation based on the Theano library [3]. Pre-training had a proportion of corruption for the stochastic mapping in each hidden layer of \(v=\{0.15, 0.20, 0.25, 0.30\}\) and a learning rate of \(\varepsilon _{0}=0.01\). Fine-tuning ran for 5,000 epochs and had a learning rate schedule with \(\varepsilon _{0}=0.05\) that annihilates linearly after 1,000 epochs. Figure 2 shows the learning curve of the stacked auto-encoder. The optimal parameters \(\theta \) for the model in Fig. 1 were found at the end of training with a normalized training MSE of 0.0127, and a normalized validation MSE of 0.0186, which corresponds to 4.79 and 6.46 mm\(^2\) respectively on the original scale. The learning curve describes several flat regions before stabilizing after 3,500 epochs.

3.4 Clustering the Codes

The K-Means++ algorithm was done using the scikit-learn library [12]. For each number of clusters \(k\) (2 through 9), the algorithm ran for 100 times with different centroid seeds in order to keep the best clustering in terms of inertia. Figure 3 depicts the validity ratio against the number of clusters. The validity ratio suggests that the optimal number of clusters should be 4 or 5. However, subsequent analysis illustrated in Table 1 indicates that 5 clusters is the right number of clusters for this dataset because all the clinical indices are statistically significant (\(\alpha =0.05\)) given that the other indices are in the model. Figure 4 presents the visualization of the five clusters using a PCA to project the codes in 3D and 2D views. However, it should be mentioned that the clustering was performed on the codes of dimension 50. Figure 5 shows the frontal, lateral and daVinci representations of the centroid of each cluster.

Fig. 3
figure 3

Validity ratio with respect to the number of clusters, to determine the optimal number of clusters

Full size image

3.5 Clinical Significance

Based on the five identified clusters, cluster 1 is composed of 50 Lenke Type-1A, 12 Type-1B and 2 Type-1C, representing hyper-kyphotic, hyper-lordotic profiles, with high curvatures in the sagittal plane. No sagittal rotation was detected in cluster 1. Cluster 2 is composed of 29 Lenke Type-1A, 7 Type-1B and 0 Type-1C, representing a high axial rotation of the apical vertebra, with the strongest thoracic deformation of all clusters. Moreover, those two clusters have no lumbar derotation.

Clusters 3, 4 and 5 represent the clusters with higher lumbar deformities. Cluster 3 includes 34 Lenke Type-1A, 17 Type-1B and 20 Type-1C, with a minimal thoracic deformation and the highest angulation of TLL plane of all clusters. Cluster 4 includes 23 observations, with 21 Lenke Type-1A, 2 Type-1B and 0 Type-1C. Cluster 4 is characterized by a hypo-kyphotic profile (mean = 7\(^{\circ }\)) and the highest angulation of the MT plane of all clusters. Finally, cluster 5 includes 70 Lenke Type-1A, 5 Type-1B and 8 Type-1C, with a low kyphosis, and medium range thoracic deformations. While this last cluster has a higher orientation of the thoracolumbar curve, its magnitude is not significant.

Table 1 Mean geometric clinical 3D parameters for the thoracic and lumbar regions, within all five clusters detected by the framework
Full size table
Fig. 4
figure 4

Visualization of the five clusters found by the K-Means++ algorithm on low-dimensional points, by projecting the 50-dimensional codes into 3 (a) and 2 (b) principal components (PC) using PCA

Full size image

Surgical strategies based on current 2D classification systems are suboptimal since they do not capture the intrinsic 3D representation of the deformation. Lenke Type-1 classification currently leads to selective thoracic arthrodesis. This very restrictive surgery treatment comes from the hard thresholds on the geometric parameters. A small change in Cobb angle could lead to two different classifications and to two different fusion recommendations subsequently [9]. Therefore, identifying groups based on their true 3D representation will help to better adjust surgery choices such as levels of fusion, biomechanical forces to apply or surgical instrumentations. In this study, the learning framework provided an optimal number of 5 clusters based on the input population. It is not possible at this stage to infer that Lenke Type-1 should be divided in 5 groups. However, this study confirms that within a defined 2D class currently used for surgical planning, there exists a number of sub-groups with different 3D signatures that are statistically significant. Therefore, each subgroup would lead to different surgical strategies. Previous studies have indicated that within Lenke Type-1 [5, 7, 15], there indeed exists 3D variability in terms of geometric parameters that could be divided in 4–6 sub-groups.

Fig. 5
figure 5

Frontal, lateral and top view profiles of cluster centers, with daVinci representations depicting planes of maximal deformities. a Centroid of cluster 1. b Centroid of cluster 2. c Centroid of cluster 3. d Centroid of cluster 4. e Centroid of cluster 5

Full size image

4 Conclusion

In this paper, we presented an automated classification method using a deep learning technique, namely with stacked auto-encoders, to discover sub-groups within a cohort of thoracic deformations. The code layer of the auto-encoder learns a distributed representation in low-dimension that aims to capture the main factors of variation in the training dataset. However, different examples from the distribution of the training dataset may potentially yield to high reconstruction errors [2]. Therefore, having a large and representative training dataset of AIS is critical. This will also prevent the model from overfitting.

The current study evaluated the 3D sub-classification of Lenke Type-1 scoliotic curves, suggesting that shape variability is present within an existing 2D group used in clinical practice. However, these types of approaches include complex synthetization tasks, which require sizeable datasets to improve the data representation within the code layer. Therefore, a multicentric dataset may help to significantly increase the number of cases from various sites and obtain a more reproducible model. Furthermore, the development of computational methods will ultimately lead to more reliable classification paradigms, helping to identify possible cases which might progress with time. Future work will include additional Lenke types, such as double major and lumbar deformations. Other works will propose to use longitudinal data for surgical treatment planning, whereas each observation is considered independently in the current framework. Finally, a reliability study will be undertaken to evaluate the relevance of classification systems.