ReliefF for Hierarchical Multi-label Classification

Abstract

In machine learning, the data available for analysis is becoming more complex both in terms of high-dimensionality and the way it is structured. This emphasises the need for developing machine learning algorithms that are able to tackle both the high-dimensionality and the complex structure of the data. Our work in this paper, focuses on extending a feature ranking algorithm that can be used as a filter method for a specific type of structured data. More specifically, we adapt the RReliefF algorithm for regression, for the task of hierarchical multi-label classification (HMC). We evaluate this algorithm experimentally in a filter-like setting by employing ensembles of predictive clustering trees for HMC as a classifier. In the experimental evaluation, we consider datasets from two prominent domains for HMC - functional genomics and image annotation. The results show that HMC-ReliefF can identify the relevant features present in the data and produces a ranking where they are placed among the top ranked ones.

1 Introduction

The current trend in machine learning is that the data available for analysis is becoming increasingly more complex. The complexity arises both from the data being high-dimensional and from the data being more structured. On one hand, high-dimensional data presents specific challenges for many machine learning algorithms, especially with the stability of the produced results [11]. On the other, mining complex data and extracting knowledge from it has been identified as one of the most challenging problems in machine learning [6, 17].

Various feature selection methods exist for dealing with the high-dimensionality of the data. They usually precede the induction of predictive models and can be classified as filter, wrapper and embedded methods [10]. Filter methods [3] are the simplest ones and they usually involve a feature ranking algorithm that produces a list of relevant features. Wrapper methods [15] rely on classification algorithms to perform feature selection and are computationally expensive. Embedded methods [10] are basically classification algorithms that have the feature selection embedded in the model induction phase.

Learning in a supervised context, where the target is structured, has also attracted much attention. Several algorithms that were previously employed only for classification or regression purposes, have been extended to also work with structured targets. These include decision trees for hierarchical targets [23], SVMs for multi-label and hierarchical multi-label problems [9], as well as tree ensembles that can be additionally employed for vectors of multiple targets [14].

Our work in this paper focuses on tackling the feature selection problem in the context of structured targets. We consider this a relevant problem in machine learning that relates to both of the previously discussed trends. So far, structured prediction has not been extensively researched in the context of feature ranking methods and we consider this a novel and interesting line of work to pursue.

More specifically, we focus on the ReliefF [20] algorithm for feature ranking. This algorithm is an intuitive, instance based algorithm and its theoretical properties have been extensively explored [20]. We extend ReliefF for a specific type of structured prediction problems, namely those from the Hierarchical Multi-Label Classification (HMC) domain [21]. The target that is predicted for these problems is defined with a hierarchy of classes and each instance in the dataset can be labelled with more than one class at a time. By definition, when an instance is labelled with one class it is also labelled with all of its parent classes according to the given hierarchy.

In practice, this type of problems appear in different domains, for example in biology for the task of gene function prediction or in image retrieval for the task of image annotation. For the task of gene function prediction, each gene can be annotated by multiple functions and the functions are organised into a tree-shaped hierarchy or a directed acyclic graph such as the Gene Ontology [2]. Thus, predicting the function of a gene from certain gene properties would have to take into account the multi-label annotation of each gene and also the hierarchical connections of these labels.

In the remainder of this paper, we present the details of our work organised as follows. In Sect. 2, we define more formally the HMC setting and present the distance measures appropriate for this setting. Next, in Sect. 3, we discuss in depth the original RReliefF algorithm for regression and explain our HMC-ReliefF extension of the algorithm. We present our experimental evaluation of the proposed HMC-ReliefF algorithm in Sect. 4. Finally, in Sect. 5, we present our conclusions and discuss directions of possible further work.

2 Hierarchical Multi-label Classification

In our work we extend the ReliefF algorithm for the task of hierarchical multi-label classification (HMC). Hierarchical classification is a specific type of a classification task in which the classes are organised in a hierarchy. An example that belongs to a given class automatically belongs to all its super-classes (this is known as the hierarchy constraint). Furthermore, if an example can belong simultaneously to multiple classes that can follow multiple paths from the root class, then the task is called hierarchical multi-label classification (HMC) [21, 23].

We formally define the hierarchical multi-label classification setting as follows:

• A description space $X$ that consists of tuples of values of primitive data types (discrete or continuous), i.e., $\forall X_{i} \in X, X_{i} = (x_{i_{1}},x_{i_{2}}, ...,x_{i_{D}})$, where $D$ is the size of the tuple (or number of descriptive variables),

• a target space $S$, defined with a class hierarchy $(C, \le _{h})$, where $C$ is a set of classes and $\le _{h}$ is a partial order (e.g., structured as a rooted tree) representing the superclass relationship ($\forall \ c_{1}, c_{2} \in C: c_{1} \le _{h} c_{2}$ if and only if $c_{1}$ is a superclass of $c_{2}$),

• a set $E$, where each example is a pair of a tuple and a set, from the descriptive and target space respectively, and each set satisfies the hierarchy constraint, i.e., $E = \{(X_{i}, S_{i})| X_{i} \in X, S_{i} \subseteq C, c \in S_{i} \Rightarrow \forall c^\prime \le _{h} c:c^\prime \in S_{i}, 1 \le i \le N \}$ and $N$ is the number of examples in $E$ ($N = |E|$)

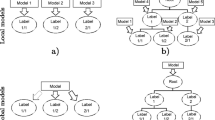
Two toy examples of classes organised in hierarchies can be seen in Fig. 1. The first hierarchy in Fig. 1(a) consists of five classes $\{c_1, c_2, c_3, c_{2.1}, c_{2.2}\}$, organised in a tree-like structure. The other hierarchy in Fig. 1(c), contains six classes ($c_1- c_6$) and they are organised in a directed acyclic graph (DAG), where each class can have multiple parents.

Calculating the distance between two different instances of the target space $S_1$ and $S_2$, can be done in different ways. These distances include: a weighted Euclidean distance for HMC [23], Jaccard distance (also known as Union-intersection distance/score) [12], simGIC (Similarity for Graph Information Content) [18] and ImageCLEF (evaluation score of the ImageCLEF image annotation task) [5]. An experimental evaluation comparing these distances in the context of HMC [1] has shown that learning predictive models that use the different distances, does not produce statistically significant differences in predictive performance.

Fig. 1.

Toy examples of hierarchies structured as a tree and a DAG. (a) Class label names contain information about the position in the hierarchy, e.g., $c_{2.1}$ is a subclass of $c_{2}$. (b) The set of classes $S_{1} = \{c_{1},c_{2},c_{2.2}\}$, shown in bold in the hierarchy, represented as a vector ($L_{k}$). (c) A class hierarchy structured as a DAG. The class $c_{6}$ has two parents: $c_{1}$ and $c_{4}$.

In our work, we chose to extend the RReliefF algorithm by using a weighted Euclidean distance for HMC [23]. With this weighted Euclidean distance, the hierarchical aspect is incorporated by relating the class weight with the depth of the class within the hierarchy. Extending RReliefF with this distance is the most straightforward choice, considering that the original algorithm uses the Euclidean distance for calculating the distance for the target variable.

Before calculating the distance between two instances of the hierarchy, they are first represented as a vector of binary values [23]. The vector is created by traversing the tree or DAG that is representing the hierarchy in pre-order and assigning a 1 or 0 sequentially in the vector for a present or absent label respectively. For example, consider an instance of the toy class hierarchy $S_1$, given in boldface in Fig. 1(b). This particular instance consists of three classes, namely $\{c_1, c_2, c_{2.2}\}$ and its corresponding vector representation would be $L_1 = [1, 1, 0, 1, 0]$.

If we additionally consider another instance $S_2$, labelled just with class $\{c_2 \}$, with a vector representation $L_2 = [0, 1, 0, 0, 0]$, then the distance between $S_1$ and $S_2$ would be obtained by simply comparing the two binary vectors. In our HMC-ReliefF algorithm we use a weighted Euclidean distance measure given with the following equation:

$$\begin{aligned} d(L_{1},L_{2}) = \sqrt{\sum _{i} w(c_{i})(L_{1,i}- L_{2,i})^2}, \end{aligned}$$

(1)

The weighting function $w(c)$ allows for the hierarchical structure of the classes to be taken into account by making the value dependent on the depth of the hierarchy:

$$\begin{aligned} w(c) = w_{0}^{depth(c)}, 0 < w_{0} < 1 . \end{aligned}$$

(2)

This scheme ensures that the differences higher in the hierarchy have larger influence on the total distance.

For the specific case of comparing $S_1$ and $S_2$, the distance is calculated as follows:

$$\begin{aligned} d(S_1,S_2) = d([1,1,0,1,0],[0,1,0,0,0]) = \sqrt{w_0+w_0^2}. \end{aligned}$$

where $w(c_1) = w_0$ and $w(c_3) = w_{0}^2$.

If the hierarchy is represented with a DAG, this scheme needs to be modified. In this case, more than one path from the root to a given class may exist and thus a node can have different depths. This problem is solved with the following recursive equation:

$$\begin{aligned} w(c) = w_{0} \cdot avg(w(parent_{j}(c))). \end{aligned}$$

(3)

By using this weighting function, the weight of the different possible parents is averaged. This is recommended [23] as a good way to take into account multiple inheritance which occurs in DAGs.

3 HMC-ReliefF Algorithm

Algorithms from the Relief family are instance-based methods for estimating feature relevance. The original Relief algorithm [13] is formulated for binary classification problems. The algorithm was extended [16] to deal with multi-class problems and the extension was named ReliefF. Later, it was also adapted for regression problems [19] and named RReliefF.

In general, the feature relevance value assigned by the Relief algorithm to a feature $F$ is an approximation of the following difference of probabilities [16]:

$$\begin{aligned} W[F]&= P(\text {diff. value of } F \vert \text {nearest inst. from diff. class}) - \\ \nonumber&\quad P(\text {diff. value of }F \vert \text {nearest inst. from same class}) \end{aligned}$$

(4)

In the case of classification, the basic intuition behind the ReliefF algorithm is to estimate the relevance of a feature according to how well it distinguishes between neighbouring instances. If the feature has different values for neighbouring instances that are of different class (nearest miss), then it is awarded a higher relevance values. However, if the values of the class for the neighbouring instances are the same (nearest hit), then the relevance value is decreased.

Although the hierarchical multi-label setting is a classification one, extending the ReliefF algorithm is not a good idea. Namely, if we simply treat two instances annotated by different parts of the hierarchy in a simple hit/miss scenario, we would simply translate the HMC problem to a multi-class one, therefore ignoring both the hierarchical and the multi-label aspect. Having in mind that the definition of the HMC distance in Sect. 2 is actually weighted Euclidean, it is more suited to be included in the RReliefF algorithm, originally designed for regression.

In a regression setting, the target space is continuous and the concept of nearest hit/miss does not apply. Therefore, the feature relevance $W[F]$ is reformulated as the difference between the following probabilities:

$$\begin{aligned} W[F]&= P(\text {diff. value of } F \vert \text {nearest inst. with diff. prediction}) - \\ \nonumber&\quad P(\text {diff. value of }F \vert \text {nearest inst. with same prediction}) \end{aligned}$$

(5)

Additionally, if we introduce the following probabilities:

$$ P_{diffF}(\text {diff. value of F} \vert \text {nearest instance}) $$

and

$$ P_{diffC}(\text {diff. prediction} \vert \text {nearest instance}), $$

as well as the conditional probability:

$$ P_{diffC \vert diffF}(\text {diff. prediction} \vert \text {diff. value of F and nearest instances}). $$

Finally, by using the Bayes rule, we obtain:

$$\begin{aligned} W[F] = \frac{P_{diffC|diffF}P_{diffF}}{P_{diffC}} - \frac{(1 - P_{diffC|diffF})P_{diffF}}{1 - P_{diffC}} \end{aligned}$$

(6)

The details of the RReliefF algorithm are given in pseudocode form in Algorithm 1. The algorithm begins by selecting a random instance ($R_i$) and finding the $k$ nearest instances $I_j$ to it. From these instances, it then approximates the relevance $W[F]$ from Eq. 6 of each feature by calculating $N_{dC}$, $N_{dF}[F]$ and $N_{dC \& dF}[F]$, described in lines 6,8 and 9 of Algorithm 1. The estimations of these values is based on the distance calculation in the feature space, $diff(F,R_i,I_j)$, (lines 8 and 9) and in the target space, $diff(\tau (\cdot ),R_i,I_j)$, (lines 6 and 9).

Our original purpose is to extend the RReliefF algorithm for hierarchical multi-label classification problems. Considering that the HMC refers to the target space, we extend the RReliefF algorithm by changing the way that $diff(\tau (\cdot ),R_i,I_j)$, from lines 6 and 9, is calculated. From Sect. 2 and Eq. 1 we obtain:

$$\begin{aligned} diff(\tau (\cdot ),R_i,I_j) = diff(S_i,S_j) = \sqrt{\sum _{k} w(c_{k})(L_{i,k}- L_{j,k})^2} \end{aligned}$$

(7)

where $S_i$ and $S_j$ are the target descriptions of $R_i$ and $I_j$ correspondingly, while $L_{i,k}$ and $L_{j,k}$ are their binary representations. In this way, by changing the way the distance is calculated, the original RReliefF algorithm is extended to work for HMC problems and we name this extension HMC-ReliefF.

4 Experiments

Our experimental evaluation of the HMC-ReliefF is based on the intuition of what is the expected output of a good feature ranking algorithm. Namely, a good feature ranking algorithm would output the relevant features on top of the ranked list of features. A bad ranking algorithm would not necessarily be the one that gives an inverse ranking according to relevance, but the one that outputs a random ranking. In the random ranking, the distribution of the relevant features is expected to be uniform throughout the list.

Having this in mind, we employ a stepwise filter-like procedure [22] to evaluate our HMC-ReliefF algorithm. The idea is that starting from the ranked list of features, we construct classifiers for different numbers of top-$k$ ranked features. If there are relevant features on top of the feature ranking, then we can construct a classifier that has a good predictive performance. If the ranking is random then the number of relevant features in the top-$k$ ranked features is expected to be smaller.

Formally, if we have a feature ranking algorithm $r$ that we use on a dataset $\fancyscript{D}$, then the output would be a feature ranking $\mathbf {R}$, namely:

$$ r (\fancyscript{D}) \rightarrow \mathbf {R} . $$

The feature ranking $\mathbf {R}$ is defined as an ordered list of features $F$, more specifically:

$$ \mathbf {R} = (F_{r1}, \dots , F_{rj}, \dots , F_{rk}) $$

where:

$$\begin{aligned} rank(F_{r1}) \le \dots \le rank(F_{rj}) \le \dots \le rank(F_{rk}) \end{aligned}$$

If we assume that we can induce and evaluate a predictive model $\fancyscript{M}(R_i, F_t)$, where $R_i \subseteq \mathbf {R}$ and $F_t$ is a target feature, then our whole evaluation procedure can be described as in Algorithm 2.

For each step $k$ of the filtering, i.e., for each subset of top-$k$ ranked feature subsets, we induce a classification model and evaluate its performance. This process of generating feature sets from the feature ranking is performed in a forward manner, by adding more and more of the top ranked features, which we name forward feature addition (FFA). At the end, we obtain a vector of model quality estimates that we can plot as a curve, thus obtaining a FFA curve that we use to estimate the performance of the feature ranking algorithm. In order to say that the FFA curve of a certain feature ranking algorithm is better than that of a random ranking, the model quality estimates of the ranking must be larger than those of the models from the random ranking. Visually, this would mean that the FFA curve of the algorithm would be above the FFA curve of the random ranking.

4.1 Experimental Setup

In the HMC-ReliefF algorithm, given in Algorithm 1, there are two basic parameters that can be specified by users and which influence the relevance estimation. These are the number of random instances $m$ that are chosen and the number of nearest neighbours $k$ that are used to calculate the feature relevance values. Therefore, in our experiments, we decided to explore a reasonable set of values of these parameters in order to evaluate the algorithm performance.

For the number of random instances $m$, instead of considering an absolute number, we consider sampling a percentage of the datasets instance space, while for the number of nearest neighbours $k$ we consider absolute values. More specifically, we consider the following parameters:

• $m =\{ 1\,\%, 5\,\%, 10\,\%, 20\,\%, 25\,\% \}$

• $k = \{5, 10, 25, 50 \}$.

As a baseline for our comparisons, we use a set of 50 random rankings for each different dataset. For each of these rankings, we perform the previously described procedure in Sect. 4 and generate a separate FFA curve. For the random rankings, we average the results of the 50 individual FFA curves, thus generating an expected FFA curve for a given dataset.

Table 1. Properties of the datasets with hierarchical targets; $N_{tr}$ is the number of instances in the training dataset, $D/C$ is the number of descriptive attributes (discrete/continuous), $|\fancyscript{H}|$ is the number of classes in the hierarchy, $\fancyscript{H}_{d}$ is the maximal depth of the classes in the hierarchy, $\overline{\fancyscript{L}}$ is the average number of labels per example, and $\overline{\fancyscript{L}}_{L}$ is the average number of leaf labels per example. Note that the values for $\fancyscript{H}_{d}$ are not always a natural number because the hierarchy has a form of a DAG and the maximal depth of a node is calculated as the average of the depths of its parents.

As a predictive model which we induce and evaluate, we use random forests of so-called predictive clustering trees for hierarchical multi-label classification (PCT-HMCs) [14, 23]. The specific parameters that we used for the random forests of PCTs were 100 trees and a feature subset size of 10 % of the all features in the dataset. For estimating the PCT-HMCs performance, we use ten-fold cross validation.

In the HMC context, there are various error measures that can be considered. We use the area of a variant of a precision-recall curve, namely the Pooled Area Under the Precision-Recall Curve ($AU(\overline{PRC})$), details discussed in [23]. For this measure, the precision and recall are micro averaged for all classes from the hierarchy. In the datasets domains that we consider, the positive examples for a given class are only few as compared to the negative ones. The Precision-Recall evaluation of these algorithms is most suitable in this context, because we are more interested in correctly predicting the positive examples (i.e., that an example belongs to a given class), rather than correctly predicting negative instances.

For the experiments, we use datasets from two domains which have classes organised in a hierarchy. We use 6 datasets from 2 domains, more specifically: biology (Yeast-GO [4], SCOP-GO [4] and SCOP-FUN [4]) and image annotation/classification (Diatoms [8], ImCLEF07D [7] and ImCLEF07A [7]). The relevant properties that characterize each dataset are given in Table 1. Note that the Yeast-GO and the SCOP-GO datasets have a hierarchy organised as a DAG, while the remaining datasets have tree-shaped hierarchies. For more details on the datasets, we refer the reader to the referenced literature.

4.2 Results and Discussion

In this section, we present the results from our experimental evaluation. In Fig. 2, we give the FFA curves for the datasets from the image annotation domain, while in Fig. 3, we present the FFA curves for datasets from the functional genomics domain. The graphs on the left-hand side of Figs. 2 and 3 represent the FFA curves for a fixed value of $m$, while the value of $k$ is varied. Correspondingly, the graphs on the right-hand side contain FFA curves for a fixed value of $k$, while the value of $m$ is varied. The fixed values of $m$ and $k$ are chosen for the best FFA curves.

Overall, it can be observed that all of the FFA curves of the HMC-ReliefF algorithm are most of the time above the FFA curves of the random rankings. This means that at the top of the rankings produced by HMC-ReliefF, for different settings of $m$ and $k$, relevant features can be found. It also means that this is not by chance, as the $AU(\overline{PRC})$ of the produced models is larger than the expected value of a random ranking. However, there are differences in the obtained curves for the different datasets, which we will discuss in detail.

Fig. 2.

Comparison of different FFA curves obtained by varying the number of $m$ and $k$ for datasets from the image annotation domain

Fig. 3.

Comparison of different FFA curves obtained by varying the number of $m$ and $k$ for datasets from the functional genomics domain

We first consider the datasets from the image annotation domain, given in Fig. 2. It can be noticed that all of the FFA curves produced by HMC-ReliefF, are only slightly higher, i.e., are only slightly better, than the expected FFA curves of the random rankings. Also, there is no great variability of the FFA curves with respect to the different number of $m$ and $k$. This is expected if we take into account this specific domain and the way the features are produced. Namely, most of the features are image descriptors, which are informative about the image and most of them are relevant. This can also be concluded if we observe just the expected FFA curve of the random rankings.

Next, if we consider the results from the functional genomics domain in Fig. 3, a more complex interpretation is necessary. First, the FFA curves of the Yeast-GO dataset in Fig. 3a and b, show only slight improvement over the random FFA curves at the beginning of the ranking (top 1 % of the features). After that, seemingly irrelevant or redundant features are added, up to 75 % of the features. After this point there is a jump in the number of relevant features that are added, as the $AU(\overline{PRC})$ values become larger. For a fixed $k$ in Fig. 3b, this effect is more pronounced as the percent of sampled instances $m$ increases.

Upon closer inspection of the produced rankings of the Yeast-GO dataset, all of the numerical features were located among the top-ranked 1 % of the features and the bottom 25 % of the features, while the binary features were in the remaining part of the ranking. Although most of the numerical features were relevant, the corresponding relevance values for part of them seemed to be underestimated. This problem of underestimation of numerical attributes was also noted by Robnik-Šikonja and Kononenko [20], especially in the domains with both numeric and nominal features. To alleviate this issue, the use of a ramp function was proposed when calculating the distance between the numerical attributes. In our implementation a ramp function was also used, however different threshold parameters of this function were not explored. Robnik-Šikonja and Kononenko in [20], noted that for different domains, different thresholds might be appropriate and we believe that this is the probable cause of the underestimation of the relevance for part of the numeric features.

The FFA curves of the SCOP-FUN dataset, in Fig. 3c and d are the only ones that show variability of the curves with respect to $m$ and $k$. Unlike the other datasets, the best FFA curves were obtained for a small number of $m$ and of $k$. This is consistent with the analysis of ReliefF in [20] where it is stated that the values of $m$ and $k$ are often problem dependent and often smaller values might be better in order to preserve “locality” of the relevance estimations.

The best results were obtained for the SCOP-GO dataset, which we present in Fig. 3e and f. Both for a fixed $m$ and $k$, the values of the FFA curves produced by HMC-ReliefF are much higher than those of the random rankings. For a fixed $m$ varying the values of $k$ does not influence the results (Fig. 3e). For a large fixed $k$, there is only a difference for the FFA curve produced for $m = 1\,\%$ of the instance space, which produces lower $AU(\overline{PRC})$ values than the other values of the parameter $m$.

5 Conclusions and Further Work

In this paper, we presented the HMC-ReliefF algorithm, which is an extension of the RReliefF algorithm for the task of Hierarchical Multi-label Classification. We believe that this is both an interesting and novel line of work, in the context of feature ranking algorithms. To the best of our knowledge, there has not been any work for feature ranking within the context of structured data. We specifically focused on the ReliefF algorithm, due to its success in both classification and regression settings. The specific type of structured problems that we considered (HMC), was motivated by the fact that this kind of data can be found in various domains including biology and image annotation.

We evaluated the HMC-ReliefF algorithm on datasets from different domains and with different properties of the hierarchies. We first investigated if our algorithm was able to detect relevant features in a dataset and put them on top of the ranking. We consider this to be a minimum requirement of any feature ranking algorithm. Additionally, we also explored a reasonable set of parameter settings of HMC-ReliefF, which have influence on the feature relevance estimations.

The results of our experiments showed that, for various datasets, the HMC-ReliefF algorithm performed well, as evaluated by a stepwise filter like approach of constructing FFA curves. This performance was compared to an expected FFA curve, obtained from a set of random rankings. The exploration of the various parameters of HMC-ReliefF showed the following. For the image annotation datasets, large values of $m$ and $k$ were preferred and the FFA curves did not show much variability with respect to the parameters. The FFA curves produced by HMC-ReliefF were above the expected FFA curves with small differences. This was due to the nature of the domain and due to the fact that most of the features in the image annotation datasets were relevant.

For the functional genomics datasets, the results were more complex. The effect of underestimation of relevance of numeric features with respect to binary ones was observed, which has also been noted in the original ReliefF. The FFA curves of one of the datasets, were sensitive to the change of $m$ and $k$, producing better FFA curves for smaller values. Finally, the last investigated dataset from this domain provided the best FFA curves, with values significantly larger than those of the expected FFA curves.

With this paper and the results presented we performed an initial investigation of the HMC-ReliefF algorithm. The directions for further work regarding our HMC-ReliefF algorithm are numerous. One major direction would be to define an artificial, controlled setting for investigating HMC problems in the context of feature ranking. Different types of hierarchies should be considered, which are also differently structured (balanced vs. unbalanced, different width, different depth), or differently populated by instances (sparse vs. non-sparse). Within this setting, the effects of the various parameters of HMC-ReliefF can be investigated and the advantages and limitations of the algorithm can be explored. Another major direction is to consider different types of structured outputs, such as multi-label or multi-target classification.