Feature Selection for Hierarchical Multi-label Classification

Abstract

In this work we study how conventional feature selection methods can be applied to Hierarchical Multi-label Classification Problems. In Hierarchical Multi-label Classification, instances can belong to two or more classes (labels) simultaneously, where such classes are hierarchically structured. Feature selection plays an important role in Machine Learning classification tasks, once it can effectively reduce the dataset dimensionality by removing irrelevant and/or redundant features, improving classification accuracy. Although many relevant real-world problems are from the hierarchical and multi-label domains, the majority of the related researches address the feature selection task focusing on single-label problems. In many works, even when the proposal deals with multi-label problems, the classes are not associated with a hierarchical structure. Therefore, in this work we study how feature selection can be applied in the Hierarchical Multi-label Classification context. For this, we propose four hierarchical strategies combining the Binary Relevance (BR) and Label Powerset (LP) multi-label transformations with the attribute evaluators ReliefF (RF) and Information Gain (IG). We tested our strategies on 10 real-world datasets from the functional genomic field, commonly used in Hierarchical Multi-label Classification works. As main results, three of the four proposed strategies produced some relevant subsets of features, while keeping predictive performances in comparison to the use of the complete set of features.

1 Introduction

In the majority of the classification tasks found in the literature, a single class is assigned to a given instance, and the classes of the problem assume a flat (non-hierarchical) structure [2]. However, in several real-world problems, the classes are organized in superclasses and subclasses, forming a hierarchical taxonomy. As an example, a protein complex or organelle can be categorized in a class taxonomy associated with its cellular localization in the Gene Ontology [4]. Other examples can be found in Botanic and Zoology, where classification structures of living beings are hierarchically organized, or in the musical field, where songs can be assigned to many genres and sub-genres.

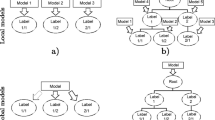
These kind of classification problems are known in the Machine Learning (ML) literature as Hierarchical Multi-label Classification (HMC), a special case of Hierarchical Classification (HC), due to the fact that an instance can be assigned to two or more paths in the hierarchy simultaneously. According to the problem domain, a hierarchical structure can be represented as a Tree or as a Directed Acyclic Graph (DAG).

In hierarchical problems where the taxonomy is a tree-shaped structure (Fig. 1a), each class node has only one parent node, which means that each class has a single depth value (number of edges between the root node and a given node). Hence, there is just one possible path between the root and any other node. On the other hand, in DAG-shaped structures (Fig. 1b), a given class node can have more than one parent node, which means a class can have multiple depth values, since there may be several paths between the root node and another hierarchical node. These hierarchical characteristics should be considered in the development and evaluation of hierarchical classifiers.

Fig. 1.

Adapted from [14].

Hierarchical structures.

Definition: Considering X the space of instances, the HMC problem consists of finding a function (classifier) f to map each instance $\mathbf{x}_i$ $\in$ X to a set of classes $C_i \in C$, with C the set of all classes in the problem. The function f must respect the constraints of the hierarchy, and optimize a quality criterion [2].

The hierarchy constraint states that when a class is predict, all its superclasses should also be predicted. As an example, in Fig. 1a, an instance classified in class 2.1.1 should also be classified in classes 2.1 and 2.

In classification problems, Feature Selection (FS) plays an important role, since it can effectively reduce the dimensionality of data by removing irrelevant and/or redundant features, improving classification performance. Although there are many real-world problems that are hierarchical and multi-label, the majority of the FS methods in the literature deal only with single-label problems. In addition, although there are works proposing FS methods for multi-label problems, they focus on non-hierarchical scenarios. Thus, we investigate here how FS can be applied to Hierarchical Multi-label Classification, focusing on tree-shaped hierarchies. We rely on the work of Spolaôr et al. [17] to propose strategies combining the Binary Relevance (BR) and Label Powerset (LP) multi-label transformations with the attribute evaluators ReliefF (RF) and Information Gain (IG).

The remainder of this paper is organized as follow. Section 2 defines the general Feature Selection task and presents the methods used in this work; Sect. 3 presents an overview of the related works in the literature, while Sect. 4 describes our proposed strategies for FS in HMC problems; Sect. 5 details our methodology, with the datasets and evaluation measures used; in Sect. 6 the experiments are presented and discussed; finally, in Sect. 7 we present our conclusions and future research directions.

2 Feature Selection

Feature Selection (FS) aims at finding a minimum number of attributes which describe a dataset as well as the original feature space. It is a pre-processing step, performing an important role in Machine Learning classification problems, once it reduces the feature space by removing redundant or irrelevant attributes, reducing training time while increasing or keeping predictive performance [10, 21].

In general, there are three basic FS approaches: Filter, Wrapper and Embedded. While the Embedded approach performs the FS within the training process of a specific algorithm [8], the Wrapper approach requires a specific learning algorithm to evaluate and determine which features to select. This approach tends to find features better suited for the specific learning algorithm. However it has a high computational cost.

Filter-based FS methods are widely used due to their efficiency and low complexity. This method scores the attributes using some criterion and discards those who weren’t selected. Different from Wrappers, they do not require the use of a learning algorithm to evaluate the features.

Among the different criteria used in the Filter approach to evaluate the importance of an attribute, ReliefF and Information Gain are very popular for single-label classification. Since we used them in our proposal, they are briefly described in the next sections.

2.1 ReliefF

The original Relief attribute estimator is limited to deal with two class problems. Its key idea is to estimate the quality of an attribute according to how well its values distinguish between instances that are near to each other. The ReliefF (RF) algorithm overcomes this limitation, being more robust and dealing with incomplete and noisy data. For that purpose, given a randomly selected instance $R_i$, RF searches for its k nearest neighbors from the same class, called nearest hits ($H_j$), and also the k nearest neighbors from each of the different classes, called nearest misses $M_j(C)$. It updates the quality estimation W[A] for all attributes A depending on their values for $R_i$, $H_j$ and misses $M_j(C)$. The contribution for each class of the misses is weighted with the prior probability of that class P(C) (estimated from the training set) [13]. The parameter k for hits and misses is the basic difference from the original Relief, and ensures greater robustness of the algorithm concerning noise. The whole process is repeated m times, where m is a user-defined parameter. For more details on ReliefF, please refer to the work of Robnik-Šikonja and Kononenko [13].

2.2 Information Gain

Information Gain (IG) is a measure based on the concept of entropy. It measures the dependency between each feature of a space of instances and a single class label. It ranks features ($a_j$) based on their amount of information; the higher is the IG value for a feature $a_j$, the stronger is the relationship between that feature $a_j$ and the label. The Information Gain measure is calculated by the difference between the entropy of a dataset D and the weighted sum of each subset $D_v \subseteq D$, where $D_v$ consists of the set of instances where $a_j$ has the value v. Therefore, if $a_j$ has 10 distinct values in D, the sum would be applied to 10 different $D_v$ datasets. For details please refer to Spolaôr et al. [18].

3 Related Work

Although scarce in the hierarchical multi-label scenarios, multi-label feature selection has gained attention from the machine learning, statistical computing and related communities. This section briefly describes some related works proposed for multi-label classification in non-hierarchical and hierarchical scenarios.

In the work of Amazal et al. [1], the authors address the multi-label feature selection task proposing a weighted Chi-square feature selection approach called Distributed Category Term Frequency Based on Chi-square (CTF-CHI), and used a Multinominal Naive Bayes (MNB) classifier to evaluate the efficiency of a selected subset of features. The authors performed feature selection by transforming the original problem into a single-label one.

Gao et al. [6] proposed a multi-label feature selection method named Feature Redundancy Maximization (FRM) to deal with the problem of overestimating the redundancy of some candidate features, entailed by traditional multi-label feature selection methods which employ the cumulative summation strategy.

Petkovic et al. [12] investigated two groups of feature ranking for multi-target regression (MTR) tasks, by studying the feature ranking scores (Symbolic, Genie3, and Random Forest scores) based on ensembles (bagging, random forest, extra trees) of predictive clustering trees, and a score derived of the RReliefF method. MTR problems consist of multiple continuous target variables, where the goal is to learn a model for predicting all of them simultaneously.

Slavkov et al. [15] address feature ranking in the context of HMC problem by focusing in the ReliefF feature importance estimator, a continuation of author’s previous work [16]. The authors tested their propose on five datasets from the biology and image fields, and obtained better results when compared with a feature ranking algorithm based on BR.

Still in feature ranking, Petkovic et al. [11] extended his work on Multi-target regression [12] for HMC. They applied a group of feature ranking approaches based on the Symbolic, Genie3 and Random Forest scoring functions, coupled with Bagging, Random Forest and Extra Trees ensembles of PCTs. The authors evaluated their approaches on 30 HMC benchmark datasets by using a kNN model that considers feature importance scores in the distance function. The results obtained outperformed the HMC-Relief feature ranking method, and demonstrated that Symbolic and Genie3 yield relevant feature rankings.

4 Applying Feature Selection in HMC

In this section we introduce our proposal for applying FS in HMC problems. We first briefly introduce the Binary Relevance (BR) and Label-Powerset (LP) multi-label transformations, which are used in our proposal.

4.1 Binary Relevance

Binary Relevance (BR) consists in learning a different classifier for each class of the problem. The original multi-label problem is transformed into |C| binary problems, where C is the set of classes from the original problem. The i-th ($i = 1 \dots |C|$) classifier decides if an instance belongs to the i-th class [5]. A final multi-label classification is then obtained combining the single-label predictions.

4.2 Label Powerset

Label Powerset (LP) considers each subset of classes from C as a new and unique class, forming a single-label multi-class problem. One multi-class classifier is trained for the new problem. Given a new instance, the classifier predicts its most probable class, which represents a set of classes. Unlike BR, LP considers the correlation among labels, but since the transformation increases the number of classes, these can end having very few positive instances [7].

4.3 Our Proposal

We use the work of Spolaôr et al. [17], which combines the BR and LP transformations with ReliefF (RF) and Information Gain (IG), resulting in four non-hierarchical multi-label feature selection methods:

• RF-BR: ReliefF based on the BR transformation;

• RF-LP: ReliefF based on the LP transformation;

• IG-BR: Information Gain based on the BR transformation;

• IG-LP: Information Gain based on the LP transformation.

We focus on HMC problems with hierarchies structured as trees. Since each hierarchical level can be considered a multi-label non-hierarchical problem (see Fig. 1a), we apply the four above methods in each level. The selected features for each level are then combined to form a new hierarchical dataset. This results in four different strategies for FS in HMC.

Let D be a Hierarchical Multi-label Dataset, with X denoting the space of instances, Y denoting the space of classes, A denoting the space of attributes, and n denoting the number of levels of the hierarchy.

We first apply a pre-processing in the tree structure level by level, transforming a HMC dataset in n non-Hierarchical (flat) Multi-label (nHMC) datasets. We thus have a new flat multi-label dataset for each of the n levels of the hierarchy. We name each of these n flat datasets as datalevels. Each datalevel inherits the original feature space A of the problem. The i-th datalevel, with $i = \{1, \dots , n\}$, contains the instances which are classified in the classes located in the i-th level of the original dataset D. To deal with the hierarchy constraint (mentioned in Sect. 1), the instances classified in classes located in the i-th level are also assigned to their superclasses. Thus, if an instance is in datalevel i, it is also in all the previous $i-1$ datalevels. As an example, in Fig. 1a, we would have three datalevels, and the instances belonging to the third datalevel (level 3) would also belong to the second (level 2) and first (level 1) datalevels simultaneously.

In a second step, we apply one the FS methods (RF-BR, RF-LP, IG-BR, IG-LP) to all datalevels. These methods return, for each feature, a score representing the importance of that feature. Thus, the features of a datalevel are sorted in a descending order according to the values of their scores. We have now to apply a score threshold in order to select a given number of features.

The choice of an optimal threshold for each datalevel is not trivial, since each datalevel has specific characteristics, such as different numbers of attributes from different domains and contexts. Low threshold values may lead to the selection of many no relevant or redundant features. In the other hand, high threshold values may leave behind relevant attributes by selecting a very small set.

Since we are not interested in selecting specific features, but instead we want to evaluate the ability of our proposal in selecting features, we adopt a different strategy to choose thresholds. We use a boxplot to analyze the position, dispersion, and symmetry regarding the attributes after obtaining their scores for each FS method applied to each datalevel. We consider features with a score above 0.

By putting all scores in a boxplot, we can analyze different numbers of selected features without having to directly apply a threshold. We select 100% of the features (corresponding to the interval between the worst and the best score), the features in the interval between the first quartile and the best score, the features in the interval between the median and the best score, and finally the features in the interval between the third quartile and the best score.

After selecting features for each level independently, a third step generates a new HMC dataset, where the new feature space A’ is the union of all the features selected in all datalevels. We execute the previous steps for each of the FS methods RF-BR, RF-LP, IG-BR and IG-LP.

Finally, we induce a Hierarchical Multi-Label classifier in the new hierarchical dataset having the reduced number of features. In our experiments, we employed Clus-HMC [19], one of the state-of-the-art HMC methods in the literature. Figure 2 illustrates all steps of our proposal.

Fig. 2.

Illustration of all the steps of our proposal.

5 Methodology

This section presents the datasets used in our experiments, the base classifier used to validate our proposal, and the evaluation measures employed.

5.1 Datasets

We used ten HMC protein function datasets modeled as a tree. They are commonly used to evaluate hierarchical multi-label classifiers [9], and are freely available¹. They come with already prepared training, validation and test partitions, which have been used by many works in the literature. Table 1 presents the main characteristics of the used datasets.

Many methods in the literature, such as Clare [3], Vens et al. [19], Cerri et al. [2], and Wehrmann et al. [20] have presented the results of their proposals on these datasets, training their models on 2/3 of each dataset and testing on the remaining 1/3. Here we use exactly the same schema, by putting together the training and validation sets, and testing on the remaining test set.

Table 1. Datasets: #attributes (|A|); #classes per level (|C|); #instances (|X|); attribute type (Type): numerical (Quanti), qualitative (Quali) or both (Mixed).

5.2 Base Classifier

Clus-HMC [19] is an algorithm which builds decision tree classifiers. It is based on Predictive Clustering Trees (PCTs), where the root node corresponds to a cluster containing all training data, which is recursively partitioned in minor clusters while going down to the leaf nodes. PCTs are built in such a way that each division aims to maximize the variance reduction within each cluster.

To apply PCTs to the HMC task, first, the instance labels are represented as binary vectors: the i-th vector component is assigned 1 if the instance belongs to class $c_i$, and 0 otherwise. To analyze the variance in the HMC context, Clus-HMC considers the similarity in higher hierarchical levels as more important than similarity in low levels. This is performed weighting classes for the calculation of the Euclidean distance between the binary vectors. Here we used the Clus-HMC implementation provided within the Clus framework, which is freely available². For more details on Clus-HMC, please refer to Vens et al. [19].

5.3 Evaluation Measures

We used Precision-Recall (PR) curves to evaluate our results. Since Clus-HMC outputs a probability of an instance to belong to each class, we can use different threshold values in the range [0.0, 1.0] in order to produce many PR points, generating a curve plotting the precision of a model as a function of its recall. In this work, we used two PR-curve variations, defined below.

• Weighted Average of the Areas Under the individual PR curves ($\overline{AUPRC}_w$): average the areas under individual PR-curves, weighting classes by their frequencies $w_i = v_i / \sum {}{}_j v_j$, with $v_i$ the frequency of class $c_i$. It gives more importance to more frequent classes. $\overline{AUPRC}_w$ is given by Eq. 1.

• Average Area Under the PR Curves ($\overline{AUPRC}$): an instantiation of the previous $\overline{AUPRC}_w$, where all weights are set to 1/|C|, with C the set of classes, $\overline{AUPRC}$ is given by Eq. 2.

6 Experiments and Discussion

Figures 3 and 4 present our results with different numbers of selected features, as described in our boxplot strategy. We executed Clus-HMC with its best hyper-parameter values as suggested by Vens et al. [19]³. We also compare our proposal with a version of PCA able to deal with both numeric and categorical features (PCAMix). Since PCA is an unsupervised method, it was applied to the whole feature set just once, without separating the original dataset in many datalevels. The figures use the following notation.

• Min: 100% of the selected features with score higher than 0, corresponding to the interval between the worst and the best score;

• 1st Quartile: the features between the first quartile and the best score;

• Median: the features between the median and the best score;

• 3rd Quartile: the features between the third quartile and the best score;

• Reference: Clus-HMC in the hierarchical dataset without feature selection;

• PCAMix: PCA applied to the hierarchical dataset without separating it in non-hierarchical datasets;

Fig. 3.

Results for $\overline{AUPRC}$.

Fig. 4.

Results for $\overline{AUPRC}_w$.

Although there is no strategy that led to predictive enhancements in all cases, three out of the four proposed FS strategies have selected relevant features in at least 6/10 cases in some boxplot partitions. The results belonging to the Min boxplot partition, which represents 100% of the features selected (score higher than 0), did not lead to predictive changes considering IG-BR, RF-BR and RF-LP. The Eisen and Seq datasets were the only ones with a predictive loss in the 1st quartile for BR in both evaluation measures. For all the strategies proposed, the Median boxplot partition was the one that led to the best results, with IG-BR producing discrete predictive gains in 8/10 datasets considering $\overline{AUPRC}_w$, such as 4% in Spo, 1% in Gasch2, 2% in Expr, 2% in Derisi, and less than 1% in the remaining datasets. The exceptions were Eisen and Seq. Still in the Median partition, BR-RF led to gains in 7/10 datasets in both evaluation measures, such as 4% in Derisi, 3% in Eisen, 5% in Gasch1, 4% in Gasch2 and about 1% in the remaining datasets. The exceptions were Cellcycle, Church and Seq. Finally, RF-LP in the Median boxplot partition led to gains in 6/10 datasets in $\overline{AUPRC}$, with the exception of Cellcycle, Gasch1, Gasch2 and Seq.

The IG-LP strategy, although selecting extremely few features, produced the worst predictive performance at all. This result is visible in Figs. 3 and 4, where the curves decay sharply in all subdivisions of quartiles referring to IG-LP. It is also possible to see that in the Derisi dataset, no features have been selected.

Although PCA considerably reduced the feature space (23.8% of the original space in Derisi and 64.2% of the original space in Seq), the evaluation measures show that the principal components actually contributed negatively to the predictive performances. In comparison to the reference value, the performances after applying PCA were 45,8% lower in the Church dataset, 38.5% lower in Derisi, and 50,5% lower in Expr. Predictive gains were obtained in Pheno, with 3.4% and 4.5% higher performances in $\overline{AUPRC}$ and $\overline{AUPRC}_w$, respectively.

Figure 5 shows the percentage of features selected by each strategy, relative to the total number of features. The figure also shows the number of principal components as a percentage of the number of original features. We show the principal components which explain 90% or more of the data variation. Note that it is possible to see a common pattern in our FS strategies. In most of them, many attributes are selected near to the first boxplot quartile, while fewer attributes are selected near to the third quartile. As an example, taking RF-BR, we see almost no features selected near to the first quartile, while 62% of the original features are selected near to the third quartile. Another observation is that, as the Min partition corresponds to the 100% selected features with scores higher than 0, some datasets may have the Min below the 100% line, since some attributes didn’t have a score. Thus, the Min partitions in the radar plots may differ from the baseline, such as the dataset Spo with IG-BR.

Fig. 5.

Percentage of selected features according to each strategy.

7 Conclusion and Future Work

In this work we proposed strategies to apply feature selection methods in hierarchical multi-label datasets. Our proposal divides the original hierarchy in many non-hierarchical (flat) multi-label datasets, applies feature selection strategies combined with multi-label transformations in each flat dataset, and then combines the features selected forming a hierarchy with a new reduced feature space.

From our experiments, we can conclude that three (IG-BR, RF-BR e RF-LP) out of the four proposed FS strategies have selected relevant subsets of features. While reducing the feature space, these three methods improved or maintained predictive performances, with the exception of some few dataset. It is also possible to conclude that PCA is not a good choice for feature space reduction when related to hierarchical structures.

As can be seen from our work, feature selection focusing on hierarchical problems still has a large space for improvements. Other FS methods could be applied using our proposal, and new specific methods still need to be developed. As future works, we would like to study how feature selection methods can be applied in HMC problems with hierarchies structured as Directed Acyclic Graphs. Since in these structures the depth of a class is dependent on the different paths between it and the root class, our proposal is not directly applicable.