Keywords

1 Introduction to Pharmacokinetic/Pharmacodynamic Concepts

The development of new drugs is time-consuming (12–15 years) and costly. A study from 2003 [9] reports costs of approximately US$ 800 million to bring a drug to the market. It is further estimated that around 90 % of compounds (drug candidates) will fail during the drug development process [23]. Hence, the pharmaceutical industry is in search of new tools to support drug discovery and development. It is stated by the U.S. Food and Drug Administration that computational modeling and simulation is a useful tool to improve the efficiency in developing safe and effective drugs, see e.g. [16].

The development of a drug is usually divided into three categories. Firstly, numerous compounds are developed and screened in vitro. Secondly, promising compounds are tested for an effect in animals (in vivo). Here, the interest is also in prediction of an appropriate dose for first in man studies. Finally, the drug is tested in humans (phase I–III).

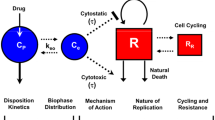
In the drug discovery and development process, so-called pharmacokinetic/pharmacodynamic experiments are conducted, which consists of two parts: The first part, called pharmacokinetics, deals with the time course of the drug concentration in blood. The interest is on absorption, distribution, metabolism and excretion of the drug in the body. The disease or more general the biological/pharmacological effect is not considered. Roughly said, one observes what the body does to the drug. The second part is the pharmacodynamics which “can be defined as the study of the time course of the biological effects of drugs, the relationship of the effects to drug exposure and the mechanism of drug action”, see [14]. That means one observes what the drug does to the body. Combining pharmacokinetics (PK) and pharmacodynamics (PD) gives an overall picture of the pharmacological effect/response, where it is assumed that the drug concentration is the driving force. In this work, the pharmacological effect is understood as the measurable therapeutic effect of the drug on a disease. In [4] it is stated: “Appropriate linking of pharmacokinetic and pharmacodynamic information provides a rational basis to understand the impact of different dosage regimens on the time course of pharmacological response.” Furthermore, it is believed “that by better understanding of the relationship between PK and PD one can shed light on situations where one or the other needs to be optimized in drug discovery and development”, see [40]. Typically, “PKPD modeling is widely used as the theoretical basis for optimization of the dosing regimen …of drugs in Phase II”, see [6]. Finally, it is stated in [34] about PKPD modeling: “When these insights are obtained in early development they can be used in translational approach to better predict efficacy and safety in the later stages of clinical development.”

From the mathematical point of view, linking of PK and PD leads to nonautonomous differential equations driven by the drug action.

Ideally, PKPD models are based on fundamental biological and pharmacological principles to mimic the underlying mechanisms of disease development and drug response. Models fulfilling these requirements are called (semi-) mechanistic. Therefore, the development of such models is in general performed in an interdisciplinary collaboration between mathematicians, biologists, pharmacologists etc.

It is written in [6]: “Not surprisingly, PKPD modeling has developed from an empirical and descriptive approach into a scientific discipline based on the (patho-) physiological mechanisms behind PKPD relationships. It is now well accepted that mechanism-based PKPD models have much improved properties for extrapolation and prediction.”

Following Mager et al. [32] and Danhof et al. [7] a PKPD model consists of four parts:

  1. (i)

    Modeling of pharmacokinetics to describe the drug concentration.

  2. (ii)

    Modeling the binding of drug molecules at the receptor/target to describe the effect concentration relationship.

  3. (iii)

    Transduction modeling, describing a cascade of processes that govern the time course of pharmacological response after drug-induced target activation.

  4. (iv)

    Modeling of the disease.

An important task of a PKPD model is to describe several dosing schedules simultaneously (at least the placebo group and one dosing group) by one set of model parameter obtained from an optimization process. In a PKPD model with an estimated set of parameter only the dosing schedule is allowed to vary. Hence, a PKPD model build without existing data is mostly useless in practice. Based on a PKPD model with an appropriate amount of data, different dosing schedules could be simulated and physiological model parameter could be inter-specifically (animals to human) scaled to support e.g. first in man dose finding in early drug development. A PKPD model could also be extended with a population approach to investigate clinical data (phase I–III), see e.g. [2]. However, this additional statistical approach will not be treated in this chapter.

2 Pharmacokinetic Models

2.1 Introduction

The pharmacokinetics (PK) describes the behavior of an administered drug in the body over time. In detail, the PK characterizes the absorption, distribution, metabolism and excretion (called ADME concept, see e.g. [14]) of a drug.

First pharmacokinetic models representing the circulatory system were published by the Swedish physiologist T. Teorell [39] in 1937. The German pediatrist F.H. Dost is deemed to be the founder of the term pharmacokinetics, see [41]. In his famous books “Der Blutspiegel” from 1953 [10] and “Grundlagen der Pharmakokinetik” from 1968 [11], he presented a broad overview and analysis of drug behavior in time based on linear differential equations.

In pharmacokinetic experiments the drug concentration in blood over time is measured. In order to develop a PK model the body is typically divided into several parts. In this work we focus on the widely used two-compartment model approach dividing the body in a heavily with blood supplied part and the rest. Such a model is based on linear differential equations and is from the modeling point of view an empirical approach to describe the drug concentration. However, the time course of most drugs could be well described by such models.

Further note, that the PK model is the driving force in a full PKPD model and therefore, a handy and descriptive representation of the solution is necessary from the computational point of view.

2.2 Two-Compartment Models

In this work we focus on two-compartment pharmacokinetic models representing the body based on linear differential equations. We consider oral absorption and intravenous administration of a drug. In practice, for drug concentration measurements, blood samples have to be taken from the patients and therefore, the availability of data is limited due to ethical constraints. It turned out in application that two compartments are sufficient to appropriate describe the time course in blood for most drugs. For a more detailed overview of pharmacokinetic models see e.g. the book from Gabrielsson [14].

A two-compartment model consists of two physiological meaningful parts (see e.g. [28]):

  • The central compartment is identified with the blood and organs heavily supplied with blood like liver or kidney.

  • The peripheral compartment describes for example tissue or more generally, the part of the body which is not heavily supplied with blood.

The compartments are connected among each other in both directions and therefore, a distribution between central and peripheral compartment takes place.

Main assumption in pharmacokinetics:

  • The drug is completely eliminated (metabolism and excretion) from the body through the central (blood) compartment.

In case of oral administration of a drug (p.o.), absorption through the gastrointestinal tract takes place. Therefore, the distribution in the blood is not immediate and also only a part of the drug will reach the blood circulation (called bioavailability). In contrast, in case of intravenous dosing (i.v.) the drug is directly applied to the blood circulation and it is assumed that the drug is immediately distributed in the body.

With the formulated assumptions a two-compartment model for oral drug administration (p.o.) at time t = 0 reads

$$\displaystyle\begin{array}{rcl} x\prime_{1}& = -k_{10}x_{1} - k_{12}x_{1} + k_{21}x_{2} + k_{31}x_{3}\,,& \qquad x_{1}(0) = 0{}\end{array}$$
(7.1)
$$\displaystyle\begin{array}{rcl} x\prime_{2}& = k_{12}x_{1} - k_{21}x_{2}\,,& \qquad x_{2}(0) = 0{}\end{array}$$
(7.2)
$$\displaystyle\begin{array}{rcl} x\prime_{3}& = -k_{31}x_{3}\,,& \qquad x_{3}(0) = f \cdot \mathit{dose}{}\end{array}$$
(7.3)

where 0 < f ≤ 1 is a fraction parameter representing the amount of drug which effectively reaches the blood. We set without loss of generality f ≡ 1. The blood compartment is described by (7.1), the peripheral compartment by (7.2) and (7.3) describes the absorption. Note that Eq. (7.3) is not a part of the body. It is understood as additional hypothetical compartment necessary to describe the absorption. The model (7.1)–(7.3) has the parameters

$$\displaystyle{\theta = \left (k_{10},k_{12},k_{21},k_{31}\right )}$$

and the variable dose.

The parameter k 10 > 0 describes the elimination rate from the body, k 12, k 21 > 0 stand for the distribution between central and peripheral compartment and k 31 > 0 is the absorption rate. In case of i.v. administration k 31 = 0 (no absorption) and x 1(0) = dose and therefore, the model reduces to (7.1)–(7.2).

In practice, the drug is measured as concentration in blood plasma. Therefore, the parameter volume of distribution V 1 > 0 of the central compartment x 1(t) is introduced to obtain the drug concentration

$$\displaystyle{ c(t) = \frac{x_{1}(t)} {V _{1}} \,. }$$
(7.4)

In this work, c(t) will always denote the drug concentration in blood.

The representation of the two-compartment model based on ordinary differential equation is unhandy in application because in a full PKPD model the drug concentration has to be evaluated many times. Also for multiple dosing the representation is not appropriate. In order to reduce the computational effort the analytical solution of the blood compartment is presented in the next section.

2.3 Single Dosage

Applying the Laplace transform to (7.1)–(7.3) gives for the blood compartment in concentration terms for p.o. administration

$$\displaystyle\begin{array}{rcl}{ c}^{p.o.}(t)& =& \frac{\mathit{dose}k_{31}(k_{21}-\alpha )} {V _{1}(k_{31}-\alpha )(\beta -\alpha )} \exp (-\alpha t) + \frac{\mathit{dose}k_{31}(k_{21}-\beta )} {V _{1}(k_{31}-\beta )(\alpha -\beta )} \exp (-\beta t) \\ & & \quad + \frac{\mathit{dose}k_{31}(k_{21} - k_{31})} {V _{1}(k_{31}-\beta )(k_{31}-\alpha )} \exp (-k_{31}t) \\ & =& \mathit{dose}A_{\mathit{po}}\exp (-\alpha t) + \mathit{dose}B_{\mathit{po}}\exp (-\beta t) \\ & & \quad -\mathit{dose}(A_{\mathit{po}} + B_{\mathit{po}})\exp (-k_{31}t) {}\end{array}$$
(7.5)

where

$$\displaystyle\begin{array}{rcl} \alpha,\beta & =& \frac{1} {2}\left (k_{12} + k_{21} + k_{10} \pm \sqrt{{(k_{12 } + k_{21 } + k_{10 } )}^{2 } - 4k_{21 } k_{10}}\right )\,. {}\\ \end{array}$$

The final parameterization of the two-compartment p.o. model with a given dose reads

$$\displaystyle\begin{array}{rcl} \theta = \left (A_{\mathit{po}},B_{\mathit{po}},\alpha,\beta,k_{31}\right )& &{}\end{array}$$
(7.6)

and is called macro constant parameterization. Typically, (7.5)–(7.6) is used to fit data. However, this parameterization is not physiological interpretable. Following the clearance concept (see e.g. [14]), one obtains the physiological parameterization (see e.g. [18]) standing in a one-to-one correspondence to (7.6)

$$\displaystyle{\theta = \left (\mathit{Cl},\mathit{Cl}_{d},V _{1},V _{2},k_{31}\right )}$$

where Cl = k 10 V 1 is the hepatitic clearance, \(\mathit{Cl}_{d} = k_{12}V _{1} = k_{21}V _{2}\) the intercompartmental clearance and V 2 the volume of distribution of the peripheral compartment.

Finally, we give a short comment on classical allometric (inter-species) scaling of physiological parameters like clearance or volume of distribution. First, to perform a scaling, the underlying pharmacokinetic mechanism for the different species has to be similar. Second, it is commonly believed that clearance or volume of distribution depend on the body weight w, see [33]. A typical allometric model for scaling a physiological parameter p is based on a power law and reads

$$\displaystyle\begin{array}{rcl} p(w) ={ \mathit{aw}}^{b}& &{}\end{array}$$
(7.7)

where a, b > 0 are allometric parameters, see [14, 33] or [42]. It is suggested that at least 4 to 5 species are necessary to predict from mouse to human. A typical chain is mouse, rat, rabbit, monkey and finally human.

2.4 Multiple Dosage

The next step to describe the pharmacokinetics of a drug is to handle multiple dosing events, that means, a drug is administered several times to the body. Hence, one has also to account the remaining drug concentration in the body from a previous dosage.

A drug is often designed for equidistant administration, i.e. every day, every second day, every week and so on. This makes the application of drugs more secure for patients and therefore, increases the success on the market.

Let τ > 0 be the length of the dosing interval, \(m \in \mathbb{N}\) the maximal number of doses and \(j \in \{ 1,\ldots,m\}\) denote the actual number of dosage. Using the superposition principle one obtains the multiple dosing formula for p.o. administration represented by a composed function. The drug concentration at time t reads

$$\displaystyle\begin{array}{rcl}{ c}^{p.o.}(t) = \left \{\begin{array}{@{}l@{\quad }l@{}} c_{j}^{p.o.}(\xi )\,,\quad t = j\tau +\xi \,,\quad \xi \in [0,\tau ]\quad &j \in \{ 1,\ldots,m - 1\} \\ c_{j}^{p.o.}(\xi )\,,\quad t = j\tau +\xi \,,\quad \xi \geq 0 \quad &j = m \end{array} \right.& & {}\\ \end{array}$$

with

$$\displaystyle\begin{array}{rcl} c_{j}^{p.o.}(\xi )& =& \mathit{dose}A_{\mathit{ po}}\frac{1 -\exp (-\tau j\alpha )} {1 -\exp (-\tau \alpha )} \exp (-\alpha \xi ) \\ & & \quad + \mathit{dose}B_{\mathit{po}}\frac{1 -\exp (-\tau j\beta )} {1 -\exp (-\tau \beta )} \exp (-\beta \xi ) \\ & & \quad -\mathit{dose}(A_{\mathit{po}} + B_{\mathit{po}})\frac{1 -\exp (-\tau jk_{31})} {1 -\exp (-\tau k_{31})} \exp (-k_{31}\xi ){}\end{array}$$
(7.8)

see e.g. the book from Gibaldi [15]. We remark that for multiple p.o. administration, c p. o. (t) is a continuous function whereas in case of i.v., c i. v. (t) is not continuous at the dosing time points.

2.5 Discussion and Outlook

The pharmacokinetics describes the behavior of a drug in the body over time. Two-compartment models are widely used in industry and academics to describe the drug concentration in blood empirically because the time course of most drugs is reflected quite well. Such models have an analytical representation and mainly serve as input (driving force) in a full nonautonomous PKPD model. Also note that in experiments often a sparse PK data situation exists because only a limited number of blood samples can be taken from the animals or patients.

A mechanistic description of pharmacokinetic processes (ADME) to predict the kinetics of drugs in the whole body is provided by physiologically based pharmacokinetic models (PBPK), see [19]. Such models are composed of several compartments representing relevant organs (like kidney, liver, lung, gut, etc.) and tissues described by weight or volume and blood perfusion rates. PBPK models admit a mechanistic understanding of the drug’s kinetics in the body and its implication to toxicological assessment. It is commonly stated that these models are superior when estimating human pharmacokinetic parameters based on animal data in contrast to classical allometric approaches based on empirical compartment PK models, see [19]. In addition, these models allow to differentiate for the prediction in PK between children and adults, see [1]. Nevertheless, in this work we skip a detailed description of PBPK because in a full PKPD model the drug concentration is usually described by empirical models.

3 Pharmacodynamic Models

3.1 Introduction

The pharmacodynamics (PD) “can be defined as the study of the time course of the biological effects of drugs, the relationship of the effects to drug exposure and the mechanism of drug action”, see [14].

Of major importance in PD is the binding of the drug at the receptor (target) because “receptors are the most important targets for therapeutic drugs”, see [31]. For that purpose we introduce effect-concentration models (compare [14]). Such models are typically used as subunits in larger systems describing the pharmacological effect/response on a disease provoked by the binding of the drug at the receptor/target.

Hence, the next step is “the process of target activation into pharmacological response. Typically, binding of a drug to its target activates a cascade of electrophysiological and/or biochemical events resulting in the observable biological response”, see [6]. For that we consider models with a zero order inflow and first order outflow and also focus on cascades of these models, so-called transit compartments.

Further, we present lifespan models to describe the lifespan of subjects in a population, e.g. typically used to describe maturation of cells. Such models have a zero order in- and outflow term, an explicit lifespan parameter and a description of the past. Finally, we show an important relationship between transit compartments and lifespan models.

From the mathematical point of view, the resulting pharmacodynamic models are differential equations. In the following we understand the existence of the solution in two different terms. If the right hand side is continuous (p.o. case) the existence of the solution is understood in terms of Picard–Lindelöf. If the right hand side is piecewise continuous in time (i.v. case) we understand the existence in the sense of Carathéodory, see [5].

3.2 Effect-Concentration Models

In Sect. 7.2, pharmacokinetic models describing the time course of the drug concentration c(t) were introduced. Now we consider models that put the drug concentration in relationship to an effect denoted by

$$\displaystyle{ e(\sigma,c(t)) }$$
(7.9)

where we call σ the drug-related parameter. The only requirement on (7.9) is

$$\displaystyle{ e(\sigma,c) \geq 0\quad \mbox{ and}\quad e(\sigma,0) = 0\,. }$$

The simplest approach for an effect of a drug is a linear term

$$\displaystyle{ e(k_{\mathit{pot}},c(t)) = k_{\mathit{pot}}c(t) }$$
(7.10)

where k pot  > 0 describes the drug potency. Such a parameter could be used to rank different compounds among each other in preclinical screening. The approach (7.10) is also useful if only few dosing groups are available for a simultaneous fit. For more dosing groups this approach is only locally true because the effect of a drug is in the majority of cases only linear in a small range of different doses.

The classical drug-receptor binding theory states that the amount of binding possibilities at the receptor is limited. Therefore, the effect of a drug will saturate and more drug will not lead to more effect. The most common nonlinear model to relate drug concentration and effect is

$$\displaystyle{ e(\sigma,c(t)) = \frac{E_{\mathit{max}}c{(t)}^{h}} {\mathit{EC}_{50}^{h} + c{(t)}^{h}} }$$
(7.11)

with \(\sigma = (E_{\mathit{max}},\mathit{EC}_{50},h)\), see [31]. E max  > 0 is the maximal effect, EC 50 > 0 is the concentration needed to produce the half-maximal effect and h > 0 is the Hill coefficient. Equation (7.11) is one of the basic principles in PKPD and called the E max model, see also Chap. 6.

3.3 Indirect Response Models

In pharmacodynamics, one is often faced with a so-called indirect drug response, that means, the drug stimulates or inhibits factors which control the response, see [8]. Further, one often assumes that the system describing the pharmacological action is in a so-called baseline condition. For example, think of heart rate, blood pressure, biomarkers etc.. The aim is to describe a perturbation of the baseline by a drug c(t). Moreover, if the perturbation vanishes, it is pharmacological assumed that the response runs back into its baseline.

The basic equation of an indirect response model (IDR) with constant inflow k in  > 0 and outflow k out  > 0 reads

$$\displaystyle{ x\prime = k_{\mathit{in}} - k_{\mathit{out}}x\,,\qquad x(0) = {x}^{0} \geq 0\,. }$$
(7.12)

For the baseline condition the initial value is set equal to the steady state \({x}^{{\ast}} =\lim \limits _{t\rightarrow \infty }x(t)\),

$$\displaystyle\begin{array}{rcl}{ x}^{0} = {x}^{{\ast}} = \frac{k_{\mathit{in}}} {k_{\mathit{out}}}\,.& & {}\\ \end{array}$$

In nonautonomous indirect response models, the drug effect is often described by an E max term modulating the in- and outflow. Depending on which rate is stimulated or inhibited, one obtains four possible models, see originally Jusko and coworkers [8] or summarized in [14], presented here in compact form

$$\displaystyle\begin{array}{rcl} x\prime& =& k_{\mathit{in}} \cdot \left \{\left (1 - \frac{I_{\mathit{max}}c{(t)}^{h}} {\mathit{IC}_{50}^{h} + c{(t)}^{h}}\right )\,,\,\left (1 + \frac{S_{\mathit{max}}c{(t)}^{h}} {\mathit{SC}_{50}^{h} + c{(t)}^{h}}\right )\right \} \\ & & -k_{\mathit{out}} \cdot \left \{\left (1 - \frac{I_{\mathit{max}}c{(t)}^{h}} {\mathit{IC}_{50}^{h} + c{(t)}^{h}}\right )\,,\,\left (1 + \frac{S_{\mathit{max}}c{(t)}^{h}} {\mathit{SC}_{50}^{h} + c{(t)}^{h}}\right )\right \} \cdot x{}\end{array}$$
(7.13)

with the initial value

$$\displaystyle{ \qquad x(0) = \frac{k_{\mathit{in}}} {k_{\mathit{out}}} }$$

where 0 < I max  ≤ 1. IDRs of the form (7.13) are one of the most popular models in PKPD and are extensively studied and applied in the last 20 years.

3.4 General Inflow–Outflow Models

Consider a state \(x: \mathbb{R}_{\geq 0} \rightarrow \mathbb{R}_{\geq 0}\) controlled by two processes, namely, an inflow into the state and an outflow from this state. A reasonable realization is by a zero-order inflow and a first-order outflow. Let \(k_{\mathit{in}}: \mathbb{R}_{\geq 0} \rightarrow \mathbb{R}_{\geq 0}\) and \(k_{\mathit{out}}: \mathbb{R}_{\geq 0} \rightarrow \mathbb{R}_{\geq 0}\) be piecewise continuous and bounded functions with

$$\displaystyle{ \lim \limits _{t\rightarrow \infty }k_{\mathit{in}}(t) = k_{\mathit{in}}^{{\ast}}\geq 0\quad \mbox{ and}\quad \lim \limits _{ t\rightarrow \infty }k_{\mathit{out}}(t) = k_{\mathit{out}}^{{\ast}} > 0 }$$

describing inflow and outflow, respectively. We call

$$\displaystyle{ x\prime(t) = k_{\mathit{in}}(t) - k_{\mathit{out}}(t)x(t)\,,\qquad x(0) = {x}^{0} \geq 0 }$$
(7.14)

an inflow–outflow model (IOM). Model (7.14) has an asymptotically stable stationary point

$$\displaystyle{ {x}^{{\ast}} =\lim \limits _{ t\rightarrow \infty }x(t) = \frac{k_{\mathit{in}}^{{\ast}}} {k_{\mathit{out}}^{{\ast}}}\,. }$$
(7.15)

Note that indirect response models are a special case of IOMs.

3.5 Transit Compartment Models

Widely used models in PKPD are transit compartment models (TCMs). Such models are chains of inflow–outflow models where the inflow in the j-compartment is just the outflow of the j − 1. The corresponding equations read

$$\displaystyle\begin{array}{rcl} x\prime_{1}& = k_{\mathit{in}}(t) -\mathit{kx}_{1},& \qquad x_{1}(0) = x_{1}^{0} \geq 0{}\end{array}$$
(7.16)
$$\displaystyle\begin{array}{rcl} x\prime_{2}& = \mathit{kx}_{1} -\mathit{kx}_{2},& \qquad x_{2}(0) = x_{2}^{0} \geq 0{}\end{array}$$
(7.17)
$$\displaystyle\begin{array}{rcl} \begin{array}{llll} &\ \ \vdots & &\ \ \vdots \\ x\prime_{n}& = \mathit{kx}_{n-1} -\mathit{kx}_{n},&x_{n}(0)& = x_{n}^{0} \geq 0\end{array} & &{}\end{array}$$
(7.18)

where \(k_{\mathit{in}}: \mathbb{R}_{\geq 0} \rightarrow \mathbb{R}_{\geq 0}\) is a piecewise continuous and bounded function. For example, k in (t) could describe the PK and therefore, in case of i.v. discontinuities exist. The transit rate between the compartments is k > 0. Roughly said, the states x 2(t), …, x n (t) can be viewed as delayed versions of x 1(t).

The application of (7.16)–(7.18) is versatile in PKPD modeling. TCMs can be motivated by signal transduction processes, see [38], and therefore, mimic biological signal pathways. But TCMs are also often used to just produce delays, see [30] (delayed drug course) or [12] (delayed cytokine growth). Hence, the states x i (t) often lose their pharmacological interpretation and the TCM concept is downgraded to a help technique. Historically, Sheiner was the first in 1979, see [36], who suggested to apply a TCM with n = 1 to describe a delay between pharmacokinetics and effect which is also called an effect compartment.

TCMs are also applied to describe populations, see e.g [37]. When looking at a TCM one sees that one could assign a mean residence/transit time of \(\frac{1} {k}\) for an individual to stay in the i-th compartment, i ∈ 1, …, n, see e.g. [38]. In this sense, a TCM could be reinterpreted as a model describing an age structured population and x i (t) describes the number of individuals with age a i , where \(a_{i} \in (\frac{i-1} {k}, \frac{i} {k}]\). Hence, spoken in terms of population, the \(x_{1}(t),\ldots,x_{n}(t)\) describe the age distribution of a total population

$$\displaystyle\begin{array}{rcl} y_{n}(t) = x_{1}(t) +\ldots +x_{n}(t)\,.& & {}\\ \end{array}$$

Therefore, the secondary parameter

$$\displaystyle\begin{array}{rcl} T = \frac{n} {k}& & {}\\ \end{array}$$

describes the mean transit/residence time needed for an object created by k in to pass through all states x i (t) for i = 1, …, n.

However, in most cases it is obvious that the choice of the number of compartments n is somehow arbitrary. In application, n is often chosen in such a way that the final PKPD model fits the data best. For example, Savic and Karlsson [35] used a TCM to describe an absorption lag which is often seen in PK p.o. data because “some time passes before drug appears in the systemic circulation.” They calculated the optimal number of compartments based on fitting results for different drugs.

A reasonable extension of (7.16)–(7.18) is to use a time-variant transit rate satisfying kg(t) > 0. This leads to

$$\displaystyle\begin{array}{rcl} x\prime_{1}& = k_{\mathit{in}}(t) -\mathit{kg}(t)x_{1},& \qquad x_{1}(0) = x_{1}^{0} \geq 0{}\end{array}$$
(7.19)
$$\displaystyle\begin{array}{rcl} x\prime_{2}& = \mathit{kg}(t)x_{1} -\mathit{kg}(t)x_{2},& \qquad x_{2}(0) = x_{2}^{0} \geq 0{}\end{array}$$
(7.20)
$$\displaystyle\begin{array}{rcl} \begin{array}{lllllll} &\ \ \vdots &&& &\ \ \vdots \\ x\prime_{n}& = \mathit{kg}(t)x_{n-1} -\mathit{kg}(t)x_{n},&&&x_{n}(0)& = x_{n}^{0} \geq 0\end{array} & &{}\end{array}$$
(7.21)

where \(g: \mathbb{R} \rightarrow \mathbb{R}_{>0}\) is a piecewise and bounded function with finitely many discontinuity points. We call (7.19)–(7.21) a generalized TCM and will have a closer look at it in Sect. 7.3.7.

3.6 Lifespan Models

Another class of pharmacodynamic models are lifespan models introduced by Krzyzanski and Jusko in 1999 [26] to PKPD. Generally, such models describe populations where the individuals have a certain lifespan. Krzyzanski and Jusko applied this approach to hematological cell populations in the context of indirect response models.

Let \(y: \mathbb{R}_{\geq 0} \rightarrow \mathbb{R}_{\geq 0}\) be a state controlled by production (birth of individuals) and loss (death of individuals). The general form of a lifespan model (LSM) is

$$\displaystyle\begin{array}{rcl} y\prime(t) = k_{\mathit{in}}(t) - k_{\mathit{out}}(t)\,,\quad y(0) = {y}^{0}& &{}\end{array}$$
(7.22)

where k in and k out are piecewise continuous and bounded functions.

In this chapter we consider two different cases. First, we present LSMs with a constant lifespan, that means every individual in the population has the same lifespan T > 0. This approach is first of all an idealized situation. However, this assumption is reasonable in most applications due to the data situation. Second, we additionally consider distributed lifespans.

3.6.1 Constant Lifespan

Assuming a constant lifespan T, the outflow from state y at time t is equal to the inflow at time t − T and we obtain the relation

$$\displaystyle{k_{\mathit{out}}(t) = k_{\mathit{in}}(t - T)\quad \mbox{ for}\,\,t \geq 0\,.}$$

Hence, the LSM for constant lifespan reads

$$\displaystyle\begin{array}{rcl} y\prime(t) = k_{\mathit{in}}(t) - k_{\mathit{in}}(t - T)\,,\quad y(0) = {y}^{0}\,.& &{}\end{array}$$
(7.23)

In applications one has seldom the freedom of choosing the initial value y(0) = y 0 arbitrarily. For example, in populations the initial value y 0 has to be set in such a way that it describes the amount of individuals already born and also died in the interval [−T, 0]. Therefore, we obtain

$$\displaystyle\begin{array}{rcl}{ y}^{0} =\int \limits _{ -T}^{0}k_{\mathit{ in}}(s)\,\mathit{ds}\,.& &{}\end{array}$$
(7.24)

The solution of (7.23)–(7.24) reads

$$\displaystyle{y(t) =\int \limits _{ t-T}^{t}k_{\mathit{ in}}(s)\,ds\quad \mbox{ for}\,\,t \geq 0\,.}$$

An important situation in application is a constant production in the past (e.g. in context of cell production)

$$\displaystyle{k_{\mathit{in}}(s) = k_{\mathit{in}}^{-}\quad \mbox{ for}\,\,s \leq 0\,.}$$

Then the initial value (7.24) is

$$\displaystyle{{y}^{0} = \mathit{Tk}_{\mathit{ in}}^{-}\,.}$$

3.6.2 Distributed Lifespan

Let X be a random variable with a probability density function \(l: \mathbb{R} \rightarrow \mathbb{R}_{\geq 0}\) where l(s) = 0 for s < 0 describes the lifespan of individuals and \(T = \mathbb{E}[X]\). The outflow term then reads

$$\displaystyle{k_{\mathit{out}}(t) =\int \limits _{ 0}^{\infty }k_{\mathit{ in}}(t-\tau )l(\tau )d\tau = (k_{\mathit{in}} {\ast} l)(t)}$$

see e.g. [25], [27]. The LSM is

$$\displaystyle{ y\prime(t) = k_{\mathit{in}}(t) - (k_{\mathit{in}} {\ast} l)(t)\,,\quad y(0) = {y}^{0}\,. }$$
(7.25)

Again the initial value y 0 has to be chosen in such a way that it describes the amount of individuals already born and died. One obtains

$$\displaystyle{ {y}^{0} =\int \limits _{ 0}^{\infty }\int \limits _{ -\tau }^{0}k_{\mathit{ in}}(s)\,\mathit{ds}\,\,l(\tau )\,d\tau }$$
(7.26)

see [20]. The solution of (7.25)–(7.26) reads

$$\displaystyle{y(t) =\int \limits _{ 0}^{\infty }\int \limits _{ t-\tau }^{t}k_{\mathit{ in}}(s)\,\mathit{ds}\,\,l(\tau )\,d\tau \quad \mbox{ for}\,\,t \geq 0\,.}$$

For constant past \(k_{\mathit{in}}(s) = k_{\mathit{in}}^{-}\) for s ≤ 0 we have \({y}^{0} = \mathit{Tk}_{\mathit{in}}^{-}\).

3.7 General Relationship Between Transit Compartments and Lifespan Models

In this section we present an important relationship between transit compartments and lifespan models with constant lifespan. Roughly said, if the number of compartments tends to infinity and the parameter

$$\displaystyle{ T = \frac{n} {k} }$$

is fixed, then in the limit the sum of all compartments is a lifespan model with constant lifespan T > 0.

An initial result was presented by Krzyzanski in 2011, see [24]. He investigated equal initial values for the generalized TCM (7.19)–(7.21) and constant past for the LSM (7.23)–(7.24).

Here, we consider (7.19)–(7.21) with arbitrary initial values \(x_{1}^{0} \geq 0,\ldots,x_{n}^{0} \geq 0\) and look for the corresponding generalized LSM with arbitrary past. This generalization covers more pharmacological situations. An important role plays

$$\displaystyle{\tau (t) =\int \limits _{ 0}^{t}g(s)\,\mathit{ds}\,,\quad t \in \mathbb{R}\,.}$$

Note that τ is a strongly increasing function with τ(0) = 0 and inverse τ −1. Furthermore, τ(t) could be interpreted as a time-transformation.

Theorem 7.1.

Consider the generalized transit compartment model

$$\displaystyle\begin{array}{rcl} x\prime_{1}& = k_{\mathit{in}}(t) -\mathit{kg}(t)x_{1},& \qquad x_{1}(0) = x_{1}^{0} \geq 0{}\end{array}$$
(7.27)
$$\displaystyle\begin{array}{rcl} x\prime_{2}& = \mathit{kg}(t)x_{1} -\mathit{kg}(t)x_{2},& \qquad x_{2}(0) = x_{2}^{0} \geq 0{}\end{array}$$
(7.28)
$$\displaystyle\begin{array}{rcl} \begin{array}{lllllll} &\ \ \vdots &&& &\ \ \vdots \\ x\prime_{n}& = \mathit{kg}(t)x_{n-1} -\mathit{kg}(t)x_{n},&&&x_{n}(0)& = x_{n}^{0} \geq 0,\end{array} & &{}\end{array}$$
(7.29)

where \(k_{\mathit{in}}: \mathbb{R} \rightarrow \mathbb{R}_{\geq 0}\) and \(g: \mathbb{R} \rightarrow \mathbb{R}_{>0}\) are piecewise continuous and bounded functions with finitely many discontinuity points and k > 0. Again let \(\tau (t) =\int \limits _{ 0}^{t}g(s)\,ds\) and let \(h: [0,1] \rightarrow \mathbb{R}_{\geq 0}\) be an arbitrary piecewise continuous function with h(0) = k in (0). Assume that the initial values of (7.27)–(7.29)satisfy

$$\displaystyle{ x_{i}(0) = \frac{1} {k}h\left ( \frac{i} {n}\right )\quad \mathit{for}\,i = 1,\ldots,n\,. }$$
(7.30)

Let

$$\displaystyle{ T = \frac{n} {k} > 0 }$$

be an arbitrary but fixed value. Further consider the total population based on (7.27)–(7.29)

$$\displaystyle{ y_{n}(t) = x_{1}(t) +\ldots +x_{n}(t)\,. }$$

Then the limit

$$\displaystyle{ y(t) =\lim \limits _{n\rightarrow \infty }y_{n}(t)\quad { \mathit{for}}\,t \geq 0 }$$
(7.31)

fulfills the lifespan model

$$\displaystyle\begin{array}{rcl} y\prime& =& k_{\mathit{in}}(t) - g(t)\frac{k_{\mathit{in}}(z)} {g(z)} \,,\quad \,y(0) = {y}^{0}{}\end{array}$$
(7.32)
$$\displaystyle\begin{array}{rcl} z\prime& =& \frac{g(t)} {g(z)}\,,\qquad \qquad \qquad \,\,\,\,\,\ z(0) {=\tau }^{-1}(-T){}\end{array}$$
(7.33)

provided the input function k in satisfies

$$\displaystyle{ \frac{k_{\mathit{in}}\left({\tau }^{-1}(t)\right )} {g\left({\tau }^{-1}(t)\right )} = h\left (-\frac{t} {T}\right )\quad { \mathit{ for }} - T \leq t \leq 0\,. }$$
(7.34)

The initial value of (7.32)reads

$$\displaystyle{ {y}^{0} = T\int \limits _{ 0}^{1}h(s)\,\mathit{ds}\,. }$$
(7.35)

Proof.

The matrix notation of (7.27)–(7.30) is

$$\displaystyle\begin{array}{rcl} x\prime& =& g(t)\mathit{Ax} + k_{\mathit{in}}(t){e}^{1}\,,\qquad x(0) = \frac{1} {k}\hat{{x}}^{0}{}\end{array}$$
(7.36)

with \(\hat{x}_{i}^{0} = h\left ( \frac{i} {n}\right ),i = 1,\ldots,n\) and

$$\displaystyle{A = \left (\begin{array}{lllll} - k& & \\ k & - k& &\\ &\ddots &\ddots & \\ & &k& - k \end{array} \right ) \in {\mathbb{R}}^{n,n}\,.}$$

Consider in addition

$$\displaystyle\begin{array}{rcl} u\prime& =& \mathit{Au} + \frac{k_{\mathit{in}}{(\tau }^{-1}(t))} {g{(\tau }^{-1}(t))} {e}^{1}\,,\qquad u(0) = \frac{1} {k}\hat{{x}}^{0}{}\end{array}$$
(7.37)

where the time dependency of the transit rate is shifted into the inflow term. Note that u 1(t), …, u n (t) describe a TCM with constant transit rate k and inflow

$$\displaystyle{ \tilde{k}_{\mathit{in}}(t) = \frac{k_{\mathit{in}}{(\tau }^{-1}(t))} {g{(\tau }^{-1}(t))} \,. }$$
(7.38)

It is obvious that the solutions of (7.36) and (7.37) are linked via

$$\displaystyle{ x(t) = u(\tau (t))\,. }$$
(7.39)

Next we use (7.39) and obtain

$$\displaystyle{y\prime_{n}(t) = x\prime_{1}(t) +\ldots +x\prime_{n}(t) = k_{\mathit{in}}(t) -\mathit{kg}(t)u_{n}(\tau (t))\,.}$$

Because (7.37) is a TCM with constant transit rate k and inflow \(\tilde{k}_{\mathit{in}}(t)\) (see (7.38)), we can apply the convergence result from [21]. This yields

$$\displaystyle{\lim \limits _{n\rightarrow \infty }\,\mathit{ku}_{n}(s) =\tilde{ k}_{\mathit{in}}(s - T) = \frac{k_{\mathit{in}}{(\tau }^{-1}(s - T))} {g{(\tau }^{-1}(s - T))} \quad {\mathit{ for }}s \in \mathbb{R}}$$

provided that (7.34) holds. Hence, the equation for the limit (7.31) reads

$$\displaystyle\begin{array}{rcl} y\prime(t)& =& k_{\mathit{in}}(t) - g(t)\lim \limits _{n\rightarrow \infty }\mathit{ku}_{n}(\tau (t)) = k_{\mathit{in}}(t) - g(t)\frac{k_{\mathit{in}}{(\tau }^{-1}(\tau (t) - T))} {g{(\tau }^{-1}(\tau (t) - T))} {}\\ \end{array}$$

with the initial value

$$\displaystyle{{y}^{0} =\lim \limits _{ n\rightarrow \infty }\sum _{i=1}^{n}x_{ i}(0) =\lim \limits _{n\rightarrow \infty }\sum _{i=1}^{n}\frac{T} {n}h\left ( \frac{i} {n}\right ) = T\int \limits _{0}^{1}h(s)\,\mathit{ds}\,.}$$

Furthermore,

$$\displaystyle{z(t) {=\tau }^{-1}(\tau (t) - T)}$$

satisfies

$$\displaystyle{z\prime(t) = \frac{1} {\tau \prime\left({\tau }^{-1}\left (\tau (t) - T\right )\right )}\tau \prime(t) = \frac{g(t)} {g(z(t))}\,,\quad z(0) {=\tau }^{-1}(-T)\,.}$$

Summarizing, we obtain the stated result. □ 

Remark 7.1.

  1. (a)

    In case of g ≡ 1 in (7.27)–(7.29), the lifespan model (7.32)–(7.33) reduces to

    $$\displaystyle{y\prime(t) = k_{\mathit{in}}(t) - k_{\mathit{in}}(t - T)\,,\quad y(0) = {y}^{0}\,,\qquad z(t) = t - T}$$

    which is well known from [21].

  2. (b)

    The assumption \(g: \mathbb{R} \rightarrow \mathbb{R}_{>0}\) is pharmacological reasonable. For example, g could describe a stimulation or inhibition term depending on the drug concentration as applied in (7.13).

  3. (c)

    The solution of (7.32)–(7.33) reads

    $$\displaystyle{y(t) =\int \limits _{ z(t)}^{t}k_{\mathit{ in}}(s)\,\mathit{ds}\,,\quad z(t) {=\tau }^{-1}\left (\tau (t) - T\right )\,.}$$

3.8 Discussion and Outlook

Typical (semi-) mechanistic pharmacodynamic models describing the pharmacological effect applied in academics and industry were presented. We introduced models to describe the effect-concentration relationship, stated inflow/outflow models typically applied to describe perturbations of a baseline and finally, presented lifespan models for populations. In Theorem 7.1 we presented an important relationship between general transit compartments and lifespan models.

In the next section we will develop a model for a disease progression (tumor growth) and the effect of drug on the disease. For that we apply an effect concentration term and mimic the dying of proliferating cells by either transit compartments or lifespan models. For another application of PKPD see Chap. 8 in this volume.

For further reading about PKPD modeling we recommend the books from Gabrielsson and Weiner [14], from Bonate [2] for a more statistical oriented data analysis and also from Macheras and Iliadis [31] for a more general biological/mathematical point of view. Finally, several excellent review articles about PKPD modeling were published in the last years where we like to highlight the manuscripts from Danhof et al. [6, 7] or Mager et al. [32].

4 Pharmacokinetic/Pharmacodynamic Tumor Growth Model for Anticancer Effects

In this section we develop a PKPD model to describe tumor growth and the anti-cancer effects of a drug along the guideline (i)–(iv) listed in Sect. 7.1. We firstly model the disease development (iv) without drug action, here called unperturbed tumor growth. Then we present the modeling of the drug effect on the disease (compare (ii)–(iii)) called perturbed tumor growth. Finally, we include the pharmacokinetics of a specific drug into the model, see (i).

4.1 Introduction and Experimental Setup

It is generally stated that the work of Laird [29] “Dynamics of tumor growth” published in 1964 initiated the mathematical modeling of tumor growth. Laird applied the Gompertz equation (here presented in the original formulation)

$$\displaystyle{ \frac{W} {W_{0}} = {e}^{\frac{A} {\alpha } (1-{e}^{-\alpha t}) } }$$

to describe unperturbed (no drug administration) tumor growth. W denotes the tumor size in time, W 0 is the initial tumor size and A, α are growth related parameters. This model realizes a sigmoid growth behavior and therefore, describes the three significant phases of tumor growth. First, a tumor grows exponentially, after a while the tumor growth becomes linear due to limits of nutrient supply and finally, the tumor growth saturates. Laird applied the Gompertz equation to data from mice, rats and rabbits.

In the book from Wheldon [43] it is stated that the saturation property of tumors could seldom be measured in patients because the host dies in the majority of cases before saturation begins. Also in preclinics, the experiments have to be terminated when a critical tumor size is reached due to ethical constraints and according to the animal welfare law. Hence, in this work we present a tumor growth model without saturation and focus on the first two tumor growth phases, namely exponential growth followed by linear growth.

We consider experiments performed in xenograft mice. Such mice are applied as a model for human tumor growth. It is stated by Bonate in [3]: “Most every drug approved in cancer was first tested in a xenograft model to determine its anticancer activity”. Xenograft mice develop human solid tumors based on implantation of human cancer cells. The tumor grows in the flank of the mice and its volume is measured by an electronic caliber and recalculated to weight based on tissue consistency assumptions. Roughly said, the tumor size could be measured “from the outside” without stressing the animals in contrast to PK where blood samples have to be taken. Therefore, in general more data is available in PD in contrast to PK.

However, we also mention two disadvantages of xenografts formulated by Bonate, see [3]: “First, these are human tumors grown in mice and so the mice must be immunocompromised for the tumor growth in order to prevent a severe transplant reaction from occurring in the host animal. Second, since these tumors are implanted in the flank, they do not mimic tumors of other origins, e.g. a lung cancer tumor grown in the flank may not representative for a lung cancer tumor in the lung.”

4.2 Unperturbed Tumor Growth

The growth of a tumor without an anticancer drug is called unperturbed growth. The aim of this section is to model this behavior with a realistic right hand side of the differential equation

$$\displaystyle\begin{array}{rcl} w\prime = f(w)\,,\quad w(0) = w_{0}& &{}\end{array}$$
(7.40)

where w 0 > 0 is the inoculated tumor weight, more precisely, the amount of implanted human tumor cells into the xenograft mouse. The tumor weight is denoted by w(t).

In 2004, Simeoni et al. [37] presented a model consisting of an exponential and a linear growth phase in order to describe the tumor growth in xenograft mice in time by the function

$$\displaystyle\begin{array}{rcl} g_{s}(w) = \left \{\begin{array}{@{}l@{\quad }l@{}} \lambda _{0}w\,,\quad &\quad w \leq w_{\mathit{th}} \\ \lambda _{1}\,, \quad &\quad w > w_{\mathit{th}} \end{array} \right.\,,\qquad w_{\mathit{th}} = \frac{\lambda _{1}} {\lambda _{0}}& &{}\end{array}$$
(7.41)

for (7.40). In (7.41), the parameter λ 0 > 0 describes the exponential growth rate and λ 1 > 0 the linear growth rate. If the weight w reaches a threshold w th , then the exponential growth switches immediately to linear growth in (7.41). This produces a fast transition between the exponential and linear phase in w(t). It is suggested by Simeoni to apply the approximation

$$\displaystyle\begin{array}{rcl} g_{a}(w) = \frac{\lambda _{0}w} {{\left [1 +{ \left (\frac{\lambda _{0}} {\lambda _{1}} w\right )}^{20}\right ]}^{ \frac{1} {20} }} & & {}\\ \end{array}$$

for (7.41) in practice.

Another growth function for (7.40)

$$\displaystyle{ g(w) = \frac{2\lambda _{0}\lambda _{1}w} {\lambda _{1} + 2\lambda _{0}w} }$$
(7.42)

was presented in [22] which is based on the Michaelis–Menten approach and produces a longer transition between these two essentially different growth phases. The parameter in (7.42) have the same meaning as in Simeoni’s model, see [22] for argumentation and derivation.

In this work we use the disease progression model

$$\displaystyle{ w\prime = \frac{2\lambda _{0}\lambda _{1}w} {\lambda _{1} + 2\lambda _{0}w}\,,\qquad w(0) = w_{0} }$$
(7.43)

for unperturbed tumor growth w(t) with the three parameter

$$\displaystyle{ \theta = (\lambda _{0},\lambda _{1},w_{0})\,. }$$

In Fig. 7.1, measurements from four different human tumor cell lines in xenograft mice, namely RKO (cancer of the colon), PC3 (prostate cancer), MDA (breast cancer) and A459 (lung cancer) were fitted with (7.43).

Fig. 7.1
figure 1

Different human tumor cell lines (RKO, PC3, MDA and A549) in xenograft mice fitted with model (7.43)

Full size image

4.3 Perturbed Tumor Growth Based on TransitCompartments

The next step towards a PKPD tumor growth model is to include the pharmacokinetics of a drug, or more precisely, the perturbation of the tumor growth by an anticancer agent. It is generally observed that the anti-cancer effect is delayed due to the drug concentration. Hence, the attacked tumor cells could be considered as a population with a lifespan. Simeoni and co-workers applied a transit compartment model and assumed that proliferating cells attacked by the drug will pass through different damaging stages until the cells finally and irrevocably die, see [37].

We apply the linear effect-concentration term

$$\displaystyle{e(k_{\mathit{pot}},c(t)) = k_{\mathit{pot}}c(t)}$$

to describe the action of the drug at the target (proliferating cells). The pharmacokinetics is denoted by c(t) and k pot  > 0 describes the potency parameter of a drug. The PK c(t) is a two-compartment model with either p.o. or i.v. administration. In our performed experiments we have two dosing groups, namely, a placebo and a drug administration group. Therefore, the linear effect term is an appropriate choice.

In a first approach we also apply a transit compartment model to describe the different stages of dying non-proliferating tumor cells initiated by the drug action. We denote by p(t) the amount of proliferating tumor cells and by d 1(t), …, d n (t) the different stages of dying tumor cells attacked by an anticancer agent. Since, the non-proliferating cells d 1, …, d n still add to total tumor mass, the total tumor w is the sum of proliferating tumor cells p and non-proliferating tumor cells d 1, …, d n . Only proliferating cells that are not affected by drug action contribute to the tumor growth. Therefore, the growth function g(w) of the total tumor consisting of proliferating and non-proliferating cells is slowed down by the factor \(\frac{p} {w}\).

The PKPD model with transit compartments reads

$$\displaystyle\begin{array}{rcl} p\prime& = \frac{2\lambda _{0}\lambda _{1}p} {\lambda _{1}+2\lambda _{0}p} \frac{p} {w(t)} - k_{\mathit{pot}}c(t)p,& \qquad p(0) = w_{0}{}\end{array}$$
(7.44)
$$\displaystyle\begin{array}{rcl} d\prime_{1}& = k_{\mathit{pot}}c(t)p -\mathit{kd}_{1},& \qquad d_{1}(0) = 0{}\end{array}$$
(7.45)
$$\displaystyle\begin{array}{rcl} d\prime_{2}& = \mathit{kd}_{1} -\mathit{kd}_{2},& \qquad d_{2}(0) = 0{}\end{array}$$
(7.46)
$$\displaystyle\begin{array}{rcl} \begin{array}{llll} &\ \ \vdots & &\ \ \vdots \\ d\prime_{n}& = \mathit{kd}_{n-1} -\mathit{kd}_{n},&d_{n}(0)& = 0\end{array} & &{}\end{array}$$
(7.47)
$$\displaystyle\begin{array}{rcl} w(t)& =& p(t) + d_{1}(t) +\ldots +d_{n}(t){}\end{array}$$
(7.48)

with the model parameter

$$\displaystyle{\theta = (\lambda _{0},\lambda _{1},w_{0},k_{\mathit{pot}},k)\,.}$$

The total tumor weight is denoted by w(t). The average lifespan of attacked tumor cells is computed after a fitting process by

$$\displaystyle{ T = \frac{n} {k}\,. }$$
(7.49)

In Fig. 7.2 we present two simultaneous fits of unperturbed and perturbed data with (7.44)–(7.48) and n = 3.

Fig. 7.2
figure 2

In every plot the unperturbed and perturbed tumor growth data was simultaneously fitted with (7.44)–(7.48) and n = 3. In the left panel the drug A1 was administered at day 15, 16, 17 and 18 and in the right panel the drug B was administered at day 12, 13, 14, 15 and 16

Full size image

4.4 Perturbed Tumor Growth Based on the LifespanApproach

In this section we apply Theorem 7.1 to the tumor growth model based on transit compartments. From a schematic point of view the model (7.44)–(7.48) can be regarded as a system with a TCM represented by (7.16)–(7.18) with input

$$\displaystyle\begin{array}{rcl} k_{\mathit{in}}(t)& =& e(\sigma,c(t))p(t)\,.{}\end{array}$$
(7.50)

On the way to a description of the pharmacological process with an LSM we set

$$\displaystyle{d(t) = d_{1}(t) +\ldots +d_{n}(t)}$$

representing the totality of cells attacked by the anticancer agent and replace the TCM (7.45)–(7.47) by a LSM for the population d(t). Using (7.50) this leads to

$$\displaystyle{d\prime(t) = k_{\mathit{in}}(t) - k_{\mathit{in}}(t - T) = e(\sigma,c(t))p(t) - e(\sigma,c(t - T))p(t - T)}$$

completed by the initial condition d(0) = 0 and the past

$$\displaystyle{ e(\sigma,c(s))p(s) = 0\,,\quad - T \leq s < 0\,. }$$
(7.51)

In applications, (7.51) is fulfilled because no drug is administered before inoculation of the tumor cells.

Then the reformulation of (7.44)–(7.48) in the lifespan model context reads

$$\displaystyle\begin{array}{rcl} p\prime(t)& = \frac{2\lambda _{0}\lambda _{1}p(t)} {\lambda _{1}+2\lambda _{0}p(t)} \frac{p(t)} {w(t)} - e(\sigma,c(t))p(t),& \qquad p(0) = w_{0}{}\end{array}$$
(7.52)
$$\displaystyle\begin{array}{rcl} d\prime(t)& = e(\sigma,c(t))p(t) - e(\sigma,c(t - T))p(t - T),& \qquad d(0) = 0{}\end{array}$$
(7.53)
$$\displaystyle\begin{array}{rcl} w(t)& =& p(t) + d(t)\,.{}\end{array}$$
(7.54)

In the LSM formulation (7.51)–(7.54) we have exactly two differential equations, one for the proliferating cells p(t) and one governing the population of the attacked tumor cells d(t). Note that it is not necessary to provide information about p(s) for − T ≤ s < 0 due to (7.51). The parameters are

$$\displaystyle{\theta = (\lambda _{0},\lambda _{1},w_{0},k_{\mathit{pot}},T)}$$

where T is the lifespan of the dying tumor cells which is now fitted directly from the data.

The sum of squares and parameter estimates of (7.51)–(7.54) and (7.44)–(7.48) are similar. The new formulation (7.51)–(7.54) is also from the modeling point of view a serious alternative to the classical formulation. Here the number of dying tumor stages is reduced to exactly one stage for the total population of cells attacked by the anticancer agent. This coincides with the situation in practice, where the choice of the number of compartments n is more or less arbitrary because the different stages could not be measured.

4.5 Discussion and Outlook

It is estimated that every third European develops cancer once in life time. Hence, mathematical modeling of tumor growth data is an important task to support drug development. The PKPD model structure presented by Simeoni et al. in 2004 [37] is one of the most applied tumor growth models in the last years.

In this work we focused on administration of one single drug. However, an important topic in anticancer drug development is the combination of different drugs and the search of synergistic effects in order to maximize the pharmacological effect. Based on a synergistic combination of drug effects the dosage could be reduced to minimize the side effects in patients. Hence, a new direction in tumor growth modeling is the development of realistic and mechanistic models for drug combination approaches. In [22] an approach which explicitly quantifies the synergy by a parameter and also describes combination therapy data was presented. The model could be used to rank different combination therapies. Nevertheless, this modeling field is subject of active research, see e.g. [17] for preclinical and [13] for clinical phase. To our knowledge no widely accepted mechanistic PKPD tumor growth combination therapy model is developed yet.