Nonlinear vibration analysis of laminated shallow shells with clamped cutouts by the R-functions method

Abstract

In present work, an effective method to research geometrically nonlinear free vibrations of elements of thin-walled constructions that can be modeled as laminated shallow shells with complex planform is applied. The proposed method is numerical–analytical. It is based on joint use of the R-functions theory, variational methods, Bubnov–Galerkin procedure and Runge–Kutta method. The mathematical formulation of the problem is performed in a framework of the refined first-order shallow shells theory. To implement the developed method, appropriate software was developed. New problems of linear and nonlinear vibrations of laminated shallow shells with clamped cutouts are solved. To confirm reliability of the obtained results, their comparison with the ones known in the literature is provided. Effect of boundary conditions is studied.

1 Introduction

Investigation of geometrically nonlinear vibrations of laminated shallow shells and plates with complex planform and cutouts is an actual problem. It is connected with wide applications of the composite shells and plates as structural components of many modern thin-walled structures. Cutouts are often required in the shell elements due to practical necessity: in order to facilitate structure, provide access and compound with other parts, for venting and other reasons. Nonlinear vibrations of the shallow shells and plates were studied and reviewed by Chia [1, 2], Chia and Chia [3], Alhaazza and Alhazza [4] and many other scientists. Surveys of the references devoted to nonlinear analysis of the laminated plates and shells with cutouts are given by Anil et al. [5], Qatu et al. [6], Sahu and Datta [7, 8], Zhang and Yang [9], Datta and Biswas [10] and so on. Extensive literature review from 2003 to 2013 of geometrically nonlinear vibrations of shells made of traditional and advanced materials is fulfilled by Alijani and Amabilli [11]. The mathematical statement of this class of problems is well developed in the literature [12, 13].

As follows from the literature reviews, a geometrically nonlinear analysis of laminated plates with cutout received a lot of attention. The number of papers devoted to the study of nonlinear analysis of shallow shells with cutouts is essentially smaller. Let us point out only few works devoted to these important problems. Large amplitude flexural vibrations of layered composite plates with cutouts were studied by Reddy [14] and Sivakumar et al. [15] using finite element method (FEM). Changshi Xu and Chia [16] have investigated nonlinear vibrations and buckling of laminated shallow spherical shells with a free circular opening at the apex. Numerical results are presented for different boundary conditions, ratios of base radius to thickness, number of layers and shell rise to thickness. Nanda and Bandypadhyay [17, 18] have investigated the large amplitude free vibrations of laminated shells of doubly curved with free square cutout. Authors of the Refs. [17, 18] have considered square cylindrical and spherical shells with $(0/90^{\circ })_{4}$ lamination scheme and free square cutout. The outer boundary is simply supported. The nonlinear strains in plane are linearized analogically to Ref. [19]. FEM is used at each step of the proposed algorithm. Authors have employed finite element model using an eight-noded element.

Note that free cutout and holes have been considered in all papers. There are practically no works about nonlinear vibrations of the laminated shallow shells with clamped or simply supported cutouts. But in practice such boundary conditions arise. The aim of the paper is study of geometrically nonlinear vibrations of the symmetrically laminated shallow shells and plates with square and rectangular clamped cutouts. It is assumed that external contour can be clamped or simply supported, while the internal cutout is clamped. The proposed method is based on the R-functions theory [20,21,22,23], variational principles and Runge–Kutta method. Theoretically, method is developed for multiple-mode approach, but presented numerical results were obtained for single mode and may be considered as the first approximation to more accurate solutions.

2 The mathematical statement of the problem

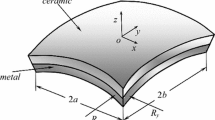
A laminated shallow shell of an arbitrary planform with radii curvature $R_x ,\;R_y$ consisted of S layers of the constant thickness $h_i$ is considered. Assume that shell under consideration has symmetric laminated scheme relatively to the midsurface. The slip and separation between the layers are absent. Investigation is carried out by the first-order shear deformation theory (FSDT). According to this theory, it is assumed that the tangent displacements are linear functions of coordinate z, and the transverse displacement w is a constant through the thickness of the shell. Normal to the midsurface remains straight after deformation, but not necessarily normal to the middle surface. For symmetrically laminated shell, the in-plane force resultants $N_{11}, N_{12}, N_{22}$, moment resultants $M_{11}, M_{12}, M_{22}$ and shear resultants $Q_x, Q_y$ are defined by

$$\begin{aligned} \left\{ {{\begin{array}{c} {N_{11} } \\ {N_{22} } \\ {N_{12} } \\ \end{array} }} \right\}= & {} \left[ {{\begin{array}{ccc} {C_{11} }&{} {C_{12} }&{} {C_{16} } \\ {C_{12} }&{} {C_{22} }&{} {C_{26} } \\ {C_{16} }&{} {C_{26} }&{} {C_{66} } \\ \end{array} }} \right] \cdot \left\{ {{\begin{array}{c} {\varepsilon _{11} } \\ {\varepsilon _{22} } \\ {\varepsilon _{12} } \\ \end{array} }} \right\} , \quad \left\{ {{\begin{array}{l} {M_{11} } \\ {M_{22} } \\ {M_{12} } \\ \end{array} }} \right\} \nonumber \\= & {} \left[ {{\begin{array}{ccc} {D_{11} }&{} {D_{12} }&{} {D_{16} } \\ {D_{12} }&{} {D_{22} }&{} {D_{26} } \\ {D_{16} }&{} {D_{26} }&{} {D_{66} } \\ \end{array} }} \right] \cdot \left\{ {{\begin{array}{l} {\chi _{11} } \\ {\chi _{22} } \\ {\chi _{12} } \\ \end{array} }} \right\} ,\nonumber \\ \left\{ {\begin{array}{l} Q_y \\ Q_x \\ \end{array}} \right\}= & {} \left[ {\begin{array}{cc} C_{44} &{} C_{45} \\ C_{45} &{} C_{55} \\ \end{array}} \right] \left\{ {\begin{array}{l} \varepsilon _{23} \\ \varepsilon _{13} \\ \end{array}} \right\} . \end{aligned}$$

(1)

The nonlinear strain–displacement relations can be presented as follows

$$\begin{aligned} \varepsilon _{11}= & {} u,_x +\frac{w}{R_x }+\frac{1}{2}w,_x^2 , \quad \nonumber \\ \varepsilon _{22}= & {} v,_y +\frac{w}{R_y }+\frac{1}{2}w,_y^2 , \quad \nonumber \\ \varepsilon _{12}= & {} u,_y +v,_x +w,_x w,_y ,\nonumber \\ \varepsilon _{13}= & {} w,_x +\psi _x -\frac{u}{R_x }, \quad \varepsilon _{23} =w,_y +\psi _y -\frac{v}{R_y }, \nonumber \\ \chi _{11}= & {} \psi _x ,_x , \quad \chi _{22} =\psi _y ,_y , \quad \chi _{12} =\psi _x ,_y +\psi _y ,_x .\nonumber \\ \end{aligned}$$

(2)

Here and throughout comma defines the function differentiation with respect to its corresponding variable. Functions $u\left( {x,y,t} \right) ,v\left( {x,y,t} \right) ,w\left( {x,y,t} \right)$ are displacements of the coordinate surface points; $\psi _x ,\psi _y$ are rotation angles of the normal to the coordinate surface. Constants $C_{ij}$ and $D_{ij}$ are the stiffness coefficients of the shell, which are defined by the following expressions [13, 14, 24, 25]:

$$\begin{aligned} \left( {C_{ij} ,D_{ij} } \right)= & {} \sum _{m=1}^S {\int \limits _{h_m }^{h_{m+1} } {B_{ij}^{\left( m \right) } } \left( {1,z^{2}} \right) \mathrm{d}z,} \quad \nonumber \\&\left( {i,j=1,2,6} \right) ,\quad \nonumber \\ C_{ij}= & {} k_i^2 \sum _{m=1}^S {\int \limits _{h_m }^{h_{m+1} } {B_{ij}^{\left( m \right) } \mathrm{d}z} } ,\quad \left( {i,j=4,5} \right) . \end{aligned}$$

(3)

Here $B_{ij}^{\left( m \right) }$ are stiffness coefficients of the mth layer, and $k_i , i=\overline{4,5}$ are shear correction factors. Next, we assume that $k_4 =k_5$, that is, $C_{45} =C_{54}$.

The problem of geometrically nonlinear vibrations of shallow shells is reduced to the solution of the system of nonlinear differential equations of motion [12,13,14]:

$$\begin{aligned}&\frac{\partial N_{11} }{\partial x}+\frac{\partial N_{12} }{\partial y}-\frac{Q_x }{R_x }=m_1 \frac{\partial ^{2}u}{\partial t^{2}};\nonumber \\&\frac{\partial N_{22} }{\partial y}+\frac{\partial N_{12} }{\partial x}-\frac{Q_y }{R_y }=m_1 \frac{\partial ^{2}v}{\partial t^{2}};\nonumber \\&\frac{\partial Q_x }{\partial x}+\frac{\partial Q_y }{\partial y}+\frac{N_{11} }{R_x }+\frac{N_{22}}{R_y} +N_{11} \frac{\partial ^{2}w}{\partial x^{2}}\nonumber \\&\qquad +\,2N_{12} \frac{\partial ^{2}w}{\partial x\partial y}+N_{22} \frac{\partial ^{2}w}{\partial y^{2}}=m_1 \frac{\partial ^{2}w}{\partial t^{2}};\nonumber \\&\frac{\partial M_{11} }{\partial x}+\frac{\partial M_{12} }{\partial y}-Q_x =m_2 \frac{\partial ^{2}\psi _x }{\partial t^{2}};\nonumber \\&\frac{\partial M_{22} }{\partial y}+\frac{\partial M_{12} }{\partial x}-Q_y =m_2 \frac{\partial ^{2}\psi _y }{\partial t^{2}}, \end{aligned}$$

(4)

where $m_1 ,m_2$ are calculated by known formulas from [12, 24, 25].

System (4) is supplemented by appropriate boundary and initial conditions.

3 The solution method

The first step of the proposed method is study of linear problem in order to find the natural frequencies and eigenfunctions $\left\{ {U^{(c)}} \right\} =\left\{ {u^{(c)},v^{(c)},w^{(c)},\psi _x^{(c)} ,\psi _y^{(c)} } \right\} ^\mathrm{T}$ satisfying the given boundary conditions of linear shells vibrations. Note that while solving linear problem we will not ignore inertia and rotation forces. Solution of linear problems has been widely discussed in [22, 24]. Let us note that in generic case this problem can be solved by the R-functions method (RFM). When solving the nonlinear problem, we will ignore the inertial terms. Then, let us present unknown function in the following form:

$$\begin{aligned} w= & {} \sum _{i=1}^n {y_i \left( t \right) w_i^{(c)} \left( {x,y} \right) } , \quad \nonumber \\ \psi _x= & {} \sum _{i=1}^n {y_i \left( t \right) \psi _{xi}^{(c)} \left( {x,y} \right) } , \quad \nonumber \\ \psi _y= & {} \sum _{i=1}^n {y_i \left( t \right) \psi _{yi}^{(c)} \left( {x,y} \right) } ,\nonumber \\ u= & {} \sum _{i=1}^n {y_i \left( t \right) u_i^{(c)} \left( {x,y} \right) } +\sum _{i=1}^n {\sum _{j=1}^n {y_i y_j u_{ij} } },\nonumber \\ v= & {} \sum _{i=1}^n {y_i \left( t \right) v_i^{(c)} \left( {x,y} \right) } +\sum _{i=1}^n {\sum _{j=1}^n {y_i y_j v_{ij} } } , \end{aligned}$$

(5)

where $y_i \left( t \right) \;$ are unknown functions in time, $w_i^{(c)} (x,y), u_i^{( c )} \left( {x,y} \right) , v_i^{( c )} \left( {x,y} \right) , \psi _{xi}^{(c)} (x,y), \psi _{yi}^{(c)} (x,y)$ are the ith eigenfunctions of linear vibrations of the shell and functions $u_{ij} \left( {x,y} \right) ,v_{ij} \left( {x,y} \right)$ should be solutions of the following system:

$$\begin{aligned} \left\{ {\begin{array}{l} L_{11} u_{ij} +L_{12} v_{ij} =-Nl_1^{\left( 2 \right) } \left( {w_i^{(c)} ,w_j^{(c)} } \right) , \\ L_{21} u_{ij} +L_{22} v_{ij} =-Nl_2^{\left( 2 \right) } \left( {w_i^{(c)} ,w_j^{(c)} } \right) , \\ \end{array}} \right. \end{aligned}$$

(6)

where linear differential operators $L_{ij} , \ \left( {i,j=\overline{1,5} } \right)$ are defined as:

$$\begin{aligned} L_{11}= & {} C_{11} \left( \,\, \right) ,_{xx} +2C_{16} \left( \,\, \right) ,_{xy} +C_{66} \left( \,\, \right) ,_{yy} ,\nonumber \\ L_{12}= & {} L_{21} =C_{16} \left( \,\, \right) ,_{xx} +\left( {C_{12} +C_{66} } \right) \left( \,\, \right) ,_{xy} \nonumber \\&+\,C_{26} \left( \,\, \right) ,_{yy} ,\nonumber \\ L_{22}= & {} C_{66} \left( \,\, \right) ,_{xx} +2C_{26} \left( \,\, \right) ,_{xy} +C_{22} \left( \,\, \right) ,_{yy} . \end{aligned}$$

(7)

The right-hand sides of Eq. (6) are nonlinear operators $Nl_k^{\left( 2 \right) } \left( {w_i^{(c)} ,w_j^{(c)} } \right) ,\;\;k=1,2$ determined by the following relations:

$$\begin{aligned} Nl_1^{\left( 2 \right) } \left( {w_i^{(c)} ,w_j^{(c)} } \right)= & {} w_i^{(c)} ,_x L_{11} w_j^{(c)} \nonumber \\&+\,w_i^{(c)} ,_y L_{12} w_j^{(c)} ,\nonumber \\ Nl_2^{\left( 2 \right) } \left( {w_i^{(c)} ,w_j^{(c)} } \right)= & {} w_i^{(c)} ,_x L_{21} w_j^{(c)} \nonumber \\&+\,w_i^{(c)} ,_y L_{22} w_j^{(c)} . \end{aligned}$$

(8)

Obtained system (6) is supplemented by the corresponding boundary conditions. It can be proved that variational formulation of problem (6) is reduced to finding stationary points of the following functional:

$$\begin{aligned} I\left( {u_{ij} ,v_{ij} } \right)= & {} \frac{1}{2}\iint \limits _\Omega \left( N_{11}^{\left( L \right) } \left( {u_{ij} ,v_{ij} } \right) \varepsilon _{11}^{\left( L \right) } \left( {u_{ij} ,v_{ij} } \right) \right. \nonumber \\&+\,N_{22}^{\left( L \right) } \left( {u_{ij} ,v_{ij} } \right) \varepsilon _{22}^{\left( L \right) } \left( {u_{ij} ,v_{ij} } \right) \nonumber \\&+\,N_{21}^{\left( L \right) } \left( {u_{ij} ,v_{ij} } \right) \varepsilon _{12}^{\left( L \right) } \left( {u_{ij} ,v_{ij} } \right) \nonumber \\&- \, 2\left( Nl_1^{\left( 2 \right) } \left( {w_i^{(c)} ,w_j^{(c)} } \right) u_{ij}\right. \nonumber \\&\left. \left. +\,Nl_2^{\left( 2 \right) } \left( {w_i^{(c)} ,w_j^{(c)} } \right) v_{ij} \right) \right) \mathrm{d}\Omega \nonumber \\&+\, \int \limits _{\partial \Omega } {\left( {N_n^{\left( N \right) } \left( {w_i^{ c)} ,w_j^{( c)} } \right) \left( {u_{ij} l+v_{ij} m} \right) } \right. } \nonumber \\&+\left. {T_n^{\left( N \right) } \left( {w_i^{( c)} ,w_j^{( c)} } \right) \left( {v_{ij} l-u_{ij} m} \right) } \right) \mathrm{d}S.\nonumber \\ \end{aligned}$$

(9)

Expressions $N_n^{\left( N \right) }$ and $T_n^{\left( N \right) }$ are

$$\begin{aligned} N_n^{\left( N \right) }= & {} N_{11}^{\left( N \right) } l^{2}+N_{22}^{\left( N \right) } m^{2}+2N_{12}^{\left( N \right) } lm, \quad \nonumber \\ T_n^{\left( N \right) }= & {} N_{12}^{\left( N \right) } \left( {l^{2}-m^{2}} \right) +\left( {N_{11}^{\left( N \right) } -N_{22}^{\left( N \right) } } \right) lm,\nonumber \\ \end{aligned}$$

(10)

where $l=\cos \left( {l^{0},Ox} \right) , m=\cos \left( {l^{o},Oy} \right)$ are the directional cosines of the external normal to border of the domain. Components $N_{11}^{\left( N \right) } ,N_{22}^{\left( N \right) } ,N_{12}^{\left( N \right) }$ are defined as

$$\begin{aligned} \left\{ {N^{\left( N \right) } } \right\}= & {} \left\{ N_{11}^{\left( N \right) } \left( {w_i^{( c)} ,w_j^{( c)} } \right) ,\right. \nonumber \\&\left. N_{22}^{\left( N \right) } \left( {w_i^{( c)} ,w_j^{( c)} ,} \right) ,N_{12}^{\left( N \right) } \left( {w_i^{( c)} ,w_j^{( c)} ,} \right) \right\} \\= & {} \left[ C \right] \left\{ \frac{1}{2}w_{i,x}^{( c)} \cdot w_{j,x}^{( c)} ;\quad \frac{1}{2}w_{i,y}^{( c)} \cdot w_{j,y}^{( c)} ;\;\;\;\right. \nonumber \\&\left. \frac{1}{2}\left( {w_{i,x}^{( c)} \cdot w_{j,x}^{( c)} +w_{j,x}^{( c)} \cdot w_{i,y}^{( c)} } \right) \right\} ^\mathrm{T}. \end{aligned}$$

Table 1 Material properties taken from Refs. [17, 28]

Fig. 1

Geometry of a shell shape in plan with a central cutout and examined boundary conditions

It can be shown that substitution of solutions (5) in the initial system turns the first, second, fourth and fifth equations into identities. Substituting expressions (5) for functions $u,v,w,\psi _x ,\psi _y$ in the third equation of system (4) and applying procedure by Bubnov–Galerkin, we drive nonlinear system of ordinary differential equations in unknown functions $y_r \left( t \right)$ of the following type:

$$\begin{aligned}&y^{//}_r \left( t \right) +\omega _{rl}^2 y_r \left( t \right) +\sum _{i=1}^n {\sum _{j=1}^n {\beta _{ji}^{( r)} y_i \left( t \right) y_j \left( t \right) } } \nonumber \\&\qquad +\sum _{i=1}^n {\sum _{j=1}^n {\sum _{k=1}^n {\gamma _{ijk}^{( r)} y_i \left( t \right) y_j \left( t \right) y_k \left( t \right) } } } \nonumber \\&\quad =0,\;(r=\overline{1,n} ). \end{aligned}$$

(11)

Expressions for coefficients $\beta _{ij}^{( r)} ,\gamma _{ijk}^{(r)}$ are presented below:

$$\begin{aligned} \beta _{ij}^{( r)}= & {} \frac{-1}{m_1 \left\| {w_r^{(c)} } \right\| ^{2}}\nonumber \\&\iint \limits _\Omega \left( {N_{11}^{(L)} w_j^{( c)} ,_{xx} +} N_{22}^{(L)} w_j^{( c)} ,_{yy} +2N_{12}^{(L)} w_j^{( c)} ,_{xy} \right. \nonumber \\&\left. -\,k_1 N_{11}^{(Np)} -k_2 N_{22}^{(Np)} \right) w_r^{(c)} \mathrm{d}\Omega , \end{aligned}$$

(12)

$$\begin{aligned} \gamma _{ijk}^{(r)}= & {} -\frac{1}{m_1 \left\| {w_r^{(c)} } \right\| ^{2}}\nonumber \\&\iint \limits _\Omega \left( N_{11}^{(Np)} w_k^{( c)} ,_{xx} +N_{22}^{(Np)} w_k^{( c)} ,_{yy}\right. \nonumber \\&\left. +\,2N_{12}^{(Np)} w_k^{( c)} ,_{xy} \right) w_r^{(c)} \mathrm{d}\Omega , \end{aligned}$$

(13)

where

$$\begin{aligned} \left\{ {N^{(L)}} \right\}= & {} \left[ C \right] \varepsilon ^{(L)}, \quad \left\{ {N^{(Np)}} \right\} =\left[ C \right] \left\{ {\varepsilon ^{(Np)}} \right\} ,\quad \\ \left\{ {\varepsilon ^{(L)}} \right\}= & {} \left\{ u_i^{( c)} ,_x +k_1 w_i^{(c)} ; v_i^{( c)} ,_y \right. \\&\left. +\,k_2 w_i^{(c)} ; \left( {u_i^{( c)} ,_y +v_i^{( c)} ,_x } \right) \right\} ^\mathrm{T},\\ \left\{ {\varepsilon ^{(Np)}} \right\}= & {} \left\{ u_{ij,x} +\frac{1}{2}w_i^{( c)} ,_x w_j^{( c)} ,_x ;v_{ij,y}\right. \nonumber \\&+\,\frac{1}{2}w_i^{( c)} ,_y w_j^{( c)} ,_y ;u_{ij,y} +v_{ij,x} \nonumber \\&\left. +\,w_i^{( c)} ,_x w_j^{( c)} ,_y \right\} ^\mathrm{T}. \end{aligned}$$

If we take only one mode, putting $n=1$, then system (11) is reduced to a single nonlinear ODE

$$\begin{aligned} {y}''_1 (t)+\omega _l^2 y_1 (t)+\beta \cdot y_1^2 (t)+\gamma \cdot y_1^3 (t)=0. \end{aligned}$$

(14)

Formulas for the coefficients $\beta ,\gamma$ in Eq. (14) are given in [25,26,27].

The solution of the obtained ordinary differential equation may be accomplished through a variety of approximation methods, for example Runge–Kutta method and Bubnov–Galerkin.

4 Numerical results

The developed theoretical approach and created software are validated by some test problems. A few of the studied problems regarding plates and shallow shells with constant thickness of layers are given below. The shear correction factors are taken as $k_4^2 =k_5^2 =5/6$. Three types of materials M1, M2, M3 are considered. Material properties used in the present study are described in Table 1.

Table 2 Convergence of the fundamental linear frequency parameters $\Lambda =\omega _{1l} (2a)^{2}\sqrt{\rho /E_{22} h^{2}}$ in polynomial approximation obtained by RFM in framework of classical theory (CST) and refined theory of the first order (FSDT)

To check reliability of the proposed method, let us start with linear vibration problems for shallow shells with free square cut and compare our results with known ones in Refs. [17, 28].

4.1 Linear vibration

Problem 1

(test). Free vibration of cylindrical and spherical cross-ply $(0^{\circ }/90^{\circ })_{4}$ shells with central free square cutout (Fig. 1a) [17, 28] is studied. Geometrical parameters are: $a/b=1,\;c/d=1,\;2a/h=100\;$, for cylindrical shell $R_x/h=\infty ,R_y/h=300$, for spherical shell $R_x/h=300,R_y /h=300$. The boundary conditions are taken as follows:

$$\begin{aligned} v= & {} w=\psi _y =0\hbox { at }x=\pm a\\&\hbox { and }u=w=\psi _x =0\hbox { at }y=\pm b. \end{aligned}$$

It was obvious that presented boundary conditions correspond to simply supported shell with free cutout (see Fig. 1a). Denote these boundary conditions as (SF).

First let us investigate the convergence of the fundamental linear frequency on the example of a square spherical shell made of material M2 increasing the numbers of the admissible functions. Size of cut is $c/2a=0.1$.

Solutions structures [20, 21] have the following forms:

CST: $w=(a^{2}-x^{2})\;\left( {a^{2}-y^{2}} \right) P_1 ,\quad u=\left( {a^{2}-y^{2}} \right) P_2 ,\;\quad v=(a^{2}-x^{2})P_3$

FSDT:

$$\begin{aligned} w= & {} (a^{2}-x^{2})\;\left( {a^{2}-y^{2}} \right) P_1 ,\quad u=\left( {a^{2}-y^{2}} \right) P_2 ,\;\quad \\ v= & {} (a^{2}-x^{2})P_3 ,\\ \psi _x= & {} \left( {a^{2}-y^{2}} \right) P_4 ,\;\quad \psi _y =(a^{2}-x^{2})P_5 , \end{aligned}$$

where $P_k \left( {x,y} \right) ,\;\left( {k=\overline{1,5} } \right)$ are undetermined components that are presented as an expansion in a series by a complete system (power polynomials or splines [29]). Taking into account that shape of the plan is doubly—symmetric nature, we will perform numerical implementation for one quarter of the investigated domain. The results obtained at approximation of uncertain components in the solution structures by power polynomials (pol) are presented in Table 2.

The analysis of Table 2 shows that in practical calculations we can take the 13th degree of polynomials $P_2 ,P_3 ,P_4 ,P_5$ (28x4 coordinate functions) to approximate the unknown functions for $u, v,\psi _x ,\psi _y$ and the 14th degree (36 coordinate functions) of the polynomial $P_1$ to approximate the deflection w. Analysis of the convergence at approximation of undermined components by splines showed that we could hold the mesh of splines 20x20. All the subsequent results have been calculated with mentioned above number of coordinate functions and indicated mesh of splines.

Fundamental linear frequency parameters $\Lambda =\omega _{1l} (2a)^{2}\sqrt{\rho /E_{22} h^{2}}$ obtained by RFM in framework of two theories (CST and FSDT) with polynomial (pol.) and spline approximation (sp.) of undetermined components are compared in Table 3 with known results presented in Refs. [17, 28]. Comparison is performed for cylindrical and spherical shells with different cut sizes.

Table 3 Comparison of fundamental linear frequency parameters $\Lambda =\omega _{1l} (2a)^{2}\sqrt{\rho /E_{22} h^{2}}$ for cross-ply $(0^{\circ }/90^{\circ })_{ 4}$ laminated simply supported shells with central free square cutout, $2a/h=100,\;R_x /h=300,\;R_y/h=300$

The maximum deviation of the obtained results with ones known in the literature does not exceed 1.5%. For thin shells ($2h/a=100$), the results obtained in the framework of two theories practically coincide. Further the refined shell theory of the first order (FSDT) will be used.

Problem 2

(test). Consider free vibration problem of three-layered cross-ply cylindrical shallow shell. Assume that external boundary is simply supported and a central square cutout is free (SF), (Fig. 1a). Mechanical properties of the layers are taken for materials M1 and M3 (see Ref. [17]).

Dimensionless geometric parameters are defined as $R_x /h=300,h/{2a}=0.01,\;\;a/b=1,\;\;c/d=1$. Comparison of the obtained fundamental linear frequency parameters $\Lambda =\omega _{1l} (2a)^{2}\sqrt{\rho /E_{22} h^{2}}$ for different materials with the known ones (see Ref. [17]) is presented in Table 4.

Table 4 Comparison of the fundamental linear frequency parameters $\Lambda =\omega _{1l} (2a)^{2}\sqrt{\rho /E_{22} h^{2}}$ for cross-ply $\left( {0^{0}/90^{0}/0^{0}} \right)$ laminated cylindrical panel with the boundary condition (SF)

Table 5 Fundamental linear frequency parameters $\Lambda =\omega _{1l} \left( {2a} \right) ^{2}\sqrt{\rho /E_{22} h^{2}}$ of shallow shells with rectangular clamped cutout ($a/b=1; c/2a=0.15; c/d=2$), thickness of $h/2a=0.1$; 0.01 and lamination scheme $(0^{0}/90^{0}/0^{0})$

The observed divergence of the obtained results with ones in Ref. [17] does not exceed 1.5%.

Further new results obtained by using RFM are presented.

Problem 3

Consider the problem of free vibration of shallow shells with two types of boundary conditions: completely clamped border (CC) (Fig. 1b) and simply supported on external edge with clamped cutout (SC) (Fig. 1c).

In order to solve this problem by RFM, we should construct a system of basic functions satisfying at least the main boundary conditions. The boundary conditions for shells clamped on external and internal borders are:

$$\begin{aligned} (\hbox {CC}) w=u=v=\psi _x =\psi _y =0,\quad \forall \left( {x,y} \right) \in \partial \Omega . \end{aligned}$$

But if shell is clamped only on cutout and simply supported on outer contour, then boundary conditions are more complex:

$$\begin{aligned}&\hbox {(SC) }w=0,\quad \forall \left( {x,y} \right) \in \partial \Omega \\&u=v=\psi _x =\psi _y =0,\quad \forall \left( {x,y} \right) \in \partial \Omega ^{( c)}\\&u=\psi _x =0,\quad y=\pm b,\\&v=\psi _y =0,\quad x=\pm a. \end{aligned}$$

Here $\partial \Omega$ and $\;\partial \Omega ^{( c)}$ are the whole border and border of the cutout relatively. For construction of the system of basic functions, we should build the corresponding solutions structures [20]. These structures have the following forms:

$$\begin{aligned} \hbox {Case (CC)}-w= & {} \omega P_1 ,\quad u=\omega P_2 ,\;v=\omega P_3 ,\;\nonumber \\ \psi _x= & {} \omega P_4 ,\;\psi _y =\omega P_5 , \end{aligned}$$

(15)

$$\begin{aligned} \hbox {Case (SC)}-w= & {} \omega P_1 ,\quad u=\omega ^{( u)}P_2 , \;v=\omega ^{( v)}P_3 ,\;\nonumber \\ \psi _x= & {} \omega ^{( u)}P_4 ,\;\psi _y =\omega ^{( v)}P_5 , \end{aligned}$$

(16)

where $P_k \left( {x,y} \right) ,\;\left( {k=\overline{1,5} } \right)$ are undetermined components of the solution structures [20, 21]. Equation $\omega =0$ is the equation of the whole boundary. It can be constructed by the R-functions theory and has the following form:

$$\begin{aligned} {\upomega } =\left( {f_1 \wedge _0 f_2 } \right) \wedge _0 \left( {f_3 \vee _0 f_4 } \right) . \end{aligned}$$

Here $f_i ,\;\left( {i=\overline{1,4} } \right)$ are defined as:

$$\begin{aligned} f_1= & {} \left( {a^{2}-x^{2}} \right) /2a\ge 0,\;f_2 =\left( {b^{2}-y^{2}} \right) /2b\ge 0,\;\\ f_3= & {} \left( {x^{2}-c^{2}} \right) /2c\ge 0,\;f_4 =\left( {y^{2}-d^{2}} \right) /2d\ge 0, \end{aligned}$$

the symbols $\wedge _0 ,\;\vee _0$ define R-operations [20].

Equations $\omega ^{( u)}=0,\;\omega ^{( v)}=0$ are defined as follows:

$$\begin{aligned} \omega ^{( u)}=f_2 \wedge _0 \left( {f_3 \vee _0 f_4 } \right) ,\quad \omega ^{( v)}=f_1 \wedge _0 \left( {f_3 \vee _0 f_4 } \right) . \end{aligned}$$

Fundamental non-dimensional frequencies $\Lambda$ and curvatures $k_1 ,k_2$ are defined as:

$$\begin{aligned} \Lambda =\omega _{1l} (2a)^{2}\sqrt{\rho /E_{22} h^{2}}, \quad k_1 =\frac{2a}{R_x },\quad k_2 =\frac{2a}{R_y }. \end{aligned}$$

The following variants of curvature values are investigated: $k_1 =k_2 =0$ (plate, Pl.); $k_1 =0.1,\quad k_2 =0$ (cylindrical shell, Cyl.); $k_1 =k_2 =0.1$ (spherical shell, Sph.); $k_1 =0.1,\quad k_2 =-0.1$ (hyperbolic paraboloid shell, Hyp.). Fundamental frequencies for cross-ply three-layered shells with rectangular clamped cutout made of three types of the materials (M1, M2, M3) with different boundary conditions (CC, SC) and thickness $h/2a=0.1,\quad h/2a=0.01$ are presented in Table 5.

As it follows from Table 6, effect of the curvature is more essential for thin plates and shells. It should be noted that results presented in Table 6 were obtained for spline-mesh 30x30. As for the polynomial approximation, for plates and shells with thickness $h/2a=0.1$, we used the same number of coordinate functions as before (Test 1 and 2). But for thinner plates and shells ($h/2a=0.01$), in the given case we had to increase the number of coordinate functions. For fully clamped (CC) plates and shells, we took 55 admissible functions for approximation of $w,\psi _x ,\psi _y$ [18th and 19th degree of the power polynomials $P_1$, and $P_4 ,P_5$ in structures (15)], and 45 admissible functions for u, v [the 15th degree of the polynomials $P_2 ,P_3$ in structures (15)]. For boundary conditions SC, we have taken 45 admissible functions for w (the 16th degree of the polynomial $P_1$) and 36 admissible functions for $u,v,\psi _x ,\psi _y$ (the 15th degree of the polynomials $P_2 ,P_3 ,P_4 ,P_5 )$ in structures (16), provided that symmetry is taken into account.

The first three eigenmodes and corresponding non-dimensional frequencies of SC three-layered $(0^{\circ }/90^{\circ }/0^{\circ })$ shells and plate made of material M2 with rectangular clamped central cutout and thickness $h/2a=0.1$ are presented in Table 6.

Table 6 First three eigenmodes and non-dimensional frequency parameters $\Lambda =\omega _{1l} \left( {2a} \right) ^{2}\sqrt{\rho /E_{22} h^{2}}$ of shallow shells $(0^{\circ }/90^{\circ }/0^{\circ })$ made of material M2 with rectangular clamped cutout and simply supported on outer contour (SC) ($a/b=1; c/2a=0.15; c/d=2, h/2a=0.1$)

Effect of thickness on fundamental linear frequency parameters of CC shell of material M2 with square cutout $c/2a=0.1$ and different laminations is given in Fig. 2.

Fig. 2

The effect of thickness on fundamental linear frequency parameters $\Lambda =\omega _{1l} \left( {2a} \right) ^{2}\sqrt{\rho /E_{22} h^{2}}$ of CC shells with square clamped cutout made of material M2: a angle ply ($45^{\circ }/-45^{\circ }/45^{\circ })$; b cross-ply ($0^{\circ }/90^{\circ }/0^{\circ }$)

We can see that with increasing thickness non-dimensional parameter of the fundamental frequency parameters $\Lambda =\omega _{1l} \left( {2a} \right) ^{2}\sqrt{\rho /E_{22} h^{2}}$ of the observed angle and cross-ply shells are decreasing. It should be noted that influence of examined parameters of curvature and types of lamination rapidly decreases with growth of thicknesses. Influence of the thickness parameter on frequencies of the shells with SC boundary condition is the same.

4.2 Nonlinear vibration

In order to check the accuracy of the present approach to nonlinear problems solution, we consider two test problems.

Problem 4

(test). Investigate free geometrically nonlinear vibrations of shallow isotropic square shell of constant thickness of doubly curved. The following geometric and material parameters are used: $a/b=1;R_x/R_y =1;R_x/R_y =0; \quad R_x =10;h/2a=0.01;\nu =0.3.$ The boundary conditions correspond to a simply supported edge. Figure 3 shows comparison of the backbone curves, obtained by RFM with the known results in Ref. [30] for cylindrical and spherical shells. To obtain the dependency of the frequencies ratio to the amplitude, Runge–Kutta method was used.

The observed divergence of obtained results with the known ones presented in Ref. [30] does not exceed 2%.

Table 7 Comparison of nonlinear frequency ratio $\omega _{nl}/\omega _l$ of laminated plates obtained by the RFM with results presented in Ref. [31]

Problem 5

test). Consider nonlinear vibrations of thin five layers composite rectangular plates using the CST taking into account the following material properties [31]: $E_1/E_2 =40, G_{12}/E_2 =0.6, G_{13}/E_2 =0.5, \nu _{12} =0.25$. All plate layers have the same thicknesses, and fiber orientations are measured from Ox-axis. The following boundary conditions are considered in the present analysis:

• (i) Immovable simply supported case (SSI):

  $$\begin{aligned}&w=0,\;M_n =0,v=0,u=0\hbox { at }x=\pm \frac{a}{2},\\&\quad y=\pm \frac{b}{2}; \end{aligned}$$

• (ii) Immovable clamped case (CCI):

  $$\begin{aligned}&w=0,\;w,_n =0,v=0,u=0\hbox { at }x=\pm \frac{a}{2},\\&\quad y=\pm \frac{b}{2}. \end{aligned}$$

Fig. 3

Non-dimensional ratio of frequencies $\omega _{nl} /\omega _l$ versus $W_{\max }/h$ of nonlinear vibration cylindrical $\left( {k_1 =0.1;\;k_2 =0} \right)$ and spherical $\left( {k_1 =0.1;\;k_2 =0.1} \right)$ isotropic panels

Fig. 4

The effect of curvature on the nonlinear to the linear frequency ratio of spherical shells ($0^{\circ }/90^{\circ }/0^{\circ }$) with square clamped cutout $\left( {h/{2a}=0.01;c/{2a}=0.1;k_1 =0.1=\;k_2}\right)$: a SC; b CC

The relation between the nonlinear frequency ratio $\omega _{nl} /\omega _l$ and non-dimensional maximum amplitude $W_{\max }/h$ regarding cross-ply $(0^{\circ }/90^{\circ }/0^{\circ }/90^{\circ }/0^{\circ })$ and angle ply $(45^{\circ }/-45^{\circ }/45^{\circ }/-45^{\circ }/45^{\circ })$ of the thin square plates $(a/b=1, h/2a=0.01)$ is reported in Table 7.

The comparison of results reported in Table 7 confirms accuracy of the proposed approach. Further new nonlinear results are discussed.

Problem 6

Let us consider the problem of nonlinear free vibration of three- layered shallow shells (Fig. 1b, c) with two types of boundary conditions: completely clamped border (CC), simply supported on external edge and clamped cutout (SC).

The effect of different curvatures on amplitude–frequency dependence for cross-ply $(0^{\circ }/90^{\circ }/0^{\circ })$ shells made of material M2 and thickness $h/2a=0.01$ with the square clamped cutout of size $c/2a=0.1$ is shown in Fig. 4.

From observed curves, it follows that with the amplitude increase the behavior of the backbone curves of investigated cross-ply shells of material M2 is more rigid for plates than for another types of curvatures despite boundary conditions. It means that ratio $\omega _{nl}/\omega _l$ is essentially greater for plates than for shells.

The effect of material on amplitude–frequency dependence for spherical shells $(0^{\circ }/90^{\circ }/0^{\circ })$ of SC and CC boundary conditions with the rectangular clamped cutout for three types of materials (M1, M2, M3) is presented in Fig. 5 ($a/b=1; c/2a=0.15; c/d=2; h/2a=0.1$ and $h/2a=0.01$).

Fig. 5

The effect of material on the nonlinear to the linear frequency ratio of spherical shells with rectangular cutout: a SC; b CC

Fig. 6

The effect of lamination on the nonlinear to the linear frequency ratio of spherical shells with square cutout: a SC; b CC

Fig. 7

The effect of layers number on the nonlinear to the linear frequency ratio of spherical shells with square cutout: a SC; b CC

Fig. 8

The effect of cutout type on the nonlinear to the linear frequency ratio of spherical ($0^{0}/90^{0}/0^{0}$) shells of M2 material: a SC; b CC

For shells with boundary conditions SC, we can state that backbone curves for shells of material M1 are more rigid than for shells of materials M2 and M3 for both thicknesses. But for CC shells backbone curves are more rigid for shells of material M3 than for shells of materials M1 and M2 for both thicknesses. Also, these curves are more rigid for thick shells.

The effect of lamination scheme on amplitude–frequency dependencies for spherical shells with SC and CC boundary conditions is shown in Fig. 6. It is assumed that shell is three layers and made of material M2. It has the square cutout of size $c/a=0.2$ and thickness $h/2a=0.01$ and $h/2a=0.1$.

We can see that for completely clamped CC shells the most rigid behavior of backbone curves is observed for cross-ply lamination $(0^{\circ }/90^{\circ }/0^{\circ })$, while for SC shells most rigid behavior is observed for angle-ply $(45^{\circ }/-45^{\circ }/45^{\circ })$ shells despite different thicknesses.

The effect of number of layers on amplitude–frequency dependence for spherical shells of SC and CC boundary conditions is presented in Fig. 7. Investigated shells consist of three $(0^{\circ }/90^{\circ }/0^{\circ })$ or five $(0^{\circ }/90^{\circ }/0^{\circ }/90^{\circ }/0^{\circ })$ layers and made of material M2. They have the square central cutout of size $c/a=0.2$. The values of thickness are accepted: $h/2a=0.01$ and $h/2a=0.1$. According to the observed graphs, we can state that the backbone curve of the three-layered shell behaves more rigid than the one of five layers for SC thick shells ($h/2a=0.1$). On the other hand, backbone curves for five- and three- layered thin SC shells ($h/2a=0.01$) practically coincide (divergence is less than 2%). As for the CC shells, we can conclude that the curves for three-layered shells are more rigid for both thicknesses.

The effect of cutout type on amplitude–frequency dependence for three-layered square spherical shells made of material M2 is presented in Fig. 8. Two types of the boundary conditions (SC, Fig. 8a) and (CC Fig. 8b) are studied. Cutouts are square ($c/2a=d/2a=0.1$) or rectangular ($c/2a=0.15; c/d=2$) ones. Lamination scheme is defined as $(0^{0}/90^{0}/0^{0})$. The values of thickness are taken as: $h/2a=0.01$ and $h/2a=0.1$.

We can see that type of cutout is not essential for behavior of backbone curves of thin ($h/2a=0.01$) CC shells (Fig. 8b). Note that for thin SC shells with rectangular cutout backbone curves are more rigid curves. As for thick shells, square cutout results in more rigid behavior of backbone curves for both types of boundary conditions.

5 Conclusions

The developed numerical–analytical approach based on the R-functions theory is used to carry out nonlinear vibration analysis of laminated shallow shells with central square and rectangular clamped cutouts. Multilayered shells made of different materials with different curvatures are investigated. Different types of boundary conditions on outer contour are examined. The new amplitude–frequency curves are constructed using the single-mode approximation by the Runge–Kutta method. Effect of different parameters (thickness of layers, lamination scheme, curvatures, number of layers, size of cutout, boundary conditions) on behavior of backbone curves is studied. Numerical results obtained by proposed method and created software are found in good agreement with those available in the open literature. The proposed method can be readily extended to shallow shells with cutouts of different form and different ways of their fixing.