Abstract
We construct new functional encryption schemes that combine the access control functionality of attribute-based encryption with the possibility of performing linear operations on the encrypted data. While such a primitive could be easily realized from fully fledged functional encryption schemes, what makes our result interesting is the fact that our schemes simultaneously achieve all the following properties. They are public-key, efficient and can be proved secure under standard and well established assumptions (such as LWE or pairings). Furthermore, security is guaranteed in the setting where adversaries are allowed to get functional keys that decrypt the challenge ciphertext. Our first results are two functional encryption schemes for the family of functions that allow users to embed policies (expressed by monotone span programs) in the encrypted data, so that one can generate functional keys to compute weighted sums on the latter. Both schemes are pairing-based and quite generic: they combine the ALS functional encryption scheme for inner products from Crypto 2016 with any attribute-based encryption schemes relying on the dual-system encryption methodology. As an additional bonus, they yield simple and elegant multi-input extensions essentially for free, thereby broadening the set of applications for such schemes. Multi-input is a particularly desirable feature in our setting, since it gives a finer access control over the encrypted data, by allowing users to associate different access policies to different parts of the encrypted data. Our second result builds identity-based functional encryption for inner products from lattices. This is achieved by carefully combining existing IBE schemes from lattices with adapted, LWE-based, variants of ALS. We point out to intrinsic technical bottlenecks to obtain richer forms of access control from lattices. From a conceptual point of view, all our results can be seen as further evidence that more expressive forms of functional encryption can be realized under standard assumptions and with little computational overhead.
You have full access to this open access chapter, Download conference paper PDF
Similar content being viewed by others
1 Introduction
Public-key encryption allows the owner of a secret key \(\mathsf {sk}\) to decrypt any ciphertext created with respect to a corresponding public key \(\mathsf {pk}\). At the same time, without \(\mathsf {sk}\), one should not be able to extract any information whatsoever about the encrypted plaintext. This all-or-nothing feature is becoming restrictive nowadays as, in many applications, a much more fine grained access control to data is required. Functional encryption addresses this need by providing an encryption mechanism where decryption keys are associated with functions. Specifically, given a ciphertext \({\mathsf {Enc}}(m)\) and a secret key \(\mathsf {sk}_f\) associated to some function f, the holder of \(\mathsf {sk}_f\) learns f(m) and nothing else.
Security for functional encryption is formalized via a variant of the standard indistinguishability notion. In a nutshell, this notion states that an adversary who is allowed to see secret keys corresponding to functions \(f_1, \ldots f_n\) should not be able to say which of the challenge messages \(m_0\) or \(m_1\) has been encrypted, as long as \(f_i(m_0)=f_i(m_1)\), for all i. This indistinguishability notion has been proposed in [25, 50] and shown inadequate for certain, somewhat complex, functionalities. These authors also suggested an alternative, simulation based, security notion that however turns out to be impossible to achieve for general functionalities without introducing additional restrictions. See [25, 50] for details.
Since its introduction, functional encryption has attracted a lot of interest. Known results can be broadly categorized as focusing on (1) feasibility results for general functionalities, and on (2) concrete, efficient realizations for restricted functionalities of practical interest. Constructions of the first type are all horrendously inefficient. Also, they either rely on quite unstable assumptions (e.g. indistinguishability obfuscation) or impose severe restrictions on the number of secret keys that can be issued. Constructions of the second type, on the other hand, are known only for the case of linear functions and quadratic functions. Over the last few years, significant research efforts have been devoted to the quest of improving these constructions along different directions. For the case of the inner-product functionality (IPFE) [3], this meant, for instance, improved security guarantees (e.g. [4, 11, 20, 26]), function hiding realizations (e.g. [22, 32, 33]), multi-input extensions (e.g. [5, 7]), decentralized schemes (e.g. [1, 2, 30, 46]), unbounded-size vectors (e.g. [34, 54]) and specialized variants (e.g. [19]). For the case of quadratic functions, current schemes are limited to [18, 35] in the public-key setting. Note that FE for inner products, which is the focus of this work, can be used a building block to obtain FE for quadratic functions. This fact, implicit in [18], is made explicit in [35] and in the private-key variants [14, 47].
In spite of these efforts, only a few convincing practical applications of the primitive have been proposed so far. Notable examples include the recent non interactive protocol for hidden-weight coin flips from [31], a practical construction of function-hiding inner product FE with applications such as in biometric authentication, nearest-neighbor search on encrypted data in [45], an application of functional encryption for quadratic functions for performing private inference on encrypted data in [51].
A possible explanation for this is that, behind its charming theoretical appearance, functional encryption hides a fragile and potentially dangerous nature: each new released secret key inherently leaks information. This becomes particularly painful for the case of inner products, as, when encrypting plaintexts of length, say, n, holding n secret keys allows, in general, to recover the full plaintext completely. While this might seem inherent in the nature of IPFE, one might wonder if additional measures might be put in place to reduce leakage and make the primitive more appealing for applications. Think for instance of the case of a medical database. To preserve privacy while maintaining the possibility of performing simple descriptive statistics (such as the weighted mean) on the data, one might decide to encrypt the database using IPFE. A drawback of this solution, however, is that the confidentiality of the whole database is compromised if a sufficiently large number of different keys is released. This is problematic since this threshold might be easy to reach when many users access the database.
A natural way to limit the inherent information leakage of existing IPFE schemes would be to use FE primitives with more sophisticated functionalities. Ideally, this primitive should allow to embed access policies in the (encrypted) data while allowing to compute weighted sums on the latter. More precisely, each key should allow to obtain the desired inner product only when some appropriate access policy is satisfied. Going back to our medical example, this means that the confidentiality of a particular database entry would be compromised only if sufficiently many different keys satisfying the ciphertext policy associated with that entry are released.
Another way to look at the question, is providing additional security guarantees with respect to basic identity or attribute based encryption schemes. These typically control who is authorized to decrypt the data. Still, once the data is accessed, no additional control is possible: authorized users get the full information, while others get nothing. In this sense, it is natural to consider encryption primitives that, beyond access control, also permit to more carefully tune the information leakage.
Notice that the mechanisms above are easy to realize if one is willing to resort to functional encryption schemes for general functionalities. The trouble with this is that such a solution would be of little (if any) practical interest. Our goal, on the other hand, is to develop a scheme that implements the features above while retaining as much as possible all the nice properties of currently known IPFEs.
This motivates the following question.
Is it possible to develop an efficient, public-key, functional encryption scheme that allows users both to embed access policies in the encrypted data and to generate decryption keys to compute inner products on the data?
A Trivial Generic Approach. Since ABE and IPFE are both well-studied primitives, the first natural question is whether we can easily combine existing schemes to achieve our target notion. In the target scheme, each ciphertext is associated with a predicate \(\mathsf {P}\) and encrypts a vector \(\varvec{x}\). Each functional decryption key \(\mathsf {sk}_{\varvec{y},\mathsf {att}}\) is associated with an attribute \(\mathsf {att}\) and a vector \(\varvec{y}\). Decryption recovers \(\langle \varvec{x}, \varvec{y} \rangle \) if \(\mathsf {P}(\mathsf {att})=1\). If it is not the case, no information about \(\varvec{x}\) should be revealed.
Now, consider the approach of encrypting a plaintext via an IPFE and then encrypting the resulting ciphertext via the ABE. This is not secure against collusions as, once the outer ciphertext is decrypted, the inner one becomes completely independent from the ABE. To see why, assume we have keys for \(\mathsf {sk}_{\varvec{y}_0,\mathsf {att}_0}\) and \(\mathsf {sk}_{\varvec{y}_1,\mathsf {att}_0}\) and a ciphertext \(\mathsf {ct}\), encrypting a vector \(\varvec{x}\) under the predicate \(\mathsf {P}\) such that \(\mathsf {P}(\mathsf {att}_0)=1\) and \(\mathsf {P}(\mathsf {att}_1)=0\). The trivial solution allows to use \(\mathsf {sk}_{\varvec{y}_0,\mathsf {att}_0}\) to obtain the original IPFE ciphertext, which can then be used with \(\mathsf {sk}_{\varvec{y}_1,\mathsf {att}_1}\) to obtain \(\langle \varvec{x},\varvec{y}_1 \rangle \) (even though we should only have been able to compute \(\langle \varvec{x},\varvec{y}_0 \rangle \)). This means that mix-and-match attacks are possible. In fact, there seems to be no trivial solution to this problem.
Another Trivial Generic Approach. One other approach to limit the leakage is by encrypting various databases under a different IPFE public key for every recipient. Apart from the fact that this leads to a prohibitive blow-up in size, it would not be possible to aggregate data between different databases. Our solution has neither of these limitations and ensures that the ciphertext size is independent of the number of potential recipients.
Our Contributions. In this paper, we construct schemes for inner-product functional encryption with fine-grained access control. Our realizations are both efficient and provably secure under standard and well-established assumptions.
The key distinguishing feature of our constructions is that they can be proved secure in the, technically more challenging, setting where the adversary is allowed to (get keys to) decrypt the challenge ciphertext. Let us explain this more in detail. Popular specializations of functional encryption (such as identity-based encryption (IBE) [23, 53] and attribute-based encryption [42, 52]) are ones where the message is interpreted as a pair \((\mathsf{I},m)\), where m is the actual message (often called the “payload”) and \(\mathsf{I}\) is a string, referred to as the index (or in the context of ciphertext-policy ABE [21], a predicate), that can be either public or private. For these schemes, confidentiality of the payload is guaranteed as long as no decryption keys associated with attributes that satisfy the predicate are issued. In our case, we still guarantee a meaningful security notion when keys which allow users to decrypt the payload are issued.
Private-index schemes also provide meaningful security guarantees when keys that decrypt are leaked, namely, they still hide the index in that case. However, as opposed to public-index schemes, for which we have constructions for all circuits from standard assumptions [24, 40], such schemes can only handle restrictive policies, that are expressed by orthogonality testing (also referred to as inner-product encryption [44]), or assume a weaker security property, called weak attribute hiding, which limits the set of keys that the adversary can get. Namely, this property dictates that the adversary is only allowed to ask secret keys corresponding to functions that cannot be used to decrypt the challenge ciphertext. As observed in [41], a fully attribute-hiding predicate encryption for circuits would bring us tantalizing close to getting indistinguishability obfuscation, which explains why they are much harder to realize in practice.
We consider both public-index schemes where policies are expressive (they can be expressed by monotone span programs, which capture Boolean formulas), and private-index schemes for orthogonality testing (which captures constant depth Boolean formulas). In both settings, we permit a fine-tuned access to the payload, which, from a technical point of view, involve providing security even when the adversary obtains keys that decrypt the challenge ciphertext (even in the public-index case).
IP-FE with fine-grained access control from pairings. Our first main result is the construction of functional encryption schemes for the family of functions that allows users to embed policies on the encrypted data, so that one can generate decryption keys that computes weighted sums on the latter. More precisely, in our schemes, each ciphertext is associated with a predicate \(\mathsf {P}\) and encrypts a (small norm) vector \(\varvec{x}\). Each functional decryption key is associated with an attribute \(\mathsf {att}\) and a (small norm) vector \(\varvec{y}\). Decryption recovers \(\langle \varvec{x}, \varvec{y} \rangle \) if \(\mathsf {att}\) satisfies \(\mathsf {P}\). If this is not the case, security guarantees that no information about \(\varvec{x}\) is revealed.
Our constructions are quite generic and show that it is possible to combine existing pairing-based attribute-based encryption with the IPFE from [11]. Our construction relies on any attribute-based encryption that uses the dual-system encryption methodology [56]. In particular, we provide a modular framework that turns any ABE that supports the class of predicates \(\mathcal {P}\) into a functional encryption scheme for the functions described by an attribute \(\mathsf {att}\in \mathcal {U}\) and a vector \(\varvec{y}\), that given as input a vector \(\varvec{x}\) and a predicate \(\mathsf {P}\in \mathcal {P}\), outputs \(\langle \varvec{x}, \varvec{y} \rangle \) if \(\mathsf {P}(\mathsf {att})=1\) and \(\bot \) otherwise. For correctness to hold we require that both \(\varvec{x}\) and \(\varvec{y}\) are vectors of polynomially-bounded dimension and norm. We consider both the case where the policy \(\mathsf {P}\) associated with a ciphertext is public, or at the contrary, remains hidden. As explained previously, leveraging state of the art pairing-based ABE, we obtain an FE for \(\mathcal {P}\) described by monotone span programs, and an FE for \(\mathcal {P}\) for any constant depth formula, where the formula itself remains hidden.
From a technical point of view, our first realization combines the IPFE from [11] with any predicate encoding for prime-order pairing groups. In a nutshell, predicate encodings [16, 57] are a one-time secure, private key, statistical variant of ABE that are much simpler to construct and to deal with. The resulting construction achieves simulation security, but only in a selective sense, and unfortunately this happens to be the case even if the underlying building blocks achieve adaptive security. Informally, this comes from the fact that our security model explicitly allows the adversary to (get keys to) decrypt the challenge ciphertext. Technically, this means that, throughout the security proof, only functional decryption keys associated with pairs \((\mathsf {att},\varvec{y})\) for which \({\mathcal {P}}^*(\mathsf {att})=0\) can be turned into semi-functional ones (here \({\mathcal {P}}^*\) denotes the predicate chosen by the adversary for the challenge ciphertext). Following the dual-system encryption methodology, semi-functional keys refer to keys that cannot decrypt successfully the challenge ciphertext, but can decrypt correctly any other honestly generated ciphertext. Keys for which \({\mathcal {P}}^*(\mathsf {att})=1\) cannot be turned semi-functional as otherwise they would fail to (correctly) decrypt the challenge ciphertext. Such a decryption issue does not arise in typical ABE settings, as their security model explicitly prevents the adversary to decrypt the challenge ciphertext.
Our second construction circumvents this difficulty and obtains adaptive security by generalizing the techniques introduced in [49], later improved in [28] in the context of fully-hiding predicate encryption for inner product testing. Indeed, in fully-hiding predicate encryption, the proof also has to explicitly deal with the decryption issue sketched above. To do so, we introduce the notion of function encoding, which is the analogue of predicate encoding for functional encryption. Recall that predicate encodings, introduced in [16, 57], are a “dumbed-down” version of ABE, and provide a framework to extend the dual system encryption methodology introduced by [56] in the context of adaptively-secure IBE to a broad class of ABE, including inner product testing, or Boolean formulas. In our case, we use the abstraction of function encoding to generalize the information-theoretic argument from [28] to capture a broad class of functional encryption, including inner-product FE with access control expressed by inner-product testing, Boolean formulas, and more.
Similarly to predicate encoding, which has received significant interest (particularly as its more general form referred to as Conditional-Disclosure of Secret, e.g. [15, 37, 39, 48]), we believe the notion of function encoding could be interesting on its own.
In a nutshell, functional encodings enhance a more sophisticated information theoretic argument than traditional Dual System Encryption, where secret keys are switched to a semi-functional mode that still allows them to decrypt the challenge ciphertext, but yield different information than normally generated secret keys. Indeed, in the security proof, the ciphertext will encode the original message \(\varvec{x}_0\), but also the message \(\varvec{x}_1\), where the pair \((\varvec{x}_0,\varvec{x}_1)\) is chosen by the adversary during the indistinguishability game. Normal keys will decrypt with respect to the message \(\varvec{x}_0\), whereas the semi-functional keys will decrypt with respect to the message \(\varvec{x}_1\), thereby successfully proving security.
Identity-Based inner-product FE from lattices. Our second main result is the construction of two identity-based inner-product FE (IB-IPFE) from the LWE assumptionFootnote 1. Both schemes combine existing LWE-based IBE with the LWE-based inner-product FE from [11]. The first one uses the IBE from [38], where the public key described a trapdoor function for which it is hard to sample short preimage. Given the trapdoor—the master key of the IBE—it is possible to efficiently compute a short preimage of any target image. Each identity \(\mathsf {id}\) yielding a different image, the corresponding preimage, a matrix of short coefficients \(\varvec{M}_\mathsf {id}\), defines the user secret key for \(\mathsf {id}\). As it turns out, to produce functional decryption keys associated with identity \(\mathsf {id}\) and vector \(\varvec{y}\), we can simply give a projection \(\varvec{M}_\mathsf {id}\varvec{y}\). We prove this remarkably simple scheme adaptively-secure in the random oracle model using the security argument of [38] to handle all functional decryption keys that do not decrypt the challenge ciphertext, whereas we use the proof techniques of [11] to take care of all keys that decrypt the challenge ciphertexts.
Our second constructions relies on the IBE from [10], where the public key can be used to derive an identity-based public key \(\mathsf {pk}_\mathsf {id}\) for any identity \(\mathsf {id}\). The public key \(\mathsf {pk}_\mathsf {id}\) describes a trapdoor function, for which, as in [38], it is hard to compute short preimages. A fixed target image, which belongs to the range of all the trapdoor functions \(\mathsf {pk}_\mathsf {id}\) is made public. The user secret key for \(\mathsf {id}\) is a short preimage of the fixed target image, for the function \(\mathsf {pk}_\mathsf {id}\). Once again, user secret keys happen to be matrices, which can be projected to obtain functional decryption keys \(\mathsf {sk}_{\mathsf {id},\varvec{y}}\) and get an IB-IPFE.
As a bonus, our schemes inherit the anonymity property of the underlying IBE, that is, the identity associated with a ciphertext remains hidden as long as no functional decryption key that decrypts is issued.
Richer access control from lattices. The puncturing technique that is used in the security proof of [10] has been generalized to obtain ABE for all circuits in [24]. However, there are intrinsic technical limitations in our proof strategy which prevent from extending our scheme to the ABE case. In particular, to use the security argument of the IPFE from [11] as part of our own security proof, we rely on a lazy sampling argument: to obtain a functional decryption key \(\mathsf {sk}_{\mathsf {id}^\star ,\varvec{y}}\) where \(\mathsf {id}^\star \) is the identity of the challenge ciphertext, we first sample a matrix with short coefficients \(\varvec{M}_{\mathsf {id}^\star }\) and set the fixed public target image such that this short matrix is a preimage of the target image by the function described by the public key \(\mathsf {pk}_{\mathsf {id}^\star }\). Concretely, the target image is a matrix \(\varvec{T}\), the public key \(\mathsf {pk}_{\mathsf {id}} = \varvec{A}_{\mathsf {id}^\star }\) is also a matrix, and we want \(\varvec{A}_{\mathsf {id}^\star } \varvec{M}_{\mathsf {id}^\star } = \varvec{T}\), where the matrices have matching dimensions. We can first sample \(\varvec{T}\), then use the trapdoor to compute \(\varvec{M}_{\mathsf {id}^\star }\) satisfying the previous equation, but we can also first sample a short \(\varvec{M}_{\mathsf {id}^\star }\), and then set \(\varvec{T} = \varvec{A}_{\mathsf {id}^\star } \varvec{M}_{\mathsf {id}^\star }\). This produces identically distributed matrices, and in the latter case, we can produce \(\varvec{M}_{\mathsf {id}^\star }\) without knowing the trapdoor, which is necessary in the security proof. The matrix \(\varvec{M}_{\mathsf {id}^\star }\) will actually correspond to the master secret key of the IPFE of [11]. The key \(\mathsf {sk}_{\mathsf {id}^\star ,\varvec{y}}\) is \(\varvec{M}_{\mathsf {id}^\star } \varvec{y}\), as described above, which corresponds to a functional decryption key for \(\varvec{y}\) in the scheme from [11]. However, this lazy sampling argument is inherently limited to the case where only one attribute (here, identity) satisfies the predicate (here, identity) of the challenge ciphertext. In the case of ABE, there can be multiple such attributes for a given predicate. We leave combining ABE for circuits with inner-product FE as a challenging open problem.
Multi-input extensions. As a final contribution, we show how to generalize our pairing-based IP-FE scheme to the multi input setting. Our realization is rather generic in the sense that it converts any single input construction of the primitive, satisfying few additional properties, into a multi input scheme supporting the same class of functionalities. Specifically, the required properties are that (1) the underlying IP-FE is pairings-based (2) its encryption and key generation algorithms can take as input large norm vectors and (3) its encryption algorithm enjoys linearly homomorphic properties. Recall that, to guarantee efficient decryption, our parings based constructions require that both the plaintext vectors \(\varvec{x}\) and the function vector \(\varvec{y}\) have small norm. What we require now is that, if one is willing to give up efficient decryption, the small norm condition can be relaxed (i.e. decryption returns an encoding of the output rather than the output itself).
On a technical level the transformation follows very closely the generic single-input to multi-input IP-FE transform by Abdalla et al. [5, 7]. In this sense, we believe that the interesting contribution is the primitive itself. Indeed, information leakage is even more problematic in the multi input setting, as here users can combine their inputs with many different ciphertexts coming from other users. In the case of n users this easily leads to an information leakage that completely destroys security. While countermeasures could be put in place to limit the encryption and key queries that the adversary is allowed to ask, by resorting for instance, to the notion of multi-client IPFE, where ciphertexts are associated with time-stamps, and only ciphertext with matching time-stamps can be combined (e.g. [30]) we believe that our proposed primitive provides a more general and versatile solution to the problem.
Our construction allows users to compute weighted sums on encrypted vectors each associated with a possibly different access structure. In our medical example above, this might be used to add even more granularity to the access control of data. That is, some users may obtain keys that can compute statistics on some, but not all, the encrypted data. For instance, doctors in a hospital may be able to compute on a different set of encrypted data then employees of a health insurance company. Moreover, multi-input allows users to aggregate data coming from different sources.
Related Works. We emphasize that the primitive considered in this paper is natural, and as such, it has also been considered in previous works, either implicitly or explicitly.
In [34], Dufour-Sans and Pointcheval describe an identity-based functional encryption scheme for inner products as a byproduct of their realization of unbounded IPFE with succinct keys. Their construction is proven selectively secure in the random-oracle model based on the standard decisional bilinear Diffie-Hellman assumption. Compared to their construction, our pairing-based schemes provide support for significantly richer functionalities and are proven secure in the standard model.
In prior works [13, 43], the authors define a so-called partially-hiding FE allowing for the computation on two inputs (x, y), where the input x is seen as a public attribute and the other one, y, remains hidden. The construction of [13] supports degree-2 computation on the private input y, and degree-1 computation on the public input x. Its security rely on the generic bilinear group model. In [43], functional secret keys support the computation of degree-2 polynomials on the private input, as in [13], but it supports \(\mathsf {NC}_0\) computation on the public input. As an additional benefit, the security of their construction rely on a standard assumption on pairing groups (namely, SXDH). In an early version of their eprint [36] dating back to 2019, Jain, Lin and Sahai provided a partially-hiding FE allowing for degree-2 computation on the private input, and \(\mathsf {NC}_1\) computation on the public inputs; relying on the SXDH assumption. All of these schemes are in the secret-key setting. Our scheme has the advantage to be public-key, although our techniques inherently rely on the linearity of the inner-product functionality. All of those works focus on simulation, selective security, and use partially-hiding FE in the context of providing indistinguishability obfuscation.
In [29], Chen, Zang and Yiu propose a construction of attribute-based functional encryption for inner products. Like ours, their construction is pairing-based, but it is less generic, and relies on three decisional assumptions on bilinear groups of composite order \(N=p_1p_2p_3\) (\(p_1,p_2,p_3\) distinct primes), which are less efficient than prime-order groups. Our realizations, on the other hand, build generically from any dual system encryption-based ABE. In terms of security, their construction guarantees indistinguishability against adaptive adversaries in the standard model, but only in the weaker setting discussed above, where keys that decrypt cannot be leaked to the adversary, which does not capture the essence of the notion that we achieve, since it does not offer any additional security guarantees with respect to standard ABE schemes. We recall that all our schemes explicitly allow the adversary to get functional keys to decrypt the challenge ciphertext. Also, while our first scheme is only selectively secure, it achieves this in the stronger simulation setting. Finally, no extensions to the multi-input case are considered in [29].
In [58], Wee builds partially hiding predicate encryption schemes which simultaneously generalize existing attribute-based and inner-product predicate encryption schemes. Although his constructions support a larger class of policies than our constructions, the decryptor still has access to the payload message (a KEM key in this case) once the access policy is satisfied or to a uniformly random value otherwise. We see it as an interesting open problem to extend his work to also permit selective computations over the payload message when the access policy is satisfied.
Organization. Section 2 recalls some standard notation together with the syntax and security definitions for functional encryption schemes. Section 3 presents our constructions of inner-product FE with fine-grained access control from pairings. Section 4 describes our first lattice-based construction of identity-based functional encryption in the random-oracle model. In the full version [6], we also describe a lattice-based standard-model construction of identity-based functional encryption and present a multi-input extension of our schemes.
2 Preliminaries
Notation. We denote with \(\lambda \in \mathbb {N}\) a security parameter. A probabilistic polynomial time (PPT) algorithm \(\mathcal{A}\) is a randomized algorithm for which there exists a polynomial \(p(\cdot )\) such that for every input x the running time of \(\mathcal{A}(x)\) is bounded by p(|x|). We say that a function \(\varepsilon : \mathbb {N}\rightarrow \mathbb {R}^+\) is negligible if for every positive polynomial \(p(\lambda )\) there exists \({\lambda }_0 \in \mathbb {N}\) such that for all \(\lambda > {\lambda }_0\): \(\varepsilon (\lambda ) < 1/p(\lambda )\). If S is a set, \(x \leftarrow _{\textsc {r}}S\) denotes the process of selecting x uniformly at random in S. If \(\mathcal{A}\) is a probabilistic algorithm, \(y \leftarrow _{\textsc {r}}\mathcal{A}(\cdot )\) denotes the process of running \(\mathcal{A}\) on some appropriate input and assigning its output to y. For a positive integer n, we denote by [n] the set \(\{1,\ldots , n\}\). We denote vectors \(\varvec{x} = (x_i)\) and matrices \(\mathbf{A}= (a_{i,j})\) in bold. For a set S (resp. vector \(\varvec{x}\)) |S| (resp. \(|\varvec{x}|\)) denotes its cardinality (resp. number of entries). Also, given two vectors \(\varvec{x}\) and \(\varvec{x}'\) we denote by \(\varvec{x} \Vert \varvec{x}'\) their concatenation. By \(\equiv \), we denote the equality of statistical distributions, and for any \(\varepsilon >0\), we denote by \(\approx _\varepsilon \) the \(\varepsilon \)-statistical difference of two distributions. For any \(x \in \mathbb {R}\), we denote by \(\lfloor x \rfloor \) the largest integer less than or equal to x, while for any \(z \in [0,1]\), we denote by \(\lfloor z \rceil \) the closest integer to z. For all \(\varvec{a}_i \in \mathbb {Z}_p^{n_i}\) for \(i\in [n]\), we denote by \((\varvec{a}_1,\ldots ,\varvec{a}_n) \in \mathbb {Z}^{\sum _{i \in [n]} n_i}_p\) a column vector, and by \((\varvec{a}^\top _1|\cdots | \varvec{a}^\top _n) \in \mathbb {Z}_p^{1 \times \sum _{i \in [n]} n_i}\) a row vector.
2.1 Pairing Groups
Let \({\mathsf {PGGen}}\) be a PPT algorithm that on input the security parameter \(1^\lambda \), returns a description \(\mathcal {PG}=({\mathbb {G}}_1, {\mathbb {G}}_2, {\mathbb {G}}_T, p, P_1, P_2, e)\) where for all \(s\in \{1,2,T\}\), \({\mathbb {G}}_s\) is an additive cyclic group of order p for a \(2\lambda \)-bit prime p. \({\mathbb {G}}_1\) and \({\mathbb {G}}_2\) are generated by \(P_1\) and \(P_2\) respectively, and \(e: {\mathbb {G}}_1 \times {\mathbb {G}}_2 \rightarrow {\mathbb {G}}_T\) is an efficiently computable (non-degenerate) bilinear map. Define \(P_T := e(P_1, P_2)\), which is a generator of \({\mathbb {G}}_T\), of order p. We use implicit representation of group elements. For \(s \in \{1,2,T\}\) and \(a \in \mathbb {Z}_p\), define \([a]_s = a \cdot P_s \in {\mathbb {G}}_s\) as the implicit representation of a in \({\mathbb {G}}_s\). More generally, for a matrix \(\mathbf {A}= (a_{ij}) \in \mathbb {Z}_p^{n\times m}\) we define \([\mathbf {A}]_s\) as the implicit representation of \(\mathbf {A}\) in \({\mathbb {G}}_s\):
Given \([a]_1\) and \([b]_2\), one can efficiently compute \([a \cdot b]_T\) using the pairing e. For matrices \(\mathbf {A}\) and \(\mathbf {B}\) of matching dimensions, define \(e([\mathbf {A}]_1, [\mathbf {B}]_2) := \left[ \mathbf {A}\mathbf {B}\right] _T\). For any matrix \(\mathbf {A}, \mathbf {B}\in \mathbb {Z}_p^{n \times m}\), any group \(s \in \{1,2,T\}\), we denote by \([\mathbf {A}]_s + [\mathbf {B}]_s = [\mathbf {A}+\mathbf {B}]_s\).
For any prime p, we define the following distributions. The \(\mathsf {DDH}\) distribution over \(\mathbb {Z}_p^2\): \(a \leftarrow _{\textsc {r}}\mathbb {Z}_p\), outputs \(\varvec{a}:= {1 \atopwithdelims ()a}\). The \(\mathsf {DLIN}\) distribution over \(\mathbb {Z}_p^{3 \times 2}\): \(a,b \leftarrow _{\textsc {r}}\mathbb {Z}_p\), outputs \(\mathbf {A}:= \begin{pmatrix} a &{} 0 \\ 0 &{} b \\ 1 &{} 1 \end{pmatrix}\).
Definition 2.1
(DDH assumption). For any adversary \(\mathcal {A}\), any group \(s \in \{1,2,T\}\) and any security parameter \(\lambda \), let
where the probabilities are taken over \(\mathcal {PG}\leftarrow _{\textsc {r}}\mathsf {GGen}(1^\lambda ,d)\), \(\varvec{a} \leftarrow _{\textsc {r}}\mathsf {DDH}\), \(r \leftarrow _{\textsc {r}}\mathbb {Z}_p\), \(\varvec{u}\leftarrow _{\textsc {r}}\mathbb {Z}_p^2\), and the random coins of \(\mathcal {A}\). We say DDH holds in \({\mathbb {G}}_s\) if for all PPT adversaries \(\mathcal {A}\), \(\mathsf {Adv}^{\mathsf {DDH}}_{{\mathbb {G}}_s,\mathcal {A}}(\lambda )\) is a negligible function of \(\lambda \).
Definition 2.2
(SXDH assumption). For any security parameter \(\lambda \) and any pairing group \(\mathcal {PG}=({\mathbb {G}}_1, {\mathbb {G}}_2, {\mathbb {G}}_T, p, P_1, P_2, e) \leftarrow _{\textsc {r}}{\mathsf {PGGen}}(1^\lambda )\), we say SXDH holds in \(\mathcal {PG}\) if DDH holds in \({\mathbb {G}}_1\) and \({\mathbb {G}}_2\).
2.2 Functional Encryption
Definition 2.3
(Functional Encryption [25, 50]). Let \(\mathcal {F}\) be a family of functions, with \(f \in \mathcal {F}\) defined as \(f : \mathcal {X}\rightarrow \mathcal {Y}\). A functional encryption scheme for \(\mathcal {F}\) consists of the following algorithms:
-
\({\mathsf {Setup}}(1^\lambda , \mathcal {F})\): takes as input the security parameter \(\lambda \) and a description of the function family \(\mathcal {F}\), and outputs a master public key \(\mathsf {mpk}\) and a master secret key \(\mathsf {msk}\). The master public key \(\mathsf {mpk}\) is assumed to be part of the input of all the remaining algorithms.
-
\({\mathsf {Enc}}(x \in \mathcal {X})\): takes as input the master public key \(\mathsf {mpk}\) and a message
 , and it outputs a ciphertext
, and it outputs a ciphertext  .
. -
 : takes as input the master secret key \(\mathsf {msk}\), a function
: takes as input the master secret key \(\mathsf {msk}\), a function  , and it outputs a decryption key
, and it outputs a decryption key  .
. -
 : takes as input a decryption key
: takes as input a decryption key  along with a ciphertext
along with a ciphertext  , and it outputs a value
, and it outputs a value  or the special symbol
or the special symbol  if it fails.
if it fails.
A scheme as defined above is correct if for all security parameter \(\lambda \),  , and
, and  , we have:
, we have:  where the probability is taken over
where the probability is taken over  ,
,  ,
,  .
.
Partial Information. For the rest of this paper, it is convenient to split the output of the function in two parts: \((f(x),\mathsf {part}(x))\), where \(\mathsf {part}(x)\) is some partial information on x that is independent from f. For instance, we will consider the case of \(x:=(\mathsf {P},\varvec{x})\), where \(\mathsf {P}\) is a predicate, and \(\varvec{x}\in \mathbb {Z}^d\) is a vector of dimension d; each function is described by a pair \((\mathsf {att},\varvec{y})\) where \(\mathsf {att}\) is an attribute, and \(\varvec{y}\in \mathbb {Z}^d\). The output f(x) reveals \(\varvec{x}^\top \varvec{y}\) and \(\mathsf {P}\) if \(\mathsf {P}(\mathsf {att})=1\); only \(\mathsf {P}\) otherwise. Note that the information \(\mathsf {P}\) is always revealed, no matter the function. Considering this part of the input separately will be helpful later.
Security Notions. We first recall the selective indistinguishability variant for the security of functional encryption here.
Definition 2.4
(SEL-IND security). For every functional encryption \(\mathcal {FE}\), every security parameter \(\lambda \), every stateful adversary \(\mathcal {A}\), we define the following experiments for \(\beta \in \{0,1\}\):

where \(\mathsf {OKeyGen}(\cdot )\) is an oracle that on input \(f \in \mathcal {F}\), outputs \({\mathsf {KeyGen}}(\mathsf {msk},f)\). Additionally, if \(\mathcal {A}\) ever calls the oracle \({\mathsf {KeyGen}}\) on an input \(f \in \mathcal {F}\), the challenge queries \(x_0,x_1\) must satisfy: \(f(x_0)=f(x_1)\) and \(\mathsf {part}(x_0)=\mathsf {part}(x_1)\).
A functional encryption scheme \(\mathcal {FE}\) is SEL-IND-secure if for every PPT adversary \(\mathcal {A}\), the following advantage is a negligible function of \(\lambda \):

Now we give the adaptive, indistinguishability based variant of security for FE. It is the same as the previous definition, except the challenge \((x^0,x^1)\) can be chosen adaptively, after seeing the public key and querying functional decryption keys.
Definition 2.5
(AD-IND security). For every functional encryption \(\mathcal {FE}\), every security parameter \(\lambda \), every stateful adversary \(\mathcal {A}\), we define the following experiments for \(\beta \in \{0,1\}\):

where \(\mathsf {OKeyGen}(\cdot )\) is an oracle that on input \(f \in \mathcal {F}\), outputs \({\mathsf {KeyGen}}(\mathsf {msk},f)\). Additionally, if \(\mathcal {A}\) ever calls the oracle \({\mathsf {KeyGen}}\) on an input \(f \in \mathcal {F}\), the challenge queries \(x_0,x_1\) must satisfy: \(f(x_0)=f(x_1)\) and \(\mathsf {part}(x_0)=\mathsf {part}(x_1)\).
A functional encryption scheme \(\mathcal {FE}\) is AD-IND-secure if for every PPT adversary \(\mathcal {A}\), the following advantage is a negligible function of \(\lambda \):

We now give the simulation-based, selective security. Note that simulation security straightforwardly implies indistinguishable security.
Definition 2.6
(SEL-SIM security). For any FE scheme \(\mathcal {FE}\) for functionality \(\mathcal {F}\), any security parameter \(\lambda \), any PPT stateful adversary \(\mathcal {A}\), and any PPT simulator \(\mathcal {S}:=(\widetilde{{\mathsf {Setup}}},\widetilde{{\mathsf {Enc}}},\widetilde{{\mathsf {KeyGen}}})\), we define the following two experiments.

In the real experiment, the key generation oracle \(\mathsf {OKeyGen}\), when given as input \(f \in \mathcal {F}\), returns \({\mathsf {KeyGen}}(\mathsf {msk},f)\). In the ideal experiment, the key generation oracle \(\mathsf {OKeyGen}\), when given as input \(f \in \mathcal {F}\), computes \(f(x^\star )\), and returns \(\widetilde{{\mathsf {KeyGen}}}(\widetilde{\mathsf {msk}},\mathsf {part}(x^\star ),f, f(x^\star ))\), where \(\mathsf {part}(x^\star )\) denotes the partial information on \(x^\star \).
We say an FE scheme is SEL-SIM secure if for all PPT adversaries \(\mathcal {A}\), there exists a PPT simulator \(\mathcal {S}:=(\widetilde{{\mathsf {Setup}}},\widetilde{{\mathsf {Enc}}},\widetilde{{\mathsf {KeyGen}}})\) such that
3 Inner-Product FE with Fine-Grained Access Control
In this section, we present functional encryption schemes for the family of functions that allows users to embed access policies in the encrypted data, and generate functional decryption keys that compute weighted sum on the latter. Namely, each ciphertext is associated with a predicate \(\mathsf {P}\), and encrypts a vector \(\varvec{x}\in [0,B]^d\) for some dimension d and some bound B. Each functional decryption key is associated with an attribute \(\mathsf {att}\) and a vector \(\varvec{y}\in [0,B]^d\). Decryption recovers the inner product \(\varvec{x}^\top \varvec{y}\in [0,dB^2]\) together with \(\mathsf {P}\) if the attribute \(\mathsf {att}\) satisfies the predicate \(\mathsf {P}\). Otherwise, it only recovers the predicate \(\mathsf {P}\), but no information about the encrypted vector \(\varvec{x}\) is revealed.
We show it is possible to combine existing pairing-based ABE together with the inner-product FE from [11]. Our generic construction works on any ABE that relies on the dual system encryption methodology, originally put forth by [56]. Namely, any such ABE that supports the class of predicates \(\mathcal {P}\), can be turned into an FE scheme for the family \(\mathcal {F}_{\mathsf {ipfe}(d,B),\mathcal {P}} := \mathcal {U}\times [0,B]^d\) of functions described by an attribute \(\mathsf {att}\in \mathcal {U}\) and a vector \(\varvec{y}\in [0,B]^d\), that given as input a predicate \(\mathsf {P}\in \mathcal {P}\) where \(\mathsf {P}: \mathcal {U}\rightarrow \{0,1\}\) and a vector \(\varvec{x}\in [0,B]^d\), returns \(\varvec{x}^\top \varvec{y}\in [0,dB^2]\) if \(\mathsf {P}(\mathsf {att})=1\), 0 otherwise. Note that this can be compactly written as \(\mathsf {P}(\mathsf {att}) \cdot \varvec{x}^\top \varvec{y}\). We will consider the case where the partial information that is leaked about \((\mathsf {P},\varvec{x})\) is \(\mathsf {P}\), which corresponds to the case of ABE with public indices, but also the case where the predicate itself is hidden, which corresponding to the case of predicate encryption, also referred to as ABE with private indices. For correctness, we require the bound B and the dimension d to be polynomially bounded.
We first give a scheme that builds upon any predicate encoding, a one-time secure, private-key, statistical variant of ABE, introduced in [16, 57], later refined in [8, 9, 12, 17] for prime-order pairing groups. Building a predicate encoding is much easier than directly building an attribute based encryption, since the heavy machinery that is being used to prove security of the resulting ABE is taken care of by these modular frameworks. We follow this line of work by giving a definition of predicate encoding which is essentially that of [27]. For simplicity, we leave the question of using more general predicate encodings, such as those from [9], which capture a larger class of ABE, as future work. Our modular construction is general enough to capture identity-based encryption, inner-product predicate encryption, and monotone span programs. A description of the corresponding concrete predicate encodings can be found in the full version of this paper [6].
3.1 FE with Simulation, Selective Security
First, we recall the definition of predicate encodings.
Definition 3.1
(predicate encoding). Let \(\mathcal {P}\) be a family of predicates and p be a prime. A predicate encoding for \((\mathcal {P},\mathbb {Z}_p)\) is given by the following polynomial-time deterministic algorithms:
-
\(\mathsf {Param}(\mathcal {P})\): takes as input the family of predicates \(\mathcal {P}\), and returns the parameters \((n,|\mathsf {ct}|,|\mathsf {sk}|) \in \mathbb {N}^3\).
-
\(\mathsf {EncCt}(\mathsf {P})\): takes as input a predicate \(\mathsf {P}\in \mathcal {P}\), and returns a matrix \(\mathbf {C}\in \mathbb {Z}_p^{n \times |\mathsf {ct}|}\).
-
\(\mathsf {EncKey}(\mathsf {att})\): takes as input an attribute \(\mathsf {att}\in \mathcal {U}\), and returns a matrix \(\mathbf {K}\in \mathbb {Z}_p^{(n+1) \times |\mathsf {sk}|}\).
-
\(\mathsf {Decode}(\mathsf {P},\mathsf {att})\): takes as input a predicate \(\mathsf {P}\in \mathcal {P}\), an attribute \(\mathsf {att}\in \mathcal {U}\), and returns a vector \(\varvec{d}\in \mathbb {Z}_p^{|\mathsf {ct}| + |\mathsf {sk}|}\).
We require the following properties.
-
Correctness. If \(\mathsf {P}\in \mathcal {P}\) and \(\mathsf {att}\in \mathcal {U}\) such that \(\mathsf {P}(\mathsf {att})=1\), \(\mathbf {C}:=\mathsf {EncCt}(\mathsf {P}) \in \mathbb {Z}_p^{n \times |\mathsf {ct}|}\), \(\mathbf {K}:= \mathsf {EncKey}(\mathsf {att}) \in \mathbb {Z}_p^{(n+1) \times |\mathsf {sk}|}\), \(\varvec{d}:= \mathsf {Decode}(\mathsf {P},\mathsf {att})\), then
 , where \(\mathbf {0}\in \mathbb {Z}_p^{1 \times |\mathsf {ct}|}\).
, where \(\mathbf {0}\in \mathbb {Z}_p^{1 \times |\mathsf {ct}|}\). -
Security. If \(\mathsf {P}\in \mathcal {P}\) and \(\mathsf {att}\in \mathcal {U}\) such that \(\mathsf {P}(\mathsf {att})=0\), then the following are identically distributed:

where \(\alpha ,v_1,\ldots ,v_n \leftarrow _{\textsc {r}}\mathbb {Z}_p\).
Example: Identity-Based Encryption.
-
\(\mathsf {Param}(\mathsf {IBE})\): takes as input the family of predicates \(\mathcal {I}\), where each predicate is described by an identity \(\mathsf {id}\in \mathcal {I}\), and returns 1 when given as an input an identity \(\mathsf {id}'\) such that \(\mathsf {id}'=\mathsf {id}\), returns 0 otherwise. It returns the parameters \((n=2,|\mathsf {ct}|=1,|\mathsf {sk}|=1) \in \mathbb {N}^3\).
-
\(\mathsf {EncCt}(\mathsf {id})\): given \(\mathsf {id}\in \mathcal {I}\), returns a matrix \(\mathbf {C}= (1,\mathsf {id}) \in \mathbb {Z}_p^{2 \times 1}\) such that \((v_1|v_2) \mathbf {C}= v_1 + \mathsf {id}v_2 \in \mathbb {Z}_p\).
-
\(\mathsf {EncKey}(\mathsf {id})\): given \(\mathsf {id}\in \mathcal {I}\), returns a matrix \(\mathbf {K}= (1,1,\mathsf {id}) \in \mathbb {Z}_p^{3 \times 1}\) such that \((\alpha |v_1|v_2) \mathbf {K}= \alpha + v_1 + \mathsf {id}v_2 \in \mathbb {Z}_p\).
-
\(\mathsf {Decode}(\mathsf {id},\mathsf {id}')\): if \(\mathsf {id}=\mathsf {id}'\), it returns the vector \(\varvec{d}:= {-1 \atopwithdelims ()1} \in \mathbb {Z}_p^{2}\).
Our simulation, selectively secure FE is described in Fig. 1.
Correctness. Observe that for all predicates \(\mathsf {P}\in \mathcal {P}\), the vector \([(\mathbf {W}^\top _1 \varvec{c}_1| \ldots | \mathbf {W}^\top _n \varvec{c}_1)]_1 \in {\mathbb {G}}_1^{2 \times n}\) can be computed from \(\mathsf {mpk}\) and the randomness  used by the encryption algorithm to compute \([\varvec{c}_1]_1 := [\varvec{a}s]_1\). Then, the encryption algorithm multiplies the resulting vector by the matrix \(\mathbf {C}:= \mathsf {EncCt}(\mathsf {P}) \in \mathbb {Z}_p^{n \times |\mathsf {ct}|}\) to obtain \([\mathbf {C}_2]_1 \in {\mathbb {G}}_1^{2 \times |\mathsf {ct}|}\). Similarly, for all attributes \(\mathsf {att}\in \mathcal {U}\), the vector \([(\mathbf {U}\varvec{y}|\mathbf {W}_1 \varvec{k}_1| \ldots | \mathbf {W}_n \varvec{k}_1)]_2 \in {\mathbb {G}}_2^{2 \times (n+1)}\) can be computed from \(\mathsf {mpk}\), \(\mathsf {msk}\), and the randomness
used by the encryption algorithm to compute \([\varvec{c}_1]_1 := [\varvec{a}s]_1\). Then, the encryption algorithm multiplies the resulting vector by the matrix \(\mathbf {C}:= \mathsf {EncCt}(\mathsf {P}) \in \mathbb {Z}_p^{n \times |\mathsf {ct}|}\) to obtain \([\mathbf {C}_2]_1 \in {\mathbb {G}}_1^{2 \times |\mathsf {ct}|}\). Similarly, for all attributes \(\mathsf {att}\in \mathcal {U}\), the vector \([(\mathbf {U}\varvec{y}|\mathbf {W}_1 \varvec{k}_1| \ldots | \mathbf {W}_n \varvec{k}_1)]_2 \in {\mathbb {G}}_2^{2 \times (n+1)}\) can be computed from \(\mathsf {mpk}\), \(\mathsf {msk}\), and the randomness  used by the key generation algorithm to compute \([\varvec{k}_1]_2 := [\varvec{b}r]_2\). Then, the key generation algorithm multiplies the resulting vector by the matrix \(\mathbf {K}:= \mathsf {EncKey}(\mathsf {att}) \in \mathbb {Z}_p^{(n+1) \times |\mathsf {sk}|}\) to obtain \([\mathbf {K}_2]_1 \in {\mathbb {G}}_2^{2 \times |\mathsf {sk}|}\).
used by the key generation algorithm to compute \([\varvec{k}_1]_2 := [\varvec{b}r]_2\). Then, the key generation algorithm multiplies the resulting vector by the matrix \(\mathbf {K}:= \mathsf {EncKey}(\mathsf {att}) \in \mathbb {Z}_p^{(n+1) \times |\mathsf {sk}|}\) to obtain \([\mathbf {K}_2]_1 \in {\mathbb {G}}_2^{2 \times |\mathsf {sk}|}\).
Let \(\mathsf {P}\in \mathcal {P}\) and \(\mathsf {att}\in \mathcal {U}\) such that \(\mathsf {P}(\mathsf {att})=1\), \(\varvec{x}, \varvec{y}\in [0,B]^d\),  , and
, and  . The values computed by the decryption algorithm are such that
. The values computed by the decryption algorithm are such that  , where \(\mathbf {C}:= \mathsf {EncCt}(\mathsf {P}) \in \mathbb {Z}_p^{n \times |\mathsf {ct}|}\), and \([\varvec{d}^\top _2]_T := [(\varvec{c}_1^\top \mathbf {U}\varvec{y}| \varvec{c}_1^\top \mathbf {W}_1 \varvec{k}_1| \ldots | \varvec{c}_1^\top \mathbf {W}_n \varvec{k}_1) \mathbf {K}]_T \in {\mathbb {G}}_T^{1\times |\mathsf {sk}|}\), where \(\mathbf {K}:= \mathsf {EncKey}(\mathsf {att}) \in \mathbb {Z}_p^{(n+1) \times |\mathsf {sk}|}\). Thus, by correctness of the predicate encoding \((\mathsf {Param}, \mathsf {EncCt}, \mathsf {EncKey}, \mathsf {Decode})\), we have \([\gamma ]_T := [\varvec{c}_1^\top \mathbf {U}\varvec{y}]_T \in {\mathbb {G}}_T\). To see why, please note that, since
, where \(\mathbf {C}:= \mathsf {EncCt}(\mathsf {P}) \in \mathbb {Z}_p^{n \times |\mathsf {ct}|}\), and \([\varvec{d}^\top _2]_T := [(\varvec{c}_1^\top \mathbf {U}\varvec{y}| \varvec{c}_1^\top \mathbf {W}_1 \varvec{k}_1| \ldots | \varvec{c}_1^\top \mathbf {W}_n \varvec{k}_1) \mathbf {K}]_T \in {\mathbb {G}}_T^{1\times |\mathsf {sk}|}\), where \(\mathbf {K}:= \mathsf {EncKey}(\mathsf {att}) \in \mathbb {Z}_p^{(n+1) \times |\mathsf {sk}|}\). Thus, by correctness of the predicate encoding \((\mathsf {Param}, \mathsf {EncCt}, \mathsf {EncKey}, \mathsf {Decode})\), we have \([\gamma ]_T := [\varvec{c}_1^\top \mathbf {U}\varvec{y}]_T \in {\mathbb {G}}_T\). To see why, please note that, since  ,
,  . Therefore, \([\mathsf {out}]_T = [\varvec{x}^\top \varvec{y}]_T\). Finally, assuming the value \(B^2d\) is polynomial in the security parameter, the decryption can efficiently recover the discrete logarithm \(\mathsf {out}\) from \([\mathsf {out}]_T\).
. Therefore, \([\mathsf {out}]_T = [\varvec{x}^\top \varvec{y}]_T\). Finally, assuming the value \(B^2d\) is polynomial in the security parameter, the decryption can efficiently recover the discrete logarithm \(\mathsf {out}\) from \([\mathsf {out}]_T\).
Theorem 3.2
(SEL-SIM security). If the underlying predicate encoding is secure, then the FE scheme from Fig. 1 is SEL-SIM secure. Namely, for any PPT adversary \(\mathcal {A}\), there exist PPT adversaries \(\mathcal {B}_1\) and \(\mathcal {B}_2\) such that:
where Q denotes the number of queries to \(\mathsf {OKeyGen}\).
Overview of ciphertext distributions appearing in the proof of Theorem 3.2, with changes between hybrids highlighted with a gray background. SF stands for semi-functional. Here, \(\mathbf {C}:=\mathsf {EncCt}(\mathsf {P}^\star )\).
Proof
The proof goes over a series of hybrid games, defined in Fig. 4. Let \(\mathcal {A}\) be a PPT adversary. For any such game \(\mathsf {G}\), we denote by \(\mathsf {Adv}_{\mathsf {G}}(\mathcal {A})\) the probability  , that is, the probability that the game outputs 1 when interacting with \(\mathcal {A}\). The probability is taken over the random coins of \(\mathcal {A}\) and the game \(\mathsf {G}\) itself. For an overview of the ciphertext and key distributions in the proof, see Figs. 2 and 3.
, that is, the probability that the game outputs 1 when interacting with \(\mathcal {A}\). The probability is taken over the random coins of \(\mathcal {A}\) and the game \(\mathsf {G}\) itself. For an overview of the ciphertext and key distributions in the proof, see Figs. 2 and 3.
-
Game \(\mathsf {G}_0\): is the same as \(\mathsf {Real}^{\mathcal {FE}}_{\mathcal {A}}(1^\lambda )\) from Definition 2.6.
-
Game \(\mathsf {G}_1\): in this game, the challenge ciphertext is switched to the semi-functional distribution (see Fig. 2). Namely, the vector \([\varvec{c}_1]_1\) contained in the challenge ciphertext is switched to uniformly random over \({\mathbb {G}}_1^2\), using the DDH assumption. The game is described fully in Fig. 4 and is indistinguishable from \(\mathsf {G}_0\) by Lemma 3.3.
Lemma 3.3
There exists a PPT adversary \(\mathcal {B}_1\), such that:
Proof
The PPT adversary \(\mathcal {B}_1\) receives the DDH challenge \(([\varvec{a}]_1, [\varvec{z}]_1)\) where  , \([\varvec{z}]_1 := [\varvec{a}s]_1\) with
, \([\varvec{z}]_1 := [\varvec{a}s]_1\) with  or
or  , then samples
, then samples  ,
,  ,
,  and simulates the experiment for \(\mathcal {A}\) in the following way:
and simulates the experiment for \(\mathcal {A}\) in the following way:
Simulation of the Master Public Key: Since \(\mathcal {B}_1\) samples \(\mathbf {U}\) and \(\mathbf {W}_i\) himself, he can use the encoding \([\varvec{a}]_1\) to compute \([\mathbf {U}^{\!\scriptscriptstyle {\top }}\varvec{a}]_1\) and \(\{[\mathbf {W}^\top _i \varvec{a}]_1\}_{i \in [n]})\). Then \(\mathcal {B}_1\), computes \(\left( [\mathbf {W}_i\varvec{b}]_2\}_{i \in [n]}\right) \) and outputs \(\mathsf {mpk}:= \left( [\varvec{a}]_1, [\varvec{b}]_2, [\mathbf {U}^\top \varvec{a}]_1, \{[\mathbf {W}^\top _i \varvec{a}]_1,[\mathbf {W}_i\varvec{b}]_2\}_{i \in [n]}\right) \).
Simulation of the Encryption Challenge: Adversary \(\mathcal {B}_1\) sets \([\varvec{c}_1]_1 := [\varvec{z}]_1\), \(\mathbf {C}:= \mathsf {EncCt}(\mathsf {P})\), \([\mathbf {C}_2]_1:=[(\mathbf {W}^\top _1 \varvec{z}| \ldots | \mathbf {W}^\top _n \varvec{z}) \mathbf {C}]_1\), \([\varvec{c}_3]_1:=[\varvec{x}^\star + \mathbf {U}^\top \varvec{z}]_1\), and returns \((\mathsf {P},[\varvec{c}_1]_1,[\mathbf {C}_2]_1,[\varvec{c}_3]_1)\). When \(\mathcal {B}_1\) gets a DDH challenge of the form \([\varvec{z}]_1 := [\varvec{a}s]_1\) with  , it simulates \(\mathsf {G}_1\), whereas it simulates \(\mathsf {G}_2\) when \([\varvec{z}]_1\) is uniformly random over \({\mathbb {G}}_1\).
, it simulates \(\mathsf {G}_1\), whereas it simulates \(\mathsf {G}_2\) when \([\varvec{z}]_1\) is uniformly random over \({\mathbb {G}}_1\).
Simulation of the Functional Keys: \(\mathcal {B}_1\) generates the keys straightforwardly as described in \(\mathsf {G}_0\), using the matrix \(\mathbf {U}\), \(\{\mathbf {W}_i\}_{i \in [n]}\), and \(\varvec{b}\). \(\square \)
Overview of key distributions appearing in the proof of Theorem 3.2, with changes between hybrids highlighted with a gray background. SF stands for semi-functional. Throughout the figure, \(\mathbf {K}=\mathsf {EncKey}(\mathsf {att})\).
-
Game \(\mathsf {G}_2\): in this game, all the functional decryption keys associated with an attribute \(\mathsf {att}\) such that \(\mathsf {P}^\star (\mathsf {att})=0\) are switched to semi-functional (see Fig. 3). That is, for these keys, the matrix \(\widetilde{\mathbf {U}}\) (defined in Fig. 4) is used in place of the master secret key \(\mathbf {U}\). Note that the matrix \(\widetilde{\mathbf {U}}\), as opposed to the master secret key \(\mathbf {U}\), can be computed (information theoretically) from \(\mathsf {mpk}\) only. These semi-functional keys decrypt successfully normal ciphertexts (which can be produced from \(\mathsf {mpk}\)), but fail to decrypt semi-functional ciphertexts.
To switch keys from normal to semi-functional, we use a hybrid argument across keys, where each key is first switched to a high entropy distribution, typically referred to as pseudo mode in the dual system methodology [56], where the vector \([\varvec{k}_1]_2\) contained in the key is switched to uniformly random over \({\mathbb {G}}_2^2\), using the DDH assumption. At this point, the proof relies on the security of the predicate encoding to switch the key a semi-functional distribution. After this statistical transition, the vector \([\varvec{k}_1]_2\) is switched back to its original distribution, and the proof proceeds to the next key. Details of the transition from game \(\mathsf {G}_1\) to game \(\mathsf {G}_2\) are given in the full version of this paper [6].
Even though the hybrid argument used here is standard in the context of dual system encryption, the crucial difference is that only the keys associated with \(\mathsf {att}\) such that \(\mathsf {P}^\star (\mathsf {att})=0\) can be switched to semi-functional. The other keys should actually decrypt the challenge ciphertext properly. This is the reason the experiment needs to know in advance the value \(\mathsf {P}^\star \), so as to determine which key can be switched. For the keys that cannot be switched, we use a security argument similar to that used in [11] instead.
-
Game \(\mathsf {Ideal}^{\mathcal {FE}}_{\mathcal {A},\mathcal {S}}(1^\lambda )\): we show this game is statistically close to \(\mathsf {G}_2\). The simulator \(\mathcal {S}:=(\widetilde{{\mathsf {Setup}}},\widetilde{{\mathsf {Enc}}},\widetilde{{\mathsf {KeyGen}}})\) is described in Fig. 5. First, we use the fact that for all \(\varvec{a}\in \mathbb {Z}_p^2\), the following distributions are within 1/p statistical distance:

The leftmost distribution corresponds to \(\mathsf {G}_2\), whereas the rightmost distribution corresponds to \(\mathsf {Ideal}^{\mathcal {FE}}_{\mathcal {A},\mathcal {S}}(1^\lambda )\).
Then, we use the fact that for all \(\varvec{x}^\star \in \mathbb {Z}^d\), the following distributions are identical:
$$\begin{aligned} (\varvec{a}, \varvec{c}_1, \widetilde{\mathbf {U}}, \mathbf {U})\ \text{ and } \ (\varvec{a}, \varvec{c}_1, \widetilde{\mathbf {U}}, \mathbf {U}- \varvec{a}^{\bot }(\varvec{x}^\star )^\top ), \end{aligned}$$where
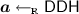 ,
,  ,
,  , \(\varvec{u}_0 := \tfrac{\mathbf {U}^\top \varvec{a}}{\Vert \varvec{a}\Vert _2^2}\), \(\widetilde{\mathbf {U}} := \varvec{a}\varvec{u}^\top _0\), and \(\varvec{a}^{\bot }\in \mathbb {Z}_p^2\) such that \(\varvec{a}^\top \varvec{a}^{\bot }=0\) and \(\varvec{c}_1^\top \varvec{a}^{\bot }=1\). This is because \(\mathbf {U}\) is a uniformly random matrix, so adding an offset \(- \varvec{a}^{\bot }(\varvec{x}^\star )^\top \) does not change its distribution. This extra offset doesn’t appear in \(\widetilde{\mathbf {U}}\) since \(\varvec{a}^\top \varvec{a}^{\bot }=0\). The leftmost distribution corresponds to \(\mathsf {G}_2\), whereas the rightmost distribution corresponds to \(\mathsf {Ideal}^{\mathcal {FE}}_{\mathcal {A},\mathcal {S}}(1^\lambda )\).
, \(\varvec{u}_0 := \tfrac{\mathbf {U}^\top \varvec{a}}{\Vert \varvec{a}\Vert _2^2}\), \(\widetilde{\mathbf {U}} := \varvec{a}\varvec{u}^\top _0\), and \(\varvec{a}^{\bot }\in \mathbb {Z}_p^2\) such that \(\varvec{a}^\top \varvec{a}^{\bot }=0\) and \(\varvec{c}_1^\top \varvec{a}^{\bot }=1\). This is because \(\mathbf {U}\) is a uniformly random matrix, so adding an offset \(- \varvec{a}^{\bot }(\varvec{x}^\star )^\top \) does not change its distribution. This extra offset doesn’t appear in \(\widetilde{\mathbf {U}}\) since \(\varvec{a}^\top \varvec{a}^{\bot }=0\). The leftmost distribution corresponds to \(\mathsf {G}_2\), whereas the rightmost distribution corresponds to \(\mathsf {Ideal}^{\mathcal {FE}}_{\mathcal {A},\mathcal {S}}(1^\lambda )\).Putting everything together, we obtain:

\(\square \)
Hybrid games for the proof of Theorem 3.2.
PPT simulator for the security proof of the FE scheme from Fig. 4.
3.2 FE with Adaptive, Indistinguishability Based Security
In this section, we build FE schemes for the family of functions \(\mathcal {F}_{\mathsf {ipfe}(d,B),\mathcal {P}}\), where \(\mathcal {P}\) corresponds to identity-based encryption, inner-product predicate encryption, or even monotone span programs. Similarly to the selective construction in Sect. 3.1, we give a modular construction that builds upon a simple, information-theoretic, one-time secure object, that generalizes the notion of predicate encoding to functions, hence called function encoding. Namely, a function encoding is a private-key version of functional encryption that only satisfies a one-time security notion.
Recall that our construction from Sect. 3.1 fails to achieve adaptive security, even if the underlying building blocks are adaptively secure. The reason is that, throughout the security proof, only the functional decryption keys associated with a pair \((\mathsf {att},\varvec{y})\) such that \(\mathsf {P}^\star (\mathsf {att})=0\) can be turned to semi-functional, where \(\mathsf {P}^\star \) is the predicate chosen by the adversary for the challenge ciphertext. In fact, the other keys cannot be turned semi-functional, since they must decrypt correctly the challenge ciphertext, and not just ciphertexts that can be generated from the public key. This challenge does not arise in the typical dual system encryption methodology used for ABE, since none of the queried keys can decrypt.
A similar situation arose in the context of fully-hiding predicate encryption for inner products, where ciphertexts are associated with a vector \(\widetilde{\varvec{x}}\in \mathbb {Z}_p^n\), functional decryption keys are associated with \(\widetilde{\varvec{y}} \in \mathbb {Z}_p^n\), and decryption successfully recovers the plaintext if \(\widetilde{\varvec{x}}^\top \widetilde{\varvec{y}}=0\), whereas no information about that plaintext is revealed otherwise. As opposed to regular inner-product encryption, the vector \(\widetilde{\varvec{x}}\) is also hidden, the only bit of information that leaks is whether \(\widetilde{\varvec{x}}^\top \widetilde{\varvec{y}}=0\) or not. In this context, the adversary can query functional decryption keys that decrypt the challenge ciphertext. This is still a meaningful security notion since \(\widetilde{\varvec{x}}\) remains hidden even when such keys are queried.
We show that the techniques introduced by [49], later improved in [28] for adaptively secure fully-hiding predicate encryption for inner products are also relevant to obtain adaptively secure inner-product FE with fine-grained access control (even when the predicate is not hidden). In fact, using function encodings, a new notion we introduce that subsumes the notion of predicate encoding introduced in [16, 57] in the context of adaptively-secure ABE, we generalize the approach of [28, 49] to a large class of functional encryption schemes, whereas their scheme corresponds to the special case of inner-product encryption. Namely, we compile any function encoding for the function family \(\mathcal {F}\) into an adaptively secure FE for the same class of functions from the SXDH assumption in asymmetric pairings. In the full version of this paper [6], we give concrete function encodings that correspond to identity-based encryption, inner-product predicate encryption, fully-hiding inner-product predicate encryption and monotone span programs.
Definition 3.4
(function encoding). Let \(\mathcal {F}\) be a family of functions where each function \(f \in \mathcal {F}\) is of the form \(f:\mathcal {X}\rightarrow \mathbb {Z}_p\), and p be a prime. A function encoding for \((\mathcal {F},\mathbb {Z}_p)\) is given by the following polynomial-time deterministic algorithms:
-
\(\mathsf {Param}(\mathcal {F})\): takes as input the family of functions \(\mathcal {F}\), and returns the parameters \((n,|\mathsf {ct}|,|\mathsf {sk}|) \in \mathbb {N}^3\).
-
\(\mathsf {EncCt}(x)\): takes as input \(x \in \mathcal {X}\), and returns a matrix \(\mathbf {C}\in \mathbb {Z}_p^{(n+1) \times |\mathsf {ct}|}\).
-
\(\mathsf {EncKey}(f)\): takes as input a function \(f \in \mathcal {F}\), and returns a matrix \(\mathbf {K}\in \mathbb {Z}_p^{(n+1) \times |\mathsf {sk}|}\).
-
\(\mathsf {Decode}(f,\mathsf {part}(x))\): takes as input the partial information \(\mathsf {part}(x)\) of \(x \in \mathcal {X}\) and \(f \in \mathcal {F}\). It returns a vector \(\varvec{d}\in \mathbb {Z}_p^{|\mathsf {ct}| + |\mathsf {sk}|}\). (See Sect. 2.2 for a discussion on the partial information).
We require the following properties.
-
Correctness. For all \(x \in \mathcal {X}\) and \(f \in \mathcal {F}\), \(\mathbf {C}:=\mathsf {EncCt}(x) \in \mathbb {Z}_p^{(n+1) \times |\mathsf {ct}|}\), \(\mathbf {K}:= \mathsf {EncKey}(f) \in \mathbb {Z}_p^{(n+1) \times |\mathsf {sk}|}\), \(\varvec{d}:= \mathsf {Decode}(f,\mathsf {part}(x))\), we have: \((\mathbf {C}|\mathbf {K}) \varvec{d}= (f(x), 0, \ldots , 0) \in \mathbb {Z}_p^{n+1}\).
-
Security. For any \(x^0,x^1 \in \mathcal {X}\) and \(f \in \mathcal {F}\) such that \(f(x^0)=f(x^1)\) and \(\mathsf {part}(x^0)=\mathsf {part}(x^1)\), the following are identically distributed:
$$\begin{aligned}\varvec{v}^\top (\mathbf {C}|\mathbf {K})&\text{ with } \mathbf {C}:= \mathsf {EncCt}(x^0), \mathbf {K}:= \mathsf {EncKey}(f)\\&\text{ and }\\ \varvec{v}^\top (\mathbf {C}|\mathbf {K})&\text{ with } \mathbf {C}:= \mathsf {EncCt}(x^1), \mathbf {K}:= \mathsf {EncKey}(f), \end{aligned}$$where
 .
.
Example: Identity-Based Encryption. Each function is described by an identity \(\mathsf {id}\in \mathbb {Z}_p\) and a vector \(\varvec{y}\in [0,B]^d\), takes as input another identity \(\mathsf {id}'\in \mathbb {Z}_p\) and a vector \(\varvec{x}\in [0,B]^d\), and outputs \(\varvec{x}^\top \varvec{y}\) if \(\mathsf {id}=\mathsf {id}'\), 0 otherwise. The partial information \(\mathsf {part}(\varvec{x},\mathsf {id})=\mathsf {id}\).
-
\(\mathsf {Param}\): returns the parameters \((2d,|\mathsf {ct}|=d,|\mathsf {sk}|=n+1)\).
-
\(\mathsf {EncCt}(\varvec{x},\mathsf {id})\): given \(\varvec{x}\in \mathbb {Z}_p^n\) and \(\mathsf {id}\in \mathbb {Z}_p\), returns a matrix \(\mathbf {C}\in \mathbb {Z}_p^{(2d+1) \times d}\) such that \(\mathbf {C}^\top (w_0,\varvec{w}_1,\varvec{w}_2) = (w_0\varvec{x}+ \varvec{w}_1 + \mathsf {id}\varvec{w}_2) \in \mathbb {Z}^{d}_p\).
-
\(\mathsf {EncKey}(\varvec{y},\mathsf {id}')\): given \(\varvec{y}\in \mathbb {Z}_p^n\) and \(\mathsf {id}' \in \mathbb {Z}_p\), returns a matrix \(\mathbf {K}\in \mathbb {Z}_p^{(2d+1) \times 1}\) such that \(\mathbf {K}^\top (w_0,\varvec{w}_1,\varvec{w}_2) = \varvec{y}^\top (\varvec{w}_1 + \mathsf {id}' \varvec{w}_2)\in \mathbb {Z}_p\).
-
\(\mathsf {Decode}(\mathsf {id},\mathsf {id}',\varvec{y})\): if \(\varvec{x}^\top \varvec{y}=0\), it returns the vector \(\varvec{d}:= (\varvec{y}, -1) \in \mathbb {Z}_p^{d+1}\).
Our modular construction is presented in Fig. 6. Proofs of correctness and security are given below.
Correctness. Observe that for all predicates \(\mathsf {P}\in \mathcal {P}\) and vectors \(\varvec{x}\in [0,B]^d\), the vector \([(\mathbf {W}^\top _0\varvec{c}_1| \mathbf {W}^\top _1 \varvec{c}_1| \ldots | \mathbf {W}^\top _n \varvec{c}_1)]_1 \in {\mathbb {G}}_1^{3 \times n}\) can be computed from \(\mathsf {mpk}\) and the randomness  used by the encryption algorithm to compute \([\varvec{c}_1]_1 := [\varvec{a}s]_1\). Then, the encryption algorithm multiplies by the matrix \(\mathbf {C}:= \mathsf {EncCt}(\mathsf {P},\varvec{x}) \in \mathbb {Z}_p^{(n+1) \times |\mathsf {ct}|}\) to obtain \([\mathbf {C}_2]_1 \in {\mathbb {G}}_1^{3 \times |\mathsf {ct}|}\). Similarly, for all attributes \(\mathsf {att}\in \mathcal {U}\), the vector \([(\mathbf {W}_0\varvec{k}_1| \mathbf {W}_1 \varvec{k}_1| \ldots | \mathbf {W}_n \varvec{k}_1)]_2 \in {\mathbb {G}}_2^{2 \times n}\) can be computed from \(\mathsf {mpk}\), \(\mathsf {msk}\), and the randomness
used by the encryption algorithm to compute \([\varvec{c}_1]_1 := [\varvec{a}s]_1\). Then, the encryption algorithm multiplies by the matrix \(\mathbf {C}:= \mathsf {EncCt}(\mathsf {P},\varvec{x}) \in \mathbb {Z}_p^{(n+1) \times |\mathsf {ct}|}\) to obtain \([\mathbf {C}_2]_1 \in {\mathbb {G}}_1^{3 \times |\mathsf {ct}|}\). Similarly, for all attributes \(\mathsf {att}\in \mathcal {U}\), the vector \([(\mathbf {W}_0\varvec{k}_1| \mathbf {W}_1 \varvec{k}_1| \ldots | \mathbf {W}_n \varvec{k}_1)]_2 \in {\mathbb {G}}_2^{2 \times n}\) can be computed from \(\mathsf {mpk}\), \(\mathsf {msk}\), and the randomness  used by the key generation algorithm to compute \([\varvec{k}_1]_2 := [\varvec{b}r]_2\). Then, the key generation algorithm multiplies by the matrix \(\mathbf {K}:= \mathsf {EncKey}(\mathsf {att},\varvec{y}) \in \mathbb {Z}_p^{(n+1) \times |\mathsf {sk}|}\) to obtain \([\mathbf {K}_2]_1 \in {\mathbb {G}}_2^{2 \times |\mathsf {sk}|}\).
used by the key generation algorithm to compute \([\varvec{k}_1]_2 := [\varvec{b}r]_2\). Then, the key generation algorithm multiplies by the matrix \(\mathbf {K}:= \mathsf {EncKey}(\mathsf {att},\varvec{y}) \in \mathbb {Z}_p^{(n+1) \times |\mathsf {sk}|}\) to obtain \([\mathbf {K}_2]_1 \in {\mathbb {G}}_2^{2 \times |\mathsf {sk}|}\).
Let \(\mathsf {P}\in \mathcal {P}\) and \(\mathsf {att}\in \mathcal {U}\) such that \(\mathsf {P}(\mathsf {att})=1\), \(\varvec{x}, \varvec{y}\in [0,B]^d\),  , and
, and  . The values computed by the decryption algorithm are such that
. The values computed by the decryption algorithm are such that  , which implies that \([\varvec{d}^\top _1]_T= [(\varvec{c}_1^\top \mathbf {W}_0 \varvec{k}_1| \varvec{c}_1^\top \mathbf {W}_1 \varvec{k}_1| \ldots | \varvec{c}_1^\top \mathbf {W}_n \varvec{k}_1)\mathbf {C}]_T \in {\mathbb {G}}_T^{1\times |\mathsf {ct}|}\), where \(\mathbf {C}:= \mathsf {EncCt}(\mathsf {P},\varvec{x}) \in \mathbb {Z}_p^{(n+1) \times |\mathsf {ct}|}\), and the second equality holds because \(\varvec{c}_1^{\!\scriptscriptstyle {\top }}\mathbf {W}_i\varvec{k}_1\in \mathbb {Z}_p\), for every \(i\in \{0\ldots n\}\). Also, \([\varvec{d}^\top _2]_T := [(\varvec{c}_1^\top \mathbf {W}_0\varvec{k}_1|\varvec{c}_1^\top \mathbf {W}_1 \varvec{k}_1| \ldots | \varvec{c}_1^\top \mathbf {W}_n \varvec{k}_1) \mathbf {K}]_T \in {\mathbb {G}}_T^{1\times |\mathsf {sk}|}\), where \(\mathbf {K}:= \mathsf {EncKey}(\mathsf {att},\varvec{y}) \in \mathbb {Z}_p^{(n+1) \times |\mathsf {sk}|}\). Thus, by correctness of the function encoding \((\mathsf {Param},\mathsf {EncCt},\mathsf {EncKey},\mathsf {Decode})\), we have \([\gamma ]_T := [\varvec{c}_1^\top \mathbf {W}_0 \varvec{k}_1 \cdot \varvec{x}^\top \varvec{y}]_T = [\varvec{c}_1^\top \varvec{k}_3 \cdot \varvec{x}^\top \varvec{y}]\in {\mathbb {G}}_T\). Therefore, assuming the value \(B^2d\) is polynomial in the security parameter, the decryption can efficiently recover \(\mathsf {out}= \varvec{x}^\top \varvec{y}\in [0,B^2d]\).
, which implies that \([\varvec{d}^\top _1]_T= [(\varvec{c}_1^\top \mathbf {W}_0 \varvec{k}_1| \varvec{c}_1^\top \mathbf {W}_1 \varvec{k}_1| \ldots | \varvec{c}_1^\top \mathbf {W}_n \varvec{k}_1)\mathbf {C}]_T \in {\mathbb {G}}_T^{1\times |\mathsf {ct}|}\), where \(\mathbf {C}:= \mathsf {EncCt}(\mathsf {P},\varvec{x}) \in \mathbb {Z}_p^{(n+1) \times |\mathsf {ct}|}\), and the second equality holds because \(\varvec{c}_1^{\!\scriptscriptstyle {\top }}\mathbf {W}_i\varvec{k}_1\in \mathbb {Z}_p\), for every \(i\in \{0\ldots n\}\). Also, \([\varvec{d}^\top _2]_T := [(\varvec{c}_1^\top \mathbf {W}_0\varvec{k}_1|\varvec{c}_1^\top \mathbf {W}_1 \varvec{k}_1| \ldots | \varvec{c}_1^\top \mathbf {W}_n \varvec{k}_1) \mathbf {K}]_T \in {\mathbb {G}}_T^{1\times |\mathsf {sk}|}\), where \(\mathbf {K}:= \mathsf {EncKey}(\mathsf {att},\varvec{y}) \in \mathbb {Z}_p^{(n+1) \times |\mathsf {sk}|}\). Thus, by correctness of the function encoding \((\mathsf {Param},\mathsf {EncCt},\mathsf {EncKey},\mathsf {Decode})\), we have \([\gamma ]_T := [\varvec{c}_1^\top \mathbf {W}_0 \varvec{k}_1 \cdot \varvec{x}^\top \varvec{y}]_T = [\varvec{c}_1^\top \varvec{k}_3 \cdot \varvec{x}^\top \varvec{y}]\in {\mathbb {G}}_T\). Therefore, assuming the value \(B^2d\) is polynomial in the security parameter, the decryption can efficiently recover \(\mathsf {out}= \varvec{x}^\top \varvec{y}\in [0,B^2d]\).
Hybrid games for the proof of Theorem 3.5.
Theorem 3.5
(AD-IND security). If the underlying function encoding is secure, then the FE scheme from Fig. 6 is AD-IND secure. Namely, for any PPT adversary \(\mathcal {A}\), there exist PPT adversaries \(\mathcal {B}_1\) and \(\mathcal {B}_2\) such that:
where Q denotes the number of queries to \(\mathsf {OKeyGen}\).
Proof
The proof uses a series of hybrid games, described in Fig. 7. For each game \(\mathsf {G}\), we define by \(\mathsf {Adv}_{\mathsf {G}}(\mathcal {A})\) the advantage of \(\mathcal {A}\) in \(\mathsf {G}\), that is:  .
.
-
Game \(\mathsf {G}_0\): is defined such that \(\mathsf {Adv}_{\mathsf {G}_0}(\mathcal {A}) = \mathsf {Adv}_{\mathcal {FE},\mathcal {A}}^{\mathsf {AD\text{- }IND}}(\lambda )\).
-
Game \(\mathsf {G}_1\): here we change the distribution of the vector \([\varvec{c}_1]_1\) that is part of the challenge ciphertext to uniformly random over \({\mathbb {G}}_1^2\), using the DDH assumption in \({\mathbb {G}}_1\). Namely, we build a PPT adversary \(\mathcal {B}_1\) such that:
$$\begin{aligned} |\mathsf {Adv}_{\mathsf {G}_0}(\mathcal {A}) - \mathsf {Adv}_{\mathsf {G}_1}(\mathcal {A})| \le \mathsf {Adv}^{\mathsf {DDH}}_{{\mathbb {G}}_1,\mathcal {B}_1}(\lambda ). \end{aligned}$$Upon receiving a challenge \((\mathcal {PG},[\varvec{a}]_1,[\varvec{z}]_1)\), where \([\varvec{z}]_1 := [\varvec{a}s]_1\) for
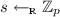 , or
, or  , the adversary \(\mathcal {B}_1\) samples \((n,|\mathsf {ct}|,|\mathsf {sk}|) \leftarrow \mathsf {Param}(\mathcal {F}_{\mathsf {ipfe}(d,B)},\mathcal {P})\), for all \(i \in [0,n]\),
, the adversary \(\mathcal {B}_1\) samples \((n,|\mathsf {ct}|,|\mathsf {sk}|) \leftarrow \mathsf {Param}(\mathcal {F}_{\mathsf {ipfe}(d,B)},\mathcal {P})\), for all \(i \in [0,n]\),  , and simulate \(\mathcal {A}\)’s view in a straightforward way, setting \([\varvec{c}_1]_1 := [\varvec{z}]_1\) in the challenge ciphertext.
, and simulate \(\mathcal {A}\)’s view in a straightforward way, setting \([\varvec{c}_1]_1 := [\varvec{z}]_1\) in the challenge ciphertext. -
Game \(\mathsf {G}_2\): here we change the distribution of the challenge ciphertext so that it doesn’t depend on the random bit
 anymore. Clearly, $$\begin{aligned} \mathsf {Adv}_{\mathsf {G}_2}(\mathcal {A})=0. \end{aligned}$$
anymore. Clearly, $$\begin{aligned} \mathsf {Adv}_{\mathsf {G}_2}(\mathcal {A})=0. \end{aligned}$$We show that \(\mathsf {G}_1\) and \(\mathsf {G}_2\) are computationally indistinguishable using the security of a private-key variant of our scheme. Namely, we exhibit a PPT adversary \(\mathcal {B}_2\) such that:
$$\begin{aligned} |\mathbf {Adv}_{\mathsf {G}_1}(\mathcal {A}) - \mathbf {Adv}_{\mathsf {G}_2}(\mathcal {A})| \le \mathsf {Adv}_{\mathsf {H}_0}(\mathcal {B}_2), \end{aligned}$$where \(\mathsf {Adv}_{\mathsf {H}_0}(\mathcal {B}_2)\) denotes the advantage of \(\mathcal {B}_2\) in game \(\mathsf {H}_0\), which is the private-key analogue of game \(\mathsf {G}_0\) (see Fig. 8). We use the fact that for any \(i \in [0,n]\): \((\mathbf {W}_i^\top \varvec{a},\mathbf {W}_i^\top \varvec{c}_1)\) with
 ,
, 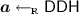 ,
, 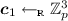 , is within negligible statistical distance from \((\mathbf {W}_i^\top \varvec{a},\varvec{w}_i)\) with
, is within negligible statistical distance from \((\mathbf {W}_i^\top \varvec{a},\varvec{w}_i)\) with  . Roughly speaking, the vectors \(\varvec{w}_i\) can be used as a fresh private-key, independent of the public key \(\{[\mathbf {W}_i^\top \varvec{a}]_1\}\). Note that when
. Roughly speaking, the vectors \(\varvec{w}_i\) can be used as a fresh private-key, independent of the public key \(\{[\mathbf {W}_i^\top \varvec{a}]_1\}\). Note that when  and
and  such that \(\varvec{a}^\top \varvec{a}^{\bot }= 0\), we have that the vectors \((\varvec{a}|\varvec{a}^{\bot })\) form a basis of \(\mathbb {Z}_p^2\). Thus we can write \(\mathbf {W}_i^\top := \widetilde{\varvec{w}_i} \varvec{a}^\top + \varvec{w}_i (\varvec{a}^{\bot })^\top \), where
such that \(\varvec{a}^\top \varvec{a}^{\bot }= 0\), we have that the vectors \((\varvec{a}|\varvec{a}^{\bot })\) form a basis of \(\mathbb {Z}_p^2\). Thus we can write \(\mathbf {W}_i^\top := \widetilde{\varvec{w}_i} \varvec{a}^\top + \varvec{w}_i (\varvec{a}^{\bot })^\top \), where  , and \(\varvec{a}^{\bot }\in \mathbb {Z}_p^2\) is such that \(\varvec{a}^\top \varvec{a}^{\bot }= 0\) and \(\varvec{c}_1^\top \varvec{a}^{\bot }=1\). This way, the public key can be written as: $$\begin{aligned} \mathsf {mpk}:= \left( [\varvec{a}]_1,\{[\widetilde{\varvec{w}_i}\varvec{a}^\top \varvec{a}]_1\}_{i \in [n]}\right) , \end{aligned}$$
, and \(\varvec{a}^{\bot }\in \mathbb {Z}_p^2\) is such that \(\varvec{a}^\top \varvec{a}^{\bot }= 0\) and \(\varvec{c}_1^\top \varvec{a}^{\bot }=1\). This way, the public key can be written as: $$\begin{aligned} \mathsf {mpk}:= \left( [\varvec{a}]_1,\{[\widetilde{\varvec{w}_i}\varvec{a}^\top \varvec{a}]_1\}_{i \in [n]}\right) , \end{aligned}$$the challenge ciphertext can be written as:
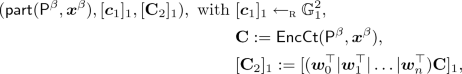
which corresponds exactly to game \(\mathsf {H}_0\). The functional decryption keys can be written as:

The adversary \(\mathcal {B}_2\) samples
 for all \(i \in [0,n]\) and
for all \(i \in [0,n]\) and  ,
,  such that \(\varvec{a}^\top \varvec{a}^{\bot }= 0\), thanks to which it can simulate the public key to \(\mathcal {A}\). To generate the challenge ciphertext, \(\mathcal {B}_2\) forwards the query \(\Big ((\mathsf {P}^0,\varvec{x}^0),(\mathsf {P}^1,\varvec{x}^1)\Big )\) to its own encryption oracle, and forwards its challenge ciphertext to \(\mathcal {A}\). When \(\mathcal {A}\) queries \(\mathsf {OKeyGen}(\mathsf {att},\varvec{y})\), \(\mathcal {B}_2\) queries its own oracle to get \(\mathsf {sk}_{\mathsf {att},\varvec{y}} := (\mathsf {att},\varvec{y},[\varvec{k}_1]_2, [\varvec{k}_2]_2,[k_3]_2)\), where \([\varvec{k}^\top _2]_2 := [(\varvec{w}_0^\top \varvec{k}_1|\ldots |\varvec{w}_n^\top \varvec{k}_1)\mathbf {K}]_2\) for \(\mathbf {K}:= \mathsf {EncKey}(\mathsf {att},\varvec{y})\), and \([k_3]_2 := [\varvec{w}_0^\top \varvec{k}_1]_2\). \(\mathcal {B}_2\) computes \([\mathbf {K}'_2]_2 := [\varvec{a}^{\bot }\varvec{k}^\top _2]_2 + [\varvec{a}(\widetilde{\varvec{w}_0}^\top |\ldots |\widetilde{\varvec{w}_n}^\top )\mathbf {K}]_2\), and \([\varvec{k}'_3]_2 := [\varvec{a}^{\bot }k_3]_2 + [\varvec{a}\widetilde{\varvec{w}_0}^\top \varvec{k}_1]_2\), and returns \(([\varvec{k}_1]_2,[\mathbf {K}'_2]_2,[\varvec{k}'_3]_2)\) to \(\mathcal {A}\). In the full version [6], we show that \(\mathsf {Adv}_{\mathsf {H}_0}(\mathcal {B}_2)\) is negligible.
such that \(\varvec{a}^\top \varvec{a}^{\bot }= 0\), thanks to which it can simulate the public key to \(\mathcal {A}\). To generate the challenge ciphertext, \(\mathcal {B}_2\) forwards the query \(\Big ((\mathsf {P}^0,\varvec{x}^0),(\mathsf {P}^1,\varvec{x}^1)\Big )\) to its own encryption oracle, and forwards its challenge ciphertext to \(\mathcal {A}\). When \(\mathcal {A}\) queries \(\mathsf {OKeyGen}(\mathsf {att},\varvec{y})\), \(\mathcal {B}_2\) queries its own oracle to get \(\mathsf {sk}_{\mathsf {att},\varvec{y}} := (\mathsf {att},\varvec{y},[\varvec{k}_1]_2, [\varvec{k}_2]_2,[k_3]_2)\), where \([\varvec{k}^\top _2]_2 := [(\varvec{w}_0^\top \varvec{k}_1|\ldots |\varvec{w}_n^\top \varvec{k}_1)\mathbf {K}]_2\) for \(\mathbf {K}:= \mathsf {EncKey}(\mathsf {att},\varvec{y})\), and \([k_3]_2 := [\varvec{w}_0^\top \varvec{k}_1]_2\). \(\mathcal {B}_2\) computes \([\mathbf {K}'_2]_2 := [\varvec{a}^{\bot }\varvec{k}^\top _2]_2 + [\varvec{a}(\widetilde{\varvec{w}_0}^\top |\ldots |\widetilde{\varvec{w}_n}^\top )\mathbf {K}]_2\), and \([\varvec{k}'_3]_2 := [\varvec{a}^{\bot }k_3]_2 + [\varvec{a}\widetilde{\varvec{w}_0}^\top \varvec{k}_1]_2\), and returns \(([\varvec{k}_1]_2,[\mathbf {K}'_2]_2,[\varvec{k}'_3]_2)\) to \(\mathcal {A}\). In the full version [6], we show that \(\mathsf {Adv}_{\mathsf {H}_0}(\mathcal {B}_2)\) is negligible.
\(\square \)
4 A Lattice-Based Identity-Based Functional Encryption in the Random-Oracle Model
In this section, we give an overview of an identity-based functional encryption (IFE) for the inner-product functionality from LWE in the random-oracle model. In the full version [6], we provide a lattice-based scheme that is proven secure in the standard model, as well as more background on lattices.
4.1 Our Construction
In this section, we describe how to obtain an identity-based inner-product functional encryption scheme based on the hardness of LWE in the random-oracle model. Our idea is to start with a modification of the ALS functional encryption scheme for inner-products [11], proposed by [55] and which we recall in the full version of this paper [6]. We modify the identity-based encryption scheme of [38] in such a way as to support functional key generation queries, as in ALS. Our construction is described in Fig. 9. Ciphertexts encode vectors \(\varvec{x}\in \mathcal{X}:=\{0,\ldots ,P-1\}^\ell \) under an identity \(\mathsf {id}\). Secret keys correspond to an identity \(\mathsf {id}\) and a vector \(\varvec{y}\in \mathcal{Y}:=\{0,\ldots ,V-1\}^\ell \). When the identities match, our scheme decrypts the bounded inner-product \(\langle \varvec{x},\varvec{y} \rangle \in \{0,\ldots , K - 1\}\) where \(K = \ell PV\).
Since our construction achieves anonymity and the size of input vectors \(\varvec{x}\) are fixed, no partial information about the input is leaked. That is, \(\mathsf {part}(\varvec{x},\mathsf {id})=\perp \).
An identity-based inner-product functional encryption scheme \(\mathcal {IFE}\) in the random-oracle model, where H denotes the random oracle. For descriptions of the algorithms \(\mathsf {TrapGen}\) and \(\mathsf {SamplePre}\), please consult the full version of this paper [6]. Distribution \(\mathcal {D}_{\mathbb {Z}^m,\sigma }\) denotes the discrete Gaussian distribution on \(\mathbb {Z}^m\), of standard deviation \(\sigma \), for more details see the full version [6].
Lemma 4.1
(Correctness). For \(q\ge 2K\ell \sqrt{\ell } V\omega (\log ^2 n)\), \(\sigma =2C\alpha q (\sqrt{m}+\sqrt{n}+\sqrt{\ell })\), \(\rho \ge \omega (\sqrt{\log n})\), \(m=2n \log q\), the scheme from Fig. 9 is correct.
Proof
When identities match, observe that decryption yields \(\varvec{y}^{\!\scriptscriptstyle {\top }}\mathbf {U}\varvec{s}+\varvec{y}^{\!\scriptscriptstyle {\top }}\varvec{f}_2+\varvec{y}^{\!\scriptscriptstyle {\top }}\mathbf {Z}\mathbf {A}\varvec{s}+\varvec{y}^{\!\scriptscriptstyle {\top }}\mathbf {Z}\varvec{f}_1+\Big \lfloor \tfrac{q}{K} \Big \rfloor \langle \varvec{x},\varvec{y} \rangle \), which is equal to:

This decrypts correctly as long as the error terms are small. As explained in the full version, we know that every entry of \(\mathbf {Z}\) is with overwhelming probability bounded by \(\omega (\log n)\), so \(\Vert \mathbf {Z} \Vert \le \sqrt{\ell }\cdot \omega (\log n)\), as long as \(\rho \ge \omega (\sqrt{\log n})\). We can bound \(\Vert \varvec{y}^{\!\scriptscriptstyle {\top }}\mathbf {Z}\varvec{e}_1 \Vert \le \ell \sqrt{\ell } V\omega (\log ^2 n)\) and \(\Vert \varvec{y}\varvec{e}_2 \Vert \le \ell V\omega (\sqrt{\log n})\), as long as \(\sigma \ge \omega (\sqrt{\log n}).\) For decryption to succeed, we want that the error terms are smaller than \(\tfrac{q}{2K}\), which implies: \(q\ge 2K\ell \sqrt{\ell } V\omega (\log ^2 n)\), which is the case for our choice of parameters. \(\square \)
Remark 4.2
(No smudging noise). We remark that in our setup, we rely on efficient lattice parameters and require no smudging or superpolynomial modulus.
Theorem 4.3
(Security). Let n be the security parameter, \(q\ge 2K\ell \sqrt{\ell } V\omega (\log ^2 n)\), \(\sigma =2C\alpha q (\sqrt{m}+\sqrt{n}+\sqrt{\ell })\), \(\rho \ge \omega (\sqrt{\log n})\), \(m=2n \log q\), \(\alpha \le \tfrac{\sigma }{2C\alpha q (\sqrt{m}+\sqrt{n}+\sqrt{\ell })}\), then the scheme from Fig. 9 is AD-IND-secure in the random-oracle model, assuming that \(\mathsf {LWE}_{q,\alpha ,n}\) is hard.
The full proof of security can be found in the full version [6]. In the following, we give an overview of the security proof. We achieve adaptive security in the random-oracle model, where the proof closely follows that of [38], while making several changes to adapt the proof techniques to functional encryption.
In the security game, the adversary will be able to ask for functional keys \(\mathsf {sk}_{\mathsf {id},\varvec{y}}\), associated to any identity \(\mathsf {id}\) and vector \(\varvec{y}\). Then, it will have to decide on two pairs (identity, plaintext) for the challenges \((\mathsf {id}_0^*,\varvec{x}^*_0)\) and \((\mathsf {id}^*_1,\varvec{x}^*_1)\). In the proof, we leverage the ROM to guess what identities \(\mathsf {id}_0^*\) and \(\mathsf {id}^*_1\) will be used for the challenge messages. Then we make the following observation: if the adversary obtained secret keys for either \(\mathsf {id}_0^*\Vert \varvec{y}\) or \(\mathsf {id}_1^*\Vert \varvec{y}\), for any \(\varvec{y}\), then it could trivially distinguish between encryptions of \(\varvec{x}_0\) under \(\mathsf {id}^*_0\) and encryptions of \(\varvec{x}_1\) under \(\mathsf {id}^*_1\).
However, this type of trivial attack should be excluded by the AD-IND definition, therefore the adversary cannot obtain decryption key queries for neither \(\mathsf {id}^*_0\) or \(\mathsf {id}^*_1\).
Then, the proof distinguishes the two cases:
-
1.
When \(\mathsf {id}^{*}_0\ne \mathsf {id}^*_1\), security will be inherited from the security of the underlying IBE scheme of [38] through a direct reduction to LWE.
-
2.
When \(\mathsf {id}^*_0=\mathsf {id}^*_1\), functional decryption keys are allowed to be issued to the adversary and the proof will make use of the security of ALS [11]. This is only possible due to the compatibility of ALS with the IBE of [38].
Please consult the full version of this paper for the full proof of security [6]. In the latter, we also show how to construct an identity-based functional encryption scheme for inner-products in the standard model, by building upon [10].
Notes
- 1.
We stress that both schemes support exponentially large input domains, as for existing LWE-based inner-product FE schemes.
References
Abdalla, M., Benhamouda, F., Gay, R.: From single-input to multi-client inner-product functional encryption. In: Galbraith, S.D., Moriai, S. (eds.) ASIACRYPT 2019, Part III. LNCS, vol. 11923, pp. 552–582. Springer, Cham (2019). https://doi.org/10.1007/978-3-030-34618-8_19
Abdalla, M., Benhamouda, F., Kohlweiss, M., Waldner, H.: Decentralizing inner-product functional encryption. In: Lin, D., Sako, K. (eds.) PKC 2019, Part II. LNCS, vol. 11443, pp. 128–157. Springer, Cham (2019). https://doi.org/10.1007/978-3-030-17259-6_5
Abdalla, M., Bourse, F., De Caro, A., Pointcheval, D.: Simple functional encryption schemes for inner products. In: Katz, J. (ed.) PKC 2015. LNCS, vol. 9020, pp. 733–751. Springer, Heidelberg (2015). https://doi.org/10.1007/978-3-662-46447-2_33
Abdalla, M., Bourse, F., De Caro, A., Pointcheval, D.: Better security for functional encryption for inner product evaluations. Cryptology ePrint Archive, Report 2016/011 (2016). http://eprint.iacr.org/2016/011
Abdalla, M., Catalano, D., Fiore, D., Gay, R., Ursu, B.: Multi-input functional encryption for inner products: function-hiding realizations and constructions without pairings. In: Shacham, H., Boldyreva, A. (eds.) CRYPTO 2018, Part I. LNCS, vol. 10991, pp. 597–627. Springer, Cham (2018). https://doi.org/10.1007/978-3-319-96884-1_20
Abdalla, M., Catalano, D., Gay, R., Ursu, B.: Inner-product functional encryption with fine-grained access control. Cryptology ePrint Archive, Report 2020/577 (2020). https://eprint.iacr.org/2020/577
Abdalla, M., Gay, R., Raykova, M., Wee, H.: Multi-input inner-product functional encryption from pairings. In: Coron, J.-S., Nielsen, J.B. (eds.) EUROCRYPT 2017, Part I. LNCS, vol. 10210, pp. 601–626. Springer, Cham (2017). https://doi.org/10.1007/978-3-319-56620-7_21
Agrawal, S., Chase, M.: A study of pair encodings: predicate encryption in prime order groups. In: Kushilevitz, E., Malkin, T. (eds.) TCC 2016, Part II. LNCS, vol. 9563, pp. 259–288. Springer, Heidelberg (2016). https://doi.org/10.1007/978-3-662-49099-0_10
Agrawal, S., Chase, M.: Simplifying design and analysis of complex predicate encryption schemes. In: Coron, J.-S., Nielsen, J.B. (eds.) EUROCRYPT 2017, Part I. LNCS, vol. 10210, pp. 627–656. Springer, Cham (2017). https://doi.org/10.1007/978-3-319-56620-7_22
Agrawal, S., Boneh, D., Boyen, X.: Efficient lattice (H)IBE in the standard model. In: Gilbert, H. (ed.) EUROCRYPT 2010. LNCS, vol. 6110, pp. 553–572. Springer, Heidelberg (2010). https://doi.org/10.1007/978-3-642-13190-5_28
Agrawal, S., Libert, B., Stehlé, D.: Fully secure functional encryption for inner products, from standard assumptions. In: Robshaw, M., Katz, J. (eds.) CRYPTO 2016, Part III. LNCS, vol. 9816, pp. 333–362. Springer, Heidelberg (2016). https://doi.org/10.1007/978-3-662-53015-3_12
Ambrona, M., Barthe, G., Schmidt, B.: Generic transformations of predicate encodings: constructions and applications. In: Katz, J., Shacham, H. (eds.) CRYPTO 2017, Part I. LNCS, vol. 10401, pp. 36–66. Springer, Cham (2017). https://doi.org/10.1007/978-3-319-63688-7_2
Ananth, P., Jain, A., Sahai, A.: Indistinguishability obfuscation without multilinear maps: iO from LWE, bilinear maps, and weak pseudorandomness. Technical report, Cryptology ePrint Archive, Report 2018/615 (2018). https://eprint.iacr.org/2018/615
Ananth, P., Sahai, A.: Projective arithmetic functional encryption and indistinguishability obfuscation from degree-5 multilinear maps. In: Coron, J.-S., Nielsen, J.B. (eds.) EUROCRYPT 2017, Part I. LNCS, vol. 10210, pp. 152–181. Springer, Cham (2017). https://doi.org/10.1007/978-3-319-56620-7_6
Applebaum, B., Arkis, B., Raykov, P., Vasudevan, P.N.: Conditional disclosure of secrets: amplification, closure, amortization, lower-bounds, and separations. In: Katz, J., Shacham, H. (eds.) CRYPTO 2017, Part I. LNCS, vol. 10401, pp. 727–757. Springer, Cham (2017). https://doi.org/10.1007/978-3-319-63688-7_24
Attrapadung, N.: Dual system encryption via doubly selective security: framework, fully secure functional encryption for regular languages, and more. In: Nguyen, P.Q., Oswald, E. (eds.) EUROCRYPT 2014. LNCS, vol. 8441, pp. 557–577. Springer, Heidelberg (2014). https://doi.org/10.1007/978-3-642-55220-5_31
Attrapadung, N.: Dual system encryption framework in prime-order groups via computational pair encodings. In: Cheon, J.H., Takagi, T. (eds.) ASIACRYPT 2016, Part II. LNCS, vol. 10032, pp. 591–623. Springer, Heidelberg (2016). https://doi.org/10.1007/978-3-662-53890-6_20
Baltico, C.E.Z., Catalano, D., Fiore, D., Gay, R.: Practical functional encryption for quadratic functions with applications to predicate encryption. In: Katz, J., Shacham, H. (eds.) CRYPTO 2017, Part I. LNCS, vol. 10401, pp. 67–98. Springer, Cham (2017). https://doi.org/10.1007/978-3-319-63688-7_3
Barbosa, M., Catalano, D., Soleimanian, A., Warinschi, B.: Efficient function-hiding functional encryption: from inner-products to orthogonality. In: Matsui, M. (ed.) CT-RSA 2019. LNCS, vol. 11405, pp. 127–148. Springer, Cham (2019). https://doi.org/10.1007/978-3-030-12612-4_7
Benhamouda, F., Bourse, F., Lipmaa, H.: CCA-secure inner-product functional encryption from projective hash functions. In: Fehr, S. (ed.) PKC 2017, Part II. LNCS, vol. 10175, pp. 36–66. Springer, Heidelberg (2017). https://doi.org/10.1007/978-3-662-54388-7_2
Bethencourt, J., Sahai, A., Waters, B.: Ciphertext-policy attribute-based encryption. In: 2007 IEEE Symposium on Security and Privacy, pp. 321–334. IEEE Computer Society Press, May 2007. https://doi.org/10.1109/SP.2007.11
Bishop, A., Jain, A., Kowalczyk, L.: Function-hiding inner product encryption. In: Iwata, T., Cheon, J.H. (eds.) ASIACRYPT 2015, Part I. LNCS, vol. 9452, pp. 470–491. Springer, Heidelberg (2015). https://doi.org/10.1007/978-3-662-48797-6_20
Boneh, D., Franklin, M.: Identity-based encryption from the Weil pairing. In: Kilian, J. (ed.) CRYPTO 2001. LNCS, vol. 2139, pp. 213–229. Springer, Heidelberg (2001). https://doi.org/10.1007/3-540-44647-8_13
Boneh, D., et al.: Fully key-homomorphic encryption, arithmetic circuit ABE and compact garbled circuits. In: Nguyen, P.Q., Oswald, E. (eds.) EUROCRYPT 2014. LNCS, vol. 8441, pp. 533–556. Springer, Heidelberg (2014). https://doi.org/10.1007/978-3-642-55220-5_30
Boneh, D., Sahai, A., Waters, B.: Functional encryption: definitions and challenges. In: Ishai, Y. (ed.) TCC 2011. LNCS, vol. 6597, pp. 253–273. Springer, Heidelberg (2011). https://doi.org/10.1007/978-3-642-19571-6_16
Castagnos, G., Laguillaumie, F., Tucker, I.: Practical fully secure unrestricted inner product functional encryption modulo p. In: Peyrin, T., Galbraith, S. (eds.) ASIACRYPT 2018, Part II. LNCS, vol. 11273, pp. 733–764. Springer, Cham (2018). https://doi.org/10.1007/978-3-030-03329-3_25
Chen, J., Gay, R., Wee, H.: Improved dual system ABE in prime-order groups via predicate encodings. In: Oswald, E., Fischlin, M. (eds.) EUROCRYPT 2015, Part II. LNCS, vol. 9057, pp. 595–624. Springer, Heidelberg (2015). https://doi.org/10.1007/978-3-662-46803-6_20
Chen, J., Gong, J., Wee, H.: Improved inner-product encryption with adaptive security and full attribute-hiding. In: Peyrin, T., Galbraith, S. (eds.) ASIACRYPT 2018, Part II. LNCS, vol. 11273, pp. 673–702. Springer, Cham (2018). https://doi.org/10.1007/978-3-030-03329-3_23
Chen, Y., Zhang, L., Yiu, S.M.: Practical attribute based inner product functional encryption from simple assumptions. Cryptology ePrint Archive, Report 2019/846 (2019). https://eprint.iacr.org/2019/846
Chotard, J., Dufour Sans, E., Gay, R., Phan, D.H., Pointcheval, D.: Decentralized multi-client functional encryption for inner product. In: Peyrin, T., Galbraith, S. (eds.) ASIACRYPT 2018, Part II. LNCS, vol. 11273, pp. 703–732. Springer, Cham (2018). https://doi.org/10.1007/978-3-030-03329-3_24
Connor, R.J., Schuchard, M.: Blind Bernoulli trials: a noninteractive protocol for hidden-weight coin flips. In: Heninger, N., Traynor, P. (eds.) USENIX Security 2019, pp. 1483–1500. USENIX Association, Berkeley (2019)
Datta, P., Dutta, R., Mukhopadhyay, S.: Functional encryption for inner product with full function privacy. In: Cheng, C.-M., Chung, K.-M., Persiano, G., Yang, B.-Y. (eds.) PKC 2016, Part I. LNCS, vol. 9614, pp. 164–195. Springer, Heidelberg (2016). https://doi.org/10.1007/978-3-662-49384-7_7
Datta, P., Okamoto, T., Tomida, J.: Full-hiding (unbounded) multi-input inner product functional encryption from the k-linear assumption. In: Abdalla, M., Dahab, R. (eds.) PKC 2018, Part II. LNCS, vol. 10770, pp. 245–277. Springer, Cham (2018). https://doi.org/10.1007/978-3-319-76581-5_9
Dufour-Sans, E., Pointcheval, D.: Unbounded inner-product functional encryption with succinct keys. In: Deng, R.H., Gauthier-Umaña, V., Ochoa, M., Yung, M. (eds.) ACNS 2019. LNCS, vol. 11464, pp. 426–441. Springer, Cham (2019). https://doi.org/10.1007/978-3-030-21568-2_21
Gay, R.: A new paradigm for public-key functional encryption for degree-2 polynomials. In: Kiayias, A., Kohlweiss, M., Wallden, P., Zikas, V. (eds.) PKC 2020, Part I. LNCS, vol. 12110, pp. 95–120. Springer, Cham (2020). https://doi.org/10.1007/978-3-030-45374-9_4
Jain, A., Lin, H., Sahai, A.: Simplifying constructions and assumptions for iO. Technical report, Cryptology ePrint Archive, Report 2019/1252 (2019). https://eprint.iacr.org/2019/1252
Gay, R., Kerenidis, I., Wee, H.: Communication complexity of conditional disclosure of secrets and attribute-based encryption. In: Gennaro, R., Robshaw, M. (eds.) CRYPTO 2015, Part II. LNCS, vol. 9216, pp. 485–502. Springer, Heidelberg (2015). https://doi.org/10.1007/978-3-662-48000-7_24
Gentry, C., Peikert, C., Vaikuntanathan, V.: Trapdoors for hard lattices and new cryptographic constructions. In: Ladner, R.E., Dwork, C. (eds.) 40th ACM STOC, pp. 197–206. ACM Press, May 2008. https://doi.org/10.1145/1374376.1374407
Gertner, Y., Ishai, Y., Kushilevitz, E., Malkin, T.: Protecting data privacy in private information retrieval schemes. J. Comput. Syst. Sci. 60(3), 592–629 (2000)
Gorbunov, S., Vaikuntanathan, V., Wee, H.: Attribute-based encryption for circuits. In: Boneh, D., Roughgarden, T., Feigenbaum, J. (eds.) 45th ACM STOC, pp. 545–554. ACM Press, June 2013. https://doi.org/10.1145/2488608.2488677
Gorbunov, S., Vaikuntanathan, V., Wee, H.: Predicate encryption for circuits from LWE. In: Gennaro, R., Robshaw, M. (eds.) CRYPTO 2015, Part II. LNCS, vol. 9216, pp. 503–523. Springer, Heidelberg (2015). https://doi.org/10.1007/978-3-662-48000-7_25
Goyal, V., Pandey, O., Sahai, A., Waters, B.: Attribute-based encryption for fine-grained access control of encrypted data. In: Juels, A., Wright, R.N., De Capitani di Vimercati, S. (eds.) ACM CCS 2006, pp. 89–98. ACM Press, October/November 2006. https://doi.org/10.1145/1180405.1180418. Available as Cryptology ePrint Archive Report 2006/309
Jain, A., Lin, H., Matt, C., Sahai, A.: How to leverage hardness of constant-degree expanding polynomials over \(\mathbb{R}\) to build \(i\cal{O}\). In: Ishai, Y., Rijmen, V. (eds.) EUROCRYPT 2019, Part I. LNCS, vol. 11476, pp. 251–281. Springer, Cham (2019). https://doi.org/10.1007/978-3-030-17653-2_9
Katz, J., Sahai, A., Waters, B.: Predicate encryption supporting disjunctions, polynomial equations, and inner products. In: Smart, N. (ed.) EUROCRYPT 2008. LNCS, vol. 4965, pp. 146–162. Springer, Heidelberg (2008). https://doi.org/10.1007/978-3-540-78967-3_9
Kim, S., Lewi, K., Mandal, A., Montgomery, H., Roy, A., Wu, D.J.: Function-hiding inner product encryption is practical. In: Catalano, D., De Prisco, R. (eds.) SCN 2018. LNCS, vol. 11035, pp. 544–562. Springer, Cham (2018). https://doi.org/10.1007/978-3-319-98113-0_29
Libert, B., Ţiţiu, R.: Multi-client functional encryption for linear functions in the standard model from LWE. In: Galbraith, S.D., Moriai, S. (eds.) ASIACRYPT 2019, Part III. LNCS, vol. 11923, pp. 520–551. Springer, Cham (2019). https://doi.org/10.1007/978-3-030-34618-8_18
Lin, H.: Indistinguishability obfuscation from SXDH on 5-linear maps and locality-5 PRGs. In: Katz, J., Shacham, H. (eds.) CRYPTO 2017, Part I. LNCS, vol. 10401, pp. 599–629. Springer, Cham (2017). https://doi.org/10.1007/978-3-319-63688-7_20
Liu, T., Vaikuntanathan, V., Wee, H.: Conditional disclosure of secrets via non-linear reconstruction. In: Katz, J., Shacham, H. (eds.) CRYPTO 2017, Part I. LNCS, vol. 10401, pp. 758–790. Springer, Cham (2017). https://doi.org/10.1007/978-3-319-63688-7_25
Okamoto, T., Takashima, K.: Adaptively attribute-hiding (hierarchical) inner product encryption. In: Pointcheval, D., Johansson, T. (eds.) EUROCRYPT 2012. LNCS, vol. 7237, pp. 591–608. Springer, Heidelberg (2012). https://doi.org/10.1007/978-3-642-29011-4_35
O’Neill, A.: Definitional issues in functional encryption. Cryptology ePrint Archive, Report 2010/556 (2010). http://eprint.iacr.org/2010/556
Ryffel, T., Pointcheval, D., Bach, F., Dufour-Sans, E., Gay, R.: Partially encrypted deep learning using functional encryption. In: Wallach, H., Larochelle, H., Beygelzimer, A., d’Alché-Buc, F., Fox, E., Garnett, R. (eds.) Advances in Neural Information Processing Systems 32, pp. 4519–4530. Curran Associates, Inc. (2019). http://papers.nips.cc/paper/8701-partially-encrypted-deep-learning-using-functional-encryption.pdf
Sahai, A., Waters, B.: Fuzzy identity-based encryption. In: Cramer, R. (ed.) EUROCRYPT 2005. LNCS, vol. 3494, pp. 457–473. Springer, Heidelberg (2005). https://doi.org/10.1007/11426639_27
Shamir, A.: Identity-based cryptosystems and signature schemes. In: Blakley, G.R., Chaum, D. (eds.) CRYPTO 1984. LNCS, vol. 196, pp. 47–53. Springer, Heidelberg (1985). https://doi.org/10.1007/3-540-39568-7_5
Tomida, J., Takashima, K.: Unbounded inner product functional encryption from bilinear maps. In: Peyrin, T., Galbraith, S. (eds.) ASIACRYPT 2018, Part II. LNCS, vol. 11273, pp. 609–639. Springer, Cham (2018). https://doi.org/10.1007/978-3-030-03329-3_21
Wang, Z., Fan, X., Liu, F.-H.: FE for inner products and its application to decentralized ABE. In: Lin, D., Sako, K. (eds.) PKC 2019, Part II. LNCS, vol. 11443, pp. 97–127. Springer, Cham (2019). https://doi.org/10.1007/978-3-030-17259-6_4
Waters, B.: Dual system encryption: realizing fully secure IBE and HIBE under simple assumptions. In: Halevi, S. (ed.) CRYPTO 2009. LNCS, vol. 5677, pp. 619–636. Springer, Heidelberg (2009). https://doi.org/10.1007/978-3-642-03356-8_36
Wee, H.: Dual system encryption via predicate encodings. In: Lindell, Y. (ed.) TCC 2014. LNCS, vol. 8349, pp. 616–637. Springer, Heidelberg (2014). https://doi.org/10.1007/978-3-642-54242-8_26
Wee, H.: Attribute-hiding predicate encryption in bilinear groups, revisited. In: Kalai, Y., Reyzin, L. (eds.) TCC 2017, Part I. LNCS, vol. 10677, pp. 206–233. Springer, Cham (2017). https://doi.org/10.1007/978-3-319-70500-2_8
Acknowledgment
The first author was supported in part by the European Union’s Horizon 2020 Research and Innovation Programme under grant agreement 780108 (FENTEC), by the ERC Project aSCEND (H2020 639554), and by the French FUI project ANBLIC. The third author was partially supported by a Google PhD Fellowship in Privacy and Security. The fourth author was partially supported by the ERC Project PREP-CRYPTO (H2020 724307). Part of this work was done while the third author was at École normale supérieure, Paris, France, at UC Berkeley, California, USA, and at Cornell Tech, NY, USA.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2020 International Association for Cryptologic Research
About this paper
Cite this paper
Abdalla, M., Catalano, D., Gay, R., Ursu, B. (2020). Inner-Product Functional Encryption with Fine-Grained Access Control. In: Moriai, S., Wang, H. (eds) Advances in Cryptology – ASIACRYPT 2020. ASIACRYPT 2020. Lecture Notes in Computer Science(), vol 12493. Springer, Cham. https://doi.org/10.1007/978-3-030-64840-4_16
Download citation
DOI: https://doi.org/10.1007/978-3-030-64840-4_16
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-64839-8
Online ISBN: 978-3-030-64840-4
eBook Packages: Computer ScienceComputer Science (R0)




 , and it outputs a ciphertext
, and it outputs a ciphertext  .
. : takes as input the master secret key
: takes as input the master secret key  , and it outputs a decryption key
, and it outputs a decryption key  .
. : takes as input a decryption key
: takes as input a decryption key  along with a ciphertext
along with a ciphertext  , and it outputs a value
, and it outputs a value  or the special symbol
or the special symbol  if it fails.
if it fails. , where
, where 




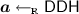 ,
,  ,
,  ,
, 


 .
.

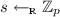 , or
, or  , the adversary
, the adversary  , and simulate
, and simulate  anymore. Clearly,
anymore. Clearly,  ,
, 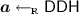 ,
, 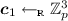 , is within negligible statistical distance from
, is within negligible statistical distance from  . Roughly speaking, the vectors
. Roughly speaking, the vectors  and
and  such that
such that  , and
, and 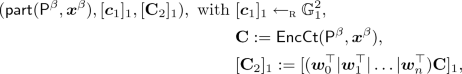

 for all
for all  ,
,  such that
such that 

