Abstract
Registered encryption (Garg et al., TCC’18) is an emerging paradigm that tackles the key-escrow problem associated with identity-based encryption by replacing the private-key generator with a much weaker entity known as the key curator. The key curator holds no secret information, and is responsible to: (i) update the master public key whenever a new user registers its own public key to the system; (ii) provide helper decryption keys to the users already registered in the system, in order to still enable them to decrypt after new users join the system. For practical purposes, tasks (i) and (ii) need to be efficient, in the sense that the size of the public parameters, of the master public key, and of the helper decryption keys, as well as the running times for key generation and user registration, and the number of updates, must be small.
In this paper, we generalize the notion of registered encryption to the setting of functional encryption (FE).
As our main contribution, we show an efficient construction of registered FE for the special case of (attribute hiding) inner-product predicates, built over asymmetric bilinear groups of prime order. Our scheme supports a large attribute universe and is proven secure in the bilinear generic group model. We also implement our scheme and experimentally demonstrate the efficiency requirements of the registered settings. Our second contribution is a feasibility result where we build registered FE for
 based on indistinguishability obfuscation and somewhere statistically binding hash functions.
based on indistinguishability obfuscation and somewhere statistically binding hash functions.
Access provided by Autonomous University of Puebla. Download conference paper PDF
Similar content being viewed by others
Keywords
1 Introduction
Functional encryption (FE) [18, 51, 53] enriches standard public-key encryption with fine-grained access control over encrypted data. This added feature is made possible by having a so-called master secret key \(\textsf{msk}\) that can be used (by an authority) to generate decryption keys \(\textsf{sk}_f\) associated with functions f, in such a way that decrypting any ciphertext c, corresponding to a plaintext m, reveals f(m) and nothing more. Recent years have seen a flourish of works exploring FE constructions in various settings and from different assumptions [1,2,3, 5, 6, 8, 9, 17, 19, 20, 27, 28, 32,33,34, 36, 37, 43,44,45, 48, 52, 56], and its applications to building powerful cryptographic tools such as reusable garbled circuits [36], adaptive garbling [40], multi-party non-interactive key exchange [31], universal samplers [31], verifiable random functions [15, 38], and indistinguishability obfuscation (iO) [7, 16] (which, in turn, implies a plethora of other cryptographic primitives [52]).
An important limitation of FE is the well-known key escrow problem: the authority holding the master secret key (sometimes referred to as the private key generator – PKG) can generate secret keys for any function, allowing it to arbitrarily decrypt messages intended for specific recipients. This requires a fully trusted PKG which severely restricts the applicability of FE in many scenarios.
Registered Encryption. A recent line of research proposes to tackle the key-escrow problem in the much simpler case of identity-based encryptionFootnote 1 (IBE) [54]. This led to the notion of registered IBE (RIBE) [29]Footnote 2, where the main idea is to replace the PKG with a much weaker entity called the key curator (KC), whose role is to register the public keys of the users (without possessing any secret key). In particular, in a RIBE scheme there is an initial setup phase in which a common reference string (CRS) is sampled. The CRS is given to the KC which publishes an (initially empty) master public key. Each user now can also use the CRS and sample its own public and secret key, and can register its identity and the chosen public key to the KC; the KC is required to generate a new master public key, which includes the newly registered public keys, and which will permit encrypting messages to any of the registered users. Moreover, since the master public key is updated over time, the KC is responsible for providing any decrypting party with a so-called helper decryption key, i.e., auxiliary information connecting its public key with the updated master public key.
Recently, the notion of RIBE has been extended to the setting of attribute-based encryption (ABE) [41], where one can encrypt messages with respect to policies, and where decryptors can recover the message if their attributes satisfy the policy embedded in the ciphertext. However, their registered ABE (RABE) schemes [41] are required to hide only messages in the ciphertext. In particular, they do not hide the policies embedded in the ciphertexts, since they are required in the clear for decryption to work. This restricts using RABE in scenarios where hiding the policy is also important.
More generally, the current state of affairs leaves open the question of building registered FE (RFE), where any user can sample its own key pair \((\textsf{pk},\textsf{sk})\) as before, along with fixing a function of its choice (say f, from a class of functions), and register \((\textsf{pk},f)\) with the KC. In such a setting, one can then encrypt messages m that the registered user can decrypt with \(\textsf{sk}\) and a helper secret key to learn only f(m). Overall, this would achieve the analogous functionality to that of the celebrated notion of FE, without suffering from the key escrow issue. The focus of our work is to make progress on this problem.
1.1 Our Contributions
We initiate the study of RFE in this paper by providing two constructions – one for a special class of FE, and another for the general class of all functions.
In particular, as our first contribution, we provide the first RFE scheme for the class of inner-product predicates (a.k.a. (attribute hiding) inner-product predicate encryption), i.e., a registered IPE (RIPE) from asymmetric bilinear maps on prime-order groups. More concretely, our scheme supports the function class \(\mathcal {F}= \{f_\textbf{x}(\cdot ,\cdot )\}_{\textbf{x}\in \mathbb {Z}^{n^+}_q}\) defined as:

where \(\textbf{x}\) and \(\textbf{y}\) are n-size vectors over \(\mathbb {Z}^{n^+}_q = \mathbb {Z}^{n}_q \setminus \{\textbf{0}^n\}\), and q is a prime. Below we summarize our result informally in Theorem 1 and also later in Table 1 (Sect. 3) when we discuss related works to compare it with existing registered encryption schemes.
Theorem 1 (Informal)
Let \(\lambda \) be a security parameter, n be the length of supported vectors, and L be a bound on the maximum number of users. There is a (black-box) construction of RIPE supporting a large universe and up to \(L\) users in the generic bilinear group model, satisfying the following properties:
-
The CRS is of size
 .
. -
The master public key and each helper decryption key is of size
 .
. -
Key-generation and registration runs in time
 and
and
 , respectively.
, respectively. -
Each registered user receives at most \(O(\log L)\) updates from the KC over the entire lifetime of the system.
Moreover, both encryption and decryption runs in time
 .
.
Our scheme is proven secure in the bilinear generic group model [12, 14]. We emphasize that our scheme supports attribute-hiding and a large universe unlike [41]. In particular, our scheme satisfies the strong notion of two-sided securityFootnote 3 [26, 46], where no information on the attribute vector \(\textbf{y}\) is revealed (besides the orthogonality test) even if decryption succeeds, akin to what [46] achieved.Footnote 4
Somewhat interestingly, our proof strategy and construction template are substantially different from the typical inner-product predicate encryption schemes in the literature (e.g., [46]). Roughly speaking, traditional proof strategies work by “programming” the function output (for the challenge ciphertext) in the key given by the adversary, and then arguing that this new key is indistinguishable from the original distribution. In the registered setting, the adversary can sample its own key, so the reduction has no control over it and cannot modify its distribution. Hence, we see RIPE as the main technical contribution of this work.
We also implemented our scheme and describe the results in Sect. 7. The benchmarks are achieved with a set of \(L = 100\) to \(L = 1000\) users with attribute vectors of length varying between \(n = 10\) and \(n = 100\). Our results demonstrate concrete, practical efficiency of our scheme beyond the realms of only feasibility. Further, following the generic and non-cryptographic transformations described in [46, Section 5], our RIPE scheme can also support constant-degree polynomial evaluations, disjunctions, conjunctions, and evaluating CNF and DNF formulas.
As our second contribution, we build RFE for all circuits from indistinguishability obfuscation (iO). This is a feasibility result extending the iO-based RABE schemes in [41] to the setting of RFE. In more detail, we achieve the following:
Theorem 2 (Informal)
Let \(\lambda \) be the security parameter. Assuming somewhere statistically binding hash functions [42, 50] and iO [13], there is a (non black-box) construction of RFE supporting arbitrary functions and an arbitrary number of users, satisfying the following properties:
-
The CRS, master public key, and each helper decryption key is of size
 .
. -
Key-generation and registration runs in time
 and
and
 , respectively, where \(L\) stands for the current number of registered users.
, respectively, where \(L\) stands for the current number of registered users. -
Each registered user receives at most \(O(\log L)\) updates from the KC over the entire lifetime of the system, where \(L\) is as defined in the previous item.
Moreover, both encryption and decryption runs in time
 . Further, the above scheme achieves the same efficiency as that of iO-based RABE from [41].
. Further, the above scheme achieves the same efficiency as that of iO-based RABE from [41].
2 Technical Overview
In the following, we first describe the notion of registered FE and its properties of interest. Next, we provide a brief overview of the techniques behind our schemes.
RFE Definition. We discuss the notion of RFE at a high level. Fundamentally, RFE allows users to generate their own keys (associated to functions of their choice) without the need of a trusted authority, which is replaced with a KC that does not hold any secret. The KC is simply responsible of managing a data structure containing the public keys (plus the corresponding functions) of registered users. Roughly, the RFE syntax goes as follows: For some security parameter \(\lambda \) and a function class \(\mathcal {F}\), the algorithm
 initializes the system to output a common reference string \(\textsf{crs}\).Footnote 5 Given \(\textsf{crs}\), the KC initializes a state \(\alpha = \bot \) (i.e., the data structure) and the master public key \(\textsf{mpk}=\bot \). A user can now register its own \((\textsf{pk},f)\) pair as follows: it samples
initializes the system to output a common reference string \(\textsf{crs}\).Footnote 5 Given \(\textsf{crs}\), the KC initializes a state \(\alpha = \bot \) (i.e., the data structure) and the master public key \(\textsf{mpk}=\bot \). A user can now register its own \((\textsf{pk},f)\) pair as follows: it samples
 and submits a registration request \((\textsf{pk},f)\) to the KC, where \(f\in \mathcal {F}\) is a function it wishes to associate with \(\textsf{pk}\). The KC updates its state as \(\alpha = \alpha '\) and \(\textsf{mpk}= \textsf{mpk}'\) where \((\textsf{mpk}',\alpha ')\) are output by the deterministic registration algorithm \(\textsf{RegPK}(\textsf{crs},\alpha ,\textsf{pk},f)\). Intuitively, a ciphertext
and submits a registration request \((\textsf{pk},f)\) to the KC, where \(f\in \mathcal {F}\) is a function it wishes to associate with \(\textsf{pk}\). The KC updates its state as \(\alpha = \alpha '\) and \(\textsf{mpk}= \textsf{mpk}'\) where \((\textsf{mpk}',\alpha ')\) are output by the deterministic registration algorithm \(\textsf{RegPK}(\textsf{crs},\alpha ,\textsf{pk},f)\). Intuitively, a ciphertext
 computed with \(\textsf{mpk}\) can be later decrypted by the users registered before or during \(\textsf{mpk}\) was generated. The registered user uses \(\textsf{sk}\) to decrypt \(c\). However, \(\textsf{mpk}\) is updated periodically (after each registration) – so the user issues an update request to the KC that, in turn, deterministically returns a helper secret key \({\textsf{hsk}}= \textsf{Update}(\textsf{crs},\alpha ,\textsf{pk})\). The \({\textsf{hsk}}\) provides necessary information to make a (previously registered) user’s secret key \(\textsf{sk}\) valid with respect to a new \(\textsf{mpk}\). With \({\textsf{hsk}}\), the user can decrypt to learn \(f(m) = \textsf{Dec}(\textsf{sk},{\textsf{hsk}},c)\). For optimal efficiency, an RFE system with \(L\) registered users should satisfy the following properties:
computed with \(\textsf{mpk}\) can be later decrypted by the users registered before or during \(\textsf{mpk}\) was generated. The registered user uses \(\textsf{sk}\) to decrypt \(c\). However, \(\textsf{mpk}\) is updated periodically (after each registration) – so the user issues an update request to the KC that, in turn, deterministically returns a helper secret key \({\textsf{hsk}}= \textsf{Update}(\textsf{crs},\alpha ,\textsf{pk})\). The \({\textsf{hsk}}\) provides necessary information to make a (previously registered) user’s secret key \(\textsf{sk}\) valid with respect to a new \(\textsf{mpk}\). With \({\textsf{hsk}}\), the user can decrypt to learn \(f(m) = \textsf{Dec}(\textsf{sk},{\textsf{hsk}},c)\). For optimal efficiency, an RFE system with \(L\) registered users should satisfy the following properties:
-
(1)
Compact parameters: The sizes of \(\textsf{crs},\textsf{mpk},{\textsf{hsk}}\) must be small, e.g.,
 .
. -
(2)
Efficiency: This measures key-generation and registration runtimes, and the number of updates as described below.
-
(a)
Each execution of \(\textsf{KGen} \) and \(\textsf{RegPK}\) should run in time
 .
. -
(b)
Each registered user receives at most \(O(\log L)\) number of new updates (i.e., new \({\textsf{hsk}}\)s) over the lifetime of the system.
-
(a)
RFE can support an unbounded or a bounded number of users. In particular, for the unbounded case, the setup is independent of the number of users. (In this case, the parameter L in efficiency conditions refer to the current number of registered users.) For the bounded case, the setup depends on a bound \(L\) (fixed a-priori). Security of RFE is analogous to that of RIBE [29] and RABE [41]. In particular, an adversary \(\textsf{A}\) corrupting a subset of k registered users (i.e., \(\textsf{A}\) knows the set \(\{(\textsf{sk}_i,(\textsf{pk}_i,f_i))\}_{i\in [k]}\)) cannot distinguish
 from
from
 , as long as \(f_i(m_0) = f_i(m_1), \forall i \in [k]\). This should hold even if \(\textsf{A}\) registers malformed public keys. We refer to the full version [25] for more details.
, as long as \(f_i(m_0) = f_i(m_1), \forall i \in [k]\). This should hold even if \(\textsf{A}\) registers malformed public keys. We refer to the full version [25] for more details.
Slotted RFE. Following Hohenberger et al. [41], we first define and use slotted RFE as a stepping stone towards building full-fledged RFE. Differently to RFE, there is only a single update (referred to as aggregation) in slotted RFE, where users are assigned to “slots” and the master public key is only computed once all slots are filled. In more detail, initialization and key generation work as before, except now that the \(\textsf{Setup} \) (resp. \(\textsf{KGen} \)) takes as an extra input the maximum number of slots/keys L that can be aggregated (resp. a user index \(i\in [L]\)). The KC takes all L pairs \(\{(\textsf{pk}_i,f_i)\}_{i\in [L]}\) together, aggregrates (i.e. updates) it to compute a short \(\textsf{mpk}\) and L helper secret keys \(\{{\textsf{hsk}}_i\}_{i\in [L]}\) for each user. Encryption and decryption again works as before.
Akin to RFE, slotted RFE security requires that, for an aggregated \(\textsf{mpk}\) w.r.t. to all L slots,
 and
and
 are computationally indistinguishable, so long as \(f_j(m_0) = f_j(m_1)\) for all corrupted slots \(j\in [L]\). We refer to the full version [25] for more details.
are computationally indistinguishable, so long as \(f_j(m_0) = f_j(m_1)\) for all corrupted slots \(j\in [L]\). We refer to the full version [25] for more details.
Hohenberger et al.[41] lifted slotted RABE to a standard RABE via a generic compiler, and the same holds for slotted RFE (with minor syntactic changes). Loosely speaking, they use a “powers-of-two” approach, where users are assigned to different slotted schemes with increasing capacities, and they are moved forward as new users join the system. The same idea yields a fully-fledged RFE that supports \(O(\log L)\) number of updates and incurs a multiplicative \(O(\log L)\) overhead on the size of \(\textsf{crs}, \textsf{mpk}, {\textsf{hsk}}\), and the key-generation and encryption runtimes compared to that of the underlying slotted RFE scheme. The registration runtime is dominated by \(O(t_\textsf{Aggr}+ L\cdot t_{\textsf{hsk}})\), where \(t_\textsf{Aggr}\) and \(t_{\textsf{hsk}}\) are the aggregation runtime and the helper decryption key size of the slotted RFE respectively. For completeness, we present the transformation in our full version [25].
2.1 (Bounded Users) Slotted RIPE from Pairings
We begin with an overview of our scheme for inner-product predicates. This is a special case of FE, where vectors \(\textbf{x}\in \mathbb {Z}^{n^+}_q( = \mathbb {Z}_q^n\setminus {\{ \textbf{0}^n \}})\) denote functions \(f_\textbf{x}\) (associated to keys), and messages consist of a tuple \(( \textbf{y},m)\). The function \(f_{\textbf{x}}\) can be recast as:
where we denote the length of vectors by \(n = n(\lambda )\), and assume the attribute space to be \({\mathcal {U}} = \mathbb {Z}_q^{n^+}\) (i.e., domain of vectors). Our scheme follows the blueprint of [41]. However, unlike [41], that reveals the policy in clear, achieving attribute-hiding security in this setting of predicate encryption requires us to introduce crucial modifications, which we highlight after the overview of our scheme below. Furthermore, the security analysis is completely different.
Single-Slot Scheme. We begin by discussing a simplified scheme with \(L = 1\) (i.e., there is a single slot). Below is a description of each algorithm in the scheme.
-
Generating the CRS: We first describe the CRS generation. The CRS can be split into three different parts, a general part, a slot-specific part, and a key-specific part. We will describe how each part is generated individually.
-
General part: First, we generate an asymmetric pairing group of prime order q, denoted as \({\mathcal {G}}= (\mathbb {G}_1,\mathbb {G}_2,\mathbb {G}_{\textsf{T}}, q,g_1,g_2 ,e)\). Then, we sample
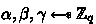 and set \(h = g_1^\beta , Z = e(g_1,g_2 )^\alpha \). (We will need \(\gamma \) for the multi-slot scheme, which we describe later.)
and set \(h = g_1^\beta , Z = e(g_1,g_2 )^\alpha \). (We will need \(\gamma \) for the multi-slot scheme, which we describe later.) -
Slot-specific part: We associate each slot with a set of group elements, for this case we sample
 and set \(A= g_2^t\) and \(B = g_2^\alpha A^\beta = g_2^{\alpha +\beta t}\).
and set \(A= g_2^t\) and \(B = g_2^\alpha A^\beta = g_2^{\alpha +\beta t}\). -
Key-specific part: We also associate a group element to each component of the key vector, plus the secret key. To do this, for each \(w \in [n+1]\), we sample \(u_w \leftarrow \mathbb {Z}_q\) and set \(U_w = g_1^{u_w}\).
In the end, we set the CRS to be:
$$ \textsf{crs}= \left( {\mathcal {G}},Z,h,A,B,\{U_w\}_{w\in [n+1]}\right) . $$ -
-
Generating keys: To compute a new pair of public/secret keys, we sample a non-zero secret key
 and set \(\textsf{pk}= U_{n+1}^{-\textsf{sk}}\). Note that we are conceptually treating the secret key as one more element of the predicate vector. This is an important structural difference with respect to [41].
and set \(\textsf{pk}= U_{n+1}^{-\textsf{sk}}\). Note that we are conceptually treating the secret key as one more element of the predicate vector. This is an important structural difference with respect to [41]. -
Key Aggregation: Since we only have one slot, given \(\textsf{pk}\) and \(\textsf{crs}\), and a predicate vector (or key) \(\textbf{x}= (x_1,\dots ,x_n)\), we set the master public key as:
$$ \textsf{mpk}= \left( {\mathcal {G}}, h,Z,\{U_w\}_{w\in [n+1]},\textsf{pk}\cdot \prod _{w=1}^{n}U_w^{-x_w}\right) . $$ -
Encryption: To encrypt a message \(m\in \mathbb {G}_{\textsf{T}}\) with respect to a non-zero attribute vector \(\textbf{y}= (y_1,\ldots ,y_n) \in \mathbb {Z}_q^{n^+}\), and the master public key \(\textsf{mpk}\), we create a ciphertext that has two components, a message-embedding component, and a key-slot-embedding component.
-
Message embedding: We sample
 , and set \(C_1 = m\cdot Z ^ s, C_2 = g_1^s\).
, and set \(C_1 = m\cdot Z ^ s, C_2 = g_1^s\). -
Key-slot embedding: First, we sample
 . Then, we set $$ C_{3,w} = h^{y_w\cdot r + s }\cdot U_w^{-z} \ (\forall w\in [n]),\ \ C_{3,n+1} = h^s \cdot U_{n+1}^{-z},\ \ \text { and } $$$$ C_{3,n+2} = h^s\cdot \textsf{pk}^{-z}\prod _{w=1}^{n}U_w^{z\cdot x_w}. $$
. Then, we set $$ C_{3,w} = h^{y_w\cdot r + s }\cdot U_w^{-z} \ (\forall w\in [n]),\ \ C_{3,n+1} = h^s \cdot U_{n+1}^{-z},\ \ \text { and } $$$$ C_{3,n+2} = h^s\cdot \textsf{pk}^{-z}\prod _{w=1}^{n}U_w^{z\cdot x_w}. $$
The final ciphertext will be \((C_1,C_2,\{ C_{3,w} \}_{w \in [n+1]})\).
-
-
Decryption: Before describing the actual decryption, let us check the intuition behind each element of the ciphertext. The first component \(C_1 = m\cdot Z^s\) is just a masking of the message with a random power of Z from the CRS. Consider B from \(\textsf{crs}\), and the ciphertext components \(C_1\) and \(C_2\), and observe:
$$\begin{aligned} \frac{C_1}{e(C_2,B)} = \frac{m\cdot e\left( g_1,g_2\right) ^{\alpha \cdot s}}{e\left( g_1,g_2\right) ^{\alpha \cdot s}\cdot e\left( g_1,g_2\right) ^{s\beta t}} =\frac{m}{e\left( h^s,A\right) }. \end{aligned}$$Thus, to recover the message, it suffices to recompute \(e(h^s,A)\). Note that \(h^s\) is already present in some form in the \(C_{3,*}\) components. We can partition \(C_{3,*}\) terms into three different groups, and see how \(h^s\) appears in each one:
-
1.
For all \(w \in [n]\), we have \(C_{3,w} = h^s \cdot h^{y_w \cdot r}\cdot U_w^{-z}\). In this case, there are extra terms \(y_w \cdot r\) as well as \(U_w\) present in the ciphertext. However, since \(\textbf{x}\) and \(\textbf{y}\) are orthogonal (otherwise decryption fails), we can eliminate these extra terms by raising each \(C_{3,w}\) to the power of \(x_w\) for \(w \in [n]\) and compute their product. Thus, we will have:
$$\begin{aligned} \prod _{w=1}^{n} C_{3,w}^{x_{w}} &= \prod _{w=1}^{n} h^{x_w \cdot s} \cdot h^{x_w \cdot y_w \cdot r}\cdot \prod _{w=1}^{n} U_w^{-z\cdot x_w} \\ &= h^{s \cdot \sum _{w=1}^{n}x_w} \cdot \underset{=1}{\underbrace{{h^{r\cdot \sum _{w=1}^{n} x_w \cdot y_w}}}}\cdot \prod _{w=1}^{n} U_w^{-z \cdot x_w}. \end{aligned}$$Therefore, we are left with two terms \(h^{s \cdot \sum _{w=1}^{n} x_w}\) and \(\prod _{w=1}^{n} U_w^{-z \cdot x_w}\).
-
2.
For \(w = n+1\), we have \(C_{3,n+1} = h^s \cdot U_{n+1}^{-z}\), where the term \(h^s\) is masked with \(U_{n+1}^{-z}\).
-
3.
For \(w = n+2\), we have \(C_{3,n+2} = h^s \cdot \textsf{pk}^{-z}\prod _{w=1}^{n}U_w^{z\cdot x_w} = h^s \cdot U_{n+1}^{z\cdot \textsf{sk}}\cdot \prod _{w=1}^{n}U_w^{z\cdot x_w}\).
Multiplying together the remaining components we obtain:
$$\begin{aligned} C_{3,n+2}\cdot C_{3,n+1}^{\textsf{sk}}\cdot \prod _{w=1}^{n} C_{3,w}^{x_{w}} = h^{s}\cdot h^{s\cdot \textsf{sk}} \cdot h^{s \cdot \sum _{w=1}^{n}x_w} = h^{s\cdot \left( 1 + \textsf{sk}+ \sum _{w=1}^{n}x_w \right) }. \end{aligned}$$The decryptor can now raise \(h^{s\cdot \left( 1 + \textsf{sk}+ \sum _{w=1}^{n}x_w \right) }\) to the power of \((1 + \textsf{sk}+ \sum _{w=1}^{n}x_w )^{-1}\) to get \(h^s\). Once \(h^s\) is obtained, it can be paired with A, available from \(\textsf{crs}\), to decrypt the message.
-
1.
Multi-slot Scheme. To gain an intuition on how our scheme handles multiple slots, we describe a toy example where \(L=2\), i.e., we are in the two-slot setting. Notice that one trivial generalization is to individually generate public keys as before, and concatenate them into the master public key. However, this approach will not work, since we want the master public key size to be independent of the number of slots. Instead, we expand the slot-specific components in the CRS to \(A_1,B_1\) (for slot 1) and \(A_2,B_2\) (for slot 2), which are generated in the same way as A, B in the one-slot setting, but using independent random elements
 in generating \(A_1,A_2\). We will also need to link the slots to the keys, so that we can use the slot in the key-generation algorithm. For this, instead of generating only one set of \(\{ U_w \}_{w \in [n]}\), we generate them with respect to both slots
in generating \(A_1,A_2\). We will also need to link the slots to the keys, so that we can use the slot in the key-generation algorithm. For this, instead of generating only one set of \(\{ U_w \}_{w \in [n]}\), we generate them with respect to both slots
where the elements \(\{ u_{w,i} \}_{i\in \{1,2\}}\) are chosen independently and uniformly at random. Accordingly, in the key generation we can set
and we aggregate the keys as
where \(\textbf{x}_1\) and \(\textbf{x}_2\) are the chosen keys. One can encrypt using the new \(\widehat{U}\) values instead of U, however, once we try to decrypt and expand the corresponding equations, we realize that many terms will not cancel out as before. For example, if a message is encrypted for slot 1, during decryption we will have,

where the terms in
 can be canceled out using a similar multiplication trick as before. However, the terms \(U_{n+1,2}^{-z\cdot \textsf{sk}_1}\), \(U_{n+1,2}^{z\cdot \textsf{sk}_2}\), \(\prod _{w\in [n]} U_{w,2}^{-z\cdot x_{w,1}}\) and \(\prod _{w=1}^{n}U_{w,2}^{z\cdot x_{w,2}}\) cannot be canceled as they do not appear anywhere else, and further we assume the decryptor only knows \(\textsf{sk}_1\), but not \(\textsf{sk}_2\). We can circumvent this issue by introducing some “cross-terms” into the CRS, and use them in the aggregation to compute helper secret keys that enables the decryptor (holding \(\textsf{sk}_1\) and \(\textbf{x}_1\)) to cancel such terms. We create these terms such that they include both slot-specific and key-specific parts. Intuitively, they bind each slot to other slots and keys together. For slots \(i,j \in [2]\) where \(i\ne j\) and key indices \(w\in [n+1]\), we define these terms as:
can be canceled out using a similar multiplication trick as before. However, the terms \(U_{n+1,2}^{-z\cdot \textsf{sk}_1}\), \(U_{n+1,2}^{z\cdot \textsf{sk}_2}\), \(\prod _{w\in [n]} U_{w,2}^{-z\cdot x_{w,1}}\) and \(\prod _{w=1}^{n}U_{w,2}^{z\cdot x_{w,2}}\) cannot be canceled as they do not appear anywhere else, and further we assume the decryptor only knows \(\textsf{sk}_1\), but not \(\textsf{sk}_2\). We can circumvent this issue by introducing some “cross-terms” into the CRS, and use them in the aggregation to compute helper secret keys that enables the decryptor (holding \(\textsf{sk}_1\) and \(\textbf{x}_1\)) to cancel such terms. We create these terms such that they include both slot-specific and key-specific parts. Intuitively, they bind each slot to other slots and keys together. For slots \(i,j \in [2]\) where \(i\ne j\) and key indices \(w\in [n+1]\), we define these terms as:
We add \(\{ W_{i,j,w} \}_{i\ne j \in [2],w \in [n+1]}\) to the CRS as:
In addition, we will let the user publish \(\{ W_{j,i,n+1}^{\textsf{sk}_i} \}_{i\in \{1,2\}, j\ne i}\) in their respective public keys, to enable the other users to cancel out the desired cross terms, and publish in the ciphertext an additional element \(C_4 = g_1^z\), to be paired with the W’s in order to compute the correct terms.
The above scheme is correct but unfortunately insecure. At a high level, the problem is that the adversary can pair \(C_4\) with wrong elements and generate unintended relations between z and other components, in the exponent. To prevent this, instead of putting \(g_1^z\) directly in the ciphertext, we introduce an extra component
 in the CRS, and set \(C_4 = \Gamma ^z\). The only other modification that we must apply is the generation of the CRS itself, where for slots \(i,j \in \{ 1,2 \}\) with \(i\ne j\), and key indices \(w\in [n+1]\), we define:
in the CRS, and set \(C_4 = \Gamma ^z\). The only other modification that we must apply is the generation of the CRS itself, where for slots \(i,j \in \{ 1,2 \}\) with \(i\ne j\), and key indices \(w\in [n+1]\), we define:
This forces a (possibly malicious) decryptor to pair \(C_4\) only with the elements \(W_{i,j,w}\) and remove the additional cross-terms described above. The rest of the construction remains the same. See Sect. 6 for more details.
Proof Sketch. We prove the above slotted RIPE scheme secure in the generic bilinear group model (\({\textsf{GGM}}\)). Recall that in the \({\textsf{GGM}}\), the adversary is supplied with handles to the corresponding group elements from the scheme. Further, it can also learn handles to arbitrary linear combinations of existing and new elements (in the same group \(\mathbb {G}_{\mathfrak {t}}, {\mathfrak {t}}\in \{1,2,{\textsf{T}}\}\)) via the group oracles it is provided with. Additionally, since we are in the bilinear setting, the adversary also gets access to the pairing oracle that allows it to learn handles referring to the product of any two terms from the source groups \(\mathbb {G}_1\) and \(\mathbb {G}_2\). However, the only crucial information it can actually learn in this whole interaction is via the zero-tests that work again only in \(\mathbb {G}_{\textsf{T}}\).
Our formal multi-slot RIPE scheme in Sect. 6 introduces several variables with different combinations of indices. To argue indistinguishability in a convenient way between subsequent hybrids in the proof, we first switch from the \({\textsf{GGM}}\) to the symbolic group model (\({\textsf{SGM}}\)) via the Schwarz-Zippel lemma. In particular, the \({\textsf{SGM}}\) allows us to represent all the terms, that the adversary can learn in the security game, as multivariate polynomials (in respective groups) from a ring of variables. The heart of the proof relies on arguing properties of the coefficients of these polynomials that correspond to successful zero-tests, which aids in proving indistinguishability directly. In particular, these claims set in while proving attribute hiding by switching the challenge attribute from \(\textbf{y}_0\) to \(\textbf{y}_1\) in the ciphertext elements \(C_{3,w}\ \forall w\in [n+2]\), and helps in arguing the following:
-
1.
Coefficients of such polynomials formed by pairing terms \(C_{3,w}\in \mathbb {G}_1\) with any element in \(\mathbb {G}_2\), except \(A_i, i\in [2]\), must be all zero.
-
2.
Such a coefficient vector must be orthogonal to \(\textbf{y}_b\) for \(b\in \{ 0,1 \}\), and in particular, either be a constant multiple of the vector \(\widetilde{\textbf{x}}_i = (\textbf{x}_i,\textsf{sk}_i), i\in [2]\) or be all zero.
The claim in Item 1 follows from observing that the monomials formed symbolically (in the exponent) when pairing \(C_{3,w}\) with anything in \(\mathbb {G}_2\) (except \(A_1\) or \(A_2\)) are all linearly independent and do not cancel out. Item 2 follows from two observations. The first one is that the randomness r (appearing as an independent symbolic term, but only in the components \(C_{3,w}\)’s) can only cancel out in zero-tests when the coefficients are orthogonal to \(\textbf{y}_b\). The second one follows additionally from linear independence of some specific symbolic terms and observing further that the vector of first \(n+1\) coefficients can be expressed as a constant multiple of \(\widetilde{\textbf{x}}_i\). Overall, these claims ensure that the only non-trivial adversarial queries can be for vectors lying in the span of both registered and valid predicates. The rest of the proof follows from the admissibility of the adversary, and by reusing these claims. We refer to Theorem 6 for more details.
Comparison with the Slotted RABE of [41]. Our slotted RIPE scheme from prime-order pairings (in Sect. 6) shares some similarities at a high level with the slotted RABE from composite-order pairings by Hohenberger et al.[41]. For instance, the message-embedding mechanism in both schemes are same, which is by masking the message with the randomness in the term \(e\left( h^s,A_i\right) \). (This is also a standard technique in many other pairing-based schemes.) The use of “slot”-based framework to embed users’ keys is also similar, but only at the level of a blueprint. In particular, that is where the similarity ends. More specifically, the way slots and attributes are “glued” together in our scheme is fundamentally different: in [41], the ciphertext has two specific components, an attribute-specific component and a slot-specific one, where one party can decrypt a message if it manages to succeed to decrypt the slot-specific component and the attribute-specific component simultaneously. But in our scheme, the slot and attribute elements are entwined in the same ciphertext component. In essence, we conceptually treat the secret key as “one more dimension” in the predicate vector, whereas the scheme in [41] uses a separate machinery that takes care of the key component. Further, unlike [41] which reveals the policy in the ciphertext, we carefully ensure attribute hiding by multiplying a randomizer \(r\in \mathbb {Z}_q^+\) to the attribute \(\textbf{y}\). As a result, we achieve totally different functionalities and stronger security notions. Finally, our scheme supports vectors from \(\mathbb {Z}^{n^+}_q\) where q is a \(\lambda \)-bit prime and n denotes supported the vector length. As stated in [41, Section 7.2], this enables our scheme to support a large attribute universe in contrast to the pairing-based RABE in [41], that only supports a small attribute universe.
2.2 (Unbounded Users) Slotted RFE from iO
As a feasibility result, we show (slotted) RFE for all circuits based on indistinguishability obfuscation (iO) [13] and (succinct) somewhere statistically binding hash functions (SSB) [42, 50]. In particular, we generalize the techniques from Hohenberger et al. [41] to get a slotted RFE from iO (which can be lifted to RFE with the powers-of-two trick). Below is a brief overview of this slotted RFE.
The CRS is set as the SSB hash key \(\textsf{hk}\), and users’ keys are generated through a PRG \(\textsf{PRG}\) and a seed s (i.e., \((\textsf{pk},\textsf{sk}) = (\textsf{PRG}(s), s)\)). To aggregate \(((\textsf{pk}_i, f_i))_{i \in [L]}\), the KC computes a Merkle tree hash \(h = \textsf{Hash}(\textsf{hk}, ((\textsf{pk}_i, f_i))_{i \in [L]})\) and sets \(\textsf{mpk}= (\textsf{hk},h)\). The helper secret key \({\textsf{hsk}}_i\) (of the i-th slot) is essentially the SSB opening \(\pi _i\) for the i-th (hashed) block \((\textsf{pk}_i,f_i)\). A ciphertext \(c\) (encrypting \(m\)) is simply the obfuscation \(\widetilde{C}\) of a circuit \(C_{h,m}\) that, on input \((i,\textsf{pk}_i,f_i,\pi _i,\textsf{sk}_i)\), returns \(f_i(m)\) if the following two conditions are satisfied: \(\pi _i\) is a valid opening for the i-th block \((\textsf{pk}_i,f_i)\) and \((\textsf{pk}_i,\textsf{sk}_i)\) is a valid key-pair. Decryption works using \(\textsf{sk}_i\) and \({\textsf{hsk}}_i = \pi _i\) to evaluate \(\widetilde{C}\) on input \((i,\textsf{pk}_i,f_i,\pi _i,\textsf{sk}_i)\). The scheme supports the function class
 . Compactness of parameters is evident from SSB succinctness. Due to a poly-logarithmic overhead from the powers-of-two trick, the final RFE can support an arbitrary number of users by setting \(L= 2^\lambda \). The registration runtime remains linear in the current/effective number of registered users at the time of registration. We provide more details in our full version [25].
. Compactness of parameters is evident from SSB succinctness. Due to a poly-logarithmic overhead from the powers-of-two trick, the final RFE can support an arbitrary number of users by setting \(L= 2^\lambda \). The registration runtime remains linear in the current/effective number of registered users at the time of registration. We provide more details in our full version [25].
 respectively denote
respectively denote
 etc. \(\mathcal {U}\) (from [41]) denotes the attribute space supported by the corresponding scheme. \(\mathcal {F}\) denotes the function space supported by our schemes (each function \(f \in \mathcal {F}\) of our RIPE is an n-length vector from \(\mathbb {Z}^{n^{+}}_q\)). Above, BB is an abbreviation for “black-box”.
etc. \(\mathcal {U}\) (from [41]) denotes the attribute space supported by the corresponding scheme. \(\mathcal {F}\) denotes the function space supported by our schemes (each function \(f \in \mathcal {F}\) of our RIPE is an n-length vector from \(\mathbb {Z}^{n^{+}}_q\)). Above, BB is an abbreviation for “black-box”.2.3 On Function Privacy in (Slotted) RFE
By definition, RFE allows users to sample their own keys and functions. Thus, the notion of function-privacy, that is typically considered in the setting of (secret-key) FE [21, 55], does not make much sense from this perspective. However, one can still define function-privacy w.r.t. any other registered or unregistered party. In more detail, in the case of RFE, a user choosing its own keys and functions may want to hide its function from any party including the KC. Capturing this requires a mild change in the RFE syntax, where the function can be input to the \(\textsf{KGen} \) algorithm instead of \(\textsf{RegPK}\) and also require that the generated user key-pair is tied to this function. The KC gets access of only the users’ public keys to aggregate and generate \(\textsf{mpk},{\textsf{hsk}}\).Footnote 6 The security definition would need to change accordingly. In particular, it would now additionally require each public key to computationally hide the function tied to it.
All our schemes can be modified to satisfy this syntax. For example, our slotted RIPE from pairings can be easily adapted to this notion since the extended key \(\widetilde{\textbf{x}}_i = (\textbf{x}_i, \textsf{sk}_i, 1)\) is embedded in the public-key \(\textsf{pk}_i\) for slot \(i\in [2]\) as \(\textsf{pk}_i = \prod _{w=1}^{n+1} U_{w,i}^{-\widetilde{x}_{w,i}}\). This holds similarly for the cross-terms as well. Using a NIZK, the users can prove that they always choose a non-zero vector as its predicate. It is also easy to verify the same for our slotted RFE from \(\textsf{iO}\). However, for simplicity, we avoid formalizing this in our definitions and schemes. Both our formal constructions from Sect. 6 and the one based on \(\textsf{iO}\) are thus in the standard registered setting (i.e., without function-privacy). Building more efficient function-private RFE for specific functions is left as a future work.
3 Related Work
The first paper [29] defined and built RIBE from iO and SSB hashes; this was later improved by Garg et al. [30] building RIBE (with the same level of efficiency) from standard assumptions (e.g., from CDH/LWE) even for anonymous IBE. Subsequent work on RIBE focused on adding verifiability [39], proving lower bounds on the number of decryption updates [49], improving on practical efficiency of the garbled circuit construction [23], providing effcient black-box construction from pairings with
 \(\textsf{mpk}\) [35]. More recently, Döttling et al. [24] obtain a lattice-based RIBE with the sizes of \(\textsf{crs}, \textsf{mpk}, {\textsf{hsk}}\) as well as key generation runtime growing as
\(\textsf{mpk}\) [35]. More recently, Döttling et al. [24] obtain a lattice-based RIBE with the sizes of \(\textsf{crs}, \textsf{mpk}, {\textsf{hsk}}\) as well as key generation runtime growing as
 , with a O(L) registration runtime and \(O(\log L)\) number of updates. Very recently, [41] extended RIBE to the setting of ABE. They built a (black-box) registered ABE (RABE) scheme supporting a bounded number of users and linear secret sharing schemes as access policies from assumptions on composite-order pairing groups. However, their (pairing-based) scheme, the size of CRS and runtime of aggregate and keygen depend linearly on the size of attribute space \(|\mathcal {U}|\). The dependence on \(|\mathcal {U}|\) allows their scheme to only support a small attribute space (e.g.,
, with a O(L) registration runtime and \(O(\log L)\) number of updates. Very recently, [41] extended RIBE to the setting of ABE. They built a (black-box) registered ABE (RABE) scheme supporting a bounded number of users and linear secret sharing schemes as access policies from assumptions on composite-order pairing groups. However, their (pairing-based) scheme, the size of CRS and runtime of aggregate and keygen depend linearly on the size of attribute space \(|\mathcal {U}|\). The dependence on \(|\mathcal {U}|\) allows their scheme to only support a small attribute space (e.g.,
 ). Notably, our (paring-based) RIPE does not suffer from this limitation since our parameters depend only on the vector length \(n = n(\lambda )\) (see Table 1); so we can support a exponential size function class \(\mathcal {F}\).
). Notably, our (paring-based) RIPE does not suffer from this limitation since our parameters depend only on the vector length \(n = n(\lambda )\) (see Table 1); so we can support a exponential size function class \(\mathcal {F}\).
In [39], the authors further introduced an RABE extension to more general access structures. Specifically, they proposed a universal definition of registration-based encryption in which the algorithms take as an additional input the description of an FE scheme (although no construction was presented). Such algorithms compile the standard algorithmic behavior of the FE scheme into a (verifiable) registration-based one. However, our tailored notion for the functional encryption setting is more natural and follows directly from the RABE definition.
Finally, we also mention a related work on dynamic decentralized FE [22] (DDFE), where there is no trusted authority and users sample their own keys. DDFE, as a notion, posits other general (and albeit unrelated) requirements like (conditional) aggregation of labelled data which comes from different users using seperate FE instances. However, a crucial difference from the registered setting, is that in DDFE there is no requirement on the master public key size, which can be as large as the number of registered users. This is a major challenge (and arguably the defining feature) of all registered settings. Chotard et al.[22] also built IP-DDFE, that outputs the inner-product value \(\langle \textbf{x}, \textbf{y}\rangle \), while our scheme is for the more challenging orthogonality-test predicate (with two-sided security).
Open Problems. We view our work as an initial first step in the world of registered FE, however many open problems remain. For example, a natural question is if registered FE can be obtained generically from any compact, polynomially-hard FE. Another interesting direction is to design schemes for specialized function classes from weaker assumptions. Finally, a technical open problem is to prove our pairing-based RIPE scheme (or some modification thereof) secure in the standard model.
4 Organization
We organize the rest of the paper as follows. The formal definitions of both RFE and slotted RFE extend the same for the RABE setting from [41] in a straighforward way. Hence, we provide the RFE definitions in our full version [25]. Our main focus in this paper is on building (slotted) registered IPE. Thus, we first define slotted RIPE formally in Sect. 5.1 and extend it to slotted RFE for the case of general functions in our full version [25]. Our slotted RIPE scheme from bilinear pairings is provided in Sect. 6. We demonstrate our implementation results of the above slotted RIPE scheme in Sect. 7. Our slotted RFE for general functions and unbounded users, built on iO (plus an SSB hash and a PRG), generalizes a construction from [41] and is presented in [25]. Further, the transformation from slotted RFE to RFE extending the generic compiler from [41] is again provided in our full version [25].
5 Preliminaries
Notations. We write \([n] = \{1,2,\ldots ,n\}\) and \([0,n] = \{0\}\cup [n]\). Capital bold-face letters (such as \(\textbf{X}\)) are used to denote random variables, small bold-face letters (such as \(\textbf{x}\)) to denote vectors, small letters (such as x) to denote concrete values, calligraphic letters (such as \({\mathcal {X}}\)) to denote sets, serif letters (such as \({\textsf{A}}\)) to denote algorithms. All of our algorithms are modeled as (possibly interactive) Turing machines. For a string \(x \in \{0,1\}^*\), we let |x| be its length; if \({\mathcal {X}}\) is a set or a list, \(|{\mathcal {X}}|\) represents the cardinality of \({\mathcal {X}}\). When x is chosen uniformly in \({\mathcal {X}}\), we write
 . If
. If
 is an algorithm, we write
is an algorithm, we write
 to denote a run of
to denote a run of
 on input x and output y; if
on input x and output y; if
 is randomized, y is a random variable and
is randomized, y is a random variable and
 denotes a run of
denotes a run of
 on input x and (uniform) randomness r. An algorithm
on input x and (uniform) randomness r. An algorithm
 is probabilistic polynomial-time (\(\text {PPT}\)) if
is probabilistic polynomial-time (\(\text {PPT}\)) if
 is randomized and for any input \(x,r \in \{0,1\}^*\) the computation of
is randomized and for any input \(x,r \in \{0,1\}^*\) the computation of
 terminates in a polynomial number of steps (in the input size). We write \(C(x) = y\) to denote the evaluation of the circuit \(C\) on input x and output y. For any integer \(k\in \mathbb {N}\), we denote \(\mathbb {Z}_q^{k^+}=\mathbb {Z}_q^k\setminus \{\textbf{0}^k\}\) as the set of all non-zero k-size vectors over \(\mathbb {Z}_q\), and \(\mathbb {Z}_q^+ = \mathbb {Z}_q\setminus \{0\}\).
terminates in a polynomial number of steps (in the input size). We write \(C(x) = y\) to denote the evaluation of the circuit \(C\) on input x and output y. For any integer \(k\in \mathbb {N}\), we denote \(\mathbb {Z}_q^{k^+}=\mathbb {Z}_q^k\setminus \{\textbf{0}^k\}\) as the set of all non-zero k-size vectors over \(\mathbb {Z}_q\), and \(\mathbb {Z}_q^+ = \mathbb {Z}_q\setminus \{0\}\).
Negligible Functions. Throughout the paper, we denote the security parameter by \(\lambda \in \mathbb {N}\) and we implicitly assume that every algorithm takes \(\lambda \) as input. A function \(\nu (\lambda )\) is called negligible in \(\lambda \in \mathbb {N}\) if it vanishes faster than the inverse of any polynomial in \(\lambda \), i.e.
 for all positive polynomials \(p(\lambda )\).
for all positive polynomials \(p(\lambda )\).
5.1 Slotted Registered Inner-Product Encryption
We now present the slotted RIPE definitions below. Let \(n = n(\lambda )\) be a polynomial in \(\lambda \) and q be a prime. A slotted RIPE with message space \(\mathcal {M}\) and attribute space \(\mathcal {U}\) is composed of the following polynomial-time algorithms:
-
\(\textsf{Setup} (1^\lambda , 1^n,1^L):\) On input the security parameter
 , the vector length n, and the number of slots \(L\), the randomized setup algorithm outputs a common reference string \(\textsf{crs}\).
, the vector length n, and the number of slots \(L\), the randomized setup algorithm outputs a common reference string \(\textsf{crs}\). -
\(\textsf{KGen} (\textsf{crs},i):\) On input the common reference string \(\textsf{crs}\) and a slot index \(i\in [L]\), the randomized key-generation algorithm outputs a public key \(\textsf{pk}_i\) and a secret key \(\textsf{sk}_i\).
-
\(\textsf{IsValid}(\textsf{crs},i,\textsf{pk}_i)\): On input the common reference string \(\textsf{crs}\), a slot index \(i \in [L]\), and a public key \(\textsf{pk}_i\), the deterministic key validation algorithm outputs a decision bit \(b \in \{ 0,1 \}\).
-
\(\textsf{Aggr} (\textsf{crs}, ((\textsf{pk}_i,\textbf{x}_i))_{i\in [L]}):\) On input the common reference string \(\textsf{crs}\) and a \(L\) pairs \((\textsf{pk}_1,\textbf{x}_1),\dots ,(\textsf{pk}_L,\textbf{x}_L)\) each composed of a public key \(\textsf{pk}_i\) and its corresponding (non-zero) vector \(\textbf{x}_i\in \mathcal {U}\), the deterministic aggregation algorithm outputs the master public key \(\textsf{mpk}\) and a \(L\) helper decryption keys \({\textsf{hsk}}_1,\dots ,{\textsf{hsk}}_L\).
-
\(\textsf{Enc} (\textsf{mpk},\textbf{y}, m)\): On input the master public key \(\textsf{mpk}\), a (non-zero) attribute vector \(\textbf{y}\in \mathcal {U}\), and a message \(m\in \mathcal {M}\), the randomized encryption algorithm outputs a ciphertext \(c\).
-
\(\textsf{Dec} (\textsf{sk},{\textsf{hsk}},c)\): On input a secret key \(\textsf{sk}\), an helper decryption key \({\textsf{hsk}}\), and a ciphertext \(c\), the deterministic decryption algorithm outputs a message \(m\in \mathcal {M}\cup \{\bot \}\).
Completeness, Correctness, and Efficiency. Completeness of slotted RIPE says that honestly generated public keys for a slot index \(i\in [L]\) are valid with respect to the same slot i, i.e., \(\textsf{IsValid}(\textsf{crs},i,\textsf{pk}_i) = 1\). Similarly, correctness says that honest ciphertexts correctly decrypt (to functions of the plaintext) under honestly generated and aggregated keys. For compactness and efficiency, we extend the requirements of RFE to the slotted RIPE setting. The formal definitions are provided in our full version [25]. Below we define the security of slotted RIPE formally.
Definition 1 (Security of slotted RIPE)
Let \(\Pi _{{\textsf{s}}{\textsf{RIPE}}} = (\textsf{Setup},\textsf{KGen},\textsf{IsValid},\textsf{Aggr},\textsf{Enc},\textsf{Dec})\) be a slotted RIPE scheme with message space \(\mathcal {M}\) and attribute space \({\mathcal {U}}\). For any adversary
 , define the following security game
, define the following security game
 with respect to a bit \(b\in \{ 0,1 \}\) between
with respect to a bit \(b\in \{ 0,1 \}\) between
 and a challenger.
and a challenger.
-
Setup phase: Upon getting an attribute length n and a slot count \(L\) from the adversary
 , the challenger samples
, the challenger samples
 and gives \(\textsf{crs}\) to
and gives \(\textsf{crs}\) to
 . The challenger also initializes a counter \(\textsf{ctr}= 0\), a dictionary \({\textsf{D}}\), and a set of slot indices \({\mathcal {C}}_L= \emptyset \) to account for corrupted slots.
. The challenger also initializes a counter \(\textsf{ctr}= 0\), a dictionary \({\textsf{D}}\), and a set of slot indices \({\mathcal {C}}_L= \emptyset \) to account for corrupted slots. -
Pre-challenge query phase:
 can issue the following queries.
can issue the following queries.-
Key-generation query:
 specifies a slot index \(i\in [L]\). As a response, the challenger increments \(\textsf{ctr}= \textsf{ctr}+1\), samples
specifies a slot index \(i\in [L]\). As a response, the challenger increments \(\textsf{ctr}= \textsf{ctr}+1\), samples
 , updates the dictionary as \({\textsf{D}}[\textsf{ctr}] = (i,\textsf{pk}_\textsf{ctr},\textsf{sk}_\textsf{ctr})\) and replies with \((\textsf{ctr}, \textsf{pk}_\textsf{ctr})\) to
, updates the dictionary as \({\textsf{D}}[\textsf{ctr}] = (i,\textsf{pk}_\textsf{ctr},\textsf{sk}_\textsf{ctr})\) and replies with \((\textsf{ctr}, \textsf{pk}_\textsf{ctr})\) to
 .
. -
Corruption query:
 specifies an index \(c\in [\textsf{ctr}]\). In response, the challenger looks up the tuple \({\textsf{D}}[c] = (i',\textsf{pk}',\textsf{sk}')\) and replies with \(\textsf{sk}'\) to
specifies an index \(c\in [\textsf{ctr}]\). In response, the challenger looks up the tuple \({\textsf{D}}[c] = (i',\textsf{pk}',\textsf{sk}')\) and replies with \(\textsf{sk}'\) to
 .
.
-
-
Challenge phase: For each \(i\in [L]\),
 specifies a tuple \((c_i, \textbf{x}_i, \textsf{pk}_i^*)\) where:
specifies a tuple \((c_i, \textbf{x}_i, \textsf{pk}_i^*)\) where:-
either \(c_i \in [\textsf{ctr}]\) that refers to a challenger-generated key from before which it associates with a non-zero predicate \(\textbf{x}_i\in \mathcal {U}\): in this case, the challenger looks up \({\textsf{D}}[c_i] = (i',\textsf{pk}',\textsf{sk}')\) and halts if \(i \ne i'\). Else, the challenger sets \(\textsf{pk}_i^* = \textsf{pk}'\). Further, if
 issued a corrupt query before on \(c_i\), the challenger adds i to \({\mathcal {C}}_L\).
issued a corrupt query before on \(c_i\), the challenger adds i to \({\mathcal {C}}_L\). -
or \(c_i = \bot \) that refers to a self-generated (and corrupt) secret key for an arbitrary non-zero predicate \(\textbf{x}_i\in \mathcal {U}\): in this case, the challenger aborts if \(\textsf{IsValid}(\textsf{crs},i,\textsf{pk}_i^*) = 0\). Else if \(\textsf{pk}_i^*\) is valid, it adds the index i to \({\mathcal {C}}_L\).
Additionally,
 sends a challenge pair \((\textbf{y}_0, m_0),(\textbf{y}_1, m_1)\in {\mathcal {U}} \times \mathcal {M}\). In response, the challenger computes \(\left( \textsf{mpk}, ({\textsf{hsk}}_i)_{i\in [L]}\right) = \textsf{Aggr} \left( \textsf{crs}, (\textsf{pk}_i^*,\textbf{x}_i)_{i\in [L]}\right) \) and
sends a challenge pair \((\textbf{y}_0, m_0),(\textbf{y}_1, m_1)\in {\mathcal {U}} \times \mathcal {M}\). In response, the challenger computes \(\left( \textsf{mpk}, ({\textsf{hsk}}_i)_{i\in [L]}\right) = \textsf{Aggr} \left( \textsf{crs}, (\textsf{pk}_i^*,\textbf{x}_i)_{i\in [L]}\right) \) and
 , and replies with \(c^*\) to
, and replies with \(c^*\) to
 .
. -
-
Output phase:
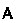 returns a bit \(b'\in \{ 0,1 \}\) which is also the output of the experiment.
returns a bit \(b'\in \{ 0,1 \}\) which is also the output of the experiment.
 is called admissible if the challenge pair \((\textbf{y}_0, m_0), (\textbf{y}_1, m_1)\) satisfy the following:
is called admissible if the challenge pair \((\textbf{y}_0, m_0), (\textbf{y}_1, m_1)\) satisfy the following:
-
\(\forall \textbf{x}_i\in {\mathcal {U}}\) with \(i\in {\mathcal {C}}_L\), it holds that:
$$\text {either } \langle \textbf{x}_i,\textbf{y}_0 \rangle = \langle \textbf{x}_i,\textbf{y}_1 \rangle = 0 \quad \text {or} \quad \text {both} \langle \textbf{x}_i,\textbf{y}_0 \rangle , \langle \textbf{x}_i,\textbf{y}_1 \rangle \ne 0,\text { and}$$ -
if \(\exists \textbf{x}_i\in {\mathcal {U}}\) with \(i\in {\mathcal {C}}_L\) such that \(\langle \textbf{x}_i,\textbf{y}_0 \rangle = \langle \textbf{x}_i,\textbf{y}_1 \rangle = 0\), then \(m_0 = m_1\).
We say that \(\Pi _{{\textsf{s}}{\textsf{RIPE}}}\) is secure if for all polynomials \(n = n(\lambda ), L= L(\lambda )\) and for all \(\text {PPT}\) and admissible
 in the above security hybrid, there exists a negligible function
in the above security hybrid, there exists a negligible function
 such that for all \(\lambda \in \mathbb {N}\),
such that for all \(\lambda \in \mathbb {N}\),

Remark 1
We argue in our full version [25] that for general RFE, security without post-challenge queries imply security with post-challenge queries in the slotted setting as well. This is because \(\textsf{Aggr}\) is deterministic and does not require any secret. Hence, an adversary can simulate the post-challenge queries itself.
6 Slotted Registered IPE from Prime-Order Pairings
Bilinear Groups. Our slotted RIPE is based on asymmetric bilinear groups. We use cyclic groups of prime order q with an asymmetric bilinear map endowed on them. We assume a \(\text {PPT}\) algorithm \({\textsf{GroupGen}}\) that takes a security parameter \(\lambda \) as input and outputs \({\mathcal {G}}= (\mathbb {G}_1,\mathbb {G}_2,\mathbb {G}_{\textsf{T}}, q, g_1,g_2, e)\), where \(\mathbb {G}_1,\mathbb {G}_2,\mathbb {G}_{\textsf{T}}\) are cyclic groups of prime order q, \(g_1\) (resp. \(g_2\)) is random generator in \(\mathbb {G}_1\) (resp. \(\mathbb {G}_2\)) and \(e:\mathbb {G}_1\times \mathbb {G}_2 \rightarrow \mathbb {G}_{\textsf{T}}\) is a non-degenerate bilinear map.
We assume the message space \({\mathcal {M}} = \mathbb {G}_{\textsf{T}}\) for our scheme. Our slotted RIPE supports an a-priori fixed number of slots \(L= L(\lambda )\), i.e., the scheme supports a bounded number of slots. Below, we describe our formal scheme.
Construction 1
The slotted RIPE scheme
 with message space \(\mathcal {M}= \mathbb {G}_{\textsf{T}}\) and attribute space \({\mathcal {U}} = \mathbb {Z}_q^{n^+}\) is as follows:
with message space \(\mathcal {M}= \mathbb {G}_{\textsf{T}}\) and attribute space \({\mathcal {U}} = \mathbb {Z}_q^{n^+}\) is as follows:
-
\(\textsf{Setup} (1^\lambda ,1^n,1^L)\): On input the security parameter \(\lambda \), the attribute size n and the number of slots \(L\), compute
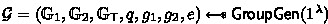 and generate the common reference string as follows.
and generate the common reference string as follows.-
1.
Sample
 and set \(h = g_1^\beta , Z = e(g_1,g_2)^\alpha , \Gamma = g_1^{\gamma },n' = n+1\).
and set \(h = g_1^\beta , Z = e(g_1,g_2)^\alpha , \Gamma = g_1^{\gamma },n' = n+1\). -
2.
For each index \(i\in [0,L]\), do the following:
-
1.
for each \(w\in [n']\), sample
 and set \(U_{w,i} = g_1^{u_{w,i}}\).
and set \(U_{w,i} = g_1^{u_{w,i}}\). -
2.
for a slot index \(i>0\), sample
 and set \(A_i = g_2^{t_i}, B_i = g_2^\alpha \cdot A_i^\beta \).
and set \(A_i = g_2^{t_i}, B_i = g_2^\alpha \cdot A_i^\beta \). -
3.
for a slot index \(i > 0\), \(\forall w\in [n'], j\in [0,L]\setminus \{ i \}\), set \(W_{i,j,w} = A_i^{u_{w,j}/\gamma }\).
-
1.
-
4.
Sample
 . Set \(\textsf{sk}_0= \widetilde{\textbf{x}}_0\) and $$T_0 = \left( \prod _{w=1}^{n}U_{w,0}^{-\widetilde{x}_{w,0}}\right) \cdot U_{n',0}^{-\widetilde{r}_0}\quad , \quad \widetilde{W}_{i,0} = \left( \prod _{w=1}^{n}W_{i,0,w}^{\widetilde{x}_{w,0}}\right) \cdot W_{i,0,n'}^{\widetilde{r}_0},\ \ \forall i\in [L].$$
. Set \(\textsf{sk}_0= \widetilde{\textbf{x}}_0\) and $$T_0 = \left( \prod _{w=1}^{n}U_{w,0}^{-\widetilde{x}_{w,0}}\right) \cdot U_{n',0}^{-\widetilde{r}_0}\quad , \quad \widetilde{W}_{i,0} = \left( \prod _{w=1}^{n}W_{i,0,w}^{\widetilde{x}_{w,0}}\right) \cdot W_{i,0,n'}^{\widetilde{r}_0},\ \ \forall i\in [L].$$Also, set \(\textsf{pk}_0 = \left( T_0, \left\{ \widetilde{W}_{i,0}\right\} _{i\in [L]}\right) \).
Finally, output the common reference string
$$\textsf{crs}= ({\mathcal {G}},Z,h,\Gamma ,\left\{ A_i, B_i\right\} _{i \in [L]},\{\left\{ U_{w,i}\right\} _{i\in [0,L]},\left\{ W_{i,j,w}\right\} _{i\in [L],j\in [0,L]\setminus \{ i \}}\}_{w\in [n']}, \textsf{pk}_0)$$ -
1.
-
\(\textsf{KGen} (\textsf{crs}, i)\): On input the common reference string \(\textsf{crs}\) and a slot index \(i\in [L]\), do the following.
-
1.
Parse the common reference string
$$\begin{aligned} \textsf{crs}&= \left( {\mathcal {G}},Z,h,\Gamma ,\left\{ A_i, B_i\right\} _{i \in [L]},\right. \\ &\qquad \left. \left\{ \left\{ U_{w,i}\right\} _{i\in [0,L]},\left\{ W_{i,j,w}\right\} _{i\in [L],j\in [0,L]\setminus \{ i \}}\right\} _{w\in [n']}, \textsf{pk}_0\right) . \end{aligned}$$ -
2.
Sample
 and pick elements \(U_{n',i}\) and \(\{W_{j,i,n'}\}_{j\in [L]\setminus \{i\}}\) from \(\textsf{crs}\).
and pick elements \(U_{n',i}\) and \(\{W_{j,i,n'}\}_{j\in [L]\setminus \{i\}}\) from \(\textsf{crs}\). -
3.
Compute \(T_i = U_{n',i}^{-\widetilde{r}_i}\) and \(\widetilde{W}_{j,i} = W_{j,i,n'}^{\widetilde{r}_i}, \forall j\in [L]\setminus \{i\}\).
-
4.
Output \(\textsf{pk}_i = \left( T_i,\{\widetilde{W}_{j,i}\}_{j\in [L]\setminus \{i\}} \right) \) and \(\textsf{sk}_i = \widetilde{r}_i\).
-
1.
-
\(\textsf{IsValid}(\textsf{crs},i,\textsf{pk}_i)\): On input the common reference string \(\textsf{crs}\), a slot index \(i\in [L]\) and a purported public key \(\textsf{pk}_i = \left( T_i, \{\widetilde{W}_{j,i}\}_{j\in [L]\setminus \{i\}}\right) \), the key-validation algorithm first affirms that each of the components in \(\textsf{pk}_i\) is a valid group element, namely: \(\left( T_i{\mathop {\in }\limits ^{?}} \mathbb {G}_1\setminus \{1_{\mathbb {G}_1}\}\quad \wedge \quad \widetilde{W}_{j,i} {\mathop {\in }\limits ^{?}} G_2\setminus \{1_{\mathbb {G}_2}\},\ \ \forall j\in [L]\setminus \{i\}\right) \) where \(1_{\mathbb {G}_{\mathfrak {t}}}\) denotes the identity in \(\mathbb {G}_{\mathfrak {t}}\) for \({\mathfrak {t}}\in [2]\). If the checks pass, it picks the elements \(U_{n',i}\) and \(\{W_{j,i,n'}\}_{j\in [L]\setminus \{i\}}\) from \(\textsf{crs}\) and checks further that
$$e\left( T_i^{-1}, W_{j,i,n'}\right) {\mathop {=}\limits ^{?}} e\left( U_{n',i}, \widetilde{W}_{j,i}\right) , \forall j\in [L]\setminus \{i\}.$$If all checks pass, it outputs 1. Else, it outputs 0.
-
\(\textsf{Aggr} (\textsf{crs}, ((\textsf{pk}_i,\textbf{x}_i))_{i\in [L]})\): On input the common reference string \(\textsf{crs}\) and a set of \(L\) public keys \(\textsf{pk}_i = \left( T_i,\{\widetilde{W}_{j,i}\}_{j\in [L]\setminus \{i\}}\right) \) together with vectors \(\textbf{x}_i = (x_{1,i},\ldots ,x_{n,i})\in \mathbb {Z}_q^{n^+}\) (representing predicates \(f_{\textbf{x}_i}\)), compute the following.
-
1.
Parse the common reference string
$$\begin{aligned} \textsf{crs}&= \left( {\mathcal {G}},Z,h,\Gamma ,\left\{ A_i, B_i\right\} _{i \in [L]},\right. \\ &\qquad \left. \left\{ \left\{ U_{w,i}\right\} _{i\in [0,L]},\left\{ W_{i,j,w}\right\} _{i\in [L],j\in [0,L]\setminus \{ i \}}\right\} _{w\in [n']}, \textsf{pk}_0\right) . \end{aligned}$$ -
2.
Fuse the predicate vector \(\textbf{x}_i\) into \(\textsf{pk}_i\) by updating each of its components as
$$T_i = \left( \prod _{w=1}^{n}U_{w,i}^{-{x}_{w,i}}\right) \cdot T_i \quad \text { , }\quad \widetilde{W}_{j,i} = \left( \prod _{w=1}^{n}W_{j,i,w}^{{x}_{w,i}}\right) \cdot \widetilde{W}_{j,i}, \forall j\in [L]\setminus \{i\}$$and set \(\textsf{pk}_i = \left( T_i,\left\{ \widetilde{W}_{j,i}\right\} _{j\in [L]\setminus \{i\}}\right) \). Further, parse \(\textsf{pk}_0\) as follows:
$$ \textsf{pk}_0 = \left( T_0, \left\{ \widetilde{W}_{j,0}\right\} _{j\in [0,L]\setminus \{0\}}\right) . $$ -
3.
For each \(w\in [n']\), compute \(\widehat{U}_w = \prod _{i\in [0,L]}U_{w,i}\) and \(\widehat{U}_{n'+1} = \prod _{i\in [0,L]}T_i\).
-
4.
Compute the cross-terms as follows. For each slot index \(i\in [L]\):
-
(a)
for each \(w\in [n']\), compute \(\widehat{W}_{w,i} = \prod _{j\in [0,L]\setminus \{ i \}}W_{i,j,w}\).
-
(b)
compute \(\widehat{W}_{n'+1,i} = \left( \prod _{j\in [0,L]\setminus \{ i \}}\widetilde{W}_{i,j}\right) ^{-1}\).
-
(a)
-
5.
Output the master public key and the slot-specific helper secret keys as \(\textsf{mpk}= \left( {\mathcal {G}},h,Z,\Gamma ,\left\{ \widehat{U}_{w}\right\} _{w\in [n'+1]}\right) \), and
$$ {\textsf{hsk}}_i = \left( {\mathcal {G}}, i,\textbf{x}_i, A_i,B_i, \left\{ \widehat{W}_{w,i}\right\} _{w\in [n'+1]} \right) , \forall i\in [L]. $$
-
1.
-
\(\textsf{Enc} (\textsf{mpk},\textbf{y},m)\): On input the master public key \(\textsf{mpk}\), a vector \(\textbf{y}= (y_1,\ldots ,y_n)\in \mathbb {Z}_q^{n^+}\) (as an attribute) and a message \(m\in \mathbb {G}_{\textsf{T}}\), the ciphertext is computed as:
-
1.
Parse \(\textsf{mpk}= \left( {\mathcal {G}},h,Z,\Gamma ,\left\{ \widehat{U}_{w}\right\} _{w\in [n'+1]}\right) \).
-
2.
Set \(\widetilde{\textbf{y}} = (\textbf{y},0,0)\in \mathbb {Z}_q^{n'+1}\) and sample
 . Also, parse \(\widetilde{\textbf{y}} = (\widetilde{y}_1,\ldots ,\widetilde{y}_{n'+1})\).
. Also, parse \(\widetilde{\textbf{y}} = (\widetilde{y}_1,\ldots ,\widetilde{y}_{n'+1})\). -
3.
Message embedding: set \(C_1 = m\cdot Z^s\) and \(C_2 = g_1^s\).
-
4.
Attribute and Slot embedding: for each \(w\in [n'+1]\), set \(C_{3,w}= h^{\widetilde{y}_w \cdot r + s}\cdot \widehat{U}_w^{-z}\). Set \(C_4 = \Gamma ^z\).
-
5.
Output the ciphertext \(c= \left( C_1,C_2,\{C_{3,w}\}_{w\in [n'+1]},C_4\right) \).
-
1.
-
\(\textsf{Dec} (\textsf{sk},{\textsf{hsk}},c)\): Parse the input secret key \(\textsf{sk}\), helper secret key \({\textsf{hsk}}\) and ciphertext \(c\) as \(\textsf{sk}= \widetilde{r}_i\), and
$$ {\textsf{hsk}}= \left( {\mathcal {G}}, i, \textbf{x}_i, A_i,B_i, \left\{ \widehat{W}_{w,i}\right\} _{w\in [n'+1]} \right) , c= \left( C_1,C_2,\{C_{3,w}\}_{w\in [n'+1]},C_4\right) , $$for some \(i\in [L]\). Let \(\widetilde{\textbf{x}}_i =(\widetilde{x}_{1,i},\dots ,\widetilde{x}_{n'+1,i}) = (\textbf{x}_i, \widetilde{r}_i, 1) \in \mathbb {Z}_q^{n'+1}, X_i = \sum _{w=1}^{n'+1}\widetilde{x}_{w,i} \in \mathbb {Z}_q\). Compute and output the following:
$$\begin{aligned} \frac{C_1}{e(C_2,B_i)} \cdot \left[ \prod _{w=1}^{n'+1} \left\{ e\left( C_{3,w}^{\widetilde{x}_{w,i}},A_i\right) \cdot e\left( C_4,\widehat{W}_{w,i}^{\widetilde{x}_{w,i}}\right) \right\} \right] ^{X_i^{-1}}. \end{aligned}$$
Remark: In the setup algorithm in our scheme, we introduce a dummy slot “0” and pre-register an honestly generated dummy key \(\textsf{pk}_0\). This slot does not impact the security definition in any way because the associated secret key \(\textsf{sk}_0\) is thrown away once the one-time setup is executed. This modification is done only for a simpler analysis of the security proof in the \({\textsf{GGM}}\).
Theorem 3
(Completeness of Construction 1). The slotted RIPE scheme \(\Pi _{{\textsf{s}}{\textsf{RIPE}}}\) with message space \(\mathcal {M}= \mathbb {G}_{\textsf{T}}\) and attribute space \({\mathcal {U}} = \mathbb {Z}_q^{n^+}\) from Construction 1 is complete.
Theorem 4
(Compactness and Efficiency of Construction 1). The slotted RIPE scheme \(\Pi _{{\textsf{s}}{\textsf{RIPE}}}\) with message space \(\mathcal {M}= \mathbb {G}_{\textsf{T}}\) and attribute space \({\mathcal {U}} = \mathbb {Z}_q^{n^+}\) from Construction 1 satisfies the following properties:
-

-
Runtime

-
Runtime

We refer to the full version [25] for the proofs of Theorems 4 and 3.
Theorem 5
(Perfect Correctness of Construction 1). The slotted RIPE scheme \(\Pi _{{\textsf{s}}{\textsf{RIPE}}}\) with message space \(\mathcal {M}= \mathbb {G}_{\textsf{T}}\) and attribute space \({\mathcal {U}} = \mathbb {Z}_q^{n^+}\) from Construction 1 is perfectly correct.
Proof
Fix some \(\lambda \), attribute size \(n = n(\lambda )\), a slot count \(L= L(\lambda )\) and an index \(i\in [L]\). Let
 and
and
 be defined as in the scheme from Construction 1. Take any set of public keys \(\left\{ \textsf{pk}_j\right\} _{j\in [L]\setminus \{i\}}\), where \(\textsf{IsValid}(\textsf{crs},j,\textsf{pk}_j) = 1\). Therefore, we have
be defined as in the scheme from Construction 1. Take any set of public keys \(\left\{ \textsf{pk}_j\right\} _{j\in [L]\setminus \{i\}}\), where \(\textsf{IsValid}(\textsf{crs},j,\textsf{pk}_j) = 1\). Therefore, we have
For each \(j\in [L]\), let \(\textbf{x}_j\in \mathbb {Z}_q^{n^+}\) be the predicate vector associated to \(\textsf{pk}_j\) and let \(\widetilde{\textbf{x}}_j = (\textbf{x}_j, \widetilde{r}_j, 1)\). Further, let \(\textsf{mpk}\) and \({\textsf{hsk}}_i\) be as computed by \(\textsf{Aggr} (\textsf{crs}, ((\textsf{pk}_j,\textbf{x}_j))_{j\in [L]})\). Now, note that in the \(\textsf{Dec} \) algorithm, the computation associated to the message components yield

Now observe that for any vector \(\textbf{x}_i\in \mathbb {Z}_q^{n^+}\) for some \(i\in [L]\) and an attribute \(\textbf{y}\in \mathbb {Z}_q^{n^+}\) with \(\langle \textbf{x}_i,\textbf{y} \rangle = 0\), it also holds that \(\langle \widetilde{\textbf{x}}_i,\widetilde{\textbf{y}} \rangle = \langle \textbf{x}_i,\textbf{y} \rangle + \langle \widetilde{r}_i,0 \rangle + 1\cdot 0 = 0\). For brevity, we set up the notations \(g_{\textsf{T}}= e\left( g_1,g_2\right) \) and the discrete logarithm as \({\textsf{DL}}{\left( K\right) }= k\), where \(K = g_{\mathfrak {t}}^k\) for any \(k\in \mathbb {Z}_q\) (i.e., irrespective of any group type \({\mathfrak {t}}\in \{1,2,{\textsf{T}}\}\)) for the rest of the proof. To ensure correctness with the rest of decryption above, it is thus enough to show that

so that \(\textsf{Dec} \) yields the message \(m\in \mathbb {G}_{\textsf{T}}\). We will analyze individual pairing products in the above form separately. Before that we note a few things about the public keys after they are fused with the predicate vectors during \(\textsf{Aggr} \). For any \(i\in [L],j\in [0,L]\), we have
where we redefined \(\widetilde{x}_{n',0} = \widetilde{r}_0\). Further, for any \(w\in [n']\) and \(i\in [L]\), we have:

Defining the first pairing product as \(\theta _1 = \prod _{w=1}^{n'+1}e\left( C_{3,w}^{\widetilde{x}_{w,i}},A_i\right) \), we have:


Defining the second pairing product as \(\theta _2 = \prod _{w=1}^{n'+1}e\left( C_4,\widehat{W}_{w,i}^{\widetilde{x}_{w,i}}\right) \), we have:

This completes the proof since
Theorem 6
(Security of Construction 1). The slotted RIPE scheme \(\Pi _{{\textsf{s}}{\textsf{RIPE}}}\) with message space \(\mathcal {M}= \mathbb {G}_{\textsf{T}}\) and attribute space \({\mathcal {U}} = \mathbb {Z}_q^{n^+}\) from Construction 1 is secure in the \({\textsf{GGM}}\).
Below, we show that our slotted RIPE scheme \(\Pi _{{\textsf{s}}{\textsf{RIPE}}}\) (Construction 1) is secure in the generic group model. We start with some notations and definitions for generic and symbolic group models.
Generic Bilinear Group Model. Our definitions for generic bilinear group model is adapted from [4, 12]. Let \({\mathcal {G}}= (\mathbb {G}_1,\mathbb {G}_2,\mathbb {G}_{\textsf{T}}, q,g_1,g_2, e)\) be a bilinear group setting, \({\mathcal {L}}_{{1}},{\mathcal {L}}_{{2}},{\mathcal {L}}_{{{\textsf{T}}}}\) be lists of group elements in \(\mathbb {G}_1, \mathbb {G}_2\), and \(\mathbb {G}_{\textsf{T}}\) respectively. Let \({\mathcal {D}}\) be a distribution over \({\mathcal {L}}_{{1}},{\mathcal {L}}_{{2}},{\mathcal {L}}_{{{\textsf{T}}}}\). The generic group model for a bilinear group setting \({\mathcal {G}}\) and a distribution \({\mathcal {D}}\) is described in Fig. 1. In this model, the challenger first initializes the lists \({\mathcal {L}}_{{1}},{\mathcal {L}}_{{2}},{\mathcal {L}}_{{{\textsf{T}}}}\) by sampling the group elements according to \({\mathcal {D}}\), and the adversary receives handles for the elements in the lists. For \({\mathfrak {t}}\in \{1,2,{\textsf{T}}\}\), \({\mathcal {L}}_{{{\mathfrak {t}}}}[h]\) denotes the h-th element in the list \({\mathcal {L}}_{{{\mathfrak {t}}}}\). The handle to this element is simply the pair \(({\mathfrak {t}},h)\). An adversary
 running in the generic bilinear group model can apply group operations and the bilinear map e to the elements in the lists. To do this,
running in the generic bilinear group model can apply group operations and the bilinear map e to the elements in the lists. To do this,
 has to call the appropriate oracle specifying handles for the input elements.
has to call the appropriate oracle specifying handles for the input elements.
 also gets access to the internal state variables of the challenger via handles, and we assume that the equality queries are “free”, in the sense that they do not count when measuring the computational complexity
also gets access to the internal state variables of the challenger via handles, and we assume that the equality queries are “free”, in the sense that they do not count when measuring the computational complexity
 . For \({\mathfrak {t}}\in \{1,2,{\textsf{T}}\}\), the challenger computes the result of a query, say \(\delta \in \mathbb {G}_{\mathfrak {t}}\), and stores it in the corresponding list as \({\mathcal {L}}_{{{\mathfrak {t}}}}[{\textsf{pos}}] = \delta \) where \({\textsf{pos}}\) is its next empty position in \({\mathcal {L}}_{{{\mathfrak {t}}}}\), and returns to
. For \({\mathfrak {t}}\in \{1,2,{\textsf{T}}\}\), the challenger computes the result of a query, say \(\delta \in \mathbb {G}_{\mathfrak {t}}\), and stores it in the corresponding list as \({\mathcal {L}}_{{{\mathfrak {t}}}}[{\textsf{pos}}] = \delta \) where \({\textsf{pos}}\) is its next empty position in \({\mathcal {L}}_{{{\mathfrak {t}}}}\), and returns to
 its (newly created) handle \(({\mathfrak {t}},{\textsf{pos}})\). Handles are not unique (i.e., the same group element may appear more than once in a list under different handles). As in [4], the equality test oracle in [12] is replaced with the zero-test oracle \({\textsf{Zt}}_{\textsf{T}}(\cdot )\) that, on input a handle \(({\mathfrak {t}},h)\), returns 1 if \({\mathcal {L}}_{{{\mathfrak {t}}}}[h]=0\) and 0 otherwise only for the case \({\mathfrak {t}} = {\textsf{T}}\).
its (newly created) handle \(({\mathfrak {t}},{\textsf{pos}})\). Handles are not unique (i.e., the same group element may appear more than once in a list under different handles). As in [4], the equality test oracle in [12] is replaced with the zero-test oracle \({\textsf{Zt}}_{\textsf{T}}(\cdot )\) that, on input a handle \(({\mathfrak {t}},h)\), returns 1 if \({\mathcal {L}}_{{{\mathfrak {t}}}}[h]=0\) and 0 otherwise only for the case \({\mathfrak {t}} = {\textsf{T}}\).
Symbolic Group Model. The symbolic group model (\({\textsf{SGM}}\)) for a bilinear group setting \({\mathcal {G}}\) and a distribution \({\mathcal {D}}\) gives to the adversary the same interface as the corresponding generic group model (\({\textsf{GGM}}\)), except that internally the challenger stores lists of elements from the ring \(\mathbb {Z}_q[{\texttt{x}}_1,\ldots ,{\texttt{x}}_k]\) instead of lists of group elements, where \(\{{\texttt{x}}_k\}_{k \in \mathbb {N}}\) are indeterminates. The \({\textsf{Add}}_{\mathfrak {t}}(\cdot ,\cdot ),{\textsf{Neg}}_{\mathfrak {t}}(\cdot ),{\textsf{Map}}_e(\cdot ,\cdot ),{\textsf{Zt}}_{\textsf{T}}(\cdot )\) oracles respectively compute addition, negation, multiplication, and zero tests in the ring. For our proof, we will work in the ring \(\mathbb {Z}_q[{\texttt{x}}_1,\ldots , {\texttt{x}}_k, 1/{\texttt{x}}_i]\) for some \(i\in [k]\). Note that any element \(f\in \mathbb {Z}_q[{\texttt{x}}_1,\ldots , {\texttt{x}}_k, 1/{\texttt{x}}_i]\) can be represented as
using \(\{\eta _{\textbf{c}}\in \mathbb {Z}_q\}_{\textbf{c}\in \mathbb {Z}^k}\), where \(\eta _\textbf{c}= 0\) for all but finite \(\textbf{c}\in \mathbb {Z}^k\). Note that this expression is unique. We now begin our proof for Theorem 6 below.
Proof
At a high level, we show a sequence of hybrids each of which is a game between a challenger and a \(\text {PPT}\) adversary
 . In the first (resp., last) hybrid, the challenger encrypts a pair \((\textbf{y}_b, m_b)\) corresponding to bit \(b=0\) (resp., \(b=1\)). The intermediate hybrids ensure that the distributions in any pair of subsequent hybrids from the first to the last one are statistically indistinguishable.
. In the first (resp., last) hybrid, the challenger encrypts a pair \((\textbf{y}_b, m_b)\) corresponding to bit \(b=0\) (resp., \(b=1\)). The intermediate hybrids ensure that the distributions in any pair of subsequent hybrids from the first to the last one are statistically indistinguishable.
Since the proof is in the \({\textsf{GGM}}\), w.l.o.g. the challenger simulates all the generic bilinear group oracle queries for
 . In particular, the challenger stores the actual computed elements in the list \({\mathcal {L}}_{{{\mathfrak {t}}}}\) based on its group type \({\mathfrak {t}}\in \{1,2,{\textsf{T}}\}\). The handle to an actual element stored in any of these lists are just a tuple \(({\mathfrak {t}},{\textsf{pos}})\) specifying the group type \({\mathfrak {t}}\) and its position in the table \({\mathcal {L}}_{{{\mathfrak {t}}}}\). Since our scheme contains several variables, we will refrain from explicitly specifying the handles to the actual elements for convenience. Further, when we move to the \({\textsf{SGM}}\), we will denote any literal variable v as \({\texttt{v}}\) and composite terms like \(v_1v_2\) (resp., \(\frac{v_1}{v_2}\)) as \({\mathtt {v_1}}{\mathtt {v_2}}\) (resp., \(\frac{{\mathtt {v_1}}}{{\mathtt {v_2}}}\)) to represent an individual monomial in a (possibly multivariate) polynomial. For variables denoted with Greek alphabets, say \(\alpha , \beta , \gamma \), we represent their corresponding formal variables as \(\upalpha ,\upbeta ,\upgamma \). We also define \(\mathbb {Z}_q\text {-}{\textsf{span}}({{\mathcal {S}}})\) as the set of \(\mathbb {Z}_q\)-linear combinations of all elements in any set \({\mathcal {S}}\). Assume
. In particular, the challenger stores the actual computed elements in the list \({\mathcal {L}}_{{{\mathfrak {t}}}}\) based on its group type \({\mathfrak {t}}\in \{1,2,{\textsf{T}}\}\). The handle to an actual element stored in any of these lists are just a tuple \(({\mathfrak {t}},{\textsf{pos}})\) specifying the group type \({\mathfrak {t}}\) and its position in the table \({\mathcal {L}}_{{{\mathfrak {t}}}}\). Since our scheme contains several variables, we will refrain from explicitly specifying the handles to the actual elements for convenience. Further, when we move to the \({\textsf{SGM}}\), we will denote any literal variable v as \({\texttt{v}}\) and composite terms like \(v_1v_2\) (resp., \(\frac{v_1}{v_2}\)) as \({\mathtt {v_1}}{\mathtt {v_2}}\) (resp., \(\frac{{\mathtt {v_1}}}{{\mathtt {v_2}}}\)) to represent an individual monomial in a (possibly multivariate) polynomial. For variables denoted with Greek alphabets, say \(\alpha , \beta , \gamma \), we represent their corresponding formal variables as \(\upalpha ,\upbeta ,\upgamma \). We also define \(\mathbb {Z}_q\text {-}{\textsf{span}}({{\mathcal {S}}})\) as the set of \(\mathbb {Z}_q\)-linear combinations of all elements in any set \({\mathcal {S}}\). Assume
 issues an arbitrary polynomial number \(Q_{\textsf{zt}}(\lambda )\) of queries to its \({\textsf{Zt}}_{\textsf{T}}\) oracle in each hybrid.
issues an arbitrary polynomial number \(Q_{\textsf{zt}}(\lambda )\) of queries to its \({\textsf{Zt}}_{\textsf{T}}\) oracle in each hybrid.
-
\(\textbf{H}_1(\lambda ):\) This is the real scheme corresponding to bit \(b=0\) in the \({\textsf{GGM}}\). In more detail, the hybrid goes as follows.
-
Setup phase:
 sends an attribute length \(n=n(\lambda )\) and slot count \(L= L(\lambda )\) to the challenger, upon which it first initializes \(\textsf{ctr}= 0\), a dictionary \({\textsf{D}}\), and the set \({\mathcal {C}}_L= \emptyset \) to account for corrupted slots. Next, it computes
sends an attribute length \(n=n(\lambda )\) and slot count \(L= L(\lambda )\) to the challenger, upon which it first initializes \(\textsf{ctr}= 0\), a dictionary \({\textsf{D}}\), and the set \({\mathcal {C}}_L= \emptyset \) to account for corrupted slots. Next, it computes
 and initializes three tables as \({\mathcal {L}}_{{{\mathfrak {t}}}}[1] = g_{\mathfrak {t}}, \forall {\mathfrak {t}}\in \{1,2,{\textsf{T}}\}\). The challenger prepares a tuple \(\left( \mathbb {G}_1,\mathbb {G}_2,\mathbb {G}_{\textsf{T}}, q, \{({\mathfrak {t}},1)\}_{{\mathfrak {t}}\in \{1,2,{\textsf{T}}\}}\right) \), where \(({\mathfrak {t}},1)\) represents the handle to \(g_{\mathfrak {t}}, \forall {\mathfrak {t}}\in \{1,2,{\textsf{T}}\}\). To allow \(\textsf{A}\) to compute the group operations including the bilinear map e, the challenger also simulates all the oracles \({\textsf{Add}}_{\mathfrak {t}}, {\textsf{Neg}}_{\mathfrak {t}}, {\textsf{Map}}_e, {\textsf{Zt}}_{\textsf{T}}\) with implicit access to the lists \(\{{\mathcal {L}}_{{{\mathfrak {t}}}}\}_{{\mathfrak {t}}\in \{1,2,{\textsf{T}}\}}\). It then computes the \(\textsf{crs}\) components as follows:
and initializes three tables as \({\mathcal {L}}_{{{\mathfrak {t}}}}[1] = g_{\mathfrak {t}}, \forall {\mathfrak {t}}\in \{1,2,{\textsf{T}}\}\). The challenger prepares a tuple \(\left( \mathbb {G}_1,\mathbb {G}_2,\mathbb {G}_{\textsf{T}}, q, \{({\mathfrak {t}},1)\}_{{\mathfrak {t}}\in \{1,2,{\textsf{T}}\}}\right) \), where \(({\mathfrak {t}},1)\) represents the handle to \(g_{\mathfrak {t}}, \forall {\mathfrak {t}}\in \{1,2,{\textsf{T}}\}\). To allow \(\textsf{A}\) to compute the group operations including the bilinear map e, the challenger also simulates all the oracles \({\textsf{Add}}_{\mathfrak {t}}, {\textsf{Neg}}_{\mathfrak {t}}, {\textsf{Map}}_e, {\textsf{Zt}}_{\textsf{T}}\) with implicit access to the lists \(\{{\mathcal {L}}_{{{\mathfrak {t}}}}\}_{{\mathfrak {t}}\in \{1,2,{\textsf{T}}\}}\). It then computes the \(\textsf{crs}\) components as follows:
-
1.
Set \(n' = n+1\). Compute \(h = g_1^\beta ,\Gamma = g_1^\gamma \in \mathbb {G}_1\) and \(Z = e(g_1,g_2)^\alpha \in \mathbb {G}_{\textsf{T}}\) as in the real \(\textsf{Setup} \) algorithm. Update \({\mathcal {L}}_{{1}}\) with the elements \(\beta ,\gamma \) and \({\mathcal {L}}_{{{\textsf{T}}}}\) with \(\alpha \) respectively.
-
2.
For each slot index \(i\in [0,L]\), do the following:
-
(a)
\(\forall w\in [n']\), compute \(U_{w,i} = g_1^{u_{w,i}}\in \mathbb {G}_1\) as in the real scheme and update \({\mathcal {L}}_{{1}}\) with \(u_{w,i}\).
-
(b)
\(\forall i>0\), compute \(A_i = g_2^{t_i}, B_i = g_2^{\alpha +\beta \cdot t_i}\in \mathbb {G}_2\) as in the real scheme and update \({\mathcal {L}}_{{2}}\) with \(t_i, (\alpha +\beta \cdot t_i)\) in order.
-
(c)
\(\forall i>0, w\in [n']\) and for each \(j\in [0,L]\setminus \{ i \}\), compute \(W_{i,j,w} = g_2^{\frac{t_i\cdot u_{j,w}}{\gamma }}\in \mathbb {G}_2\) as in the real scheme and update \({\mathcal {L}}_{{2}}\) with \(\frac{t_i\cdot u_{j,w}}{\gamma }\).
-
(a)
-
3.
For
 , set \(\textsf{pk}_0 = \left( T_0, \left\{ \widetilde{W}_{i,0}\right\} _{i\in [L]}\right) \) as in the real scheme. Define \(u'_{0} = \sum _{w=1}^{n'}u_{w,0}\cdot \widetilde{x}_{w,0} = -{\textsf{DL}}{\left( T_0\right) }\) so that $$T_0 = g_1^{u'_0}\in \mathbb {G}_1\quad , \quad \widetilde{W}_{i,0} = g_2^{\frac{t_i\cdot u'_0}{\gamma }}\in \mathbb {G}_2,\forall i\in [L].$$
, set \(\textsf{pk}_0 = \left( T_0, \left\{ \widetilde{W}_{i,0}\right\} _{i\in [L]}\right) \) as in the real scheme. Define \(u'_{0} = \sum _{w=1}^{n'}u_{w,0}\cdot \widetilde{x}_{w,0} = -{\textsf{DL}}{\left( T_0\right) }\) so that $$T_0 = g_1^{u'_0}\in \mathbb {G}_1\quad , \quad \widetilde{W}_{i,0} = g_2^{\frac{t_i\cdot u'_0}{\gamma }}\in \mathbb {G}_2,\forall i\in [L].$$Update \({\mathcal {L}}_{{1}}\) with \(u'_0\) and \({\mathcal {L}}_{{2}}\) with \(\left\{ \frac{t_i\cdot u'_0}{\gamma }\right\} _{i\in [L]}\) in order.
-
4.
Set
$$\begin{aligned} \textsf{crs}&= \left( {\mathcal {G}},Z,h,\Gamma ,\left\{ A_i, B_i\right\} _{i \in [L]}, \right. \\ & \qquad \left. \left\{ \left\{ U_{w,i}\right\} _{i\in [0,L]},\left\{ W_{i,j,w}\right\} _{i\in [L],j\in [0,L]\setminus \{ i \}}\right\} _{w\in [n']}, \textsf{pk}_0\right) . \end{aligned}$$ -
5.
Return to
 a tuple \(\textsf{crs}'\) that includes \(\left( \mathbb {G}_1,\mathbb {G}_2,\mathbb {G}_{\textsf{T}}, q, \{({\mathfrak {t}},1)\}_{{\mathfrak {t}}\in \{1,2,{\textsf{T}}\}}\right) \) along with the handles to all elements in the same order as they are arranged in the \(\textsf{crs}\) above.
a tuple \(\textsf{crs}'\) that includes \(\left( \mathbb {G}_1,\mathbb {G}_2,\mathbb {G}_{\textsf{T}}, q, \{({\mathfrak {t}},1)\}_{{\mathfrak {t}}\in \{1,2,{\textsf{T}}\}}\right) \) along with the handles to all elements in the same order as they are arranged in the \(\textsf{crs}\) above.
-
Pre-challenge query phase:
 can issue key generation queries or corruption queries in this phase.
can issue key generation queries or corruption queries in this phase.
-
1.
Consider the key-generation queries first. Upon getting a slot index \(i\in [L]\), the challenger updates \(\textsf{ctr}= \textsf{ctr}+1\), sets \(\textbf{x}^\textsf{ctr}_i = \textbf{x}_i\) and does the following:
-
(a)
Sample
 and compute \(\textsf{pk}^\textsf{ctr}_i = \left( T^\textsf{ctr}_i, \left\{ \widetilde{W}^\textsf{ctr}_{j,i}\right\} _{j\in [L]\setminus \{i\}}\right) \) as in \(\textsf{KGen} \).
and compute \(\textsf{pk}^\textsf{ctr}_i = \left( T^\textsf{ctr}_i, \left\{ \widetilde{W}^\textsf{ctr}_{j,i}\right\} _{j\in [L]\setminus \{i\}}\right) \) as in \(\textsf{KGen} \). -
(b)
Note that the element \(T^\textsf{ctr}_i\in \mathbb {G}_1\) from \(\textsf{pk}^\textsf{ctr}_i\) has the following structure:
$$T^\textsf{ctr}_i = g_1^{-\widetilde{r}^\textsf{ctr}_iu_{n',i}},\text { where } \textsf{sk}^\textsf{ctr}_i = \widetilde{r}^\textsf{ctr}_i \text { is the secret key}.$$Even given the handle to \(u_{n',i}\),
 cannot compute a handle for \({\textsf{DL}}{\left( T_i^\textsf{ctr}\right) } = -\widetilde{r}^\textsf{ctr}_iu_{n',i}\) on its own. Hence, the challenger updates \({\mathcal {L}}_{{1}}\) with \({\textsf{DL}}{\left( T_i^\textsf{ctr}\right) }\).
cannot compute a handle for \({\textsf{DL}}{\left( T_i^\textsf{ctr}\right) } = -\widetilde{r}^\textsf{ctr}_iu_{n',i}\) on its own. Hence, the challenger updates \({\mathcal {L}}_{{1}}\) with \({\textsf{DL}}{\left( T_i^\textsf{ctr}\right) }\). -
(c)
Further, each term in \(\left\{ \widetilde{W}^\textsf{ctr}_{j,i}\in \mathbb {G}_2\right\} _{j\in [L]\setminus \{i\}}\) has the following structure:
$$\widetilde{W}^\textsf{ctr}_{j,i} = W_{j,i,n'}^{\widetilde{r}^\textsf{ctr}_i} = g_2^{\frac{t_ju_{n',i}}{\gamma }\cdot \widetilde{r}^\textsf{ctr}_{i}}$$For reasons similar to Item (b) above, the challenger updates \({\mathcal {L}}_{{2}}\) with each element individually from the set \(\big \{\widetilde{r}_i^\textsf{ctr}\cdot \frac{t_ju_{n',i}}{\gamma }\big \}_{j\in [L]\setminus \{i\}}\).
-
(d)
Define \(\textsf{pk}_\textsf{ctr}= \textsf{pk}^\textsf{ctr}_i, \textsf{sk}_\textsf{ctr}= \textsf{sk}^\textsf{ctr}_i\) and \(\textsf{pk}_\textsf{ctr}'\) as a sequence of handles to all elements in the same order as they are arranged in \(\textsf{pk}_\textsf{ctr}\).
-
(e)
Return the tuple \((\textsf{ctr}, \textsf{pk}_\textsf{ctr}')\) to
 and update \({\textsf{D}}[\textsf{ctr}] = (i, \textsf{pk}_\textsf{ctr},\textsf{sk}_\textsf{ctr})\).
and update \({\textsf{D}}[\textsf{ctr}] = (i, \textsf{pk}_\textsf{ctr},\textsf{sk}_\textsf{ctr})\).
-
(a)
-
2.
When
 sends \(c\in [\textsf{ctr}]\) issuing a corruption query, the challenger returns \(\textsf{sk}'\) to
sends \(c\in [\textsf{ctr}]\) issuing a corruption query, the challenger returns \(\textsf{sk}'\) to
 where \({\textsf{D}}[c] = (i',\textsf{pk}',\textsf{sk}')\).
where \({\textsf{D}}[c] = (i',\textsf{pk}',\textsf{sk}')\).
-
Challenge phase: In this phase,
 specifies the following challenge information: $$ \left\{ (c_i, \textbf{x}_i, \textsf{pk}_i^*)\right\} _{i\in [L]} \quad \text { and }\quad ((\textbf{y}_0,m_0),(\textbf{y}_1,m_1))\in (\mathbb {Z}_q^{n+}\times \mathbb {G}_{\textsf{T}})^2. $$
specifies the following challenge information: $$ \left\{ (c_i, \textbf{x}_i, \textsf{pk}_i^*)\right\} _{i\in [L]} \quad \text { and }\quad ((\textbf{y}_0,m_0),(\textbf{y}_1,m_1))\in (\mathbb {Z}_q^{n+}\times \mathbb {G}_{\textsf{T}})^2. $$
Preprocessing the challenge information. For each \(i\in [L]\), the challenger checks that \(\textbf{x}_i \ne \textbf{0}^n\) and does the following:
-
1.
If \(c_i\in [\textsf{ctr}]\), it checks \({\textsf{D}}[c_i] = (i',\textsf{pk}',\textsf{sk}')\). If \(i \ne i'\), it halts. Else, it sets \(\textsf{pk}_i^* = \textsf{pk}'\). Further, if
 issued a corruption query for \(c_i\) before, it updates \({\mathcal {C}}_L= {\mathcal {C}}_L\cup \{i\}\).
issued a corruption query for \(c_i\) before, it updates \({\mathcal {C}}_L= {\mathcal {C}}_L\cup \{i\}\). -
2.
If \(c_i = \bot \), \(\textsf{pk}_i^*\) represents a corrupt secret key generated by
 itself. Hence, it parses \(\textsf{pk}_i^*\) and halts if \(\textsf{IsValid}(\textsf{crs},i,\textsf{pk}_i^*)=0\).Footnote 7 Else, it updates \({\mathcal {C}}_L= {\mathcal {C}}_L\cup \{i\}\).
itself. Hence, it parses \(\textsf{pk}_i^*\) and halts if \(\textsf{IsValid}(\textsf{crs},i,\textsf{pk}_i^*)=0\).Footnote 7 Else, it updates \({\mathcal {C}}_L= {\mathcal {C}}_L\cup \{i\}\).
Computing key aggregation. The challenger then computes
Computing the challenge ciphertext. The challenger now uses \(\textsf{mpk}\) and the pair \((\textbf{y}_0,m_0)\), and generates
 where \(c^* = \left( C_1 , C_2, \{C_{3,w}\}_{w\in [n'+1]}, C_4\right) \).
where \(c^* = \left( C_1 , C_2, \{C_{3,w}\}_{w\in [n'+1]}, C_4\right) \).
-
1.
Note that \(C_1 = m_0\cdot e(g_1,g_2)^{\alpha s} \in \mathbb {G}_{\textsf{T}}\) and \(C_2 = g_1^s \in \mathbb {G}_1\). Accordingly, the challenger updates \({\mathcal {L}}_{{{\textsf{T}}}}\) with \(\alpha s\) and \({\mathcal {L}}_{{1}}\) with s respectively.
-
2.
With \(\widetilde{\textbf{y}}_0 = (\textbf{y}_0, 0, 0) = (y^0_1,\ldots ,y^0_n, 0, 0)\), note that the elements \(\{C_{3,w} \in \mathbb {G}_1\}_{w\in [n'+1]}\) have the following structure:
$$\begin{aligned} \text {for all } w\in [n],\ C_{3,w} = & {} h^{y^0_w\cdot r+s}\cdot \widehat{U}_w^{-z} = g_1^{r\beta y^0_w+s\beta - z\cdot u_w}\\ \text {for } w=n',\ C_{3,n'} = & {} g_1^{r\beta \cdot 0 + s\beta - z\cdot u'_n} = g_1^{s\beta - z\cdot u_{n'}}\\ \text {for } w=n'+1, C_{3,n'+1} = & {} g_1^{r\beta \cdot 0 + s\beta }\cdot \widehat{U}_{n'+1}^{-z} = g_1^{s\beta }\cdot \prod _{i=0}^{L}T_i^{-z} \\ = & {} g_1^{s\beta }\cdot \prod _{i=0}^{L}g_1^{z\sum _{w=1}^{n'}\widetilde{x}_{w,i}\cdot u_{w,i}}\\ = & {} g_1^{s\beta }\cdot \prod _{i=0}^{L}g_1^{z\cdot u'_i} = g_1^{s\beta + z\cdot u'_0 -z\sum _{i=1}^{L}{\textsf{DL}}{\left( T_i\right) }}\\{ where } u_w = & {} \sum _{i=0}^{L}u_{w,i} \text { ,and } u_{n'} = \sum _{i=0}^{L}u_{n',i}. \end{aligned}$$Accordingly, the challenger updates \({\mathcal {L}}_{{1}}\) with the elements \(\{r\beta y_w^0+s\beta -z\cdot u_w\}_{w\in [n]}\), \(\left( s\beta -z\cdot u_{n'}\right) \), and \(\left[ s\beta +z\cdot u'_0 - z\cdot \sum _{i=1}^{L}{\textsf{DL}}{\left( T_i\right) }\right] \) in order.
-
3.
Since \(C_4 = g_1^{\gamma z} \in \mathbb {G}_1\), it updates \({\mathcal {L}}_{{1}}\) with \(z\gamma \).
 Since \(\textsf{Aggr} \) is deterministic,
Since \(\textsf{Aggr} \) is deterministic,
 is able to compute \(\left( \textsf{mpk}, ({\textsf{hsk}}_i)_{i\in [L]}\right) \) on its own. In the \({\textsf{GGM}}\),
is able to compute \(\left( \textsf{mpk}, ({\textsf{hsk}}_i)_{i\in [L]}\right) \) on its own. In the \({\textsf{GGM}}\),
 is able to compute handles for the elements in \(\textsf{mpk}\) and \(\{{\textsf{hsk}}_i\}_{i\in [L]}\). To this end, it queries the appropriate group oracles to generate such handles as follows:
is able to compute handles for the elements in \(\textsf{mpk}\) and \(\{{\textsf{hsk}}_i\}_{i\in [L]}\). To this end, it queries the appropriate group oracles to generate such handles as follows:
-
1.
 only needs to compute the handles for \(\{{\widehat{U}_w}\}_{w\in [n'+1]}\) to complete its information about \(\textsf{mpk}\). Note that \(\forall w\in [n']\), \(\widehat{U}_w = \prod _{i=0}^{L}U_{w,i} = g_1^{u_w}\), where \(u_w = \sum _{i=0}^{L}u_{w,i}\). Hence, \(\forall w\in [n']\),
only needs to compute the handles for \(\{{\widehat{U}_w}\}_{w\in [n'+1]}\) to complete its information about \(\textsf{mpk}\). Note that \(\forall w\in [n']\), \(\widehat{U}_w = \prod _{i=0}^{L}U_{w,i} = g_1^{u_w}\), where \(u_w = \sum _{i=0}^{L}u_{w,i}\). Hence, \(\forall w\in [n']\),
 invokes the \({\textsf{Add}}_1\) oracle \(L\) times iteratively on the handles in \({\mathcal {L}}_{{1}}\) for \(\{u_{w,i}\}_{i\in [0,L]}\) and gets a handle for \(u_w\). Further, to get a handle for \(\widehat{U}_{n'+1} = \prod _{i=0}^{L}T_i\), it has to first a get a handle for each \(T_i\) that is fused with the predicate \(\textbf{x}_i\). Note the structure of each \(T_i\) after Step (2) in \(\textsf{Aggr} \): $$T_i = g_1^{\sum _{w=1}^{n'} -\widetilde{x}_{w,i}\cdot u_{w,i}} = g_1^{\sum _{w=1}^{n} \left( -x_{w,i}\cdot u_{w,i}\right) }\times g_1^{\left( -\widetilde{r}_i\cdot u_{n',i}\right) } \in \mathbb {G}_1.$$
invokes the \({\textsf{Add}}_1\) oracle \(L\) times iteratively on the handles in \({\mathcal {L}}_{{1}}\) for \(\{u_{w,i}\}_{i\in [0,L]}\) and gets a handle for \(u_w\). Further, to get a handle for \(\widehat{U}_{n'+1} = \prod _{i=0}^{L}T_i\), it has to first a get a handle for each \(T_i\) that is fused with the predicate \(\textbf{x}_i\). Note the structure of each \(T_i\) after Step (2) in \(\textsf{Aggr} \): $$T_i = g_1^{\sum _{w=1}^{n'} -\widetilde{x}_{w,i}\cdot u_{w,i}} = g_1^{\sum _{w=1}^{n} \left( -x_{w,i}\cdot u_{w,i}\right) }\times g_1^{\left( -\widetilde{r}_i\cdot u_{n',i}\right) } \in \mathbb {G}_1.$$Given a handle for the second multiplicand, it is easy to note that the first one is publicly computable using \({\textsf{Neg}}_1\) and \({\textsf{Add}}_1\) oracles. Once
 obtains the handles for \(\{T_i\}_{i\in [L]}\), it can call \({\textsf{Add}}_1\) oracle on these handles to get the same for \(\widehat{U}_{n'+1}\).
obtains the handles for \(\{T_i\}_{i\in [L]}\), it can call \({\textsf{Add}}_1\) oracle on these handles to get the same for \(\widehat{U}_{n'+1}\). -
2.
 only needs to compute the handles for \(\{\widehat{W}_{w,i}\}_{w\in [n'+1]}\) to get complete information about \({\textsf{hsk}}_i\) for each \(i\in [L]\). Note that \(\forall w\in [n']\), \(\widehat{W}_{w,i} = \prod _{j\in [0,L]\setminus \{ i \}}W_{i,j,w} = g_2^{t_i\cdot \left( u_w-u_{w,i}\right) /\gamma }\), since \((u_w - u_{w,i}) = \sum _{j\in [0,L]\setminus \{ i \}}u_{w,j}\). It is again easy to see that a handle for such an element can be computed by calling the \({\textsf{Add}}_2\) oracle \(L-1\) times iteratively on the handles in \({\mathcal {L}}_{{2}}\) for \(\big \{\frac{t_i\cdot u_{w,j}}{\gamma }\big \}_{j\in [0,L]\setminus \{i\}}\). Further, note that to get a handle for \(\widehat{W}_{n'+1,i} = \prod _{j\in [0,L]\setminus \{ i \}}\widetilde{W}_{i,j}^{-1}\), it has to first a get a handle for each \(\widetilde{W}_{j,i}\) that is fused with the predicate \(\textbf{x}_i\). Note the structure of each \(\widetilde{W}_{j,i}\) after Step (2) in \(\textsf{Aggr} \): $$\widetilde{W}_{j,i} = \left( \prod _{w=1}^{n} W_{i,j,w}^{\widetilde{x}_{w,i}}\right) \cdot W_{i,j,n'}^{\widetilde{r}_i} = g_2^{\sum _{w=1}^{n} \frac{t_ju_{w,i}}{\gamma }\cdot x_{w,i}} \times g_2^{\left( \frac{t_ju_{n',i}}{\gamma }\cdot \widetilde{r}_{i}\right) } \in \mathbb {G}_2.$$
only needs to compute the handles for \(\{\widehat{W}_{w,i}\}_{w\in [n'+1]}\) to get complete information about \({\textsf{hsk}}_i\) for each \(i\in [L]\). Note that \(\forall w\in [n']\), \(\widehat{W}_{w,i} = \prod _{j\in [0,L]\setminus \{ i \}}W_{i,j,w} = g_2^{t_i\cdot \left( u_w-u_{w,i}\right) /\gamma }\), since \((u_w - u_{w,i}) = \sum _{j\in [0,L]\setminus \{ i \}}u_{w,j}\). It is again easy to see that a handle for such an element can be computed by calling the \({\textsf{Add}}_2\) oracle \(L-1\) times iteratively on the handles in \({\mathcal {L}}_{{2}}\) for \(\big \{\frac{t_i\cdot u_{w,j}}{\gamma }\big \}_{j\in [0,L]\setminus \{i\}}\). Further, note that to get a handle for \(\widehat{W}_{n'+1,i} = \prod _{j\in [0,L]\setminus \{ i \}}\widetilde{W}_{i,j}^{-1}\), it has to first a get a handle for each \(\widetilde{W}_{j,i}\) that is fused with the predicate \(\textbf{x}_i\). Note the structure of each \(\widetilde{W}_{j,i}\) after Step (2) in \(\textsf{Aggr} \): $$\widetilde{W}_{j,i} = \left( \prod _{w=1}^{n} W_{i,j,w}^{\widetilde{x}_{w,i}}\right) \cdot W_{i,j,n'}^{\widetilde{r}_i} = g_2^{\sum _{w=1}^{n} \frac{t_ju_{w,i}}{\gamma }\cdot x_{w,i}} \times g_2^{\left( \frac{t_ju_{n',i}}{\gamma }\cdot \widetilde{r}_{i}\right) } \in \mathbb {G}_2.$$Again, given a handle for the second multiplicand, the same can be computed publicly for the entire product using handles for \(\{W_{i,j,w}\}\). Once
 obtains the handles to each element in \(\{\widetilde{W}_{j,i}\}_{j\in [L]\setminus \{i\}}\), it can call \({\textsf{Add}}_2\) oracle on these handles to get the same for \(\widehat{W}_{n+1,i}\).
obtains the handles to each element in \(\{\widetilde{W}_{j,i}\}_{j\in [L]\setminus \{i\}}\), it can call \({\textsf{Add}}_2\) oracle on these handles to get the same for \(\widehat{W}_{n+1,i}\). -
3.
Finally, it defines \(\textsf{mpk}'\) and each \({\textsf{hsk}}_i'\) as sequences of handles to all elements (except \(i,\textbf{x}_i\)) in the same order as arranged in \(\textsf{mpk}\) and each \({\textsf{hsk}}_i, \forall i\in [L]\).
-
Output phase:
 outputs a bit \(b'\in \{ 0,1 \}\).
outputs a bit \(b'\in \{ 0,1 \}\).
For ease of presentation, in Table 2 we show all unit and composite terms generated in the scheme itself, and stored in the respective lists.
-
\(\textbf{H}_2(\lambda ):\) In this hybrid, we switch to the \({\textsf{SGM}}\) partially. Namely, the interaction between challenger and
 remains exactly as it was in \(\textbf{H}_1(\lambda )\), but now the challenger stores formal variables for all the terms from Table 2 in the respective lists \({\mathcal {L}}_{{{\mathfrak {t}}}},\forall {\mathfrak {t}}\in \{1,2,{\textsf{T}}\}\). Thus, all the handles
remains exactly as it was in \(\textbf{H}_1(\lambda )\), but now the challenger stores formal variables for all the terms from Table 2 in the respective lists \({\mathcal {L}}_{{{\mathfrak {t}}}},\forall {\mathfrak {t}}\in \{1,2,{\textsf{T}}\}\). Thus, all the handles
 receives refer to multivariate polynomials from the following ring:
receives refer to multivariate polynomials from the following ring:
Concretely,
 gets handles to formal polynomials from \({\mathcal {L}}_{{{\mathfrak {t}}}}\) for each \({\mathfrak {t}}\in \{1,2,{\textsf{T}}\}\), where:
gets handles to formal polynomials from \({\mathcal {L}}_{{{\mathfrak {t}}}}\) for each \({\mathfrak {t}}\in \{1,2,{\textsf{T}}\}\), where:
-
1.
\({\mathcal {L}}_{{{\textsf{T}}}} = \left\{ 1, \upalpha ,{\textsf{DL}}{\left( m\right) }+\upalpha {\texttt{s}}\right\} \).
-
2.
\({\mathcal {L}}_{{1}} = {\mathcal {L}}_{{1}}^\textsf{crs}\cup {\mathcal {L}}_{{1}}^{\textsf{key}} \cup {\mathcal {L}}_{{1}}^c\), where
-
(a)
\({\mathcal {L}}_{{1}}^\textsf{crs}=\left( 1, \upbeta , \upgamma , {\mathtt {u_0'}}, {\mathtt {\{u_{w,i}\}_{i\in [0,L],w\in [n']}}}\right) \),
-
(b)
\({\mathcal {L}}_{{1}}^{\textsf{key}} = \left( \left\{ {\mathtt {-\widetilde{r}^c_iu_{n',i}}}\right\} _{c \in [Q_{\textsf{k}}]} \right) \) for some \(i\in [L]\), and
-
(c)
\({\mathcal {L}}_{{1}}^c= \left( {\texttt{s}}, {\mathtt {z\upgamma }}, \left\{ {\mathtt {r\upbeta y_w}}+{\mathtt {s\upbeta }}-{\mathtt {z\sum _{i=0}^{L}u_{w,i}}}\right\} _{w\in [n]}, {\mathtt {s\upbeta -zu_{n'}}}, {\mathtt {s\upbeta - z{\textsf{DL}}{\left( T\right) }}}\right) \).
-
(a)
-
3.
\({\mathcal {L}}_{{2}} = {\mathcal {L}}_{{2}}^\textsf{crs}\cup {\mathcal {L}}_{{2}}^{\textsf{key}}\), where
-
(a)
\({\mathcal {L}}_{{2}}^\textsf{crs}= \left( 1, {\mathtt {\{t_i,\upalpha +\upbeta t_i\}_{i\in [L]}}}, {\mathtt {\frac{t_iu_0'}{\upgamma }}}, {\mathtt {\left\{ \frac{t_iu_{w,j}}{\upgamma }\right\} _{i\in [L], j\in [0,L]\setminus \{i\},w\in [n']}}} \right) \), and
-
(b)
\({\mathcal {L}}_{{2}}^{\textsf{key}} = \left( \left\{ {\mathtt { \frac{\widetilde{r}_i^ct_ju_{n',i}}{\upgamma }}}\right\} _{{j\in [L]\setminus \{i\},}{c\in [Q_{\textsf{k}}]}} \right) \) for some \(i\in [L]\).
-
(a)
However, when
 issues any zero-test query via \({\textsf{Zt}}_{\textsf{T}}\) oracle, the challenger replaces the formal variables with their corresponding elements from \(\mathbb {Z}_q\). In this case, if the variable is not assigned a value in \(\mathbb {Z}_q\), it samples the corresponding value from the same distribution as it did in \(\textbf{H}_1(\lambda )\). However, once a value is assigned to a variable, it is fixed throughout the rest of \(\textbf{H}_2(\lambda )\). We show in [25] that \(\textbf{H}_1(\lambda ) \equiv \textbf{H}_2(\lambda )\).
issues any zero-test query via \({\textsf{Zt}}_{\textsf{T}}\) oracle, the challenger replaces the formal variables with their corresponding elements from \(\mathbb {Z}_q\). In this case, if the variable is not assigned a value in \(\mathbb {Z}_q\), it samples the corresponding value from the same distribution as it did in \(\textbf{H}_1(\lambda )\). However, once a value is assigned to a variable, it is fixed throughout the rest of \(\textbf{H}_2(\lambda )\). We show in [25] that \(\textbf{H}_1(\lambda ) \equiv \textbf{H}_2(\lambda )\).
Given the tuple \(\textsf{P} = \left( {\mathcal {L}}_{{1}},{\mathcal {L}}_{{2}}, {\mathcal {L}}_{{{\textsf{T}}}}\right) \), we define \({\mathcal {C}}({\mathcal {L}}_{{{\textsf{T}}}}) = {\mathcal {L}}_{{{\textsf{T}}}} \cup \{V_1\cdot V_2~|~\forall V_1\in {\mathcal {L}}_{{1}}, V_2 \in {\mathcal {L}}_{{2}}\}\). Basically, it is the set of all monomials from \(\upzeta \) with variables in \(\mathbb {G}_{\textsf{T}}\) that \(\mathcal {A}\) can compute querying \({\textsf{Map}}_e\) on the handles it received for elements in \({\mathcal {L}}_{{1}}, {\mathcal {L}}_{{2}}\). We estimate the size of \({\mathcal {C}}({\mathcal {L}}_{{{\textsf{T}}}})\) as follows. Note that we have \(\left| {\mathcal {C}}({\mathcal {L}}_{{{\textsf{T}}}})\right| = \left| {\mathcal {L}}_{{{\textsf{T}}}}\right| + \left| {\mathcal {L}}_{{1}}\right| \cdot \left| {\mathcal {L}}_{{2}}\right| \) where \(\left| {\mathcal {L}}_{{{\textsf{T}}}}\right| =3\),

There are several variables in \(\upzeta \) and several terms in \({\mathcal {L}}_{{1}}, {\mathcal {L}}_{{2}}\). Hence, for brevity, we do not state all the elements of \({\mathcal {C}}({\mathcal {L}}_{{{\textsf{T}}}})\) explicitly with all possible cross combinations of the monomials from \({\mathcal {L}}_{{1}},{\mathcal {L}}_{{2}}\). However, it is easy to see by inspection that the maximal total degree of each term in \({\mathcal {C}}({\mathcal {L}}_{{{\textsf{T}}}})\) is \(d=7\) corresponding to the term \(\left[ {\mathtt {r\upbeta y_w\cdot \frac{\widetilde{r}_i^ct_ju_{n',i}}{\upgamma }}}\right] \) for any \(w\in [n'],i\in [L], j\in [0,L]\setminus \{i\}, c\in [Q_{\textsf{k}}]\). We also note that any handle submitted by \(\mathcal {A}\) to the \({\textsf{Zt}}_{\textsf{T}}\) oracle during its interaction refers to a polynomial \(f\in \upzeta \) as
where the coefficients \(\{\eta _\varTheta \in \mathbb {Z}_q\}_{\varTheta \in {\mathcal {C}}({\mathcal {L}}_{{{\textsf{T}}}})}\) can be computed efficiently. Further, since all the monomials in \({\mathcal {C}}({\mathcal {L}}_{{{\textsf{T}}}})\) are distinct, the coefficients \(\eta _\varTheta \) are unique.
-
\(\textbf{H}_3(\lambda ):\) In this hybrid, all queries to \({\textsf{Zt}}_{\textsf{T}}\) oracle are answered using formal variables. Namely, for any \({\textsf{Zt}}_{\textsf{T}}\) query on a handle to a polynomial \(f\in \upzeta \), the challenger returns 1 if:
We show in [25] that \(\textbf{H}_2(\lambda )\approx \textbf{H}_3(\lambda )\).
-
\(\textbf{H}_4(\lambda ):\) In this hybrid, the challenge ciphertext computes an encryption of \(m_0\) with respect to \(\textbf{y}_1\). That is, everything remains as it is in \(\textbf{H}_3(\lambda )\) except that the challenger generates

Arguing indistinguishability between \(\textbf{H}_3(\lambda )\) and \(\textbf{H}_4(\lambda )\) is the crux of this proof. We provide this analysis in our full version [25]. From here on, the challenger moves to \(\textbf{H}_6(\lambda )\) directly if \(m_0 = m_1\). Else if \(m_0 \ne m_1\), it still moves to \(\textbf{H}_6(\lambda )\), but via the next hybrids.
-
\(\textbf{H}_{5,1}(\lambda ):\) In this hybrid, \(Z^s\in \mathbb {G}_{\textsf{T}}\) is replaced with
 .
. -
\(\textbf{H}_{5,2}(\lambda ):\) In this hybrid, the challenge ciphertext encrypts \(m_1\) instead of \(m_0\).
-
\(\textbf{H}_{5,3}(\lambda ):\) In this hybrid, \({\mathfrak {U}}\) is changed to the honestly computed \(Z^s\) again.
-
\(\textbf{H}_6(\lambda ):\) In this hybrid, the challenger moves to \({\textsf{GGM}}\) from the symbolic setting of \({\textsf{SGM}}\). This is the real scheme corresponding to bit \(b=1\) in the \({\textsf{GGM}}\).
Hybrid Indistinguishability. Due to space constraints, we defer all the formal proofs for the indistinguishability of hybrids in our full version [25].
Final pairing-based RIPE scheme. By combining the slotted RIPE scheme of Construction 1 and the (“powers-of-two”) transformation provided in our full version [25] , we obtain a secure registered IPE with an extra \(O(\log L)\) factor in all its compactness and efficiency measures.
7 Implementation and Benchmarks
We developed a Python prototypeFootnote 8 of our \({\textsf{s}}{\textsf{RIPE}}\) scheme from Sect. 6 with the \(\textsf{BLS12}\)-\(\textsf{381}\) elliptic curve for pairings, which we implemented via the \(\mathsf petrelic\) Python wrapper [47] around RELIC [10]. This configuration allows each element in \(\mathbb {G}_1,\mathbb {G}_2,\mathbb {G}_T\) to be represented using 49, 97 and 384 bytes respectively. We obtained the benchmarks below on a personal computer with an Intel Core i7-10700 3.8GHz CPU and 128GB of RAM running Ubuntu 22.04.1 LTS with kernel 5.15.0-58-generic. Exponentiations in \(\mathbb {G}_1\) (resp., \(\mathbb {G}_2\)) and each pairing took 0.13 (resp., 0.18) milliseconds and 0.68 milliseconds on average on our machine.
Benchmarks. We provide benchmarks in Fig. 2, showing the sizes of \(\textsf{mpk}\) and the \(|\textsf{crs}|\) as well as the execution times of setup, aggregate, encrypt and decrypt in relation to parameters \(L\) and n. For encryption and decryption, we executed the algorithms 100 times for each pair \((L,n)\), and then computed the average runtime. The setup and aggregate were run once for each unique pair of \((L,n)\). We did not plot the sizes of the ciphertexts, but these can be determined deterministically based on n as \(|c| = 580+49n\) bytes. The size of the helper secret key for each user is \(|{\textsf{hsk}}| = 340+97n\) bytes. Note that the setup and aggregation time grows acutely with \(L\) and n. Improving the efficiency of our \({\textsf{s}}{\textsf{RIPE}}\) scheme is left as a future work.
Notes
- 1.
IBE can be seen as a special case of FE for equality predicates \(f_y\) such that \(f_y(x,m) = m\) if and only if \(y = x\) (and \(\bot \) otherwise). Here, x and y have the role of the parties’ identities (which do not need to be secret), and m is the encrypted message.
- 2.
The original paper define the primitive as registration based encryption. However, we choose to call it as registered IBE, in line with the more recent work in [41].
- 3.
Two-sided security in PE allows an adversary to obtain secret keys for predicates that can decrypt a challenge ciphertext, provided the challenge message pair consists of the same message.
- 4.
Generic compilers from any ABE for LSSS (or equivalently, monotone span programs) to (hierarchical) IPE are known (e.g., [11]). However, such compilers do not ensure attribute-privacy which we crucially require from our (registered) IPE scheme.
- 5.
Although the common reference string is generated by a trusted setup, the important difference is that there is no long-term secret that needs to be stored throughout the lifetime of the system. Furthermore, in some cases, the setup algorithm could be “transparent”, and therefore computable using just a hash function.
- 6.
In such a setting (rogue) users can try to register arbitrary functions of their choice which would allow them to learn arbitrary information about encrypted messages. To prevent this, one can restrict the function class at setup meaningfully (e.g., excluding trivial functions like identity). Any user wanting to register its public key would then need to prove the validity of its chosen function w.r.t. this class of functions.
- 7.
By Definition 1,
 is supposed to send well-formed keys that passes the \(\textsf{IsValid}(\textsf{crs},\cdot ,\cdot )\) test. Hence, from now on we do not mention it any more, but assume the challenger checks it implicitly.
is supposed to send well-formed keys that passes the \(\textsf{IsValid}(\textsf{crs},\cdot ,\cdot )\) test. Hence, from now on we do not mention it any more, but assume the challenger checks it implicitly. - 8.
References
Agrawal, S.: Indistinguishability obfuscation without multilinear maps: new methods for bootstrapping and instantiation. In: Ishai, Y., Rijmen, V. (eds.) EUROCRYPT 2019. LNCS, vol. 11476, pp. 191–225. Springer, Cham (2019). https://doi.org/10.1007/978-3-030-17653-2_7
Agrawal, S., Kitagawa, F., Modi, A., Nishimaki, R., Yamada, S., Yamakawa, T.: Bounded functional encryption for turing machines: adaptive security from general assumptions. In: Kiltz, E., Vaikuntanathan, V. (eds.) Theory of Cryptography: 20th International Conference, TCC 2022, Chicago, IL, USA, 7–10 November 2022, Proceedings, Part I, pp. 618–647. Springer, Heidelberg (2022). https://doi.org/10.1007/978-3-031-22318-1_22
Agrawal, S., Maitra, M., Vempati, N.S., Yamada, S.: Functional encryption for turing machines with dynamic bounded collusion from LWE. In: Malkin, T., Peikert, C. (eds.) CRYPTO 2021. LNCS, vol. 12828, pp. 239–269. Springer, Cham (2021). https://doi.org/10.1007/978-3-030-84259-8_9
Agrawal, S., Yamada, S.: Optimal broadcast encryption from pairings and LWE. In: Canteaut, A., Ishai, Y. (eds.) EUROCRYPT 2020. LNCS, vol. 12105, pp. 13–43. Springer, Cham (2020). https://doi.org/10.1007/978-3-030-45721-1_2
Ananth, P., Brakerski, Z., Segev, G., Vaikuntanathan, V.: From selective to adaptive security in functional encryption. In: Gennaro, R., Robshaw, M. (eds.) CRYPTO 2015. LNCS, vol. 9216, pp. 657–677. Springer, Heidelberg (2015). https://doi.org/10.1007/978-3-662-48000-7_32
Ananth, P., Jain, A., Lin, H., Matt, C., Sahai, A.: Indistinguishability obfuscation without multilinear maps: new paradigms via low degree weak pseudorandomness and security amplification. In: Boldyreva, A., Micciancio, D. (eds.) CRYPTO 2019. LNCS, vol. 11694, pp. 284–332. Springer, Cham (2019). https://doi.org/10.1007/978-3-030-26954-8_10
Ananth, P., Jain, A.: Indistinguishability obfuscation from compact functional encryption. In: Gennaro, R., Robshaw, M. (eds.) CRYPTO 2015. LNCS, vol. 9215, pp. 308–326. Springer, Heidelberg (2015). https://doi.org/10.1007/978-3-662-47989-6_15
Ananth, P., Sahai, A.: Projective arithmetic functional encryption and indistinguishability obfuscation from degree-5 multilinear maps. In: Coron, J.-S., Nielsen, J.B. (eds.) EUROCRYPT 2017. LNCS, vol. 10210, pp. 152–181. Springer, Cham (2017). https://doi.org/10.1007/978-3-319-56620-7_6
Ananth, P., Vaikuntanathan, V.: Optimal bounded-collusion secure functional encryption. In: Hofheinz, D., Rosen, A. (eds.) TCC 2019. LNCS, vol. 11891, pp. 174–198. Springer, Cham (2019). https://doi.org/10.1007/978-3-030-36030-6_8
Aranha, D.F., Gouvêa, C.P.L., Markmann, T., Wahby, R.S., Liao, K.: RELIC is an Efficient LIbrary for Cryptography (2020). https://github.com/relic-toolkit/relic
Attrapadung, N., Hanaoka, G., Yamada, S.: Conversions among several classes of predicate encryption and applications to ABE with various compactness tradeoffs. In: Iwata, T., Cheon, J.H. (eds.) ASIACRYPT 2015. LNCS, vol. 9452, pp. 575–601. Springer, Heidelberg (2015). https://doi.org/10.1007/978-3-662-48797-6_24
Baltico, C.E.Z., Catalano, D., Fiore, D., Gay, R.: Practical functional encryption for quadratic functions with applications to predicate encryption. In: Katz, J., Shacham, H. (eds.) CRYPTO 2017. LNCS, vol. 10401, pp. 67–98. Springer, Cham (2017). https://doi.org/10.1007/978-3-319-63688-7_3
Barak, B., et al.: On the (im) possibility of obfuscating programs. J. ACM (JACM) 59(2), 1–48 (2012)
Barthe, G., Fagerholm, E., Fiore, D., Mitchell, J.C., Scedrov, A., Schmidt, B.: Automated analysis of cryptographic assumptions in generic group models. J. Cryptol. 32(2), 324–360 (2019)
Bitansky, N.: Verifiable random functions from non-interactive witness-indistinguishable proofs. J. Cryptol. 33(2), 459–493 (2020)
Bitansky, N., Vaikuntanathan, V.: Indistinguishability obfuscation from functional encryption. In: Guruswami, V. (ed.) 56th FOCS, pp. 171–190. IEEE Computer Society Press (2015)
Boneh, D., et al.: Fully key-homomorphic encryption, arithmetic circuit ABE and compact garbled circuits. In: Nguyen, P.Q., Oswald, E. (eds.) EUROCRYPT 2014. LNCS, vol. 8441, pp. 533–556. Springer, Heidelberg (2014). https://doi.org/10.1007/978-3-642-55220-5_30
Boneh, D., Sahai, A., Waters, B.: Functional encryption: definitions and challenges. In: Ishai, Y. (ed.) TCC 2011. LNCS, vol. 6597, pp. 253–273. Springer, Heidelberg (2011). https://doi.org/10.1007/978-3-642-19571-6_16
Brakerski, Z., Döttling, N., Garg, S., Malavolta, G.: Candidate iO from homomorphic encryption schemes. In: Canteaut, A., Ishai, Y. (eds.) EUROCRYPT 2020, Part I. LNCS, vol. 12105, pp. 79–109. Springer, Heidelberg (May (2020). https://doi.org/10.1007/s00145-023-09471-5
Brakerski, Z., Döttling, N., Garg, S., Malavolta, G.: Factoring and pairings are not necessary for io: circular-secure lwe suffices. In: 49th International Colloquium on Automata, Languages, and Programming (ICALP 2022). Schloss Dagstuhl-Leibniz-Zentrum für Informatik (2022)
Brakerski, Z., Segev, G.: Function-private functional encryption in the private-key setting. In: Dodis, Y., Nielsen, J.B. (eds.) TCC 2015. LNCS, vol. 9015, pp. 306–324. Springer, Heidelberg (2015). https://doi.org/10.1007/978-3-662-46497-7_12
Chotard, J., Dufour-Sans, E., Gay, R., Phan, D.H., Pointcheval, D.: Dynamic decentralized functional encryption. In: Micciancio, D., Ristenpart, T. (eds.) CRYPTO 2020. LNCS, vol. 12170, pp. 747–775. Springer, Cham (2020). https://doi.org/10.1007/978-3-030-56784-2_25
Cong, K., Eldefrawy, K., Smart, N.P.: Optimizing registration based encryption. In: Paterson, M.B. (ed.) IMACC 2021. LNCS, vol. 13129, pp. 129–157. Springer, Cham (2021). https://doi.org/10.1007/978-3-030-92641-0_7
Döttling, N., Kolonelos, D., Lai, R.W.F., Lin, C., Malavolta, G., Rahimi, A.: Efficient laconic cryptography from learning with errors. In: Hazay, C., Stam, M. (eds.) EUROCRYPT 2023. LNCS, vol. 14006, pp. 417–446. Springer, Cham (2023). https://doi.org/10.1007/978-3-031-30620-4_14
Francati, D., Friolo, D., Maitra, M., Malavolta, G., Rahimi, A., Venturi, D.: Registered (inner-product) functional encryption. Cryptology ePrint Archive (2023)
Francati, D., Friolo, D., Malavolta, G., Venturi, D.: Multi-key and multi-input predicate encryption from learning with errors. In: Advances in Cryptology-EUROCRYPT 2023: 42nd Annual International Conference on the Theory and Applications of Cryptographic Techniques, Lyon, France, 23–27 April 2023, Proceedings, Part III, pp. 573–604. Springer, Heidelberg (2023). https://doi.org/10.1007/978-3-031-30620-4_19
Garg, S., Gentry, C., Halevi, S., Raykova, M., Sahai, A., Waters, B.: Candidate indistinguishability obfuscation and functional encryption for all circuits. In: 54th FOCS, pp. 40–49. IEEE Computer Society Press (2013)
Garg, S., Gentry, C., Halevi, S., Zhandry, M.: Functional encryption without obfuscation. In: Kushilevitz, E., Malkin, T. (eds.) TCC 2016. LNCS, vol. 9563, pp. 480–511. Springer, Heidelberg (2016). https://doi.org/10.1007/978-3-662-49099-0_18
Garg, S., Hajiabadi, M., Mahmoody, M., Rahimi, A.: Registration-based encryption: removing private-key generator from IBE. In: Beimel, A., Dziembowski, S. (eds.) TCC 2018. LNCS, vol. 11239, pp. 689–718. Springer, Cham (2018). https://doi.org/10.1007/978-3-030-03807-6_25
Garg, S., Hajiabadi, M., Mahmoody, M., Rahimi, A., Sekar, S.: Registration-based encryption from standard assumptions. In: Lin, D., Sako, K. (eds.) PKC 2019. LNCS, vol. 11443, pp. 63–93. Springer, Cham (2019). https://doi.org/10.1007/978-3-030-17259-6_3
Garg, S., Pandey, O., Srinivasan, A., Zhandry, M.: Breaking the sub-exponential barrier in obfustopia. In: Coron, J.-S., Nielsen, J.B. (eds.) EUROCRYPT 2017. LNCS, vol. 10212, pp. 156–181. Springer, Cham (2017). https://doi.org/10.1007/978-3-319-56617-7_6
Gay, R., Jain, A., Lin, H., Sahai, A.: Indistinguishability obfuscation from simple-to-state hard problems: new assumptions, new techniques, and simplification. In: Canteaut, A., Standaert, F.-X. (eds.) EUROCRYPT 2021. LNCS, vol. 12698, pp. 97–126. Springer, Cham (2021). https://doi.org/10.1007/978-3-030-77883-5_4
Gay, R., Pass, R.: Indistinguishability obfuscation from circular security. In: Proceedings of the 53rd Annual ACM SIGACT Symposium on Theory of Computing, pp. 736–749 (2021)
Gentry, C., Lewko, A.B., Sahai, A., Waters, B.: Indistinguishability obfuscation from the multilinear subgroup elimination assumption. In: Guruswami, V. (ed.) 56th FOCS, pp. 151–170. IEEE Computer Society Press (2015)
Glaeser, N., Kolonelos, D., Malavolta, G., Rahimi, A.: Efficient registration-based encryption. Cryptology ePrint Archive, Paper 2022/1505 (2022). https://eprint.iacr.org/2022/1505
Goldwasser, S., Kalai, Y.T., Popa, R.A., Vaikuntanathan, V., Zeldovich, N.: Reusable garbled circuits and succinct functional encryption. In: Boneh, D., Roughgarden, T., Feigenbaum, J. (eds.) 45th ACM STOC, pp. 555–564. ACM Press (2013)
Gorbunov, S., Vaikuntanathan, V., Wee, H.: Functional encryption with bounded collusions via multi-party computation. In: Safavi-Naini, R., Canetti, R. (eds.) CRYPTO 2012. LNCS, vol. 7417, pp. 162–179. Springer, Heidelberg (2012). https://doi.org/10.1007/978-3-642-32009-5_11
Goyal, R., Hohenberger, S., Koppula, V., Waters, B.: A generic approach to constructing and proving verifiable random functions. In: Kalai, Y., Reyzin, L. (eds.) TCC 2017. LNCS, vol. 10678, pp. 537–566. Springer, Cham (2017). https://doi.org/10.1007/978-3-319-70503-3_18
Goyal, R., Vusirikala, S.: Verifiable registration-based encryption. In: Micciancio, D., Ristenpart, T. (eds.) CRYPTO 2020. LNCS, vol. 12170, pp. 621–651. Springer, Cham (2020). https://doi.org/10.1007/978-3-030-56784-2_21
Hemenway, B., Jafargholi, Z., Ostrovsky, R., Scafuro, A., Wichs, D.: Adaptively secure garbled circuits from one-way functions. In: Robshaw, M., Katz, J. (eds.) CRYPTO 2016. LNCS, vol. 9816, pp. 149–178. Springer, Heidelberg (2016). https://doi.org/10.1007/978-3-662-53015-3_6
Hohenberger, S., Lu, G., Waters, B., Wu, D.J.: Registered attribute-based encryption. Cryptology ePrint Archive (2022)
Hubacek, P., Wichs, D.: On the communication complexity of secure function evaluation with long output. In: Roughgarden, T. (ed.) ITCS 2015, pp. 163–172. ACM (2015)
Jain, A., Lin, H., Matt, C., Sahai, A.: How to leverage hardness of constant-degree expanding polynomials overa \(\mathbb{R} \) to build \(i\cal{O} \). In: Ishai, Y., Rijmen, V. (eds.) EUROCRYPT 2019. LNCS, vol. 11476, pp. 251–281. Springer, Cham (2019). https://doi.org/10.1007/978-3-030-17653-2_9
Jain, A., Lin, H., Sahai, A.: Indistinguishability obfuscation from well-founded assumptions. In: Proceedings of the 53rd Annual ACM SIGACT Symposium on Theory of Computing, pp. 60–73 (2021)
Jain, A., Lin, H., Sahai, A.: Indistinguishability obfuscation from LPN over \(\mathbb{F} _p\), DLIN, and PRGs in \({NC}^0\). In: Dunkelman, O., Dziembowski, S. (eds.) EUROCRYPT 2022, Part I. LNCS, vol. 13275, pp. 670–699. Springer, Heidelberg (2022). https://doi.org/10.1007/978-3-031-06944-4_23
Katz, J., Sahai, A., Waters, B.: Predicate encryption supporting disjunctions, polynomial equations, and inner products. In: Smart, N. (ed.) EUROCRYPT 2008. LNCS, vol. 4965, pp. 146–162. Springer, Heidelberg (2008). https://doi.org/10.1007/978-3-540-78967-3_9
Laurent Girod, W.L.: Petrelic is a python wrapper around relic (2022). https://github.com/spring-epfl/petrelic
Lin, H.: Indistinguishability obfuscation from constant-degree graded encoding schemes. In: Fischlin, M., Coron, J.-S. (eds.) EUROCRYPT 2016. LNCS, vol. 9665, pp. 28–57. Springer, Heidelberg (2016). https://doi.org/10.1007/978-3-662-49890-3_2
Mahmoody, M., Qi, W., Rahimi, A.: Lower bounds for the number of decryption updates in registration-based encryption. Cryptology ePrint Archive, Report 2022/1285 (2022). https://eprint.iacr.org/2022/1285
Okamoto, T., Pietrzak, K., Waters, B., Wichs, D.: New realizations of somewhere statistically binding hashing and positional accumulators. In: Iwata, T., Cheon, J.H. (eds.) ASIACRYPT 2015. LNCS, vol. 9452, pp. 121–145. Springer, Heidelberg (2015). https://doi.org/10.1007/978-3-662-48797-6_6
O’Neill, A.: Definitional issues in functional encryption. Cryptology ePrint Archive, Report 2010/556 (2010). https://eprint.iacr.org/2010/556
Sahai, A., Waters, B.: How to use indistinguishability obfuscation: deniable encryption, and more. In: Shmoys, D.B. (ed.) 46th ACM STOC, pp. 475–484. ACM Press (2014)
Sahai, A., Waters, B.: Fuzzy identity-based encryption. In: Cramer, R. (ed.) EUROCRYPT 2005. LNCS, vol. 3494, pp. 457–473. Springer, Heidelberg (2005). https://doi.org/10.1007/11426639_27
Shamir, A.: Identity-based cryptosystems and signature schemes. In: Blakley, G.R., Chaum, D. (eds.) CRYPTO 1984. LNCS, vol. 196, pp. 47–53. Springer, Heidelberg (1985). https://doi.org/10.1007/3-540-39568-7_5
Shen, E., Shi, E., Waters, B.: Predicate privacy in encryption systems. In: Reingold, O. (ed.) TCC 2009. LNCS, vol. 5444, pp. 457–473. Springer, Heidelberg (2009). https://doi.org/10.1007/978-3-642-00457-5_27
Wee, H., Wichs, D.: Candidate obfuscation via oblivious LWE sampling. In: Canteaut, A., Standaert, F.-X. (eds.) EUROCRYPT 2021. LNCS, vol. 12698, pp. 127–156. Springer, Cham (2021). https://doi.org/10.1007/978-3-030-77883-5_5
Acknowledgments
The authors thank the anonymous reviewers for their helpful comments. The first author was supported by the Carlsberg Foundation under the Semper Ardens Research Project CF18-112 (BCM). The second and the sixth author were partially supported by project SERICS (PE00000014) under the MUR National Recovery and Resilience Plan funded by the European Union - NextGenerationEU and by Sapienza University under the project SPECTRA. The third author was partially supported by the European Union (ERC AdG REWORC - 101054911), and by True Data 8 (Distributed Ledger & Multiparty Computation) under the Hessen State Ministry for Higher Education, Research and the Arts within their joint support of the National Research Center for Applied Cybersecurity ATHENE. The fourth author was partially funded by the German Federal Ministry of Education and Research (BMBF) in the course of the 6GEM research hub under grant number 16KISK038 and by the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation) under Germany’s Excellence Strategy - EXC 2092 CASA - 390781972.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2023 International Association for Cryptologic Research
About this paper
Cite this paper
Francati, D., Friolo, D., Maitra, M., Malavolta, G., Rahimi, A., Venturi, D. (2023). Registered (Inner-Product) Functional Encryption. In: Guo, J., Steinfeld, R. (eds) Advances in Cryptology – ASIACRYPT 2023. ASIACRYPT 2023. Lecture Notes in Computer Science, vol 14442. Springer, Singapore. https://doi.org/10.1007/978-981-99-8733-7_4
Download citation
DOI: https://doi.org/10.1007/978-981-99-8733-7_4
Published:
Publisher Name: Springer, Singapore
Print ISBN: 978-981-99-8732-0
Online ISBN: 978-981-99-8733-7
eBook Packages: Computer ScienceComputer Science (R0)





 .
. .
. and
and
 , respectively.
, respectively. .
. and
and
 , respectively, where
, respectively, where  .
. .
.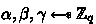 and set
and set  and set
and set  and set
and set  , and set
, and set  . Then, we set
. Then, we set  , the vector length n, and the number of slots
, the vector length n, and the number of slots  , the challenger samples
, the challenger samples
 and gives
and gives  . The challenger also initializes a counter
. The challenger also initializes a counter  can issue the following queries.
can issue the following queries. specifies a slot index
specifies a slot index  , updates the dictionary as
, updates the dictionary as  .
. specifies an index
specifies an index  .
. specifies a tuple
specifies a tuple  issued a corrupt query before on
issued a corrupt query before on  sends a challenge pair
sends a challenge pair  , and replies with
, and replies with  .
. returns a bit
returns a bit 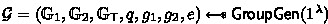 and generate the common reference string as follows.
and generate the common reference string as follows. and set
and set  and set
and set  and set
and set  . Set
. Set  and pick elements
and pick elements  . Also, parse
. Also, parse 



 sends an attribute length
sends an attribute length  and initializes three tables as
and initializes three tables as  , set
, set  a tuple
a tuple  can issue key generation queries or corruption queries in this phase.
can issue key generation queries or corruption queries in this phase. and compute
and compute  cannot compute a handle for
cannot compute a handle for  and update
and update  sends
sends  where
where  specifies the following challenge information:
specifies the following challenge information:  issued a corruption query for
issued a corruption query for  itself. Hence, it parses
itself. Hence, it parses  only needs to compute the handles for
only needs to compute the handles for  invokes the
invokes the  obtains the handles for
obtains the handles for  only needs to compute the handles for
only needs to compute the handles for  obtains the handles to each element in
obtains the handles to each element in  outputs a bit
outputs a bit  remains exactly as it was in
remains exactly as it was in  receives refer to multivariate polynomials from the following ring:
receives refer to multivariate polynomials from the following ring:
 .
.
 is supposed to send well-formed keys that passes the
is supposed to send well-formed keys that passes the