Polar Representation of Bipolar Information: A Case Study to Compare Intuitionistic Entropies

Abstract

In this paper, a new approach to compare measures of entropy in the setting of the intuitionistic fuzzy sets introduced by Atanassov. A polar representation is introduced to represent such bipolar information and it is used to study the three main intuitionistic fuzzy sets entropies of the literature. A theoretical comparison and some experimental results highlight the interest of such a representation to gain knowledge on these entropies.

1 Introduction

Measuring information is a very crucial task in Artificial intelligence. First of all, one main challenge is to define what is information, as it is done by Lotfi Zadeh [15] who considers different approaches to define information: the probabilistic approach, the possibilistic one, and their combination. In the literature, we can also cite the seminal work by J. Kampé de Fériet who introduced a new way to consider information and its aggregation [10, 11].

In previous work, we have focused on the monotonicity of entropy measures and highlighted the fact that there exist several forms of monotonicity [4, 5]. But highlighting that two measures share the same monotonicity property is often not sufficient in an application framework: to choose between two measures, their differences in behaviour are usually more informative.

In this paper, we do not focus on defining information but we discuss on the comparison of measures of information in the particular case of Intuitionistic Fuzzy Sets introduced by Atanassov (AIFS) [2] and related measures of entropy (simply called hereafter AIFS entropies) that have been introduced to measure intuitionistic fuzzy set-based information.

In this case, we highlight the fact that trying to interpret such a measure according to variations of the AIFS could not be clearly understandable. Instead, we propose to introduce a polar representation of AIFS in order to help the understanding of the behaviour of AIFS entropies. As a consequence, in a more general context, we argue that introducing a polar representation for bipolar information could be a powerful way to improve the understandability of the behaviour for related measures.

This paper is organized as follows: in Sect. 2, we recall the basis of intuitionistic fuzzy sets and some known measures of entropy in this setting. In Sect. 3, we propose an approach to compare measures of entropy of intuitionistic fuzzy sets that is based on a polar representation of intuitionistic membership degrees. In Sect. 4, some experiments are presented that highlight the analytical conclusions drawn in the previous section. The last section concludes the paper and presents some future works.

2 Intuitionistic Fuzzy Sets and Entropies

First of all, in this section, some basic concepts related to intuitionistic fuzzy sets are presented. Afterwards, existing AIFS entropies are recalled.

2.1 Basic Notions

Let $U=\{u_1,\ldots , u_n\}$ be a universe, an intuitionistic fuzzy set introduced by Atanassov (AIFS) A of U is defined [2] as:

$$A=\{(u, \mu _A(u), \nu _A(u)) | u \in U\}$$

with $\mu _A: U \rightarrow [0,1]$ and $\nu _A: U \rightarrow [0,1]$ such that $0\le \mu _A(u) + \nu _A(u) \le 1$, $\forall u\in ~U$. Here, $\mu _A(u)$ and $\nu _A(u)$ represent respectively the membership degree and the non-membership degree of u in A.

Given an intuitionistic fuzzy set A of U, the intuitionistic index of u to A is defined for all $u\in U$ as: $\pi _A(u)=1-(\mu _A(u) + \nu _A(u))$. This index represents the margin of hesitancy lying on the membership of u in A or the lack of knowledge on A. In [6], an AIFS A such that $\mu _A(u) = \nu _A(u) = 0$, $\forall u \in U$ is called completely intuitionistic.

2.2 Entropies of Intuitionistic Fuzzy Sets

Existing Entropies. In the literature, there exist several definitions of the entropy of an intuitionistic fuzzy set and several works proposed different ways to define such entropy, for instance from divergence measures [12]. In this paper, in order to illustrate the polar representation, we focus on three classical AIFS entropies.

In [13], the entropy of the AIFS A is defined as:

$$E_{1}(A) = \displaystyle 1 - \frac{1}{2n}\sum _{i=1}^{n}|\mu _A (u_i)- \nu _A(u_i)|, $$

where n is the cardinality of the considered universe.

Other definitions are introduced in [6] based on extensions of the Hamming distance and the Euclidean distance to intuitionistic fuzzy sets. For instance, the following entropy is proposed:

$$E_{2}(A)= \displaystyle \sum _{i=1}^{n} \pi _A(u_i) = n- \sum _{i=1}^{n} (\mu _A(u_i)+\nu _A(u_i)). $$

In [9], another entropy is introduced:

$$ E_{3}(A) = \displaystyle \frac{1}{2n}\sum _{i=1}^{n}\big (1 - |\mu _A (u_i)-\nu _A(u_i)|\big ) (1+\pi _A(u_i)). $$

Definitions of Monotonicity. All AIFS entropies share a property of monotonicity, but authors don’t agree about a unique definition of monotonicity.

Usually, monotonicity is defined according to the definition of a partial order $\le$ on AIFS. Main definitions of monotonicity for entropies that have been proposed are based on different definition of the partial order In the following, we show the definitions of the partial order less fuzzy proposed by [6, 9, 13].

Let E(A) be the entropy of the AIFS A. The following partial orders (M1) or (M2) can be used:

(M1) $E(A) \le E(B)$, if A is less fuzzy than B.

i.e. $\mu _A(u) \le \mu _B(u)$ and $\nu _A(u) \ge \nu _B(u)$ when $\mu _B(u) \le \nu _B(u)$, $\forall u\in U$, or $\mu _A(u) \ge \mu _B(u)$ and $\nu _A(u) \le \nu _B(u)$ when $\mu _B(u) \ge \nu _B(u)$, $\forall u\in ~U$.

(M2) $E(A) \le E(B)$ if $A \le B$

i.e. $\mu _A(u) \le \mu _B(u)$ and $\nu _A(u) \le ~\nu _B(u)$, $\forall u\in ~U$.

Each definition of the monotonicity produces the definition of a particular form of E:

• it is easy to show that $E_{1}$ satisfies (M1);

• $E_{2}$ has been introduced by [6] to satisfy (M2);

• $E_{3}$ has been defined by [9] from (M1).

Indeed, these three AIFS entropies are different by definition as they are based on different definitions of monotonicity. However, if we want to choose the best entropy to use for a given application, it may not be so clear. A comparative study as those presented in Fig. 2 do not bring out much information about the way they are different. In the following section, we introduce a new approach to better highlight differences in the behaviour of these entropies.

3 Comparing AIFS Entropies

Usually, the study of measures, either entropies or other kinds of measures, is done by means of a given set of properties. In the previous section, we focused on the property of monotonicity showing that several definitions exist and could be used. Thus, if any measure could be built according to a given definition of monotonicity, at the end, this could not be very informative to understand clearly their differences in behaviour.

A first approach focuses on the study of the variations of an entropy according to the variations of each of its AIFS components $\mu$ and $\nu$. However, this can only highlight the “horizontal” variations (when $\mu$ varies) or the “vertical” variations (when $\nu$ varies) and fails to enable a good understandability when both quantities vary.

In this paper, we introduce a polar representation of AIFS in order to be able to understand more clearly the dual influence of this bipolar information. Indeed, we show that the comparison of measures can be made easier with such a representation. We focus on AIFS, but we believe that such a study can also be useful for other bipolar information measures.

3.1 Polar Representation of an AIFS

In this part, we introduce a polar representation of an AIFS and we represent an AIFS as a complex number. In [3], this kind of representation is a way to show a geometric representation of an AIFS. In a more analytic way, such a representation could also be used to represent basic operations (intersection, union,...) on AIFS [1, 14], or for instance on the Pythagorean fuzzy sets [7].

Indeed, as each $u \in U$ is associated with two values $\mu _A(u)$ and $\nu _A(u)$, the membership of u to A can thus be represented as a point in a 2-dimensional space. In this sense, $\mu _A(u)$ and $\nu _A(u)$ represent the Cartesian coordinates of this point. We can then think of a complex number representation as we did in [5] or, equivalently, a representation of such a point by means of polar coordinates. In the following, we show that such a representation makes easier specific studies of these measures.

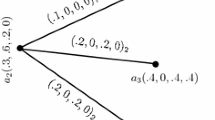
The AIFS A is defined for $u\in U$ as $\mu _A(u)$ and $\nu _A(u)$, that can be represented as the complex number $z_A(u)= \mu _A(u) + i\,\nu _A(u)$ (see Fig. 1). Thus, for this u, an AIFS is a point under (or on) the straight line $y=1-x$. When it belongs to the line $y=1-x$, it corresponds to the special case of a fuzzy set.

Another special case corresponds to the straight line $y=x$ that corresponds to AIFS such that $\mu _A(u)= \nu _A(u)$: AIFS above this line are such that $\mu _A(u)~\le ~\nu _A(u)$ and those under this line are such that $\mu _A(u) \ge \nu _A(u)$.

Fig. 1.

Geometrical representation of an intuitionistic fuzzy set.

Hereafter, using classical notation from complex numbers, given $z_{A}(u)$, we note $\theta _A(u)=\arg (z_{A}(u))$ and $r_A(u) = |z_A(u)|=\sqrt{\mu _A(u)^2 + \nu _A(u)^2}$ (see Fig. 1).

The values $r_A(u)$ and $\theta _A(u)$ provide the polar representation of the AIFS $(u, \mu _A(u), \nu _A(u))$ for all $u\in U$. Following classical complex number theory, we have $\mu _A(u)=r_A(u)\cos \theta _A(u)$ and $\nu _A(u)=r_A(u)\sin \theta _A(u)$.

To alleviate the notations, in the following, when there is no ambiguity, $r_A(u)$ and $\theta _A(u)$ will be noted r and $\theta$ respectively.

Using trigonometric identities, we have:

$$\begin{aligned} \mu _A(u)+\nu _A(u)&= r(\cos \theta +\sin \theta ) \\&= r \sqrt{2}\; (\frac{\sqrt{2}}{2}\cos \theta + \frac{\sqrt{2}}{2}\sin \theta ) \\&= r \sqrt{2}\; \sin (\theta + \frac{\pi }{4}) \end{aligned}$$

The intuitionistic index can thus be rewritten as $\pi _A(u)=1- r \sqrt{2}\sin (\theta +~\frac{\pi }{4})$.

Moreover, let d be the distance from $(\mu _A(u), \nu _A(u))$ to the straight line $y=x$ and $\delta$ be the projection according to the U axis of $(\mu _A(u), \nu _A(u))$ on $y=x$ (ie. $\delta = |\mu _A(u)-\nu _A(u)|$).

It is easy to see that $d= r |\sin (\frac{\pi }{4}-~\theta )|$ and $\delta = \frac{d}{\sin \frac{\pi }{4}}$. Thus, we have $\delta =\sqrt{2}\;r |\sin (\frac{\pi }{4}-\theta )|$.

In the following, for the sake of simplicity, when there is no ambiguity, $\mu _A(u_i)$, $\nu _A(u_i)$, $r_A(u_i)$ and $\theta _A(u_i)$ will be respectively noted $\mu _i$, $\nu _i$, $r_i$ and $\theta _i$.

3.2 Rewriting AIFS Entropies

With the notations introduced in the previous paragraph, entropy $E_1$ can be rewritten as:

$$E_{1}(A) = \displaystyle 1 - \frac{\sqrt{2}}{2n}\sum _{i=1}^{n}r_i |sin(\frac{\pi }{4}-\theta _i)|. $$

With this representation of the AIFS, it is easy to see that:

• if $\theta _i$ is given, $E_{1}$ decreases when $r_i$ increases (ie. when the AIFS gets closer to $y=1-x$, and thus, when it tends to be a classical fuzzy set): the nearer an AIFS is from the straight line $y=1-x$, the lower its entropy.

• if $r_i$ is given, $E_{1}$ increases when $\theta _i$ tends to $\frac{\pi }{4}$ (ie. when the knowledge on the non-membership decreases): the closer to $y=x$ it is, the higher its entropy.

A similar study can be done with $E_{2}$. In our setting, it can be rewritten as:

$$E_{2}(A)= \displaystyle n- \sqrt{2}\sum _{i=1}^{n} r_i\sin (\theta _i+\frac{\pi }{4}). $$

With this representation of the AIFS, we can see that:

• if $\theta _i$ is given, then $E_{2}$ decreases when $r_i$ increases: the closer to (0, 0) (ie. the more “completely intuitionistic”) the AIFS is, the lower its entropy.

• if $r_i$ is given, $E_{2}$ decreases when $\theta _i$ increases: the farther an AIFS is from $y=x$, the higher its entropy.

A similar study can be done with $E_{3}$ that can be rewritten as:

$$E_{3}(A)= \displaystyle \frac{1}{2n}\sum _{i=1}^{n}\big (1-r_i \sqrt{2} |\sin (\frac{\pi }{4}-\theta _i)|\big ) \big (2-r_i \sqrt{2} \sin (\frac{\pi }{4}+\theta _i\big )). $$

It is interesting to highlight here two elements of comparison: on one hand a behavioural difference between $E_{1}$ (resp. $E_3$) and $E_{2}$: if they vary similarly according to $r_i$, they vary in an opposite way according to $\theta _i$; on the other hand, a similar behaviour between $E_1$ and $E_3$.

To illustrate these similarities and differences, a set of experiments have been conducted and results are provided in Sect. 4.

Fig. 2.

Correlations between $E_1(A)$, $E_2(A)$ and $E_3(A)$ for 5000 random AIFS.

4 Experimental Study

In this section, we present some results related to experiments conducted to compare AIFS entropies.

4.1 Correlations Between AIFS Entropies

The first experiment has been conducted to see if some correlations could be highlighted between each of the three presented AIFS entropies.

First of all, an AIFS A is randomly generated. It is composed of n points, n also randomly generated and selected from 1 to $n_{max}=20$. Afterwards, the AIFS entropy of A is valued for each of the three AIFS entropies presented in Sect. 2: $E_1$, $E_2$ and $E_3$. Then, a set of $n_{AIFS} = 5000$ such random AIFS is built.

A correlogram to highlight possible correlations between the values of $E_1(A)$, $E_2(A)$ and $E_3(A)$ is thus plot and presented in Fig. 2.

In this figure, each of these 9 spots (i, j) should be read as follows. The spot line i and column j corresponds to:

• if $i=j$: the distribution of the values of $E_i(A)$ for all A;

• if $i\not =j$: the distribution of $(E_j(A), E_i(A))$ for each random AIFS A.

This process has been conducted several times, with different values for $n_{max}$ and for $n_{AIFS}$, with similar results.

It is clear that there is no correlation between the entropies. It is noticeable that $E_1$ and $E_2$ could yield to very different values for the same AIFS A. For instance, if $E_1(A)$ equals 1, the value of $E_2(A)$ could be either close to 0 or equals to 1 too.

As a consequence, it is clear that these entropies are highly different but no conclusion can be drawn about the elements that bring out this difference.

Fig. 3.

Variations related to $\theta$ when $r=0.01$ (left) or $r=0.5$ (right) ($E_1$ in solid line (red), $E_2$ in dashed line (blue), $E_3$ in dash-dot line (green)). (Color figure online)

4.2 Variations of AIFS Entropies

To better highlight behaviour differences between the presented AIFS entropies, we introduce the polar representation to study the variations of the values of the entropy according to r or to $\theta$.

Variations Related to $\varvec{\theta }$. In Fig. 3, the variations of the entropies related to $\theta$ for an AIFS A composed of a single element are shown. The polar representation is used to study these variations. The value of r is set to either 0.01 (left) to highlight the variations when r is low, or 0.5 (right) to highlight variations when r is high (this value corresponds to the highest possible value to have a complete range of variations for $\theta$).

It is easy to show in this figure an illustration of the conclusions drawn in Sect. 3:

• $E_1$ and $E_3$ varies in the same way;

• $E_1$ (resp. $E_3$) and $E_2$ varies in an opposite way;

• all of these AIFS entropies reach an optimum for $\theta =\frac{\pi }{4}$. It is a maximum for $E_1$ and $E_3$ and a minimum for $E_2$.

• the optimum is always 1 for $E_1$ for any r, but it depends on r for $E_2$ and $E_3$.

• for all entropies, the value when $\theta =0$ (resp. $\theta =\frac{\pi }{2}$) depends on r.

Variations Related to $\varvec{r}$. In Fig. 4, the variations of the entropies related to r for an AIFS A composed of a single element are shown. Here again, the polar representation is used to study these variations.

According to the polar representations of the AIFS entropies, it is easy to see that $E_1$ and $E_2$ vary linearly with r, and in a quadratic form for $E_3$.

We provided here the variations when $\theta =0$ (ie. the AIFS is on the horizontal axis), $\theta =\frac{\pi }{8}$ (ie. the AIFS is under $y=x$), $\theta =\frac{\pi }{4}$ (ie. the AIFS is on $y=x$) and when $\theta =\frac{\pi }{2}$ (ie. the AIFS is on the vertical axis). We don’t provide results when the AIFS is below $y=x$ as it is similar to the results when the AIFS is under with a symmetry related to $y=x$ (as it can be seen with the variations when $\theta =\frac{\pi }{2}$ which are similar to the ones when $\theta =0$).

For each experiment, r varies from 0 to $r=(\sqrt{2}\cos (\frac{\pi }{4}-\theta ))^{-1}$ when $\theta \not =\frac{\pi }{2}$.

It is easy to highlight from these results some interesting behaviour of the AIFS entropies when r varies:

• they all varies in the same way but not with the same amplitude;

• all of these AIFS entropies reach an optimum when $r=0$ (ie. the AIFS is completely intuitionistic;

• $E_1$ takes the optimum value for any r when $\theta =\frac{\pi }{4}$.

Fig. 4.

Variations related to r when $\theta$ varies ($E_1$ in solid line (red), $E_2$ in dashed line (blue), $E_3$ in dash-dot line (green)). (Color figure online)

5 Conclusion

In this paper, we introduce a new approach to compare measures of entropy in the setting of intuitionistic fuzzy sets. We introduce the use of a polar representation to study the three main AIFS entropies of the literature.

This approach is very promising as it enables us to highlight the main differences in behaviour that can exist between measures. Beyond this study on the AIFS, such a polar representation could thus be an interesting way to study bipolar information-based measures.

In future work, our aim is to develop this approach and apply it to other AIFS entropies, for instance [8], and other bipolar representations of information.