Topological Relations Between Bipolar Fuzzy Sets Based on Mathematical Morphology

Abstract

In many domains of information processing, both vagueness, or imprecision, and bipolarity, encompassing positive and negative parts of information, are core features of the information to be modeled and processed. This led to the development of the concept of bipolar fuzzy sets, and of associated models and tools. Here we propose to extend these tools by defining algebraic relations between bipolar fuzzy sets, including intersection, inclusion, adjacency and RCC relations widely used in mereotopology, based on bipolar connectives (in a logical sense) and on mathematical morphology operators.

1 Introduction

In many domains, such as knowledge representation, preference modeling, argumentation, multi-criteria decision analysis, spatial reasoning, both vagueness or imprecision and bipolarity, encompassing positive and negative parts of information, are core features of the information to be modeled and processed. Bipolarity corresponds to a recent trend in contemporary information processing, both from a knowledge representation point of view, and from a processing and reasoning one. It allows distinguishing between (i) positive information, which represents what is guaranteed to be possible, for instance because it has already been observed or experienced, and (ii) negative information, which represents what is impossible or forbidden, or surely false [12]. This domain has recently motivated work in several directions, for instance for applications in knowledge representation, preference modeling, argumentation, multi-criteria decision analysis, cooperative games, among others [12]. Three types of bipolarity are distinguished in [14]: (i) symmetric univariate, where a unique totally ordered scale covers the range from negative (not satisfactory) to positive (satisfactory) information (e.g. modeled by probabilities); (ii) symmetric bivariate, where two separate scales are linked together and concern related information (e.g. modeled by belief functions); (iii) asymmetric or heterogeneous, where two types of information are not necessarily linked together and may come from different sources. This last type is particularly interesting in image interpretation and spatial reasoning. In order to include the precise nature of information, fuzzy and possibilistic formalisms for bipolar information have been proposed (see e.g. [14]). This led to the development of the concept of bipolar fuzzy sets, and of associated models and tools, such as fusion and aggregation, similarity and distances, mathematical morphology, etc.

Here we propose to extend this set of tools by defining algebraic relations between bipolar fuzzy sets, including intersection, inclusion, adjacency and relations of region connection calculus (RCC) widely used in mereotopology¹. Formal definitions are proposed, based on bipolar connectives and on mathematical morphology operators (here we consider only the deterministic part of mathematical morphology and use mostly erosions and dilations). They are shown to have the desired properties and to be consistent with existing definitions on sets and fuzzy sets, while providing an additional bipolar feature. The proposed relations can be used for instance for preference modeling or spatial reasoning, accounting for both bipolarity and imprecision. Any type of bipolar fuzzy set is considered, and the proposed definitions are not restricted to objects with indeterminate or broad boundaries as in the egg-yolk [10] or 9-intersection [9] models.

In Sect. 2, definitions of bipolar fuzzy sets and bipolar connectives are summarized. Extensions of basic set theoretical relations to bipolar fuzzy sets are given in Sect. 3. Mathematical morphology operators are recalled in Sect. 4. Adjacency is addressed in Sect. 5, based on morphological dilation. Finally RCC relations are extended to bipolar fuzzy sets in Sect. 6.²

2 Background on Bipolar Fuzzy Sets and Connectives

In this section, we recall some useful definitions on bipolar fuzzy sets and basic connectives (negation, conjunction, disjunction, implication). As mentioned in the introduction, bipolar information has two components, one related to positive information, and one related to negative information. These pieces of information can take different forms, according to the application domain, such as preferences and constraints, observations and rules, possible and forbidden places for an object in space, etc. Let us assume that bipolar information is represented by a pair $(\mu , \nu )$, where $\mu$ represents the positive information and $\nu$ the negative information, under a consistency constraint [14], which guarantees that the positive information is compatible with the constraints or rules expressed by the negative information. From a formal point of view, bipolar information can be represented in different settings. Here we consider the representation where $\mu$ and $\nu$ are membership functions to fuzzy sets, defined over a space ${\mathcal S}$ (for instance the spatial domain, a set of potential options in preference modeling...). As noticed e.g. in [13] and the subsequent discussion, bipolar fuzzy sets are formally equivalent (but with important differences in their semantics) to interval-valued fuzzy sets and to intuitionistic fuzzy sets, and all these are also special cases of L-fuzzy sets introduced in [16]. Despite these formal equivalences, since the semantics are very different, we keep here the terminology of bipolarity.

Definition 1

A bipolar fuzzy set on ${\mathcal S}$ is defined by an ordered pair of functions $(\mu , \nu )$ from ${\mathcal S}$ into [0, 1] such that $\forall x \in {\mathcal S}, \mu (x) + \nu (x) \le 1$ (consistency constraint).

We consider here that $\mu$ and $\nu$ are really two different functions, which may represent different types of information or may be issued from different sources (third type bipolarity according to [14]). However, this may also include the symmetric case, reducing the consistency constraint to a duality relation such as $\nu = 1 - \mu$. For each point x, $\mu (x)$ defines the membership degree of x (positive information) and $\nu (x)$ its non-membership degree (negative information). This formalism allows representing both bipolarity and fuzziness. The set of bipolar fuzzy sets defined on ${\mathcal S}$ is denoted by ${\mathcal B}$.

Let us denote by ${\mathcal L}$ the set of ordered pairs of numbers (a, b) in [0, 1]³ such that $a\, +\, b \le 1$ (hence $(\mu ,\nu ) \in {\mathcal B}\Leftrightarrow \forall x \in {\mathcal S}, (\mu (x),\nu (x)) \in {\mathcal L}$). In all what follows, for each $(\mu , \nu ) \in {\mathcal B}$, we will note $(\mu , \nu )(x) = (\mu (x), \nu (x))$ ($\in {\mathcal L}$), $\forall x \in {\mathcal S}$. Note that fuzzy sets can be considered as particular cases of bipolar fuzzy sets, either when $\forall x \in {\mathcal S}, \nu (x) = 1 - \mu (x)$, or when only one information is available, i.e. $(\mu (x), 0)$ or $(0, 1 - \mu (x))$. Furthermore, if $\mu$ (and $\nu$) only takes values 0 and 1, then bipolar fuzzy sets reduce to classical sets.

Let $\preceq$ be a partial ordering on ${\mathcal L}$ such that $({\mathcal L}, \preceq )$ is a complete lattice. We denote by $\bigvee$ and $\bigwedge$ the supremum and infimum, respectively. The smallest element is denoted by $0_{\mathcal L}$ and the largest element by $1_{\mathcal L}$. The partial ordering on ${\mathcal L}$ induces a partial ordering on ${\mathcal B}$, also denoted by $\preceq$ for the sake of simplicity:

$$\begin{aligned} (\mu _1,\nu _1) \preceq (\mu _2,\nu _2) \text { iff } \forall x \in {\mathcal S}, (\mu _1,\nu _1)(x) \preceq (\mu _2,\nu _2)(x). \end{aligned}$$

(1)

Then $({\mathcal B}, \preceq )$ is a complete lattice, for which the supremum and infimum are also denoted by $\bigvee$ and $\bigwedge$. The smallest element is the bipolar fuzzy set $0_{\mathcal B}= (\mu _0,\nu _0)$ taking value $0_{\mathcal L}$ at each point, and the largest element is the bipolar fuzzy set $1_{\mathcal B}= (\mu _\mathbb {I}, \nu _\mathbb {I})$ always equal to $1_{\mathcal L}$.

Let us now recall definitions and properties of connectives, that will be useful in the following and that extend to the bipolar case the connectives classically used in fuzzy set theory. In all what follows, increasingness and decreasingness are intended according to the partial ordering $\preceq$. Similar definitions can also be found e.g. in [11] in the case of interval-valued fuzzy sets of intuitionistic fuzzy sets, for a specific partial ordering (Pareto ordering).

Definition 2

A negation, or complementation, on ${\mathcal L}$ is a decreasing operator N such that $N(0_{\mathcal L})=1_{\mathcal L}$ and $N(1_{\mathcal L})=0_{\mathcal L}$. In this paper, we restrict ourselves to involutive negations, such that $\forall \mathbf{a} \in {\mathcal L}, N(N(\mathbf{a}))=\mathbf{a}$ (these are the most interesting ones for mathematical morphology).

A conjunction is an operator C from ${\mathcal L}\times {\mathcal L}$ into ${\mathcal L}$ such that $C(0_{\mathcal L}, 0_{\mathcal L}) = C(0_{\mathcal L}, 1_{\mathcal L}) = C(1_{\mathcal L}, 0_{\mathcal L}) = 0_{\mathcal L}$, $C(1_{\mathcal L},1_{\mathcal L}) = 1_{\mathcal L}$, and that is increasing in both arguments⁴. A t-norm is a commutative and associative bipolar conjunction such that $\forall \mathbf{a} \in {\mathcal L}, C(\mathbf{a},1_{\mathcal L}) = C(1_{\mathcal L},\mathbf{a}) = \mathbf{a}$ (i.e. the largest element of ${\mathcal L}$ is the unit element of C). If only the property on the unit element holds, then C is called a semi-norm.

A disjunction is an operator D from ${\mathcal L}\times {\mathcal L}$ into ${\mathcal L}$ such that $D(1_{\mathcal L},1_{\mathcal L}) = D(0_{\mathcal L},1_{\mathcal L}) = D(1_{\mathcal L},0_{\mathcal L}) = 1_{\mathcal L}$, $D(0_{\mathcal L},0_{\mathcal L}) = 0_{\mathcal L}$, and that is increasing in both arguments. A t-conorm is a commutative and associative bipolar disjunction such that $\forall \mathbf{a} \in {\mathcal L}, D(\mathbf{a},0_{\mathcal L}) = D(0_{\mathcal L},\mathbf{a}) = \mathbf{a}$ (i.e. the smallest element of ${\mathcal L}$ is the unit element of D).

An implication is an operator I from ${\mathcal L}\times {\mathcal L}$ into ${\mathcal L}$ such that $I(0_{\mathcal L},0_{\mathcal L}) = I(0_{\mathcal L},1_{\mathcal L}) = I(1_{\mathcal L},1_{\mathcal L}) = 1_{\mathcal L}$, $I(1_{\mathcal L},0_{\mathcal L}) = 0_{\mathcal L}$ and that is decreasing in the first argument and increasing in the second argument.

In the following, we will call these connectives bipolar to make their instantiation on bipolar information explicit. Similarly, elements of ${\mathcal L}$ should be considered as pairs, quantifying the positive and negative parts of information. The properties of these connectives are detailed for instance in [6, 11], as well as the links between them. Let us mention of few of them useful in the sequel: given a t-norm C and a negation N, a t-conorm can be defined as $D((a_1,b_1), (a_2,b_2)) = N(C(N((a_1,b_1)), N((a_2,b_2))))$; an implication I induces a negation N defined as $N((a,b)) = I((a,b), 0_{\mathcal L})$; an implication can be derived from a negation N and a disjunction D as $I_N((a_1,b_1),(a_2,b_2)) = D(N((a_1,b_1)),(a_2,b_2))$; an implication can also be defined by residuation from a conjunction C such that $\forall (a,b) \in {\mathcal L}\setminus 0_{\mathcal L}, C(1_{\mathcal L}, (a,b)) \ne 0_{\mathcal L}$ as: $I_R((a_1,b_1),(a_2,b_2)) = \bigvee \{ (a_3,b_3) \in {\mathcal L}\; | \; C((a_1,b_1),(a_3,b_3)) \preceq (a_2,b_2) \}$ (and we have $C((a_1,b_1),(a_3,b_3)) \preceq (a_2,b_2) \Leftrightarrow (a_3,b_3) \preceq I((a_1,b_1),(a_2,b_2))$, expressing the adjunction property); if C is a conjunction that admits $1_{\mathcal L}$ as unit element, then $C((a,b),(a',b')) \preceq (a,b) \wedge (a',b')$; if I is an implication that admits $1_{\mathcal L}$ as unit element on the left, then $(a',b') \preceq I((a,b),(a',b'))$; if I is an implication that admits $0_{\mathcal L}$ as unit element on the right, then $(a,b) \preceq I((a,b),(a',b'))$; a residual implication I defined from a bipolar t-norm satisfies $I((a,b),(a',b')) = 1_{\mathcal L}\Leftrightarrow (a,b) \preceq (a',b')$. In the following we will mostly consider conjunctions which are bipolar t-norms, and the associated residual implications.

The marginal partial ordering on ${\mathcal L}$, or Pareto ordering (by reversing the scale of negative information) is defined as:

$$\begin{aligned} (a_1,b_1) \preceq (a_2,b_2) \; \text {iff} \; a_1 \le a_2 \text { and } b_1 \ge b_2. \end{aligned}$$

(2)

This ordering, often used in economics and social choice, has also been used for bipolar information [15], and intuitionistic fuzzy sets (or interval valued fuzzy sets) e.g. in [11]. For this partial ordering, $({\mathcal L}, \preceq )$ is a complete lattice. The greatest element is $1_{\mathcal L}= (1,0)$ and the smallest element is $0_{\mathcal L}= (0,1)$. The supremum and infimum are respectively defined as:

$$\begin{aligned} \bigvee ((a_1,b_1), (a_2,b_2)) = (\max (a_1,a_2), \min (b_1,b_2)), \end{aligned}$$

(3)

$$\begin{aligned} \bigwedge ((a_1,b_1), (a_2,b_2)) = (\min (a_1,a_2), \max (b_1,b_2)). \end{aligned}$$

(4)

In this paper, we restrict our developments to this partial ordering, as an example. Other partial orderings are discussed in [6], where dilations and erosions based on any ordering are proposed.

Let us now mention a few connectives. In Definition 2, the monotony properties have now to be intended according to the Pareto ordering.

An example of negation, which will be used in the following, is the standard negation, defined by $N((a,b))=(b,a)$.

Two types of t-norms and t-conorms are considered in [11] (actually in the intuitionistic case) and will be considered here as well in the bipolar case. The first class consists of operators called t-representable bipolar t-norms and t-conorms, which can be expressed using usual t-norms t and t-conorms T as $C((a_1,b_1),(a_2,b_2)) = (t(a_1,a_2), T(b_1,b_2))$, and $D((a_1,b_1),(a_2,b_2)) = (T(a_1,a_2), t(b_1,b_2))$. A typical example is obtained for $t = \min$ and $T = \max$. In the following we will use dual operators t and T. The second class includes bipolar Lukasiewicz operators, which are not t-representable, and are not detailed here.

3 Basic Set Theoretical Relations on Bipolar Fuzzy Sets

Inclusion and intersection can be simply defined as bipolar numbers (i.e. in ${\mathcal L}$) (see e.g. [6] and the references therein):

Definition 3

A bipolar degree of inclusion of $(\mu _1,\nu _1)$ in $(\mu _2,\nu _2)$ is defined from a bipolar implication I as:

$$ Inc((\mu _1,\nu _1), (\mu _2,\nu _2)) = \bigwedge _{x \in {\mathcal S}} I((\mu _1,\nu _1)(x), (\mu _2,\nu _2)(x)). $$

Definition 4

A bipolar degree of intersection of $(\mu _1,\nu _1)$ and $(\mu _2,\nu _2)$ is defined from a bipolar conjunction C as:

$$ Int((\mu _1,\nu _1), (\mu _2,\nu _2)) = \bigvee _{x \in {\mathcal S}} C((\mu _1,\nu _1)(x), (\mu _2,\nu _2)(x)). $$

Proposition 1

The bipolar degrees of inclusion and intersection in Definitions 3 and 4 are consistent with the corresponding definitions in the crisp and fuzzy cases.

The bipolar degree of inclusion is an element of ${\mathcal L}$ and is decreasing in the first argument and increasing in the second one.

The bipolar degree of intersection is an element of ${\mathcal L}$ and is increasing in both arguments. It is symmetrical in particular if C is a bipolar t-norm.

If the conjunction is t-representable (i.e. $C=(t,T)$ with t a t-norm and T the dual t-conorm), then we have: $Int((\mu _1,\nu _1), (\mu _2,\nu _2)) = (\mu _{int}(\mu _1,\mu _2), 1 - \mu _{int}(1 - \nu _1, 1 - \nu _2))$ where $\mu _{int}$ is the degree of intersection between fuzzy sets, defined as $\mu _{int}(\mu ,\mu ') = \sup _{x \in {\mathcal S}} t(\mu (x),\mu '(x))$.

4 Mathematical Morphology on Bipolar Fuzzy Sets

Mathematical morphology on bipolar fuzzy sets was proposed for the first time in [2], by considering the complete lattice defined from the Pareto ordering. Then it was further developed, with additional properties, geometric aspects and applications to spatial reasoning, in [3, 5]. In [6], any partial ordering was considered, and derived operators were also proposed. Similar work has been developed independently, in the setting of intuitionistic fuzzy sets and interval-valued fuzzy sets, also based on Pareto ordering (e.g. [18]). This group proposed an extension to L-fuzzy sets [24], besides its important contribution to connectives (e.g. [11]). Here, while relying on the general algebraic framework of mathematical morphology on the one hand, and on L-fuzzy sets [16] on the other hand, we restrict ourselves to the special case of bipolar fuzzy sets, according to Definition 1, and use the definitions proposed in [2, 6], in their particular form involving structuring elements. A structuring element is a binary bipolar relation between elements of ${\mathcal S}$ and its value at “$x-y$” represents the bipolar degree to which this relation is satisfied between x and y. If ${\mathcal S}$ is endowed with a translation (for instance ${\mathcal S}$ is a subset of $\mathbb {R}^n$ or $\mathbb {Z}^n$, representing a spatial domain), then the value of a structuring element at $x-y$ represents the value at point y of the translation of the structuring element at point x.

Definition 5

Let $(\mu _B,\nu _B)$ be a bipolar fuzzy structuring element (in ${\mathcal B}$). The erosion of any $(\mu , \nu )$ in ${\mathcal B}$ by $(\mu _B,\nu _B)$ is defined from a bipolar implication I as:

$$\begin{aligned} \forall x \in {\mathcal S}, \; \varepsilon _{(\mu _B,\nu _B)}((\mu ,\nu ))(x) = \bigwedge _{y \in {\mathcal S}} I((\mu _B,\nu _B)(y-x), (\mu ,\nu )(y)). \end{aligned}$$

(5)

Definition 6

Let $(\mu _B,\nu _B)$ be a bipolar fuzzy structuring element (in ${\mathcal B}$). The dilation of any $(\mu , \nu )$ in ${\mathcal B}$ by $(\mu _B,\nu _B)$ is defined from a bipolar conjunction C as:

$$\begin{aligned} \forall x \in {\mathcal S}, \; \delta _{(\mu _B,\nu _B)}((\mu ,\nu ))(x) = \bigvee _{y \in {\mathcal S}} C ((\mu _B,\nu _B)(x-y), (\mu ,\nu )(y)). \end{aligned}$$

(6)

These definitions are proved to provide bipolar fuzzy sets, and express erosion (respectively dilation), as a degree of inclusion (respectively intersection) of the translation (if defined on ${\mathcal S}$) of the structuring element and the bipolar fuzzy set to be transformed, according to Definitions 3 and 4.

The properties of these definitions are detailed in [6]. In particular, we will exploit in the following the fact that dilation commutes with the supremum of the lattice, and is increasing. It is extensive if and only if the origin of ${\mathcal S}$ completely belongs to the structuring element (i.e. with bipolar degree (1, 0)). We will restrict ourselves to extensive dilations in the following, i.e. such that $(\mu ,\nu ) \preceq \delta (\mu ,\nu )$. The two operations $\varepsilon$ and $\delta$ form an adjunction if and only if I is the residuated implication of C (i.e. I and C are adjoint). Finally, these definitions are equivalent to the fuzzy definitions if no bipolarity is taken into account (the dilation of a fuzzy set $\mu$ by a structuring element $\mu _B$ is defined as $\delta _{\mu _B}(\mu )(x) = \sup _{y \in {\mathcal S}} t(\mu _B(x-y),\mu (y))$ where t is a t-norm [4], and a similar expression for erosion).

5 Adjacency Between Bipolar Fuzzy Sets Based on Mathematical Morphology

In this section, we extend our previous work on adjacency between fuzzy sets [8] to the case of bipolar fuzzy sets. The underlying idea is similar, and relies on the fact that two entities (e.g. objects in space) are adjacent if they do not intersect, but as soon as one of them is dilated, they intersect.

Definition 7

Let $\delta$ be a bipolar fuzzy dilation, C a bipolar conjunction, N a bipolar negation, and Int a bipolar degree of intersection (Definition 4). The adjacency between two bipolar fuzzy sets $(\mu _1,\nu _1)$ and $(\mu _2,\nu _2)$ is defined as a bipolar number in ${\mathcal L}$ as:

$$ Adj((\mu _1,\nu _1), (\mu _2,\nu _2)) = C(N(Int((\mu _1,\nu _1), (\mu _2,\nu _2))), Int((\mu _1,\nu _1), \delta (\mu _2,\nu _2))). $$

This definition formalizes the conjunction (C(.)) between the non intersection of the two entities (N(Int(.))) and the intersection of one entities and the dilation of the other one.

The dilation can be defined according to the application. For instance for applications in the spatial domain, we may define a structuring element representing the smallest discernable spatial unit, or the imprecision related to objects or points positions. The dilation is then computed using this structuring element. The simplest one in a discrete domain would be composed of one central point and its neighbors according to a pre-defined discrete connectivity. It would then be a classical set.

Let us detail the case where C is a t-representable conjunction [11], i.e. $C((a_1,b_1),(a_2,b_2)) = (t(a_1,a_2), T(b_1,b_2))$ where t is a t-norm and T is a t-conorm. We consider here the Pareto ordering and $N(a,b)=(b,a)$, and we denote by $\delta ^+$ and $\delta ^-$ the positive and negative parts of the dilation. For instance for the dilation of a bipolar fuzzy set $(\mu _2,\nu _2)$ by a structuring element $(\mu _B,\nu _B)$ we have:

$$\begin{aligned} \delta ^+(x)= & {} \sup _{y \in {\mathcal S}} t(\mu _B(x-y), \mu _2(y)) = \delta _{\mu _B}(\mu _2)(x),\\ \delta ^-(x)= & {} \inf _{y \in {\mathcal S}} T(\nu _B(x-y), \nu _2(y)) = \varepsilon _{1-\nu _B}(\nu _2). \end{aligned}$$

These equations show that the positive part of the dilation is the fuzzy dilation of $\mu$ (positive part of the bipolar fuzzy set) by $\mu _B$ (positive part of the structuring element), and its negative part is the fuzzy erosion of $\nu$ (negative part of the bipolar fuzzy set) by $1 - \nu _B$ (negation of the negative part of the structuring element).

Proposition 2

For a t-representable conjunction defined from a t-norm t and its dual t-conorm T, we have ($\mu _{int}$ being the classical degree of intersection of fuzzy sets):

$$\begin{aligned} \begin{array}{c} Adj((\mu _1,\nu _1), (\mu _2,\nu _2)) =\\ (t(1 - \mu _{int}(1-\nu _1, 1-\nu _2), \mu _{int}(\mu _1, \delta ^+)), T(\mu _{int}(\mu _1, \mu _2), 1 - \mu _{int}(1\!-\!\nu _1, 1\!-\!\delta ^-))). \end{array} \end{aligned}$$

This result has an interpretation that corresponds to the intuition: (i) the positive part evaluates to which extent $1-\nu _1$ and $1-\nu _2$ do not intersect, and $\mu _1$ and $\delta ^+$ intersect; (ii) the negative part evaluates to which extent $\mu _1$ and $\mu _2$ intersect, or $1-\nu _1$ and $1 - \delta ^-$ do not intersect.

The non representable case, for instance for Lukasiewicz bipolar conjunction, can be developed in a similar way. The interpretation is slightly more complicated and may be less directly intuitive.

Other properties are expressed in the following proposition.

Proposition 3

The adjacency defined in Definition 7 has the following properties: (i) it is symmetrical if C is left continuous (according to a metric on ${\mathcal L}$, e.g. Euclidean distance), (ii) it is invariant under geometric transformations such as translation and rotation (if ${\mathcal S}$ is a spatial domain, e.g. a subset of $\mathbb {R}^n$ or $\mathbb {Z}^n$), (iii) it is consistent with the definitions in the binary case and in the fuzzy case.

Note that this relation is not considered in other works such as [9, 10, 17, 20]. Due to the indetermination in the objects and in the relations, in some cases the adjacency relation may be close to relations such as “nearly overlap” in [9]. However, as mentioned in the introduction, the proposed model is more general since it is not restricted to objects with imprecise or broad boundaries (which are the ones considered in these other works).

Fig. 1.

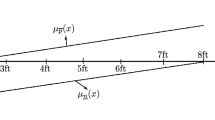
A few typical situations illustrating the adjacency between bipolar fuzzy sets in the spatial domain. The positive part ($\mu$) is inside the plain lines, and the negative part ($\nu$) is outside the dashed lines. For the sake of simplicity, membership degrees are not represented. The blue lines correspond to $(\mu _1,\nu _1)$ and the red ones to $(\mu _2,\nu _2)$. (Color figure online)

A few typical adjacency situations are illustrated in Fig. 1. For the sake of simplicity, degrees in the positive and negative parts are not represented. In case (a) in this figure, the two positive parts are adjacent, and the indeterminate parts are overlapping, thus resulting in a strong indeterminacy in the spatial relation. The proposed definition provides a bipolar number where both positive and negative parts are less than 1. In case (b), the positive part is equal to 0, showing that the relation is less satisfied than in case (a), as expected. The relation is best satisfied in case (c), with no ambiguity, which is reflected by the $(1,0) = 1_{\mathcal L}$ bipolar value provided by the proposed definition. In case (d), the two negative parts of the sets are the same. This is an illustration where the bipolarity does not correspond to broad boundaries. Here the resulting bipolar adjacency value is $(0,1) = 0_{\mathcal L}$, which corresponds to the fact that the possible region for the two objects is very large (the left half-plane), with potentially no adjacency between them because of overlapping. Finally, in case (d), the negative parts are different half-planes, and this situation is close to the perfect adjacency case. The largest value (1, 0) would be obtained if the two positive regions were strictly adjacent. As a concrete example, the spatial entities in the two last situations may correspond to brain structures situated in the same hemisphere (then $\nu$ is the contra-lateral hemisphere), or in different hemispheres.

6 RCC Relations Extended to Bipolar Fuzzy Sets

In this section, we propose extensions of the now classical RCC relations [19] to bipolar fuzzy sets. The connection predicate, a reflexive and symmetrical relation⁵, is denoted by C, so we will denote conjunctions and bipolar t-norms by Conj in all this section.

Using Connectives. A first approach consists of a direct formal extension of the equations on classical sets, similar to the extension proposed in [22] for the fuzzy case. The proposed extension relies on the connectives and bipolar degrees of intersection and inclusion (see Sects. 2 and 3). Thus we start with a bipolar connection predicate C, which is reflexive and symmetrical. Bipolar fuzzy sets are denoted by capital letters ($A, B ... \in {\mathcal B}$).

Definition 8

Let I be a bipolar implication, Conj a bipolar t-norm and N a bipolar negation. The RCC relations on bipolar fuzzy sets are defined as bipolar degrees of satisfaction as follows:

• Part: $P(A,B)= \bigwedge _{Z\in {\mathcal B}} I(C(A,Z),C(B,Z))$;

• Overlaps: $O(A,B)= \bigvee _{Z\in {\mathcal B}} Conj(P(Z,A), P(Z,B))$;

• Non tangential part: $NTP(A,B) = \bigwedge _{Z\in {\mathcal B}} I(C(Z,A), O(Z,B))$;

• Disconnected: $DC(A,B) = N(C(A,B))$;

• Proper part: $PP(A,B) = \bigwedge (P(A,B), N(P(B,A)))$ (or any bipolar conjunction Conj instead of $\bigwedge$ in this definition and the next ones);

• Equals: $EQ(A,B) = \bigwedge (P(A,B), P(B,A))$;

• Distinct regions: $DR(A,B) = N(O(A,B))$;

• Partially overlaps: $PO(A,B) = \bigwedge (O(A,B), N(P(B,A)), N(P(A,B)))$;

• Externally connected: $EC(A,B) = \bigwedge (C(A,B), N(O(A,B)))$;

• Tangential proper part: $TPP(A,B) = \bigwedge (PP(A,B), N(NTP(A,B)))$;

• Non tangential proper part: $NTPP(A,B) = \bigwedge (PP(A,B), NTP(A,B))$.

Using Mathematical Morphology. Another approach relies on the parthood predicate P as starting point. Then we can directly derive the five relations O, PP, EQ, DR, PO as above, thus leading to RCC-5. To get more relations, as in RCC-8 (where the eight relations are DC, EC, TPP, $TPP^{-1}$, PO, EQ, NTPP, $NTPP^{-1}$, where $^{-1}$ denotes the inverse relation), in Definition 8 the predicate C is involved. Here we propose another set of definitions, based on an extensive dilation $\delta$ (defined abstractly here, without referring to points of the underlying space). These links between RCC relations and mathematical morphology have been suggested in [7] in the crisp case (on classical sets).

Definition 9

Given a parthood predicate P (supposed to be reflexive) and an extensive dilation $\delta$, the relations O, PP, EQ, DR, PO are defined as in Definition 8 and the other ones as follows:

• $DC(A,B) = \bigwedge (DR(A,B), DR(A, \delta (B))) = \bigwedge (DR(A,B), DR(\delta (A), B))$;

• $EC(A,B) = \bigwedge (DR(A,B),O(A, \delta (B))) = \bigwedge (DR(A,B), O(\delta (A), B))$;

• $TPP(A,B) = \bigwedge (PP(A,B), O(\delta (A), N(B)))$;

• $NTPP(A,B) = \bigwedge (P(A,B), P(\delta (A), B)) = P(\delta (A), B)$.

These definitions are simple to implement and provide very concise expressions.

Properties. For crisp and fuzzy sets, the proposed definitions reduce to the existing ones [19, 22], which is a desired consistency. Moreover, the following properties hold.

Proposition 4

The relations in Definitions 8 and 9 have the following properties:

• The relations O, DC, EQ, DR, PO, EC are symmetrical;

• P (in Definition 8), O, EQ are reflexive;

• $TPP \preceq PP$, $NTPP \preceq PP$, $PP \preceq P$, $EQ \preceq P$, $PO \preceq O$, $P \preceq O$, $EC \preceq DR$, $DC \preceq DR$, and for Definition 8 $O \preceq C$ and $EC \preceq C$;

• $D_W(DC, C) = D_W(DR, C) = 1_{\mathcal L}$ (for Definition 8), and $D_W(DR,O)$;

• if C is increasing in both arguments, then P is decreasing in the first argument and increasing in the second one (for Definition 8), and if it is supposed to have these monotony properties in Definition 9, then O is increasing, DC and DR are decreasing, NTPP and PP are decreasing in the first argument and increasing in the second one.

Interpretations in Concrete Domains. In Definitions 8 and 9, the relations are abstract and do not make any reference to elements of ${\mathcal S}$ (points). Reasoning can then be performed on any bipolar (spatial) entities. Now, if we move to the concrete domain ${\mathcal S}$, which is often necessary for practical applications, then, we can assign to each abstract bipolar fuzzy set an interpretation in ${\mathcal S}$. Interpretations of the RCC relations then require concrete definitions of C, or P and $\delta$. This can be achieved in different ways: (i) C can be defined as a degree of intersection (Definition 4) and then $O = C$; (ii) can be defined as a closeness relations (as in [21] for the fuzzy case), for instance from a dilation and a degree of intersection; (iii) P can be defined as an inclusion relation (Definition 3) and $\delta$ as a dilation with a given structuring element (Definition 6). Note that the morphological definition of EC is then exactly the proposed definition for adjacency in Sect. 5.

7 Conclusion

In this paper, we proposed original definitions of algebraic relations (intersection, inclusion, adjacency and RCC relations) between bipolar fuzzy sets, using mathematical morphology operators, in particular dilation. This problem had never been addressed before, and could be useful in spatial reasoning, but also in other domains, such as preference modeling, where preferences can be considered as bipolar fuzzy sets. Future work aims at exploring such applications, with concrete examples. Other aspects will be investigated as well, such as links with existing works on objects with imprecise, indeterminate or broad boundaries [9, 10, 17, 20] (although our approach is not restricted to such objects). Another interesting direction concerns composition tables and reasoning, extending the work in the crisp and fuzzy cases [19, 23]. Finally, other types of spatial relations can be addressed, such as directional relations.