Abstract
In ASIACRYPT 2016, Bellare, Fuchsbauer and Scafuro studied security of non-interactive zero-knowledge (NIZK) arguments in the face of parameter subversion. They showed that achieving subversion soundness (soundness without trusting to the third party) and standard zero-knowledge is impossible at the same time. On the positive side, in the best case, they showed that one can achieve subversion zero-knowledge (zero-knowledge without trusting to the third party) and soundness at the same time. In this paper, we show that one can amplify their best positive result and construct NIZK arguments that can achieve subversion zero-knowledge and simulation (knowledge) soundness at the same time. Simulation (knowledge) soundness is a stronger notion in comparison with (knowledge) soundness, as it also guarantees non-malleability of proofs. Such stronger security guarantee is a must in practical systems. To prove the result, we show that given a NIZK argument that achieves Sub-ZK and (knowledge) soundness, one can use an OR-based construction to define a new language and build a NIZK argument that will guarantee Sub-ZK and simulation (knowledge) soundness at the same time. We instantiate the construction with the state-of-the-art zk-SNARK proposed by Groth [Eurocrypt 2016] and obtain an efficient SNARK that guarantees Sub-ZK and simulation knowledge soundness.
Access provided by Autonomous University of Puebla. Download conference paper PDF
Similar content being viewed by others
Keywords
1 Introduction
Non-Interactive Zero-Knowledge (NIZK) proofs are one of the central design tools in cryptographically secure systems, allowing one to verify the veracity of statements without leaking extra information. Technically speaking, a NIZK allows a prover to prove that, for a public statement \(\mathsf {x}\) she knows a witness \(\mathsf {w}\) which hold in a relation \(\mathbf {R}\), \((\mathsf {x}, \mathsf {w}) \in \mathbf {R}\), without leaking any information about her witness \(\mathsf {w}\). In the Common Reference String (CRS) model [BFM88], a NIZK requires a setup phase which is supposed to be done by a trusted third party. Under a trusted setup phase, usually a NIZK is required to guarantee three essential properties known as completeness, zero-knowledge and soundness. The property completeness guarantees that a honest prover always convinces a honest verifier. The soundness ensures that a malicious prover cannot convince the honest verifier except with negligible probability. Zero-knowledge property assures that the proof generated by prover does not leak any information about the witness \(\mathsf {w}\). Moreover, following some stronger requirements in practical systems, there have been various constructions for NIZKs that can achieve more stronger notions than bare soundness. The notions knowledge soundness and simulation knowledge soundness (a.k.a.simulation extractability) are two flavours of soundness that guarantee more security than what soundness achieves. Knowledge-soundness guarantees that if an adversarial prover manages to come out with an acceptable proof, there exists an efficient extractor which given some secret information can efficiently extract the witness from the proof. Zero-knowledge Succinct Non-interactive Arguments of Knowledge (zk-SNARKs) [Gro10, Lip12, PHGR13, BCTV13, Gro16, GM17, Lip19] are the most known and practically-interested NIZK arguments that guarantee knowledge soundness. By the date, the most efficient zk-SNARK is proposed by Groth [Gro16] in Eurocrypt 2016, which is constructed for Quadratic Arithmetic Programs (QAPs) and works in a biliner group. As an stronger notion, simulation knowledge soundness guarantees that knowledge-soundness is satisfied even if adversary already has seen arbitrary number of simulated proofs for any statements. Roughly speaking, simulation extractability guarantees that the proofs are also non-malleable and consequently secure against man-in-the-middle attacks. In Crypto 2017, Groth and Maller [GM17] proposed the first zk-SNARK in the CRS model for Square Arithmetic Programs (SAPs) that achieves (non-black-box) simulation extractability. Recently, Atapoor and Baghery [AB19] used a folklore OR technique [BG90] with a particular instantiation from C\(\emptyset \)C\(\emptyset \) framework [KZM+15]Footnote 1 and presented a variation of the state-of-the-art zk-SNARK proposed by Groth [Gro16] and showed that it can achieve (non-black-box) simulation extractability and outperforms Groth and Maller’s zk-SNARK [GM17] considerably [AB19]. Concurrently, Lipmaa [Lip19] proposed several (non-black-box) simulation-extractable zk-SNARKs in the CRS model for different languages including QAPs, SAPs, Quadratic Span Programs (QSPs) and Square Span Programs (SSPs). By deploying zk-SNARKs in some bigger cryptographic systems that should guarantee universal composability (UC), some studies construct zk-SNARKs with black-box simulation extractability [KZM+15, Bag19a] which is a necessary requirement for using zk-SNARKs in the UC-secure protocols.
Importance of Setup Phase in the CRS Model. By deploying cryptographic primitives in various applications, recently there have been various attacks or flaw reports on the setup phase of cryptographic systems that rely on public parameters supposed to be generated honestly. In some cases, attacks are caused from maliciously (or incorrectly) generated public parameters or modifying cryptographic protocol specifications to embed backdoors, with intent to violate security of the main system [BBG+13, PLS13, Gre14, Gab19, LPT19, Hae19]. Specially, after the Snowden revelations, there have been various endeavours in constructing cryptographic primitives and protocols secure against active subversion. The primitives constructed in this setting, guarantee their pre-defined security with trusted parameters, even in the case that the public parameters are subverted. Initiated by Bellare et al. [BPR14] for symmetric encryption schemes, there have been various studies about subversion resistant of various cryptograph ic primitives, including signature schemes [AMV15], non-interactive zero-knowledge proofs [BFS16], public-key encryption schemes [ABK18] and commitment schemes [Bag19b].
Subversion Security in NIZK Arguments. In the context of NIZKs, in [BFS16], Bellare, Fuchsbauer and Scafuro tackled the discussed problem by studying how much security one can still achieve when the CRS generator cannot be trusted. They first defined three new notions called subversion witness indistinguishability (Sub-WI), subversion zero-knowledge (Sub-ZK) and subversion soundness (Sub-SND) as a variant of the standard notions witness indistinguishability (WI), zero-knowledge (ZK) and soundness (SND) in NIZK arguments. The main difference of proposed notions with the standard ones is that in the new ones the setup phase is compromised and the parameters can be generated maliciously. For instance, the notion Sub-ZK guarantees that even if an adversary generates the CRS elements, still the NIZK proof does not leak any information about the witness of the prover. Intuitively, Sub-ZK implies that the ZK is guaranteed even if an adversary generates the CRS. In the rest, Bellare et al. showed that the definitions of Sub-SND and ZK are not compatible; as the former requires that a prover should not be able to generate a fake proof even if he generates the CRS, but the later implies that there exists a simulation algorithm that given trapdoors of CRS can generate a (fake) simulated proof indistinguishable from the real ones. This resulted a negative result that we cannot construct a NIZK argument which will guarantee ZK and Sub-SND simultaneously.
The above negative result opened two possible directions for positive results on subversion-resistant proof systems. One direction was achieving Sub-ZK and a version of soundness (i.e. one of notions soundness, knowledge soundness or simulation knowledge soundness) and the second direction was achieving Sub-WI (the best notion weaker than ZK) and a notion of Sub-SND (one of notions subversion soundness, subversion knowledge soundness or subversion simulation knowledge soundness). Along the first direction, Bellare et al. showed that one can construct NIZK arguments which achieve Sub-ZK and SND at the same time [BFS16]. Their main idea to achieve Sub-ZK is to use a knowledge assumption in the proof of zero-knowledge to extract the trapdoors of CRS from untrusted CRS and then use them to simulate the argument. After this positive result, Abdolmaleki et al. [ABLZ17] showed that the state-of-the-art zk-SNARK [Gro16] can achieve Sub-ZK and knowledge soundness with minimal changes in the CRS and executing an efficient public algorithm to check the well-formedness of CRS elements. In a concurrent work, Fuchsbauer [Fuc18] showed that most of paring-based zk-SNARKs including Groth’s scheme can achieve Sub-ZK and knowledge soundness simultaneously. In the same direction, Abdolmaleki et al. [ALSZ18] showed that one can achieve Sub-ZK and SND in the Quasi-Adaptive NIZK arguments which are a particular type of NIZK proof systems.
In the second direction of possible positive results, Bellare et al. [BFS16] showed that Zap schemes proposed by Groth, Ostrovsky and Sahai [GOS06] achieves Sub-WI and Sub-SND at the same time; as such proof systems do not require particular CRS (consequently they do not require a tru-sted setup phase) but provides weaker security guarantee than ZK. Recently, Fuchsbauer and Orru [FO18] showed that one can achieve even more in this direction, by presenting a Sub-WI and knowledge sound Zap scheme.
Problem Statement. By considering the summarized subversion-resistant constructions, one may ask if we can construct NIZK arguments with more stronger security guarantees in the face of subverted CRS. For instance, can we construct NIZK arguments that can guarantee Sub-ZK and simulation knowledge soundness at the same time, such that the prover will not trust a third party to achieve ZK and the verifier will obtain more security guarantee (more precisely non-malleable proofs) than knowledge soundness. In comparison with non-subversion-resistant simulation-extractable zk-SNARKs, our target constructions can eliminate the trust on CRS generators from prover side.
Our Contribution. We answer the question discussed above positively by constructing NIZK arguments that can achieve Sub-ZK and simulation knowledge soundness at the same time. Such construction guarantees that the prover does not need to trust a third party to achieve ZK, on the other side, extra from knowledge soundness verifier will get sure that the proofs are non-malleable. To construct such NIZK arguments, inspired by a folklore OR technique [BG90], we use a part of the C\(\emptyset \)C\(\emptyset \) framework [BG90, DDO+01, KZM+15] that recently is also used by Atapoor and Baghery [AB19] to achieve simulation (knowledge) soundness in Gorth’s zk-SNARK [Gro16]. We show that using such construction, given NIZK arguments that guarantees Sub-ZK and (knowledge) soundness, we can construct Sub-ZK and simulation (knowledge) sound NIZK arguments.
As an instantiation, we show that a recent variation of Groth’s zk-SNARK proposed by Atapoor and Baghery [AB19] can achieve Sub-ZK with minimal extra computational cost. The cost is that similar to NIZK arguments that achieve Sub-ZK and (knowledge) soundness [ABLZ17, Fuc18], the prover only needs to execute an efficient algorithm (CRS verification) to check the well-formedness of CRS elements before using them. If CRS verification passed, the protocol ensures that the generated proof does not leak any information about the witnesses even if CRS generators collude with the verifier. This allows prover to achieve ZK without trusting to the CRS generators.
Table 1 summarizes current subversion-resistant constructions and compares with an instantiation of our result. First row shows the negative result that achieving Sub-SND and ZK at the same time is impossible as their definitions are incompatible [BFS16]. Next rows indicate the notions achieved in various presented non-interactive proof systems [ABLZ17, Fuc18, FO18, ALSZ18].
Our Technique. In the proposed construction, we use a part of the C\(\emptyset \)C\(\emptyset \) framework and show that this part can be used to construct non-interactive arguments that will satisfies Sub-ZK and (non-black-box) simulation (knowledge) soundness. We define a new language \(\mathbf {L}'\) based on an OR construction (that is added to achieve non-malleability) and the original language \(\mathbf {L}\) in the input non-interactive argument that guarantees Sub-ZK. Then we use the basic property of an OR construction, i.e. that OR proofs can be simulated using the trapdoors of one branch. We show that if the input NIZK argument achieves Sub-ZK, then the lifted non-interactive argument also guarantees Sub-ZK. As in the notion of Sub-ZK the prover does not trust to the CRS generators and consequently the simulator does not trust to the simulation trapdoors, so in proof of Sub-ZK, different form C\(\emptyset \)C\(\emptyset \) framework, we use a technique in subversion-resistant schemes and simulate the protocol. In this road, a key point is that the proofs for an OR-based language can be simulated by trapdoors of either first or second branch. Next, as an instantiation, we use the above result and show that since the state-of-the-art zk-SNARK proposed by Groth [Gro16] achieves Sub-ZK after some verifications on CRS elements [ABLZ17, Fuc18], its recent variation proposed in [AB19] (which uses the same OR construction) can achieve Sub-ZK after some efficient verifications on CRS elements.
Rest of the paper is organized as follows; Sect. 2 introduces notations and necessary preliminaries for the paper. The proposed transformation for constructing subversion-resistant simulation (knowledge) sound NIZK arguments is described in Sect. 3. In Sect. 4, we show that recent variation of Groth’s zk-SNARK [Gro16] proposed by Atapoor and Baghery [AB19] can achieve Sub-ZK and simulation knowledge soundness with minimal extra computational cost. Finally, we conclude the paper in Sect. 5.
2 Preliminaries
Let PPT denote probabilistic polynomial-time. Let  be the information-theoretic security parameter, say
be the information-theoretic security parameter, say  . All adversaries will be stateful. For an algorithm
. All adversaries will be stateful. For an algorithm  , let
, let  be the image of
be the image of  , i.e. the set of valid outputs of
, i.e. the set of valid outputs of  , let
, let  denote the random tape of
denote the random tape of  , and let
, and let  denote sampling of a randomizer r of sufficient length for
denote sampling of a randomizer r of sufficient length for  ’s needs. By
’s needs. By  we denote the fact that
we denote the fact that  , given an input x and a randomizer r, outputs y. For algorithms
, given an input x and a randomizer r, outputs y. For algorithms  and
and  , we write
, we write  as a shorthand for “
as a shorthand for “ ,
,  ”. We denote by
”. We denote by  an arbitrary negligible function. For distributions A and B, \(A \approx _c B\) means that they are computationally indistinguishable. In pairing-based groups, we use additive notation together with the bracket notation, i.e., in group \(\mathbb {G}_{\mu }\), \(\left[ a\right] _{\mu } = a \left[ 1\right] _{\mu }\), where \(\left[ 1\right] _{\mu }\) is a fixed generator of \(\mathbb {G}_{\mu }\). A bilinear group generator
an arbitrary negligible function. For distributions A and B, \(A \approx _c B\) means that they are computationally indistinguishable. In pairing-based groups, we use additive notation together with the bracket notation, i.e., in group \(\mathbb {G}_{\mu }\), \(\left[ a\right] _{\mu } = a \left[ 1\right] _{\mu }\), where \(\left[ 1\right] _{\mu }\) is a fixed generator of \(\mathbb {G}_{\mu }\). A bilinear group generator  returns \((p, \mathbb {G}_1, \mathbb {G}_2, \mathbb {G}_T, \hat{e}, \left[ 1\right] _{1}, \left[ 1\right] _{2})\), where \(p\) (a large prime) is the order of cyclic abelian groups \(\mathbb {G}_1\), \(\mathbb {G}_2\), and \(\mathbb {G}_T\). Finally, \(\hat{e} : \mathbb {G}_1 \times \mathbb {G}_2 \rightarrow \mathbb {G}_T\) is an efficient non-degenerate bilinear pairing, s.t. \(\hat{e} (\left[ a\right] _{1}, \left[ b\right] _{2}) = \left[ a b\right] _{T}\). Denote \(\left[ a\right] _{1} \bullet \left[ b\right] _{2} = \hat{e}(\left[ a\right] _{1}, \left[ b\right] _{2})\).
returns \((p, \mathbb {G}_1, \mathbb {G}_2, \mathbb {G}_T, \hat{e}, \left[ 1\right] _{1}, \left[ 1\right] _{2})\), where \(p\) (a large prime) is the order of cyclic abelian groups \(\mathbb {G}_1\), \(\mathbb {G}_2\), and \(\mathbb {G}_T\). Finally, \(\hat{e} : \mathbb {G}_1 \times \mathbb {G}_2 \rightarrow \mathbb {G}_T\) is an efficient non-degenerate bilinear pairing, s.t. \(\hat{e} (\left[ a\right] _{1}, \left[ b\right] _{2}) = \left[ a b\right] _{T}\). Denote \(\left[ a\right] _{1} \bullet \left[ b\right] _{2} = \hat{e}(\left[ a\right] _{1}, \left[ b\right] _{2})\).
Next we review QAPs that defines NP-complete language specified by a quadratic equation over polynomials and have reduction from the language Circuit-SAT [GGPR13, Gro16].
Quadratic Arithmetic Programs. QAP was introduced by Gennaro et al. [GGPR13] as a language where for an input \(\mathsf {x}\) and witness \(\mathsf {w}\), \((\mathsf {x}, \mathsf {w}) \in \mathbf {R}\) can be verified by using a parallel quadratic check. Consequently, any efficient simulation-extractable zk-SNARK for QAP results in an efficient simulation-extractable zk-SNARK for Circuit-SAT.
An QAP instance \(\mathcal {Q}_p\) is specified by the so defined \((\mathbb {Z}_p, m_0, \ell , \{u_j, v_j, w_j\}_{j = 0}^m)\), where \(m_0\) is the length of the statement (e.g. public inputs and outputs in an arithmetic circuit), \(\ell \) is a target polynomial (defined based on the number of constraints, e.g. number of multiplication gates in an arithmetic circuit), and \(u_j, v_j, w_j\) are three set of polynomials that encodes the wires in the target arithmetic circuit. More discussions about encoding an arithmetic circuit to an QAP instance can be found in [GGPR13]. A QAP instance \(\mathcal {Q}_p\) defines the following relation, where we assume that \(A_0 = 1\):

Alternatively, \((\mathsf {x}, \mathsf {w}) \in \mathbf {R}\) if there exists a (degree \(\le n - 2\)) polynomial \(h(X)\), s.t.
where \(\ell (X) = \prod _{i = 1}^\mathsf {n}(X - \omega ^{i - 1}) \) is a polynomial related to Lagrange interpolation, and \(\omega \) is an \(\mathsf {n}\)-th primitive root of unity modulo p.
Roughly speaking, the goal of the prover of a zk-SNARK for QAP [GGPR13] is to prove that for public \((A_1, \dots , A_{m_0})\) and \(A_0 = 1\), she knows \((A_{m_0+ 1}, \dots , A_m)\) and a degree \(\le n - 2\) polynomial \(h(X)\), such that above equation holds.
2.1 Definitions
We use the definitions of subversion secure and standard NIZK arguments from [ABLZ17, Gro16, GM17]. Let \(\mathcal {R}\) be a relation generator, such that  returns a polynomial-time decidable binary relation \(\mathbf {R}= \{(\mathsf {x}, \mathsf {w})\}\). Here, \(\mathsf {x}\) is the statement and \(\mathsf {w}\) is the witness. Security parameter
returns a polynomial-time decidable binary relation \(\mathbf {R}= \{(\mathsf {x}, \mathsf {w})\}\). Here, \(\mathsf {x}\) is the statement and \(\mathsf {w}\) is the witness. Security parameter  can be deduced from the description of \(\mathbf {R}\). The relation generator also outputs auxiliary information \(\xi \) that will be given to the honest parties and the adversary. As in [Gro16, ABLZ17], \(\xi \) is the value returned by
can be deduced from the description of \(\mathbf {R}\). The relation generator also outputs auxiliary information \(\xi \) that will be given to the honest parties and the adversary. As in [Gro16, ABLZ17], \(\xi \) is the value returned by  , so \(\xi \) is given as an input to the honest parties; if needed, one can include an additional auxiliary input to the adversary. Let \(\mathbf {L}_{\mathbf {R}} = \{\mathsf {x}: \exists \mathsf {w}, (\mathsf {x}, \mathsf {w}) \in \mathbf {R}\}\) be an NP-language. A (subversion-resistant) NIZK argument system \(\varPsi \) for \(\mathcal {R}\) consists a tuple of PPT algorithms
, so \(\xi \) is given as an input to the honest parties; if needed, one can include an additional auxiliary input to the adversary. Let \(\mathbf {L}_{\mathbf {R}} = \{\mathsf {x}: \exists \mathsf {w}, (\mathsf {x}, \mathsf {w}) \in \mathbf {R}\}\) be an NP-language. A (subversion-resistant) NIZK argument system \(\varPsi \) for \(\mathcal {R}\) consists a tuple of PPT algorithms  , such that:
, such that:
CRS Generator: \(\mathsf {K}\) is a PPT algorithm that, given \((\mathbf {R}, \xi )\) where  , outputs
, outputs  and stores trapdoors of \({\mathbf {\mathsf {crs} }}\) as \(\mathbf {\mathsf {ts}}\). We distinguish
and stores trapdoors of \({\mathbf {\mathsf {crs} }}\) as \(\mathbf {\mathsf {ts}}\). We distinguish  (needed by the prover) from
(needed by the prover) from  (needed by the verifier).
(needed by the verifier).
CRS Verifier: \(\mathsf {CV}\) is a PPT algorithm that, given \((\mathbf {R}, \xi , {\mathbf {\mathsf {crs} }})\), returns either 0 (the CRS is incorrectly formed) or 1 (the CRS is correctly formed).
Prover:  is a PPT algorithm that, given
is a PPT algorithm that, given  for \(\mathsf {CV}(\mathbf {R}, \xi , {\mathbf {\mathsf {crs} }})=1\) and \((\mathsf {x}, \mathsf {w}) \in \mathbf {R}\), outputs an argument \(\pi \). Otherwise, it outputs \(\bot \).
for \(\mathsf {CV}(\mathbf {R}, \xi , {\mathbf {\mathsf {crs} }})=1\) and \((\mathsf {x}, \mathsf {w}) \in \mathbf {R}\), outputs an argument \(\pi \). Otherwise, it outputs \(\bot \).
Verifier:  is a PPT algorithm that, given
is a PPT algorithm that, given  , returns either 0 (reject) or 1 (accept).
, returns either 0 (reject) or 1 (accept).
Simulator:  is a PPT algorithm that, given \((\mathbf {R}, \xi , {\mathbf {\mathsf {crs} }}, \mathsf {x}, \mathbf {\mathsf {ts}})\), outputs a simulated argument \(\pi \).
is a PPT algorithm that, given \((\mathbf {R}, \xi , {\mathbf {\mathsf {crs} }}, \mathsf {x}, \mathbf {\mathsf {ts}})\), outputs a simulated argument \(\pi \).
Strictly speaking, a zk-SNARK system is required to be complete, (computationally) knowledge-sound, (statistically) ZK, and succinct as in the following definitions.
Definition 1
(Perfect Completeness). A non-interactive argument \(\varPsi \) is perfectly complete for \(\mathcal {R}\), if for all  , all
, all  , and \((\mathsf {x}, \mathsf {w}) \in \mathbf {R}\),
, and \((\mathsf {x}, \mathsf {w}) \in \mathbf {R}\), 
Definition 2
(Computationally Knowledge-Soundness [Gro16]). A non-interactive argument \(\varPsi \) is computationally (adaptively) knowledge-sound for \(\mathcal {R}\), if for every PPT  , there exists a PPT extractor
, there exists a PPT extractor  , s.t. for all
, s.t. for all  ,
,

Here, \(\xi \) can be seen as a common auxiliary input to  and
and  that is generated by using a benign [BCPR14] relation generator.
that is generated by using a benign [BCPR14] relation generator.
Definition 3
(Statistically Zero-Knowledge (ZK) [Gro16]). A non-interactive argument \(\varPsi \) is statistically ZK for \(\mathcal {R}\), if for all  , all
, all  , and for all PPT
, and for all PPT  ,
,  , where
, where

Here, the oracle \(\mathsf {O}_0 (\mathsf {x}, \mathsf {w})\) returns \(\bot \) (reject) if \((\mathsf {x}, \mathsf {w}) \not \in \mathbf {R}\), and otherwise it returns  . Similarly, \(\mathsf {O}_1 (\mathsf {x}, \mathsf {w})\) returns \(\bot \) (reject) if \((\mathsf {x}, \mathsf {w}) \not \in \mathbf {R}\), otherwise it returns
. Similarly, \(\mathsf {O}_1 (\mathsf {x}, \mathsf {w})\) returns \(\bot \) (reject) if \((\mathsf {x}, \mathsf {w}) \not \in \mathbf {R}\), otherwise it returns  . \(\varPsi \) is perfect ZK for \(\mathcal {R}\) if one requires that \(\varepsilon _0 = \varepsilon _1\).
. \(\varPsi \) is perfect ZK for \(\mathcal {R}\) if one requires that \(\varepsilon _0 = \varepsilon _1\).
Definition 4
(Succinctness [GM17]). A non-interactive argument \(\varPsi \) is succinct if the proof size is polynominal in  and the verifier’s computation time is polynominal in security parameter
and the verifier’s computation time is polynominal in security parameter  and the size of instance \(\mathsf {x}\).
and the size of instance \(\mathsf {x}\).
In the rest, we recall the definition of (non-black-box) (or simulation knowledge soundness) and Sub-ZK [ABLZ17] that we aim to achieve in new constructions.
Definition 5
((Non-Black-Box) Simulation Extractability [GM17]). A non-interactive argument \(\varPsi \) is (non-black-box) simulation-extractable for \(\mathcal {R}\), if for any PPT  , there exists a PPT extractor
, there exists a PPT extractor  s.t. for all
s.t. for all  ,
,

Here, Q is the set of \((\mathsf {x}, \pi )\)-pairs generated by the adversary’s queries to \(\mathsf {O}(.)\). Note that (non-black-box) simulation extractability implies knowledge-soundness (given in Definition 2), as the former additionally allows the adversary to send query to the proof simulation oracle.
Definition 6
(Statistically Subversion Zero-Knowledge [ABLZ17]). A non-interactive argument \(\varPsi \) is statistically Sub-ZK for \(\mathcal {R}\), if for any PPT subverter \(\mathsf {X}\) there exists a PPT extractor \(\mathsf {ext}_\mathsf {X}\), such that for all  , all
, all  , and for all PPT
, and for all PPT  ,
,  , where
, where

Here, \(\xi _{\mathsf {X}}\) is auxiliary information generated by subverter \(\mathsf {X}\), and the oracle \(\mathsf {O}_0 (\mathsf {x}, \mathsf {w})\) returns \(\bot \) (reject) if \((\mathsf {x}, \mathsf {w}) \not \in \mathbf {R}\), and otherwise it returns  . Similarly, \(\mathsf {O}_1 (\mathsf {x}, \mathsf {w})\) returns \(\bot \) (reject) if \((\mathsf {x}, \mathsf {w}) \not \in \mathbf {R}\), and otherwise it returns
. Similarly, \(\mathsf {O}_1 (\mathsf {x}, \mathsf {w})\) returns \(\bot \) (reject) if \((\mathsf {x}, \mathsf {w}) \not \in \mathbf {R}\), and otherwise it returns  . \(\varPsi \) is perfectly Sub-ZK for \(\mathcal {R}\) if one requires that \(\varepsilon _0 = \varepsilon _1\).
. \(\varPsi \) is perfectly Sub-ZK for \(\mathcal {R}\) if one requires that \(\varepsilon _0 = \varepsilon _1\).
3 Subversion-Resistant Simulation-Extractable NIZKs
As we discussed in the introduction, currently we have NIZK constructions that can achieve Sub-ZK (defined in Definition 6) and knowledge soundness (defined in Definition 2) at the same time [ABLZ17, Fuc18], which means prover achieves ZK without trusting to a third party and verifier achieves knowledge soundness but with trusting to the CRS generator. On the other hand, currently there are simulation knowledge sound (defined in Definition 5) NIZK arguments [GM17, Lip19, AB19] but none of them are known to achieve Sub-ZK, which means both prover and verifier needs to trust the CRS generators.
In this section, we aim to construct NIZK arguments that similar to NIZKs studied in [ABLZ17, Fuc18], the prover does not need to trust CRS generators to achieve ZK, but the protocol will guarantee simulation knowledge soundness, as in simulation-extractable zk-SNARKs [GM17, Lip19]. Recently, the scheme proposed in [Lip19] also was updated to achieve Sub-ZK. However, in the rest, we will observe that our proposed construction can be instantiated with any of current subversion-resistant NIZKs which basically allows to use it as a framework to achieve simulation (knowledge) soundness in all NIZKs that guarantee Sub-ZK and (knowledge) soundness. Subversion ZK in new constructions guarantees that even an adversary generates the CRS, still it cannot break the ZK of protocol. To mitigate the level of trust or to improve security in the setup phase even more, particularly for verifier, one can use Multi-Party Computation (MPC) protocols for CRS generation [BCG+15, ABL+19].
3.1 Construction
In this section, we presented the proposed construction which can act as a compiler that transforms Sub-ZK and (knowledge) sound NIZKs into ones that satisfy Sub-ZK and simulation (knowledge) soundness. We use a folklore OR technique with a particular instantiation proposed in [KZM+15, AB19]. Indeed, the proposed OR compiler can be viewed as using the Bellare-Goldwasser paradigm [BG90], which is proposed to construct signatures from NIZK arguments, in a non-black-box way.
Consider a subversion-resistant NIZK argument \(\varPsi \) for \(\mathcal {R}_{\mathbf {L}}\) which consists of PPT algorithms  and guarantees Sub-ZK and (knowledge) soundness. Let
and guarantees Sub-ZK and (knowledge) soundness. Let  be a one-time secure signature scheme and \((\mathsf {Com}, \mathsf {ComVerify})\) be a perfectly binding commitment scheme. Using a variation of a construction proposed by Bellare-Goldwasser [BG90] (used in [KZM+15, AB19], given the language \(\mathbf {L}\) with the corresponding NP relation \(\mathbf {R}_{\mathbf {L}}\), we define a new language \({\mathbf {L}'}\) such that \(((\mathsf {x}, \mu , pk_{\mathsf {Sign}}, \rho ), (\mathsf {w}, s, r)) \in \mathbf {R}_{\mathbf {L}'}\) iff:
be a one-time secure signature scheme and \((\mathsf {Com}, \mathsf {ComVerify})\) be a perfectly binding commitment scheme. Using a variation of a construction proposed by Bellare-Goldwasser [BG90] (used in [KZM+15, AB19], given the language \(\mathbf {L}\) with the corresponding NP relation \(\mathbf {R}_{\mathbf {L}}\), we define a new language \({\mathbf {L}'}\) such that \(((\mathsf {x}, \mu , pk_{\mathsf {Sign}}, \rho ), (\mathsf {w}, s, r)) \in \mathbf {R}_{\mathbf {L}'}\) iff:
where  is a pseudo-random function family. Due to OR-based construction of new language \({\mathbf {L}'}\), a user to be able to generate an acceptable proof will require either the witness \(\mathsf {w}\) or the trapdoors of CRS, and since it is assumed that the CRS trapdoors are kept secret, so soundness is guaranteed as long as CRS trapdoors are secret. We note that due to using the pseudo-random function \(f_s\) with a random secret trapdoor s, the output of \(f_s\) is indistinguishable from the outputs of a truly random function. By considering new language, the subversion-resistant NIZK argument \(\varPsi \) for the relation \(\mathbf {R}_{\mathbf {L}}\) with PPT algorithms
is a pseudo-random function family. Due to OR-based construction of new language \({\mathbf {L}'}\), a user to be able to generate an acceptable proof will require either the witness \(\mathsf {w}\) or the trapdoors of CRS, and since it is assumed that the CRS trapdoors are kept secret, so soundness is guaranteed as long as CRS trapdoors are secret. We note that due to using the pseudo-random function \(f_s\) with a random secret trapdoor s, the output of \(f_s\) is indistinguishable from the outputs of a truly random function. By considering new language, the subversion-resistant NIZK argument \(\varPsi \) for the relation \(\mathbf {R}_{\mathbf {L}}\) with PPT algorithms  that achieves Sub-ZK and (knowledge) soundness, can be lifted to a subversion-resistant NIZK \(\varPsi '\) with PPT algorithms
that achieves Sub-ZK and (knowledge) soundness, can be lifted to a subversion-resistant NIZK \(\varPsi '\) with PPT algorithms  that guarantees Sub-ZK and simulation (knowledge) soundness. Based on the language \(\mathbf {L}'\), the construction of NIZK \(\varPsi '\) and the corresponding algorithms are described in Fig. 1.
that guarantees Sub-ZK and simulation (knowledge) soundness. Based on the language \(\mathbf {L}'\), the construction of NIZK \(\varPsi '\) and the corresponding algorithms are described in Fig. 1.
Recently, Atapoor and Baghery [AB19] used the same construction to achieve simulation knowledge soundness in Groth’s zk-SNARK [Gro16] which led to the most efficient zk-SNARK which also guarantees non-malleability of proofs. Here, we show that such OR-based language can be extended and used to build subversion-resistant NIZK arguments which will also guarantee simulation (knowledge) soundness.
An extension of the proposed construction in [AB19] that outputs a Sub-ZK and simulation (knowledge) sound NIZK argument \(\varPsi '\). Note that in our construction, we assumed that the input NIZK \(\varPsi \) guarantees Sub-ZK and (knowledge) soundness. Due to this fact, we have a new algorithm \(\mathsf {CV}'\) to verify the well-formedness of CRS elements, and a new simulation procedure by  to simulate the proofs without trusting to the CRS generators.
to simulate the proofs without trusting to the CRS generators.
Recall that one of two main differences between a Sub-ZK NIZK argument and a common NIZK argument is the existence of a public CRS verification algorithm \(\mathsf {CV}\) in the former ones. Basically, given a CRS \({\mathbf {\mathsf {crs} }}\) the algorithm \(\mathsf {CV}\) verifies the well-formedness of its elements. Additionally, in simulation of a Sub-ZK NIZK argument there exists a (non-black-box) extractor \(\mathsf {ext}_\mathsf {X}\) that can extract the simulation trapdoors from a (possibly malicious) CRS generator \(\mathsf {X}\). More detailed discussions can be found in [BFS16, ABLZ17, Fuc18, ALSZ18].
So similar to other subversion-resistant NIZK arguments, as we aim to achieve Sub-ZK (not standard ZK) and simulation (knowledge) soundness in our constructions, so there are two key differences between new proposed constructions and the one presented in [AB19] (that are shown in  form in Fig. 1). The first key difference is that we have an extra algorithm \(\mathsf {CV}'\) which will be used by prover to check the well-formedness of CRS elements before using them. This is actually the cost that prover needs to pay insted of trusting to the CRS generators. The second key difference is that in new constructions, the simulator
form in Fig. 1). The first key difference is that we have an extra algorithm \(\mathsf {CV}'\) which will be used by prover to check the well-formedness of CRS elements before using them. This is actually the cost that prover needs to pay insted of trusting to the CRS generators. The second key difference is that in new constructions, the simulator  does not get simulation trapdoors directly, as the prover does not trust to the CRS generators in this setting. Instead, the simulator
does not get simulation trapdoors directly, as the prover does not trust to the CRS generators in this setting. Instead, the simulator  calls the extraction algorithm \(\mathsf {ext}_{\mathsf {X}}\) constructed for the input NIZK argument \(\varPsi \) and extracts simulation trapdoors \(\mathbf {\mathsf {ts}}\) of it, and then uses them for the rest of simulation.
calls the extraction algorithm \(\mathsf {ext}_{\mathsf {X}}\) constructed for the input NIZK argument \(\varPsi \) and extracts simulation trapdoors \(\mathbf {\mathsf {ts}}\) of it, and then uses them for the rest of simulation.
3.2 Efficiency
In the rest, by considering Fig. 1, we consider efficiency of new constructions for different important metrics in (subversion-resistant) NIZK arguments.
Setup Phase. The setup needs to be done for a new language \(\mathbf {L}'\). Roughly speaking, it means the setup phase of original NIZK \(\varPsi \) needs to be executed for a new arithmetic circuit that has slightly larger number of gates. Again with a particular instantiation [KMS+16, AB19], new changes will add around 52.000 multiplication gates to the QAP-based arithmetic circuits that encode \(\mathbf {L}\). The number of gates comes from the case that both commitment scheme and pseduo-random function used in construction are instantiated with a SHA512 hash function [KMS+16, AB19]. Implementations show that this will add a constant amount (e.g. 10 megabyte) to the size of original CRS, that for arithmetic circuits with large number of gates (that usually is the case in practical application) the overhead is negligible [AB19].
CRS Verification. In new construction, in order to verify the well-formedness of CRS elements one needs to execute \(\mathsf {CV}'\) algorithm which almost has the same efficiency as \(\mathsf {CV}\) algorithm in original NIZK argument \(\varPsi \). In practice, it is shown that running time of \(\mathsf {CV}\) can be less than running time of  [ABLZ17].
[ABLZ17].
Prover. In new schemes, prover needs to give a proof for the new language \(\mathbf {L}'\) and sign the proof with a one-time secure signature scheme. Empirical performances presented in [AB19] show that the overhead for a QAP-based zk-SNARK is very small in practical cases. For instance, in the fixed setting, for an arithmetic circuit that prover already needed 83 s to generate a proof, in new construction the proof generation took 90.1 s.
Proof Size. In new constructions the size of new proof \(\pi ' := (z_0, \pi , pk_{\mathsf {Sign}}, \sigma )\) will be equal to the size of original proof \(\pi \) plus the size of three elements \((z_0, pk_{\mathsf {Sign}}, \sigma )\). Similarly, with a particular instantiation for 128-bit security (e.g. the one in [AB19]), these three elements totally can add less than 128 bytes to the size of original proof \(\pi \).
Verifier. Extra from the verification of NIZK argument \(\varPsi \), the verifier of argument \(\varPsi '\) will verify the validity of a one-time secure signature. Similarly, for a particular instantiation [AB19], verification of the signature scheme adds 1 equation to the verification of original scheme that needs two parings and one exponentiation. They show that a proper instantiation can even give a verification faster than the verification of current simulation knowledge sound NIZKs arguments in the CRS model [GM17, Lip19].
3.3 Security Proofs
In this section, we show that the given a subversion-resistant NIZK argument that guarantees completeness, Sub-ZK, and (knowledge) soundness, the described construction in Sect. 3.1 results a NIZK argument that achieves completeness, Sub-ZK and simulation (knowledge) soundness.
Theorem 1 (Completeness)
If the NIZK argument \(\varPsi \) ensures completeness, Sub-ZK, and (knowledge) soundness, and the one-time signature scheme  is secure, then the proposed construction in Fig. 1 guarantees completeness.
is secure, then the proposed construction in Fig. 1 guarantees completeness.
Proof
By considering the completeness of NIZK argument \(\varPsi \) and the fact that \(\mathsf {SigVerify}(pk_{\mathsf {Sign}}, m, \mathsf {Sign}(m,sk_{\mathsf {Sign}}))=1\), we conclude that the output NIZK argument \(\varPsi '\) guarantees completeness. \(\square \)
Theorem 2 (Subversion Zero-Knowledge)
If the NIZK argument \(\varPsi \) guarantees completeness, Sub-ZK, and (knowledge) soundness, the pseudo-random function family is secure, and the one-time signature scheme is secure, then the proposed construction in Fig. 1 achieves Sub-ZK.
Before going through the proof, it is worth to mention that proving Sub-ZK of a subversion-resistant NIZK argument is a bit tricky than proving standard notion of ZK. The reason is that in the proof of standard ZK, CRS generator is trusted and the CRS trapdoors (simulation trapdoors) are honestly provided to the simulator  . But in proving Sub-ZK, since the prover does not trust to the CRS generator any more, consequently the simulator
. But in proving Sub-ZK, since the prover does not trust to the CRS generator any more, consequently the simulator  cannot trust to the provided trapdoors. To address this issue, the proposed solution [BFS16] is that the prover checks the well-formedness of CRS elements before using them and in simulating proofs, the simulator uses a non-black-box extraction procedure to extract the simulation trapdoors directly from the (possibly malicious) CRS generator and then uses them for the simulation [BFS16, ABLZ17, Fuc18, ALSZ18, Bag19b]. The non-black-box extraction usually is done using various knowledge assumptions [Dam92, BFS16]. For instance [ABLZ17] used Bilinear Diffie-Hellman Knowledge of Exponents (BDH-KE) assumptionFootnote 2 to prove Sub-ZK of Groth’s zk-SNARK [Gro16], while Fuchsbauer [Fuc18] did the same but with the Square Knowledge of Exponent (SKE) assumptionFootnote 3 which led to prove Sub-ZK of Groth’s zk-SNARK [Gro16] without modifying its CRS. But, intuitively in all cases one relies on the fact that if a (malicious) CRS generator manages to come out with some well-formed CRS elements, there exists a non-black-box extractor that given access to the source code and random coins of the (malicious) CRS generator, it can extract the simulation trapdoors. Once the simulation trapdoors are extracted, the simulator
cannot trust to the provided trapdoors. To address this issue, the proposed solution [BFS16] is that the prover checks the well-formedness of CRS elements before using them and in simulating proofs, the simulator uses a non-black-box extraction procedure to extract the simulation trapdoors directly from the (possibly malicious) CRS generator and then uses them for the simulation [BFS16, ABLZ17, Fuc18, ALSZ18, Bag19b]. The non-black-box extraction usually is done using various knowledge assumptions [Dam92, BFS16]. For instance [ABLZ17] used Bilinear Diffie-Hellman Knowledge of Exponents (BDH-KE) assumptionFootnote 2 to prove Sub-ZK of Groth’s zk-SNARK [Gro16], while Fuchsbauer [Fuc18] did the same but with the Square Knowledge of Exponent (SKE) assumptionFootnote 3 which led to prove Sub-ZK of Groth’s zk-SNARK [Gro16] without modifying its CRS. But, intuitively in all cases one relies on the fact that if a (malicious) CRS generator manages to come out with some well-formed CRS elements, there exists a non-black-box extractor that given access to the source code and random coins of the (malicious) CRS generator, it can extract the simulation trapdoors. Once the simulation trapdoors are extracted, the simulator  can simulate the proofs. It is worth to mention that the well-formedness of CRS elements are checked by a public efficient CRS verification algorithm known as \(\mathsf {CV}\). Using different knowledge-assumptions in proving Sub-ZK of particular NIZK arguments might lead to different \(\mathsf {CV}\) algorithms, as Abdolmaleki et al. [ABLZ17] and Fuchsbauer [Fuc18] proposed two different \(\mathsf {CV}\) algorithms for Groth’s zk-SNARK [Gro16].
can simulate the proofs. It is worth to mention that the well-formedness of CRS elements are checked by a public efficient CRS verification algorithm known as \(\mathsf {CV}\). Using different knowledge-assumptions in proving Sub-ZK of particular NIZK arguments might lead to different \(\mathsf {CV}\) algorithms, as Abdolmaleki et al. [ABLZ17] and Fuchsbauer [Fuc18] proposed two different \(\mathsf {CV}\) algorithms for Groth’s zk-SNARK [Gro16].
Proof
Sub-ZK in the input NIZK implies that there exists a simulation algorithm  which first uses extraction algorithm \(\mathsf {ext}_{\mathsf {X}}\) and extracts the simulation trapdoors from (malicious) CRS generator \(\mathsf {X}\) and then uses the extracted trapdoors to simulate the argument. We note that due to OR-based construction of new language \(\mathbf {L}'\), the proofs for new language can be simulated using either simulation trapdoors of NIZK argument \(\varPsi \) (first branch) or simulation trapdoors (s, r) of that are hidden in the committed value \(\rho := \mathsf {Com}(s, r)\) (second branch). Here for simulation we use simulation trapdoors of NIZK argument \(\varPsi \) which can be extracted by \(\mathsf {ext}_{\mathsf {X}}\). Now, consider the following experiences,
which first uses extraction algorithm \(\mathsf {ext}_{\mathsf {X}}\) and extracts the simulation trapdoors from (malicious) CRS generator \(\mathsf {X}\) and then uses the extracted trapdoors to simulate the argument. We note that due to OR-based construction of new language \(\mathbf {L}'\), the proofs for new language can be simulated using either simulation trapdoors of NIZK argument \(\varPsi \) (first branch) or simulation trapdoors (s, r) of that are hidden in the committed value \(\rho := \mathsf {Com}(s, r)\) (second branch). Here for simulation we use simulation trapdoors of NIZK argument \(\varPsi \) which can be extracted by \(\mathsf {ext}_{\mathsf {X}}\). Now, consider the following experiences,
 (simulator)
(simulator)
-
Setup: Sample
 ;
;  ; \(\rho :=Com(s, r)\); and output \({\mathbf {\mathsf {crs} }}':= ({\mathbf {\mathsf {crs} }}, \rho )\); where \(\mathbf {\mathsf {ts}}\) contains trapdoors of CRS \({\mathbf {\mathsf {crs} }}\) and (s, r) are hidden trapdoors of the committed value \(\rho \).
; \(\rho :=Com(s, r)\); and output \({\mathbf {\mathsf {crs} }}':= ({\mathbf {\mathsf {crs} }}, \rho )\); where \(\mathbf {\mathsf {ts}}\) contains trapdoors of CRS \({\mathbf {\mathsf {crs} }}\) and (s, r) are hidden trapdoors of the committed value \(\rho \). -
Define function \(\mathsf {O}(\mathsf {x},\mathsf {w})\): Abort \(\mathsf {if} \ (\mathsf {x}, \mathsf {w}) \not \in \mathbf {R}_{\mathbf {L}}\); call the extraction algorithm \(\mathsf {ext}_{\mathsf {X}}\) constructed in simulation of subversion-resistant NIZK \(\varPsi \) and extract simulation trapdoors \(\mathbf {\mathsf {ts}}\) of \(\varPsi \) from CRS generator \(\mathsf {X}\); generate
 sample
sample  ; generate
; generate  ; sign
; sign  ; return \(\pi ' := (z_0, \pi , pk_{\mathsf {Sign}}, \sigma )\).
; return \(\pi ' := (z_0, \pi , pk_{\mathsf {Sign}}, \sigma )\). -

 (prover)
(prover)
-
Setup: Sample \(({\mathbf {\mathsf {crs} }}\,\Vert \,\mathbf {\mathsf {ts}}) \leftarrow \mathsf {K}(\mathbf {R}_{\mathbf {L}'}, \xi )\);
 ; \(\rho := Com(s, r)\); and output \({\mathbf {\mathsf {crs} }}':= ({\mathbf {\mathsf {crs} }}, \rho )\); where \(\mathbf {\mathsf {ts}}\) contains trapdoors of CRS \({\mathbf {\mathsf {crs} }}\) and (s, r) are hidden trapdoors of the committed value \(\rho \).
; \(\rho := Com(s, r)\); and output \({\mathbf {\mathsf {crs} }}':= ({\mathbf {\mathsf {crs} }}, \rho )\); where \(\mathbf {\mathsf {ts}}\) contains trapdoors of CRS \({\mathbf {\mathsf {crs} }}\) and (s, r) are hidden trapdoors of the committed value \(\rho \). -
Define function \(\mathsf {O}(\mathsf {x},\mathsf {w})\): Abort \(\mathsf {if} \ (\mathsf {x}, \mathsf {w}) \not \in \mathbf {R}_{\mathbf {L}}\); generate
 sample
sample  ; generate
; generate  ; sign \(\sigma \leftarrow \mathsf {Sign}(sk_{\mathsf {Sign}}, (\mathsf {x}, z_0, \pi ))\); return \(\pi ' := (z_0, \pi , pk_{\mathsf {Sign}}, \sigma )\).
; sign \(\sigma \leftarrow \mathsf {Sign}(sk_{\mathsf {Sign}}, (\mathsf {x}, z_0, \pi ))\); return \(\pi ' := (z_0, \pi , pk_{\mathsf {Sign}}, \sigma )\). -

Lemma 1
If the NIZK argument \(\varPsi \) guarantees Sub-ZK, and the one-time signature scheme is secure, for two above experiments we have \(\Pr [\mathsf {EXP}_{1}^{zk}] \approx \Pr [\mathsf {EXP}_{2}^{zk}]\).
Proof
Two experiments \(\mathsf {EXP}_{2}^{zk}\) and \(\mathsf {EXP}_{1}^{zk}\) model the real prover and simulator of new construction described in Fig. 1. As the NIZK argument \(\varPsi \) guarantees Sub-ZK it, consequently it guarantees ZK, so one can conclude that the proof generated by prover in experiment \(\mathsf {EXP}_{2}^{zk}\) is indistinguishable from the proof generated by the simulator in \(\mathsf {EXP}_{1}^{zk}\). Intuitively, this is because of OR-based construction of new language \(\mathbf {L}'\), and consequently the fact that all new elements added to the new construction are chosen randomly and independently. \(\square \)
This results that the constructed NIZK arguments in Sect. 3.1 ensures Sub-ZK. \(\square \)
Theorem 3 ((Non-black-Box) Simulation Knowledge Soundness)
If the NIZK argument \(\varPsi \) is complete, Sub-ZK, and knowledge sound, then the proposed construction in Fig. 1 guarantees (non-black-box) simulation knowledge soundness.
Before going through the proof of theorem, recall that simulation knowledge soundness states that given a honestly generated CRS \({\mathbf {\mathsf {crs} }}\), an adversary cannot come out with a valid fresh proof, even if he access to an oracle which returns simulated proofs for an arbitrary statement, unless he knows the witness. The existing of an oracle which returns simulated proofs shows that the protocol is simulatable, so the proofs should be zero-knowledge. In the last theorem, we observed that the constructed NIZK argument in Sect. 3.1 guarantees Sub-ZK and consequently ZK. In proving this theorem, as verifier trusts to the CRS generator and as Sub-ZK implies ZK, so we use the simulator of standard ZK to prove this theorem.
Proof
The proof is simplified and generalized version of the proof of simulation knowledge soundness presented in [KZM+15] and in [AB19], respectively, but for all (Sub-)ZK and (knowledge) sound NIZK arguments. For the sake of completeness, we provide the proof in the rest. The proof is for the case that the input NIZK argument guarantees knowledge soundness. Similarly, we write consecutive hybrid experiments and at the end show that success probability of an adversary to break the simulation knowledge soundness of new constructions are negligible. Consider the following experiments,
 (main experiment)
(main experiment)
-
Setup: Sample \(({\mathbf {\mathsf {crs} }}\,\Vert \,\mathsf {ts}) \leftarrow \mathsf {K}(\mathbf {R}_{\mathbf {L}'}, \xi )\);
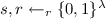 ; \(\rho := \mathsf {Com}(s, r)\); and output \(({\mathbf {\mathsf {crs} }}' \,\Vert \,\mathsf {ts}') := (({\mathbf {\mathsf {crs} }}, \rho ) \,\Vert \,(\mathsf {ts}, (s, r)))\); where \(\mathsf {ts}'\) is new CRS trapdoor.
; \(\rho := \mathsf {Com}(s, r)\); and output \(({\mathbf {\mathsf {crs} }}' \,\Vert \,\mathsf {ts}') := (({\mathbf {\mathsf {crs} }}, \rho ) \,\Vert \,(\mathsf {ts}, (s, r)))\); where \(\mathsf {ts}'\) is new CRS trapdoor. -
Define function \(\mathsf {O}(\mathsf {x})\):
 set \(\mu = f_{s} (pk_{\mathsf {Sign}})\); generate
set \(\mu = f_{s} (pk_{\mathsf {Sign}})\); generate  ; sign \(\sigma \leftarrow \mathsf {Sign}(sk_{\mathsf {Sign}}, (\mathsf {x}, \mu , \pi ))\); return \(\pi ' := (\mu , \pi , pk_{\mathsf {Sign}}, \sigma )\).
; sign \(\sigma \leftarrow \mathsf {Sign}(sk_{\mathsf {Sign}}, (\mathsf {x}, \mu , \pi ))\); return \(\pi ' := (\mu , \pi , pk_{\mathsf {Sign}}, \sigma )\). -
 .
. -
Parse \(\pi ' := (\mu , \pi , pk_{\mathsf {Sign}}, \sigma )\);
 .
. -
Return 1
 ; where Q shows the set of statment-proof pairs generated by \(\mathsf {O}(\mathsf {x})\).
; where Q shows the set of statment-proof pairs generated by \(\mathsf {O}(\mathsf {x})\).
 (relaxing the return checking)
(relaxing the return checking)
-
Setup: Sample \(({\mathbf {\mathsf {crs} }}\,\Vert \,\mathsf {ts}) \leftarrow \mathsf {K}(\mathbf {R}_{\mathbf {L}'}, \xi )\);
 ; \(\rho := \mathsf {Com}(s, r)\); and output \(({\mathbf {\mathsf {crs} }}' \,\Vert \,\mathsf {ts}') := (({\mathbf {\mathsf {crs} }}, \rho ) \,\Vert \,(\mathsf {ts}, (s, r)))\); where \(\mathsf {ts}'\) is new CRS trapdoor.
; \(\rho := \mathsf {Com}(s, r)\); and output \(({\mathbf {\mathsf {crs} }}' \,\Vert \,\mathsf {ts}') := (({\mathbf {\mathsf {crs} }}, \rho ) \,\Vert \,(\mathsf {ts}, (s, r)))\); where \(\mathsf {ts}'\) is new CRS trapdoor. -
Define function \(\mathsf {O}(\mathsf {x})\):
 set \(\mu = f_{s} (pk_{\mathsf {Sign}})\); generate
set \(\mu = f_{s} (pk_{\mathsf {Sign}})\); generate  ; sign \(\sigma \leftarrow \mathsf {Sign}(sk_{\mathsf {Sign}}, (\mathsf {x}, \mu , \pi ))\); return \(\pi ' := (\mu , \pi , pk_{\mathsf {Sign}}, \sigma )\).
; sign \(\sigma \leftarrow \mathsf {Sign}(sk_{\mathsf {Sign}}, (\mathsf {x}, \mu , \pi ))\); return \(\pi ' := (\mu , \pi , pk_{\mathsf {Sign}}, \sigma )\). -
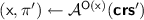 .
. -
Parse \(\pi ' := (\mu , \pi , pk_{\mathsf {Sign}}, \sigma )\);
 .
. -
Return
 \(\wedge \)
\(\wedge \)  ; where Q is the set of statment-proof pairs and \(\mathcal {PK}\) is the set of signature verification keys, both generated by \(\mathsf {O}(\mathsf {x})\).
; where Q is the set of statment-proof pairs and \(\mathcal {PK}\) is the set of signature verification keys, both generated by \(\mathsf {O}(\mathsf {x})\).
Lemma 2
If the underlying one-time signature scheme is strongly unforgeable, and the NIZK argument guarantees knowledge-soundness, then  .
.
Proof
We note that if \((\mathsf {x}, \pi ') \not \in Q\) and “\(pk_{\mathsf {Sign}}\) from \((\mathsf {x},\pi ')\), has been generated by \(\mathsf {O}(\cdot )\)”, then the \((\mathsf {x},\mu ,\pi )\) is a valid message/signature pair. Therefore by security of the signature scheme, we know that \((\mathsf {x}, \pi ) \not \in Q\) and “\(pk_{\mathsf {Sign}}\) has been generated by \(\mathsf {O}(\cdot )\)” happens with negligible probability, which allows us to focus on \(pk_{\mathsf {Sign}} \not \in \mathcal {PK}\).
Now, due to knowledge soundness of the original scheme (there is an extractor  where can extract witness from
where can extract witness from  ), if some witness is valid for \(\mathbf {L}'\) and \((\mathsf {x}, \mathsf {w}) \not \in \mathbf {R}_{\mathbf {L}}\), so we conclude it must be the case that there exists some \(s'\), such that \(\rho \) is valid commitment of \(s'\) and \(\mu = f_{s'}(pk_{\mathsf {Sign}})\), which by perfectly binding property of the commitment scheme, it implies \(\mu = f_{s}(pk_{\mathsf {Sign}})\). \(\square \)
), if some witness is valid for \(\mathbf {L}'\) and \((\mathsf {x}, \mathsf {w}) \not \in \mathbf {R}_{\mathbf {L}}\), so we conclude it must be the case that there exists some \(s'\), such that \(\rho \) is valid commitment of \(s'\) and \(\mu = f_{s'}(pk_{\mathsf {Sign}})\), which by perfectly binding property of the commitment scheme, it implies \(\mu = f_{s}(pk_{\mathsf {Sign}})\). \(\square \)
 (simulator)
(simulator)
-
Setup: Sample \(({\mathbf {\mathsf {crs} }}\,\Vert \,\mathsf {ts}) \leftarrow \mathsf {K}(\mathbf {R}_{\mathbf {L}'}, \xi )\);
 ; \(\rho := Com(s, r)\); and output \(({\mathbf {\mathsf {crs} }}' \,\Vert \,\mathsf {ts}') := (({\mathbf {\mathsf {crs} }}, \rho ) \,\Vert \,(\mathsf {ts}, (s, r)))\); where \(\mathsf {ts}'\) is new CRS trapdoor.
; \(\rho := Com(s, r)\); and output \(({\mathbf {\mathsf {crs} }}' \,\Vert \,\mathsf {ts}') := (({\mathbf {\mathsf {crs} }}, \rho ) \,\Vert \,(\mathsf {ts}, (s, r)))\); where \(\mathsf {ts}'\) is new CRS trapdoor. -
Define function \(\mathsf {O}(\mathsf {x})\):
 set \(\mu = f_{s} (pk_{\mathsf {Sign}})\); generate
set \(\mu = f_{s} (pk_{\mathsf {Sign}})\); generate  ; sign \(\sigma \leftarrow \mathsf {Sign}(sk_{\mathsf {Sign}}, (\mathsf {x}, \mu , \pi ))\); return \(\pi ' := (\mu , \pi , pk_{\mathsf {Sign}}, \sigma )\).
; sign \(\sigma \leftarrow \mathsf {Sign}(sk_{\mathsf {Sign}}, (\mathsf {x}, \mu , \pi ))\); return \(\pi ' := (\mu , \pi , pk_{\mathsf {Sign}}, \sigma )\). -
 .
. -
Parse \(\pi ' := (\mu , \pi , pk_{\mathsf {Sign}}, \sigma )\);
 .
. -
Return
 ; where Q is the set of statment-proof pairs and \(\mathcal {PK}\) is the set of signature verification keys, both generated by \(\mathsf {O}(\mathsf {x})\).
; where Q is the set of statment-proof pairs and \(\mathcal {PK}\) is the set of signature verification keys, both generated by \(\mathsf {O}(\mathsf {x})\).
Lemma 3
If the NIZK argument \(\varPsi \) guarantees zero-knowledge, then for two experiments \(\mathsf {EXP}_{3}^{SimExt}\) and \(\mathsf {EXP}_{2}^{SimExt}\), we have  .
.
Proof
As the NIZK argument \(\varPsi \) ensures Sub-ZK and consequently ZK, so it implies no polynomial time adversary can distinguish a proof generated by the simulator from a proof that is generated by the prover. So, as we are running in polynomial time, thus two experiments are indistinguishable. \(\square \)
 (separating secret key of pseudo random function)
(separating secret key of pseudo random function)
-
Setup: Sample \(({\mathbf {\mathsf {crs} }}\,\Vert \,\mathsf {ts}) \leftarrow \mathsf {K}(\mathbf {R}_{\mathbf {L}'}, \xi )\);
 ;
;  ; and output \(({\mathbf {\mathsf {crs} }}' \,\Vert \,\mathsf {ts}') := (({\mathbf {\mathsf {crs} }}, \rho ) \,\Vert \,(\mathsf {ts}, (s,s', r)))\); where \(\mathsf {ts}'\) is new trapdoor.
; and output \(({\mathbf {\mathsf {crs} }}' \,\Vert \,\mathsf {ts}') := (({\mathbf {\mathsf {crs} }}, \rho ) \,\Vert \,(\mathsf {ts}, (s,s', r)))\); where \(\mathsf {ts}'\) is new trapdoor. -
Define function \(\mathsf {O}(\mathsf {x})\):
 set \(\mu = f_{s} (pk_{\mathsf {Sign}})\); generate
set \(\mu = f_{s} (pk_{\mathsf {Sign}})\); generate  ; sign \(\sigma \leftarrow \mathsf {Sign}(sk_{\mathsf {Sign}}, (\mathsf {x}, \mu , \pi ))\); return \(\pi ' := (\mu , \pi , pk_{\mathsf {Sign}}, \sigma )\).
; sign \(\sigma \leftarrow \mathsf {Sign}(sk_{\mathsf {Sign}}, (\mathsf {x}, \mu , \pi ))\); return \(\pi ' := (\mu , \pi , pk_{\mathsf {Sign}}, \sigma )\). -
 .
. -
Parse \(\pi ' := (\mu , \pi , pk_{\mathsf {Sign}}, \sigma )\);
 .
. -
Return
 ; where Q is the set of statment-proof pairs and \(\mathcal {PK}\) is the set of signature verification keys, both generated by \(\mathsf {O}(\mathsf {x})\).
; where Q is the set of statment-proof pairs and \(\mathcal {PK}\) is the set of signature verification keys, both generated by \(\mathsf {O}(\mathsf {x})\).
Lemma 4
If the commitment scheme used in the CRS generation is computationally hiding, then  .
.
Proof
Computationally hiding of a commitment scheme implies that \(Com(m_1, r)\) and \(Com(m_2, r)\) are computationally indistinguishable, as in this lemma. \(\square \)
 (replace pseudo random function \(f_s(\cdot )\) with true random function \({F(\cdot )}\)):
(replace pseudo random function \(f_s(\cdot )\) with true random function \({F(\cdot )}\)):
-
Setup: Sample \(({\mathbf {\mathsf {crs} }}|| \mathsf {ts}) \leftarrow \mathsf {K}(\mathbf {R}_{\mathbf {L}'}, \xi )\); \(s'\),
 ,
,  ; \(\rho := \mathsf{Com}(s', r)\); and output
; \(\rho := \mathsf{Com}(s', r)\); and output  ; where \(\mathsf {ts}'\) is new CRS trapdoor.
; where \(\mathsf {ts}'\) is new CRS trapdoor. -
Define function \(\mathsf {O}(\mathsf {x})\):
 set
set  ; generate
; generate  ; sign \(\sigma \leftarrow \mathsf {Sign}(sk_{\mathsf {Sign}}, (\mathsf {x}, \mu , \pi ))\); return \(\pi ' := (\mu , \pi , pk_{\mathsf {Sign}}, \sigma )\).
; sign \(\sigma \leftarrow \mathsf {Sign}(sk_{\mathsf {Sign}}, (\mathsf {x}, \mu , \pi ))\); return \(\pi ' := (\mu , \pi , pk_{\mathsf {Sign}}, \sigma )\). -
 .
. -
Parse \(\pi ' := (\mu , \pi , pk_{\mathsf {Sign}}, \sigma )\);
 .
. -
Return
 ); where Q is the set of statment-proof pairs and \(\mathcal {PK}\) is the set of signature verification keys, both generated by \(\mathsf {O}(\mathsf {x})\).
); where Q is the set of statment-proof pairs and \(\mathcal {PK}\) is the set of signature verification keys, both generated by \(\mathsf {O}(\mathsf {x})\).
Lemma 5
If the underlying truly random function \(F(\cdot )\) is secure, then \(\Pr [\mathsf {EXP}_{4}^{SimExt}] \le \Pr [\mathsf {EXP}_{5}^{SimExt}]\).
Proof
By assuming function \(F(\cdot )\) is secure, we can conclude no polynomial time adversary can distinguish an output of the true random function \(F(\cdot )\) from an output of the pseudo random function \(f_s(\cdot )\). Indeed, experiment \(\mathsf {EXP}_{5}^{SimExt}\) can be converted to an adversary for the game of a true random function. \(\square \)
Claim
For experiment \(\mathsf {EXP}_{5}^{SimExt}\), we have  .
.
Proof
From verification we know \(pk_{\mathsf {Sign}} \not \in \mathcal {PK}\), therefore \(F(pk_{\mathsf {Sign}})\) has not been queried already. Thus, we will see \(F(pk_{\mathsf {Sign}})\) as a newly generated random string independent from \(\mu \), which implies adversary only can guess. \(\square \)
This completes proof of the main theorem. \(\square \)
4 A Sub-ZK Simulation-Extractable SNARK
In this section, we aim to instantiate the construction proposed in Sect. 3.1, and achieve a NIZK argument that can guarantee Sub-ZK and simulation knowledge soundness. In such a scheme, the prover will get sure that the proof is ZK without trusting to the CRS generators but to achieve simulation knowledge soundness they will trust the CRS generators. Based on discussions in Sect. 3.1 and Fig. 1, we need to instantiate some primitives including the pseudo-random function, the commitment scheme, and the one-time secure signature scheme and also use a subversion-resistant NIZK argument as a subroutine.
A Subversion-Resistant NIZK. Currently Groth’s zk-SNARK is the most efficient subversion-resistant NIZK argument that is proven to achieve Sub-ZK [ABLZ17, Fuc18] and knowledge soundness [Gro16] in the generic group model. While proving Sub-ZK, Abdolmaleki et al. [ABLZ17] and Fuchsbauer [Fuc18] have proposed two different CRS verification \(\mathsf {CV}\) algorithms for Groth’s zk-SNARK, which the later works for original version but the first one requires some changes in the CRS of Groth’s zk-SNARK.
Instantiation of Primitives. As mentioned before, recently Atapoor and Baghery [AB19] used a similar construction to achieve simulation knowledge soundness in Groth’s zk-SNARK [Gro16]. Their main goal was to construct an efficient version of Groth’s zk-SNARK that can also guarantee non-malleability of proofs and outperforms Groth and Maller’s zk-SNARK [GM17]. They instantiate pseudo-random function and commitment scheme with SHA512 hash function which requires an arithmetic circuit with \({\approx }26.000\) multiplication gates [KMS+16]. They used Boneh and Boyen’s signature scheme [BB08] to instantiate the one-time secure signature scheme which is a paring-based signature scheme and works as follows:
Key Generation,  : Given a bilinear group description \((p, \mathbb {G}_1, \mathbb {G}_2, \mathbb {G}_T, \hat{e}, \left[ 1\right] _{1}, \left[ 1\right] _{2})\), selects
: Given a bilinear group description \((p, \mathbb {G}_1, \mathbb {G}_2, \mathbb {G}_T, \hat{e}, \left[ 1\right] _{1}, \left[ 1\right] _{2})\), selects  , and returns
, and returns  .
.
Signing,  : Given the group description,
: Given the group description,  , and a message m, returns
, and a message m, returns  .
.
Verification,  : Given
: Given  , m, and \([\sigma ]_2\), checks whether
, m, and \([\sigma ]_2\), checks whether  and returns either 1 or 0.
and returns either 1 or 0.
A CRS verification algorithm for the variation of Groth’s zk-SNARK [Gro16] proposed by Atapoor and Baghery [AB19]. Note that \({\mathbf {\mathsf {crs} }}':=({\mathbf {\mathsf {crs} }}, \rho )\), where \(\rho := Com(s, r)\) and \({\mathbf {\mathsf {crs} }}\) is the CRS of Groth’s zk-SNARK that is shown above the figure.
Subversion-Resistant Simulatioo-Extractable SNARK. In the rest, we use the instantiations used in [AB19] and the \(\mathsf {CV}\) algorithm proposed by Fuchsbauer [Fuc18] to construct a variation of Groth’s zk-SNARK that will guarantee Sub-ZK and simulation knowledge soundness. In Fig. 2 we presented a CRS verification algorithm \(\mathsf {CV}'\) which basically is a minimally changed version of the \(\mathsf {CV}\) algorithm proposed by Fuchsbauer [Fuc18]. In \(\mathsf {CV}'\) we also check whether  , and basically this is the only difference between \(\mathsf {CV}'\) and \(\mathsf {CV}\) algorithms.
, and basically this is the only difference between \(\mathsf {CV}'\) and \(\mathsf {CV}\) algorithms.
Finally, as we used the same instantiations used in [AB19], so the other three algorithms  will be the same as in the variation of Groth’s zk-SNARK proposed in [AB19]. Basically, we propose to add the new algorithm \(\mathsf {CV}'\) to their variation and with minimal computational cost, achieve Sub-ZK as well. To this end, the prover first needs to check the well-formedness of CRS elements with executing the algorithm \(\mathsf {CV}'\) (shown in Fig. 2) and if it returned 1 (the CRS is well-formed) it continues and generates the proof as described in Fig. 1. Abodlmaleki et al. [ABLZ17] showed that using batching techniques a similar \(\mathsf {CV}'\) algorithm can be executed very efficiently; specially faster than running time of prover.
will be the same as in the variation of Groth’s zk-SNARK proposed in [AB19]. Basically, we propose to add the new algorithm \(\mathsf {CV}'\) to their variation and with minimal computational cost, achieve Sub-ZK as well. To this end, the prover first needs to check the well-formedness of CRS elements with executing the algorithm \(\mathsf {CV}'\) (shown in Fig. 2) and if it returned 1 (the CRS is well-formed) it continues and generates the proof as described in Fig. 1. Abodlmaleki et al. [ABLZ17] showed that using batching techniques a similar \(\mathsf {CV}'\) algorithm can be executed very efficiently; specially faster than running time of prover.
5 Conclusion
Recently, Atapoor and Baghery [AB19] used a folklore OR technique [BG90] with a particular instantiation [KZM+15, AB19] to construct a variation of Groth’s zk-SNARK [Gro16] that achieves simulation knowledge soundness; consequently it guarantees non-malleability of proofs.
In this paper, we showed that the same technique can be used to amplify the best result in constructing subversion-resistant NIZK arguments [BFS16, ABLZ17, Fuc18, FO18, ALSZ18]. Technically speaking, we proved that if the input NIZK argument already achieves Sub-ZK (ZK without trusting to a third party) and (knowledge) soundness, by applying the mentioned technique, the lifted NIZK argument will also guarantee Sub-ZK and simulation (knowledge) soundness. Simulation knowledge soundness (a.k.a. simulation-extractability) ensures non-malleability of proofs which is a necessary requirement in practical applications.
We emphasize that, the used compiler can be applied on any subversion-resistant NIZK argument, e.g. the ones studied in [Fuc18], but we focused on the state-of-the-art zk-SNARK which is proposed by Groth in [Gro16]. From a different perspective, basically we showed that the recent construction proposed by Atapoor and Baghery [AB19] can also achieve Sub-ZK with minimal efficiency loss. The cost is that prover will check the well-formedness of CRS elements by an efficient CRS verification algorithm before using them.
To sum up, we note that as currently Atapoor and Baghery’s variation [AB19] of Groth’s zk-SNARK is the most efficient simulation-extractable zk-SNARK in the CRS model, so adding Sub-ZK to their scheme will result the most efficient SNARK that can guarantee Sub-ZK and simulation-extractability.
Notes
- 1.
A framework with practically optimized primitives which given a sound NIZK lifts it to a universally composable or more precisely a black-box simulation extractable NIZK argument [KZM+15].
- 2.
It states that in an asymetric bilinear group, given \(\left[ 1\right] _{1}\) and \(\left[ 1\right] _{1}\), if an adversary manages to come out with \(\left[ a\right] _{1}\) and \(\left[ a\right] _{2}\), he must know a. Knowing a is formalized by showing that there exists an efficient non-black-box extractor that given access to source code and random coins of the adversary, it can extract a [Dam92].
- 3.
It states that in a symmetric bilinear group, given \(\left[ 1\right] _{1}\), if an adversary manages to come out with \(\left[ a\right] _{1}\) and \(\left[ a^2\right] _{1}\), he must know a.
References
Atapoor, S., Baghery, K.: Simulation extractability in groth’s zk-SNARK. In: Pérez-Solá, C., Navarro-Arribas, G., Biryukov, A., Garcia-Alfaro, J. (eds.) DPM/CBT-2019. LNCS, vol. 11737, pp. 336–354. Springer, Cham (2019). https://doi.org/10.1007/978-3-030-31500-9_22
Auerbach, B., Bellare, M., Kiltz, E.: Public-key encryption resistant to parameter subversion and its realization from efficiently-embeddable groups. In: Abdalla, M., Dahab, R. (eds.) PKC 2018, Part I. LNCS, vol. 10769, pp. 348–377. Springer, Cham (2018). https://doi.org/10.1007/978-3-319-76578-5_12
Abdolmaleki, B., Baghery, K., Lipmaa, H., Siim, J., Zając, M.: UC-secure CRS generation for SNARKs. In: Buchmann, J., Nitaj, A., Rachidi, T. (eds.) AFRICACRYPT 2019. LNCS, vol. 11627, pp. 99–117. Springer, Cham (2019). https://doi.org/10.1007/978-3-030-23696-0_6
Abdolmaleki, B., Baghery, K., Lipmaa, H., Zając, M.: A subversion-resistant SNARK. In: Takagi, T., Peyrin, T. (eds.) ASIACRYPT 2017, Part III. LNCS, vol. 10626, pp. 3–33. Springer, Cham (2017). https://doi.org/10.1007/978-3-319-70700-6_1
Abdolmaleki, B., Lipmaa, H., Siim, J. and Zajac, M.: On QA-NIZK in the BPK model. IACR Cryptology ePrint Archive, 2018:877 (2018). http://eprint.iacr.org/2018/877
Ateniese, G., Magri, B., Venturi, D.: Subversion-resilient signatures: definitions, constructions and applications. Cryptology ePrint Archive, Report 2015/517 (2015). http://eprint.iacr.org/2015/517
Baghery, K.: On the efficiency of privacy-preserving smart contract systems. In: Buchmann, J., Nitaj, A., Rachidi, T. (eds.) AFRICACRYPT 2019. LNCS, vol. 11627, pp. 118–136. Springer, Cham (2019). https://doi.org/10.1007/978-3-030-23696-0_7
Baghery, K.: Subversion-resistant commitment schemes: definitions and constructions. Cryptology ePrint Archive, Report 2019/1065 (2019). http://eprint.iacr.org/2019/1065
Boneh, D., Boyen, X.: Short signatures without random oracles and the SDH assumption in bilinear groups. J. Cryptol. 21(2), 149–177 (2008)
Ball, J., Borger, J., Greenwald, G., et al.: Revealed: how us and uk spy agencies defeat internet privacy and security. The Guardian 6, 2–8 (2013)
Ben-Sasson, E., Chiesa, A., Green, M., Tromer, E., Virza, M.: Secure sampling of public parameters for succinct zero knowledge proofs. In: 2015 IEEE Symposium on Security and Privacy, pp. 287–304. IEEE Computer Society Press (2015)
Bitansky, N., Canetti, R., Paneth, O., Rosen, A.: On the existence of extractable one-way functions. In: Shmoys, D.B. (ed.) 46th ACM STOC, pp. 505–514. ACM Press, May/June 2014
Ben-Sasson, E., Chiesa, A., Tromer, E., Virza, M.: Succinct non-interactive arguments for a von neumann architecture. Cryptology ePrint Archive, Report 2013/879 (2013). http://eprint.iacr.org/2013/879
Blum, M., Feldman, P., Micali, S.: Non-interactive zero-knowledge and its applications (extended abstract). In: 20th ACM STOC, pp. 103–112. ACM Press, May 1988
Bellare, M., Fuchsbauer, G., Scafuro, A.: NIZKs with an untrusted CRS: security in the face of parameter subversion. In: Cheon, J.H., Takagi, T. (eds.) ASIACRYPT 2016, Part II. LNCS, vol. 10032, pp. 777–804. Springer, Heidelberg (2016). https://doi.org/10.1007/978-3-662-53890-6_26
Bellare, M., Goldwasser, S.: New paradigms for digital signatures and message authentication based on non-interactive zero knowledge proofs. In: Brassard, G. (ed.) CRYPTO 1989. LNCS, vol. 435, pp. 194–211. Springer, New York (1990). https://doi.org/10.1007/0-387-34805-0_19
Bellare, M., Paterson, K.G., Rogaway, P.: Security of symmetric encryption against mass surveillance. In: Garay, J.A., Gennaro, R. (eds.) CRYPTO 2014, Part I. LNCS, vol. 8616, pp. 1–19. Springer, Heidelberg (2014). https://doi.org/10.1007/978-3-662-44371-2_1
Damgård, I.: Towards practical public key systems secure against chosen ciphertext attacks. In: Feigenbaum, J. (ed.) CRYPTO 1991. LNCS, vol. 576, pp. 445–456. Springer, Heidelberg (1992). https://doi.org/10.1007/3-540-46766-1_36
De Santis, A., Di Crescenzo, G., Ostrovsky, R., Persiano, G., Sahai, A.: Robust non-interactive zero knowledge. In: Kilian, J. (ed.) CRYPTO 2001. LNCS, vol. 2139, pp. 566–598. Springer, Heidelberg (2001). https://doi.org/10.1007/3-540-44647-8_33
Fuchsbauer, G., Orrù, M.: Non-interactive zaps of knowledge. In: Preneel, B., Vercauteren, F. (eds.) ACNS 2018. LNCS, vol. 10892, pp. 44–62. Springer, Cham (2018). https://doi.org/10.1007/978-3-319-93387-0_3
Fuchsbauer, G.: Subversion-zero-knowledge SNARKs. In: Abdalla, M., Dahab, R. (eds.) PKC 2018, Part I. LNCS, vol. 10769, pp. 315–347. Springer, Cham (2018). https://doi.org/10.1007/978-3-319-76578-5_11
Gabizon, A.: On the security of the BCTV pinocchio zk-SNARK variant. IACR Cryptology ePrint Archive, 2019:119 (2019)
Gennaro, R., Gentry, C., Parno, B., Raykova, M.: Quadratic span programs and succinct NIZKs without PCPs. In: Johansson, T., Nguyen, P.Q. (eds.) EUROCRYPT 2013. LNCS, vol. 7881, pp. 626–645. Springer, Heidelberg (2013). https://doi.org/10.1007/978-3-642-38348-9_37
Groth, J., Maller, M.: Snarky Signatures: minimal signatures of knowledge from simulation-extractable SNARKs. In: Katz, J., Shacham, H. (eds.) CRYPTO 2017, Part II. LNCS, vol. 10402, pp. 581–612. Springer, Cham (2017). https://doi.org/10.1007/978-3-319-63715-0_20
Groth, J., Ostrovsky, R., Sahai, A.: Non-interactive zaps and new techniques for NIZK. In: Dwork, C. (ed.) CRYPTO 2006. LNCS, vol. 4117, pp. 97–111. Springer, Heidelberg (2006). https://doi.org/10.1007/11818175_6
Greenwald, G.: No Place to Hide: Edward Snowden, the NSA, and the US Surveillance State. Macmillan, London (2014)
Groth, J.: Short pairing-based non-interactive zero-knowledge arguments. In: Abe, M. (ed.) ASIACRYPT 2010. LNCS, vol. 6477, pp. 321–340. Springer, Heidelberg (2010). https://doi.org/10.1007/978-3-642-17373-8_19
Groth, J.: On the size of pairing-based non-interactive arguments. In: Fischlin, M., Coron, J.-S. (eds.) EUROCRYPT 2016, Part II. LNCS, vol. 9666, pp. 305–326. Springer, Heidelberg (2016). https://doi.org/10.1007/978-3-662-49896-5_11
Haenni, R.: Swiss post public intrusion test: undetectable attack against vote integrity and secrecy (2019). https://e-voting.bfh.ch/app/download/7833162361/PIT2.pdf?t=1552395691
Kosba, A., Miller, A.: The blockchain model of cryptography and privacy-preserving smart contracts. In: 2016 IEEE Symposium on Security and Privacy, pp. 839–858. IEEE Computer Society Press, May 2016
Kosba, A.E., et al.: A framework for building composable zero-knowledge proofs. Technical report 2015/1093, 10 November 2015. http://eprint.iacr.org/2015/1093. Accessed 9 Apr 2017
Lipmaa, H.: Progression-free sets and sublinear pairing-based non-interactive zero-knowledge arguments. In: Cramer, R. (ed.) TCC 2012. LNCS, vol. 7194, pp. 169–189. Springer, Heidelberg (2012). https://doi.org/10.1007/978-3-642-28914-9_10
Lipmaa, H.: Simulation-extractable SNARKs revisited. Cryptology ePrint Archive, Report 2019/612 (2019). http://eprint.iacr.org/2019/612
Lewis, S.J., Pereira, O., Teague, V.: Trapdoor commitments in the swisspost e-voting shuffle proof (2019). https://people.eng.unimelb.edu.au/vjteague/SwissVote
Parno, B., Howell, J., Gentry, C., Raykova, M.: Pinocchio: nearly practical verifiable computation. In: 2013 IEEE Symposium on Security and Privacy, pp. 238–252. IEEE Computer Society Press, May 2013
Perlroth, N., Larson, J., Shane, S.: NSA able to foil basic safeguards of privacy on web. The New York Times, 5 (2013)
Acknowledgement
This work was supported in part by the Estonian Research Council grant PRG49.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2019 Springer Nature Switzerland AG
About this paper
Cite this paper
Baghery, K. (2019). Subversion-Resistant Simulation (Knowledge) Sound NIZKs. In: Albrecht, M. (eds) Cryptography and Coding. IMACC 2019. Lecture Notes in Computer Science(), vol 11929. Springer, Cham. https://doi.org/10.1007/978-3-030-35199-1_3
Download citation
DOI: https://doi.org/10.1007/978-3-030-35199-1_3
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-35198-4
Online ISBN: 978-3-030-35199-1
eBook Packages: Computer ScienceComputer Science (R0)



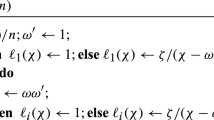


 ;
;  ;
;  sample
sample  ; generate
; generate  ; sign
; sign  ; return
; return 
 ;
;  sample
sample  ; generate
; generate  ; sign
; sign 
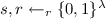 ;
;  set
set  ; sign
; sign  .
. .
. ; where Q shows the set of statment-proof pairs generated by
; where Q shows the set of statment-proof pairs generated by  ;
;  set
set  ; sign
; sign 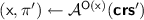 .
. .
.
 ; where Q is the set of statment-proof pairs and
; where Q is the set of statment-proof pairs and  ;
;  set
set  ; sign
; sign  .
. .
. ; where Q is the set of statment-proof pairs and
; where Q is the set of statment-proof pairs and  ;
;  ; and output
; and output  set
set  ; sign
; sign  .
. .
. ; where Q is the set of statment-proof pairs and
; where Q is the set of statment-proof pairs and  ,
,  ;
;  ; where
; where  set
set  ; generate
; generate  ; sign
; sign  .
. .
. ); where Q is the set of statment-proof pairs and
); where Q is the set of statment-proof pairs and 