Abstract
Zero-knowledge SNARKs (zk-SNARKs) have recently found various applications in verifiable computation and blockchain applications (Zerocash), but unfortunately they rely on a common reference string (CRS) that has to be generated by a trusted party. A standard suggestion, pursued by Ben Sasson et al. [IEEE S&P, 2015], is to generate CRS via a multi-party protocol. We enhance their CRS-generation protocol to achieve UC-security. This allows to safely compose the CRS-generation protocol with the zk-SNARK in a black-box manner with the insurance that the security of the zk-SNARK is not influenced. Differently from the previous work, the new CRS-generation protocol also avoids the random oracle model which is typically not required by zk-SNARKs themselves. As a case study, we apply the protocol to the state-of-the-art zk-SNARK by Groth [EUROCRYPT, 2016].
Access provided by Autonomous University of Puebla. Download conference paper PDF
Similar content being viewed by others
Keywords
1 Introduction
A zero-knowledge argument is a cryptographic protocol between a prover and a verifier where the objective is to prove the validity of some statement while not leaking any other information. In particular, such an argument should be sound (it should be impossible to prove false statements) and zero-knowledge (the only leaked information should be the validity of the statement). Practical applications often require a non-interactive zero-knowledge (NIZK) argument where the prover outputs a single message which can be checked by many different verifiers.
Zero-knowledge succinct non-interactive arguments of knowledge (zk-SNARKs) are particularly efficient instantiations of NIZK, and have thus found numerous application ranging from verifiable computation [29] to privacy-preserving cryptocurrencies [5] and privacy-preserving smart contracts [25]. In most of such zk-SNARKs (see, e.g., [13, 15, 19, 20, 26, 29]), the verifier’s computation is dominated by a small number of exponentiations and pairings in a bilinear group, while the argument consists of a small number of group elements. Importantly, a zk-SNARK exists for any NP-language.
One drawback in the mentioned pairing-based zk-SNARKs is their reliance on the strong common reference string (CRS) model. It assumes that in the setup phase of the protocol a trusted party publishes a CRS, sampled from some specialized distribution, while not leaking any side information. Subverting the setup phase can make it easy to break the security, e.g., leaking a CRS trapdoor makes it trivial to prove false statements. This raises the obvious question of how to apply zk-SNARKs in practice without completely relying on a single trusted party. The issue is further amplified since in all of the mentioned zk-SNARKs, one has to generate a new CRS each time the relation changes.
Reducing trust on CRS generation is indeed a long-standing open question. Several different approaches for this are known, but each one has its own problems. Some recent papers [6, 8, 9] have proposed efficient CRS-generation multi-party computation protocols, where only 1 out of \(\mathsf {N}_{p}\) parties has to be honest, for a large class of known zk-SNARKs (in fact, most of the efficient pairing-based zk-SNARKs belong to this class, possibly after the inclusion of a small number of new elements to their CRSs) for which the CRS can be computed by a fixed well-defined class \(\mathcal {C}^{\mathsf {S}}\) of circuits. Following [6], we will call this class of zk-SNARKs \(\mathcal {C}^{\mathsf {S}}\)-SNARKs. However, the CRS-generation protocols of [6, 8, 9] have the following two weaknesses:
-
1.
They are not secure in the universal composability (UC) setting [10]. Hence, they might not be secure while running in parallel with other protocols, as is often the case in real life scenarios. Moreover, some systems require a UC-secure NIZK [22, 25], but up to now their CRS is still be generated in a standalone setting. We note that [6, 9] do prove some form of simulatability but not for full UC-security. Protocol of [8] is for one specific zk-SNARK.
-
2.
All use the random oracle model and [8, 9] additionally use knowledge assumption. Non-falsifiable assumptions [28] (e.g., knowledge assumptions) and the random oracle model are controversial (in particular, the random oracle model is uninstantiable [12, 17] and thus can only be thought of as a heuristic), and it is desirable to avoid them in situations where they are not known to circumvent impossibility results. Importantly, construction of zk-SNARKs under falsifiable assumptions is impossible [16] and hence they do rely on non-falsifiable assumptions but usually not on the random oracle model. Relying on the random oracle model in the setup phase means that the complete composed system (CRS-generation protocol + zk-SNARK) relies on both random oracle model and non-falsifiable assumptions. Hence, we end up depending on two undesirable assumptions rather than one.
Updatable CRS [21] is another recent solution to the problem. Essentially, this can be viewed as a single round MPC protocol where each party needs to participate just once in the CRS computation. Current zk-SNARKs in updatable CRS model [21, 27] are still less efficient, than the state-of-the-art non-updatable counterparts like the zk-SNARK by Groth [20].
As a different approach, in order to minimize the trust of NIZKs in the setup phase, Bellare et al. [4] defined the notion of subversion-resistance, which guarantees that a security property (like soundness) holds even if the CRS generators are all malicious. As proven in [4], achieving subversion-soundness and (even non-subversion) zero knowledge at the same time is impossible for NIZK arguments. On the other hand, one can construct subversion-zero knowledge (Sub-ZK) and sound NIZK arguments. Abdolmaleki et al. [2] showed how to design efficient Sub-ZK SNARKs: essentially, a zk-SNARK can be made Sub-ZK by constructing an efficient public CRS-verification algorithm \(\mathsf {CV}\) that guarantees the well-formedness of its CRS. In particular, [2] did this for the most efficient known zk-SNARK by Groth [20] after inserting a small number of new elements to its CRS. Fuchsbauer [14] proved that Groth’s zk-SNARK (with a slightly different simulation) is Sub-ZK even without changing its CRS.
Our Contributions. We propose a new UC-secure multi-party CRS-generation protocol for \(\mathcal {C}^{\mathsf {S}}\)-SNARKs that crucially relies only on falsifiable assumptions and does not require a random oracle. Conceptually, the new protocol follows similar ideas as the protocol of [6], but it does not use any proofs of knowledge. Instead, we use a discrete logarithm extractable (DL-extractable) UC commitment functionality \(\mathcal {F}_{\mathsf {dlmcom}}\) that was recently defined by Abdolmaleki et al. [1]. A DL-extractable commitment scheme allows to commit to a field element x and open to the group element \(g^x\). Since \(\mathcal {F}_{\mathsf {dlmcom}}\) takes x as an input, the committer must know x and thus x can be extracted by the UC-simulator. As we will show, this is sufficient to prove UC-security of the new CRS-generation protocol.
In addition, we show that the Sub-ZK SNARK of [2] is a Sub-ZK \(\mathcal {C}^{\mathsf {S}}\)-SNARK after just adding some more elements to its CRS. We also improve the efficiency of the rest of the CRS-generation protocol by allowing different circuits for each group, considering special multiplication-division gates, and removing a number of NIZK proofs that are used in [6]. Like in the previous CRS-generation protocols [6, 8, 9], soundness and zero-knowledge will be guaranteed as long as 1 out of \(\mathsf {N}_{p}\) parties participating in the CRS generation is honest. If SNARK is also Sub-ZK [2, 14], then zero-knowledge is guaranteed even if all \(\mathsf {N}_{p}\) parties are dishonest, given that the prover executes a public CRS verification algorithm.
Since it is impossible to construct UC commitments in the standard model [11], the new UC-secure CRS-generation protocol necessarily relies on some trust assumption. The DL-extractable commitment scheme of [1] is secure in the registered public key (RPK) modelFootnote 1 that is a weaker trust model than the CRS model. However, we stay agnostic to the concrete implementation of \(\mathcal {F}_{\mathsf {dlmcom}}\), proving the security of the CRS-generation protocol in the \(\mathcal {F}_{\mathsf {dlmcom}}\)-hybrid model. Thus, the trust assumption of the CRS-generation protocol is directly inherited from the trust assumption of the used DL-extractable commitment scheme. Constructing DL-extractable commitment schemes in a weaker model like the random string model or the multi-string model is an interesting open question. Note that CRS-s of known efficient \(\mathcal {C}^{\mathsf {S}}\)-SNARKs, with a few exceptions, contain \(\varOmega (\mathsf {n})\) group elements, where \(\mathsf {n}\) is the circuit size (e.g., in the last CRS generation of Zcash [5], \(\mathsf {n}\approx 2\,000\,000\)Footnote 2). Hence, even a relatively inefficient DL-extractable commitment scheme (that only has to be called once per CRS trapdoor) will not be the bottleneck in the CRS-generation protocol.
We proceed as follows. First, we describe an ideal functionality \(\mathcal {F}_{\mathsf {mcrs}}\), an explicit multi-party version of the CRS generation functionality. Intuitively (the real functionality is slightly more complicated), first, \(\mathsf {N}_{p}\) key-generators  send to \(\mathcal {F}_{\mathsf {mcrs}}\) their shares of the trapdoors, s.t. the shares of the honest parties are guaranteed to be uniformly random. Second, \(\mathcal {F}_{\mathsf {mcrs}}\) combines the shares to create the trapdoors and the CRS, and then sends the CRS to each
send to \(\mathcal {F}_{\mathsf {mcrs}}\) their shares of the trapdoors, s.t. the shares of the honest parties are guaranteed to be uniformly random. Second, \(\mathcal {F}_{\mathsf {mcrs}}\) combines the shares to create the trapdoors and the CRS, and then sends the CRS to each  .
.
We propose a protocol \(\mathsf {K}_{\mathsf {mcrs}}\) that UC-realizes \(\mathcal {F}_{\mathsf {mcrs}}\) in the \(\mathcal {F}_{\mathsf {dlmcom}}\)-hybrid model, i.e., assuming the availability of a UC-secure realization of \(\mathcal {F}_{\mathsf {dlmcom}}\). In \(\mathsf {K}_{\mathsf {mcrs}}\), the parties  first \(\mathcal {F}_{\mathsf {dlmcom}}\)-commit to their individual share of each trapdoor. After opening the commitments,
first \(\mathcal {F}_{\mathsf {dlmcom}}\)-commit to their individual share of each trapdoor. After opening the commitments,  compute \(\mathsf {crs}\) by combining their shares with a variation of the protocol from [6]. The structure of this part of the protocol makes it possible to publicly check that it was correctly followed.
compute \(\mathsf {crs}\) by combining their shares with a variation of the protocol from [6]. The structure of this part of the protocol makes it possible to publicly check that it was correctly followed.
Next, we prove that a \(\mathcal {C}^{\mathsf {S}}\)-SNARK that is complete, sound, and Sub-ZK in the CRS model is also complete, sound, and Sub-ZK in the \(\mathcal {F}_{\mathsf {mcrs}}\)-hybrid model. Sub-ZK holds even if all CRS creators were malicious, but for soundness we need at least one honest party. We then show that the Sub-ZK secure version [2, 14] of the most efficient known zk-SNARK by Groth [20] remains sound and Sub-ZK if the CRS has been generated by using \(\mathsf {K}_{\mathsf {mcrs}}\). The main technical issue here is that since Groth’s zk-SNARK is not \(\mathcal {C}^{\mathsf {S}}\)-SNARK (see Sect. 3), we need to add some new elements to its CRS and then reprove its soundness against an adversary who is given access to the new CRS elements. We note that Bowe et al. [9] proposed a different modification of Groth’s zk-SNARK together with a CRS-generation protocol, but under strong assumptions of random beacon model, random oracle model, and knowledge assumptions. Role of the commitment in their case is substituted with a random beacon which in particular means that they do not need to fix parties in the beginning of the protocol.
We constructed a UC-secure CRS-generation protocol \(\mathsf {K}_{\mathsf {mcrs}}\) in the \(\mathcal {F}_{\mathsf {dlmcom}}\)-hybrid model for any \(\mathcal {C}^{\mathsf {S}}\)-SNARK and in particular proved that a small modification of Groth’s zk-SNARK is secure when composed with \(\mathsf {K}_{\mathsf {mcrs}}\). Moreover, the resulting CRS-generation protocol is essentially as efficient as the prior protocols from [6, 8, 9]. However, (i) we proved the UC-security of the new CRS-generation protocol, and (ii) the new protocol is falsifiable, i.e., it does not require either the random oracle model or any knowledge assumption.
2 Preliminaries
Let PPT denote probabilistic polynomial-time. Let  be the information-theoretic security parameter, in practice, e.g.,
be the information-theoretic security parameter, in practice, e.g.,  . All adversaries will be stateful. For an algorithm
. All adversaries will be stateful. For an algorithm  , let
, let  be the image of
be the image of  , i.e., the set of valid outputs of
, i.e., the set of valid outputs of  , let
, let  denote the random tape of
denote the random tape of  , and let
, and let  denote sampling of a randomizer r of sufficient length for
denote sampling of a randomizer r of sufficient length for  ’s needs. By
’s needs. By  we denote that
we denote that  , given an input x and a randomizer r, outputs y. We denote by
, given an input x and a randomizer r, outputs y. We denote by  an arbitrary negligible function, and by
an arbitrary negligible function, and by  an arbitrary polynomial function. \(A \approx _c B\) means that distributions A and B are computationally indistinguishable. We write
an arbitrary polynomial function. \(A \approx _c B\) means that distributions A and B are computationally indistinguishable. We write  if x is sampled according to distribution
if x is sampled according to distribution  or uniformly in case
or uniformly in case  is a set. By
is a set. By  we denote the set of all elements in
we denote the set of all elements in  that have non-zero probability.
that have non-zero probability.
Assume that  are different parties of a protocol. Following previous work [6], we will make the following assumptions about the network and the adversary. It is possible that the new protocols can be implemented in the asynchronous model but this is out of scope of the current paper.
are different parties of a protocol. Following previous work [6], we will make the following assumptions about the network and the adversary. It is possible that the new protocols can be implemented in the asynchronous model but this is out of scope of the current paper.
Synchronicity Assumptions: We assume that the computation can be divided into clearly divided rounds. As it is well-known, synchronous computation can be simulated, assuming bounded delays and bounded time-drift. For the sake of simplicity, we omit formal treatment of UC-secure synchronous execution, see [23] for relevant background.
Authentication: We assume the existence of an authenticated broadcast between the parties. In particular, (i) if an honest party broadcasts a message, we assume that all parties (including, in the UC-setting, the simulator) receive it within some delay, and (ii) an honest party  accepts a message as coming from
accepts a message as coming from  only if it was sent by
only if it was sent by  .
.
Covertness: We assume that an adversary in the multi-party protocols is covert, i.e., it will not produce outputs that will not pass public verification algorithms. In the protocols we write that honest parties will abort under such circumstances, but in the proofs we assume that adversary will not cause abortions.
For pairing-based groups we will use additive notation together with the bracket notation, i.e., in group \(\mathbb {G}_{\iota }\), \(\left[ a\right] _{\iota } = a \left[ 1\right] _{\iota }\), where \(\left[ 1\right] _{\iota }\) is a fixed generator of \(\mathbb {G}_{\iota }\). A deterministic bilinear group generator  returns
returns  , where \(p\) (a large prime) is the order of cyclic abelian groups \(\mathbb {G}_1\), \(\mathbb {G}_2\), and \(\mathbb {G}_T\), and \(\hat{e} : \mathbb {G}_1 \times \mathbb {G}_2 \rightarrow \mathbb {G}_T\) is an efficient non-degenerate bilinear pairing, s.t. \(\hat{e} (\left[ a\right] _{1}, \left[ b\right] _{2}) = \left[ a b\right] _{T}\). Denote \(\left[ a\right] _{1} \bullet \left[ b\right] _{2} = \hat{e}(\left[ a\right] _{1}, \left[ b\right] _{2})\); this extends to vectors in a natural way. Occasionally we write \(\left[ a\right] _{\iota } \bullet \left[ b\right] _{3 - \iota }\) for \(\iota \in \{1,2\}\) and ignore the fact that for \(\iota = 2\) it should be written \(\left[ b\right] _{3 - \iota } \bullet \left[ a\right] _{\iota }\). Let \([a]_{\star } := ([a]_{1}, [a]_{2})\). As in [4], we will implicitly assume that
, where \(p\) (a large prime) is the order of cyclic abelian groups \(\mathbb {G}_1\), \(\mathbb {G}_2\), and \(\mathbb {G}_T\), and \(\hat{e} : \mathbb {G}_1 \times \mathbb {G}_2 \rightarrow \mathbb {G}_T\) is an efficient non-degenerate bilinear pairing, s.t. \(\hat{e} (\left[ a\right] _{1}, \left[ b\right] _{2}) = \left[ a b\right] _{T}\). Denote \(\left[ a\right] _{1} \bullet \left[ b\right] _{2} = \hat{e}(\left[ a\right] _{1}, \left[ b\right] _{2})\); this extends to vectors in a natural way. Occasionally we write \(\left[ a\right] _{\iota } \bullet \left[ b\right] _{3 - \iota }\) for \(\iota \in \{1,2\}\) and ignore the fact that for \(\iota = 2\) it should be written \(\left[ b\right] _{3 - \iota } \bullet \left[ a\right] _{\iota }\). Let \([a]_{\star } := ([a]_{1}, [a]_{2})\). As in [4], we will implicitly assume that  is generated deterministically from
is generated deterministically from  ; in particular, the choice of
; in particular, the choice of  cannot be subverted.
cannot be subverted.
UC Security. We work in the standard universal composability framework of Canetti [10] with static corruptions of parties. The UC framework defines a PPT environment machine \(\mathcal {Z}\) that oversees the execution of a protocol in one of two worlds. The “ideal world” execution involves “dummy parties” (some of whom may be corrupted by an ideal adversary/simulator  ) interacting with a functionality \(\mathcal {F}\). The “real world” execution involves PPT parties (some of whom may be corrupted by a PPT real world adversary
) interacting with a functionality \(\mathcal {F}\). The “real world” execution involves PPT parties (some of whom may be corrupted by a PPT real world adversary  ) interacting only with each other in some protocol \(\pi \). We refer to [10] for a detailed description of the executions, and a definition of the real world ensemble
) interacting only with each other in some protocol \(\pi \). We refer to [10] for a detailed description of the executions, and a definition of the real world ensemble  and the ideal world ensemble
and the ideal world ensemble  . A protocol \(\pi \) UC-securely computes \(\mathcal {F}\) if there exists a PPT
. A protocol \(\pi \) UC-securely computes \(\mathcal {F}\) if there exists a PPT  such that for every non-uniform PPT \(\mathcal {Z}\) and PPT
such that for every non-uniform PPT \(\mathcal {Z}\) and PPT  ,
,  .
.
The importance of this definition is a composition theorem that states that any protocol that is universally composable is secure when run concurrently with many other arbitrary protocols; see [10] for discussions and definitions.
CRS Functionality. The CRS model UC functionality  parameterized by a distribution
parameterized by a distribution  and a function f intuitively works as follows. Functionality samples a trapdoor \(\mathsf {tc}\) from
and a function f intuitively works as follows. Functionality samples a trapdoor \(\mathsf {tc}\) from  , computes \(\mathsf {crs}= f (\mathsf {tc})\), and stores \(\mathsf {crs}\) after a confirmation from the simulator. Subsequently on each retrieval query \((\mathtt {retrieve}, \mathsf {sid})\) it responds by sending \((\mathtt {CRS}, \mathsf {sid}, \mathsf {crs})\). For full details see Fig. 1.
, computes \(\mathsf {crs}= f (\mathsf {tc})\), and stores \(\mathsf {crs}\) after a confirmation from the simulator. Subsequently on each retrieval query \((\mathtt {retrieve}, \mathsf {sid})\) it responds by sending \((\mathtt {CRS}, \mathsf {sid}, \mathsf {crs})\). For full details see Fig. 1.
DL-extractable UC Commitment. Abdolmaleki et al. [1] recently proposed a discrete logarithm extractable (DL-extractable) UC-commitment scheme. Differently from the usual UC-commitment, a committer will open the commitment to \([m]_{1}\), but the functionality also guarantees that the committer knows x. Hence, in the UC security proof it is possible to extract the discrete logarithm of \([m]_{1}\). Formally, the ideal functionality \(\mathcal {F}_{\mathsf {dlmcom}}\) takes m as a commitment input (hence the user must know m), but on \(\mathtt {open}\) signal only reveals \([m]_{1}\). See Fig. 2. We refer to [1] for a known implementation of \(\mathcal {F}_{\mathsf {dlmcom}}\) in the RPK model.
Non-interactive Zero-Knowledge. Let \(\mathcal {R}\) be a relation generator, such that  returns a polynomial-time decidable binary relation \(\mathbf {R}= \{(\mathsf {x}, \mathsf {w})\}\). Here, \(\mathsf {x}\) is the statement and \(\mathsf {w}\) is the witness. We assume that
returns a polynomial-time decidable binary relation \(\mathbf {R}= \{(\mathsf {x}, \mathsf {w})\}\). Here, \(\mathsf {x}\) is the statement and \(\mathsf {w}\) is the witness. We assume that  is explicitly deducible from the description of \(\mathbf {R}\). The relation generator also outputs auxiliary information \({\xi _{\mathbf {R}}}\) that will be given to the honest parties and the adversary. As in [2, 20], \({\xi _{\mathbf {R}}}\) is the value returned by
is explicitly deducible from the description of \(\mathbf {R}\). The relation generator also outputs auxiliary information \({\xi _{\mathbf {R}}}\) that will be given to the honest parties and the adversary. As in [2, 20], \({\xi _{\mathbf {R}}}\) is the value returned by  . Because of this, we also give \({\xi _{\mathbf {R}}}\) as an input to the honest parties; if needed, one can include an additional auxiliary input to the adversary. Let \(\mathbf {L}_{\mathbf {R}} = \{\mathsf {x}: \exists \mathsf {w}, (\mathsf {x}, \mathsf {w}) \in \mathbf {R}\}\) be an \(\mathbf {NP}\)-language.
. Because of this, we also give \({\xi _{\mathbf {R}}}\) as an input to the honest parties; if needed, one can include an additional auxiliary input to the adversary. Let \(\mathbf {L}_{\mathbf {R}} = \{\mathsf {x}: \exists \mathsf {w}, (\mathsf {x}, \mathsf {w}) \in \mathbf {R}\}\) be an \(\mathbf {NP}\)-language.
A (subversion-resistant) non-interactive zero-knowledge argument system [2] \(\varPsi \) for \(\mathcal {R}\) consists of six PPT algorithms:
-
CRS trapdoor generator: \(\mathsf {K}_{\mathsf {tc}}\) is a PPT algorithm that, given
 , outputs a CRS trapdoor \(\mathsf {tc}\). Otherwise, it outputs \(\bot \).
, outputs a CRS trapdoor \(\mathsf {tc}\). Otherwise, it outputs \(\bot \). -
CRS generator: \(\mathsf {K}_{\mathsf {crs}}\) is a deterministic algorithm that, given \((\mathbf {R}, {\xi _{\mathbf {R}}}, \mathsf {tc})\), where
 and \(\mathsf {tc}\in {\text {im}}(\mathsf {K}_{\mathsf {tc}}(\mathbf {R}, {\xi _{\mathbf {R}}})) \setminus \{\bot \}\), outputs \(\mathsf {crs}\). Otherwise, it outputs \(\bot \). We distinguish three parts of \(\mathsf {crs}\):
and \(\mathsf {tc}\in {\text {im}}(\mathsf {K}_{\mathsf {tc}}(\mathbf {R}, {\xi _{\mathbf {R}}})) \setminus \{\bot \}\), outputs \(\mathsf {crs}\). Otherwise, it outputs \(\bot \). We distinguish three parts of \(\mathsf {crs}\):  (needed by the prover),
(needed by the prover),  (needed by the verifier), and
(needed by the verifier), and  (needed by \(\mathsf {CV}\) algorithm).
(needed by \(\mathsf {CV}\) algorithm). -
CRS verifier: \(\mathsf {CV}\) is a PPT algorithm that, given
 , returns either 0 (the CRS is ill-formed) or 1 (the CRS is well-formed).
, returns either 0 (the CRS is ill-formed) or 1 (the CRS is well-formed). -
Prover:
 is a PPT algorithm that, given
is a PPT algorithm that, given  , where \((\mathsf {x}, \mathsf {w}) \in \mathbf {R}\), outputs an argument \(\pi \). Otherwise, it outputs \(\bot \).
, where \((\mathsf {x}, \mathsf {w}) \in \mathbf {R}\), outputs an argument \(\pi \). Otherwise, it outputs \(\bot \). -
Verifier:
 is a PPT algorithm that, given
is a PPT algorithm that, given  , returns either 0 (reject) or 1 (accept).
, returns either 0 (reject) or 1 (accept). -
Simulator:
 is a PPT algorithm that, given \((\mathbf {R}, {\xi _{\mathbf {R}}}, \mathsf {crs}, \mathsf {tc}, \mathsf {x})\), outputs an argument \(\pi \).
is a PPT algorithm that, given \((\mathbf {R}, {\xi _{\mathbf {R}}}, \mathsf {crs}, \mathsf {tc}, \mathsf {x})\), outputs an argument \(\pi \).
We also define the CRS generation algorithm \(\mathsf {K}(\mathbf {R}, {\xi _{\mathbf {R}}})\) that first sets \(\mathsf {tc}\leftarrow \mathsf {K}_{\mathsf {tc}}(\mathbf {R}, {\xi _{\mathbf {R}}})\) and then outputs \(\mathsf {crs}\leftarrow \mathsf {K}_{\mathsf {crs}}(\mathbf {R}, {\xi _{\mathbf {R}}}, \mathsf {tc})\).
\(\varPsi \) is perfectly complete for \(\mathcal {R}\), if for all  ,
,  ,
,  , and
, and  ,
,

\(\varPsi \) is computationally adaptively knowledge-sound for \(\mathcal {R}\) [20], if for every non-uniform PPT  , there exists a non-uniform PPT extractor
, there exists a non-uniform PPT extractor  , s.t. \(\forall \)
, s.t. \(\forall \)  ,
,

Here, \({\xi _{\mathbf {R}}}\) can be seen as a common auxiliary input to  and
and  that is generated by using a benign [7] relation generator; we recall that we just think of \({\xi _{\mathbf {R}}}\) as being the description of a secure bilinear group.
that is generated by using a benign [7] relation generator; we recall that we just think of \({\xi _{\mathbf {R}}}\) as being the description of a secure bilinear group.
\(\varPsi \) is statistically unbounded ZK for \(\mathcal {R}\) [18], if for all  , all
, all  , and all computationally unbounded
, and all computationally unbounded  ,
,  , where
, where

Here, the oracle \(\mathsf {O}_0 (\mathsf {x}, \mathsf {w})\) returns \(\bot \) (reject) if  , and otherwise it returns
, and otherwise it returns  . Similarly, \(\mathsf {O}_1 (\mathsf {x}, \mathsf {w})\) returns \(\bot \) (reject) if
. Similarly, \(\mathsf {O}_1 (\mathsf {x}, \mathsf {w})\) returns \(\bot \) (reject) if  , and otherwise it returns
, and otherwise it returns  . \(\varPsi \) is perfectly unbounded ZK for \(\mathcal {R}\) if one requires that \(\varepsilon ^{unb}_0 = \varepsilon ^{unb}_1\).
. \(\varPsi \) is perfectly unbounded ZK for \(\mathcal {R}\) if one requires that \(\varepsilon ^{unb}_0 = \varepsilon ^{unb}_1\).
\(\varPsi \) is statistically unbounded Sub-ZK for \(\mathcal {R}\), if for any non-uniform PPT subverter \(\mathsf {X}\) there exists a non-uniform PPT  , such that for all
, such that for all  ,
,  , and computationally unbounded
, and computationally unbounded  ,
,  , where
, where

Here, the oracle \(\mathsf {O}_0 (\mathsf {x}, \mathsf {w})\) returns \(\bot \) (reject) if  , and otherwise it returns
, and otherwise it returns  . Similarly, \(\mathsf {O}_1 (\mathsf {x}, \mathsf {w})\) returns \(\bot \) (reject) if
. Similarly, \(\mathsf {O}_1 (\mathsf {x}, \mathsf {w})\) returns \(\bot \) (reject) if  , and otherwise it returns
, and otherwise it returns  . \(\varPsi \) is perfectly unbounded Sub-ZK for \(\mathcal {R}\) if one requires that \(\varepsilon ^{unb}_0 = \varepsilon ^{unb}_1\).
. \(\varPsi \) is perfectly unbounded Sub-ZK for \(\mathcal {R}\) if one requires that \(\varepsilon ^{unb}_0 = \varepsilon ^{unb}_1\).
Intuitively the previous definition says that an argument is Sub-ZK when for any untrusted (efficient) CRS generator \(\mathsf {X}\), some well-formedness condition  implies that \(\mathsf {X}\) knows a trapdoor which would allow him to simulate the proof. Hence, to protect privacy from malicious CRS generators, the prover just needs to verify that the CRS satisfies the \(\mathsf {CV}\) algorithm.
implies that \(\mathsf {X}\) knows a trapdoor which would allow him to simulate the proof. Hence, to protect privacy from malicious CRS generators, the prover just needs to verify that the CRS satisfies the \(\mathsf {CV}\) algorithm.
Finally, a non-interactive argument system is succinct if the argument length is polynomial in  and the verifier runs in time polynomial in
and the verifier runs in time polynomial in  .
.
3 Multi-party CRS Generation
Recently, [6, 8, 9] proposed several multi-party CRS-generation protocols for SNARKs. In particular, [6] proposes a specific class of arithmetic circuits \(\mathcal {C}^{\mathsf {S}}\), shows how to evaluate \(\mathcal {C}^{\mathsf {S}}\)-circuits in an MPC manner, and claims that \(\mathcal {C}^{\mathsf {S}}\)-circuits can be used to compute CRS-s for a broad class of SNARKs, in this paper called \(\mathcal {C}^{\mathsf {S}}\)-SNARKs. The CRS of each \(\mathcal {C}^{\mathsf {S}}\)-SNARK is an output of some \(\mathcal {C}^{\mathsf {S}}\)-circuit taken into exponent. The input of such circuit is the CRS trapdoor. In the following, we review and modify the framework of [6] redefining slightly the class \(\mathcal {C}^{\mathsf {S}}\) and the CRS-generation protocol.
\(\mathcal {C}^{\mathsf {S}}\)-Circuits. For an arithmetic circuit  over a field \(\mathbb {F}\), denote by
over a field \(\mathbb {F}\), denote by  and
and  the set of wires and gates of
the set of wires and gates of  (each gate can have more than one output wire), and by
(each gate can have more than one output wire), and by  the set of input and output wires of
the set of input and output wires of  . There can also be wires with hard-coded constant values, but these are not considered to be part of
. There can also be wires with hard-coded constant values, but these are not considered to be part of  . The size of
. The size of  is
is  . For a wire w we denote the value on the wire by \(\bar{w}\); this notation also extends to tuples, say,
. For a wire w we denote the value on the wire by \(\bar{w}\); this notation also extends to tuples, say,  denotes the tuple of values of
denotes the tuple of values of  .
.
For a gate g,  is the output wire and the tuple of all input wires is denoted by
is the output wire and the tuple of all input wires is denoted by  . Let \(g_w\) be the gate with
. Let \(g_w\) be the gate with  . We consider circuits with addition and multiplication-division gates. For an addition gate (
. We consider circuits with addition and multiplication-division gates. For an addition gate ( ),
),  ,
,  , and it outputs a value \(\bar{w} = a_0 + \sum _{j = 1}^f a_j \bar{w}_j\). For a \(\mathsf {multdiv}\) gate (
, and it outputs a value \(\bar{w} = a_0 + \sum _{j = 1}^f a_j \bar{w}_j\). For a \(\mathsf {multdiv}\) gate ( ),
),  ,
,  is the left multiplication input,
is the left multiplication input,  is the right multiplication input,
is the right multiplication input,  is the division input, and
is the division input, and  . The output wire w contains the value \(\bar{w} = a \bar{w}_1 \bar{w}_2 / \bar{w}_3\). Previous works either only considered multiplication gates [6] or separate multiplication and division gates [9]. Using \(\mathsf {multdiv}\) gates can, in some cases, reduce the circuit size compared to separate multiplication and division gates.
. The output wire w contains the value \(\bar{w} = a \bar{w}_1 \bar{w}_2 / \bar{w}_3\). Previous works either only considered multiplication gates [6] or separate multiplication and division gates [9]. Using \(\mathsf {multdiv}\) gates can, in some cases, reduce the circuit size compared to separate multiplication and division gates.
Class \(\mathcal {C}^{\mathsf {S}}\) contains \(\mathbb {F}\)-arithmetic circuits  , such that:
, such that:
-
(1)
For any
 , there exists
, there exists  such that
such that 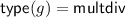 ,
,  , and
, and 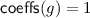 . That is, each trapdoor itself should be a part of the output of the circuit. Adding those \(\mathsf {multdiv}\) gates corresponds to the MPC protocol combining the shares of trapdoor \(\mathsf {ts}_{}{}\) of each party to get \([\mathsf {tc}]_{\iota }\).
. That is, each trapdoor itself should be a part of the output of the circuit. Adding those \(\mathsf {multdiv}\) gates corresponds to the MPC protocol combining the shares of trapdoor \(\mathsf {ts}_{}{}\) of each party to get \([\mathsf {tc}]_{\iota }\). -
(2)
For any
 :
:-
(a)
 . Hence, each gate output is a CRS element.
. Hence, each gate output is a CRS element. -
(b)
If
 then
then  ,
,  . That is, the left multiplication input can be a constant or an output of a previous gate, the right multiplication and division inputs have to be one of the inputs of the circuit. This allows to easily verify the computation in the MPC. For convenience, we require further that constant value of
. That is, the left multiplication input can be a constant or an output of a previous gate, the right multiplication and division inputs have to be one of the inputs of the circuit. This allows to easily verify the computation in the MPC. For convenience, we require further that constant value of  can only be 1; from computational point of view nothing changes since
can only be 1; from computational point of view nothing changes since  can be any constant.
can be any constant. -
(c)
If
 then
then  . Addition is done locally in MPC (does not require additional rounds) with the outputs of previous gates, since outputs correspond to publicly known CRS elements.
. Addition is done locally in MPC (does not require additional rounds) with the outputs of previous gates, since outputs correspond to publicly known CRS elements.
-
(a)
The sampling depth \({\text {depth}}_{\mathsf {S}}\) of a gate  is defined as follows:
is defined as follows:
-
1.
\({\text {depth}}_{\mathsf {S}}(g) = 1\) if g is a \(\mathsf {multdiv}\) gate and
 is a constant.
is a constant. -
2.
\({\text {depth}}_{\mathsf {S}}(g) = \max \{{\text {depth}}_{\mathsf {S}}(g'): g' \text { an input of } g\}\) for other \(\mathsf {multdiv}\) gates,
-
3.
\({\text {depth}}_{\mathsf {S}}(g) = b_g + \max \{{\text {depth}}_{\mathsf {S}}(g'): g' \text { an input of } g\}\) for any \(\mathsf {add}\) gate, where
(i) \(b_g = 0\) iff all the input gates of g are \(\mathsf {add}\) gates. (ii) \(b_g = 1\), otherwise.
Denote  . We again defined \({\text {depth}}_{\mathsf {S}}\) slightly differently compared to [6]; our definition emphasizes the fact that addition gates can be executed locally. Essentially, \(\mathsf {N}_{p}\cdot {\text {depth}}_{\mathsf {S}}(g_w)\) will be the number of rounds that it takes to compute \([\bar{w}]_{\iota }\) with our MPC protocol. The multiplicative depth of a circuit (denoted by
. We again defined \({\text {depth}}_{\mathsf {S}}\) slightly differently compared to [6]; our definition emphasizes the fact that addition gates can be executed locally. Essentially, \(\mathsf {N}_{p}\cdot {\text {depth}}_{\mathsf {S}}(g_w)\) will be the number of rounds that it takes to compute \([\bar{w}]_{\iota }\) with our MPC protocol. The multiplicative depth of a circuit (denoted by  ) is the maximum number of multiplication gates from any input to any output. An exemplary \(\mathcal {C}^{\mathsf {S}}\)-circuit is given in Fig. 3.
) is the maximum number of multiplication gates from any input to any output. An exemplary \(\mathcal {C}^{\mathsf {S}}\)-circuit is given in Fig. 3.
Multi-party Circuit Evaluation Protocol. We describe the circuit evaluation protocol, similar to the one in [6], that allows to evaluate any \(\mathcal {C}^{\mathsf {S}}\)-circuits “in the exponent”. We assume there are \(\mathsf {N}_{p}\) parties  , each having published a share \([\mathsf {ts}_{i, s}]_{\star } \in \mathbb {F}^*\), for \(s \in [1 \, .. \, t]\). The goal of the evaluation protocol is to output
, each having published a share \([\mathsf {ts}_{i, s}]_{\star } \in \mathbb {F}^*\), for \(s \in [1 \, .. \, t]\). The goal of the evaluation protocol is to output  where
where  are \(\mathcal {C}^{\mathsf {S}}\)-circuits and \(\mathsf {tc}= (\prod _j \mathsf {ts}_{j, 1}, \ldots , \prod _j \mathsf {ts}_{j, t})\). This protocol constructs a well-formed CRS, given that \(\mathsf {tc}\) is the CRS trapdoor and
are \(\mathcal {C}^{\mathsf {S}}\)-circuits and \(\mathsf {tc}= (\prod _j \mathsf {ts}_{j, 1}, \ldots , \prod _j \mathsf {ts}_{j, t})\). This protocol constructs a well-formed CRS, given that \(\mathsf {tc}\) is the CRS trapdoor and  ,
,  are respectively all the \(\mathbb {G}_1\) and \(\mathbb {G}_2\) elements of the CRS. In Sect. 4, we combine the circuit evaluation protocol with a UC-secure commitment scheme to obtain a UC-secure CRS-generation protocol. Each step in the circuit evaluation protocol is publicly verifiable and hence, no trust is needed at all; except that to get the correct distribution we need to trust one party.
are respectively all the \(\mathbb {G}_1\) and \(\mathbb {G}_2\) elements of the CRS. In Sect. 4, we combine the circuit evaluation protocol with a UC-secure commitment scheme to obtain a UC-secure CRS-generation protocol. Each step in the circuit evaluation protocol is publicly verifiable and hence, no trust is needed at all; except that to get the correct distribution we need to trust one party.
We make two significant changes to the circuit evaluation protocol compared to [6]: (i) we do not require that  , allowing CRS elements in \(\mathbb {G}_1\) and \(\mathbb {G}_2\) to be different, and (ii) instead of multiplication gates we evaluate \(\mathsf {multdiv}\) gates.
, allowing CRS elements in \(\mathbb {G}_1\) and \(\mathbb {G}_2\) to be different, and (ii) instead of multiplication gates we evaluate \(\mathsf {multdiv}\) gates.
Let us first describe the computation of \([\bar{w}]_{\iota }\) for a single gate \(g_w\). For an \(\mathsf {add}\) gate, given that all input gates have already been computed, that is, \([\bar{w}_1, \dots , \bar{w}_f]_{\iota }\) are already public, each  computes \([\bar{w}]_{\iota } = a_0 + \sum _{j = 1}^f a_j [\bar{w}_j]_{\iota }\) locally. A \(\mathsf {multdiv}\) gate g, with
computes \([\bar{w}]_{\iota } = a_0 + \sum _{j = 1}^f a_j [\bar{w}_j]_{\iota }\) locally. A \(\mathsf {multdiv}\) gate g, with  and
and  , can be implemented by the \(\mathsf {N}_{p}\)-round protocol \(\mathsf {Eval_{md}}\) from Fig. 4. Here, each party
, can be implemented by the \(\mathsf {N}_{p}\)-round protocol \(\mathsf {Eval_{md}}\) from Fig. 4. Here, each party  takes as input \([b]_{\iota }\) (the output of the preceding gate or just \([1]_{\iota }\) if there is none), runs \(\mathsf {C}_{\mathsf {md}}\) procedure on
takes as input \([b]_{\iota }\) (the output of the preceding gate or just \([1]_{\iota }\) if there is none), runs \(\mathsf {C}_{\mathsf {md}}\) procedure on  ,
,  (her shares of the trapdoor that are also g’s inputs), and broadcasts its output. Note that \([b]_{\iota }\) corresponds to the left multiplication, \(\mathsf {ts}_{i, s}\) to the right multiplication, and \(\mathsf {ts}_{i, k}\) to the division input of g.
(her shares of the trapdoor that are also g’s inputs), and broadcasts its output. Note that \([b]_{\iota }\) corresponds to the left multiplication, \(\mathsf {ts}_{i, s}\) to the right multiplication, and \(\mathsf {ts}_{i, k}\) to the division input of g.
Importantly, since each party  published \([\{\mathsf {ts}_{i, j}\}_{j = 1}^{t}]_{\star }\), everybody can verify that
published \([\{\mathsf {ts}_{i, j}\}_{j = 1}^{t}]_{\star }\), everybody can verify that  executed \(\mathsf {C}_{\mathsf {md}}\) correctly by checking if \(\mathsf {V}_{\mathsf {md}}([b_i]_{\iota }, [b_{i - 1}]_{\iota }, a, [\mathsf {ts}_{i, s}, \mathsf {ts}_{i, k}]_{3 - \iota }) = 1\), where \([b_i]_{\iota }\) is
executed \(\mathsf {C}_{\mathsf {md}}\) correctly by checking if \(\mathsf {V}_{\mathsf {md}}([b_i]_{\iota }, [b_{i - 1}]_{\iota }, a, [\mathsf {ts}_{i, s}, \mathsf {ts}_{i, k}]_{3 - \iota }) = 1\), where \([b_i]_{\iota }\) is  ’s output and \([b_{i - 1}]_{\iota }\) is her input (the output of the party
’s output and \([b_{i - 1}]_{\iota }\) is her input (the output of the party  ). We assume \([b_0]_{\iota } = [1]_{\iota }\) to allow the parties to check the computations of
). We assume \([b_0]_{\iota } = [1]_{\iota }\) to allow the parties to check the computations of  . Just running \(\mathsf {Eval_{md}}\) to evaluate each \(\mathsf {multdiv}\) gate in
. Just running \(\mathsf {Eval_{md}}\) to evaluate each \(\mathsf {multdiv}\) gate in  would require
would require  rounds. Next we see that computation can be parallelized to obtain
rounds. Next we see that computation can be parallelized to obtain  rounds.
rounds.
Optimised Multi-party Circuit Evaluation Protocol. Before presenting the complete (parallelised) circuit evaluation protocol, we provide an illustrative example of how \(\mathcal {C}^{\mathsf {S}}\)-circuits can be evaluated efficiently using multiple parties. The idea behind this approach is to allow parties to evaluate the circuit not gate-by-gate but all the gates of the same sampling depth. We say that gates are in the same layer if they have the same \({\text {depth}}_{\mathsf {S}}\). Following the definition of \({\text {depth}}_{\mathsf {S}}\), layers are separated by add gates. That is, two gates, say \(g_1\) and \(g_2\) are in different layers if there is an add gate \(g_{add}\) such that \(g_1\) (or \(g_2\)) depends on \(g_{add}\)’s output, while the other gate does not. In each layer, each gate is computed using only trapdoor elements and outputs from gates of some preceding layer. Parties evaluate the layer in a round-robin manner broadcasting intermediate values which allows other parties to verify the computation.
This is how the optimised protocol and the naive MPC protocol differ. Since naive protocol evaluates circuit gate-by-gate, one gate’s output can be another’s input even if both share the same layer. For instance, consider gates \(g_1\) and \(g_3\) from Fig. 3. There, \(g_1\)’s output is \(g_3\)’s input and they are both in the same layer. Since the output of \(g_1\) is computed before \(g_3\) is evaluated, it can be used in the computation. On the other hand, in the optimised version of circuit evaluation all gates in the same layer are evaluated at the same time, thus \(g_3\) is computed at the same time when \(g_1\) is computed.
Example 1
Suppose we have parties  ,
,  ,
,  that wish to compute \(\mathsf {crs}= \{[\mathsf {tc}_1]_{\star }, [\mathsf {tc}_2]_{\star }, [\mathsf {tc}_1^2 / \mathsf {tc}_2]_{1}, [\mathsf {tc}_1^2 / \mathsf {tc}_2 + \mathsf {tc}_2]_{1}\}\). Let us only focus on the computation of \(\mathbb {G}_1\) elements. This is represented by a \(\mathcal {C}^{\mathsf {S}}\)-circuit in Fig. 3 where we have (i) a \(\mathsf {multdiv}\) gate \(g_1\) with input values \((1, \mathsf {tc}_1, 1)\), (ii) a \(\mathsf {multdiv}\) gate \(g_2\) with input values \((1, \mathsf {tc}_2, 1)\), (iii) a \(\mathsf {multdiv}\) gate \(g_3\) that takes the output of \(g_1\) as
that wish to compute \(\mathsf {crs}= \{[\mathsf {tc}_1]_{\star }, [\mathsf {tc}_2]_{\star }, [\mathsf {tc}_1^2 / \mathsf {tc}_2]_{1}, [\mathsf {tc}_1^2 / \mathsf {tc}_2 + \mathsf {tc}_2]_{1}\}\). Let us only focus on the computation of \(\mathbb {G}_1\) elements. This is represented by a \(\mathcal {C}^{\mathsf {S}}\)-circuit in Fig. 3 where we have (i) a \(\mathsf {multdiv}\) gate \(g_1\) with input values \((1, \mathsf {tc}_1, 1)\), (ii) a \(\mathsf {multdiv}\) gate \(g_2\) with input values \((1, \mathsf {tc}_2, 1)\), (iii) a \(\mathsf {multdiv}\) gate \(g_3\) that takes the output of \(g_1\) as  , the circuit’s inputs \(\mathsf {tc}_1\) as
, the circuit’s inputs \(\mathsf {tc}_1\) as  , and \(\mathsf {tc}_2\) as
, and \(\mathsf {tc}_2\) as  , that is, the input values of \(g_3\) are \((\mathsf {tc}_1, \mathsf {tc}_1, \mathsf {tc}_2)\), and (iv) an add gate \(g_{add}\) that adds outputs of \(g_2\) and \(g_3\). The parties respectively publish shares \([\mathsf {ts}_{1,1}, \mathsf {ts}_{1,2}]_{\star }\), \([\mathsf {ts}_{2,1}, \mathsf {ts}_{2,2}]_{\star }\), \([\mathsf {ts}_{3,1}, \mathsf {ts}_{3,2}]_{\star }\).
, that is, the input values of \(g_3\) are \((\mathsf {tc}_1, \mathsf {tc}_1, \mathsf {tc}_2)\), and (iv) an add gate \(g_{add}\) that adds outputs of \(g_2\) and \(g_3\). The parties respectively publish shares \([\mathsf {ts}_{1,1}, \mathsf {ts}_{1,2}]_{\star }\), \([\mathsf {ts}_{2,1}, \mathsf {ts}_{2,2}]_{\star }\), \([\mathsf {ts}_{3,1}, \mathsf {ts}_{3,2}]_{\star }\).
-
In the first round,
 broadcasts \([b_{g_1}^{1}]_{1} \leftarrow [\mathsf {ts}_{1,1}]_{1}\) for gate \(g_1\), \([b_{g_2}^1]_{1} \leftarrow [\mathsf {ts}_{1,2}]_{1}\) for gate \(g_2\), and \([b_{g_3}^1]_{1} \leftarrow [\mathsf {ts}_{1,1}^2 / \mathsf {ts}_{1,2}]_{1}\) for gate \(g_3\).
broadcasts \([b_{g_1}^{1}]_{1} \leftarrow [\mathsf {ts}_{1,1}]_{1}\) for gate \(g_1\), \([b_{g_2}^1]_{1} \leftarrow [\mathsf {ts}_{1,2}]_{1}\) for gate \(g_2\), and \([b_{g_3}^1]_{1} \leftarrow [\mathsf {ts}_{1,1}^2 / \mathsf {ts}_{1,2}]_{1}\) for gate \(g_3\). -
In the second round,
 broadcasts \([b_{g_1}^2]_{1} \leftarrow \mathsf {ts}_{2,1} \cdot [b_{g_1}^1]_{1}\) for gate \(g_1\), \([b_{g_2}^2]_{1} \leftarrow \mathsf {ts}_{2,2} \cdot [b_{g_2}^1]_{1}\) for gate \(g_2\), and \([b_{g_3,1}^2]_{1} \leftarrow \mathsf {ts}_{2,1} \cdot [b_{g_3}^1]_{1}\), \([b_{g_3,2}^2]_{1} \leftarrow (\mathsf {ts}_{2,1} / \mathsf {ts}_{2,2}) \cdot [b_{g_3,1}^2]_{1}\) for \(g_3\) (note that \(g_3\) required two computations rather than one).
broadcasts \([b_{g_1}^2]_{1} \leftarrow \mathsf {ts}_{2,1} \cdot [b_{g_1}^1]_{1}\) for gate \(g_1\), \([b_{g_2}^2]_{1} \leftarrow \mathsf {ts}_{2,2} \cdot [b_{g_2}^1]_{1}\) for gate \(g_2\), and \([b_{g_3,1}^2]_{1} \leftarrow \mathsf {ts}_{2,1} \cdot [b_{g_3}^1]_{1}\), \([b_{g_3,2}^2]_{1} \leftarrow (\mathsf {ts}_{2,1} / \mathsf {ts}_{2,2}) \cdot [b_{g_3,1}^2]_{1}\) for \(g_3\) (note that \(g_3\) required two computations rather than one). -
In the third round,
 broadcasts \([b_{g_1}^3]_{1} \leftarrow \mathsf {ts}_{3,1} \cdot [b_{g_1}^2]_{1}\) for gate \(g_1\), \([b_{g_2}^3]_{1} \leftarrow \mathsf {ts}_{3,2} \cdot [b_{g_2}^2]_{1}\) for gate \(g_2\), and \([b_{g_3, 1}^3]_{1} \leftarrow \mathsf {ts}_{3,1} \cdot [b_{g_3, 2}^2]_{1}\), \([b_{g_3, 2}^3]_{1} \leftarrow (\mathsf {ts}_{3,1}/\mathsf {ts}_{3,2}) \cdot [b_{g_3, 1}^3]_{1}\) for \(g_3\). For \(g_{add}\) each party computes \([b_{g_{add}}]_{1} \leftarrow [b_{g_2}^3]_{1} + [b_{g_3, 2}^3]_{1}\).
broadcasts \([b_{g_1}^3]_{1} \leftarrow \mathsf {ts}_{3,1} \cdot [b_{g_1}^2]_{1}\) for gate \(g_1\), \([b_{g_2}^3]_{1} \leftarrow \mathsf {ts}_{3,2} \cdot [b_{g_2}^2]_{1}\) for gate \(g_2\), and \([b_{g_3, 1}^3]_{1} \leftarrow \mathsf {ts}_{3,1} \cdot [b_{g_3, 2}^2]_{1}\), \([b_{g_3, 2}^3]_{1} \leftarrow (\mathsf {ts}_{3,1}/\mathsf {ts}_{3,2}) \cdot [b_{g_3, 1}^3]_{1}\) for \(g_3\). For \(g_{add}\) each party computes \([b_{g_{add}}]_{1} \leftarrow [b_{g_2}^3]_{1} + [b_{g_3, 2}^3]_{1}\).
Finally, if we define \(\mathsf {tc}_1 := \mathsf {ts}_{1,1} \cdot \mathsf {ts}_{2,1} \cdot \mathsf {ts}_{3,1}\) and \(\mathsf {tc}_2 := \mathsf {ts}_{1,2} \cdot \mathsf {ts}_{2,2} \cdot \mathsf {ts}_{3,2}\), then the outputs of  contain \([b_{g_1}^3]_{1} = [\mathsf {tc}_1]_{1}\), \([b_{g_2}^3]_{1} = [\mathsf {tc}_2]_{1}\), and \([b_{g_3, 2}^3]_{1} = [\mathsf {tc}_1^2 / \mathsf {tc}_2]_{1}\); moreover, \([b_{g_{add}}]_{1} = [\mathsf {tc}_2 + \mathsf {tc}_1^2 / \mathsf {tc}_2]_{1}\). Besides addition, each element is built up one share multiplication at a time and hence the computation can be verified with pairings, e.g, the last output \([b_{g_3,2}^2]_{1}\) of
contain \([b_{g_1}^3]_{1} = [\mathsf {tc}_1]_{1}\), \([b_{g_2}^3]_{1} = [\mathsf {tc}_2]_{1}\), and \([b_{g_3, 2}^3]_{1} = [\mathsf {tc}_1^2 / \mathsf {tc}_2]_{1}\); moreover, \([b_{g_{add}}]_{1} = [\mathsf {tc}_2 + \mathsf {tc}_1^2 / \mathsf {tc}_2]_{1}\). Besides addition, each element is built up one share multiplication at a time and hence the computation can be verified with pairings, e.g, the last output \([b_{g_3,2}^2]_{1}\) of  is correctly computed exactly when \([b_{g_3,2}^2]_{1} \bullet [\mathsf {ts}_{2,2}]_{2} = [b_{g_3,1}^2]_{1} \bullet [\mathsf {ts}_{2,1}]_{2}\). \(\square \)
is correctly computed exactly when \([b_{g_3,2}^2]_{1} \bullet [\mathsf {ts}_{2,2}]_{2} = [b_{g_3,1}^2]_{1} \bullet [\mathsf {ts}_{2,1}]_{2}\). \(\square \)
Motivated by the example above, we give the full and formal description of the circuit evaluation protocol. Let  , for \(\iota \in \{1,2\}\), and
, for \(\iota \in \{1,2\}\), and  be a circuit layer that contains all \(\mathsf {multdiv}\) gates g at sampling depth d. For any
be a circuit layer that contains all \(\mathsf {multdiv}\) gates g at sampling depth d. For any  let
let  output the longest path \((g_1, \dots , g_q = g)\) such that each
output the longest path \((g_1, \dots , g_q = g)\) such that each  , and, for \(j < q\),
, and, for \(j < q\),  . Intuitively, this is the path of gates in
. Intuitively, this is the path of gates in  that following only the left inputs lead up to the gate g, say,
that following only the left inputs lead up to the gate g, say,  for the circuit
for the circuit  in Fig. 3. For simplicity, we describe a \(\mathsf {multdiv}\) gate g by a tuple \(([b]_{\iota }, a, s, k)\) where \([b]_{\iota } = [\overline{\mathsf {L\text {-}input}} (g)]_{\iota }\) is the left input value, assumed already to be known by the parties,
in Fig. 3. For simplicity, we describe a \(\mathsf {multdiv}\) gate g by a tuple \(([b]_{\iota }, a, s, k)\) where \([b]_{\iota } = [\overline{\mathsf {L\text {-}input}} (g)]_{\iota }\) is the left input value, assumed already to be known by the parties,  ,
,  , and
, and  .
.
The parties evaluate \(\mathsf {multdiv}\) gates of the circuit in order  , where \(D_{\iota }\) is the sampling depth of
, where \(D_{\iota }\) is the sampling depth of  . After each layer \(C_{\iota , d}\) each party locally evaluates all the addition gates at depth \(d + 1\). The evaluation of
. After each layer \(C_{\iota , d}\) each party locally evaluates all the addition gates at depth \(d + 1\). The evaluation of  proceeds in a round-robin fashion. First,
proceeds in a round-robin fashion. First,  evaluates
evaluates  with her input shares \(\mathsf {ts}_{1,k}\) alone. Next,
with her input shares \(\mathsf {ts}_{1,k}\) alone. Next,  multiplies her shares \(\mathsf {ts}_{2,k}\) to each output of
multiplies her shares \(\mathsf {ts}_{2,k}\) to each output of  . However, to make computation verifiable, if
. However, to make computation verifiable, if  is supposed to compute \([b_{g}^1 \cdot \mathsf {ts}_{2, \alpha _1} \cdot \dots \mathsf {ts}_{2, \alpha _q}]_{\iota }\), where \([b_{g}^1]_{\iota }\) is some output of
is supposed to compute \([b_{g}^1 \cdot \mathsf {ts}_{2, \alpha _1} \cdot \dots \mathsf {ts}_{2, \alpha _q}]_{\iota }\), where \([b_{g}^1]_{\iota }\) is some output of  , then it is done one multiplication at a time. Namely, she outputs \([b_{g,1}^2]_{\iota } = [b_{g}^1 \cdot \mathsf {ts}_{2, \alpha _1}]_{\iota }\), \([b_{g,2}^2]_{\iota } = [b_{g,1}^2 \cdot \mathsf {ts}_{2, \alpha _2}]_{\iota }\), ..., \([b_{g,q}^2]_{\iota } = [b_{g,q-1}^2 \cdot \mathsf {ts}_{2, \alpha _q}]_{\iota }\). Each multiplication would correspond to exactly one gate in
, then it is done one multiplication at a time. Namely, she outputs \([b_{g,1}^2]_{\iota } = [b_{g}^1 \cdot \mathsf {ts}_{2, \alpha _1}]_{\iota }\), \([b_{g,2}^2]_{\iota } = [b_{g,1}^2 \cdot \mathsf {ts}_{2, \alpha _2}]_{\iota }\), ..., \([b_{g,q}^2]_{\iota } = [b_{g,q-1}^2 \cdot \mathsf {ts}_{2, \alpha _q}]_{\iota }\). Each multiplication would correspond to exactly one gate in  . The elements \([b_{g,1}^2, \dots , b_{g,q-1}^2]_{\iota }\) are used only for verification; \([b_{g,q}^2]_{\iota }\) is additionally used by
. The elements \([b_{g,1}^2, \dots , b_{g,q-1}^2]_{\iota }\) are used only for verification; \([b_{g,q}^2]_{\iota }\) is additionally used by  to continue the computation. Each subsequent party
to continue the computation. Each subsequent party  multiplies her shares to the output of
multiplies her shares to the output of  in a similar fashion. This protocol requires only
in a similar fashion. This protocol requires only  rounds.
rounds.
Let \(\mathsf {cert}^\iota = (\mathsf {cert}^{\iota }_1, \dots , \mathsf {cert}^{\iota }_{D_{\iota }})\) be the total transcript (certificate) in \(\mathbb {G}_{\iota }\) corresponding to the output of the multi-party evaluation of  where \(\mathsf {cert}^{\iota }_r\) is the transcript in round r. Denote \(\mathsf {cert}:= (\mathsf {cert}^1, \mathsf {cert}^2)\). All gates of depth r of
where \(\mathsf {cert}^{\iota }_r\) is the transcript in round r. Denote \(\mathsf {cert}:= (\mathsf {cert}^1, \mathsf {cert}^2)\). All gates of depth r of  are evaluated by a uniquely fixed party
are evaluated by a uniquely fixed party  . In what follows, let \(i = \mathsf {rndplayer}(r)\) be the index of this party.
. In what follows, let \(i = \mathsf {rndplayer}(r)\) be the index of this party.
The complete description of evaluation and verification of a layer  is given in Fig. 5 with function \(\mathsf {C}_{\mathsf {layer}}\) and \(\mathsf {V}_{\mathsf {layer}}\) that have the following interface. First, for \(i = \mathsf {rndplayer}(r)\) and for both \(\iota \in \{1, 2\}\), in round r to compute
is given in Fig. 5 with function \(\mathsf {C}_{\mathsf {layer}}\) and \(\mathsf {V}_{\mathsf {layer}}\) that have the following interface. First, for \(i = \mathsf {rndplayer}(r)\) and for both \(\iota \in \{1, 2\}\), in round r to compute  ,
,  computes
computes  , given a circuit layer
, given a circuit layer  , the shares \(\mathsf {ts}_{i, k}\) for all \(t\) trapdoors of \(\mathsf {tc}_k\), and the transcript \(\{\mathsf {cert}^{\iota }_{j}\}_{j = 1}^{r-1}\) of all previous computation. Second, any party can verify, by using the algorithm
, the shares \(\mathsf {ts}_{i, k}\) for all \(t\) trapdoors of \(\mathsf {tc}_k\), and the transcript \(\{\mathsf {cert}^{\iota }_{j}\}_{j = 1}^{r-1}\) of all previous computation. Second, any party can verify, by using the algorithm  , that the computation of the circuit layer
, that the computation of the circuit layer  in round r has been performed correctly by
in round r has been performed correctly by  . In particular,
. In particular,  checks that \(\mathsf {V}_{\mathsf {layer}}\) outputs 1 for all rounds since
checks that \(\mathsf {V}_{\mathsf {layer}}\) outputs 1 for all rounds since  ’s previous round before executing \(\mathsf {C}_{\mathsf {layer}}\) for her new round. Importantly, executing \(\mathsf {V}_{\mathsf {layer}}\) does not assume the knowledge of any trapdoors.
’s previous round before executing \(\mathsf {C}_{\mathsf {layer}}\) for her new round. Importantly, executing \(\mathsf {V}_{\mathsf {layer}}\) does not assume the knowledge of any trapdoors.
4 UC-Secure CRS Generation
We propose a functionality \(\mathcal {F}_{\mathsf {mcrs}}\) for multi-party CRS generation of any \(\mathcal {C}^{\mathsf {S}}\)-SNARK. Finally, we construct a protocol \(\mathsf {K}_{\mathsf {mcrs}}\) that UC-realizes \(\mathcal {F}_{\mathsf {mcrs}}\) in the \(\mathcal {F}_{\mathsf {dlmcom}}\)-hybrid model.
New Ideal Functionality. In Fig. 6, we define the new ideal functionality  for pairing-based (since it outputs elements from \(\mathbb {G}_{\iota }\)) multi-party CRS-generation protocol. The CRS is described by a \(t\)-input arithmetic circuits
for pairing-based (since it outputs elements from \(\mathbb {G}_{\iota }\)) multi-party CRS-generation protocol. The CRS is described by a \(t\)-input arithmetic circuits  over a field
over a field  such that
such that  for
for  , where
, where  is a samplable distribution over
is a samplable distribution over  .
.
The trapdoor \(\mathsf {tc}\) is constructed by combining shares  of each party
of each party  by a function \(\mathsf {comb}\). For each honest party
by a function \(\mathsf {comb}\). For each honest party  , the ideal functionality picks
, the ideal functionality picks  , whereas for malicious parties we only know
, whereas for malicious parties we only know  . The function \(\mathsf {comb}\) should be defined so that if there exists at least one honest party then \(\mathsf {tc}\leftarrow \mathsf {comb}(\mathsf {ts}_{1}, \dots , \mathsf {ts}_{\mathsf {N}_{p}})\) is also distributed accordingly to
. The function \(\mathsf {comb}\) should be defined so that if there exists at least one honest party then \(\mathsf {tc}\leftarrow \mathsf {comb}(\mathsf {ts}_{1}, \dots , \mathsf {ts}_{\mathsf {N}_{p}})\) is also distributed accordingly to  . In such case we say that
. In such case we say that  is \(\mathsf {comb}\)-friendly. It is true for example when \(\mathsf {comb}\) is point-wise multiplication and
is \(\mathsf {comb}\)-friendly. It is true for example when \(\mathsf {comb}\) is point-wise multiplication and  is a uniform distribution over
is a uniform distribution over  as, e.g., in [6, 8, 9]. This guarantees the correct distribution of \(\mathsf {crs}\) if at least one party is honest.
as, e.g., in [6, 8, 9]. This guarantees the correct distribution of \(\mathsf {crs}\) if at least one party is honest.
We believe \(\mathcal {F}_{\mathsf {mcrs}}\) captures essentially any reasonable pairing-based multi-party CRS-generation protocol, where the trapdoor is shared between \(\mathsf {N}_{p}\) parties. Note that specifying distinct honest and corrupted inputs to the functionality is common in the UC literature, [3, 24]. In Theorem 2, we will establish the relation between \(\mathcal {F}_{\mathsf {crs}}\) and \(\mathcal {F}_{\mathsf {mcrs}}\).
New Protocol. We define the new multi-party CRS-generation protocol  (see Fig. 7) in the \(\mathcal {F}_{\mathsf {dlmcom}}\)-hybrid model. This allows us to instantiate the protocol with any DL-extractable commitment and, moreover, the only trust assumption that the protocol needs is the one inherited from the commitment scheme, e.g., using construction from [1] gives security in the RPK model. Given that \(D_{\iota }\) is the sampling depth of
(see Fig. 7) in the \(\mathcal {F}_{\mathsf {dlmcom}}\)-hybrid model. This allows us to instantiate the protocol with any DL-extractable commitment and, moreover, the only trust assumption that the protocol needs is the one inherited from the commitment scheme, e.g., using construction from [1] gives security in the RPK model. Given that \(D_{\iota }\) is the sampling depth of  , then \(R = \mathsf {N}_{p}\cdot \max (D_1, D_2)\) is the number of rounds needed to evaluate both circuits in parallel. For the sake of simplicity, we assume \(\mathsf {cert}^{\iota }_r\) is the empty string for \(r > \mathsf {N}_{p}\cdot D_{\iota }\).
, then \(R = \mathsf {N}_{p}\cdot \max (D_1, D_2)\) is the number of rounds needed to evaluate both circuits in parallel. For the sake of simplicity, we assume \(\mathsf {cert}^{\iota }_r\) is the empty string for \(r > \mathsf {N}_{p}\cdot D_{\iota }\).
\(\mathsf {K}_{\mathsf {mcrs}}\) proceeds in rounds: (i) In round 1, each  gets a signal
gets a signal  ; parties commit to their shares of trapdoor \(\mathsf {tc}\). (ii) In round 2, each party
; parties commit to their shares of trapdoor \(\mathsf {tc}\). (ii) In round 2, each party  gets a signal \((\mathtt {mcrsopen}, \mathsf {sid})\); parties open their shares. (iii) In round \(r \in [3 \, .. \, R+2]\),
gets a signal \((\mathtt {mcrsopen}, \mathsf {sid})\); parties open their shares. (iii) In round \(r \in [3 \, .. \, R+2]\),  is triggered, where \(i = \mathsf {rndplayer}(r)\); parties jointly compute \(\mathsf {crs}\) from the trapdoor shares; before party
is triggered, where \(i = \mathsf {rndplayer}(r)\); parties jointly compute \(\mathsf {crs}\) from the trapdoor shares; before party  performs her computation, she checks if previous computation were done correctly. (iv) In round \(R + 3\), each party
performs her computation, she checks if previous computation were done correctly. (iv) In round \(R + 3\), each party  gets the signal
gets the signal  and extracts the \(\mathsf {crs}\) from \(\mathsf {cert}\). The CRS will be output by
and extracts the \(\mathsf {crs}\) from \(\mathsf {cert}\). The CRS will be output by  only if all the verifications succeeded. The signals \(\mathtt {sc}\), \(\mathtt {mcrsopen}\), \(\mathtt {mcrscertok}\), and \(\mathtt {mcrsfinal}\) can be sent either by a controller server or by the internal clock of
only if all the verifications succeeded. The signals \(\mathtt {sc}\), \(\mathtt {mcrsopen}\), \(\mathtt {mcrscertok}\), and \(\mathtt {mcrsfinal}\) can be sent either by a controller server or by the internal clock of  . The construction uses a secure broadcast channel; thus, if a message is broadcast, then all parties are guaranteed to receive the same message. Note that after
. The construction uses a secure broadcast channel; thus, if a message is broadcast, then all parties are guaranteed to receive the same message. Note that after  obtains \((\mathtt {rcpt}, \mathsf {lbl}_{i j k})\), for \(i \in [1 \, .. \, \mathsf {N}_{p}], j \not = i, k \in [1 \, .. \, t]\), she broadcasts \((\mathtt {mcrsreceipt}, \mathsf {lbl}_{i j k})\) since \(\mathtt {rcpt}\) is not broadcast.
obtains \((\mathtt {rcpt}, \mathsf {lbl}_{i j k})\), for \(i \in [1 \, .. \, \mathsf {N}_{p}], j \not = i, k \in [1 \, .. \, t]\), she broadcasts \((\mathtt {mcrsreceipt}, \mathsf {lbl}_{i j k})\) since \(\mathtt {rcpt}\) is not broadcast.
Security. To prove UC-security of \(\mathsf {K}_{\mathsf {mcrs}}\), we restrict \(\mathcal {F}_{\mathsf {mcrs}}\) as follows: (i)  such that
such that  for \(\iota \in \{1,2\}\). Note that this means that for any trapdoor element \(\mathsf {tc}_k \in \mathsf {tc}\), \([\mathsf {tc}_k]_{\star } \in \mathsf {crs}\). (ii)
for \(\iota \in \{1,2\}\). Note that this means that for any trapdoor element \(\mathsf {tc}_k \in \mathsf {tc}\), \([\mathsf {tc}_k]_{\star } \in \mathsf {crs}\). (ii)  is the uniform distribution on
is the uniform distribution on  , (iii) \(\mathsf {comb}(\mathsf {ts}_{1}, \dots , \mathsf {ts}_{\mathsf {N}_{p}}) := \mathsf {ts}_{1} \circ \ldots \circ \mathsf {ts}_{\mathsf {N}_{p}}\), where \(\circ \) denotes point-wise multiplication, and \(\mathsf {ts}_{i k}\) is
, (iii) \(\mathsf {comb}(\mathsf {ts}_{1}, \dots , \mathsf {ts}_{\mathsf {N}_{p}}) := \mathsf {ts}_{1} \circ \ldots \circ \mathsf {ts}_{\mathsf {N}_{p}}\), where \(\circ \) denotes point-wise multiplication, and \(\mathsf {ts}_{i k}\) is  ’s share of \(\mathsf {tc}_k\).
’s share of \(\mathsf {tc}_k\).
Theorem 1
\(\mathsf {K}_{\mathsf {mcrs}}\) UC-realizes \(\mathcal {F}_{\mathsf {mcrs}}\) in the \(\mathcal {F}_{\mathsf {dlmcom}}\)-hybrid model with perfect security against a static adversary. Formally, there exits a PPT simulator  such that for every static (covert) PPT adversary
such that for every static (covert) PPT adversary  and for any non-uniform PPT environment \(\mathcal {Z}\), \(\mathcal {Z}\) cannot distinguish \(\mathsf {K}_{\mathsf {mcrs}}\) composed with \(\mathcal {F}_{\mathsf {dlmcom}}\) and
and for any non-uniform PPT environment \(\mathcal {Z}\), \(\mathcal {Z}\) cannot distinguish \(\mathsf {K}_{\mathsf {mcrs}}\) composed with \(\mathcal {F}_{\mathsf {dlmcom}}\) and  from
from  composed with \(\mathcal {F}_{\mathsf {mcrs}}\). That is,
composed with \(\mathcal {F}_{\mathsf {mcrs}}\). That is,  .
.
Proof
(Sketch). To prove UC-security, we have to construct an algorithm  that is able to simulate behaviour of honest parties for \(\mathcal {Z}\) in the ideal world without knowing their real inputs. Since we are in \(\mathcal {F}_{\mathsf {dlmcom}}\)-hybrid model,
that is able to simulate behaviour of honest parties for \(\mathcal {Z}\) in the ideal world without knowing their real inputs. Since we are in \(\mathcal {F}_{\mathsf {dlmcom}}\)-hybrid model,  simulates \(\mathcal {F}_{\mathsf {dlmcom}}\) for the malicious parties and hence learns their shares. At first,
simulates \(\mathcal {F}_{\mathsf {dlmcom}}\) for the malicious parties and hence learns their shares. At first,  picks random shares \(\mathsf {ts}_{i k}'\) to simulate all the honest parties. Once the ideal functionality has received
picks random shares \(\mathsf {ts}_{i k}'\) to simulate all the honest parties. Once the ideal functionality has received  from all the honest parties and
from all the honest parties and  for all the dishonest parties (forwarded by
for all the dishonest parties (forwarded by  ), then
), then  receives \((\mathtt {CRS}, \mathsf {sid}, \mathsf {crs})\) from the ideal functionality. Now,
receives \((\mathtt {CRS}, \mathsf {sid}, \mathsf {crs})\) from the ideal functionality. Now,  fixes one honest party
fixes one honest party  and opens its commitments to \([\mathsf {ts}_{h k}^*]_{1} \leftarrow [\mathsf {tc}_k]_{1} / (\prod _{i \in [1 \, .. \, \mathsf {N}_{p}] \setminus \{h\}} \mathsf {ts}_{i k}')\) for \([\mathsf {tc}_k]_{1} \in \mathsf {crs}\) and \(\mathsf {ts}_{i k}'\) collected through \(\mathcal {F}_{\mathsf {dlmcom}}\). Since \([\mathsf {tc}_k]_{1}\) is uniformly random, then so is \([\mathsf {ts}_{h k}^*]_{1}\) (the same distribution as in the real protocol). With a similar strategy
and opens its commitments to \([\mathsf {ts}_{h k}^*]_{1} \leftarrow [\mathsf {tc}_k]_{1} / (\prod _{i \in [1 \, .. \, \mathsf {N}_{p}] \setminus \{h\}} \mathsf {ts}_{i k}')\) for \([\mathsf {tc}_k]_{1} \in \mathsf {crs}\) and \(\mathsf {ts}_{i k}'\) collected through \(\mathcal {F}_{\mathsf {dlmcom}}\). Since \([\mathsf {tc}_k]_{1}\) is uniformly random, then so is \([\mathsf {ts}_{h k}^*]_{1}\) (the same distribution as in the real protocol). With a similar strategy  simulates each gate output for
simulates each gate output for  such that the final output of the simulated protocol is \(\mathsf {crs}\), matching the output of the ideal functionality.
such that the final output of the simulated protocol is \(\mathsf {crs}\), matching the output of the ideal functionality.
We discuss challenges of adaptive security and give the full proof of this theorem in the full version of the paper. \(\square \)
5 Secure MPC for NIZKs
Next, we show that \(\mathsf {K}_{\mathsf {mcrs}}\) can be used to generate the CRS of any \(\mathcal {C}^{\mathsf {S}}\)-SNARK without harming the completeness, soundness, or (subversion) zero-knowledge properties. It could also be used to generate CRS of other primitives which can be represented by \(\mathcal {C}^{\mathsf {S}}\)-circuits, but it is especially well suited for the intricate structure of SNARK CRS. Finally, we apply the protocol to the Sub-ZK secure version [2, 14] of the most efficient zk-SNARK by Groth [20].
NIZK in the MCRS Model. Let \(\varPsi \) be a NIZK argument system secure in the \(\mathcal {F}_{\mathsf {crs}}\)-hybrid model. We show that by instantiating \(\mathcal {F}_{\mathsf {crs}}\) with \(\mathcal {F}_{\mathsf {mcrs}}\), the NIZK remains complete, sound, and zero-knowledge, provided that the adversary  controls up to \(\mathsf {N}_{p}- 1\) out of \(\mathsf {N}_{p}\) parties. Here we require that
controls up to \(\mathsf {N}_{p}- 1\) out of \(\mathsf {N}_{p}\) parties. Here we require that  is \(\mathsf {comb}\)-friendly. See Fig. 8 for the high-level description of MPC protocol for the CRS generation.
is \(\mathsf {comb}\)-friendly. See Fig. 8 for the high-level description of MPC protocol for the CRS generation.
Theorem 2
Let  and
and  be such that
be such that  is \(\mathsf {comb}\)-friendly. \(\mathsf {K}_\mathsf {crs}^{\mathcal {F}_{\mathsf {mcrs}}}\) securely realizes
is \(\mathsf {comb}\)-friendly. \(\mathsf {K}_\mathsf {crs}^{\mathcal {F}_{\mathsf {mcrs}}}\) securely realizes  in the \(\mathcal {F}_{\mathsf {mcrs}}\)-hybrid model given (covert)
in the \(\mathcal {F}_{\mathsf {mcrs}}\)-hybrid model given (covert)  corrupts up to \(\mathsf {N}_{p}- 1\) out of \(\mathsf {N}_{p}\) parties (i.e. CRS generators).
corrupts up to \(\mathsf {N}_{p}- 1\) out of \(\mathsf {N}_{p}\) parties (i.e. CRS generators).
The proof of this theorem is given in the full version of the paper. Next corollary immediately follows from the universal composition theorem [10].
Corollary 1
Let \(\varPsi \) be a NIZK argument that is complete, sound, computationally ZK, and computationally Sub-ZK in the  -hybrid model. By instantiating
-hybrid model. By instantiating  with \(\mathsf {K}_\mathsf {crs}^{\mathcal {F}_{\mathsf {mcrs}}}\), the following holds:
with \(\mathsf {K}_\mathsf {crs}^{\mathcal {F}_{\mathsf {mcrs}}}\), the following holds:
-
1.
\(\varPsi \) is complete, sound, and computationally zero-knowledge in the \(\mathcal {F}_{\mathsf {mcrs}}\)-hybrid model, given that (covert)
 corrupts up to \(\mathsf {N}_{p}- 1\) out of \(\mathsf {N}_{p}\) parties.
corrupts up to \(\mathsf {N}_{p}- 1\) out of \(\mathsf {N}_{p}\) parties. -
2.
\(\varPsi \) is Sub-ZK in the \(\mathcal {F}_{\mathsf {mcrs}}\)-hybrid model, even if (covert)
 corrupts all \(\mathsf {N}_{p}\) parties.
corrupts all \(\mathsf {N}_{p}\) parties. -
3.
If
 is a uniform distribution over
is a uniform distribution over  , \(\mathsf {comb}\) the point-wise multiplication and the CRS can be computed by \(\mathcal {C}^{\mathsf {S}}\)-circuits, then properties 1 and 2 hold in the \(\mathcal {F}_{\mathsf {dlmcom}}\)-hybrid model since \(\mathsf {K}_{\mathsf {mcrs}}\) realizes \(\mathcal {F}_{\mathsf {mcrs}}\) in that setting.
, \(\mathsf {comb}\) the point-wise multiplication and the CRS can be computed by \(\mathcal {C}^{\mathsf {S}}\)-circuits, then properties 1 and 2 hold in the \(\mathcal {F}_{\mathsf {dlmcom}}\)-hybrid model since \(\mathsf {K}_{\mathsf {mcrs}}\) realizes \(\mathcal {F}_{\mathsf {mcrs}}\) in that setting.
CRS of \(\mathsf {Z}^{*}\) Sub-ZK SNARK from [2]
Applying \(\mathsf {K}_{\mathsf {mcrs}}\) to Groth’s zk-SNARK. Figure 9 contains the description of the CRS for the Sub-ZK version of Groth’s zk-SNARK \(\mathsf {Z}^{*}\) as was proposed in [2]. We have omitted the element \([\alpha \beta ]_{T}\) that can be computed from \([\alpha ]_{1}\) and \([\beta ]_{2}\). The CRS from [2] differs from the original CRS for Groth’s zk-SNARK [20] by the entries in  which make the CRS verifiable using a \(\mathsf {CV}\) algorithm. Here, \(\ell _i (X)\) are Lagrange basis polynomials and \(\ell (X) = X^\mathsf {n}- 1\), \(u_j (X)\), \(v_j (X)\), \(w_j (X)\) are publicly-known circuit-dependent polynomials. Due to the lack of space, we do not present other algorithms of \(\mathsf {Z}^{*}\).
which make the CRS verifiable using a \(\mathsf {CV}\) algorithm. Here, \(\ell _i (X)\) are Lagrange basis polynomials and \(\ell (X) = X^\mathsf {n}- 1\), \(u_j (X)\), \(v_j (X)\), \(w_j (X)\) are publicly-known circuit-dependent polynomials. Due to the lack of space, we do not present other algorithms of \(\mathsf {Z}^{*}\).
We recall that to use the algorithm \(\mathsf {K}_\mathsf {crs}^{\mathcal {F}_{\mathsf {mcrs}}}\) the CRS has to be of the form  , where
, where  . In Fig. 9, the
. In Fig. 9, the
 entries cannot be computed from trapdoors by a \(\mathcal {C}^{\mathsf {S}}\)-circuit unless we add \( \mathsf {crs}_\mathsf {TV}= ([ (w_j (\chi ), \beta u_j (\chi ), \alpha v_j (\chi ))_{j = 0}^{\mathsf {m}}, \chi ^\mathsf {n}]_{1},[(\ell _i (\chi ))_{i = 1}^\mathsf {n}, (\chi ^{k})_{k = 1}^{\mathsf {n}- 1}]_{2}) \) to the CRS. To obtain better efficiency we additionally add \([\left( \ell _i (\chi )\right) _{i = 1}^\mathsf {n}]_{2}\) to the CRS, although they can be computed from the existing elements \([\left( \chi ^{k}\right) _{k = 1}^{\mathsf {n}- 1}]_{2}\). However, since we are adding elements to the CRS, we also need to reprove the soundness. We do this in the full version of the paper.
entries cannot be computed from trapdoors by a \(\mathcal {C}^{\mathsf {S}}\)-circuit unless we add \( \mathsf {crs}_\mathsf {TV}= ([ (w_j (\chi ), \beta u_j (\chi ), \alpha v_j (\chi ))_{j = 0}^{\mathsf {m}}, \chi ^\mathsf {n}]_{1},[(\ell _i (\chi ))_{i = 1}^\mathsf {n}, (\chi ^{k})_{k = 1}^{\mathsf {n}- 1}]_{2}) \) to the CRS. To obtain better efficiency we additionally add \([\left( \ell _i (\chi )\right) _{i = 1}^\mathsf {n}]_{2}\) to the CRS, although they can be computed from the existing elements \([\left( \chi ^{k}\right) _{k = 1}^{\mathsf {n}- 1}]_{2}\). However, since we are adding elements to the CRS, we also need to reprove the soundness. We do this in the full version of the paper.
We give a brief description of the CRS-generation protocol for \(\mathsf {Z}^{*}\) without explicitly describing the circuits  and
and  . Without directly saying it, it is assumed that parties verify all the computations as shown in Fig. 7.
. Without directly saying it, it is assumed that parties verify all the computations as shown in Fig. 7.
Share Collection Phase. Parties proceed as is in Fig. 7 to produce random and independent shares \([\mathsf {ts}_{i}]_{\star } = [\alpha _i, \beta _i, \gamma _i, \delta _i, \chi _i]_{\star }\) for each  .
.
CRS Generation Phase. (i) On layers  parties jointly compute \([\alpha , \beta , \gamma , \delta ]_{\star }\), \([(\chi ^{k})_{k = 1}^{\mathsf {n}- 1}]_{\star }\) and \([\chi ^\mathsf {n}]_{1}\). (ii) Each
parties jointly compute \([\alpha , \beta , \gamma , \delta ]_{\star }\), \([(\chi ^{k})_{k = 1}^{\mathsf {n}- 1}]_{\star }\) and \([\chi ^\mathsf {n}]_{1}\). (ii) Each  locally computes \([\left( \ell _k(\chi )\right) _{k = 1}^{\mathsf {n}}]_{\star }\), \([ (w_j (\chi ), u_j (\chi ))_{j = 0}^{\mathsf {m}} ]_{1}\), and \([(v_j (\chi ))_{j=0}^\mathsf {m}]_{\star }\) using \([(\chi ^{k})_{k = 1}^{\mathsf {n}- 1}]_{\star }\); and also computes \([\ell (\chi )]_{1} = [\chi ^\mathsf {n}]_{1} - [1]_{1}\). (iii) On layer
locally computes \([\left( \ell _k(\chi )\right) _{k = 1}^{\mathsf {n}}]_{\star }\), \([ (w_j (\chi ), u_j (\chi ))_{j = 0}^{\mathsf {m}} ]_{1}\), and \([(v_j (\chi ))_{j=0}^\mathsf {m}]_{\star }\) using \([(\chi ^{k})_{k = 1}^{\mathsf {n}- 1}]_{\star }\); and also computes \([\ell (\chi )]_{1} = [\chi ^\mathsf {n}]_{1} - [1]_{1}\). (iii) On layer  , from input \([\ell (\chi )]_{1}\), parties jointly compute \([(\chi ^{k} \ell (\chi ) / \delta )_{k=0}^{\mathsf {n}- 2}]_{1}\) using \(\mathsf {n}- 1\) \(\mathsf {multdiv}\) gates. Moreover, they compute \([\left( \beta u_l(\chi ), \alpha v_l(\chi )\right) _{l = 0}^{\mathsf {m}}]_{1}\). (iv) Each party computes locally \([\left( \beta u_l(\chi ) + \alpha v_l(\chi ) + w_l (\chi )\right) _{l = 0}^{\mathsf {m}}]_{1}\). (v) On layer
, from input \([\ell (\chi )]_{1}\), parties jointly compute \([(\chi ^{k} \ell (\chi ) / \delta )_{k=0}^{\mathsf {n}- 2}]_{1}\) using \(\mathsf {n}- 1\) \(\mathsf {multdiv}\) gates. Moreover, they compute \([\left( \beta u_l(\chi ), \alpha v_l(\chi )\right) _{l = 0}^{\mathsf {m}}]_{1}\). (iv) Each party computes locally \([\left( \beta u_l(\chi ) + \alpha v_l(\chi ) + w_l (\chi )\right) _{l = 0}^{\mathsf {m}}]_{1}\). (v) On layer  parties compute jointly \([\left( \beta u_l(\chi ) + \alpha v_l(\chi ) + w_l (\chi ) / \gamma \right) _{l = 0}^{m_0}]_{1}\) and \([\left( \beta u_l(\chi ) + \alpha v_l(\chi ) + w_l(\chi ) / \delta \right) _{l = m_0+ 1}^{\mathsf {m}}]_{1}\).
parties compute jointly \([\left( \beta u_l(\chi ) + \alpha v_l(\chi ) + w_l (\chi ) / \gamma \right) _{l = 0}^{m_0}]_{1}\) and \([\left( \beta u_l(\chi ) + \alpha v_l(\chi ) + w_l(\chi ) / \delta \right) _{l = m_0+ 1}^{\mathsf {m}}]_{1}\).
The cost of the CRS generation for \(\mathsf {Z}^{*}\) can be summarised as follows: the circuits  and
and  have both sampling depth 3; the multi-party protocol for computing the \(\mathsf {crs}\) takes \(3 \mathsf {N}_{p}+ 6\) rounds and requires \(3 \mathsf {m}+ 3 \mathsf {n}+ 9\) \(\mathsf {multdiv}\) gates. Note that with separate multiplication and division gates one would need \(2 \mathsf {m}+ 3 \mathsf {n}+ 8\) multiplication gates and \(\mathsf {m}+ \mathsf {n}\) division gates which would be less efficient.
have both sampling depth 3; the multi-party protocol for computing the \(\mathsf {crs}\) takes \(3 \mathsf {N}_{p}+ 6\) rounds and requires \(3 \mathsf {m}+ 3 \mathsf {n}+ 9\) \(\mathsf {multdiv}\) gates. Note that with separate multiplication and division gates one would need \(2 \mathsf {m}+ 3 \mathsf {n}+ 8\) multiplication gates and \(\mathsf {m}+ \mathsf {n}\) division gates which would be less efficient.
Notes
- 1.
In the RPK model, each party registers his public key with an authority of his choosing. It is assumed that even authorities of untrusted parties are honest to the extent that they verify the knowledge (e.g., by using a standalone ZK proof) of the corresponding secret key.
- 2.
References
Abdolmaleki, B., Baghery, K., Lipmaa, H., Siim, J., Zajac, M.: DL-Extractable UC-Commitment Schemes. Technical Report 2019/201, IACR (2019). https://eprint.iacr.org/2019/201
Abdolmaleki, B., Baghery, K., Lipmaa, H., Zając, M.: A subversion-resistant SNARK. In: Takagi, T., Peyrin, T. (eds.) ASIACRYPT 2017. LNCS, vol. 10626, pp. 3–33. Springer, Cham (2017). https://doi.org/10.1007/978-3-319-70700-6_1
Barak, B., Canetti, R., Nielsen, J.B., Pass, R.: Universally composable protocols with relaxed set-up assumptions. In: 45th FOCS, pp. 186–195
Bellare, M., Fuchsbauer, G., Scafuro, A.: NIZKs with an untrusted CRS: security in the face of parameter subversion. In: Cheon, J.H., Takagi, T. (eds.) ASIACRYPT 2016. LNCS, vol. 10032, pp. 777–804. Springer, Heidelberg (2016). https://doi.org/10.1007/978-3-662-53890-6_26
Ben-Sasson, E., et al.: Zerocash: Decentralized anonymous payments from bitcoin. In: 2014 IEEE Symposium on Security and Privacy, pp. 459–474 (2014)
Ben-Sasson, E., Chiesa, A., Green, M., Tromer, E., Virza, M.: Secure sampling of public parameters for succinct zero knowledge proofs. In: 2015 IEEE Symposium on Security and Privacy, pp. 287–304 (2015)
Bitansky, N., Canetti, R., Paneth, O., Rosen, A.: On the existence of extractable one-way functions. In: 46th ACM STOC, pp. 505–514
Bowe, S., Gabizon, A., Green, M.D.: A multi-party protocol for constructing the public parameters of the pinocchio zk-SNARK. Cryptology ePrint Archive, Report 2017/602 (2017). http://eprint.iacr.org/2017/602
Bowe, S., Gabizon, A., Miers, I.: Scalable multi-party computation for zk-SNARK parameters in the random beacon model. Cryptology ePrint Archive, Report 2017/1050 (2017). http://eprint.iacr.org/2017/1050
Canetti, R.: Universally composable security: a new paradigm for cryptographic protocols. In: 42nd FOCS, pp. 136–145
Canetti, R., Fischlin, M.: Universally composable commitments. In: Kilian, J. (ed.) CRYPTO 2001. LNCS, vol. 2139, pp. 19–40. Springer, Heidelberg (2001). https://doi.org/10.1007/3-540-44647-8_2
Canetti, R., Goldreich, O., Halevi, S.: The random oracle methodology, revisited (preliminary version). In: 30th ACM STOC, pp. 209–218
Danezis, G., Fournet, C., Groth, J., Kohlweiss, M.: Square span programs with applications to succinct NIZK arguments. In: Sarkar, P., Iwata, T. (eds.) ASIACRYPT 2014. LNCS, vol. 8873, pp. 532–550. Springer, Heidelberg (2014). https://doi.org/10.1007/978-3-662-45611-8_28
Fuchsbauer, G.: Subversion-zero-knowledge SNARKs. In: Abdalla, M., Dahab, R. (eds.) PKC 2018. LNCS, vol. 10769, pp. 315–347. Springer, Cham (2018). https://doi.org/10.1007/978-3-319-76578-5_11
Gennaro, R., Gentry, C., Parno, B., Raykova, M.: Quadratic span programs and succinct NIZKs without PCPs. In: Johansson, T., Nguyen, P.Q. (eds.) EUROCRYPT 2013. LNCS, vol. 7881, pp. 626–645. Springer, Heidelberg (2013). https://doi.org/10.1007/978-3-642-38348-9_37
Gentry, C., Wichs, D.: Separating succinct non-interactive arguments from all falsifiable assumptions. In: 43rd ACM STOC, pp. 99–108
Goldwasser, S., Kalai, Y.T.: On the (in)security of the Fiat-Shamir paradigm. In: 44th FOCS, pp. 102–115
Groth, J.: Simulation-sound NIZK proofs for a practical language and constant size group signatures. In: Lai, X., Chen, K. (eds.) ASIACRYPT 2006. LNCS, vol. 4284, pp. 444–459. Springer, Heidelberg (2006). https://doi.org/10.1007/11935230_29
Groth, J.: Short pairing-based non-interactive zero-knowledge arguments. In: Abe, M. (ed.) ASIACRYPT 2010. LNCS, vol. 6477, pp. 321–340. Springer, Heidelberg (2010). https://doi.org/10.1007/978-3-642-17373-8_19
Groth, J.: On the size of pairing-based non-interactive arguments. In: Fischlin, M., Coron, J.-S. (eds.) EUROCRYPT 2016. LNCS, vol. 9666, pp. 305–326. Springer, Heidelberg (2016). https://doi.org/10.1007/978-3-662-49896-5_11
Groth, J., Kohlweiss, M., Maller, M., Meiklejohn, S., Miers, I.: Updatable and universal common reference strings with applications to zk-SNARKs. In: Shacham, H., Boldyreva, A. (eds.) CRYPTO 2018. LNCS, vol. 10993, pp. 698–728. Springer, Cham (2018). https://doi.org/10.1007/978-3-319-96878-0_24
Juels, A., Kosba, A.E., Shi, E.: The ring of Gyges: investigating the future of criminal smart contracts. In: ACM CCS 16, pp. 283–295 (2016)
Katz, J., Maurer, U., Tackmann, B., Zikas, V.: Universally composable synchronous computation. In: Sahai, A. (ed.) TCC 2013. LNCS, vol. 7785, pp. 477–498. Springer, Heidelberg (2013). https://doi.org/10.1007/978-3-642-36594-2_27
Kidron, D., Lindell, Y.: Impossibility results for universal composability in public-key models and with fixed inputs. J. Cryptol. 24(3), 517–544 (2011)
Kosba, A.E., Miller, A., Shi, E., Wen, Z., Papamanthou, C.: Hawk: the blockchain model of cryptography and privacy-preserving smart contracts. In: 2016 IEEE Symposium on Security and Privacy, pp. 839–858 (2016)
Lipmaa, H.: Progression-free sets and sublinear pairing-based non-interactive zero-knowledge arguments. In: Cramer, R. (ed.) TCC 2012. LNCS, vol. 7194, pp. 169–189. Springer, Heidelberg (2012). https://doi.org/10.1007/978-3-642-28914-9_10
Maller, M., Bowe, S., Kohlweiss, M., Meiklejohn, S.: Sonic: zero-knowledge snarks from linear-size universal and updateable structured reference strings. Cryptology ePrint Archive, Report 2019/099 (2019). https://eprint.iacr.org/2019/099
Naor, M.: On cryptographic assumptions and challenges. In: Boneh, D. (ed.) CRYPTO 2003. LNCS, vol. 2729, pp. 96–109. Springer, Heidelberg (2003). https://doi.org/10.1007/978-3-540-45146-4_6
Parno, B., Howell, J., Gentry, C., Raykova, M.: Pinocchio: Nearly practical verifiable computation. In: 2013 IEEE Symposium on Security and Privacy, pp. 238–252 (2013)
Acknowledgement
The authors were supported by the European Union’s Horizon 2020 research and innovation programme under grant agreements No. 653497 (project PANORAMIX) and No. 780477 (project PRIViLEDGE), and by the Estonian Research Council grant (PRG49).
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2019 Springer Nature Switzerland AG
About this paper
Cite this paper
Abdolmaleki, B., Baghery, K., Lipmaa, H., Siim, J., Zając, M. (2019). UC-Secure CRS Generation for SNARKs. In: Buchmann, J., Nitaj, A., Rachidi, T. (eds) Progress in Cryptology – AFRICACRYPT 2019. AFRICACRYPT 2019. Lecture Notes in Computer Science(), vol 11627. Springer, Cham. https://doi.org/10.1007/978-3-030-23696-0_6
Download citation
DOI: https://doi.org/10.1007/978-3-030-23696-0_6
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-23695-3
Online ISBN: 978-3-030-23696-0
eBook Packages: Computer ScienceComputer Science (R0)








 , outputs a CRS trapdoor
, outputs a CRS trapdoor  and
and  (needed by the prover),
(needed by the prover),  (needed by the verifier), and
(needed by the verifier), and  (needed by
(needed by  , returns either 0 (the CRS is ill-formed) or 1 (the CRS is well-formed).
, returns either 0 (the CRS is ill-formed) or 1 (the CRS is well-formed). is a PPT algorithm that, given
is a PPT algorithm that, given  , where
, where  is a PPT algorithm that, given
is a PPT algorithm that, given  , returns either 0 (reject) or 1 (accept).
, returns either 0 (reject) or 1 (accept). is a PPT algorithm that, given
is a PPT algorithm that, given  , there exists
, there exists  such that
such that 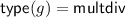 ,
,  , and
, and 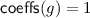 . That is, each trapdoor itself should be a part of the output of the circuit. Adding those
. That is, each trapdoor itself should be a part of the output of the circuit. Adding those  :
: . Hence, each gate output is a CRS element.
. Hence, each gate output is a CRS element. then
then  ,
,  . That is, the left multiplication input can be a constant or an output of a previous gate, the right multiplication and division inputs have to be one of the inputs of the circuit. This allows to easily verify the computation in the MPC. For convenience, we require further that constant value of
. That is, the left multiplication input can be a constant or an output of a previous gate, the right multiplication and division inputs have to be one of the inputs of the circuit. This allows to easily verify the computation in the MPC. For convenience, we require further that constant value of  can only be 1; from computational point of view nothing changes since
can only be 1; from computational point of view nothing changes since  can be any constant.
can be any constant. then
then  . Addition is done locally in MPC (does not require additional rounds) with the outputs of previous gates, since outputs correspond to publicly known CRS elements.
. Addition is done locally in MPC (does not require additional rounds) with the outputs of previous gates, since outputs correspond to publicly known CRS elements. is a constant.
is a constant.

 broadcasts
broadcasts  broadcasts
broadcasts 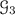 broadcasts
broadcasts 



 corrupts up to
corrupts up to  corrupts all
corrupts all  is a uniform distribution over
is a uniform distribution over  ,
, 