Abstract
Functional encryption (FE) is advanced encryption that enables us to issue functional decryption keys where functions are hardwired. When we decrypt a ciphertext of a message m by a functional decryption key where a function f is hardwired, we can obtain f(m) and nothing else. We say FE is selectively or adaptively secure when target messages are chosen at the beginning or after function queries are sent, respectively. In the weakly-selective setting, function queries are also chosen at the beginning. We say FE is single-key/collusion-resistant when it is secure against adversaries that are given only-one/polynomially-many functional decryption keys, respectively. We say FE is sublinearly-succinct/succinct when the running time of an encryption algorithm is sublinear/poly-logarithmic in the function description size, respectively.
In this study, we propose a generic transformation from weakly-selectively secure, single-key, and sublinearly-succinct (we call “building block”) PKFE for circuits into adaptively secure, collusion-resistant, and succinct (we call “fully-equipped”) one for circuits. Our transformation relies on neither concrete assumptions such as learning with errors nor indistinguishability obfuscation (IO). This is the first generic construction of fully-equipped PKFE that does not rely on IO.
As side-benefits of our results, we obtain the following primitives from the building block PKFE for circuits: (1) laconic oblivious transfer (2) succinct garbling scheme for Turing machines (3) selectively secure, collusion-resistant, and succinct PKFE for Turing machines (4) low-overhead adaptively secure traitor tracing (5) key-dependent message secure and leakage-resilient public-key encryption. We also obtain a generic transformation from simulation-based adaptively secure garbling schemes that satisfy a natural decomposability property into adaptively indistinguishable garbling schemes whose online complexity does not depend on the output length.
Access provided by Autonomous University of Puebla. Download conference paper PDF
Similar content being viewed by others
1 Introduction
1.1 Background
Achieving stronger cryptographic primitives by using weaker ones is one of the central and fundamental tasks in cryptography. We would like to minimize assumptions to achieve more secure and advanced cryptography. A typical example is how to achieve IND-CCA secure public-key encryption from IND-CPA secure one [21, 48, 50]. The objective of this study is showing how to achieve more secure and efficient functional encryption (FE) from less secure and efficient one in a generic way.
FE [15] is an encryption scheme that enables us to issue functional decryption keys \(\mathsf {sk}_f\) where a function f is hardwired. We can decrypt a ciphertext \(\mathsf {ct}_\mathsf {m}\) of a message \(\mathsf {m}\) by using \(\mathsf {sk}_f\). A notable feature of FE is that we obtain \(f(\mathsf {m})\) and nothing else when we decrypt \(\mathsf {ct}_\mathsf {m}\) by \(\mathsf {sk}_f\). If we can encrypt messages by a public-key (resp. a master secret key), then we call public-key (resp. secret-key) FE (PKFE and SKFE for short). FE can control what information of messages can be given to owners of functional decryption keys by using various functions. Moreover, FE is a versatile tool to achieve useful cryptographic primitives such as trapdoor permutations, universal samplers, non-interactive multi-party key-exchange [28]. The most prominent application of FE is achieving indistinguishability obfuscation (IO) [10, 24] from FE [3, 13, 14, 41, 43].
There are three main performance measures of FE. One is the number of issuable functional decryption keys. Another is the level of security. The other is the size of an encryption circuit. If an FE scheme can securely release one/polynomially-many functional decryption key/s, we call it a single-key/collusion-resistant scheme. Roughly speaking, an FE scheme is secure if adversaries cannot distinguish whether a target ciphertext is an encryption of \(\mathsf {m}_0\) or \(\mathsf {m}_1\) chosen by them. In the security game, adversaries can send functional decryption key queries and receives \(\mathsf {sk}_f\) for queried f as long as \(f(\mathsf {m}_0) = f(\mathsf {m}_1)\). If adversaries are required to commit target messages \((\mathsf {m}_0,\mathsf {m}_1)\) (resp. and queries \(f_1,\ldots ,f_q\)) at the beginning of the game, we call it selective (resp. weakly selective) security. If adversaries can decide target messages after they send functional decryption key queriesFootnote 1, then we call it adaptive security. The size of an encryption circuit must depend on the length of messages to be encrypted. Moreover, the size might depend on the size of functions supported by the scheme as several known FE schemes do [33, 51]. The dependence on the size of functions should be as low as possible to achieve better efficiency. FE is called succinct/sublinearly-succinct if the dependence is logarithmic/sublinear.
It is desirable to achieve the best properties of all performance measures simultaneously. Therefore, the following question is natural.

This question has been extensively studied [1, 4, 14, 29, 30, 35, 37, 44], but all previous studies gave only partial answers. The work of Garg and Srinivasan [30] is the most close to an answer to the above problem, but that is not sufficient since they need an additional algebraic assumption and the ciphertext size of the resulting scheme depends on output-length of circuits supported by the scheme. In this study, we give an affirmative answer to the open question above, which was clearly stated by Garg and Srinivasan [29]. We sometimes call the building-block and goal-primitive in the question above obf-minimumFootnote 2 and fully-equipped PKFE, respectively in this paper.
One might wonder why we do not start with weakly-selectively secure, single-key, and non-succinct FE. This is because there is a huge gap between non-succinct FE and sublinearly-succinct one. We know that sub-exponentially-secure sublinearly-succinct FE implies IO for circuits [3, 14, 29, 39,40,41,42]. We also know that non-succinct PKFE (resp. SKFE) is achieved by plain public-key encryption (resp. one-way function) [33, 51]. It is unlikely that we can achieve IO from plain public-key encryption. Thus, we start with sublinearly-succinct FE. We also emphasize that we focus on transformations with polynomial security loss in this study. If sub-exponential security loss is allowed, we can achieve IO from obf-minimum SKFE/PKFE. We rely on neither sub-exponential security nor IO in this study. We stress that one of the big issues in cryptography is to avoid sub-exponential security loss. Sub-exponential security loss significantly degrades security and efficiency of cryptographic schemes in general. In particular, in the area of obfuscation-based (or FE-based) cryptography, avoiding sub-exponential security loss has been actively studied [2, 5, 6, 27,28,29, 31, 46].
Hereafter, we use the following notations. Relationships between different notions of PKFE and SKFE are parameterized by \((\#\mathsf {key},\#\mathsf {ct},\mathsf {sec},\mathsf {eff})\). Here, \(\#\mathsf {key}\in \{1_\mathsf {key},\mathsf {unb}_\mathsf {key}\}\) and \(\#\mathsf {ct} \in \{1_\mathsf {ct},\mathsf {unb}_\mathsf {ct}\}\) denote the number of functional-decryption-keys/ciphertexts: \(\mathsf {unb}\) means unbounded polynomially many, \(\mathsf {sec} \in \{\mathsf {w}\text {-}\mathsf {sel},\mathsf {sel},\mathsf {ada}\}\) denotes weakly-selective, selective or adaptive security, and \(\mathsf {eff} \in \{\mathsf {ns},\mathsf {sls},\mathsf {fs}\}\) denotes the efficiency: \(\mathsf {ns}\), \(\mathsf {sls}\), and \(\mathsf {fs}\) denote non-succinct, sublinearly-succinct, and succinct, respectively. In the case of PKFE, we omit \(\#\mathsf {ct}\)Footnote 3.
Known Transformations for Better Security and Efficiency. There are several techniques to strengthen security and/or improve the efficiency of FE. Ananth, Brakerski, Segev, and Vaikuntanathan [1] presented a transformation from selectively secure FE to adaptively secure FE. Unfortunately, this transformation does not preserve (sublinear-)succinctness. This is because the transformation uses a  -SKFE schemeFootnote 4 [33] as a key building block. Garg and Srinivasan [29], and Li and Micciancio [44] presented transformations from single-key and sublinearly-succinct PKFE to collusion-resistant one. More specifically, the transformation by Garg and Srinivasan [29] is from \((1_\mathsf {key},\mathsf {w}\text {-}\mathsf {sel},\mathsf {sls})\)-PKFE to \((\mathsf {unb}_\mathsf {key},\mathsf {sel},\mathsf {fs})\)-PKFE. However, these transformations do not preserve adaptive security. Ananth, Jain, and Sahai [4] and Bitansky and Vaikuntanathan [14] presented a transformation from \((\mathsf {unb}_\mathsf {key},\mathsf {sel},\mathsf {ns})\)-PKFE to \((\mathsf {unb}_\mathsf {key},\mathsf {sel},\mathsf {fs})\)-PKFE. This transformation also does not preserve adaptive security. Ananth and Sahai [7] presented a transformation (denoted by AS16 transformation) from \((\mathsf {unb}_\mathsf {key},\mathsf {sel},\mathsf {fs})\)-PKFE for circuits to \((\mathsf {unb}_\mathsf {key},\mathsf {ada},\mathsf {fs})\)-PKFE for Turing machines (TMs) by using \((1_\mathsf {key},1_\mathsf {ct},\mathsf {ada},\mathsf {fs})\)-SKFE for TMs. If the building block \((1_\mathsf {key},1_\mathsf {ct},\mathsf {ada},\mathsf {fs})\)-SKFE is for circuits, then the transformation also works and we obtain the resulting PKFE for circuits. The difference from the transformation by Ananth et al. [1] is that we can start with
-SKFE schemeFootnote 4 [33] as a key building block. Garg and Srinivasan [29], and Li and Micciancio [44] presented transformations from single-key and sublinearly-succinct PKFE to collusion-resistant one. More specifically, the transformation by Garg and Srinivasan [29] is from \((1_\mathsf {key},\mathsf {w}\text {-}\mathsf {sel},\mathsf {sls})\)-PKFE to \((\mathsf {unb}_\mathsf {key},\mathsf {sel},\mathsf {fs})\)-PKFE. However, these transformations do not preserve adaptive security. Ananth, Jain, and Sahai [4] and Bitansky and Vaikuntanathan [14] presented a transformation from \((\mathsf {unb}_\mathsf {key},\mathsf {sel},\mathsf {ns})\)-PKFE to \((\mathsf {unb}_\mathsf {key},\mathsf {sel},\mathsf {fs})\)-PKFE. This transformation also does not preserve adaptive security. Ananth and Sahai [7] presented a transformation (denoted by AS16 transformation) from \((\mathsf {unb}_\mathsf {key},\mathsf {sel},\mathsf {fs})\)-PKFE for circuits to \((\mathsf {unb}_\mathsf {key},\mathsf {ada},\mathsf {fs})\)-PKFE for Turing machines (TMs) by using \((1_\mathsf {key},1_\mathsf {ct},\mathsf {ada},\mathsf {fs})\)-SKFE for TMs. If the building block \((1_\mathsf {key},1_\mathsf {ct},\mathsf {ada},\mathsf {fs})\)-SKFE is for circuits, then the transformation also works and we obtain the resulting PKFE for circuits. The difference from the transformation by Ananth et al. [1] is that we can start with  -SKFE. AS16 transformation is the closest to what we want, but not satisfactory since it uses IO (that is, sub-exponentially secure FE). All these transformations sacrifice either adaptive security or succinctness or rely on IO. Thus, the transformation in the question above has been remaining open in the area of FE.
-SKFE. AS16 transformation is the closest to what we want, but not satisfactory since it uses IO (that is, sub-exponentially secure FE). All these transformations sacrifice either adaptive security or succinctness or rely on IO. Thus, the transformation in the question above has been remaining open in the area of FE.
Crucial Ingredient: Adaptive Garbling. As we saw above, if we can obtain \((1_\mathsf {key},1_\mathsf {ct},\mathsf {ada},\mathsf {fs})\)-SKFE for circuits from \((1_\mathsf {key},\mathsf {w}\text {-}\mathsf {sel},\mathsf {sls})\)-PKFE, then we resolve the open question above by using the transformations of Garg and Srinivasan [29] and Ananth and Sahai [7]. In fact, \((1_\mathsf {key},1_\mathsf {ct},\mathsf {ada},\mathsf {fs})\)-SKFE for circuits is essentially the same as adaptively indistinguishable garbling schemes (indistinguishability-based definition [37]) whose online computational complexity is \({\mathrm {poly}}(\log {|C|},n,\lambda )\) where C is a circuit to be garbled, n is the input length of C, and \(\lambda \) is the security parameterFootnote 5. Here, the online computational complexity means the computational complexity to encode an input. We call garbling schemes whose online computational complexity is \({\mathrm {poly}}(\log {|C|},n,\lambda )\) circuit-succinct garbling schemes.Footnote 6 Thus, we focus on adaptive and circuit-succinct garbling schemes.
Several previous works [11, 30, 35,36,37,38] have proposed adaptively secure garbling schemes. The garbling scheme of Bellare, Hoang, and Rogaway is not circuit-succinct, that is, the online computational complexity is \({\mathrm {poly}}(|C|,\lambda )\). The garbling scheme of Hemenway, Jafargholi, Ostrovsky, Scafuro, and Wichs [35] achieves online computational complexity \((n+m+w){\mathrm {poly}}(\lambda )\) where n, m, and w are the input length, output length, and width of a circuit to be garbled, respectively (they also presented a garbling scheme for \(\mathsf {NC}^1\) circuits whose complexity is \((n+m){\mathrm {poly}}(\lambda )\)). Jafargholi, Scafuro, and Wichs [37] presented an adaptively indistinguishable garbling scheme whose online computational complexity is \((n+w){\mathrm {poly}}(\lambda )\). The garbling scheme of Garg and Srinivasan [30] (we call GS18 scheme in this paper) achieved online computational complexity \(O(n+m)+{\mathrm {poly}}(\log {|C|},\lambda )\). Others [36, 38] are garbling scheme for \(\mathsf {NC}^1\) circuits. None of these is satisfactory for our goal since the complexity depends on a polynomial of \(|C|\), w, d, or m.
GS18 scheme is closest to our goal. However, there are two issues as follows.
-
1.
GS18 scheme is based on a concrete assumption (the CDH, LWE, or factoring assumptions). More specifically, the scheme is based on updatable laconic oblivious transfer (LOT) [19], which is achieved by the CDH, LWE, or factoring assumptions [16, 19, 23].
-
2.
GS18 scheme is simulation-based secure. Therefore, the online computational complexity must be at least linear in m since Applebaum, Ishai, Kushilevitz, and Waters [8] showed the lower bound of online complexity for simulation-based secure garbled circuits.
Getting Rid of the Dependence on Output Length. If we can generically transform a simulation-based adaptively secure garbling scheme whose online computational complexity is \({\mathrm {poly}}(n,m,g(|C|),\lambda )\) where \(g(\cdot )\) is some function (such as \(\log (\cdot )\)) into an adaptively indistinguishable garbling scheme whose online computational complexity is \({\mathrm {poly}}'(n,g(|C|),\lambda )\), then we can solve the second issue explained above by using GS18 scheme [30] as a building block. In fact, Jafargholi et al. left such a transformation as an open problem [37]. We quote their sentence in a footnote.Footnote 7 This open question is related to our main question since \((1_\mathsf {key},1_\mathsf {ct},\mathsf {ada},\mathsf {fs})\)-SKFE is the crucial ingredient as explained above.
1.2 Our Contributions
We solved the open problem explained in the previous section. In particular, we prove the following theorem.
Theorem 1.1
(Main theorem). Assume that there exists weakly-selectively secure, single-key, and sublinearly-succinct PKFE for circuits, then there exists adaptively secure, collusion-resistant, and succinct PKFE for circuits.
All our constructions and transformations in this study incur only polynomial security loss. To obtain our crucial ingredient, \((1_\mathsf {key},1_\mathsf {ct},\mathsf {ada},\mathsf {fs})\)-SKFE, we will prove the (informal) theorems below, which are of independent interests, and construct an adaptively secure garbling scheme whose online computational complexity is \({\mathrm {poly}}(\log {|C|},n,\lambda )\) by combining (a variant of) GS18 scheme.
Theorem 1.2
(Informal, see Theorem 4.5). Assume that there exists \((1_\mathsf {key},\mathsf {w}\text {-}\mathsf {sel},\mathsf {sls})\)-PKFE for circuits, then there exists updatable laconic oblivious transfer.
That is, we can generically construct updatable LOT from obf-minimum FE. This solves the first issue of GS18 scheme. This itself is interesting since this is the first construction of LOT that relies on neither specific number theoretic assumptions nor IO.Footnote 8 Therefore, we obtain an adaptively secure garbling scheme whose online computational complexity is \(O(n+m)+{\mathrm {poly}}(\log {|C|},\lambda )\) from obf-minimum PKFE via GS18 scheme. Note that, to achieve this, we need some tweaks for the garbling scheme since the security level of our updatable LOT is slightly weaker than that used in GS18 scheme. In fact, we prove that such a weaker LOT is sufficient to achieve an adaptively secure garbling scheme that we need. However, for simplicity, we give only informal theorems here. See Sect. 2 for more details.
We propose two solutions for the second issue of GS18 scheme. One is proposing an extension of AS16 transformation [7] in the following theorem.
Theorem 1.3
(Informal, see Theorem 6.1). If there exists \((\mathsf {unb}_\mathsf {key},\mathsf {sec},\mathsf {eff})\)-PKFE for single-bit output circuits, then there exists \((\mathsf {unb}_\mathsf {key},\mathsf {sec},\mathsf {eff})\)-PKFE for multi-bit output circuits where \(\mathsf {sec}\in \{\mathsf {w}\text {-}\mathsf {sel},\mathsf {sel},\mathsf {ada}\}\) and \(\mathsf {eff} \in \{\mathsf {ns},\mathsf {sls},\mathsf {fs}\}\). This transformation preserves adaptive security and succinctness.
If we set \(m=1\) (that is, single-bit output) in adaptively secure garbling scheme whose online computational complexity is \(O(n,m,\log {|C|},\lambda )\), then we obtain adaptively secure circuit-succinct garbling scheme for single-bit output circuits. We plug this into AS16 transformation, and then we obtain \((\mathsf {unb}_\mathsf {key},\mathsf {ada},\mathsf {fs})\)-PKFE for single-bit output circuits. Lastly, by applying the informal theorem above, we can obtain fully-equipped PKFE. See the next section for more details. Note that it is easy to transform our variant of GS18 scheme into \((1_\mathsf {key},1_\mathsf {ct},\mathsf {ada},\mathsf {fs})\)-SKFE for single-bit output circuits. See the full version for details.
The other is using the transformation in the following theorem.
Theorem 1.4
(Informal). Assume that there exists a simulation-based adaptively secure garbling scheme whose online computational complexity depends on the output length of circuits and that satisfies a natural decomposability property, then there exists an indistinguishability-based adaptively secure garbling scheme whose online computational complexity does not depend on the output length of circuits. The overhead of the transformation is not large, that is, the online complexity affected by other parameters (\(|C|\), n, and \(\lambda \)) do not change in an asymptotic sense.
Known adaptive garbling schemes satisfy the natural decomposability property. That is, we solve the open question by Jafargholi et al. [37]. Note that the first solution is much simpler than the second one. However, the technique used in the transformation in Theorem 1.4 is related to other our techniques in this study, and adaptively secure circuit-succinct garbling schemes are closely related to our goal as we explained so far. Moreover, Theorem 1.4 solves the open problem presented by Jafargholi et al. [37] (We think this is of an independent interest). Therefore, we also include the second solution in this paper.
More Implications of Our Results. Ananth and Lombardi [5] proved that if there exists single-key and succinct PKFE for circuits and one of CDH/LWE/factoring assumptions holds, then there exists succinct garbling scheme for TMs. The concrete assumptions come from that they use LOT. We can replace their LOT with our LOT based on FEFootnote 9. Thus, we obtain the following corollary.
Corollary 1.1
If there exists \((1_\mathsf {key},\mathsf {w}\text {-}\mathsf {sel},\mathsf {sls})\)-PKFE for circuits, then there exists a succinct garbling scheme for TMs.
We also obtain the following corollary by combining with the known results [7, 29].
Corollary 1.2
If there exists \((1_\mathsf {key},\mathsf {w}\text {-}\mathsf {sel},\mathsf {sls})\)-PKFE for circuits, then there exists \((\mathsf {unb}_\mathsf {key},\mathsf {sel},\mathsf {fs})\)-PKFE for TMs.
That is, we remove the concrete assumptions from the theorems of Ananth and Lombardi.Footnote 10 Agrawal and Maitra [6] also proved that if there exists succinct PKFE for circuits, then there exists PKFE for TMs. However, their PKFE for TMs supports only single/constant-bit output TMs. That is, our corollary above improves their result since ours supports multi-bit output TMs.Footnote 11
Nishimaki, Wichs, and Zhandry [49] presented a traitor tracing scheme that supports an exponentially large identity space and whose ciphertext overhead is \(O(\log {n})\) where n is the length of identities. Their scheme is based on fully-equipped PKFE that was instantiated by IO previously. Thus, we obtain the following corollary.
Corollary 1.3
If there exists \((1_\mathsf {key},\mathsf {w}\text {-}\mathsf {sel},\mathsf {sls})\)-PKFE for circuits, there exists an adaptively secure traitor tracing scheme whose master key size is \({\mathrm {poly}}(\log {n})\), secret key size is \({\mathrm {poly}}(n)\), and ciphertext size is \(|\mathsf {m}| + {\mathrm {poly}}(\log {n})\) where \(|\mathsf {m}|\) is the message length.
Brakerski, Lombardi, Segev, and Vaikuntanathan [16] showed key-dependent message (KDM) secure and leakage-resilient PKE can be based on batch encryption, which is essentially the same as LOT. Thus, we obtain the following corollary (See the reference [16] for the details of parameters in the statement).
Corollary 1.4
If there exists \((1_\mathsf {key},\mathsf {w}\text {-}\mathsf {sel},\mathsf {sls})\)-PKFE for circuits, then there exists a PKE scheme that satisfies (1) KDM security with respect to affine functions of the secret key and (2) leakage-resilience with leakage rate \(1-o(1)\).
To the best of our knowledge, except constructions based on IO [20, 47], all existing generic constructions of PKE satisfying KDM security or leakage resilience of \(1- o(1)\) rate assume some algebraic property such as homomorphism to the underlying primitive. Our construction is a generic construction of PKE satisfying the above security notions based on a polynomially secure primitive without such algebraic properties.
2 Technical Overview
In this section, we give high level overviews of our techniques. We briefly summarize how to arrive at fully-equipped PKFE from obf-minimum PKFE in Fig. 1.
Illustration of the path from our starting point to the goal: In this figure, “SKFE single” denotes SKFE for single-bit output circuits. “Updatable sd-LOT” denotes selective-database updatable laconic OT. Regarding garbling scheme, “Garbling-Opt” denotes garbling schemes with nearly optimal online complexity and “Output-independence” denotes the online complexity does not depends on output-length (See Sects. 5 and 7 for more details). Ada-SIM/Ada-IND denote simulation-/indistinguishability-based adaptively secure garbling schemes, respectively. Solid thin arrows denote known or trivial implications. Thick solid and dotted arrows denote implications that we prove in this study. Here, in the case of dotted lines, we assume specific properties of underlying tools. See each section for details.
2.1 Laconic OT from Succinct PKFE
We first show an overview of our LOT protocol based on sublinearly succinct PKFE. More precisely, we construct updatable LOT with arbitrary compression factor based on \((1,\mathsf {w}\text {-}\mathsf {sel},\mathsf {sls})\)-PKFE.
By the transformation of Cho et al. [19] and an observation by Ananth and Lombardi [5]Footnote 12, we can transform non-updatable LOT with compression factor 2 into updatable one with arbitrary compression factor using Merkle tree. Thus, to achieve our goal, we can focus on constructing non-updatable LOT with compression factor 2. Our first observation is that we might construct such LOT based on IBE. In this overview, let the length of a database \(D\) be \({ s}\), that is \(D\in \{0,1\}^s\), and \(D[i]\) denotes the i-th bit of \(D\).
Laconic OT Based on IBE and Its Problem. We first review the definition of LOT. An LOT consists of four algorithms \(\mathsf {Gen}, \mathsf {Hash}, \mathsf {Send}\), and \(\mathsf {Receive}\). We generate a CRS \(\mathsf {crs}\) using \(\mathsf {Gen}\). \(\mathsf {Hash}\), given \(\mathsf {crs}\) and a database \(D\), outputs a short digest \(d\) and private state \(\widehat{D}\). The algorithm \(\mathsf {Send}\), given \(d\), a database location \(L\), and two messages \(m_0\) and \(m_1\), outputs LOT ’s ciphertext \(e\). By using \(\mathsf {Receive}\), a receiver who has the secret state \(\widehat{D}\) can decrypt \(e\) and obtain \(m_{D[L]}\). For security, we require that an honest receiver cannot obtain the other message \(m_{1-D[L]}\) even if he has \(\widehat{D}\).
Our basic idea for constructing LOT is as follows. When hashing a database \(D\), we first generate a master public-key and master secret-key \((\mathsf {MPK},\mathsf {MSK})\) of \(\mathsf {IBE}\) and \(\mathsf {sk}_{i,D[i]}\leftarrow \mathsf {KG}(\mathsf {MSK},i\Vert D[i])\) for every \(i\in [{ s}]\). Then, we set \(\mathsf {MPK}\) as a digest of \(D\) and \(\{\mathsf {sk}_{i,D[i]}\}_{i\in [{ s}]}\) as a secret state \(\widehat{D}\). When generating LOT ’s ciphertext \(e\) for location \(L\in [{ s}]\) and two messages \(m_0\) and \(m_1\), we generate \(e=(\mathsf {Enc}(\mathsf {MPK},L\Vert 0,m_0),\mathsf {Enc}(\mathsf {MPK},L\Vert 1,m_1))\). We see that a receiver who has \(\widehat{D}=\{\mathsf {sk}_{i,D[i]}\}_{i\in [{ s}]}\) can obtain \(m_{D[L]}\). If the receiver honestly generates \(\widehat{D}\) and deletes \(\mathsf {MSK}\), he cannot obtain \(m_{D[L]}\) based on the security of \(\mathsf {IBE}\). Moreover, if the size of a master public-key of \(\mathsf {IBE}\) is independent of the identity length, the size of a digest is also independent of the database size. This construction resembles the one-time signature with encryption from IBE by Döttling and Garg [22].
The above construction seems to satisfy the syntactic and security requirement of LOT. However, the construction has a problem that the hash procedure is randomized. Though the definition of LOT by Cho et al. does not explicitly require that the hash algorithm be deterministic, we observe that the hash algorithm needs to be deterministic for the security notion defined by Cho et al. [19] to be meaningful. In fact, the above basic construction has a crucial problem that if a receiver computes a hash value by himself, he obtains a master secret-key of IBE and can decrypt any ciphertext.
Moreover, it is not clear whether we can apply the bootstrap method proposed by Cho et al. [19] if the hash function of the underlying LOT is randomized. Their bootstrapping method implicitly assumes the hash algorithm of the underlying LOT is deterministic.
Derandomization Using IO. For the above reasons, we need to derandomize the hash algorithm of the above construction. We can make the hash procedure of the above construction deterministic by using IO and puncturable pseudorandom function (PRF) as follows.
In a modified construction, we generate a CRS by obfuscating a circuit that, given a database \(D\), first generates a random coin by using \(D\) and a puncturable PRF key and then perform the hash procedure of the basic construction using the random coin. This circuit outputs a digest that is a master public-key of IBE and secret state that is secret-keys of IBE corresponding to \(D\), but not master secret-key.
We can prove the security of the modified construction based on the punctured programming technique proposed by Sahai and Waters [52]. However, to complete the proof, we need to require an adversary to declare the challenge database before seeing a CRS. This is because, in the security proof, we need to generate a CRS as an obfuscated circuit that has the challenge database hardwired. This security notion for LOT is weaker than that used by Garg and Srinivasan [30] to construct adaptive garbling scheme.
Selective-Database Security. In this work, we show that we can construct an adaptive garbling scheme based on LOT whose security holds only when the challenge database is selectively determined. We call an LOT scheme satisfying such a security notion selective-database LOT. Note that we allow an adversary for LOT to adaptively choose the challenge location and messages. In fact, in our construction of adaptive garbling scheme, we need LOT whose security holds even if the challenge messages are adaptively chosen. In contrast, the security notion defined by Cho et al. [19] that requires an adversary to declare all challenge instances before seeing CRS is not sufficient for our adaptive garbling scheme. In Sect. 2.2, we explain this issue in more detail.
By weakening the required security notion to selective-database security, LOT no longer imply collision-resistant hash function while the LOT satisfying an adaptive security notion used by Garg and Srinivasan does. This weakening seems to be necessary to achieve LOT from IO due to the substantial barrier that was shown by Asharov and Segev [9].
Replacing IO with Sublinearly Succinct PKFE. We can replace IO in the above construction with sublinearly succinct PKFE by relying on the result shown by Liu and Zhandry [46].
Liu and Zhandry generalized previous works [27,28,29], and showed we can replace IO with decomposable obfuscation (dO) that can be based on polynomially secure \((1,\mathsf {w}\text {-}\mathsf {sel},\mathsf {sls})\)-PKFE if the circuit pair to be obfuscated satisfies some condition. Roughly speaking, they showed that if there is a polynomial size “witness” for the functional equivalence of a circuit pair to be obfuscated, IO can be replaced with dO. One particular situation where this condition is satisfied is that in the security proof we modify a circuit to be obfuscated so that it outputs a hardwired value for a single input and otherwise it runs in the same way as the original one.
Using the terminology by Liu and Zhandry, hardwiring a single output for an input into a circuit corresponds to decompose the circuit to the input. We explain this in more detail. Let C be a circuit of 3-bit input. For a bit string x of length less than 3, let \(C_x\) be a circuit \(C(x\Vert \cdot )\), that is, C in which x is hardwired as the first \(|x|\) bit of the input. We call such a circuit partial evaluation of C. When decomposing C to the input say 100, we represent C as the tuple of partial evaluations \((C_{0},C_{11},C_{100},C_{101})\). When considering C as a complete binary tree, \((C_{0},C_{11},C_{100},C_{101})\) corresponds to the cover of minimum size that contains 100. We see that computation of C on any input can be done using \((C_{0},C_{11},C_{100},C_{101})\). This is essentially the same as hardwiring a single output C(100) on input 100 into C.
Liu and Zhandry showed if C is obfuscated by dO, we can replace it with an obfuscated circuit that is constructed from partial evaluations \((C_{0},C_{11},C_{100},C_{101})\) without affecting the behavior of an adversary. At a high level, this change can be done by removing C and embedding \((C_{0},C_{11},C_{100},C_{101})\) into functional keys of the underlying PKFE. Then, we can perform security proofs in a similar way as the punctured programming.
Consider a circuit of the form \(C(x)=C'(x;\mathsf {F}_K(x))\), where \(C'\) is a circuit, \(\mathsf {F}\) is a PRF, and K is a PRF key. For simplicity, let C be a circuit of 3 bit input as above. We show how to change the distribution of C(100). By obfuscating C with dO, we can decompose C to 100, that is, we can replace obfuscated C with obfuscated circuit constructed from \((C_{0},C_{11},C_{100},C_{101})\). Next, we change \(\mathsf {F}_K(100)\) with a truly random string. To accomplish this step, we require that \(\mathsf {F}_K(100)\) is pseudorandom even if partial evaluations of \(\mathsf {F}_K(\cdot )\) for 0, 11, and 101 are given. Liu and Zhandry call such PRF decomposing compatible PRF and the construction of PRF by Goldreich, Goldwasser, and Micali [32] satisfies such a property. Once we can replace \(\mathsf {F}_K(100)\) with a truly random string, we can change the distribution of C(100). Thus, we can complete the security proof.
Instantiating Our Construction with Sublinearly Succinct PKFE. The circuit to be obfuscated in our construction is of the form \(C(x)=C'(x;\mathsf {F}_K(x))\), where \(C'\) is a circuit executes a setup and key generation algorithm of IBE. In a similar manner as above, we can change the security game so that the master public-key and secret-keys related to the challenge database are generated using a truly random string. Then, we can prove the selective-database security of our LOT based on the selective security of IBE. Note that in the reduction, the challenge identity in the security game of IBE is \(L^*\Vert 1-D^*[L^*]\), where \(D^*\) and \(L^*\) are challenge database and position in the security game of LOT. The identity \(L^*\Vert 1-D^*[L^*]\) depends on the choice of \(L^*\) by an adversary for LOT. However, the reduction algorithm can guess the location with the probability at least \(\frac{1}{{ s}+1}\), which is inverse polynomial. Thus, a selectively secure IBE is sufficient for this construction.
Therefore, we can replace IO in our construction with dO, which can be based on \((1_\mathsf {key},\mathsf {w}\text {-}\mathsf {sel},\mathsf {sls})\)-PKFE. Moreover, selectively secure IBE can be constructed from \((1_\mathsf {key},\mathsf {w}\text {-}\mathsf {sel},\mathsf {sls})\)-PKFE based on the result by Garg and Srinivasan [29]. Their collusion-resistant PKFE based on \((1_\mathsf {key},\mathsf {w}\text {-}\mathsf {sel},\mathsf {sls})\)-PKFE can be used as an identity-based key encapsulation mechanism the size of whose master public-key is independent of the length of identities.Footnote 13 Thus, we can construct selective-database LOT based only on \((1_\mathsf {key},\mathsf {w}\text {-}\mathsf {sel},\mathsf {sls})\)-PKFE.
Comparison with the Construction by Ananth and Lombardi [5]. Ananth and Lombardi showed a construction of LOT based on IO. As they noted, it seems difficult to replace IO in their construction with polynomially secure PKFE. The reason why they need IO is that they constructed LOT based on witness encryption [25] by modifying the construction proposed by Cho et al. [19].
Witness encryption based on IO is outside of the framework by Liu and Zhandry. Thus, we cannot construct witness encryption from sublinearly succinct PKFE using the result by Liu and Zhandry. In fact, it is believed to be hard to construct witness encryption based on some polynomially secure primitive including PKFE [25].
2.2 Adaptive Garbling from Selective-Database Updatable Laconic OT
The adaptive garbling scheme by Garg and Srinivasan (we write GS18 scheme for short) is based on adaptively secure updatable LOT [30], where adversaries can select a database after they see a CRS. However, our LOT achieves only selective-database updatable LOT, where adversaries must commit a database before a CRS is given. In fact, we prove that we can achieve an adaptive garbling scheme by using a selective-database updatable LOT.
Where is the Adaptive Property of LOT Used in GS18 Scheme? In GS18 scheme, a database of an updatable LOT is determined by an input x. More specifically, the current database is determined by x, each intermediate wire values determined by x and each gate, and output values. A CRS \(\mathsf {crs}\) of updatable LOT is generated at the offline phase (i.e., when we generate a garbled circuit \(\widetilde{C}\)) and \(\mathsf {crs}\) is hardwired in circuits to be garbled by selectively secure garbling. At this point, x might not be determined yet since we consider the adaptive setting. Thus, a simulator must have \(\mathsf {crs}\) before x (and a database) is fixed. This is why Garg and Srinivasan used the adaptive security of LOT.
Overcoming the Issue. The issues is that we need \(\mathsf {crs}\) at the offline phase. Our idea is deferring using \(\mathsf {crs}\) until we generate a garbled input (i.e., online phase). To look closer at our idea, we need to explain more on GS18 scheme. In GS18 scheme, “step circuits” are garbled by selectively secure garbling. Each step circuit has the description of each gate of the circuit C to be garbled by the adaptive garbling scheme. Roughly speaking, a step circuit takes as input a digest \(d\) of updatable LOT and does the following two procedures.
-
Updating the database according to the output wire value of the gate computed from input x.
-
Outputting encrypted labels of selectively secure garbling for the next gate via updatable LOT.
The important point is that \(\mathsf {crs}\) of updatable LOT is hardwired in each step circuit to run \(\mathsf {Send}\) and \(\mathsf {SendWrite}\) algorithms, which was explained in Sect. 2.1. This is the problem since we do not fix \(\mathsf {crs}\) at the offline phase. Here our idea comes in.
Instead of hardwiring \(\mathsf {crs}\) in each step circuit, we define modified step circuits that take as input not only digest \(d\) but also \(\mathsf {crs}\). Now \(\mathsf {crs}\) is an input for step circuits. By this change, to generate (simulated) garbled modified step circuits, we do not need \(\mathsf {crs}\). As a result, \(\mathsf {crs}\) need not be determined at the offline phase. In the construction, we put \(\mathsf {crs}\) in the state information though we generate \(\mathsf {crs}\) at the offline phase in the construction. In the proof, a simulator can adaptively set the state information when the simulator needs it since the state information is not revealed.
The CRS \(\mathsf {crs}\) must be fixed when a garbled input \(\widetilde{x}\) is generated. However, at this point, input x and a database were already determined. Therefore, we can use the selective-database security of updatable LOT because, in the simulation, an adversary of updatable LOT can simulate garbled step circuits without \(\mathsf {crs}\), and when x is fixed, the adversary fixes a database based on x and can receive \(\mathsf {crs}\) in the reduction. This is the main idea behind our adaptive garbling scheme based on selective-database updatable LOT.
Although we can generate \(\mathsf {crs}\) at the online phase, we select that we put \(\mathsf {crs}\) in the state information for better online complexity and compatibility with the transformation given in Sect. 7.
Note that, to make our proof work, reduction algorithms attacking updatable LOT need to set the challenge messages as values computed by using CRS. That is, we allow the challenge messages to depend on the CRS. This is why we introduce a new security notion selective-database security for LOT. Our LOT satisfies this security.
From Adaptive Garbling to Adaptively Secure 1-Key 1-Ciphertext SKFE. By combining two transformations explained in this section and the previous section, we obtain an adaptive garbling scheme whose online complexity is \(O(n+m)+{\mathrm {poly}}(\log {|C|},\lambda )\) based on \((1_\mathsf {key},\mathsf {w}\text {-}\mathsf {sel},\mathsf {sls})\)-PKFE. Especially, by restricting circuits supported by garbling schemes to single-bit output circuits, we obtain an adaptive garbling scheme whose online complexity is \(O(n)+{\mathrm {poly}}(\log {|C|},\lambda )\) based on the same assumption.
In the next step, we use the transformation proposed by Ananth and Sahai [7]. In order to use their transformation, we have to transform the constructed adaptive garbling scheme into \((1_\mathsf {key},1_\mathsf {ct},\mathsf {ada},\mathsf {fs})\)-SKFE. Although adaptive garbling scheme with succinct online encoding and \((1_\mathsf {key},1_\mathsf {ct},\mathsf {ada},\mathsf {fs})\)-SKFE are essentially the same primitives, there is a difference between them. The security game for \((1_\mathsf {key},1_\mathsf {ct},\mathsf {ada},\mathsf {fs})\)-SKFE allows an adversary to make an encryption query and key query in arbitrary order while that for adaptive garbling scheme requires an adversary to always make circuit query first. We can solve this issue with a simple transformation using a one-time pad. See the full version for details.
2.3 From Single-bit to Multi-bit Succinct FE by Leveraging Collusion-Resistance
As explained in the previous section, we obtained \((1_\mathsf {key},1_\mathsf {ct},\mathsf {ada},\mathsf {fs})\)-SKFE for single-bit output functions from \((1_\mathsf {key},\mathsf {w}\text {-}\mathsf {sel},\mathsf {sls})\)-PKFE. By using \((1_\mathsf {key},1_\mathsf {ct},\mathsf {ada},\mathsf {fs})\)-SKFE for single-bit output functions in the transformation by Ananth and Sahai [7], we obtain \((\mathsf {unb}_\mathsf {key},\mathsf {ada},\mathsf {fs})\)-PKFE for single-bit output functions. Here, we show that we can transform \((\mathsf {unb}_\mathsf {key},\mathsf {ada},\mathsf {fs})\)-PKFE for single-bit output functions to one for multi-bit output functions.
The transformation is very simple. We construct a PKFE scheme \(\mathsf {MultiPKFE}\) for multi-bit output functions from a PKFE scheme \(\mathsf {OnePKFE}\) for single-bit output functions as follows. The encryption algorithm of \(\mathsf {MultiPKFE}\) works completely in the same manner as that of \(\mathsf {OnePKFE}\). The key generation algorithm of \(\mathsf {MultiPKFE}\), given a function f with m-bit output, first decomposes the function to \(\{f_i\}_{i\in [m]}\) where \(f_i\) is a function that computes the i-th bit of \(f(\mathsf {m})\) on input \(\mathsf {m}\). Then it generates decryption keys \(\mathsf {sk}_{f_i}\) for the function \(f_i\) for \(i\in [m]\) by the key generation algorithm of \(\mathsf {OnePKFE}\), and outputs  . The decryption algorithm of \(\mathsf {MultiPKFE}\), given a ciphertext \(\mathsf {CT}\) of a message \(\mathsf {m}\) and a decryption key \(\mathsf {sk}_f=\{\mathsf {sk}_{f_i}\}_{i\in [m]}\), computes \(f_i(\mathsf {m})\) for \(i\in [m]\) by using the decryption algorithm of \(\mathsf {OnePKFE}\), and outputs
. The decryption algorithm of \(\mathsf {MultiPKFE}\), given a ciphertext \(\mathsf {CT}\) of a message \(\mathsf {m}\) and a decryption key \(\mathsf {sk}_f=\{\mathsf {sk}_{f_i}\}_{i\in [m]}\), computes \(f_i(\mathsf {m})\) for \(i\in [m]\) by using the decryption algorithm of \(\mathsf {OnePKFE}\), and outputs  .
.
In the above construction, if \(\mathsf {OnePKFE}\) is adaptively collusion-resistant, then so is \(\mathsf {MultiPKFE}\) since a decryption key of \(\mathsf {MultiPKFE}\) consists of a polynomial number of decryption keys of \(\mathsf {OnePKFE}\). Moreover, the transformation also preserves the succinctness of a ciphertext since a ciphertext of \(\mathsf {MultiPKFE}\) consists of a ciphertext of \(\mathsf {OnePKFE}\).
We note that this transformation has not been explicitly pointed out before despite its simplicity. Although researchers in this filed might already observe this transformation, we explicitly write it since to the best of our knowledge, nobody explicitly claims.
By combining the transformation with the results of previous sections, we obtain fully-equipped PKFE for all polynomial-size functions from \((1,\mathsf {w}\text {-}\mathsf {sel},\mathsf {sls})\)-PKFE.
2.4 Adaptively Indistinguishable Garbling with Near-Optimal Online Complexity
We explained how to construct fully-equipped PKFE for all polynomial-size functions from \((1_\mathsf {key},\mathsf {w}\text {-}\mathsf {sel},\mathsf {sls})\)-PKFE through Sects. 2.1, 2.2, and 2.3. As mentioned in Sect. 1, we have another option to achieve it.
In the option, after constructing adaptive garbling scheme as explained in Sect. 2.2, we transform it into adaptively indistinguishable garbling with near-optimal online complexity. More specifically, we construct an adaptively indistinguishable garbling scheme whose online complexity only logarithmically depends on the size of a circuit being garbled, and does not depend on the output length of the circuit. Similarly to adaptive garbling scheme, adaptively indistinguishable garbling with such online complexity can be easily transformed into \((1_\mathsf {key},1_\mathsf {ct},\mathsf {ada},\mathsf {fs})\)-SKFE for (multi-bit output) circuits using one-time pad. Thus, by using the transformation by Ananth and Sahai [7] with the resulting \((1_\mathsf {key},1_\mathsf {ct},\mathsf {ada},\mathsf {fs})\)-SKFE, we obtain fully equipped PKFE for circuits.
We can generalize the transformation from adaptive garbling scheme into adaptively indistinguishable garbling that removes the dependence on the output-length of online encoding so that it captures not only our (and GS18) adaptive garbling scheme but also those proposed by Hemenway et al. [35] and Jafargholi and Wichs [38]. Thus, this transformation solves the open question posed by Jafargholi et al. [37]. Here, we give an overview of the transformation.
Basic Idea. Our starting point is the simulation-based adaptive garbling given in Sect. 5 (or in [30]), which we denote by \(\mathsf {adGC}^{\prime }_{{\mathsf {gs}}}\). Recall that the online communication complexity of \(\mathsf {adGC}^{\prime }_{{\mathsf {gs}}}\) is \(n+m+{\mathrm {poly}}(\lambda ,\log |C|)\) where C is the circuit being garbled with n-bit input and m-bit output. Especially, we remark that if we only consider circuits of single-bit output, then the online communication complexity is \(n+{\mathrm {poly}}(\lambda ,\log |C|)\). Our first attempt is to decompose a circuit of m-bit output to circuits of single-bit output, and garble each of them by using \(\mathsf {adGC}^{\prime }_{{\mathsf {gs}}}\). Namely, for garbling a circuit C of m-bit output, we garble \(C_i\), which is a circuit that outputs the i-th bit of an output of C, for each \(i\in [m]\). For an input x, the input garbling algorithm generates a single garbled input \(\widetilde{x}\) by \(\mathsf {adGC}^{\prime }_{{\mathsf {gs}}}\).
At first glance, this idea would lead to a garbling scheme with online communication complexity \(n+{\mathrm {poly}}(\lambda ,\log |C|)\) since we only garble circuits of single-bit output. However, this idea does not work since a garbling scheme is defined so that 1 garbled input is associated with 1 garbled circuit whereas we need a variant of garbling scheme where 1 garbled input is associated with multiple garbled circuits. Here, we notice that such a variant of garbling scheme can be seen as a single-key SKFE (with function privacyFootnote 14) by interpreting garbled circuits and garbled inputs as ciphertexts and decryption keys of SKFE, respectively. By this interpretation, the online communication and computational complexity as garbling are translated into the secret key length and running time of key generation, and the size of a circuit being garbled is translated into the message length. Based on this observation, we can see that what we need to construct an adaptively indistinguishable garbling with succinct online complexity is an adaptively secure single-key SKFE scheme with succinct decryption key and key generation in the sense that they only logarithmically depend on the message-length.
Single-Key SKFE with Succinct Decryption Key and Key Generation. Our idea to construct such an SKFE scheme is to plug \(\mathsf {adGC}^{\prime }_{{\mathsf {gs}}}\) into the construction of adaptively secure single-key SKFE by Gorbunov, Vaikuntanathan and Wee [33].Footnote 15 We first briefly review their construction. In their construction, for a message \(\mathsf {m}\), the encryption algorithm garbles the universal circuit \(U(\mathsf {m},\cdot )\), which is given a description of a function f as input and outputs \(f(\mathsf {m})\), by Yao’s garbling scheme to generate a garbled circuit \(\widetilde{U}\) along with labels that are needed to evaluate the garbled circuit. Then it encrypts \(\widetilde{U}\) and labels by a secret-key non-committing encryption for receiver (SK-NCER) to generate a ciphertext of the SKFE scheme.Footnote 16 Here, SK-NCER is a special type of SKE in which we can generate a “fake” ciphertext that can be opened to any message that is later chosen along with a corresponding “fake” decryption key. We note that we can construct an SK-NCER scheme whose decryption-key-length is proportional to the message-length from any SKE scheme by “double-encryption” construction similarly to some previous works [18, 34]. Namely, we encrypt each bit of the message under two different keys either of which is given to the decryptor. A decryption key of the SKFE scheme for a function f consists of secret keys of SK-NCER that enable one to recover labels corresponding to f. By using the decryption key, one first recovers labels corresponding to f and then evaluates the garbled circuit \(\widetilde{U}\) with these labels to obtain \(U(\mathsf {m},f)=f(\mathsf {m})\). Intuitively, the security of the SKFE scheme holds since an adversary who has a decryption key for f cannot obtain labels that do not correspond to f, and thus \(\widetilde{U}\) does not reveal information of \(\mathsf {m}\) beyond the value of \(U(\mathsf {m},f)=f(\mathsf {m})\) by the security of Yao’s garbling. We note that it is essential to encrypt \(\widetilde{U}\) by SK-NCER for achieving the adaptive security since Yao’s garbling only has the selective security and thus we cannot simulate \(\widetilde{U}\) before an input is determined.Footnote 17 Since the size of \(\widetilde{U}\) is proportional to the message-length of the SKFE scheme and the decryption-key-length of SK-NCER depends on its message-length, the decryption-key-length of their SKFE scheme is proportional to the message-length of the SKFE scheme.
Here, we observe that if we use an adaptive garbling scheme instead of Yao’s garbling, then we need not encrypt \(\widetilde{U}\) since we can simulate \(\widetilde{U}\) before an input is determined by the adaptive security, and we only need to encrypt labels by SK-NCER. Since the number of labels corresponds to the online communication complexity of the underlying garbling scheme, we expect that we could obtain an SKFE scheme with succinct decryption key by plugging \(\mathsf {adGC}^{\prime }_{{\mathsf {gs}}}\) into this construction. However, there is a problem that \(\mathsf {adGC}^{\prime }_{{\mathsf {gs}}}\) does not have the decomposability, which means that a garbled input is obtained by choosing labels according to each bit of the input whereas the above construction requires the garbling scheme to have the decomposability. Nonetheless, we observe that \(\mathsf {adGC}^{\prime }_{{\mathsf {gs}}}\) has a similar property to the decomposability called the quasi-decomposability, which we introduce in this paper. The quasi-decomposability roughly means that there exists a hash function \(\mathsf {H}\) such that a garbled input for an input x is generated by choosing labels according to each bit of \(\mathsf {H}(x)\) instead of x. We prove that the quasi-decomposability is sufficient to realize the above idea.
Now, we obtained adaptively secure single-key SKFE with succinct decryption key.Footnote 18 We can also see that the key generation algorithm of the scheme is also succinct. As discussed in the previous paragraph, such an SKFE scheme yields an adaptively indistinguishable garbling scheme with succinct online communication/computational complexity.
Other Instantiations. The above construction gives a generic construction of an adaptively indistinguishable garbling scheme whose online complexity does not depend on the output length of the circuit being garbled based on any (quasi-)decomposable adaptive garbling scheme. For example, we can also instantiate the construction with adaptive garbling schemes proposed by Hemenway et al. [35] and Jafargholi and Wichs [38] (the latter is Yao’s garbling itself) since they are decomposable. As a result, we obtain adaptively indistinguishable garbling schemes for corresponding circuit classes whose online complexity do not depend on output-length. Previously, such garbling schemes are constructed in an ad hoc manner by Jafargholi et al. [37]. On the other hand, our construction is generic, and thus resolves the open question posed by Jafargholi et al. [37].
Alternative Ad-hoc Way. Knowledgeable readers might think that we can achieve an adaptively indistinguishable garbling scheme that we need by replacing selectively secure garbling schemes in the somewhere adaptive garbling scheme by Garg, Miao, and Srinivasan [26] with GS18 scheme. This idea might work. However, the idea is an ad-hoc solution. Moreover, to formally prove its security, we must use the specific property (and internal structure) of Yao’s garbling scheme [45, 53] and GS18 scheme at least. We cannot use those schemes in a black-box way.Footnote 19 To avoid this issue, prove security in a modular way, and achieve a general transformation, we selected the design explained above.
3 Preliminaries
Definitions of standard notations and primitives are omitted here. Omitted definitions can be found in the full version.
3.1 Known Results on Functional Encryption
Ananth and Sahai [7] proved the following theorem.
Theorem 3.1
([7]). If there exist \((\mathsf {unb}_\mathsf {key},\mathsf {sel},\mathsf {fs})\)-PKFE for circuits and \((1_\mathsf {key},1_\mathsf {ct}, \mathsf {ada},\mathsf {fs})\)-SKFE for multi-bit output (resp. single-bit output) circuits, then there exists \((\mathsf {unb}_\mathsf {key},\mathsf {ada},\mathsf {fs})\)-PKFE for multi-bit output (resp. single-bit output) circuits.
Garg and Srinivasan [29] proved the following theorem.
Theorem 3.2
([29]). If there exists \((1_\mathsf {key},\mathsf {w}\text {-}\mathsf {sel},\mathsf {sls})\)-PKFE for circuits, then there exists \((\mathsf {unb}_\mathsf {key},\mathsf {sel},\mathsf {fs})\)-PKFE for circuits.
By combining these theorems, we obtain the following theorem.
Theorem 3.3
([7, 29]). If there exist \((1_\mathsf {key},\mathsf {w}\text {-}\mathsf {sel},\mathsf {sls})\)-PKFE for circuits and \((1_\mathsf {key},1_\mathsf {ct},\mathsf {ada},\mathsf {fs})\)-SKFE for multi-bit output (resp. single-bit output) circuits, then there exists \((\mathsf {unb}_\mathsf {key},\mathsf {ada},\mathsf {fs})-\text {PKFE} \) for multi-bit output (resp. single-bit output) circuits.
4 Selective-Database Laconic OT from PKFE
In this section, we show how to construct (updatable) laconic OT satisfying a security notion we call selective-database security from sublinearly succinct PKFE. We first show that by using IO, we can construct selective-database laconic OT with the compression factor 2. Then, we show that we can replace IO in our construction with sublinearly succinct PKFE by relying on the result of Liu and Zhandry [46]. Finally, we transform our selective-database laconic OT with compression factor 2 into updatable one based on the transformation using Merkle tree proposed by Cho et al. [19].
4.1 Definition of Selective-Database Laconic OT
We use (updatable) laconic OT proposed by Cho et al. [19]. However, the security level that we need in this work is slightly different from those by Cho et al., Garg and Srinivasan [30], and Ananth and Lombardi [5].
Definition 4.1
(Selective-Database Laconic OT). A laconic OT (LOT) A laconic OT protocol consists of four algorithms.
-
\(\mathsf {Gen}(1^\lambda ) \rightarrow \mathsf {crs}\): This algorithm takes as input the security parameter and outputs a common reference string \(\mathsf {crs}\).
-
 : This deterministic algorithm takes as input \(\mathsf {crs}\) and a database \(D\in \{0,1\}^{*}\) and outputs a digest \(d\) of \(D\) and a state \(\widehat{D}\).
: This deterministic algorithm takes as input \(\mathsf {crs}\) and a database \(D\in \{0,1\}^{*}\) and outputs a digest \(d\) of \(D\) and a state \(\widehat{D}\). -
\(\mathsf {Send}(\mathsf {crs},d,L,m_0,m_1) \rightarrow e\): This algorithm takes as input \(\mathsf {crs}\), \(d\), a database location \(L\in \mathbb {N}\), and two messages \(m_0\) and \(m_1\) of length \(p(\lambda )\), and outputs a ciphertext \(e\).
-
\(\mathsf {Receive}^{\widehat{D}}(\mathsf {crs},e,L) \rightarrow m\): This is a RAM algorithm with random read access to \(\widehat{D}\). It takes as input \(\mathsf {crs}\), \(e\), and \(L\in \mathbb {N}\), and outputs a message m.
These algorithms satisfy the following three properties.
Correctness. For any database \(D\) of size at most \(M={\mathrm {poly}}(\lambda )\), any memory location \(L\in [M]\), any pair of messages \((m_0,m_1) \in \{0,1\}^{p(\lambda )}\), it holds that \(m_{D[L]}=\mathsf {Receive}^{\widehat{D}} (\mathsf {crs},\mathsf {Send}(\mathsf {crs},d,L,m_0,m_1),L)\), where \(\mathsf {crs}\leftarrow \mathsf {Gen}(1^{\lambda })\) and  .
.
Selective-Database Adaptive-Message Sender Privacy Against Semi-honest Receivers. There exists a PPT simulator \(\mathsf {Sim}\) that satisfies \( |\Pr [\mathsf {Real}^{\mathsf {sel}\text {-}\mathsf {db}}_{\ell \mathsf {OT}}(\lambda )=1] - \Pr [\mathsf {Sim}^{\mathsf {sel}\text {-}\mathsf {db}}_{\ell \mathsf {OT}}(\lambda )=1]| \le {\mathsf {negl}}(\lambda ) \), where the experiments \(\mathsf {Real}^{\mathsf {sel}\text {-}\mathsf {db}}_{\ell \mathsf {OT}}(\lambda )\) and \(\mathsf {Sim}^{\mathsf {sel}\text {-}\mathsf {db}}_{\ell \mathsf {OT}}(\lambda )\) are defined as follows.

where \(|D|=M = {\mathrm {poly}}(\lambda )\), \(L\in [M]\), and \(m_0,m_1 \in \{0,1\}^{p(\lambda )}\).
We call this security selective-database sender privacy for short in this paper.
Efficiency. We require that \(|d|\) is bounded by a fixed polynomial in \(\lambda \) independent of \(|D|\), the running time of \(\mathsf {Hash}\) is \(|D|\cdot {\mathrm {poly}}(\log {|D|},\lambda )\), and the running time of \(\mathsf {Send}\) and \(\mathsf {Receive}\) are \({\mathrm {poly}}(\log {|D|},\lambda )\).
Selective-database adaptive-message sender privacy for updatable laconic OT [19] is defined similarly. A formal definition can be found in the full version.
4.2 Selective-Database Laconic OT with Compression Factor 2 from IO
We show how to construct laconic OT from IO in this subsection. Let \(\mathsf {IBE}=(\mathsf {IBE}.\mathsf {Setup}, \mathsf {IBE}.\mathsf {KG}, \mathsf {IBE}.\mathsf {Enc}, \mathsf {IBE}.\mathsf {Dec})\) be an IBE scheme. For simplicity, we assume that the randomness space of \(\mathsf {IBE}.\mathsf {Setup}\) is \(\{0,1\}^\lambda \) and \(\mathsf {IBE}.\mathsf {KG}\) is deterministic.Footnote 20 We let the length of a master public-key of \(\mathsf {IBE}\) be bounded by some fixed polynomial \({\mathrm {poly}}_\mathsf {MPK}(\lambda ,n)\), where n is the length of identities. Then, there exists a polynomial \(s={\mathrm {poly}}(\lambda )\) such that \(s \ge {\mathrm {poly}}_\mathsf {MPK}(\lambda ,\log s+2)\). Let \(\mathsf {PPRF}=(\mathsf {F},\mathsf {Punc})\) be a puncturable PRF whose domain and range are \(\{0,1\}^{2s}\) and \(\{0,1\}^\lambda \), respectively. Let \(i\mathcal {O}\) be an IO.
We construct an LOT protocol \(\ell \mathsf {OT}=(\mathsf {Gen},\mathsf {Hash}, \mathsf {Send}, \mathsf {Receive})\) whose hash algorithm \(\mathsf {Hash}\) hashes a 2s bit database to a digest of \({\mathrm {poly}}_\mathsf {MPK}(\lambda ,\log s+2)\le s\) bits. Thus, our construction achieves compression factor 2. In the construction, for an integer \(i\in [2s]\), \(\mathsf {str}(i)\) denotes the bit representation of i.
-
\(\mathsf {Gen}(1^\lambda ):\)
-
1.
Generates \(K \xleftarrow {\mathsf {r}}\{0,1\}^\lambda \).
-
2.
Computes \(\mathsf {crs}\leftarrow i\mathcal {O}\left( 1^\lambda , \mathsf {SetupKG}[K]\right) \). The circuit \(\mathsf {SetupKG}\) is defined in Fig. 2.
-
3.
Outputs \(\mathsf {crs}\).
-
1.
-
\(\mathsf {Hash}(\mathsf {crs}, D):\)
-
1.
Outputs \(\left( d,\widehat{D}\right) \leftarrow \mathsf {crs}(D)\).
-
1.
-
\(\mathsf {Send}(\mathsf {crs}, d, L, \mathsf {m}_0,\mathsf {m}_1):\)
-
1.
Parses \(\mathsf {MPK}\leftarrow d\).
-
2.
For \(\alpha \in \{0,1\}\), computes \(\mathsf {CT}_\alpha \leftarrow \mathsf {IBE}.\mathsf {Enc}(\mathsf {MPK}, \mathsf {str}(L)\Vert \alpha , \mathsf {m}_\alpha )\).
-
3.
Outputs \(e := (\mathsf {CT}_0,\mathsf {CT}_1)\).
-
1.
-
\(\mathsf {Receive}^{\widehat{D}}(\mathsf {crs},e,L):\)
-
1.
Sets \(\widehat{D}:=\left( D,\{\mathsf {sk}_i\}_{i\in [2s]}\right) \).
-
2.
Parses \(e \leftarrow (\mathsf {CT}_0,\mathsf {CT}_1)\).
-
3.
Outputs \(m \leftarrow \mathsf {IBE}.\mathsf {Dec}\left( \mathsf {sk}_L, \mathsf {CT}_{D[L]}\right) \).
-
1.
Theorem 4.1
Let \(\mathsf {IBE}\) be a selectively secure IBE scheme and \(\mathsf {PPRF}\) be a puncturable PRF. Let \(i\mathcal {O}\) be IO. Then, \(\ell \mathsf {OT}\) be a selective-database laconic OT.
The proof can be found in the full version.
4.3 Replacing IO with Sublinearly Succinct PKFE
IO in our construction can be replaced with sublinearly succinct PKFE by relying on the result of Liu and Zhandry [46]. Liu and Zhandry showed we can replace IO with decomposable obfuscation (dO) that can be based on sublinearly succinct PKFE if the circuit pair to be obfuscated satisfies some condition by generalizing previous works [27,28,29]. Roughly speaking, they showed that if there is a polynomial size “witness” for the functional equivalence of a circuit pair to be obfuscated, IO can be replaced with dO. One particular situation where this condition is satisfied is that in the security proof we modify a circuit to be obfuscated so that it outputs a hard-wired value for a single input and otherwise it runs in the same way as the original one. More formally, we obtain the following theorem as a special case of the result by Liu and Zhandry.
Theorem 4.2
([46]). Let \(C'(x,r)\) be a circuit. Let \(\mathsf {PPRF}=(\mathsf {F},\mathsf {Punc})\) be a punctured PRF and \(K\in \{0,1\}^\lambda \). Let \(\mathsf {Punc}\) be deterministic. We define a circuit \(C_K\) as \(C_K(x)=C'(x,\mathsf {F}_K(x))\). Moreover, we define a circuit \(C^*\) as
where \(x^*\), \(K^*\leftarrow \mathsf {Punc}(K,x^*)\), and \(y^*=C(x^*)\) are hardwired into \(C^*\). \(C_K\) and \( C^*_{x^*,K^*,y^*}\) are parameterized by K and \(x^*\), and they are functionally equivalent for all K and \(x^*\).
Assuming \((1_\mathsf {key},\mathsf {w}\text {-}\mathsf {sel},\mathsf {sls})\)-PKFE, there exists a special type of punctured PRF and decomposable obfuscation whose indistinguishability property holds for each pair of circuits \(\{(C_K,C^*_{x^*,K^*,y^*})\}_{K,x^*}\) by implementing them using the PRF.
In the above theorem, “a special type of punctured PRF” is a primitive called decomposing compatible PRF by Liu and Zhandry. Decomposing compatible PRF can be constructed from one-way functions via the construction proposed by Goldreich et al. [32], and thus its existence is implied by that of PKFE. See Sect. 2.1 or the paper by Liu and Zhandry [46] for details.
In the construction of selective-database laconic OT based on IO in Sect. 4.2, we apply IO for a pair of circuits \(\mathsf {SetupKG}\) and \(\mathsf {SetupKG}^*\). We see that when we apply IO to these circuits, they have exactly the same functional relationship as C and \(C^*\) in Theorem 4.2. That is, we obtain the following.
Lemma 4.1
Circuits \(\mathsf {SetupKG}[K]\) and \(\mathsf {SetupKG}^*[D^*\!,K\{D^*\}\!,\mathsf {MPK}^*\!,\{\mathsf {sk}^*_i\}_{i\in [2s]}]\) in Sect. 4.2 fall into the circuit class \(C_K\) and \(C^*_{x^*,K^*,y^*}\) defined in Theorem 4.2.
Therefore, from Theorem 4.2 and Lemma 4.1, IO that is needed in our construction of selective-database laconic OT in Sect. 4.2 can be instantiated based on sublinearly succinct PKFE.
Moreover, selectively secure IBE can be constructed from sublinearly succinct PKFE [29], and puncturable PRF can be based on one-way functions. Thus, we obtain the following theorem.
Theorem 4.3
Assume that there exists \((1_\mathsf {key},\mathsf {w}\text {-}\mathsf {sel},\mathsf {sls})\)-PKFE for circuits. Then, there exists selective-database laconic OT with compression factor 2.
4.4 From Non-updatable to Updatable
Cho et al. [19] showed we could bootstrap a laconic OT with the compression factor 2 into an updatable laconic OT with arbitrary compression factor using a garbling scheme and Merkle hash tree. Their bootstrapping method considers laconic OT that satisfies a weak security notion where in addition to the challenge database, the challenge location and messages are also fixed at the beginning of the security game. As Ananth and Lombardi [5] pointed out, if we use selective-database laconic OT as a building block for the bootstrapping method, then we have to use a minor variant of the method to obtain selective-database updatable laconic OT (the original bootstrapping method is not sufficient for us). More specifically, we have to sample fresh \(\mathsf {crs}_j\) for each depth j of the Merkle hash tree in the bootstrapping method. We use this variant since our laconic OT is selective-database secure. That is, we have the following theorem.
Theorem 4.4
([5, 19]). Assume that there exists selective-database laconic OT with the compression factor 2. Then, there exists selective-database updatable laconic OT with arbitrary compression factor.
By combining Theorems 4.3 and 4.4, we obtain the following theorem.
Theorem 4.5
Assume that there exists \((1_\mathsf {key},\mathsf {w}\text {-}\mathsf {sel},\mathsf {sls})\)-PKFE. Then, there exists selective-database updatable laconic OT with arbitrary compression factor.
5 Adaptive Garbling from Selective-Database Laconic OT
In this section, we present an adaptive garbling scheme with nearly optimal online communication/computational complexity based on selective-database updatable LOT. Garg and Srinivasan presented such an adaptive garbling scheme based on adaptively secure updatable LOT [30], which is instantiated by concrete assumptions such as CDH [16, 19, 23]. However, we cannot directly use their adaptive garbling scheme due to the following two reasons.
-
1.
Our goal in this section is achieving adaptive garbling scheme from succinct PKFE (i.e., we do not rely on any specific assumption such as the CDH assumption).
-
2.
The updatable LOT protocol presented in Sect. 4 is selective-database updatable LOT.
We will show that we can achieve an adaptive garbling scheme with nearly optimal online communication/computational complexity from selective-database updatable LOT in the rest of this section.
5.1 Description of Our Adaptive Garbling Scheme
In this section, we present our adaptive garbling scheme and properties that it satisfies.
Theorem 5.1
If there exist selective-database updatable LOT, somewhere equivocal encryption, and selectively secure garbled circuits, then there exists an adaptively secure garbling scheme for circuits with online communication complexity \(n+m+{\mathrm {poly}}(\lambda ,\log {|C|})\) and online computational complexity \(O(n+m)+{\mathrm {poly}}(\lambda ,\log {|C|})\).
From this theorem, Theorem 4.5, and the fact that selectively secure garbled circuits and somewhere equivocal encryption can be constructed from one-way functions [35], we obtain the following theorem.
Theorem 5.2
If there exists \((1_\mathsf {key},\mathsf {w}\text {-}\mathsf {sel},\mathsf {sls})\)-PKFE, then there exists an adaptively secure garbling scheme for circuits with online communication complexity \(n+m+{\mathrm {poly}}(\lambda ,\log {|C|})\) and online computational complexity \(O(n+m)+{\mathrm {poly}}(\lambda ,\log {|C|})\).
Conventions. Without loss of generality, we assume that circuits consist of only NAND gates. Let n, m, and \(N-n\) be the input length, output length, and the number of NAND gates of the circuit. An index is assigned to each input and gate. That is, from 1 to n are input wires, from \(n+1\) to \(N-m\) are intermediate NAND gates, and \(N-m+1\) to N are output gates of the circuit. Note that a gate whose inputs come from gate i and j has an index greater than i and j. Each gate \(g\in [n+1,N]\) is represented by a pair \((i,j) \in [g-1]\times [g-1]\). That is, the inputs of g are outputs of gates i and j. In this section, we use \(r_i\), \(x_i\), and \(y_i\) instead of r[i], x[i], and y[i] to mean the i-th bit of r, x, and y, respectively for notational simplicity.
A Variant of GS18 Garbling Scheme. We prove Theorem 5.1 in the rest of this section. First, we describe our adaptive garbling scheme. We put  at different points from the adaptive garbling scheme by Garg and Srinivasan [30]. Let
at different points from the adaptive garbling scheme by Garg and Srinivasan [30]. Let  ,
,  , and
, and  be a somewhere equivocal encryption scheme, a (selectively secure) garbling scheme with a corresponding simulator \(\mathsf {GC}.\mathsf {Sim}\), and an updatable LOT protocol, respectively. Our adaptive garbling scheme
be a somewhere equivocal encryption scheme, a (selectively secure) garbling scheme with a corresponding simulator \(\mathsf {GC}.\mathsf {Sim}\), and an updatable LOT protocol, respectively. Our adaptive garbling scheme  is as follows.
is as follows.
-
\(\mathsf {GbCkt}(1^\lambda ,C)\): This algorithm garbles a circuit \(C: \{0,1\}^{n} \rightarrow \{0,1\}^{m}\) as follows.
-
1.
Generates \(\mathsf {sek}\leftarrow \mathsf {KeyGen}(1^\lambda )\), and chooses \(r\leftarrow \{0,1\}^{N}\).
-
2.
Generates \(\mathsf {crs}\leftarrow \mathsf {Gen}(1^\lambda )\).
-
3.
Chooses \(\mathsf {label}_{k,b}^{g} \leftarrow \{0,1\}^{\lambda }\) and
 for \(g\in [n+1,N+1]\), \(k\in [\lambda ]\), and \(b\in \{0,1\}^{}\).
for \(g\in [n+1,N+1]\), \(k\in [\lambda ]\), and \(b\in \{0,1\}^{}\). -
4.
From \(g = N\) to \(g=n+1\) (decrement g), does the following.
-
(a)
Interprets gate g as (i, j).
-
(b)
Computes

-
(a)
-
5.
Generates \(\varvec{c}\leftarrow \mathsf {Enc}(\mathsf {sek},\{\widetilde{\mathsf {SC}}_g\}_{g\in [n+1,N]})\).
-
6.
Outputs
 and
and  .
.
-
1.
-
\(\mathsf {GbInp}(\mathsf {st},x)\): This algorithm garbles an input \(x \in \{0,1\}^{n}\) as follows.
-
1.
Parses
 .
. -
2.
Sets
 .
. -
3.
Computes
 .
. -
4.
Outputs
 .
.
-
1.
-
\(\mathsf {GbEval}(\widetilde{C},\widetilde{x})\): This evaluation algorithm does the following.
-
1.
Parses \(\widetilde{C}= \varvec{c}\) and
 .
. -
2.
Sets
 .
. -
3.
Computes
 .
. -
4.
Computes \(\{\widetilde{\mathsf {SC}}_g\}_{g \in [n+1,N]} \leftarrow \mathsf {Dec}(\mathsf {sek},\varvec{c})\).
-
5.
Set
 and
and  .
. -
6.
For \(g=n+1, \ldots , N\)
-
(a)
Interprets g as (i, j).
-
(b)
Computes
 .
. -
(c)
Computes
 .
. -
(d)
Sets
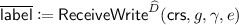 and
and  .
.
-
(a)
-
7.
Reads \(D\) from \(\widehat{D}\).
-
8.
Outputs
 .
.
-
1.
Remark 5.1
We assume that the length of \(\mathsf {crs}\) is \(\lambda \) for ease of notation instead of writing \(\{\mathsf {label}_{k',b}^{g,\mathsf {crs}}\}_{k' \in [{\mathrm {poly}}(\lambda )],b\in \{0,1\}^{}}\). We often omit the region where indices (k, b) run if it is clear from the context. That is, we often write \(\{\mathsf {label}_{k,b}^{g}\}\) and \(\{\mathsf {label}_{k,b}^{g,\mathsf {crs}}\}\) to denote \(\{\mathsf {label}_{k,b}^{g}\}_{k \in [\lambda ], b \in \{0,1\}^{}}\) and \(\{\mathsf {label}_{k,b}^{g,\mathsf {crs}}\}_{k \in [\lambda ], b \in \{0,1\}^{}}\).
Proofs of correctness and security can be found in the full version.
Online Complexity of \(\mathsf {GbInp}\). We confirm that our garbling scheme satisfies the complexity described in Theorem 5.2.
-
Online Communication Complexity: We see that \(|\widetilde{x}| = \lambda ^2 + \lambda + |\mathsf {crs}| + n + m + |\mathsf {sek}|\). By the efficiency of updatable LOT, \(|\mathsf {crs}| = \lambda \) holdsFootnote 21. Recall that \(|\mathsf {sek}| = t \cdot s \cdot {\mathrm {poly}}(\lambda )\) where s is the block-length and t is the equivocation parameter. In our setting, we set
 and
and  . Moreover, by the efficiency of updatable LOT, \(|\widetilde{\mathsf {SC}}| = {\mathrm {poly}}(\log {N},\lambda )\). Therefore, \(|\mathsf {sek}| = {\mathrm {poly}}(\log {N},\lambda )\). Thus, \(|\widetilde{x}| = n + m + {\mathrm {poly}}(\log {|C|},\lambda )\) (note that \(|C| = N\)).
. Moreover, by the efficiency of updatable LOT, \(|\widetilde{\mathsf {SC}}| = {\mathrm {poly}}(\log {N},\lambda )\). Therefore, \(|\mathsf {sek}| = {\mathrm {poly}}(\log {N},\lambda )\). Thus, \(|\widetilde{x}| = n + m + {\mathrm {poly}}(\log {|C|},\lambda )\) (note that \(|C| = N\)). -
Online Computational Complexity: The running time of our \(\mathsf {GbInp}\) depends on N since it computes \(\mathsf {Hash}(\mathsf {crs},D)\). However, we can reduce the computational complexity using a specific structure of the updatable LOT by Cho et al. [19] (recall that our updatable LOT in Sect. 4 also uses this structure) by using the same technique as GS18 scheme. We briefly review it. The construction uses Merkle hash tree technique. Therefore, we can efficiently update a hash value. Let y and \(y'\) consist of \(\ell \) blocks of \(\lambda \)-bits strings. Assume that y is different from \(y'\) only in the first k blocks. Given the Merkle hash on y and a set of \(\log {|y|}\) hash values, there exists an efficient algorithm that computes the Merkle hash on \(y'\) and whose running time is \(O(\lambda (k+\log {|y|}))\). By using this efficient update algorithm, we can reduce the computational complexity as follows. At offline phase, we compute a hash value on \(0^N\). We set each block length to be 1. That is, when \(x\in \{0,1\}^{n}\) is given, we update the first \(\left\lceil {n}\right\rceil \) blocks. For updating the hash value on \(0^N\) to the hash value on
 , it takes \(O(1 \cdot (n + \log {N}))\) time. That is, the running time of \(\mathsf {GbInp}\) is \(O(n + m) + {\mathrm {poly}}(\log {|C|},\lambda )\) since \(\mathsf {GbInp}\) computes the hash value and outputs \({\mathrm {poly}}(\lambda )+n+m\) values. Note that \(\mathsf {GbInp}\) need not output \((r_{n+1},\ldots ,r_{N - m})\).
, it takes \(O(1 \cdot (n + \log {N}))\) time. That is, the running time of \(\mathsf {GbInp}\) is \(O(n + m) + {\mathrm {poly}}(\log {|C|},\lambda )\) since \(\mathsf {GbInp}\) computes the hash value and outputs \({\mathrm {poly}}(\lambda )+n+m\) values. Note that \(\mathsf {GbInp}\) need not output \((r_{n+1},\ldots ,r_{N - m})\).
5.2 Secret-Key FE from Our Adaptive Garbling
We observe that \(\mathsf {adGC}^{\prime }_{{\mathsf {gs}}}\) can be seen as a single-key and single-ciphertext adaptive SKFE by considering a garbled circuit and a garbled input to be a decryption key and a ciphertext, respectively, where a master secret key is set as  .Footnote 22 Moreover, if we only consider single-bit output circuits as a function class, the scheme is fully succinct due to the succinct online complexity of \(\mathsf {adGC}^{\prime }_{{\mathsf {gs}}}\). See the full version for details. By combining Theorem 5.2 with the above observation, we obtain the following theorem.
.Footnote 22 Moreover, if we only consider single-bit output circuits as a function class, the scheme is fully succinct due to the succinct online complexity of \(\mathsf {adGC}^{\prime }_{{\mathsf {gs}}}\). See the full version for details. By combining Theorem 5.2 with the above observation, we obtain the following theorem.
Theorem 5.3
If there exists \((1_\mathsf {key},\mathsf {w}\text {-}\mathsf {sel},\mathsf {sls})\)-PKFE for circuits, then there exists \((1_\mathsf {key},1_\mathsf {ct},\mathsf {ada},\mathsf {fs})\)-SKFE for single-bit output circuits.
By combining Theorems 3.3 and 5.3, we obtain the following theorem.
Theorem 5.4
If there exists \((1_\mathsf {key},\mathsf {w}\text {-}\mathsf {sel},\mathsf {sls})\)-PKFE for circuits, then there exists \((\mathsf {unb}_\mathsf {key},\mathsf {ada},\mathsf {fs})\)-PKFE for single-bit output circuits.
6 Adaptively Secure, Collusion-Resistant, and Succinct FE
In this section, we show a conversion from collusion-resistant PKFE for single-bit output circuits to one for multi-bit output circuits without sacrificing succinctness. Combined with Theorem 5.4, this gives our main theorem, Theorem 1.1.
6.1 From Single-Bit to Multi-bit Succinct FE by Leveraging Collusion-Resistance
Let \(\mathsf {OnePKFE}=(\mathsf {OnePKFE}.\mathsf {Setup}, \mathsf {OnePKFE}.\mathsf {KG}, \mathsf {OnePKFE}.\mathsf {Enc}, \mathsf {OnePKFE}.\mathsf {Dec})\) be an PKFE scheme for \(\mathcal {M}\),  , and single-bit output circuits. Then, we construct an PKFE scheme \(\mathsf {MultiPKFE}=(\mathsf {MultiPKFE}.\mathsf {Setup}, \mathsf {MultiPKFE}.\mathsf {KG}, \mathsf {MultiPKFE}.\mathsf {Enc}, \mathsf {MultiPKFE}.\mathsf {Dec})\) for \(\mathcal {M}\),
, and single-bit output circuits. Then, we construct an PKFE scheme \(\mathsf {MultiPKFE}=(\mathsf {MultiPKFE}.\mathsf {Setup}, \mathsf {MultiPKFE}.\mathsf {KG}, \mathsf {MultiPKFE}.\mathsf {Enc}, \mathsf {MultiPKFE}.\mathsf {Dec})\) for \(\mathcal {M}\),  , and circuits as follows.
, and circuits as follows.
-
\(\mathsf {MultiPKFE}.\mathsf {Setup}(1^\lambda )\):
-
1.
Computes \((\mathsf {MPK},\mathsf {MSK}) \leftarrow \mathsf {OnePKFE}.\mathsf {Setup}(1^{\lambda })\).
-
2.
Outputs \((\mathsf {MPK},\mathsf {MSK})\).
-
1.
-
\(\mathsf {MultiPKFE}.\mathsf {KG}(\mathsf {MSK},f)\):
-
1.
Computes \(\mathsf {sk}_i \leftarrow \mathsf {OnePKFE}.\mathsf {KG}(\mathsf {MSK},f_i)\) for every \(i\in [\ell ]\) where \(f_i(\mathsf {m})\) outputs the i-th bit of \(f(\mathsf {m})\).
-
2.
Outputs
 .
.
-
1.
-
\(\mathsf {MultiPKFE}.\mathsf {Enc}(\mathsf {MPK},\mathsf {m})\):
-
1.
Computes \(\mathsf {CT}_\mathsf {m}\leftarrow \mathsf {OnePKFE}.\mathsf {Enc}(\mathsf {MPK},\mathsf {m})\).
-
2.
Outputs
 .
.
-
1.
-
\(\mathsf {MultiPKFE}.\mathsf {Dec}(\mathsf {sk}_f,\mathsf {CT}_\mathsf {m})\):
-
1.
Parses \(\{\mathsf {sk}_{f_i}\}_{i\in [\ell ]}\leftarrow \mathsf {sk}_f\).
-
2.
Computes \(y_i\leftarrow \mathsf {OnePKFE}.\mathsf {Dec}(\mathsf {sk}_{f_i},\mathsf {CT}_\mathsf {m})\) for every \(i\in [\ell ]\).
-
3.
Outputs
 .
.
-
1.
Correctness. Correctness of \(\mathsf {MultiPKFE}\) easily follows from correctness of \(\mathsf {OnePKFE}\).
Security. The security of \(\mathsf {MultiPKFE}\) can be stated as follows.
Theorem 6.1
If \(\mathsf {OnePKFE}\) is \((\mathsf {unb}_\mathsf {key},\mathsf {sec},\mathsf {eff})\)-PKFE for single-bit output circuits, then \(\mathsf {MultiPKFE}\) is \((\mathsf {unb}_\mathsf {key},\mathsf {sec},\mathsf {eff})\)-PKFE for multi-bit output circuits where \(\mathsf {sec} \in \{\mathsf {w}\text {-}\mathsf {sel},\mathsf {sel},\mathsf {ada}\}\) and \(\mathsf {eff} \in \{\mathsf {ns},\mathsf {sls},\mathsf {fs}\}\).
This can be proven by a standard hybrid argument.
The Running Time of Encryption Algorithm. Since the encryption algorithm of \(\mathsf {MultiPKFE}\) only runs the encryption algorithm of \(\mathsf {OnePKFE}\), the running time of \(\mathsf {MultiPKFE}.\mathsf {Enc}\) is the same as that of \(\mathsf {OnePKFE}.\mathsf {Enc}\). \(\mathsf {OnePKFE}.\mathsf {Enc}\) is succinct, so \(\mathsf {MultiPKFE}.\mathsf {Enc}\) is.
6.2 Fully-Equipped PKFE
By combining Theorems 5.4 and 6.1, we obtain the main theorem in this study, that is, Theorem 1.1. We obtain adaptively secure, collusion-resistant, and succinct public-key FE for circuits from weakly-selectively secure, single-key, and sublinearly-succinct public-key FE for circuits.
7 Adaptively Indistinguishable Garbling with Near-Optimal Online Complexity
In this section, we give a construction of an adaptively indistinguishable garbling scheme for all circuits whose online complexity does not depend on output-length of the circuit to garble. Namely, the length of online part in our construction is \(2n+{\mathrm {poly}}(\log |C|,\lambda )\) where n and |C| denote the input-length and circuit size, respectively. This is done by transforming our adaptive garbling scheme given in Sect. 4 (or the one by Garg and Srinivasan [30]). Our result can be stated as follows.
Theorem 7.1
If one of the {CDH, Factoring, LWE} assumptions holds or \((1_\mathsf {key},\mathsf {w}\text {-}\mathsf {sel},\mathsf {sls})\)-PKFE for circuits exists, then there exists an adaptively indistinguishable garbling scheme whose online communication complexity is \(2n+{\mathrm {poly}}(\log |C|,\lambda )\) and online computational complexity is \(O(n)+{\mathrm {poly}}(\log |C|,\lambda )\) where C is the circuit being garbled of n-bit input.
We note the adaptively indistinguishable garbling scheme obtained by the above theorem can be seen as \((1_\mathsf {key},1_\mathsf {ct},\mathsf {ada},\mathsf {fs})\)-SKFE for all circuits. This gives an alternative way to construct fully-equipped PKFE by Theorem 3.1.
Moreover, our construction gives a generic way to convert simulation-secure adaptive garbling (with a particular structure which we call quasi-decomposability) whose online complexity depends on output-length into adaptively indistinguishable garbling whose online complexity does not depend on output-length. By instantiating the conversion with known adaptive garbling schemes from one-way functions [35, 38], we obtain the following corollary.
Corollary 7.1
(Also proven in [37]). If one-way function exists, the following garbling schemes exist:
-
1.
Adaptively indistinguishable garbling scheme for \(\mathsf {NC}^1\) whose online communication/computational complexity are \(n\cdot {\mathrm {poly}}(\lambda )\).
-
2.
Adaptively indistinguishable garbling scheme for all circuits whose online communication/computational complexity are \((n+w)\cdot {\mathrm {poly}}(\lambda )\).
where n is the input-length and w is the width of the circuit being garbled.
Though Jafargholi et al. [37] already proved the same statement, their construction is obtained by modifying (simulation-based) adaptive garbling scheme by Hemenway et al. [35] in an ad hoc and complicated manner. On the other hand, our construction is generic, and gives a modular construction. See the full version for the details of these results.
Notes
- 1.
Of course, adversaries can send queries after they decided a pair of target messages.
- 2.
See the subsequent paragraph for the reason of naming “obf-minimum”.
- 3.
In the case of PKFE, \(\#\mathsf {ct}\) is trivially \(\mathsf {unb}\).
- 4.
In the setting of SKFE, only an entity that has a master secret-key can generate ciphertexts. Thus, adversaries is allowed to send messages as queries and receives ciphertexts in its security game. When adversaries can send one/polynomially-many message(s), we say one/many-ciphertext SKFE.
- 5.
In fact, there are subtle issues to transform a garbling scheme into a single-key and single-ciphertext SKFE (the opposite is easy). See the full version for more details.
- 6.
- 7.
Jafargholi et al. wrote “It remains an open problem whether it is possible to show a more general transformation from garbled circuits with adaptive security (and maybe other natural properties) to garbled circuits with indistinguishability based adaptive security and online complexity independent of the output size.” [37].
- 8.
Ananth and Lombardi present an LOT protocol based on IO [5].
- 9.
The security level of our LOT is sufficient for their purpose.
- 10.
Note that we cannot obtain an adaptively secure scheme in Corollary 1.2 since the succinct garbling for TMs by Ananth and Lombardi is not adaptively secure.
- 11.
Note that their FE for TMs satisfies a stronger security notion called distributional indistinguishability than standard indistinguishability.
- 12.
Cho et al.’s bootstrapping method is not sufficient for LOT whose security holds only when an adversary declares the challenge database before seeing CRS. Therefore, we cannot use the bootstrapping method of Cho et al. directly to make our selective-database (explained later) LOT updatable. However, we can use a minor variant of the bootstrapping method observed by Ananth and Lombardi [5] to bootstrap selective-database LOT into updatable one.
- 13.
To achieve \(\frac{1}{2}\) compression in our construction, it is sufficient that the size of a master public-key is logarithmic in the length of identities. This requirement is more natural for IBE, and thus we assume only this mild condition in the actual construction.
- 14.
We say that an SKFE scheme is function private if a decryption key does not reveal the associated function. As shown by Brakerski and Segev [17], we can generically add the function privacy to any SKFE scheme. Thus we do not care about function privacy in this overview.
- 15.
Though Gorbunov et al. [33] presented their construction in the public key setting, the same construction works in the secret key setting.
- 16.
Though Gorbunov et al. [33] does not use an abstraction as NCER, we observe that their construction can be seen like this.
- 17.
Though Jafargholi and Wichs [38] showed that Yao’s garbling scheme is adaptively secure for certain class of circuits like \(\mathsf {NC}^1\), we do not know how to prove its adaptive security for all circuits.
- 18.
Strictly speaking, the SKFE scheme achieves a security notion called key-adaptive security slightly weaker than the adaptive security, in which an adversary cannot make any encryption queries after making the key query. We note that this is sufficient for constructing an adaptively indistinguishable garbling scheme since the adaptive security of a garbling scheme only considers the case where a garbled input is generated after a garbled circuit is generated.
- 19.
We can formally prove adaptive security of the somewhere adaptive garbling scheme by Garg et al. [26] by using specific properties of Yao’s selectively secure garbling scheme instead of using selective security in a black-box way.
- 20.
We can always modify any IBE scheme so that it satisfies these two conditions by using PRF.
- 21.
In fact, in our LOT protocol in Sect. 4, \(|\mathsf {crs}| = {\mathrm {poly}}(\lambda )\). However, it does not matter here since it is absorbed in \({\mathrm {poly}}(\log {|C|},\lambda )\) part.
- 22.
Actually, the direct adaptation only achieves ciphertext-adaptive security where a decryption key must be queried before the challenge ciphertext is given to an adversary. This can be easily overcome by using one-time pad without sacrificing succinctness.
References
Ananth, P., Brakerski, Z., Segev, G., Vaikuntanathan, V.: From selective to adaptive security in functional encryption. In: Gennaro, R., Robshaw, M. (eds.) CRYPTO 2015, Part II. LNCS, vol. 9216, pp. 657–677. Springer, Heidelberg (2015). https://doi.org/10.1007/978-3-662-48000-7_32
Agrikola, T., Couteau, G., Hofheinz, D.: The usefulness of sparsifiable inputs: how to avoid subexponential iO. Cryptology ePrint Archive, Report 2018/470 (2018)
Ananth, P., Jain, A.: Indistinguishability obfuscation from compact functional encryption. In: Gennaro, R., Robshaw, M. (eds.) CRYPTO 2015, Part I. LNCS, vol. 9215, pp. 308–326. Springer, Heidelberg (2015). https://doi.org/10.1007/978-3-662-47989-6_15
Ananth, P., Jain, A., Sahai, A.: Indistinguishability obfuscation from functional encryption for simple functions. Cryptology ePrint Archive, Report 2015/730 (2015)
Ananth, P., Lombardi, A.: Succinct garbling schemes from functional encryption through a local simulation paradigm. In: Beimel, A., Dziembowski, S. (eds.) TCC 2018, Part II. LNCS, vol. 11240, pp. 455–472. Springer, Cham (2018). https://doi.org/10.1007/978-3-030-03810-6_17
Agrawal, S., Maitra, M.: FE and iO for turing machines from minimal assumptions. In: Beimel, A., Dziembowski, S. (eds.) TCC 2018, Part II. LNCS, vol. 11240, pp. 473–512. Springer, Cham (2018). https://doi.org/10.1007/978-3-030-03810-6_18
Ananth, P.V., Sahai, A.: Functional encryption for Turing machines. In: Kushilevitz, E., Malkin, T. (eds.) TCC 2016-A, Part I. LNCS, vol. 9562, pp. 125–153. Springer, Heidelberg (2016). https://doi.org/10.1007/978-3-662-49096-9_6
Applebaum, B., Ishai, Y., Kushilevitz, E., Waters, B.: Encoding functions with constant online rate, or how to compress garbled circuit keys. SIAM J. Comput. 44(2), 433–466 (2015)
Asharov, G., Segev, G.: Limits on the power of indistinguishability obfuscation and functional encryption. In: 56th FOCS, pp. 191–209 (2015)
Barak, B., et al.: On the (im)possibility of obfuscating programs. J. ACM 59(2), 6:1–6:48 (2012)
Bellare, M., Hoang, V.T., Rogaway, P.: Adaptively secure garbling with applications to one-time programs and secure outsourcing. In: Wang, X., Sako, K. (eds.) ASIACRYPT 2012. LNCS, vol. 7658, pp. 134–153. Springer, Heidelberg (2012). https://doi.org/10.1007/978-3-642-34961-4_10
Bitansky, N., et al.: Indistinguishability obfuscation for RAM programs and succinct randomized encodings. SIAM J. Comput. 47(3), 1123–1210 (2018)
Bitansky, N., Nishimaki, R., Passelègue, A., Wichs, D.: From cryptomania to obfustopia through secret-key functional encryption. In: Hirt, M., Smith, A. (eds.) TCC 2016-B, Part II. LNCS, vol. 9986, pp. 391–418. Springer, Heidelberg (2016). https://doi.org/10.1007/978-3-662-53644-5_15
Bitansky, N., Vaikuntanathan, V.: Indistinguishability obfuscation from functional encryption. In: 56th FOCS, pp. 171–190 (2015)
Boneh, D., Sahai, A., Waters, B.: Functional encryption: definitions and challenges. In: Ishai, Y. (ed.) TCC 2011. LNCS, vol. 6597, pp. 253–273. Springer, Heidelberg (2011). https://doi.org/10.1007/978-3-642-19571-6_16
Brakerski, Z., Lombardi, A., Segev, G., Vaikuntanathan, V.: Anonymous IBE, leakage resilience and circular security from new assumptions. In: Nielsen, J.B., Rijmen, V. (eds.) EUROCRYPT 2018, Part I. LNCS, vol. 10820, pp. 535–564. Springer, Cham (2018). https://doi.org/10.1007/978-3-319-78381-9_20
Brakerski, Z., Segev, G.: Function-private functional encryption in the private-key setting. In: Dodis, Y., Nielsen, J.B. (eds.) TCC 2015, Part II. LNCS, vol. 9015, pp. 306–324. Springer, Heidelberg (2015). https://doi.org/10.1007/978-3-662-46497-7_12
Canetti, R., Halevi, S., Katz, J.: Adaptively-secure, non-interactive public-key encryption. In: Kilian, J. (ed.) TCC 2005. LNCS, vol. 3378, pp. 150–168. Springer, Heidelberg (2005). https://doi.org/10.1007/978-3-540-30576-7_9
Cho, C., Döttling, N., Garg, S., Gupta, D., Miao, P., Polychroniadou, A.: Laconic oblivious transfer and its applications. In: Katz, J., Shacham, H. (eds.) CRYPTO 2017, Part II. LNCS, vol. 10402, pp. 33–65. Springer, Cham (2017). https://doi.org/10.1007/978-3-319-63715-0_2
Dachman-Soled, D., Dov Gordon, S., Liu, F.-H., O’Neill, A., Zhou, H.-S.: Leakage-resilient public-key encryption from obfuscation. In: Cheng, C.-M., Chung, K.-M., Persiano, G., Yang, B.-Y. (eds.) PKC 2016, Part II. LNCS, vol. 9615, pp. 101–128. Springer, Heidelberg (2016). https://doi.org/10.1007/978-3-662-49387-8_5
Dolev, D., Dwork, C., Naor, M.: Nonmalleable cryptography. SIAM J. Comput. 30(2), 391–437 (2000)
Döttling, N., Garg, S.: From selective IBE to Full IBE and selective HIBE. In: Kalai, Y., Reyzin, L. (eds.) TCC 2017, Part I. LNCS, vol. 10677, pp. 372–408. Springer, Cham (2017). https://doi.org/10.1007/978-3-319-70500-2_13
Döttling, N., Garg, S., Hajiabadi, M., Masny, D.: New constructions of identity-based and key-dependent message secure encryption schemes. In: Abdalla, M., Dahab, R. (eds.) PKC 2018, Part I. LNCS, vol. 10769, pp. 3–31. Springer, Cham (2018). https://doi.org/10.1007/978-3-319-76578-5_1
Garg, S., Gentry, C., Halevi, S., Raykova, M., Sahai, A., Waters, B.: Candidate indistinguishability obfuscation and functional encryption for all circuits. SIAM J. Comput. 45(3), 882–929 (2016)
Garg, S., Gentry, C., Sahai, A., Waters, B.: Witness encryption and its applications. In: 45th ACM STOC, pp. 467–476 (2013)
Garg, S., Miao, P., Srinivasan, A.: Two-round multiparty secure computation minimizing public key operations. In: Shacham, H., Boldyreva, A. (eds.) CRYPTO 2018, Part III. LNCS, vol. 10993, pp. 273–301. Springer, Cham (2018). https://doi.org/10.1007/978-3-319-96878-0_10
Garg, S., Pandey, O., Srinivasan, A.: Revisiting the cryptographic hardness of finding a Nash equilibrium. In: Robshaw, M., Katz, J. (eds.) CRYPTO 2016, Part II. LNCS, vol. 9815, pp. 579–604. Springer, Heidelberg (2016). https://doi.org/10.1007/978-3-662-53008-5_20
Garg, S., Pandey, O., Srinivasan, A., Zhandry, M.: Breaking the sub-exponential barrier in obfustopia. In: Coron, J.-S., Nielsen, J.B. (eds.) EUROCRYPT 2017, Part III. LNCS, vol. 10212, pp. 156–181. Springer, Cham (2017). https://doi.org/10.1007/978-3-319-56617-7_6
Garg, S., Srinivasan, A.: Single-key to multi-key functional encryption with polynomial loss. In: Hirt, M., Smith, A. (eds.) TCC 2016-B, Part II. LNCS, vol. 9986, pp. 419–442. Springer, Heidelberg (2016). https://doi.org/10.1007/978-3-662-53644-5_16
Garg, S., Srinivasan, A.: Adaptively secure garbling with near optimal online complexity. In: Nielsen, J.B., Rijmen, V. (eds.) EUROCRYPT 2018, Part II. LNCS, vol. 10821, pp. 535–565. Springer, Cham (2018). https://doi.org/10.1007/978-3-319-78375-8_18
Garg, S., Srinivasan, A.: A simple construction of iO for Turing machines. In: Beimel, A., Dziembowski, S. (eds.) TCC 2018, Part II. LNCS, vol. 11240, pp. 425–454. Springer, Cham (2018). https://doi.org/10.1007/978-3-030-03810-6_16
Goldreich, O., Goldwasser, S., Micali, S.: How to construct random functions. J. ACM 33(4), 792–807 (1986)
Gorbunov, S., Vaikuntanathan, V., Wee, H.: Functional encryption with bounded collusions via multi-party computation. In: Safavi-Naini, R., Canetti, R. (eds.) CRYPTO 2012. LNCS, vol. 7417, pp. 162–179. Springer, Heidelberg (2012). https://doi.org/10.1007/978-3-642-32009-5_11
Hazay, C., Patra, A., Warinschi, B.: Selective opening security for receivers. In: Iwata, T., Cheon, J.H. (eds.) ASIACRYPT 2015, Part I. LNCS, vol. 9452, pp. 443–469. Springer, Heidelberg (2015). https://doi.org/10.1007/978-3-662-48797-6_19
Hemenway, B., Jafargholi, Z., Ostrovsky, R., Scafuro, A., Wichs, D.: Adaptively secure garbled circuits from one-way functions. In: Robshaw, M., Katz, J. (eds.) CRYPTO 2016, Part III. LNCS, vol. 9816, pp. 149–178. Springer, Heidelberg (2016). https://doi.org/10.1007/978-3-662-53015-3_6
Jafargholi, Z., Kamath, C., Klein, K., Komargodski, I., Pietrzak, K., Wichs, D.: Be adaptive, avoid overcommitting. In: Katz, J., Shacham, H. (eds.) CRYPTO 2017, Part I. LNCS, vol. 10401, pp. 133–163. Springer, Cham (2017). https://doi.org/10.1007/978-3-319-63688-7_5
Jafargholi, Z., Scafuro, A., Wichs, D.: Adaptively indistinguishable garbled circuits. In: Kalai, Y., Reyzin, L. (eds.) TCC 2017, Part II. LNCS, vol. 10678, pp. 40–71. Springer, Cham (2017). https://doi.org/10.1007/978-3-319-70503-3_2
Jafargholi, Z., Wichs, D.: Adaptive security of Yao’s garbled circuits. In: Hirt, M., Smith, A. (eds.) TCC 2016-B, Part I. LNCS, vol. 9985, pp. 433–458. Springer, Heidelberg (2016). https://doi.org/10.1007/978-3-662-53641-4_17
Kitagawa, F., Nishimaki, R., Tanaka, K.: From single-key to collusion-resistant secret-key functional encryption by leveraging succinctness. Cryptology ePrint Archive, Report 2017/638 (2017)
Kitagawa, F., Nishimaki, R., Tanaka, K.: Indistinguishability obfuscation for all circuits from secret-key functional encryption. Cryptology ePrint Archive, Report 2017/361 (2017)
Kitagawa, F., Nishimaki, R., Tanaka, K.: Obfustopia built on secret-key functional encryption. In: Nielsen, J.B., Rijmen, V. (eds.) EUROCRYPT 2018, Part II. LNCS, vol. 10821, pp. 603–648. Springer, Cham (2018). https://doi.org/10.1007/978-3-319-78375-8_20
Kitagawa, F., Nishimaki, R., Tanaka, K.: Simple and generic constructions of succinct functional encryption. In: Abdalla, M., Dahab, R. (eds.) PKC 2018, Part II. LNCS, vol. 10770, pp. 187–217. Springer, Cham (2018). https://doi.org/10.1007/978-3-319-76581-5_7
Komargodski, I., Segev, G.: From minicrypt to obfustopia via private-key functional encryption. In: Coron, J.-S., Nielsen, J.B. (eds.) EUROCRYPT 2017, Part I. LNCS, vol. 10210, pp. 122–151. Springer, Cham (2017). https://doi.org/10.1007/978-3-319-56620-7_5
Li, B., Micciancio, D.: Compactness vs collusion resistance in functional encryption. In: Hirt, M., Smith, A. (eds.) TCC 2016-B, Part II. LNCS, vol. 9986, pp. 443–468. Springer, Heidelberg (2016). https://doi.org/10.1007/978-3-662-53644-5_17
Lindell, Y., Pinkas, B.: A proof of security of Yao’s protocol for two-party computation. J. Cryptol. 22(2), 161–188 (2009)
Liu, Q., Zhandry, M.: Decomposable obfuscation: a framework for building applications of obfuscation from polynomial hardness. In: Kalai, Y., Reyzin, L. (eds.) TCC 2017, Part I. LNCS, vol. 10677, pp. 138–169. Springer, Cham (2017). https://doi.org/10.1007/978-3-319-70500-2_6
Marcedone, A., Pass, R., Shelat, A.: Bounded KDM security from iO and OWF. In: Zikas, V., De Prisco, R. (eds.) SCN 2016. LNCS, vol. 9841, pp. 571–586. Springer, Cham (2016). https://doi.org/10.1007/978-3-319-44618-9_30
Naor, M., Yung, M.: Public-key cryptosystems provably secure against chosen ciphertext attacks. In: 22nd ACM STOC, pp. 427–437 (1990)
Nishimaki, R., Wichs, D., Zhandry, M.: Anonymous traitor tracing: how to embed arbitrary information in a key. In: Fischlin, M., Coron, J.-S. (eds.) EUROCRYPT 2016, Part II. LNCS, vol. 9666, pp. 388–419. Springer, Heidelberg (2016). https://doi.org/10.1007/978-3-662-49896-5_14
Sahai, A.: Non-malleable non-interactive zero knowledge and adaptive chosen-ciphertext security. In: 40th FOCS, pp. 543–553 (1999)
Sahai, A., Seyalioglu, H.: Worry-free encryption: functional encryption with public keys. In: ACM CCS 2010, pp. 463–472 (2010)
Sahai, A., Waters, B.: How to use indistinguishability obfuscation: deniable encryption, and more. In: 46th ACM STOC, pp. 475–484 (2014)
Yao, A.C.-C.: How to generate and exchange secrets (extended abstract). In: 27th FOCS, pp. 162–167 (1986)
Acknowledgments
The third author was supported by NTT Secure Platform Laboratories, JST OPERA JPMJOP1612, JST CREST JPMJCR14D6, JSPS KAKENHI JP16H01705, JP17H01695.
Author information
Authors and Affiliations
Corresponding authors
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2019 International Association for Cryptologic Research
About this paper
Cite this paper
Kitagawa, F., Nishimaki, R., Tanaka, K., Yamakawa, T. (2019). Adaptively Secure and Succinct Functional Encryption: Improving Security and Efficiency, Simultaneously. In: Boldyreva, A., Micciancio, D. (eds) Advances in Cryptology – CRYPTO 2019. CRYPTO 2019. Lecture Notes in Computer Science(), vol 11694. Springer, Cham. https://doi.org/10.1007/978-3-030-26954-8_17
Download citation
DOI: https://doi.org/10.1007/978-3-030-26954-8_17
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-26953-1
Online ISBN: 978-3-030-26954-8
eBook Packages: Computer ScienceComputer Science (R0)






 : This deterministic algorithm takes as input
: This deterministic algorithm takes as input 
 for
for 
 and
and  .
. .
. .
. .
. .
. .
. .
. .
. and
and  .
. .
. .
.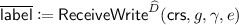 and
and  .
. .
. and
and  . Moreover, by the efficiency of updatable LOT,
. Moreover, by the efficiency of updatable LOT,  , it takes
, it takes 
 .
. .
. .
.