Abstract
We propose simple and generic constructions of succinct functional encryption. Our key tool is exponentially-efficient indistinguishability obfuscator (XIO), which is the same as indistinguishability obfuscator (IO) except that the size of an obfuscated circuit (or the running-time of an obfuscator) is slightly smaller than that of a brute-force canonicalizer that outputs the entire truth table of a circuit to be obfuscated. A “compression factor” of XIO indicates how much XIO compresses the brute-force canonicalizer. In this study, we propose a significantly simple framework to construct succinct functional encryption via XIO and show that XIO is a powerful enough to achieve cutting-edge cryptography. In particular, we prove the followings:
-
Single-key weakly succinct secret-key functional encryption (SKFE) is constructed from XIO (even with a bad compression factor) and one-way function.
-
Single-key weakly succinct public-key functional encryption (PKFE) is constructed from XIO with a good compression factor and public-key encryption.
-
Single-key weakly succinct PKFE is constructed from XIO (even with a bad compression factor) and identity-based encryption.
Our new framework has side benefits. Our constructions do not rely on any number theoretic or lattice assumptions such as decisional Diffie-Hellman and learning with errors assumptions. Moreover, all security reductions incur only polynomial security loss. Known constructions of weakly succinct SKFE or PKFE from XIO with polynomial security loss rely on number theoretic or lattice assumptions.
F. Kitagawa—This work was done while the author was visiting NTT Secure Platform Laboratories as a summer internship student.
You have full access to this open access chapter, Download conference paper PDF
Similar content being viewed by others
1 Introduction
1.1 Background
In cryptography, it is one of major research topics to construct more complex cryptographic primitives from simpler ones in a generic way. Here, “generic” means that we use only general cryptographic tools such as one-way function and public-key encryption. For such a generic construction, we do not use any specific or concrete algebraic assumptions such as the factoring, decisional Diffie-Hellman (DDH), learning with errors (LWE) assumptions. Generic constructions are useful in cryptography because they do not rely on any specific structure of underlying primitives. It means that even if a specific number theoretic assumption is broken, say the DDH, a generic construction based on public-key encryption is still secure since there are many instantiations of public-key encryption from other assumptions. Moreover, generic constructions are useful to deeply understand the nature of cryptographic primitives.
Many generic constructions have been proposed. For example, one-way functions imply pseudo-random function (PRF) [32], and many other primitives. However, we understand little of how to construct functional encryption [13, 45] in a generic way despite its usefulness as explained below.
Functional encryption is a generalization of public-key encryption and enables us to generate functional keys that are tied with a certain function f. Given such a functional key, we can obtain f(x) by decryption of ciphertext \(\mathsf {Enc}(x)\) where x is a plaintext. Functional encryption is a versatile cryptographic primitive since it enables us to achieve not only fine-grained access control systems over encrypted data but also indistinguishability obfuscation (IO) [3, 8, 11, 27].
IO converts computer programs into those that hide secret information in the original programs while preserving their functionalities. An obvious application of IO is protecting softwares from reverse engineering. Moreover, IO enables us to achieve many cutting-edge cryptographic tasks that other standard cryptographic tools do (or can) not achieve such as (collusion-resistant) functional encryption, program watermarking, and deniable encryption [21, 27, 47]. We basically focus on functional encryption and IO for all circuits in this study.
Many concrete functional encryption and IO constructions have been proposed since the celebrated invention of a candidate graded encoding system by Garg et al. [26]. However, regarding designing secure functional encryption and IO, we are still at the “embryonic” stageFootnote 1. A few candidates of graded encoding schemes have been proposed [24, 26, 30]. However, basically speaking, all are attacked, and most applications (including functional encryption) that use graded encoding schemes are also insecure [5, 18,19,20, 22, 23, 43]. As an exception, a few IO constructions are still standing [25, 28]Footnote 2.
The purpose of this study is that we shed new light on how to achieve functional encryption and IO.
The number of functional keys and the size of encryption circuit. In fact, the hardness of constructing functional encryption depends on certain features of functional encryption such as the number of issuable functional keys and ciphertexts and the size of encryption circuit.
We say “single-key” if only one functional key can be issued. We also say q-key or bounded collusion-resistant when a-priori bounded q functional keys can be issued. If q is an a-priori unbounded polynomial, then we say “collusion-resistant”. It is known that a single-key secret-key and public-key functional encryption (SKFE and PKFE) are constructed from standard one-way function and public-key encryption, respectively [46]. It is also known that a bounded collusion-resistant PKFE (resp. SKFE) is constructed from public-key encryption (resp. one-way function) and pseudo-random generator computed by polynomial degree circuits [34]. However, it is not known whether collusion-resistant functional encryption is constructed without expensive cryptographic tools such as graded encoding systems [24, 26, 30] or IO [26].
It is also known that we can construct collusion-resistant PKFE from single-key weakly succinct PKFE [29, 40]. The notion of succinctness for functional encryption schemes [3, 11]Footnote 3 means the size of encryption circuit is independent of the function-size. Weak succinctness means the size of the encryption circuit is \(s^{\gamma }\cdot {\mathrm {poly}}(\lambda ,n)\) where \(\lambda \) is a security parameter, s is the size of f that is embedded in a functional key, n is the length of a plaintext, and \(\gamma \) is a constant such that \(0<\gamma <1\). The results of Garg and Srinivasan [29] and Li and Micciancio [40] mean that we can arbitrarily increase the number of issuable functional keys by using succinctness. Moreover, succinct SKFE and PKFE are constructed from collusion-resistant SKFE and PKFE, respectively [4]. Thus, it is also a difficult task to construct succinct functional encryption schemes without graded encoding systems or IO.
The succinctness of functional encryption is also key feature to achieve IO. Ananth and Jain [3] and Bitansky and Vaikuntanathan [11] show that a sub-exponentially secure single-key weakly succinct PKFE implies IO.
These facts indicate that it is a challenging task to achieve either collusion-resistance or succinctness.
Running time of obfuscator. Not only the encryption-time of functional encryption but also the size of obfuscated circuits and the running time of obfuscators are important measures.
Lin et al. [41] introduced the notion of exponentially-efficient indistinguishability obfuscator (XIO), which is a weaker variant of IO. XIO is almost the same as IO, but the size of the obfuscated circuits is \({\mathrm {poly}}(\lambda ,|C|)\cdot 2^{\gamma n}\) where \(\lambda \) is a security parameter, C is a circuit to be obfuscated, n is the length of input for C, and a compression factor \(\gamma \) is some value such that \(0<\gamma <1\). We note that the running time of XIO on an input a circuit of n-bit inputs can be \(2^n\). They prove that if we assume that there exists XIO for circuits and the LWE problem is hard, then there exists single-key weakly succinct PKFE (and IO if sub-exponential security is additionally assumed).
Bitansky et al. [9] extend the notion of XIO and define strong XIO (SXIO). If the running time of the obfuscator is \({\mathrm {poly}}(\lambda ,|C|) \cdot 2^{\gamma n}\), then we say it is SXIO. Bitansky et al. show that sub-exponentially secure SXIO and public-key encryption imply IO. In addition, they prove that single-key weakly succinct PKFE is constructed from SXIO, public-key encryption, and weak PRF in \(\mathsf {NC}^1\), which is implied by the DDH [44] or LWE assumptions [7].
Thus, (S)XIO is useful enough to achieve weakly succinct functional encryption and IO. In this study, we discuss more applications of SXIO to functional encryption. In particular, we discuss significantly simple and generic constructions of weakly succinct functional encryption by using SXIO.
From SKFE to PKFE. Bitansky et al. [9] also prove that SXIO is constructed from collusion-resistant SKFE. Thus, we can construct weakly succinct PKFE from a weaker primitive than PKFE by the results of Lin et al. and Bitansky et al., though it is not known whether we can construct collusion-resistant SKFE from standard cryptographic primitives.
The works of Lin et al. and Bitansky et al. are advancements on how to construct succinct PKFE from weaker primitives. In particular, Bitansky et al. provide a nice generic framework for constructing weakly succinct PKFE from SKFE and public-key encryption. However, their technique is very complicated. Moreover, they still use the DDH or LWE assumptions to achieve weakly succinct PKFE with polynomial security loss. Thus, it is not known whether we can construct weakly succinct PKFE with polynomial security loss from SKFE and public-key encryption in a generic way.
1.2 Our Contributions
The primary contribution of this study is that we propose a significantly simple and generic framework to construct single-key weakly succinct functional encryption by using SXIO. In particular, our constructions are significantly simpler than those by Bitansky et al. [9]. More specifically, we prove the following theorems via our framework:
-
Main theorem 1 (informal): A single-key weakly succinct PKFE is implied by public-key encryption and SXIO with a sufficiently small compression factor.
-
Main theorem 2 (informal): A single-key weakly succinct PKFE is implied by identity-based encryption and SXIO with a compression factor that is only slightly smaller than 1.
-
Main theorem 3 (informal): A single-key weakly succinct SKFE is implied by one-way function and SXIO with a compression factor that is only slightly smaller than 1.
Readers might find that the technique (see the overview in Sect. 1.3) in our framework is a little bit straightforward and a combination of (minor variants of) well-known or implicitly known techniques. However, we stress that it is not a disadvantage but the advantage of our study. We reveal that such a simple combination of known techniques yields highly non-trivial results above for the first time. We believe that our simple technique is useful to construct better functional encryption (and IO). In fact, Kitagawa, Nishimaki, and Tanaka extend our technique and obtain an IO construction based only on SKFE [37]. As side benefits of our new framework, our functional encryption schemes have advantages over previous constructions. In particular, the third main theorem is totally new. We highlight that all these new theorems incur only polynomial security loss and do not rely on any specific number theoretic or lattice assumption. These are advantages over the constructions of Lin et al. and Bitansky et al. [9, 41] and the secondary contributions of this study. We explain details of our results below.
Implication of first and second theorems. There are transformations from a single-key weakly succinct PKFE scheme to a collusion-resistant one with polynomial security loss [29, 40]. Thus, by combining the first or second theorems with the transformation, we obtain two collusion-resistant PKFE schemes with polynomial security loss. One is based on public-key encryption and collusion-resistant (non-succinct) SKFE since collusion-resistant (non-succinct) SKFE implies SXIO with an arbitrarily small constant compression factor [9]. The other is based on identity-based encryption and single-key weakly succinct SKFE since single-key weakly succinct SKFE implies SXIO with a compression factor that is slightly smaller than 1 [10]. Note that we can also obtain IO constructions from the same building blocks if we assume that they are sub-exponentially secure by using the result of Ananth and Jain [3] or Bitansky and Vaikuntanathan [11].
As well as one-way function and public-key encryption, identity-based encryption [48] is also a standard cryptographic primitive since there are many instantiations of identity-based encryption based on widely believed number theoretic assumptions and lattice assumptions [12, 31]. Thus, our second result indicates that all one needs is to slightly compress the brute-force canonicalizer that outputs an entire truth table of a circuit to be obfuscated to construct single-key weakly succinct (or collusion-resistant) PKFE and IO.
Advantages over previous constructions. We look closer at previous works for comparison. Readers who are familiar with the previous works on PKFE can skip this part and jump into the part about implication of the third theorem.
-
Lin et al. [41]: They construct single-key weakly succinct PKFE from XIO and single-key succinct PKFE for Boolean circuits. It is known that a single key succinct PKFE for Boolean circuits is constructed from the LWE assumption [33].
Both their construction and ours are generic constructions using (S)XIO. However, their construction additionally needs single-key succinct PKFE for Boolean circuits. We have only one instantiation of such PKFE based on the LWE assumption while our additional primitives (i.e., public-key encryption and identity-based encryption) can be instantiated based on wide range of assumptions. This is the advantage of our construction over that of Lin et al.
-
Bitansky et al. [9]: They construct single-key weakly succinct PKFE from SXIO and public-key encryption with \(2^{O(d)}\) security loss where d is the depth of a circuit. They introduce decomposable garbled circuit, which is an extension of Yao’s garbled circuit [49], to achieve succinctness [9]. Decomposable garbled circuit is implied by one-way function. However, it has two disadvantages. One is that it incurs the \(2^{O(d)}\) security loss. The other is that its security proof is complex.
When we construct single-key weakly succinct (or collusion-resistant) PKFE only with polynomial security loss, the exponential security loss in the depth of circuits is a big issue. Thus, Bitansky et al. need weak PRF in \(\mathsf {NC}^1\) to achieve single-key weakly succinct (or collusion-resistant) PKFE with polynomial security loss due to the \(2^{O(d)}\) security loss [9, Sect. 5.3]Footnote 4. If our goal is constructing IO, then the \(2^{O(d)}\) security loss is not an issue in the sense that we need sub-exponential security of PKFE to achieve IO [3, 11], and we can cancel the \(2^{O(d)}\) security loss by complexity leveraging.
Decomposable garbled circuit is a useful tool for Bitansky et al.’s construction. However, the definition is complicated and it is not easy to understand the security proof. Our unified design strategy significantly simplifies a construction of single-key weakly succinct PKFE based on SXIO. In fact, our constructions use decomposable randomized encoding [6, 35], but decomposable randomized encoding is a simple tool and does not incur \(2^{O(d)}\) security loss.
Using identity-based encryption. We show that we can relax the requirements on SKFE to achieve PKFE and IO if we are allowed to use identity-based encryption.
Our construction of PKFE using identity-based encryption needs SXIO with compression factor slightly smaller than 1 that is implied by single-key (weakly) succinct SKFE while the constructions using public-key encryption need SXIO with sufficiently small compression factor that is implied by collusion-resistant SKFE. It is not known whether single-key (weakly) succinct SKFE implies collusion-resistant SKFE though the opposite is known [4]. Of course, regarding additional assumptions (public-key encryption and identity-based encryption), the existence of identity-based encryption is a stronger assumption than that of public-key encryption. However, identity-based encryption is a standard cryptographic primitive and the assumption is reasonably mild since many instantiations of identity-based encryption are known [12, 31]. Readers who are familiar with the construction of Bitansky et al. might think the second theorem is easily obtained from the result of Bitansky et al., which actually uses an identity-based encryption scheme constructed from SXIO and public-key encryption as a building block.Footnote 5 This is not the case because their construction uses an SXIO three times in a nested manner to construct their single-key weakly succinct PKFE scheme. They construct a single-key weakly succinct PKFE scheme for Boolean functions by using SXIO and identity-based encryption, and then transform it into a single-key weakly succinct PKFE scheme for non-Boolean functions by using SXIO again. Therefore, even if we replace their identity-based encryption scheme based on SXIO and public-key encryption with an assumption that there exists identity-based encryption, their construction still requires the use of SXIO two times in a nested manner, and due to this nested use, it still needs SXIO with sufficiently small compression factor.
Thus, the advantages of our single-key weakly succinct PKFE schemes over Bitansky et al.’s construction are as follows:
-
Our single-key weakly succinct PKFE scheme does not incur \(2^{O(d)}\) security loss thus does not need weak PRF in \(\mathsf {NC}^1\) (implied by the DDH or LWE assumptions) to support all circuits.
-
Our PKFE schemes and proofs are much simpler.
-
We can use single-key weakly succinct SKFE instead of collusion-resistant SKFE (if we use identity-based encryption instead of public-key encryption).
-
Komargodski and Segev [39]: Komargodski and Segev construct IO for circuits with inputs of poly-logarithmic length and sub-polynomial size from a quasi-polynomially secure and collusion-resistant SKFE scheme for \(\mathsf {P/poly}\). They also construct PKFE for circuits with inputs of poly-logarithmic length and sub-polynomial size from a quasi-polynomially secure and collusion-resistant SKFE scheme for \(\mathsf {P/poly}\) and sub-exponentially secure one-way function. Their reduction incurs super-polynomial security loss. Thus, the advantages of our single-key weakly succinct PKFE schemes and IO over Komargodski and Segev’s construction are as follows:
-
Our PKFE schemes support all circuits. (When constructing IO by combining previous results [3, 11], the construction also supports all circuits.)
-
We can use single-key weakly succinct SKFE instead of collusion-resistant SKFE (if we use identity-based encryption).
-
Our PKFE schemes are with polynomial security loss and do not need sub-exponentially secure one-way function (though we additionally use a public-key primitive).
-
We summarize differences between these previous constructions of single-key weakly succinct (or collusion-resistant) PKFE schemes and ours in Table 1.
Implication of third theorem. We can obtain interesting by-products from the third theorem.
-
By-product 1: We show that single-key weakly succinct SKFE is equivalent to one-way function and SXIO since it is known that such SKFE implies SXIO with a compression factor that is slightly smaller than 1 [10].
-
By-product 2: We show that the existence of output-compact updatable randomized encoding with unbounded number of updates [2] and one-way function is equivalent to that of single-key weakly succinct SKFE. Previously, it is known that the existence of output-compact updatable randomized encoding with unbounded number of updates and the hardness of the LWE problem imply the existence of single-key weakly succinct SKFE [2]. It is also known that single-key weakly succinct SKFE implies output-compact updatable randomized encoding with unbounded number of updates. Thus, we replace the LWE assumption in the results by Ananth, Cohen, and Jain [2] with one-way function.
1.3 Overview of Our Construction Technique
Our core schemes are q-key weakly collusion-succinct functional encryption schemes for a-priori fixed polynomial q that are constructed from SXIO and an additional cryptographic primitive (one-way function, public-key encryption, or identity-based encryption). Weak collusion-succinctness means the size of the encryption circuit is sub-linear in the number of issuable functional keys. See Definition 3 for more details on succinctness. It is known that weakly collusion-succinct functional encryption is transformed into weakly-succinct one [4, 11].
We explain our ideas to achieve q-key weakly collusion-succinct functional encryption schemes below.
Our main idea in one sentence. We compress parallelized encryption circuits of a non-succinct scheme based on standard cryptographic primitives by using SXIO to achieve weak collusion-succinctness.
Starting point. A naive idea to construct a q-key functional encryption scheme from a single-key non-succinct functional encryption scheme is running q single-key non-succinct functional encryption schemes in parallel where q is a polynomial fixed in advance. A master secret/public key consist of q master secret/public keys of the single-key scheme, respectively. A ciphertext consists of q ciphertexts of a plaintext x under q master secret or public keys. This achieves q-key functional encryption.Footnote 6 However, this simply parallelized scheme is clearly not weakly collusion-succinct since the size of the encryption circuit is linear in q. Note that a single-key non-succinct functional encryption scheme is constructed from a standard cryptographic primitive (such as one-way function, public-key encryption) [34, 46].
Compressing by SXIO. Our basic idea is compressing the encryption circuit of the simply parallelized scheme by using SXIO. Instead of embedding all q keys in an encryption circuit, our encryption algorithm obfuscates a circuit that generates the i-th master secret/public key of the simply parallelized scheme and uses it to generate a ciphertext under the i-th key where i is an input to the circuit.
For simplicity, we consider the SKFE case. We set a pseudo-random function (PRF) key K as a master secret key. For a plaintext x, our weakly collusion-succinct encryption algorithm generates a circuit \(\mathsf {E}'[K,x]\) that takes as an input an index \(i\in [q]\), generates the i-th master secret key \(\mathsf {MSK}_i\) by using the hard-wired K and the index i, and outputs a ciphertext \(\mathsf {Enc}(\mathsf {MSK}_i,x)\) of the single-key schemeFootnote 7. A ciphertext of our scheme is \(\mathsf {sxi}\mathcal {O}(\mathsf {E}'[K,x])\). In \(\mathsf {E}'[K,x]\), each master secret key is generated in an on-line manner by using the PRF (it is determined only by K and input i). The encryption circuit size of each \(\mathsf {Enc}(\mathsf {MSK}_i,x)\) is independent of q because it is the encryption algorithm of the single-key scheme. The input space of \(\mathsf {E}'[K,x]\) is [q]. Thus, the time needed to generate the ciphertext \(\mathsf {sxi}\mathcal {O}(\mathsf {E}'[K,x])\) is \({\mathrm {poly}}(\lambda ,|x|,|f|)\cdot q^{\gamma }\) from the efficiency guarantee of SXIO. This achieves weak collusion-succinctness. The size depends on \(|f|\), but it is not an issue since our goal at this step is not (weak) succinctness. The security is proved using the standard punctured programming technique [47].
Extension to public-key setting. We achieve a q-key weakly collusion-succinct PKFE by a similar idea to the SKFE case. Only one exception is that we need an SXIO to generate not only a ciphertext but also a master public-key to prevent the size of a master public-key from linearly depending on q. That is, a master public-key is an obfuscated circuit that outputs a master public-key of a single-key scheme by using a PRF key. We give the simplified description of this setup circuit (denoted by \(\mathsf {S}\)) below for clarity. For the formal description of \(\mathsf {S}\), see Fig. 2 in Sect. 3.2. If we do not use \(\mathsf {sxi}\mathcal {O}(\mathsf {S})\) as the master public key, we must use \(\{\mathsf {MPK}_i\}_{i\in [q]}\) as the master public-key and embed them in a public encryption circuit \(\mathsf {E}''\) since we cannot make PRF key K public. This leads to linear dependence on q of the encryption time.

Encryption circuit \(\mathsf {E}''\) is almost the same as \(\mathsf {E}'\) in the SKFE construction except that \(\mathsf {MPK}= \mathsf {sxi}\mathcal {O}(\mathsf {S})\) is hardwired to generate a master public-key in an on-line manner. Similarly to the SKFE construction, a ciphertext is \(\mathsf {sxi}\mathcal {O}(\mathsf {E}'')\). This incurs two applications of SXIO in a nested manner (i.e., we obfuscate a circuit in which another obfuscated circuit is hard-wired). Although the input space of \(\mathsf {E}''\) is [q] and the size of the encryption circuit of the single-key scheme is independent of q, the size of \(\mathsf {sxi}\mathcal {O}(\mathsf {E}'')\) polynomially depends on \(\mathsf {sxi}\mathcal {O}(\mathsf {S})\). Thus, a better compression factor of SXIO for \(\mathsf {S}\) is required to ensure the weak collusion-succinctness of the resulting scheme. Such better SXIO is implied by collusion-resistant (non-succinct) SKFE [9]. See Sect. 3.2 for details of the efficiency analysis.
Using power of identity-based encryption. To overcome the nested applications of SXIO, we directly construct a q-key weakly collusion-succinct PKFE from SXIO, identity-based encryption, and garbled circuit. The main idea is the same. Our starting point is the single-key non-succinct PKFE scheme of Sahai and Seyalioglu [46], which is based on a public-key encryption scheme \(\mathsf {PKE}\). We use a universal circuit \(U(\cdot ,x)\) in which a plaintext x is hard-wired and takes as an input a function f, which will be embedded in a functional key. Let \(s\, : =|f|\). The scheme of Sahai and Seyalioglu is as follows.
-
Setup: A master public-key consists of 2s public-keys of \(\mathsf {PKE}\), \(\{\mathsf {pk}_0^{j},\mathsf {pk}_1^{j}\}_{j\in [s]}\).
-
Functional Key: A functional key for f consists of s secret-keys of \(\mathsf {PKE}\), \(\{\mathsf {sk}_{f_j}^j\}_{j\in [s]}\) where \(f = f_1\ldots f_s\) and \(f_j\) is a single bit for every \(j \in [s]\).
-
Encryption: A ciphertext of a plaintext x consists of a garbled circuit of \(U(\cdot ,x)\) and encryptions of 2s labels of the garbled circuit under \(\mathsf {pk}_b^{j}\) for all \(j\in [s]\) and \(b\in \{0,1\}\).
-
Decryption: We obtain labels corresponding to f by using \(\{\mathsf {sk}_{f_j}^j\}_{j\in [s]}\) and evaluate the garbled \(U(\cdot ,x)\) with those labels.
We can replace \(\mathsf {PKE}\) with an identity-based encryption scheme \(\mathsf {IBE}\) by using identities in \([s]\times \{0,1\}^{}\). That is, \(\{\mathsf {pk}_0^j,\mathsf {pk}_1^j\}_{j\in [s]}\) is aggregated into a master public-key of \(\mathsf {IBE}\). A functional key for f consists of secret keys for identities \((1,f_1),\ldots ,(s,f_s)\). In addition, encryptions of 2s labels consist of 2s ciphertexts for identities (j, b) for all \(j\in [s]\) and \(b\in \{0,1\}^{}\). We parallelize this by extending the identity space into \([q]\times [s]\times \{0,1\}^{}\) to achieve a q-key scheme. We need compression to achieve weak collusion-succinctness since simple parallelization incurs the linearity in q.
Our encryption algorithm obfuscates the following circuit \(\widetilde{\mathsf {E}}\) by using an SXIO. A master public-key of \(\mathsf {IBE}\) and plaintext x are hard-wired in \(\widetilde{\mathsf {E}}\). Given index i, \(\widetilde{\mathsf {E}}\) generates a garbled circuit of \(U(\cdot ,x)\) with 2s labels and outputs the garbled circuit and encryptions of the 2s labels under appropriate identities. Identities consist of \((i,j,f_j) \in [q]\times [s]\times \{0,1\}\) for every \(j\in [s]\). A ciphertext of our scheme is \(\mathsf {sxi}\mathcal {O}(\widetilde{\mathsf {E}})\). Therefore, if secret keys for identities \(\left\{ (i,j,f_j)\right\} _{j\in [s]}\) are given as functional keys, then we can obtain labels only for f from corresponding ciphertexts of \(\mathsf {IBE}\) output by \(\mathsf {sxi}\mathcal {O}(\widetilde{\mathsf {E}})\) on the input i, and compute \(U(f,x)=f(x)\).
A master public-key and encryption circuit of the identity-based encryption are succinct in the sense that their size is sub-linear in \(|\mathcal {ID}|\) where \(\mathcal {ID}\) is the identity space of \(\mathsf {IBE}\). That is, the size depends on \(|\mathcal {ID}|^{\alpha }\) for sufficiently small constant \(\alpha \).Footnote 8 In addition, the input space of \(\widetilde{\mathsf {E}}\) is just [q] and the garbled circuit part of \(\widetilde{\mathsf {E}}\) is independent of q. Therefore, the time needed to generate a ciphertext \(\mathsf {sxi}\mathcal {O}(\widetilde{\mathsf {E}})\) is sub-linear in q from the efficiency property of SXIO. Thus, the scheme is weakly collusion-succinct.
In fact, this PKFE construction is similar to that of Bitansky et al. [9], but we do not need decomposable garbled circuit because our goal is achieving weak collusion-succinctness, which allows encryption circuits to polynomially depend on the size of f (our goal is not weak succinctness at this stage). Thus, a standard garbled circuit is sufficient for our construction. Moreover, SXIO with a bad compression factor is sufficient since we use an SXIO only once.
Uniting pieces. It is known that public-key encryption (resp. one-way function) implies single-key non-succinct PKFE (resp. SKFE) [34, 46] and bounded-key weakly collusion-succinct PKFE (resp. SKFE) implies single-key weakly succinct PKFE (resp. SKFE) [4, 11]. Thus, via our weakly collusion-succinct PKFE (resp. SKFE), we can obtain single-key weakly succinct PKFE (resp. SKFE) based on SXIO and standard cryptographic primitives. Figure 1 illustrates our first and third informal theorems.
Concurrent and independent work. Lin and Tessaro [42] prove that a collusion-resistant PKFE scheme for \(\mathsf {P/poly}\) is constructed from any single-key PKFE scheme for \(\mathsf {P/poly}\) (e.g., a PKFE scheme based on public-key encryption proposed by Gorbunov et al. [34]) and IO for \(\omega (\log {\lambda })\)-bit-input circuits.
Their construction is similar to that of our single-key weakly succinct PKFE scheme for \(\mathsf {P/poly}\) from public-key encryption and SXIO. One notable difference is that they use IO for \(\omega (\log {\lambda })\)-bit-input circuits while we use SXIO for \(\mathsf {P/poly}\) based on collusion-resistant SKFE for \(\mathsf {P/poly}\) with polynomial security loss, which is a weaker tool than theirs.
Organization. This paper consists of the following parts. In Sect. 2, we provide preliminaries and basic definitions. In Sect. 3, we present our constructions of weakly collusion-succinct functional encryption schemes based on SXIO and standard cryptographic primitives. In Sect. 4, we provide a statement about how to transform weakly collusion-succinct functional encryption schemes into single-key weakly succinct functional encryption schemes. In Sect. 5, we summarize our results.
2 Preliminaries
We now define some notations and cryptographic primitives. We omit some notations and definitions due to limited space.
If \(\mathcal {X}^{(b)}=\{X^{(b)}_{\lambda }\}_{\lambda \in \mathbb {N}}\) for \(b \in \{0,1\}\) are two ensembles of random variables indexed by \(\lambda \in \mathbb {N}\), we say that \(\mathcal {X}^{(0)}\) and \(\mathcal {X}^{(1)}\) are computationally indistinguishable if for any PPT distinguisher \(\mathcal {D}\), there exists a negligible function \({\mathsf {negl}}(\lambda )\), such that \(\varDelta \, : =| \Pr [\mathcal {D}(X^{(0)}_\lambda )=1] - \Pr [\mathcal {D}(X^{(1)}_\lambda )=1] | \le {\mathsf {negl}}(\lambda ). \) We write \(\mathcal {X}^{(0)} {\mathop {\approx }\limits ^{\mathsf {c}}}_{\delta } \mathcal {X}^{(1)}\) to denote that the advantage \(\varDelta \) is bounded by \(\delta \).
2.1 Functional Encryption
Secret-Key Functional Encryption (SKFE). We introduce the syntax of an index based variant SKFE scheme that we call an index based SKFE (iSKFE) scheme. “Index based” means that, to generate the i-th functional decryption key, we need to feed an index i to a key generation algorithm. For a single-key scheme, an iSKFE scheme is just a standard SKFE scheme in which the key generation algorithm does not take an index as an input since the index is always fixed to 1. See Remark 2 for details.
Definition 1
(Index Based Secret-key Functional Encryption). Let \(\mathcal {M}\, : =\left\{ \mathcal {M}_\lambda \right\} _{\lambda \in \mathbb {N}}\) be a message domain, \(\mathcal {Y}\, : =\left\{ \mathcal {Y}_\lambda \right\} _{\lambda \in \mathbb {N}}\) a range, \(\mathcal {I}\, : =[q_k(\lambda )]\) an index space where \(q_k\) is a fixed polynomial, and \(\mathcal {F}\, : =\left\{ \mathcal {F}_\lambda \right\} _{\lambda \in \mathbb {N}}\) a class of functions \(f:\mathcal {M}\rightarrow \mathcal {Y}\). An iSKFE scheme for \(\mathcal {M},\mathcal {Y},\mathcal {I},\) and \(\mathcal {F}\) is a tuple of algorithms \(\mathsf {SKFE}= (\mathsf {Setup},\mathsf {iKG},\mathsf {Enc},\mathsf {Dec})\) where:
-
\(\mathsf {Setup}(1^\lambda )\) takes as input the security parameter and outputs a master secret key \(\mathsf {MSK}\).
-
\(\mathsf {iKG}(\mathsf {MSK},f,i)\) takes as input \(\mathsf {MSK}\), a function \(f\in \mathcal {F}\), and an index \(i\in \mathcal {I}\), and outputs a secret key \(\mathsf {sk}_f\) for f.
-
\(\mathsf {Enc}(\mathsf {MSK},x)\) takes as input \(\mathsf {MSK}\) and a message \(x\in \mathcal {M}\) and outputs a ciphertext \(\mathsf {CT}\).
-
\(\mathsf {Dec}(\mathsf {sk}_f,\mathsf {CT})\) takes as input \(\mathsf {sk}_f\) for \(f\in \mathcal {F}\) and \(\mathsf {CT}\) and outputs \(y\in \mathcal {Y}\), or \(\bot \).
-
Correctness: We require \(\mathsf {Dec}(\mathsf {iKG}(\mathsf {MSK}, f, i), \mathsf {Enc}(\mathsf {MSK}, x)) = f(x)\) for any \(x \in \mathcal {M}\), \(f \in \mathcal {F}\), \(i \in \mathcal {I}\), and \(\mathsf {MSK}\leftarrow \mathsf {Setup}(1^\lambda )\).
Next, we introduce selective-message message privacy [17].
Definition 2
(Selective-Message Message Privacy). Let \(\mathsf {SKFE}\) be an iSKFE scheme whose message space, function space, and index space are \(\mathcal {M}\), \(\mathcal {F}\), and \(\mathcal {I}\), respectively. We define the selective-message message privacy experiment \(\mathsf {Exp}_{\mathcal {A}}^{ \mathsf {sm} \text{- } \mathsf {mp}}(1^\lambda ,b)\) between an adversary \(\mathcal {A}\) and a challenger as follows.
-
1.
\(\mathcal {A}\) is given \(1^\lambda \) and sends \((x_0^{(1)},x_1^{(1)}),\cdots ,(x_0^{(q_m)},x_1^{(q_m)})\) to the challenger, where \(q_m\) is an a-priori unbounded polynomial of \(\lambda \).
-
2.
The challenger chooses \(\mathsf {MSK}\leftarrow \mathsf {Setup}(1^\lambda )\) and a challenge bit \(b \leftarrow \{0,1\}\).
-
3.
The challenger generates \(\mathsf {CT}^{(j)} \leftarrow \mathsf {Enc}(\mathsf {MSK}, x_b^{(j)})\) for \(j \in [q_m]\) and sends them to \(\mathcal {A}\).
-
4.
\(\mathcal {A}\) is allowed to make arbitrary function queries at most \(|\mathcal {I}|=q_k\) times. For the \(\ell \)-th key query \(f_{\ell }\in \mathcal {F}\) from \(\mathcal {A}\), the challenger generates \(sk_{f_{\ell }} \leftarrow \mathsf {iKG}(\mathsf {MSK}, f_{\ell }, \ell )\) and returns \(sk_{f_\ell }\) to \(\mathcal {A}\).
-
5.
\(\mathcal {A}\) outputs \(b' \in \{0,1\}\). The experiment output \(b'\) if \(f_{\ell }(x_0^{(j)}) = f_{\ell }(x_1^{(j)})\) for all \(j\in [q_m]\) and \(\ell \in [q_k]\), where \(q_k\) is the number of key queries made by \(\mathcal {A}\); otherwise \(\bot \).
We say that \(\mathsf {SKFE}\) is \(q_k\)-selective-message message private (or selectively secure for short) if for any PPT \(\mathcal {A}\), it holds that
We further say that \(\mathsf {SKFE}\) is \((q_k,\delta )\)-selective-message message private, for some concrete negligible function \(\delta (\cdot )\), if for any PPT \(\mathcal {A}\) the above advantage is smaller than \(\delta (\lambda )^{\varOmega (1)}\).
Remark 1
(Regarding the number of key queries). Let \(\mathsf {FE}\) be a functional encryption scheme. If \(q_k\) is an unbounded polynomial, then we say \(\mathsf {FE}\) is a collusion-resistant functional encryption. If \(q_k\) is a bounded polynomial (i.e., fixed in advance), then we say \(\mathsf {FE}\) is a bounded collusion-resistant functional encryption. If \(q_k = 1\), we say \(\mathsf {FE}\) is a single-key functional encryption. In this study, our constructions are bounded collusion-resistant.
Remark 2
(Regarding an index for algorithm \(\mathsf {iKG}\) ). Our definitions of functional encryptions slightly deviates from the standard ones (e.g., the definition by Ananth and Jain [3] or Brakerski and Segev [17]). Our key generation algorithm takes not only a master secret key and a function but also an index, which is used to bound the number of functional key generations. This index should be different for each functional key generation. One might think this is a limitation, but this is not the case in this study because our goal is constructing single-key PKFE. For a single-key scheme, \(|\mathcal {I}|=1\) and we do not need such an index. Index based bounded collusion-resistant functional encryption schemes are just intermediate tools in this study. In fact, such an index has been introduced by Li and Micciancio in the context of PKFE [40].Footnote 9
Next, we introduce notions regarding efficiency, called succinctness for functional encryption schemes.
Definition 3
(Succinctness of Functional Encryption [11]). For a class of functions \(\mathcal {F}=\left\{ \mathcal {F}_\lambda \right\} \) over message domain \(\mathcal {M}=\left\{ \mathcal {M}_\lambda \right\} \), we let \(n(\lambda )\) be the input length of the functions in \(\mathcal {F}\), \(s(\lambda ) = \max _{f\in \mathcal {F}_\lambda }|f|\) the upper bound on the circuit size of functions in \(\mathcal {F}_\lambda \), and \(d(\lambda ) = \max _{f\in \mathcal {F}_\lambda }\mathsf {depth}(f)\) the upper bound on the depth, and a functional encryption scheme is
-
succinct if the size of the encryption circuit is bounded by \({\mathrm {poly}}(n,\lambda ,\log {s})\), where \({\mathrm {poly}}\) is a fixed polynomial.
-
weakly succinct if the size of the encryption circuit is bounded by \(s^{\gamma }\cdot {\mathrm {poly}}(n,\lambda )\), where \({\mathrm {poly}}\) is a fixed polynomial, and \(\gamma <1\) is a constant.
-
weakly collusion-succinct if the size of the encryption circuit is bounded by \(q^{\gamma }\cdot {\mathrm {poly}}(n,\lambda ,s)\), where q is the upper bound of issuable functional keys in bounded-key schemes (that is, the size of the index space of the scheme), \({\mathrm {poly}}\) is a fixed polynomial, and \(\gamma <1\) is a constant.
We call \(\gamma \) the compression factor. The following theorem states that one can construct IO from any single-key weakly succinct PKFE. We recall that single-key iPKFE is also single-key PKFE, and vice versa.
Theorem 1
[11]. If there exists a single-key sub-exponentially weakly selectively secure weakly succinct PKFE scheme for \(\mathsf {P}/\mathsf {poly}\), then there exists an indistinguishability obfuscator for \(\mathsf {P}/\mathsf {poly}\).
2.2 Indistinguishability Obfuscation
Definition 4
(Indistinguishability Obfuscator). A PPT algorithm \(i\mathcal {O}\) is an IO for a circuit class \(\{\mathcal {C}_\lambda \}_{\lambda \in \mathbb {N}}\) if it satisfies the following two conditions.
-
Functionality: For any security parameter \(\lambda \in \mathbb {N}\), \(C \in \mathcal {C}_\lambda \), and input x, we have that \(\Pr [C'(x)=C(x) : C' \leftarrow i\mathcal {O}(C)] = 1\).
-
Indistinguishability: For any PPT distinguisher \(\mathsf {D}\) and for any pair of circuits \(C_0, C_1 \in \mathcal {C}_\lambda \) such that for any input x, \(C_0(x) = C_1(x)\) and \(|C_0|=|C_1|\), it holds that \( | \Pr \left[ \mathsf {D}(i\mathcal {O}(C_0))= 1\right] - \Pr \left[ \mathsf {D}(i\mathcal {O}(C_1))= 1\right] | \le {\mathsf {negl}}(\lambda )\). We further say that \(i\mathcal {O}\) is \(\delta \)-secure, for some concrete negligible function \(\delta (\cdot )\), if for any PPT \(\mathsf {D}\) the above advantage is smaller than \(\delta (\lambda )^{\varOmega (1)}\).
Definition 5
(Strong Exponentially-Efficient Indistinguishability Obfuscation). Let \(\gamma < 1\) be a constant. An algorithm \(\mathsf {sxi}\mathcal {O}\) is a \(\gamma \)-compressing SXIO for a circuit class \(\{\mathcal {C}_\lambda \}_{\lambda \in \mathbb {N}}\) if it satisfies the functionality and indistinguishability in Definition 4 and the following efficiency requirement:
-
Non-trivial time efficiency: We require that the running time of \(\mathsf {sxi}\mathcal {O}\) on input \((1^\lambda , C)\) is at most \(2^{n\gamma } \cdot {\mathrm {poly}}(\lambda , |C|)\) for any \(\lambda \in \mathbb {N}\) and any circuit \(C \in \{C_\lambda \}_{\lambda \in \mathbb {N}}\) with input length n.
Remark 3
In this paper, when we write “SXIO for \(\mathsf {P/poly}\)”, we implicitly mean that SXIO for polynomial-size circuits with inputs of logarithmic length. This follows the style by Bitansky et al. [9] though Lin et al. [41] use the circuit class \(\mathsf {P}^{\log }\mathsf {/poly}\) to denote the class of polynomial-size circuits with inputs of logarithmic length. The reason why we use the style is that we can consider the polynomial input length if we do not care about the polynomial running time of \(\mathsf {sxi}\mathcal {O}\) and the input length n obviously must be logarithmic for the polynomial running time of \(\mathsf {sxi}\mathcal {O}\) from the definition.
3 Collusion-Succinct Functional Encryption from SXIO
In our bounded-key weakly collusion-succinct iSKFE and iPKFE schemes, we use single-key non-succinct SKFE and PKFE schemes that are implied from one-way function and public-key encryption, respectively.
Theorem 2
[34]Footnote 10 . If there exists a \(\delta \)-secure one-way function, then there exists a \((1,\delta )\)-selectively-secure and non-succinct SKFE scheme for \(\mathsf {P/poly}\). If there exists a \(\delta \)-secure public-key encryption, then there exists a \((1,\delta )\)-selectively-secure and non-succinct PKFE scheme for \(\mathsf {P/poly}\).
Throughout this paper, let n and s be the length of a message x and size of a function f of a functional encryption scheme, respectively as in Definition 3.
3.1 Collusion-Succinct SKFE from SXIO and One-Way Function
We put only our theorem in this section due to limited space. We can understand an essence of the theorem from the construction in the next section.
Theorem 3
If there exists non-succinct \((1,\delta )\)-selective-message message private SKFE for \(\mathsf {P/poly}\) and \(\delta \)-secure \(\widetilde{\gamma }\)-compressing SXIO for \(\mathsf {P/poly}\) where \(0<\widetilde{\gamma }<1\) (\(\widetilde{\gamma }\) might be close to 1), then there exists weakly collusion-succinct \((q,\delta )\)-selective-message message private iSKFE for \(\mathsf {P/poly}\) with compression factor \(\gamma '\) such that \(0<\widetilde{\gamma }<\gamma '<1\), where \(q\) is an a-priori fixed polynomial of \(\lambda \).
3.2 Collusion-Succinct PKFE from SXIO and Public-Key Encryption
In this section, we discuss how to construct a bounded-key weakly collusion-succinct iPKFE scheme from an SXIO and PKE scheme.
Overview and proof strategy. Before we proceed to details, we give a main idea for our iPKFE scheme.
Analogously to SKFE setting in Sect. 3.1, to achieve collusion-succinctness, we consider to set a ciphertext as a circuit obfuscated by SXIO that can generate q ciphertexts of a single-key non-succinct scheme. We need to maintain q encryption keys succinctly. In the SKFE setting, we maintain q master secret-keys as one puncturable PRF key. However, we cannot directly use this solution in the PKFE setting. If we do so in the PKFE setting, since the puncturable PRF key should be the master secret-key, an encryptor cannot use it. Thus, we need some mechanism that makes all master public-keys of single-key non-succinct schemes available to an encryptor maintaining them succinctly.
To generate a succinct master public-key, we generate a setup circuit (denoted by \(\mathsf {S}_{\mathsf {1fe}}\) in our scheme) that outputs i-th master public-key of a single-key non-succinct scheme corresponding to an input i, and obfuscate the circuit by SXIO as explained in Sect. 1.3. An encryptor embeds \(\mathsf {MPK}\, : =\mathsf {sxi}\mathcal {O}(\mathsf {S}_{\mathsf {1fe}})\) into an encryption circuit and outputs an obfuscation of this encryption circuit as a ciphertext. This encryption circuit is hardwired a plaintext x and can output ciphertexts under all q master public-keys like the encryption circuit in Sect. 3.1.
Our solution means that we must obfuscate a circuit in which an obfuscated circuit is hardwired (nested applications of SXIO). The nested application still increases the size of a ciphertext. However, if the compression factor of SXIO for \(\mathsf {S}_{\mathsf {1fe}}\) is sufficiently small, we can achieve weak collusion-succinctness.
In the security proof, we use the security of a single-key non-succinct scheme to change a ciphertext of \(x_0\) under each master public-key into that of \(x_1\) via the punctured programming approach as the SKFE case. However, in the reduction to the single-key security, a target master public-key should be given from the security experiment. This means that we must embed the target master public-key into the setup circuit instead of generating it in an on-line manner. Thus, we must apply the punctured programming technique to the setup circuit too before the reduction to the single-key security. This is what the first hybrid step in the security proof does. The rest of the proof is almost the same as that of our iSKFE scheme.
Our construction. The construction of an iPKFE scheme \(\mathsf {qFE}\) whose index space is [q] from an SXIO and public-key encryption scheme is as follows, where q is a fixed polynomial of \(\lambda \). Let \(\mathsf {1FE}=(\mathsf {1FE}.\mathsf {Setup}, \mathsf {1FE}.\mathsf {KG}, \mathsf {1FE}.\mathsf {Enc}, \mathsf {1FE}.\mathsf {Dec})\) be a single-key non-succinct PKFE scheme and \((\mathsf {PRF}.\mathsf {Gen},\mathsf {F},\mathsf {Punc})\) a puncturable PRF.
-
\(\mathsf {qFE}.\mathsf {Setup}(1^\lambda )\) :
-
Generate \(K \leftarrow \mathsf {PRF}.\mathsf {Gen}(1^\lambda )\) and \(\mathsf {S}_{\mathsf {1fe}}[K]\) defined in Fig. 2.
-
Return \((\widehat{\mathsf {MPK}},\widehat{\mathsf {MSK}}) \, : =(\mathsf {sxi}\mathcal {O}(\mathsf {S}_{\mathsf {1fe}}),K)\).
-
-
\(\mathsf {qFE}.\mathsf {i}\mathsf {KG}(\widehat{\mathsf {MSK}}, f, i)\) :
-
Parse \(K \, : =\widehat{\mathsf {MSK}}\).
-
Compute \(r_i \leftarrow \mathsf {F}_K(i)\) and \((\mathsf {MSK}_i, \mathsf {MPK}_i) \leftarrow \mathsf {1FE}.\mathsf {Setup}(1^\lambda ; r_i)\).
-
Compute \(\mathsf {sk}^i_f \leftarrow \mathsf {1FE}.\mathsf {KG}(\mathsf {MSK}_i,f)\) and return \(\widehat{\mathsf {sk}}_f \leftarrow (i, \mathsf {sk}^i_f)\).
-
-
\(\mathsf {qFE}.\mathsf {Enc}(\widehat{\mathsf {MPK}}, x)\) :
-
Generate \(K' \leftarrow \mathsf {PRF}.\mathsf {Gen}(1^\lambda )\) and \(\mathsf {E}_\mathsf {1fe}[\widehat{\mathsf {MPK}},K',x]\) defined in Fig. 3.
-
Return \(\widehat{\mathsf {CT}}\leftarrow \mathsf {sxi}\mathcal {O}(\mathsf {E}_\mathsf {1fe}[\widehat{\mathsf {MPK}},K',x])\).
-
-
\(\mathsf {qFE}.\mathsf {Dec}(\widehat{\mathsf {sk}}_f, \widehat{\mathsf {CT}})\) :
-
Parse \((i, \mathsf {sk}^i_f) \, : =\widehat{\mathsf {sk}}_f\).
-
Compute the circuit \(\widehat{\mathsf {CT}}\) on input i, that is \(\mathsf {CT}_i \leftarrow \widehat{\mathsf {CT}}(i)\).
-
Return \(y \leftarrow \mathsf {1FE}.\mathsf {Dec}(\mathsf {sk}^i_f, \mathsf {CT}_i)\).
-
Theorem 4
If there exists \((1,\delta )\)-selectively-secure non-succinct PKFE for \(\mathsf {P/poly}\) and \(\delta \)-secure \(\gamma \)-compressing SXIO for \(\mathsf {P/poly}\) where \(\gamma \) is an arbitrarily small constant such that \(0<\gamma <1\), then there exists \((q,\delta )\)-selectively-secure weakly collusion-succinct iPKFE for \(\mathsf {P/poly}\) with compression factor \(\beta \), where q is an a-priori fixed polynomial of \(\lambda \), and \(\beta \) is a constant such that \(0<\beta <1\) specified later.
Proof of Theorem 4
We start with the security proof, then move on to analyzing succinctness.
Security Proof. Let us assume that the underlying primitives are \(\delta \)-secure. Let \(\mathcal {A}\) be an adversary attacking the selective security of \(\mathsf {qFE}\). We define a sequence of hybrid games.
-
\(\mathsf {Hyb}_{0}\) : The first game is the original selective security experiment for \(b=0\), that is \(\mathsf {Expt}_{\mathcal {A}}^{\mathsf {sel}}(1^\lambda ,0)\). \(\mathcal {A}\) first selects the challenge messages \((x_0^*,x_1^*)\) and receives the master public key \(\widehat{\mathsf {MPK}}:=\mathsf {sxi}\mathcal {O}(\mathsf {S}_\mathsf {1fe}[K])\) and target ciphertext \(\mathsf {sxi}\mathcal {O}(\mathsf {E}_{\mathsf {1fe}}[\widehat{\mathsf {MPK}},K',x_0^*])\). Next, \(\mathcal {A}\) adaptively makes q function queries \(f_1,\ldots ,f_q\) such that \(f_i(x_0^*) = f_i(x_1^*)\) for all \(i \in [q]\) and receives functional keys \(\widehat{\mathsf {sk}}_{f_1},\ldots , \widehat{\mathsf {sk}}_{f_q}\).
-
\(\mathsf {Hyb}_{1}^{i^*}\) : Let \(i^* \in [q]\). We generate \(\widehat{\mathsf {MPK}}\) as obfuscated \(\mathsf {S}^*_\mathsf {1fe}\) described in Fig. 4. In this hybrid game, we set \(r_{i^*} \leftarrow \mathsf {F}_{K}(i^*)\), \(K\{{i^*}\} \leftarrow \mathsf {Punc}(K,{i^*})\) and \((\mathsf {MPK}_{i^*},\mathsf {MSK}_{i^*}) \leftarrow \mathsf {1FE}.\mathsf {Setup}(1^\lambda ;r_{i^*})\).
When \(i^*=1\), the behavior of \(\mathsf {S}^*_\mathsf {1fe}\) is the same as that of \(\mathsf {S}_\mathsf {1fe}\) since the hard-wired \(\mathsf {MPK}_{1}\) in \(\mathsf {S}^*_\mathsf {1fe}\) is the same as the output of \(\mathsf {S}_\mathsf {1fe}\) on the input 1. Their size is also the same since we pad circuit \(\mathsf {S}_\mathsf {1fe}\) to have the same size as \(\mathsf {S}_\mathsf {1fe}^*\). Then, we can use the indistinguishability guarantee of \(\mathsf {sxi}\mathcal {O}\) and it holds that \(\mathsf {Hyb}_{0}{\mathop {\approx }\limits ^{\mathsf {c}}}_{\delta }\mathsf {Hyb}_{1}^{1}\).
-
\(\mathsf {Hyb}_{2}^{i^*}\) : The challenge ciphertext is generated by obfuscating \(\mathsf {E}^*_\mathsf {1fe}\) described in Fig. 5. In this hybrid game, we set \(r'_{i^*} \leftarrow \mathsf {F}_{K'}(i^*)\), \(K'\{{i^*}\} \leftarrow \mathsf {Punc}(K',{i^*})\), \(\mathsf {CT}_{i^*} \leftarrow \mathsf {1FE}.\mathsf {Enc}(\mathsf {MPK}_{i^*},x_0^* ;r'_{i^*})\), and \(\mathsf {MPK}_{i^*}\leftarrow \widehat{\mathsf {MPK}}({i^*})\).
When \(i^*=1\), the behavior of \(\mathsf {E}^*_\mathsf {1fe}\) is the same as that of \(\mathsf {E}_\mathsf {1fe}\) since the hard-wired \(\mathsf {CT}_1\) in \(\mathsf {E}^*_\mathsf {1fe}\) is the same as the output of \(\mathsf {E}_\mathsf {1fe}\) on the input 1. Moreover, both circuits have the same size by padding \(\mathsf {pad}_\mathsf {E}\). Then, we can use the indistinguishability guarantee of \(\mathsf {sxi}\mathcal {O}\) and it holds that \(\mathsf {Hyb}_{1}^{1}{\mathop {\approx }\limits ^{\mathsf {c}}}_{\delta }\mathsf {Hyb}_{2}^{1}\).
In addition, for \({i^*}\ge 2\), the behavior of \(\mathsf {E}^*_\mathsf {1fe}\) does not change between \(\mathsf {Hyb}_{1}^{i^*}\) and \(\mathsf {Hyb}_{2}^{i^*}\). Thus, \(\mathsf {Hyb}_{1}^{i^*} {\mathop {\approx }\limits ^{\mathsf {c}}}_{\delta } \mathsf {Hyb}_{2}^{i^*}\) holds for every \({i^*}\in \{2,\cdots ,q\}\) due to the security guarantee of \(\mathsf {sxi}\mathcal {O}\).
-
\(\mathsf {Hyb}_{3}^{i^*}\) : We change \(r_{i^*} = \mathsf {F}_{K}(i^*)\) and \(r'_{i^*} = \mathsf {F}_{K'}(i^*)\) into uniformly random \(r_{i^*}\) and \(r'_{i^*}\). Due to the pseudo-randomness at punctured points of puncturable PRF, it holds that \(\mathsf {Hyb}_{2}^{i^*}{\mathop {\approx }\limits ^{\mathsf {c}}}_{\delta }\mathsf {Hyb}_{3}^{i^*}\) for every \({i^*}\in [q]\).
-
\(\mathsf {Hyb}_{4}^{i^*}\) : We change \(\mathsf {CT}_{i^*}\) from \(\mathsf {1FE}.\mathsf {Enc}(\mathsf {MPK}_{i^*},x_0^*)\) to \(\mathsf {1FE}.\mathsf {Enc}(\mathsf {MPK}_{i^*},x_1^*)\). In \(\mathsf {Hyb}_{3}^{i^*}\) and \(\mathsf {Hyb}_{4}^{i^*}\), we do not need randomness to generate \(\mathsf {MPK}_{i^*}\) and \(\mathsf {CT}_{i^*}\). We just hardwire \(\mathsf {MPK}_{i^*}\) and \(\mathsf {CT}_{i^*}\) into \(\mathsf {S}^*_\mathsf {1fe}\) and \(\mathsf {E}^*_\mathsf {1fe}\), respectively. Therefore, for every \({i^*}\in [q]\), \(\mathsf {Hyb}_{3}^{i^*} {\mathop {\approx }\limits ^{\mathsf {c}}}_{\delta } \mathsf {Hyb}_{4}^{i^*}\) follows from the selective security of \(\mathsf {1FE}\) under the master public key \(\mathsf {MPK}_{i^*}\).
-
\(\mathsf {Hyb}_{5}^{i^*}\) : We change \(r_i^*\) and \(r'_{i^*}\) into \(r_{i^*} = \mathsf {F}_{K}(i^*)\) and \(r'_{i^*} = \mathsf {F}_{K'}(i^*)\). We can show \(\mathsf {Hyb}_{4}^{i^*} {\mathop {\approx }\limits ^{\mathsf {c}}}_{\delta } \mathsf {Hyb}_{5}^{i^*}\) for every \({i^*}\in [q]\) based on the pseudo-randomness at punctured point of puncturable PRF.
From the definition of \(\mathsf {S}^*_{\mathsf {1FE}}\), \(\mathsf {E}^*_{\mathsf {1FE}}\), and \(\mathsf {Hyb}_{1}^{i^*}\), the behaviors of \(\mathsf {S}^*_{\mathsf {1FE}}\) and \(\mathsf {E}^*_{\mathsf {1FE}}\) in \(\mathsf {Hyb}_{5}^{i^*}\) and \(\mathsf {Hyb}_{1}^{i^* +1}\) are the same. Thus, \(\mathsf {Hyb}_{5}^{i^*} {\mathop {\approx }\limits ^{\mathsf {c}}}_{\delta } \mathsf {Hyb}_{1}^{i^* +1}\) holds for every \({i^*}\in [q-1]\) due to the security guarantee of \(\mathsf {sxi}\mathcal {O}\). It also holds that \(\mathsf {Hyb}_{5}^{q} {\mathop {\approx }\limits ^{\mathsf {c}}}_{\delta } \mathsf {Expt}_{\mathcal {A}}^{\mathsf {sel}}(1^\lambda ,1)\) based on the security guarantee of \(\mathsf {sxi}\mathcal {O}\). This completes the security proof.
Padding Parameter. The proof of security relies on the indistinguishability of obfuscated \(\mathsf {S}_{\mathsf {1fe}}\) and \(\mathsf {S}^*_{\mathsf {1fe}}\) defined in Figs. 2 and 4, and that of obfuscated \(\mathsf {E}_\mathsf {1fe}\) and \(\mathsf {E}_\mathsf {1fe}^*\) defined in Figs. 3 and 5. Accordingly, we set \(\mathsf {pad}_{\mathsf {S}} \, : =\max (|\mathsf {S}_{\mathsf {1fe}}|,|\mathsf {S}_{\mathsf {1fe}}^*|)\) and \(\mathsf {pad}_{\mathsf {E}} \, : =\max (|\mathsf {E}_{\mathsf {1fe}}|,|\mathsf {E}_{\mathsf {1fe}}^*|)\).
The circuits \(\mathsf {S}_\mathsf {1fe}\) and \(\mathsf {S}_\mathsf {1fe}^*\) compute a puncturable PRF over domain \([q]\) and a key pair of \(\mathsf {1FE}\), and may have punctured PRF keys and a master public key hardwired. The circuits \(\mathsf {E}_\mathsf {1fe}\) and \(\mathsf {E}_\mathsf {1fe}^*\) run the circuit \(\widehat{\mathsf {MPK}}\) and compute a puncturable PRF over domain \([q]\) and a ciphertext of \(\mathsf {1FE}\), and may have punctured PRF keys and a hard-wired ciphertext. Note that the size of instances of \(\mathsf {1FE}\) is independent of q. Thus, it holds that
Weak Collusion-Succinctness. To clearly analyze the size of \(\mathsf {qFE}.\mathsf {Enc}\), we suppose that \(\text {SXIO} \) used to obfuscate \(\mathsf {S}_\mathsf {1fe}\) and that used to obfuscate \(\mathsf {E}_\mathsf {1fe}\) are different.
Let \(\gamma '\) be the compression factor of the SXIO for \(\mathsf {S}_\mathsf {1fe}\). The input space for \(\mathsf {S}_\mathsf {1fe}\) is [q]. Therefore, by the efficiency guarantee of SXIO, we have
Let \(\gamma \) be the compression factor of the SXIO for \(\mathsf {E}_\mathsf {1fe}\). The input space of \(\mathsf {E}_\mathsf {1fe}\) is also [q]. The size of the encryption circuit \(\mathsf {qFE}.\mathsf {Enc}\) (dominated by generating the obfuscated \(\mathsf {E}_\mathsf {1fe}\)) is
where c is some constant.
We assume there exists SXIO with an arbitrarily small compression factor. Thus, by setting \(\gamma '\) as \(\gamma ' < \frac{1-\gamma }{c}\), we can ensure that \(\beta \, : =\gamma + c\gamma ' < 1\), that is \(\mathsf {qFE}\) is weakly collusion-succinct.
This completes the proof of Theorem 4.\(\blacksquare \)
3.3 Collusion-Succinct PKFE from SXIO and Identity-Based Encryption
In this section, we directly construct a weakly collusion-succinct and weakly selectively secure iPKFE scheme from an SXIO and identity-based encryption scheme.
Our construction. The construction of a weakly collusion-succinct and weakly selectively secure q-key iPKFE scheme \(\mathsf {qFE}\) for any fixed polynomial q of \(\lambda \) is based on an SXIO, identity-based encryption schemeFootnote 11, and garbled circuit which is implied by a one-way function. Our collusion-succinct iPKFE scheme is weakly selectively secure because we use function descriptions as identities of identity-based encryption, and the selective security of identity-based encryption requires adversaries to submit a target identity at the beginning of the game.
We assume that we can represent every function f by a \(s\) bit string \((f[1],\cdots , f[s])\) where \(s = {\mathrm {poly}}(\lambda )\). Let \(\mathsf {IBE}=(\mathsf {IBE}.\mathsf {Setup},\mathsf {IBE}.\mathsf {KG}, \mathsf {IBE}.\mathsf {Enc},\) \(\mathsf {IBE}.\mathsf {Dec})\) be an identity-based encryption scheme whose identity space is \([q] \times [s] \times \{0,1\}\), \(\mathsf {GC}=(\mathsf {Grbl}, \mathsf {Eval})\) a garbled circuit, and \((\mathsf {PRF}.\mathsf {Gen},\mathsf {F},\mathsf {Punc})\) a PRF whose domain is \([q] \times [s] \times \{0,1,2\}\).
-
\(\mathsf {qFE}.\mathsf {Setup}(1^\lambda )\) :
-
Generate \((\mathsf {MPK}_{\mathsf {ibe}},\mathsf {MSK}_{\mathsf {ibe}}) \leftarrow \mathsf {IBE}.\mathsf {Setup}(1^\lambda )\).
-
Set \(\mathsf {MPK}\, : =\mathsf {MPK}_{\mathsf {ibe}}\) and \(\mathsf {MSK}\, : =\mathsf {MSK}_{\mathsf {ibe}}\) and return \((\mathsf {MPK}, \mathsf {MSK})\).
-
-
\(\mathsf {qFE}.\mathsf {i}\mathsf {KG}(\mathsf {MSK}, f, i)\) :
-
Parse \(\mathsf {MSK}_{\mathsf {ibe}} \leftarrow \mathsf {MSK}\) and \((f[1],\cdots , f[s]) \, : =f\).
-
For every \(j \in [s]\), compute \(\mathsf {SK}_{}^j \leftarrow \mathsf {IBE}.\mathsf {KG}(\mathsf {MSK}_{\mathsf {ibe}}, (i,j,f[j]))\).
-
Return \(\mathsf {sk}_f \, : =(i, f, \{\mathsf {SK}_{}^j\}_{j \in [s]})\).
-
-
\(\mathsf {qFE}.\mathsf {Enc}(\mathsf {MPK}, x)\) :
-
Parse \(\mathsf {MPK}_{\mathsf {ibe}} \leftarrow \mathsf {MPK}\) and choose \(K \leftarrow \mathsf {PRF}.\mathsf {Gen}(1^\lambda )\).
-
Return \(\mathsf {CT}_{\mathsf {fe}} \leftarrow \mathsf {sxi}\mathcal {O}(\mathsf {E}\mathsf {L}_{\mathsf {gc}}[\mathsf {MPK}_{\mathsf {ibe}},K,x])\). \(\mathsf {E}\mathsf {L}_\mathsf {gc}\) is defined in Fig. 6.
-
-
\(\mathsf {qFE}.\mathsf {Dec}(\mathsf {sk}_f, \mathsf {CT}_{\mathsf {fe}})\) :
-
Parse \((i, f, \{\mathsf {SK}_{}^j\}_{j \in [s]}) \leftarrow \mathsf {sk}_f\).
-
Compute the circuit \(\mathsf {CT}_\mathsf {fe}\) on input i, that is \((\widetilde{U}, \{\mathsf {CT}_{}^{j,\alpha }\}_{j \in [s], \alpha \in \{0,1\}}) \leftarrow \mathsf {CT}_{\mathsf {fe}}(i)\).
-
For every \(j \in [s]\), compute \(L_j \leftarrow \mathsf {IBE}.\mathsf {Dec}(\mathsf {SK}_{}^j, \mathsf {CT}_{}^{j, f[j]})\).
-
Return \(y \leftarrow \mathsf {Eval}(\widetilde{U}, \{L_j\}_{j \in [s]})\).
-
Theorem 5
If there exists \(\delta \)-selectively-secure succinct identity-based encryption with \(\alpha \)-compression (\(\alpha \) is a sufficiently small constant) and \(\delta \)-secure \(\widetilde{\gamma }\)-compressing SXIO for \(\mathsf {P/poly}\) for a constant \(\widetilde{\gamma }\) such that \(0< \widetilde{\gamma } < 1\) (\(\widetilde{\gamma }\) might be close to 1), then there exists weakly collusion-succinct \((q,\delta )\)-weakly-selectively secure iPKFE for circuits of size at most s with compression factor \(\beta \), where s and q are a-priori fixed polynomials of \(\lambda \) and \(\beta \) is a constant such that \(\widetilde{\gamma }<\beta <1\) specified later.
Proof of Theorem 5
We start with the security proof then moving to analyzing succinctness.
Security Proof. Let us assume that the underlying primitives are \(\delta \)-secure. Let \(\mathcal {A}\) be an adversary attacking weakly selective security of \(\mathsf {qFE}\). We define a sequence of hybrid games.
-
\(\mathsf {Hyb}_{0}\) : The first game is the original weakly selective security experiment for \(b=0\), that is \(\mathsf {Expt}_{\mathcal {A}}^{\mathsf {sel^*}}(1^\lambda ,0)\). In this game, \(\mathcal {A}\) first selects the challenge messages \((x_0^*,x_1^*)\) and queries q functions \(f_1,\ldots ,f_q\) such that \(f_i(x_0^*) = f_i(x_1^*)\) for all \(i\in [q]\). Then \(\mathcal {A}\) obtains an encryption of \(x_0^*\), the master public key, and functional keys \(\mathsf {sk}_{f_1},\ldots , \mathsf {sk}_{f_q}\).
-
\(\mathsf {Hyb}_{1}^{i^*}\) : Let \({i^*}\in [q]\). The challenge ciphertext is generated by obfuscating \(\mathsf {E}\mathsf {L}^*_\mathsf {gc}\) described in Fig. 7. In this hybrid game, we set \(r_\mathsf {gc}^* \leftarrow \mathsf {F}_{K}(i^* \Vert 1\Vert 2)\), \(r_{i^*\Vert j\Vert \alpha }^* \leftarrow \mathsf {F}_{K}(i^* \Vert j\Vert \alpha )\) for all \(j\in [s]\) and \(\alpha \in \{0,1\}\), \(K\{S^*\} \leftarrow \mathsf {Punc}(K,S^*)\) where \(S^* \, : =\left\{ i^*\Vert 1\Vert 2,\left\{ i^*\Vert j \Vert \alpha \right\} _{j\in [s],\alpha \in \{0,1\}^{}}\right\} \), \((\widetilde{U}^*, \{L^*_{j,\alpha }\}_{j \in [s], \alpha \in \{0,1\}}) \leftarrow \mathsf {Grbl}(1^\lambda , U(\cdot , x_0^*); r_\mathsf {gc}^*)\), and \(\mathsf {CT}_{i^{*}}^{j,\alpha } \leftarrow \mathsf {IBE}.\mathsf {Enc}(\mathsf {MPK}_{\mathsf {ibe}},(i^* , j,\alpha ), L_{j,\alpha } ;r_{i^*\Vert j\Vert \alpha }^*)\) for all \(j \in [s]\) and \(\alpha \in \{0,1\}\). Hereafter, we use \(r_{j\Vert \alpha }^*\) instead of \(r_{i^*\Vert j\Vert \alpha }^*\) for ease of notation.
When \(i^*=1\), the behaviors of \(\mathsf {E}\mathsf {L}_\mathsf {gc}\) and \(\mathsf {E}\mathsf {L}_\mathsf {gc}^*\) are the same from the definition of \(\mathsf {E}\mathsf {L}_{\mathsf {gc}}^*\), and so are their size since we pad circuit \(\mathsf {E}\mathsf {L}_\mathsf {gc}\) to have the same size as \(\mathsf {E}\mathsf {L}_\mathsf {gc}^*\). Then, we can use the indistinguishability guarantee of \(\mathsf {sxi}\mathcal {O}\), and it holds that \(\mathsf {Hyb}_{0}{\mathop {\approx }\limits ^{\mathsf {c}}}_{\delta }\mathsf {Hyb}_{1}^{1}\).
-
\(\mathsf {Hyb}_{2}^{i^*}\) : We change \(r_\mathsf {gc}^* = \mathsf {F}_{K}(i^* \Vert 1 \Vert 2)\) and \(r^*_{j\Vert \alpha } = \mathsf {F}_{K}(i^* \Vert j \Vert \alpha )\) into uniformly random \(r_\mathsf {gc}^*\) and \(r^*_{j\Vert \alpha }\) for all \(j \in [s]\) and \(\alpha \in \{0,1\}^{}\). Due to the pseudo-randomness at punctured points of puncturable PRF, it holds that \(\mathsf {Hyb}_{1}^{i^*}{\mathop {\approx }\limits ^{\mathsf {c}}}_{\delta }\mathsf {Hyb}_{2}^{i^*}\) for every \({i^*}\in [q]\).
-
\(\mathsf {Hyb}_{3}^{i^*}\) : For ease of notation, let \(f^* \, : =f_{i^*}\) and
 be the complement of f, that is,
be the complement of f, that is,  . Moreover, we omit each randomness for \(\mathsf {IBE}.\mathsf {Enc}\) since it is uniformly random at this hybrid game. For every \(j\in [s]\), we change
. Moreover, we omit each randomness for \(\mathsf {IBE}.\mathsf {Enc}\) since it is uniformly random at this hybrid game. For every \(j\in [s]\), we change-
normal ciphertexts
 into
into -
junk ciphertexts
 , where \(\ell \) is a polynomial denoting the length of labels output by \(\mathsf {Grbl}\).
, where \(\ell \) is a polynomial denoting the length of labels output by \(\mathsf {Grbl}\).
That is, for identities which do not correspond to the \({i^*}\)-th function queried by \(\mathcal {A}\), we do not encrypt labels of garbled circuit. We do not change \(\mathsf {CT}_{i^*}^{j,f^*[j]}\) for all \(j\in [s]\). Note that all \(f_{1},\ldots , f_{q}\) are known in advance since we consider weakly selective security. \(\mathcal {A}\) is not given secret keys of \(\mathsf {IBE}\) for identity
 , so it is hard for \(\mathcal {A}\) to detect this change. We show \(\mathsf {Hyb}_{2}^{i^*} {\mathop {\approx }\limits ^{\mathsf {c}}}_{\delta } \mathsf {Hyb}_{3}^{i^*}\) more formally in Lemma 1 by using the selective security of \(\mathsf {IBE}\).
, so it is hard for \(\mathcal {A}\) to detect this change. We show \(\mathsf {Hyb}_{2}^{i^*} {\mathop {\approx }\limits ^{\mathsf {c}}}_{\delta } \mathsf {Hyb}_{3}^{i^*}\) more formally in Lemma 1 by using the selective security of \(\mathsf {IBE}\). -
The description of \(\mathsf {E}\mathsf {L}^*_\mathsf {gc}\). The description depends on \({i^*}\), but we use the notion \(\mathsf {E}\mathsf {L}^*_\mathsf {gc}\) instead of \(\mathsf {E}\mathsf {L}^{i^*}_\mathsf {gc}\) for simpler notations. \(U(\cdot , x)\) is a universal circuit in which x is hardwired as the second input.
Lemma 1
It holds that \(\mathsf {Hyb}_{2}^{i^*} {\mathop {\approx }\limits ^{\mathsf {c}}}_{\delta } \mathsf {Hyb}_{3}^{i^*}\) for all \({i^*}\in [q]\) if \(\mathsf {IBE}\) is selectively secure.
Proof
First, we define more hybrid games \(\mathsf {H}_{j^*}\) for \(j^*\in \{0,\cdots ,s\}\) as follows.
-
\(\mathsf {H}_{j^*}\) : This is the same as \(\mathsf {Hyb}_{2}^{i^*}\) except that for \(j\le j^*\),
 . We see that \(\mathsf {H}_{0}\) and \(\mathsf {H}_{s}\) are the same as \(\mathsf {Hyb}_{2}^{i^*}\) and \(\mathsf {Hyb}_{3}^{i^*}\), respectively.
. We see that \(\mathsf {H}_{0}\) and \(\mathsf {H}_{s}\) are the same as \(\mathsf {Hyb}_{2}^{i^*}\) and \(\mathsf {Hyb}_{3}^{i^*}\), respectively.
We show that \(\mathsf {H}_{j^* -1} {\mathop {\approx }\limits ^{\mathsf {c}}}_{\delta } \mathsf {H}_{j^*}\) holds for all \(j^* \in [s]\). This immediately implies the lemma.
We construct an adversary \(\mathcal {B}\) in the selective security game of \(\mathsf {IBE}\) as follows. To simulate the weakly selective security game of iPKFE, \(\mathcal {B}\) runs \(\mathcal {A}\) attacking \(\mathsf {qFE}\) and receives a message pair \((x_0^*,x_1^*)\) and function queries \(f_1,\cdots ,f_q\). \(\mathcal {B}\) simulates the game of \(\mathsf {qFE}\) as follows.
-
Setup and Encryption: \(\mathcal {B}\) sets
 as the target identity to the challenger of \(\mathsf {IBE}\). Note that \(f^* = f_{i^*}\).
as the target identity to the challenger of \(\mathsf {IBE}\). Note that \(f^* = f_{i^*}\).To set challenge messages of IBE, \(\mathcal {B}\) computes \((\widetilde{U}^*, \{L^*_{j,\alpha }\}_{j \in [s], \alpha \in \{0,1\}}) \leftarrow \mathsf {Grbl}(1^\lambda , U(\cdot , x_0^*))\) and sets
 and \(m_1 \, : =0^{\ell (\lambda )}\). \(\mathcal {B}\) sends \(\mathsf {id}^*\) and \((m_0^*,m_1^*)\) to the challenger of IBE, and receives \(\mathsf {MPK}_{\mathsf {ibe}}\) and
and \(m_1 \, : =0^{\ell (\lambda )}\). \(\mathcal {B}\) sends \(\mathsf {id}^*\) and \((m_0^*,m_1^*)\) to the challenger of IBE, and receives \(\mathsf {MPK}_{\mathsf {ibe}}\) and 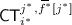 as the master public-key and target ciphertext of IBE. \(\mathcal {B}\) sets \(\mathsf {MPK}\, : =\mathsf {MPK}_{\mathsf {ibe}}\). To simulate ciphertexts of \(\mathsf {qFE}\), \(\mathcal {B}\) does the followings.
as the master public-key and target ciphertext of IBE. \(\mathcal {B}\) sets \(\mathsf {MPK}\, : =\mathsf {MPK}_{\mathsf {ibe}}\). To simulate ciphertexts of \(\mathsf {qFE}\), \(\mathcal {B}\) does the followings.-
For all \(j \le j^* -1\), \(\mathcal {B}\) computes \(\mathsf {CT}_{i^{*}}^{j,f^* [j]} \leftarrow \mathsf {IBE}.\mathsf {Enc}(\mathsf {MPK}_{\mathsf {ibe}},i^*\Vert \) \( j \Vert f^* [j],L_{j,f^* [j]} )\) and
 .
. -
For \(j = j^*\), \(\mathcal {B}\) computes \(\mathsf {CT}_{i^{*}}^{j^*,f^*[j^*]} \leftarrow \mathsf {IBE}.\mathsf {Enc}(\mathsf {MPK}_{\mathsf {ibe}},i^* \Vert j^* \Vert f^*[j^*],\) \( L_{j^*,f^*[j^*]})\).
-
For all \(j \ge j^* +1\) and \(\alpha \in \{0,1\}^{}\), \(\mathcal {B}\) computes \(\mathsf {CT}_{i^{*}}^{j,\alpha } \leftarrow \mathsf {IBE}.\mathsf {Enc}\) \((\mathsf {MPK}_{\mathsf {ibe}}, i^*\Vert j \Vert \alpha ),L_{j,\alpha } )\).
By using these ciphertexts \(\{\mathsf {CT}_{i^*}^{j,\alpha }\}_{j\in [s],\alpha \in \{0,1\}^{}}\), \(\mathcal {B}\) constructs program \(\mathsf {E}\mathsf {L}^*_{\mathsf {gc}}\) and sets \(\mathsf {CT}^*_{\mathsf {fe}} \, : =\mathsf {sxi}\mathcal {O}(\mathsf {E}\mathsf {L}^*_{\mathsf {gc}})\) as the target ciphertext of \(\mathsf {qFE}\).
-
-
Key Generation: Then, \(\mathcal {B}\) queries identities \((i,1,f_i [1]),\ldots , (i,s,f_i [s])\) for all \(i\in [q]\) to the challenger of \(\mathsf {IBE}\), receives \(\mathsf {SK}_i^j \leftarrow \mathsf {IBE}.\mathsf {KG}(\mathsf {MSK}_{\mathsf {ibe}},i\Vert j \Vert f_i [j])\), and sets \(\mathsf {SK}_{f_i} \, : =(i,f_i,\{\mathsf {SK}_{i}^{j}\}_{j\in [s]})\) for all \(i\in [q]\). Note that \(\mathcal {B}\) does not have to query the challenge identity
 .
.
Now \(\mathcal {B}\) sets all values for \(\mathcal {A}\) and sends \(\mathsf {MPK}\), \(\mathsf {CT}_{\mathsf {fe}}^*\), and \(\{\mathsf {SK}_{f_i}\}_{i\in [q]}\) to \(\mathcal {A}\). If \(\mathcal {B}\) is given  , then \(\mathcal {B}\) perfectly simulates \(\mathsf {H}_{j^* -1}\). If \(\mathcal {B}\) is given
, then \(\mathcal {B}\) perfectly simulates \(\mathsf {H}_{j^* -1}\). If \(\mathcal {B}\) is given  , then \(\mathcal {B}\) perfectly simulates \(\mathsf {H}_{j^*}\). Therefore, the advantage of \(\mathcal {A}\) between \(\mathsf {H}_{j^* -1}\) and \(\mathsf {H}_{j^*}\) is bounded by that of \(\mathcal {B}\) attacking \(\mathsf {IBE}\) and it holds that \(\mathsf {H}_{j^* -1}{\mathop {\approx }\limits ^{\mathsf {c}}}_{\delta }\mathsf {H}_{j^*}\). This completes the proof of the lemma.\(\blacksquare \)
, then \(\mathcal {B}\) perfectly simulates \(\mathsf {H}_{j^*}\). Therefore, the advantage of \(\mathcal {A}\) between \(\mathsf {H}_{j^* -1}\) and \(\mathsf {H}_{j^*}\) is bounded by that of \(\mathcal {B}\) attacking \(\mathsf {IBE}\) and it holds that \(\mathsf {H}_{j^* -1}{\mathop {\approx }\limits ^{\mathsf {c}}}_{\delta }\mathsf {H}_{j^*}\). This completes the proof of the lemma.\(\blacksquare \)
-
\(\mathsf {Hyb}_{4}^{i^*}\) : We change \((\widetilde{U}^*, \{L^*_{j,\alpha }\}_{j \in [s], \alpha \in \{0,1\}}) \leftarrow \mathsf {Grbl}(1^\lambda , U(\cdot , x_0^*))\) into a simulated output \((\widetilde{U}^*, \{L^*_{j,f^* [j]}\}_{j \in [s]}) \leftarrow \mathsf {Sim.GC}(1^\lambda , y^*))\) where \(y^* \, : =f^*(x_0^*) = f^*(x_1^*)\). By the requirement of the game, \(f^*(x_0^*)=f^*(x_1^*)\) holds. In this game,
 are not generated since the simulator of GC does not generate them. This is not a problem since for such labels, junk ciphertexts are generated as in \(\mathsf {Hyb}_{3}^{i^*}\). It holds that \(\mathsf {Hyb}_{3}^{i^*} {\mathop {\approx }\limits ^{\mathsf {c}}}_{\delta } \mathsf {Hyb}_{4}^{i^*}\) for every \({i^*}\in [q]\) due to the security of the garbled circuit.
are not generated since the simulator of GC does not generate them. This is not a problem since for such labels, junk ciphertexts are generated as in \(\mathsf {Hyb}_{3}^{i^*}\). It holds that \(\mathsf {Hyb}_{3}^{i^*} {\mathop {\approx }\limits ^{\mathsf {c}}}_{\delta } \mathsf {Hyb}_{4}^{i^*}\) for every \({i^*}\in [q]\) due to the security of the garbled circuit. -
\(\mathsf {Hyb}_{5}^{i^*}\) : We change the simulated garbled circuit, junk ciphertexts, and punctured PRF keys hardwired into \(\mathsf {E}\mathsf {L}^*_\mathsf {gc}\) back into the real garbled circuit, normal IBE ciphertexts, and un-punctured PRF keys. In this hybrid game, we set \(r_\mathsf {gc}^* = \mathsf {F}_{K}(i^* \Vert 1\Vert 2)\), \(r_{j\Vert \alpha }^* = \mathsf {F}_{K}(i^* \Vert j\Vert \alpha )\) for all \(j\in [s]\) and \(\alpha \in \{0,1\}\), \((\widetilde{U}^*, \{L^*_{j,\alpha }\}_{j \in [s], \alpha \in \{0,1\}}) \leftarrow \mathsf {Grbl}(1^\lambda , U(\cdot , x_1^*);r_\mathsf {gc}^*)\), and \(\mathsf {CT}_{i^{*}}^{j,\alpha } \leftarrow \mathsf {IBE}.\mathsf {Enc}(\mathsf {MPK}_{\mathsf {ibe}}, (i^* , j,\alpha ),L_{j,\alpha } ;r_{j\Vert \alpha }^*)\). We can show \(\mathsf {Hyb}_{4}^{i^*} {\mathop {\approx }\limits ^{\mathsf {c}}}_{\delta } \mathsf {Hyb}_{5}^{i^*}\) for every \({i^*}\in [q]\) in a reverse manner.
It holds \(\mathsf {Hyb}_{5}^{i^*}{\mathop {\approx }\limits ^{\mathsf {c}}}_{\delta }\mathsf {Hyb}_{1}^{i^* + 1}\) for every \({i^*}\in [q-1]\) by the definition of \(\mathsf {E}\mathsf {L}_{\mathsf {gc}}^*\) and \(\mathsf {sxi}\mathcal {O}\). That is, \(\mathsf {Expt}_{\mathcal {A}}^{\mathsf {sel^*}}(1^\lambda ,0) = \mathsf {Hyb}_{0} {\mathop {\approx }\limits ^{\mathsf {c}}}_{\delta } \mathsf {Hyb}_{1}^{1} {\mathop {\approx }\limits ^{\mathsf {c}}}_{\delta } \cdots {\mathop {\approx }\limits ^{\mathsf {c}}}_{\delta } \mathsf {Hyb}_{5}^{q} {\mathop {\approx }\limits ^{\mathsf {c}}}_{\delta } \mathsf {Expt}_{\mathcal {A}}^{\mathsf {sel^*}}(1^\lambda ,1)\) holds. This completes the security proof.
Padding Parameter. The proof of security relies on the indistinguishability of obfuscated \(\mathsf {E}\mathsf {L}_\mathsf {gc}\) and \(\mathsf {E}\mathsf {L}_\mathsf {gc}^*\) defined in Figs. 6 and 7, respectively. Accordingly, we set \(\mathsf {pad}_{\mathsf {E}\mathsf {L}} \, : =\max (|\mathsf {E}\mathsf {L}_\mathsf {gc}|,|\mathsf {E}\mathsf {L}_\mathsf {gc}^*|)\).
The circuits \(\mathsf {E}\mathsf {L}_\mathsf {gc}\) and \(\mathsf {E}\mathsf {L}_\mathsf {gc}^*\) compute a puncturable PRF over domain \([q]\), 2s IBE ciphertexts, and garbled circuit of \(U(\cdot ,x)\), and may have punctured PRF keys and a hard-wired ciphertext. Note that the size of set \(S^*\) of punctured points of PRF in \(\mathsf {E}\mathsf {L}_\mathsf {gc}^*\) is logarithmic in q. Note also that \(|\mathcal {ID}| = 2qs\). Thus, due to the efficiency of \(\mathsf {IBE}\), it holds that
where \(\alpha \) is a constant such that \(0<\alpha <1\).
Weak Collusion-Succinctness. The input space for \(\mathsf {E}\mathsf {L}_\mathsf {gc}\) is \([q]\). Thus, by the efficiency guarantee of SXIO, the size of the encryption circuit \(\mathsf {qFE}.\mathsf {Enc}\) (dominated by generating an obfuscated \(\mathsf {E}\mathsf {L}_\mathsf {gc}\)) is
where \(\widetilde{\gamma }\) is a constant such that \(0<\widetilde{\gamma }<1\) and c is some constant.
By using an identity-based encryption scheme whose compression factor \(\alpha \) satisfies \(\alpha <\frac{1-\widetilde{\gamma }}{c}\), we ensure that \(\beta \, : =\widetilde{\gamma }+c\alpha < 1\), that is \(\mathsf {qFE}\) is weakly collusion succinct. This completes the proof of Theorem 5.\(\blacksquare \)
4 Weak Succinctness from Collusion-Succinctness
We state only the theorem due to limited space.
Theorem 6
If there exists weakly collusion-succinct \((\mu ,\delta )\)-weakly-selectively secure iPKFE (resp. iSKFE) for circuits of size at most \(s = s(\lambda )\) with \(n = n(\lambda )\) inputs with encryption circuit of size \(\mu ^{\gamma }\cdot {\mathrm {poly}}(\lambda ,n,s)\) where \(\mu = s \cdot {\mathrm {poly}}_\mathsf {RE}(\lambda ,n)\) and \({\mathrm {poly}}_\mathsf {RE}\) is a fixed polynomial determined by \(\mathsf {RE}\), then there exists weakly succinct \((1,\delta )\)-weakly-selectively secure PKFE (resp. SKFE) for circuits of size at most \(s = s(\lambda )\) with encryption circuit of size \(s^{\gamma '}\cdot {\mathrm {poly}}(\lambda ,n)\), where \(\gamma '\) is a fixed constant such that \(\gamma< \gamma ' <1\).
We can obtain this theorem by slightly modifying the analysis of the transformation by Bitansky and Vaikuntanathan [11, Proposition IV.1].
5 Putting it Altogether
Before summarizing our results, we introduce the following theorems regarding SKFE and SXIO obtained by the results of Brakerski et al. [16] and Bitansky et al. [9, 10]. Note that \({\mathrm {poly}}\) denotes an unspecified polynomial below.
Theorem 7
[9, 16]. If there exists \(({\mathrm {poly}},\delta )\)-selective-message message private and non-succinct SKFE for \(\mathsf {P/poly}\), then there exists \(\delta \)-secure and \(\gamma \)-compressing SXIO for \(\mathsf {P/poly}\) where \(\gamma \) is an arbitrary constant such that \(0<\gamma <1\). (\(\gamma \) could be sufficiently small)
Theorem 8
[10]. If there exists \((1,\delta )\)-selective-message message private and weakly succinct SKFE for \(\mathsf {P/poly}\), then there exists \(\delta \)-secure and \(\widetilde{\gamma }\)-compressing SXIO for \(\mathsf {P/poly}\) where \(\widetilde{\gamma }\) is a constant such that \(1/2\le \widetilde{\gamma }<1\).
We also introduce the following result shown by Garg and Srinivasan [29] stating that we can transform single-key PKFE into collusion-resistant one strengthening selective security and succinctness.
Theorem 9
[29]. If there exists a \((1,\delta )\)-weakly-selectively secure and weakly succinct PKFE scheme for \(\mathsf {P/poly}\), then there exists a \(({\mathrm {poly}},\delta )\)-selectively secure and succinct PKFE scheme for \(\mathsf {P/poly}\).
5.1 Transformation from SKFE to PKFE
By Theorems 2, 4, 6 and 7, we obtain the following theorem. We note that Theorem 4 requires a sufficiently small compression factor for SXIO.
Theorem 10
If there exists \(\delta \)-secure plain public-key encryption and \(({\mathrm {poly}},\delta )\)-selective-message message private and non-succinct SKFE for \(\mathsf {P/poly}\), then there exists \((1,\delta )\)-selectively secure and weakly succinct PKFE for \(\mathsf {P/poly}\).
From this theorem and Theorem 9, we obtain the following corollary stating that collusion-resistant PKFE is constructed from collusion-resistant SKFE if we additionally assume public-key encryption.
Corollary 1
If there exists \(\delta \)-secure plain public-key encryption and \(({\mathrm {poly}},\delta )\)-selective-message message private and non-succinct SKFE for \(\mathsf {P/poly}\), then there exists \(({\mathrm {poly}},\delta )\)-selectively secure and succinct PKFE for \(\mathsf {P/poly}\).
We stress that the transformations above incur only polynomial security loss.
We next see that single-key weakly-succinct SKFE is also powerful enough to yield PKFE if we additionally assume identity-based encryption. By Theorems 5, 6 and 8, we obtain the following theorem since Theorem 5 just requires that the compression factor of SXIO \(\widetilde{\gamma }\) is slightly smaller than 1 (no need to be sufficiently small).
Theorem 11
If there exists \(\delta \)-secure identity-based encryption and \((1,\delta )\)-selective-message message private and weakly succinct SKFE for \(\mathsf {P/poly}\), then there exists \((1,\delta )\)-weakly-selectively secure and weakly succinct PKFE for \(\mathsf {P/poly}\).
We stress that the transformation above incurs only polynomial security loss. We note the following two facts. It was not known whether \((1,\delta )\)-selective-message message private and weakly succinct SKFE for \(\mathsf {P/poly}\) implies \(({\mathrm {poly}},\delta )\)-selective-message message private SKFE for \(\mathsf {P/poly}\) or not before the recent work of Kitagawa et al. [38]. Moreover, the transformation of Kitagawa et al. incurs quasi-polynomial security loss.
By combining this theorem with Theorem 9, we obtain the following corollary stating that we can construct collusion-resistant PKFE from single-key weakly succinct SKFE if we additionally assume identity-based encryption.
Corollary 2
If there exists \(\delta \)-selectively-secure identity-based encryption and \((1,\delta )\)-selectively-secure weakly succinct SKFE for \(\mathsf {P/poly}\), then there exists \(({\mathrm {poly}},\delta )\)-selectively secure and succinct PKFE for \(\mathsf {P/poly}\).
We stress that the transformation above incurs only polynomial security loss. Figure 8 illustrates our results stated above.
Illustration of our theorems. Dashed lines denote known facts or trivial implications. White boxes denote our ingredients or goal. Purple boxes denote our key schemes. Green boxes denote our intermediate tools. All transformations in this figure incur only polynomial security loss. \(\gamma \)-SXIO (resp. \(\widetilde{\gamma }\)-SXIO) denotes SXIO with compression factor \(\gamma \) (resp. \(\widetilde{\gamma }\)), which is sufficiently small constant of less than 1 (resp. arbitrary constant of less than 1). We ignore garbled circuit, puncturable PRF, and decomposable RE in this figure. They are implied by one-way function. (Color figure online)
5.2 Equivalence of SKFE, SXIO, and Updatable RE
By Theorems 2, 3 and 6, we obtain the following theorem.
Theorem 12
If there exists \(\delta \)-secure one-way function and \(\delta \)-secure and \(\widetilde{\gamma }\)-compressing SXIO for \(\mathsf {P/poly}\) for a constant \(\widetilde{\gamma }\) such that \(0<\widetilde{\gamma }<1\) (\(\widetilde{\gamma }\) might be close to 1), then there exists \((1,\delta )\)-selective-message message private and weakly succinct SKFE for \(\mathsf {P/poly}\).
By combining this theorem and Theorem 8, we obtain the following corollary stating that the existence of single-key weakly-succinct SKFE is equivalent to those of SXIO and \(\text {one-way function} \). Note that single-key weakly succinct SKFE for \(\mathsf {P/poly}\) trivially implies one-way function.
Corollary 3
A single-key weakly succinct SKFE for \(\mathsf {P/poly}\) is equivalent to one-way function and \(\widetilde{\gamma }\)-compressing SXIO for \(\mathsf {P/poly}\) such that \(0<\widetilde{\gamma }<1\) (\(\widetilde{\gamma }\) might be close to 1).
We can also obtain equivalence of these primitives and updatable randomized encoding (URE). We introduce the following results related to URE shown by Ananth et al. [2].
Theorem 13
[2]. A single-key weakly succinct SKFE for \(\mathsf {P/poly}\) implies output-compact URE with an unbounded number of updates.
Theorem 14
[2]. Output-compact URE with an unbounded number of updates implies a \(\widetilde{\gamma }\)-compressing SXIO for \(\mathsf {P/poly}\) where \(\frac{1}{2}\le \widetilde{\gamma }<1\).
Note that Ananth et al. prove Theorem 14 for a \(\widetilde{\gamma }\)-compressing XIO, but it is easy to observe that their construction of XIO can be extended to \(\widetilde{\gamma }\)-compressing SXIO. By Theorems 12 to 14, we can obtain the following corollary.
Corollary 4
A single-key weakly succinct SKFE for \(\mathsf {P/poly}\) is equivalent to one-way function and output-compact updatable randomized encoding with an unbounded number of updates.
Ananth et al. show that single-key weakly-succinct SKFE is equivalent to the combination of updatable randomized encoding and the LWE assumption. Regarding the result, Corollary 4 shows that the LWE assumption is replaced with weaker and general assumption, that is one-way function.
Notes
- 1.
We borrow this term from the talk by Amit Sahai at MIT, “State of the IO: Where we stand in the quest for secure obfuscation” http://toc.csail.mit.edu/node/981.
- 2.
Martin Albrecht and Alex Davidson maintain the status of graded encoding schemes and IO constructions at http://malb.io/are-graded-encoding-schemes-broken-yet.html.
- 3.
In some papers, the term “compactness” is used for this property, but we use the term by Bitansky and Vaikuntanathan [11] in this study.
- 4.
They use a bootstrapping technique by Ananth et al. [1], which transforms functional encryption for \(\mathsf {NC}^1\) into one for \(\mathsf {P/poly}\).
- 5.
Note that our requirements on an identity-based encryption scheme is the same as theirs on their identity-based encryption scheme.
- 6.
- 7.
We ignore the issue regarding randomness of the ciphertext in this section.
- 8.
When we say identity-based encryption, we assume that it satisfies this type of succinctness. In fact, most identity-based encryption schemes based on number theoretic or lattice assumptions satisfy it.
- 9.
The security definition of Li and Micciancio for index based functional encryption and ours is slightly different. Their definition allows an adversary to use indices for key generation in an arbitrary order. On the other hand, our definition does not allow it. The difference comes from the fact that their goal is constructing collusion-resistant functional encryption while our goal is constructing single-key functional encryption. By restricting an adversary to use indices successively from one, we can describe security proofs more simply.
- 10.
More precisely, Gorbunov et al. prove that we can construct adaptively secure schemes, in which adversaries are allowed to declare a target message pair after the function query phase. However, selective security is sufficient for our purpose.
- 11.
We stress that the size of the encryption circuit of an identity-based encryption scheme is \(|\mathcal {ID}|^{\alpha }\cdot {\mathrm {poly}}(\lambda ,\ell )\) where \(\ell \) is the length of plaintext, \(\mathcal {ID}\) is the identity-space, and \(\alpha \) is a constant such that \(0<\alpha <1\). Most identity-based encryption schemes based on concrete assumptions have such succinct encryption circuits. In our scheme, \(\mathcal {ID}\) is just a polynomial size.
References
Ananth, P., Brakerski, Z., Segev, G., Vaikuntanathan, V.: From selective to adaptive security in functional encryption. In: Gennaro, R., Robshaw, M. (eds.) CRYPTO 2015. LNCS, vol. 9216, pp. 657–677. Springer, Heidelberg (2015). https://doi.org/10.1007/978-3-662-48000-7_32
Ananth, P., Cohen, A., Jain, A.: Cryptography with updates. In: Coron, J.-S., Nielsen, J.B. (eds.) EUROCRYPT 2017. LNCS, vol. 10211, pp. 445–472. Springer, Cham (2017). https://doi.org/10.1007/978-3-319-56614-6_15
Ananth, P., Jain, A.: Indistinguishability obfuscation from compact functional encryption. In: Gennaro, R., Robshaw, M. (eds.) CRYPTO 2015. LNCS, vol. 9215, pp. 308–326. Springer, Heidelberg (2015). https://doi.org/10.1007/978-3-662-47989-6_15
Ananth, P., Jain, A., Sahai, A.: Indistinguishability obfuscation from functional encryption for simple functions. Cryptology ePrint Archive, Report 2015/730
Apon, D., Döttling, N., Garg, S., Mukherjee, P.: Cryptanalysis of indistinguishability obfuscations of circuits over GGH13. In: ICALP 2017 (2017)
Applebaum, B., Ishai, Y., Kushilevitz, E.: Computationally private randomizing polynomials and their applications. Comput. Complex. 15(2), 115–162 (2006)
Banerjee, A., Peikert, C., Rosen, A.: Pseudorandom functions and lattices. In: Pointcheval, D., Johansson, T. (eds.) EUROCRYPT 2012. LNCS, vol. 7237, pp. 719–737. Springer, Heidelberg (2012). https://doi.org/10.1007/978-3-642-29011-4_42
Barak, B., Goldreich, O., Impagliazzo, R., Rudich, S., Sahai, A., Vadhan, S.P., Yang, K.: On the (im)possibility of obfuscating programs. J. ACM 59(2), 6 (2012)
Bitansky, N., Nishimaki, R., Passelègue, A., Wichs, D.: From cryptomania to obfustopia through secret-key functional encryption. In: Hirt, M., Smith, A. (eds.) TCC 2016. LNCS, vol. 9986, pp. 391–418. Springer, Heidelberg (2016). https://doi.org/10.1007/978-3-662-53644-5_15
Bitansky, N., Nishimaki, R., Passelègue, A., Wichs, D.: From cryptomania to obfustopia through secret-key functional encryption. Cryptology ePrint Archive, Report 2016/558 (2016)
Bitansky, N., Vaikuntanathan, V.: Indistinguishability obfuscation from functional encryption. In: 56th FOCS, pp. 171–190 (2015)
Boneh, D., Franklin, M.K.: Identity-based encryption from the weil pairing. SIAM J. Comput. 32(3), 586–615 (2003)
Boneh, D., Sahai, A., Waters, B.: Functional encryption: definitions and challenges. In: Ishai, Y. (ed.) TCC 2011. LNCS, vol. 6597, pp. 253–273. Springer, Heidelberg (2011). https://doi.org/10.1007/978-3-642-19571-6_16
Boneh, D., Waters, B.: Constrained pseudorandom functions and their applications. In: Sako, K., Sarkar, P. (eds.) ASIACRYPT 2013. LNCS, vol. 8270, pp. 280–300. Springer, Heidelberg (2013). https://doi.org/10.1007/978-3-642-42045-0_15
Boyle, E., Goldwasser, S., Ivan, I.: Functional signatures and pseudorandom functions. In: Krawczyk, H. (ed.) PKC 2014. LNCS, vol. 8383, pp. 501–519. Springer, Heidelberg (2014). https://doi.org/10.1007/978-3-642-54631-0_29
Brakerski, Z., Komargodski, I., Segev, G.: Multi-input functional encryption in the private-key setting: stronger security from weaker assumptions. In: Fischlin, M., Coron, J.-S. (eds.) EUROCRYPT 2016. LNCS, vol. 9666, pp. 852–880. Springer, Heidelberg (2016). https://doi.org/10.1007/978-3-662-49896-5_30
Brakerski, Z., Segev, G.: Function-private functional encryption in the private-key setting. In: Dodis, Y., Nielsen, J.B. (eds.) TCC 2015. LNCS, vol. 9015, pp. 306–324. Springer, Heidelberg (2015). https://doi.org/10.1007/978-3-662-46497-7_12
Chen, Y., Gentry, C., Halevi, S.: Cryptanalyses of candidate branching program obfuscators. In: Coron, J.-S., Nielsen, J.B. (eds.) EUROCRYPT 2017. LNCS, vol. 10212, pp. 278–307. Springer, Cham (2017). https://doi.org/10.1007/978-3-319-56617-7_10
Cheon, J.H., Fouque, P.-A., Lee, C., Minaud, B., Ryu, H.: Cryptanalysis of the new CLT multilinear map over the integers. In: Fischlin, M., Coron, J.-S. (eds.) EUROCRYPT 2016. LNCS, vol. 9665, pp. 509–536. Springer, Heidelberg (2016). https://doi.org/10.1007/978-3-662-49890-3_20
Cheon, J.H., Han, K., Lee, C., Ryu, H., Stehlé, D.: Cryptanalysis of the multilinear map over the integers. In: Oswald, E., Fischlin, M. (eds.) EUROCRYPT 2015. LNCS, vol. 9056, pp. 3–12. Springer, Heidelberg (2015). https://doi.org/10.1007/978-3-662-46800-5_1
Cohen, A., Holmgren, J., Nishimaki, R., Vaikuntanathan, V., Wichs, D.: Watermarking cryptographic capabilities. In: 48th ACM STOC, pp. 1115–1127 (2016)
Coron, J.-S., Gentry, C., Halevi, S., Lepoint, T., Maji, H.K., Miles, E., Raykova, M., Sahai, A., Tibouchi, M.: Zeroizing without low-level zeroes: new MMAP attacks and their limitations. In: Gennaro, R., Robshaw, M. (eds.) CRYPTO 2015. LNCS, vol. 9215, pp. 247–266. Springer, Heidelberg (2015). https://doi.org/10.1007/978-3-662-47989-6_12
Coron, J.-S., Lee, M.S., Lepoint, T., Tibouchi, M.: Zeroizing attacks on indistinguishability obfuscation over CLT13. In: Fehr, S. (ed.) PKC 2017. LNCS, vol. 10174, pp. 41–58. Springer, Heidelberg (2017). https://doi.org/10.1007/978-3-662-54365-8_3
Coron, J.-S., Lepoint, T., Tibouchi, M.: Practical multilinear maps over the integers. In: Canetti, R., Garay, J.A. (eds.) CRYPTO 2013. LNCS, vol. 8042, pp. 476–493. Springer, Heidelberg (2013). https://doi.org/10.1007/978-3-642-40041-4_26
Fernando, R., Rasmussen, P.M.R., Sahai, A.: Preventing CLT attacks on obfuscation with linear overhead. In: Takagi, T., Peyrin, T. (eds.) ASIACRYPT 2017. LNCS, vol. 10626, pp. 242–271. Springer, Cham (2017). https://doi.org/10.1007/978-3-319-70700-6_9
Garg, S., Gentry, C., Halevi, S.: Candidate multilinear maps from ideal lattices. In: Johansson, T., Nguyen, P.Q. (eds.) EUROCRYPT 2013. LNCS, vol. 7881, pp. 1–17. Springer, Heidelberg (2013). https://doi.org/10.1007/978-3-642-38348-9_1
Garg, S., Gentry, C., Halevi, S., Raykova, M., Sahai, A., Waters, B.: Candidate indistinguishability obfuscation and functional encryption for all circuits. In: 54th FOCS, pp. 40–49. IEEE Computer Society Press (2013)
Garg, S., Miles, E., Mukherjee, P., Sahai, A., Srinivasan, A., Zhandry, M.: Secure obfuscation in a weak multilinear map model. In: Hirt, M., Smith, A. (eds.) TCC 2016. LNCS, vol. 9986, pp. 241–268. Springer, Heidelberg (2016). https://doi.org/10.1007/978-3-662-53644-5_10
Garg, S., Srinivasan, A.: Single-Key to multi-key functional encryption with polynomial loss. In: Hirt, M., Smith, A. (eds.) TCC 2016. LNCS, vol. 9986, pp. 419–442. Springer, Heidelberg (2016). https://doi.org/10.1007/978-3-662-53644-5_16
Gentry, C., Gorbunov, S., Halevi, S.: Graph-induced multilinear maps from lattices. In: Dodis, Y., Nielsen, J.B. (eds.) TCC 2015. LNCS, vol. 9015, pp. 498–527. Springer, Heidelberg (2015). https://doi.org/10.1007/978-3-662-46497-7_20
Gentry, C., Peikert, C., Vaikuntanathan, V.: Trapdoors for hard lattices and new cryptographic constructions. In: 40th ACM STOC, pp. 197–206. ACM Press (2008)
Goldreich, O., Goldwasser, S., Micali, S.: How to construct random functions. J. ACM 33(4), 792–807 (1986)
Goldwasser, S., Kalai, Y.T., Popa, R.A., Vaikuntanathan, V., Zeldovich, N.: Reusable garbled circuits and succinct functional encryption. In: STOC 2013, pp. 555–564 (2013)
Gorbunov, S., Vaikuntanathan, V., Wee, H.: Functional encryption with bounded collusions via multi-party computation. In: Safavi-Naini, R., Canetti, R. (eds.) CRYPTO 2012. LNCS, vol. 7417, pp. 162–179. Springer, Heidelberg (2012). https://doi.org/10.1007/978-3-642-32009-5_11
Ishai, Y., Kushilevitz, E.: Randomizing polynomials: a new representation with applications to round-efficient secure computation. In: 41st FOCS, pp. 294–304 (2000)
Kiayias, A., Papadopoulos, S., Triandopoulos, N., Zacharias, T.: Delegatable pseudorandom functions and applications. In: ACM CCS 2013, pp. 669–684 (2013)
Kitagawa, F., Nishimaki, R., Tanaka, K.: Indistinguishability obfuscation for all circuits from secret-key functional encryption. Cryptology ePrint Archive, Report 2017/361 (2017)
Kitagawa, F., Nishimaki, R., Tanaka, K.: From single-key to collusion-resistant secret-key functional encryption by leveraging succinctness. Cryptology ePrint Archive, Report 2017/638 (2017)
Komargodski, I., Segev, G.: From minicrypt to obfustopia via private-key functional encryption. In: Coron, J.-S., Nielsen, J.B. (eds.) EUROCRYPT 2017. LNCS, vol. 10210, pp. 122–151. Springer, Cham (2017). https://doi.org/10.1007/978-3-319-56620-7_5
Li, B., Micciancio, D.: Compactness vs collusion resistance in functional encryption. In: Hirt, M., Smith, A. (eds.) TCC 2016. LNCS, vol. 9986, pp. 443–468. Springer, Heidelberg (2016). https://doi.org/10.1007/978-3-662-53644-5_17
Lin, H., Pass, R., Seth, K., Telang, S.: Indistinguishability obfuscation with non-trivial efficiency. In: Cheng, C.-M., Chung, K.-M., Persiano, G., Yang, B.-Y. (eds.) PKC 2016. LNCS, vol. 9615, pp. 447–462. Springer, Heidelberg (2016). https://doi.org/10.1007/978-3-662-49387-8_17
Lin, H., Tessaro, S.: Indistinguishability obfuscation from trilinear maps and block-wise local PRGs. Cryptology ePrint Archive, Report 2017/250 (2017)
Miles, E., Sahai, A., Zhandry, M.: Annihilation attacks for multilinear maps: cryptanalysis of indistinguishability obfuscation over GGH13. In: Robshaw, M., Katz, J. (eds.) CRYPTO 2016. LNCS, vol. 9815, pp. 629–658. Springer, Heidelberg (2016). https://doi.org/10.1007/978-3-662-53008-5_22
Naor, M., Reingold, O.: Number-theoretic constructions of efficient pseudo-random functions. J. ACM 51(2), 231–262 (2004)
O’Neill, A.: Definitional issues in functional encryption. Cryptology ePrint Archive, Report 2010/556 (2010)
Sahai, A., Seyalioglu, H.: Worry-free encryption: functional encryption with public keys. In: ACM CCS 2010, pp. 463–472. ACM Press (2010)
Sahai, A., Waters, B.: How to use indistinguishability obfuscation: deniable encryption, and more. In: 46th ACM STOC, pp. 475–484. ACM Press (2014)
Shamir, A.: Identity-based cryptosystems and signature schemes. In: Blakley, G.R., Chaum, D. (eds.) CRYPTO 1984. LNCS, vol. 196, pp. 47–53. Springer, Heidelberg (1985). https://doi.org/10.1007/3-540-39568-7_5
Yao, A. C.-C.: How to generate and exchange secrets (extended abstract). In: 27th FOCS, pp. 162–167. IEEE Computer Society Press, October 1986
Acknowledgement
The first and third authors are supported by NTT Secure Platform Laboratories, JST CREST JPMJCR14D6, JST OPERA, JSPS KAKENHI JP16H01705, JP16J10322, JP17H01695.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2018 International Association for Cryptologic Research
About this paper
Cite this paper
Kitagawa, F., Nishimaki, R., Tanaka, K. (2018). Simple and Generic Constructions of Succinct Functional Encryption. In: Abdalla, M., Dahab, R. (eds) Public-Key Cryptography – PKC 2018. PKC 2018. Lecture Notes in Computer Science(), vol 10770. Springer, Cham. https://doi.org/10.1007/978-3-319-76581-5_7
Download citation
DOI: https://doi.org/10.1007/978-3-319-76581-5_7
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-319-76580-8
Online ISBN: 978-3-319-76581-5
eBook Packages: Computer ScienceComputer Science (R0)











 be the complement of f, that is,
be the complement of f, that is,  . Moreover, we omit each randomness for
. Moreover, we omit each randomness for  into
into , where
, where  , so it is hard for
, so it is hard for 
 . We see that
. We see that  as the target identity to the challenger of
as the target identity to the challenger of  and
and 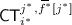 as the master public-key and target ciphertext of IBE.
as the master public-key and target ciphertext of IBE.  .
. .
. are not generated since the simulator of GC does not generate them. This is not a problem since for such labels, junk ciphertexts are generated as in
are not generated since the simulator of GC does not generate them. This is not a problem since for such labels, junk ciphertexts are generated as in 
