A New Strategy for Scattered Data Approximation Using Radial Basis Functions Respecting Points of Inflection

Abstract

The approximation of scattered data is known technique in computer science. We propose a new strategy for the placement of radial basis functions respecting points of inflection. The placement of radial basis functions has a great impact on the approximation quality. Due to this fact we propose a new strategy for the placement of radial basis functions with respect to the properties of approximated function, including the extreme and the inflection points. Our experimental results proved high quality of the proposed approach and high quality of the final approximation.

The research was supported by projects Czech Science Foundation (GACR) No. 17-05534S and partially by SGS 2019-016.

1 Introduction

The Radial basis functions (RBF) are well known technique for scattered data approximation in d-dimensional space in general. A significant advantage of the RBF application is its computational complexity, which is nearly independent of the problem dimensionality. The formulation is leading to a solution of a linear system of equations $\varvec{Ax}=\varvec{b}$. There exists several modifications and specifications of the RBF use for approximation. The method of RBF was originally introduced by Hardy in a highly influential paper in 1971 [8, 9]. The paper [8] presented an analytical method for representation of scattered data surfaces. The method computes the sum of quadric surfaces. The paper also stated the importance of the location of radial basis functions. This issue is solved by several papers. Some solutions are proposed by the papers [3, 15, 16], which use the regularization in the forward selection of radial basis function centers. The paper [31] presents an improvement for the problem with the behavior of RBF interpolants near boundaries. The paper [13] compares RBF approximations with different radial basis functions and different placement of those radial basis functions. However, all the radial basis functions are placed with some random or uniform distribution. A bit more sophisticated placement is presented in [14].

The selection of a shape parameter is another problem. Wrong selection of this parameter can lead to an ill-conditioned problem or to an inaccurate approximation. The selection of the best shape parameter is thus very important. Fornberg and Wright [5] presents an algorithm which avoids this difficulty, and which allows numerically stable computations of Multi-Quadric RBF interpolants for all shape parameter values. The paper [29] derives a range of suitable shape parameters using the analysis of the condition number of the system matrix, error of energy and irregularity of node distribution. A lot of approaches for selection of a good value of the shape parameter use some kind of random generator. Examples of this approaches are [2, 20]. The paper [1] proposes a genetic algorithm to determine a good variable shape parameter, however the algorithm is very slow.

2 Radial Basis Functions

The Radial basis function (RBF) is a technique for scattered data interpolation [17] and approximation [4, 27]. The RBF interpolation and approximation is computationally more expensive compared to interpolation and approximation methods that use an information about mesh connectivity, because input data are not ordered and there is no known relation between them, i.e. tessellation is not made. Although RBF has a higher computational cost, it can be used for d-dimensional problem solution in many applications, e.g. solution of partial differential equations [11, 33], image reconstruction [28], neural networks [7, 10, 32], vector fields [24, 26], GIS systems [12, 18], optics [19] etc. It should be noted that it does not require any triangulation or tessellation mesh in general. There is no need to know any connectivity of interpolation points, all points are tied up only with distances of each other. Using all these distances we can form the interpolation or approximation matrix, which will be shown later.

The RBF is a function whose value depends only on the distance from its center point. Due to the use of distance functions, the RBFs can be easily implemented to reconstruct the surface using scattered data in 2D, 3D or higher dimensional spaces. It should be noted that the RBF interpolation and approximation is not separable by dimension. For the readers reference a compressed description of the RBF is given in the following paragraphs, for details consider [25, 26].

Radial function interpolants have a helpful property of being invariant under all Euclidean transformations, i.e. translations, rotations and reflections. It does not matter whether we first compute the RBF interpolation function and then apply a Euclidean transformation, or if we first transform all the data and then compute the radial function interpolants. This is a result of the fact that Euclidean transformations are characterized by orthonormal transformation matrices and are therefore two-norm invariant. Radial basis functions can be divided into two groups according to their influence. The first group are “global” RBFs [21]. Application of global RBFs usually leads to ill-conditioned system, especially in the case of large data sets with a large span [13, 23]. An example of “global” RBF is the Gauss radial basis function.

$$\begin{aligned} \varphi (r) = e^{-\epsilon r^2} , \end{aligned}$$

(1)

where r is the distance of two points and $\epsilon$ is a shape parameter.

The “local” RBFs were introduced in [30] as compactly supported RBF (CSRBF) and satisfy the following condition:

$$\begin{aligned} \begin{aligned} \varphi (r)&=(1-r)^{q}_{+} P(r) \\&= {\left\{ \begin{array}{ll} (1-r)^{q} P(r) &{} \quad 0\le r \le 1 \\ 0 &{} \quad r>1 \end{array}\right. } \end{aligned} \end{aligned}$$

(2)

where P(r) is a polynomial function, r is the distance of two points and q is a parameter.

2.1 Radial Basis Function Approximation

RBF interpolation was originally introduced by [8] and is based on computing the distance of two points in any k-dimensional space. The interpolated value, and approximated value as well, is determined as (see [22]):

$$\begin{aligned} h(\varvec{x})= \sum \limits _{j=1}^M { \lambda _{j} \varphi (\left\| \varvec{x} - \varvec{\xi }_j \right\| ) } \end{aligned}$$

(3)

where $\lambda _{j}$ are weights of the RBFs, M is the number of the radial basis functions, $\varphi$ is the radial basis function and $\varvec{\xi }_j$ are centers of radial basis functions. For a given dataset of points with associated values, i.e. in the case of scalar values $\{\varvec{x}_i,h_i\}_{1}^{N}$, where $N \gg M$, the following overdetermined linear system of equations is obtained:

$$\begin{aligned} h_i = h(\varvec{x}_i)= \sum \limits _{j=1}^M { \lambda _{j} \varphi (\left\| \varvec{x}_i - \varvec{\xi }_j \right\| ) } \\ \nonumber \quad \text {for } \forall i \in \{ 1, \ldots , N \} \end{aligned}$$

(4)

where $\lambda _{j}$ are weights to be computed; see Fig. 1 for a visual interpretation of (3) or (4) for a $2\frac{1}{2}D$ function. Point in $2\frac{1}{2}D$ is a 2D point associated with a scalar value.

Equation (4) can be rewritten in a matrix form as

$$\begin{aligned} \varvec{A \lambda } = \varvec{h} , \end{aligned}$$

(5)

where $A_{ij}=\varphi (\left\| \varvec{x}_i - \varvec{\xi }_j \right\| )$ is the entry of the matrix in the $i-$th row and $j-$th column, the number of rows $N \gg M$, M is the number of unknown weights $\varvec{\lambda }=[\lambda _1,\ldots ,\lambda _M]^T$, i.e. a number of reference points, and $\varvec{h}=[h_1,\ldots ,h_N]^T$ is a vector of values in the given points. The presented system is overdetermined, i.e. the number of equations N is higher than the number of variables M. This linear system of equations can be solved by the least squares method (LSE) as

$$\begin{aligned} \varvec{A}^T\varvec{A\lambda }=\varvec{A}^T\varvec{h} , \end{aligned}$$

(6)

where the matrix $\varvec{A}^T\varvec{A}$ is symmetrical. Another possibility to solve the overdetermined system of linear equations $\varvec{A\lambda }=\varvec{h}$ is using the QR decomposition.

Fig. 1.

(from [26]).

Data values, the RBF collocation functions, the resulting interpolant

The RBF approximation can be done using “global” or “local” functions. When using “global” radial basis functions, the matrix $\varvec{A}$ will be full and ill conditioned in general. When using “local” radial basis functions, the matrix $\varvec{A}$ might be sparse, which can be beneficial when solving the overdetermined system of linear equations $\varvec{A \lambda } = \varvec{h}$.

3 Proposed Approach

We propose a new approach for scattered data approximation of $2\frac{1}{2}D$ functions using Radial basis functions with respecting inflection points of the function. Inflection points are computed from the discrete mesh and from curves given by implicit points. For a simplicity, the proposed approach is demonstrated on sampled regular grid.

The input $2\frac{1}{2}D$ function f(x, y) is for the sake of simplicity of evaluation sampled on a regular grid. For a general case neighbours have to be determined, e.g. by using a kd-tree. One important feature when computing the RBF approximation is the location of radial basis functions. We will show two main groups of locations, where the radial basis functions should be placed.

The first group are extreme points of the input data set. Most of the radial basis functions have the property of having its maximum at its center (we will use only those) and thus it is very suitable to place the radial basis functions at the locations of extreme points.

The second group are inflection points of the input data set. The inflection points are important as the surface crosses its tangent plane, i.e. the surface changes from being concave to being convex, or vice versa. The surface at those locations should be approximated as accurately as possible in order to maintain the main features of the surface.

3.1 Determination of Extreme Points

The local extreme points of the function f(x, y) can be either minimum or maximum, i.e.

$$ \begin{aligned} \displaystyle \frac{\partial f}{\partial x} = 0 \quad \& \quad \displaystyle \frac{\partial f}{\partial y} = 0 . \end{aligned}$$

(7)

The decision if a point is a local extreme point can be done using only surrounding points. In our case, i.e. regular grid, we use four surrounding points, i.e. point on the right, left, up and down. In general case, neighbor points need to be determined, e.g. using a kd-tree. If a point is a local maximum, then all four surrounding points must be lower. The same also applies to a local minimum, i.e all four surrounding points must be higher (Fig. 2).

Fig. 2.

Location of local extreme points. The values 1 and 8 (green) are local extremes, i.e. local minimum and local maximum. The value 4 (red) is not a local extreme as the four surrounding values are higher and smaller as well. (Color figure online)

The situation on the border of the input data set is a little bit different as we cannot use all four surrounding points, there will always be at least one missing. One solution is to skip the border of the input data set, however in this way we could omit some important extremes. Therefore, we determine the extremes from only three or two surrounding points.

3.2 Determination of Inflection Points

The second group of important locations for radial basis functions placement are inflection points, which forms actually curves of implicit points. The inflection points are located where the Gaussian curvature is equal zero. The Gaussian curvature for $2\frac{1}{2}D$ function f(x, y) is computed as

$$\begin{aligned} k_{gauss} = \displaystyle \frac{\displaystyle \frac{\partial ^2 f}{\partial x^2} \displaystyle \frac{\partial ^2 f}{\partial y^2} - \left( \displaystyle \frac{\partial ^2 f}{\partial x \partial y} \right) ^2}{\left( \left( \displaystyle \frac{\partial f}{\partial x} \right) ^2 + \left( \displaystyle \frac{\partial f}{\partial y} \right) ^2 + 1 \right) ^2} . \end{aligned}$$

(8)

The Gaussian curvature is equal zero when

$$\begin{aligned} \displaystyle \frac{\partial ^2 f}{\partial x^2} \displaystyle \frac{\partial ^2 f}{\partial y^2} - \left( \displaystyle \frac{\partial ^2 f}{\partial x \partial y} \right) ^2 = 0 . \end{aligned}$$

(9)

This formula is equivalent to the calculation using the Hessian matrix, i.e.

$$\begin{aligned} \begin{vmatrix} \displaystyle \frac{\partial ^2 f}{\partial x^2}&\displaystyle \frac{\partial ^2 f}{\partial x \partial y} \\ \displaystyle \frac{\partial ^2 f}{\partial y \partial x}&\displaystyle \frac{\partial ^2 f}{\partial y^2} \\ \end{vmatrix} = 0 . \end{aligned}$$

(10)

To find out the locations, where the Gaussian curvature, i.e. the determinant of Hessian matrix, is equal zero, we can sample the following function from the input discrete data set.

$$\begin{aligned} I(x, y) = \displaystyle \frac{\partial ^2 f}{\partial x^2} \displaystyle \frac{\partial ^2 f}{\partial y^2} - \left( \displaystyle \frac{\partial ^2 f}{\partial x \partial y} \right) ^2 . \end{aligned}$$

(11)

An application example of (11) can be seen in Fig. 3.

Now, we need to find out the locations, where this sampled function is equal zero. We again use the four surrounding points. If at least one is positive and at least one is negative, then there must be a zero value in between them. For the simplicity and to speed-up the calculation we consider the center point as the inflection point (see Figs. 3 and 4 for illustration).

Fig. 3.

Location of inflection points. The green positions with values 1 are considered as inflection points. The red position with value 4 is not an inflection point as all four surrounding values from (11) are positive. (Color figure online)

Fig. 4.

An example of $2\frac{1}{2}D$ function with the curves of inflection points. The red curve represents the location of inflection points calculated using (11). (Color figure online)

The resulting inflection points form a curve of implicit points. It is quite densely sampled. However, for the purpose of the RBF approximation, we can reduce the inflection points to obtain a specific number of inflection points or reduce them as the distance between the closest two is larger than some threshold value.

3.3 RBF Approximation with Respecting Inflection Points

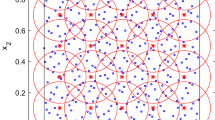
In the previous chapters, we presented the location of radial basis functions for $2\frac{1}{2}D$ function approximation. These locations are well placed to capture the main shape of the function f(x, y). However we should add some more additional points to cover the whole approximation space. One set of additional radial basis functions is placed on the border and in the corners. The last additional radial basis functions are placed at locations with Halton distribution [4]

$$\begin{aligned} Halton(p)_k = \sum _{i=0}^{\lfloor \log {_{p}k} \rfloor } {\displaystyle \frac{1}{p^{i+1}} \left( \left\lfloor \displaystyle \frac{k}{p^i} \right\rfloor \text {mod } p \right) } , \end{aligned}$$

(12)

where p is the prime number and k is the index of the calculated element, see Fig. 5 for an example of denerated points distribution. It is recommended to use different primes for x and y coordinate.

Fig. 5.

The example of $10^3$ Halton points. The Halton sequence was generated using two prime numbers [2, 3], i.e. for x coordinates a Halton sequence with the prime number 2 and for y coordinates a Halton sequence with the prime number 3.

Knowing all the positions of radial basis functions, we can compute the RBF approximation of the $2\frac{1}{2}D$ function. For the calculation we use the approach described in Sect. 2.1.

4 Experimental Results

In this section, we test the proposed approach for Radial basis function approximation. We tested the approach on all standard testing functions from [6]. In this paper we present the experimental results on only three testing functions, while the results for other testing functions are similar. The selected testing functions are the following

$$\begin{aligned} f_1(x, y) =&\displaystyle \frac{2}{11} \left( \sin {\left( 4x^2 + 4y^2 \right) } - \left( x+y \right) + \frac{5}{2} \right) \end{aligned}$$

(13)

$$\begin{aligned} f_2(x, y) =&\displaystyle \frac{3}{4}e^{-\frac{1}{4}((9x-2)^2+(9y-2)^2)} +\displaystyle \frac{3}{4}e^{-\frac{1}{49}(9x+1)^2-\frac{1}{10}(9y+1)^2} \nonumber \\&+\displaystyle \frac{1}{2}e^{-\frac{1}{4}(9x-7)^2-\frac{1}{4}(9y-3)^2} -\displaystyle \frac{1}{5}e^{-(9x-4)^2-(9y-7)^2}\end{aligned}$$

(14)

$$\begin{aligned} f_3(x, y) =&\displaystyle \frac{1}{9} \tanh {(9y-9x)} + 1 \end{aligned}$$

(15)

All testing functions $z = f(x, y)$ were “normalized” to the interval $x, y \in \langle -1, 1 \rangle$ and the “height” z to $\langle 0, 1 \rangle$ in order to easily compare the proposed approximation properties and approximation error for all testing functions and we used Gaussian radial basis function in all experiments.

$$\begin{aligned} \varphi (r) = e^{-\epsilon r^2} . \end{aligned}$$

(16)

Only some representative results are presented in this chapter. The visualization of (13) is in Fig. 6, the visualization of (14) is in Fig. 9 and the visualization of (15) is in Fig. 12.

The first function (13) is an inclined sine wave. This function contains inflection points formed in the elliptical shapes as can be seen in Fig. 8b. In the experiments we used the Gaussian radial basis function with a shape parameter $\epsilon =1$. The visualization of original function together with the RBF approximation is in Fig. 6. The approximation consists of 246 radial basis functions (78 are at locations of inflection points and extremes, 24 are at the borders and 144 are Halton points). It can be seen that the RBF approximation is visually identical to the original one. Also precision of approximation is very high, see Fig. 8a

Fig. 6.

The RBF approximation of $2\frac{1}{2}D$ function (13). The total number of RBF centers is 246 (red marks). (Color figure online)

To have a more closer look at the quality of RBF approximation, we computed the isocontours of the both original and approximated functions, see Fig. 7. Those isocontours are again visualy identical and cannot be seen any difference.

Fig. 7.

The comparison of function isocontours.

To compare the original and RBF approximated functions, we can compute the approximation error using the following formula for each point of evaluation.

$$\begin{aligned} Err = \vert f(x,y) - f_{RBF}(x,y) \vert , \end{aligned}$$

(17)

where f(x, y) is the value from input data set and $f_{RBF}(x,y)$ is the approximated value. Absolute error is used for evaluations data are normalized to $\langle -1, 1\rangle \times \langle -1, 1\rangle \times \langle 0, 1\rangle$ as described recently. If we compute the approximation error for all input sample points, then we can calculate the average approximation error, which is $2.37\cdot 10^{-4}$, and also the histogram of approximation error, see Fig. 8a. It can be seen that the most common approximation errors are quite low values below $0.4\%$. The higher approximation errors appear only few times. This proves a good properties of the approximation method.

Fig. 8.

The histogram (a) of approximation error for the function (13). The horizontal axis represents the absolute approximation error computed as (17). It should be noted, that the vertical axis is in logarithmic scale. The visualization (b) of all located inflection and extreme points.

Fig. 9.

The RBF approximation of $2\frac{1}{2}D$ function (14). The total number of RBF centers is 244 (red marks). (Color figure online)

Fig. 10.

The comparison of function isocontours.

The next testing function (14) is visualized together with the RBF approximation in Fig. 9. This function consists of four hills and the RBF approximation preserves the main shape. The only small difference is at the borders, which can be seen in more details in Fig. 10. The Gauss function with the shape parameter $\epsilon =26$ was used as radial basis function.

The average approximation error is $2.75\cdot 10^{-3}$ and the distribution of the approximation error can be seen in the histogram in Fig. 11.

Fig. 11.

The histogram of approximation error for the function (14). The horizontal axis represents the absolute approximation error computed as (17). It should be noted, that the vertical axis is in logarithmic scale.

Fig. 12.

The RBF approximation of $2\frac{1}{2}D$ function (15). The total number of RBF centers is 244 (red marks). (Color figure online)

Fig. 13.

The visualization of approximated function isocontours (a). The visualization of approximation error as isocontours plot (b), please note that the average approximation error is $1.22\cdot 10^{-2}$.

The last function (15) for testing the proposed RBF approximation is visualized in Fig. 12a. This function is quite exceptional, because it has a sharp cliff on $x=y$. Such sharp cliffs are always very hard to approximate using the RBF. However using the proposed distribution of the radial basis functions, we are able to approximate the sharp cliff quite well, see Fig. 12b. The problem, that comes up, is the wavy surface for $y > x$, see more details in Fig. 13. The Gauss function with the shape parameter $\epsilon =25$ was used as the radial basis function.

The average approximation error for this specific function is $1.22\cdot 10^{-2}$. This result is quite positive as the function is very hard to approximate using the RBF approximation technique. The histogram of the approximation error is visualized in Fig. 14.

Fig. 14.

The histogram of approximation error for the function (15). The horizontal axis represents the absolute approximation error computed as (17). It should be noted, that the vertical axis is in logarithmic scale.

5 Conclusion

We presented a new approach for approximation of $2\frac{1}{2}D$ scattered data using Radial basis functions respecting inflection points in the given data set. The RBF approximation uses the properties of the input data set, namely the extreme and the inflection points to determine the location of radial basis functions. This sophisticated placement of radial basis functions significantly improves the quality of the RBF approximation. It reduces the needed number of radial basis functions and thus creates even more compressed RBF approximation, too.

In future, the proposed approach is to be extended to approximate $3\frac{1}{2}D$ scattered data, while utilizing the properties of the input data set for the optimal placement of radial basis functions. Also efficient finding a shape parameters is to be explored.