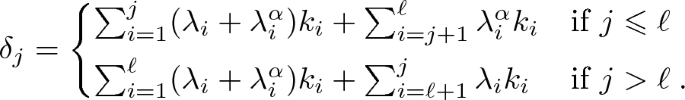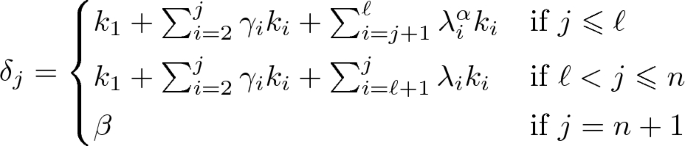bison Instantiating the Whitened Swap-Or-Not Construction

Abstract

We give the first practical instance – bison – of the Whitened Swap-Or-Not construction. After clarifying inherent limitations of the construction, we point out that this way of building block ciphers allows easy and very strong arguments against differential attacks.

1 Introduction

Block ciphers are among the most important cryptographic primitives as they are at the core responsible for a large fraction of all our data that is encrypted. Depending on the mode of operation (or used construction), a block cipher can be turned into an encryption function, a hash-function, a message authentication code or an authenticated encryption function.

Due to their importance, it is not surprising that block ciphers are also among the best understood primitives. In particular the Advanced Encryption Standard (AES) [2] has been scrutinized by cryptanalysts ever since its development in 1998 [19] without any significant security threat discovered for the full cipher (see e.g. [6, 7, 23, 26,27,28,29]).

The overall structure of AES, being built on several (round)-permutations interleaved with a (binary) addition of round keys is often referred to as key-alternating cipher and is depicted in Fig. 1.

Fig. 1.

Key-alternating construction for r rounds, using unkeyed round permutations $R_1$ to $R_r$. In practical instantiations, the round keys $k_i$ are typically derived from a master key by some key schedule.

The first cipher following this approach was, to the best of our knowledge, the cipher MMB [17], while the name key-alternating cipher first appears in [20] and in the book describing the design of the AES [21]. Nowadays many secure ciphers follow this construction.

Interestingly, besides its overwhelming use in practice and the intense cryptanalytic efforts spent to understand its practical security, the generic (or idealized) security of key-alternating ciphers has not been investigated until 2012. Here, generic or idealized security refers to the setting where the round functions $R_i$ are modeled as random permutations. An (computational unbounded) attacker is given access to those round functions via oracle queries and additional oracle access to either the block cipher or a random permutation. The goal of the attacker is to tell apart those two cases. As any attack in this setting is obviously independent of any particular structure of the round function, those attacks are generic for all key-alternating ciphers. In this setting, the construction behind key-alternating ciphers is referred to as the iterated Even-Mansour construction. Indeed, the Even-Mansour cipher [25] can be seen as a one-round version of the key-alternating cipher where the round function is a random permutation.

The first result on the iterated Even-Mansour construction (basically focusing on the two-round version) was given in [10]. Since then, quite a lot of follow-up papers, e.g. [3, 30, 32, 38], managed to improve and generalize this initial result significantly. In particular, [15] managed to give a tight security bound for any number of rounds. Informally, for breaking the r-round Even-Mansour construction, any attacker needs to make roughly $2^{\frac{r}{r+1}n}$ oracle queries.

While this bound can be proven tight for the iterated Even-Mansour construction, it is unsatisfactory for two reasons. First, one might hope to get better security bounds with different constructions and second one might hope to lower the requirement of relying on r random permutations.

Motivated by this theoretical defect and the importance of encrypting small domains with full security (see e.g. [42]), researchers started to investigate alternative ways to construct block ciphers with the highest possible security level under minimal assumptions in ideal models. The most interesting result along those lines is the construction by Tessaro [48]. His construction is based on the Swap-or-Not construction by [31], which was designed for the setting where the component functions are secret. Instead of being based on random permutations, this construction requires only a set of random (Boolean) functions. Tessaro’s construction, coined Whitened Swap-Or-Not (WSN for short), requires only two public random (Boolean) functions $f_i$ with n-bit input, and can be proven to achieve full security, see Sect. 2 for more details.

However, and this is the main motivation for our work, no instance of this construction is known. This situation is in sharp contrast to the case of the iterated Even-Mansour construction, where many secure instances are known for a long time already, as discussed above.

Without such a concrete instance, the framework of [48] remains of no avail. As soon as one wants to use the framework in any way, one fundamentally has to instantiate the Boolean functions modeled as ideal functionalities by efficiently computable functions. Clearly, the above mentioned bound in the ideal model does not say anything about any concrete instance. Tessaro phrases this situation as follows:

Heuristically, however, one hopes for even more: Namely, that under a careful implementation of the underlying component, the construction retains the promised security level [48].

There has actually been one instance of the previous construction [31], but this has been broken almost instantaneously and completely, as parts of the encryption function were actually linear, see [52]. This failure to securely instantiate the construction points to an important hurdle. Namely, proving the generic bounds and analyzing the security of an instance are technically very different tasks. The security of any block cipher is, with the current state of knowledge, always the security against known attacks. In particular, when designing any concrete block cipher, one has to argue why linear and differential attacks do not threaten the construction.

Our Contribution

Consequently, in this paper we investigate the important, but so far overlooked, aspect of instantiating the WSN construction with a practical secure instance. Practical secure meaning, just like in the case of AES, that the block cipher resists all known attacks. We denote this instance as (for Bent whItened Swap Or Not). Our insights presented here are twofold.

First, we derive some inherent restrictions on the choice of the round function $f_i$. In a nutshell, we show that $f_i$ has to be rather strong, in the sense that its output bit has to basically depend on all input bits. Moreover, we show that using less than n rounds will always result in an insecure construction. Those, from a cryptanalytic perspective rather obvious, results are presented in Sect. 3. Again, but from a different angle, this situation is in sharp contrast to key-alternating ciphers. In the case of key-alternating ciphers, even with a rather small number of rounds (e.g. ten in the case of AES-128) and rather weak round functions (in case of the AES round function any output bit depends on 32 input bits only and the whole round function decomposes into four parallel functions on 32 bits each) we get ciphers that provide, to the best of our knowledge today and after a significant amount of cryptanalysis, full security.

Second, despite those restrictions of the WSN construction, that have significant impact on the performance of any instance, there are very positive aspects of the WSN construction as well. In Sect. 4, we first define a family of WSN instances which fulfill our initial restrictions.

As we will show in detail, this allows to argue very convincingly that our instance is secure against differential attacks. Indeed, under standard assumptions, we can show that the probability of any (non-trivial) differential is upper bounded by $2^{-n+1}$ where $n$ is the block size, a value that is close to the ideal case. This significantly improves upon what is the state of the art for key-alternating ciphers. Deriving useful bounds on differentials is notoriously hard and normally one therefore has to restrict to bounding the probability of differential characteristics only. Our results for differential cryptanalysis can be of independent interest in the analysis of maximally unbalanced Feistel networks or nonlinear feedback shift registers.

We specify our concrete instance as a family of block ciphers for varying input length in Sect. 5. In our instance, we attach importance to simplicity and mathematical clarity. It is making use of bent functions, i.e. maximally non-linear Boolean functions, for instantiating f and linear feedback shift registers (lfsrs) for generating the round keys. Another advantage of bison is that it defines a whole family of block ciphers, one for any odd block size. In particular it allows the straightforward definition of small scale variants to be used for experiments.

Finally we discuss various other attacks and argue why they do not pose a threat for bison in Sect. 6. Particularly the discussion on algebraic attacks might be of independent interest. For this we analyse the growth of the algebraic degree over the rounds. In contrast to what we intuitively expect – an exponential growth (until a certain threshold) as in the case for SPNs [11] – the degree of the WSN construction grows linearly in the degree of the round function $f_i$. This result can also be applied in the analysis of maximally unbalanced Feistel networks or nonlinear feedback shift registers.

Related Work

The first cipher, a Feistel structure, that allowed similarly strong arguments against differential attacks was presented by Nyberg and Knudsen [45], see also [44] for a nice survey on the topic. This cipher was named CRADIC, as Cipher Resistant Against DIfferential Cryptanalysis but is often simply referenced as the KN cipher. However, the cipher has been broken quickly afterwards, with the invention of interpolation attacks [34]. Another, technically very different approach to get strong results on resistance against attacks we would like to mention is the decorrelation theory [51]. Interestingly, both previous approaches rely rather on one strong component, i.e. round function, to ensure security, while the WSN approach, and in particular bison, gains its resistance against differential attacks step by step.

Regarding the analysis of differentials, extensive efforts have been expended to evaluate the MEDP/MELP of SPN ciphers, and in particular of the AES. Some remarkable results were published by [46] and then subsequently improved by [35] with a sophisticated pruning algorithm. Interestingly, further work by [22] and later by [13] revealed that such bounds are not invariant under affine transformations – an equivalence notion often exploited for classification of S-boxes when studying their strength against differential cryptanalysis. All these works stress out how difficult it is to evaluate the MEDP/MELP of SPNs, even for a small number of rounds. On the contrary, and as we are going to elaborate in the remaining of this paper, computing the MEDP of bison is rather straightforward and independent of the exact details of the components. This can be compared to the wide trail strategy that, making use of the branch number and the superbox argument, allows bounding the probability of any differential characteristic for a large class of SPNs. Our arguments allow to bound the differential probability for a large class of WSN instances.

2 Preliminaries

We briefly recall the Whitened Swap-or-Not construction, recapitulate properties of Boolean functions and shortly cover differential and linear cryptanalysis. We denote by $\mathbb {F}_2$ the finite field with two elements and by $\mathbb {F}_2^n$ the n-dimensional vector space over $\mathbb {F}_2$, i.e. the set of all n-bit vectors with a bitwise xor as the addition.

2.1 Whitened Swap-or-Not

The WSN is defined as follows. Given two round keys $k_i$, $w_i$, the ith round $R_{k_i,w_i}$ computes

where $f_{0,1} : \mathbb {F}_2^n \rightarrow \mathbb {F}_2$ are modeled as two ideal random functions, the $\max$ function returns the lexicographic biggest value in the input set, and $+$ denotes the addition in $\mathbb {F}_2$ (the bitwise xor). The index b(i) equals zero for the first half of the rounds and one for the second half (see Fig. 2 for a graphical overview of the encryption process).

In the remainder of the paper, we denote by $E_{k,w}^r(x)$ the application of r rounds of the construction to the input x with round keys $k_i$ and $w_i$ derived from the master key (k, w). Every round is involutory, thus for decryption one only has to reverse the order of the round keys.

Fig. 2.

Schematic view of the WSN construction.

Note that the usage of the maximum function is not decisive but that it can be replaced by any function $\varPhi _k$ that returns a unique representative of the set , see [48]. In other words it can be replaced by any function such that $\varPhi _k(x) = \varPhi _k(y)$ if and only if $y \in \{x,x+k\}$.

The main result given by Tessaro on the security of the WSN is the following:

Proposition 1

(Security of the WSN (Informal) [48]). The WSN construction is $(2^{n-\mathcal {O}(\log n)}, 2^{n-\mathcal {O}(1)} )$-secure for ${\mathcal {O}(n)}$ rounds.

Thus, any adversary trying to distinguish the WSN construction from a random permutation and making at most $2^{n-\mathcal {O}(\log n)}$ queries to the block cipher and $2^{n-\mathcal {O}(1)}$ queries to the underlying function has negligible advantage. Here, the round keys are modeled as independent and uniformly distributed random variables.

2.2 Boolean Functions

A Boolean function is defined as a function f mapping n bits to one bit. Any Boolean function

$$\begin{aligned} f: \mathbb {F}_2^n\rightarrow \mathbb {F}_2 \end{aligned}$$

can be uniquely expressed by its algebraic normal form (ANF), i.e. as a (reduced) multivariate polynomial with n variables $x_0,\dots , x_{n-1}$. For $u\in \mathbb {F}_2^n$ we denote

$$\begin{aligned} x^u= \prod _{i=0}^{n-1} x_i^{u_i}. \end{aligned}$$

The ANF of f can be expressed as

$$\begin{aligned} f(x) = \sum _{u \in \mathbb {F}_2^n} \lambda _u x^u \end{aligned}$$

for suitable choices of $\lambda _u \in \mathbb {F}_2$. The degree of f, denoted by $\deg (f)$ is defined as the maximal weight of a monomial present in the ANF of f. That is

$$\begin{aligned} \deg (f)=\max \{ {{\,\mathrm{wt}\,}}(u) \ |\ u \in \mathbb {F}_2^n \text { such that } \lambda _u \ne 0 \}. \end{aligned}$$

In the context of symmetric cryptography, the differential and linear behavior of a Boolean function play an important role.

The derivative of a function f in direction $\alpha$ is defined as . Informally, studying the behavior of this derivative is at the core of differential cryptanalysis. If we generalize to the derivative of a vectorial Boolean function $F : \mathbb {F}_2^n \rightarrow \mathbb {F}_2^n$, we can additionally specify an output difference $\beta$. The differential distribution table (ddt) captures the distribution of all possible derivatives; its entries are

where we leave out the subscript, if it is clear from the context. Note that $\alpha$ is usually referred to as the input difference and $\beta$ as the output difference.

In a similar way, we can approach the linear behavior of a Boolean function, that is its similarity to any linear function. The Fourier coefficient of a function $f : \mathbb {F}_2^n \rightarrow \mathbb {F}_2$, which is defined as

is a very useful way to measure this similarity. Here, the notation denotes the inner product, defined as . Recall that any affine Boolean function can be written as for some fixed $\alpha \in \mathbb {F}_2^n$ and a constant $c \in \mathbb {F}_2$. In particular, it follows that any such affine function has one Fourier coefficient equal to $\pm 2^n$. More generally, the nonlinearity of f, defined as , measures the minimal Hamming-distance of f to the set of all affine functions.

Analogously to the ddt, for a vectorial Boolean function $F : \mathbb {F}_2^n \rightarrow \mathbb {F}_2^n$, we define

and the linear approximation table (lat) contains the Fourier coefficients

Again we leave out the subscript, if it is clear from the context. Here $\alpha$ is usually referred to as the input mask and $\beta$ as the output mask. Another representation that is sometimes preferred is the correlation matrix that in a similar way contains the correlation values for all possible linear approximations, see [18]. The correlation values are simply scaled versions of the Fourier coefficients, i.e.

The advantage of the correlation matrix notation is that the correlation matrix of a composition of functions is nothing but the product of the corresponding matrices. For the linear approximation table, additional scaling is required.

Bent Functions. As they will play an important role in our design of bison, we recall the basic facts of bent functions. Boolean functions on an even number n of input bits that achieve the highest possible nonlinearity of $2^{n} - 2^{\frac{n}{2}}$ are called bent. Bent functions have been introduced by Rothaus [47] and studied ever since, see also [14, Section 8.6]. Even so bent functions achieve the highest possible nonlinearity, their direct use in symmetric cryptography is so far very limited. This is mainly due to the fact that bent functions are not balanced, i.e. the distribution of zeros and ones is (slightly) biased.

Using Parseval’s equality, it is easy to see that a function is bent if and only if all its Fourier coefficients are $\pm 2^{\frac{n}{2}}$. Moreover, an alternative classification that will be of importance for bison, is that a function is bent if and only if all (non-trivial) derivatives $\varDelta _\alpha (f)$ are balanced Boolean functions [41].

While there are many different primary and secondary constructions¹ of bent functions known, for simplicity and for the sake of ease of implementation, we decided to focus on the simplest known bent functions which we recall next, see also [14, Section 6.2].

Lemma 1

([24]). Let $n = 2 m$ be an even integer. The function

is a quadratic bent function. Moreover, any quadratic bent function is affine equivalent to f.

2.3 Differential and Linear Cryptanalysis

The two most important attacks on symmetric primitives are differential and linear cryptanalysis, respectively developed by Biham and Shamir [5] and by Matsui [40] for the analysis of the Data Encryption Standard. The general idea for both is to find a non-random characteristic in the differential, resp/linear, behavior of the scheme under inspection. Such a property can then be used as a distinguisher between the cipher and a random permutation and in many cases leads to key-recovery attacks.

It is inherently hard to compute these properties for the whole function, thus one typically exploits the special structure of the cipher. For round-based block ciphers one usually makes use of linear and differential characteristics that specify not only the input and output masks (resp/differences) but also all intermediate masks after the single rounds.

In the case of differential cryptanalysis, an r-round characteristic $\delta$ is defined by $(r+1)$ differences

$$\begin{aligned} \delta = (\delta _0,\ldots ,\delta _r) \in \mathbb {F}_2^{(r+1)n}. \end{aligned}$$

For so-called Markov ciphers and assuming the independence of round keys, we can compute the probability of a characteristic averaged over all round-key sequences:

where the encryption iterates the round function F for r rounds. Moreover we usually assume the hypothesis of stochastic equivalence introduced by Lai et al. [37], stating that the actual probability for any fixed round key equals the average.

In contrast to the normal characteristic that defines the exact differences before and after each round, a differential takes every possible intermediate differences into account and fixes only the overall input and output differences (which are the two values an attacker can typically control).

However, while bounding the average probability of a differential characteristic is easily possible for many ciphers (using in particular the wide-trail strategy introduced in [16]), bounding the average probability of a differential, which is denoted as the expected differential probability (EDP), is not. Nevertheless, some effort was spent to prove bounds on the maximum EDP (MEDP) for two rounds of some key-alternating ciphers [13, 21, 33, 46].

Similarly, for linear cryptanalysis, an r-round characteristic (also called trail or path) for a round function F is defined by $(r+1)$ masks

$$\begin{aligned} \theta =(\theta _0,\dots ,\theta _r) \in \mathbb {F}_2^{(r+1)n} \end{aligned}$$

and its correlation is defined as

$$\begin{aligned} {{\,\mathrm{\mathbf {cor}}\,}}_F(\theta ) := \prod _{i=0}^{r-1} {{\,\mathrm{\mathbf {cor}}\,}}_F(\theta _i,\theta _{i+1}) = \prod _{i=0}^{r-1} \frac{{\widehat{F}}(\theta _i,\theta _{i+1})}{2^n} \end{aligned}$$

and it can be shown that the correlation of a composition can be computed as the sum over the trail correlations. More precisely,

$$\begin{aligned} {{\,\mathrm{\mathbf {cor}}\,}}_{E_{k}^r}(\alpha ,\beta ) = \sum _{\genfrac{}{}{0.0pt}{}{\theta }{\theta _0 = \alpha , \theta _r = \beta }} {{\,\mathrm{\mathbf {cor}}\,}}_F(\theta ), \end{aligned}$$

(1)

where the encryption $E_{k}^r$ iterates the round function F for r rounds.

This is referred to as the linear hull (see [43]). While not visible in order to simplify notation, the terms in Eq. (1) are actually key dependent and thus for some keys they either could cancel out or amplify the overall correlation. For more background, we refer to e.g. [9] and [36]. For a key-alternating cipher with independent round keys, the average over all round-key sequences of the correlation ${{\,\mathrm{\mathbf {cor}}\,}}_{E_{k}^r}(\alpha ,\beta )$ is zero for any pair of nonzero masks $(\alpha ,\beta )$ (see e.g. [21, Section 7.9]). Then, the most relevant parameter of the distribution is its variance, which corresponds to the average square correlation, and is called the expected linear potential. Again, bounding the ELP is out of reach for virtually any practical cipher, while for bounding the correlation of a single trail, one can again use the wide-trail strategy mentioned above. Upper bounds for the MELP of two rounds of AES are also given in [13, 33, 46].

Finally we would like to note that the round keys in an actual block cipher instance are basically never independent and identically distributed over the full key space, but instead derived from a key schedule, rendering the above assumption plain wrong. While the influence of key schedules is a crucially understudied topic and for specific instances strange effects can occur, see [1, 36], the above assumption are seen as valid heuristics for most block ciphers.

3 Inherent Restrictions

In this section we point out two inherent restrictions on any practical secure instance, i.e. generic for the WSN construction. Those restrictions result in general conditions on both the minimal number of rounds to be used and general properties of the round functions $f_{b(i)}$. In particular, those insights are taken into account for bison. While these restrictions are rather obvious from a cryptanalytic point of view, they have a severe impact on the performance of any concrete instance. We discuss performance in more detail in the full version [12, Section 7].

3.1 Number of Rounds

As in every round of the cipher, we simply add (or not) the current round key $k_i$, the ciphertext can always be expressed as the addition of the plaintext and a (message dependent) linear combination of all round keys $k_i$. The simple but important observation to be made here is that, as long as the round keys do not span the full space, the block cipher is easily attackable.

Phrased in terms of linear cryptanalysis we start with the following lemma.

Lemma 2

For any number of rounds $r<n$ there exists an element $u \in \mathbb {F}_2^n\setminus \{0\}$ such that

$$\begin{aligned} {\widehat{E_{k,w}^r}}(u,u)=2^n, \end{aligned}$$

that is the equation

holds for all $x \in \mathbb {F}_2^n$.

Proof

Let $k_1, \dots , k_{r}$ be the round keys derived from k and denote by

the dual space of the space spanned by the round keys, i.e.

As $r<n$ by assumption, the dimension of is smaller than n and thus . Therefore, U contains a non-zero element

and it holds that

(2)

Even more importantly, this observation leads directly to a known plaintext attack with very low data-complexity. Given a set of t plaintext/ciphertext $(p_i,c_i)$ pairs, an attacker simply computes

Given $t > r$ slightly more pairs than rounds, and assuming that $p_i+c_i$ is uniformly distributed in (otherwise the attack only gets even stronger)² implies that

with high probability and V can be efficiently computed. Furthermore, as above is at most r, we have $V^{\perp } \ne \{0\}$. Given any $u \ne 0$ in $V^\perp$ allows to compute one bit of information on the plaintext given only the ciphertext and particularly distinguish the cipher from a random permutation in a chosen-plaintext setting efficiently.

A similar argument shows the following:

Lemma 3

For any number of rounds r smaller than $2n-3$ there exist nonzero $\alpha$ and $\beta$, such that

$$\begin{aligned} \widehat{E_{k,w}^r}(\alpha , \beta ) = 0 \end{aligned}$$

Proof

We restrict to the case $r \geqslant n$ as otherwise the statement follows directly from the lemma above. Indeed, from Parseval equality, the fact that $\widehat{E_{k,w}^r}(\alpha , \alpha )=2^n$ implies that $\widehat{E_{k,w}^r}(\alpha , \beta )=0$ for all $\beta \ne \alpha$. Let $k_1, \ldots , k_{r}$ be the round keys derived from k and choose non-zero elements $\alpha \ne \beta$ such that

Note that, as $r \le 2n-3$ by assumption such elements always exist. Next, we split the encryption function in two parts, the first $n-2$ rounds $E_1$ and the remaining $r-(n-2)<n$ rounds $E_2$, i.e.

$$\begin{aligned} E_{k,w}^r = E_2 \circ E_1. \end{aligned}$$

We can compute the Fourier coefficient of $E_{k,w}^r$ as

$$\begin{aligned} {\widehat{E_{k,w}^r}}(\alpha ,\beta )=\sum _{\gamma \in \mathbb {F}_2^n} \frac{{\widehat{E_1}}(\alpha ,\gamma )}{2^n} \cdot \frac{{\widehat{E_2}}(\gamma ,\beta )}{2^n}. \end{aligned}$$

Now, the above lemma and the choices of $\alpha$ and $\beta$ imply that ${\widehat{E_1}}(\alpha ,\gamma ) = 0$ for $\gamma \ne \alpha$ and ${\widehat{E_2}}(\gamma ,\beta ) = 0$ for $\gamma \ne \beta$. Recalling that $\alpha \ne \beta$ by construction concludes the proof.

However, as the masks $\alpha$ and $\beta$ depend on the key, and unlike above there does not seem to be an efficient way to compute those, we do not see a direct way to use this observation for an attack.

Summarizing the observations above, we get the following conclusion:

Rationale 1

Any practical instance must iterate at least n rounds. Furthermore, it is beneficial if any set of n consecutive round keys are linearly independent.³

After having derived basic bounds on the number of rounds for any secure instance, we move on to criteria on the round function itself.

3.2 Round Function

Here, we investigate a very basic criterion on the round function, namely dependency on all input bits. Given the Boolean functions $f_{b(i)}:\mathbb {F}_2^n \rightarrow \mathbb {F}_2$ used in the round function of $E_{k,w}^r$, an important question is, if it is necessary that the output bit of $f_{b(i)}$ has to depend on all input bits. It turns out that this is indeed strictly necessary for any secure instance, as summarized in the next rational.

Rationale 2

For a practical instance, the functions $f_{b(i)}$ has to depend on all bits. Even more, for any $\delta \in \mathbb {F}_2^n$ the probability of

$$\begin{aligned} f_{b(i)}(x)=f_{b(i)}(x+\delta ) \end{aligned}$$

should be close to $\frac{1}{2}$.

Due to page constraints, we refer to [12, Lemma 4] for more details. It is worth noticing that the analysis leading to Rationale 2 applies to the original round function. However, as pointed out in [49, Section 3.1], in the definition of the round function, we can replace the function

by any function $\varPhi _k$ such that $\varPhi _k(x)=\varPhi _k(x+k)$ for all $x$. While the following sections will focus on the case when $\varPhi _k$ is linear, we will prove that Rationale 2 is also valid in this other setting.

Again, this should be compared to key-alternating ciphers, where usually not all output bits of a single round function depend on all input bits. For example for AES any output bit after one round depends only on 32 input bits and for Present any output bit only depends on 4 input bits. However, while for key-alternating ciphers this does not seem to be problematic, and indeed allows rather weak round functions to result in a secure scheme, for the WSN construction the situation is very different.

Before specifying our exact instance, we want to discuss differential cryptanalysis of a broader family of instances.

4 Differential Cryptanalysis of bison-Like Instances

We coin an instance of the WSN construction “bison-like”, if it iterates at least n rounds with linearly independent round keys $k_1, \ldots , k_n$ and applies Boolean functions $f_{b(i)}$. As explained in [49, Section 3.1], in order to enable decryption it is required that the Boolean functions $f_{b(i)}$ return the same result for both x and $x+k$. In the original proposition by Tessaro, this is achieved by using the $\max$ function in the definition of the round function. Using this technique reduces the number of possible inputs for the $f_{b(i)}$ to $2^{n-1}$. To simplify the analysis and to ease notation, we replace the $\max$ function with a linear function $\varPhi _k : \mathbb {F}_2^n \rightarrow \mathbb {F}_2^{n-1}$ with $\ker (\varPhi _k)=\{0,k\}$. From now on, we assume that any bison-like instance uses such a $\varPhi _k$ instead of the $\max$ function. The corresponding round function has then the following form

(3)

With the above conditions, any bison-like instance of the WSN construction is resistant to differential cryptanalysis, as we show in the remainder of this section.

For our analysis, we make two standard assumptions in symmetric cryptanalysis as mentioned above: the independence of whitening round keys $w_i$ and the hypothesis of stochastic equivalence with respect to these round keys. That is, we assume round keys $w_i$ to be independently uniformly drawn and the resulting EDP to equal the differential probabilities averaged over all $w$. Thus, the keys $w_i$ act very much like the round key for a key-alternating cipher with respect to the probabilities of characteristics. We further back up this intuition by practical experiments (see Sect. 6.3 and [12, Appendix B]). For the round keys $k_i$ we do not have to make such assumptions.

We first discuss the simple case of differential behaviour for one round only and then move up to an arbitrary number of rounds and devise the number of possible output differences and their probabilities.

4.1 From One-Round Differential Characteristics

Looking only at one round, we can compute the ddt explicitly:

Proposition 2

Let $R_{k_i,w_i} : \mathbb {F}_2^n \rightarrow \mathbb {F}_2^n$ be the WSN round function as in Eq. (3). Then its ddt consists of the entries

(4)

Most notably, if $f$ is bent, we have

Proof

We have to count the number of solutions of $R(x) + R(x + \alpha ) = \beta$:

Since $f$ takes its values in $\mathbb {F}_2$, the only output differences $\beta$ such that $\textsc {ddt}_{R}[\alpha ,\beta ]$ may differ from $0$ are $\beta =\alpha$ and $\beta =\alpha +k$. When $\beta =\alpha$, we have

Similarly,

Most notably, when $\alpha \in \{0,k\}$, $\widehat{\varDelta _{\varPhi _k(\alpha )}(f)}(0) = 2^{n-1}$. Moreover, when $f$ is bent, $\widehat{\varDelta _{\varPhi _k(\alpha )}(f)}(0) = 2^{n-2}$ for all other values of $\alpha$.

4.2 To Differentials over More Rounds

As previously explained, it is possible to estimate the probability of a differential characteristic over several rounds, averaged over the round keys, when the cipher is a Markov cipher. We now show that this assumption holds for any bison-like instance of the WSN construction.

Lemma 4

Let $R_{k,w} : \mathbb {F}_2^n \rightarrow \mathbb {F}_2^n$ be the WSN round function as in Eq. (3). For any fixed $k \in \mathbb {F}_2^n$ and any differential $(\alpha , \beta ) \in \mathbb {F}_2^n \times \mathbb {F}_2^n$, we have that

$$\begin{aligned} {{\,\mathrm{Pr}\,}}_w \left[ R_{k,w}(x+\alpha ) + R_{k,w}(x) =\beta \right] \end{aligned}$$

is independent of $x$. More precisely

$$\begin{aligned} {{\,\mathrm{Pr}\,}}_w \left[ R_{k,w}(x+\alpha ) + R_{k,w}(x) =\beta \right] = {{\,\mathrm{Pr}\,}}_x \left[ R_{k,w}(x+\alpha ) + R_{k,w}(x) =\beta \right] \;. \end{aligned}$$

Proof

We have

where $\textsf {Supp}(g)$ denotes the support of a Boolean function $g$, i.e., the values $x$ for which $g(x)=1$. Clearly, the cardinality of this set does not depend on $x$. Moreover, this cardinality, divided by $2^{n-1}$, corresponds to the value of

$$\begin{aligned} {{\,\mathrm{Pr}\,}}_x \left[ R_{k,w}(x+\alpha ) + R_{k,w}(x) =\beta \right] \end{aligned}$$

computed in the previous proposition.

By induction on the number of rounds, we then directly deduce that any bison-like instance of the WSN construction is a Markov cipher in the sense of the following corollary.

Corollary 1

Let $E_{k,w}^i$ denote $i$ rounds of a bison-like instance of the WSN construction with round function $R_{k_i,w_i}$. For any number of rounds $r$ and any round keys $(k_1, \ldots , k_r)$, the probability of an $r$-round characteristic $\delta$ satisfies

For many ciphers several differential characteristics can cluster in a differential over more rounds. This is the main reason why bounding the probability of differentials is usually very difficult if possible at all. For bison-like instances the situation is much nicer; we can actually compute the EDP, i.e., the probabilities of the differentials averaged over all whitening key sequences $(w_1, \ldots , w_r)$. This comes from the fact that any differential for less than n rounds contains at most one differential characteristic with non-zero probability. To understand this behavior, let us start by analyzing the EDP (averaged over the $w_i$) and by determining the number of possible output differences.

In the following, we assume that the input difference $\alpha$ is fixed, and we calculate the number of possible output differences. We show that this quantity depends on the relation between $\alpha$ and the $k_i$.

Lemma 5

Let us consider $r$ rounds of a bison-like instance of the WSN construction with round function involving Boolean functions $f_{b(i)}$ having no (non-trivial) constant derivative. Assume that the first $n$ round keys $k_1, \dots , k_n$ are linearly independent, and that $k_{n+1}=k_1 + \sum _{i=2}^n \gamma _i k_i$ for $\gamma _i \in \mathbb {F}_2$. For any non-zero input difference $\alpha$, the number of possible output differences $\beta$ such that

is

Proof

By combining Corollary 1 and Proposition 2, we obtain that the average probability of a characteristic $(\delta _0, \delta _1, \ldots , \delta _{r-1}, \delta _r)$ can be non-zero only if $\delta _i \in \{ \delta _{i-1} , \delta _{i-1}+k_i\}$ for all $1 \leqslant i \leqslant r$. Therefore, the output difference $\delta _r$ must be of the form $\delta _r= \delta _0 + \sum _{i=1}^r \lambda _i k_i$ with $\lambda _i \in \mathbb {F}_2$. Moreover, for those characteristics, the average probability is non-zero unless there exists $1 \leqslant i < r$ such that $|\widehat{\varDelta _{\varPhi _{k_i}(\delta _i)}(f_{b(i)})}(0)|=2^{n-1}$, i.e. $\varDelta _{\varPhi _{k_i}(\delta _i)}(f_{b(i)})$ is constant. By hypothesis, this only occurs when $\delta _i \in \{0,k_i\}$, and the impossible characteristics correspond to the case when either $\delta _i=0$ or $\delta _{i+1}=0$. It follows that the valid characteristics are exactly the characteristics of the form

$$ \delta _i = \delta _0 + \sum _{j=1}^i \lambda _j k_j $$

where none of the $\delta _i$ vanishes.

• When the input difference , for any given output difference $\beta = \alpha + \sum _{i=1}^r \lambda _i k_i$, the $r$-round characteristic

  $$ (\alpha , \alpha + \lambda _1 k_1, \alpha + \lambda _1 k_1+ \lambda _2 k_2, \ldots , \alpha + \sum _{i=1}^r \lambda _i k_i) $$

  is valid since none of the intermediate differences vanishes.

• When $r \leqslant n$ and $\alpha = k_\ell + \sum _{i=1}^{\ell -1} \lambda _i^\alpha k_i$, the only possible characteristic from $\alpha$ to $\beta = \alpha + \sum _{i=1}^r \lambda _i k_i$ satisfies

  

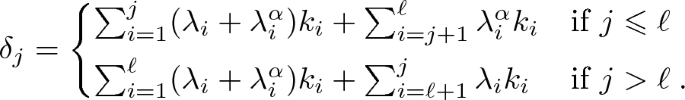
  Since the involved round keys are linearly independent, we deduce that $\delta _j=0$ only when $j=\ell$ and $\lambda _i = \lambda _i^\alpha$ for all $1 \leqslant i \leqslant \ell$. It then follows that there exists a valid characteristic from $\alpha$ to $\beta$ unless $\lambda _i = \lambda _i^\alpha$ for all $1 \leqslant i \leqslant \ell$. The number of possible outputs $\beta$ is then

  $$ (2^\ell -1)2^{r-\ell }= 2^r - 2^{r-\ell }. $$

• If we increase the number of rounds to more than n, we have $\alpha = k_\ell + \sum _{i=1}^{\ell -1} \lambda _i^\alpha k_i$ for some $\ell \leqslant n$. If $\beta = \alpha + \sum _{i=1}^n \lambda _i k_i$ with $\sum _{i=1}^\ell \lambda _i k_i \ne \alpha$, then we can obviously extend the previous $n$-round characteristic to

  $$ (\alpha , \alpha +\lambda _1 k_1, \ldots , \alpha + \sum _{i=1}^{n-1}\lambda _i k_i, \beta , \beta , \ldots , \beta ). $$

  If $\sum _{i=1}^\ell \lambda _i k_i = \alpha$, $\beta$ cannot be the output difference of an $n$-round characteristic. However, the following $(n+1)$-round characteristic starting from $\delta _0=\alpha$ is valid:

  

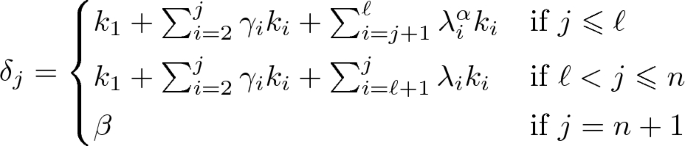
  Indeed, $\delta _n = \beta +k_n$ implying that the last transition is valid. Moreover, it can be easily checked that none of these $\delta _j$ vanishes, unless $\beta =0$. This implies that all non-zero output differences $\beta$ are valid.

The last case in the above lemma is remarkable, as it states any output difference is possible after $n+1$ rounds. To highlight this, we restate it as the following corollary.

Corollary 2

For bison-like instances with more than n rounds whose round keys $k_1, \ldots , k_{n+1}$ satisfy the hypothesis of Lemma 5, and for any non-zero input difference, every non-zero output difference is possible.

We now focus on a reduced version of the cipher limited to exactly n rounds and look at the probabilities for every possible output difference. Most notably, we exhibit in the following lemma an upper-bound on the MEDP which is minimized when $n$ is odd and the involved Boolean functions $f_{b(i)}$ are bent. In other words, Rationale 2 which was initially motivated by the analysis in Sect. 3 for the original round function based on $x \mapsto \max (x,x+k)$ [48] is also valid when a linear function $\varPhi _k$ is used.

Lemma 6

Let us consider $n$ rounds of a bison-like instance of the WSN construction with round function involving Boolean functions $f_{b(i)}$. Let $k_1, \dots , k_n$ be any linearly independent round keys. Then, for any input difference $\alpha \ne 0$ and any $\beta$, we have

More precisely, if all $f_{b(i)}$ are bent,

where $\ell$ denotes as previously the latest round key that appears in the decomposition of $\alpha$ into the basis $(k_1, \ldots , k_n)$, that is $\alpha = k_\ell + \sum _{i=1}^{\ell -1} \lambda _i k_i$.

Fig. 3.

Probabilities of output differences for three rounds and the cases of the input difference $\alpha = k_1 + k_2$, thus $\ell = 2$. Dotted transitions are impossible.

The case of bent functions is visualized in Fig. 3, where we give an example of the three possibilities for three rounds.

Proof

As proved in Lemma 5, $(\alpha , \beta )$ is an impossible differential if and only if $\beta = \sum _{i=\ell + 1}^n \lambda _i k_i$. For all other values of $\beta = \alpha + \sum _{i=1}^n \lambda _i k_i$, we have

where $\delta _i = \alpha + \sum _{j=1}^i \lambda _j k_j$. The $i$-th term in the product is upper-bounded by

except if $\varPhi _{k_i}(\delta _i) =0$, i.e., $\delta _i \in \{0, k_i\}$. As seen in Lemma 5, the case $\delta _i=0$ cannot occur in a valid characteristic. The case $\delta _i=k_i$ occurs if and only if $i=\ell$ and $\beta = k_\ell + \sum _{j=\ell + 1}^n \lambda _j k_j$. In this situation, the $\ell$-th term in the product equals $1$. In the tree of differences this is visible as the collapsing of the two branches from two possible succeeding differences into only one, which then of course occurs with probability one, see upper branch of Fig. 3.

Most notably, all $f_{b(i)}$ are bent if and only if

leading to the result.

This can be seen on Fig. 3: the $2^{n-\ell }$ possible differences coming from the collapsed branch have a transition of probability one in that round, resulting in an overall probability of $2^{-n+1}$, see Eq. (6). For the lower part of Fig. 3, all the other differences are not affected by this effect and have a probability of $2^{-n}$, see Eq. (7).

Because they allow us to minimize the MEDP, we now concentrate on the case of bent functions for the sake of simplicity, which implies that the block size is odd. However, if an even block size is more appropriate for implementation reasons, we could also define bison-like instances based on maximally nonlinear functions.

It would be convenient to assume in differential cryptanalysis that the EDP of a differential does not increase when adding more rounds, while this does not hold in general. However, this argument can easily be justified for bison-like instances using bent functions, when averaging over the whitening keys w.

Proposition 3

Let us consider $r \geqslant n$ rounds of a bison-like instance of the WSN construction with bent functions $f_{b(i)}$. Let $k_1, \dots , k_n$ be any linearly independent round keys. Then the probability of any non-trivial differential, averaged over all whitening key sequences w is upper bounded by $2^{-n + 1}$.

In other words, the MEDP of bison-like instances with bent $f_{b(i)}$ for $r \geqslant n$ rounds is $2^{-n+1}$.

Proof

By induction over r. The base case for $r=n$ rounds comes from Lemma 6. In the induction step, we first consider the case when the output difference $\beta$ after $r$ rounds differs from $k_{r}$. Then the output difference $\delta _{r} = \beta$ can be reached if and only if the output difference after $(r-1)$ rounds $\delta _{r-1}$ belongs to $\{\beta , \beta + k_{r}\}$. Then,

When the output difference $\beta$ after $r$ rounds equals $k_r$, it results from $\delta _{r-1}=k_r$ with probability $1$. In this case

$$ \mathrm {EDP}^r(\alpha , \beta ) = \mathrm {EDP}^{r-1}(\alpha , \beta ) \leqslant 2^{-n+1}\;. $$

This bound is close to the ideal case, in which each differential has probability $1/(2^{n}-1)$.

We now give a detailed description of our instance bison.

5 Specification of bison

As bison-like instances should obviously generalise bison, this concrete instance inherits the already specified parts. Thus bison uses two bent functions $f_{b(i)}$, replaces the $\max$ function by $\varPhi _k$, and uses a key schedule that generates round keys, where all n consecutive round keys are linearly independent. The resulting instance for n bits iterates the WSN round function as defined below over $3 \cdot n$ rounds. The chosen number of rounds mainly stems from the analysis of the algebraic degree that we discuss in Sect. 6.

Security Claim

We claim n-bit security for bison in the single-key model. We emphasize that we do not claim any security in the related-key, chosen-key or known-key model.

5.1 Round Function

For any nonzero round key $k$, we define $\varPhi _{k} : \mathbb {F}_2^{n} \rightarrow \mathbb {F}_2^{n-1}$ as

(8)

where i(k) denotes the index of the lowest bit set to 1 in k, and the notation $x[1,\ldots ,j-1,j+1,\ldots ,n]$ returns the $(n-1)$-bit vector, consisting of the bits of x except the jth bit.

Lemma 7

The function $\varPhi _k : \mathbb {F}_2^{n} \rightarrow \mathbb {F}_2^{n-1}$ is linear and satisfies

$$\begin{aligned} \ker (\varPhi _{k}) = \{0,k\}. \end{aligned}$$

The proof can be done by simply computing both outputs for x and $x+k$.

For the preimage of $y \in \mathbb {F}_2^{n-1}$ and $j = i(k)$ we have

(9)

Due to the requirement for the $f_{b(i)}$ being bent, we are limited to functions taking an even number of bits as input. The simplest example of a bent function is the inner product.

Eventually we end up with the following instance of the WSN round.

5.2 Key Schedule

In the ith round, the key schedule has to compute two round keys: $k_i \in \mathbb {F}_2^n$ and $w_i \in \mathbb {F}_2^{n-1}$. We compute those round keys as the states of lfsrs after i clocks, where the initial states are given by a master key K. The master key consists of two parts of n and $n-1$ bits, i.e.

$$\begin{aligned} K=(k,w) \in \mathbb {F}_2^n \times \mathbb {F}_2^{n-1}. \end{aligned}$$

As the all-zero state is a fixed point for any lfsr, we exclude the zero key for both k and w. In particular $k=0$ is obviously a weak key that would result in a ciphertext equal to the plaintext $p = E_{0,w}^r(p)$ for all p, independently of w or of the number of rounds r.

It is well-known that choosing a feedback polynomial of an lfsr to be primitive results in an lfsr of maximal period. Clocking the lfsr then corresponds to multiplication of its state with the companion matrix of this polynomial. Interpreted as elements from the finite field, this is the same as multiplying with a primitive element.

In order to avoid structural attacks, e.g. invariant attacks [28, 39, 50], as well as the propagation of low-weight inputs, we add round constants $c_i$ to the round key $w_i$.

These round constants are also derived from the state of an lfsr with the same feedback polynomial as the $w_i$ lfsr, initialized to the unit vector with the least significant bit set. To avoid synchronization with the $w_i$ lfsr, the $c_i$ lfsr clocks backwards.

As discussed above, this key schedule has the following property, see also Rationale 1.

Lemma 8

For bison’s key schedule, the following property holds: Any set of n consecutive round keys $k_i$ are linearly independent. Moreover there exist coefficients $\lambda _i$ such that

$$\begin{aligned} k_{n+i} = k_i + \sum _{j=i+1}^{n+i-1} \lambda _j k_j. \end{aligned}$$

Proof

To prove this, we start by showing that the above holds for the first n round keys, the general case then follows from a similar argumentation. We need to show that there exists no non-trivial $c_i \in \mathbb {F}_2$ so that , which is equivalent to showing that there exists no non-trivial $c_i \in \mathbb {F}_2$ so that . In this regard, we recall the notion of minimal polynomial of k with respect to $C(p_{k})$, defined as the monic polynomial of smallest degree $Q_L(k)(x) = \sum _{i=0}^{d} q_i x^i \in \mathbb {F}_2[x]$ such that . Referring to a discussion that has been done for instance in [4], we know that the minimal polynomial of k is a divisor of the minimal polynomial of $C(p_{k})$. Since in our case our construction has been made so that this later is equal to $p_k$ which is a primitive polynomial, we deduce that the minimal polynomial of $k \ne 0$ is $p_{k}$ itself. Since the degree of $p_{k}$ is equal to n, this prove that the first n keys are linearly independent.

The equation holds, since $p_k(0) = 1$.

6 Security Analysis

As we have already seen, bison is resistant to differential cryptanalysis. In this section, we argue why bison is also resistant to other known attacks.

6.1 Linear Cryptanalysis

For linear cryptanalysis, given the fact that bison is based on a bent function, i.e. a maximally non-linear function, arguing that no linear characteristic with high correlation exist is rather easy. Again, we start by looking at the Fourier coefficients for one round.

From One Round. Using the properties of f being bent, we get the following.

Proposition 4

Let $R_{k,w} : \mathbb {F}_2^n \rightarrow \mathbb {F}_2^n$ be the round function as defined in Eq. (10). Then, its lat consists of the entries

(11)

We prove the proposition in [12, Section 6.1.1, Proposition 4].

To More Rounds. When we look at more than one round, we try to approximate the linear hull by looking at the strongest linear trail. As already discussed in Lemma 2, for $r < n$ there are trails with probability one. We now show that any trail’s correlation for $r \geqslant n$ rounds is actually upper bounded by $2^{-\frac{n+1}{2}}$:

Proposition 5

For $r \geqslant n$ rounds, the correlation of any non-trivial linear trail for bison is upper bounded by $2^{-\frac{n+1}{2}}$.

Proof

It is enough to show the above for any n-round trail. By contradiction, assume there exists a non-trivial trail $\theta = (\theta _0, \ldots , \theta _n)$ with correlation one. Following Proposition 4, for every round i the intermediate mask $\theta _i$ has to fulfill . Further $\theta _i = \theta _{i+1}$ for $0 \leqslant i < n$. Because all n round keys are linearly independent, this implies that $\theta _i = 0$, which contradicts our assumption. Thus, in at least one round the second or third case of Eq. (11) has to apply.

It would be nice to be able to say more about the linear hull, analogously to the differential case. However, for the linear cryptanalysis this looks much harder, due to the denser lat. In our opinion developing a framework where bounding linear hulls is similarly easy as it is for bison with respect to differentials is a fruitful future research topic.

6.2 Higher-Order Differentials and Algebraic Attacks

High-order differential attacks, cube attacks, algebraic attacks and integral attacks all make use of non-random behaviour of the ANF of parts of the encryption function. In all these attacks the algebraic degree of (parts of) the encryption function is of particular interest. In this section, we argue that those attacks do not pose a threat to bison.

We next elaborate in more detail on the algebraic degree of the WSN construction. In particular, we are going to show that the algebraic degree increases at most linearly with the number of rounds. More precisely, if the round function is of degree d, the algebraic degree after r rounds is upper bounded by $r(d-1)+1$.

Actually, we are going to consider a slight generalization of the WSN construction and prove the above statement for this generalization.

General Setting. Consider an initial state of n bits given as $x=(x_0,\dots ,x_{n-1})$ and a sequence of Boolean functions

$$\begin{aligned} f_i :\mathbb {F}_2^{n+i} \rightarrow \mathbb {F}_2 \end{aligned}$$

for $0 \leqslant i < r$. We define a sequence of values $y_i$ by setting $y_0=f_0(x)$ and

$$\begin{aligned} y_i=f_i(x_0,\dots ,x_{n-1},y_0, \dots , y_{i-1}), \end{aligned}$$

for $1 \leqslant i < r$. Independently of the exact choice of $f_i$ the degree of any $y_\ell$, as a function of x can be upper bounded as stated in the next proposition.

Proposition 6

Let $f_i$ be a sequence of functions as defined above, such that $\deg (f_i)\leqslant d$. The degree of $y_\ell$ at step $\ell$ seen as a function of the bits of the initial state $x_0,\dots ,x_{n-1}$ satisfies

$$\begin{aligned} \deg (y_\ell )\leqslant (d-1)(\ell +1)+1. \end{aligned}$$

Moreover, for any $I \subseteq \{0,\dots , \ell \}$,

$$\begin{aligned} \deg (\prod _{i \in I} y_i)\leqslant (d-1)(\ell +1)+ |I|. \end{aligned}$$

Proof

The first assertion is of course a special case of the second one, but we add it for the sake of clarity. We prove the second, more general, statement by induction on $\ell$.

Starting with $\ell =0$, we have to prove that $\deg (y_0)\leqslant d$, which is obvious, as

$$\begin{aligned} y_0=f_0(x_0,\dots ,x_{n-1}) \end{aligned}$$

and $\deg (f_0) \le d$.

Now, we consider some $I \subseteq \{0, \ldots , \ell \}$ and show that

$$\begin{aligned} \deg (\prod _{i \in I} y_i)\leqslant (d-1)(\ell +1) +|I|. \end{aligned}$$

We assume that $\ell \in I$, otherwise the result directly follows the induction hypothesis.

Since $f_\ell$ depends both on $y_0, \ldots , y_{\ell -1}$ and $x$, we decompose it as follows:

$$\begin{aligned} y_\ell =f_\ell (y_0, \ldots , y_{\ell -1},x) = \sum _{{\begin{array}{c}J \subseteq \{0, \ldots , \ell -1\}\\ 0 \leqslant | J| \leqslant \min (d,\ell )\end{array}}} \left( \prod _{j \in J}y_j\right) g_J(x) \end{aligned}$$

with $\deg (g_J)\leqslant d - |J|$ for all $J$ since $\deg (f_\ell )\leqslant d$.

Then, for $I = \{\ell \} \cup I'$, we look at

$$\begin{aligned} y_\ell \left( \prod _{i \in I'} y_i \right) = \sum _{{\begin{array}{c}J \subseteq \{0, \ldots , \ell -1\}\\ 0 \leqslant |J| \leqslant \min (d,\ell )\end{array}}} \left( \prod _{j \in J \cup I'} y_j \right) g_J(x)\;. \end{aligned}$$

From the induction hypothesis, the term of index $J$ in the sum has degree at most

$$\begin{aligned} (d-1)\ell +|J \cup I'| + \deg (g_J)= & {} (d-1)\ell +|J \cup I'| + d - |J| \\\leqslant & {} (d-1)(\ell +1) + |J \cup I'| - |J| +1\\\leqslant & {} (d-1)(\ell +1) + |J| + |I'| - |J| + 1\\\leqslant & {} (d-1)(\ell +1) + |I|\;. \end{aligned}$$

Special Case of . In the case of bison, we make use of quadratic functions, and thus Proposition 6 implies that after r rounds the degree is upper bounded by $r+1$ only. Thus, it will take at least $n-2$ rounds before the degree reaches the maximal possible degree of $n-1$. Moreover, due to the construction of WSN, if all component functions of $E_{k,w}^r$ are of degree at most d, there will be at least one component function of $E_{k,w}^{r+n-1}$ of degree at most d. That is, there exist a vector $\beta \in \mathbb {F}_2^n$ such that

$$\begin{aligned} \langle \beta , E_{k,w}^{r+n-1}(x) \rangle \end{aligned}$$

has degree at most d. Namely, for

it holds that

$$\begin{aligned} \deg \left( \langle \beta , E_{k,w}^{r+s}(x) \rangle \right) =\deg \left( \langle \beta , E_{k,w}^r(x) \rangle + \sum _{i=r}^{r+s} \lambda _i \langle \beta , k_i \rangle \right) = \deg \left( \langle \beta , E_{k,w}^r(x) \rangle \right) . \end{aligned}$$

We conclude there exists a component function of $E_{k,w}^{r+s}$ of non-maximal degree, as long as $0 \leqslant r \leqslant n-2$ and $0\leqslant s \leqslant n-1$. Thus for bison there will be at least one component function of degree less than $n-1$ for any number of rounds $0\leqslant r\leqslant 2n-3$. However, similarly to the case of zero-correlation properties as described in Lemma 3, the vector $\beta$ is key dependent and thus this property does not directly lead to an attack.

Finally, so far we only discussed upper bounds on the degree, while for arguing security, lower bounds on the degree are more relevant. As it seems very hard (just like for any cipher) to prove such lower bounds, we investigated experimentally how the degree increases in concrete cases. As can be seen in [12, Figure 4] the maximum degree is reached for almost any instance for $n+5$ rounds. Most importantly, the fraction of instances where it takes more than $n+2$ rounds decreases with increasing block length n. Moreover, the round function in bison experimentally behaves with this respect as a random function, as can be seen in [12, Figure 5]. Thus, as the number of rounds is 3n, we are confident that attacks exploiting the algebraic degree do not pose a threat for bison.

Besides the WSN construction, a special case of the above proposition worth mentioning is a non linear feedback generator (NLFSR).

Degree of NLFSRs. One well-known special case of the above general setting is an NLFSR or, equivalently a maximally unbalanced Feistel cipher, depicted below.

Proposition 6 implies that the degree of any NLFSR increases linearly with the number of rounds. To the best of our knowledge, this is the first time this have been observed in this generality. We like to add that this is in sharp contrast to how the degree increases for SPN ciphers. For SPN ciphers the degree usually increases exponentially until a certain threshold is reached [11].

6.3 Other Attacks

We briefly discuss other cryptanalytic attacks.

Impossible Differentials. In Lemma 5 and Corollary 2, we discuss that every output difference is possible after more than n rounds. Consequently, there are no impossible differentials for bison.

Truncated Differentials. Due to our strong bounds on differentials it seems very unlikely that any strong truncated differential exists.

Zero Correlation Linear Cryptanalysis. In Lemma 3 we already discussed generic zero correlation linear hulls for the WSN construction. Depending on the actual key used, this technique may be used to construct a one-round-longer zero-correlation trail. For this, we need two distinct elements , , and construct the trail analogously to Lemma 3 (which may not exist, due to the key dependency).

Invariant Attacks. For an invariant attack, we need a Boolean function g, s.t. $g(x) + g(E_{k,w}^r(x))$ is constant for all x and some weak keys (k, w). As the encryption of any message is basically this message with some of the round keys added, key addition is the only operation which is performed. It has been shown in [4, Proposition 1] that any g which is invariant for a linear layer followed by the addition of the round key $k_i$ as well as for the same up to addition of a different $k_j$, has a linear space containing $k_i + k_j$. In the case of the linear layer being the identity, the linear space actually contains also the $k_i$ and $k_j$ (by definition).

Thus, the linear space of any invariant for our construction has to contain which is obviously the full space $\mathbb {F}_2^n$. Following the results of [4], there are thus no invariant subspace or nonlinear invariant attack on bison.

Related-Key Attacks. In generic related-key attacks, the attacker is also allowed to exploit encryptions under a related, that is $k^\prime = f(k)$, key – in the following, we restrict our analysis to the case where f is the addition with a constant. That is, the attacker cannot only request $E_{k,w}(x)$, and $E_{k,w}(x + \alpha )$, but also $E_{k+\beta ,w+\beta ^\prime }(x)$ or $E_{k+\beta ,w+\beta ^\prime }(x + \alpha )$, for $\alpha$ (difference in the input x), $\beta$ (difference in the key k) and $\beta ^\prime$ (difference in the key w) of her choice. As $\beta = \beta ^\prime = 0$ would result in the standard differential scenario, we exclude it for the remainder of this discussion. Similar, $\beta = k$ results in $\varPhi _{k+\beta } = \varPhi _0$, which we did not define, thus we also skip this case and refer to the fact that if an attacker chooses $\beta = k$, she basically already has guessed the secret key correctly.

For bison, the following proposition holds.

Proposition 7

For r rounds, the probability of any related-key differential characteristic for bison, averaged over all whieting key sequences $(w_1, \ldots , w_r)$, is upper bounded by .

For more details and a proof of the proposition, see [12, Section 6.3.5, Proposition 7].

Further Observations. During the design process, we observed the following interesting point: For sparse master keys k and w and message m, e.g. $k = w = m = 1$, in the first few rounds, nothing happens. This is mainly due to the choice of sparse key schedule polynomials $p_w$ and $p_k$ and the fact that $f_0$ outputs 0 if only one bit in its input is set (as for any x).

To the best of our knowledge, this observation cannot be exploited in an attack.

Experimental Results. We conducted experiments on small-scale versions of bison with $n=5$. The ddts and lats, depicted using the “Jackson Pollock representation” [8], for one to ten rounds are listed in [12, Appendix B]. In [12, Appendix B.1] one can see that the two cases of averaging over all possible $w_i$ and choosing a fixed $w_i$ results in very similar differential behaviors. Additionally, after $5 = n$ rounds, the plots do not change much.

The results in the linear case, see [12, Appendix B.2], are quite similar. The major difference here, is the comparable bigger entries for a fixed $w_i$. Nonetheless, most important is that there are no high entries in the average lat which would imply a strong linear approximation for many keys. Additionally one also expects for a random permutation not too small lat entries. Note that one can well observe the probability-one approximation for $4 = n-1$ rounds (lower right corner of the corresponding plot).

7 Conclusion

Efficiency of symmetric ciphers have been significantly improved further and further, in particular within the trend of lightweight cryptography. However, when it comes to arguing about the security of ciphers, the progress is rather limited and the arguments basically did not get easier nor stronger since the development of the AES. In our opinion it might be worth shifting the focus to improving security arguments for new designs rather than (incrementally) improving efficiency. We see bison as a first step in this direction.

With our instance for the WSN construction and its strong resistance to differential cryptanalysis, this framework emerges as an interesting possibility to design block ciphers. Unfortunately, we are not able to give better then normal arguments for the resistance to linear cryptanalysis. It is thus an interesting question, if one can find a similar instance of the WSN construction for which comparable strong arguments for the later type of cryptanalysis exist.

Alternative designs might also be worth looking at. For example many constructions for bent functions are known and could thus be examined as alternatives for the scalar product used in bison. One might also look for a less algebraic design – but we do not yet see how this would improve or ease the analysis or implementation of an instance.

Finally, for an initial discussion of implementation figures, see [12, Section 7]. Another line of future work in this direction is the in-depth analysis of implementation optimizations and side channel-resistance of bison.