Abstract
At CRYPTO ’12, Landecker et al. introduced the cascaded LRW2 (or CLRW2) construction and proved that it is a secure tweakable block cipher up to roughly \( 2^{2n/3} \) queries. Recently, Mennink has presented a distinguishing attack on CLRW2 in \( 2n^{1/2}2^{3n/4} \) queries. In the same paper, he discussed some non-trivial bottlenecks in proving tight security bound, i.e., security up to \( 2^{3n/4} \) queries. Subsequently, he proved security up to \( 2^{3n/4} \) queries for a variant of CLRW2 using 4-wise independent AXU assumption and the restriction that each tweak value occurs at most \( 2^{n/4} \) times. Moreover, his proof relies on a version of mirror theory which is yet to be publicly verified. In this paper, we resolve the bottlenecks in Mennink’s approach and prove that the original CLRW2 is indeed a secure tweakable block cipher up to roughly \( 2^{3n/4} \) queries. To do so, we develop two new tools: First, we give a probabilistic result that provides improved bound on the joint probability of some special collision events, and second, we present a variant of Patarin’s mirror theory in tweakable permutation settings with a self-contained and concrete proof. Both these results are of generic nature and can be of independent interests. To demonstrate the applicability of these tools, we also prove tight security up to roughly \( 2^{3n/4} \) queries for a variant of DbHtS, called DbHtS-p, that uses two independent universal hash functions.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Tweakable Block Ciphers: A tweakable block cipher (or TBC for short) is a cryptographic primitive that has an additional public indexing parameter called tweak in addition to the usual secret key of a standard block cipher. This means that a tweakable block cipher, \( {\widetilde{E}}: {\mathcal {K}}\times {\mathcal {T}}\times {\mathcal {M}}\rightarrow {\mathcal {M}}\), is a family of permutations on the plaintext/ciphertext space \( {\mathcal {M}}\) indexed by two parameters: the secret key \( k \in {\mathcal {K}}\) and the public tweak \( t \in {\mathcal {T}}\). Liskov, Rivest and Wagner formalized the concept of TBCs in their renowned work [1]. Tweakable block ciphers are more versatile than a standard block cipher and find a broad range of applications, most notably in authenticated encryption schemes, such as TAE [1], \( \mathsf {\Theta } \mathsf {CB}\) [2] (TBC-based generalization of the OCB family [2,3,4]), PIV [5], COPA [6], SCT [7] (used in Deoxys [7, 8]) and AEZ [9]; and message authentication codes, such as PMAC_TBC3K and PMAC_TBC1K [10], PMAC2x and PMACx [11], ZMAC [12], NaT and HaT [13], ZMAC+ [14], DoveMAC [15]. Apart from this, TBCs have also been employed in encryption schemes [16,17,18,19,20,21].
Birthday-Bound Secure TBCs: Although there are some TBC constructions designed from scratch, notably Deoxys-BC [8] and Skinny [8, 22], still the wide availability of secure and well-analyzed block ciphers make them perfect candidates for constructing TBCs. Liskov et al. [1] proposed two constructions for TBCs based on a secure block cipher. The second construction, called LRW2, is defined as follows:
where E is a block cipher, k is the block cipher key and h is an XOR universal hash function. The LRW2 construction is strongly related to the \( \textsf {XEX} \) construction by Rogaway [2] and its extensions by Chakraborty and Sarkar [23], Minematsu [24] and Granger et al. [25]. All these schemes are inherently birthday-bound secure due to the internal hash XOR collisions, i.e., the adversary can choose approx. \( 2^{n/2} \) queries in such a way that there will be two queries (t, m) and \( (t',m') \) with \( m \oplus h(t) = m' \oplus h(t') \). This leads to a simple distinguishing event \( c \oplus c' = m \oplus m' \).
Beyond-Birthday-Bound Secure TBCs: Landecker et al. [26] first suggested the cascading of two independent LRW2 instances to get a beyond-birthday-bound (BBB) secure TBC, called CLRW2, i.e.,
They proved that CLRW2 is a secure TBC up to approx. \( 2^{2n/3} \) queries. Later on, Procter [27] pointed out a flaw in the security proof of CLRW2. The proof was subsequently fixed by both Landecker et al. and Procter to recover the claimed security bounds. Lampe and Seurin [28] studied the \( \ell \ge 2 \) independent cascades of LRW2 and proved that it is secure up to approx. \( 2^{\frac{\ell n}{\ell +2}} \) queries. They further conjectured that the \( \ell \) cascade is secure up to \(2^{\frac{\ell n}{\ell +1}} \) queries. Recently, Mennink [29] has showed a \(2n^{1/2}2^{3n/4} \)-query attack on CLRW2. In the same paper, he also proved security up to \( 2^{3n/4} \) queries, albeit for a variant of CLRW2 with strong assumptions on the hash functions and restrictions on tweak repetitions.
All of the above constructions are proved to be secure in standard model. However, there are TBC constructions in public random permutation and ideal cipher model as well. In [13], Cogliati, Lampe and Seurin introduced the tweakable Even–Mansour construction and its cascaded variant. They showed that the two-round construction is secure up to approx. \( 2^{2n/3} \) queries. A simple corollary of this result also gives security of CLRW2 up to \( 2^{2n/3} \) queries. The bound is tight in the ideal permutation model as one can simply fix the tweak and use the \( 2^{2n/3} \) queries attack on key alternating cipher by Bogdanov et al. [30]. Some notable BBB secure TBC constructions in the ideal cipher model include Mennink’s \(\tilde{\textsf {F}}[1]\) and \(\tilde{\textsf {F}}[2]\) [31, 32], Wang et al. 32 constructions [33] and their generalization, called XHX, by Jha et al. [34]. All of these constructions are at most birthday-bound secure in the sum of key size and block size.Footnote 1 Recently, Lee and Lee [35] have proved that a two-level cascade of XHX, called XHX2, achieves BBB security in terms of the sum of key size and block size.
1.1 Recent Developments in the Analysis of CLRW2
In [29], Mennink presented an improved security analysis of CLRW2. The major contribution was an attack in approx. \(n^{1/2}2^{3n/4} \) queries. The attack works by finding four queries \( (t,m_1,c_1) \), \( (t',m_2,c_2) \), \( (t,m_3,c_3) \) and \((t',m_4,c_4) \) such that
This leads to a simple distinguishing attack since, in case of CLRW2,
happens with probability 1, given \( \texttt {AltColl} \) holds. In contrast, this happens with probability close to \( 1/2^n \) for an ideal tweakable random permutation.
Following on the insights from the attack, Mennink [29] also gives a security proof of the same order for a variant of CLRW2. Basically, the proof bounds the probability that the above-given four equations hold. Additionally, inspired by [36], Patarin’s mirror theory [37,38,39] is used which requires a bound on the probability of some more bad events. The major bottleneck in proving the security beyond \( 2^{2n/3} \) queries comes from two directions:
First, there is no straightforward way of proving the upper bound of the probability of occurrence of \( \texttt {AltColl}\) to \(\frac{q^4}{2^{3n}} \), where q is the number of queries. This is due to two reasons: (1) the adversary has full control over the tweak usages and (2) the hash functions are just 2-wise independent XOR universal.
Second, mirror theory was primarily developed to lower bound the number of solutions to equations arising for some random system which is trying to mimic a random function. This is not the case here, and as we will see in later sections, the mirror theory bound is directly dependent on tweak repetitions.
In order to bypass the two bottlenecks, the following assumptions are made in [29]:
- 1.
The hash functions are 4-wise independent AXU.
- 2.
The maximum number of tweak repetitions is restricted to \( 2^{n/4} \).
- 3.
A limited variant of mirror theory result is true for \( q < 2^{3n/4} \).
Among the three assumptions, the first two are at least plausible. But the last assumption is questionable as barring certain restricted cases, the proof of mirror theory has many gaps which are still open or unproved, as has been noted in [40, 41].
1.2 Contributions of this Work
In light of the above discussion, we revisit the proof strategy of [29] (see Sect. 3), explicitly considering each of the issues. We show that all three assumptions used in [29] are dispensable. In order to do so, we develop some new tools which are described below:
- 1.
The Alternating Events Lemma We derive a generic tool (see Sect. 4) to bound the probability of events of the form \( \texttt {AltColl} \). In CLRW2 analysis, only a special case is required, where the randomness comes from two independent universal hash functions.
- 2.
Mirror Theory in Tweakable Permutation Setting We adapt the mirror theory line of argument (see Sect. 5) to get suitable bounds in tweakable permutation setting. This is a generalization of the existing mirror theory result in function setting.
Using the above-mentioned tools, we prove that CLRW2 is secure up to approx. \( 2^{3n/4} \) queries (see Sect. 6). Our result, in combination with the attack in [29] (see supplementary material B), gives the tight (up to a logarithmic factor) security of CLRW2.
As a side result on the application of our tools, we also prove tight security up to roughly \( 2^{3n/4} \) queries for a variant of DbHtS [42], called \(\textsf {DbHtS-p}\), that uses two independent universal hash functions (see Sect. 7).
Here, we explicitly remark that our bound on CLRW2 is not derivable from the recent result on XHX2 [35].
2 Preliminaries
Notational Setup: For \( n \in {{\mathbb {N}}}\), [n] denotes the set \( \{1,2,\ldots ,n\} \), \( \{0,1\}^n \) denotes the set of bit strings of length n, and \( {\textsf {Perm}}(n) \) denotes the set of all permutations over \( \{0,1\}^n \). For \( n,\kappa \in {{\mathbb {N}}}\), \({\textsf {BPerm}}(\kappa ,n) \) denotes the set of all families of permutations \( \pi _k := \pi (k,\cdot ) \in {\textsf {Perm}}(n) \), indexed by \(k \in \{0,1\}^{\kappa } \). We sometimes extend this notation, whereby \( {\textsf {BPerm}}(\kappa ,\tau ,n) \) denotes the set of all families of permutations \( \pi _{(k,t)} \), indexed by \( (k,t) \in \{0,1\}^\kappa \times \{0,1\}^\tau \). For \( n,r \in {{\mathbb {N}}}\), such that \( n \ge r \), we define the falling factorial \( (n)_r :=n!/(n-r)! = n(n-1)\cdots (n-r+1) \).
For \( q \in {{\mathbb {N}}}\), \( x^q \) denotes the q-tuple \((x_1,x_2,\ldots ,x_q) \), and \( {\widehat{x}}^q \) denotes the set \(\{x_i : i \in [q]\} \). By an abuse of notation, we also use \( x^q \) to denote the multiset \( \{x_i : i \in [q]\} \) and \( \mu (x^q,x') \) to denote the multiplicity of \( x' \in x^q \). For a set \( {\mathcal {I}}\subseteq [q] \) and a q-tuple \( x^q \), \( x^{{\mathcal {I}}} \) denotes the tuple \( (x_i)_{i \in {\mathcal {I}}} \). For a pair of tuples \( x^q \) and \(y^q\), \( (x^q,y^q) \) denotes the 2-ary q-tuple \(((x_1,y_1),\ldots ,(x_q,y_q)) \). An n-ary q-tuple is defined analogously. For \( q \in {{\mathbb {N}}}\), for any set \( {\mathcal {X}}\), \( ({\mathcal {X}})_q\) denotes the set of all q-tuples with distinct elements from \({\mathcal {X}}\). For \( q \in {{\mathbb {N}}}\), a 2-ary tuple \( (x^q,y^q) \) is called permutation compatible, denoted \({x^q}\leftrightsquigarrow {y^q} \), if \(x_i = x_j \iff y_i =y_j \). Extending notations, a 3-ary tuple \((t^q,x^q,y^q) \) is called tweakable permutation compatible, denoted by \( ({t^q}, {x^q})\leftrightsquigarrow ({t^q}, {y^q}) \), if \( (t_i,x_i) = (t_j,x_j) \iff (t_i,y_i) = (t_j,y_j) \). For any tuple \( x^q \in {\mathcal {X}}^q \), and for any function \( f: {\mathcal {X}}\rightarrow {\mathcal {Y}}\), \( f(x^q) \) denotes the tuple \((f(x_1),\ldots ,f(x_q)) \). We use shorthand notation \(\exists ^*\) to represent the phrase “there exists distinct.”
We use the conventions: Uppercase and lowercase letters denote variables and values, respectively, and Serif font letters are used to denote random variables, unless stated otherwise. For a finite set \( {\mathcal {X}}\), \( \textsf {X} \leftarrow \!\!{\$}\,{\mathcal {X}}\) denotes the uniform and random sampling of \( \textsf {X} \) from \({\mathcal {X}}\).
2.1 Some Useful Inequalities
Definition 2.1
For \( r \ge s \), let \( a = (a_i)_{i \in [r]} \) and \( b = (b_j)_{j \in [s]} \) be two sequences over \( {{\mathbb {N}}}\). We say that acompresses tob, if there exists a partition \( {\mathcal {P}}\) of [r] such that \( {\mathcal {P}}\) contains exactly s cells, say \( {\mathcal {P}}_1,\ldots ,{\mathcal {P}}_s \), and \( \forall i\in [s],~~b_i = \sum _{j \in {\mathcal {P}}_i}a_j \).
Proposition 1
For \( r \ge s \), let \( a=(a_i)_{i \in [r]} \) and \( b=(b_j)_{j \in [s]} \) be sequences over \( {{\mathbb {N}}}\), such that a compresses to b. Then for any \( n \in {{\mathbb {N}}}\), such that \( 2^n \ge \sum _{i=1}^{r} a_i \), we have \( \prod _{i=1}^{r}(2^n)_{a_i} \ge \prod _{j=1}^{s}(2^n)_{b_j} \).
In [34, Proof of Lemma 3], the authors refer to a variant of Proposition 1. We remark that this variant [34, Fact 1] is in fact false. However, [34, Proof of Lemma 3] implicitly used Proposition 1 and hence stands correct.
Proposition 2
For \( r \ge 2 \), let \( c=(c_i)_{i\in [r]} \) and \( d =(d_i)_{i\in [r]}\) be two sequences over \( {{\mathbb {N}}}\). Let \(a_1,a_2,b_1,b_2 \in {{\mathbb {N}}}\), such that \( c_i \le a_j \), \( c_i + d_i \le a_j + b_j \) for all \( i \in [r] \) and \( j \in [2] \), and \(\sum _{i=1}^{r}d_i = b_1+b_2 \). Then, for any \( n \in {{\mathbb {N}}}\), such that \( a_j + b_j \le 2^n \) for \(j \in [2] \), we have \(\prod _{i=1}^{r} (2^n-c_i)_{d_i} \ge (2^n-a_1)_{b_1}(2^n-a_2)_{b_2}\).
Proposition 2 is quite intuitive, in the sense, that the starting value in each of the falling factorial terms on the left is at least as much as the starting values on the right, and the total number of terms is same on both the sides. The formal proofs of Proposition 1 and 2 are given in supplementary material A.
2.2 (Tweakable) Block Ciphers and Random Permutations
A block cipher with key size \( \kappa \) and block size n is a family of permutations \( {E}\in {\textsf {BPerm}}(\kappa ,n) \). For \( k \in \{0,1\}^\kappa \), we denote \( {E}_k(\cdot ) := {E}(k,\cdot ) \) and \({E}^{-1}_k(\cdot ) := {E}^{-1}(k,\cdot ) \). A tweakable block cipher with key size \( \kappa \), tweak size \( \tau \) and block size n is a family of permutations \( {\widetilde{E}}\in {\textsf {BPerm}}(\kappa ,\tau ,n) \). For \( k \in \{0,1\}^\kappa \) and \( t \in \{0,1\}^\tau \), we denote \({\widetilde{E}}_k(t,\cdot ) := {\widetilde{E}}(k,t,\cdot ) \) and \( {\widetilde{E}}^{-1}_k(t,\cdot ) :={\widetilde{E}}^{-1}(k,t,\cdot ) \). Throughout this paper, we fix \(\kappa ,\tau ,n \in {{\mathbb {N}}}\) as the key size, tweak size and block size, respectively, of the given (tweakable) block cipher.
We say that \( \Pi \) is an (ideal) random permutation on block space \( \{0,1\}^n\) to indicate that \( \Pi \leftarrow \!\!{\$}\,{\textsf {Perm}}(n) \). Similarly, we say that \( {{\widetilde{\Pi }}}\) is an (ideal) tweakable random permutation on tweak space \( \{0,1\}^\tau \) and block space \(\{0,1\}^n\) to indicate that \( {{\widetilde{\Pi }}}\leftarrow \!\!{\$}\,{\textsf {BPerm}}(\tau ,n) \).
2.3 (T)SPRP Security Definitions
In this paper, we assume that the distinguisher is non-trivial, i.e., it never makes a duplicate query, and it never makes a query for which the response is already known due to some previous query. For instance, say an oracle gives bidirectional access (permutation P with inverse). If the adversary has made a forward call x and gets response \( y = P(x) \). Then, making an inverse query y is redundant. Note that such redundancies are necessary in certain security games, most notably in indifferentiability, where the adversary can use these redundancies to catch a simulator. Let \({{\mathbb {A}}}(q,t) \) be the class of all non-trivial distinguishers limited to q oracle queries and t computations.
(Tweakable) Strong Pseudorandom Permutation (SPRP): The SPRP advantage of distinguisher \( {{\mathscr {A}}} \) against \( {E}\) instantiated with a key \({\textsf {K}} \leftarrow \!\!{\$}\,\{0,1\}^\kappa \) is defined as
The SPRP security of \( {E}\) is defined as \(\displaystyle \mathbf {Adv}^{{\textsf {sprp}}}_{{E}}(q,t) := \max _{{{\mathscr {A}}} \in {{\mathbb {A}}}(q,t)} \mathbf {Adv}^{{\textsf {sprp}}}_{E}({{\mathscr {A}}}) \). Similarly, the TSPRP advantage of distinguisher \( {{\mathscr {A}}} \) against \({\widetilde{E}}\) instantiated with a key \( {\textsf {K}} \leftarrow \!\!{\$}\,\{0,1\}^\kappa \) is defined as
The TSPRP security of \( {\widetilde{E}}\) is defined as \(\displaystyle \mathbf {Adv}^{{\textsf {tsprp}}}_{{\widetilde{E}}}(q,t) := \max _{{{\mathscr {A}}} \in {{\mathbb {A}}}(q,t)} \mathbf {Adv}^{{\textsf {tsprp}}}_{{\widetilde{E}}}({{\mathscr {A}}}) \).
2.4 The Expectation Method
Let \( {{\mathscr {A}}} \) be a computationally unbounded and deterministic distinguisher that tries to distinguish between two oracles \({\mathcal {O}}_0 \) and \( {\mathcal {O}}_1 \) via black box interaction with one of them. We denote the query–response tuple of \({{\mathscr {A}}}\)’s interaction with its oracle by a transcript \( \omega \). This may also include any additional information the oracle chooses to reveal to the distinguisher at the end of the query–response phase of the game. We denote by  (res.
(res.  ) the random transcript variable when \( {{\mathscr {A}}} \) interacts with \( {\mathcal {O}}_1 \) (res. \({\mathcal {O}}_0 \)). The probability of realizing a given transcript \(\omega \) in the security game with an oracle \( {\mathcal {O}}\) is known as the interpolation probability of \( \omega \) with respect to \( {\mathcal {O}}\). Since \( {{\mathscr {A}}} \) is deterministic, this probability depends only on the oracle \( {\mathcal {O}}\) and the transcript \( \omega \). A transcript \( \omega \) is said to be attainable if
) the random transcript variable when \( {{\mathscr {A}}} \) interacts with \( {\mathcal {O}}_1 \) (res. \({\mathcal {O}}_0 \)). The probability of realizing a given transcript \(\omega \) in the security game with an oracle \( {\mathcal {O}}\) is known as the interpolation probability of \( \omega \) with respect to \( {\mathcal {O}}\). Since \( {{\mathscr {A}}} \) is deterministic, this probability depends only on the oracle \( {\mathcal {O}}\) and the transcript \( \omega \). A transcript \( \omega \) is said to be attainable if  . The expectation method (stated below) is quite useful in obtaining improved bounds in many cases [43,44,45]. The H-coefficient technique due to Patarin [46] is a simple corollary of this result where the \(\epsilon _{{\textsf {ratio}}}\) is a constant function.
. The expectation method (stated below) is quite useful in obtaining improved bounds in many cases [43,44,45]. The H-coefficient technique due to Patarin [46] is a simple corollary of this result where the \(\epsilon _{{\textsf {ratio}}}\) is a constant function.
Lemma 2.1
(Expectation Method [43]) Let \( \varOmega \) be the set of all transcripts. For some \( \epsilon _{\textsf {bad} }> 0 \) and a nonnegative function \({\epsilon _{\textsf {ratio} }}: \varOmega \rightarrow [0,\infty ) \), suppose there is a set \( \varOmega _\textsf {bad} \subseteq \varOmega \) satisfying the following:
 ;
;For any \( \omega \notin \varOmega _\textsf {bad} \), \( \omega \) is attainable and
 .
.
Then for an distinguisher \( {{\mathscr {A}}} \) trying to distinguish between \( {\mathcal {O}}_1 \) and \( {\mathcal {O}}_0 \), we have the following bound on its distinguishing advantage:

2.5 Patarin’s Mirror Theory
In [37], Patarin defines mirror theory as a technique to estimate the number of solutions of linear systems of equalities and linear non-equalities in finite groups. In its most general case, the mirror theory proof is tractable up to the order of \( 2^{2n/3} \) security bound, but it readily becomes complex and extremely difficult to verify, as one aims for the optimal bound [40, 41]. We remark here that this in no way suggests that the result is incorrect, and in future, we might even get some independent verifications of the result.
We restrict ourselves to the binary field \( {{\mathbb {F}}}_{2}^{n}\) with \( \oplus \) as the group operation. We will use the Mennink and Neves interpretation [36] of mirror theory. For ease of understanding and notational coherency, we sometimes use different parametrization and naming conventions. Let \( q \ge 1 \) and let \({\mathcal {L}}\) be the system of linear equations
where \( Y^q \) and \( V^q \) are unknowns, and \( \lambda ^q \in (\{0,1\}^n)^q \) are knowns. In addition, there are (in)equality restrictions on \( Y^q \) and \( V^q \), which uniquely determine \({\widehat{Y}}^q \) and \( {\widehat{V}}^q \). We assume that \({\widehat{Y}}^q \) and \( {\widehat{V}}^q \) are indexed in an arbitrary order by the index sets \( [q_Y] \) and \( [q_V] \), where \( q_Y =|{\widehat{Y}}^q| \) and \( q_V = |{\widehat{V}}^q| \). This assumption is without any loss of generality as this does not affect the system \({\mathcal {L}}\). Given such an ordering, we can view \( {\widehat{Y}}^q \) and \({\widehat{V}}^q \) as ordered sets \( \{Y'_1,\ldots ,Y'_{q_Y}\} \) and \(\{V'_1,\ldots ,V'_{q_V}\} \), respectively. We define two surjective index mappings:
It is easy to verify that \( {\mathcal {L}}\) is uniquely determined by \((\varphi _Y,\varphi _V,\lambda ^q) \), and vice versa. Consider a labeled bipartite graph \( {\mathcal {G}}({\mathcal {L}}) = ([q_Y],[q_V],{\mathcal {E}}) \) associated with \( {\mathcal {L}}\), where \( {\mathcal {E}}= \{(\varphi _Y(i),\varphi _V(i),\lambda _i) : i \in [q]\} \), \(\lambda _i\) being the label of edge. Clearly, each equation in \({\mathcal {L}}\) corresponds to a unique labeled edge (assuming no duplicate equations). We give three definitions with respect to the system \({\mathcal {L}}\) using \({\mathcal {G}}({\mathcal {L}})\).
Definition 2.2
(cycle-freeness) \({\mathcal {L}}\) is said to be cycle-free if and only if \( {\mathcal {G}}({\mathcal {L}}) \) is acyclic.
Definition 2.3
(\(\xi _{\max }\)-component) Two distinct equations (or unknowns) in \( {\mathcal {L}}\) are said to be in the same component if and only if the corresponding edges (res. vertices) in \( {\mathcal {G}}({\mathcal {L}}) \) are in the same component. The size of any component \( {\mathcal {C}}\) in \( {\mathcal {L}}\), denoted \( \xi ({\mathcal {C}}) \), is the number of vertices in the corresponding component of \({\mathcal {G}}({\mathcal {L}})\), and the maximum component size is denoted by \(\xi _{\max }({\mathcal {L}})\) (or simply \( \xi _{\max } \)).
Definition 2.4
(non-degeneracy) \({\mathcal {L}}\) is said to be non-degenerate if and only if there does not exist a path of even length at least 2 in \( {\mathcal {G}}({\mathcal {L}}) \) such that the labels along the edges on this path sum up to zero.
Theorem 2.1
(Fundamental Theorem of Mirror Theory [37]) Let \({\mathcal {L}}\) be a system of equations over the unknowns \(({\widehat{Y}}^q, {\widehat{V}}^q) \), that is, (i) cycle-free, (ii) non-degenerate and (iii) \( \xi _{\max }^2 \cdot \max \{q_Y,q_V\} \le 2^n/67 \). Then, the number of solutions \((y_1,\ldots ,y_{q_Y},v_1,\ldots ,v_{q_V}) \) of \( {\mathcal {L}}\), denoted \(h_q \), such that \( y_i \ne y_j \) and \( v_i \ne v_j \) for all \(i\ne j \), satisfies
A proof of this theorem is given in [37]. As mentioned before, the proof is quite involved with some claims remaining open or unproved. On the other hand, the same paper contains results for various other cases. For instance, for \(\xi =2\), several sub-optimal bounds have been shown. By sub-optimal, we mean that a factor of \( (1-\epsilon ) \), for some \( \epsilon > 0 \), is multiplied to the right-hand side of Eq. (3). Inspired by this, we give the following terminology which will be useful in later references to mirror theory.
For \( \xi \ge 2 \), \( \epsilon > 0 \), we write \((\xi ,\epsilon )\)-restricted mirror theory theorem to denote the mirror theory result in which the number of solutions, \( h_q \), of a system of equations with \( \xi _{\max } = \xi \), satisfies \( h_q \ge \left( 1-\epsilon \right) \frac{(2^n)_{q_Y}(2^n)_{q_V}}{2^{nq}} \).
Mirror theory has been primarily used for bounding the pseudorandomness of sum of permutations [37, 40, 47, 48] with respect to a random function. For instance, suppose we sample elements in \({\widehat{Y}}^q \) and \( {\widehat{V}}^q \) as outputs of two independent random permutations \( \Pi _1 \) and \( \Pi _2 \), respectively, over \(q_Y\) and \( q_V \) distinct inputs, respectively. Let \({\textsf {pr}}_{1} \) be the probability of realizing the system of equations \( {\mathcal {L}}\) and \( {\textsf {pr}}_{0} \) be the probability of realizing the q-tuple \( \lambda ^q \) through random function outputs over q distinct inputs. Then, it is easy to see that \( {\textsf {pr}}_{1} = h_q/(2^n)_{q_Y}(2^n)_{q_V}\) and \( {\textsf {pr}}_{0} = 1/2^{nq} \). Clearly, the above-given lower bound on \( h_q \) implies that \( {\textsf {pr}}_{1} \ge (1 - \epsilon ) {\textsf {pr}}_{0} \). When combined with the H-coefficient technique, we get an \( \epsilon \) term in the distinguishing advantage bound for sum of random permutations. Here, \( \epsilon \) can be viewed as the degree of deviation from random function behavior. This is precisely the reason that one finds terms of the form \( (2^n)_{q_Y}(2^n)_{q_V} \) and \( 2^{nq} \) in mirror theory bounds. We refer the readers to [36, 37] for a more detailed exposition on the aim and motivations behind mirror theory.
In [29], \( (4,{3q}/{2^{n}}) \)-restricted mirror theory theorem is used. In Sect. 5, we study the \( (\xi ,{q^4}/{2^{3n}}) \) case, for \( \xi \le 2^n/2q \) and present a variant of mirror theory suitable for tweakable permutation scenario.
3 Revisiting Mennink’s Improved Bound on CLRW2
We first describe the notion of \( \ell \)-wise independent XOR universal hash functions as given in [29]. This notion will be used for the description of CLRW2 (for \( \ell = 2 \)), as well as Mennink’s improved bound on CLRW2 (for \( \ell = 4 \)).
Definition 3.1
For \( \ell \ge 2 \), \( \epsilon \ge 0 \), a family of functions \({\mathcal {H}}= \{h: \{0,1\}^\tau \rightarrow \{0,1\}^n\} \) is called an \(\ell \)-wise independent XOR universal hash up to the bound \(\epsilon \), denoted \( \epsilon \text {-AXU}_{\ell } \), if for any \( j \in \{2,\ldots ,\ell \}\), any \( t^j \in (\{0,1\}^\tau )_{j} \) and a \(\delta ^{j-1} \in (\{0,1\}^n)^{j-1} \), we have
For \( \ell = 2 \), this is nothing but the notion of AXU hash functions, first introduced by Krawczyk [49] and later by Rogaway [50]. In [29], the author suggested a simple \( \text {AXU}_\ell \) hash function family using finite field arithmetic for small domain (\( \tau =n \)). Basically, the hash function family is defined as follows
for \( h = (h_1,\ldots ,h_{\ell -1}) \), where \( \odot \) denotes field multiplication operator with respect to some irreducible polynomial over the binary field \( {{\mathbb {F}}}_{2}^{n}\). For \( \ell =2 \), this yields the popular polyhash function. In general, this function requires \(\ell -1 \) keys and \( \ell -1 \) field multiplications to achieve \(2^{-n}\text {-AXU}_\ell \). Alternatively, secure block ciphers can also be used to construct \( (2^{n}-\ell +1)^{-1}\text {-AXU}_\ell \) hash functions over sufficiently large domains.
3.1 Description of the Cascaded LRW2 Construction
Let \( {E}\in {\textsf {BPerm}}(\kappa ,n) \) be a block cipher. Let \( {\mathcal {H}}\) be a hash function family from \( \{0,1\}^\tau \) to \( \{0,1\}^n\). We define the tweakable block cipher \( \textsf {LRW2} [{E},{\mathcal {H}}] \), based on the block cipher \( {E}\) and the hash function family \( {\mathcal {H}}\), by the following mapping: \( \forall (k,h,t,m) \in \{0,1\}^\kappa \times {\mathcal {H}}\times \{0,1\}^\tau \times \{0,1\}^n\),
For \( \ell \in {{\mathbb {N}}}\), the \( \ell \)-round cascaded LRW2 construction, denoted \( \textsf {CLRW2} [{E},{\mathcal {H}},\ell ] \), is a cascade of \(\ell \) independent LRW2 instances, i.e., \( \textsf {CLRW2} [{E},{\mathcal {H}},\ell ] \) is a tweakable block cipher, based on the block cipher \( {E}\) and the hash function family \( {\mathcal {H}}\), defined as follows: \( \forall (k^\ell ,h^\ell ,t,m) \in \{0,1\}^{\kappa \ell } \times {\mathcal {H}}^\ell \times \{0,1\}^\tau \times \{0,1\}^n\),
The two-round CLRW2 was first analyzed by Landecker et al. [26], whereas the \( \ell > 2 \) case was studied by Lampe and Seurin [28]. Since we mainly focus on the \(\ell = 2 \) case, we use the nomenclatures, CLRW2 and cascaded LRW2, interchangeably with two-round CLRW2. Figure 1 gives a pictorial description of the cascaded LRW2 construction. Throughout the rest of the paper, we use the notations from Fig. 1 in the context of CLRW2.
In [26] the CLRW2 construction was shown to be a BBB secure (up to \( 2^{2n/3} \) queries) TSPRP, provided the underlying block cipher is an SPRP, and the hash function families are AXU.
3.2 Mennink’s Proof Approach
The proof in [29] applies H-coefficient technique coupled with mirror theory. The main focus is to identify a suitable class of bad events on \( (x^q,u^q) \), where q is the number of queries, which makes mirror theory inapplicable. Crudely, the bad events correspond to cases where for some query there is no randomness left (in the sampling of \( y^q \) and \( v^q \)) in the ideal world. Given a good transcript, mirror theory is applied to bound the number of solutions of the system of equation \( \{Y_i \oplus V_i = \lambda _i : i \in [q]\} \), where \( Y_i \) and \( V_i \) are unknowns satisfying \( {x^q}\leftrightsquigarrow {Y^q} \) and \( {V^q}\leftrightsquigarrow {u^q} \), and \( \lambda ^q \) is fixed. The proof relies on three major assumptions:
Assumption 1. \( {\mathcal {H}}\) is \( \text {AXU}_4 \) hash function family.
Assumption 2. For any \( t' \in \{0,1\}^\tau \), \(\mu _{t'} = \mu (t^q,t') \le \gamma = 2^{n/4} \).
Assumption 3. \( \left( 4,\frac{3q}{2^{n}}\right) \)-restricted mirror theory theorem is correct.
Transcript Graph: A graphical view on \( x^q \) and \( u^q \) was used to characterize all bad events. Basically, each transcript is mapped to a unique bipartite graph on \( x^q,u^q \), as defined in Definition 3.2.
Definition 3.2
(Transcript Graph) A transcript graph \( {\mathcal {G}}= ({\mathcal {X}},{\mathcal {U}},{\mathcal {E}}) \) associated with \((x^q,u^q) \), denoted \( {\mathcal {G}}(x^q,u^q) \), is defined as \( {\mathcal {X}}:=\{(x_i,0) : i \in [q]\};~ {\mathcal {U}}:= \{(u_i,1) : i \in [q]\};~\text {and } {{\mathcal {E}}} := \{((x_i,0),(u_i,1)) : i \in [q]\}\). We also associate the value \( \lambda _i = h_1(t_i) \oplus h_2(t_i)\) with edge \( ((x_i,0),(u_i,1)) \in {\mathcal {E}}\).
Note that the graph may not be simple, i.e., it can contain parallel edges. For all practical purposes, we may drop the 0 and 1 for \( (x,0) \in {\mathcal {X}}\) and \( (u,1) \in {\mathcal {U}}\), as they can be easily distinguished from the context and notations. Further, for some \( i,j \in [q] \), if \( x_i = x_j \) (or \( u_i=u_j \)), then they share the same vertex \( x_i = x_j = x_{i,j} \) (or \( u_i = u_j =u_{i,j} \)). The event \( x_i=x_j \) and \( u_i=u_j \), although extremely unlikely, will lead to a parallel edge in \( {\mathcal {G}}\). Finally each edge \( (x_i,u_i) \in {\mathcal {E}}\) corresponds to a query index \( i \in [q] \), so we can equivalently view (and call) the edge \( (x_i,u_i) \) as index i. Figure 2 gives an example graph for \( {\mathcal {G}}\).
Bad Transcripts: A transcript graph \({\mathcal {G}}(x^q,u^q) \) is called bad if:
- 1.
it has a cycle of size \( = 2 \).
- 2.
it has two adjacent edges i and j such that \(\lambda _i \oplus \lambda _j = 0 \).
- 3.
it has a component with number of edges \( \ge 4 \).
All subgraphs in Fig. 2, except the first two from left, are considered bad in [29]. Conditions 1 and 2 correspond to the cases which might lead to degeneracy in the real world. Condition 3 may lead to a cycle of length \( \ge 4 \) edges. The non-fulfillment of conditions 1, 2 and 3 satisfies the cycle-free and non-degeneracy properties required in mirror theory. It also bounds \( \xi _{\max } \le 4 \). Conditions 1 and 2 contribute small and insignificant terms and can be ignored from this discussion. We focus on the major bottleneck, i.e., condition 3. The subgraphs corresponding to condition 3 are given in Fig. 3. Configurations (D), (E) and (F) are symmetric to (A), (B) and (C). So we can study (A), (B) and (C), and the other three can be similarly analyzed.
Bottleneck 1: Bound on the probability of (A), (C), (D) and (F)—This can be divided into two parts:
- (a)
Configuration (A) arises for the event
$$\begin{aligned} \exists ^{*}i,j,k,l \text { such that } x_i = x_j = x_k = x_\ell . \end{aligned}$$This event is upper bounded to \( q^4\epsilon ^3 \) using assumption 1 on hash functions. Similar argument holds for (D).
- (b)
Configuration (C) (similarly for F) arises for the event
$$\begin{aligned} \exists ^{*}i,j,k,\ell \in [q] \text { such that } x_i = x_j = x_k \wedge u_k = u_\ell . \end{aligned}$$In this case, we can apply assumption 1 (even \( \text {AXU}_3 \) would suffice) to get an upper bound of \( q^4\epsilon ^3 \).
Bottleneck 2: Bound on the probability of (B)—Configuration (B) arises for the event
This is probably the trickiest case, which requires assumption 2, i.e., restriction on tweak repetition. Specifically, consider the case \( t_i = t_k \) and \( t_j = t_\ell \). This is precisely the case exploited in Mennink’s attack on CLRW2 [29] (see supplementary material B). In this case, for a fixed \( i,j,k,\ell \) the probability is bounded by \( \epsilon ^2 \). There are at most \( q^2 \) choices for (i, j), at most \((\mu _{t_i}-1) \) choices for k and a single choice for \( \ell \) given i, j and k. Thus, the probability is bounded by \(q^2\gamma \epsilon ^2 \) (using assumption 2). Similar argument holds for (E).
Bottleneck 3: Mirror theory bound—The final hurdle is the use of mirror theory in computation of real-world interpolation probability, which requires assumption 3. Yet another issue is the nature of the mirror theory bound. A straightforward application of mirror theory bound leads to a term of the form

in the ratio of interpolation probabilities (as required for H-coefficient technique), where \( \sum _{t' \in {\widehat{t}}^q} \mu _{t'} = q \). The boxed expression (particularly, the numerator in the expression) is of main interest. In the worst case, \( \mu _{t'} =O(q) \), which gives a lower bound of the form \( 1-{q^2}/{2^n} \) for the boxed expression. But using assumption 2, we get a lower bound of \( 1-{q\gamma }/{2^n} \) as \( \mu _{t'} \le \gamma \).
3.2.1 Severity of the Assumptions in [29]
Among the three assumptions, assumptions 1 and 2 are plausible in the sense that real-life use cases exist for assumption 2 and practical instantiations are possible for assumption 1. Another point of note is the fact that \( \gamma < 2^{n/4} \) is imposed due to bottleneck 3. Otherwise, a better bound of \( \gamma < 2^{n/2} \) could have been used. While assumptions 1 and 2 are plausible to a large extent, assumption 3 is disputable. This is because no publicly verifiable proof exists for the generalized mirror theory. In fact, the proof for a special case of mirror theory also has some unproved gaps and mistakes. See Remark 1 for one such issue.
Although the proof in [29] requires the above-mentioned assumptions, the proof approach seems quite simple, and in some cases, it highlights the bottlenecks in getting tight security. In the remainder of this paper, we aim to resolve all the bottlenecks discussed here, while relaxing all the assumptions made in [29]. Specifically, bottleneck 2 is resolved using the tools from Sect. 4, and bottlenecks 1 and 3 are resolved using the tools from Sects. 4 and 5, and a careful application of the expectation method in Sect. 6.
4 Results on (Multi)Collisions in Universal Hash
Let \( {\mathcal {H}}= \{h\ |\ h: {\mathcal {T}}\rightarrow {\mathcal {B}}\} \) be a family of functions. A pair of distinct elements \( (t, t') \) from \( {\mathcal {T}}\) is said to be colliding for a function \( h \in {\mathcal {H}}\), if \( h(t) =h(t') \). A family of functions \( {\mathcal {H}}= \{h\ |\ h: {\mathcal {T}}\rightarrow {\mathcal {B}}\} \) is called an \( \epsilon \)-universal hash if for all \( t \ne t' \in {\mathcal {T}}\),
Throughout this section, we fix \( t^q = (t_1, \ldots , t_q) \in ({\mathcal {T}})_q \). For a randomly chosen hash function \({\textsf {H}} \leftarrow \!\!{\$}\,{\mathcal {H}}\), the probability of having at least one colliding pair in \( t^q \) is at most \( {q \atopwithdelims ()2} \cdot \epsilon \). This is straightforward from the union bound.
4.1 The Alternating Collisions and Events Lemmata
Suppose \( {\mathcal {H}}\) is an \( \epsilon \)-universal hash, and \({\textsf {H}}_1,{\textsf {H}}_2 \leftarrow \!\!{\$}\,{\mathcal {H}}\) are two independently drawn universal hash functions. Then, by applying independence and union bound, we have
Now we go one step further. We would like to bound the probability of the following event:
For any fixed distinct i, j, k and l, we cannot claim that the probability of the event \( {\textsf {H}}_1(t_i) ={\textsf {H}}_1(t_j) \ \wedge \ {\textsf {H}}_2(t_j) ={\textsf {H}}_2(t_k)\ \wedge \ {\textsf {H}}_1(t_k) ={\textsf {H}}_1(t_l)\) is \(\epsilon ^3\) as the first and last events are no longer independent. Now, we show how we can get an improved bound even in the dependent situation. In particular, we prove the following lemma.
Lemma 4.1
(Alternating Collisions Lemma) Suppose \(\textsf {H} _1,\textsf {H} _2 \leftarrow \!\!{\$}\,{\mathcal {H}}\) are two independently drawn \( \epsilon \) universal hash functions and \( t^q \in ({\mathcal {T}})_q \). Then,
Proof
For any \( h \in {\mathcal {H}}\), we define the following useful set:
Let us denote the size of the above set by \( I_h \). So, \( I_h \) is the number of colliding pairs for the hash functions h. We also define a set \( {\mathcal {H}}_{\le } = \{h: I_h \le \frac{1}{\sqrt{\epsilon }} \} \) which collects all hash functions having a small number of colliding pairs. We denote the complement set by \( {\mathcal {H}}_> \). Now, by using double counting of the set \( \{(h, i,j) : h(t_i) = h(t_j)\} \) we get
Basically for every h, we have exactly \( I_h \) choices of (i, j), and so, the size of the set \( \{(h, i,j) : h(t_i) = h(t_j)\} \) is exactly \( \sum _h I_h \). On the other hand, for any \( 1 \le i <j \le q \), there are at most \( \epsilon \cdot |{\mathcal {H}}| \) hash functions h, such that \( (t_i, t_j) \) is a colliding pair for h. This follows from the definition of the universal hash function. From Eq. (8) and the definition of \({\mathcal {H}}_{\le } \), we have
Let \( \texttt {E} \) denote the event that there exist distinct i, j, k and l such that \( {\textsf {H}}_1(t_i) ={\textsf {H}}_1(t_j)\ \wedge \ {\textsf {H}}_1(t_k) ={\textsf {H}}_1(t_l)\ \wedge \ {\textsf {H}}_2(t_j) ={\textsf {H}}_2(t_k) \). Now, we proceed to bound the probability of this event.
First, we justify inequality 1. Given \( {\textsf {H}}_1 = h \), the probability of the event \( \texttt {E} \) is same as the probability of the following event:
There are at most \( I_h^2 \) pairs of pairs and for each pair of pairs and the collision probability of \( {\textsf {H}}_2(t_j) = {\textsf {H}}_2(t_k) \) is at most \( \epsilon \). So probability of the above event can be at most \( \min \{1, I_h^2\cdot \epsilon \} \). Now, we justify inequality 2 using two facts. First, \( {\textsf {H}}_1 \leftarrow \!\!{\$}\,{\mathcal {H}}\), i.e., \({\Pr _{}\left[ {{\textsf {H}}_1 = h}\right] } = |{\mathcal {H}}|^{-1} \) for all \( h \in {\mathcal {H}}\). Second, for all \( h \in {\mathcal {H}}_{\le } \), \( I_h \le 1/\sqrt{\epsilon } \). Inequality 3 follows from Eq. (9). \(\square \)
Now, we generalize the above result for a more general setting. The proof of the result is similar to the previous proof, and hence, we skip it (given in supplementary material C).
Lemma 4.2
(Alternating Events Lemma) Let \( \textsf {X} ^q =(\textsf {X} _1,\ldots , \textsf {X} _q) \) be a q-tuple of random variables. Suppose for all \( i < j \in [q] \), \(\texttt {E} _{i,j} \) are events associated with \( \textsf {X} _i \) and \(\textsf {X} _j\), possibly dependent. Each event holds with probability at most \( \epsilon \). Moreover, for any distinct \( i, j, k, l \in [q] \), \(\texttt {F} _{i,j, k, l} \) are events associated with \(\textsf {X} _i \), \( \textsf {X} _j\), \(\textsf {X} _k \) and \( \textsf {X} _l \), which holds with probability at most \( \epsilon ' \). Moreover, the collection of events \((\texttt {F} _{i,j, k, l})_{i,j,k,l} \) is independent with the collection of event \((\texttt {E} _{i,j})_{i,j} \). Then,
Note that Lemma 4.1 is a direct corollary of the above lemma. (The event \( \texttt {E}_{i,j} \) denotes that \( (t_i, t_j) \) is a colliding pair of \( {\textsf {H}}_1 \) and \( \texttt {F}_{i,j,k,l} \) denotes that \( (t_j, t_k) \) is a colliding pair of \( {\textsf {H}}_2 \).)
4.2 Expected Multicollisions in Universal Hash
Suppose \( {\mathcal {H}}\) is an \( \epsilon \)-universal hash, and \({\textsf {H}} \leftarrow \!\!{\$}\,{\mathcal {H}}\). Let \( {\textsf {X}}^q ={\textsf {H}}(t^q) \). We define an equivalence relation \(\sim \) on [q] as: \( \alpha \sim \beta \) if and only if \({\textsf {X}}_\alpha = {\textsf {X}}_\beta \) (i.e., \(\sim \) is simply the multicollision relation). Let \({\mathcal {P}}_1,{\mathcal {P}}_2,\ldots ,{\mathcal {P}}_r \) denote those equivalence classes of [q] corresponding to \( \sim \), such that \( {\nu }_i =|{\mathcal {P}}_i| \ge 2 \) for all \( i \in [r] \). In the following lemma, we present a simple yet powerful result on multicollisions in universal hash functions.
Lemma 4.3
Let \( \textsf {C} \) denote the number of colliding pairs in \( \textsf {X} ^q \). Then, we have
Proof
For \( i \in [r] \), each of the \( {\nu _i \atopwithdelims ()2} \) pairs in \(({\mathcal {P}}_i)_2 \) correspond to 1 colliding pair. And each colliding pair belongs to \( ({\mathcal {P}}_i)_2 \) for some \( i \in [r] \), as equality implies that the corresponding indices are related by \(\sim \). Thus, we have
The result follows from the fact that \( {\textsf {Ex} _{}\left[ {{\textsf {C}}}\right] } \le {q \atopwithdelims ()2} \epsilon \). \(\square \)
Lemma 4.3 results in a simple corollary given below, which was independently proved in [51].
Corollary 4.1
Let \( {\nu }_{\max } = \max \{{\nu }_i:i\in [r]\} \). Then, for some \(a\ge 2 \), we have
Proof
We have
where the last inequality follows from Markov’s inequality. \(\square \)
Dutta et al. [52] proved a weakerFootnote 2 variant of Corollary 4.1, using an elegant combinatorial argumentation.
5 Mirror Theory in Tweakable Permutation Setting
As evident from bottleneck 3 of Sect 3.2, a straightforward application of mirror theory bound would lead to a sub-optimal bound. In order to circumvent this sub-optimality, Mennink [29] used a restriction on tweak repetitions (assumption 2 of Sect. 3.2). Specifically, a bound of the form \( O(q/2^{3n/4}) \) requires \( \mu (t^q,t') <2^{n/4}\) for all \( t' \in {\widehat{t}}^q \), where \( t^q \) denotes the q-tuple of tweaks used in the q queries. In order to avoid this assumption, we need a different approach.
A closer inspection of the mirror theory proof reveals that we can actually avoid the restrictions on tweak repetitions. In fact, rather surprisingly, we will see that tweak repetitions are actually helpful in the sense that mirror theory bound is good. In the remainder of this section, we develop a modified version of mirror theory, apt for applications in tweakable permutation settings.
5.1 General Setup and Notations
Isolated and Star Components: In an edge-labeled bipartite graph \( {\mathcal {G}}= ({\mathcal {Y}},{\mathcal {V}},{\mathcal {E}}) \), an edge \( (y,v,\lambda ) \) is called isolated edge if both y and v have degree 1. A component \( {\mathcal {S}}\) of \( {\mathcal {G}}\) is called star, if \(\xi ({\mathcal {S}}) \ge 3 \) and there exists a unique vertex v in \({\mathcal {S}}\) with degree \( \xi ({\mathcal {S}})-1 \). We call v the center of \({\mathcal {S}}\). Further, we call \( {\mathcal {S}}\) a \( {{\mathcal {Y}}}_{\text {-}\star }\) (res. \( {{\mathcal {V}}}_{\text {-}\star }\)) component if its center lies in \( {\mathcal {Y}}\) (res. \( {\mathcal {V}}\)).
The System of Equation: Following the notations and definitions from Sect. 2.5, consider a system of equation \( {\mathcal {L}}\)
such that each component in \( {\mathcal {G}}({\mathcal {L}}) \) is either an isolated edge or a star. Let \( c_1 \), \( c_2 \) and \( c_3 \) denote the number of components of isolated, \( {{\mathcal {Y}}}_{\text {-}\star }\) and \( {{\mathcal {V}}}_{\text {-}\star }\) types, respectively. Let \( q_1 \), \( q_2 \) and \( q_3 \) denote the number of equations of isolated, \( {{\mathcal {Y}}}_{\text {-}\star }\) and \( {{\mathcal {V}}}_{\text {-}\star }\) types, respectively. Therefore, \( c_1 = q_1 \).
Note that the equations in \( {\mathcal {L}}\) can be arranged in any arbitrary order without affecting the number of solutions. For the sake of simplicity, we fix the ordering in such a way that all isolated edges occur first, followed by the star components.
Now, our goal is to give a lower bound on the number of solutions of \( {\mathcal {L}}\), such that the \( Y'_i \) values are pairwise distinct and \(V'_i\) values are pairwise distinct. More formally, we aim to prove the following result.
Theorem 5.1
Let \( {\mathcal {L}}\) be the system of linear equations as described above with \( q < 2^{n-2} \) and \( \xi _{\max }q \le 2^{n-1} \). Then, the number of tuples \( (y_1,\ldots ,y_{q_Y},v_1,\ldots ,v_{q_V}) \) that satisfy \( {\mathcal {L}}\), denoted \( h_q \), such that \( y_i \ne y_j \) and \(v_i \ne v_j \), for all \( i \ne j \), satisfies:
where \( \eta _{j} = \xi _{j}-1 \) and \( \xi _{j} \) denotes the size (number of vertices) of the jth component, for all \(j\in [c_1+c_2+c_3] \).
We note here that the bound in Theorem 5.1 is parametrized in q and \(\xi \). This is a bit different from the traditional mirror theory bounds. Further, we note that the bounds in Theorem 5.1 becomes \( 1-O(q^4/2^{3n}) \), when the value of \( \sum _{i=1}^{c_2+c_3}\eta ^2_{c_1+i} \) is \(O(q^2/2^{n}) \). When we apply this result to CLRW2 and \(\textsf {DbHtS-p}\), we can show that the expected value of the term is indeed \(O(q^2/2^{n})\) (a good time to revisit Lemma 4.3). Corollary 5.1 is useful for random function setting.
Corollary 5.1
Let \( {\mathcal {L}}\) be the system of linear equations as described above with \( q < 2^{n-2} \) and \( \xi _{\max }q < 2^{n-1} \). Then, the number of tuples \( (y_1,\ldots ,y_{q_Y},v_1,\ldots ,v_{q_V}) \) that satisfy \({\mathcal {L}}\), denoted \( h_q \), such that \( y_i \ne y_j \) and \( v_i \ne v_j \), for all \( i \ne j \), satisfies:
where \( \eta _{j} = \xi _{j}-1 \) and \( \xi _{j} \) denotes the size (number of vertices) of the jth component, for all \(j\in [c_1+c_2+c_3] \).
Note the difference between the expressions given in Theorem 5.1 and Corollary 5.1. Looking back at the discussion given toward the end of Sect. 2.5, one can see the motivation behind the denominator given in Corollary 5.1. Since we aim to apply mirror theory in tweakable permutation setting, the denominator is changed accordingly in Theorem 5.1.
The proof of Theorem 5.1 uses an inductive approach similar to the one in [37]. We postpone the complete proof to supplementary material D.
6 Tight Security Bound of CLRW2
Based on the tools, we developed in Sects. 4 and 5, and we now show that the CLRW2 construction achieves security up to the query complexity approximately \( 2^{3n/4} \). Given Mennink’s attack [29] (see supplementary material B) in roughly these many queries, we can conclude that the bound is tight.
Theorem 6.1
Let \( \kappa ,\tau ,n \in {{\mathbb {N}}}\) and \( \epsilon > 0 \). Let \( {E}\in {\textsf {BPerm} }(\kappa ,n) \), and let \( {\mathcal {H}}\) be an \( (\{0,1\}^\tau ,\{0,1\}^n,\epsilon ) \)-AXU hash function family. Consider
For \( q \le 2^{n-2} \) and \( t > 0 \), the TSPRP security of \(\text {\textsf {CLRW2}}[{E},{\mathcal {H}}] \) against \( {{\mathbb {A}}}(q,t) \) is given by
where \( t' = c(t + qt_{{\mathcal {H}}}) \), \( t_{{\mathcal {H}}} \) being the time complexity for computing the hash function \( {\mathcal {H}}\), \( c > 0 \) is a constant depending upon the computation model, and
On putting \( \epsilon = 1/2^n \), in Eq. (10) and further simplifying, we get
Corollary 6.1
For \( \epsilon = \frac{1}{2^n} \), we have
Specifically, the advantage bound is meaningful up to \( q \approx 2^{\frac{3n}{4}-1.43} \) queries.
The proof of Theorem 6.1 employs the expectation method coupled with an adaptation of \( (2^n/2q,q^4/2^{3n}) \)-restricted mirror theory [37] in tweakable permutation settings. While our use of mirror theory is somewhat inspired by its recent use in [29], in contrast to [29], we apply a modified version of mirror theory and that too for a restricted subset of queries. The complete proof of Theorem 6.1 is given in the remainder of this section.
6.1 Initial Step
Consider the instantiation \( \textsf {CLRW2} [{E}_{{\textsf {K}}_1},{E}_{{\textsf {K}}_2},{\textsf {H}}_1,{\textsf {H}}_2] \) of \( \textsf {CLRW2} [{E},{\mathcal {H}}] \), where \( {\textsf {K}}_1\), \({\textsf {K}}_2\), \( {\textsf {H}}_1\), \({\textsf {H}}_2 \) are independent and \( ({\textsf {K}}_1, {\textsf {K}}_2) \leftarrow \!\!{\$}\,(\{0,1\}^{\kappa })^2 \), \( ({\textsf {H}}_1,{\textsf {H}}_2) \leftarrow \!\!{\$}\,{\mathcal {H}}^2 \). As the first step, we switch to the information-theoretic setting, i.e., we replace \( ({E}_{{\textsf {K}}_1},{E}_{{\textsf {K}}_2}) \) with \( (\Pi _1,\Pi _2) \leftarrow \!\!{\$}\,{\textsf {Perm}}(n)^2 \). For the sake of simplicity, we write the modified instantiation \( \textsf {CLRW2} [\Pi _1,\Pi _2,{\textsf {H}}_1,{\textsf {H}}_2] \) as \( \textsf {CLRW2} \), i.e., without any parametrization. This switching is done via a standard hybrid argument that incurs a cost of \( 2\mathbf {Adv}^{{\textsf {sprp}}}_{{E}}(q,t') \) where \( t' = O(t + qt_{{\mathcal {H}}}) \). Thus, we have
So, in Eq. (12), we have to give an upper bound on \( \mathbf {Adv}^{{\textsf {tsprp}}}_{\textsf {CLRW2}}(q) \). At this point, we are in the information-theoretic setting. In other words, we consider computationally unbounded distinguisher \( {{\mathscr {A}}} \). Without loss of generality, we assume that \( {{\mathscr {A}}} \) is deterministic and non-trivial. Under this setup, we are now ready to apply the expectation method.
6.2 Oracle Description
The two oracles of interest are: \( {\mathcal {O}}_1 \), the real oracle, that implements \( \textsf {CLRW2} \); and \( {\mathcal {O}}_0 \), the ideal oracle, that implements \( {{\widetilde{\Pi }}}\leftarrow \!\!{\$}\,{\textsf {BPerm}}(\tau ,n) \). We consider an extended version of these oracles, the one in which they release some additional information. We use notations analogously as given in Fig. 1 to describe the transcript generated by \( {{\mathscr {A}}} \)’s interaction with its oracle.
6.2.1 Description of the Real Oracle, \( {\mathcal {O}}_1 \):
The real oracle \( {\mathcal {O}}_1 \) faithfully runs \( \textsf {CLRW2} \). We denote the transcript random variable generated by \( {{\mathscr {A}}} \)’s interaction with \( {\mathcal {O}}_1 \) by the usual notation  , which is a 10-ary q-tuple
, which is a 10-ary q-tuple
defined as follows: The initial transcript consists of \( ({\textsf {T}}^q,{\textsf {M}}^q,{\textsf {C}}^q) \), where for all \( i \in [q] \):
\( {\textsf {T}}_i \): ith tweak value, \( {\textsf {M}}_i \): ith plaintext value, \( {\textsf {C}}_i \): ith ciphertext value
where \( {\textsf {C}}^q = \textsf {CLRW2} ({\textsf {T}}^q,{\textsf {M}}^q) \). At the end of the query–response phase, \( {\mathcal {O}}_1 \) releases some additional information \( ({\textsf {X}}^q,{\textsf {Y}}^q,{\textsf {V}}^q,{\textsf {U}}^q,{\lambda }^q,{\textsf {H}}_1,{\textsf {H}}_2) \), where for all \( i \in [q] \):
\( ({\textsf {X}}_i,{\textsf {Y}}_i) \): ith input–output pair for \( \Pi _1 \),
\( ({\textsf {V}}_i,{\textsf {U}}_i) \): ith input–output pair for \( \Pi _2 \),
\( {\lambda }_i \): ith internal masking, \( {\textsf {H}}_1,{\textsf {H}}_2 \): the hash keys.
Note that \( {\textsf {X}}^q \), \( {\textsf {U}}^q \) and \( {\lambda }^q \) are completely determined by the hash keys \( {\textsf {H}}_1,{\textsf {H}}_2 \) and the initial transcript \( ({\textsf {T}}^q,{\textsf {M}}^q,{\textsf {C}}^q) \). But, we include them anyhow to ease the analysis.
6.2.2 Description of the Ideal Oracle, \( {\mathcal {O}}_0 \):
The ideal oracle \( {\mathcal {O}}_0 \) has access to \( {{\widetilde{\Pi }}}\). Since \( {\mathcal {O}}_1 \) releases some additional information, \( {\mathcal {O}}_0 \) must generate these values as well. The ideal transcript random variable  is also a 10-ary q-tuple
is also a 10-ary q-tuple
defined below. Note that we use the same notation to represent the variables of transcripts in the both worlds. However, the probability distributions of these would be determined from their definitions. The initial transcript consists of \( ({\textsf {T}}^q,{\textsf {M}}^q,{\textsf {C}}^q) \), where for all \( i \in [q] \):
\( {\textsf {T}}_i \): ith tweak value, \( {\textsf {M}}_i \): ith plaintext value, \( {\textsf {C}}_i \): ith ciphertext value,
where \( {\textsf {C}}^q = {{\widetilde{\Pi }}}({\textsf {T}}^q,{\textsf {M}}^q) \). Once the query–response phase is over \( {\mathcal {O}}_0 \) first samples \( ({\textsf {H}}_1,{\textsf {H}}_2) \leftarrow \!\!{\$}\,{\mathcal {H}}^2 \) and computes \( {\textsf {X}}^q,{\textsf {U}}^q,{\lambda }^q \), where for all \( i \in [q] \):
\( {\textsf {X}}_i := {\textsf {H}}_1({\textsf {T}}_i) \oplus {\textsf {M}}_i \), \( {\textsf {U}}_i := {\textsf {H}}_2({\textsf {T}}_i) \oplus {\textsf {C}}_i \), \( {\lambda }_i := {\textsf {H}}_1({\textsf {T}}_i) \oplus {\textsf {H}}_2({\textsf {T}}_i) \).
This means that \( {\textsf {X}}^q \), \( {\textsf {U}}^q \) and \( {\lambda }^q \) are defined honestly. Given the partial transcript  we wish to characterize the hash key \( {\textsf {H}} := ({\textsf {H}}_1,{\textsf {H}}_2) \) as good or bad. We write \( {\mathcal {H}}_{{\textsf {bad}}} \) for the set of bad hash keys, and \( {\mathcal {H}}_{\textsf {good}}= {\mathcal {H}}^2{\setminus }{\mathcal {H}}_{{\textsf {bad}}} \). We say that a hash key \( {\textsf {H}} \in {\mathcal {H}}_{{\textsf {bad}}} \) (or \( {\textsf {H}} \) is bad) if and only if one of the following predicates is true:
we wish to characterize the hash key \( {\textsf {H}} := ({\textsf {H}}_1,{\textsf {H}}_2) \) as good or bad. We write \( {\mathcal {H}}_{{\textsf {bad}}} \) for the set of bad hash keys, and \( {\mathcal {H}}_{\textsf {good}}= {\mathcal {H}}^2{\setminus }{\mathcal {H}}_{{\textsf {bad}}} \). We say that a hash key \( {\textsf {H}} \in {\mathcal {H}}_{{\textsf {bad}}} \) (or \( {\textsf {H}} \) is bad) if and only if one of the following predicates is true:
- 1.
\({\texttt {H}}_1\):\( \exists ^{*}i,j \in [q] \) such that \( {\textsf {X}}_i = {\textsf {X}}_j \wedge {\textsf {U}}_i = {\textsf {U}}_j \).
- 2.
\({\texttt {H}}_2\):\( \exists ^{*}i,j \in [q] \) such that \( {\textsf {X}}_i = {\textsf {X}}_j \wedge {\lambda }_i = {\lambda }_j \).
- 3.
\(\texttt {H}_3\):\( \exists ^{*}i,j \in [q] \) such that \( {\textsf {U}}_i = {\textsf {U}}_j \wedge {\lambda }_i = {\lambda }_j \).
- 4.
\(\texttt {H}_4\):\( \exists ^{*}i,j,k,\ell \in [q] \) such that \( {\textsf {X}}_i = {\textsf {X}}_j \wedge {\textsf {U}}_j = {\textsf {U}}_k \wedge {\textsf {X}}_k = {\textsf {X}}_\ell \).
- 5.
\(\texttt {H}_5\):\( \exists ^{*}i,j,k,\ell \in [q] \) such that \( {\textsf {U}}_i = {\textsf {U}}_j \wedge {\textsf {X}}_j = {\textsf {X}}_k \wedge {\textsf {U}}_k = {\textsf {U}}_\ell \).
- 6.
\(\texttt {H}_6\):\( \exists k \ge 2^n/2q, \exists ^{*}i_1,i_2,\ldots ,i_{k} \in [q] \) such that \( {\textsf {X}}_{i_1} = \cdots = {\textsf {X}}_{i_{k}} \).
- 7.
\(\texttt {H}_7\):\( \exists k \ge 2^n/2q, \exists ^{*}i_1,i_2,\ldots ,i_{k} \in [q] \) such that \( {\textsf {U}}_{i_1} = \cdots = {\textsf {U}}_{i_{k}} \).
Case 1.\( {\textsf {H}} \)is bad: If the hash key \( {\textsf {H}} \) is bad, then \( {\textsf {Y}}^q \) and \( {\textsf {V}}^q \) values are sampled degenerately as \( {\textsf {Y}}_i = {\textsf {V}}_i = 0 \) for all \( i \in [q] \). It means that we sample without maintaining any specific conditions, which may lead to inconsistencies.
Case 2.\( {\textsf {H}} \)is good: To characterize the transcript corresponding to a good hash key, it will be useful to study a graph, similar to the one in Sect. 3, associated with \( ({\textsf {X}}^q,{\textsf {U}}^q) \). Specifically, we consider the random transcript graph \( {\mathcal {G}}({\textsf {X}}^q,{\textsf {U}}^q) \) arising due to \( {\textsf {H}} \in {\mathcal {H}}_{\textsf {good}}\). Lemma 6.1 and Fig. 4 characterize the different types of possible components in \( {\mathcal {G}}({\textsf {X}}^q,{\textsf {U}}^q) \). Note that type 2, type 3, type 4 and type 5 graphs are the same as configurations (A), (D), (C) and (F) of Fig. 3, for \( \ge 4 \) edges. These graphs are considered as bad in [29], whereas we allow such components.
Enumerating all possible types of components of a transcript graph corresponding to a good hash key: type 1 is the only possible component of size \( = 1 \) edge; type 2 and type 3 are \( {\mathcal {X}}_{\text {-}\star } \) and \( {\mathcal {U}}_{\text {-}\star } \) components, respectively; type 4 and type 5 are the only possible components that are not isolated or star (can have degree 2 vertices in both \( {\mathcal {X}}\) and \( {\mathcal {U}}\))
Lemma 6.1
The transcript graph \( {\mathcal {G}}\) corresponding to \( (\textsf {X} ^q,\textsf {U} ^q) \) generated by a good hash key \( \textsf {H} \) has the following properties:
- 1.
\( {\mathcal {G}}\) is simple, acyclic and has no isolated vertices.
- 2.
\( {\mathcal {G}}\) has no two adjacent edges i and j such that \( {\lambda }_i \oplus {\lambda }_j = 0 \).
- 3.
\( {\mathcal {G}}\) has no component of size \( > 2^n/2q \) edges.
- 4.
\( {\mathcal {G}}\) has no component such that it has 2 distinct degree 2 vertices in \( {\mathcal {X}}\) or \( {\mathcal {U}}\).
In fact, the all possible types of components of \( {\mathcal {G}}\) are enumerated in Fig. 4.
The proof of Lemma 6.1 is elementary and given in supplementary material E for the sake of completeness.
In what follows, we describe the sampling of \( {\textsf {Y}}^q \) and \( {\textsf {V}}^q \) when \( {\textsf {H}} \in {\mathcal {H}}_{\textsf {good}}\). We collect the indices \( i \in [q] \) corresponding to the edges in all type 1, type 2, type 3, type 4 and type 5 components, in the index sets \( {\mathcal {I}}_{1} \), \( {\mathcal {I}}_{2} \), \( {\mathcal {I}}_{3} \), \( {\mathcal {I}}_{4} \) and \( {\mathcal {I}}_{5} \), respectively. Clearly, the five sets are disjoint, and \( [q] = {\mathcal {I}}_{1} \sqcup {\mathcal {I}}_{2} \sqcup {\mathcal {I}}_{3} \sqcup {\mathcal {I}}_{4} \sqcup {\mathcal {I}}_{5} \). Let \( {\mathcal {I}}= {\mathcal {I}}_{1} \sqcup {\mathcal {I}}_{2} \sqcup {\mathcal {I}}_{3} \). Consider the system of equation
where \( Y_i = Y_j \) (res. \( V_i = V_j \)) if and only if \( {\textsf {X}}_i ={\textsf {X}}_j \) (res. \( {\textsf {U}}_i ={\textsf {U}}_j \)) for all \( i,j \in [q] \). The solution set of \( {\mathcal {L}}\) is precisely the set
Given these definitions, the ideal oracle \( {\mathcal {O}}_0 \) samples \( ({\textsf {Y}}^q,{\textsf {V}}^q) \) as follows:
\( ({\textsf {Y}}^{{\mathcal {I}}},{\textsf {V}}^{{\mathcal {I}}}) \leftarrow \!\!{\$}\,{\mathcal {S}}\), i.e., \( {\mathcal {O}}_0 \) uniformly samples one valid assignment from the set of all valid assignments.
Let \( {\mathcal {G}}{\setminus } {\mathcal {I}}\) denote the subgraph of \( {\mathcal {G}}\) after the removal of edges and vertices corresponding to \( i \in {\mathcal {I}}\). For each component \( {\mathcal {C}}\) of \( {\mathcal {G}}{\setminus } {\mathcal {I}}\):
Suppose \( ({\textsf {X}}_i,{\textsf {U}}_i) \in {\mathcal {C}}\) corresponds to the edge in \( {\mathcal {C}}\), where both \( {\textsf {X}}_i \) and \( {\textsf {U}}_i \) have degree \( \ge 2 \). Then, \( {\textsf {Y}}_i \leftarrow \!\!{\$}\,\{0,1\}^n\) and \( {\textsf {V}}_i = {\textsf {Y}}_i \oplus {\lambda }_i \).
For each edge \( ({\textsf {X}}_{i'},{\textsf {U}}_{i'}) \ne ({\textsf {X}}_i,{\textsf {U}}_i) \in {\mathcal {C}}\), either \( {\textsf {X}}_{i'} = {\textsf {X}}_i \) or \( {\textsf {U}}_{i'} = {\textsf {U}}_i \). Suppose, \( {\textsf {X}}_{i'} = {\textsf {X}}_i \). Then, \( {\textsf {Y}}_{i'} = {\textsf {Y}}_i \) and \( {\textsf {V}}_{i'} = {\textsf {Y}}_{i'} \oplus {\lambda }_{i'} \). Now, suppose \( {\textsf {U}}_{i'} = {\textsf {U}}_i \). Then, \( {\textsf {V}}_{i'} = {\textsf {V}}_i \) and \( {\textsf {Y}}_{i'} = {\textsf {V}}_{i'} \oplus {\lambda }_{i'} \).
At this point,  is completely defined. In this way, we maintain both the consistency of equations of the form \( {\textsf {Y}}_i \oplus {\textsf {V}}_i = {\lambda }_i \) (as in the case of real world) and the permutation consistency within each component, when \( {\textsf {H}} \in {\mathcal {H}}_{\textsf {good}}\). However, there might be collisions among \( {\textsf {Y}} \) or \( {\textsf {V}} \) values from different components.
is completely defined. In this way, we maintain both the consistency of equations of the form \( {\textsf {Y}}_i \oplus {\textsf {V}}_i = {\lambda }_i \) (as in the case of real world) and the permutation consistency within each component, when \( {\textsf {H}} \in {\mathcal {H}}_{\textsf {good}}\). However, there might be collisions among \( {\textsf {Y}} \) or \( {\textsf {V}} \) values from different components.
6.3 Definition and Analysis of Bad Transcripts
Given the description of the transcript random variable corresponding to the ideal oracle, we can define the set of transcripts \( \varOmega \) as the set of all tuples \( \omega = (t^q,m^q,c^q,x^q,y^q,v^q,u^q,\lambda ^q,h_1,h_2) \), where \( t^q \in (\{0,1\}^\tau )^q \); \( m^q,c^q,y^q,v^q \in (\{0,1\}^n)^q \); \( (h_1,h_2) \in {\mathcal {H}}^2 \); \( x^q = h_1(t^q) \oplus m^q \); \( u^q = h_2(t^q) \oplus c^q \); \( \lambda ^q = h_1(t^q) \oplus h_2(t^q) \); and \( ({t^q}, {m^q})\leftrightsquigarrow ({t^q}, {c^q}) \).
Our bad transcript definition is inspired by two requirements:
- 1.
Eliminate all \( x^q \), \( u^q \) and \( \lambda ^q \) tuples such that both \( y^q \) and \( v^q \) are trivially restricted by way of linear dependence. For example, consider the condition \( \texttt {H}_2 \). This leads to \( y_i = y_j \), which would imply \( v_i = y_i \oplus \lambda _i = y_j \oplus \lambda _j = v_j \). Assuming \( i > j \), \( v_i \) is trivially restricted (\( = v_j \)) by way of linear dependence. This may lead to
 as \( u_i \) may not be equal to \( u_j \).
as \( u_i \) may not be equal to \( u_j \). - 2.
Eliminate all \( x^q \), \( u^q \), \( y^q \), \( v^q \) tuples such that
 or
or  .
.
Among the two, requirement 2 is trivial as \( {x^q}\leftrightsquigarrow {y^q} \) and \( {u^q}\leftrightsquigarrow {v^q} \) are always true for real-world transcript. Requirement 1 is more of a technical one that helps in the ideal world sampling of \( y^q \) and \( v^q \).
Bad Transcript Definition: We first define certain transcripts as bad depending upon the characterization of hash keys. Inspired by the ideal world description, we say that a hash key \( (h_1,h_2) \in {\mathcal {H}}_{{\textsf {bad}}} \) (or \( (h_1,h_2) \) is bad) if and only if the following predicate is true:
We say that \( \omega \) is hash-induced bad transcript, if \( (h_1,h_2) \in {\mathcal {H}}_{\textsf {bad}} \). We write this event as \( \texttt {BAD-HASH}\), and by a slight abuse of notations,Footnote 3 we have
This takes care of the first requirement. For the second one, we have to enumerate all the conditions which might lead to  or
or  . Since we sample degenerately when the hash key is bad, the transcript is trivially inconsistent in this case. For good hash keys, if \( x_i=x_j \) (or \( u_i=u_j \)) then we always have \( y_i=y_j \) (res. \( v_i=v_j \)); hence, the inconsistency would not arise. So, given that the hash key is good, we say that \( \omega \) is sampling-induced bad transcript, if one of the following conditions is true:
. Since we sample degenerately when the hash key is bad, the transcript is trivially inconsistent in this case. For good hash keys, if \( x_i=x_j \) (or \( u_i=u_j \)) then we always have \( y_i=y_j \) (res. \( v_i=v_j \)); hence, the inconsistency would not arise. So, given that the hash key is good, we say that \( \omega \) is sampling-induced bad transcript, if one of the following conditions is true:
For some \( \alpha \in [5] \) and \( \beta \in \{\alpha ,\ldots ,5\} \), we have
\(\texttt {Ycoll}_{{\alpha }{\beta }}:\exists i \in {\mathcal {I}}_{\alpha }, j \in {\mathcal {I}}_{\beta } \), such that \( x_i \ne x_j \wedge y_i = y_j \), and
\(\texttt {Vcoll}_{{\alpha }{\beta }}:\exists i \in {\mathcal {I}}_{\alpha }, j \in {\mathcal {I}}_{\beta } \), such that \( u_i \ne u_j \wedge v_i = v_j \),
where \( {\mathcal {I}}_i \) is defined as before in Sect. 6.2. By varying \( \alpha \) and \( \beta \) over all possible values, we get all 30 conditions which might lead to  or
or  . Here, we remark that some of these 30 conditions are never satisfied due to the sampling mechanism prescribed in Sect. 6.2. These are \( \texttt {Ycoll}_{{1}{1}} \), \( \texttt {Ycoll}_{{1}{2}} \), \( \texttt {Ycoll}_{{1}{3}} \), \( \texttt {Ycoll}_{{2}{2}} \), \( \texttt {Ycoll}_{{2}{3}} \), \( \texttt {Ycoll}_{{3}{3}} \), \( \texttt {Vcoll}_{{1}{1}} \), \( \texttt {Vcoll}_{{1}{2}} \), \( \texttt {Vcoll}_{{1}{3}} \), \( \texttt {Vcoll}_{{2}{2}} \), \( \texttt {Vcoll}_{{2}{3}} \) and \( \texttt {Vcoll}_{{3}{3}} \). We listed them here only for the sake of completeness. We write the combined event that one of the 30 conditions hold as \( \texttt {BAD-SAMP}\). Again by an abuse of notations, we have
. Here, we remark that some of these 30 conditions are never satisfied due to the sampling mechanism prescribed in Sect. 6.2. These are \( \texttt {Ycoll}_{{1}{1}} \), \( \texttt {Ycoll}_{{1}{2}} \), \( \texttt {Ycoll}_{{1}{3}} \), \( \texttt {Ycoll}_{{2}{2}} \), \( \texttt {Ycoll}_{{2}{3}} \), \( \texttt {Ycoll}_{{3}{3}} \), \( \texttt {Vcoll}_{{1}{1}} \), \( \texttt {Vcoll}_{{1}{2}} \), \( \texttt {Vcoll}_{{1}{3}} \), \( \texttt {Vcoll}_{{2}{2}} \), \( \texttt {Vcoll}_{{2}{3}} \) and \( \texttt {Vcoll}_{{3}{3}} \). We listed them here only for the sake of completeness. We write the combined event that one of the 30 conditions hold as \( \texttt {BAD-SAMP}\). Again by an abuse of notations, we have
Finally, a transcript \( \omega \) is called bad, i.e., \( \omega \in \varOmega _{{\textsf {bad}}} \), if it is either a hash- or a sampling-induced bad transcript. All other transcripts are called good. It is easy to see that all good transcripts are attainable (as required in the H-coefficient technique or the expectation method).
Bad Transcript Analysis: We analyze the probability of realizing a bad transcript in the ideal world. By definition, this is possible if and only if one of \( \texttt {BAD-HASH}\) or \( \texttt {BAD-SAMP}\) occurs. So, we have

Lemma 6.2 upper bounds \( \epsilon _{\textsf {hash} }\) to \( 2q^2\epsilon ^2 + 2q^2\epsilon ^{1.5} + 16q^4\epsilon 2^{-2n} \) and Lemma 6.3 upper bounds \( \epsilon _{{\textsf {samp}}}\) to \( 9q^4\epsilon ^22^{-n} \). Substituting these values in Eq. (15), we get
Lemma 6.2
\( \displaystyle {\epsilon _{\textsf {hash} }} \le 2q^2\epsilon ^2 + 2q^2\epsilon ^{1.5} + \frac{16q^4\epsilon }{2^{2n}} \).
Proof
Using Eqs. (13) and (15), we have
\( {\texttt {H}}_1\) is true if for some distinct i, j both \( {\textsf {X}}_i = {\textsf {X}}_j \) and \( {\textsf {U}}_i = {\textsf {U}}_j \). Now \( {\textsf {T}}_i = {\textsf {T}}_j \implies {\textsf {M}}_i \ne {\textsf {M}}_j \). Hence, \( {\textsf {X}}_i \ne {\textsf {X}}_j \) and \( {\texttt {H}}_1\) is not true. So suppose \( {\textsf {T}}_i \ne {\textsf {T}}_j \). Then for a fixed i, j we get an upper bound of \( \epsilon ^2 \) as \( {\mathcal {H}}\) is \( \epsilon \)-AXU, and we have at most \( {q \atopwithdelims ()2} \) pairs of i, j. Thus, \( {\Pr _{}\left[ {{\texttt {H}}_1}\right] } \le {q \atopwithdelims ()2}\epsilon ^2 \). Following a similar line of argument, one can bound \( {\Pr _{}\left[ {{\texttt {H}}_2}\right] } \le {q \atopwithdelims ()2}\epsilon ^2 \) and \( {\Pr _{}\left[ {\texttt {H}_3}\right] } \le {q \atopwithdelims ()2}\epsilon ^2 \).
In the remaining, we bound the probability of \( \texttt {H}_4\) and \( \texttt {H}_6\), while the probability of \( \texttt {H}_5\) and \( \texttt {H}_7\) can be bounded analogously. For any function \( f: \{0,1\}^\tau \in \{0,1\}^n\), let \( f': \{0,1\}^\tau \times \{0,1\}^n\rightarrow \{0,1\}^n\) be defined as \( f'(t,m) = f(t) \oplus m \). So \( {\textsf {X}}_i = {\textsf {H}}'_1({\textsf {T}}_i,{\textsf {M}}_i) \), and \( {\textsf {U}}_i = {\textsf {H}}'_2({\textsf {T}}_i,{\textsf {C}}_i) \), for all \( i \in [q] \). It is easy to see that \( {\textsf {H}}'_b \) is \( \epsilon \)-universal if \( {\textsf {H}}_b \) is \( \epsilon \)-AXU for \( b \in [2] \). Using the renewed description, \( \texttt {H}_4\) is true if for some distinct \( i,j,k,\ell \),
Since \( (t_i,m_i) \ne (t_j,m_j) \) and \( (t_i,c_i) \ne (t_j,c_j) \) for distinct i and j, we can apply the alternating collisions lemma of Lemma 4.1 to get \( {\Pr _{}\left[ {\texttt {H}_4}\right] } \le q^2\epsilon ^{1.5} \).
For \( \texttt {H}_6\), we have
where \( k \ge 2^n/2q \). Since \( (t_{i_{j}},m_{i_{j}}) \ne (t_{i_l},m_{i_l}) \) for all \( j \ne l \), we can apply Corollary 4.1 with \( a = 2^n/2q \) to get \( {\Pr _{}\left[ {\texttt {H}_6}\right] } \le \frac{8q^4\epsilon }{2^{2n}} \). \(\square \)
Lemma 6.3
\( \displaystyle \epsilon _{{\textsf {samp}}}\le \frac{9q^4\epsilon ^2}{2^n} \).
Proof
Using Eqs. (14) and (15), we have
We bound the probabilities of the events on the right-hand side in groups as given below:
\({{1.\hbox { Bounding } \sum _{\alpha \in [3],\beta \in \{\alpha ,\ldots ,3\}}{\Pr _{}\left[ {\texttt {Ycoll}_{{\alpha }{\beta }}}\right] }+{\Pr _{}\left[ {\texttt {Vcoll}_{{\alpha }{\beta }}}\right] } }}\): Recall that the sampling of \( {\textsf {Y}} \) and \( {\textsf {V}} \) values is always done consistently for indices belonging to \( {\mathcal {I}}= {\mathcal {I}}_1 \sqcup {\mathcal {I}}_2 \sqcup {\mathcal {I}}_3 \). Hence,
\({{2.\hbox { Bounding } \sum _{\alpha \in [3],\beta \in \{4,5\}} {\Pr _{}\left[ {\texttt {Ycoll}_{{\alpha }{\beta }}}\right] }+{\Pr _{}\left[ {\texttt {Vcoll}_{{\alpha }{\beta }}}\right] } }}\): Let us consider the event \( \texttt {Ycoll}_{{1}{4}} \), which translates to existing indices \( i \in {\mathcal {I}}_{1} \) and \( j \in {\mathcal {I}}_{4} \) such that \( {\textsf {X}}_i \ne {\textsf {X}}_j \wedge {\textsf {Y}}_i = {\textsf {Y}}_j \). Since \( j \in {\mathcal {I}}_{4} \), there must exist \( k,\ell \in {\mathcal {I}}_{4}{\setminus }\{j\} \), such that one of the following happens
We analyze the first case, while the other two cases can be similarly bounded. To bound the probability of \( \texttt {Ycoll}_{{1}{4}} \), we can thus look at the joint event
Note that the event \( {\textsf {Y}}_i = {\textsf {Y}}_j \) is independent of \( {\textsf {X}}_j = {\textsf {X}}_k \wedge {\textsf {U}}_k = {\textsf {U}}_\ell \), as both \( {\textsf {Y}}_i \) and \( {\textsf {Y}}_j \) are sampled independent of the hash key. Thus, we get
where the last inequality follows from the uniform randomness of \( {\textsf {Y}}_j \) and the AXU property of \( {\textsf {H}}_1 \) and \( {\textsf {H}}_2 \). The probability of the other two cases is similarly bounded to \( q{q \atopwithdelims ()3}\frac{\epsilon ^2}{2^n} \), whence we get
We can bound the probabilities of \( \texttt {Ycoll}_{{2}{4}} \), \( \texttt {Ycoll}_{{3}{4}} \), \( \texttt {Ycoll}_{{\alpha }{5}} \), \( \texttt {Vcoll}_{{\alpha }{4}} \) and \( \texttt {Vcoll}_{{\alpha }{5}} \), for \( \alpha \in [3] \), in a similar manner as in the case of \( \texttt {Ycoll}_{{1}{4}} \). So, we skip the argumentation for these cases and summarize the probability for this group as
\({{3.\hbox { Bounding } \sum _{\alpha \in \{4,5\},\beta \in \{\alpha ,5\}}{\Pr _{}\left[ {\texttt {Ycoll}_{{\alpha }{\beta }}}\right] }+{\Pr _{}\left[ {\texttt {Vcoll}_{{\alpha }{\beta }}}\right] } }}\): Consider the event \( \texttt {Ycoll}_{{4}{4}} \), which translates to there exists distinct indices \( i,j \in {\mathcal {I}}_4 \) such that \( {\textsf {X}}_i \ne {\textsf {X}}_j \wedge {\textsf {Y}}_i = {\textsf {Y}}_j \). Here, as \( i,j \in {\mathcal {I}}_4 \), there must exist \( k,\ell \in {\mathcal {I}}_4{\setminus }\{j\} \) such that one of the following happens
The analysis of these cases is similar to 2 above. So, we skip it and provide the final bound
The probabilities of all the remaining events in this group can be bounded in a similar fashion.
The result follows by combining Eqs. (17–19), followed by some algebraic simplifications. \(\square \)
6.4 Good Transcript Analysis
From Sect. 6.2, we know the types of components present in the transcript graph corresponding to a good transcript \( \omega \) are exactly as in Fig. 4. Let \( \omega = (t^q,m^q,c^q,x^q,y^q,v^q, u^q,\lambda ^q,h_1,h_2) \) be the good transcript at hand. From the bad transcript description of Sect. 6.3, we know that for a good transcript \( ({t^q}, {m^q})\leftrightsquigarrow ({t^q}, {c^q}) \), \( {x^q}\leftrightsquigarrow {y^q} \), \( {v^q}\leftrightsquigarrow {u^q} \) and \( y^q \oplus v^q = \lambda ^q \).
We add some new parameters with respect to \( \omega \) to aid our analysis of good transcripts. For \( i \in [{5}] \), let \( c_i(\omega ) \) and \( q_i(\omega ) \) denote the number of components and number of indices (corresponding to the edges), respectively, of type i in \( \omega \). Note that \( q_1(\omega ) = c_1(\omega ) \), \( q_i(\omega ) \ge 2c_i(\omega ) \) for \( i \in \{2,3\} \), and \( q_i(\omega ) \ge 3c_i(\omega ) \) for \( i \in \{4,5\} \). Obviously, for a good transcript \( q = \sum _{i=1}^{5} q_i(\omega ) \). For all these parameters, we will drop the \( \omega \) parametrization whenever it is understood from the context.
Interpolation probability for the real oracle: In the real oracle, \( ({\textsf {H}}_1,{\textsf {H}}_2) \leftarrow \!\!{\$}\,{\mathcal {H}}^2 \), \( \Pi _1 \) is called exactly \( q_1+c_2+q_3+2c_4+q_5-c_5 \) times and \( \Pi _2 \) is called exactly \( q_1+q_2+c_3+q_4-c_4+2c_5 \) times. Thus, we have

Interpolation probability for the ideal oracle: In the ideal oracle, the sampling is done in parts:
- I.:
\({{\widetilde{\Pi }}}\)sampling: Let \( (t'_1,t'_2,\cdots ,t'_r) \) denote the tuple of distinct tweaks in \( t^q \), and for all \( i \in [r] \), let \( a_i = \mu (t^q,t'_i) \), i.e., \( r \le q \) and \( \sum _{i=1}^{r} a_i = q \). Then, we have
$$\begin{aligned} {\Pr _{}\left[ {{{\widetilde{\Pi }}}(t^q,m^q)=c^q}\right] } \le \frac{1}{\prod _{i = 1}^{r}(2^n)_{a_i}}. \end{aligned}$$- II.:
Hash key sampling: The hash keys are sampled uniformly from \( {\mathcal {H}}^2 \), i.e., \( {\Pr _{}\left[ {({\textsf {H}}_1,{\textsf {H}}_2)=(h_1,h_2)}\right] } = \frac{1}{|{\mathcal {H}}|^2} \).
- III.:
Internal variables sampling: The internal variables \( {\textsf {Y}}^q \) and \( {\textsf {V}}^q \) are sampled in two stages.
- (A).:
type 1, type 2 and type 3 sampling: Recall the sets \( {\mathcal {I}}_{1} \), \( {\mathcal {I}}_{2} \) and \({\mathcal {I}}_{3} \), from Sect. 6.3. Consider the system of equation
$$\begin{aligned} {\mathcal {L}}= \{{\textsf {Y}}_i \oplus {\textsf {V}}_i = \lambda _i~:~i \in {\mathcal {I}}\}. \end{aligned}$$Let \( (\lambda '_1,\lambda '_2,\cdots ,\lambda '_s) \) denote the tuple of distinct elements in \( \lambda ^{\mathcal {I}}\), and for all \( i \in [s] \), let \( b_i = \mu (\lambda ^{\mathcal {I}},\lambda '_i) \). Figure 4 shows that \( {\mathcal {L}}\) is cycle-free and non-degenerate. Further, \( \xi _{\max }({\mathcal {L}}) \le 2^n/2q \), since the transcript is good. So, we can apply Theorem 5.1 to get a lower bound on the number of valid solutions, \( |{\mathcal {S}}| \) for \( {\mathcal {L}}\). Using the fact that \( ({\textsf {Y}}^{{\mathcal {I}}},{\textsf {V}}^{{\mathcal {I}}}) \leftarrow \!\!{\$}\,{\mathcal {S}}\) and Theorem 5.1, we have
$$\begin{aligned} {\Pr _{}\left[ {({\textsf {Y}}^{{\mathcal {I}}},{\textsf {V}}^{{\mathcal {I}}}) = (y^{{\mathcal {I}}},v^{{\mathcal {I}}})}\right] } \le \frac{\prod _{i=1}^{s}(2^n)_{b_i}}{\zeta (\omega )(2^n)_{q_1+c_2+q_3}(2^n)_{q_1+q_2+c_3}}, \end{aligned}$$where
$$\begin{aligned} \zeta (\omega ) = \left( 1 - \frac{13q^4}{2^{3n}} - \frac{2q^2}{2^{2n}} - \left( \sum _{i=1}^{c_2+c_3}\eta ^2_{c_1+i}\right) \frac{4q^2}{2^{2n}}\right) . \end{aligned}$$- (B).:
type 4 and type 5 sampling: For the remaining indices, one value is sampled uniformly for each of the components, i.e., we have
$$\begin{aligned} {\Pr _{}\left[ {\left( {\textsf {Y}}^{[q] {\setminus } {\mathcal {I}}},{\textsf {V}}^{[q] {\setminus } {\mathcal {I}}}\right) = \left( y^{[q] {\setminus } {\mathcal {I}}},v^{[q] {\setminus } {\mathcal {I}}}\right) }\right] } = \frac{1}{(2^n)^{c_4+c_5}}. \end{aligned}$$
By combining I, II, III, and rearranging the terms, we have
 (21)
(21)where \( p_1 = q_1+c_2+q_3 \) and \( p_2 = q_1+q_2+c_3 \).
6.5 Ratio of Interpolation Probabilities
On dividing Eq. (20) by Eq. (21), and simplifying the expression, we get

At inequality 1, we rewrite the numerator such that \( d_i = \mu (t^{\mathcal {I}},t'_i) \) for \( i \in [r] \). Further, \( r \ge s \), as number of distinct internal masking values is at most the number of distinct tweaks, and \( {\widehat{t}}^{\mathcal {I}}\) compresses to \( {\widehat{\lambda }}^{\mathcal {I}}\). So using Proposition 1, we can justify inequality 2. At inequality 2, for \( i \in \{2,3,4,5\} \), \( c_i(\omega ) > 0 \) if and only if \( r \ge 2 \). Also, \( d_i \le c_1 + c_2 + c_3 \le p_1+c_4 \) and \( d_i \le p_2+c_5 \) for \( i \in [r] \). Similarly, \( a_i \le c_1 + c_2 + c_3 + 2c_4 + 2c_5 \le p_1 + 2c_4 + q_5 - c_5 \), and \( a_i \le p_2 + q_4 - c_4 + 2c_5 \). Also, \( \sum _{i=1}^{r}a_i-d_i = q_4+q_5 \). Thus, A satisfies the conditions given in Proposition 2, and hence, \( A \ge 1 \). This justifies inequality 3.
We define \( \epsilon _{{\textsf {ratio}}}: \varOmega \rightarrow [0,\infty ) \) by the mapping
Clearly, \( \epsilon _{{\textsf {ratio}}}\) is nonnegative and the ratio of real to ideal interpolation probabilities is at least \( 1 - \epsilon _{{\textsf {ratio}}}(\omega ) \) (using Eq. (22)). Thus, we can use Lemma 2.1 to get
Let \( \sim _1 \) (res. \( \sim _2 \)) be an equivalence relation over [q], such that \( \alpha \sim _1 \beta \) (res. \( \alpha \sim _2 \beta \)) if and only if \( {\textsf {X}}_\alpha = {\textsf {X}}_\beta \) (res. \( {\textsf {U}}_\alpha = {\textsf {U}}_\beta \)). Now, each \( \eta _i \) random variable denotes the cardinality of some non-singleton equivalence class of [q] with respect to either \( \sim _1 \) or \( \sim _2 \). Let \( {\mathcal {P}}^1_1,\ldots ,{\mathcal {P}}^1_r \) and \( {\mathcal {P}}^2_1,\ldots ,{\mathcal {P}}^2_s \) denote the non-singleton equivalence classes of [q] with respect to \( \sim _1 \) and \( \sim _2 \), respectively. Further, for \( i \in [r] \) and \( j \in [s] \), let \( {\nu }_i = |{\mathcal {P}}^1_i| \) and \( {\nu }'_j = |{\mathcal {P}}^2_j| \). Then, we have
where the first inequality follows from the fact that \( {\textsf {H}}_1 \) and \( {\textsf {H}}_2 \) are independently sampled, and the second inequality follows from Lemma 4.3 and the fact that \( {\textsf {H}}_1,{\textsf {H}}_2 \leftarrow \!\!{\$}\,{\mathcal {H}}\). Theorem 6.1 follows from Eqs. (12), (16), (23)–(24). \(\square \)
7 Further Discussion
In this paper, our chief contribution is a tight (up to a logarithmic factor) security bound for the cascaded LRW2 tweakable block cipher. We developed two new tools: First, we provide a probabilistic result, called alternating collisions (events) lemma, which gives improved bounds for some special collision events, which are encountered frequently in BBB security analysis. Second, we adapt a restricted variant of mirror theory in tweakable permutations setting.
7.1 Applications of Alternating Events Lemma and Mirror Theory
The combination of alternating events lemma and mirror theory seems to have some nice applications. Here, we give some applications based on the double-block hash-then-sum (or DbHtS) paradigm by Datta et al. [42]. The DbHtS paradigm is a variable input length pseudorandom function or PRF construction, based on a block cipher \( {E}\) and a hash function \( {\mathcal {H}}\), which is defined as:
\( \forall (k^2,h,m) \in \{0,1\}^{2\kappa } \times {\mathcal {H}}\times \{0,1\}^* \),
where \( \{0,1\}^* \) denotes the set of all bit strings, and \( (x,u) = h(m) \).
PRF Security: Let \( F\) be a keyed function family from \( \{0,1\}^* \) to \( \{0,1\}^n\) indexed by the key space \( \{0,1\}^\kappa \). We define the PRF advantage of an adversary \( {{\mathscr {A}}}\) against \( F\) as,
where \( {\textsf {K}}\leftarrow \!\!{\$}\,\{0,1\}^\kappa \) and \( \Gamma \) is a uniform random function chosen from the set of all functions from \( \{0,1\}^* \) to \( \{0,1\}^n\). The PRF security of \( F\) against any adversary class \( {{\mathbb {A}}}(q,t) \) is defined analogously to SPRP and TSPRP security given in Sect. 2.3.
7.1.1 Application 1: \(\textsf {DbHtS-p}\)—
As a first application, we relax the DbHtS construction to \(\textsf {DbHtS-p}\), where the hash function h is made up of independent universal hash functions \( h_1 \) and \( h_2 \), such that \( h(m) = (h_1(m),h_2(m)) \). This construction was also analyzed in [51], though they showed security up to \( q \ll 2^{2n/3} \).
We show that \(\textsf {DbHtS-p}\) achieves higher security (i.e., security up to \( q \ll 2^{3n/4} \)). Further, the attack by Leurent et al. [53] in roughly \( 2^{3n/4} \) queries seems to apply to \(\textsf {DbHtS-p}\) for algebraic hash functions. Thus, our bound is tight.
Theorem 7.1
For \( q \le 2^{n-2} \) and \( t > 0 \), the PRF security of \( {\textsf {DbHtS-p}}[{E},{\mathcal {H}}] \) against \( {{\mathbb {A}}}(q,t) \) is given by
where \( t' = c(t + qt_{{\mathcal {H}}}) \), \( t_{{\mathcal {H}}} \) being the time complexity for computing the hash function \( {\mathcal {H}}\), \( c > 0 \) is a constant depending upon the computation model, and
Note that the PRP security game is similar to SPRP, except that the adversary is not given inverse access to the oracle. The proof of Theorem 7.1 is given in supplementary material F.
7.1.2 Application 2: DbHtS-f—
The \(\textsf {DbHtS-f}\) is another relaxation of DbHtS, where the hash function h is made up of independent universal hash functions \( h_1 \) and \( h_2 \), and the finalization is done via keyed functions \( F_{k_1} \) and \( F_{k_2} \), i.e., \( \textsf {DbHtS-f} (m) = \lambda = F_{k_1}(x) \oplus F_{k_2}(u) \), where \( x = h_1(m) \) and \( u = h_2(m) \). We show that \(\textsf {DbHtS-f}\) is secure up to \( q \ll 2^{3n/4} \).
Theorem 7.2
For \( q \le 2^{n-2} \) and \( t > 0 \), the PRF security of \({\textsf {DbHtS-f}}[F,{\mathcal {H}}] \) against \( {{\mathbb {A}}}(q,t) \) is given by
where \( t' = c(t + qt_{{\mathcal {H}}}) \), \( t_{{\mathcal {H}}} \) being the time complexity for computing the hash function \( {\mathcal {H}}\), and \( c > 0 \) is a constant depending upon the computation model.
Proof
This can be argued using the previous line of research on sum of PRFs, starting from the work by Aiello and Venkatesan [54], followed by the works by Patarin et al. [55, 56]. Basically, one can show that the sum of PRFs is a perfectly secure PRF if there is no “alternating cycles” in the inputs (see [54, 55] for details). We can use the alternating collisions lemma to bound the probability of getting such alternating cycles. \(\square \)
7.1.3 Modified Benes [54,55,56]
mBenes-f of [54] is a 2n-bit to 2n-bit PRF construction, which is defined as \( \textsf {mBenes-f}(a,b) := (e,f) \), where
where \( F_{k_i} \) are independently sampled PRFs. In [54], the authors conjectured that mBenes-f is secure up to \( q \ll 2^n \). In [55, 56], the authors have given a very high-level sketch for proof of security up to \( q \ll 2^{n-\epsilon } \) for all \( \epsilon > 0 \). Let us define the mappings \( (a,b) \mapsto c \) and \( (a,b) \mapsto d \) as functions \( h_1 \) and \( h_2 \). Then, it is easy to see that \( h_1 \) and \( h_2 \) are \( 2^{-n} \) universal hash functions. Hence, as a direct consequence of Theorem 7.2, one can argue that mBenes-f is secure up to \( q \ll 2^{3n/4} \). Suppose mBenes-p denotes the natural variant of mBenes-f, when \( F_{k_i} \)’s are independently sampled PRPs. In a similar vein as mBenes-f, mBenes-p can be shown to be secure up to \( q \ll 2^{3n/4} \) as a direct consequence of Theorem 7.1.
7.2 Open Problems
We remark here that the alternating events lemma is not applicable when the hash functions are dependent. Thus, we cannot apply it to other DbHtS instantiations, such as \(\textsf {PMAC+}\) [57] and \(\textsf {LightMAC+}\) [58], in a straightforward manner. It would be an interesting future work to somehow bypass the independence requirement of the alternating events lemma. Yet another future work could be to look for the repercussions of this result on the security of XHX2 [35] in both the ideal cipher and the standard model. Note that XHX2 in the standard model is same as two-round cascade of XTX [59]. It seems that the bounds can be improved up to three-fourth of sum of block size and key size (or tweak size in the standard model). Our result does not seem to generalize to the cascaded LRW2 for \( \ell > 2 \), and it would be interesting to see some improved analysis on the generalized \( \ell \)-round cascaded LRW2 for \( \ell > 2 \).
Notes
\(\tilde{\textsf {F}}[1]\), \(\tilde{\textsf {F}}[2]\) and Wang et al. constructions assume key size to be same as block size.
The bound is \( \frac{q^2\epsilon }{a} \).
We use the notation \( \texttt {H}_i \) to denote the event that the predicate \( \texttt {H}_i \) is true.
References
M. Liskov, R.L. Rivest, D.A. Wagner, Tweakable block ciphers. J. Cryptol. 24(3), 588–613 (2011)
P. Rogaway, Efficient instantiations of tweakable blockciphers and refinements to modes OCB and PMAC, in Advances in Cryptology—ASIACRYPT ’04, Proceedings (2004), pp. 16–31
P. Rogaway, M. Bellare, J. Black, T. Krovetz, OCB: a block-cipher mode of operation for efficient authenticated encryption, in ACM Conference on Computer and Communications Security—ACM-CCS ’01, Proceedings (2001), pp. 196–205
T. Krovetz, P. Rogaway, The software performance of authenticated-encryption modes, in Fast Software Encryption—FSE ’11, Revised Selected Papers (2011), pp. 306–327
T. Shrimpton, R.S. Terashima, A modular framework for building variable-input-length tweakable ciphers, in Advances in Cryptology—ASIACRYPT ’13, Proceedings, Part I (2013), pp. 405–423
E. Andreeva, A. Bogdanov, A. Luykx, B. Mennink, E. Tischhauser, Yasuda, K., Parallelizable and authenticated online ciphers, in Advances in Cryptology—ASIACRYPT ’13, Proceedings, Part I (2013), pp. 424–443
T. Peyrin, Y. Seurin, Counter-in-tweak: authenticated encryption modes for tweakable block ciphers, in Advances in Cryptology—CRYPTO ’16, Proceedings, Part I (2016), pp. 33–63
J. Jean, I. Nikolic, T. Peyrin, Tweaks and keys for block ciphers: the TWEAKEY framework, in Advances in Cryptology—ASIACRYPT ’14, Proceedings, Part II (2014), pp. 274–288
V.T. Hoang, T. Krovetz, P. Rogaway, Robust authenticated-encryption AEZ and the problem that it solves, in Advances in Cryptology—EUROCRYPT ’15, Proceedings, Part I (2015), pp. 15–44
Y. Naito, Full prf-secure message authentication code based on tweakable block cipher, in Provable Security—ProvSec ’15, Proceedings (2015), pp. 167–182
E. List, M. Nandi, Revisiting full-prf-secure PMAC and using it for beyond-birthday authenticated encryption, in Topics in Cryptology—CT-RSA ’17, Proceedings (2017), pp. 258–274
T. Iwata, K. Minematsu, T. Peyrin, Y. Seurin, ZMAC: A fast tweakable block cipher mode for highly secure message authentication, in Advances in Cryptology—CRYPTO ’17, Proceedings, Part III (2017), pp. 34–65
B. Cogliati, R. Lampe, Y. Seurin, Tweaking even-mansour ciphers, in Advances in Cryptology—CRYPTO ’15, Proceedings, Part I (2015), pp. 189–208
E. List, M. Nandi, ZMAC+—an efficient variable-output-length variant of ZMAC. IACR Trans. Symmetric Cryptol. 2017(4) (2017) 306–325
T. Grochow, E. List, M. Nandi, Dovemac: a tbc-based PRF with smaller state, full security, and high rate. IACR Trans. Symmetric Cryptol. 2019(3) (2019) 43–80
K. Minematsu, Beyond-birthday-bound security based on tweakable block cipher, in Fast Software Encryption—FSE ’09, Revised Selected Papers (2009), pp. 308–326
P. Rogaway, H. Zhang, Online ciphers from tweakable blockciphers, in Topics in Cryptology—CT-RSA ’11, Proceedings (2011), pp. 237–249
C. Forler, E. List, S. Lucks, J. Wenzel, Poex: a beyond-birthday-bound-secure on-line cipher. Cryptogr. Commun. 10(1), 177–193 (2018)
A. Jha, M. Nandi, On rate-1 and beyond-the-birthday bound secure online ciphers using tweakable block ciphers. Cryptogr. Commun. 10(5), 731–753 (2018)
A. Dutta, M. Nandi, Tweakable HCTR: a BBB secure tweakable enciphering scheme, in Progress in cryptology—INDOCRYPT ’18, Proceedings (2018), pp. 47–69
R. Bhaumik, E. List, M. Nandi, ZCZ—achieving n-bit SPRP security with a minimal number of tweakable-block-cipher calls, in Advances in Cryptology—ASIACRYPT ’18, Proceedings, Part I (2018), pp. 336–366
C. Beierle, J. Jean, S. Kölbl, G. Leander, A. Moradi, T. Peyrin, Y. Sasaki, P. Sasdrich, S.M. Sim, The SKINNY family of block ciphers and its low-latency variant MANTIS, in Advances in Cryptology—CRYPTO ’16, Proceedings, Part II (2016), pp. 123–153
D. Chakraborty, P. Sarkar, A general construction of tweakable block ciphers and different modes of operations. IEEE Trans. Inf. Theory 54(5), 1991–2006 (2008)
K. Minematsu, Improved security analysis of XEX and LRW modes, in Selected Areas in Cryptography—SAC ’06, Revised Selected Papers (2006), pp. 96–113
R. Granger, P. Jovanovic, B. Mennink, S. Neves, Improved masking for tweakable blockciphers with applications to authenticated encryption, in Advances in Cryptology—EUROCRYPT ’16, Proceedings, Part I (2016), pp. 263–293
W. Landecker, T. Shrimpton, R.S. Terashima, Tweakable blockciphers with beyond birthday-bound security, in Advances in Cryptology—CRYPTO ’12, Proceedings (2012), pp. 14–30
G. Procter, A note on the CLRW2 tweakable block cipher construction. IACR Cryptol. ePrint Arch. 2014, 111 (2014)
R. Lampe, Y. Seurin, Tweakable blockciphers with asymptotically optimal security, in Fast Software Encryption—FSE ’13, Revised Selected Papers (2013), pp. 133–151
B. Mennink, Towards tight security of cascaded LRW2, in Theory of Cryptography—TCC ’18, Proceedings, Part II (2018), pp. 192–222
A. Bogdanov, L.R. Knudsen, G. Leander, F. Standaert, J.P. Steinberger, E. Tischhauser, Key-alternating ciphers in a provable setting: encryption using a small number of public permutations—(extended abstract), in Advances in Cryptology—EUROCRYPT ’12, Proceedings (2012), pp. 45–62
B. Mennink, Optimally secure tweakable blockciphers, in Fast Software Encryption—FSE ’15, Revised Selected Papers (2015), pp. 428–448
B. Mennink, Optimally secure tweakable blockciphers. IACR Cryptol. ePrint Arch. 2015, 363 (2015)
L. Wang, J. Guo, G. Zhang, J. Zhao, D. Gu, How to build fully secure tweakable blockciphers from classical blockciphers, in Advances in Cryptology—ASIACRYPT ’16, Proceedings, Part I (2016), pp. 455–483
A. Jha, E. List, K. Minematsu, S. Mishra, M. Nandi, XHX—a framework for optimally secure tweakable block ciphers from classical block ciphers and universal hashing, in Progress in Cryptology—LATINCRYPT ’17, Revised Selected Papers (2017), pp. 207–227
B. Lee, J. Lee, Tweakable block ciphers secure beyond the birthday bound in the ideal cipher model, in Advances in Cryptology—ASIACRYPT ’18, Proceedings, Part I (2018), pp. 305–335
B. Mennink, S. Neves, Encrypted Davies–Meyer and its dual: towards optimal security using mirror theory, in Advances in Cryptology—CRYPTO ’17, Proceedings, Part III (2017), pp. 556–583
J. Patarin, Introduction to mirror theory: analysis of systems of linear equalities and linear non equalities for cryptography. IACR Cryptol. ePrint Arch. 2010, 287 (2010)
J. Patarin, Mirror theory and cryptography. Appl. Algebra Eng. Commun. Comput. 28(4), 321–338 (2017)
V. Nachef, J. Patarin, E. Volte, Feistel Ciphers—Security Proofs and Cryptanalysis. Springer, Berlin (2017)
W. Dai, V.T. Hoang, S. Tessaro, Information-theoretic indistinguishability via the chi-squared method, in Advances in Cryptology—CRYPTO ’17, Proceedings, Part III (2017), pp. 497–523
N. Datta, A. Dutta, M. Nandi, K. Yasuda, Encrypt or decrypt? To make a single-key beyond birthday secure nonce-based MAC, in Advances in Cryptology—CRYPTO ’18, Proceedings, Part I. (2018), pp. 631–661
N. Datta, A. Dutta, M. Nandi, G. Paul, Double-block hash-then-sum: a paradigm for constructing bbb secure prf. IACR Trans. Symmetric Cryptol. 2018(3), 36–92 (2018)
V.T. Hoang, S. Tessaro, Key-alternating ciphers and key-length extension: exact bounds and multi-user security, in Advances in Cryptology—CRYPTO ’16, Proceedings, Part I (2016), pp. 3–32
V.T. Hoang, S. Tessaro, The multi-user security of double encryption, in Advances in Cryptology—EUROCRYPT ’17, Proceedings, Part II (2017), pp. 381–411
C. Guo, L. Wang, Revisiting key-alternating feistel ciphers for shorter keys and multi-user security, in Advances in Cryptology—ASIACRYPT ’18, Proceedings, Part I (2018), pp. 213–243
J. Patarin, Etude des Générateurs de Permutations Pseudo-aléatoires Basés sur le Schéma du DES. PhD thesis, Université de Paris (1991)
C. Hall, D.A. Wagner, J. Kelsey, B. Schneier, Building PRFs from PRPs, in Advances in Cryptology—CRYPTO ’98, Proceedings (1998), pp. 370–389
M. Bellare, R. Impagliazzo, A tool for obtaining tighter security analyses of pseudorandom function based constructions, with applications to PRP to PRF conversion. IACR Cryptol. ePrint Arch. 1999, 24 (1999)
H. Krawczyk, LFSR-based hashing and authentication, in Advances in Cryptology—CRYPTO ’94, Proceedings (1994), pp. 129–139
P. Rogaway, Bucket hashing and its application to fast message authentication. J. Cryptol. 12(2), 91–115 (1999)
A. Moch, E. List, Parallelizable MACs based on the sum of PRPs with security beyond the birthday bound, in Applied Cryptography and Network Security—ACNS ’19, Proceedings (2019), pp. 131–151
A. Dutta, M. Nandi, S. Talnikar, Beyond birthday bound secure MAC in faulty nonce model, in Advances in Cryptology—EUROCRYPT ’19, Proceedings, Part I (2019), pp. 437–466
G. Leurent, M. Nandi, F. Sibleyras, Generic attacks against beyond-birthday-bound MACs, in Advances in Cryptology—CRYPTO ’18, Proceedings, Part I (2018), pp. 306–336
W. Aiello, R. Venkatesan, Foiling birthday attacks in length-doubling transformations—benes: a non-reversible alternative to feistel, in Advances in Cryptology—EUROCRYPT ’96, Proceedings (1996), pp. 307–320
J. Patarin, A. Montreuil, Benes and butterfly schemes revisited, in Information Security and Cryptology—ICISC ’05, Revised Selected Papers (2005), pp. 92–116
J. Patarin, A proof of security in o(2\({}^{\text{n}}\)) for the benes scheme, in Progress in Cryptology—AFRICACRYPT ’08, Proceedings (2008), pp. 209–220
K. Yasuda, A new variant of PMAC: beyond the birthday bound, in Advances in Cryptology—CRYPTO ’11, Proceedings (2011), pp. 596–609
Y. Naito, Blockcipher-based MACs: beyond the birthday bound without message length, in Advances in Cryptology—ASIACRYPT ’17, Proceedings, Part III (2017), pp. 446–470
K. Minematsu, T. Iwata, Tweak-length extension for tweakable blockciphers, in Cryptography and Coding—IMACC ’15, Proceedings (2015), pp. 77–93
Acknowledgements
We thank the anonymous reviewers of EUROCRYPT 2019, CRYPTO 2019 and the Journal of Cryptology for their comments and suggestions. We also thank Bart Mennink for his comments and suggestions on an earlier version of this paper.
Author information
Authors and Affiliations
Corresponding author
Additional information
Communicated by Serge Vaudenay.
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendices
Supplementary Material
Proofs of Propositions 1 and 2
1.1 Proof of Proposition 1
Suppose a compresses to b due to a partition \( {\mathcal {P}}\). Then, we call \( {\mathcal {P}}\) the compressing partition of a and b. For \( s \ge 1 \), let p(s) denote the claimed statement. We prove the result by induction on s. We first handle the base case, \( s=1 \). In this case, we have \( b_1=\sum _{i=1}^{r}a_i \). Thus, \( a_i \le b_1 \) for all \( i \in [r] \). Now, a term-by-term comparison gives
which shows that the base case p(1) is true. Suppose p(s) is true for all \( s = n \), for some \( n > 1 \). We now show that \( p(n+1) \) is true.
Let \( a = (a_i)_{i \in [r]} \) and \( b = (b_j)_{j \in [s+1]} \) be two sequences over \( {{\mathbb {N}}}\), such that \( r \ge s+1 \) and a compresses to b. Suppose \( {\mathcal {P}}\) is a compressing partition of a and b. Consider the sequences \( a'=(a_i)_{i\in {\mathcal {P}}_{s+1}} \) and \( b'=(b_{s+1}) \). We have \( |{\mathcal {P}}_{s+1}| \ge 1 \) and \( b_{s+1} = \sum _{i \in {\mathcal {P}}_{s+1}} a_i \), which means \( a' \) compresses to \( b' \). Further, \( 2^n \ge \sum _{i \in {\mathcal {P}}_{s+1}} a_i \). Thus, we can apply p(1) result on \( a' \) and \( b' \) to get
For the remaining, let \( a{''}=(a_i)_{i\in [r]{\setminus }{\mathcal {P}}_{s+1}} \) and \( b{''}=(b_j)_{j \in [s]} \). Again, we have \( r-|{\mathcal {P}}_{s+1}| \ge s \), and \( b_i = \sum _{j\in {\mathcal {P}}_{i}} a_j \) for all \( i \in [s] \). Thus, we can apply the induction hypothesis for p(s) on \( a{''} \) and \( b{''} \) to get
The combination of Eqs. (27) and (28) shows that \( p(s+1) \) is true. The result follows by induction. \(\square \)
1.2 Proof of Proposition 2
For \( r \ge 2 \), let p(r) denote the claimed statement. We prove the result by induction on r. For now, assume p(2) to be true, as we handle this case later. Suppose the proposition statement, denoted p(r), is true for all \( r \ge 2 \). We show that the statement \( p(r+1) \) is true. Fix some arbitrary \( n \in {{\mathbb {N}}}\).
Let \( a_1,a_2,b_1,b_2,c_1,\ldots ,c_{r+1},d_1,\ldots ,d_{r+1} \in {{\mathbb {N}}}\), such that \( c_i \le a_i \) and \( c_i + d_i \le a_i + b_j \le 2^n \), for all \( i \in [r+1] \) and \( j \in [2] \). Let \( i ' \) be the smallest index in \( [r+1] \), such that \( d_{i'} = \min \{d_1,\ldots ,d_{r+1}\} \) (such an element exists by well-ordering principle). Without loss of generality, we assume that \( b_1 \ge b_2 \). We compare the terms, \( (2^n-c_{i'}-j+1) \) and \( (2^n-a_{1}-j+1) \), for all \( j \in [d_{i'}] \). Since \( c_{i'} \le a_{1} \), we must have \( (2^n-c_{i'}-j+1) \ge (2^n-a_{1}-j+1) \), for all \( j \in [d_{i'}] \). Now, we must have \( d_{i'} \le b_1 \); otherwise, \( d_{i'} > b_1 \ge b_2 \) which leads to \( \sum _{i \in [r]} d_i > b_1+b_2 \). Suppose \( d_{i'} < b_1 \), then using \( (2^n-c_{i'}-j+1)/(2^n-a_{1}-j+1) \ge 1 \), we remove all the \( (2^n-c_{i'}-j+1) \), \( (2^n-a_{1}-j+1) \) terms for all \( j \in [d_{i'}] \). This reduces the claimed statement to p(r), which is true by hypothesis. If \( d_{i'} = b_1 \), then we are left with \( \prod _{i \in [r+1]{\setminus }\{i'\}}(2^n-c_i)\cdots (2^n-c_i-d_i+1) \) on the left, where \( r \ge 2 \), and \( (2^n-a_2)\cdots (2^n-a_2-b_2+1) \) on the right. Using a similar line of argument as above, we can again reduce the claimed statement to p(r), which is true by hypothesis. So \( p(r+1) \) is true.
Now the base case p(2) can be handled in a similar manner. In this case, we assume without loss of generality that \( d_1 \le d_2 \) and \( b_1 \ge b_2 \), where \( d_1 + d_2 = b_1 + b_2 \). Since \( c_1 \le a_{1} \), we must have \( (2^n-c_1-j+1) \ge (2^n-a_{1}-j+1) \), for all \( j \in [d_1] \). Now, we must have \( d_1 \le b_1 \); otherwise, \( d_1 > b_1 \ge b_2 \) which leads to \( d_1 + d_2 > b_1+b_2 \). If \( d_1 = b_1 \), then after removing all the terms corresponding to \( (c_1,d_1) \) and \( (a_1,b_1) \), we have \( (2^n-c_2)\cdots (2^n-c_2-d_2+1) \) on the left and \( (2^n-a_2)\cdots (2^n-a_2-b_2+1) \), where \( c_2 \le a_2 \) and \( c_2+b_2 \le a_2+b_2 \), whence \( (2^n-c_2)\cdots (2^n-c_2-d_2+1) \ge (2^n-a_2)\cdots (2^n-a_2-b_2+1) \). If \( d_1 < b_1 \), then we compare terms from \( (2^n-c_2)\cdots (2^n-c_2-d_2+1) \) with \( (2^n-a_1-d_1)\cdots (2^n-a_1-b_1+1)(2^n-a_2)\cdots (2^n-a_2-b_2+1) \). First \( (2^n-c_2-d_2+j) \ge (2^n-a_2-b_2+j) \) for \( j \in [b_2] \), as \( c_2+d_2 \le a_2+b_2 \). We remove all these terms to get \( (2^n-c_2)\cdots (2^n-c_2-d_2+b_2+1) \) on the left and \( (2^n-a_1-d_1)\cdots (2^n-a_1-b_1+1) \) on the right, where the number of terms \( d_2-b_2=b_1-d_1 \). Since \( c_2 \le a_1 \), \( (2^n-c_2-j+1) \ge (2^n-a_1-d_1-j+1) \) for all \( j \in [b_1-d_1] \). This shows that p(2) is true. \(\square \)
Mennink’s Attack on CLRW2
In [29], Mennink gave an \( O(n^{1/2}2^{3n/4}) \) query attack on CLRW2. The attack is generic in nature as it does not exploit the weaknesses in the underlying block cipher. Rather it assumes that the block cipher instances are independent random permutations. Also the attack works for any hash function, including \( \text {AXU} \). We briefly describe the attack and refer the readers to [29] for a more concrete and formal description, analysis and experimental verification of the attack.
Attack Description: Suppose in the transcript generated by a distinguisher, there exist four queries \( (t,m_1,c_1) \), \( (t',m_2,c_2) \), \( (t, m_3,c_3) \) and \( (t',m_4,c_4) \), such that the following equations hold:
Using notations analogous to Fig. 1, we equivalently have \( x_1 = x_2 \); \( u_2 = u_3 \); and \( x_3 = x_4 \). Since \( {x^4}\leftrightsquigarrow {y^4} \) and \( {v^4}\leftrightsquigarrow {u^4} \), looking at the equations generated by the corresponding y and v values, we have \( v_1 = y_1 \oplus \lambda (t) = y_2 \oplus \lambda (t) = v_2 \oplus \lambda (t') \oplus \lambda (t) = v_3 \oplus \lambda (t) \oplus \lambda (t') = y_3 \oplus \lambda (t') = v_4 \). This immediately gives \( u_1 = u_4 \), i.e.,
In other words, Eq. (30) is implied by the existence of Eq. (29), and by combining all four equations, we have
where \( \alpha = h_1(t) \oplus h_1(t') \) and \( \beta = h_2(t) \oplus h_2(t') \). While the distinguisher does not know \( \alpha \) and \( \beta \), it can exploit the relations:
If for some value a we have about \( 2^n \) quadruples satisfying
then, for CLRW2, the expected number of solutions for Eqs. (31)–(32) is approximately 2 for \( a = \alpha \). On the other hand, for \({{\widetilde{\Pi }}}\), the expected number of solutions is always close to 1 for any \( a \in \{0,1\}^n\). In [29], it has been shown that approximately \( 2n^{1/2}2^{3n/4} \) queries are sufficient for the distinguisher to ensure that Eq. (33) has about \( 2^n \) solutions. Given these many queries, the distinguisher can attack by observing the number of solutions for Eqs. (31)–(32) for each value of a.
Proof of Lemma 4.2
Proof
We follow a similar proof approach as considered in Lemma 4.1. We define a binary random vector \( {\textsf {I}} = ({\textsf {I}}_{i,j}: i \ne j)\) where \( {\textsf {I}}_{i,j} \) takes value 1 if \( \texttt {E}_{i,j} \) holds, otherwise zero. The sample space of the random vector is \(\varOmega \), the set of all binary vectors indexed by all pairs (i, j). For any vector \(w \in \varOmega \), we write \(\#w\) to represent the number of 1’s that appear in w. Let \(\varOmega _{\le } = \{w: \#w \le \frac{1}{\sqrt{\epsilon '}} \}\) and its complement set by \(\varOmega _>\).
We define a random variable \({\textsf {N}} = \sum _{i\ne j} {\textsf {I}}_{i,j}\): The number of \(\texttt {E}\) events holds. As \(\texttt {E}_{i,j}\) holds with probability at most \(\epsilon \),
Let \( \texttt {EEF} \) denote the event that there exists distinct i, j, k and l such that \( \texttt {E}_{i,j}\ \wedge \ \texttt {E}_{k,l}\ \wedge \ \texttt {F}_{i,j,k,l} \). Now we proceed for bounding the probability of the event.
The first inequality follows exactly by the same reason argued in the proof of Lemma 4.1. The last inequality follows from Eq. (34). This completes the proof. \(\square \)
Proof of Mirror Theory in Tweakable Settings
The induction is defined on the number of components. Apropos of this, we consider some new parameters. For \( i \in [c_1+c_2+c_3] \):
\( X_i \) denotes the number of Y vertices in the previous \( i-1 \) components.
\( U_i \) denotes the number of V vertices in the previous \( i-1 \) components.
\( \xi _i \) denotes the size (number of vertices) of the ith component. We actually use \( \eta _i:=\xi _i-1 \) (number of edges in the ith component).
for \( j \in [\eta _i] \) and \( r = \sum _{k=1}^{i-1}\eta _k+j \),
\( \lambda ^i_j := \lambda _r \) (\( \lambda \) value corresponding to the jth equation of ith component).
\( \delta ^i_j := \mu (\lambda ^{r-1},\lambda ^i_j) \), where \( \delta ^1_1 = 0 \) by convention.
\( {\mathfrak {h}}_i \) denotes the number of solutions for the sub-system consisting of the first i components of \( {\mathcal {L}}\), denoted \( {\mathcal {L}}_{|i} \). Note that \( h_i = {\mathfrak {h}}_i \) for \( i \in [c_1] \), and \( h_q = {\mathfrak {h}}_{c_1+c_2+c_3} \).
\( H_i := \prod _{j \in [\eta _i]}(2^n)_{\mu (\lambda ^{s},\lambda ^i_j)} \cdot {\mathfrak {h}}_i \), where \( s = \sum _{k=1}^{i}\eta _k \).
\( J_i := {\left\{ \begin{array}{ll} (2^n)_{X_i+1}(2^n)_{U_i+1} &{} i\text {th component is isolated,}\\ (2^n)_{X_i+1}(2^n)_{U_i+\eta _i} &{} i\text {th component is a } {{\mathcal {Y}}}_{\text {-}\star },\\ (2^n)_{X_i+\eta _i}(2^n)_{U_i+1} &{} i\text {th component is a } {{\mathcal {V}}}_{\text {-}\star }. \end{array}\right. } \)
Proof Sketch: Inspired by Patarin’s mirror theory argument [37, 39], we will study the relation between \( H_i \) and \( J_i \) for all \( i \in [c_1+c_2+c_3] \). Our goal is to bound \( {\mathfrak {h}}_{c_1+c_2+c_3} \) in terms of \( H_{c_1+c_2+c_3} \) and \( J_{c_1+c_2+c_3} \). We show that \( H_{c_1+c_2+c_3} \ge (1-\epsilon ) J_{c_1+c_2+c_3} \), where \( \epsilon = O\left( q^2/2^{2n} + \sum _{i=1}^{c_2+c_3}\eta ^2_{c_1+i}q^2/2^{2n}\right) \), which immediately gives the bound for \( {\mathfrak {h}}_{c_1+c_2+c_3} \). This is precisely the motivation behind the definition of H and J.
The proof is given in two steps. First, in Sect. D.1, we bound the number of solutions for the sub-system of equations corresponding to isolated edges, i.e., the first \( c_1 \) components. The idea is to apply induction on \( H_i/J_i \) for \( i \in [c_1] \).
Given the number of solutions for the first \( c_1 \) components, we then bound the number of solutions for the remaining \( c_2+c_3 \) components (corresponding to star components) in section D.2, which essentially gives a bound for the complete system \( {\mathcal {L}}\). Again, \( H_{i'}/J_{i'} \) is analyzed for \( i' = c_1+i \) and \( i \in [c_2+c_3] \). However, we keep the expression in terms of q and \( \eta \) intact.
1.1 Bound for Sub-system Corresponding to Isolated Edges
As noted before, we want to bound \( {\mathfrak {h}}_{i} \) by induction on i, i.e., we want to evaluate \( {\mathfrak {h}}_{i+1} \) from \( {\mathfrak {h}}_i \). Since isolated components have only one edge, we simply write \( \lambda _i \) and \( \delta _i \) instead of \( \lambda ^i_1 \) and \( \delta ^i_1 \). We first give two supplementary results in Lemmas D.1 and D.2, which will be used later on to prove the main result.
Lemma D.1
For \( i \in [q_1] \),
where
and \( {\mathfrak {h}}'_i(j,k,\lambda _{i+1}) \) denotes the number of solutions of \( {\mathcal {L}}'_{|i}(j,k,\lambda _{i+1}) := {\mathcal {L}}_{|i} \cup \{Y_j \oplus V_k = \lambda _{i+1}\} \), for some \( j,k \in [i] \).
Proof
Let \( {\mathcal {S}}_i \) denote the solution space of \( {\mathcal {L}}_{|i} \), i.e., \( {\mathfrak {h}}_i = |{\mathcal {S}}_i| \). For a fix \( (y^i,v^i) \in {\mathcal {S}}_i \), we want to compute the number of \( (y_{i+1},v_{i+1}) \) pairs such that \( (y^{i+1},v^{i+1}) \in {\mathcal {S}}_{i+1} \). Now, some pair \( (x,x \oplus \lambda _{i+1}) \) is valid if \( x \ne y_j \) and \( x \oplus \lambda _{i+1} \ne v_k \), for \( j,k \in [i] \). This means that \( x \notin {\mathcal {Y}}\cup {\mathcal {V}}\), where \( {\mathcal {Y}}= \{y_j:j \in [i]\} \) and \( {\mathcal {V}}= \{v_j \oplus \lambda _{i+1}:j \in [i]\} \). As all \( y_j \) values are pairwise distinct and \( v_j \) values are pairwise distinct, we must have \( |{\mathcal {Y}}| = |{\mathcal {V}}| = i \). Thus, we have
where \( \phi (j,k) \) is the indicator variable that takes the value of 1 when \( y_j \oplus v_k = \lambda _{i+1} \), and 0 otherwise. Equality 1 follows from the definition of \( {\mathfrak {h}}'_i(j,k,\lambda _{i+1}) \), and equality 2 follows from the fact that exactly \( \delta _{i+1} \) (j, k) pairs exist such that \( k = j \), \( \lambda _{i+1} = \lambda _j \), and \( y_j \oplus v_j = \lambda _{i+1} \). For these, the number of solutions is exactly the same as \( {\mathfrak {h}}_i \) (since \( Y_j \oplus V_k = \lambda _{i+1} \) is already in \( {\mathcal {L}}_{|i} \)). The remaining valid (j, k) pairs must have \( \lambda _j,\lambda _k \ne \lambda _{i+1} \); else, they contradict \( {\mathcal {L}}\). The set of these remaining (j, k) pairs is the set \( {\mathcal {M}}\). \(\square \)
The following corollary of Lemma D.1 will be quite useful. The proof is immediate from the proof of Lemma D.1.
Corollary D.1
For \( i \ge 1 \), let \( {\widehat{{\mathcal {L}}}}_{i+1} \) be a system of \( i+1 \) equations such that \( \xi _{\max }({\widehat{{\mathcal {L}}}}_{i+1}) = 2 \). Then, for any sub-system \( {\widehat{{\mathcal {L}}}}_i \) consisting of i equations from \( {\widehat{{\mathcal {L}}}}_{i+1} \), we have
where \( {\widehat{{\mathfrak {h}}}}_i \) and \( {\widehat{{\mathfrak {h}}}}_{i+1} \) denote the number of solutions of \( {\widehat{{\mathcal {L}}}}_i \) and \( {\widehat{{\mathcal {L}}}}_{i+1} \), respectively.
Lemma D.2
For all \( (j,k) \in {\mathcal {M}}\), and for all \( \beta \in \{0,1\}^n \),
Proof
We are interested in \( {\mathfrak {h}}_i'(j,k,\beta ) \), which is the number of solutions of \( {\mathcal {L}}'_{|i}(j,k,\beta ) \), \( j,k \in {\mathcal {M}}\). The sub-system containing j and k equations is of the form
where once we fix \( Y_j = y_j \), all other unknowns are completely determined by linearity. Thus, \( {\mathfrak {h}}_i'(j,k,\beta ) \) is at most \( {\widehat{{\mathfrak {h}}}}_{i-1} \), where \( {\widehat{{\mathfrak {h}}}}_{i-1} \) is the number of solutions of \( {\widehat{{\mathcal {L}}}}_{|i-1} := {\mathcal {L}}'_{|i}(j,k,\beta ){\setminus }\{Y_j \oplus V_k = \beta ,Y_k \oplus V_k = \lambda _k\} \), the system obtained by removing the equations \( Y_j \oplus V_k = \beta \) and \( Y_k \oplus V_k = \lambda _k \) from \( {\mathcal {L}}'_{|i}(j,k,\beta ) \). Now a solution among the \( {\widehat{{\mathfrak {h}}}}_{i-1} \) solutions of \( {\widehat{{\mathcal {L}}}}_{|i-1} \) is not valid to be counted in \( {\mathfrak {h}}_i'(j,k,\beta ) \), if there exists \( \ell \in [i]{\setminus }\{k\} \), such that \( y_j \oplus v_\ell = \beta \) or \( y_j \oplus v_\ell = \beta \oplus \lambda _{k} \oplus \lambda _\ell \). The first case leads to \( V_k = V_\ell \), and the second case leads to \( Y_k = Y_\ell \), where \( k \ne \ell \) is obvious. Let \( {\widehat{{\mathcal {L}}}}'_{|i-1}(j,\ell ,\beta ) := {\widehat{{\mathcal {L}}}}_{|i-1} \cup \{Y_j \oplus V_\ell = \beta \} \) and \( {\widehat{h}}'_{i-1}(j,\ell ,\beta ) \) be the number of solutions \( {\widehat{{\mathcal {L}}}}'_{|i-1}(j,\ell ,\beta ) \). Therefore, the two cases correspond to the terms \( {\widehat{{\mathfrak {h}}}}'_{i-1}(j,\ell ,\beta ) \) and \( {\widehat{{\mathfrak {h}}}}'_{i-1}(j,\ell ',\beta \oplus \lambda _k \oplus \lambda _{\ell '}) \), whence we have
Let \( {\widehat{{\mathcal {L}}}}_{|i-2,\ell } := {\widehat{{\mathcal {L}}}}'_{|i-1}(j,\ell ,\beta ){\setminus }\{Y_j \oplus V_{\ell } = \beta ,Y_{\ell } \oplus V_{\ell } = \lambda _{\ell }\} \) and \( {\widehat{{\mathcal {L}}}}_{|i-2,\ell '} := {\widehat{{\mathcal {L}}}}'_{|i-1}(j,\ell ',\beta \oplus \lambda _{k}\oplus \lambda _{\ell '}){\setminus }\{Y_j \oplus V_{\ell '} = \beta \oplus \lambda _{k}\oplus \lambda _{\ell '},Y_{\ell '} \oplus V_{\ell '} = \lambda _{\ell '}\} \). Let \( {\widehat{{\mathfrak {h}}}}_{i-2,\ell } \) and \( {\widehat{{\mathfrak {h}}}}_{i-2,\ell '} \) be the number of solutions for \( {\widehat{{\mathcal {L}}}}_{|i-2,\ell } \) and \( {\widehat{{\mathcal {L}}}}_{|i-2,\ell '} \). Using similar line of argument as above, we bound \( {\widehat{{\mathfrak {h}}}}_{i-1}'(j,\ell ,\beta ) \le {\widehat{{\mathfrak {h}}}}_{i-2,\ell } \) and \( {\widehat{{\mathfrak {h}}}}_{i-1}'(j,\ell ',\beta \oplus \lambda _k \oplus \lambda _{\ell '}) \le {\widehat{{\mathfrak {h}}}}_{i-2,\ell '} \). Finally, we have
where inequalities 1 and 2 follow from Corollary D.1. Note that we switch from \( {\widehat{{\mathfrak {h}}}}_{i-2,\ell } \) and \( {\widehat{{\mathfrak {h}}}}_{i-2,\ell '} \) to \( {\widehat{{\mathfrak {h}}}}_{i-1} \) by reintroducing the equation \( Y_\ell \oplus V_\ell = \lambda _\ell \) and \( Y_{\ell '} \oplus V_{\ell '} = \lambda _{\ell '} \), respectively, and from \( {\widehat{{\mathfrak {h}}}}_{i-1} \) to \( {\mathfrak {h}}_i \) by reintroducing the equation \( Y_k \oplus V_k = \lambda _k \). The readers may use Fig. 5 to get a pictorial view of the switchings between different systems of equations. \(\square \)
Switchings used in the proof of Lemma D.2. From left to right: \( {\mathcal {L}}'_{|i}(j,k,\beta ) \) is the system \( {\mathcal {L}}_{|i}\cup \{Y_j \oplus V_k = \beta \} \); \( {\widehat{{\mathcal {L}}}}_{|i-1} \) is obtained by removing the equations involving \( V_k \) from \( {\mathcal {L}}'_{|i}(j,k,\beta ) \); \( {\widehat{{\mathcal {L}}}}'_{|i-1}(j,\ell ,\beta ) \) is the system \( {\widehat{{\mathcal {L}}}}_{|i-1}\cup \{Y_j \oplus V_\ell = \beta \} \); \( {\widehat{{\mathcal {L}}}}'_{|i-1}(j,\ell ',\beta ') \) is the system \( {\widehat{{\mathcal {L}}}}_{|i-1}\cup \{Y_j \oplus V_{\ell '} = \beta '\} \), where \( \beta ' = \beta \oplus \lambda _k \oplus \lambda _{\ell '} \); \( {\widehat{{\mathcal {L}}}}_{|i-2,\ell } \) is obtained by removing the equations involving \( V_\ell \) from \( {\widehat{{\mathcal {L}}}}'_{|i-1}(j,\ell ,\beta ) \). Note that there should have been two \( {\widehat{{\mathcal {L}}}}_{|i-2} \) switchings, one each for \( {\widehat{{\mathcal {L}}}}'_{|i-1}(j,\ell ,\beta ) \) and \( {\widehat{{\mathcal {L}}}}'_{|i-1}(j,\ell ',\beta ') \). We have drawn just once for economical reasons. Similar clarification applies to switchings from \( {\widehat{{\mathcal {L}}}}_{|i-2} \) to \( {\widehat{{\mathcal {L}}}}_{|i-1} \) (we only show for \( \ell \))
Remark 1
In [37, Theorem 11], a result similar to Lemma D.2 has been proved for random function scenario. While the proof of that theorem is correct, there is a notational issue which is worth pointing out. The \( {\mathfrak {h}}' \) notation is used in an unparametrized fashion, with an explicit hint in [37, Theorem 8] that this is done for simplification. But this simplification leads to a rather peculiar technical issue in [37, Theorem 11], where both lower and upper bounds are required on \( {\mathfrak {h}}' \) values, requiring different switchings. Without the parametrization, it is difficult to understand (and verify) the switchings.
Remark 2
The proof of Lemma D.2 should also give an idea of the proof complexity. Since we only want \( \epsilon = O(q^4/2^{3n}) \), we needed a somewhat crude estimate of \( {\mathfrak {h}}' \) values. In actual mirror theory as we move toward \( \epsilon = O(q/2^n) \), we have to make a good estimate of \( {\mathfrak {h}}' \) values, which does not seem easy.
Now, we state the main result of this section.
Lemma D.3
For \( q_1 < 2^{n-2} \), we have
Proof
We prove by induction on \( i \in [q_1] \), the number of components. First, \( H_1 = 2^{2n} = J_1 \). So the statement is true for \( i = 1 \). By definition, the ratio \( \frac{H_{i+1}}{H_i} = (2^n-\delta _{i+1}) \cdot \frac{{\mathfrak {h}}_{i+1}}{{\mathfrak {h}}_i} \), and \( J_{i+1} = (2^n - i)^2 J_i \). So we have
From Lemmas D.1 and D.2, we have
Recall that \( {\mathcal {M}}= \{(j,k):j,k \in [i],j \ne k,\lambda _j,\lambda _k \ne \lambda _{i+1}\} \). As there are \( \delta _{i+1} \)\( i' \in [i] \) such that \( \lambda _{i+1} = \lambda _{i'} \), we must have \( |{\mathcal {M}}| \ge (i - \delta _{i+1})(i-\delta _{i+1}-1) \). On substituting this value for \( |{\mathcal {M}}| \) in Eq. (37), and using the resulting lower bound for \( {\mathfrak {h}}_{i+1} \) in Eq. (36), we get

Let the boxed expression be A. We first simplify this term.
At inequality 1, we use \( i \le q_1 \le 2^{n-2} \), \( (i-2),(i-\delta _{i+1}) < i \), and \( (2^n-\delta _{i+1}),(2^n-i+1) < 2^n \); inequality 2 is just a simplification; and at inequality 3, we use \( (i-\delta _{i+1}),\delta _{i+1} \le i \) and \( (2^n-i)^2 \le 2^{n-1} \). Now, we have
Inequality 1 follows from recursive application of the induction hypothesis. The result follows by induction. \(\square \)
1.2 Bound for Sub-system Corresponding to Star Components
At this point, we have the bound for the sub-system corresponding to the \( q_1 \) isolated edges, and we want to extend it to get the bound on \( {\mathfrak {h}}_{q_1+c_2+c_3} \). For simplicity, we let \( i' = q_1+i = c_1+i \). Thus, \( c_1+c_2+c_3 = (c_2+c_3)' \). We follow exactly the same approach as before in case of isolated edges.
For \( i'-1 \ge 0 \), we analyze the ratio \( \frac{H_{i'}}{J_{i'}} \). Note that \( J_{i'} \) depends on the type of \( i' \)th component (\( {{\mathcal {Y}}}_{\text {-}\star }\) or \( {{\mathcal {V}}}_{\text {-}\star }\)). However, it can be easily seen that the two expressions are symmetric. Without loss of generality, we assume that the \( i' \)th component is \( {{\mathcal {Y}}}_{\text {-}\star }\). Then, we have

Let the boxed expression be A. We first simplify this term. In Lemma D.5, we show that
Thus, we have
We need both lower and upper bounds on B. Using the facts that \( X_{i'},U_{i'}+\eta _{i'} < q \), and \( \xi _{\max }q < 2^{n-1} \), we get \( B \ge 2^{n(\eta _{i'}+1)-1} \). Now, we derive an upper bound on B.
We also need a lower bound on C.
On substituting the bounds of B and C in Eq. (38), we get
At inequality 1, we use the fact that \( X_{i'},Y_{i'} \le q \) and \( \sum _{j=1}^{\eta _{i'}}\delta ^{i'}_j < q \) (\( \lambda ^{i'}_j \) can occur at most once in any component). At inequality 2, we use the fact that \( \eta ^2_{i'} > \eta _{i'}+1 \) as \( \eta _{i'} > 2 \). Therefore, we have
In combination with Lemma D.3, this immediately gives the bound on \( \frac{H_{c_1+c_2+c_3}}{J_{c_1+c_2+c_3}} \) in Lemma D.4.
Lemma D.4
For \( q \le 2^{n-2} \) and \( \xi _{\max } \le 2^n/2q \), we have
Theorem 5.1 follows from the definition of H, J and Lemma D.4.
Lemma D.5
\( \displaystyle {\mathfrak {h}}_{i'} \ge \left( 2^n - X_{i'} - \eta _{i'}U_{i'} + \sum _{j=1}^{\eta _{i'}}\delta ^{i'}_j\right) \cdot {\mathfrak {h}}_{i'-1}. \)
Proof
Let \( {\mathcal {S}}_{i'-1} \) denote the solution space of \( {\mathcal {L}}_{|i'-1} \). Let \( r = \sum _{j=1}^{i'-1}\eta _{j} \). For a fixed \( (y^r,v^r) \in {\mathcal {S}}_{i'-1} \), we want to compute the number of solutions for \( {\mathcal {L}}_{|i'} \). Since this is a \( {{\mathcal {Y}}}_{\text {-}\star }\) component, it is sufficient to choose an assignment for \( Y_{i'} \) (center of the \( i' \)th component) value and \( V^{i'}_j = Y_{i'} \oplus \lambda ^{i'}_{j} \). Now, an assignment x is invalid if \( x \in {\mathcal {Y}}\cup {\mathcal {V}}\), where \( {\mathcal {Y}}= \{y_j:j \in [r]\} \) and \( {\mathcal {V}}= \{v_j\oplus \lambda ^{i'}_k: j\in [r],k \in [\eta _{i'}]\} \). Clearly, \( |{\mathcal {Y}}| = X_{i'} \) and \( |{\mathcal {V}}| \le \eta _{i'}U_{i'} \). Further, exactly \( \sum _{j=1}^{\eta _{i'}}\delta ^{i'}_j \) previous equations share \( \lambda \) value with some equation in the \( i' \)th component, whence \( |{\mathcal {Y}}\cap {\mathcal {V}}| \ge \sum _{j=1}^{\eta _{i'}}\delta ^{i'}_j \). Thus, we have
\(\square \)
Proof of Lemma 6.1
Property 1 holds by definition and the nonexistence of bad hash key condition 1. Property 2 holds due to the nonexistence of bad hash key conditions 2 and 3. Property 3 holds due to the nonexistence of bad hash key conditions 4, 5, 6 and 7. Property 4 holds due to nonexistence of bad hash key conditions 4 and 5. It is easy to verify that given Properties 1, 2, 3 and 4, Fig. 4 enumerates all possible types of components of \( {\mathcal {G}}\). \(\square \)
Proof of Security of \(\textsf {DbHtS-p}\)
The analysis of \(\textsf {DbHtS-p}\) would be similar to the analysis of CLRW2 presented in this paper. The variables arising in \(\textsf {DbHtS-p}\) computation are analogously notated as in CLRW2 (see Fig. 6). Specifically, we have the following connection between the notations for \(\textsf {DbHtS-p}\) and CLRW2:
\( x^q \) and \( u^q \) in \(\textsf {DbHtS-p}\) correspond to \( x^q \) and \( u^q \) in CLRW2. Here, \( x^q = h_1(m^q) \) and \( u^q = h_2(m^q) \).
\( y^q \) and \( v^q \) in \(\textsf {DbHtS-p}\) correspond to \( y^q \) and \( v^q \) in CLRW2.
Similar to CLRW2, in \(\textsf {DbHtS-p}\)\( {x^q}\leftrightsquigarrow {y^q} \) and \( {u^q}\leftrightsquigarrow {v^q} \). Note that in \(\textsf {DbHtS-p}\)\( v^q = {E}_{k_2}(u^q) \), whereas in CLRW2\( u^q = {E}_{k_2}(v^q) \). However, this does not affect the permutation compatibility property.
\( \lambda ^q \) in \(\textsf {DbHtS-p}\) corresponds to \( \lambda ^q \) in CLRW2. Therefore, \( v^q \oplus y^q = \lambda ^q \).
Initial Setup: The first step of replacing the block cipher instantiations with independent uniform random permutations \( \Pi _1 \) and \( \Pi _2 \) incurs a cost of \( 2\mathbf {Adv}^{{\textsf {prp}}}_{{E}}(q,t') \). For the sake of simplicity, we call the resulting construction \(\textsf {DbHtS-p}\).
Oracle Description and Sampling Mechanism: The real and ideal oracles can be described in a similar manner as in case of CLRW2, except a small change. For all \( i \in [q] \), \( {\lambda }_i \leftarrow \!\!{\$}\,\{0,1\}^n\) in the ideal world, and \( {\lambda }_i = \textsf {DbHtS-p} (m_i) \) in the real world.
Definition of Bad Transcript and its Analysis: We again use the same set of bad transcripts and bound the probability of realizing a bad transcript, denoted \( {\epsilon _{{\textsf {bad}}}} \), as
Here, the only notable difference is the bound on \( {\Pr _{}\left[ {{\texttt {H}}_2}\right] } \) and \( {\Pr _{}\left[ {\texttt {H}_3}\right] } \). Since now the \( {\lambda } \) values are uniform at random, \( {\Pr _{}\left[ {{\texttt {H}}_2}\right] } \le {q \atopwithdelims ()2}\epsilon 2^{-n} \) and \( {\Pr _{}\left[ {\texttt {H}_3}\right] } \le {q \atopwithdelims ()2}\epsilon 2^{-n} \). All other bad events are bounded identically to the bad events in case of CLRW2.
Good Transcript Analysis: For a fixed good transcript \( \omega \), in the real world the interpolation probability is bounded as in case of CLRW2, i.e.,

In the ideal world, using Corollary 5.1 we get

where \( p_1 = q_1+c_2+q_3 \), \( p_2=q_1+q_2+c_3 \), and
On dividing Eq. (43) by (44) and doing some simplification, we get

Using Lemma 2.1, we get
The result follows from Eqs. (42) and (45). \(\square \)
Note that the application of alternating events/collisions lemma (or a similar result) seems indispensable, even if one assumes that the fundamental theorem of mirror theory holds.
Rights and permissions
About this article
Cite this article
Jha, A., Nandi, M. Tight Security of Cascaded LRW2. J Cryptol 33, 1272–1317 (2020). https://doi.org/10.1007/s00145-020-09347-y
Received:
Revised:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00145-020-09347-y




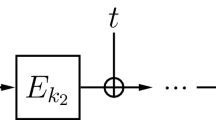
 ;
; .
.



 as
as  or
or  .
.

