Abstract
Signcryption with non-interactive non-repudiation is a public key primitive which aims at combining the functionalities of encryption and signature schemes, while offering to a judge the ability to settle a repudiation dispute without engaging in a costly multi-roundprotocol. We propose a new RSA based identification scheme together with a strongly unforgeable signature scheme. We derive a practical and efficient signcryption scheme with non-interactive non-repudiation we show to be insider secure, under the RSA assumption and the Random Oracle model. The communication overhead of our signcryption scheme, compared to the corresponding signature scheme is one group element.
This Research was supported by the African Center of Excellence in Mathematics, Computer Science and ICT of UGB.
Access provided by Autonomous University of Puebla. Download conference paper PDF
Similar content being viewed by others
Keywords
- Identification
- Signature
- Signcryption
- Insider security
- Non-interactive non-repudiation
- Signed quadratic residues
1 Introduction
Signcryption is a public key primitive introduced by Zheng [23], with the aim of combining the functionalities of encryption and signature schemes. Since Zheng’s seminal work, many security models and constructions have been proposed [3]. In a recent work, Badertscher et al. [2] consider, from an application-centric perspective, the security goals a signcryption scheme should achieve depending on the secret keys the attacker knows. They conclude, in opposition to [3, p. 29], that insider security should be considered as the standard security goal.
An important attribute which is not considered in the “standard” insider security model is non-interactive non-repudiation. As discussed in [2], the natural usage of signcrytion is to achieve a confidential and authenticated channel between two parties over an insecure network. The same can be achieved using non-interactive or one pass-key exchange protocols, which often outperform signcryption schemes. So, a major benefit of signcryption schemes compared to non-interactive and one-pass key exchange is non-interactive non-repudiation (NINR), i.e. a non-repudiation attribute wherein a judge does not have to engage in a costly multi-round interactive protocol to settle a repudiation dispute.
A first attempt to achieve NINR in a signcryption design was proposed by Bao and Deng [6]. Unfortunately their scheme fails in providing both NINR and confidentiality [17, 22]. In [17], Malone–Lee propose a design with NINR. However, he analyses his design, under the Gap Diffie–Hellman Assumption [19] and the Random Oracle (RO) model [8], in a security definition which is closer to the outsider model than to the insider one [3, Chap. 2–4]. Fan et al. [11] propose a strengthening of Malone–Lee’s security model which considers, not only confidentiality and unforgeability in the insider model, but also soundness and unforgeability of non-repudiation evidence. They propose a design they show to be insider secure under the Decisional Bilinear Diffie–Hellman assumption, without resorting to the RO model.
In this paper, we propose a new identification scheme, inspired from the FXCR [20, 21] and Guillou–Quisquater (GQ) [13] schemes, over the group of signed quadratic residues [14].
We derive a signature scheme which is strongly unforgeable against chosen message attacks. A significant advantage of our signature scheme, compared to the FXCR or GQ schemes is that it is defined over a group wherein the strong Diffie–Hellman assumption is known to hold under the factoring assumption [14]. Then, using a variant of Cash et al.’s trapdoor test technique [10], we derive a signcryption scheme with non-interactive non-repudiation (SCNINR) we show to be insider secure, under the RSA assumption and the RO model, in a variant of Fan et al.’s security definition [11].
This paper is organized as follows. In Sect. 2, we present some preliminaries. In Sect. 3, we propose the identification scheme, discuss its attributes, and derive the signature scheme. We present the new SCNINR scheme and its security arguments in Sect. 4.
2 Preliminaries
Notations. If n is an integer, |n| denotes its bit-length and [n] denotes the set \(\{0, \cdots , n\}\). For a real l, \(\lceil l\rceil \) denotes the smallest integer which is greater than or equal to l. We refer to the length of a list \(\mathcal {L}\) by \(|\mathcal {L}|\), and to the cardinality of a set S by |S|. If P is a probabilistic algorithm which takes as parameters \(u_1, \cdots , u_n\) and outputs a result V which belongs to a set \(\mathbf {V}\), we write  . We denote by \(\{P(u_1,\cdots , u_n)\}\) the set \(\{v\in \mathbf {V} : \Pr (V=v)\ne 0\}\). If S is a set, the notation
. We denote by \(\{P(u_1,\cdots , u_n)\}\) the set \(\{v\in \mathbf {V} : \Pr (V=v)\ne 0\}\). If S is a set, the notation  means that a is chosen uniformly at random from S. \(\mathsf {Exp}(\mathbb {Z}_N, t, l)\) denotes the computational effort required to perform t exponentiations with l bit exponents in \(\mathbb {Z}_N\); \(\mathsf {Exp}(\mathbb {Z}_N, l)\) stands for \(\mathsf {Exp}(\mathbb {Z}_N, 1, l)\). \(\mathsf {Jcb}(\mathbb {Z}_N)\) denotes the effort required to compute a Jacobi symbol in \(\mathbb {Z}_N\). For two bit strings \(m_1\) and \(m_2\), \(m_1{||}m_2\) denotes their concatenation; \(\epsilon \) denotes the empty string. If \(x_1, x_2, \cdots , x_k\) are objects belonging to different structures (group, bit-string, etc.) \((x_1, x_2, \cdots , x_k)\) denotes a representation of the tuple such that each component can be unequivocally parsed.
means that a is chosen uniformly at random from S. \(\mathsf {Exp}(\mathbb {Z}_N, t, l)\) denotes the computational effort required to perform t exponentiations with l bit exponents in \(\mathbb {Z}_N\); \(\mathsf {Exp}(\mathbb {Z}_N, l)\) stands for \(\mathsf {Exp}(\mathbb {Z}_N, 1, l)\). \(\mathsf {Jcb}(\mathbb {Z}_N)\) denotes the effort required to compute a Jacobi symbol in \(\mathbb {Z}_N\). For two bit strings \(m_1\) and \(m_2\), \(m_1{||}m_2\) denotes their concatenation; \(\epsilon \) denotes the empty string. If \(x_1, x_2, \cdots , x_k\) are objects belonging to different structures (group, bit-string, etc.) \((x_1, x_2, \cdots , x_k)\) denotes a representation of the tuple such that each component can be unequivocally parsed.
RSA Public Key Generator. Let k be a security parameter, n(k) be a function of k and \(0\leqslant \delta < 1/2\) be a constant. An algorithm \({\mathsf {RSAGen}}\) (which may be distributed) is said to be a \((n(k), \delta )\) RSA public key generator if on input \(1^k\), it outputs a n(k) bit Blum integer \(N=pq\) together with a public exponent e such that all the prime factors of \(\phi (N)/4\) are: (i) pairwise distinct, and (ii) at least \(\delta {}n\) bit integers, and (iii) e is a \((k+1)\) bit prime.
RSA and Factoring Assumptions. Let \(\mathcal {A}\) be an algorithm. We define the quantity

The RSA assumption for an \((n(k), \delta )\) RSA public key generator is said to hold if for all efficient adversary \(\mathcal {A}\), \({\mathsf {Adv}}^{\text {RSA}}_{\mathcal {A}, {\mathsf {RSAGen}}}(k)\) is negligible. For an instance  and an efficiently sampleable and recognizable subset \(\mathsf {J}\) of \(\mathbb {Z}_N\), we say that the RSA problem is \((t(k), \varepsilon (k))\) hard in \(\mathsf {J}\), if for all \(\mathcal {A}\) running in time at most t,
and an efficiently sampleable and recognizable subset \(\mathsf {J}\) of \(\mathbb {Z}_N\), we say that the RSA problem is \((t(k), \varepsilon (k))\) hard in \(\mathsf {J}\), if for all \(\mathcal {A}\) running in time at most t, 
Let \(\mathcal {A}\) be a factoring algorithm and

The factoring assumption for an \((n, \delta )\) RSA public key generator is said to hold if for all efficient adversary \(\mathcal {A}\), \({\mathsf {Adv}}^{\mathsf {fac}}_{\mathcal {A}, {\mathsf {RSAGen}}}(k)\) is negligible.
Diffie–Hellman Assumptions. Let \(\mathcal {G}=\langle G\rangle \) be a cyclic group, which order is a function of the security parameter k and is not necessarily known. For \(X\in \mathcal {G}\), \(\log _GX\) denotes the smallest non-negative integer x such that \(G^x=X\). For, \(X, Y\in \mathcal {G}\), we denote \(G^{(\log _GX)(\log _GY)}\) by \(\text {CDH}(X, Y)\). The computational Diffie–Hellman (CDH) Assumption is said to hold in \(\mathcal {G}\) if for all efficient algorithm \(\mathcal {A}\),

is negligible in k. The strong Diffie–Hellman (sCDH) assumption is said to hold in \(\mathcal {G}\) if the CDH assumption holds even if \(\mathcal {A}\) is endowed with a decisional Diffie–Hellman oracle \(\mathcal {O}_{\text {DDH}, X}(\cdot , \cdot )\) for a some fixed X, which on input \(U, V\in \mathcal {G}\) outputs 1 if \(V=\text {CDH}(X, U)\) and 0 otherwise.
Signed Quadratic Residues. For an odd integer N, we consider \(\{-(N-1)/2, \cdots ,\) \((N-1)/2\}\) as a set of representatives of the residue classes modulo N. We denote by \(\mathbb {J}_N\) the subgroup of elements of \(\mathbb {Z}_N^*\) with Jacobi symbol 1, and consider the quotient group \(\mathbb {J}_N/\{-1, 1\}\). We define \(\mathbb {J}_N^+=\mathbb {J}_N\cap \{1,\cdots , (N-1)/2\}\), and the binary operation \(\circ \) over \(\mathbb {J}_N^+\) by \(X\circ Y=|X\cdot {}Y \mod N|\). For \(X\in \mathbb {J}_N^+\) and \(t\in \mathbb {N},\) we write  for \(\overbrace{X\circ \cdots \circ X}^{t\text { times}} = |X^t \mod N|\in \mathbb {J}_N^+.\) Then \((\mathbb {J}_N^+, \circ )\) is a group, termed group of signed quadratic residues. Moreover the mapping which associates \(\{-X, X\}\in \mathbb {J}_N/\{-1, 1\}\) to \(|X|\in \mathbb {J}_N^+\) is an isomorphism. We identify the quotient group \(\mathbb {J}_N/\{-1, 1\}\) with \(\mathbb {J}_N^+\). From [14], we have the following Lemma.
for \(\overbrace{X\circ \cdots \circ X}^{t\text { times}} = |X^t \mod N|\in \mathbb {J}_N^+.\) Then \((\mathbb {J}_N^+, \circ )\) is a group, termed group of signed quadratic residues. Moreover the mapping which associates \(\{-X, X\}\in \mathbb {J}_N/\{-1, 1\}\) to \(|X|\in \mathbb {J}_N^+\) is an isomorphism. We identify the quotient group \(\mathbb {J}_N/\{-1, 1\}\) with \(\mathbb {J}_N^+\). From [14], we have the following Lemma.
Lemma 1
If N is a Blum integer then (a) \((\mathbb {J}_N^+, \circ )\) is a subgroup of \(\mathbb {Z}_N^*\) of order \(\phi (N)/4\); (b) \(\mathbb {J}_N^+\) is efficiently recognizable given only N; and (c) if \(\mathbb {J}_N\) is cyclic then so is \(\mathbb {J}_N^+\).
Canonical Identification Schemes
Definition 1
A canonical identification scheme \(\mathcal {I}=({\mathsf {Gen}}, {\mathsf {P}}, {\mathsf {V}}, \mathsf {ChSet})\) is a triple of algorithms together with a challenge set, such that:
-
\({\mathsf {Gen}}\) is a probabilistic algorithm which takes as input a domain parameters \(dp\) and returns a key pair \((sk, pk)\).
-
\({\mathsf {P}}=({\mathsf {P}}_1, {\mathsf {P}}_2)\) is a pair of algorithms such that: (i) \({\mathsf {P}}_1\) takes as input a secret key \(sk\) and outputs a commitment X together with a state \(st\); and (ii) \({\mathsf {P}}_2\) takes as inputs a private key \(sk\), a commitment X, a challenge \(c\in \mathsf {ChSet}\), and a state \(st\) and outputs a response \(s\in \{0, 1\}^*\).
-
\({\mathsf {V}}\) is a deterministic verification algorithm which takes as inputs a public key \(pk\), a commitment X, a challenge c, and a response s and outputs \(d\in \{0,1\}\).
-
And, for all \((sk, pk) \in \{{\mathsf {Gen}}(dp)\}\), all \((X, st)\in \{{\mathsf {P}}_1(sk)\}\), all \(c\in \mathsf {ChSet}\), and all \(s\in \{{\mathsf {P}}_2(sk, X, c, st)\}\), \({\mathsf {V}}(pk, X, c, s)=1\).
A transcript (X, c, s) is said to be accepting with respect to \(pk\) if \({{\mathsf {V}}(pk, X, c, s)=1}\).
An identification scheme is said to be unique if for all \((sk, pk)\in \{{\mathsf {Gen}}(dp)\}\), all \((X, st)\in \{{\mathsf {P}}_1(sk)\}\), and all \(c\in \mathsf {ChSet}\), there is at most one \(s\in \{0, 1\}^*\) such that \({\mathsf {V}}(pk, X, c, s)=1\). It is said to have \({\alpha \text {-bits}}\) of min entropy if for all \((sk, pk)\in \{{\mathsf {Gen}}(dp)\}\), the commitments generated through \({\mathsf {P}}_1(sk)\) are chosen from a distribution with min entropy at least \(\alpha \); i.e., for all commitment \(X_0\), if  was honestly generated then \(\Pr (X=X_0)\leqslant 2^{-\alpha }\).
was honestly generated then \(\Pr (X=X_0)\leqslant 2^{-\alpha }\).
Definition 2
Let \(\mathcal I=({\mathsf {Gen}},\) \({\mathsf {P}},{\mathsf {V}}, \mathsf {ChSet})\) be a canonical identification scheme.
-
(a)
\(\mathcal I\) is said to provide special soundness (SpS) if there exists an efficient deterministic algorithm \(\mathsf {Ext}\) (an extractor) such that for all accepting conversations with respect to a public key \(pk\), (X, c, s) and \((X, c', s')\), if \(c\ne c'\) then \(sk^*\leftarrow \mathsf {Ext}(pk, X, c, s, c', s')\) is such that \((sk^*, pk)\in \{{\mathsf {Gen}}(dp)\}\).
-
(b)
It is said to be honest verifier zero knowledge (HVZK) if there exists an efficient probabilistic algorithm \(\mathsf {sim}\) (a simulator) such that for all \((sk, pk)\in \{{\mathsf {Gen}}(dp)\}\), the output distribution of \(\mathsf {sim}\) on input \(pk\) is identical to that of a real transcript between \({\mathsf {P}}(sk)\) and \({\mathsf {V}}(pk)\).
-
(c)
It is said to be random self reducible (RSR) if there is a probabilistic algorithm \(\mathsf {Rerand}\) together with two deterministic algorithms \(\mathsf {Tran}\) and \(\mathsf {Derand}\) such that for all \((sk, pk)\in \{{\mathsf {Gen}}(dp)\}\):
-
if
 and
and  then \(pk_1\) and \(pk_2\) have the same distribution;
then \(pk_1\) and \(pk_2\) have the same distribution; -
for all \((sk_1, pk_1)\in \{{\mathsf {Gen}}(dp)\}\), for all \(\tau \) such that \((\tau , pk_1)\in \{\mathsf {Rerand}(pk)\}\), if \(sk^*\leftarrow \mathsf {Derand}(pk, pk_1, sk_1, \tau )\) then \((sk^*, pk)\in \{{\mathsf {Gen}}(dp)\}\);
-
for all \((sk_1, pk_1)\in \{{\mathsf {Gen}}(dp)\}\) and all \((X, c, s_1)\) such that \({{\mathsf {V}}(pk_1, X, c, s_1)=1}\), if \((X, c, s)\leftarrow \mathsf {Tran}(pk, pk_1, \tau , (X, c, s_1))\) then \({\mathsf {V}}(pk, X, c, s)=1\).
-
Definition 3
A canonical identification scheme \(\mathcal I=({\mathsf {Gen}}, {\mathsf {P}}, {\mathsf {V}}, \mathsf {ChSet})\) is said to be \((t, \varepsilon )\)-secure against Key Recovery against Key Only Attacks (KR-KOA), if for all adversary \(\mathcal {A}\) running in time at most t

Symmetric Encryption, Digital Signature
Definition 4
A symmetric encryption scheme \(\mathcal {E}=( \mathsf {E}, \mathsf {D}, \mathbf {K}(k), \mathbf {M}(k), \mathbf {C}(k))\) is a pair of efficient algorithms \((\mathsf {E}, \mathsf {D})\) together with a triple of sets \((\mathbf {K}(k), \mathbf {M}(k), \mathbf {C}(k))\) such that for all \(\tau \in \mathbf {K}\) and all \(m\in \mathbf {M}\), \(\mathsf {E}(\tau , m)\in \mathbf {C}\), \(m = \mathsf {D}(\tau , \mathsf {E}(\tau , m))\).
Definition 5
Let \(\mathcal {A}\) be an adversary against an encryption scheme \(\mathcal {E}\); its semantic security advantage is

where \(m_0, m_1\in \mathbf {M}\) are distinct equal length messages. The scheme \(\mathcal {E}\) is said to be \((t, \varepsilon )\)-semantically secure if for all adversary \(\mathcal {A}\) running in time t \({{\mathsf {Adv}}^{\mathsf {ss}}_{\mathcal {A}, \mathcal {E}}(k)\leqslant \varepsilon }\).
Definition 6
A signature scheme \(\mathcal {S}=({\mathsf {Gen}}, \mathsf {Sign}, \mathsf {Vrfy})\) is a triple of efficient algorithms together with a message space \(\mathbf {M}\), such that:
-
\({\mathsf {Gen}}\) is probabilistic algorithm which takes as input a domain parameter \(dp\) and returns a key pair \((sk, pk)\);
-
\(\mathsf {Sign}\) is a probabilistic algorithm which takes as inputs a secret key \(sk\) and a message \(m\in \mathbf {M}\) and outputs a signature \(\sigma \);
-
\(\mathsf {Vrfy}\) is a deterministic algorithm which takes as inputs a public key \(pk\), a message m, and a signature \(\sigma \) and outputs \(d\in \{0, 1\}\); and
-
for all \((sk, pk)\in \{{\mathsf {Gen}}(dp)\}\), all \(m\in \mathbf {M}\), \(\Pr \left[ \mathsf {Vrfy}(pk, m, \mathsf {Sign}(sk, m))=1\right] =1.\)

Definition 7
Let \(\mathcal {S}=({\mathsf {Gen}}, \mathsf {Sign}, \mathsf {Vrfy})\) be a signature scheme such that the execution of \(\mathsf {Sign}\) involves the computation of one digest value, at least. \(\mathcal {S}\) is said to be \((t, U, Q_{\mathsf {Sign}}, Q_{\mathsf {H}},\varepsilon )\) multi-user strongly unforgeable against chosen message attacks (MU-SUF-CMA) in the RO model, if for all adversary \(\mathcal {A}\) playing Game 1 (wherein we consider U and \(dp\) as implicit parameters), if \(\mathcal {A}\) runs in time at most t, issues at most \(Q_{\mathsf {Sign}}\) and \(Q_{\mathsf {H}}\) queries to the signing and hashing oracles respectively, the probability it succeeds is at most \(\varepsilon \).
Signcryption Schemes
Definition 8
A signcryption scheme is a quintuple of algorithms \(\mathcal {SC}=({\mathsf {Setup}},\) \({\mathsf {Gen}}_S, {\mathsf {Gen}}_R, {\mathsf {Sc}}, \mathsf {Usc})\) wherein:
-
(a)
\({\mathsf {Setup}}\) is a probabilistic algorithm which takes a security parameter \(1^k\) as input, and outputs a domain parameter \(dp\).
-
(b)
\({\mathsf {Gen}}_S\) is a probabilistic algorithm which takes as input a domain parameter \(dp\) and outputs a sender key pair \((sk_S, pk_S)\) wherein \(sk_S\) is the signing key.
-
(c)
\({\mathsf {Gen}}_R\) is a probabilistic algorithm which takes \(dp\) as input and outputs a receiver key pair \((sk_R, pk_R)\).
-
(d)
\({\mathsf {Sc}}\) is a probabilistic algorithm which takes as inputs \(dp\), a sender private key \(sk_S\) and a receiver public key \(pk_R\), and outputs a signcrypted text C. We consider \(dp\) as an implicit parameter and write
 .
. -
(e)
\(\mathsf {Usc}\) is a deterministic algorithm which takes as input \(dp\), a sender public key \(pk_S\), a receiver secret key \(sk_R\) and outputs either a message \(m\in \mathcal {M}\) or an error symbol \(\bot \notin \mathcal {M}\).
The above algorithms are such that for all \(dp\in \{{\mathsf {Setup}}(1^k)\}\), all \(m\in \mathcal {M}\), all \((sk_S, pk_S)\in \{{\mathsf {Gen}}_S(dp)\}\), and all \((sk_R, pk_R)\in \{{\mathsf {Gen}}_R(dp)\}\), \(m = \mathsf {Usc}(sk_R, pk_S,\) \({\mathsf {Sc}}(sk_S, pk_R, m)).\) The scheme is said to provide NINR if there is a non-repudiation evidence generation algorithm \({\mathsf {N}}\) together with a pubic verification algorithm \({\mathsf {PV}}\) such that:
-
\({\mathsf {N}}\) takes as inputs a receiver secret key \(sk_R\), a sender public key \(pk_S\), and a signcrypted text C, and outputs a non-repudiation evidence \(nr\) or a failure symbol \(\bot \); we write \(nr\leftarrow {\mathsf {N}}(sk_R, pk_S, C)\).
-
\({\mathsf {PV}}\) takes as inputs a signcryptext C a message m, a non-repudiation evidence \(nr\), and two public keys \(pk_S\) and \(pk_R\) and outputs, a decision \(d\in \{0,1\}\); we write \(d\leftarrow {\mathsf {PV}}(C, m, nr, pk_S, pk_R)\).
-
And, for all \(dp\in \{{\mathsf {Setup}}(1^k)\}\), all \(C\in \{0, 1\}^*\), all \((sk_S, pk_S)\in \{{\mathsf {Gen}}_S(dp)\}\), and all \((sk_R, pk_R)\in \{{\mathsf {Gen}}_R(dp)\}\), if \(\bot \ne m\leftarrow \mathsf {Usc}(sk_R, pk_S, C)\) and \(nr\leftarrow {\mathsf {N}}(sk_R, pk_S, C)\) then \(1=d\leftarrow {\mathsf {PV}}(C, m, nr, pk_S, pk_R)\).
Confidentiality. We propose in Game 2 an extension of the Secret Key Ignorant Multi-User (SKI-MU) insider confidentiality in the Flexible Signcryption/Unsigncryption Oracle (FSO/FUO) model [4, 5] geared to SCNINR.

Definition 9
A SCNINR \(\mathcal {SC}\) is said to be \((t, q_{{\mathsf {Sc}}}, q_{\mathsf {Usc}},q_{{\mathsf {N}}}, \varepsilon )\)-secure in the SKI-MU insider confidentiality in the FSO/FUO-IND-CCA2 sense if for all adversary \(\mathcal {A}\) playing Game 2, if \(\mathcal {A}\) runs in time t, and issues respectively \(q_{{\mathsf {Sc}}}\), \(q_{\mathsf {Usc}}\), and \(q_{{\mathsf {N}}}\) queries to the signcryption, unsigncryption, and non-repudiation evidence generation oracles then \({\mathsf {Adv}}^{\mathsf {cca2}}_{\mathcal {A}, \mathcal {SC}}(1^k)\leqslant \varepsilon \).
Unforgeability. We recall here the multi-user insider unforgeability in the FSO/FUO-sUF-CMA sense for SCNINR.

Definition 10
A SCNINR is said to be \((t, q_{{\mathsf {Sc}}}, \varepsilon )\) multi-user insider unforgeable in the FSO/FUO-sUF-CMA sense if for all attacker \(\mathcal {A}\) playing Game 3, if \(\mathcal {A}\) runs in time t and issues \(q_{{\mathsf {Sc}}}\) signcryption queries then \(\mathsf {Adv}_{\mathcal {A}, \mathcal {SC}}^{\mathsf {suf}}(1^k)\leqslant \varepsilon \).
Soundness of Non-repudiation. This attribute ensures that public verification always yields a correct result.

Definition 11
A signcryption scheme \(\mathcal {SC}\) is said to achieve \((t, q_{{\mathsf {Sc}}}, \varepsilon )\) computational soundness of non-repudiation if for all adversary \(\mathcal {A}\) playing Game 4, if \(\mathcal {A}\) runs in time t and issues \(q_{{\mathsf {Sc}}}\) signcryption queries then \(\mathsf {Adv}_{\mathcal {A}, \mathcal {SC}}^{\mathsf {snr}}(1^k)\leqslant \varepsilon \).
Unforgeability of Non-repudiation (NR) Evidence. Contrary to Malone–Lee [17], Fan et al. [11] consider unforgeability of non-repudiation evidence. However, their definition seems too restrictive. Indeed, they consider the capability of both the sender and receiver of a signcrypted text to generate a non-repudiation evidence as a security weakness. As a motivating example, they consider a malicious patient who receives a signcrypted medical report from his doctor, generates a non-repudiation evidence, and exposes the signcryted text together with the NR evidence. The patient can then claim that the doctor has exposed his report. In such a situation a judge cannot decide who, among the patient and the doctor, exposed the report.
As for us, non-repudiation ensures that a message sender (the doctor in the example) cannot deny that the message in the signcryted text (the medical record) is from him. The question considered in the example is not about the non-repudiation of the signcrypted message (the report), but about the non-repudiation of the (non-repudiation) evidence. Moreover in many settings, a non-repudiation evidence may be used both for credit (the ability of the sender to later claim being the sender of the message) and responsibility (the ability of the receiver to hold the sender accountable for the message contents) [9, Chap. 3]. It seems then important that NR evidences can be generated by both the sender (at signcrypted text generation) and the receiver of a signcrypted text.

Definition 12
A SCNINR is said to achieve \((t, q_{{\mathsf {Sc}}}, q_{\mathsf {Usc}}, q_{{\mathsf {N}}}, \varepsilon )\) unforgeability of non-repudiation evidence if for all adversary \(\mathcal {A}\) playing Game 5, if \(\mathcal {A}\) runs in time t and issues respectively \(q_{{\mathsf {Sc}}}\), \(q_{\mathsf {Usc}}\), and \(q_{{\mathsf {N}}}\) queries to the signcryption, unsigncryption, and non-repudiation evidence generation oracles then \({\mathsf {Adv}_{\mathcal {A}, \mathcal {SC}}^{\mathsf {unr}}(1^k)\leqslant \varepsilon }\).
3 New Identification and Signature Schemes
A domain parameter is given by \(dp= (N, G, R, e, k)\) wherein
-
\(N=pq\) is an RSA modulus, \(p=2p'+1\) and \(q=2q'+1\) being safe primes.
-
e is a \((k+1)\) bit prime. To improve the scheme’s efficiency, it can be chosen to be a sparse prime. It is used as an RSA public exponent.
-
R is a generator of \(\mathbb {J}_N^+\), and
 .
. -
k is a security parameter, \(n(k)= |N|\) is chosen such that the best known algorithm for factoring N runs in time \({\approx }2^k\).
For domain parameter generation, if there is a party which is trusted by all the users, he can generate the domain parameter. Alternatively, an perhaps preferably, the domain parameter may be generated by a set of parties such that each user of the scheme trusts at least one of them. In this case, the parties generating the domain parameter may perform as follows:
-
(1)
They run the distributed shared RSA modulus generation following the protocol given in [1], to get product of two safe primes N, while each party has a share of the primes.
-
(2)
They choose a \((k+1)\) bit prime e and
 , and compute
, and compute  (R is a generator of \(\mathbb {J}_N^+\), with all but negligible probability).
(R is a generator of \(\mathbb {J}_N^+\), with all but negligible probability). -
(3)
The domain parameter is \(dp= (N, G, R, e, k)\).
Description of the Scheme. Let \(dp= (N, G, R, e, k)\) be a domain parameter, and \(l=\lceil N/4\rceil \). We derive the scheme \(\mathcal {I}_{SSN}=({\mathsf {Gen}}, {\mathsf {P}},{\mathsf {V}}, \mathsf {ChSet})\) wherein \({\mathsf {Gen}}\), \({\mathsf {P}}=({\mathsf {P}}_1, {\mathsf {P}}_2)\), and \({\mathsf {V}}\) are as described hereunder; we denote \([2^k-1]\) by \(\mathsf {ChSet}\).
-

 ;
;  Return \((sk, pk)\).
Return \((sk, pk)\). -

 ;
;  ; Return \((X, st)\).
; Return \((X, st)\). -
 \(Y\leftarrow st\);
\(Y\leftarrow st\);  ; Return s.
; Return s. -
 If
If  then Return 1, Else return 0.
then Return 1, Else return 0.
For all \((sk, pk)\in \{{\mathsf {Gen}}(dp)\}\), if (X, c, s) is a transcript generated through \({\mathsf {P}}\) then \(1={\mathsf {V}}(pk, X, c, s)\), as 
Uniqueness and Min Entropy. As the function \(\text {Exp}_e: \; \mathbb {J}_N^+\rightarrow \mathbb {J}_N^+\) which maps Y to  is bijective, for all \(X, pk\in \mathbb {J}_N^+\), all \(c\in \mathsf {ChSet}\), there is one and only one \(s\in \mathbb {J}_N^+\) such that
is bijective, for all \(X, pk\in \mathbb {J}_N^+\), all \(c\in \mathsf {ChSet}\), there is one and only one \(s\in \mathbb {J}_N^+\) such that  . Let \(\delta _0\) denote \(\max (1/p', 1/q')\). If
. Let \(\delta _0\) denote \(\max (1/p', 1/q')\). If  and
and  the statistical distance between \(x_1\) and \(x_2\) is \({\varDelta (x_1, x_2) \leqslant \tfrac{N/4 - \phi (N)/4}{N/4} \leqslant \delta _0}.\) So, if
the statistical distance between \(x_1\) and \(x_2\) is \({\varDelta (x_1, x_2) \leqslant \tfrac{N/4 - \phi (N)/4}{N/4} \leqslant \delta _0}.\) So, if  and
and  , then \(\varDelta (X_1, X_2)\leqslant \delta _0\). Then, if X is generated through \({\mathsf {P}}_1(\cdot )\), the statistical distance between the distribution of X and the uniform distribution over \(\mathbb {J}_N^+\) is not greater than \(\delta _0\). And then for all \(X_0\in \mathbb {J}_N^+\), if X is generated through \({\mathsf {P}}_1(\cdot )\), \({\mid }\Pr (X=X_0)- 1/|\mathbb {J}_N^+|{\mid }\; \leqslant \delta _0\); the identification scheme has \(\alpha \approx -\log _2(\delta _0)\) bits of min-entropy.
, then \(\varDelta (X_1, X_2)\leqslant \delta _0\). Then, if X is generated through \({\mathsf {P}}_1(\cdot )\), the statistical distance between the distribution of X and the uniform distribution over \(\mathbb {J}_N^+\) is not greater than \(\delta _0\). And then for all \(X_0\in \mathbb {J}_N^+\), if X is generated through \({\mathsf {P}}_1(\cdot )\), \({\mid }\Pr (X=X_0)- 1/|\mathbb {J}_N^+|{\mid }\; \leqslant \delta _0\); the identification scheme has \(\alpha \approx -\log _2(\delta _0)\) bits of min-entropy.
Special Soundness. If (X, c, s) and \((X, c', s')\) are two accepting transcripts with respect to a public key \(pk\) such that \(c\ne c'\) then  , and then
, and then  . Now, as \(c, c'\in \mathsf {ChSet}=[2^k-1]\), and \(e>2^k\) is prime, it follows that \(\gcd (e, c-c') = 1\). Let \(\alpha , \beta \in \mathbb {Z}\) be such that \(e\alpha +(c-c')\beta =1\) and
. Now, as \(c, c'\in \mathsf {ChSet}=[2^k-1]\), and \(e>2^k\) is prime, it follows that \(\gcd (e, c-c') = 1\). Let \(\alpha , \beta \in \mathbb {Z}\) be such that \(e\alpha +(c-c')\beta =1\) and  , then
, then 
Honest Verifier Zero Knowledge. For all public key \(pk\in \mathbb {J}_N^+\), the following simulator yields transcripts with the same distribution as real transcripts.
-

 ;
;  ;
;  ;
;  ; Return (X, c, s).
; Return (X, c, s).
Random Self Reducibility. The \(\mathsf {Rerand}\), \(\mathsf {Tran}\) and \(\mathsf {Derand}\) algorithms are:
-

 ;
;  ; Return \((\tau , pk_1)\);
; Return \((\tau , pk_1)\); -

 ; Return \(sk^*\);
; Return \(sk^*\); -
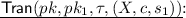
 ; \(s\leftarrow Z\circ s_1\); Return (X, c, s).
; \(s\leftarrow Z\circ s_1\); Return (X, c, s).
The \(\mathsf {Rerand}\) algorithm outputs a public key \(pk_1\) which has the same distribution as the keys generated through \({\mathsf {Gen}}(dp)\). The \(\mathsf {Derand}\) algorithm provides the static private key corresponding to \(pk\). The \(\mathsf {Tran}\) algorithm produces a valid transcript with respect to the public key \(pk\).
KR-KOA Security. For \(sk, pk\in \mathbb {J}_N^+\), if  then \((\pm sk)^{e}=pk\). Then under the RSA assumption over \(\mathbb {J}_N^+\), \(\mathcal {I}_{SSN}\) is secure against KR-KOA.
then \((\pm sk)^{e}=pk\). Then under the RSA assumption over \(\mathbb {J}_N^+\), \(\mathcal {I}_{SSN}\) is secure against KR-KOA.
Lemma 2
If the RSA problem is \((t, \varepsilon )\)-hard over \(\mathbb {J}_N^+\) then the identification scheme \(\mathcal {I}_{SSN}\) is \((t,\varepsilon )\)-KR-KOA-secure.
The Signature Scheme. As the identification scheme is commitment recoverable, using the (alternative) Fiat–Shamir transform [12], we derive the signature scheme \(\mathcal {S}_{SSN}=({\mathsf {Gen}}, \mathsf {Sign}, \mathsf {Vrfy})\) we describe hereunder. \(\mathsf {H}_1:\{0, 1\}^* \rightarrow \mathsf {ChSet}\) is a hash function.
-
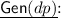
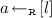 ;
;  Return \((sk, pk)\).
Return \((sk, pk)\). -

 ;
;  ; \(h\leftarrow \mathsf {H}_1(X, m)\)
; \(h\leftarrow \mathsf {H}_1(X, m)\)  ; Return (h, s).
; Return (h, s). -
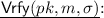 Parse \(\sigma \) as \((h,s)\in \mathsf {ChSet}\times \mathbb {Z}_N\);
Parse \(\sigma \) as \((h,s)\in \mathsf {ChSet}\times \mathbb {Z}_N\); 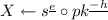 ; \(h'=\mathsf {H}_1(X, m)\).
; \(h'=\mathsf {H}_1(X, m)\).If \(pk, s\in \mathbb {J}_N^+\) and \(h=h'\) then Return 1; Else Return 0.
Security and Efficiency of the Signature Scheme. We have the following theorem; its proof follows straightly from the SpS, HVZN, RSR, min-entropy, and KR-KOA security attributes of the identification scheme and Theorem 3.1 from [15].
Theorem 1
If the RSA problem is \((t, \varepsilon )\) hard on (N, e), then the scheme \(\mathcal {S}_{SSN}\) is \((t',\varepsilon ',U,Q_s,Q_h)\)-MU-SUF-CMA secure in the random oracle model, where \({\varepsilon '}/{t'} \leqslant 24(Q_h + 1)\cdot {\varepsilon }/{t} + {Q_s}/{2^{\alpha }} + {1}/{2^k}.\)
Although efficient, the signature scheme is slightly less efficient than the GQ scheme [13]. A key pair generation requires \(\mathsf {Exp}(\mathbb {Z}_N, 2,l)\) operations for our scheme while it requires \(\mathsf {Exp}(\mathbb {Z}_N, k)\) operations for the GQ scheme. We stress that, using simultaneous exponentiation techniques [18, Sect. 14.6], \(\mathsf {Exp}(\mathbb {Z}_N, 2,l)\) \(\approx 1.17\cdot \mathsf {Exp}(\mathbb {Z}_N, l)\). A \(\mathcal {S}_{SSN}\) signature generation can be performed in \({1.17\cdot \mathsf {Exp}(\mathbb {Z}_N,l)}\) \(+\mathsf {Exp}(\mathbb {Z}_N,k)\) operations, while it requires \(2\cdot \mathsf {Exp}(\mathbb {Z}_N,k)\) operations for the GQ scheme. In both schemes, only \(\mathsf {Exp}(\mathbb {Z}_N,k)\) operations need to be performed online, all the other operations can be performed offline. A signature verification requires \(2\cdot \mathsf {Jcb}(N)\) + \(\mathsf {Exp}(\mathbb {Z}_N, 2, k)\) operations for \(\mathcal {S}_{SSN}\) and \(\mathsf {Exp}(\mathbb {Z}_N, 2, k)\) operations for the GQ scheme.
4 The Signcryption Scheme
From the \(\mathcal {S}_{SSN}\) scheme, which has the advantage of being defined over a group wherein the strong DH assumption is known to hold under the factoring assumption [14], we derive \(\mathcal {SC}_{SSN}=({\mathsf {Setup}}, {\mathsf {Gen}}_S,{\mathsf {Gen}}_R,{\mathsf {Sc}}, \) \( \mathsf {Usc}, {\mathsf {N}}, {\mathsf {PV}})\). The \({\mathsf {Setup}}\) algorithm generates a domain parameter \(dp'\) as in Sect. 3, together with an encryption scheme \(\mathcal {E}\) and two hash functions \(\mathsf {H}_1:\{0, 1\}^*\rightarrow \mathsf {ChSet}\) and \(\mathsf {H}_2:\{0, 1\}^*\rightarrow \mathbf {K}\). We consider \(dp=(dp', \mathsf {H}_1, \mathsf {H}_2, \mathcal {E})\) as an implicit parameter.
-

 ;
;  Return \((sk_S, pk_S)\);
Return \((sk_S, pk_S)\); -

 ;
;  Return \((sk_R, pk_R)\);
Return \((sk_R, pk_R)\); -


\(\tau _1\leftarrow \mathsf {H}_2(X_1,X_2,Z_1, Z_2, pk_S, pk_R);\) \(\tau _2\leftarrow \mathsf {H}_2(X_2, X_1, Z_2, Z_1, pk_S, pk_R);\) \(h\leftarrow \mathsf {H}_1(X_1, X_2, m, \tau _1);\) \({c\leftarrow \mathsf {E}(\tau _2, m);}\)
 Return \((h, X_2, s, c)\);
Return \((h, X_2, s, c)\); -
 Parse C as \((h, X_2, s, c)\). If \(X_2, pk_S\not \in \mathbb {J}_N^+\) then Return \(\bot \);
Parse C as \((h, X_2, s, c)\). If \(X_2, pk_S\not \in \mathbb {J}_N^+\) then Return \(\bot \);

 \(\tau _1\leftarrow \mathsf {H}_2(X_1, X_2, Z_1, Z_2, pk_S, pk_R);\)
\(\tau _2\leftarrow \mathsf {H}_2(X_2, X_1, \)
\(Z_2, Z_1,pk_S, pk_R);\)
\(m\leftarrow \mathsf {D}(\tau _2, c);\)
\(\tau _1\leftarrow \mathsf {H}_2(X_1, X_2, Z_1, Z_2, pk_S, pk_R);\)
\(\tau _2\leftarrow \mathsf {H}_2(X_2, X_1, \)
\(Z_2, Z_1,pk_S, pk_R);\)
\(m\leftarrow \mathsf {D}(\tau _2, c);\)
If \(h=h'\leftarrow \mathsf {H}_1(X_1, X_2, m, \tau _1)\) then Return m; Else return \(\bot \);
-
 Parse C as \((h, X_2, s, c)\). If \(X_2, pk_S\not \in \mathbb {J}_N^+\) then Return \(\bot \);
Parse C as \((h, X_2, s, c)\). If \(X_2, pk_S\not \in \mathbb {J}_N^+\) then Return \(\bot \);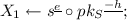

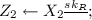 \(\tau _1\leftarrow \mathsf {H}_2(X_1, X_2,Z_1, Z_2, pk_S, pk_R);\)
\(\tau _2\leftarrow \mathsf {H}_2(X_2, X_1,\)
\( Z_2, Z_1, pk_S, pk_R);\)
\(m\leftarrow \mathsf {D}(\tau _2, c);\)
\(\tau _1\leftarrow \mathsf {H}_2(X_1, X_2,Z_1, Z_2, pk_S, pk_R);\)
\(\tau _2\leftarrow \mathsf {H}_2(X_2, X_1,\)
\( Z_2, Z_1, pk_S, pk_R);\)
\(m\leftarrow \mathsf {D}(\tau _2, c);\)
If \(h=h'\leftarrow \mathsf {H}_1(X_1, X_2, m, \tau _1)\) then Return \((\tau _1, \tau _2)\); Else return \(\bot \);
-
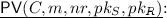 Parse C as \((h, X_2, s, c)\) and \(nr\) as \((\tau _1, \tau _2)\); \(m'\leftarrow \mathsf {D}(\tau _2, c);\)
Parse C as \((h, X_2, s, c)\) and \(nr\) as \((\tau _1, \tau _2)\); \(m'\leftarrow \mathsf {D}(\tau _2, c);\)If \(m'\ne m\) then Return 0;
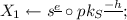
If
 then Return 1; Else return 0;
then Return 1; Else return 0;
For the consistency of the scheme, one can observe that for all \(dp\in \{{\mathsf {Setup}}(1^k)\}\), all \(m\in \mathcal {M}\), all \((sk_S, pk_S)\in \{{\mathsf {Gen}}_S(dp)\}\), and all \((sk_R, pk_R)\in \{{\mathsf {Gen}}_R(dp)\}\), \(m = \mathsf {Usc}(sk_R, pk_S, {\mathsf {Sc}}(sk_S, pk_R, m))\). Moreover, if \(nr\leftarrow {\mathsf {N}}(sk_R, pk_S, {\mathsf {Sc}}(sk_S, pk_R, m))\) then \(1=d\leftarrow {\mathsf {PV}}(C, m, nr, pk_S, pk_R)\).
Efficiency of the Scheme. Since Malone–Lee’s scheme [17] is defined over any Diffie–Hellman group, and Fan et al.’s [11] design makes use of bilinear pairings, it is rather difficult to compare the efficiency of these schemes with our (we use an RSA instance), without considering concrete instances. Nonetheless, our design is a practical and efficient one; it uses the RSA primitive, which remains probably the most widely deployed public key primitive [16]. A sender key pair generation requires \(\mathsf {Exp}(\mathbb {Z}_n, 2, l)\) operations (the exponentiations use the same exponent); a receiver key pair generation requires \(\mathsf {Exp}(\mathbb {Z}_n, l)\) operations. A signcryption generation requires \(\mathsf {Exp}(\mathbb {Z}_n, 6, l)\) operations (we neglect the cost of the three digest operations together with the symmetric encryption). Five of the six exponentiations can be performed off-line. Moreover, three of the five off-line exponentiations share the same exponent, and the remaining two exponentiations have also the same exponent. An unsigncryption or a non-repudiation evidence generation requires four exponentiations; we recall that e can be chosen to be a sparse prime so that exponentiations involving e can be performed using few multiplications. A public verification requires \(\mathsf {Exp}(\mathbb {Z}_n, 2, l)\) operations. Assuming that \(|c|=|m|\), the communication overhead compared to a signature is one group element.
4.1 Confidentiality of the \(\mathcal {SC}_{SSN}\) Signcryption Scheme
We need the following result, its proof is given in the full version of this paper.
Theorem 2
If \({X}_1, {r}, {s}\) be mutually independent random variables, such r and s are uniformly distributed over [N/4]. Let \({X}_2\) be defined by  , and suppose that \(Y, Z_1,\) and \(Z_2\) are random variables taking values in \(\mathbb {J}_N^+\), and are defined as some functions of \(X_1\) and \({X}_2\), then: (a) the statistical distance between \({X}_2\) and the uniform distribution over \(\mathbb {J}_N^+\) is not greater than \(2\delta _0\);(b) If
, and suppose that \(Y, Z_1,\) and \(Z_2\) are random variables taking values in \(\mathbb {J}_N^+\), and are defined as some functions of \(X_1\) and \({X}_2\), then: (a) the statistical distance between \({X}_2\) and the uniform distribution over \(\mathbb {J}_N^+\) is not greater than \(2\delta _0\);(b) If  and
and  , then the probability that the truth value of
, then the probability that the truth value of

does not agree with

is at most \(5\delta _0\); and if (2) holds then so does (1).
Theorem 3
Under the RO model, if the factorization of N is \((t(k), \varepsilon _{\mathsf {fac}}(k))\)-hard and the encryption scheme \(\mathcal {E}\) is \((t(k), \varepsilon _{\mathsf {ss}}(k))\)-semantically secure, then \(\mathcal {SC}_{SSN}\) is \((t(k), q_{{\mathsf {Sc}}}, q_{\mathsf {Usc}}, q_{{\mathsf {N}}}, \varepsilon '(k))\)-secure in the SKI-MU insider confidentiality in the FSO/FUO-IND-CCA2 sense, wherein
Proof
We call the steps (1) and (2), (3) and (4), and (5) and (6) of Game 2 the pre-challenge, challenge, and post-challenge phases respectively. We provide a simulator which answers to \(\mathcal {A}\)’s queries in all phases. The
 procedure is executed at the beginning of the game. When the variable abort is set to 1, the whole simulation fails. If the simulation does not fail, the
procedure is executed at the beginning of the game. When the variable abort is set to 1, the whole simulation fails. If the simulation does not fail, the
 procedure is executed at the end of the game. The oracle \(\text {DDH}_{Y_0}(\cdot , \cdot )\) takes \(U, V\in \mathbb {J}_N^+\) as inputs and outputs 1 if \(\text {CDH}(Y_0, U)=V\) and 0 otherwise. For a list L and an element X, \(\mathsf {Apd}(L,X)\) adds X to L.
procedure is executed at the end of the game. The oracle \(\text {DDH}_{Y_0}(\cdot , \cdot )\) takes \(U, V\in \mathbb {J}_N^+\) as inputs and outputs 1 if \(\text {CDH}(Y_0, U)=V\) and 0 otherwise. For a list L and an element X, \(\mathsf {Apd}(L,X)\) adds X to L.

In the pre-challenge phase, the simulator answers to \(\mathcal {O}_{\mathsf {H}_1}(\cdot )\), \(\mathcal {O}_{\mathsf {H}_2}(\cdot )\), \(\mathcal {O}_{\mathsf {Usc}}(\cdot , \cdot )\), and \(\mathcal {O}_{{\mathsf {N}}}(\cdot , \cdot )\) queries. The lines 10–22 describe both \(\mathcal {O}_{\mathsf {Usc}}(\cdot , \cdot )\) and \(\mathcal {O}_{{\mathsf {N}}}(\cdot ,\cdot )\). When executing \(\mathcal {O}_{\mathsf {Usc}}(\cdot , \cdot )\) (resp. \(\mathcal {O}_{{\mathsf {N}}}(\cdot , \cdot )\)), the instruction \(\mathsf { return }\, (\tau _1, \tau _2)\) (resp. \(\mathsf {return }\, m\)) at line 22 is omitted. Digest queries are answered using input-output tables. The \(\mathcal {O}_{\mathsf {H}_2}(\cdot )\) digest values of strings with format \((X_1, X_2, Z_1, Z_2, pk, pk_R)\) are not only assigned by the \(\mathcal {O}_{\mathsf {H}_2}(\cdot )\) oracle, but also through executions of \(\mathcal {O}_{\mathsf {Usc}}(\cdot , \cdot )\) and \(\mathcal {O}_{{\mathsf {N}}}(\cdot , \cdot )\); in the latter two cases \(Z_1=\text {CDH}(X_1, pk_R)\) and \(Z_2=\text {CDH}(X_2, pk_R)\) are unknown. So, for consistency, in addition to \(\mathcal {S}_{\mathsf {H}_2}\), we use a list \(\mathcal {S}_{\mathsf {k}}\) to store the values of \(\mathcal {O}_{\mathsf {H}_2}(X_1, X_2, Z_1, Z_2, pk, pk_R)\) which was assigned while \(Z_1\) and \(Z_2\) are unknown (see at lines 14–20). Doing so, the simulator consistently answers to all digest queries with the help of the \(\text {DDH}_{Y_0=pk_R}(\cdot , \cdot )\) oracle (see at lines 6–8).
In the challenge phase, we essentially simulate a signature generation (at line 24), then \(X_2\) is set to \(X_0\) (the simulator takes \(X_0\) and \(Y_0=pk_R\) as input). The secret keys, \(\tau _1\) and \(\tau _2\) are chosen uniformly at random from \(\mathbf {K}\), and savings are performed for \(\mathcal {O}_{\mathsf {H}_2}(\cdot )\) digests consistency (lines 27–28). In the post-challenge phase, the changes, compared to the pre-challenge phase, are the (re)definitions of the \(\mathcal {O}_{{\mathsf {Sc}}}(\cdot , \cdot )\) and \(\mathcal {O}_{\mathsf {H}_2}(\cdot )\) oracles. When computing \(\mathcal {O}_{{\mathsf {Sc}}}(pk, m)\), the simulator ignores both \(sk_S\) and the secret key corresponding to \(pk\). For consistency, we simulate a signature generations (see at line 30), choose r and \(s_2\), and generate \(X_2\) (see at line 31) such that: (i) the statistical distance between the distribution of the \(X_2\) we generate in this way and the distribution of \(X_2\) we obtain through a real execution of \({\mathsf {Sc}}(\cdot , \cdot , \cdot )\) is not greater than \(2\delta _0 = 2\max (1/p', 1/q')\); (ii) if \(Z_1\) and \(Z_2\) are such that  , then \(Z_1=\text {CDH}(X_1, pk)\) and \(Z_2=\text {CDH}(X_2, pk)\) with overwhelming probability (see Theorem 2). Doing so, we have a way to assign values to \(\tau _1\) and \(\tau _2\), while keeping the outputs of \(\mathcal {O}_{\mathsf {H}_2}(\cdot )\) consistent (see at lines 31–35 and 43–46). Let \(\mathsf {bad}\) be the event: “(a) the simulator aborts (see at lines 26 and 32) or (b) in some execution of \(\mathcal {O}_{\mathsf {H}_2}(\cdot )\), \(Z_1\) and \(Z_2\) are such that
, then \(Z_1=\text {CDH}(X_1, pk)\) and \(Z_2=\text {CDH}(X_2, pk)\) with overwhelming probability (see Theorem 2). Doing so, we have a way to assign values to \(\tau _1\) and \(\tau _2\), while keeping the outputs of \(\mathcal {O}_{\mathsf {H}_2}(\cdot )\) consistent (see at lines 31–35 and 43–46). Let \(\mathsf {bad}\) be the event: “(a) the simulator aborts (see at lines 26 and 32) or (b) in some execution of \(\mathcal {O}_{\mathsf {H}_2}(\cdot )\), \(Z_1\) and \(Z_2\) are such that  while \(\text {CDH}(X_1, pk)\ne Z_1 \text { or } \text {CDH}(X_2, pk)\ne Z_2\) (see at lines 43–46).” Then, from Theorem 2
while \(\text {CDH}(X_1, pk)\ne Z_1 \text { or } \text {CDH}(X_2, pk)\ne Z_2\) (see at lines 43–46).” Then, from Theorem 2
Let \(\mathsf {Succ}^{\mathsf {cca2}}_{\mathcal {A}, \mathsf {sim}}\) denote the event “\(\mathcal {A}\) succeeds in the simulated environment”. Under the RO model, if \(\lnot \mathsf {bad}\) then, \(\mathcal {A}\)’s views in the real and simulated environments are the same; so, \(\Pr (\mathsf {Succ}^{\mathsf {cca2}}_{\mathcal {A}}\wedge \lnot \mathsf {bad}) =\Pr (\mathsf {Succ}^{\mathsf {cca2}}_{\mathcal {A}, \mathsf {sim}}\wedge \lnot \mathsf {bad})\). Then
Let \(\mathsf {CDHfound}\) be the event the “
 procedure outputs \(\hat{Z}_2\ne \bot \)”. By the definition of \(\mathsf {CDHfound}\), \(\Pr (\mathsf {Succ}^{\mathsf {cca2}}_{\mathcal {A}, \mathsf {sim}} \wedge \lnot \mathsf {bad}\wedge \mathsf {CDHfound}) \leqslant \mathsf {Adv}^{\text {sCDH}}_{\mathcal {B}_1}(\mathbb {J}_N^+),\) where \(\mathcal {B}_1\) is obtained from \(\mathcal {A}\) and the simulator. Using [14, Theorem 2], we obtain
procedure outputs \(\hat{Z}_2\ne \bot \)”. By the definition of \(\mathsf {CDHfound}\), \(\Pr (\mathsf {Succ}^{\mathsf {cca2}}_{\mathcal {A}, \mathsf {sim}} \wedge \lnot \mathsf {bad}\wedge \mathsf {CDHfound}) \leqslant \mathsf {Adv}^{\text {sCDH}}_{\mathcal {B}_1}(\mathbb {J}_N^+),\) where \(\mathcal {B}_1\) is obtained from \(\mathcal {A}\) and the simulator. Using [14, Theorem 2], we obtain
Now, if \(\mathsf {Succ}^{\mathsf {cca2}}_{\mathcal {A}, \mathsf {sim}} \wedge \lnot \mathsf {bad}\wedge \lnot \mathsf {CDHfound}\), then \(\mathcal {A}\) is essentially playing a semantic security game against \(\mathcal {E}\), so using \(\mathcal {A}\) and the simulator we build an adversary \(\mathcal {B}_2\) against \(\mathcal {E}\) such that
The result follows from (3)–(6). \(\square \)
4.2 Unforgeability of the \(\mathcal {SC}_{SSN}\) Scheme
Theorem 4
Under the RO model, if the RSA problem is \((t(k), \varepsilon _0(k))\)-hard over \(\mathbb {J}_N^+\), then \(\mathcal {SC}_{SSN}\) is \((t, q_{{\mathsf {Sc}}}, \varepsilon ')\)-MU insider unforgeable in the FSO/FUO-sUF-CMA sense, with \(\varepsilon ' \leqslant \sqrt{q\varepsilon _0} + (q+1){|\mathsf {ChSet}|}^{-1} + q_{{\mathsf {Sc}}}(q_{{\mathsf {Sc}}}-1) \left( 2(p'q')^{2}|\mathbf {K}|\right) ^{-1}+ 5q_{{\mathsf {Sc}}}\delta _0,\) with \(q=q_{\mathsf {H}_1}+q_{{\mathsf {Sc}}}\) wherein \(q_{\mathsf {H}_1}\) is an upper bound on the number of \(\mathcal {O}_{\mathsf {H}_1}(\cdot )\) queries the adversary issues.
Proof
Let \(q_{\mathsf {H}_1}\) and \(q_{{\mathsf {Sc}}}\) be upper bounds on the number of queries \(\mathcal {A}\) issues to the \(\mathcal {O}_{\mathsf {H}_1}(\cdot )\) and \(\mathcal {O}_{{\mathsf {Sc}}}(\cdot , \cdot )\) oracles respectively, and \(q=q_{\mathsf {H}_1}+q_{{\mathsf {Sc}}}\). In addition to the domain parameter and  , the simulator takes as an additional input \(L_{\mathsf {H}_1}=(h_1, \cdots , h_q)\) such that for all i,
, the simulator takes as an additional input \(L_{\mathsf {H}_1}=(h_1, \cdots , h_q)\) such that for all i,  .
.

As in the previous analysis, \(\mathsf {bad}\) denotes the event: “(a) \(\mathsf {abort}\) is set to 1 (see at line 115) or (b) in the execution of \(\mathcal {O}_{\mathsf {H}_2}(\cdot )\), \(Z_1\) and \(Z_2\) are such that (see at lines 108 and 110)  and \(\text {CDH}(X_1, pk)\ne Z_1 \text { or } \text {CDH}(X_2, pk)\ne Z_2\).”
and \(\text {CDH}(X_1, pk)\ne Z_1 \text { or } \text {CDH}(X_2, pk)\ne Z_2\).”
Then
and then
Let \(\mathsf {fail}\) be the event “the
 procedure outputs \((0, \epsilon , \epsilon )\)”. If the event \({\mathsf {Succ}_{\mathcal {A}}^{\mathsf {suf}}\wedge \lnot \mathsf {bad}\wedge \mathsf {fail}}\) occurs then the oracle \(\mathcal {O}_{\mathsf {H}_1}(\cdot )\) was never queried with value \((\hat{X}_1, \hat{X}_2, \hat{m}, \hat{\tau }_1)\). Which means that \(\mathcal {A}\) successfully guessed \(\mathcal {O}_{\mathsf {H}_1}(\hat{X}_1, \hat{X}_2, \hat{m}, \hat{\tau }_1)\). Under the RO model,
procedure outputs \((0, \epsilon , \epsilon )\)”. If the event \({\mathsf {Succ}_{\mathcal {A}}^{\mathsf {suf}}\wedge \lnot \mathsf {bad}\wedge \mathsf {fail}}\) occurs then the oracle \(\mathcal {O}_{\mathsf {H}_1}(\cdot )\) was never queried with value \((\hat{X}_1, \hat{X}_2, \hat{m}, \hat{\tau }_1)\). Which means that \(\mathcal {A}\) successfully guessed \(\mathcal {O}_{\mathsf {H}_1}(\hat{X}_1, \hat{X}_2, \hat{m}, \hat{\tau }_1)\). Under the RO model,
Using \(\mathcal {A}\) and the simulator, we obtain a machine \(\mathcal {B}\) which takes \((dp, \mathcal {E}, Y_0, L_{\mathsf {H}_1}=(h_1, \cdots , h_q))\) as input and outputs \((j_0, \hat{X}_1, \hat{s})\) such that  with probability \(\varepsilon _1=\Pr (\mathsf {Succ}_{\mathcal {A}}^{\mathsf {suf}}\wedge \lnot \mathsf {bad}\wedge \lnot \mathsf {fail})\). Let \(\mathsf {F}_B\) be the forking algorithm [7, Sect. 3] associated to \(\mathcal {B}\). By the General Forking Lemma [7, Lemma 1], from \(\mathsf {F}_B\)’s output, we have \((h_{j_0}, h'_{j_0}, X_1, \hat{s}, \hat{s'})\) such that \(h_{j_0} \ne h'_{j_0}\),
with probability \(\varepsilon _1=\Pr (\mathsf {Succ}_{\mathcal {A}}^{\mathsf {suf}}\wedge \lnot \mathsf {bad}\wedge \lnot \mathsf {fail})\). Let \(\mathsf {F}_B\) be the forking algorithm [7, Sect. 3] associated to \(\mathcal {B}\). By the General Forking Lemma [7, Lemma 1], from \(\mathsf {F}_B\)’s output, we have \((h_{j_0}, h'_{j_0}, X_1, \hat{s}, \hat{s'})\) such that \(h_{j_0} \ne h'_{j_0}\),  , and
, and  with probability \(\varepsilon _0\geqslant \varepsilon _1(\varepsilon _1/q - 1/|\mathsf {ChSet}|)\). Then, using \(\mathsf {F}_B\) and Shamir’s trick (we use on page 9 when proving that \(\mathcal {I}_{SSN}\) provides special soundness), we obtain a machine \(\mathcal {B}_2\) which, on input \(Y_0\), outputs \(X_0\) such that
with probability \(\varepsilon _0\geqslant \varepsilon _1(\varepsilon _1/q - 1/|\mathsf {ChSet}|)\). Then, using \(\mathsf {F}_B\) and Shamir’s trick (we use on page 9 when proving that \(\mathcal {I}_{SSN}\) provides special soundness), we obtain a machine \(\mathcal {B}_2\) which, on input \(Y_0\), outputs \(X_0\) such that  with probability \(\varepsilon _0\). Again, from the General Forking Lemma [7, Lemma 1],
with probability \(\varepsilon _0\). Again, from the General Forking Lemma [7, Lemma 1],
The result follows from (8)–(10).
4.3 Soundness of Non-repudiation
Theorem 5
Under the RO model, \(\mathcal {SC}_{SSN}\) achieves \((t, q_{{\mathsf {Sc}}}, \varepsilon )\)-computational soundness of non-repudiation, with \(\varepsilon \leqslant {1/2}\cdot q(q-1){|\mathsf {ChSet}|}^{-1} + {1/2}\cdot q_{{\mathsf {Sc}}}(q_{{\mathsf {Sc}}}-1)(p'q')^{-2}{|\mathbf {K}|}^{-1}+ 5q_{{\mathsf {Sc}}}\delta _0,\) where \(q=q_{\mathsf {H}_1} + q_{{\mathsf {Sc}}}\), wherein \(q_{\mathsf {H}_1}\) is an upper bound on the number of \(\mathcal {O}_{\mathsf {H}_1}(\cdot )\) queries \(\mathcal {A}\) issues.
Proof
First, we provide a simulation for Game 4. The simulator takes \(dp=(N, G, R, e, k)\) and \(\mathcal {E}=(\mathsf {E}, \mathsf {D}, \mathbf {K}, \mathbf {M}, \mathbf {C})\) as inputs. The
 simply sets \(\mathcal {S}_{\mathsf {H}_1}\leftarrow ()\); \(\mathcal {S}_{\mathsf {k}}\leftarrow ()\); \( \mathcal {S}_{\mathsf {k \& r}}\leftarrow ()\); \(\mathcal {S}_{\mathsf {H}_2}\leftarrow ().\) The \(\mathcal {O}_{\mathsf {H}_1}(\cdot )\) oracle is as described in lines 2–3 in the simulation for the confidentiality game. The \(\mathcal {O}_{\mathsf {H}_2}(\cdot )\) and \(\mathcal {O}_{{\mathsf {Sc}}}(\cdot , \cdot )\) oracles are as in lines 104–111 and 112–117 in the simulation for the unforgeability game, except that the lines 113 and 115 are replaced respectively with the lines 200 and 201, hereunder:
simply sets \(\mathcal {S}_{\mathsf {H}_1}\leftarrow ()\); \(\mathcal {S}_{\mathsf {k}}\leftarrow ()\); \( \mathcal {S}_{\mathsf {k \& r}}\leftarrow ()\); \(\mathcal {S}_{\mathsf {H}_2}\leftarrow ().\) The \(\mathcal {O}_{\mathsf {H}_1}(\cdot )\) oracle is as described in lines 2–3 in the simulation for the confidentiality game. The \(\mathcal {O}_{\mathsf {H}_2}(\cdot )\) and \(\mathcal {O}_{{\mathsf {Sc}}}(\cdot , \cdot )\) oracles are as in lines 104–111 and 112–117 in the simulation for the unforgeability game, except that the lines 113 and 115 are replaced respectively with the lines 200 and 201, hereunder:

Defining \(\mathsf {bad}\) as in the proof of Theorem 4, the inequality (7) still holds. Then
If \(\mathcal {A}\) succeeds and \(\lnot \mathsf {bad}\), \(\mathcal {A}\) outputs \((sk_R, pk_R, C^*, m', nr)\) such that \(m'\ne m\leftarrow \mathsf {Usc}(sk_R, pk_S, C^*)\) and \(1=d\leftarrow {\mathsf {PV}}(C^*, m', nr, pk_S, pk_R)\). Let \(C^*=(\hat{h}, \hat{X}_2, \hat{s}, \hat{c})\), \(nr=(\tau _1, \tau _2)\), \(\widehat{nr}=(\hat{\tau }_1, \hat{\tau }_2)\leftarrow {\mathsf {N}}(sk_R, pk_S, C^*)\), and  . As \(m\ne m'\) and \(1=d\leftarrow {\mathsf {PV}}(C^*, m', nr, pk_S, pk_R)=d'\leftarrow {\mathsf {PV}}(C^*, m, \widehat{nr}, pk_S, pk_R).\) \(\mathcal {A}\) have found \((m, \hat{\tau }_1)\) and \((m', \tau _1)\) such that \(\hat{h}=h_1\leftarrow \mathcal {O}_{\mathsf {H}_{1}}(\hat{X}_1, \hat{X}_2,m, \hat{\tau }_1)=h_2\leftarrow \mathcal {O}_{\mathsf {H}_{1}}(\hat{X}_1, \hat{X}_2,m', \tau _1).\) Then
. As \(m\ne m'\) and \(1=d\leftarrow {\mathsf {PV}}(C^*, m', nr, pk_S, pk_R)=d'\leftarrow {\mathsf {PV}}(C^*, m, \widehat{nr}, pk_S, pk_R).\) \(\mathcal {A}\) have found \((m, \hat{\tau }_1)\) and \((m', \tau _1)\) such that \(\hat{h}=h_1\leftarrow \mathcal {O}_{\mathsf {H}_{1}}(\hat{X}_1, \hat{X}_2,m, \hat{\tau }_1)=h_2\leftarrow \mathcal {O}_{\mathsf {H}_{1}}(\hat{X}_1, \hat{X}_2,m', \tau _1).\) Then
The Theorem follows from (11) and (12). \(\square \)
4.4 Unforgeability of Non-repudiation Evidence
Theorem 6
Under the RO model, if the factoring problem is \((t(k), \varepsilon (k))\) hard, then the \({\mathcal {SC}}_{SSN}\) scheme achieves \((t, q_{{\mathsf {Sc}}}, q_{\mathsf {Usc}}, q_{{\mathsf {N}}}, \varepsilon ')\) unforgeability of non-repudiation evidence with \(\varepsilon '\leqslant \varepsilon + |\mathbf {K}|^{-1} + q_{{\mathsf {Sc}}}(q_{{\mathsf {Sc}}}-1)\left( 2(p'q')^{2}\right) ^{-1} + (5q_{{\mathsf {Sc}}}+2)\delta _0.\)
Proof
We consider the following simulation.

Let \(\mathsf {bad}\) denote the event “the same couple \((X_1, X_2)\) is generated in two executions of \(\mathcal {O}_{\mathsf {Sign}}(\cdot , \cdot )\)”. Then, under the RO model,
Let \(\mathsf {fail}\) be the event “the
 procedure outputs \( \epsilon \)”. If \(\mathsf {Succ}_{\mathcal {A}}^{\mathsf {unr}}\wedge \lnot \mathsf {bad}\wedge \mathsf {fail}\) occurs, \(\mathcal {A}\) never query the \(\mathcal {O}_{\mathsf {H}2}\) oracle on \((\hat{X}_1, \hat{X}_2, \text {CDH}(pk_R, \hat{X}_1),\) \(\text {CDH}(pk_R, \hat{X}_2),\) \(pk_S, pk_R)\); then \(\mathcal {A}\) successfully guessed the corresponding digest value. It follows
procedure outputs \( \epsilon \)”. If \(\mathsf {Succ}_{\mathcal {A}}^{\mathsf {unr}}\wedge \lnot \mathsf {bad}\wedge \mathsf {fail}\) occurs, \(\mathcal {A}\) never query the \(\mathcal {O}_{\mathsf {H}2}\) oracle on \((\hat{X}_1, \hat{X}_2, \text {CDH}(pk_R, \hat{X}_1),\) \(\text {CDH}(pk_R, \hat{X}_2),\) \(pk_S, pk_R)\); then \(\mathcal {A}\) successfully guessed the corresponding digest value. It follows
If \(\mathsf {Succ}_{\mathcal {A}}^{\mathsf {unr}}\wedge \lnot \mathsf {bad}\wedge \lnot \mathsf {fail}\) occurs, as  and \(\hat{Z}_2 = \text {CDH}(X_2, pk_R=Y_0)\)
and \(\hat{Z}_2 = \text {CDH}(X_2, pk_R=Y_0)\)

Using \(\mathcal {A}\) and the simulator, we have a machine which takes \(X_0, Y_0\) as input and outputs \(\text {CDH}(X_0, Y_0)\) with probability \(\Pr (\mathsf {Succ}_{\mathcal {A}}^{\mathsf {unr}}\wedge \lnot \mathsf {bad}\wedge \lnot \mathsf {fail})\). The result follows from (13), (14), and [14, Theorem 2]. \(\square \)
5 Concluding Remarks
We have proposed a new identification scheme over the group of signed quadratic residues, wherein the strong Diffie–Hellman assumption holds under the factoring assumption. Using the identification scheme, we derived a new signature scheme we have shown to be strongly unforgeable against chosen message attacks, under the RSA assumption and the Random Oracle model. We proposed an efficient signcryption scheme with non-interactive non-repudiation, we have shown to be insider secure, under the RSA assumption and the RO model, in a variant of Fan et al.’s security model. The communication overhead of the signcryption scheme, compared to the corresponding signature scheme is one group element.
Compared to Fan et al.’s design which uses bilinear maps, our scheme is RSA based and can be easily deployed in most of the existing platforms.
In a forthcoming stage, we will be interested in the conditions under which our design can be generalized to generic Diffie–Hellman groups. We will investigate also signcryption designs with a tight security reduction.
References
Algesheimer, J., Camenisch, J., Shoup, V.: Efficient computation modulo a shared secret with application to the generation of shared safe-prime products. In: Yung, M. (ed.) CRYPTO 2002. LNCS, vol. 2442, pp. 417–432. Springer, Heidelberg (2002). https://doi.org/10.1007/3-540-45708-9_27
Badertscher, C., Banfi, F., Maurer, U.: A constructive perspective on signcryption security. In: Catalano, D., De Prisco, R. (eds.) SCN 2018. LNCS, vol. 11035, pp. 102–120. Springer, Cham (2018). https://doi.org/10.1007/978-3-319-98113-0_6
Baek, J., Steinfeld, R.: Security for signcryption: the multi-user model. In: Dent, A., Zheng, Y. (eds.) Practical Signcryption. ISC, pp. 43–53. Springer, Heidelberg (2010). https://doi.org/10.1007/978-3-540-89411-7_3
Baek, J., Steinfeld, R., Zheng, Y.: Formal proofs for the security of signcryption. In: Naccache, D., Paillier, P. (eds.) PKC 2002. LNCS, vol. 2274, pp. 80–98. Springer, Heidelberg (2002). https://doi.org/10.1007/3-540-45664-3_6
Baek, J., Steinfeld, R., Zheng, Y.: Formal proofs for the security of signcryption. J. Cryptol. 20(2), 203–235 (2007)
Bao, F., Deng, R.H.: A signcryption scheme with signature directly verifiable by public key. In: Imai, H., Zheng, Y. (eds.) PKC 1998. LNCS, vol. 1431, pp. 55–59. Springer, Heidelberg (1998). https://doi.org/10.1007/BFb0054014
Bellare, M., Neven, G.: Multi-signatures in the plain public-key model and a general forking lemma. In: Proceedings of the 13th ACM Conference on Computer and Communications Security, pp. 390–399. ACM (2006)
Bellare, M., Rogaway, P.: Random oracle are practical: a paradigm for designing efficient protocols. In: ACM-CCS 1993, pp. 62–73. ACM (1993)
Boyd, C., Mathuria, A.: Protocols for Authentication and Key Establishment. Springer Science & Business Media, Heidelberg (2003). https://doi.org/10.1007/978-3-662-09527-0
Cash, D., Kiltz, E., Shoup, V.: The twin Diffie-Hellman problem and applications. J. Cryptol. 22(4), 470–504 (2009)
Fan, J., Zheng, Y., Tang, X.: Signcryption with non-interactive non-repudiation without random oracles. In: Gavrilova, M.L., Tan, C.J.K., Moreno, E.D. (eds.) Transactions on Computational Science X. LNCS, vol. 6340, pp. 202–230. Springer, Heidelberg (2010). https://doi.org/10.1007/978-3-642-17499-5_9
Fiat, A., Shamir, A.: How to prove yourself: practical solutions to identification and signature problems. In: Odlyzko, A.M. (ed.) CRYPTO 1986. LNCS, vol. 263, pp. 186–194. Springer, Heidelberg (1987). https://doi.org/10.1007/3-540-47721-7_12
Guillou, L.C., Quisquater, J.-J.: A practical zero-knowledge protocol fitted to security microprocessor minimizing both transmission and memory. In: Barstow, D., Brauer, W., Brinch Hansen, P., Gries, D., Luckham, D., Moler, C., Pnueli, A., Seegmüller, G., Stoer, J., Wirth, N., Günther, C.G. (eds.) EUROCRYPT 1988. LNCS, vol. 330, pp. 123–128. Springer, Heidelberg (1988). https://doi.org/10.1007/3-540-45961-8_11
Hofheinz, D., Kiltz, E.: The group of signed quadratic residues and applications. In: Halevi, S. (ed.) CRYPTO 2009. LNCS, vol. 5677, pp. 637–653. Springer, Heidelberg (2009). https://doi.org/10.1007/978-3-642-03356-8_37
Kiltz, E., Masny, D., Pan, J.: Optimal security proofs for signatures from identification schemes. In: Robshaw, M., Katz, J. (eds.) CRYPTO 2016. LNCS, vol. 9815, pp. 33–61. Springer, Heidelberg (2016). https://doi.org/10.1007/978-3-662-53008-5_2
Lenstra, A.K., Hughes, J.P., Augier, M., Bos, J.W., Kleinjung, T., Wachter, C.: Public keys. In: Safavi-Naini, R., Canetti, R. (eds.) CRYPTO 2012. LNCS, vol. 7417, pp. 626–642. Springer, Heidelberg (2012). https://doi.org/10.1007/978-3-642-32009-5_37
Malone-Lee, J.: Signcryption with non-interactive non-repudiation. Des. Codes Crypt. 37(1), 81–109 (2005)
Menezes, A., van Oorschot, P., Vanstone, S.: Handbook of Applied Cryptography. CRC Press, Boca Raton (1996)
Okamoto, T., Pointcheval, D.: The gap-problems: a new class of problems for the security of cryptographic schemes. In: Kim, K. (ed.) PKC 2001. LNCS, vol. 1992, pp. 104–118. Springer, Heidelberg (2001). https://doi.org/10.1007/3-540-44586-2_8
Sarr, A.P., Elbaz–Vincent, P.: On the security of the (F)HMQV protocol. In: Pointcheval, D., Nitaj, A., Rachidi, T. (eds.) AFRICACRYPT 2016. LNCS, vol. 9646, pp. 207–224. Springer, Cham (2016). https://doi.org/10.1007/978-3-319-31517-1_11
Sarr, A.P., Elbaz-Vincent, P., Bajard, J.-C.: A secure and efficient authenticated Diffie–Hellman protocol. In: Martinelli, F., Preneel, B. (eds.) EuroPKI 2009. LNCS, vol. 6391, pp. 83–98. Springer, Heidelberg (2010). https://doi.org/10.1007/978-3-642-16441-5_6
Shin, J.-B., Lee, K., Shim, K.: New DSA-verifiable signcryption schemes. In: Lee, P.J., Lim, C.H. (eds.) ICISC 2002. LNCS, vol. 2587, pp. 35–47. Springer, Heidelberg (2003). https://doi.org/10.1007/3-540-36552-4_3
Zheng, Y.: Digital signcryption or how to achieve cost(signature & encryption) \(\ll \) cost(signature) + cost(encryption). In: Kaliski, B.S. (ed.) CRYPTO 1997. LNCS, vol. 1294, pp. 165–179. Springer, Heidelberg (1997). https://doi.org/10.1007/BFb0052234
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2019 Springer Nature Switzerland AG
About this paper
Cite this paper
Sarr, A.P., Seye, P.B., Ngarenon, T. (2019). A Practical and Insider Secure Signcryption with Non-interactive Non-repudiation. In: Carlet, C., Guilley, S., Nitaj, A., Souidi, E. (eds) Codes, Cryptology and Information Security. C2SI 2019. Lecture Notes in Computer Science(), vol 11445. Springer, Cham. https://doi.org/10.1007/978-3-030-16458-4_24
Download citation
DOI: https://doi.org/10.1007/978-3-030-16458-4_24
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-16457-7
Online ISBN: 978-3-030-16458-4
eBook Packages: Computer ScienceComputer Science (R0)





 and
and  then
then  .
. .
. , and compute
, and compute  (R is a generator of
(R is a generator of 
 ;
;  Return
Return 
 ;
;  ; Return
; Return 
 ; Return s.
; Return s. If
If  then Return 1, Else return 0.
then Return 1, Else return 0.
 ;
;  ;
;  ;
;  ; Return (X, c, s).
; Return (X, c, s).
 ;
;  ; Return
; Return 
 ; Return
; Return 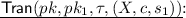
 ;
; 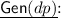
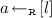 ;
;  Return
Return 
 ;
;  ;
;  ; Return (h, s).
; Return (h, s).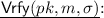 Parse
Parse 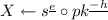 ;
; 
 ;
;  Return
Return 
 ;
;  Return
Return 

 Return
Return  Parse C as
Parse C as 


 Parse C as
Parse C as 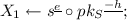

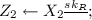
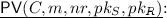 Parse C as
Parse C as 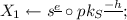
 then Return 1; Else return 0;
then Return 1; Else return 0;