Abstract
We present a generic construction of an insider secure signcryption scheme with non-interactive non-repudiation. Our construction uses as building blocks a signature scheme, a key encapsulation mechanism (KEM), a keyed hash function, a symmetric encryption scheme, and a pseudo-random function. We show that our construction is insider secure in the dynamic multi-user model, without resorting the random oracle or the key registration model. Our generic scheme provides also non-interactive non-repudiation.
Access provided by Autonomous University of Puebla. Download conference paper PDF
Similar content being viewed by others
Keywords
1 Introduction
Signcryption schemes provide both the functionalities of signature and encryption schemes. These schemes were proposed for the first time by Zheng [24]. Since Zheng’s seminal work, many designs have been proposed, e.g. [2, 5, 7, 8, 10, 12, 18,19,20,21,22]. For the analysis of signcryption schemes, two important lines of separations in the security definitions are: two-party versus multi-party models, and outsider versus insider security models [1, 3, 4]. Broadly, in a two-party security model, only one sender and one receiver are considered. Whereas in a multi-party model, an attacker can use any public key of its choice. In an outsider model, it is assumed that an attacker cannot access a legitimate sender or receiver long-term secret. In an insider model, an attacker has access to all the secrets except the one “being attacked”; for confidentiality, it is assumed that the attacker knows the sender’s static private key, and for unforgeability that the attacker knows the receiver’s static private key. The strongest among these models is insider security in the (dynamic) multi-user model.
Some “natural” constructions of signcryption schemes are “encrypt and sign (E &S), “Encrypt then Sign” (EtS) and Sign then Encrypt (StE). Unfortunately, these natural constructions do not yield secure signcryption schemes in the dynamic multi-user insider model [1, Sect. 2.3]. For instance, In an E &S construction, the signature may reveal the encrypted message, confidentiality is not then achieved. In the EtS and StE constructions the difficulty is to maintain the security of the operation performed first. For instance in the EtS construction, for confidentiality, an attacker (a probabilistic polynomial time machine) which knows the sender’s static private key can resign and submit the resigned signcrypted text to a decryption oracle. In the StE construction, for unforgeability, an adversary which knows the receiver static private key can decrypt the ciphertext and re-encrypt and submit the resulting signcrypted text as a forgery.
A nice property of signcryption schemes is Non-Interactive Non-Repudiation (NINR), which allows a third party to settle a non-repudiation dispute without engaging a costly protocol. NINR is a main advantage of signcryption schemes compared to one pass key exchange protocols, which often outperform signcryption schemes.
Building high-level secure and efficient cryptographic schemes from low-level primitives is a main focus in modern cryptography. In the case of signcryption schemes, insider security appears to be the right security definition [3]. As far as we are aware, there are only three works, that aim to propose generic insider secure constructions of signcryption schemes in the dynamic multi-user model, [10, 19] and [2]. Unfortunately the designs from [19] and [2] are shown to be secure in the registered key model, wherein an attacker has to show that it knows the private keys corresponding to the public keys it uses. This model does not capture some realistic attacks on certificate authorities, e.g. [11, 13]. In [10], Chiba et al. propose two generic StE type constructions that they show to be insider secure in the dynamic multi-user model, without resorting the random oracle or registered key model. As their constructions are StE, they inherit NINR from the base signature scheme.
In this work, we build a simple and efficient generic EtS signcryption scheme with NINR (SCNINR), termed \(\textsf{SN}\) (Signcryption with Non-interactive non-repudiation). We propose a detailed analysis of our construction, in the insider dynamic multi-user model, without using the random oracle or registered key model.
This paper is organized as follows. In Sect. 2, we present some preliminaries on signcryption schemes and on the building blocks we use in our design. In Sect. 3, we propose our generic SCNINR scheme. In Sect. 4, we propose a detailed security analysis of our construction in the dynamic multi-user model. We compare our design with the previous proposals in Sect. 5.
2 Preliminaries
If S is a set,
 means that a is chosen uniformly at random from S; we write
means that a is chosen uniformly at random from S; we write
 as a shorthand for
as a shorthand for
 , etc. We denote by \({\textsf{sz}}(a)\) the number of bits required to represent a. If S and \(S'\) are two sets, \(\textsf{Func}(S, S')\) denotes the set of functions with domain S and range \(S'\).
, etc. We denote by \({\textsf{sz}}(a)\) the number of bits required to represent a. If S and \(S'\) are two sets, \(\textsf{Func}(S, S')\) denotes the set of functions with domain S and range \(S'\).
For a probabilistic algorithm \(\mathcal {A}\) with parameters \(u_1, \cdots , u_n\) and output \(V\in \textbf{V}\), we write
 . We denote by \(\{\mathcal {A}(u_1,\cdots , u_n)\}\) the set \(\{v\in \textbf{V}: \Pr (V=v)\ne 0\}\). If \(x_1, x_2, \cdots , x_k\) are objects belonging to different structures (group, bit-string, etc.) \((x_1, x_2, \cdots , x_k)\) denotes a representation as a bit-string of the tuple such that each element can be unequivocally parsed. For a list L, \(\textsf{Apd}(L,X)\) adds X to L. For a positive integer n, [n] denotes the set \(\{ 1, 2, \cdots , n\}\).
. We denote by \(\{\mathcal {A}(u_1,\cdots , u_n)\}\) the set \(\{v\in \textbf{V}: \Pr (V=v)\ne 0\}\). If \(x_1, x_2, \cdots , x_k\) are objects belonging to different structures (group, bit-string, etc.) \((x_1, x_2, \cdots , x_k)\) denotes a representation as a bit-string of the tuple such that each element can be unequivocally parsed. For a list L, \(\textsf{Apd}(L,X)\) adds X to L. For a positive integer n, [n] denotes the set \(\{ 1, 2, \cdots , n\}\).
A Symmetric Encryption. A symmetric encryption scheme \(\mathcal {E}=(\textsf{E}, \textsf{D}, \textbf{K}(k), \textbf{M}(k),\) \(\textbf{C}(k))\) is a pair of efficient algorithms \((\textsf{E}, \textsf{D})\), an encryption and a decryption algorithm, together with a triple of sets \((\textbf{K}, \textbf{M}, \textbf{C})\), which depend on a security parameter k, such that for all \(\tau \in \textbf{K}\) and all \(m\in \textbf{M}\), it holds that \(\textsf{E}(\tau , m)\in \textbf{C}\) and \(m = \textsf{D}(\tau , \textsf{E}(\tau , m))\).
Definition 1
Let \(\mathcal {A}=(\mathcal {A}_1, \mathcal {A}_2)\) be an adversary against \(\mathcal {E}\) and let

and \({\textsf{Adv}}^{\textsf{ss}}_{\mathcal {A}, \mathcal {E}}(k)\) denote the quantity
where \(m_0, m_1\in \textbf{M}\) are distinct messages of equal length. The scheme \(\mathcal {E}\) is said to be \((t(k), \varepsilon (k))\)–semantically secure if for all adversaries \(\mathcal {A}\) running in time t(k), it holds that \({{\textsf{Adv}}^{\textsf{ss}}_{\mathcal {A}, \mathcal {E}}(k)\leqslant \varepsilon (k)}\).
We will need also the following definition.
Definition 2
Let \(\mathcal {E}=(\textsf{E}, \textsf{D}, \textbf{K}(k), \textbf{M}(k), \textbf{C}(k))\) be an encryption scheme. The scheme \(\mathcal {E}\) is said to be \((t(k), \varepsilon (k))\)–secure against key clustering attacks if for all adversaries \(\mathcal {A}\) running in time \(\leqslant t(k)\),

Pseudo-Random Function (PRF). A PRF is a deterministic algorithm \(\textsf{Prf}\) together with a triple of sets \((\textbf{K}(k),\textbf{D}(k),\textbf{R}(k))\) (which depends on the security parameter k) such that for all \(\tau \in \textbf{K}\) and all \(m\in \textbf{D}\), \(\textsf{Prf}(\tau ,m)\in \textbf{R}\). Notice that for all fixed \(\tau \in \textbf{K}\), \(\textsf{Prf}(\tau , \cdot )\in \textsf{Func}(\textbf{D}, \textbf{R})\).
Definition 3
Let \(\textsf{Prf}\) be a pseudo-random function and \(\mathcal {A}\) be an adversary,


and
The PRF \(\textsf{Prf}\) is said to be \((t(k), \varepsilon (k))\)–secure if for all efficient adversaries \(\mathcal {A}\) running in time \(\leqslant t\), it holds that \(\textsf{Adv}_{\mathcal {A}, \textsf{Prf}}(k)\leqslant \varepsilon (k)\).
Collision Resistant Hash Function. Let \(\textbf{K}(k)\), \(\textbf{M}'(k)\) and \(\textbf{T}(k)\) be sets which depend on a security parameter k and \(\textsf{H}\) be a keyed hash function defined over \((\textbf{K}, \textbf{M}', \textbf{T})\), i. e. \(\textsf{H}\) takes as inputs \(\tau _0\in \textbf{K}\) and \(m\in \textbf{M}'\) and outputs \(t\in \textbf{T}\); we write \(t\leftarrow \textsf{H}(\tau _0, m)\).
Definition 4
A keyed hash function \(\textsf{H}:\textbf{K}\times \textbf{M}'\rightarrow \textbf{T}\) is said to be \((t(k), \varepsilon (k))\) collision resistant if for all efficient adversaries \(\mathcal {A}\) running in time \(\leqslant t(k)\),

Definition 5
Let \(\textsf{H}:\textbf{K}\times \textbf{M}'\rightarrow \textbf{T}\) be a keyed hash function and \(\textsf{Pfx}\) be a subset of \(\{0, 1\}^*\). \(\textsf{H}\) is said to be \((t(k), \varepsilon (k))\) resistant to collisions with identical prefix from \(\textsf{Pfx}\), if for all efficient adversaries \(\mathcal {A}\) running in time \(\leqslant t(k)\),

Notice that resistance to collisions with identical prefix may be a weaker assumption than classical collision resistance. We consider now the following game parameterized by a pseudo-random function \(\textsf{Prf}\).

Definition 6
Let \(\textsf{H}:\textbf{K}\times \textbf{M}'\rightarrow \textbf{T}\) be a keyed hash function and \(\textsf{Pfx}\) and \(\textsf{Sfx}\) be respectively some sets of message prefixes and suffixes. For an adversary \(\mathcal {A}\) playing Game 1, let \(\textsf{Succ}_{\mathcal {A}, \textsf{H}}(k)\) denote the event “\(\mathcal {A}\) wins Game 1”. \(\textsf{H}\) is said to be \((t(k), \varepsilon (k))\) secure against pre-image attacks with chosen prefix from \(\textsf{Pfx}\) and suffix from \(\textsf{Sfx}\), if for all efficient adversaries \(\mathcal {A}\) running in time \(\leqslant t(k)\), \(\Pr (\textsf{Succ}_{\mathcal {A}, \textsf{H}}(k))\leqslant \varepsilon (k).\)
The following lemma shows that the pre-image resistance (from Definition 6) follows from identical prefix collision resistance. The proof is given in the appendix.
Lemma 1
Let \(\textsf{H}:\textbf{K}\times \textbf{M}'\rightarrow \textbf{T}\) be a keyed hash function. If \(\textsf{H}\) is \((t(k), \varepsilon (k))\) secure against collisions with identical prefix from \(\textsf{Pfx}\), then it is \((t(k), \varepsilon '(k))\) secure in the sense of Definition 6, where
Key Encapsulation Mechanism (KEM). A KEM is a four-tuple of efficient algorithms \(\mathcal {K}=({\textsf{Setup}_\textsf{K}}, {\textsf{Gen}_\textsf{K}}, \textsf{Ecp}, \textsf{Dcp})\) together with a key space \(\textbf{K}'(k)\) and encapsulated keys space \(\textbf{C}'\), such that:
-
\({\textsf{Setup}_\textsf{K}}\) is a probabilistic algorithm which takes as input a security parameter k and outputs a domain parameter \(dp_{\textsf{K}}\);
-
\({\textsf{Gen}_\textsf{K}}\) is a key pair generator, it takes as input the domain parameter \(dp_{\textsf{K}}\) and outputs a key pair \((sk_{\textsf{K}}, pk_{\textsf{K}})\);
-
\(\textsf{Ecp}\) is a probabilistic algorithm which takes as input a public key \(pk_{\textsf{K}}\) and outputs a key \(\tau \in \textbf{K}'\) together with an encapsulated key \(c\in \textbf{C}'\), we write \((\tau , c)\leftarrow _R\textsf{Ecp}(pk_{\textsf{K}})\);
-
\(\textsf{Dcp}\) takes as inputs a private key \(sk_{\textsf{K}}\) together with an encapsulated key c and outputs \(\tau \in \textbf{K}'\) or and error symbol \(\bot \).
It is required that for all \(k\in \mathbb {N}^*\), all \(dp_{\textsf{K}}\in \{{\textsf{Setup}_\textsf{K}}(k)\}\), all \((sk_{\textsf{K}}, pk_{\textsf{K}})\in \{{\textsf{Gen}_\textsf{K}}(dp_{\textsf{K}})\}\), if \((\tau , c)\in \{\textsf{Ecp}(pk_{\textsf{K}})\}\), \(\Pr \left[ \textsf{Dcp}(sk_{\textsf{K}}, c)=\tau \right] =1\).
Definition 7
Let \(\mathcal {K}\) be a KEM, and \(\mathcal {A}\) an adversary against \(\mathcal {K}\). Let

wherein the notation \(\mathcal {A}^{\mathcal {O}_{\textsf{Dcp}}(sk_{\textsf{K}}, \cdot )}\) means that \(\mathcal {A}\) is given access to a decapsulation oracle \(\mathcal {O}_{\textsf{Dcp}}(sk_{\textsf{K}}, \cdot )\) which, on input \(c'\ne c\), outputs \({\textsf{Dcp}}(sk_{\textsf{K}}, c')\) (\(\mathcal {A}\) is not allowed to issue \({\textsf{Dcp}}(sk_{\textsf{K}}, c)\)). Let \({\textsf{Adv}}^{\textsf{cca}}_{\mathcal {A}, \mathcal {K}}(k)= \left| \Pr (U_0) - \Pr (U_1) \right| .\) \(\mathcal {K}\) is said to be \((t(k), \varepsilon (k))\) indistinguishable against chosen-ciphertext attacks ( \(\textsf{IND}\text {-}\textsf{CCA}\) ), if for all efficient adversaries \(\mathcal {A}\) running in time \(\leqslant t(k)\), it holds that \({\textsf{Adv}}^{\textsf{cca}}_{\mathcal {A}, \mathcal {K}}(k)\leqslant \varepsilon (k)\).
Remark 1
In a KEM security experiment, we refer to the challenge \((\tau _0, c)\) and \((\tau _1, c)\) defined in (1) by \(\textsf{Chall}_{\mathcal {K}_{E_0}}\) and \(\textsf{Chall}_{\mathcal {K}_{E_1}},\) respectively.
Digital Signature. A digital signature scheme is a four-tuple of efficient algorithms \(\mathcal {S}=({\textsf{Setup}_\textsf{S}}, {\textsf{Gen}_\textsf{S}}, \textsf{Sign}, \textsf{Vrfy})\) together with a message space \(\textbf{M}_S\), such that:
-
\({\textsf{Setup}_\textsf{S}}\) takes as input a security parameter k and outputs a domain parameter \(dp_{\textsf{S}}\);
-
\({\textsf{Gen}_\textsf{S}}\) is a probabilistic algorithm which takes as input a domain parameter \(dp_{\textsf{S}}\) and outputs a key pair \((sk_{\textsf{S}}, pk_{\textsf{S}})\);
-
\(\textsf{Sign}\) takes as inputs a secret key \(sk_{\textsf{S}}\) and a message \(m\in \textbf{M}_S\) and outputs a signature \(\sigma \in \mathbf {\Sigma }\);
-
\(\textsf{Vrfy}\) is deterministic; it takes as inputs a public key \(pk_{\textsf{S}}\), a message m, and a signature \(\sigma \) and outputs \(d\in \{0, 1\}\); and
-
\(\mathcal {S}\) is such that for all \(k\in \mathbb {N}^*,\) all \(dp_{\textsf{S}}\in \{{\textsf{Setup}_\textsf{S}}(k)\},\) all \((sk_{\textsf{S}}, pk_{\textsf{S}})\in \{{\textsf{Gen}_\textsf{S}}(dp_{\textsf{S}})\},\) and all \(m\in \textbf{M}_S\), \({\Pr \left[ \textsf{Vrfy}(pk_{\textsf{S}}, m, \textsf{Sign}(sk_{\textsf{S}}, m))=1\right] =1.}\)

Definition 8
Let \(\mathcal {S}\) be a signature scheme; \(\mathcal {S}\) is said to be \((t(k), Q_{\textsf{Sign}}(k), \varepsilon (k))\) strongly Unforgeable against Chosen Message Attacks if for any adversary \(\mathcal {A}\) playing Game 2, if \(\mathcal {A}\) runs in time at most t(k) and issues at most \(Q_{\textsf{Sign}}(k)\) queries to the signing oracle, then it succeeds in the \(\textsf{sUF}\text {-}\textsf{CMA}\) game with probability \(\leqslant \varepsilon (k) \).
Notice that when \(\varepsilon (k)\) does not depend on \(Q_{\textsf{Sign}}(k)\), we say simply that \(\mathcal {S}\) is \((t(k), \varepsilon (k))\)–secure. We will need also the following notion, which is not captured in the \(\textsf{sUF}\text {-}\textsf{CMA}\) security definition, although it seems naturally achieved by many usual signature schemes (which uses a hash function), such as the Full Domain Hash, for instance.
Definition 9
A signature scheme is said to be \((t(k), \varepsilon (k))\) secure against colliding signatures if for all efficient adversaries \(\mathcal {A}\) running in time \(\leqslant t(k)\),

2.1 Insider Security for SCNINR
This subsection deals with the syntax of a SCNINR scheme and the insider security definitions in the dynamic Multi-User model [2] (also termed the Flexible Signcryption/ Flexible Unsigncryption Oracle (FSO/FUO) model [5]).
Definition 10
A signcryption scheme is a quintuple of algorithms \(\mathcal{S}\mathcal{C}=({\textsf{Setup}},\) \({\textsf{Gen}_\textsf{sd}}, {\textsf{Gen}_\textsf{rcv}}, {\textsf{Sc}}, \textsf{Usc})\) where:
-
a)
\({\textsf{Setup}}\) takes a security parameter k as input, and outputs a public domain parameter \(dp\);
-
b)
\({\textsf{Gen}_\textsf{sd}}\) takes as input \(dp\) and outputs a sender key pair \((sk_\textsf{sd}, pk_\textsf{sd})\), \(sk_\textsf{sd}\) is the signcrypting key;
-
c)
\({\textsf{Gen}_\textsf{rcv}}\) takes \(dp\) as input and outputs a receiver key pair \((sk_\textsf{rcv}, pk_\textsf{rcv})\);
-
d)
\({\textsf{Sc}}\) takes as inputs a sender private key \(sk_\textsf{sd}\), a receiver public key \(pk_\textsf{rcv}\), and a message m, and outputs a signcryptext C; we write
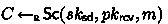 ;
; -
e)
\(\textsf{Usc}\) is a deterministic algorithm. It takes as inputs \(dp\), a receiver secret key \(sk_\textsf{rcv}\), a sender public key \(pk_\textsf{sd}\), and a signcryptext C, and outputs either a valid message \(m\in \textbf{M}\) or an error symbol \(\bot \not \in \textbf{M}\).
And, for all \(dp\in \{{\textsf{Setup}}(k)\}\), all \(m\in \textbf{M}\), all \((sk_\textsf{sd}, pk_\textsf{sd})\in \{{\textsf{Gen}_\textsf{sd}}(dp)\}\), and all \((sk_\textsf{rcv}, pk_\textsf{rcv})\in \{{\textsf{Gen}_\textsf{rcv}}(dp)\}\), \(m = \textsf{Usc}(sk_\textsf{rcv}, pk_\textsf{sd},{\textsf{Sc}}(sk_\textsf{sd}, pk_\textsf{rcv}, m)).\) The scheme is said to provide NINR if there are two algorithms \({\textsf{N}}\) and \({\textsf{PV}}\), a non-repudiation evidence generation and a pubic verification algorithms, such that:
-
\({\textsf{N}}\) takes as inputs a receiver secret key \(sk_\textsf{rcv}\), a sender public key \(pk_\textsf{sd}\), and a signcrypted text C, and outputs a non-repudiation evidence \(nr\) or a failure symbol \(\bot \).
-
\({\textsf{PV}}\) takes as inputs a signcryptext C, a message m, a non-repudiation evidence \(nr\), a sender public key \(pk_\textsf{sd}\), and a receiver public key \(pk_\textsf{rcv}\), and outputs \(d\in \{0,1\}\).
-
For all \(dp\in \{{\textsf{Setup}}(k)\}\), all \(C\in \{0, 1\}^*\), all \((sk_\textsf{sd}, pk_\textsf{sd})\in \{{\textsf{Gen}_\textsf{sd}}(dp)\}\), and all \((sk_\textsf{rcv}, pk_\textsf{rcv})\in \{{\textsf{Gen}_\textsf{rcv}}(dp)\}\), if \(\bot \ne m\leftarrow \textsf{Usc}(sk_\textsf{rcv}, pk_\textsf{sd}, C)\) and \(nr\leftarrow {\textsf{N}}(sk_\textsf{rcv}, pk_\textsf{sd}, C)\) then \(1=d\leftarrow {\textsf{PV}}(C, m, nr, pk_\textsf{sd}, pk_\textsf{rcv})\).
Definition 11
(Confidentiality in the \(\textsf{dM}{-}\textsf{IND}{-}\textsf{iCCA}\) ). A SCNINR \(\mathcal{S}\mathcal{C}\) is said to be \((t(k), q_{\textsf{Usc}}(k),q_{{\textsf{N}}}(k), \varepsilon (k))\) \(\textsf{dM}{-}\textsf{IND}{-}\textsf{iCCA}\)-secure, if for all adversaries \(\mathcal {A}\) playing Game 3, running in time \(\leqslant t(k)\), and issuing at most respectively \(q_{\textsf{Usc}}(k)\) and \(q_{{\textsf{N}}}(k)\) queries to the unsigncryption and non-repudiation evidence generation oracles,
\({{\textsf{Adv}}^{\textsf{cca2}}_{\mathcal {A}, \mathcal{S}\mathcal{C}}(k)\leqslant \varepsilon (k).}\)


Definition 12
(Unforgeability in the \(\textsf{dM}{-}\textsf{sUF}{-}\textsf{iCCA}\) model). A SCNINR is said to be \((t(k), q_{{\textsf{Sc}}}(k), \varepsilon (k))\) unforgeable in the \(\textsf{dM}{-}\textsf{sUF}{-}\textsf{iCCA}\) model if for all attackers \(\mathcal {A}\) playing Game 4, running in time \(\leqslant t(k)\), and issuing at most \(q_{{\textsf{Sc}}}(k)\) signcryption queries, \({\textsf{Adv}_{\mathcal {A}, \mathcal{S}\mathcal{C}}^{\textsf{suf}}(k)\leqslant \varepsilon (k).}\)

Definition 13
(Soundness of non-repudiation). A SCNINR is said to achieve \((t(k), \varepsilon (k))\)–computational soundness of non-repudiation if for any adversary \(\mathcal {A}\) playing Game 5 and running in time \(\leqslant t(k)\), \({\textsf{Adv}_{\mathcal {A}, \mathcal{S}\mathcal{C}}^{\textsf{snr}}(k)\leqslant \varepsilon (k).}\)

Definition 14
(Unforgeability of non-repudiation evidence). A SCNINR is said to achieve \((t, q_{{\textsf{Sc}}}, q_{\textsf{Usc}}, q_{{\textsf{N}}}, \varepsilon )\) unforgeability of non-repudiation evidence if for all adversaries \(\mathcal {A}\) playing Game 6, running in time t, and issuing respectively \(q_{{\textsf{Sc}}}\), \(q_{\textsf{Usc}}\), and \(q_{{\textsf{N}}}\) queries to the signcryption, unsigncryption, and non-repudiation evidence generation oracles, \({\textsf{Adv}_{\mathcal {A}, \mathcal{S}\mathcal{C}}^{\textsf{unr}}(k)\leqslant \varepsilon }\).
3 An Efficient Generic Insider Secure SCNINR
We present our generic SCNINR design termed \(\textsf{SN}\); it uses as building blocks (i) a KEM \(\mathcal {K}=({\textsf{Setup}_\textsf{K}}, {\textsf{Gen}_\textsf{K}}, \textsf{Ecp}, \textsf{Dcp})\), (ii) a symmetric encryption scheme \(\mathcal {E}=(\textsf{E}, \textsf{D}, \textbf{K}, \textbf{M},\) \(\textbf{C})\), (iii) a PRF \(\textsf{Prf}\) defined over \((\textbf{K}, \textbf{D}, \textbf{R}=\textbf{K})\), (iv) a hash function \(\textsf{H}\) defined over \((\textbf{K}, \textbf{M}', \textbf{T})\), and (v) a signature scheme \(\mathcal {S}=({\textsf{Setup}_\textsf{S}}, {\textsf{Gen}_\textsf{S}}, \textsf{Sign}, \textsf{Vrfy})\) with message space \(\textbf{M}_S\). We assume that \(\textbf{M}\subset \textbf{D}\), \(\mathbf {\Sigma }\subset \textbf{D}\), \(\textbf{T}\subset \textbf{M}_S\), and that for all \((\tau , \tau ', \tau '')\in \textbf{K}^2\), all \(c'\in \textbf{C}'\), all \(c\in \textbf{C}\), all \(pk_\textsf{sd}\) such that \((sk_\textsf{sd}, pk_\textsf{sd})\in \{{\textsf{Gen}_\textsf{S}}(dp_2)\}\) for some \(sk_\textsf{sd}\), and all \(pk_\textsf{rcv}\) such that \((sk_\textsf{rcv}, pk_\textsf{rcv})\in \{{\textsf{Gen}_\textsf{S}}(dp_1)\}\), \((pk_\textsf{sd},\tau , \tau ', \tau '',\) \(c, c', pk_\textsf{rcv})\in \textbf{M}'\). We assume that the KEM is such that \(\textbf{K}'=\textbf{K}^4\) (this can be achieved by using, if needed, an appropriate key derivation function and/or a pseudo-random generator), and that \(dp_{\textsf{K}}\) defines both \(\textbf{K}'\) and \(\textbf{C}'\).
In an encrypt-then-sign design (which aims also at NINR), the signed data cannot be the plain-text m (or publicly depend on it), as otherwise even outsider confidentiality cannot be achieved. Moreover, for insider confidentiality (wherein the attacker knows the sender’s private key) it should not be possible to recover the signed data from the sender’s private key, as an attacker could resign the data and submit the resulting signcrypted cipher-text for decryption, and then succeed in an insider confidentiality game. To overcome these difficulties, we compute the signed data as a function of the encapsulated key and the plain text m such that it cannot be recovered by an attacker which does not know the receiver’s private key. Besides, we append a (PFR based MAC) tag of the signature, to make a “re-signing attack” not feasible. The design we obtain is described hereunder.

For the consistency of the scheme, one can observe that as \(\textsf{Dcp}(sk_\textsf{rcv}, c_1)\) yields \((\tau _1, \tau '_1, \tau _2, \tau '_2)\), the receiver can compute \(\tau _3\leftarrow \textsf{Prf}(\tau _2, m)\) and \(\hat{m}\), and then verify whether \(1=\textsf{Vrfy}(pk_\textsf{sd}, \hat{m}, \sigma )\) and \(t=\textsf{Prf}(\tau '_1, \sigma )\) to accept or reject m. So, for all \(dp\in \{{\textsf{Setup}}(k)\}\), all \(m\in \mathcal {M}\), all \((sk_\textsf{sd}, pk_\textsf{sd})\in \{{\textsf{Gen}_\textsf{sd}}(dp)\}\), and all \((sk_\textsf{rcv}, pk_\textsf{rcv})\in \{{\textsf{Gen}_\textsf{rcv}}(dp)\}\), \(m = \textsf{Usc}(sk_\textsf{rcv}, pk_\textsf{sd}, {\textsf{Sc}}(sk_\textsf{sd}, pk_\textsf{rcv}, m))\). Besides, if \(nr\leftarrow {\textsf{N}}(sk_\textsf{rcv}, pk_\textsf{sd}, {\textsf{Sc}}(sk_\textsf{sd}, pk_\textsf{rcv}, m))\) then \(1=d\leftarrow {\textsf{PV}}(C, m, nr, pk_\textsf{sd}, pk_\textsf{rcv})\). Our construction is a signcryption scheme with non-interactive non-repudiation.
4 Security Analysis of the \(\textsf{SN}\) Scheme
We propose in this section a detailed security analysis of our generic construction.
4.1 Insider Confidentiality
Theorem 1
If the encryption scheme \(\mathcal {E}\) is \((t(k), \varepsilon _{\textsf{ss}}(k))\)–semantically secure, the pseudo random function \(\textsf{Prf}\) is \((t(k), \varepsilon _{\textsf{Prf}}(k))\)–secure, the key encapsulation mechanism is \((t(k), \varepsilon _{\mathcal {K}}(k))\)–secure, and the signature scheme is \((t(k), \varepsilon _{\mathcal {S}}(k))\) resistant against colliding signatures, then the \(\textsf{SN}\) signcryption scheme is \((t(k), \varepsilon (k))\)–\(\textsf{dM}{-}\textsf{IND}{-}\textsf{iCCA}\) secure, where
wherein \(q_{\textsf{Usc}}\) and \(q_{{\textsf{N}}}\) are upper bounds on the number of unsigncryption and non-repudiation evidence generation queries the attacker issues.
Proof
We denote the steps (1) and (2), (3) and (4), and (5) and (6) of Game 3 by pre-challenge, challenge, and post-challenge stages respectively. We consider the following simulator to answer \(\mathcal {A}\)’s queries. The Initialization procedure is executed once at the beginning of the game. The Finalization procedure is also executed once, after \(\mathcal {A}\) produces its output, at the end of the game. To keep the description simple, we omit public key validations.

At lines 103 to 109 we describe simultaneously the \(\mathcal {O}_{\textsf{Usc}}(\cdot , \cdot )\) and \(\mathcal {O}_{{\textsf{N}}}(\cdot ,\cdot )\) oracles. When one of the oracles is queried, at line 109, the boxed instruction with corresponding header is executed.
Besides the experiment \(E_0\) in the \(\textsf{dM}{-}\textsf{IND}{-}\textsf{iCCA}\) security game, we define three other experiments \(E_0^{(1)}\), \(E_0^{(2)}\), and \(E_0^{(3)}\). For each experiment, at a line with boxed codes, only the code with corresponding header is executed. The simulator is efficient in all the experiments. We give a summary of the changes between the experiments hereunder.
-
1)
From \(E_0\) to \(E_0^{(1)}\):
-
a)
in \(E_0^{(1)}\), the simulator \(\textsf{Sim}\) does not generate \((sk_\textsf{rcv}, pk_\textsf{rcv})\), instead it receives \(pk_\textsf{rcv}\) from a KEM challenger (see at line 103),
-
b)
to compute \(\textsf{Dcp}(sk_\textsf{rcv}, c_1)\), the simulator sends \(c_1\) to the KEM challenger and receives \((\tau _1, \tau '_1, \tau _2, \tau '_2)\leftarrow \textsf{Dcp}(sk_\textsf{rcv}, c_1)\) from the challenger (see at line 106),
-
c)
and in the challenge phase, the value of
 is received from the KEM challenger; we note \(((\tau _1, \tau '_1, \tau _2, \tau '_2), c)\leftarrow \textsf{Chall}_{\mathcal {K}_{E_0}}.\)
is received from the KEM challenger; we note \(((\tau _1, \tau '_1, \tau _2, \tau '_2), c)\leftarrow \textsf{Chall}_{\mathcal {K}_{E_0}}.\) -
d)
Besides, in the \(\textsf{Usc}\) and \({\textsf{N}}\) oracles, whenever \(\mathcal {A}\) provides the simulator with a signcrypted cipher-text \(C=(t, \sigma , c_1, c_2)\) with \(c_1=\bar{c}_1\), the simulator considers t as an invalid PRF based MAC and returns \(\bot \) (see at line 105).
-
a)
-
2)
From \(E_0^{(1)}\) to \(E_0^{(2)}\), the only change is at line 102 of the challenge phase, wherein the KEM challenger provides \(\mathcal {S}\) with \(\textsf{Chall}_{\mathcal {K}_{E_1}}\) instead of \(\textsf{Chall}_{\mathcal {K}_{E_0}}\).
-
3)
From \(E_0^{(2)}\) to \(E_0^{(3)}\), the change is in the challenge phase, where \(\tau _3\) is computed as \(\tau _3\leftarrow \textsf{Prf}(\tau _2, m_0)\) in \(E_0^{(2)}\), and as
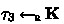 in \(E_0^{(3)}\) (see at line 101). Notice that
in \(E_0^{(3)}\) (see at line 101). Notice that
 is equivalent to
is equivalent to
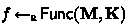 ; \(\tau _3\leftarrow f(m)\).
; \(\tau _3\leftarrow f(m)\).
Let \(\Pr (\textsf{out}_0)\) and \(\Pr (\textsf{out}^{(i)}_0),\) for \(i\in \{1, 2, 3\}\) denote the probability that \(\mathcal {A}\) outputs 1 in the experiments \(E_0\) and \(E^{(i)}_0\), respectively. Notice that the Finalization procedure outputs exactly whatever \(\mathcal {A}\) returns. Given the difference between \(E_0\) and \(E^{(1)}_0\), whenever \(\mathcal {A}\) provides the \(\mathcal {O}_{\textsf{Usc}}\) or \(\mathcal {O}_{{\textsf{N}}}\) oracles with a valid \(C=(t, \sigma , c_1, c_2)\) with \(c_1=\bar{c}_1\) then:
-
a)
If this occurs before the challenge phase, t is a no-message (PRF-based) MAC forgery.
-
b)
If this occurs after the challenge phase (with the restriction \(C\ne C^*\)), if \((t, \sigma )\ne (t^*, \sigma ^*)\), then \((t^*, \sigma ^*)\) is MAC forgery. Otherwise, we necessarily have \((pk, c_1, c_2)\ne (pk_\textsf{sd}, c^*_1, c^*_2)\). And then, if \(\hat{m}=\hat{m}^*\), we have a \(\textsf{H}\) collision, otherwise we have colliding signatures.
So, using [9, Theorem 6.2, p. 224], it holds that
The difference between \(E_0^{(1)}\) and \(E_0^{(2)}\) is: in \(E_0^{(1)}\) the simulator receives \(\textsf{Chall}_{\mathcal {K}_{E_0}}\) from the KEM challenger, while it receives \(\textsf{Chall}_{\mathcal {K}_{E_1}}\) in \(E_0^{(2)}\). As \(\mathcal {K}\) is \((t(k), \varepsilon _{\mathcal {K}}(k))\)–secure, it follows that
Also, given that \(\textsf{Prf}\) is \((t(k), \varepsilon _{\textsf{Prf}}(k))\)–secure, we have
Now, we consider the experiments \(E_1^{(3)}, E_1^{(2)}, E_1^{(1)}\) and \(E_1\) where the only difference between \(E_1\) (resp. \(E_1^{(3)}, E_1^{(2)}, E_1^{(1)}\)) and \(E_0\) (resp. \(E_0^{(3)}, E_0^{(2)}, E_0^{(1)}\)) is that the lines 112 and 113 in the challenge phase are modified, to use \(m_1\) instead of \(m_0\), as hereunder:

With similar arguments, applied to the experiments \(E_1\) and \(E_1^{(i)}\), \(i=1, 2, 3\), we obtain
and
We consider now, the challenge phases in the experiments \(E_b^{(3)}, b=0, 1\), wherein the secret key \(\tau _1\) is used only in the encryption
 . Recall that in \(E_{b, b=0, 1}^{(3)}\), \((\tau _1,\tau '_1, \tau _2, \tau '_2)\) is computed at the KEM challenger as
. Recall that in \(E_{b, b=0, 1}^{(3)}\), \((\tau _1,\tau '_1, \tau _2, \tau '_2)\) is computed at the KEM challenger as
 . Now, we consider the experiments \(E_{b, b=0, 1}^{(3a)}\), such that the difference between \(E_{b, b=0, 1}^{(3)}\) and \(E_{b, b=0, 1}^{(3a)}\) is that in \(E_{b, b=0, 1}^{(3a)}\) the simulator ignores the value of \(\tau _1\) generated by the KEM challenger; it does not compute \(c_2\). Instead, it receives \(c_2\) from a semantic security challenger. The challenger computes \(c_2\) using the instructions:
. Now, we consider the experiments \(E_{b, b=0, 1}^{(3a)}\), such that the difference between \(E_{b, b=0, 1}^{(3)}\) and \(E_{b, b=0, 1}^{(3a)}\) is that in \(E_{b, b=0, 1}^{(3a)}\) the simulator ignores the value of \(\tau _1\) generated by the KEM challenger; it does not compute \(c_2\). Instead, it receives \(c_2\) from a semantic security challenger. The challenger computes \(c_2\) using the instructions:
 . Given the change, it holds that
. Given the change, it holds that
and the difference between \(E_{0}^{(3a)}\) and \(E_{1}^{(3a)}\) is that in \(E_{0}^{(3a)}\) \(c_2\) is computed as
 wherein
wherein
 , while in \(E_{0}^{(3a)}\) it is computed as
, while in \(E_{0}^{(3a)}\) it is computed as
 , it then follows that
, it then follows that
From the inequalities (3) to (10), we obtain

\(\square \)
4.2 Unforgeability of the \(\textsf{SN}\) Scheme
Theorem 2
If the signature scheme is \((t(k),\varepsilon _{\mathcal {S}}(k))\)–\(\textsf{sUF}\text {-}\textsf{CMA}\) secure and the hash function \(\textsf{H}\) is \((t(k),\varepsilon _{\textsf{H}}(k))\) collision resistant, then the \(\textsf{SN}\) signcryption scheme is \((t(k),\varepsilon (k))\) \(\textsf{dM}{-}\textsf{sUF}{-}\textsf{iCCA}\)–secure, where \( \varepsilon (k) \leqslant \varepsilon _{\textsf{H}}(k)+\varepsilon _{\mathcal {S}}(k). \)
Proof
We consider the following simulation to answer \(\mathcal {A}\)’s queries.

In experiment \(E_0\) the simulator answers \(\mathcal {A}'s\) queries exactly as in an \(\textsf{dM}{-}\textsf{sUF}{-}\textsf{iCCA}\) security game. In \(E_1\), we modify the simulator such that it receives \(pk_\textsf{sd}\) from a signature challenger, and whenever \(\mathcal {S}\) needs a signature on some \(\hat{m}\), it sends it to its signature challenger and receives the corresponding signature (see at line 205). Let \(\textsf{Ev}_{b, b=0,1}\) be the event: “the conditions (i) and (ii) in the Finalization procedure are satisfied in experiment \(E_b\).” It is clear that \(\Pr (\textsf{Ev}_0)=\Pr (\textsf{Ev}_1).\) Let \(\textsf{Coll}\) be the event simulator outputs \((x_1, x_2)\) such that \(\textsf{H}(\tau _0, x_1)=\textsf{H}(\tau _0, x_2)\).
And, if \(\textsf{Ev}_1\wedge \lnot \textsf{Coll}\) occurs, the simulator outputs a signature forgery, ı. e.
It follows that \(\varepsilon (k)=\Pr (\textsf{Ev})\leqslant \varepsilon _{\textsf{H}}(k)+\varepsilon _{\mathcal {S}}(k).\) \(\square \)
4.3 Soundness of Non-Repudiation
Theorem 3
If the hash function \(\textsf{H}\) is \((t(k), \varepsilon _{\textsf{H}}(k))\)–collision resistant and the signature scheme is \((t(k), \varepsilon _{\mathcal {S}}(k))\) secure against colliding signatures, then the \(\textsf{SN}\) scheme achieves \((t(k), \varepsilon (k))\) soundness of non-repudiation, where \(\varepsilon (k)\leqslant \varepsilon _{\textsf{H}}(k)+ \varepsilon _{\mathcal {S}}(k)\).
Proof
We consider the following simulator.

Clearly, our simulator is efficient and if \(\mathcal {A}\) succeeds in the soundness of non-repudiation game, its output \((C^*, pk_\textsf{sd}, sk_\textsf{rcv}, pk_\textsf{rcv}, C^*, m', nr^*)\) is such that the conditions (i) and (ii) at line 303 are satisfied. Then the simulator outputs either \((s_1, s_2)\) such that \(s_1\ne s_2\) and \(\textsf{H}(\tau _0, s_1)=\textsf{H}(\tau _0, s_2)\), or \((pk_\textsf{sd}, \hat{m}, \hat{m}^*, \sigma ^*)\) such that \(\hat{m}\ne \hat{m}^*\) and \(1=\textsf{Vrfy}(pk, \hat{m}, \sigma ^*)=\textsf{Vrfy}(pk, \hat{m}^*, \sigma ^*).\) Hence, \( \varepsilon (k)\leqslant \varepsilon _{\textsf{H}}(k)+ \varepsilon _{\mathcal {S}}(k). \) \(\square \)
4.4 Unforgeability of Non-Repudiation Evidence
Theorem 4
If the encryption scheme is \((t(k), \varepsilon _{\mathcal {E}}(k))\) resistant to clustering key attacks, the signature scheme is \((t(k), \varepsilon _{\mathcal {S}}(k))\) resistant to colliding signatures, the hash function is \((t(k), \varepsilon _{\textsf{H}}(k))\) resistant to collisions with identical prefix, and the KEM is \((t(k), \varepsilon _{\mathcal {K}}(k))\) \(\textsf{IND}\text {-}\textsf{CCA}\) secure, then \(\textsf{SN}\) achieves \((t(k), \varepsilon (k))\) unforgeability of non-repudiation evidence with
wherein \(q_{{\textsf{Sc}}}\), \(q_{\textsf{Usc}}\), and \(q_{{\textsf{N}}}\) are upper bounds on the number of times the attacker issues respectively the signcryption, unsigncryption, and non-repudiation evidence generation oracles.
Proof
Let \(\textsf{Ev}\) be the event: \(\mathcal {A}\) outputs \((C^*, m^*, nr^*)\) such that the conditions
-
(i)
 was issued by \(\mathcal {A}\), for some \(m\in \textbf{M}\);
was issued by \(\mathcal {A}\), for some \(m\in \textbf{M}\); -
(ii)
\(1=d\leftarrow {\textsf{PV}}(C^*, m^*, nr^*, pk_\textsf{sd}, pk_\textsf{rcv})\);
-
(iii)
\(\mathcal {O}_{{\textsf{N}}}(pk_\textsf{sd}, C^*)\) was never issued by \(\mathcal {A}\).
We consider the following simulation; when \(\textsf{abort}\) is set to \(\textsf{true}\), the simulation aborts.


We consider the experiments \(E_i\), for \(i=0, 1, 2, 3\). In \(E_0\) \(\mathcal {A}\) plays Game 6; the simulator guesses the execution of the signcryption oracle wherein \(C^*\) will be generated, and answers \(\mathcal {A}\)’s queries consistently. Let \(\textsf{Ev}\) be the event \(\mathcal {A}\) succeeds and \(\textsf{Guess}\) be the event the simulator’s guess is correct. If \(\textsf{Ev}\wedge \textsf{Guess}\) occurs, the simulator outputs \((\tau ^*_2,{\tau '}^*_2)\) such that \(\hat{m}_0\leftarrow \textsf{H}(\tau _0, (pk, \tau ^*_2,{\tau '}^*_2, {\tau }^*_3, c_1, c_2,pk_\textsf{rcv}))\) wherein \({\tau }^*_3\leftarrow \textsf{Prf}(\tau ^*_2, m_0)\). As the guess’s correctness is independent from \(\mathcal {A}\)’s success,
Let \(\textsf{out}_i\) denote the event \(\textsf{Ev}\wedge \textsf{Guess}\) in experiment \(E_i\), for \(i=0,1,2,3\). We now consider the experiment \(E_1\), wherein instead of generating \((\bar{\tau }_1, \bar{\tau }'_1, \bar{\tau }_2, \bar{\tau }'_2, \bar{c}_1)\) for the guessed \({\textsf{Sc}}\) query (see at lines 403 and 409), the simulator receives \((\bar{\tau }_1,\bar{\tau }'_1, \bar{\tau }_2, \bar{\tau }'_2, \bar{c}_1)\) from a KEM challenger as \(\textsf{Chall}_{\mathcal {K}_{E_0}}\). In \(E_1\), when \(\mathcal {A}\) provides the \(\mathcal {O}_{\textsf{Usc}}\) or \(\mathcal {O}_{{\textsf{N}}}\) oracles with a signcrypted cipher text \((t, \sigma , c_1, c_2)\) with \(c_1=\bar{c}_1\), the simulator returns \(\bot \). Indeed, for such a query to succeeds (except \(C_0\), which is allowed only for \(\mathcal {O}_{\textsf{Usc}}\)), it must hold that \(t=t'\leftarrow \textsf{Prf}(\bar{\tau }'_1, \sigma )\). As \((t, \sigma , c_1, c_2)\ne (\bar{t}, \bar{\sigma }, \bar{c}_1, \bar{c}_2)\), if \((t, \sigma )\ne (\bar{t}, \bar{\sigma })\), this yields a PRF MAC forgery, otherwise (we must have \((c_1, c_2)\ne (\bar{c}_1, \bar{c}_2)\)) we obtain a collision for \(\textsf{H}\) or colliding signatures. Hence
We consider the experiment \(E_2\), where the only difference compared to \(E_1\) is that \((\bar{\tau }_1,\bar{\tau }'_1, \bar{\tau }_2, \bar{\tau }'_2, c_1)\) is received from a KEM challenger as \(\textsf{Chall}_{\textbf{K}_{E_1}}\) instead of \(\textsf{Chall}_{\mathcal {K}_{E_0}}\). It holds that
In experiment \(E_3\), the challenger receives \((\bar{\tau }_1, \bar{\tau }'_1, \bar{\tau }_2, \bar{\tau }'_2, c_1)\) as \(\textsf{Chall}_{\mathcal {K}_{E_1}}\)from the KEM challenger, however it does not use \(\bar{\tau }_2\) and \(\bar{\tau }'_2\), instead the values of \(\bar{\tau }_2\) and \(\bar{\tau }'_2\) are generated by a pre-image challenger, as \(\bar{\tau }_2\) and \(\bar{\tau }'_2\) are generated following the same distribution as at the KEM challenger, it follows that
Now if \(\textsf{out}_3\) occurs, the simulator succeeds in its pre-image game. So, from Lemma 1,
And then,
\(\square \)
5 Comparison with Previous Constructions
As far as we are aware, only Chiba et al. [10] propose generic constructions of insider secure signcryption schemes (in the dynamic multi-user model) in the standard model. They propose two generic designs, we refer to by \(\textsf{CMSM1}\) [10, Sect. 4.1] and \(\textsf{CMSM2}\) [10, Sect. 4.2]. Both constructions use as building blocks:
-
an \(\textsf{IND}\text {-}\textsf{CCA}\)–secure symmetric encryption scheme (only semantic security is required for \(\textsf{CMSM2}\)), and
-
a \(\textsf{sUF}\text {-}\textsf{CMA}\)–secure signature scheme.
The construction \(\textsf{CMSM1}\) uses also an \(\textsf{IND}\text {-}\textsf{CCA}\)–secure tag–based–KEM (a KEM which takes a tag as additional input for encapsulation/decapsulation).
The design \(\textsf{CMSM2}\) uses as additional building blocks:
-
an \(\textsf{IND}\text {-}\textsf{CCA}\)–secure KEM, and
-
a one-to-one and sUF–OT secure MAC.
In comparison, in our design, we use as building blocks:
-
a semantically secure symmetric encryption scheme,
-
a \(\textsf{sUF}\text {-}\textsf{CMA}\)–secure signature scheme,
-
an \(\textsf{IND}\text {-}\textsf{CCA}\)–secure KEM,
-
a collision resistant hash function, and
-
a secure pseudo-random function.
Although tag-based-KEMs can be built from any \(\textsf{IND}\text {-}\textsf{CCA}\)–secure public key encryption scheme [10], KEMs seem to be more common. For instance, cryptography standards, such as HPKE [6], use KEMs as building block, not tag-based-KEMs. And, any tag-based KEM can be transformed into a KEM, by using an empty tag. In this respect, compared to \(\textsf{CMSM1}\), the \(\textsf{SN}\) scheme uses more common low level primitives.
The construction \(\textsf{CMSM2}\) uses very common low level primitives. Unfortunately, to achieve strong unforgeability, there is a significant restriction on the MAC, which is required to be one-to-one, i. e. it is required that given a key \(\tau \) and a message m, there is one and only one t such that \(\textsf{MAC}(\tau , m)=t\). This requirement excludes a large class of hash based MACs such as HMAC [16], UMAC [17], or KMAC [15]. The same restriction exists on the encryption scheme; this precludes the use a randomized encryption scheme, such as a bloc cipher with a mode of operation using a (pseudo-)random initialization vector, for instance. In comparison, in the \(\textsf{SN}\) construction, we require the signature scheme to be resistant against colliding signatures and the encryption scheme to be resistant against clustering key attacks. In many signatures, wherein the message to be signed is hashed first (the Full Domain Hash [14], for instance), colliding signatures yield a digest collision. The requirement is then naturally achieved in usual signature schemes. And, given the commonly required avalanche effect in substitution permutation network based encryption schemes (each cipher-text bit is changed with probability 1/2, when a single bit of the key is modified), one can reasonably expect common encryption schemes to be resistant against key clustering attacks. To instantiate the PFR, given the public parameter \(\tau _0\) and a secure block cipher, from the PFR–PRP switching lemma [9, p. 134], \(\textsf{Prf}(\tau , x)\) can be computed using the instructions:

It appears that, compared to \(\textsf{CMSM2}\), the \(\textsf{SN}\) scheme offers a wider range of choices for an instantiation of the low level primitives. This may be of prime importance in a constrained environment wherein only a limited number of low level primitives can be implemented.
Contrary to Tan’s design [23] and the generic constructions from [2] and [19], the \(\textsf{SN}\) scheme does not require the registered key model; it then offers a superior security. Also, compared to the constructions from [20,21,22], \(\textsf{SN}\) does not use the random oracle model. Another security advantage of the \(\textsf{SN}\) scheme compared to these constructions is its generic nature; it can be instantiated with adequate present and future (including quantum-resistant) primitives.
From an efficiency perspective, the computational cost of the \(\textsf{CMSM1}\), \(\textsf{CMSM2}\), and \(\textsf{SN}\) schemes, comes mainly from the asymmetric operations (the cost of the symmetric operations is usually neglected): encapsulation and signature for signcryption, and decapsulation and signature verification, for unsigncryption. Given that any tag-based-KEM can be transformed (for free) into a KEM, for any instantiation of \(\textsf{CMSM1}\) or \(\textsf{CMSM2}\), there is an instantiation of \(\textsf{SN}\) that achieves the same efficiency for the asymmetric operations, if not better. For a comparison with direct constructions [20,21,22,23], \(\textsf{SN}\) can be instantiated with any signature scheme \(\mathcal {S}\) and symmetric encryption scheme \(\mathcal {E}\), and an appropriate KEM, PRF and hash function, provided \(\mathcal {S}\) is strongly unforgeable and \(\mathcal {S}\) is semantically secure and the KEM is \(\textsf{IND}\text {-}\textsf{CCA}\)–secure. Given that hash and PRF evaluations are negligible compared to signature and KEM operations, SN will yield a comparable efficiency.
The bit length of a \(\textsf{CMSM1}\) signcrypted cipher-text corresponding to a message m is the bit length of m (assuming that the encryption scheme \(\mathcal {E}\) is length preserving) added with that of a signature on m and that of a encapsulated key, i.e. \({\textsf{sz}}(m)+{\textsf{sz}}(\textsf{Sign}(sk_\textsf{sd}, m))+ {\textsf{sz}}(\textsf{Ecp}(sk_\textsf{sd}, pk_\textsf{rcv}))\), where \(sk_\textsf{sd}\) and \(pk_\textsf{rcv}\) are respectively the sender’s private key and the receiver’s public key. The \(\textsf{CMSM2}\) and \(\textsf{SN}\) schemes add to this quantity the size of a MAC (a PRF based MAC in the case of \(\textsf{SN}\)). So, the \(\textsf{SN}\) and \(\textsf{CMSM2}\) have the same communication overhead, which is slightly greater than that of \(\textsf{CMSM1}\).
An interesting feature of the \(\textsf{SN}\) scheme, is that all the security reductions are tight, except for the unforgeability of non-repudiation evidence wherein we use a guessing strategy. A concrete instance of \(\textsf{SN}\) may be re-analyzed for unforgeability of non-repudiation evidence, if the underlying KEM is build upon a random self-reducible problem.
References
An, J.H., Rabin, T.: Security for signcryption: the two-user model. In: Dent, A., Zheng, Y. (eds.) Practical Signcryption, pp. 21–42. Springer, Heidelberg (2010). https://doi.org/10.1007/978-3-540-89411-7_2
Arriaga, A., Barbosa, M., Farshim, P.: On the joint security of signature and encryption schemes under randomness reuse: efficiency and security amplification. In: Bao, F., Samarati, P., Zhou, J. (eds.) ACNS 2012. LNCS, vol. 7341, pp. 206–223. Springer, Heidelberg (2012). https://doi.org/10.1007/978-3-642-31284-7_13
Badertscher, C., Banfi, F., Maurer, U.: A constructive perspective on signcryption security. In: Catalano, D., De Prisco, R. (eds.) SCN 2018. LNCS, vol. 11035, pp. 102–120. Springer, Cham (2018). https://doi.org/10.1007/978-3-319-98113-0_6
Baek, J., Steinfeld, R.: Security for signcryption: the multi-user model. In: Dent, A., Zheng, Y. (eds.) Practical Signcryption, pp. 43–53. Springer, Heidelberg (2010). https://doi.org/10.1007/978-3-540-89411-7_3
Baek, J., Steinfeld, R., Zheng, Y.: Formal proofs for the security of signcryption. J. Cryptol. 20(2), 203–235 (2007)
Barnes, R., Bhargavan, K., Lipp, B., Wood, C.: RFC 9180: Hybrid public key encryption (2022)
Bao, F., Deng, R.H.: A signcryption scheme with signature directly verifiable by public key. In: Imai, H., Zheng, Y. (eds.) PKC 1998. LNCS, vol. 1431, pp. 55–59. Springer, Heidelberg (1998). https://doi.org/10.1007/BFb0054014
Bjørstad, T.E., Dent, A.W.: Building better signcryption schemes with tag-KEMs. In: Yung, M., Dodis, Y., Kiayias, A., Malkin, T. (eds.) PKC 2006. LNCS, vol. 3958, pp. 491–507. Springer, Heidelberg (2006). https://doi.org/10.1007/11745853_32
Boneh, D., Shoup, V.: A graduate course in applied cryptography. Draft 0.6 (2023). https://toc.cryptobook.us/
Chiba, D., Matsuda, T., Schuldt, J.C.N., Matsuura, K.: Efficient generic constructions of signcryption with insider security in the multi-user setting. In: Lopez, J., Tsudik, G. (eds.) ACNS 2011. LNCS, vol. 6715, pp. 220–237. Springer, Heidelberg (2011). https://doi.org/10.1007/978-3-642-21554-4_13
Ducklin, P.: Serious security: google finds fake but trusted SSL certificates for its domains, made in France. Naked Security-Award-Winning Computer Security, News, Opinion, Advice and Research from SOPHOS, pp. 09–12 (2013)
Fan, J., Zheng, Y., Tang, X.: Signcryption with non-interactive non-repudiation without random oracles. In: Gavrilova, M.L., Tan, C.J.K., Moreno, E.D. (eds.) Transactions on Computational Science X. LNCS, vol. 6340, pp. 202–230. Springer, Heidelberg (2010). https://doi.org/10.1007/978-3-642-17499-5_9
Fisher, D.: Final Report on DigiNotar Hack Shows Total Compromise of CA Servers. Threatpost, 10/31/12. https://threatpost.com/final-report-diginotar-hack-shows-total-compromise-ca-servers-103112/77170/
Kakvi, S.A., Kiltz, E.: Optimal security proofs for full domain hash, revisited. In: Pointcheval, D., Johansson, T. (eds.) EUROCRYPT 2012. LNCS, vol. 7237, pp. 537–553. Springer, Heidelberg (2012). https://doi.org/10.1007/978-3-642-29011-4_32
Kelsey, J., Chang, S.J., Perlner, R.: SHA-3 derived functions: cSHAKE, KMAC, TupleHash, and ParallelHash. NIST Special Publication, vol. 800, p. 185 (2016)
Krawczyk, H., Bellare, M., Canetti, R.: RFC2104: HMAC: Keyed-hashing for message authentication (1997)
Krovetz, T. (Ed.): RFC 4418: UMAC: Message Authentication Code using Universal Hashing (2006)
Malone-Lee, J.: Signcryption with non-interactive non-repudiation. Des. Codes Cryptogr. 37(1), 81–109 (2005)
Matsuda, T., Matsuura, K., Schuldt, J.C.N.: Efficient constructions of signcryption schemes and signcryption composability. In: Roy, B., Sendrier, N. (eds.) INDOCRYPT 2009. LNCS, vol. 5922, pp. 321–342. Springer, Heidelberg (2009). https://doi.org/10.1007/978-3-642-10628-6_22
Ngarenon, T., Sarr, A.P.: A Computational Diffie-Hellman based Insider Secure Signcryption with Non Interactive Non Repudiation (full version) (2022). https://hal.science/hal-03628351/document
Ngarenon, T., Sarr, A.P.: A computational Diffie-Hellman based insider secure signcryption with non-interactive non-repudiation. In: Rushi Kumar, B., Ponnusamy, S., Giri, D., Thuraisingham, B., Clifton, C.W., Carminati, B. (eds.) ICMC 2022. Springer Proceedings in Mathematics & Statistics, vol. 415. Springer, Cham (2023). https://doi.org/10.1007/978-981-19-9307-7_8
Sarr, A.P., Seye, P.B., Ngarenon, T.: A practical and insider secure signcryption with non-interactive non-repudiation. In: Carlet, C., Guilley, S., Nitaj, A., Souidi, E.M. (eds.) C2SI 2019. LNCS, vol. 11445, pp. 409–429. Springer, Cham (2019). https://doi.org/10.1007/978-3-030-16458-4_24
Tan, C.H.: Signcryption scheme in multi-user setting without random oracles. In: Matsuura, K., Fujisaki, E. (eds.) IWSEC 2008. LNCS, vol. 5312, pp. 64–82. Springer, Heidelberg (2008). https://doi.org/10.1007/978-3-540-89598-5_5
Zheng, Y.: Digital signcryption or how to achieve cost(signature & encryption) \(\ll \) cost(signature) + cost(encryption). In: Kaliski, B.S. (ed.) CRYPTO 1997. LNCS, vol. 1294, pp. 165–179. Springer, Heidelberg (1997). https://doi.org/10.1007/BFb0052234
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
A Proof of Lemma 1
A Proof of Lemma 1
Let \(\mathcal {A}\) be an adversary playing Game 1. We build an adversary \(\mathcal {B}\) against the collision (with identical prefix) resistance of \(\textsf{H}\) a follows.
-
1)
\(\mathcal {B}\) receives
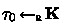 from its challenger and sends \(\tau _0\) to \(\mathcal {A}\).
from its challenger and sends \(\tau _0\) to \(\mathcal {A}\). -
2)
When \(\mathcal {B}\) receives \((p_0, m_0, s_0)\) from \(\mathcal {A}\), it chooses
 and computes \(\tau ''_0\leftarrow \textsf{Prf}(\tau ', m_0)\), \(\hat{m}_0\leftarrow \textsf{H}(\tau _0, (p_0, \tau , \tau ', \tau '', s_0))\) and sends \(\hat{m}_0\) to \(\mathcal {A}\).
and computes \(\tau ''_0\leftarrow \textsf{Prf}(\tau ', m_0)\), \(\hat{m}_0\leftarrow \textsf{H}(\tau _0, (p_0, \tau , \tau ', \tau '', s_0))\) and sends \(\hat{m}_0\) to \(\mathcal {A}\). -
3)
When \(\mathcal {A}\) outputs \((\tau ^*, \tau '^*)\) such that \(\hat{m}_0=\hat{m}^*_0\leftarrow \textsf{H}(\tau _0, (p_0, \tau ^*, \tau '^*, \tau ''^*, s_0))\) wherein \(\tau ''^*\leftarrow \textsf{Prf}(\tau '^*, m_0)\), if \((\tau , \tau ')\ne (\tau ^*, \tau '^*)\) then \(\mathcal {B}\) outputs \((s, s')\) wherein \(s=(p_0, \tau , \tau ', \tau '', s_0)\) and \(s'=(p_0, \tau ^*, \tau '^*, \tau ''^*, s_0)\) as messages with identical prefix \(p_0\) and colliding hashes under \(\tau _0\).
Let \(\textsf{bad}\) be the event: the chosen pair \((\tau , \tau ')\) is such that for all \((\bar{\tau }, \bar{\tau }')\ne (\tau , \tau ')\), \(\hat{m}_0\ne \textsf{H}(\tau _0, (p_0, \bar{\tau }, \bar{\tau }', \bar{\tau }'', s_0))\), i. e. there is no other pair \((\bar{\tau }, \bar{\tau }')\in \textbf{K}^2\) such that \(\textsf{H}(\tau _0, (p_0, \bar{\tau }, \bar{\tau }', \bar{\tau }'', s_0)) =\textsf{H}(\tau _0, (p_0, \tau , \tau ', \tau '', s_0))\). It holds that
If \(\textsf{Succ}_{\mathcal {A}, \textsf{H}}\) denotes the event \(\mathcal {A}\) succeeds in Game 1,
Now let \(\textsf{Eq}\) be the event \((\tau , \tau ')=(\tau ^*, \tau '^*)\).
Now, as if \(\textsf{Succ}_{\mathcal {A}, \textsf{H}}\wedge \lnot \textsf{bad}\) occurs, there at least one \((\tau ^*, \tau '^*)\ne (\tau , \tau ')\) such that \(\hat{m}_0=\hat{m}^*_0\leftarrow \textsf{H}(\tau _0, (p_0, \tau ^*, \tau '^*, \tau ''^*, s_0))\), and \(\mathcal {A}\) has no information about \((\tau , \tau ')\) besides \(\hat{m}_0\), it holds that
Hence
And, whenever \(\textsf{Succ}_{\mathcal {A}, \textsf{H}}\wedge \lnot \textsf{bad}\wedge \lnot \textsf{Eq}\) occurs \(\mathcal {B}\) outputs \(s, s'\) with identical prefix such that \(\textsf{H}(\tau _0,s)=\textsf{H}(\tau _0, s')\). \(\square \)
Rights and permissions
Copyright information
© 2024 The Author(s), under exclusive license to Springer Nature Switzerland AG
About this paper
Cite this paper
Togde, N., Sarr, A.P. (2024). An Efficient Generic Insider Secure Signcryption with Non-Interactive Non-Repudiation. In: Regazzoni, F., Mazumdar, B., Parameswaran, S. (eds) Security, Privacy, and Applied Cryptography Engineering. SPACE 2023. Lecture Notes in Computer Science, vol 14412. Springer, Cham. https://doi.org/10.1007/978-3-031-51583-5_8
Download citation
DOI: https://doi.org/10.1007/978-3-031-51583-5_8
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-031-51582-8
Online ISBN: 978-3-031-51583-5
eBook Packages: Computer ScienceComputer Science (R0)





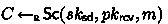 ;
; is received from the KEM challenger; we note
is received from the KEM challenger; we note 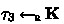 in
in  is equivalent to
is equivalent to
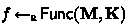 ;
;  was issued by
was issued by 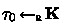 from its challenger and sends
from its challenger and sends  and computes
and computes