Abstract
In Side-Channel Analysis (SCA), several papers have shown that neural networks could be trained to efficiently extract sensitive information from implementations running on embedded devices. This paper introduces a new tool called Gradient Visualization that aims to proceed a post-mortem information leakage characterization after the successful training of a neural network. It relies on the computation of the gradient of the loss function used during the training. The gradient is no longer computed with respect to the model parameters, but with respect to the input trace components. Thus, it can accurately highlight temporal moments where sensitive information leaks. We theoretically show that this method, based on Sensitivity Analysis, may be used to efficiently localize points of interest in the SCA context. The efficiency of the proposed method does not depend on the particular countermeasures that may be applied to the measured traces as long as the profiled neural network can still learn in presence of such difficulties. In addition, the characterization can be made for each trace individually. We verified the soundness of our proposed method on simulated data and on experimental traces from a public side-channel database. Eventually we empirically show that the Sensitivity Analysis is at least as good as state-of-the-art characterization methods, in presence (or not) of countermeasures.
Access provided by Autonomous University of Puebla. Download conference paper PDF
Similar content being viewed by others
Keywords
1 Introduction
Side-channel analysis is a class of cryptanalytic attacks that exploits weaknesses of a physical implementation of a cryptographic primitive. During its execution, the primitive processes values, called sensitive, that both depend on a piece of public data (e.g. a plaintext) and on some chunk of a secret value (e.g. a key). As the processing is invertible, knowing the value of this variable (or at least having some information about it) and the plaintext enables an attacker to recover the piece of secret key. Secure cryptographic algorithms such as the Advanced Encryption Standard (AES) can then be defeated by recovering each byte of the secret key separately thanks to a divide-and-conquer strategy, thereby breaking the high complexity usually required to defeat such an algorithm. This information is usually gathered thanks to physical leakages such as the power consumption or the electromagnetic emanations measured on the target device. Actually, conducting an SCA is equivalent as studying the conditional probability distribution of the sensitive variables given the physical measure. It can be done for example through the computation of statistics such as a difference of means [16] or a correlation coefficient [3].
For the specific type of SCA called profiling attacks, an attacker will try to estimate the whole conditional distribution thanks to a profiling phase during which she has access to an open sample for which she knows the value of the target variable. Such an access allows her to estimate the conditional distribution. Historically, Gaussian Template Attacks (GTA) have first been proposed in the early 2000’s [7]. Their complexity is however strongly impacted by the number of time samples contained in the exploited traces. A first pre-processing step is hence required to extract, from each trace, few points called Points of Interest (PoIs). Tools like Signal-to-Noise Ratio (SNR) can efficiently extract those PoIs [22] (see Sect. 4.3). Other characterization methods based on statistical tools such as the T-Test [24] or the \(\chi ^2\)-Test [26] may also be used.Footnote 1 However, in presence of countermeasures such as masking or de-synchronization [33], both estimation with GTA and PoIs extraction with SNR are no longer efficient (or at least much less). Likewise, other dimensionality reduction techniques like dedicated variants of Principal Component Analysis (PCA) [4, 8, 9, 11, 37] or Kernel Discriminant Analysis (KDA) [6] can be used, without guarantee that relevant components will be extracted.
Recently, the SCA community has benefited the resurgence of Convolutional Neural Networks (CNNs) in the 2010’s [17] to apply them to profiling attacks, as first proposed in [12, 20, 23]. They are seen as a black-box tool and their results have been afterwards experimentally shown to be robust to the most common countermeasures, namely masking [21] and de-synchronization [5]. Their main advantage is that they do not require pre-processing, and are at least as efficient as the other state-of-the-art profiling attacks. However, from the evaluator’s point-of-view, this is not sufficient. On the one hand she wants to make sure that a CNN attack succeeded for good reasons i.e. that the learned model can generalize to new data. On the other hand the evaluator also wants to help the developer to localize and understand where the vulnerability comes from in order to remove or at least reduce it. This issue is part of a more general problematic in Deep Learning based systems, namely their explainability and interpretability. To address it, a theoretical framework has recently been proposed in [25], and several methods have been tested to tackle the issue. In particular, some computer vision research groups have studied the so-called Sensitivity Analysis [35, 36] which is derived from the computation of the loss function gradient with respect to the input data during the training phase.
In this paper, we propose to apply a particular Sensitivity Analysis method called Gradient Visualization (GV) in order to better understand how a CNN can learn to predict the sensitive variable based on the analysis of a single trace. The main claim is that CNN based models succeed in discriminating PoIs from non-informative points, and their localization can be deduced by simply looking at the gradient of the loss function with respect to the input traces for a trained model. We theoretically show that this method can be used to localize PoIs in the case of a perfect model. The efficiency of the proposed method does not decrease when countermeasures like masking or misalignment are applied. In addition, the characterization can be made for each trace individually. We verified the efficiency of our proposed method on simulated data and on experimental traces from a public Side Channel database. We empirically show that Gradient Visualization is at least as good as state-of-the-art characterization methods, in presence or not of different countermeasures.
The paper is organized as follows. In Sect. 3 we start by considering the optimal model an ideal attacker may get during profiling, and we deduce some properties of its derivatives with respect to the input traces that can be related to the PoIs. In Sect. 4 we use these properties on a model estimated with CNNs and we explain how to practically implement the visualization method. A toy example applied on simulated data is proposed for illustration. Sections 5 and 6 are eventually dedicated to an experimental validation of the effectiveness of our proposal in realistic attacks scenarios.
2 Preliminaries
2.1 Notations
Throughout the paper we use calligraphic letters as \(\mathcal {X}\) to denote sets, the corresponding upper-case letter X to denote random variables (resp. random vectors \(\mathbf X \)) over \(\mathcal {X}\), and the corresponding lower-case letter x (resp. \(\mathbf x \) for vectors) to denote realizations of X (resp. \(\mathbf X \)). The i-th entry of a vector \(\mathbf x \) is denoted by \(\mathbf x [i]\). We denote the probability space of a set \(\mathcal {X}\) by \(\mathcal {P}(\mathcal {X})\). If \(\mathcal {X}\) is discrete, it corresponds to the set of vectors \([0, 1]^{|\mathcal {X}|}\) such that the coordinates sum to 1. If a random variable X is drawn from a distribution \(\mathcal {D}\), then \(\mathcal {D}^N\) denotes the joint distribution over the sequence of N i.i.d. random variables of same probability distribution than X. The symbol \(\mathbb {E}\) denotes the expected value, and might be subscripted by a random variable \(\mathbb {E}_{X}\), or by a probability distribution \(\underset{X \sim \mathcal {D}}{\mathbb {E}}\) to specify under which probability distribution it is computed. Likewise, \(\mathrm {Var}\) denotes the variance of a random variable. If \(f: x, y \mapsto f(x, y) \) is a multivariate function, \(\frac{\partial }{\partial x}\) denotes the partial derivative with respect to the input variable x. Likewise, if f is a function from \(\mathbb {R}^n\) to \(\mathbb {R}\), then \(\nabla f(\mathbf x )\) denotes the gradient of f computed in \(\mathbf x \in \mathbb {R}^n\), which corresponds to the vector of the partial derivatives with respect to each coordinate of \(\mathbf x \) respectively. If there is an ambiguity, the gradient will be denoted \(\nabla _\mathbf{x }f(\mathbf x , \mathbf y )\) to emphasize that the gradient is computed with respect to \(\mathbf x \) only. Eventually if f is a function from \(\mathbb {R}^n\) to \(\mathbb {R}^m\), then \(J_f(\mathbf x ) \in \mathbb {R}^{m, n}\) denotes the (m, n) matrix whose rows are the transposed gradient of each elementary function \(\mathbf x \mapsto f(\mathbf x )[i] \in \mathbb {R}\). The output of a cryptographic primitive \({\mathbf {C}}\) is considered as the target sensitive variable \(Z= {\mathbf {C}}(P, K)\), where \(P\) denotes some public variable, e.g. a plaintext chunk, where \(K\) denotes the part of secret key the attacker aims to retrieve, and where \(Z\) takes values in \(\mathcal {Z}= \{s_1, \ldots , s_{|\mathcal {Z}|}\}\). Among all the possible values \(K\) may take, \(k^{\star }\) will denote the right key hypothesis. A side-channel trace will be viewed as a realization of a \(D\)-dimensional random column vector \(\mathbf X \in \mathcal {X}\subset \mathbb {R}^{D}\).
2.2 Profiling Attacks
We will consider attacking a device through a profiling attack, made of the following steps:
-
Profiling acquisition: a dataset of \(N_p\) profiling traces is acquired on the prototype device: \(S_p\triangleq \{(\mathbf x _1, z_1), \ldots , (\mathbf x _{N_p}, z_{N_p})\}\).
-
Model building: a model that returns a discrete probability distribution (pdf) \(F(\mathbf x )\) is built. If the model is accurate, the returned discrete pdf, viewed as a vector, is assumed to be a good approximation of the conditional pdf \(\mathrm {Pr}[Z| \mathbf X = \mathbf x ]\).
-
Attack acquisition: a dataset of \(N_a\) attack traces is acquired on the target device: \(S_{a}\triangleq \{(\mathbf x _1, z_1), \ldots , (\mathbf x _{N_a}, z_{N_a})\}\).
-
Predictions: a prediction vector is computed on each attack trace, based on the previously built model:
 . It assigns a score to each key hypothesis, for each trace.
. It assigns a score to each key hypothesis, for each trace. -
Guessing: the scores are combined over all the attack traces to output a likelihood for each key hypothesis; the candidate with the highest likelihood is predicted to be the right key.
Let us denote by \(g_{S_{a}}(k^{\star })\) the actual rank of the correct key hypothesis returned by the attack. If \(g_{S_{a}}(k^{\star })=1\), then the attack is considered as successful. More details about the score vector and the rank definitions can be found in Appendix A. The difficulty of attacking the target device is often defined as the number of traces required to get a successful attack. As many random factors may be involved during the attack, it is preferred to study its expected value, the so-called Guessing Entropy (\(\mathrm {GE}\)) [38]:
The goal of an evaluator is therefore to find a model \(F\) that minimizes \(N_a\) such that \(\mathrm {GE}(N_a) < 2\). We will assume that this is equivalent to the problem of accurately estimating the conditional probability distribution \(\mathbf x \mapsto \mathrm {Pr}[Z| \mathbf X = \mathbf x ]\). As mentioned in the introduction, we distinguish the security evaluator as a particular attacker who additionally wishes to interpret the attack results. One step of this diagnosis is to temporally localize where the information leakage appeared in \(\mathbf x \). This task is usually called characterization. It consists in emphasizing Points of Interest (PoIs) where the information leakage may come from. Section 4.3 will present an usual characterization technique while a new method will be introduced through this paper.
3 Study of an Optimal Model
In this section, we address the evaluator interpretation problem in the ideal situation when the conditional distribution is known (i.e. when the model is perfect). The latter will be denoted as \(F^*\). We will show how the study of the derivatives of such a model with respect to each coordinate of an input trace can highlight information about our PoIs. To this end, we need two assumptions.
Assumption 1
(Sparsity). There only exists a small set of coordinates \(\mathcal {I}_{Z}\triangleq \{t_1, \ldots , t_{C} | C\ll D\}\) such that \(\mathrm {Pr}[Z| \mathbf X ] = \mathrm {Pr}\left[ Z| \mathbf X \left[ t_1\right] , \ldots , \mathbf X \left[ t_{C}\right] \right] \).
Assumption 2
(Regularity). The conditional probability distribution \(F^*\) is differentiable over \(\mathcal {X}\) and thereby continuous.
Informally, Assumption 1 tells that the leaking information is non-uniformly distributed over the trace. Both assumptions are realistic in a SCA context (this point is discussed in Appendix B).
Once Assumptions 1 and 2 are stated, we may want to observe their impact on the properties verified by the optimal model derivatives. For such a purpose we start by considering an example on a trace \(\mathbf x \). Figure 1 (left) illustrates such a trace in blue, and the green line depicts a PoI, namely a peak of SNR (in other words the set of PoIs \(\mathcal {I}_{Z}\) is reduced to a single time index). The prediction pdfs \(F^*(\mathbf x )\) are given at the right of the same figure: they are here represented by a histogram over the 256 possible values of a byte. We may fairly suppose that a slight variation on one coordinate that does not belong to \(\mathcal {I}_{Z}\) (dotted in gray in Fig. 1, left) should not radically change the output of the optimal model. The pdf remains the same, as the gray bars and blue bars perfectly match in Fig. 1 (right). However, applying a slight variation on the coordinate from \(\mathcal {I}_{Z}\) (dotted in red in Fig. 1, left) may radically change the output distribution (red bars in Fig. 1, right).
This example illustrates the more general idea that small variations applied to the trace at a coordinate \(t \in \mathcal {I}_{Z}\) should radically change the output prediction whereas small variations at \(t \notin \mathcal {I}_{Z}\) have no impact. As a consequence, if \(F^*\) is differentiable with respect to the input trace (according to Assumption 2), there should exist \(s\in \mathcal {Z}\) such that:
The latter observation can be stated in terms of the Jacobian matrix of the estimator, denoted as \(J_{F^*}(\mathbf x )\). Its coefficients should be zero almost everywhere, except in columns \(t \in \mathcal {I}_{Z}\):
where \(\mathbf Y _t = \left( \frac{\partial }{\partial \mathbf x [t]} F^*(\mathbf x )[s_1], \frac{\partial }{\partial \mathbf x [t]} F^*(\mathbf x )[s_2], \ldots , \frac{\partial }{\partial \mathbf x [t]} F^*(\mathbf x )\left[ s_{|\mathcal {Z}|}\right] \right) ^\intercal \) and \(\mathbf 0 \) denotes the zero column vector.
The properties verified by the Jacobian matrix in (3) form the cornerstone of this paper, as it implies that we can guess from this matrix whether a coordinate from an input trace belongs to \(\mathcal {I}_{Z}\) or not, i.e. whether a coordinate has been recognized as a PoI when designing the optimal model \(F^*\). Such a technique is part of Sensitivity Analysis.Footnote 2 Moreover, except Assumption 1, no more assumption on the nature of the leakage model is required.
4 Our Characterization Proposal
So far we have shown that the Jacobian of an optimal model may emphasize PoIs. In practice however, the evaluator does not have access to the optimal model, but a trained estimation of it. A natural idea is hence to look at the Jacobian matrix of the model estimation, hoping that its coefficients will be close to the optimal model derivatives. Here we follow this idea in contexts where the approximation is modeled by training Convolutional Neural Networks, described in Sect. 4.1 (discussions can be found in Appendix C about this approximation). Section 4.2 illustrates our claim with a toy example. Finally, Sect. 4.3 is dedicated to the comparison of our approach with state-of-the-art methods for leakage characterization.
4.1 Gradient Approximation with Neural Networks
Neural Networks (NN) [19] aim at constructing a function \(F:\mathcal {X}\rightarrow \mathcal {P}(\mathcal {Z})\) composed of several simple operations called layers. All the layers are entirely parametrized by (a) a real vector called trainable weights and denoted by \(\theta \) that can be automatically set; (b) other parameters defining the general architecture of the model which are gathered under the term hyper-parameter. The latter ones are defined by the attacker/evaluator.
Convolutional Neural Networks (CNN) form a specific type of Neural Network where particular constraints are applied on the trainable weights [18]. The training phase consists in an automatic tuning of the trainable weights and it is done via an iterative approach that locally applies the Stochastic Gradient Descent algorithm to minimize a loss function that quantifies the classification error of the function \(F\) over the training set. For further details, the interested reader may refer to [13].
To accurately and efficiently compute the Jacobian matrix of a CNN, an algorithm called backward propagation (or back-propagation) can exactly compute the derivatives with the same time complexity as computing \(F(\mathbf x , \theta )\) [13]. As a consequence, computing such a matrix can be done with a negligible overhead during an iteration of a Stochastic Gradient Descent. Actually the modern Deep Learning libraries [2, 28] are optimized to compute the required derivatives for Stochastic Gradient Descent in the back-propagation, so the Jacobian matrix is never explicitly stored, and it is easier to get the loss function gradient with respect to the input trace \(\nabla _\mathbf{x }\ell (F(\mathbf x , \theta ), z^*)\), where \(\ell : \mathcal {P}(\mathcal {Z}) \times \mathcal {Z}\rightarrow \mathbb {R}_+\) denotes the loss function, and \(z^*\) denotes the true sensitive value. Hopefully, studying either the latter one or \(J_{F}(\mathbf x )\) is fairly equivalent, as one coordinate of the loss function gradient is a function of elements from the corresponding column in the Jacobian matrix:
That is why we propose to visualize the latter gradient to characterize PoIs in the context of a CNN attack, instead of the Jacobian matrix (unless explicit mention). To be more precise, we visualize the absolute value of each coordinate of the gradient in order to get the sensitivity magnitude. In the following, such a method is named Gradient Visualization (GV for short).
4.2 Example on Simulated Data
To illustrate and explain the relevance of the GV method, and before going on experimental data, we here propose to apply it on a toy example, aiming at simulating simple \(D\)-dimensional leakages from an n-bit sensitive variable \(Z\). The traces are defined such that for every \(t \in \llbracket 1, D\rrbracket \):
where \((U_i)_i, (B_i)_i\) and all \((z_{t,i})_i\) are independent, \(U_i \sim \mathcal {B}(n, 0.5)\), \(B_i \sim \mathcal {N}(0, \sigma ^2)\) and where \((z_{1,i}, \ldots , z_{m,i})\) is a m-sharing of \(z_i\) for the bitwise addition law. This example corresponds to a situation where the leakages on the shares are hidden among values that have no relation with the target.
Every possible combination of the m-sharing has been generated and replicated 100 times before adding the noise, in order to have an exhaustive dataset. Therefore, it contains \(100 \times 2^{mn}\) simulated traces. We ran the experiment for \(n = 4\) bits, \(m \in \{2, 3\}, D = 100\), and a varying noise \(\sigma ^2 \in [0, 1]\). Once the data were generated, we trained a neural network with one hidden layer made of D neurons. Figure 2 presents some examples obtained for 2 (left) and 3 shares (right). We clearly see some peaks at the coordinates where the meaningful information have been placed. Interestingly, this simulation shows that a second order masking has been defeated, though it required 16 times more simulated data and less noised data (\(\sigma ^2 \ge 0.1\)) than for the same experiment against first order masking. Further works might study how much the noise magnitude \(\sigma ^2\) and the number of shares impact the efficiency of the training. It is however beyond the scope of this paper.
4.3 Comparison with SNR for Characterization
Now we have shown that Gradient Visualization is relevant for characterization on simulated data, one may wonder to what extent this method would be useful compared to other characterization techniques. In this section, we compare our contribution to the SNR used for PoIs selection in SCA. For each time sample t, it is estimated by the following statistics:
where the numerator denotes the signal magnitude and the denominator denotes the noise magnitude estimate (see [22] for more details on its application in the SCA context). One has to keep in mind that the SNR is a statistical tool, andproduces a single characterization from all the profiling traces; whereas our method gives one map for each trace, though we might average them. This observation has two consequences. First, if an SNR characterization is launched in presence of masking, every trace coordinate \(\mathbf X [t]\) is likely to be independent from \(Z\), which will lead the numerator to converge towards 0. Secondly, if an SNR characterization is launched in presence of de-synchronization (which is likely to introduce a lot of noise in the traces), then the denominator is expected to explode as argued in [33, Section 3.2]. To sum-up, an SNR characterization cannot directly highlight higher order leakages when the random material (used to mask and/or desynchronise the data) is not assumed to be known. Some solutions to deal with this issue have been proposed, e.g. by pre-processing the traces with some functions combining tuple of points [31] or by applying realignment techniques [10, 27, 39].
4.4 Related Works
The idea to use the derivatives of differentiable models to visualize information is not new. Following the emergence of deep convolutional networks, [35] has first proposed the idea of GV to generate a so-called Sensitivity Map for image recognition. The approach was motivated by the fact that such a map can be computed for free thanks to the back-propagation algorithm. A derived method, called Guided Backpropagation has also been proposed in [36]. The latter one slightly modifies the back-propagation rule in a ReLU layer in order to filter the contributions from the upper layers. Actually [25] states that visualizing the gradient only tracks an explanation to the variation of a final decision (\(F(\mathbf x )\) in our context), and not directly the decision itself. To this end, they propose a visualization method called Layerwise Relevance Propagation (LRP). Another method called Deconvolution has been proposed in [40] in order to give insight about the regions of an input data that contribute to the activation of a given feature in a model (either in an intermediate layer or in the output layer). In the domain of Image Recognition, these methods have been shown to be more relevant than GV.
However, the SCA and Image Recognition domains differ. In the latter one, the decision is highly diluted among lots of pixels, and the decision surface might be locally flat, though we are in a very determining area. Hopefully in a SCA context, Assumption 1 states that it is reasonable to consider that the information is very localized. That is why we are in a particular case where looking at the output sensitivity may be more interesting than other visualization methods.
5 Experiment Description
So far we have claimed that relevant information can be extracted from the loss gradient of a differentiable model. Following this idea, it has been shown to be efficient to localize PoIs on simulated data and validated that this method might overcome some weaknesses of state-of-the-art techniques. We now plan to experimentally verify these claims. Before introducing the results in Sect. 6, we first describe our investigations. In Sect. 5.1, we present the CNN architecture that will be used for profiling. Finally, Sect. 5.2 gives an exhaustive description of all the considered parameters for our experiments.
5.1 CNN Architecture
For these experiments, we will consider the same architecture as proposed in [5, 32], with the same notations since the training will be done on the same dataset (see Sect. 5.2):
where \(\gamma \) denotes a convolutional layer, \(\sigma \) denotes an activation function i.e. a non-linear function applied elementwise, \(\mu \) denotes a batch-normalization layer, \(\delta \) denotes an average pooling layer, \(\lambda \) denotes a dense layer and \(\mathrm {s}\) denotes the softmax layer. Furthermore, \(n_1\) denotes the number of dense blocks, namely the composition \([\lambda \circ \sigma ]\). Likewise, \(n_3\) denotes the number of convolutional blocks, namely \([\delta \circ \sigma \circ \mu \circ \gamma ]\).
As the ultimate goal is not to get the better possible architecture, but rather having a simple and efficient one, a lighter baseline has been chosen compared to the original architecture proposed in the cited papers:
-
The number of filters in the first layers has been decreased (10 instead of 64), though it is still doubled between each block; and the filter size has been set to 5.
-
The dense layers contain less neurons: 1,000 instead of 4,096.
-
A global pooling layer \(\delta _G\), has been added at the top of the last block. Its pooling size equals the width of the feature maps in the last convolutional layer, so that each feature maps are reduced to one point. While it acts as a regularizer (since it will drastically reduce the number of neurons in the first dense layer), the global pooling layer also forces the convolutional filters to better localize the discriminative features [41].
5.2 Settings
Our experiments have been done with the 50, 000 EM traces from the ASCAD database [32]. Each trace is made of 700 time samples.Footnote 3 Here-after, the three different configurations investigated in this paper are presented with the notations taken from [32]. For each experiment we precise the label to be learned. This label is known during the training/profiling phase but not during the test/attack phase:
-
Experiment 1 (no countermeasure): the traces are synchronized, the label to be learned by the Neural Network is \(Z= \mathrm {Sbox}(P\oplus K) \oplus r_{out}\) (in other terms, \(r_{out}\) is assumed to be known, like \(P\)). The traces correspond to the dataset
 , and the labels are recomputed from the
, and the labels are recomputed from the
 field of the
field of the
 structure.
structure. -
Experiment 2 (artificial shift): the labels are the same as in Exp. 1 but the traces are artificially shifted to the left of a random number of points drawn from a uniform distribution over \(\llbracket 0, 100\rrbracket \). Concretely, the traces correspond to the dataset
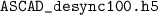 .
. -
Experiment 3 (synchronized traces, with unknown masking): we target \(Z= \mathrm {Sbox}(P\oplus K)\), i.e. we have no knowledge of the masks \(r_{out}\) (neither during profiling or attack phase). Concretely, the traces correspond to the dataset
 and the labels are directly imported from the field
and the labels are directly imported from the field
 in the
in the
 structure.
structure.
It is noticeable that in every case, as the key is fixed, and both the plaintext and \(r_{out}\) are completely random and independent. Therefore, the labels are always balanced.
The Neural Networks source code is implemented on Python thanks to the Pytorch [28] library and is run on a workstation with a Nvidia Quadro M4000 GP-GPU with 8 GB memory and 1664 cores.
We will use the Cross-Entropy (also known as Negative Log Likelihood) as a loss function. It particularly fits our context as it is equivalent as minimizing the Kullback-Leibler divergence, which measures a divergence between two probability distributions, namely \(F^*(\mathbf x )\) and \(F(\mathbf x , \theta )\) in our case. Therefore, the model \(F(., \theta )\) will converge towards \(F^*\) during the training.
For each tested neural network architecture, a 5-fold cross-validation strategy has been followed. Namely, the ASCAD database has been split into 5 sets \(S_1, \ldots , S_5\) of 10, 000 traces each, and the i-th cross-validation, denoted by \(\mathrm {CV}_i\), corresponds to a training dataset \(S_p=\cup _{j\ne i} S_j\) and a validation dataset \(S_{v}= S_i\). The given performance metrics and the visualizations are averaged over these 5 folds. The optimization is actually done with a slight modification of Stochastic Gradient Descent called Adam [15]. The learning rate is always set to \(10^{-4}\). Likewise, the batch size has been fixed to 64. For each training, we operate 100 epochs, i.e. each couple \((\mathbf x _i, z_i)\) is passed 100 times through an SGD iteration, and we keep as the best model the one that has the lowest GE on the validation set.Footnote 4
6 Experimental Results
This section presents experimentations of the GV in different contexts, namely (Exp. 1) when the implementation embeds no countermeasure, (Exp. 2) when traces are de-synchronized and (Exp. 3) when masking is applied. The methods used to train the CNNs, to tune their hyper-parameters and to generate the GV have been presented in Sect. 5.
6.1 Application Without Countermeasure
In application context (Exp. 1) (i.e. no countermeasure) several CNNs have been trained with the architecture hyper-parameters in (7) specified as listed in Table 1 (left). Since the masked data are here directly targeted (i.e. the masks are supposed to be known), no recombination (thereby no dense layer) should be required, according to [32], Sec.4.2.4. The parameter \(n_1\) should therefore be null. However, to validate this intuition we let it vary in \(\{0,1,2\}\). The validation loss corresponding to these values is given in Table 1 (center), where \(N^*\) denotes the minimum number of traces required to have a GE lower than 1. Even if this minimum is roughly the same for the 3 different configurations, we selected the best one (i.e. \(n_1=1\)) for our best CNN architecture. Figure 3 (left) presents the corresponding GV, and the corresponding SNR (right).Footnote 5 It may be observed that the peaks obtained with GV and SNR are identical: the highest point in the SNR is the second highest point in GV, whereas the highest point in GV is ranked 7-th in the SNR peaks. More generally both methods target the same clock cycle (the 19-th). These observations validate the fact that our characterization method is relevant for an unprotected target.
6.2 Application with an Artificial De-synchronization
We now add a new difficulty by considering the case of de-synchronization as described in Sect. 5.2. The hyper-parameter grid is exactly the same as in Sect. 6.1, and the corresponding loss is given in Table 1 (right). Faced to misalignment, the considered architectures have still good performances, and the attacks succeeded in roughly the same number of traces than before. Interestingly, Fig. 4 shows that the GV succeeds to recover the leakage localization while the SNR does not (see Fig. 9 in Appendix D). Actually, the gradient averaged over the profiling traces Fig. 4 (left) shows that, instead of having a small number of peaks, a band is obtained whose width approximately equals the maximum quantity of shift applied in the traces, namely 100 points. Moreover, individual gradients Fig. 4 (right) bring a single characterization for each trace, enabling to guess approximately the shift applied to each trace.
6.3 Application with a First Order Masking
The last experiment concerns the application of GV in presence of masking. Several model configurations have been tested which correspond to the hyper-parameters listed in Table 2 (left). We eventually selected the 8 models that achieved the best GE convergence rate (right).
For the selected architectures, our first attempt to use GV did not give full satisfaction. As an illustration, Fig. 5 (left) presents it for one of the tested architectures (averaged over the 5 folds of the cross-validation). Indeed, it looks difficult to distinguish PoIs (i.e. those identified by our SNR characterization, see the right-hand side of Fig. 6) from ghost peaks (i.e. peaks a priori independent of the sensitive target). To explain this phenomenon, we decided to study the validation loss of the trained models. Figure 5 (right) presents it for one model and for each of the 5 cross-validation folds \(\mathrm {CV}_i\), \(i\in [0..4]\).
It may be observed in Fig. 5 (right) that the training and validation loss curves proceeded a fast big decrease after an initial plateau during the first 15 epochs. After that, the validation loss starts increasing while the training loss still decreases. After roughly 50 epochs, the validation loss goes on a regime with unstable results, but still higher than the training loss. These observations are clues of overfitting. It means that the model exploits (non-informative) leakage not localized in the PoIs to memorize the training data and to improve the training loss. Such a strategy should not generalize well on the validation traces. As we are looking for models that implement a strategy that are generalizable on unseen traces, we propose to use a regularization technique called early-stopping [13]: the training is stopped after a number of epochs called patience (in our case 10) if no remarkable decrease (i.e. up to a tolerance term, 0.25 bits here) is observed in the validation loss. With this slight modification, the previous architectures are trained again from scratch, and a better GV is produced (see the left-hand side of Fig. 6). As the main peaks are separated enough, an evaluator may conclude that they represent different leakages.
6.4 Comparison in the Context of Template Attacks
A careful observation of Fig. 6 shows that the main peaks given by the GV are not exactly aligned with those given by the SNR characterization (performed under the hypothesis that the masks are known). For GV, the main peak appears at the points corresponding to the 20-th clock cycle, which is one cycle after the one previously targeted by both the GV and the SNR in the previous case where no countermeasure was considered (Sect. 6.1). We validated that this phenomenon occurred for every successful visualization produced by GV. Furthermore, concerning the peaks related to the mask leakage, the GV only emphasizes one clock cycle (the 6-th) whereas the SNR highlights two of them: the 6-th and the 7-th. It implies that the GV should not be taken as an exact equivalent to the SNR. We have not found any track of explanation to justify this slight shift but it raises the question whether the PoIs highlighted by GV represent relevant leakages and can be used in the context of Template Attacks.
To give an answer, we decided to use our characterization method as a pre-processing for a Template Attack, and compare it to two pre-processing methods: SNR (through PoIs selection) and PCA (through dimensionality reduction).
The input dimension of the traces are reduced to \(2^n, n \in \{1, 2, 3, 4, 5\}\) points, based on the following methods:
-
SNR strategy: the \(2^{n-1}\) highest PoIs from the mask SNR and the \(2^{n-1}\) highest PoIs from the masked data SNR are selected;
-
PCA strategy: the \(2^n\) first components in a decreasing order of contribution are selected;
-
GV strategy: the \(2^{n-1}\) highest PoIs from the GV are selected from the area around the 6-th clock cycle. Likewise, the other half comes from the peaks in the area around the 20-th clock cycle.
Remark 1
To make a fair comparison in the context of a first order masking, we assume that we know the mask during the characterization phase for SNR, so that we can localize PoIs for the mask and the masked data. Notice that we do not assume the mask knowledge neither during the profiling phase nor for the other strategies. Obviously, this scenario is not realistic as if one has access to the mask during characterization, then the latter one is very likely to be also available during the profiling phase.
Once reduced, the traces are processed with a first order Template Attack [7], and the GE is estimated. The results are given on Fig. 7. The plain curves denote the GE for GV whereas the dotted curves denote either GE obtained with SNR (left) or PCA (right).
From Fig. 7 we can observe several things:
-
Only a few PoIs from the GV strategy are needed to get a successful attack. The optimal number of extracted PoIs is 4. Beyond that, the other PoIs bring more difficulty in the Template Attack than they bring new information (due to the increasing dimensionality).
-
When the SNR strategy is followed, the optimal attack is done with 2 PoIs and the more PoIs are used, the less efficient are the attacks. This observation confirms that SNR selects relevant PoIs as expected. However, when comparing the SNR and GV strategies with a same number of PoIs, the latter one appears to be always better, except for 32 PoIs where both strategies seem equal.
-
The PCA strategy does not work well for the two or four first extracted components. However, when considering eight components and above, it achieves an efficiency as good as the GV strategy, and even sometimes better.
-
In any case, the Template Attacks need much more traces to get a GE converging towards zero than the optimal CNN attack presented in Table 2.
Based on the presented experiments, we may draw several conclusions on the GV efficiency. First of all, it seems to be an accurate characterization method, almost always much better than that based on an SNR. This first conclusion enables to answer the question previously asked: the targeted PoIs in GV are relevant leakages and can be used in the context of Template Attacks. A possible and informal explanation would be that choosing the couples of samples that maximize the information about the sensitive variable is not equivalent as selecting the single samples that independently maximize the information on each share.
Secondly, GV can be used as a reliable dimensionality reduction pre-processing in presence of counter-measures, even more reliable than PCA in our cases where one makes a reduction to a very few dimensions (2 or 4). However, this conclusion has a minor interest, as the GV seen as a pre-processing method is done post-mortem, and the training of a CNN model did not suffer from a high dimension input. And last, but not least, the GV method unfortunately faces a drawback: if the trained CNN overfits, then the GV might suffer from the presence of ghost peaks. That is why the overfitting must be carefully monitored. In this sense, visualizing the gradient can hopefully help to assess whether it is the case or not.
7 Conclusion
In this paper, we have theoretically shown that a method called Gradient Visualization can be used to localize Points of Interest. This result relies on two assumptions that can be considered as realistic in a Side Channel context.
Generally, the efficiency of the proposed method only depends on the ability of the profiling model to succeed in the attack. In the case where countermeasures like masking or misalignment are considered, CNNs are shown to still build good pdf estimations, and thereby the Gradient Visualization provides a good characterization tool. In addition, such a visualization can be made for each trace individually, and the method does not require more work than needed to perform a profiling with CNNs leading to a successful attack. Therefore, characterization can be done after the profiling phase whereas profiling attacks with Templates often requires to proceed a characterization phase before.
We verified the efficiency of our proposed method on simulated data. It has been shown that as long as a Neural Network is able to have slightly better performance than randomness, it can localize points that contain the informative leakage.
On experimental traces, we have empirically shown that Gradient Visualization is at least as good as state-of-the-art characterization methods, in different cases corresponding to the presence or not of different countermeasures. Not only it can still localize Points of Interest in presence of desynchronization or masking but it has also been shown that different PoIs can be emphasized compared to the first ones highlighted by SNR. These new PoIs have been shown to be at least as relevant as the ones proposed by SNR.
Further work would study such a technique in presence of both desynchronization and masking, or in presence of higher order masking scheme.
Notes
- 1.
In practice, the latter methods usually emphasize the same PoIs than SNR. This claim has been empirically verified on the data considered in this study. For this reason, we will only focus on the SNR when challenging the effectiveness of our method in the remaining of this paper.
- 2.
A general definition of Sensitivity Analysis is the study of how the uncertainty in the output of a mathematical model or system (numerical or otherwise) can be apportioned to different sources of uncertainty in its inputs [1].
- 3.
It corresponds to 26 clock cycles.
- 4.
Following the recent work in [29], the classical Machine Learning metrics (accuracy, recall) are ignored, as they are not proved to fit well the context of SCA.
- 5.
References
Sensitivity analysis - Wikipedia. https://en.wikipedia.org/wiki/Sensitivity_analysis
Abadi, M., et al.: TensorFlow: a system for large-scale machine learning. arXiv:1605.08695 [cs], 27 May 2016
Brier, E., Clavier, C., Olivier, F.: Correlation power analysis with a leakage model. In: Joye, M., Quisquater, J.-J. (eds.) CHES 2004. LNCS, vol. 3156, pp. 16–29. Springer, Heidelberg (2004). https://doi.org/10.1007/978-3-540-28632-5_2
Cagli, E., Dumas, C., Prouff, E.: Enhancing dimensionality reduction methods for side-channel attacks. In: Homma, N., Medwed, M. (eds.) CARDIS 2015. LNCS, vol. 9514, pp. 15–33. Springer, Cham (2016). https://doi.org/10.1007/978-3-319-31271-2_2
Cagli, E., Dumas, C., Prouff, E.: Convolutional neural networks with data augmentation against jitter-based countermeasures. In: Fischer, W., Homma, N. (eds.) CHES 2017. LNCS, vol. 10529, pp. 45–68. Springer, Cham (2017). https://doi.org/10.1007/978-3-319-66787-4_3
Cagli, E., Dumas, C., Prouff, E.: Kernel discriminant analysis for information extraction in the presence of masking. In: Lemke-Rust, K., Tunstall, M. (eds.) CARDIS 2016. LNCS, vol. 10146, pp. 1–22. Springer, Cham (2017). https://doi.org/10.1007/978-3-319-54669-8_1
Chari, S., Rao, J.R., Rohatgi, P.: Template attacks. In: Kaliski, B.S., Koç, K., Paar, C. (eds.) CHES 2002. LNCS, vol. 2523, pp. 13–28. Springer, Heidelberg (2003). https://doi.org/10.1007/3-540-36400-5_3
Choudary, M.O., Kuhn, M.G.: Efficient stochastic methods: profiled attacks beyond 8 bits. In: Joye, M., Moradi, A. (eds.) CARDIS 2014. LNCS, vol. 8968, pp. 85–103. Springer, Cham (2015). https://doi.org/10.1007/978-3-319-16763-3_6
Choudary, O., Kuhn, M.G.: Efficient template attacks. In: Francillon, A., Rohatgi, P. (eds.) CARDIS 2013. LNCS, vol. 8419, pp. 253–270. Springer, Cham (2014). https://doi.org/10.1007/978-3-319-08302-5_17
Durvaux, F., Renauld, M., Standaert, F.-X., van Oldeneel tot Oldenzeel, L., Veyrat-Charvillon, N.: Efficient removal of random delays from embedded software implementations using hidden Markov models. In: Mangard, S. (ed.) CARDIS 2012. LNCS, vol. 7771, pp. 123–140. Springer, Heidelberg (2013). https://doi.org/10.1007/978-3-642-37288-9_9
Eisenbarth, T., Paar, C., Weghenkel, B.: Building a side channel based disassembler. In: Gavrilova, M.L., Tan, C.J.K., Moreno, E.D. (eds.) Transactions on Computational Science X. LNCS, vol. 6340, pp. 78–99. Springer, Heidelberg (2010). https://doi.org/10.1007/978-3-642-17499-5_4
Gilmore, R., Hanley, N., O’Neill, M.: Neural network based attack on a masked implementation of AES. In: 2015 IEEE International Symposium on Hardware Oriented Security and Trust (HOST), pp. 106–111, May 2015. https://doi.org/10.1109/HST.2015.7140247
Goodfellow, I., Bengio, Y., Courville, A.: Deep Learning. Adaptive Computation and Machine Learning Series. MIT Press, Cambridge (2017)
Hardt, M.: Off the convex path. http://offconvex.github.io/
Kingma, D.P., Ba, J.: Adam: a method for stochastic optimization. arXiv:1412.6980 [cs], 22 December 2014
Kocher, P., Jaffe, J., Jun, B.: Differential power analysis. In: Wiener, M. (ed.) CRYPTO 1999. LNCS, vol. 1666, pp. 388–397. Springer, Heidelberg (1999). https://doi.org/10.1007/3-540-48405-1_25
Krizhevsky, A., Sutskever, I., Hinton, G.E.: ImageNet classification with deep convolutional neural networks. In: Advances in Neural Information Processing Systems, pp. 1097–1105 (2012)
LeCun, Y., Bengio, Y.: Convolutional networks for images, speech, and time series. In: The Handbook of Brain Theory and Neural Networks, pp. 255–258. MIT Press, Cambridge (1998). http://dl.acm.org/citation.cfm?id=303568.303704
LeCun, Y., Bengio, Y., Hinton, G.: Deep learning. Nature 521(7553), 436–444 (2015). https://doi.org/10.1038/nature14539. http://www.nature.com/articles/nature14539
Lerman, L., Bontempi, G., Markowitch, O.: A machine learning approach against amasked AES: reaching the limit of side-channel attacks with a learningmodel. J. Cryptographic Eng. 5(2), 123–139 (2015). https://doi.org/10.1007/s13389-014-0089-3
Maghrebi, H., Portigliatti, T., Prouff, E.: Breaking cryptographic implementations using deep learning techniques. In: Carlet, C., Hasan, M.A., Saraswat, V. (eds.) SPACE 2016. LNCS, vol. 10076, pp. 3–26. Springer, Cham (2016). https://doi.org/10.1007/978-3-319-49445-6_1
Mangard, S., Oswald, E., Popp, T.: Power Analysis Attacks: Revealing the Secrets of Smart Cards. Springer, Boston (2007). https://doi.org/10.1007/978-0-387-38162-6. OCLC: ocm71541637
Martinasek, Z., Dzurenda, P., Malina, L.: Profiling power analysis attack based on MLP in DPA contest v4.2. In: 2016 39th International Conference on Telecommunications and Signal Processing (TSP), pp. 223–226, June 2016. https://doi.org/10.1109/TSP.2016.7760865
Mather, L., Oswald, E., Bandenburg, J., Wójcik, M.: Does my device leak information? An a priori statistical power analysis of leakage detection tests. In: Sako, K., Sarkar, P. (eds.) ASIACRYPT 2013. LNCS, vol. 8269, pp. 486–505. Springer, Heidelberg (2013). https://doi.org/10.1007/978-3-642-42033-7_25
Montavon, G., Samek, W., Müller, K.R.: Methods for interpreting and understanding deep neural networks. Digit. Sig. Process. 73, 1–15 (2018). https://doi.org/10.1016/j.dsp.2017.10.011. http://linkinghub.elsevier.com/retrieve/pii/S1051200417302385
Moradi, A., Richter, B., Schneider, T., Standaert, F.X.: Leakage detection with the x2-test. IACR Trans. Cryptographic Hardware Embed. Syst. 2018(1), 209–237 (2018)
Nagashima, S., Homma, N., Imai, Y., Aoki, T., Satoh, A.: DPA using phase-based waveform matching against random-delay countermeasure. In: 2007 IEEE International Symposium on Circuits and Systems, pp. 1807–1810, May 2007. https://doi.org/10.1109/ISCAS.2007.378024
Paszke, A., et al.: Automatic differentiation in Pytorch. In: NIPS-W (2017)
Picek, S., Heuser, A., Jovic, A., Bhasin, S., Regazzoni, F.: The curse of class imbalance and conflicting metrics with machine learning for side-channel evaluations. IACR Trans. Cryptographic Hardware Embed. Syst. 2019(1), 209–237 (2018). https://doi.org/10.13154/tches.v2019.i1.209-237. https://tches.iacr.org/index.php/TCHES/article/view/7339
Picek, S., Samiotis, I.P., Heuser, A., Kim, J., Bhasin, S., Legay, A.: On the performance of deep learning for side-channel analysis. IACR Cryptology ePrint Archive 2018, 4 (2018). http://eprint.iacr.org/2018/004
Prouff, E., Rivain, M., Bevan, R.: Statistical analysis of second order differential power analysis. IEEE Trans. Comput. 58(6), 799–811 (2009). https://doi.org/10.1109/TC.2009.15. http://ieeexplore.ieee.org/document/4752810/
Prouff, E., Strullu, R., Benadjila, R., Cagli, E., Dumas, C.: Study of deep learning techniques for side-channel analysis and introduction to ASCAD database. IACR Cryptology ePrint Archive 2018, 53 (2018). http://eprint.iacr.org/2018/053
Rivain, M., Prouff, E., Doget, J.: Higher-order masking and shuffling for software implementations of block ciphers. In: Clavier, C., Gaj, K. (eds.) CHES 2009. LNCS, vol. 5747, pp. 171–188. Springer, Heidelberg (2009). https://doi.org/10.1007/978-3-642-04138-9_13
Shalev-Shwartz, S., Ben-David, S.: Understanding Machine Learning: From Theoryto Algorithms. Cambridge University Press (2014). https://doi.org/10.1017/CBO9781107298019. http://ebooks.cambridge.org/ref/id/CBO9781107298019
Simonyan, K., Vedaldi, A., Zisserman, A.: Deep inside convolutional networks: visualising image classification models and saliency maps. arXiv:1312.6034 [cs], 20 December 2013
Springenberg, J.T., Dosovitskiy, A., Brox, T., Riedmiller, M.: Striving for simplicity: the all convolutional net. arXiv:1412.6806 [cs], 21 December 2014
Standaert, F.-X., Archambeau, C.: Using subspace-based template attacks to compare and combine power and electromagnetic information leakages. In: Oswald, E., Rohatgi, P. (eds.) CHES 2008. LNCS, vol. 5154, pp. 411–425. Springer, Heidelberg (2008). https://doi.org/10.1007/978-3-540-85053-3_26
Standaert, F.-X., Malkin, T.G., Yung, M.: A unified framework for the analysis of side-channel key recovery attacks. In: Joux, A. (ed.) EUROCRYPT 2009. LNCS, vol. 5479, pp. 443–461. Springer, Heidelberg (2009). https://doi.org/10.1007/978-3-642-01001-9_26
van Woudenberg, J.G.J., Witteman, M.F., Bakker, B.: Improving differential power analysis by elastic alignment. In: Kiayias, A. (ed.) CT-RSA 2011. LNCS, vol. 6558, pp. 104–119. Springer, Heidelberg (2011). https://doi.org/10.1007/978-3-642-19074-2_8. http://dl.acm.org/citation.cfm?id=1964621.1964632
Zeiler, M.D., Fergus, R.: Visualizing and understanding convolutional networks. arXiv:1311.2901 [cs], 12 November 2013
Zhou, B., Khosla, A., Lapedriza, A., Oliva, A., Torralba, A.: Learning deep features for discriminative localization. In: 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), pp. 2921–2929, June 2016. https://doi.org/10.1109/CVPR.2016.319
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Appendices
A Profiling Attacks
As the model is aiming at approximating the conditional pdf, a Maximum Likelihood score can be used for the guessing:

Based on these scores, the key hypotheses are ranked in a decreasing order. Finally, the attacker chooses the key that is ranked first (resp. the set of first o ranked keys). More generally, the rank \(g_{S_{a}}(k^{\star })\) of the correct key hypothesis \(k^{\star }\) is defined as:

Remark 2
In practice, to compute \(\mathrm {GE}(N_a)\), sampling many attack sets may be very prohibitive in an evaluation context, especially if we need to reproduce the estimations for many values of \(N_a\); one solution to circumvent this problem is, given a validation set \(S_{v}\) of \(N_v\) traces, to sample some attack sets by permuting the order of the traces into the validation set.  can then be computed with a cumulative sum to get a score for each \(N_a\in [|1, N_v|]\), and so is \(g_{S_{a}}(k^{\star })\). While this trick gives good estimations for \(N_a\ll N_v\), one has to keep in mind that the estimates become biased when \(N_a\rightarrow N_v\). This problem also happens in Machine Learning when one lacks data to validate a model. A technique called Cross-Validation [34] enables to circumvent this problem by splitting the dataset into q parts called folds. The profiling is done on \(q-1\) folds and the model is evaluated with the remaining fold. By repeating this step q times, the measured results can be averaged so that they are less biased.
can then be computed with a cumulative sum to get a score for each \(N_a\in [|1, N_v|]\), and so is \(g_{S_{a}}(k^{\star })\). While this trick gives good estimations for \(N_a\ll N_v\), one has to keep in mind that the estimates become biased when \(N_a\rightarrow N_v\). This problem also happens in Machine Learning when one lacks data to validate a model. A technique called Cross-Validation [34] enables to circumvent this problem by splitting the dataset into q parts called folds. The profiling is done on \(q-1\) folds and the model is evaluated with the remaining fold. By repeating this step q times, the measured results can be averaged so that they are less biased.
B Study of an Optimal Model
Informally, Assumption 1 tells that the leaking information is non-uniformly distributed over the trace \(\mathbf X \), i.e. only a few coordinates contain clues about the attacked sensitive variable. Assumption 1 has been made in many studies such as [4]. Depending on the countermeasures implemented into the attacked device, the nature of \(\mathcal {I}_{Z}\) may be precised. Without any countermeasure, and supposing that the target sensitive variable only leaks once, Assumption 1 states that \(\mathcal {I}_{Z}\) is only a set of contiguous and constant coordinates, regardless the input traces.
Adding masking will split \(\mathcal {I}_{Z}\) into several contiguous and fixed sets whose number is equal to the number of shares in the masking scheme (or at least equal to the number of shares if we relax the hypothesis of one leakage per share). For example if M (resp. \(Z \oplus M\)) denotes the mask (resp. masked data) variable leaking at coordinate \(t_1\) (resp. \(t_2\)), then M and X[t] with \(t \ne t_1\) are independent (resp. Z and X[t] with \(t \ne t_2\) are independent). The conditional probability \(\mathrm {Pr}[Z= z\vert \mathbf X = \mathbf x ]\) satisfies:

Adding de-synchronization should force \(\mathcal {I}_{Z}\) to be non-constant between each trace.
Likewise, Assumption 2 is realistic because it is a direct corollary of a Gaussian leakage model for the traces [7, 9]. Such an hypothesis is common for Side Channel Analysis [7]. It implies that \(\mathbf x \mapsto \mathrm {Pr}[\mathbf X = \mathbf x | Z= z]\) is differentiable and:
where \(\mu _{z}\) and \(\varSigma _{z}^{-1}\) respectively denote the mean vector and the covariance matrix of the normal probability distribution related to the target sensitive value hypothesis \(z\). Then, from Bayes’ theorem, (11) and the basic rules for derivatives computation, it gives an analytic expression of \(\nabla _\mathbf{x }F^*(\mathbf x )\), thereby proving that \(F^*\) is differentiable with respect to the input trace.
C Neural Networks
Neural Networks (NN) are nowadays the privileged tool to address the classification problem in Machine Learning [19]. They aim at constructing a function \(F:\mathcal {X}\rightarrow \mathcal {P}(\mathcal {Z})\) that takes data \(\mathbf x \) and outputs vectors \(\mathbf y \) of scores. The classification of \(\mathbf x \) is done afterwards by choosing the label  , but the output can be also directly used for soft decision contexts, which corresponds more to Side Channel Analysis as the NN outputs on attack traces will be used to compute the score vector in (8). In general \(F\) is obtained by combining several simpler functions, called layers. An NN has an input layer (the identity over the input datum \(\mathbf x \), an output layer (the last function, whose output is the scores vector \(\mathbf y \) and all other layers are called hidden layers. The nature (the number and the dimension) of the layers is called the architecture of the NN. All the parameters that define an architecture, together with some other parameters that govern the training phase, have to be carefully set by the attacker, and are called hyper-parameters. The so-called neurons, that give the name to the NNs, are the computational units of the network and essentially process a scalar product between the coordinate of its input and a vector of trainable weights (or simply weights) that have to be trained. We denote \(\theta \) the vector containing all the trainable weights. Therefore, for a fixed architecture, an NN is completely parameterized by \(\theta \). Convolutional Neural Networks (CNN) implement other operations, but can be rewritten as regular NN with specific constraints on the weights [18]. Each layer processes some neurons and the outputs of the neuron evaluations will form new input vectors for the subsequent layer.
, but the output can be also directly used for soft decision contexts, which corresponds more to Side Channel Analysis as the NN outputs on attack traces will be used to compute the score vector in (8). In general \(F\) is obtained by combining several simpler functions, called layers. An NN has an input layer (the identity over the input datum \(\mathbf x \), an output layer (the last function, whose output is the scores vector \(\mathbf y \) and all other layers are called hidden layers. The nature (the number and the dimension) of the layers is called the architecture of the NN. All the parameters that define an architecture, together with some other parameters that govern the training phase, have to be carefully set by the attacker, and are called hyper-parameters. The so-called neurons, that give the name to the NNs, are the computational units of the network and essentially process a scalar product between the coordinate of its input and a vector of trainable weights (or simply weights) that have to be trained. We denote \(\theta \) the vector containing all the trainable weights. Therefore, for a fixed architecture, an NN is completely parameterized by \(\theta \). Convolutional Neural Networks (CNN) implement other operations, but can be rewritten as regular NN with specific constraints on the weights [18]. Each layer processes some neurons and the outputs of the neuron evaluations will form new input vectors for the subsequent layer.
The ability of a Neural Network to approximate well a target probabilistic function \(F^*\) by minimizing a loss function on sampled training data with Stochastic Gradient Descent is still an open question. This is what we call the mystery of Deep Learning. It theoretically requires a huge quantity of training data so that the solution obtained by loss minimization generalizes well, though it empirically works with much less data. Likewise, finding the minimum with Stochastic Gradient Descent is theoretically not proved, but has been empirically shown to be a good heuristic. For more information, see [14]. Indeed, though it raises several theoretical issues, it has been empirically shown to be efficient, especially in SCA with CNN based attacks [5, 30].
D Experimental Results
1.1 D.1 The Jacobian Matrix
In this appendix, we present the Jacobian matrix visualization, equivalent to the GV. It shows, in addition, that some target values seem more sensitive, especially those whose Hamming weight is shared by only few other values (so it gives clues about how the traces leak sensitive information). Figure 8 (top) shows such a matrix in application context (Exp. 1) as described in Sect. 6, while Fig. 8 (bottom) shows the Jacobian matrix corresponding to the application context (Exp. 2). Fig. 9 shows the SNR computed on de-synchronized traces.
Rights and permissions
Copyright information
© 2019 Springer Nature Switzerland AG
About this paper
Cite this paper
Masure, L., Dumas, C., Prouff, E. (2019). Gradient Visualization for General Characterization in Profiling Attacks. In: Polian, I., Stöttinger, M. (eds) Constructive Side-Channel Analysis and Secure Design. COSADE 2019. Lecture Notes in Computer Science(), vol 11421. Springer, Cham. https://doi.org/10.1007/978-3-030-16350-1_9
Download citation
DOI: https://doi.org/10.1007/978-3-030-16350-1_9
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-16349-5
Online ISBN: 978-3-030-16350-1
eBook Packages: Computer ScienceComputer Science (R0)





 . It assigns a score to each key hypothesis, for each trace.
. It assigns a score to each key hypothesis, for each trace.

 , and the labels are recomputed from the
, and the labels are recomputed from the
 field of the
field of the
 structure.
structure.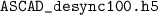 .
. and the labels are directly imported from the field
and the labels are directly imported from the field
 in the
in the
 structure.
structure.





