Keywords

1 Introduction

To maintain safety in malicious environment, implementing cryptographic technologies such as secure multi-party computations and zero-knowledge proofs are indispensable. While these technologies must be useful, usefulness alone is not always sufficient for technology diffusion, as Hanaoka pointed out [13]. In other words, we need to convince not only researchers but also everyone from engineers to non-experts of the importance of such techniques.

To understand the concept of zero-knowledge proof, games and puzzles can serve as powerful models of computation. Indeed, in game-theoretic terms, the P vs NP asks whether an optimal puzzle player can be simulated efficiently by a Turing machine [15]. The NP class is that of problems for which a given solution correctness is easy to verify. There, a zero-knowledge proof is such a verification procedure, but which prevents the verifier from gaining any knowledge about the solution other than its correctness. For instance, there exist generic cryptographic zero-knowledge proofs for all problems in NP [10], via a reduction to an NP-Complete problem with a known zero-knowledge proof.

More precisely, a Zero Knowledge Proof of knowledge (ZKP) is a secure two-party protocol that allows a prover P to convince a verifier V that he knows a solution s to the instance \(\mathcal {I}\) of a problem \(\mathcal {P}\), without revealing any information about s. In fact, when both randomization and interaction are allowed, the proofs that can be verified in polynomial time are exactly those proofs that can be generated within polynomial space [36]. More than the mere existence of a cryptographic interactive protocol, it is interesting to obtain direct (rather than via a reduction) and physical (rather than computer-aided) proofs in order to improve on their understandability. Further, sometimes, an interplay of physical and cryptographic protocols can improve efficiency or practicality due to the reduced cryptographic overhead [33]. With this in mind, finding direct physical proofs for puzzles actually augments the number of constraints that can be very efficiently proven in zero knowledge. For instance, we know how to guarantee the presence of all numbers in some set without revealing their order [12], or how to guarantee that two numbers are distinct without revealing their respective values [2]. In this paper, via providing a complete physical zero-knowledge proof for the Nikoli puzzle Makaro, we will show in particular that it is possible to physically prove that a number is the largest in a list, without revealing any value in the list.

Formally, for a solution s to any instance \(\mathcal {I}\) of a problem P, a convincing interactive zero-knowledge protocol between P and V must then satisfy the three following propertiesFootnote 1:

Completeness: If P knows s, then he is able to convince V.

ExtractabilityFootnote 2: If P does not know s, then he is not able to convince V except with some small probability. More precisely, we want a negligible probability, i.e., the probability should be a function f of a security parameter \(\lambda \) (for example the number of repetitions of the protocol) such that f is negligible, that is for every polynomial Q, there exists \(n_0 > 0\) such that \(\forall ~ x > n_0,f(x)<1/Q(x)\).

Zero-Knowledge: V learns nothing about s except \(\mathcal {I}\), i.e. there exists a probabilistic polynomial time algorithm \(\texttt {Sim}(\mathcal {I})\) (called the simulator) such that outputs of the real protocol and outputs of \(\texttt {Sim}(\mathcal {I})\) follow the same probability distribution.

As already mentioned, there exist two kinds of ZKP: interactive and non-interactive. In an interactive ZKP the prover can exchange messages with verifier in order to convince him, while in the non-interactive case the prover can just create the proof in order to convince the verifier.

ZKPs are usually executed by computers. They are often used in electronic voting to prove that some parties correctly mix some ballots without cheating, or in multi-party computation [4, 6, 34].

In this paper, we consider physical ZKPs, such proofs only rely on physical objects such as cards or envelopes and are executed by humans.

Contributions: In this paper we construct a secure physical ZKP for Makaro. This provides in particular a physical zero-knowledge proof of knowledge of the largest element in a list. Our construction uses only \(2k-1 + n+(k-1)(n+4)\) cards where n is the number of empty cells and k is the maximum room size of the Makaro’s grid. The salient feature of our protocol is to use efficient zero knowledge shuffle and shift operations together with a positional encoding in order to obtain an efficient implementation of zero-knowledge proof. Our construction physically proves that a number is the largest in a list, without revealing any value in the list.

As mentioned above, our protocol uses a deck of physical cards, and such card-based cryptography has attracted many people from researchers to non-experts, and many card-based protocols have been published in top-tier conferences in cryptography such as Crypto, Eurocrypt, and Asiacrypt [5, 8, 20, 22, 26]. Thus, card-based cryptography has contributed to increasing the number of people who have strong interest in cryptography and information security. We hope that the protocol in this paper also will motivate potential users to understand and use zero-knowledge proof to attain safety in malicious environment.

Related Work: Secure computation without computers have been widely studied and constructed based on various objects: a deck of cards [8] (including polarizing plates [37], polygon cards [38], and the standard deck of playing cards [23]), a PEZ dispenser [1], tamper-evident seals [28], a dial lock [24], and a 15 puzzle [25], Among them, secure computations with cards, referred to as card-based protocols, especially has been studied recently, due to its simplicity and applicability. Indeed, card-based protocols can be used to compute many boolean functions as shown in [5], later improved in terms of efficiency by [22, 27, 30, 39], or to perform specific computations [14, 17, 29, 32].

Sudoku, introduced under this name in 1986 by the Japanese puzzle company Nikoli, and similar games such as Akari, Takuzu, Ken-Ken or Makaro have gained immense popularity in recent years. Many of them have been proved to be NP-complete [7, 19, 21], and, in 2007, Gradwohl, Naor, Pinkas, and Rothblum proposed the first physical zero-knowledge proof protocols for Sudoku [12]. A novel protocol for Sudoku using fewer cards and with no soundness error was then proposed [35]. Physical protocols for other games, such as Hanjie, Akari, Kakuro, KenKen and Takuzu have then extended the physically verifiable set of functions [2, 3].

Outline: We first present the rules of the game, Makaro, in Sect. 2. We construct our zero-knowledge proof in Sect. 3. We start with some notations in Subsect. 3.1, then we describe the shuffling and shifting subroutines in Subsect. 3.2 as well as our construction in Subsect. 3.3. Finally we prove the security of our protocol in Sect. 4. We also propose some optimizations and conclude in the last section.

2 Rules of Makaro

Makaro is a pencil puzzle published in the famous puzzle magazine Nikoli. The puzzle instance is a rectangular grid of cells. All cells are colored either white or black. All white cells are divided into rooms enclosed by bold lines. Some white cells already contain numbers while most white cells are empty. The former is called a (white) filled cell and the latter is called a (white) empty cell. Some black cells contain an arrow and they are called (black) arrow cells. The goal of the puzzle is to fill in all empty white cells with numbers according to the following rules [31]:

  1. 1.

    Room condition: Each room contains all the numbers from 1 up to the number of cells in the room.

  2. 2.

    Neighbor condition: A number can not be next (adjacent) to the same number in another room.

  3. 3.

    Arrow condition: Every black arrow cell must point at the largest number among the numbers in the adjacent cells of the black cell (possibly the fours cells: right, left, above, and bottom).

In Fig. 1, we give a simple example of a Makaro game, where all black cells are arrow cells and all white cells are empty cells except for one filled cell with three. It is easy to verify that the three constraints are satisfied in the solution on the right part of the figure. We remark that in a solution all white cells are filled with numbers between 1 and k, where k is the maximum size of all the rooms of the grid.

Solving Makaro was shown to be NP-complete via a reduction from 3-SAT in [19].

Fig. 1.
figure 1

Example of a Makaro grid and its solution.

Full size image

3 Zero-Knowledge Proof for Makaro

In this section, we construct our protocol of zero-knowledge proof for Makaro. We first introduce some notations in order to properly give our encoding of the values of a Makaro’s solution using some cards. We also describe a few tricks that we use in our construction in order to obtain the extractability and the zero-knowledgeness.

3.1 Notations

Card. We use the following cards:

We call binary cards and the others number cards. We note that binary cards are not necessary when are regarded as binary cards. However, we believe that the use of binary cards makes it easier to understand our protocol. In our construction, binary cards are used to encode the value of a cell, while number cards are used for rearrangement.

All the back sides of the cards are assumed to be indistinguishable. Our protocol also works when all back sides of binary cards are indistinguishable and all back sides of number cards are indistinguishable, but these back sides of the former and the latter are distinguishable. For ease of explanation, we assume that all of them are indistinguishable and denote them by .

Encoding. Let k be an integer. For a number \(x \in \{1, 2, \cdots , k\}\), we use the following encoding:

The position of the corresponds to the value of x. Note that in our actual construction, encodings are placed face-down in order not to reveal encoded values.

Matrix. In our construction, we often place a sequence of cards as a matrix. The following is an example of a \(4 \times 6\) matrix (of face-down cards).

It contains four rows and six columns. We refer to the leftmost column as the 1st column and to the topmost row as the 1st row.

Pile-Shifting Shuffle. Given an \({\ell \times k}\) matrix M, a Pile-shifting shuffle, which is first used in [38], generates a new “randomly shifted” \({\ell \times k}\) matrix \(M'\): a random number r is uniformly chosen in \(\{0,1,\cdots , k-1\}\); and then, each column of M is cyclically shifted by r. Here, the shifting number r is hidden from all parties. This operation is performed on cards face-down. For example if we consider the following \(4 \times 6\) matrix with a shift of \(r=2\).

We obtain the following matrix, where columns have been shifted by to position on the right side.

In order to implement a pile-shifting shuffle, we first put each columns of cards in an envelope; and then, we cyclically shuffle them by applying a Hindu cut to the sequence of envelopes, which is widely used in games of playing cards (see, e.g., [40] for the implementation of random shifting by the Hindu cut).

Pile-Scramble Shuffle. Given an \(\ell \times k\) matrix M, a Pile-scramble shuffle, which is first used in [17], generates a new “randomly scrambled” \(\ell \times k\) matrix \(M'\): a random permutation \(\pi \) is uniformly chosen in \( S_k\), the set of all possible permutations of length k; and then, the i-th column of M is moved to the \(\pi (i)\)-th column of \(M'\). Here, the random permutation \(\pi \) is hidden from all parties. This operation is performed on cards face-down. For example if we consider the following \(4 \times 6\) matrix with the following permutation \(\pi =(13652)\).

We obtain the following matrix, where columns have been mixed according to \(\pi \).

In order to implement a pile-scramble shuffle, similar to the pile-shifting shuffle, we first put each columns of cards in an envelope; and then, we mix them completely randomly.

Miscellaneous Definitions. We define two sequences of cards as follows:

Moreover, we call the former the identity commitment of degree k. Again, we note that they are placed face-down in our actual construction. We define “\(\circ \)” as a concatenation of sequences. For example, \(\mathsf{E}_3(2)\circ \beta _3\) is a concatenation of \(\mathsf{E}_3(2)\) and \(\beta _3\) as shown in the following:

This results in \(\mathsf{E}_6(2)\). In general, it holds that \(\mathsf{E}_k(x) \circ \beta _{\ell } = \mathsf{E}_{k+\ell }(x)\).

3.2 Rearrangement Protocol

In this section, we present the Rearrangement Protocol which is invoked by our main construction as a subroutine. This protocol is implicitly used in some previous works of card-based protocols with permutations (e.g., Ibaraki et al. [16], Hashimoto et al. [14], and Sasaki et al. [35]).

The input of our Rearrangement Protocol is an \(\ell \times k\) matrix whose first row consists of number cards in an arbitrary order. It outputs an \(\ell \times k\) matrix such that the i-th column of the resultant matrix is the column of the input matrix containing the number card (without revealing the original order). It proceeds as follows:

  1. 1.

    Apply a pile-scramble shuffle to the matrix .

  2. 2.

    Turn over the first row. Suppose that the opened cards are such that \(\{v_1, v_2, \cdots , v_k\} = \{1, \cdots ,k\}\).

  3. 3.

    Sort the columns of the matrix so that the \(v_i\)-th column of the new matrix is the i-th column of the old matrix.

3.3 Our Construction

In this section, we present our construction of zero-knowledge proof for Makaro. Suppose that a puzzled instance M has n empty cells and the maximum room-size is k. The protocol is played with two players, a verifier V and a prover P, where only P has a solution of M. It requires \(2k-1\) numbered cards (from 1 up to \(2k-1\)) and \(n+(k-1)(n+4)\) binary cards (n cards of type and \((k-1)(n+4)\) cards of type ). Our protocol proceeds as follows.

Setup. In the setup phase, the prover P places an encoding of the number x on each empty cell, where x is the value of the cell according to the solution. Note that they are placed face-down in order to hide the solution. Similarly, the prover P and the verifier V (cooperatively) place k face-down cards on each filled cell according to the value given by the Makaro grid, in the same way.

Verification. The verification proceeds as follows:

  1. 1.

    The prover P convinces the verifier V of the validity of the room condition by performing the following for each room: Let \(k'\) be the room-size of the room and let \(\alpha _1, \cdots , \alpha _{k'}\) be the sequence of cards on each cell in the room. The prover P and the verifier V interact as follows:

    1. (a)

      Arrange a \(k\times k'\) matrix A such that the i-th column is \(\alpha _i\).

      $$\begin{aligned} A = \begin{bmatrix} \alpha _1^{\mathrm {T}}&\alpha _2^{\mathrm {T}}&\cdots&\alpha _{k'}^{\mathrm {T}} \end{bmatrix} \end{aligned}$$
    2. (b)

      Append \(\mathbf{e}_{k'}\) to the topmost row of A. The following is an example when \(k = 4\), \(k' = 3\), \(\alpha _1 = \mathsf{E}_4(2)\), \(\alpha _2 = \mathsf{E}_4(3)\), and \(\alpha _3 = \mathsf{E}_4(1)\):

      Note that all cards are face-down in an actual execution.

    3. (c)

      Apply a pile-scramble shuffle to the matrix.

    4. (d)

      Turn over all cards except for the topmost row. If the columns do not contain the encodings \(\mathsf{E}_k(1), \mathsf{E}_k(2), \cdots , \mathsf{E}_k(k')\), then the verifier outputs 0 and the protocol terminates.

    5. (e)

      Turn over all face-up cards so that all cards are face-down; then, apply the Rearrangement Protocol explained in Sect. 3.2; finally, put back \(\alpha _1, \cdots , \alpha _{k'}\) to their original cells.

  2. 2.

    The prover P convinces the verifier V of the validity of the neighbor condition by performing the following verification for each two adjacent cells that are in different rooms: Let \(\alpha _1\) and \(\alpha _2\) be two sequences on these two adjacent cells. The prover P and the verifier V interact as follows:

    1. (a)

      Arrange the following \(3\times k\) matrix:

      $$\begin{aligned} \begin{bmatrix} \mathbf{e}_k\\\ \alpha _1 \\ \alpha _2 \end{bmatrix} \end{aligned}$$

      The following is an example when \(k=4\) and \(\alpha _1 = \mathsf{E}_4(2)\) and \(\alpha _2 = \mathsf{E}_4(1)\).

      Note that all cards are face-down in an actual execution.

    2. (b)

      Apply a pile-scramble shuffle to the matrix.

    3. (c)

      Turn over the second and third rows. If two s are in distinct columns, it proceeds to Step 2-(d). Otherwise, the verifier outputs 0 and the protocol terminates. The following is an example when the turning result is valid.

    4. (d)

      Turn over all face-up cards so that all cards are face-down; then, apply the Rearrangement Protocol; finally, put back \(\alpha _1\) and \(\alpha _2\) to their original cells.

  3. 3.

    The prover P convinces the verifier V of the validity of the arrow condition by performing the following verification for each black arrow cell: Suppose that the black cell has four adjacent white cells and that the arrow of the cell points to the above cell. We note that three-neighbors case and two-neighbors case can be performed in the same way. Let \(\alpha _\mathsf{a}, \alpha _\mathsf{b}, \alpha _\mathsf{r}\), and \(\alpha _\mathsf{l}\) be sequences of k cards placed respectively on the above, bottom, right, and left cells of the black cell. The prover P and the verifier V interact as follows:

    1. (a)

      Arrange the following \(5\times (2k-1)\) matrix:

      $$\begin{aligned} \begin{bmatrix} \mathbf{e}_{2k-1}\\\ \alpha _\mathsf{a}\circ \beta _{k-1} \\ \alpha _\mathsf{b}\circ \beta _{k-1} \\ \alpha _\mathsf{r}\circ \beta _{k-1} \\ \alpha _\mathsf{l}\circ \beta _{k-1} \end{bmatrix} \end{aligned}$$

      The following is an example when \(k=4\) and \(\alpha _\mathsf{a} = \mathsf{E}_4(4), \alpha _\mathsf{b} = \mathsf{E}_4(2), \alpha _\mathsf{r} = \mathsf{E}_4(3)\), and \(\alpha _\mathsf{l} = \mathsf{E}_4(2)\).

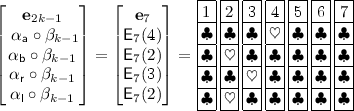
      Note that all cards are face-down in an actual execution.

    2. (b)

      Apply a pile-shifting shuffle to the matrix.

    3. (c)

      Turn over the second row. Let \(v \in \{1,\cdots ,2k-1\}\) be the position of . The following is an example when \(v = 3\) and other parameters are the same as in the previous example.

    4. (d)

      Turn over \({k-1}\) columns, \({v+1, v+2, \cdots , v+k-1}\) columns in a cyclic sense, of the third, fourth, and fifth rows of the matrix. If they are not \(3(k-1)\) \(\clubsuit \)s, the verifier outputs 0 and the protocol terminates. The following is an example when the parameters are the same as in the previous example. In this example, three columns, \({v+1, v+2}\), and \({v+3}\) columns, are turned over.

    5. (e)

      Turn over all face-up cards so that all cards are face-down; then, apply the Rearrangement Protocol; finally, put back \(\alpha _\mathsf{a}, \alpha _\mathsf{b}, \alpha _\mathsf{r}\), and \(\alpha _\mathsf{l}\) to their original cells (unless these cells are not used in the next verification of the Arrow condition).

  4. 4.

    The verifier accepts by outputting 1.

4 Security Proofs for Our Construction

In this section, we prove the completeness, the extractability, and the zero-knowledge property of our construction.

Lemma 1

(Completeness). If the prover P has a solution for the Makaro puzzle, then P can always convince the verifier V (i.e., V outputs 1).

Proof

We show that for prover P with a solution, the verifier never outputs 0.

  • First, let us consider Step 1. Due to the room condition, for each room of room-size \(k'\), all cells in the room have distinct numbers from 1 up to \(k'\). Thus, the \(k\times k'\) matrix A in Step 1-(a) contains all encodings \(\mathsf{E}_k(1), \cdots , \mathsf{E}_k(k')\). Therefore, the verifier never outputs 0 after the turning over in Step 1-(d).

  • Let us move to Step 2. Due to the Neighbor condition, for each pair of cells between different rooms, they have different numbers. Thus, the turning over in Step 2-(c) brings one \((\heartsuit ,\clubsuit )\) column, one \((\clubsuit ,\heartsuit )\) column, and \(k-2\) \((\clubsuit ,\clubsuit )\) columns. Therefore, the verifier never outputs 0 in Step 2-(c).

  • Let us consider Step 3. Due to the Arrow condition, for each black arrow cell, the arrow points to the largest number in adjacent cells. Let \(x_\mathsf{a}, x_\mathsf{b}, x_\mathsf{r}, x_\mathsf{l} \in \{1, 2, \cdots , k\}\) be numbers in adjacent cells and suppose that \(x_\mathsf{a}\) is the largest number pointed by the arrow. Then, the position of of \(\mathsf{E}_k(x_\mathsf{a})\) is also the largest number among other encodings \(\mathsf{E}_k(x_\mathsf{b}), \mathsf{E}_k(x_\mathsf{r})\), and \(\mathsf{E}_k(x_\mathsf{l})\). Therefore, the turning over in Step 3-(d) brings \(3(k-1)\) \(\clubsuit \) cards which never causes the verifier to output 0.

Therefore, the protocol always proceeds to Step 4 and the verifier outputs 1.   \(\square \)

Lemma 2

(Extractability). If the prover does not know a solution for the Makaro puzzle, then the verifier V always rejects (i.e., V outputs 0) regardless of the prover P’s behavior.

Proof

If some of encodings are invalid, i.e., do not form the encoding format, then this fact is always exposed in Step 1-(d). Thus, we can assume that all encodings are valid. Because the verifier does not know a solution, at least one condition among three conditions must be violated. The following three cases occur:

  • Suppose that room condition is violated for some room. In this case, the turning over in Step 1-(d) does not bring \(\mathsf{E}_k(1), \cdots , \mathsf{E}_k(k')\), which causes the verifier to output 0.

  • Suppose that Neighbor condition is violated for some pair of cells. In this case, the turning over in Step 2-(c) brings two \((\heartsuit , \heartsuit )\) in one column, which causes the verifier to output 0.

  • Suppose that Arrow condition is violated for some black cell with an arrow. Let \(\alpha _\mathsf{a}, \alpha _\mathsf{b}, \alpha _\mathsf{r}\), and \(\alpha _\mathsf{l}\) be encodings on the adjacent cells of such a black cell such that \(\alpha _\mathsf{a} = \mathsf{E}_k(x_\mathsf{a}), \alpha _\mathsf{b} = \mathsf{E}_k(x_\mathsf{b}), \alpha _\mathsf{r} = \mathsf{E}_k(x_\mathsf{r})\), and \(\alpha _\mathsf{l} = \mathsf{E}_k(x_\mathsf{l})\) for some \(x_\mathsf{a}, x_\mathsf{b}, x_\mathsf{r}, x_\mathsf{l} \in \{1, 2, \cdots , k\}\). Due to the violation of Arrow condition, one of \(x_\mathsf{b}, x_\mathsf{r}\), and \(x_\mathsf{l}\) is larger than \(x_\mathsf{a}\) while the arrow points to the above cell. In this case, the turning over in Step 3-(d) brings at least one , which causes the verifier to output 0.

In any case, the verifier always outputs 0.   \(\square \)

Lemma 3

(Zero-knowledge). During an execution of our protocol, the verifier V learns nothing about P’s solution.

Proof

In order to prove this, it is sufficient to show that all distributions of opening values are simulated without knowing the prover’s solution.

  • In Step 1, the “turning over” appears only in Step 1-(d) and 1-(e). The opening in Step 1-(d) brings a set of encodings \(\mathsf{E}_k(1), \cdots , \mathsf{E}_k(k')\), where \(k'\) is the room-size. Their order is uniformly distributed among \(S_{k'}\) due to the pile-scramble shuffle. Thus, it can be simulated without knowing the solution. The opening in Step 1-(e), specifically the Rearrangement Protocol, brings number cards from 1 up to \(k'\). Their order is uniformly distributed among \(S_{k'}\) due to the pile-scramble shuffle. Thus, it can be simulated without knowing the solution.

  • In Step 2, there are two steps with a “turning over”: Steps 2-(c) and 2-(d). The opening in Step 2-(c) brings one \((\heartsuit ,\clubsuit )\) column, one \((\clubsuit ,\heartsuit )\) column, and \(k-2\) \((\clubsuit ,\clubsuit )\) columns. The position of the former two columns are uniformly distributed due to the pile-scramble shuffle. Thus, it can be simulated without knowing the solution. The opening in Step 2-(d), specifically the Rearrangement Protocol, brings number cards from 1 up to k. Their order is uniformly distributed among \(S_k\) due to the pile-scramble shuffle. Thus, it can be simulated without knowing the solution.

  • In Step 3, there are three steps containing a “turning over”: Steps 3-(c), 3-(d), and 3-(e). The opening in Step 3-(c) brings one and \(k-1\) cards. The position of is uniformly distributed among \(\{1, 2, \cdots , 2k-1\}\) due to the pile-shifting shuffle. Thus, it can be simulated without knowing the solution. The opening in Step 3-(d) brings \(3(k-1)\) cards. Thus, it can be trivially simulated without knowing the solution. The opening in Step 3-(e), specifically the Rearrangement Protocol, brings number cards from 1 up to \(2k-1\). Their order is uniformly distributed among \(S_{2k-1}\) due to the pile-scramble shuffle. Thus, it can be simulated without knowing the solution.

Therefore, the verifier V learns nothing about the solution.   \(\square \)

5 Conclusion

In this paper we construct the first physical zero-knowledge proof for Makaro. Our construction uses a special encoding of the values of a Makaro solution. This allows us to design a physical zero-knowledge proof that uses a reasonable number of cards and hence, our proposed protocol is efficient. This number can even be further reduced via the following two optimizations:

Optimization 1. For each room, use encodings \(\mathsf{E}_{k'}(x)\) for the room-size \(k'\) instead of \(\mathsf{E}_k(x)\), where k is the maximum room-size. When encodings in different rooms appear in Steps 1 and 2, append additional cards. This idea reduces the number of cards.

Optimization 2. Do not place cards in the initially (white) filled cells although other cards on empty cells are still placed. Instead, make an encoding of filled cells only when it is needed. Indeed those numbers are part of the input problem and are thus known to the verifier, so no secrecy is required there. This idea also reduces the overall number of cards.

We finally note that our technique especially for the Arrow condition can also be reused for other interesting problems including zero-knowledge proofs for other games or real-world problems related to auctions, stock markets, and so on. We leave it as an open problem to find such interesting applications.