Physical Zero-Knowledge Proofs for Five Cells

Abstract

Five Cells is a logic puzzle consisting of a rectangular grid, with some cells containing a number. The player has to partition the grid into pentominoes such that the number in each cell must be equal to the number of edges of that cell that are borders of pentominoes. In this paper, we propose two physical zero-knowledge proof protocols for Five Cells using a deck of playing cards, which allow a prover to physically show that he/she knows a solution of the puzzle without revealing it. In the optimization of our first protocol, we also develop a technique to reduce the number of required cards from quadratic to linear in the number of cells, which can be used in other zero-knowledge proof protocols related to graph coloring as well.

1 Introduction

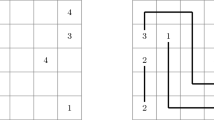
Five Cells is a logic puzzle developed by Nikoli, a Japanese company that published many popular puzzles including Sudoku, Kakuro, and Numberlink. A Five Cells puzzle consists of a rectangular grid, with some cells containing a number. The objective of the puzzle is to partition the grid into pentominoes called blocks. The number in each cell must be equal to the number of edges of that cell that are borders of pentominoes (including the outer boundary of the grid) [14]. See Fig. 1.

Fig. 1.

An example of a Five Cells puzzle (left) and its solution (right)

Determining whether a given Five Cells puzzle has a solution has been proved to be NP-complete [9].

1.1 Zero-Knowledge Proof

We are interested in constructing a zero-knowledge proof (ZKP) for Five Cells, which allows a prover P to convince a verifier V that P knows a solution of the puzzle without revealing any information about it. Formally, a ZKP is an interactive protocol between P and V, where both of them are given a computational problem x, but only P knows its solution w. A ZKP has to satisfy the following three properties.

• 1. Completeness: If P knows w, then V accepts with high probability. (Here, we consider the perfect completeness property where V always accepts.)

• 2. Soundness: If P does not know w, then V rejects with high probability. (Here, we consider the perfect soundness property where V always rejects.)

• 3. Zero-knowledge: V obtains no information about w, i.e. there exists a probabilistic polynomial time algorithm S (called a simulator) that does not know w but has an access to V, and the outputs of S follow the same probability distribution as the ones of the real protocol.

The concept of a ZKP was introduced by Goldwasser et al. [7] in 1989. In the past decade, many researchers have been focusing on constructing physical ZKPs using portable objects such as a deck of cards and envelopes. These protocols have benefits that they require only objects easily found in everyday life and do not require computers. They also allow external observers to verify that the prover truthfully executes the protocol (which is a challenging task for digital protocols). Moreover, these protocols have didactic values and can be used to teach the concept of a ZKP to non-experts.

1.2 Related Work

Physical card-based ZKP protocols for many logic puzzles have been developed in the recent years, including Sudoku [8, 23, 29], Nonogram [4, 20], Akari [1], Takuzu [1, 12], Kakuro [1, 13], KenKen [1], Makaro [2, 28], Norinori [5], Slitherlink [11], Juosan [12], Numberlink [25], Suguru [15], Ripple Effect [26], Nurikabe [16], Hitori [16], Bridges [27], Masyu [11], Heyawake [16], Shikaku [24], Usowan [18], Nurimisaki [17], ABC End View [6, 22], Ball sort puzzle [21], and Goishi Hiroi [22].

1.3 Our Contribution

In this paper, we propose two physical ZKP protocols for Five Cells with perfect completeness and soundness using a deck of cards.

Most of the paper will cover our first protocol, which combines many existing protocols to construct each block on the grid in a straightforward way. The most important part is the optimization of the protocol. We develop a color shifting protocol, which enables P to gradually color a graph while maintaining that no two adjacent vertices have the same color without revealing any information about the coloring. This technique reduces the number of required cards in the protocol from quadratic to linear in the number of cells, and it can also be used in other ZKP protocols related to graph coloring.

In Appendix A, we describe our second protocol, which takes a completely different approach from the first one. It uses a newly developed printing protocol to directly put each block on the grid. The number of required cards in the second protocol is also linear in the number of cells, but is asymptotically lower than that of the first one.

2 Verifying Connected Area

First, P needs to convince V that each block is a pentomino, i.e. consists of exactly five cells connected to each other horizontally or vertically. The following tools and subprotocols are necessary for this phase.

2.1 Cards

Each card used in our protocol has a non-negative integer on the front side. All cards have indistinguishable back sides denoted by .

For $1 \le y \le q$, define $E_q(y)$ to be a sequence of q cards, all of them being except the y-th leftmost card being a , e.g. $E_4(2)$ is . Also, define $E_q(0)$ to be a sequence of q , e.g. $E_4(0)$ is . We may sometimes stack the cards in $E_q(y)$ into a single stack.

2.2 Pile-Shifting Shuffle

A pile-shifting shuffle [30] shifts the columns of a matrix of cards by a uniformly random cyclic shift (see Fig. 2). It can be implemented in real world by putting the cards in each column into an envelope and then applying several Hindu cuts (taking some envelopes from the bottom and putting them on the top) to the pile of envelopes [32].

Note that each card in the matrix may be replaced by a stack of cards, as long as each stack in the same row has the same number of cards.

Fig. 2.

A pile-shifting shuffle on a $4 \times 5$ matrix

2.3 Chosen Pile Cut Protocol

Suppose there is a sequence of q face-down stacks $A = (a_1,a_2,...,a_q)$, where each stack has the same number of cards. A chosen pile cut protocol [10] allows P to select a desired stack $a_i$ (to use in other protocols) without revealing the index i to V. The protocol also reverts the sequence A back to its original state after P finishes using $a_i$.

Fig. 3.

A $3 \times n$ matrix M constructed in Step 1 of the chosen pile cut protocol

In the chosen pile cut protocol, P performs the following steps.

• 1. Construct the following $3 \times q$ matrix M (see Fig. 3).

  • (a) In Row 1, publicly place the sequence A.

  • (b) In Row 2, secretly place a face-down sequence $E_q(i)$.

  • (c) In Row 3, publicly place a sequence $E_q(1)$.

• 2. Turn over all face-up cards and apply the pile-shifting shuffle to M.

• 3. Turn over all cards in Row 2. Locate the position of the only . A stack in Row 1 directly above this will be the desired stack $a_i$.

• 4. After finishing using $a_i$, place $a_i$ back in M at the same position.

• 5. Turn over all face-up cards and apply the pile-shifting shuffle to M again.

• 6. Turn over all cards in Row 3. Locate the position of the only . Shift the columns of M cyclically such that this moves to Column 1. The sequence A is now reverted back to its original state.

2.4 Sea Formation Protocol

A sea formation protocol [16] allows P to convince V that an area in an $m \times n$ grid consists of t cells that are connected to each other horizontally or vertically, without revealing any other information about the area. A technique similar to the one in this protocol will be implicitly used in our main protocol.

The idea of this protocol is that P first colors all cells with color 1. Then, for each of the t cells in the given area, P will change its color from color 1 to color 2 one cell at a time, each time selecting a cell adjacent to some cell selected earlier.

A cell with color c is represented by a sequence $E_k(c)$ for a fixed $k \ge 2$. First, P publicly places an $E_k(1)$ on every cell in the grid. To handle edge cases where the selected cell is on the grid boundary, P also publicly appends a row and a column of “dummy stacks” $E_k(0)$s to the bottom and to the right of the grid. Then, turn all cards face-down. We now have an $(m+1) \times (n+1)$ matrix of stacks (see Fig. 4).

Fig. 4.

The way P appends dummy stacks to a $3 \times 4$ grid

If we arrange all $(m+1)(n+1)$ stacks in the matrix into a single sequence $A=(a_1,a_2,...,$ $a_{(m+1)(n+1)})$, starting at the top-left corner and going from left to right in Row 1, then from left to right in Row 2, and so on, we can locate exactly where the four neighbors of any given stack are. Namely, the stacks on the neighbor to the left, right, top, and bottom of a cell containing $a_i$ are $a_{i-1}$, $a_{i+1}$, $a_{i-n-1}$, and $a_{i+n+1}$, respectively. Hence, P can apply the chosen pile cut protocol to select a desired neighbor without revealing which one (since the chosen pile cut protocol preserves the cyclic order of the input sequence).

In the sea formation protocol to verify an area of size t, P performs the following steps.

• 1. Apply the chosen pile cut protocol (for $(m+1)(n+1)$ stacks) to select a desired $E_k(1)$.

• 2. Reveal the selected stack that it is an $E_k(1)$ (otherwise V rejects) and replace it with an $E_k(2)$.

• 3. Perform the following steps for $t-1$ iterations.

  • (a) Apply the chosen pile cut protocol (for $(m+1)(n+1)$ stacks) to select a desired $E_k(2)$.

  • (b) Reveal the selected stack that it is an $E_k(2)$ (otherwise V rejects).

  • (c) Pick the four neighbors of the selected stack and apply the chosen pile cut protocol (for four stacks) to select a desired neighbor.

  • (d) Reveal the selected neighbor that it is an $E_k(1)$ (otherwise V rejects) and replace it with an $E_k(2)$.

Observe that in each iteration, the “sea” of cells with color 2 expands by one cell, while all cells with color 2 remain connected to each other horizontally or vertically. Therefore, after $t-1$ iterations, V is convinced that there is an area of t cells with color 2 in the grid that are connected to each other.

3 Verifying Border Condition

Also, P needs to convince V that the number in each cell is equal to the number of edges of that cell that are borders of blocks. Note that this condition means if a cell contains a number x, then exactly $4-x$ of its four neighbors (including the “dummy neighbors” outside the grid) must be in the same block as that cell. The following tools and subprotocols are necessary for this phase.

3.1 Enhanced Matrix

Starting from a $p \times q$ matrix of cards, publicly place cards , , ..., from left to right on top of Row 1; this new row is called Row 0. Then, place cards , ..., from top to bottom (starting at Row 2) to the left of Column 1; this new column is called Column 0. This modified matrix is called a $p \times q$ enhanced matrix (see Fig. 5).

Fig. 5.

A $4 \times 5$ enhanced matrix

3.2 Double-Scramble Shuffle

To perform a double-scramble shuffle [25] on a $p \times q$ enhanced matrix, first turn all cards face-down. Then, rearrange Columns 1, 2, ..., q (including Row 0) by a uniformly random permutation (which can be implemented in real world by putting the cards in each column into an envelope and scrambling all envelopes together). After that, leave Row 1 as it is and rearrange Rows 2, 3, ..., p (including Column 0) by a uniformly random permutation unknown to all parties.

3.3 Rearrangement Protocol

A rearrangement protocol [25] reverts an enhanced matrix back to its original state. To perform the rearrangement protocol on a $p \times q$ enhanced matrix, first apply the double-scramble shuffle to the matrix. Then, turn over all cards in Row 0 and rearrange the columns such that each card with number i will be in Column i. Analogously, turn over all cards in Column 0 and rearrange Rows 2, 3, ..., p accordingly.

3.4 Neighbor Counting Protocol

Suppose there are p sequences $E_q(y_1),E_q(y_2),...,E_q(y_p)$ of cards, with $1 \le y_1 \le q$ and $0 \le y_i \le q$ for each $i=2,3,...,p$. A neighbor counting protocol [25] allows P to show to V the number of indices $i \ge 2$ such that $y_i=y_1$ without revealing any other information about the sequences.

In the neighbor counting protocol, P performs the following steps.

• 1. Construct a $p \times q$ matrix with each Row i ($i=1,2,...,p$) consisting of the sequence $E_q(y_i)$.

• 2. Place cards in Row 0 and Column 0 to make the matrix become a $p \times q$ enhanced matrix M.

• 3. Apply the double-scramble shuffle to M.

• 4. Turn over all cards in Row 1. Locate the position of the only . Suppose it is at Column j.

• 5. Turn over all cards in Column j (except Row 0). Count the number of besides the one in Row 1. This is the number of indices as desired.

• 6. Turn over all face-up cards and apply the rearrangement protocol to M.

4 Putting Together

Let $b = mn/5$ be the number of blocks in the Five Cells grid. Let $B_2,B_3,...,B_{b+1}$ be the blocks in the grid.¹ The idea of our protocol is that P initially colors all cells with color 1. Then, for each $i=2,3,...,b+1$, P will apply the sea formation protocol to change the color of each cell in $B_i$ from color 1 to color i.

After that, for each cell with a number x written on it, P will apply the neighbor counting protocol to verify that exactly $4-x$ of its neighbors have the same color as that cell.

The formal steps of our protocols are as follows.

Initially, P publicly places an $E_{b+1}(1)$ on every cell in the grid. P also publicly appends a row and a column of dummy stacks $E_k(0)$s to the bottom and to the right of the grid. Then, P turns all card face-down. We now have an $(m+1) \times (n+1)$ matrix of stacks.

In the first phase (to verify the connected area), for each $i=2,3,...,b+1$, P performs the following steps.

• 1. Apply the chosen pile cut protocol (for $(m+1)(n+1)$ stacks) to select a desired $E_{b+1}(1)$ in block $B_i$.

• 2. Reveal the selected stack that it is an $E_{b+1}(1)$ (otherwise V rejects) and replace it with an $E_{b+1}(i)$.

• 3. Perform the following steps for four iterations.

  • (a) Apply the chosen pile cut protocol (for $(m+1)(n+1)$ stacks) to select a desired $E_{b+1}(i)$ in block $B_i$.

  • (b) Reveal the selected stack that it is an $E_{b+1}(i)$ (otherwise V rejects).

  • (c) Pick the four neighbors of the selected stack and apply the chosen pile cut protocol (for four stacks) to select a desired neighbor in block $B_i$.

  • (d) Reveal the selected neighbor that it is an $E_{b+1}(1)$ (otherwise V rejects) and replace it with an $E_{b+1}(i)$.

Now V is convinced that the grid is partitioned into b disjoint blocks, each consisting of exactly five cells.

In the second phase (to verify the border condition), for each cell with a number x written on it, P performs the following steps.

• 1. Pick a sequence of cards on that cell. Call this sequence $E_{b+1}(y_1)$.

• 2. Pick the four neighbors of that cell (including dummy neighbors if that cell is on the grid boundary). Call these sequences $E_{b+1}(y_2)$, $E_{b+1}(y_3)$, $E_{b+1}(y_4)$, and $E_{b+1}(y_5)$.

• 3. Apply the neighbor counting protocol on the sequences $E_{b+1}(y_1)$, $E_{b+1}(y_2)$, ..., $E_{b+1}(y_5)$ to show that the number of indices $i \ge 2$ such that $y_i=y_1$ is $4-x$ (otherwise V rejects).

Now V is convinced that each number satisfies the border condition of the puzzle. If both verification phases pass, then V accepts.

Our protocol uses $(b+3)(m+1)(n+1)+b+13 = \varTheta (bmn) = \varTheta (m^2n^2)$ cards.

5 Optimization

Our protocol in Sect. 4 requires $\varTheta (m^2n^2)$ cards, which is quadratic in the number of cells, making it impractical to implement in real world. Therefore, we will modify our protocol to reduce the number of required cards to linear in the number of cells.

The key idea is that P does not need to color the blocks with as many as b colors. If we view each block as a vertex and two vertices have en edge if the corresponding blocks touch each other horizontally or vertically, then the resulting graph is a planar graph. Using an appropriate algorithm such as the ones in [3, 31], P can color this graph with five colors in linear time such that no two adjacent vertices have the same color.² Note that this coloring is known to only P but not V (as V must not know the structure of the graph).

An extra step to add is that, during the sea formation protocol, when coloring a block $B_i$ with color c, P has to show that none of the cells in $B_i$ is adjacent to a cell in another block with the same color c. To accommodate this, let the five colors used in P’s 5-coloring be colors 3, 4, 5, 6, and 7. When coloring a block $B_i$, P first changes color of each cell in $B_i$ from color 1 to color 2, and at the same time applies the neighbor counting protocol to show that none of its neighbor has color c. After all cells in $B_i$ become color 2, P applies the chosen pile cut protocol five times, each time changing color of a cell with color 2 to color c. Note that a cell with color j is represented by a sequence $E_7(j)$.

However, this modified protocol has a major problem: it is not zero-knowledge. Since P reveals the color of each block, V will know the number of blocks having each color and thus will gain some information about the structure of the graph. For example, if P colors the blocks with only three colors, then V will gain information that the graph is 3-colorable.

We can prevent this by making the colors dynamic in a cyclic order: $7 \rightarrow 6 \rightarrow 5 \rightarrow 4 \rightarrow 3 \rightarrow 7$. Before P starts coloring each new block, the colors of all blocks will be shifted by a random cyclic shift known only to P. By doing this, V will gain no information about the number of blocks with each color, while the property that adjacent blocks must have different colors is still preserved.

We introduce the following subprotocol to shift the colors cyclically.

5.1 Color Shifting Protocol

A color shifting protocol shifts the colors of all cells in a cyclic order $7 \rightarrow 6 \rightarrow 5 \rightarrow 4 \rightarrow 3 \rightarrow 7$ by r steps for a uniformly random $r \in \{0,1,2,3,4\}$ known only to P. For instance, if $r=1$, then all cells with color 7 will become color 6, all cells with color 6 will become color 5, and so on.

In the color shifting protocol, P performs the following steps.

• 1. Secretly choose a uniformly random integer $r \in \{0,1,2,3,4\}$.

• 2. Construct the following $5 \times (m+1)(n+1)+1$ matrix M.

  • (a) In Row 1, secretly place a sequence $E_5(r+1)$.

  • (b) In each Row i ($i=2,3,...,(m+1)(n+1)+1$), publicly place a sequence consisting of five rightmost cards taken from from a sequence on each cell in the Five Cells grid.

• 3. Apply the pile-shifting shuffle to M.

• 4. Turn over all cards in Row 1. Locate the position of the only . Shift the columns of M cyclically such that this moves to Column 1.

• 5. Place cards in Row $2,3,...,(m+1)(n+1)+1$ back to their corresponding cells.

Note that this protocol shifts the color of each cell by r steps if it has color 3, 4, 5, 6, or 7; on the other hand, if a cell has color 0, 1, or 2, its color will not change.

5.2 Optimized Protocol

The formal steps of the optimized protocol are as follows.

Initially, P publicly places an $E_7(1)$ on every cell in the grid. P also publicly appends a row and a column of dummy stacks $E_7(0)$s to the bottom and to the right of the grid. Then, P turns all card face-down. We now have an $(m+1) \times (n+1)$ matrix of stacks.

In the first phase, for $i=2,3,...,b+1$, P performs the following steps.

• 1. Apply the color shifting protocol and announce that P will color a block $B_i$ with color $c \in \{3,4,5,6,7\}$.

• 2. Apply the chosen pile cut protocol (for $(m+1)(n+1)$ stacks) to select a desired $E_7(1)$ in block $B_i$.

• 3. Reveal the selected stack that it is an $E_7(1)$ (otherwise V rejects) and replace it with an $E_7(2)$.

• 4. Pick the four neighbors of the cell in Step 3 (including dummy neighbors if that cell is on the grid boundary). Apply the neighbor counting protocol on a sequence $E_7(c)$ and the four selected sequences to show that none of these four sequences is $E_7(c)$ (otherwise V rejects).

• 5. Perform the following steps for four iterations.

  • (a) Apply the chosen pile cut protocol (for $(m+1)(n+1)$ stacks) to select a desired $E_7(2)$ in block $B_i$.

  • (b) Reveal the selected stack that it is an $E_7(2)$ (otherwise V rejects).

  • (c) Pick the four neighbors of the selected stack and apply the chosen pile cut protocol (for four stacks) to select a desired neighbor in block $B_i$.

  • (d) Reveal the selected neighbor that it is an $E_7(1)$ (otherwise V rejects) and replace it with an $E_7(2)$.

  • (e) Pick the four neighbors of the cell in Step 5(d) (including dummy neighbors if that cell is on the grid boundary). Apply the neighbor counting protocol on a sequence $E_7(c)$ and the four selected sequences to show that none of these four sequences is $E_7(c)$ (otherwise V rejects).

• 6. Perform the following steps for five iterations.

  • (a) Apply the chosen pile cut protocol (for $(m+1)(n+1)$ stacks) to select a desired $E_7(2)$ in block $B_i$.

  • (b) Reveal the selected stack that it is an $E_7(2)$ (otherwise V rejects) and replace it with an $E_7(c)$.

Note that in Steps 2 to 5, P changes the color of all cells in $B_i$ from color 1 to color 2, while also verifying that none of them is adjacent to a cell with color c. Then, in Step 6, P changes the color of all cells in $B_i$ from color 2 to color c.

In the second phase, the optimized protocol works exactly the same way as in the original protocol in Sect. 4 (except the size of the matrix). If both verification phases pass, then V accepts.

The optimized protocol uses $9(m+1)(n+1)+26 = \varTheta (mn)$ cards, which is linear in the number of cells.

6 Proof of Correctness and Security

We will prove the perfect completeness, perfect soundness, and zero-knowledge properties of the optimized protocol.

Lemma 1 (Perfect Completeness)

If P knows a solution of the Five Cells puzzle, then V always accepts.

Proof

Suppose P knows a solution of the puzzle. In P’s solution, P picks a 5-coloring of the blocks such that adjacent blocks always have different colors.

Consider the first phase for each block $B_i$. After applying the color shifting protocol, suppose that the color of $B_i$ according to P’s 5-coloring becomes color c. Since the color shifting protocol only shifts the colors in a cyclic order $7 \rightarrow 6 \rightarrow 5 \rightarrow 4 \rightarrow 3 \rightarrow 7$, the property that adjacent blocks must have different colors is still preserved. Therefore, none of the cell in $B_i$ is adjacent to a cell with color c, so the first phase will pass.

Now consider the second phase for each cell $\alpha$ with color c and with a number x. Since P’s solution is correct, exactly x edges of $\alpha$ are borders of blocks, meaning that exactly x of $\alpha$’s neighbors are in adjacent blocks (or are dummy cells) and thus cannot have color c. Therefore, exactly $4-x$ of $\alpha$’s neighbors are in the same block and thus have color c, so the second phase will pass.

Hence, we can conclude that V always accepts.    $\square$

Lemma 2 (Perfect Soundness)

If P does not know a solution of the Five Cells puzzle, then V always rejects.

Proof

We will prove the contrapositive of this statement. Suppose that V accepts, meaning that the coloring phase passes for every iteration, and the verification of the border condition passes for every numbered cell.

Consider each iteration of the first phase. In Steps 2 to 5, P selects five cells with color 1 that are connected horizontally or vertically, and changes them to color 2. P also shows that none of these cells is adjacent to a cell with color c. After that, in Step 6, P selects five cells with color 2 and changes them to color c. As the cells that have been colored in previous iterations must have color 3, 4, 5, 6, or 7, and the cells that have not been colored must have color 1, the only cells with color 2 are the exact five cells P selected in this iteration. Therefore, at the end of this iteration, a new block of five connected cells with color c that is not adjacent to any other block with color c is formed.

After b iterations, the grid is now partitioned into b blocks, each consisting of five cells. Since the color shifting protocol only shifts the colors in a cyclic order $7 \rightarrow 6 \rightarrow 5 \rightarrow 4 \rightarrow 3 \rightarrow 7$, the property that adjacent blocks must have different colors is still preserved.

Now consider the second phase for each cell $\alpha$ with color c and with a number x. Since the verification passes, exactly $4-x$ of $\alpha$’s neighbors must have color c. However, cells in adjacent blocks (or dummy cells) cannot have color c, which means these $4-x$ cells must be in the same block as $\alpha$. Therefore, exactly x edges of $\alpha$ are borders of blocks. Since the verification passes for every numbered cell, the border condition must hold for every numbered cell.

Hence, we can conclude that P knows a correct solution of the puzzle.    $\square$

Lemma 3 (Zero-Knowledge)

During the verification, V obtains no information about P’s solution.

Proof

We will prove that the interaction between P and V can be simulated by a simulator S that does not know P’s solution.

First, we will prove the zero-knowledge property of the three subprotocols used in our main protocol: the chosen pile cut protocol in Sect. 2.3, the neighbor counting protocol in Sect. 3.4, and the color shifting protocol in Sect. 5.1. In these subprotocols, it is sufficient to show that all distributions of cards that are turned face-up can be simulated by S.

• In Steps 3 and 6 of the chosen pile cut protocol, the has an equal probability to be at any of the q columns (due to the pile-shifting shuffles), so these two steps can be simulated by S.

• In Step 4 of the neighbor counting protocol, the has an equal probability to be at any of the q columns (due to the double-scramble shuffle), so this step can be simulated by S.

• In Step 5 of the neighbor counting protocol, suppose there are t s besides the one in Row 1 (t is public information). The order of Rows 2, 3, ..., p is uniformly distributed among all possible permutations (due to the double-scramble shuffle). Hence, all t s have an equal probability to be at any of the $\left( {\begin{array}{c}p-1\\ t\end{array}}\right)$ combinations of rows, so this step can be simulated by S.

• In Step 4 of the color shifting protocol, the has an equal probability to be at any of the five columns (as r is uniformly selected from $\{0,1,2,3,4\}$ at random), so this step can be simulated by S.

Now consider our main (optimized) protocol.

• In Step 1, 5(e) and 6(b), the information V receives solely depends on the value of c. However, c has an equal probability to be any element of $\{3,4,5,6,7\}$ (due to the color shifting protocol), so this step can be simulated by S.

• In Steps 3, 5(b), 5(d), and 6(b), there is only one deterministic pattern of the cards that are turned face-up, so these steps can be simulated by S.

Hence, we can conclude that V obtains no information about P’s solution.    $\square$

7 Future Work

We constructed a card-based ZKP protocol for Five Cells, and also developed an optimization technique to reduce the number of required cards in our protocol from quadratic to linear in the number of cells.

Some existing card-based ZKP protocols for other logic puzzles, such as the one for Numberlink [25], require the number of cards quadratic in the number of cells. These protocols have a common theme that it involves partitioning a grid into several parts (where the number of parts can be linear in the number of cells) and coloring each part with a color different from each other. Therefore, the number of cards on each cell is also linear in the number of cells (due to the encoding rule in Sect. 2.1), resulting in the total number of cards quadratic. A future work is to apply our optimization technique to reduce the total number of cards in these protocols from quadratic to linear.

AAlternative ZKP Protocol for Five Cells

For the sake of completeness, we also provide an alternative ZKP protocol for Five Cells. This protocol takes a completely different approach from our first protocol. It is based on the fact that there are only $\varTheta (1)$ different types of pentomino. Namely, there are 63 of them.³ Furthermore, inside each pentomino, a number in each cell according to the border condition of Five Cells is fixed, which is exactly the number of edges of that cell that are borders of the pentomino.

In this protocol, P first creates 63 templates, one for each type of pentomino. A template consists of a $5 \times 5$ matrix of card. In each template, a cell inside the pentomino is represented by a card with a number equal to the number of edges of that cell that are borders of the pentomino, while a cell outside the pentomino is represented by a (see Fig. 6).

Fig. 6.

Templates of the X-shaped pentomino and the P-shaped pentomino

The idea of this protocol is that P initially places a on each cell in the Five Cells grid. Then, P applies the following printing protocol to “print” each pentomino from a template onto the grid one by one for b times.

1.1 A.1 Printing Protocol

Suppose we have a template of a pentomino, and another $5 \times 5$ matrix of cards from the Five Cells grid. A printing protocol verifies that an area from the grid corresponding to the pentomino is initially empty, then prints the numbers inside the pentomino from the template onto that area.

In the printing protocol, P performs the following steps.

• 1. Place each card from the template on top of each corresponding card from the grid, creating 25 stacks of two cards.

• 2. Perform the following steps for five iterations.

  • (a) Apply the chosen pile cut protocol (for 25 stacks) to select a desired stack.

  • (b) Reveal the bottom card of the stack that it is a (otherwise V rejects).

  • (c) Swap the top card and bottom card of that stack.

• 3. Remove the top cards of all stacks and reveal that they are all s (otherwise V rejects).

1.2 A.2 Main Protocol

The formal steps of the protocol are as follows.

Initially, P publicly places a on every cell in the grid. To handle edge cases, P also publicly appends four rows and four columns of “dummy cards” to the bottom and to the right of the grid. Then, P turns all card face-down. We now have an $(m+4) \times (n+4)$ matrix of cards.

In addition, P prepares 63 templates of all 63 types of pentomino and lets V verify that the templates are correct (otherwise V rejects).

For $i=2,3,...,b+1$, P performs the following steps.

• 1. Apply the chosen pile cut protocol (for $(m+4)(n+4)$ stacks) to select a $5 \times 5$ area containing block $B_i$. (To be precise, P actually selects just the top-left corner cell of the area, and the rest will follow as the chosen pile cut protocol preserves the cyclic order).

• 2. Apply the chosen pile cut protocol (for 63 stacks) to select a template of a pentomino with the same type as block $B_i$. Apply the printing protocol on the selected template and the selected area to print numbers onto block $B_i$.

• 3. Reconstruct a template that has been used and replenish the pile of templates with it. Let V verify again that all 63 templates are correct (otherwise V rejects). Note that V does not know which template has been used.

Finally, P reveals all cards on the cells that contain a number (in the original Five Cell puzzle). V verifies that the numbers on the cards match the numbers on the cells (otherwise V rejects). If all verification steps pass, then V accepts.

While this protocol also uses $\varTheta (mn)$ cards, the number of required cards is only $4mn+\varTheta (m+n)$, which is asymptotically better than that of our first protocol.