Abstract
Double-authentication preventing signatures (DAPS) are a variant of digital signatures which have received considerable attention recently (Derler et al. EuroS&P 2018, Poettering Africacrypt 2018). They are unforgeable signatures in the usual sense and sign messages that are composed of an address and a payload. Their distinguishing feature is the property that signatures on two different payloads with respect to the same address allow to publicly extract the secret signing key. Thus, they are a means to disincentivize double-signing and are a useful tool in various applications.
DAPS are known in the factoring, the discrete logarithm and the lattice setting. The majority of the constructions are ad-hoc. Only recently, Derler et al. (EuroS&P 2018) presented the first generic construction that allows to extend any discrete logarithm based secure signature scheme to DAPS. However, their scheme has the drawback that the number of potential addresses (the address space) used for signing is polynomially bounded (and in fact small) as the size of secret and public keys of the resulting DAPS are linear in the address space. In this paper we overcome this limitation and present a generic construction of DAPS with constant size keys and signatures. Our techniques are not tailored to a specific algebraic setting and in particular allow us to construct the first DAPS without structured hardness assumptions, i.e., from symmetric key primitives, yielding a candidate for post-quantum secure DAPS.
The full version of this paper is available as IACR Cryptology ePrint Archive Report. All authors have been supported by EU H2020 project Prismacloud, grant agreement n\(^{\circ }\)644962.
Access provided by CONRICYT-eBooks. Download conference paper PDF
Similar content being viewed by others
Keywords
- Digital signatures
- Double-authentication prevention
- Shamir secret sharing
- Provable-security
- Generic construction
- Exponential size address space
1 Introduction
Digital signatures are an important cryptographic primitive used to provide strong integrity and authenticity guarantees for digital messages. Among many other applications, they are used to issue digital certificates for public keys within public-key infrastructures, to guarantee the origin of executable code, to sign digital documents such as PDF documents (in a legally binding way), as well as in major cryptographic protocols such as TLS. Recently, signatures also emerged to be a cornerstone of distributed cryptocurrencies such as Bitcoin, i.e., are used to bind coins to users (by means of public keys) and to sign transactions.
Double-authentication preventing signatures (DAPS) are a variant of digital signatures used to sign messages of the form \(m=(a,p)\) with a being the so called address and p the payload. They provide unforgeability guarantees in the sense of conventional signatures but have the special property that signing two different payloads \(p\ne p'\) using the same address a allows to publicly extract the secret signing key from the respective signatures. In the literature, various compelling applications for DAPS have been proposed. Those applications include penalizing double spending attacks in cryptocurrencies [27] or penalizing certification authorities for issuing two certificates with respect to the same domain name, but for two different public keys [25], for example. In this work we purely focus on DAPS constructions and we refer the reader to [25, 26] for a comparison with other types of self-enforcing digital signatures.
Currently, DAPS are known in the factoring [6, 25, 26], the discrete logarithm [16, 24, 27] and the lattice setting [10]. The majority of the constructions (the only exception being [16]) are ad-hoc. Unfortunately, such an approach yields very specific constructions, whose security may not be well understood. Having generic DAPS constructions, in contrast, yields much more flexibility, as it allows to plug in building blocks whose security is well understood. In addition, this yields simplicity and modularity in the security analysis. Only recently, Derler et al. (EuroS&P 2018) presented the first generic construction that allows to extend any discrete logarithm based EUF-CMA secure signatures scheme to DAPS. However, their scheme has the drawback that the number of potential addresses (the address space) used for signing is polynomially bounded (and in fact small) as the size of secret and the public keys of the resulting DAPS are linear in the address space. We ask whether we can come up with a generic construction without this drawback.
Somewhat orthogonal to the motivational discussion above, our work is also driven by the question whether it is possible to construct DAPS without relying on structured hardness assumptions, i.e., solely from symmetric key primitives (following up on a very recent line of work [9, 12, 15, 22]). This is interesting, because symmetric key primitives are conjectured to remain secure in the advent of sufficiently powerful quantum computers. Such quantum computers would break all discrete log and RSA based public key cryptosystems [30].
1.1 Existing DAPS Constructions
DAPS have been introduced by Poettering and Stebila [25, 26] in a factoring-based setting. Ruffing, Kate and Schröder later introduced the notion of accountable assertions (AS) in [27], being a related but weaker primitive than DAPS. In addition they present one AS that also is a DAPS (RKS henceforth). The RKS construction is based on Merkle tress and chameleon hash functions in the discrete logarithm setting. Very recently, Bellare, Poettering and Stebila [6] proposed new factoring-based DAPS from trapdoor identification-schemes using an adaption and extension of a transform from [5]. Their two transforms applied to the Guillou-Quisquater (GQ) [20] and Micali-Reyzin (MR) [23] identification scheme yield signing and verification times as well as signature sizes comparable (or slightly above) standard RSA signatures. Boneh et al. [10] propose constructions of DAPS from lattices. They consider DAPS as a special case of what they call predicate-authentication-preventing signatures (PAPS). In PAPS one considers a k-ary predicate on the message space and given any k valid signatures that satisfy the predicate reveal the signing key. Consequently, DAPS are PAPS for a specific 2-ary predicate. Derler, Ramacher and Slamanig (DRS henceforth) in [16] recently provided the first black-box construction of DAPS from digital signatures schemes and demonstrate how this approach can be used to construct N-times-authentication-preventing signatures (NAPS) (a notion called k-way DAPS in [10]). In addition, they introduced weaker extraction notions, where the focus of the extraction is on the signing key of the underlying signature scheme only. A drawback of their work is that the constructions have O(n) secret and public key size where n is the size of the address space. So their constructions are only suitable for small message spaces. In a follow up work Poettering [24], also focusing on DAPS for small address spaces, showed how for a certain class of signature schemes (obtained via Fiat-Shamir from certain identification schemes), the DRS approach can be improved by reducing the signature size by a factor of five and the size of the secret key from O(n) to O(1). However, this comes at the cost of no longer being able to do a black-box reduction to the underlying signature scheme. In Table 1 we provide a comparison of existing DAPS approaches with the ones presented in this paper regarding address space, extraction capabilities, algebraic setting as well as their characteristic as either being tailored to a specific setting or generic.
1.2 Contribution
Our contributions can be summarized as follows:
-
We propose a generic DAPS, respectively NAPS, construction building upon DRS’ secret-sharing approach, which resolves the address-space limitation in the DRS construction, and, in particular, supports an exponentially large address space. This improvement is achieved by deriving the coefficients of the secret sharing polynomial from the address using a carefully chosen pseudorandom function with an output domain being compatible with the secret key space of the underlying signature scheme. Consequently, the overhead in the public-key reduces to a constant factor. Like the DRS approach, our generic approach satisfies a relaxed notion of extractability. Interestingly, we can instantiate this construction solely from symmetric-key primitives, yielding a candidate for post-quantum secure DAPS/NAPS.
-
While the aforementioned construction thus closes an important gap in the literature, the signature sizes are somewhat large compared to signatures in the discrete log or RSA setting. To this end, we additionally follow a different direction which basically targets the extension of any digital signature scheme (such as ECDSA or EdDSA, for example) to a DAPS. Essentially, we present a compiler which uses an arbitrary DAPS scheme to extend any given signature scheme to a DAPS. While this might sound somewhat odd at first sight, we want to stress that all existing DAPS which have compact keys and exponentially large address space are ad-hoc constructions, whereas practical applications most likely will use standardized signature schemes. Using our construction it is possible to generically bring extraction to any signature scheme. Hence we obtain more efficient DAPS being compatible with standardized signature schemes such as ECDSA or EdDSA.
2 Preliminaries
In this section we firstly present a formal model for the security of signature and DAPS schemes, recall non-interactive zero-knowledge proof systems and Shamir’s secret sharing.
2.1 Digital Signature Schemes
Subsequently we formally recall the notion of digital signature schemes.
Definition 1
(Signature Scheme). A signature scheme \({\mathsf {\varSigma }}\) is a triple \((\mathsf {KGen}_{\mathsf {\varSigma }},\mathsf {Sign}_{\mathsf {\varSigma }}, \mathsf {Verify}_{\mathsf {\varSigma }})\) of PPT algorithms, which are defined as follows:
-
\(\mathsf {KGen}_{\mathsf {\varSigma }}(1^\kappa )\): This algorithm takes a security parameter \(\kappa \) as input and outputs a secret (signing) key \(\mathsf {sk}_\mathsf {\varSigma }\) and a public (verification) key \(\mathsf {pk}_\mathsf {\varSigma }\) with associated message space \(\mathcal {M}\) (we may omit to make the message space \(\mathcal {M}\) explicit).
-
\(\mathsf {Sign}_{\mathsf {\varSigma }}(\mathsf {sk}_\mathsf {\varSigma }, m)\): This algorithm takes a secret key \(\mathsf {sk}_\mathsf {\varSigma }\) and a message \(m\in \mathcal {M}\) as input and outputs a signature \(\sigma \).
-
\(\mathsf {Verify}_{\mathsf {\varSigma }}(\mathsf {pk}_\mathsf {\varSigma },m,\sigma )\): This algorithm takes a public key \(\mathsf {pk}_\mathsf {\varSigma }\), a message \(m\in \mathcal {M}\) and a signature \(\sigma \) as input and outputs a bit \(b \in \{0,1\}\).
We require a signature scheme to be correct and to provide existential unforgeability under adaptively chosen message attacks (\(\mathsf {EUF}\text {-}\mathsf {CMA}\) security). For correctness we require that for all \(\kappa \in \mathbb {N}\), for all \((\mathsf {sk}_\mathsf {\varSigma }, \mathsf {pk}_\mathsf {\varSigma }) \leftarrow \mathsf {KGen}_{\mathsf {\varSigma }}(1^\kappa )\) and for all \(m\in \mathcal {M}\) it holds that
Definition 2
(\(\mathsf {EUF}\text {-}\mathsf {CMA}\)). For a PPT adversary \(\mathcal {A}\), we define the advantage function in the sense of \(\mathsf {EUF}\text {-}\mathsf {CMA}\) as
where the corresponding experiment is depicted in Fig. 1. If for all PPT adversaries \(\mathcal {A}\) there is a negligible function \(\varepsilon (\cdot )\) such that
we say that \({\mathsf {\varSigma }}\) is \(\mathsf {EUF}\text {-}\mathsf {CMA}\) secure.
2.2 Double-Authentication-Preventing Signatures
Double-authentication-preventing signatures (DAPS) are signature schemes being capable of signing messages from a message space \(\mathcal {M}\) of the form \(\mathsf{A}\times \mathsf{P}\). Each message \(m= (a, p)\in \mathcal {M}\) thereby consists of an address a in address space \(\mathsf{A}\) and a payload p from payload space \(\mathsf P\). In addition to the algorithms provided by conventional signature schemes, a DAPS scheme provides a fourth algorithm \(\mathsf {Ex}_{\mathsf {D}}\) that extracts the secret key from signatures on two colliding messages, i.e., two different messages sharing the same address. Formally, a pair of colliding messages is defined as follows:
Definition 3
(Colliding Messages). We call two messages \(m_1 = (a_1, p_1)\) and \(m_2 = (a_2, p_2)\) colliding if \(a_1 = a_2\), but \(p_1 \ne p_2\).
Below, we now formally define DAPS following [25, 26].
Definition 4
(DAPS). A double-authentication-preventing signature scheme \({\mathsf {DAPS}}\) is a tuple \((\mathsf {KGen}_{\mathsf {D}}, \mathsf {Sign}_{\mathsf {D}}, \mathsf {Verify}_{\mathsf {D}},\mathsf {Ex}_{\mathsf {D}})\) of PPT algorithms, which are defined as follows:
-
\(\mathsf {KGen}_{\mathsf {D}}(1^\kappa ):\) This algorithm takes a security parameter \(\kappa \) as input and outputs a secret (signing) key \(\mathsf {sk}_{\mathsf {D}}\) and a public (verification) key \(\mathsf {pk}_{\mathsf {D}}\) with associated message space \(\mathcal {M}\) (we may omit to make the message space \(\mathcal {M}\) explicit).
-
\(\mathsf {Sign}_{\mathsf {D}}(\mathsf {sk}_{\mathsf {D}}, m):\) This algorithm takes a secret key \(\mathsf {sk}_{\mathsf {D}}\) and a message \(m\in \mathcal {M}\) as input and outputs a signature \(\sigma \).
-
\(\mathsf {Verify}_{\mathsf {D}}(\mathsf {pk}_{\mathsf {D}}, m,\sigma ):\) This algorithm takes a public key \(\mathsf {pk}_{\mathsf {D}}\), a message \(m\in \mathcal {M}\) and a signature \(\sigma \) as input and outputs a bit \(b \in \{0,1\}\).
-
\(\mathsf {Ex}_{\mathsf {D}}(\mathsf {pk}_{\mathsf {D}}, m_1, m_2, \sigma _1, \sigma _2):\) This algorithm takes a public key \(\mathsf {pk}_{\mathsf {D}}\), two colliding messages \(m_1\) and \(m_2\) and signatures \(\sigma _1\) for \(m_1\) and \(\sigma _2\) for \(m_2\) as inputs and outputs a secret key \(\mathsf {sk}_{\mathsf {D}}\).
Note that the algorithms \(\mathsf {KGen}_{\mathsf {D}}\), \(\mathsf {Sign}_{\mathsf {D}}\), and \(\mathsf {Verify}_{\mathsf {D}}\) match the definition of the algorithms of a conventional signature scheme. For DAPS one requires a restricted but otherwise standard notion of unforgeability [25, 26], where adversaries can adaptively query signatures for messages but only on distinct addresses. Figure 2 details the unforgeability security experiment.
Definition 5
(\(\mathsf {EUF}\text {-}\mathsf {CMA}\) [25]). For a PPT adversary \(\mathcal {A}\), we define the advantage function in the sense of \(\mathsf {EUF}\text {-}\mathsf {CMA}\) as
where the corresponding experiment is depicted in Fig. 2. If for all PPT adversaries \(\mathcal {A}\) there is a negligible function \(\varepsilon (\cdot )\) such that
we say that \({\mathsf {DAPS}}\) is \(\mathsf {EUF}\text {-}\mathsf {CMA}\) secure.
The interesting property of a DAPS scheme is the notion of double-signature extractability (DSE). It requires that whenever one obtains signatures on two colliding messages, one should be able to extract the signing key using the extraction algorithm \(\mathsf {Ex}_{\mathsf {D}}\). We present the security definition denoted as DSE in Fig. 3. Thereby, we consider the common notion which requires extraction to work if the key pair has been generated honestly. In this game, the adversary is given a key pair and outputs two colliding messages and corresponding signatures. The adversary wins the game if the key produced by \(\mathsf {Ex}_{\mathsf {D}}\) is different from the signing key, although extraction should have succeeded, i.e., the messages were colliding and their signatures were valid.
Definition 6
(\(\mathsf {DSE}\) [25]). For a PPT adversary \(\mathcal {A}\), we define the advantage function in the sense of double-signature extraction (\(\mathsf {DSE}\)) as
where the corresponding experiment is depicted in Fig. 3. If for all PPT adversaries \(\mathcal {A}\) there is a negligible function \(\varepsilon (\cdot )\) such that
then \({\mathsf {DAPS}}\) provides \(\mathsf {DSE}\).
In the full version we recall the strong variant of extractability under malicious keys (denoted as \(\mathsf {DSE^*}\)), where the adversary is allowed to generate the key arbitrarily. The \(\mathsf {DSE^*}\) notion is very interesting from a theoretical perspective, but no practically efficient DAPS construction can achieve this notion so far.
DRS in [16] argue that when DAPS are constructed by extending a conventional signature scheme \({\mathsf {\varSigma }}\), extraction of the part of the signing key corresponding to \({\mathsf {\varSigma }}\) is already sufficient to disincentivizes double-authentication for many applications. Hence, Derler et al. [16] defined two weaker double-signature extraction notions that cover extraction of the signing key of the underlying signature scheme for honestly and maliciously generated DAPS keys. The security games for weak double-signature extraction (\(\mathsf {wDSE}\)) and weak double-signature extraction under malicious keys (\(\mathsf {wDSE^*}\)) are depicted in Figs. 4 and 5. \(\mathsf {DSE}\) and \(\mathsf {DSE^*}\) imply their weaker counterparts and \(\mathsf {wDSE^*}\) implies \(\mathsf {wDSE}\).
Definition 7
(\(T \in \{ \mathsf {wDSE}, \mathsf {wDSE^*}\}\) ). For a PPT adversary \(\mathcal {A}\), we define the advantage function in the sense of weak double-signature extraction (\(T = \mathsf {wDSE}\)) and weak double-signature extraction under malicious keys (\(T = \mathsf {wDSE^*}\)), as
where the corresponding experiments are depicted in Figs. 4 and 5 respectively. If for all PPT adversaries \(\mathcal {A}\) there is a negligible function \(\varepsilon (\cdot )\) such that
then \({\mathsf {DAPS}}\) provides T.
Finally, for our constructions we may sometimes require a very mild additional property of DAPS which we call verifiability of secret keys. Informally it requires that there is an additional efficient algorithm \(\mathsf{VKey}\) which, given a key pair, outputs 1 if the given secret key is the key corresponding to the given public key. Formally we define verifiability of keys as follows:
Definition 8
(Verifiability of Keys). We say that a DAPS scheme \({\mathsf {DAPS}}= (\mathsf {KGen}_{\mathsf {D}}, \mathsf {Sign}_{\mathsf {D}}, \mathsf {Verify}_{\mathsf {D}}, \mathsf {Ex}_{\mathsf {D}})\) provides verifiability of keys, if it provides an additional efficient algorithm \(\mathsf VKey\) so that for all \(\kappa \in \mathbb {N}\), for all \((\mathsf {sk}, \mathsf {pk})\) it holds that
2.3 Non-interactive ZK Proof Systems (NIZK)
We recall a standard definition of non-interactive zero-knowledge proof systems. Let \(L \subseteq \mathsf{X}\) be an \(\mathbf NP\)-language with associated witness relation R so that \(L = \{x ~|~ \exists w : R(x, w) = 1\}\).
Definition 9
(Non-Interactive Zero-Knowledge Proof System). A non-interactive proof system \(\mathsf {\Pi }\) is a tuple of algorithms \((\mathsf {Setup}_{\mathsf {\Pi }}, \mathsf {Proof}_{\mathsf {\Pi }}, \mathsf {Verify}_{\mathsf {\Pi }})\), which are defined as follows:
-
\(\mathsf {Setup}_{\mathsf {\Pi }}(1^\kappa ):\) This algorithm takes a security parameter \(\kappa \) as input, and outputs a common reference string \(\mathsf {crs}\).
-
\(\mathsf {Proof}_{\mathsf {\Pi }}(\mathsf {crs}, x, w):\) This algorithm takes a common reference string \(\mathsf {crs}\), a statement x, and a witness w as input, and outputs a proof \(\pi \).
-
\(\mathsf {Verify}_{\mathsf {\Pi }}(\mathsf {crs}, x, \pi ):\) This algorithm takes a common reference string \(\mathsf {crs}\), a statement x, and a proof \(\pi \) as input, and outputs a bit \(b \in \{0,1\}\).
From a non-interactive zero-knowledge proof system we require completeness, soundness and adaptive zero-knowledge and simulation-sound extractability. In the full version we recall formal definitions of those properties.
NIZK from \(\varSigma \)-protocols. A \(\varSigma \)-protocol for language L is an interactive three move protocol between a prover and a verifier, where the prover proves knowledge of a witness w to the statement \(x \in L\). We recall the formal definition of \(\varSigma \)-protocols in the full version. One can obtain a non-interactive proof system with the above properties by applying the Fiat-Shamir transform [17] to any \(\varSigma \)-protocol where the min-entropy \(\mu \) of the commitment \(\mathsf a\) sent in the first message of the \(\varSigma \)-protocol is so that \(2^{-\mu }\) is negligible in the security parameter \(\kappa \) and its challenge space \(\mathsf C\) is exponentially large in the security parameter. Essentially, the transform removes the interaction between the prover and the verifier by using a hash function H (modelled as a random oracle) to obtain the challenge. That is, the algorithm \(\mathsf {Challenge}\) obtains the challenge as \(H(\mathsf {a}, x)\). Due to the lack of space we postpone a formal presentation to the full version.
Efficient NIZK Proof Systems for General Circuits. Over the last few years NIZK proof systems for general circuits have seen significant progress improving their overall efficiency. Based on the MPC-in-the-head paradigm by Ishai et al. [21], \(\textsc {ZKBoo}\) [19] and the optimized version \(\textsc {ZKB++}\) [12] are zero-knowledge proof systems covering languages over arbitrary circuits. They roughly work as follows: The prover simulates all parties of a multiparty computation (MPC) protocol implementing the joint evaluation of some function, say \(y = \mathrm {SHA\text {-}3}(x)\), and computes commitments to the states of all players. The verifier then randomly corrupts a subset of the players and checks whether those players performed the computation correctly. Following the same paradigm, Katz et al. [22] recently proposed to use a MPC protocol with a preprocessing phase, which allows to significantly reduce the proof sizes. This proof system, denoted as KKW, allows one to choose a larger number of players then in the case of \(\textsc {ZKBoo}\) and \(\textsc {ZKB++}\), where larger numbers lead to smaller proofs. For all three proof systems, the number of binary multiplication gates is the main factor influencing the proof size, as the proof size grows linearly with the number of those gates.
Finally, Ames et al. [4] introduced Ligero, which offers proofs of logarithmic size in the number of multiplication gates if the circuit is represented using a prime field. When considering binary circuits, the number of addition respectively XOR gates has also to be accounted for in the proof size. But, as noted by Katz et al. in [22], especially for large circuits with more than 100,000 gates Ligero beats \(\textsc {ZKBoo}\), \(\textsc {ZKB++}\) and KKW in term of proof size.
2.4 Shamir’s Secret Sharing
Shamir’s \((k,\ell )\)-threshold secret sharing [29] is a secret sharing scheme which allows to information-theoretically share a secret s among a set of \(\ell \) parties so that any collection of at least k shares allow to reconstruct s. Let s be the constant term of an otherwise randomly chosen \(k-1\) degree polynomial
over a finite field \(\mathbb {F}\). A share is computed as f(i) for party i, \(1\le i\le \ell \). Let \(\mathcal {S}\) be any set of cardinality at least k of these \(\ell \) shares and let \(I_\mathcal {S}\) be the set of indices corresponding to shares in \(\mathcal {S}\). Using Lagrange interpolation one can then can reconstruct the secret s by computing \(s=f(0)\) as
As long as only \(k-1\) or less shares are available the secret s is information-theoretically hidden.
3 DAPS Without Structured Hardness Assumptions
For our first construction we follow the basic idea of Derler et al. [16] and build DAPS by including secret shares of the signing key in the signatures. To resolve the address space limitation of their approach, however, we derive the coefficients of the sharing polynomial using a pseudorandom function (PRF). By then additionally proving the correct evaluation of the PRF, it is no longer necessary to store encrypted versions of the coefficients in the public key. The only issue which remains, is to additionally prove consistency with respect to a “commitment” to the PRF secret key contained in the public key (we commit to it using a fixed-value key-binding PRF as defined in Appendix A). To bind the message to the proof, we use a signature-of-knowledge style methodology [14].
More precisely, we start from a one-way function \(f : S \rightarrow P\), which we use to define the relation between public and secret keys, i.e., so that \(\mathsf {pk}_\mathsf {\varSigma }= f(\mathsf {sk}_\mathsf {\varSigma })\). In addition we carefully choose a PRF \(\mathcal {F}\), which maps to the secret key space S. At the core of our DAPS construction we use a NIZK proof to prove consistency of the secret signing key, as well as the correctness of the secret sharing. For this proof we define an language L with associated witness relation R in the following way:
In this statement we cover three aspects: First, we prove that the polynomial for Shamir’s secret sharing is derived from the address and that the secret share is correctly calculated. Second, we prove the relation between the secret and public key of the signature scheme. Third, we “commit” to the PRF secret key using a fixed-value key-binding PRF. The full scheme is depicted in Scheme 1.
It is important to note that the PRF needs to be compatible with the signature scheme, in the sense that secret-key space of \({\mathsf {\varSigma }}\), i.e., S, and \(\mathsf {R}\) match. For simplicity, we assume that \(\mathsf {R} = S\). Additionally, the domain and codomain of the PRF also define the message space of the \({\mathsf {DAPS}}\). In the following theorem we prove that Scheme 1 is an \(\mathsf {EUF}\text {-}\mathsf {CMA}\)-secure DAPS.
Theorem 1
If the NIZK proof system \(\mathsf {\Pi }\) is simulation-sound extractable, \(\mathcal {F}\) is a PRF, and f is an OWF, then Scheme 1 provides \(\mathsf {EUF}\text {-}\mathsf {CMA}\) security.
Proof
We prove this theorem using a sequence of games. We denote the winning event of game \(G_i\) as \(S_i\). We let \(Q_{\mathsf {\varSigma }}\) be the number of signing oracle queries.
-
Game 0: The original game.
-
Game 1: As before, but we modify \(\mathsf {KGen}_{\mathsf {D}}\) as follows:
-
\(\mathsf {KGen}_{\mathsf {D}}(1^\kappa ):\) As before, but let
 and store
and store  .
.
-
-
Transition \(0 \Rightarrow 1\): Both games are indistinguishable under adaptive zero-knowledge of the proof system, i.e. \(| \Pr [S_0] - \Pr [S_1] | \le \mathsf {Adv}^{\mathsf {Sim}}_{{\mathcal {A},\mathsf {S}},{\mathsf {\Pi }}}(\kappa )\).
-
Game 2: As Game 1, but we modify \(\mathsf {Sign}_{\mathsf {D}}\) as follows:
-
\(\mathsf {Sign}_{\mathsf {D}}(\mathsf {sk}, m):\) As before, but let
 .
.
-
-
Transition \(1 \Rightarrow 2\): Both games are indistinguishable under adaptive zero-knowledge of the proof system, i.e. \(| \Pr [S_1] - \Pr [S_2] | \le \mathsf {Adv}^{\mathsf {ZK}}_{{\mathcal {A},\mathsf {S}},{\mathsf {\Pi }}}(\kappa )\).
-
Game 3: As before, but we modify \(\mathsf {KGen}_{\mathsf {D}}\) and \(\mathsf {Sign}_{\mathsf {D}}\) as follows.
-
\(\mathsf {KGen}_{\mathsf {D}}(1^\kappa ):\) As before, but let
 .
. -
\(\mathsf {Sign}_{\mathsf {D}}(\mathsf {sk}_{\mathsf {D}}, m):\) As before, but let
 .
.
-
-
Transition \(2 \Rightarrow 3\): We engage with a PRF challenger \(\mathcal {C}\) against \(\mathcal {F}\). We modify \(\mathsf {Sign}_{\mathsf {D}}\) as follows:
-
\(\mathsf {KGen}_{\mathsf {D}}(1^\kappa ):\) As before, but let
 .
. -
\(\mathsf {Sign}_{\mathsf {D}}(\mathsf {sk}_{\mathsf {D}}, m):\) As before, but let
 .
.
Thus an adversary distinguishing the two games also distinguishes the PRF from a random function, i.e. \(|\Pr [S_4] - \Pr [S_3]| \le \mathsf {Adv}^{}_{\mathcal {D},F}(\kappa )\).
-
-
Game 4: As before, but we modify \(\mathsf {Sign}_{\mathsf {D}}\) as follows.
-
\(\mathsf {Sign}_{\mathsf {D}}(\mathsf {sk}_{\mathsf {D}}, m):\) As before, but track all \((a, \rho )\) pairs in \(\mathcal {Q}\).
We abort if there exists \((a_1, \rho ), (a_2, \rho ) \in \mathcal {Q}\) such that \(a_1 \ne a_2\).
-
-
Transition \(3 \Rightarrow 4\): Both games proceed identically, unless the abort event happens. The probability of the abort event is bounded by
 , i.e.
, i.e.  .
. -
Game 5: As before, but we modify \(\mathsf {Sign}_{\mathsf {D}}\) as follows.
-
\(\mathsf {Sign}_{\mathsf {D}}(\mathsf {sk}_{\mathsf {D}}, m):\) As before, but let
 .
.
-
-
Transition \(4 \Rightarrow 5\): This change is conceptional. Note that \(\rho \) is uniformly random and not revealed, and thus z is uniformly random.
-
Game 6: As before, but we modify \(\mathsf {KGen}_{\mathsf {D}}\) as follows:
-
\(\mathsf {KGen}_{\mathsf {D}}(1^\kappa ):\) As before, but let
 and store
and store  .
.
-
-
Transition \(5 \Rightarrow 6\): Both games are indistinguishable under simulation-sound extractability of the proof system, i.e. \(| \Pr [S_6] - \Pr [S_5] | \le \mathsf {Adv}^{\mathsf {Ext_1}}_{{\mathcal {A},\mathcal {E}},{\mathsf {\Pi }}}(\kappa )\).
-
Game 7: As before, but we now use the extractor to obtain \(\mathsf {sk}_\mathsf {\varSigma }^* \leftarrow \mathcal {E}_{\mathsf {2,\Pi }}(\mathsf {crs}, \xi ,(\mathsf {pk}_\mathsf {\varSigma }, \beta , c, a, z, m), \pi )\) and abort in case the extraction fails.
-
Transition \(6 \Rightarrow 7\): Both games proceed identically, unless we abort. The probability of that happening is bounded by the simulation-sound extractablity of the proof system, i.e. \(|\Pr [S_7] - \Pr [S_6]| \le \mathsf {Adv}^{\mathsf {Ext_2}}_{{\mathcal {A},\mathcal {E}},{\mathsf {\Pi }}}(\kappa )\).
Reduction. Now we are ready to present a reduction which engages with an OWF challenger \(\mathcal {C}\). In particular, we obtain a challenge and embed it in the public key, i.e.
-
\(\mathsf {KGen}_{\mathsf {D}}(1^\kappa ):\) As before, but
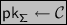 .
.
Once the adversary returns a forgery, we extract \(\mathsf {sk}_\mathsf {\varSigma }^*\) and forward the solution to the OWF challenger. Hence \(\Pr [S_7] \le \mathsf {Adv}^{\mathsf {OWF}}_{{\mathcal {A}},{f}}(\kappa )\), which concludes the proof. \(\square \)
We now show that Scheme 1 also provides \(\mathsf {wDSE}\) security. We note that in the proof of Theorem 2 we do not need to simulate proofs, so a weaker extraction notion would suffice. The proof of Theorem 1, however, already requires simulation-sound extractability which is why we directly resort to simulation-sound extractability.
Theorem 2
If the NIZK proof system \(\mathsf {\Pi }\) is simulation-sound extractable and the PRF \(\mathcal {F}\) is computationally fixed-value-key-binding, then Scheme 1 provides \(\mathsf {wDSE}\) security.
Proof
We prove this theorem using a sequence of games. We denote the winning event of game \(G_i\) as \(S_i\). Let \(m_1, m_2, \sigma _1, \sigma _2\) denote the output of \(\mathcal {A}\). For simplicity we write \(m_j = (a, p_j)\), \(\sigma _j = (z_j, \pi _{j})\) for \(j \in [2]\). Now, we have proofs attesting that \(z_j = \rho p_j + \mathsf {sk}_\mathsf {\varSigma }\) for \(j \in [2]\).
-
Game 0: The original game.
-
Game 1: As before, but we modify \(\mathsf {KGen}_{\mathsf {D}}\) as follows:
-
\(\mathsf {KGen}_{\mathsf {D}}(1^\kappa ):\) As before, but let
 and store
and store  .
.
-
-
Transition \(0 \Rightarrow 1\): Both games are indistinguishable under adaptive zero-knowledge of the proof system, i.e. \(| \Pr [S_0] - \Pr [S_1] | \le \mathsf {Adv}^{\mathsf {Sim}}_{{\mathcal {A},\mathsf {S}},{\mathsf {\Pi }}}(\kappa )\).
-
Game 2: As before, but we modify \(\mathsf {KGen}_{\mathsf {D}}\) as follows:
-
\(\mathsf {KGen}_{\mathsf {D}}(1^\kappa ):\) As before, but let
 and store
and store  .
.
-
-
Transition \(1 \Rightarrow 2\) : Both games are indistinguishable under simulation-sound extractability of the proof system, i.e. \(| \Pr [S_2] - \Pr [S_1] | \le \mathsf {Adv}^{\mathsf {Ext_1}}_{{\mathcal {A},\mathcal {E}},{\mathsf {\Pi }}}(\kappa )\).
-
Game 3: As before, but we now use the extractor to obtain \((\mathsf {sk}_{{\mathsf {\varSigma }},j}^*, \mathsf {sk}_{\mathsf {PRF},j}^*) \leftarrow \mathcal {E}_{\mathsf {2,\Pi }}(\mathsf {crs}, \xi , (\mathsf {pk}_\mathsf {\varSigma }, \beta , c, a, z_j, m_j), \pi )\) for \(j \in [2]\) and abort if the extraction fails.
-
Transition \(2 \Rightarrow 3\): Both games proceed identically, unless we abort. The probability of that happening is bounded by the simulation-sound extractablity of the proof system, i.e. \(|\Pr [S_3] - \Pr [S_2]| \le 2 \cdot \mathsf {Adv}^{\mathsf {Ext_2}}_{{\mathcal {A},\mathcal {E}},{\mathsf {\Pi }}}(\kappa )\).
-
Game 4:] As before, but we abort if \(\mathsf {sk}_{\mathsf {PRF}}\ne \mathsf {sk}_{\mathsf {PRF},j}^*\) for any \(j \in [2]\).
-
Transition \(3 \Rightarrow 4\): Both games proceed identically, unless we abort. Let \(j \in [2]\) be such that \(\mathsf {sk}_{\mathsf {PRF}}\ne \mathsf {sk}_{\mathsf {PRF},j}^*\). We bound the abort probability using \(\mathcal {F}\). Let \(\mathcal {C}\) be a computational fixed-value-key-binding challenger. We modify \(\mathsf {KGen}_{\mathsf {D}}\) as follows:
-
\(\mathsf {KGen}_{\mathsf {D}}(1^\kappa )\mathbf{:}\) As before, but let
 .
.
Then we have that \(\mathcal {F}(\mathsf {sk}_{\mathsf {PRF}}, \beta ) = \mathcal {F}(\mathsf {sk}_{\mathsf {PRF},j}^*, \beta )\), hence we forward \(\mathsf {sk}_{\mathsf {PRF},j}^*\) to \(\mathcal {C}\). Thus we built an adversary \(\mathcal {B}\) against fixed-value-key-binding of \(\mathcal {F}\), i.e. \(| \Pr [S_4] - \Pr [S_3] | \le \mathsf {Adv}^{\mathsf {cFKVB}}_{{\mathcal {B}},{\mathcal {F}}}(\kappa ) = \varepsilon (\kappa )\).
-
As we have now ensured that the correct PRF secret key was used to generate \(\rho \) from a, \(\mathsf {sk}_\mathsf {\varSigma }\) is now uniquely determined via the secret sharing. Thus the adversary can no longer win, i.e. \(\Pr [S_4] = 0\). \(\square \)
Extension to NAPS. Following the ideas outlined in [16], Scheme 1 can be extended to an N-time authentication-preventing signature scheme by changing the sharing polynomial \(\rho X + \mathsf {sk}_\mathsf {\varSigma }\) to a polynomial of degree \(N-1\) with coefficients \(\rho _1, \ldots , \rho _{N-1}\) obtained from the PRF via \(\rho _i = \mathcal {F}(\mathsf {sk}_{\mathsf {PRF}}, a\Vert i)\).
Instantiations. The requirement on the signature scheme are very weak, yet finding a suitable combination of primitives can be difficult. Thus we discuss some possible instantiations. One candidate scheme on top of which the DAPS extension can be applied is Picnic [12, 13]. In Picnic the public key \(\mathsf {pk}_\mathsf {\varSigma }\) is the image of the secret key \(\mathsf {sk}_\mathsf {\varSigma }\) under a one-way function built from LowMC [2, 3]. Signatures are then generated by proving this relation using a NIZK from \(\textsc {ZKB++}\) made non-interactive. In this case it is straight forward to use the block cipher LowMC (denoted by \(\mathcal {E}\)) as PRF by setting \(\mathcal {F}(s, x) = \mathcal {E}(s, x) \oplus x\). We argue that this PRF can also be considered a computational fixed-value-key-binding PRF, since it is reasonable to assume that finding a new key which maps one particular input to one particular output is no easier than generic key search. Furthermore, when increasing the block size of LowMC relative to the key size, the existence of second key mapping to the same output becomes increasingly unlikely.
The circuit for the secret sharing can either be implemented using a binary circuit realizing the required arithmetic, or, more efficiently, by computing the sharing bit-wise. For the latter, we consider \(\rho \), p and \(\mathsf {sk}_\mathsf {\varSigma }\) as n bit values, and compute secret shares \(z_i = \rho _i p_i + \mathsf {sk}_{{\mathsf {\varSigma }},i}\) for each bit \(i \in [n]\). Thus only n ANDs are required to implemented the secret sharing. All in all Picnic signatures can be easily extended to a DAPS without requiring extensive changes. We also note that the Fiat-Shamir transformed \(\textsc {ZKB++}\) is in fact simulation-sound extractable NIZK proof systems as confirmed in [15]. Using the signature size formulas, we can estimate DAPS signatures sizes at around 408 KB, meaning there is a overhead of 293 KB compared to Picnic signatures requiring roughly 115 KB in the ROM targeting 256 bit classical security. Analogously to the QROM security of Picnic, Unruh’s transform [31,32,33] can be used to obtain QROM security for the DAPS construction.
Also hash-based signatures such as SPHINCS [8] are well suited for this construction. Similar to the case of Picnic, the PRF can be instantiated using LowMC. However, the consistency proof is more expensive, as computing the public key requires multiple evaluations of hash functions.
Relying on Structured Hardness Assumptions. The situation is different for signature schemes relying on structured hardness assumptions, e.g., those in the discrete logarithm setting such as Schnorr signatures [28], ECDSA and EdDSA [7]. While they would fulfill the requirement for the secret-key-to-public-key relation, i.e., here working in a group \(\mathbb {G}\) with generator g the OWF is of the form \(f(x):=g^x\), the problem is finding an efficient NIZK proof system to prove statements over \(\mathbb {Z}_p\) and in a prime order group \(\mathbb {G}\) simultaneously. Furthermore the NIZK proof system would also need to support statements over binary circuits for the PRF evaluation. Recently, Agrawal et al. [1] made progress in this direction, enabling non-interactive proofs of composite statements for relations over multiple groups and binary circuits. Using these techniques to construct DAPS is an interesting open problem.
4 Extending Any Signature Scheme Using DAPS
Finally, we follow a different direction for our second approach. Here we start from an already existing DAPS and use it to extend any unforgeable signature scheme to a DAPS. Interestingly, both the unforgeability and extraction follow in a black-box way from the signature scheme and the underlying DAPS, respectively. In this construction, the secret key consists of the secret keys of the underlying DAPS and signature scheme. To guarantee extraction of the full secret key, we apply the technique of Bellare et al. [6] and encrypt the key of the signature scheme using a one-time pad derived from the secret key of the DAPS scheme. The public key then consists of that encrypted key and the public keys of the underlying DAPS and signature scheme. However, for extraction of maliciously generated keys, i.e., \(\mathsf {DSE^*}\)-security, this means that public keys need to be extended with a NIZK proof that the encryption was performed correctly. For the sake of simplicity, we thus concentrate on the \(\mathsf {DSE}\) security of the scheme. We present the compiler in Scheme 2.
In the following theorem we formally state that the DAPS construction in Scheme 2 yields an \(\mathsf {EUF}\text {-}\mathsf {CMA}\)-secure DAPS.
Theorem 3
If \({\mathsf {\varSigma }}\) is unforgeable, \({\mathsf {DAPS}}\) is unforgeable and provides verifiability of keys, then the DAPS construction in Scheme 2 is unforgeable in the ROM.
The theorem above is proven in the full version. Additionally, Scheme 1 provides \(\mathsf {DSE}\)-security if the underlying \({\mathsf {DAPS}}\) provides it as well.
Theorem 4
If \({\mathsf {DAPS}}\) provides \(\mathsf {DSE}\)-security, then the construction of DAPS in Scheme 2 provides \(\mathsf {DSE}\)-security as well.
The theorem above is proven in the full version.
5 Conclusion
In this work, we close two important gaps in the literature on DAPS. First, we present a generic DAPS construction, which, in contrast to [16], does not come with the drawback of a polynomially bounded address space. Our construction only relies on assumptions related to symmetric key primitives, which is why we also obtain a candidate for a post-quantum DAPS construction. Second, we also present an alternative generic construction of DAPS which basically shows how to bring DAPS features to any signature scheme. This is of particular practical importance, as it allows to extend arbitrary signature schemes with double signature extraction features. As our compiler works by using an arbitrary DAPS scheme to extend a given signature scheme in a black-box way, this yields more efficient DAPS than previously known for standardized and widely used signature schemes such as ECDSA or EdDSA.
References
Agrawal, S., Ganesh, C., Mohassel, P.: Non-interactive zero-knowledge proofs for composite statements. In: Shacham, H., Boldyreva, A. (eds.) CRYPTO 2018. LNCS, vol. 10993, pp. 643–673. Springer, Cham (2018). https://doi.org/10.1007/978-3-319-96878-0_22
Albrecht, M.R., Rechberger, C., Schneider, T., Tiessen, T., Zohner, M.: Ciphers for MPC and FHE. In: Oswald, E., Fischlin, M. (eds.) EUROCRYPT 2015. LNCS, vol. 9056, pp. 430–454. Springer, Heidelberg (2015). https://doi.org/10.1007/978-3-662-46800-5_17
Albrecht, M.R., Rechberger, C., Schneider, T., Tiessen, T., Zohner, M.: Ciphers for MPC and FHE. IACR Cryptology ePrint Archive 2016/687 (2016)
Ames, S., Hazay, C., Ishai, Y., Venkitasubramaniam, M.: Ligero: lightweight sublinear arguments without a trusted setup. In: CCS, pp. 2087–2104. ACM (2017)
Bellare, M., Poettering, B., Stebila, D.: From identification to signatures, tightly: a framework and generic transforms. In: Cheon, J.H., Takagi, T. (eds.) ASIACRYPT 2016. LNCS, vol. 10032, pp. 435–464. Springer, Heidelberg (2016). https://doi.org/10.1007/978-3-662-53890-6_15
Bellare, M., Poettering, B., Stebila, D.: Deterring certificate subversion: efficient double-authentication-preventing signatures. In: Fehr, S. (ed.) PKC 2017. LNCS, vol. 10175, pp. 121–151. Springer, Heidelberg (2017). https://doi.org/10.1007/978-3-662-54388-7_5
Bernstein, D.J., Duif, N., Lange, T., Schwabe, P., Yang, B.: High-speed high-security signatures. J. Cryptographic. Eng. 2(2), 77–89 (2012)
Bernstein, D.J., et al.: SPHINCS: practical stateless hash-based signatures. In: Oswald, E., Fischlin, M. (eds.) EUROCRYPT 2015. LNCS, vol. 9056, pp. 368–397. Springer, Heidelberg (2015). https://doi.org/10.1007/978-3-662-46800-5_15
Boneh, D., Eskandarian, S., Fisch, B.: Post-quantum group signatures from symmetric primitives. IACR Cryptology ePrint Archive 2018/261 (2018)
Boneh, D., Kim, S., Nikolaenko, V.: Lattice-based DAPS and generalizations: self-enforcement in signature schemes. In: Gollmann, D., Miyaji, A., Kikuchi, H. (eds.) ACNS 2017. LNCS, vol. 10355, pp. 457–477. Springer, Cham (2017). https://doi.org/10.1007/978-3-319-61204-1_23
Canetti, R., Micciancio, D., Reingold, O.: Perfectly one-way probabilistic hash functions (preliminary version). In: STOC, pp. 131–140. ACM (1998)
Chase, M., et al.: Post-quantum zero-knowledge and signatures from symmetric-key primitives. In: CCS, pp. 1825–1842. ACM (2017)
Chase, M., et al.: The Picnic Signature Algorithm Specification (2017). https://github.com/Microsoft/Picnic/blob/master/spec.pdf
Chase, M., Lysyanskaya, A.: On signatures of knowledge. In: Dwork, C. (ed.) CRYPTO 2006. LNCS, vol. 4117, pp. 78–96. Springer, Heidelberg (2006). https://doi.org/10.1007/11818175_5
Derler, D., Ramacher, S., Slamanig, D.: Post-quantum zero-knowledge proofs for accumulators with applications to ring signatures from symmetric-key primitives. In: Lange, T., Steinwandt, R. (eds.) PQCrypto 2018. LNCS, vol. 10786, pp. 419–440. Springer, Cham (2018). https://doi.org/10.1007/978-3-319-79063-3_20
Derler, D., Ramacher, S., Slamanig, D.: Short double- and n-times-authentication-preventing signatures from ECDSA and more. In: EuroS&P, pp. 273–287. IEEE (2018)
Fiat, A., Shamir, A.: How to prove yourself: practical solutions to identification and signature problems. In: Odlyzko, A.M. (ed.) CRYPTO 1986. LNCS, vol. 263, pp. 186–194. Springer, Heidelberg (1987). https://doi.org/10.1007/3-540-47721-7_12
Fischlin, M.: Pseudorandom function tribe ensembles based on one-way permutations: improvements and applications. In: Stern, J. (ed.) EUROCRYPT 1999. LNCS, vol. 1592, pp. 432–445. Springer, Heidelberg (1999). https://doi.org/10.1007/3-540-48910-X_30
Giacomelli, I., Madsen, J., Orlandi, C.: ZKBoo: faster zero-knowledge for Boolean circuits. In: USENIX Security Symposium, pp. 1069–1083. USENIX Association (2016)
Guillou, L.C., Quisquater, J.-J.: A “Paradoxical” indentity-based signature scheme resulting from zero-knowledge. In: Goldwasser, S. (ed.) CRYPTO 1988. LNCS, vol. 403, pp. 216–231. Springer, New York (1990). https://doi.org/10.1007/0-387-34799-2_16
Ishai, Y., Kushilevitz, E., Ostrovsky, R., Sahai, A.: Zero-knowledge proofs from secure multiparty computation. SIAM J. Comput. 39(3), 1121–1152 (2009)
Katz, J., Kolesnikov, V., Wang, X.: Improved non-interactive zero knowledge with applications to post-quantum signatures. IACR Cryptology ePrint Archive 2018/475 (2018)
Micali, S., Reyzin, L.: Improving the exact security of digital signature schemes. J. Cryptol. 15(1), 1–18 (2002)
Poettering, B.: Shorter double-authentication preventing signatures for small address spaces. In: Joux, A., Nitaj, A., Rachidi, T. (eds.) AFRICACRYPT 2018. LNCS, vol. 10831, pp. 344–361. Springer, Cham (2018). https://doi.org/10.1007/978-3-319-89339-6_19
Poettering, B., Stebila, D.: Double-authentication-preventing signatures. In: Kutyłowski, M., Vaidya, J. (eds.) ESORICS 2014. LNCS, vol. 8712, pp. 436–453. Springer, Cham (2014). https://doi.org/10.1007/978-3-319-11203-9_25
Poettering, B., Stebila, D.: Double-authentication-preventing signatures. Int. J. Inf. Sec. 16(1), 1–22 (2017)
Ruffing, T., Kate, A., Schröder, D.: Liar, liar, coins on fire! Penalizing equivocation by loss of bitcoins. In: ACM Conference on Computer and Communications Security, pp. 219–230. ACM (2015)
Schnorr, C.P.: Efficient identification and signatures for smart cards. In: Brassard, G. (ed.) CRYPTO 1989. LNCS, vol. 435, pp. 239–252. Springer, New York (1990). https://doi.org/10.1007/0-387-34805-0_22
Shamir, A.: How to share a secret. Commun. ACM 22(11), 612–613 (1979)
Shor, P.W.: Polynomial-time algorithms for prime factorization and discrete logarithms on a quantum computer. SIAM J. Comput. 26(5), 1484–1509 (1997)
Unruh, D.: Quantum proofs of knowledge. In: Pointcheval, D., Johansson, T. (eds.) EUROCRYPT 2012. LNCS, vol. 7237, pp. 135–152. Springer, Heidelberg (2012). https://doi.org/10.1007/978-3-642-29011-4_10
Unruh, D.: Non-interactive zero-knowledge proofs in the quantum random oracle model. In: Oswald, E., Fischlin, M. (eds.) EUROCRYPT 2015. LNCS, vol. 9057, pp. 755–784. Springer, Heidelberg (2015). https://doi.org/10.1007/978-3-662-46803-6_25
Unruh, D.: Computationally binding quantum commitments. In: Fischlin, M., Coron, J.-S. (eds.) EUROCRYPT 2016. LNCS, vol. 9666, pp. 497–527. Springer, Heidelberg (2016). https://doi.org/10.1007/978-3-662-49896-5_18
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
A One-Way Functions and Pseudorandom Function Families
A One-Way Functions and Pseudorandom Function Families
We recall the definitions of one-way functions and pseudorandom function (families).
Definition 10
(OWF). Let \(f: S \rightarrow P\) be a function. For a PPT adversary \(\mathcal {A}\) we define the advantage function as

The function f is one-way function (OWF) if it is efficiently computable and for all PPT adversaries \(\mathcal {A}\) there exists a negligible function \(\varepsilon (\cdot )\) such that
Definition 11
(PRF). Let \(\mathcal {F}: \mathcal {S} \times D \rightarrow \mathsf {R}\) be a family of functions and let \(\varGamma \) be the set of all functions \(D \rightarrow \mathsf{R}\). For a PPT distinguisher \(\mathcal {D}\) we define the advantage function as

\(\mathcal {F}\) is a pseudorandom function (family) if it is efficiently computable and for all PPT distinguishers \(\mathcal {D}\) there exists a negligible function \(\varepsilon (\cdot )\) such that
Below, we provide a slightly stronger variant of a definition of a notion introduced in [11, 18].
Definition 12
(Fixed-Value-Key-Binding PRF). A PRF family \(\mathcal {F}: \mathcal {S} \times D \rightarrow \mathsf {R}\) and a \(\beta \in D\), is fixed-value-key-binding if for all adversaries \(\mathcal {A}\)

Moreover, we present a relaxed (computational) version of the above definition.
Definition 13
(Computational Fixed-Value-Key-Binding PRF). For a PRF family \(\mathcal {F}: \mathcal {S} \times D \rightarrow \mathsf {R}\) and a \(\beta \in D\), we define the advantage function of a PPT adversary \(\mathcal {A}\) as

\(\mathcal {F}\) is computationally fixed-value-key-binding if for all PPT adversaries there exists as negligible function \(\varepsilon (\cdot )\) such that
Rights and permissions
Copyright information
© 2018 Springer Nature Switzerland AG
About this paper
Cite this paper
Derler, D., Ramacher, S., Slamanig, D. (2018). Generic Double-Authentication Preventing Signatures and a Post-quantum Instantiation. In: Baek, J., Susilo, W., Kim, J. (eds) Provable Security. ProvSec 2018. Lecture Notes in Computer Science(), vol 11192. Springer, Cham. https://doi.org/10.1007/978-3-030-01446-9_15
Download citation
DOI: https://doi.org/10.1007/978-3-030-01446-9_15
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-01445-2
Online ISBN: 978-3-030-01446-9
eBook Packages: Computer ScienceComputer Science (R0)











 and store
and store  .
. .
. .
. .
. .
. .
. , i.e.
, i.e.  .
. .
. and store
and store  .
.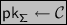 .
. and store
and store  .
. and store
and store  .
. .
.