Incremental Bond Graphs

Abstract

Incremental true bond graphs are used for a matrix-based determination of first-order parameter sensitivities of transfer functions, of residuals of analytical redundancy relations, and of the transfer matrix of the inverse model of a linear multiple-input–multiple-output system given that the latter exists. Existing software can be used for this approach for the derivation of equations from a bond graph and from its associated incremental bond graph and for building the necessary matrices in symbolic form. Parameter sensitivities of transfer functions are obtained by multiplication of matrix entries. Symbolic differentiation of transfer functions is not needed. The approach is illustrated by means of hand derivation of results for small well-known examples.

1 Introduction

Initially, the author of this chapter introduced incremental true bond graphs for bond graph-based determination of frequency domain parameter sensitivities of state and output variables in symbolic form assuming a linearised time-invariant (LTI) model [1, 2]. Contrary to sensitivity pseudo-bond graphs introduced by Cabanellas and his co-workers [3] and used by Gawthrop [4] as well as by Kam and Dauphin-Tanguy [5], bonds in incremental bond graphs do not carry first-order sensitivities of power variables with respect to a parameter but variations (increments) of power variables due to small incremental component parameter changes. Further study of incremental bond graphs has shown that they can be used for other problems due to parameter variations as well. Incremental bond graphs have proven useful for the derivation of the canonical as well as the standard interconnection form of state equations in symbolic form as needed in robustness study [6, 7].

Furthermore, during recent years, the bond graph methodology has also been applied in the field of model-based fault detection and isolation (FDI) and supervision, especially by Samantaray and others at Indian Institute of Technology, Kharagpur, India, and by members of the bond graph modelling group at École Centrale de Lille, France [8–13]. In FDI, analytical redundancy relations (ARRs) , being constraints between known variables, give rise to residuals that can serve as fault indicators . Studying the effect of component parameter uncertainties on the residuals of ARRs helps in fault isolation. In bond graph model-based FDI, ARRs can be obtained from balances at 0- and 1-junctions in symbolic form if unknown variables can be eliminated. Given symbolic processing capabilities either integrated in a bond graph modelling and simulation software environment or separately available by means of a computer algebra system, ARRs can be differentiated with respect to parameters. The residual sensitivities obtained can be used to identify those parameter uncertainties that affect residuals most significantly, which is important because FDI should be robust in the presence of parameter uncertainties.

Alternatively, in [8], parameter sensitivities of residuals of ARRs have been determined by adding sensitivities of power variables at junctions in a sensitivity pseudo-bond graph to which a virtual detector of the parameter sensitivity of the residual has been attached. The sensitivity pseudo-bond graph is connected to a bond graph of the process model under consideration by signals from the bond graph that control modulated elements in the sensitivity bond graph. Recently, it has been briefly shown that incremental bond graphs can serve the same purpose [14].

This chapter demonstrates how the incremental bond graph approach can be used to solve some further problems. To that end, first, the construction of incremental bond graphs (incBGs) and the systematic derivation of sensitivities of output variables is revisited. In the following two sections, incremental true bond graphs are used for a matrix-based determination of parameter sensitivities of transfer functions in symbolic form for linear multiple-input–multiple-output (MIMO) models and for their inverse model (if it exists). Clearly, in case of models of small size, transfer functions can be derived by hand by direct application of Mason’s loop rule on the causal bond graph [15]. More generally, bond graph-based software such as 20-sim^{® 1} [16] or SYMBOLS Shakti™² [17] can be used for this purpose. Once transfer functions have been obtained, they can be partially differentiated symbolically with respect to a component parameter by means of computer algebra systems such as Mathematica^{® 3} or Maple™.⁴ Kam and Dauphin-Tanguy [5] have derived parameter sensitivities by direct application of Mason’s loop rule to a sensitivity pseudo-bond graph.

Advantages of the incremental true bond graph-based approach presented in this chapter are that the matrices can be automatically set up in symbolic form from an original bond graph and its associated incremental bond graph by available software. Parameter sensitivities of transfer functions are then obtained by multiplication of matrix entries which can be performed by software in symbolic form. There is no need for symbolic differentiation of transfer functions. The purpose of determining sensitivities of transfer functions in symbolic form is that, in the design of a robust control, it may be useful to know how sensitive transfer functions are with respect to certain parameter uncertainties.

Furthermore, studying the effect of component parameter uncertainties on the residuals of ARRs helps in fault isolation. Therefore, Section 4.6 addresses the systematic derivation of parameter sensitivities of residuals of ARRs from an incremental bond graph.

The proposed matrix-based approach is illustrated by manual derivation of results for small, well-known examples. For more complex system models, software such as CAMP-G/MATLAB^® together with the Symbolic Math Toolbox™⁵ can be used.

2 Basics of Incremental Bond Graphs

In contrast to sensitivity pseudo-bond graphs, bonds of incremental bond graphs carry variations of power variables instead of their sensitivities with respect to a parameter. The idea is that a parameter variation $\varDelta\varTheta$ results in a perturbation of both power variables at the ports of an element due to the interaction of the element with the rest of the model [1]. Hence, a power variable $v(t)$ (either an effort or a flow) has a nominal part $v_n(t)$ and a variation $\varDelta v(t)$ due to a parameter change:

$$v(t) = v_n(t) + \varDelta v(t)$$

((4.1))

The product $(\varDelta e)(\varDelta f)$ of the incremental power variables of a bond clearly has the physical dimension of power. This suggests to consider incremental bond graphs as true bond graphs, although the product $(\varDelta e)(\varDelta f)$ is only a part of the power change $\varDelta {\mathcal P}$ due to a parameter change [1].

Given a bond graph BG of a system, then the associated incremental bond graph incBG is constructed by just replacing each element by its incremental model. The latter one may be obtained by taking the total differential of the element’s constitutive relations. That is, the Taylor series of the variation $\varDelta v$ of a power variable v is approximated by neglecting higher order terms. Accordingly, the incremental bond graph model built this way is linear, while the model represented by the initial bond graph may be nonlinear. For the determination of first-order parameter sensitivities, it is justified to neglect higher order terms in the Taylor series expansion. In [7], incremental bond graphs are applied for the derivation of two special forms of state equations used for robustness study and in this context the full variation $\varDelta v(t)$ is taken into account, i.e. higher order terms are not neglected. The structure of the incremental bond graph model of a bond graph element is the same in both cases (cf. also [6]). Exact incremental bond graphs have also been used by Junco in the context of Lyapunov’s stability analysis applied on bond graphs without parameter variations but input and state variations [18]. In his 1993 paper, the term incremental bond graph was possibly used for the first time.

As sources do not depend on system parameters, their incremental bond graph model is a source of value zero. Clearly, the incremental model of a 0- (1-) junction again is a 0- (1-) junction. The incremental bond graph representation of other elements differs from the initial bond graph element by additional sinks attached to junctions.

2.1 Incremental Models of Bond Graph Elements

First, the total differential is applied to the constitutive equations of linear 1-port elements, 2-port transformers, and gyrators, in order to keep the presentation simple. As an example, consider a linear 1-port C element with the nominal capacitance C _n . Taking a first-order variation of the constitutive relation

$$q = C \times e_{C}$$

((4.2))

yields after resolving for $\varDelta e_C$

$$\varDelta e_C = \frac{1}{C_n} \, \varDelta q - \frac{\varDelta C}{C_n} \, e_{C_n}$$

((4.3))

The result can be represented by the incremental bond graph model in Fig. 4.1. Note that the output of the MSe source is modulated by a variable from the original bond graph. In case full variations are taken into account, the equation

$$q_n + \varDelta q = (C_n + \varDelta C)(e_n + \varDelta e)$$

((4.4))

leads to the same incremental bond graph model except that the effort source instead of the nominal value $e_n(t)$ is modulated by the perturbed effort $e(t) = e_n (t) + \varDelta e(t)$.

Fig. 4.1

First-order incremental bond graph model of a linear 1-port C element

A first-order incremental bond graph model of a linear 1-port resistor with the nominal resistance R _n is easily obtained in the same way. Taking the total differential of the constitutive relation

$$e_R = R \times f_R$$

((4.5))

gives

$$\varDelta e_R = R_n (\varDelta f_R) + (\varDelta R) f_R$$

((4.6))

or

$$\varDelta f_R = \frac{1}{R_n} \left( \varDelta e_R - \frac{\varDelta R}{R_n} e_R \right)$$

((4.7))

Equation (4.6) may be represented by Fig. 4.2 a, while Fig. 4.2 b depicts (4.7). Hence, the incremental bond graph model does not depend on the assignment of causality.

Fig. 4.2

Incremental bond graph of a 1-port R element in (a) impedance and (b) admittance causality

Let m _n denote the nominal modulus of a 2-port transformer. Then, taking the total differential of its constitutive equations gives

$$\varDelta e_1 = m_n \, \varDelta e_2 + e_{2_n} \, \varDelta m$$

((4.8a))

$$\varDelta f_2 = m_n \, \varDelta f_1 + f_{1_n} \, \varDelta m$$

((4.8b))

In the incremental model of a transformer in Fig. 4.3, the second term on the right-hand side of these equations is represented by modulated sources on both sides of the transformer.

Fig. 4.3

First-order incremental bond graph model of a 2-port transformer

Furthermore, consider an effort-modulated effort source with the constitutive equation

$$E(t) = k \times e(t) \;$$

((4.9))

where $k \in \mathbb{R}$ and $k > 0$. The associated incremental model is depicted in Fig. 4.4 where k _n denotes the nominal value of k.

Fig. 4.4

First-order incremental bond graph model of an effort-modulated effort source

The outlined construction of incremental models is also applicable to linear multiport fields (Section 4.4.3). Finally, the first-order variation of the constitutive equations of nonlinear multiport elements can be represented by an incremental model [2, 14]. Consider, for instance, a nonlinear 1-port resistor with multiple parameters $\varTheta_j \in \mathbb{R}$, $\varTheta_j > 0$, $j = 1, \ldots, m$, $\boldsymbol{ \varTheta} := [ \varTheta_1 \ldots \varTheta_m ]^T$ and the constitutive equation

$$e_R (t) = \varPhi_R ( f_R(t), \boldsymbol{ \varTheta} )$$

((4.10))

The total differential

$$\varDelta e_R (t) = \frac{\partial}{\partial f_R} \varPhi_R ( f_R(t), \boldsymbol{ \varTheta} ) \, \varDelta f_R(t) + \sum_{j = 1}^m \frac{\partial}{\partial \varTheta_j} \varPhi_R ( {f_R}_n(t), \boldsymbol{ \varTheta} ) \, \varDelta \varTheta_j\quad\quad$$

((4.11))

is easily represented by the incremental model in Fig. 4.5.

Fig. 4.5

First-order incremental bond graph model of a nonlinear 1-port R element

In case of a hydraulic orifice described by Bernoulli’s square root law

$$f_R = c_\mathrm{d} \times A \times \mathrm{sign}(e_R) \, \sqrt{ \frac{2}{\rho} | e_R | }$$

((4.12))

the incremental model takes the form depicted in Fig. 4.6. In (4.12), c _d denotes the discharge coefficient, A is the cross section area of the orifice, and ρ is a constant value for the fluid density. In Fig. 4.6, $k := A \sqrt{2/\rho}$. Moreover, it is assumed that $e_R > 0$.

Fig. 4.6

First-order incremental bond graph model of a hydraulic orifice

2.2 Derivation of Output Sensitivity Functions from an Incremental Bond Graph

The previous development of incremental models of bond graph elements implies that the incremental bond graph has the same structure as the original bond graph from which it is obtained except the additional sources or sinks respectively modulated by a power variable of the original bond graph. Their number equals the number of varying parameters. If the original model is linear so is the incremental bond graph. Hence, a combination of software programs such as CAMP-G/MATLAB^® and the Symbolic Math Toolbox™ can be used to symbolically set up the matrices of the state space model for the original as well as for the associated incremental bond graph. In both state space models, the system matrix A is the same. The same holds for the matrix C in the quadruple of matrices of a linear state space model. Again, let Θ denote the vector of all component parameters and an index n indicate a dependency from nominal parameter values. The state space model for the incremental bond graph then reads

$$\varDelta\dot{\textbf{x}}(t) = {\textbf{A}}_n \, \varDelta{\textbf{x}}(t) \, + \, {\textbf{B}}^{*}(\boldsymbol{\varTheta}_n) \, {\textbf{w}}(t)\\$$

((4.13a))

$$\varDelta{\textbf{y}}(t) = {\textbf{C}}_n \, \varDelta{\textbf{x}}(t) \, + \, {\textbf{D}}^{*}(\boldsymbol{\varTheta}_n) \, {\textbf{w}}(t) \;$$

((4.13b))

where the matrices A _n and C _n are set up from the original bond graph with nominal parameters, while the matrices B ^* and D ^* can be set up automatically from the incremental bond graph. The vector w denotes the outputs of the modulated sinks representing parameter variations (cf. Fig. 4.1). It can be written in the form

$${\textbf{w}}(t) \, = \, {\textbf{W}}(t, \boldsymbol{\varTheta}_n) \varDelta\boldsymbol{\varTheta}$$

((4.14))

where ${\textbf{W}}(t, \boldsymbol{\varTheta}_n)$ is a diagonal matrix.

Assuming initial values $\varDelta \textbf{x}(0)$ to be null, then taking the Laplace transform of (4.13a) and (4.13b) and substituting the vector w finally yields the matrix of output sensitivity functions

$${\mathcal L }\frac{\partial\textbf{y}}{\partial \boldsymbol\varTheta} = \underbrace{ [ {\textbf{C}}_n\,(s{\textbf{I}} \, - \, {\textbf{A}}_n)^{-1} \, {\textbf{B}}^* \, + \, {\textbf{D}}^*]}_{\displaystyle =: \textbf{F}^{*}} ({\mathcal L}{\textbf{W}})(s)$$

((4.15))

with $s \in \mathbb{C}$. F ^* the transfer matrix of the incremental bond graph and I the identity matrix of appropriate dimension.

3 Direct and Inverse Models

In subsequent sections, the notions direct model and inverse model will be used.

3.1 Direct Models

The term direct bond graph model refers to a bond graph model in preferred integral causality that enables to compute the dynamics of the state x and the output y in terms of the input u and known parameters Θ (see also Section 6.2.1.1). In the case of a linear time-invariant (LTI) system, the model equations are of state space form

$$\dot{\textbf{x}}(t) = \textbf{A}(\boldsymbol{\varTheta}) \textbf{x}(t) + \textbf{B}(\boldsymbol{\varTheta}) \textbf{u}(t)$$

((4.16a))

$$\textbf{y}(t) = \textbf{C}(\boldsymbol{\varTheta}) \textbf{x}(t) + \textbf{D}(\boldsymbol{\varTheta}) \textbf{u}(t)$$

((4.16b))

with constant coefficient matrices $\textbf{A}, \textbf{B}, \textbf{C}, \textbf{D}$ of appropriate dimensions.

3.2 Inverse Models

Gawthrop and Smith [19] state that ‘A system inverse gives the system input required to generate a given system output.’

In other words, given known parameters Θ, model inversion means to determine the input u in terms of the state, the output y, and time derivatives of y.

Assume that the inverse model of a LTI system exists. Then, the equations of the inverse model can be expressed in the form

$$\dot{\textbf{z}}(t) = \textbf{A}^{*}(\boldsymbol{\varTheta}) \textbf{z}(t) + \sum_{j = 0}^m \textbf{B}_j^{*}(\boldsymbol{\varTheta}) \textbf{y}^{(j)} (t)\\$$

((4.17a))

$$\textbf{u}(t) = \textbf{C}^{*}(\boldsymbol{\varTheta}) \textbf{z}(t) + \sum_{j = 0}^m \textbf{D}_j^{*}(\boldsymbol{\varTheta}) \textbf{y}^{(j)} (t)$$

((4.17b))

where z with $\mathrm{dim}(\textbf{z}) \le \mathrm{dim}(\textbf{x})$ denotes the state vector of the inverse model and y ^(j) the jth time derivative of y (cf. Section 6.2.1.2). The matrices $\textbf{A}^{*}, \textbf{B}_j^{*}, \textbf{C}^{*}, \textbf{D}_j^{*}$ are constant coefficient matrices.

Let initial values $\textbf{z}(0)$ and $\textbf{y}^{(j)}(0)$ be zero. Then Laplace transform of the inverse model equations gives

$$s {\mathcal L} \textbf{z} = \textbf{A}^{*} {\mathcal L} \textbf{z} + \textbf{B}^{*}(s) {\mathcal L} \textbf{y}$$

((4.18a))

$${\mathcal L} \textbf{u} = \textbf{C}^{*} {\mathcal L} \textbf{z} + \textbf{D}^{*}(s) {\mathcal L} \textbf{y}$$

((4.18b))

where $\textbf{B}^{*}(s) := \sum_{j = 0}^m \textbf{B}_j^{*} s^j$ and $\textbf{D}^{*}(s) := \sum_{j = 0}^m \textbf{D}_j^{*} s^j$.

Let $\textbf{H}(s)$ denote the transfer matrix of the direct model. That is,

$${\mathcal L}\textbf{y} = \textbf{H}(s) \, {\mathcal L}\textbf{u}$$

((4.19))

Then, the inverse model exists if H is invertible. In that case, (4.18a) and (4.18b) give for the transfer matrix of the inverse matrix

$$\textbf{H}^{*}(s) := \textbf{H}^{-1}(s) = \textbf{C}^{*}( s \textbf{I} - \textbf{A}^{*} )^{-1} \textbf{B}^{*}(s) + \textbf{D}^{*}(s)$$

((4.20))

Equations (4.17a) and (4.17b) can be considered a generalised state space realisation of $\textbf{H}^{-1}(s)$ [20].

Note that the inverse of a state space model, in general, is not a state space model. In contrast, the inverse of a descriptor system, in general, is again a descriptor system.

The determination of parameter sensitivities of transfer functions from incremental linear inverse bond graph models is considered in Section 4.5.

4 Parameter Sensitivities of Transfer Functions from Direct Bond Graph Models

Let z _j be the variable from the system bond graph controlling the modulated source (sink) representing the jth parameter variation $\varDelta \varTheta_j$ in the incremental bond graph. Then, according to (4.14), the output of the modulated source is

$$w_j = \delta_j \, z_j \, \varDelta \varTheta_j$$

((4.21))

where the coefficient δ _j depends on the type of the element that has been replaced by its incremental model. In case of a capacitor $\delta_j = 1 / C^j_n$ and $z_j = e^j_{C_n}$ (cf. Fig. 4.1) or $\delta_j = 1 / (C^j_n)^2$ and $z_j = q^j_n$. For a linear resistor with the nominal resistance R _n , $\delta_R = 1$, $z_R = f_R$ or $\delta_R = 1 / R_n$ and $z_R = e_R$.

According to (4.15), the ith output sensitivity function with respect to Θ _j , ${\mathcal L} \partial y_i / \partial \varTheta_j$, is a transfer function $F^{*}_{ij}$ multiplied by the Laplace transform of the output $w_j = \delta_j z_j$ of the jth modulated source representing the parameter variation $\varDelta \varTheta_j$:

$${\mathcal L}\frac{\partial y_i}{\partial \varTheta_j} = F^{*}_{ij} \, \delta_j \, {\mathcal L} z_j$$

((4.22))

The Laplace transform ${\mathcal L} z_j$ may be considered one of the output variables ${\mathcal L} y_{j'}$ of the original bond graph related through transfer functions $F_{j'\kappa}$ to its n inputs u _κ :

$${\mathcal L} z_j = {\mathcal L} y_{j'} = \sum_{\kappa = 1}^{n} F_{j'\kappa} \, {\mathcal L} u_\kappa$$

((4.23))

Substitute index j′ by i. Then,

$${\mathcal L} y_i = \sum_{\kappa = 1}^{n} F_{i \kappa} \, {\mathcal L} u_\kappa$$

((4.24))

Hence,

$$\frac{\partial {\mathcal L} y_i}{\partial \varTheta_j} = \sum_{\kappa = 1}^{n} \frac{\partial F_{i \kappa}}{\partial \varTheta_j} {\mathcal L} u_\kappa$$

((4.25))

The entry ${\mathcal L} \partial y_i / \partial \varTheta_j$ of the matrix $\partial {\mathcal L}\textbf{y} / \partial \boldsymbol{\varTheta}$ is obtained from (4.15) and (4.21).

$$\frac{\partial}{\partial \varTheta_j} {\mathcal L} y_i = \sum_{\kappa = 1}^n \, F^{*}_{ij} \delta_j F_{j' \kappa} {\mathcal L} u_\kappa$$

((4.26))

Comparison of (4.25) and (4.26) finally leads to the result

$$\frac{\partial F_{i \kappa}}{\partial \varTheta_j} = F^{*}_{ij} \delta_j F_{j' \kappa}$$

((4.27))

An advantage of this matrix-based approach to a determination of parameter sensitivities of transfer functions is that available software such as CAMP-G/MATLAB^® and the Symbolic Math Toolbox™ can be used for the steps of the procedure. First, equations are automatically derived from both the original bond graph and its associated incremental bond graph, and the matrices of their state space models are built in symbolic form.

Once the transfer matrices $\textbf{F} := (F_{ij})$ for the bond graph and $\textbf{F}^{*} = (F^{*}_{ij})$ for the incremental bond graph have been set up in symbolic form, the factors of the right-hand side of (4.27) are known so that any first-order parameter sensitivity of a transfer function of interest can be determined symbolically by multiplying entries from both matrices. Clearly, given a transfer function derived from a causal bond graph, its sensitivity with respect to a parameter may also be obtained by symbolic differentiation. If the incremental bond graph approach is used then the symbolic differentiation is not necessary. The use of first-order incremental bond graph models implies that the total differential of constitutive element equations has already been taken.

The incremental bond graph has the same structure as the bond graph. Therefore, the expression for both transfer functions F and F ^* includes the factor $(s \textbf{I} - \textbf{A}_n)^{-1}$ (cf. (4.15)). Hence, since the inverse of a matrix M can be written as $\textbf{M}^{-1} = \mathrm{Adj}(\textbf{M}) / \mathrm{det}(\textbf{M})$, the denominator in the right-hand side product of (4.27) equals the square of $\mathrm{det}(s \textbf{I} - \textbf{A}_n)$.

In the next two sections, the approach is illustrated by application to two often considered small example systems. Note that in all examples in this chapter the co-energy variables of energy stores in integral causality are chosen as state variables.

Fig. 4.7

Schematic of a coupled hydraulic tank system

4.1 Example: Coupled Hydraulic Tanks

Consider the coupled hydraulic tanks depicted in Fig. 4.7. The nonlinear characteristic of the valves is given by Bernoulli’s well-known square root law. It is assumed that the constitutive equations of the valves have been linearised around an operating point so that the model equations are linear and Laplace transform can be applied.

The two tank pressures and the flow through the second valve are measured as indicated by the detectors in the bond graph in Fig. 4.8. In the following, the pressure in the right-hand side tank, p ₂, and the outflow, Q _o, from this tank are considered the output variables of interest. Then, the following linear state space model can be derived from the bond graph of Fig. 4.8.

$$\underbrace{ \left[ \begin{array}{c} \dot{p}_1 \\ \dot{p}_2 \end{array} \right]}_{\displaystyle \dot{\textbf{x}}} = \underbrace{ \left[ \begin{array}{cc} \displaystyle - \frac{1}{C_1 R_1} & \displaystyle \frac{1}{C_1 R_1} \\ \displaystyle \frac{1}{C_2 R_1} & \displaystyle - \frac{1}{C_2} \left( \frac{1}{R_1} + \frac{1}{R_2} \right) \end{array} \right]}_{\displaystyle \textbf{A}_n} \, \underbrace{ \left[ \begin{array}{c} p_1 \\ p_2 \end{array} \right]}_{\displaystyle \textbf{x}} + \underbrace{ \left[ \begin{array}{c} \displaystyle \frac{1}{C_1} \\ \displaystyle 0 \end{array} \right]}_{\displaystyle \textbf{B}_n} \, \underbrace{ \left[ Q_p \right]}_{\displaystyle \textbf{u}}$$

((4.28a))

$$\underbrace{ \left[ \begin{array}{c} p_2 \\ Q_o \end{array} \right]}_{\displaystyle \textbf{y}} = \underbrace{ \left[ \begin{array}{cc} \displaystyle 0 & \displaystyle 1 \\ \displaystyle 0 & \displaystyle \frac{1}{R_2} \end{array} \right]}_{\displaystyle \textbf{C}_n} \, \left[ \begin{array}{c} p_1 \\ p_2 \end{array} \right] + \underbrace{ \left[ 0 \right]}_{\displaystyle \textbf{D}_n} \, \left[ Q_p \right]$$

((4.28b))

Fig. 4.8

Bond graph of the coupled hydraulic tank system

4.1.1 Symbolic Differentiation of a Transfer Function with Respect to a Parameter

For a general linear MIMO system, Laplace transform of the equations of the state space model results in the matrix F of transfer functions:

$$\begin{array}{rcl}{\mathcal L}\textbf{y} & = & \underbrace{ \left[ \textbf{C}_n \left( s \textbf{I} - \textbf{A}_n \right)^{-1} \textbf{B}_n + \textbf{D}_n \right]}_{\displaystyle \textbf{F}} {\mathcal L}\textbf{u} \\ & = & \left[ \textbf{C}_n \frac{1}{\varDelta} {\mathrm{Adj}}\left( s \textbf{I} - \textbf{A}_n \right) \textbf{B}_n + \textbf{D}_n \right] {\mathcal L}\textbf{u} \; \end{array}$$

((4.29))

where $\varDelta := \mathrm{det}\left( s \textbf{I} - \textbf{A}_n \right)$.

In the case of the example under consideration, evaluation of (4.29) yields

$$\begin{aligned} \left[ \begin{array}{c} {\mathcal L}p_2 \\ {\mathcal L}Q_o \end{array} \right] & = & \left[ \begin{array}{cc} \displaystyle 0 & \displaystyle 1 \\ \displaystyle 0 & \displaystyle \frac{1}{R_2} \end{array} \right] \frac{1}{\varDelta} \left[ \begin{array}{cc} \displaystyle s + \frac{1}{C_2} \left( \frac{1}{R_1} + \frac{1}{R_2} \right) & \displaystyle \frac{1}{C_1 R_1} \\ \displaystyle \frac{1}{C_2 R_1} & \displaystyle s + \frac{1}{C_1 R_1} \end{array} \right] \, \left[ \begin{array}{c} \displaystyle \frac{1}{C_1} \\ \displaystyle 0 \end{array} \right] \, \left[ {\mathcal L} Q_p \right] \\ & = & \underbrace{ \frac{1}{\varDelta} \frac{1}{C_1} \left[ \begin{array}{c} 1 \\ \displaystyle \frac{1}{R_2} \end{array} \right] \frac{1}{C_2 R_1}}_{\displaystyle \textbf{F}} \left[ {\mathcal L}Q_p \right] \end{aligned}$$

((4.30))

Let $F_1 := {\mathcal L}p_2 / {\mathcal L}Q_p$. Then, for instance,

$$\frac{\partial F_1}{\partial R_2} = - \displaystyle \frac{1}{C_1 C_2 R_1} \frac{1}{\varDelta^2} \frac{\partial \varDelta}{\partial R_2}$$

((4.31))

where

$$- \displaystyle \frac{\partial \varDelta}{\partial R_2} = \frac{1}{C_2} \frac{1}{R_2^2} \left( s + \frac{1}{C_1 R_1} \right)$$

((4.32))

4.1.2 Application of the Incremental Bond Graph Approach

Figure 4.9 depicts the associated incremental bond graph accounting for parameter variation $\varDelta R_2$. Clearly, due to the linearity of the model, further parameter variations can be superimposed by replacing bond graph elements by their incremental model, which basically means adding a modulated sink accounting for the parameter variation.

Fig. 4.9

Incremental bond graph of the coupled hydraulic tank system accounting for parameter variation $\varDelta R_2$

The state space model derived from the associated incremental bond graph reads

$$\left[ \begin{array}{c} \varDelta\dot{p}_1 \\ \varDelta\dot{p}_2 \end{array} \right] = \textbf{A}_n \left[ \begin{array}{c} \varDelta p_1 \\ \varDelta p_2 \end{array} \right] + \underbrace{ \left[ \begin{array}{c} \displaystyle 0 \\ \displaystyle \frac{1}{C_2 R_2} \end{array} \right]}_{\displaystyle \textbf{B}^{*}} \, \underbrace{ \left[ Q_o \varDelta R_2 \right]}_{\displaystyle \textbf{w}}$$

((4.33a))

$$\left[ \begin{array}{c} \varDelta p_2 \\ \varDelta Q_o \end{array} \right] = \textbf{C}_n \left[ \begin{array}{c} \varDelta p_1 \\ \varDelta p_2 \end{array} \right] + \underbrace{ \left[ \begin{array}{c} 0 \\ \displaystyle - \frac{1}{R_2} \end{array} \right]}_{\displaystyle \textbf{D}^{*}} \textbf{w}$$

((4.33b))

According to (4.29), the matrix of transfer functions, F ^*, is given by the equation

$${\mathcal L}\varDelta\textbf{y} = \underbrace{ \left[ \textbf{C}_n \left( s \textbf{I} - \textbf{A}_n \right)^{-1} \textbf{B}^{*} + \textbf{D}^{*} \right]}_{\displaystyle \textbf{F}^{*}} {\mathcal L}\textbf{w}$$

((4.34))

In the case of the coupled hydraulic tank system, (4.34) reads

$${\mathcal L} \left[ \begin{array}{c} \varDelta p_2 \\ \varDelta Q_o \end{array} \right] = \left[ \begin{array}{c} \displaystyle \frac{1}{C_2 R_2} \frac{1}{\varDelta} \left( s + \frac{1}{C_1 R_1} \right) \\ \displaystyle \frac{1}{C_2 R_2^2} \frac{1}{\varDelta} \left( s + \frac{1}{C_1 R_1} \right) - \frac{1}{R_2} \end{array} \right] \, {\mathcal L} \left[ Q_o \varDelta R_2 \right]$$

((4.35))

Substituting ${\mathcal L}Q_o$ by means of (4.30) gives

$$\varDelta {\mathcal L}p_2 = \underbrace{ \displaystyle \frac{1}{C_2 R_2} \frac{1}{\varDelta} \left( s + \frac{1}{C_1 R_1} \right)}_{\displaystyle F^{*}_1} \times \underbrace{1}_{\displaystyle \delta_{R_2}} \times \underbrace{\frac{1}{\varDelta} \frac{1}{C_1} \frac{1}{R_2} \frac{1}{C_2 R_1}}_{\displaystyle F_2} {\mathcal L}Q_p \, \varDelta R_2\quad\quad$$

((4.36))

Hence,

$$\frac{\partial F_1}{\partial R_2} = \frac{\partial}{\partial R_2} \left( \frac{{\mathcal L}p_2}{{\mathcal L}Q_p} \right) \; = \; \frac{1}{C_1 C_2 R_1} \frac{1}{\varDelta^2} \underbrace{ \frac{1}{C_2 R_2^2} \left( s + \frac{1}{C_1 R_1} \right)}_{\displaystyle - \frac{\partial \varDelta}{\partial R_2}}$$

((4.37))

in accordance with (4.31).

This example illustrates that a parameter sensitivity of a transfer function such as $\partial F_1 / \partial R_2$ (4.31) can be obtained by multiplication of an entry of the transfer matrix F of the original bond graph model and an entry of the transfer matrix F ^* of the associated incremental bond graph.

For other sensitivities of transfer functions, e.g. $\partial F_1 / \partial C_1$, the coefficients of the polynomials in the numerator and in the denominator are complex expressions. Accordingly, more effort is necessary to show by manual formulae manipulation that the result obtained by the incremental bond graph approach equals the one that direct symbolic differentiation of the transfer function yields. For instance,

$$\frac{\partial F_1}{\partial C_1} = \frac{1}{C_2 R_1} \frac{\partial}{\partial C_1} \left( \frac{1}{\varDelta} \frac{1}{C_2} \right)$$

((4.38))

Performing the right-hand side differentiation results in a lengthy expression.

In any case, software such as CAMP-G/MATLAB^® in cooperation with the Symbolic Math Toolbox™ can set up the matrices needed for establishing both transfer matrices in symbolic form from both bond graphs.

4.2 Example: Fixed Field DC Motor

The second illustrative example is the well-known voltage-driven separately excited DC motor that drives a mechanical load against an external moment (Fig. 4.10). Figure 4.11 shows a direct bond graph model. Like the previous example, this model also has two inputs and two outputs. That is, a transfer matrix H with four transfer functions F _ij can be derived:

$$\left[ \begin{array}{c} {\mathcal L} i_a \\ {\mathcal L} \omega \end{array} \right] = \underbrace{ \left[ \begin{array}{cc} F_{11} & F_{12} \\ F_{21} & F_{22} \end{array} \right]}_{\displaystyle \textbf{H}} \, \left[ \begin{array}{l} {\mathcal L} E \\ {\mathcal L} M_\mathrm{load} \end{array} \right]$$

((4.39))

Fig. 4.10

Fixed field DC motor

Fig. 4.11

Direct bond graph model of a fixed field DC motor

A question that might be of interest is how sensitive these transfer functions are with respect to variations of the mechanical friction on the mechanical load side. Suppose that $\partial F_{21} / \partial R_m$ is to be determined. In this case, the associated incremental bond graph is obtained from the original bond graph by just replacing the resistor R : R _m by its incremental bond graph model. Figure 4.12 shows the result.

Fig. 4.12

Incremental true bond graph of the DC motor accounting for a variation in mechanical friction

4.2.1 Symbolic Differentiation of a Transfer Function with Respect to a Parameter

Derivation of the Laplace transformed state equations from the original bond graph in Fig. 4.11 yields

$$\underbrace{ \left[ \begin{array}{cccc} \displaystyle s + \frac{R_a}{L_a} & \displaystyle \frac{k_T}{L_a} \\ \displaystyle - \frac{k_T}{J_m} & \displaystyle s + \frac{R_m}{J_m} \end{array} \right]}_{\displaystyle ( s \textbf{I} - \textbf{A}_n )} \underbrace{ \left[ \begin{array}{c} {\mathcal L } i_a \\ {\mathcal L} \omega \end{array} \right]}_{\displaystyle {\mathcal L} \textbf{x}} = \underbrace{ \left[ \begin{array}{cc} \displaystyle \frac{1}{L_a} & 0 \\ 0 & \displaystyle \frac{1}{J_m} \end{array} \right]}_{\displaystyle \textbf{B}_n} \underbrace{ \left[ \begin{array}{l} {\mathcal L} E \\ {\mathcal L} M_\mathrm{load} \end{array} \right]}_{\displaystyle {\mathcal L} \textbf{u}}$$

((4.40))

Solving for ${\mathcal L}\textbf{x}$ gives for the second component ${\mathcal L} x_2 = {\mathcal L} \omega = {\mathcal L} y_2$

$${\mathcal L} \omega = \underbrace{\frac{k_T}{(L_a J_m) \varDelta }}_{\displaystyle F_{21}} {\mathcal L} E + \underbrace{\frac{L_a s + R_a}{(L_a J_m) \varDelta }}_{\displaystyle F_{22}} {\mathcal L} M_\mathrm{load}$$

((4.41))

where

$$\varDelta := \mathrm{det} (s \textbf{I} - \textbf{A}_n )\, = \, \left(s + \displaystyle \frac{R_a}{L_a}\right)\left(s + \displaystyle \frac{R_m}{J_m}\right) + \displaystyle \frac{k_T^2}{J_m L_a}$$

Accordingly,

$$\begin{aligned} \frac{\partial F_{21}}{\partial R_m} & = & \frac{\partial}{\partial R_m} \left( \frac{{\mathcal L}\omega}{{\mathcal L}E} \right) \\ & = & \underbrace{\frac{k_T}{(L_a J_m) \varDelta}}_{\displaystyle F_{21}} \, \frac{-1}{\varDelta} \frac{\partial \varDelta}{\partial R_m} \; = \; F_{21} \, \frac{-1}{J_m \, \varDelta} \left( s + \frac{R_a}{L_a} \right) \end{aligned}$$

((4.42))

4.2.2 Application of the Incremental Bond Graph Approach

Derivation of the state equations from the incremental bond graph yields

$$\underbrace{ \left[ \begin{array}{c} {\mathcal L} \varDelta i \\ {\mathcal L} \varDelta \omega \end{array} \right]}_{\displaystyle {\mathcal L} \varDelta {\textbf{x}}} = ( s \textbf{I} - \textbf{A}_n )^{-1} \underbrace{ \left[ \begin{array}{c} 0 \\ - \displaystyle \frac{1}{J_m} \end{array} \right]}_{\displaystyle\textbf{B}^{*}} \underbrace{ \left[ {\mathcal L} \omega \right] \left[ \varDelta R_m \right]}_{\displaystyle {\mathcal L} \textbf{w}}$$

((4.43))

$$= - \frac{1}{J_m \varDelta} \left[ \begin{array}{c} \displaystyle - \frac{k_T}{L_a} \\ \displaystyle s + \frac{R_a}{L_a} \end{array} \right] \left[ {\mathcal L} \omega \right] \left[ \varDelta R_m \right]$$

((4.44))

Hence,

$$\varDelta {\mathcal L} \omega = \underbrace{ - \frac{1}{J_m \, \varDelta } \left( s + \frac{R_a}{L_a} \right)}_{\displaystyle F^{*}_{21}} ( {\mathcal L} \omega ) \varDelta R_m$$

((4.45))

Combining this result derived from the incremental bond graph with the one obtained from the initial bond graph (cf.(4.41)) gives

$$\varDelta {\mathcal L} \omega = F^{*}_{21} \, \left[ \, F_{21} {\mathcal L} E + F_{22} {\mathcal L}M _\mathrm{load} \, \right] \varDelta R_m$$

((4.46))

Partial differentiation of (4.39) yields

$$\frac{\partial {\mathcal L}\omega}{\partial R_m} = \frac{\partial F_{21}}{\partial R_m} {\mathcal L}E \, + \, \frac{\partial F_{22}}{\partial R_m} {\mathcal L}M_\mathrm{load}$$

((4.47))

Comparison of the last two equations finally gives the result

$$\frac{\partial F_{21}}{\partial R_m} = F^{*}_{21} F_{21}$$

((4.48))

in accordance with (4.42) observing (4.45).

A Bode plot of $\partial F_{21} / \partial R_m$ can be easily constructed by means of the low-frequency and the high-frequency asymptotes of its factors observing that Δ is a second-order polynomial in s. The amplitude drops for $\omega > \omega_n :\,= [(R_a R_m + k_T^2)/(L_a J_m)]^{1/2}$ with a slope of −3 and the phase drops from $180^{\circ}$ to $-90^{\circ}$.

Figure 4.13 shows a Bode plot for the numerical values in Table 4.1 obtained by using Scilab [21].

Fig. 4.13

Parameter sensitivity of transfer function F ₂₁ with respect to R _m

Table 4.1 Parameter values of the fixed field DC motor

4.3 Bond Graphs with Linear Multiport Fields

In this section, energy stores and resistors are allowed to be linear multiport fields.

4.3.1 I-Fields

For illustration, consider the simple electrical circuit with mutually interacting coils depicted in Fig. 4.14. The full circles above the coils denote their relative orientation. As the two currents, i ₁ and i ₂, both enter their coil at the end marked by the full circle, the mutual inductance coefficient M ₁₂ in the constitutive equations is positive.

Fig. 4.14

Electrical circuit with mutually interacting coils

In the bond graph of Fig. 4.15, the mutually interacting coils are represented by a 2-port I-field. Its constitutive equations read

$$\left[ \begin{array}{c} \lambda_1 \\ \lambda_2 \end{array} \right] \; = \; \underbrace{ \left[ \begin{array}{cc} L_1 & M_{12} \\ M_{12} & L_2 \end{array} \right]}_{\displaystyle \textbf{L}} \, \left[ \begin{array}{c} i_1 \\ i_2 \end{array} \right] \;$$

((4.49))

where L ₁ and L ₂ denote the self-inductance coefficients of the two coils, M ₁₂ the mutual inductance coefficient, and λ ₁ and λ ₂ the flux linkages.

Fig. 4.15

Bond graph of the circuit in Fig. 4.14

Taking the total differential of the two flux linkages yields

$$\varDelta \lambda_1 = L_1 \varDelta i_1 + M_{12} \varDelta i_2 + (\varDelta L_1) i_1 + (\varDelta M_{12}) i_2$$

((4.50a))

$$\varDelta \lambda_2 = M_{12} \varDelta i_1 + L_2 \varDelta i_2 + (\varDelta M_{12}) i_1 + (\varDelta L_2) i_2$$

((4.50b))

Now, in both equations, the flux linkages $\varDelta \lambda_i$ are expressed by voltages $\varDelta u_i$. After Laplace transform the equations take the form

$$\begin{aligned} \underbrace{ \left[ \begin{array}{c} {\mathcal L}\varDelta u_1 \\ {\mathcal L}\varDelta u_2 \end{array} \right]}_{\displaystyle {\mathcal L}\varDelta \textbf{x}} & = & s \textbf{L} \underbrace{ \left[ \begin{array}{c} {\mathcal L}\varDelta i_1 \\ {\mathcal L}\varDelta i_2 \end{array} \right]}_{\displaystyle {\mathcal L}\varDelta \textbf{i}} + s \underbrace{ \left[ \begin{array}{c} (\varDelta L_1){\mathcal L}i_1 + (\varDelta M_{12}){\mathcal L}i_2 \\ (\varDelta M_{12}){\mathcal L}i_1 + (\varDelta L_2){\mathcal L}i_2 \end{array} \right]}_{\displaystyle {\mathcal L}\textbf{w}} \\ & = & s \textbf{L} {\mathcal L}\varDelta \textbf{i} + s (\varDelta \textbf{L}) {\mathcal L}\textbf{i} \end{aligned}$$

((4.51))

Equation (4.51) can be represented by a linear I-field in derivative causality and modulated effort sinks accounting for the parameter variations added to 1-junctions. The incremental bond graph model of a linear 2-port I-field is depicted in Fig. 4.16. The prime denotes differentiation with respect to time. Accordingly, Fig. 4.17 shows the incremental bond graph of the circuit in Fig. 4.14.

Fig. 4.16

Incremental bond graph model of a linear two-port I-field

Fig. 4.17

Incremental bond graph of the circuit in Fig. 4.14

The variations of the currents are determined by the two resistors in the incremental bond graph of Fig. 4.17.

$${\mathcal L}\varDelta i = \underbrace{ \left[ \begin{array}{cc} \displaystyle - \frac{1}{R_1} & 0 \\ 0 & \displaystyle - \frac{1}{R_2} \end{array} \right]}_{\displaystyle \textbf{A}} {\mathcal L}\varDelta \textbf{x}$$

((4.52))

Substitution into (4.16) gives the transfer matrix F ^* relating the inputs into the incremental bond graph to the current variations considered as outputs:

$${\mathcal L}\varDelta i = \underbrace{ (\textbf{I} - s \textbf{A} \textbf{L})^{-1} s \textbf{A}}_{\displaystyle \textbf{F}^{*}} {\mathcal L}\textbf{w}$$

((4.53))

$$= \textbf{F}^{*} (\varDelta \textbf{L}) {\mathcal L}\textbf{i}$$

((4.54))

The following equations are obtained from the bond graph of the circuit (Fig. 4.15). The first one is the constitutive equation of the I-field:

$${\mathcal L}\textbf{x} = s \textbf{L} {\mathcal L} \textbf{i}$$

((4.55))

and

$${\mathcal L}\textbf{i} = \textbf{A}{\mathcal L}\textbf{x} + \underbrace{ \left[ \begin{array}{c} \displaystyle \frac{1}{R_1} \\ 0 \end{array} \right]}_{\displaystyle \textbf{B}} \underbrace{ [ {\mathcal L}E ]}_{\displaystyle {\mathcal L} \textbf{u}}$$

((4.56))

Substitution of (4.55) into (4.56) gives the transfer matrix F relating the input ${\mathcal L}\textbf{u}$ into the bond graph to the current ${\mathcal L}\textbf{i}$:

$${\mathcal L}\textbf{i} = \underbrace{ (\textbf{I} - s\textbf{A} \textbf{L})^{-1} \textbf{B}}_{\displaystyle \textbf{F}} {\mathcal L}\textbf{u}$$

((4.57))

Finally, replacing ${\mathcal L}\textbf{i}$ in (4.54) by (4.57) shows again that the Laplace transformed variation of an output variable of the incremental bond graph is determined by the product of a transfer matrix F ^* from the incremental bond graph and a transfer matrix F from the original bond graph:

$${\mathcal L}\varDelta \textbf{i} = \textbf{F}^{*} ( \varDelta \textbf{L} ) \textbf{F} {\mathcal L}\textbf{u}$$

((4.58))

Let $\varDelta \varTheta$ be any of the three parameter variations $\varDelta L_1, \varDelta L_2,$ and $\varDelta M_{12}$. Then the sensitivity $\partial \textbf{F} / \partial \varDelta \varTheta$ can be obtained from (4.58). For instance, assume that the mutual inductance M ₁₂ is the only varying parameter, i.e.

$$\varDelta \textbf{L} = \varDelta M_{12} \left[ \begin{array}{cc} 0 & 1 \\ 1 & 0 \end{array} \right]$$

((4.59))

then (4.58) takes the form

$$\begin{aligned} \left[ \begin{array}{c} {\mathcal L} \varDelta i_1 \\ {\mathcal L} \varDelta i_2 \end{array} \right] & = & \left[ \begin{array}{cc} F^{*}_{11} & F^{*}_{12} \\ F^{*}_{21} & F^{*}_{22} \end{array} \right] \varDelta M_{12} \left[ \begin{array}{cc} 0 & 1 \\ 1 & 0 \end{array} \right] \left[ \begin{array}{c} F_{11} \\ F_{21} \end{array} \right] \, [ {\mathcal L}E ] \\ & = & \underbrace{ \left[ \begin{array}{c} F^{*}_{12} F_{11} + F^{*}_{11} F_{21} \\ F^{*}_{22} F_{11} + F^{*}_{21} F_{21} \end{array} \right]}_{\displaystyle \frac{\partial \textbf{F}}{\partial M_{12}}} \varDelta M_{12} {\mathcal L}E \end{aligned}$$

((4.60))

4.3.2 C-Fields

Two-port C-fields are suitable for a convenient representation of devices such as the movable plate capacitor, an air gap between a fixed and a movable magnetic pole [22], or piezoelectric crystals [6]. Again, taking the total differential of the output variables of a linear 2-port C-field results in relations between incremental power variables that can be depicted by an incremental bond graph similar to the one in Fig. 4.16.

For instance, consider a piezoelectric crystal. Assume a one-dimensional model of the crystal and let F be the force acting on the crystal, x the mechanical deformation, u the voltage across the crystal, and q its electrical charge for the time instant t. Then a commonly known form of the constitutive equations is

$$\left[ \begin{array}{c} x \\ q \end{array} \right] = \left[ \begin{array}{cc} C_\mathrm{m} & d_{\varepsilon} \\ d_{\varepsilon} & C_\mathrm{e} \end{array} \right] \, \left[ \begin{array}{c} F \\ u \end{array} \right]$$

((4.61))

where C _m denotes the mechanical compliance, d _ε the piezoelectric coupling, and C _e the electrical capacitance. Accordingly, the equations for the first-order variations of x and q differentiated with respect to time read

$$\varDelta \dot{x} = C_\mathrm{m} \varDelta \dot{F} + d_{\varepsilon} \varDelta \dot{u} + (\varDelta C_\mathrm{m}) \dot{F} + (\varDelta d_{\varepsilon}) \dot{u}$$

((4.62a))

$$\varDelta \dot{q} = d_{\varepsilon} \varDelta \dot{F} + C_\mathrm{e} \varDelta \dot{u} + (\varDelta d_{\varepsilon}) \dot{F} + (\varDelta C_\mathrm{e}) \dot{u}$$

((4.62b))

and can be depicted by the incremental bond graph model in Fig. 4.18.

Fig. 4.18

Incremental bond graph model of a linear 2-port C-field

5 Parameter Sensitivities of Transfer Functions of Linear Inverse Models

So far, parameter sensitivities of transfer functions of direct models have been considered. This section presents an incremental bond graph-based procedure to the symbolic determination of parameter sensitivities of transfer functions of linear inverse models given that the latter exist.

A bond graph representation of the inverse model can serve several purposes. For instance, in the case of a single-input–single-output (SISO) system, the number of energy stores in integral causality in the bond graph of the inverse model equals the number of poles of the transfer function of the inverse model and thus equals the number of zeros of the transfer function of the direct model. The number and the location of the zeros of a linear time-invariant (LTI) system are of importance for its control. The poles of a transfer function of the direct model arise from the C and I stores in integral causality. In contrast, as has been pointed out by Gawthrop [23], the dynamics giving rise to zeros in the direct model cannot be readily identified from its bond graph.

In general, an inverse model does not have a physical realisation. The behaviour of a physical system can approximate the one of an inverse model. Nevertheless, inverse models and transfer functions of inverse models are needed, e.g. in the design of a control that ensures trajectory tracking and disturbance rejection. Clearly, the control should be robust in the presence of some uncertain parameter values.

Ngwompo and his co-authors [24] state that a LTI SISO system is structurally invertible if there is at least one causal path in the causal direct bond graph between the input variable and the output variable ([24, Proposition 1, p. 162]). Furthermore, they show how the state equations of the inverse system can be directly determined from a causal direct bond graph model or from a bicausal bond graph. (In order to support tasks such as bond graph-based system inversion, Gawthrop extended the concept of computational causality by introducing the notion of bicausality [25, 19].) Clearly, the state equations of the inverse model of a SISO system can be converted into a transfer function.

5.1 Construction of the Bond Graph of the Inverse Model

For a linear multiple-input–multiple-output system, Ngwompo and his co-workers have developed criteria that can be checked on the causal bond graph of a direct model to decide whether the inverse model exists [26–28]. Moreover, they provide a procedure for constructing an inverse bond graph model that represents the inverse system of minimal order. Basically, the procedure requires to identify a unique set of disjoint input–output causal paths in the direct bond graph, to replace both sources and detectors by source–sensors (usually denoted by the symbol SS [19]), to assign and propagate bicausality along the bonds of each disjoint input–output causal path from the sensor to the source, and to apply the standard causality assignment procedure (SCAP) to the rest of the bond graph ([26, Algorithm 1, p. 111]).

In case the inverse model exists and input–output pairs are collocated, the bond graph of the inverse model can be obtained from the direct bond graph model by replacing sources by their dual or by source–sensors, by applying inverted causality to the latter, and by reassigning causality to the graph.

Let H ^* denote the transfer matrix of the inverse model . Then

$${\mathcal L} \textbf{u} = \textbf{H}^{*} {\mathcal L} \textbf{y}$$

((4.63))

Hence, the partial derivative with respect to a parameter Θ _i is

$$\frac{\partial {\mathcal L} \textbf{u}}{\partial {\varTheta_i}} = \frac{\partial \textbf{H}^{*}}{\partial {\varTheta_i}} {\mathcal L} \textbf{y} + \textbf{H}^{*} \frac{\partial {\mathcal L} \textbf{y}}{\partial {\varTheta_i}}$$

((4.64))

if the input vector y may depend on Θ _i .

5.2 Construction of the Incremental Bond Graph of the Inverse Model

The incremental bond graph of the inverse model is constructed by replacing all elements with varying parameters by their incremental model in the bond graph of the inverse model. Thus, the latter contains modulated sources (sinks) controlled by output variables z _i of the direct model. That is, in addition to the vector $\varDelta \textbf{y}$, output variables $w_i = \delta_i \, z_i \, \varDelta \varTheta_i$ of the modulated sources (sinks) are inputs into the incremental bond graph of the inverse model. Moreover, assignment of causalities to the bond graph of the inverse model commonly leads to derivative causality at the port of at least some of the energy stores. That is, the order of the inverse model is lower than the one of the direct model. For linear time-invariant (LTI) models, storage ports with differential causality imply that time derivatives of inputs will occur in the equations for the states of the energy stores in integral causality [29].

5.3 Matrix-Based Determination of Transfer Function Sensitivities for the Inverse Model

Now, let $\varDelta \textbf{x}_i^{*}$ denote variations of the states of all storage elements in integral causality, $\varDelta \textbf{x}_d^{*}$ the variations of the non-states of all energy stores in differential causality in the incremental bond graph of the inverse model, and $\varDelta \textbf{x}^{*}$ the descriptor vector $\varDelta \textbf{x}^{*} := [ \varDelta \textbf{x}_i^{*} \; \varDelta \textbf{x}_d^{*} ]^T$. Furthermore, may $\varDelta \boldsymbol{\varTheta}$ denote the vector of parameter variations. Then, matrices can be built so that

$$\varDelta\dot{\textbf{x}}^{*} = \textbf{A}^{*} \varDelta\textbf{x}^{*} + \textbf{B}^{*} \varDelta\textbf{y} + \textbf{B}^{*}_1 \varDelta\dot{\textbf{y}} + \textbf{B}^{*}_2 \textbf{W} \varDelta \boldsymbol{\varTheta} + \textbf{B}^{*}_3 \dot{\textbf{W}} \varDelta \boldsymbol{\varTheta}$$

((4.65a))

$$\varDelta\textbf{u} = \textbf{C}^{*} \varDelta\textbf{x}^{*} + \textbf{D}^{*} \varDelta\textbf{y} + \textbf{D}^{*}_1 \varDelta\dot{\textbf{y}} + \textbf{D}^{*}_2 \textbf{W}\varDelta \boldsymbol{\varTheta} + \textbf{D}^{*}_3 \dot{\textbf{W}} \varDelta \boldsymbol{\varTheta}$$

((4.65b))

(see the Appendix).

Given that $( s \textbf{I} - \textbf{A}^{*})^{-1}$ exists, then Laplace transform of (4.65b) yields

$${\mathcal L} \varDelta \textbf{u} = \textbf{M}_1 {\mathcal L} \varDelta \textbf{y} + \textbf{M}_2 ({\mathcal L} \textbf{W}) \varDelta \boldsymbol{\varTheta} \;$$

((4.66))

where

$$\textbf{M}_1 = \textbf{C}^{*}( s \textbf{I} - \textbf{A}^{*})^{-1} ( \textbf{B}^{*} + s \textbf{B}^{*}_1 ) + ( \textbf{D}^{*} + s \textbf{D}^{*}_1 )$$

((4.67a))

$$\textbf{M}_2 = \textbf{C}^{*}( s \textbf{I} - \textbf{A}^{*})^{-1} ( \textbf{B}^{*}_2 + s \textbf{B}^{*}_3 ) + ( \textbf{D}^{*}_2 + s \textbf{D}^{*}_3 )$$

((4.67b))

The vector ${\mathcal L}\textbf{w} = ({\mathcal L}\textbf{W}) \varDelta \boldsymbol{\varTheta}$ in (4.66) can be expressed by the output vector y of the direct model

$${\mathcal L}\textbf{w} = ({\mathcal L}\textbf{W}) \varDelta \boldsymbol{\varTheta} = (\varDelta \textbf{W}) {\mathcal L}\textbf{z} \; = \; (\varDelta \textbf{W}) ( \textbf{M}_{\textbf{3}} {\mathcal L}\textbf{y} )$$

((4.68))

where $\varDelta \textbf{W}$ is a diagonal matrix with $\varDelta W_{ii} = \delta_i \varDelta \varTheta_i$ and M ₃ a matrix with $m^{ij}_3 \in \mathbb{C}$. Substitution of (4.68) into (4.66) yields

$$\frac{\partial {\mathcal L} \textbf{u}}{\partial {\varTheta_i}} = \textbf{M}_1 \frac{\partial {\mathcal L} \textbf{y}}{\partial {\varTheta_i}} + \left(\textbf{M}_2 \frac{\partial \textbf{W}}{\partial \varTheta_i} \textbf{M}_3\right) {\mathcal L} \textbf{y}$$

((4.69))

Comparison of (4.69) and (4.64) finally gives the result

$$\textbf{M}_1 = \textbf{H}^{*} \label{(4.70)}$$

((4.70))

$$\textbf{M}_2 \frac{\partial \textbf{W}}{\partial \varTheta_i} \textbf{M}_3 = \frac{\partial \textbf{H}^{*}}{\partial {\varTheta_i}}$$

((4.71))

where $\partial W_{ij} / \partial \varTheta_i = \delta_i$ for $i = j$. Otherwise $\partial W_{ij} / \partial \varTheta_i = 0$.

In the following section, for illustration, this matrix-based approach is applied to two simple examples.

5.4 Example: Inverse Model of a Linear Network

Consider the simple linear electrical network depicted in Fig. 4.19. It can be viewed as an electrical analogue of the coupled hydraulic tank system considered in Section 4.4.1. A bond graph of the direct model with the two inputs $I(t)$ and $E(t)$ and the two outputs e ₁ and f ₂ appears in Fig. 4.20. There is one set of two disjoint input–output causal paths

$$\begin{aligned} &I(t) \rightarrow f_{C_1} \rightarrow x_1 \rightarrow e_1 \\ &E(t) \rightarrow e_{R_2} \rightarrow f_{R_2} \rightarrow f_2 \end{aligned}$$

The order of the first path is 1 and the order of the second one equals 0. Hence, the model is structurally invertible ([26, Criterion 2], or [30, p. 165]) and the order of the inverse model is 1 ([26, Proposition 2]).

Fig. 4.19

Schematic of a linear electrical network

Fig. 4.20

Bond graph of the direct model of the linear electrical network

Figure 4.21 shows a bond graph representation of the inverse model. Contrary to the bond graph of the direct model, the bond graph of the inverse model has one energy store in differential causality (C : C ₁) as to be expected from the structural analysis of the direct bond graph. Hence, the order of the inverse model is 1.

Fig. 4.21

Bond graph of the inverse model of the linear electrical network using bicausality

In this example, input–output pairs $I(t), e_1$ and $E(t), f_2$, respectively, are collocated. Hence, the left-hand side flow source and the effort detector in Fig. 4.20 can be combined into one source–sensor element SS. The same holds for the right-hand side effort source and the flow detector . The bond graph of the inverse model is obtained by just reversing causality at the source–sensor elements and by propagating this information [19]. Figure 4.22 shows the result.

Fig. 4.22

Bond graph of the inverse model with two source–sensors

5.4.1 Symbolic Differentiation of the Transfer Matrix of the Inverse Model with Respect to a Parameter

Let $\textbf{y} = [ e_1 \; f_2 ]^T$ and $\textbf{u} = [ f_1 \; e_2 ]^T$ according to Fig. 4.22. Derivation of equations from the bond graph of the inverse model and Laplace transform yields

$$\underbrace{ \left[ \begin{array}{c} {\mathcal L}f_1 \\ {\mathcal L}e_2 \end{array} \right]}_{\displaystyle {\mathcal L}\textbf{u}} = \underbrace{ \left[ \begin{array}{cc} H^*_{11} & H^*_{12} \\ H^*_{21} & H^*_{22} \end{array} \right]}_{\displaystyle \textbf{H}^*} \, \underbrace{ \left[ \begin{array}{c} {\mathcal L}e_1 \\ {\mathcal L}f_2 \end{array} \right]}_{\displaystyle {\mathcal L}\textbf{y}}$$

((4.72))

where

$$H^*_{11} = C_1 s + \frac{1}{R_1} - \frac{1}{R_1} \frac{1}{d}$$

((4.73a))

$$H^*_{12} = \frac{1}{d}$$

((4.73b))

$$H^*_{21} = \frac{1}{d}$$

((4.73c))

$$H^*_{22} = - \left( \frac{R_1}{d} + R_2 \right)$$

((4.73d))

and $d := R_1 C_2 s + 1$. Hence,

$$\frac{\partial \textbf{H}^*}{\partial R_2} = \left[ \begin{array}{cc} 0 & 0 \\ 0 & -1 \end{array} \right]$$

((4.74))

and

$$\frac{\partial \textbf{H}^*}{\partial C_2} = \frac{s}{d^2} \, \left[ \begin{array}{cc} 1 & - R_1 \\ -R_1 & R_1^2 \end{array} \right]$$

((4.75))

Remark 4.1

The above transfer functions of the inverse model have a pole due to the term d in their denominator. It can be identified in the bond graph of the inverse model by the causal path from the store C : C ₁ to the resistor R : R ₁. Let H denote the transfer matrix of the direct model. Then, because of $\textbf{H} = (\textbf{H}^{*})^{-1}$, this pole gives rise to a zero in the transfer functions of H that is not evident in the direct bond graph.

5.4.2 Incremental Bond Graph Approach

In the following, the results (4.74) and (4.75) obtained by symbolic differentiation will be derived from the incremental bond graph of the inverse model (Fig. 4.23) by building the matrices used in the approach presented in the previous section.

Fig. 4.23

Incremental bond graph of the inverse model of the linear electrical network

As parameters R ₂ and C ₂ are assumed to vary, the bond graph elements $\mathrm{R} : R_2$ and $\mathrm{C} : C_2$ have been replaced by their incremental models. Derivation of equations from the incremental bond graph in Fig. 4.23 results in the following matrices:

$$\begin{aligned} \underbrace{ \left[ \begin{array}{c} \varDelta\dot{x}^*_2 \\ \varDelta\dot{x}^*_1 \end{array} \right]}_{\displaystyle\varDelta\dot{\textbf{x}}^*} = \underbrace{ \left[ \begin{array}{cc} \displaystyle - \frac{1}{R_1 C_2} & 0 \\ 0 & 0 \end{array} \right]}_{\displaystyle\textbf{A}^*} \, \underbrace{ \left[ \begin{array}{c} \varDelta {x}^*_2 \\ \varDelta {x}^*_1 \end{array} \right]}_{\displaystyle\varDelta {\textbf{x}}^*} \, + \, \underbrace{ \left[ \begin{array}{cc} \displaystyle \frac{1}{R_1 C_2} & \displaystyle - \frac{1}{C_2} \\ 0 & 0 \end{array} \right]}_{\displaystyle\textbf{B}^*} \, \underbrace{ \left[ \begin{array}{c} \varDelta e_1 \\ \varDelta f_2 \end{array} \right]}_{\displaystyle\varDelta {\textbf{y}}} \\ & & \, + \, \underbrace{ \left[ \begin{array}{cc} 0 & 0 \\ 1 & 0 \end{array} \right]}_{\displaystyle\textbf{B}^*_1} \, \underbrace{ \left[ \begin{array}{c} \varDelta\dot{e}_1 \\ \varDelta\dot{f}_2 \end{array} \right]}_{\displaystyle\varDelta\dot{\textbf{y}}} \, + \, \underbrace{ \left[ \begin{array}{cc} -1 & 0 \\ 0 & 0 \end{array} \right]}_{\displaystyle\textbf{B}^*_3} \, \underbrace{ \left[ \begin{array}{c} \displaystyle \frac{1}{c_2} \, \dot{e}_{C_2} \, \varDelta C_2 \\ \displaystyle \dot{f}_{R_2} \, \varDelta R_2 \end{array} \right]}_{\displaystyle\dot{\textbf{W}}\varDelta\boldsymbol{\varTheta}} \end{aligned}$$

((4.76))

Furthermore,

$$\begin{aligned} \underbrace{ \left[ \begin{array}{c} \varDelta {f}_1 \\ \varDelta {e}_2 \end{array} \right]}_{\displaystyle\varDelta {\textbf{u}}} = \underbrace{ \left[ \begin{array}{cc} \displaystyle - \frac{1}{R_1} & 0 \\ 1 & 0 \end{array} \right]}_{\displaystyle\textbf{C}^*} \, \underbrace{ \left[ \begin{array}{c} \varDelta {x}^*_2 \\ \varDelta {x}^*_1 \end{array} \right]}_{\displaystyle\varDelta {\textbf{x}}^*} \, + \, \underbrace{ \left[ \begin{array}{cc} \displaystyle \frac{1}{R_1} & 0 \\ 0 & - R_2 \end{array} \right]}_{\displaystyle\textbf{D}^*} \, \underbrace{ \left[ \begin{array}{c} \varDelta e_1 \\ \varDelta f_2 \end{array} \right]}_{\displaystyle\varDelta {\textbf{y}}} \\ & & \, + \, \underbrace{ \left[ \begin{array}{cc} C_1 & 0 \\ 0 & 0 \end{array} \right]}_{\displaystyle\textbf{D}^*_1} \, \underbrace{ \left[ \begin{array}{c} \varDelta \dot{e}_1 \\ \varDelta \dot{f}_2 \end{array} \right]}_{\displaystyle\varDelta {\dot{\textbf{y}}}} \, + \, \underbrace{ \left[ \begin{array}{cc} 0 & 0 \\ 0 & -1 \end{array} \right]}_{\displaystyle\textbf{D}^*_2} \, \underbrace{ \left[ \begin{array}{c} \displaystyle \frac{1}{C_2}\, e_{C_2} \, \varDelta C_2 \\ f_{R_2} \, \varDelta R_2 \end{array} \right]}_{\displaystyle \textbf{W}\varDelta \boldsymbol{\varTheta}} \end{aligned}$$

((4.77))

With these matrices and $\textbf{B}^*_2 = \textbf{0}$, $\textbf{D}^*_3 = \textbf{0}$, the right-hand side expression in (4.67b) can be built. The result is

$$\textbf{M}_2 = \frac{C_2}{d} s \left[ \begin{array}{cc} 1 & 0 \\ - R_1 & \displaystyle - \frac{d}{C_2 s} \end{array} \right]$$

((4.78))

The vector $({\mathcal L}\textbf{W})\varDelta \boldsymbol{\varTheta}$ is easily reformulated

$$\begin{aligned} ({\mathcal L}W)\varDelta \boldsymbol{\varTheta} & = & \underbrace{ \left[ \begin{array}{cc} \displaystyle \frac{\varDelta C_2}{C_2} & 0 \\ 0 & \varDelta R_2 \end{array} \right]}_{\displaystyle \varDelta \textbf{W}} \underbrace{ \left[ \begin{array}{c} {\mathcal L} e_{c_2} \\ {\mathcal L} f_{R_2} \end{array} \right]}_{\displaystyle \textbf{z}} \\ & = & ( \varDelta \textbf{W}) \left[ \begin{array}{c} \displaystyle \frac{1}{d} ( {\mathcal L}e_1 - R_1 {\mathcal L}f_2 ) \\ \varDelta R_2 {\mathcal L}f_2 \end{array} \right] \\ & = & \varDelta \textbf{W} \underbrace{ \left[ \begin{array}{cc} \displaystyle \frac{1}{d} & \displaystyle - \frac{R_1}{d} \\ 0 & 1 \end{array} \right]}_{\displaystyle \textbf{M}_3} \underbrace{ \left[ \begin{array}{c} {\mathcal L}e_1 \\ {\mathcal L}f_2 \end{array} \right]}_{\displaystyle {\mathcal L}\textbf{y}} \end{aligned}$$

((4.79))

Multiplication of matrices proves that, in fact,

$$\textbf{M}_2 \frac{\partial \textbf{W}}{\partial R_2} \textbf{M}_3 = \frac{\partial \textbf{H}^*}{\partial R_2}$$

((4.80))

$$\textbf{M}_2 \frac{\partial \textbf{W}}{\partial C_2} \textbf{M}_3 = \frac{\partial \textbf{H}^*}{\partial C_2}$$

((4.81))

(cf. (4.74) and (4.75)).

Finally, evaluation of the expression for M ₁ in (4.67a) confirms (4.70).

5.5 Example: Inverse Model of a Fixed Field DC Motor

The second illustrative example is the well-known voltage-driven separately excited DC motor that drives a mechanical load against an external moment (Fig. 4.10).

The inverse bond graph is obtained from the direct bond graph (Fig. 4.11) by replacing each of the two effort sources representing the voltage source and the external moment by a flow source–effort sensor, SS, as depicted in Fig. 4.24. The source–sensor elements lead to differential causality at the ports of the two I elements accounting for the self-inductance L _a of the rotor winding and the mechanical inertia J _m of rotor and load. That is, the inverse model has no states. Hence, the denominator of all transfer functions of the inverse model is a constant.

Fig. 4.24

Inverse bond graph model of the fixed field DC motor

Assume that the friction parameter R _m is subject to variations. Then, the element R : R _m is to be replaced by its incremental model. This means that a modulated effort sink MSe : $\omega \varDelta \varTheta$ is attached to the 1-junction representing the variation $\varDelta R_m$ (Fig. 4.25). Figure 4.25 shows the resulting incremental inverse bond graph.

Fig. 4.25

Incremental inverse bond graph of the DC motor accounting for a variation in mechanical friction

From the incremental inverse bond graph in Fig. 4.25, the following equations can be immediately derived:

$$\varDelta\dot{\textbf{x}}^{*} = \varDelta\dot{\textbf{y}}$$

((4.82))

and

$$\begin{aligned} \underbrace{ \left[ \begin{array}{c} \varDelta u_1 \\ \varDelta u_2 \end{array} \right]}_{\displaystyle\varDelta\textbf{u}} = \underbrace{ \left[ \begin{array}{cc} R_a & k_T \\ - k_T & R_m \end{array} \right]}_{\displaystyle \textbf{D}^{*}} \underbrace{ \left[ \begin{array}{c} \varDelta y_1 \\ \varDelta y_2 \end{array} \right]}_{\displaystyle\varDelta\textbf{y}} + \underbrace{ \left[ \begin{array}{cc} L_a & 0 \\ 0 & J_m \end{array} \right]}_{\displaystyle \textbf{D}^{*}_1} \underbrace{ \left[ \begin{array}{c} \varDelta \dot{y}_1 \\ \varDelta \dot{y}_2 \end{array} \right]}_{\displaystyle\varDelta\dot{\textbf{y}}} \\ & & + \underbrace{ \left[ \begin{array}{cc} 0 & 0 \\ 0 & 1 \end{array} \right]}_{\displaystyle \textbf{D}^{*}_2} \underbrace{ \left[ \begin{array}{cc} 0 & 0 \\ 0 & \varDelta R_m \end{array} \right]}_{\displaystyle \varDelta \textbf{W}} \underbrace{ \left[ \begin{array}{cc} 0 & 0 \\ 0 & 1 \end{array} \right]}_{\displaystyle \textbf{M}_3} \underbrace{ \left[ \begin{array}{c} y_1 \\ y_2 \end{array} \right]}_{\displaystyle \textbf{y}} \end{aligned}$$

((4.83))

Substitution of these matrices in the right-hand side expressions in (4.67) immediately gives

$$\textbf{M}_1 = \left[ \begin{array}{cc} L_a s + R_a & k_T \\ - k_T & J_m s + R_m \end{array} \right] \; = \; \textbf{H}^{*}$$

((4.84))

and

$$\textbf{M}_2 = \left[ \begin{array}{cc} 0 & 0 \\ 0 & 1 \end{array} \right]$$

((4.85))

Finally,

$$\frac{\partial \textbf{H}^{*}}{\partial R_m} = \textbf{M}_2 \frac{\partial \textbf{W}}{\partial R_m} \textbf{M}_{\textbf{3}} \; = \; \left[ \begin{array}{cc} 0 & 0 \\ 0 & 1 \end{array} \right]$$

((4.86))

This result obtained from the incremental inverse bond graph can be verified by derivation of the transfer matrix H from the direct bond graph in Fig. 4.11 and by differentiating its inverse H ^* with respect to the parameter R _m . Derivation of Laplace transformed equations from the direct bond graph yields

$$\left[ \begin{array}{c} {\mathcal L}i_a \\ {\mathcal L} \omega \end{array} \right] = \underbrace{ \frac{1}{\varDelta} \left[ \begin{array}{cc} J_m s + R_m & -k_T \\ k_T & L_a s + R_a \end{array} \right]}_{\displaystyle \textbf{H}} \, \left[ \begin{array}{c} {\mathcal L}E \\ {\mathcal L}M \end{array} \right]$$

((4.87))

where $\varDelta := \left( L_a s + R_a \right) \left( J_m s + R_m \right) + k_T^2$.

Hence,

$$\textbf{H}^{*} = \textbf{H}^{-1} \; = \; \left[ \begin{array}{cc} L_a s + R_a & k_T \\ - k_T & J_m s + R_m \end{array} \right]$$

((4.88))

and

$$\frac{\partial \textbf{H}^{*}}{\partial R_m} = \left[ \begin{array}{cc} 0 & 0 \\ 0 & 1 \end{array} \right]$$

((4.89))

in accordance with (4.86).

As the inverse model has no states in this example, (4.18a) and (4.18b) reduce to

$$\begin{aligned} {\mathcal L}\textbf{u} & = & \textbf{D}^{*}(s) {\mathcal L}\textbf{y} \; = \; \textbf{H}^{*}(s) {\mathcal L}\textbf{y} \\ & = & \left\{ \left[ \begin{array}{cc} R_a & k_T \\ -k_T & R_m \end{array} \right] + s \left[ \begin{array}{cc} L_a & 0 \\ 0 & J_m \end{array} \right] \right\} {\mathcal L}\textbf{y} \\ & = & \left( \textbf{D}_0^{*} + \textbf{D}_1^{*} s \right) {\mathcal L}\textbf{y} \end{aligned}$$

((4.90))

In the SISO case $u_1 = E$ and $y_1 = \omega$, the matrix H ^* reduces to the scalar transfer function

$$h^{*}(s) := \frac{L_a J_m}{k_T} s^2 + \left( \frac{L_a R_m}{k_T} + \frac{R_a J_m}{k_T} \right) s + \left( \frac{R_a R_m}{k_T} + k_T \right)$$

((4.91))

That is,

$$u_1(t) = \left( \frac{R_a R_m}{k_T} + k_T \right) y_1(t) + \left( \frac{L_a R_m}{k_T} + \frac{R_a J_m}{k_T} \right) \dot{y}_1 (t) + \frac{L_a J_m}{k_T} \ddot{y}_1 (t)\quad\quad\quad$$

((4.92))

6 Parameter Sensitivities of ARR Residuals

In [14], the author of this chapter briefly showed that incremental bond graphs can also be used to determine parameter sensitivities of the residuals of analytical redundancy relations (ARRs) used in model-based fault detection and isolation. This section elaborates this aspect and gives an illustration.

6.1 ARRs for Continuous Systems

Analytical redundancy relations are balance equations of effort or flow variables, in which unknown variables have been replaced by input variables and measured output variables and in which parameters are known. Evaluation of an ARR provides a residual that theoretically should be zero. In practice, however, the residual of an ARR is within certain error bounds as long as no faults occur during system operation. The value is not exactly zero over some time interval due to noise in measurement, parameter uncertainties, and numerical inaccuracies. If, however, the numerical value of a residual exceeds certain thresholds, then this is an indicator to a fault in one of the system’s components. Noise in measured output variables may result in residual values indicating a fault that does not exist. Hence, measured data should pass appropriate filters before being used in ARRs.

To give an example of an ARR, consider the bond graph of the coupled tanks in Fig. 4.8. The sum of volume flows at the right-hand side 0-junction reads

$$0 = Q_{R_1} - Q_{C_2} - Q_\mathrm{o}$$

((4.93))

Replacing unknowns by means of constitutive component equations yields

$$r_2 = k_1 \mathrm{sign}(p_1 - p_2) \sqrt{| p_1 \, - \, p_2|} \, - \, C_2 \dot{p}_2 \, - \, Q_\mathrm{o}$$

((4.94))

This equation is an ARR because it relates the measured quantities p ₁, p ₂, and Q _o. The variable r ₂ holds the numerical value that is obtained by evaluation of the right-hand side of the equation. That is, r ₂ is the residual of the ARR. (k ₁ is a known constant in the constitutive equation of valve 1.) As can be seen, valve 1 between the two tanks, the sensed pressures, p ₁, p ₂, and the sensed outlet flow, Q _o, contribute to this ARR.

If nonlinearities of constitutive equations permit the elimination of unknowns in balance equations so that ARRs can be obtained in symbolic form, then the result of their structural analysis is usually presented as structural fault signature matrix (FSM) [6, 13, 31]. In the fault signature matrix, an entry ‘1’ in the ith row and jth column indicates that the ith component contributes to the jth residual. The entries in the jth column constitute the signature of residual r _j . Residuals are called structurally independent if their signatures differ. As has been shown by Samantaray et al. [12], the entries in the fault signature matrix can be directly determined by inspection of their diagnostic bond graph by following causal paths from inputs (sources and measurements) to the virtual sensor of a residual (cf. Chapter 7).

The set of ARRs is not unique. In general, for an observable system, the number of structurally independent residuals equals the number of sensors added to the system [32].

Structural analysis of ARRs also enables to decide whether a fault can be detected and moreover can be isolated. It is common to add two columns to the fault signature matrix holding information about whether a fault can be detected and moreover can be isolated.

In case the signature matrix is not diagonal, Samantaray and Ghoshal use parameter estimation for isolation of simultaneous faults [11]. Parameters are estimated by least squares optimisation of residuals. In that approach, values for sensitivities of residuals with respect to parameters are needed. Beyond this optimisation problem, knowledge of how sensitive residuals are with respect to certain parameters helps assessing the information in a fault signature matrix.

As to parameter sensitivities of residuals, the parameter sensitivity of r ₂ with respect to the parameter C ₂, for instance, equals $(- \dot{p}_2)$.

6.2 ARRs for Hybrid Systems

For dynamic systems with very fast state transitions in some components, e.g. caused by an abrupt fault, it is appropriate to model these state transitions as discrete events. That is, besides time continuous changes also discrete changes happen. In other words, there are a number of system modes and discrete changes between them. For each mode, the continuous dynamic behaviour is described by a continuous model [6]. Such systems are known as hybrid systems. One way to model such systems by bond graphs is to use controlled 1- and 0-junctions [33]. If the local state automation of a controlled junction forces a state change, resulting local causality changes must be propagated into the bond graph. This affects causal paths. For the purpose of FDI, Low et al. [34, 35] recently proposed a causality assignment to hybrid bond graphs so that causal paths remain unchanged under state switches of controlled junctions. Only some parts of the paths are cut off due to controlled junctions in OFF state. As a consequence, by following causal paths in hybrid bond graphs, ARRs may be derived that hold for all system modes. Low and his co-authors call these ARRs Global ARRs (GARRs) [34]. They include binary variables that can switch off parts in the symbolic expression of a GARR. In other words, the signature of a fault and the question of whether it can be detected and isolated depends on the system mode. That is, there is not one global fault signature matrix (FSM) but one for each system mode of operation.

6.3 Determination of Parameter Sensitivities of ARR Residuals

As ARRs in symbolic form cannot always be obtained by elimination of unknown variables, sensitivities of their residuals with respect to parameters sometimes cannot be derived by symbolic differentiation. Therefore, sensitivity bond graphs have been used for numerical computation of residual sensitivities [8, 11]. In the following, it is shown that once the matrices of the state space model have been derived from the original bond graph with nominal parameters and from the associated incremental bond graph, parameter sensitivities of residuals of ARRs can also be determined in symbolic form by multiplication of transfer matrix entries.

6.3.1 Matrix-Based Determination of Parameter Sensitivities of ARR Residuals

Let $\varDelta\textbf{r}$ denote the vector of variations of the residuals and let the vector $\varDelta\textbf{y}$ of output variables of the incremental bond graph be $\varDelta\textbf{r}$. Then, according to (4.34) the variation of the Laplace transform of the residuals reads

$$\varDelta {\mathcal L} \textbf{r} = \underbrace{ \left[ \textbf{C}_n \left( s \textbf{I} - \textbf{A}_n \right)^{-1} \textbf{B}^{*} + \textbf{D}^{*} \right]}_{\displaystyle \textbf{F}^{*}} {\mathcal L}\textbf{W} \varDelta\boldsymbol{\varTheta}$$

((4.95))

where Θ denotes the vector of parameters. As W is a diagonal matrix, the ith component is the weighted sum of m parameter variations:

$$\varDelta {\mathcal L} r_i = \sum_{j = 1}^m F^{*}_{ij} {\mathcal L} W_{jj} \, \varDelta \varTheta_j$$

((4.96))

Hence, the parameter sensitivities of residuals are

$$\frac{\partial {\mathcal L} r_i}{\partial \varTheta_j} = F^{*}_{ij} {\mathcal L} W_{jj} \; = \; F^{*}_{ij} \delta_j \underbrace{\sum_{k = 1}^n F_{jk} {\mathcal L} u_k }_{\displaystyle z_j}$$

((4.97))

Equation (4.97) indicates that the jth parameter sensitivity of the ith residual is obtained using the entries in the ith row of the transfer matrix of the incremental bond graph and variables from the original nominal bond graph. The latter are the signals z _j into the modulated sources of the incremental bond graph representing the parameter variations. Again, these modulating signals are output variables of the nominal bond graph and as such are a weighted sum of the Laplace transforms of input variables u _k of the nominal bond graph. In the latter sum, the weighting factors are entries in a row of the transfer matrix F of the original bond graph.

Performing these operations by hand is practically hardly feasible even for small systems. However, software programs such as CAMP-G, MATLAB^®, and the Symbolic Math Toolbox™ can set up the matrices of the state space models, perform multiplications of matrix entries, and build the sum of terms.

6.3.2 Manual Determination of Parameter Sensitivities of ARR Residuals

For small systems, parameter sensitivities of residuals of ARRs can be manually determined in the following way. First, junctions to which detectors have been attached are identified in the bond graph of the system. The number of structurally independent residuals equals the number of sensors present in the system [13]. Then, virtual detectors are attached to corresponding junctions in the incremental bond graph. Adding variations of flows or efforts, respectively, at these junctions yields variations of residuals of ARRs and thus parameter sensitivities of the residuals.

6.4 Example: Analog Integrator

For illustration, consider the circuit schematic of a simple functional model of an analog integrator depicted in Fig. 4.26. In reality, an integrated operational amplifier is built by means of a number of transistors. The macro-model in Fig. 4.26 reproduces the input–output behaviour of an operational amplifier. It is sufficiently accurate for low frequencies. Its parameters that can be tuned are the gain, A, the input resistance R _i, and the output resistance R _o. The measurement at internal nodes of a real integrated circuit requires special equipment such as a probe station. The output voltage V _o of a bonded and packaged operational amplifier chip can be measured at one of its pins and may be used for the detection of possible failures in the circuit [36].

Fig. 4.26

Functional model of an analog integrator

The circuit representation is easily converted into the bond graph in Fig. 4.27. It includes an effort detector representing the sensor of the output voltage V _o.

Fig. 4.27

Bond graph representation of the macro-model in Fig. 4.26

Assume that the operational amplifier is operated so that the gain limitation is not effective but that its gain A and input resistance R _i are subject to variations. Then, the incremental bond graph is obtained by replacing the input resistor $\mathrm{R} : R_i$ and the modulated effort source A: MSe by their incremental model. The effort detector sensing the output voltage V _o is replaced by a virtual flow detector Df^* representing a sensor of the residual variation Δ r. Figure 4.28 displays the resulting incremental bond graph.

Fig. 4.28

Incremental bond graph of the macro-model in Fig. 4.26

Summation of flow variations at junction 0₃ of the incremental bond graph in Fig. 4.28 and some substitutions yield

$${\mathcal L}\varDelta r = \left( \frac{A}{R_o} - C \, s \right) {\mathcal L}\varDelta V_d + \frac{1}{R_o} {\mathcal L} w_2$$

((4.98))

where $s \in \mathbb{C}$.

Adding voltage variations at junction 1₂ and substituting current variations give

$$\underbrace{ \left[ 1 + R_i \left( \frac{1}{R_1} + C \, s \right) \right]}_{\displaystyle a} {\mathcal L} \varDelta V_d = {\mathcal L} w_1$$

((4.99))

That is, the output variable ${\mathcal L}\varDelta r$ of the incremental bond graph model is a weighted sum of the two input variables ${\mathcal L} w_1$ and ${\mathcal L} w_2$

$${\mathcal L}\varDelta r = \underbrace{ \left( \frac{A}{R_o} - C \, s \right) \frac{1}{a}}_{\displaystyle F^{*}_{11}} \, \underbrace{ ({\mathcal L} i_i) \, \varDelta R_i}_{\displaystyle {\mathcal L}w_1} \; + \; \underbrace{ \frac{1}{R_o}}_{\displaystyle F^{*}_{12}} \underbrace{({\mathcal L} V_d) \, \varDelta A}_{\displaystyle {\mathcal L} w_2}$$

((4.100))

At the same time, ${\mathcal L}\varDelta r$ is a weighted sum of the parameter variations $\varDelta R_i$ and $\varDelta A$.

Hence,

$${\mathcal L} \frac{\partial r}{\partial R_i} = F^{*}_{11} \, {\mathcal L} i_i$$

((4.101a))

$${\mathcal L} \frac{\partial r}{\partial A} = F^{*}_{12} \, {\mathcal L} V_d$$

((4.101b))

These results can be verified by derivation of the residual r from the bond graph in Fig. 4.27 and by partial differentiation with respect to A and R _i , respectively. In fact, adding currents at junction 0₃ in the bond graph of Fig. 4.27 and expressing them by voltages gives

$${\mathcal L}r = \left( \frac{A}{R_o} - C \, s \right) {\mathcal L}V_d \; - \; \left( \frac{1}{R_o} + \frac{1}{R_L} + C s \right) {\mathcal L}V_\mathrm{o}$$

((4.102))

Partial differentiation with respect to A yields the same expression as in (4.101b). Furthermore, expressing currents i ₁ and i _C in the equation

$$V_\mathrm{d} = R_\mathrm{i} \, i_\mathrm{i} \; = \; - R_i ( i_1 + i_C )$$

((4.103))

by voltages yields

$$\left[ \frac{1}{R_\mathrm{i}} + \frac{1}{R_1} + C s \right] {\mathcal L}V_\mathrm{d} = - \, \frac{1}{R_1} {\mathcal L} V_\mathrm{i} \; - \; C s \, {\mathcal L} V_\mathrm{o}$$

((4.104))

Partial differentiation of this equation with respect to R _i and subsequent rearranging the result gives

$$\frac{\partial {\mathcal L}V_\mathrm{d}}{\partial R_\mathrm{i}} = \frac{1}{a} {\mathcal L} i_\mathrm{i}$$

((4.105))

and finally

$$\frac{\partial {\mathcal L} r}{\partial R_\textit{i}} = \left( \frac{A}{R_\mathrm{o}} - C \, s \right) \frac{\partial {\mathcal L}V_\mathrm{d}}{\partial R_i} \; = \; \left( \frac{A}{R_\mathrm{o}} - C \, s \right) \frac{1}{a} {\mathcal L} i_\mathrm{i} \; = \; F^{*}_{11} \, {\mathcal L} i_\mathrm{i}$$

((4.106))

The current i _i is an output variable of the bond graph model. It is a weighted sum of the input voltage V _i and the measured, hence known, output voltage V _o. According to (4.104)

$${\mathcal L} i_\mathrm{i} = \underbrace{ \left( - \frac{1}{a} \frac{1}{R_1} \right)}_{\displaystyle F_{11}} {\mathcal L}V_\mathrm{i} \; + \; \underbrace{ \left( - \frac{C s}{a} \right)}_{\displaystyle F_{12}} {\mathcal L} V_\mathrm{o}$$

((4.107))

As a result,

$${\mathcal L} \frac{\partial r}{\partial R_\mathrm{i}} = F^{*}_{11} F_{11} {\mathcal L}V_\mathrm{i} \; + \; F^{*}_{11} F_{12} {\mathcal L}V_\mathrm{o}$$

((4.108))

That is, ${\mathcal L} \partial r / \partial R_\mathrm{i}$ is obtained by multiplication of a transfer function $F^{*}_{11}$ of the incremental bond graph and transfer functions F ₁₁ and F ₁₂ of the bond graph with nominal parameters.

7 Conclusions

An incremental true bond graph approach to a matrix-based determination of parameter sensitivities of transfer functions of linear MIMO models and of residuals of ARRs in symbolic form has been presented. The approach has the following advantages:

• The incremental bond graph is systematically constructed by replacing elements with varying parameters by their incremental model. This step could be implemented in software.

• Existing software such as CAMP-G/MATLAB^® supported by the Symbolic Math Toolbox™ can derive equations from the bond graph and from its associated incremental bond graph and can build the matrices of the state space equations and the output equations for both bond graphs in symbolic form.

• A parameter sensitivity of a transfer function out of the multiple possible ones of a linear MIMO model is obtained in symbolic form by multiplication of appropriate matrix entries. This can be performed by computer algebra systems.

• Adding variations of power variables at junctions of the incremental bond graph immediately leads to parameter sensitivities of residuals of ARRs.

• Furthermore, if the linear inverse model of a linear MIMO model exists, equations from the bond graph of the direct model and the incremental bond graph of the inverse model can be automatically derived and matrices can be built. Computer algebra systems can be used to determine parameter sensitivities of the transfer matrix of the inverse model from these matrices.

For small linear models, the above steps can be carried out by hand as has been shown by means of the illustrating examples. In any case, no symbolic differentiation of transfer functions has to be performed. The use of an incremental bond graph means that the total differential of constitutive equations has already been taken.

Appendix

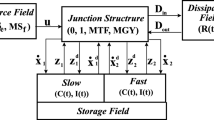
It is assumed that the bond graph of a LTI MIMO system has only 1-port storage elements some of which must take differential causality. Let x _i denote the energy vector of the storage elements in integral causality, x _d the energy vector of the stores in differential causality, and $\textbf{x} := [ \textbf{x}_\mathrm{i} \; \textbf{x}_\mathrm{d} ]^T$.

As has been shown by Rosenberg [29], a linear state space equation in terms of x _i and the input vector u can be derived from the equations of the bond graph junction structure and the linear constitutive equations of the storage fields and the dissipative fields by eliminating x _d and other variables. The result is

$$\dot{\textbf{x}}_\mathrm{i} = \textbf{A}_\mathrm{i} \textbf{x}_\mathrm{i} + {\textbf{B}_{\mathrm{i}1}} \textbf{u} + {\textbf{B}_{\mathrm{i}2}} \dot{\textbf{u}}$$

((4.109))

with constant matrices $\textbf{A}_{\rm i} , {\textbf{B}_{\rm i1}} , {\textbf{B}_{\rm i2}}$. Note that the elimination of x _d entails the time derivative of the input vector $\dot{\textbf{u}}$.

On the other hand, the junction structure equations and the constitutive equations of the dependent storage elements yield matrices A _d, B _d so that

$$\textbf{x}_\mathrm{d} = \textbf{A}_\mathrm{d} \textbf{x}_\mathrm{i} + \textbf{B}_\mathrm{d} \textbf{u}$$

((4.110))

(cf. [29, Equation 29]).

Combining (4.109) and (4.110) results in an ODE for x:

$$\underbrace{ \left[ \begin{array}{c} \dot{\textbf{x}}_i \\ \dot{\textbf{x}}_d \end{array} \right]}_{\displaystyle \dot{\textbf{x}}} = \underbrace{ \left[ \begin{array}{cc} \textbf{A}_1 & \textbf{0} \\ \textbf{A}_2 & \textbf{0} \end{array} \right]}_{\displaystyle \textbf{A}} \, \underbrace{ \left[ \begin{array}{c} \textbf{x}_i \\ \textbf{x}_d \end{array} \right]}_{\displaystyle \textbf{x}} + \underbrace{ \left[ \begin{array}{c} {\textbf{B}_{11}} \\ {\textbf{B}_{12}} \end{array} \right]}_{\displaystyle \textbf{B}_1} \, \left[ \textbf{u} \right] + \underbrace{ \left[ \begin{array}{c} {\textbf{B}_{21}} \\ {\textbf{B}_{22}} \end{array} \right]}_{\displaystyle \textbf{B}_2} \, \left[ \dot{\textbf{u}} \right]$$

((4.111))

where

$$\textbf{A}_1 = \textbf{A}_\mathrm{i}$$

((4.112))

$$\textbf{A}_2 = \textbf{A}_\mathrm{d} \textbf{A}_\mathrm{i}$$

((4.113))

$${\textbf{B}_{11}} = {\textbf{B}_{\mathrm{i}1}}$$

((4.114))

$${\textbf{B}_{12}} = \textbf{A}_\mathrm{d} {\textbf{B}_{\mathrm{i}1}}$$

((4.115))

$${\textbf{B}_{21}} = {\textbf{B}_{\mathrm{i}2}}$$

((4.116))

$${\textbf{B}_{22}} = \textbf{A}_\mathrm{d} {\textbf{B}_{\mathrm{i}2}} + \textbf{B}_\mathrm{d}$$

((4.117))

The expression for the output vector y takes the form

$$\textbf{y} = \textbf{C}_\mathrm{i} \textbf{x}_\mathrm{i} + \textbf{D}_\mathrm{d} \dot{\textbf{x}}_\mathrm{d} + \textbf{D}_\mathrm{i} \textbf{u}$$

((4.118))

with constant matrices C _i, D _i, D _d (cf., e.g. [19], p. 123, Equation 4.56).

Using (4.109), (4.110), and the time derivative of (4.110) leads to matrices C, D, and D ₁ so that (4.118) can be written in the form

$$\textbf{y} = \textbf{C} \textbf{x} + \textbf{D} \textbf{u} + \textbf{D}_1 \dot{\textbf{u}}$$

((4.119))