Dynamic Causality in Hybrid Bond Graphs

Abstract

Hybrid models are those containing continuous and discontinuous behaviour. In constructing dynamic systems models, it is frequently desirable to abstract rapidly changing, highly nonlinear behaviour to a discontinuity. Bond graphs lend themselves to systems modelling by being multi-disciplinary and reflecting the physics of the system. The causally dynamic hybrid bond graph is therefore suitable for simulation as well as providing engineering insight through analysis. There is a distinction between structural and parametric switching. The controlled junction is used for the former, and gives rise to dynamic causality. A controlled element is developed for the latter. Dynamic causality is unconstrained so as to aid insight. The junction structure matrix (JSM) for the hybrid bond graph features Boolean terms to reflect the controlled junctions in the graph structure. This hybrid JSM is used to generate a mixed-Boolean state equation. When storage elements are in dynamic causality, the resulting system equation is implicit. Control properties can be seen in the structure and causal assignment. An impulsive mode may occur when storage elements are in dynamic causality, but otherwise there are no energy losses associated with commutation because this method dictates the way discontinuities are abstracted. An impulsive model can be derived if required to further aid simulation. The mixed-Boolean mathematical model can be implemented in an environment such as Matlab.

1 Introduction

In constructing dynamic systems models, it is frequently desirable to abstract rapidly changing, highly nonlinear behaviour to a discontinuity. When rapidly changing behaviour is described by a continuous differential equation, it must be integrated using very small time steps in order to achieve any level of accuracy. Abstracting rapidly changing behaviour to a discontinuous equation can therefore aid solvability and improve computer simulation times. In addition, a user may find it intuitive to think of certain elements (like an electrical switch or hydraulic valve) or phenomena (such as contact, dry friction or breakage) as discontinuous.

Hybrid models are those containing any continuous and any discontinuous behaviour. They can be visualised as continuous modes on areas of state space linked by a discontinuous state mapping [42], and described as a hybrid automaton, i.e. one that contains both finite and continuous state spaces [58]. The dynamics consist of discrete transitions plus an evolution of the continuous part in each location.

Definition 4.1.

Hybrid Model: any model which describes both continuous and discontinuous behaviour.

The terms ‘hybrid’ and ‘switched’ system are used almost interchangeably in the bond graph literature, but there is a subtle difference. Switching models ‘comprise a family of dynamical subsystems together with a switching signal determining the active system at a current time’ [61]. They are a subset of hybrid systems, where there is some discontinuous behaviour modelled by an on/off switch or other binary signal. Switched models can be used to describe multimodal systems and variable-structure systems . The hybrid bond graph therefore usually yields a switched system, and some variants are referred to as switching bond graphs .

Definition 4.2.

Switching Model: a subset of hybrid model, which contains continuous equations and binary switching devices. The ‘switches’ select the active continuous equation(s) or behaviours at a given time.

Branicky et al. [7] categorise hybrid models into Switching and Impulse models , which can be Controlled or Autonomous. Switching models are defined as those where the vector field changes discontinuously when the state hits a boundary. Impulse models are those where the continuous state changes impulsively on hitting prescribed regions of state space, i.e. there is a ‘jump’ between the continuous equations in state space. The classic example is Newton’s Collision law, where the state of a body changes from positive to negative velocity on impact, and any dissipative effects are accounted for by a coefficient of restitution. These types of models have been created by some hybrid bond graph practitioners [36, 65].

Definition 4.3.

Impulse Model: a subset of hybrid model where the state changes impulsively, i.e. there is an impulse loss on commutation.

Variable topology systems are those where the size of the state equation matrices changes, such as contact (Fig. 4.1). They are frequently represented by impulse models [7] such as Newton’s Collision Law with restitution. This type of model exhibits an impulsive ‘jump’ in state space on commutation, which violates the conservation of energy fundamental to the bond graph. The state variables are unknown after commutation, necessitating the use of state reinitialisation [35, 36] and state estimation techniques [45].

Fig. 4.1

The three ‘Modes’ of a bouncing ball: falling, contact and rebound

A number of hybrid and switching bond graphs have been proposed to model discontinuities in the bond graph framework. From early on in the development of bond graphs, there was a need to model discontinuities in the form of elements like switches and valves. Borutzky gives an overview in his text [6], and Margetts presents a survey and discussion [29]. The different methods appear to reflect the different backgrounds and motivations of the users, with switched sources and controlled/switched junctions falling into more common usage than the other methods. One of the main differences between methods is the treatment of dynamic causality, and its consequences for analysis and computation.

1.1 Dynamic Causality

Bond graphs are constructed as acausal models, and an ideal computational causality is assigned to the model once complete. However, in a hybrid system the ideal causal assignment can change with commutation. For example, two rigid bodies might be in integral causality, but when they make contact one body will be forced into derivative causality (reflecting a genuine kinematic constraint: the two rigid bodies now act as one).

Dynamic causality is a feature of all ideal switching. Variable topology is an example of this, where the model changes significantly with commutation, e.g. a contact problem where the state equations change size.

Dynamic causality can be minimised and controlled using ‘Causality Resistance’ as originally proposed by Asher [2], to give a causally static model. This technique has been used successfully in the commercial bond graph package 20-Sim [8, 9, 59]. Dynamic causality can also be minimised by revising the causality assignment procedure, i.e. the use of Hybrid-SCAP [28].

The debate regarding static versus dynamic causality is ongoing at the time of writing. The body of work using switched sources and controlled junctions generally accepts dynamic causality, but many practitioners use methods that give static or near-static causality for ease of representation and computation. However, this chapter argues the case for embracing dynamic causality.

One of the many strengths of the bond graph method is its physical relevance. It is an Idealised Physical Modelling method, where an engineer uses the physical model to build an acausal representation, from which a mathematical model is derived. It aligns with the principles of behavioural modelling and object orientation, as opposed to the ‘input-output thinking’ used in block diagrams and signal flow graphs which results in the ‘control/physics barrier’ [62]. From early in the bond graph’s inception, structural analysis and causality exploitation were used to provide information about the system [34, 47]. ‘Structural Analysis’ refers to information that can be obtained from the bond graph structure, either by investigating the graph or the junction structure matrix. This information includes the form of the state equations, solvability, etc., and is analogous to the structural analysis of state matrices in control engineering. An analyst can easily see derivative causality and algebraic loops in a bond graph’s causal assignment, and causality can guide the engineer in assembling submodels and suggesting suitable test conditions. There is also the potential to look at interaction between nonlinear constitutive equations and uniqueness of system response [47].

It is therefore logical that a hybrid bond graph should continue to uphold these values and be suitable for qualitative analysis. Although causally dynamic models may at first appear difficult to simulate, they do provide valuable information to the user. Constraining causality is a move away from the real physics of the system. Adding parasitic elements or causality resistance can create an overly complex model with undesirable high-frequency dynamics [11]. The use of switched or modulating resistance and transformer components wrongly implies that switching is dissipative [38]. And there is a danger that compliances and resistances may be added purely to aid computation with no consideration of the physical system: a modeller can unwittingly create physically meaningless or computationally inefficient models. In contrast, a causally dynamic model offers engineering insight [14].

1.2 Categorising Discontinuities

A discontinuity is an abstraction made in order to simplify a model. It is possible to model any system using continuous functions. Discontinuities are therefore artificial, and made at the discretion of the user. Their purpose is to simplify the equations used to describe a system’s behaviour; where a system’s behaviour changes rapidly with time, describing that change as a discontinuity can improve simulation time, and aid engineering insight and analysis. They usually describe highly nonlinear behaviour which would be difficult to describe and time-consuming to compute using continuous functions. They can also describe variable topology problems, which are where the equations used for each mode of operation change significantly, with varying numbers of states and boundary conditions (for example, contact).

The term ‘discontinuity’ is fairly vague, and so a classification is made to aid application to engineering problems. Discontinuities are often classified as ideal (no losses) or non-ideal (associated with an energy loss) [46], switching or impulse [7] or according to whether they are autonomous or externally controlled. If they are assumed to be controlled by some form of automaton, they can be classified according to whether the controlling automata are time-scale dependant or parameter dependent [40]. Here, an additional distinction is made between structural and parametric discontinuities [29]. This distinction is necessary to describe where in the model (and underlying equations) the discontinuity should occur: between elements or internal to an element.

Definition 4.4.

Structural Discontinuities: discontinuities which occur when parts of the model are connected or disconnected, interrupting power flow between components. These discontinuities often give rise to variable topology models.

Engineering examples of this type of discontinuity are the hydraulic valve, mechanical clutch, ideal electrical switch or contact between bodies.

Definition 4.5.

Parametric Discontinuities: discontinuities which occur when an element has a highly nonlinear constitutive equation, and the user has abstracted this to a piecewise-continuous function. The structure of the model is unchanged, it is the equation describing the behaviour of an element which changes.

Common examples of parametric discontinuities are dry friction, tyre forces, a nonlinear damper ‘breaking out’ or saturation of an electrical capacitor or hydraulic accumulator.

These two types of discontinuity can be represented differently in a hybrid bond graph: a controlled junction with dynamic causality for structural switching and a controlled element for parametric switching.

In many cases—particularly the mechanical domain—the distinction between structural and parametric switching is clear. However, there are cases where it is less so. An electrical switch is physically an element which the user inserts into a circuit, and is often visualised in control theory as a discontinuous input, hence the use of switching sources and elements in the literature. Consequently, there is a case for treating it as parametric switching. Here the dynamic causal assignment is key: disconnecting a voltage or current source can force electrical storage elements to discharge, which is consistent with them switching to derivative causality. The controlled junction proposed for structural switching clearly shows where structure is disconnected and ideal causality assignment changes with commutation.

2 Structural Discontinuities

Structural switching activates or deactivates part of a system, and a controlled junction can be used to (dis)connect or (de)activate part of the model accordingly. Controlled junctions as described by Mosterman and Biswas [39] are selected to represent structural switching because they clearly show where structure connects and disconnects, and breaks the path of power flow. They are preferable to the use of switched sources which imply the switch is an energy-processing element when it is, in fact, a control element [6, 37]. This is not only important from the point of view of engineering insight, but also the controlled junction lends itself to being represented in the junction structure matrix and hence developing hybrid system equations.

2.1 The Controlled Junction

A controlled junction behaves as a normal 1- or 0-junction when ON and a source of zero flow or effort (respectively) when OFF. A controlled 1-junction is therefore used to break or inhibit flow (for example, an electrical switch which breaks the flow of current) and a controlled 0-junction is used to inhibit effort (for example, a clutch or other physical non-contact in a mechanical system). This always gives rise to dynamic causality on one of the attached bonds. The commonly accepted notation for controlled junctions is X1 and X0, which will be used in this paper.

Based on the above description, controlled junctions X1 and X0 can be formally defined as elements with associated Boolean parameters. They are initially defined as 2-ports for clarity, and the definition can easily be extended to more than 2 ports. The bond graph representations of controlled junctions X1 and X0 are as shown in Fig. 4.2, and their defining relationships are given by Eqs. (4.1) and (4.2), respectively.

$$\displaystyle\begin{array}{rcl} \left \{\begin{array}{rl} \lambda f_{1} =\lambda f_{2}, \\ \lambda (e_{1} - e_{2}) = 0, \\ \bar{\lambda }f_{1} = 0, \\ \bar{\lambda }f_{2} = 0\end{array} \right.& &{}\end{array}$$

(4.1)

$$\displaystyle\begin{array}{rcl} \left \{\begin{array}{rl} \lambda e_{1} =\lambda e_{2}, \\ \lambda (f_{1} - f_{2}) = 0, \\ \bar{\lambda }e_{1} = 0, \\ \bar{\lambda }e_{2} = 0\end{array} \right.& &{}\end{array}$$

(4.2)

Fig. 4.2

Bond graph representation of switched junctions X1 and X0

The Boolean parameter λ selects the set of equations that are valid given the state of the switch: 1 when the switch is ON and 0 when the switch is OFF. For each controlled junction, the defining Eqs. (4.1) and (4.2) lead to three possible causal configurations:

• Two causal configurations when the switch is ON, i.e. (first two equations equivalent to a normal 1 or 0 junction)

• a unique causal configuration when the switch is OFF, i.e. (last two equations equivalent to null sources of flow or null sources of effort imposed by the element to both power ports with conjugate variables externally imposed to the element).

In switching between ON and OFF states, the causal assignment around a controlled junction must change. In the ON state, where it behaves as a regular junction, there must be a causal input (i.e. a bond with a causal stroke defining the common effort for a 0-junction or common flow for a 1-junction). In the OFF state, where the controlled junction becomes a null source on each incident bond, there is no causal input and the causal assignment on that one bond changes. This is known as dynamic causality, and using this definition of a controlled junction it is unavoidable.

2.2 Simplification of the Hybrid Bond Graph

If a bond graph is constructed from the schematic diagram of a system, there is often potential to simplify the bond graph model. Since a controlled junction only behaves as a junction in one state, it cannot be eliminated and the rules for simplifying bond graphs must be augmented as follows:

Rule 1: :

2-Port Controlled Junctions

A controlled junction with only two ports cannot be removed and replaced with a single bond (whereas a regular junction could).

A regular junction with 2-ports can be replaced by a single bond, since the efforts and flows on the two incident bonds are equal. A controlled junction with 2-ports connects and disconnects its incident bonds with commutation: in principle like a switching bond or Boolean-modulated transformer (with dynamic causality). Removing the controlled junction would result in the surrounding structure being connected at all times.

Rule 2: :

Neighbouring Junctions: Controlled and Regular Junctions

When a regular junction and controlled junction of the same type are neighbouring, they can be merged into a single controlled junction.

That is, when a 1-junction and X1-junction are next to each other, they can be merged into a single X1-junction.

Likewise, a 0-junction and X0-junction next to each other can be merged into a single X0-junction.

When two like regular junctions are next to each other, they can be merged into a single junction. When one of those junctions is controlled, the commutating behaviour must be retained. This simplification results in elements being disconnected with commutation, whereas they would have remained connected to some substructure without the simplification (shown in Fig. 4.3).

Rule 3: :

Neighbouring Junctions: Multiple Controlled Junctions

When neighbouring controlled junctions have two ports only, they can be combined into a single controlled junction. This controlled junction is ON only when the states of both the constituent controlled junctions are ON.

When neighbouring controlled junctions have more than two ports, they cannot be combined. This is because the power to the incident elements or subsystems depends on the state of the individual controlled junction.

Fig. 4.3

An example subsystem with neighbouring regular and controlled junctions: unsimplified (left) and simplified (right)

Figure 4.4 demonstrates how two neighbouring 2-port controlled junctions can be combined: the power source is only connected to the resistor when controlled junction 1 AND controlled junction 2 are ON. The causal conflict arising between the junctions when both are OFF may be ignored.

Fig. 4.4

An example subsystem with neighbouring controlled junctions: 2-port junctions, simplified to a single junction which is ON when λ ₁ AND λ ₂ are true (left) and additional elements giving 3-port junctions (right)

However, when the controlled junctions have additional elements attached, it is no longer appropriate to combine them. There is power flow across each junction when it is ON and the other is OFF. The two controlled junctions cannot be combined in any manner which would reflect this behaviour.

Structure which adds nothing to the model can frequently be removed. This often happens in the case of electrical and hydraulics circuits where there is a return line to a zero ground or open tank. Ground parts are source elements which also act as a sink. For example, a mechanical ground is represented by a Sf-element (which has zero velocity and is a sink for force), and grounds in other domains are represented by Se-elements (e.g. an electrical ground, which is a source of 0V and a sink for current). They are usually null sources, but can have nonzero values (such as a pressurised hydraulic tank or undulating mechanical ground).

Rule 4: :

Removal of Ground Parts

When a controlled junction is positioned between a dissimilar ground and the main structure, it is not appropriate to remove the ground. That is, a null source of flow connected via an X0-junction cannot be removed. Likewise, a null source of effort connected via an X1-junction cannot be removed.

When the ground or tank is a null source, and it is not a causal input to the structure of interest, it can be deleted. An example is given in Fig. 4.5: the ground is a source of zero effort, and it adds nothing to the 1-junctions it is attached to (about which efforts are summed).

Fig. 4.5

An example system with a ground: full model (left) and simplified (right)

When a controlled junction exists between the ground and the main structure, it may not be appropriate to remove the ground. For example, in the system in Fig. 4.6, an electrical switch (represented by a X1-junction) could be inserted so that the resistance is now a non-ideal switch, shown in Fig. 4.6. In real terms, this breaks the circuit and changes its behaviour. In bond graph terms, this means that incident structure has a zero flow imposed on it when the X1-junction is OFF, rather than a zero effort (from the ground) which will have implications for the causal assignment. In simplifying the bond graph, the controlled junction and null source group must therefore be kept, because they can have a significant effect on the system.

Fig. 4.6

An example system with a ground and a controlled junction: full model (left) and simplified (right)

2.3 The Dynamic Causality Assignment Procedure

Causality in a bond graph is typically assigned using the Sequential Causality Assignment Procedure (SCAP) [22]. Using controlled junctions, dynamic causality is unavoidable (N.b. it can be minimised using Hybrid-SCAP and a variant of the controlled junction which is deleted when ‘OFF’ [28] but this can result in hanging junctions [29]).

The causality assignment procedure for the hybrid bond graph proposed in this paper starts with a reference mode of operation. This is defined with a maximum number of elements in integral causality, and controlled junctions preferably ON. This is the mode which should be easiest to simulate. Deviations from this reference due to dynamic causality are marked as dashed causal strokes. This enables the user to see the effects of commutation on causality, and aids in equation generation. The Dynamic Sequential Causality Assignment Procedure (DSCAP) to represent all modes of a hybrid bond graph model can be summarised in the following procedure:

Procedure 1: Dynamic Sequential Causality Assignment Procedure (DSCAP) for hybrid bond graph

Step 1.:

Assign causality according to SCAP with preferred integral causality, stopping when a controlled junction is reached. That is, start by assigning causality to a source element, and propagate causality throughout the bond graph as far as any controlled junctions. Repeat for other source elements, and then for any storage elements which have not yet been assigned causality. If causal conflict occurs in this stage, the model should be changed.

The causal assignment from step 1 may dictate whether some switches are ON or OFF.

Step 2.:

Choose a controlled junction which does not have its causality fully assigned. Assign causality around the controlled junctions assuming the switch to be ON and propagate as far as possible. Repeat this stage until all controlled junctions have their causality fully assigned.

Step 3.:

Finish propagating causality throughout the bond graph to any resistance elements or remaining bonds and propagate as far as possible.

Step 4.:

Taking each controlled junction in turn, consider the causality assignment when it is in the other state to the reference configuration. Mark this causality assignment with a dashed causal stroke, and propagate throughout the bond graph. If causal conflict occurs in this stage, then the other state of the controlled junction is not allowed.

Remark.

Causal propagations in step 2 and step 4 of the algorithm above may dictate the state (ON or OFF) of some controlled junctions as a result of the assigned state of others. This reveals some constraints in the state of switches indicating the allowed configurations or physically feasible modes of operation.

Figure 4.7 shows a simple example of the effect of the causality assignment around a controlled junction when ON and OFF.

Fig. 4.7

An example of causality assignments and their effect around a controlled junction. (a ) The junction in the ON (reference) mode. (b ) The junction shown by null sources when OFF. (c ) Dynamic causality notation

2.4 Dynamic Causality Notation and the Reference Configuration

The dynamic causality notation differs from that typically used [5] as it is designed to aid structural analysis and equation generation by hand. A reference configuration is used which indicates the mode of operation where most storage elements are in integral causality (giving information about model order and solvability). The dashed causal stroke notation aids the user in identifying regions of dynamic causality. Rather than assuming 2ⁿ modes of operation (where n is the number of switches), the user can inspect individual regions of the chart and generate a truth table or similar for a relatively small subsystem.

Note that the parameter λ of a switch indicates the absolute state of the switch, i.e. λ = 1 when the switch is ON and λ = 0 when the switch is OFF.

3 Parametric Discontinuities

Parametric switching has been defined as the case where an element has a piecewise-continuous constitutive equation. These may be hard nonlinearities, where the behaviour of an element changes so quickly that it can be considered instantaneous. Alternatively, they can occur where some relationship (gained via empirical data or a high-order function) is best described using a piecewise-continuous function. Classic examples are friction and tyre lateral stiffness, shown in Table 4.1.

Table 4.1 Examples of piecewise-continuous equations

The controlled element is recommended for the modelling of parametric switching. It should not be confused with the existing switched element, which has an on/off behaviour [20].

Parametric switching can be considered as mode switching, i.e. a collection of continuous modes of operation. These are controlled by an automaton, petri-net or similar, which allows the system to switch between modes of operation. Mode switching is historically modelled by a ‘tree’ of ideal switches and elements. Each element gives the constitutive equation for a specific mode of operation, and the ideal switches (de)activate it as required. Naturally, only one ideal switch can be ON at any time during a simulation. Strömberg [52] formulates mode switching trees of switched sources, and Mosterman and Biswas [39] present a multi-bond controlled junction selecting a continuous bond graph element from a number of possibilities.

Mode switching has a conceptual advantage in that it aids the development of finite state automata for simulation. However, the ‘tree’ notation means a model can rapidly grow to a vast size with multiple inputs and outputs for all possible modes of operation. This makes it less ideal for structural analysis and equation generation purposes. The multi-bond notation suggested by Mosterman and Biswas goes some way to controlling this, but it is a little confusing because multi-bond notation is typically used for multiple degrees of freedom in a model. Their idea is used as a basis for the controlled element defined here.

3.1 The Controlled Element

Consider an element with a piecewise-continuous constitutive function. A mode-switching tree can be constructed using the controlled junctions with associated Boolean terms (as used for structural switching), as shown in Fig. 4.8. Note that a resistance element is shown, but the principle holds true for inertia and compliance elements.

Fig. 4.8

Bond graph ‘Trees’ for a piecewise linear resistance element, assuming three modes of operation: a ‘Tree’ of X0-junctions (left) and a ‘Tree’ of X1-junctions (right)

In this tree, controlled junctions (de)activate the modes of operation, which are given by resistance elements on each branch. These ‘branches’ are then connected by a regular junction which sums the output values.

• In Fig. 4.8 (left) efforts are summed about a 1-junction: these efforts are the effort exerted by the resistance when a junction is ON plus the zero efforts exerted by the X0-junctions when they are OFF.

• In Fig. 4.8 (right), it is flows which are summed around a zero junction: these flows are the flow exerted by the resistance when a junction is ON plus the zero flows exerted by the X1-junctions when they are OFF.

In a bond graph tree it is important to note that the controlled junctions are constrained so that only one may be ON at any time.

In order to condense the ‘tree’ into a single controlled element, consider the underlying equations. Quantities are shown in Fig. 4.9, which also includes some source elements in order to obtain the equations. A reference configuration of λ ₁ = 1, λ ₂ = 0, λ ₃ = 0 is arbitrarily assumed. Note that dynamic causality is internal to the tree: there is static causality on the resistance elements and the input bond.

Fig. 4.9

The piecewise linear resistance element subsystem, showing quantities used in equation generation

This controlled element has the general constitutive function:

$$\displaystyle{ \mathrm{output} =\sum _{ n=1}^{i}\lambda _{ n}\varPhi _{n}(\mathrm{input}) }$$

(4.3)

where n is the number of branches to the tree, λ _n is the Boolean term associated with nth controlled junction and Φ _n is the constitutive function of the nth element.

The controlled element may be in dynamic causality (i.e. the output is effort in some modes and flow in others) it can be treated in the same way as a standard element in dynamic causality, i.e. having two input/output pairs for the two causal assignments [32]. For example, a hydraulic accumulator is a compliance element with an effort output in normal operation, but when it saturates it becomes a source of zero flow.

4 Deriving the Mixed-Boolean State Equation

Generating a state equation from a bond graph is well established. Here, a similar process is used to show that a causally dynamic hybrid bond graph can be used to generate a state equation which is mixed-Boolean.

4.1 Pseudo-States and Dynamic Causality

For a regular (causally static) bond graph, the inputs and outputs to the system from the various elements are used in generating equations. Specifically, the inputs to the system from the storage fields (i.e. the outputs of the compliance and inertia elements in integral causality) are usually taken as the time-derivatives of the state variables. The state variables are consequently displacement (for compliance elements) and momentum (for inertia elements).

When elements are in derivative causality, the state equations are no longer independent: there are dependent states associated with the elements in derivative causality which yield algebraic equations. Pseudo-state variables (associated with each element in derivative causality) have therefore been used to generate an implicit mathematical model containing the relevant algebraic constraints [12, 53].

When causality is dynamic, storage elements may switch from integral to derivative causality, and the inputs and outputs of the resistance elements may consequently reverse. The resulting state space matrices can change size depending on the mode. Storage elements in dynamic causality are therefore described using a variable for each of the two possible causal assignments: a state variable for the integral causality case and a pseudo-state variable for derivative causality. The model then describes all possible modes of operation by including input and output variables for both possible states of an element in dynamic causality. These are (de)activated in the appropriate modes of operation.

4.2 The General Hybrid Bond Graph

A causal bond graph model can be represented in matrix format, as a Junction Structure Matrix (JSM) consisting of ones and zeros which relate the system inputs and outputs. The JSM based on the Paynter Junction Structure is used here, since it has reached common use in bond graph structural analysis. The coefficients in the transformer field (representing any transformer or gyrator elements, sometimes expressed outside the junction structure matrix) are brought inside the JSM to give terms other than one and zero.

The General Bond Graph structure is shown in Fig. 4.10, with a modified ‘hybrid’ version to capture structural switching behaviour and the induced dynamic causality. There are two significant differences:

• 1. Using the Dynamic Sequential Causality Assignment Procedure (DSCAP), the causal hybrid bond graph displays some elements with static causality and some with dynamic causality (represented by dashed causal strokes, as shown in Fig. 4.10). The Hybrid Junction Structure Matrix (relating all possible system inputs and outputs) and state equation can be derived from this representation.

• 2. The Hybrid Junction Structure Matrix S contains Boolean parameters λ indicating the state of controlled junctions (used to describe structural switching). These Boolean ‘switching terms’ in the submatrices of S will therefore be carried through into the state equations derived from it.

Fig. 4.10

The junction structure matrix and generalised bond graph: general junction structure (left) and hybrid junction structure incorporating switching coefficients and dynamic causality (right)

Note that the Boolean terms λ appearing in the Junction Structure Matrix reflect controlled junctions between elements, and indicate where casual paths are severed or connected with commutation. There may be additional Boolean terms in the storage and resistance fields where parametric discontinuities exist within controlled elements.

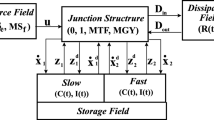
Figure 4.11 shows the key variables used in the causally dynamic hybrid bond graph, which are defined as follows. Note that the inputs to the elements are the outputs from the junction structure, and vice versa.

• 1. Elements with static causality have the usually defined variables:

  • Input vectors denoted $\dot{\hat{\boldsymbol{X}}} _{i}$ composed of $\dot{p}$ and $\dot{q}$ on I and C elements in integral causality, $\hat{\boldsymbol{Z}} _{d}$ composed of f and e on I and C elements in derivative causality, and $\hat{\boldsymbol{D}} _{\mathrm{out}}$ composed of effort or flow variables into dissipative elements (N.b. the output from the JSM is the input to the element).

  • Output vectors denoted $\hat{\boldsymbol{Z}} _{i}$ and $\dot{\hat{\boldsymbol{X}}} _{d}$ for storage elements, and $\hat{\boldsymbol{D}} _{\mathrm{in}}$ for dissipative elements

• 2. However, dynamic causality is captured in the block diagram by specifying two sets of inputs and output variables:

  • Two input vectors. For storage elements in dynamic causality, these inputs are $\dot{\tilde{\boldsymbol{X}}} _{i}$ for the integral causality case and $\tilde{\boldsymbol{Z}} _{d}$ for the derivative causality case, and are composed of $\dot{p}$, $\dot{q}$, f and e. For dissipative elements in dynamic causality, there is an effort input $\tilde{\boldsymbol{D}} _{e(\mathrm{out})}$ and flow output $\tilde{\boldsymbol{D}} _{f(\mathrm{out})}$. In any single mode of operation, one input is active and the other is redundant.

  • Two output vectors which are the complements of the inputs above. For storage elements in dynamic causality, these are $\dot{\tilde{\boldsymbol{X}}} _{d}$ and $\tilde{\boldsymbol{Z}} _{i}$ composed of $\dot{p}$, $\dot{q}$, f and e. For dissipative elements in dynamic causality, there is an effort output $\tilde{\boldsymbol{D}} _{e(\mathrm{in})}$ and flow output $\tilde{\boldsymbol{D}} _{f(\mathrm{in})}$. Again, in any single mode of operation, one output is active and the other is redundant.

  It is worth noting that an element can only have two modes of operation (flow input/effort output and effort input/flow output), although a model can have several modes of operation overall if it contains multiple controlled junctions.

Fig. 4.11

Quantities used in hybrid junction structure matrix and subsequent development

Controlled junctions in the bond graph are assigned Boolean variables λ in the Junction Structure. λ has a value of 1 when the junction is ON and 0 when OFF, signifying that there is a connection between two quantities when the junction is ON. A single bond graph therefore represents all possible modes of operation and causal assignments. Vectors $\boldsymbol{X}_{i} = [\hat{\boldsymbol{X}} _{i}\ \tilde{\boldsymbol{X}} _{i}]^{T}$ and $\boldsymbol{X}_{d} = [\hat{\boldsymbol{X}} _{d}\ \tilde{\boldsymbol{X}} _{d}]^{T}$ are the state and pseudo-state of the storage fields in integral and derivative causality, respectively. $\boldsymbol{Z}_{i} = [\hat{\boldsymbol{Z}} _{i}\ \tilde{\boldsymbol{Z}} _{i}]^{T}$ and $\boldsymbol{Z}_{d} = [\hat{\boldsymbol{Z}} _{d}\ \tilde{\boldsymbol{Z}} _{d}]^{T}$ are the complementary vectors of these states (shown in Fig. 4.10), related by $\boldsymbol{Z}_{i} =\boldsymbol{ F}_{i}\boldsymbol{X}_{i}$ and $\boldsymbol{Z}_{d} =\boldsymbol{ F}_{d}\boldsymbol{X}_{d}$. Resistive field also have inputs and outputs $\boldsymbol{D}_{\mathrm{in}} = [\hat{\boldsymbol{D}} _{\mathrm{in}}\ \tilde{\boldsymbol{D}} _{\mathrm{in}}]^{T}$ and $\boldsymbol{D}_{\mathrm{out}} = [\hat{\boldsymbol{D}} _{\mathrm{out}}\ \tilde{\boldsymbol{D}} _{\mathrm{out}}]^{T}$ related by $\boldsymbol{D}_{\mathrm{in}} =\boldsymbol{ L}\boldsymbol{D}_{\mathrm{out}}$.

There are two inputs and two outputs for each 1-port element in dynamic causality. The input/output sets are exclusive of each other, and the Boolean terms in the Hybrid Junction Structure Matrix (HJSM) will activate one of these for each mode of operation.

In order to establish which outputs of the junction structure are active, the vector of outputs must be multiplied by a diagonal matrix of Boolean expressions $\varLambda (\boldsymbol{\lambda })$. In any one mode of operation, some rows of the matrices will be set to zeros and others will give the Junction Structure for that mode. Therefore, outputs which are in static causality are assigned a 1 in the diagonal of the matrix $\varLambda (\boldsymbol{\lambda })$ because they are fixed outputs, while variables associated with elements in dynamic causality are assigned a Boolean function f(λ) determined by the combination of the switch parameters λ that dictate the output status of the variable. For each Boolean term f(λ), there will always be a NOT term $\overline{f(\lambda )}$ present in the matrix $\varLambda (\boldsymbol{\lambda })$ which activates another row to describe the dynamic element’s behaviour in its other state.

In order to construct the matrix $\varLambda (\boldsymbol{\lambda })$, consider each 1-port element in Dynamic Causality in turn, determine any causal path between this elements and the controlled junctions and report the state of the switch and the output variable in a truth table. A truth table (e.g. Table 4.2) can therefore be used to construct the combination of states, and hence function of Boolean variables, that result in each causal change. For example, if a storage element is in integral causality only when two switches are ON, this could be expressed by assigning the state variable a term in $\varLambda (\boldsymbol{\lambda })$ of (λ ₁ ⋅ λ ₂), i.e. switch 1 AND switch 2 are true or ON (Table 4.2). The pseudo-state complementary variable Z _d would therefore be assigned $(\overline{\lambda _{1} \cdot \lambda _{2}})$ because the element is in derivative causality when switch 1 AND switch 2 is NOT true, i.e. OFF.

Table 4.2 Example truth table for two switches

Often a controlled junction simply creates a path of Dynamic Causality between it and a nearby element, and the term in $\varLambda (\boldsymbol{\lambda })$ can be quickly and easily assessed. There is the potential to reduce the amount of work required to obtain the equations by modularising and reusing submodels for larger systems.

The hybrid JSM is thus represented mathematically as:

$$\displaystyle\begin{array}{rcl} \left [\begin{array}{ccc} \boldsymbol{\varLambda }_{11} & 0 & 0 \\ 0 &\boldsymbol{\varLambda }_{22} & 0 \\ 0 & 0 &\boldsymbol{\varLambda }_{33} \end{array} \right ]\left [\begin{array}{c} \dot{\boldsymbol{X}}_{i} \\ \boldsymbol{Z}_{d} \\ \boldsymbol{D}_{\mathrm{out}} \end{array} \right ] = \left [\begin{array}{cccc} \mathbf{S}_{11} & \mathbf{S}_{12} & \mathbf{S}_{13} & \mathbf{S}_{14} \\ -\mathbf{S}_{12}^{T}& 0 & 0 &\mathbf{S}_{24} \\ -\mathbf{S}_{13}^{T}& 0 &\mathbf{S}_{33} & \mathbf{S}_{34}\\ \end{array} \right ]\left [\begin{array}{c} \boldsymbol{Z}_{i} \\ \dot{\boldsymbol{X}}_{d} \\ \boldsymbol{D}_{\mathrm{in}} \\ \boldsymbol{U} \end{array} \right ]& &{}\end{array}$$

(4.4)

4.3 Notation and the Reference Configuration

A reference configuration has been used to aid the construction of the causally dynamic bond graph, and to act as a basis for the proposed dynamic causality notation. However, the Junction Structure matrix encapsulates all possible modes of operation and it is therefore of little consequence which mode is selected for the reference. The parameter λ of a switch indicates the absolute state of the switch, i.e. λ = 1 when the switch is ON and λ = 0 when the switch is OFF.

4.4 The Unique Hybrid Implicit Equation

The state equations express the time-derivatives of the states and (where there is derivative causality) the pseudo-states —$\boldsymbol{X}_{i}$ and $\boldsymbol{X}_{d}$—in terms of their derivatives and the system inputs $\boldsymbol{U}$. An implicit form can be derived from the junction structure matrix which, like the JSM, is mixed-Boolean . The LTI form remains valid because the switching behaviour is not necessarily a function of time: the equations capture the model at all time points.

$$\displaystyle\begin{array}{rcl} \mathbf{E}(\boldsymbol{\varLambda })\dot{\boldsymbol{X}}& =& \mathbf{A}(\boldsymbol{\lambda })\boldsymbol{X} + \mathbf{B}(\boldsymbol{\lambda })\boldsymbol{U}{}\end{array}$$

(4.5)

$$\displaystyle\begin{array}{rcl} \left [\begin{array}{cc} \varLambda _{11} & -\mathbf{S}_{12}\\ 0 & 0 \end{array} \right ]\left [\begin{array}{c} \dot{\boldsymbol{X}}_{i} \\ \dot{\boldsymbol{X}}_{d} \end{array} \right ]& =& \left [\begin{array}{cc} \mathbf{KF}_{i} & \mathbf{KF} \\ -\mathbf{S}_{12}^{T}\mathbf{F}_{i} -\boldsymbol{\varLambda }_{22}\mathbf{F}^{T}& -\mathbf{S}_{12}^{T}\mathbf{F} -\boldsymbol{\varLambda }_{22}\mathbf{F}_{d} \end{array} \right ]\left [\begin{array}{c} \boldsymbol{X}_{i} \\ \boldsymbol{X}_{d} \end{array} \right ] \\ & & +\left [\begin{array}{c} \mathbf{S}_{14} + \mathbf{S}_{13}\mathbf{H}\mathbf{S}_{34} \\ \mathbf{S}_{24} \end{array} \right ]\left [\begin{array}{c} \boldsymbol{U} \end{array} \right ]{}\end{array}$$

(4.6)

Again, linear coefficients are assumed in order to derive the LTI form. These matrices could contain any number of functions and off-diagonal terms (including terms in F ) in a nonlinear model, and a similar derivation process can be followed to obtain nonlinear system equations which would take the general form:

$$\displaystyle\begin{array}{rcl} \boldsymbol{\varLambda }\boldsymbol{\dot{X}}& =& f_{1}(\boldsymbol{X},\boldsymbol{Z},\boldsymbol{U},\boldsymbol{\lambda },t){}\end{array}$$

(4.7)

$$\displaystyle\begin{array}{rcl} \boldsymbol{0}& =& f_{2}(\boldsymbol{X},\boldsymbol{Z},\boldsymbol{U},\boldsymbol{\lambda },t){}\end{array}$$

(4.8)

To obtain the implicit system equation (4.6) the following procedure is proposed:

Procedure 2: A Procedure for finding the implicit system equations of a hybrid bond graph

• 1. Construct the diagonal matrix Λ

  • Consider each 1-port element in dynamic causality in turn, and determine all paths of dynamic causality between these elements and the controlled junctions.

  • Use a truth table to construct the combination of states, and hence function of Boolean variables, that result in each causal change.

• 2. Construct the Hybrid Junction Structure Matrix (HJSM) in form of Eq. (4.13).

  • The HJSM relates system inputs to outputs. For elements in static causality, there will be one input and one output. For elements in dynamic causality, there are two inputs (effort and flow) and two outputs.

  • For static causality, the HJSM is constructed by using 1’s and 0’s to denote whether quantities are related or not.

  • Where a path between two elements crosses a TF or GY element, a variable or function other than one may appear in the Hybrid Junction Structure Matrix.

  • Where a path between two elements crosses a controlled junction, a λ (or function of λ) is used to show that the relationship only occurs when the junction is ON (or OFF).

  • Where an element is in dynamic causality (shown by a dotted causal stroke in addition to the solid one) each variable will only be an input to the system in certain modes of operation. Referring to the truth table constructed in step 1, assign a function of λ which denotes the modes in which the variable is an input.

  • Recall that the matrix should be skew-symmetric, and submatrices S ₂₂, S ₂₃ and S ₃₂ should be zeros.

• 3. Derive the LTI Implicit form.

  • Find matrices L and F from the (linear) relationships in the 1-port elements.

  • Take the submatrices of S and Λ from the Junction Structure Matrix equation, and insert them into the general implicit LTI form in Eq. (4.6).

  • Simplify this equation to give the state equations plus some additional equations relating to the pseudo-states.

5 Solving the Hybrid Mathematical Model

Solving hybrid models by computer is not a new concept: there has been a tremendous amount of work in this area. However, the mixed-Boolean state model generated from the causally dynamic hybrid bond graph is particularly simple to implement.

5.1 Background

There is a body of work on simulation of hybrid bond graphs using causally static models (e.g. the use of causality resistance in 20-Sim), transforming the models to other environments such as the acausal modelling language Modelica [44], its commercial GUI Dymola [50], and formalising the transformation of bond graph models into block diagrams for simulation in SIMULINK [3, 4, 13, 21]. Hybrid Process Algebra (HyPA) has been applied to bond graphs [15, 16]. The potential for cosimulation of bond graphs and block diagrams has been explored [54], as has deriving input/output port-Hamiltonian models which allow the bond graph model to be embedded in or cosimulated with other environments [55–57]. These moves make sense from a computational point of view (and much of the research here was conducted by computer scientists) but lose the graphical advantages and relation to the physical system which are important to the systems engineer. This work in other software packages typically using controlled junctions also yielded results in the field of FDI [18, 43] where the focus was on efficient simulation rather than exploiting the bond graph [23, 45, 49].

5.2 Simulating the Mixed-Boolean State Model

At the time of writing, there are no commercial environments for simulating causally dynamic hybrid bond graphs (although there are controlled junctions in the latest versions of 20-Sim). The user therefore has two options:

• insert an equational subsystem into a Bond Graph environment (e.g. 20-Sim)

• transfer the mixed-Boolean state model to a programming environment (e.g. Modelica, Matlab).

Matlab has been used successfully to simulate the mixed-Boolean State Model [30]. Conditional statements and loops can be used to assign values to the Boolean parameters at any given time step, and the system can then be solved using regular solvers. Where the model is implicit in some modes of operation, an implicit solver such as BDF or ode15i (in Matlab) must be used. An example Matlab script is provided in the appendix.

Immediately after a discontinuity, the state (or pseudo-state) variable is assigned the same value that the corresponding state (or pseudo-state) had immediately before the discontinuity. This is because the model is inherently a switching model, and the causally dynamic hybrid bond graph described here guides the user towards developing a switching model rather than an impulsive one. There are no unknown energy losses, and hence no need for state reinitialisation. This is discussed in more detail in Sect. 4.6.6.

There is a body of literature on the simulation of hybrid and nonsmooth dynamical systems which has developed in parallel with the hybrid bond graph . A number of issues merit consideration [1]:

• Switching must always occur at the end of a time step, in order to be captured. This usually motivates an event-driven method. However, this can be impractical where there is a large number of switching instants or it is not known where they occur.

• Chattering may occur where a sliding mode cannot be reached due to numerical approximation.

• A procedure for accurately finding the location of events may be required, along with some method for reinitialising states after the event.

• Where there are a number of events, there may be a finite accumulation point past which the event-driven method cannot progress.

• There may be an impulsive term on commutation giving a Dirac or Steltjes measure. For example, the differential measure of velocity which manifests on impact between bodies.

Acary and Brogliato [1] suggest the use of discrete-time Moreau’s second-order sweeping process for solving problems such as the bouncing ball discussed here. There are no detection times, and hence no accumulation point. Nonsmooth measures are treated rigorously with no ‘jump’ in acceleration, and hence no impulse losses or need to reinitialise states.

5.3 Developing an Impulse Model

Where a mode of operation is very short (e.g. the ‘in contact with the ground’ mode of a bouncing ball) it can be computationally inefficient to simulate it. This is why these kinds of problems are often abstracted to impulsive models. The problem with impulsive models is that the impulse loss on commutation is unknown, and the values of state variables after the discontinuity are consequently unknown. The impulse must be explicitly modelled (as in Impulse Bond Graphs [65]) or the states must be reinitialised using some algorithm [36, 45].

The [switching] hybrid bond graph can be used to generate an impulsive model, with the benefit of allowing the impulse loss to be calculated rather than simply estimated. For example, in the bouncing ball problem, the model can be simplified to give Newton’s Collision Law (an impulsive model) with a coefficient of restitution calculated from the model [31].

6 Structural Analysis in Causally Dynamic HBGs

Here the term ‘structural analysis’ refers to the qualitative analyses that can be carried out on the bond graph prior to simulation. They can guide the user in revisiting their modelling assumptions or even the design of the system. They will also provide some information about computation, such as whether the model is explicit or implicit. The structural analyses mirror those carried out on state equations, because the bond graph and state model are closely linked.

6.1 State and Implicit Models

Control properties are usually found from the state space representation of the model with causality assigned (i.e. the input/output model). An overview is given by the most standard control textbooks such as Sontag [51]. Although there have been significant developments in control theory since that time, these basic parameters are still widely taught and used today, often in the context of the explicit linear time-invariant (LTI) state space equation. Authors typically strive to obtain the explicit regular state space system for ease of both computation and analysis. Since state equations are easily derived from the bond graph, it follows that control properties normally found from the state equations are reflected in the bond graph’s structure and causal assignment. A body of work by Sueur, Dauphin-Tanguy and others brings the notions of structural analysis and exploiting causality closer together. These properties (controllability, stability, (in)finite structure, etc.) aid with instrumentation for experimentation and fault diagnosis and identification (FDI).

However, implicit systems in various forms appear to arise naturally when looking at interconnected systems, and Lewis [25] argues that they are more suitable for signal processing and modelling tasks than explicit state space models. Specific implicit forms which have been investigated in detail are singular systems, semistate systems and descriptor systems. Yip and Sincovec [64] establish properties of the descriptor system , and Verghese et al. [60] develop a generalised theory for singular systems: both essentially present control properties for implicit systems which mirror those established for explicit ones. Lewis [24–26] gives a useful review of implicit systems and techniques for analysing them, and Dai [17] looks specifically at matrix-rank criteria for singular systems. Their results will be extended to the equations generated by the causally dynamic hybrid bond graph here.

The main considerations for a singular system are the presence and treatment of impulsive modes, and of causality. Causality in this sense refers to whether a value can be calculated from past values (causal) or depends on both past and forward values (noncausal): implicit systems are by nature noncausal. This allows them to be manipulated into a state space form and perhaps more significantly they can be considered as behavioural models. Willems [62, 63] demonstrates that control can be studied from a behavioural point of view without introducing inputs and outputs. Lewis and Ozcaldiran [27] therefore investigate the geometric properties of implicit models referencing Willems, arguing that they give increased engineering insight.

6.2 Observations on the Dynamic Causality Assignment

The dynamic causality notation was designed to give some insight into the model and be more usable than existing notation [5]. This section presents a series of observations on dynamic causality manifesting in the hybrid bond graph.

An immediate observation is that paths of dynamic causality between controlled junctions and elements can be identified, and these clearly show the elements affected by commutation of a controlled junction. This means that compiling a truth table for the model and constructing the Λ-matrix for any subsequent equation derivation is greatly simplified. Rather than constructing a truth table for the whole model with 2ⁱ possible modes of operation (where i is the number of controlled junctions), a series of smaller truth tables can be constructed for each segment of the model in dynamic causality.

Additional observations on the paths of dynamic causality can be made in line with those already made for causally static bond graphs, such as Margolis and Rosenberg’s work on exploiting causality [34, 47] and Rosenberg and Andry’s work on solving causal loops [48].

The number of storage elements in dynamic causality is a measure of the variation in model size. Recall that elements in integral causality provide the state variables in deriving the state equations. Therefore, when all of storage elements are in integral causality, the maximum number of states is active. In a well-constructed model, there are no elements in static derivative causality and this mode (the reference mode) gives a fully explicit state space model. Likewise, the mode of operation where most storage elements are in derivative causality gives the minimum number of state variables (and the maximum number of pseudo-states which yield additional algebraic equations). Dynamic causality on resistance elements does not affect the model size.

If dynamic causality is not controlled, it can be exploited in much the same way as static causality. Causal paths between elements (in the reference or other modes) can be traced, and signify various types of algebraic or kinematic constraint. In addition to identifying these paths in the case of dynamic causality, it is possible to further classify them.

The classic variable topology problem—ideal ‘hard’ contact resulting in coalescence—is visible via a controlled junction which is OFF in the reference mode and results in a kinematic constraint between rigid bodies (i.e. a causal path between two I-elements, one of which will be in derivative causality) when it is ON. This usually manifests as a path of dynamic causality between a controlled junction and I-element, shown in Fig. 4.12. It is also possible for compliance elements to become kinematically constrained.

Fig. 4.12

Example of a type 1 discontinuity: ‘Hard’ contact resulting in a kinematic constraint between bodies 1 and 2 (top), compliant contact (middle) and compliant contact with resistance (lower)

A user may choose to break the kinematic constraint by revising modelling assumptions: the classic approach is to redefine a hard contact problem as stiff contact, by adding a stiff compliance between the inertia elements. This may not always be appropriate, especially if a ‘proper model’ or model devoid of high-frequency stiff dynamics is required. If the mode(s) of operation for which the constraint exists were to be considered in isolation, the constrained storage elements could be lumped together: this may be laborious by hand, but a computer programme could feature an algorithm for lumping constrained elements or using relaxed causalities [22] in the appropriate modes of operation.

Where there is compliant contact, the inertia elements will remain in integral causality and there is no kinematic constraint. There will be a path of dynamic causality between the junction and a compliance element instead. There is typically some dissipation associated with this type of contact, and a resistance element may be added which will act as causality resistance: in this case the path of dynamic causality will be between the controlled junction and resistance element.

Definition 4.6.

Type 1 Structural Discontinuity: The controlled junction is OFF in the reference configuration. When it is ON, two subsystems are joined and a kinematic constraint may result.

The alternative situation is a controlled junction which is ON in the reference configuration, and divides the model into subsystems when it is OFF, as shown in Fig. 4.13. Disconnecting a power source—for example, in an electrical or hydraulic circuit—can result in storage elements discharging, and this is reflected by them switching to derivative causality. As with the type 1 structural discontinuities, parasitic elements (additional compliance, causality resistance) can be used to control this dynamic causality but must be used with caution.

Fig. 4.13

Example of a type 2 discontinuity

Definition 4.7.

Type 2 Structural Discontinuity: The controlled junction is ON in the reference configuration. When it is OFF, the system is divided into subsystems, and storage elements may discharge to compensate for a lack of power source in a subsystem.

As dynamic causality occurs, various other paths and loops may be created or broken with commutation. These are not a feature of the type of discontinuity.

Some observations may be made regarding the control properties of the system. Assume a system is [structurally] controllable and observable in the reference mode. If the system contains type 1 discontinuities, the system’s finite dynamics remain controllable and observable after commutation. If it contains type 2 discontinuities, the model may be subdivided into uncontrollable and unobservable subsystems with commutation.

In assigning the causality around a controlled junction, the user may make an arbitrary decision regarding which element to place in dynamic causality. Consider the ‘hard contact’ in Fig. 4.12: dynamic causality was assigned to Body 2 but could just as easily have been assigned to Body 1. The basic effects on the system are the same:

• When the controlled junction is OFF the I-elements

  • are both in integral causality and

  • both yield a state variable and equation.

• When the controlled junction is ON,

  • one of the I-elements switches to derivative causality,

  • the order of the model is reduced by one and

  • the elements yield one state variable and equation, and an additional pseudo-state providing an algebraic constraint between the two bodies.

The only time that the choice of element to place in derivative causality may be significant is when there is an existing causal path between an element and some other structure. This will still be captured via the new causal paths, but may be less immediately obvious to the user and computationally inefficient. An example is shown in Fig. 4.14.

Fig. 4.14

Hard contact with a causal path (indicated by arrow): Body 2 in dynamic causality (top) and Body 1 in dynamic causality (lower)

The causality assignment in Fig. 4.14 (top) results in a static causal path between Body 1 and the spring. The equally legitimate causality assignment in Fig. 4.14 (lower) does not have this static causal path. Instead, there is a causal path between the spring and Body 1 only when the controlled junction is OFF. When the controlled junction is ON, this path no longer exists but another causal path appears between the spring and Body 2. Inspecting the structure and causality of the systems (using the notation in Fig. 4.15) yields the equations in Table 4.3. It can be seen that the first set of equations is more elegant and concise. The second set still relates the spring to Body 1, but when the controlled junction is ON this is done via the algebraic constraint between the bodies.

Fig. 4.15

Notation used in equation derivation for the hard contact example

Table 4.3 Junction Structure & Implicit State Equations for the Hybrid Bond Graph in Figure 4.14

Where a causal conflict occurs in the dynamic causal assignment, this indicates a conflict in a specific mode of operation, and the mode is a ‘forbidden mode’. Forbidden modes may be a consequence of the modelling assumptions, or reflect a real case such as a short-circuit.

A mode in which there is a causal conflict is ‘forbidden’ in the sense that causality cannot be assigned, and hence the mathematical model cannot be constructed for that mode, and the model cannot be simulated. An interesting property of the hybrid bond graph is that causal conflicts reflect modes that would be undesirable or impossible in reality. This is because the method was developed to reflect the physics of the system.

6.3 Transfer Function Using Shannon-Mason Loop Rule

It is well-documented that causal paths in a bond graph are equivalent to signal loops, and a transfer function can therefore be found directly from the causal bond graph using Shannon-Mason loop rule [10]. In the hybrid bond graph proposed here, commutation clearly affects the causal paths in the model (where they cross a controlled junction) , and commutation will therefore also clearly manifest in the transfer function. By looking at the causal paths present in the reference configuration, and then each path of dynamic causality, a transfer function for all possible modes of operation can be obtained. Where the paths cross a controlled junction, or are induced by a certain combination of operations, the relevant Boolean term can be inserted into the expression for gain in the transfer function.

In constructing the transfer function, causal paths between elements and sources are used to generate gain terms in the determinant. Where that path crosses a controlled junction, it only exists in the ON state. Multiplying the gain term by the Boolean factor ensures it is sent to zero when OFF. An example of this situation is shown in Fig. 4.16, where the causal path indicated by the arrow has a gain of $\frac{-\lambda } {s^{2}\mathrm{IC}}$.

Fig. 4.16

A causal path crossing a controlled junction

Where a causal path is dynamic or partially dynamic, the gain is factored by the Boolean function (term in Λ) which activates the path to give the signal loop under consideration.

Where a path between two elements is in dynamic causality, the complete path only exists in a certain mode of operation. For the example in Fig. 4.17, the causal path between the I- and R-elements (shown by the arrow) is partially in dynamic causality. This means that there is a path between the two elements in some modes of operation only (those where the I-element is in integral causality). Hence, the Boolean function associated with activating integral causality of the I-element must be used as a factor in the gain, giving $-\frac{(\lambda _{1}\oplus \lambda _{2})R} {sI}$. When the I-element is in derivative causality, there is no causal path and the gain term is sent to zero.

Fig. 4.17

A causal path in dynamic causality

The general form of the transfer function is therefore identical to that of the standard bond graph:

$$\displaystyle{ h_{ij} = \frac{1} {\varDelta } \sum _{k}^{}G_{k}\varDelta _{k} }$$

(4.9)

where k denotes the kth path between input and output, and the graph determinant is

$$\displaystyle{ \varDelta = 1 -\sum _{i}^{}G_{i} +\sum _{ i,j}^{}G_{i}G_{j} -\sum _{i,j,k}^{}G_{i}G_{j}G_{k} + \cdots }$$

(4.10)

However, for the hybrid bond graph G is not only a function of any resistance, inertia or compliance coefficients relating to elements in the loop, but can also contain Boolean terms.

Where a controlled junction breaks/joins the causal paths in a model, the dynamic behaviour of the system is affected with commutation. The following points follow logically:

• If a controlled junction is in a path, then a Boolean term will be present in the graph determinant and hence the denominator of the transfer function. The roots of the denominator are the eigenvalues of the system, so it follows that the system will lose/gain one or more poles with commutation.

• If a controlled junction is in a path which does not ‘touch’ the input–output path (i.e. the paths do not share any nodes), then the ‘reduced determinant’ and hence the numerator of the transfer function will also contain a Boolean term. It follows that the system will lose/gain zeros with commutation.

• If a controlled junction is on the input–output path, the gain of the system will be affected. The numerator of the transfer function will again contain a Boolean and the system will lose/gain zeros with commutation.

• Where elements are in derivative causality, a path will only be present in some modes of operation and a Boolean function will denote this. Some paths will never touch because they are in exclusive modes of operation, and this must be taken into account when calculating the determinants.

6.4 The LTI Full Descriptor System

The states of the bond graph model can be used to generate an implicit system equation from the junction structure. For models where all storage elements are in integral causality, E = I (i.e. E is non-singular) and the well-known explicit or regular state space equation is generated. For models where some storage elements are in derivative or dynamic causality, E is singular and the system is implicit [26]. Hybrid bond graphs with storage elements in dynamic causality will always generate implicit equations, because the derivative causality cases generate algebraic equations with no differential term (and hence a zero term in E ) and the constraints they represent give off-diagonal coupling terms in E.

The LTI implicit equation forms one part of a descriptor system (4.11), the other part being given by the output equation (4.12).

$$\displaystyle\begin{array}{rcl} \mathbf{E}(\boldsymbol{\varLambda })\dot{\boldsymbol{X}}& = \mathbf{A}(\boldsymbol{\lambda })\boldsymbol{X} + \mathbf{B}(\boldsymbol{\lambda })\boldsymbol{U}&{}\end{array}$$

(4.11)

$$\displaystyle\begin{array}{rcl} \boldsymbol{Y }& = \mathbf{C}(\boldsymbol{\lambda })\boldsymbol{X} + \mathbf{D}(\boldsymbol{\lambda })\boldsymbol{U}&{}\end{array}$$

(4.12)

The A, B, C, D and E matrices of these equations are used in defining control parameters such as controllability and observability, usually using matrix-rank criteria [17].

There is no standard output element in the bond graph framework. Some authors take an output as being the complementary variable of an input, which is logical in systems where source elements are also used as sinks. A fairly common notation is that of detector elements (De- or Df-elements) which are essentially null sources added to junctions. These act in precisely the same manner as a source/sink, and simply have a different notation for clarity. However, output is not a property of a system, and the use of detector elements with a power flow suggests that sensors are energy-processing.

Signal detectors similar to those in the commercial package 20-Sim are used here to indicate output. The use of detector elements (De- or Df-elements)—which are essentially null sources added to junctions—was avoided as they imply that output is a system property and that the sensors are energy-processing. Signal detectors are not energy-processing, and can output quantities other than effort and flow.

Outputs can be added to the junction structure, shown graphically in Fig. 4.18, and hence expressed in terms of the junction structure and system inputs, shown in Eq. (4.13):

$$\displaystyle\begin{array}{rcl} \left [\begin{array}{cccc} \boldsymbol{\varLambda }_{11} & 0 & 0 &0 \\ 0 &\boldsymbol{\varLambda }_{22} & 0 &0 \\ 0 & 0 &\boldsymbol{\varLambda }_{33} & 0 \\ 0 & 0 & 0 & \mathbf{I} \end{array} \right ]\left [\begin{array}{c} \dot{\boldsymbol{X}}_{i} \\ \boldsymbol{Z}_{d} \\ \boldsymbol{D}_{\mathrm{out}} \\ \boldsymbol{Y } \end{array} \right ] = \left [\begin{array}{cccc} \mathbf{S}_{11} & \mathbf{S}_{12} & \mathbf{S}_{13} & \mathbf{S}_{14} \\ -\mathbf{S}_{12}^{T}& 0 & 0 &\mathbf{S}_{24} \\ -\mathbf{S}_{13}^{T}& 0 &\mathbf{S}_{33} & \mathbf{S}_{34} \\ \mathbf{S}_{41} & \mathbf{S}_{42} & \mathbf{S}_{43} & \mathbf{S}_{44} \end{array} \right ]\left [\begin{array}{c} \boldsymbol{Z}_{i} \\ \dot{\boldsymbol{X}}_{d} \\ \boldsymbol{D}_{\mathrm{in}} \\ \boldsymbol{U} \end{array} \right ]& &{}\end{array}$$

(4.13)

Fig. 4.18

The general hybrid bond graph with signal detectors giving outputs

This can be used to derive an output equation :

$$\displaystyle{ \boldsymbol{Y } = \mathbf{J}\mathbf{F}_{i}\boldsymbol{X}_{i} + \mathbf{JF}\boldsymbol{X}_{d} + \mathbf{S}_{42}\dot{\boldsymbol{X}}_{d} + (\mathbf{S}_{43}\mathbf{HS}_{34} + \mathbf{S}_{44})\boldsymbol{U} }$$

(4.14)

where J = S ₄₁ −S ₄₃ HS ₁₃ ^T. This is a rather unorthodox form of the output equation, since it is a function of $\dot{\boldsymbol{X}}_{d}$. When all storage elements are in static causality, this is of little consequence, since $\dot{\boldsymbol{X}}_{d} = 0$. The expected descriptor system can then be found, and standard matrix-rank criteria can be used to analyse the hybrid bond graph.

The output equation takes the usual LTI Descriptor System form if there is static causality on all of the storage elements. However, in a hybrid bond graph, storage elements can take dynamic causality and the $\dot{\boldsymbol{X}}_{d}$ term must be considered.

The hybrid bond graph can therefore be used to generate the standard LTI Descriptor System form. This allows comparison with control properties using established techniques such as matrix-rank criteria.

$$\displaystyle\begin{array}{rcl} \left [\begin{array}{cc} \varLambda _{11} & -\mathbf{S}_{12}\\ 0 & 0 \end{array} \right ]\left [\begin{array}{c} \dot{\boldsymbol{X}}_{i} \\ \dot{\boldsymbol{X}}_{d} \end{array} \right ]& =& \left [\begin{array}{cc} \mathbf{KF}_{i} & \mathbf{KF} \\ -\mathbf{S}_{12}^{T}\mathbf{F}_{i} -\boldsymbol{\varLambda }_{22}\mathbf{F}^{T}& -\mathbf{S}_{12}^{T}\mathbf{F} -\boldsymbol{\varLambda }_{22}\mathbf{F}_{d} \end{array} \right ]\left [\begin{array}{c} \boldsymbol{X}_{i} \\ \boldsymbol{X}_{d} \end{array} \right ] \\ & & +\left [\begin{array}{c} \mathbf{S}_{14} + \mathbf{S}_{13}\mathbf{H}\mathbf{S}_{34} \\ \mathbf{S}_{24} \end{array} \right ]\left [\begin{array}{c} \boldsymbol{U} \end{array} \right ]{}\end{array}$$

(4.15)

$$\displaystyle\begin{array}{rcl} \left [\begin{array}{c} \boldsymbol{Y } \end{array} \right ]& =& \left [\begin{array}{cc} (\mathbf{S}_{41} -\mathbf{S}_{43}\mathbf{HS}_{13}^{T})\mathbf{F}_{i}&(\mathbf{S}_{41} -\mathbf{S}_{43}\mathbf{HS}_{13}^{T})\mathbf{F} \end{array} \right ]\left [\begin{array}{c} \boldsymbol{X}_{i} \\ \boldsymbol{X}_{d} \end{array} \right ] \\ & & +\left [\begin{array}{c} \mathbf{S}_{43}\mathbf{HS}_{34} + \mathbf{S}_{44} \end{array} \right ]\left [\begin{array}{c} \boldsymbol{U} \end{array} \right ]{}\end{array}$$

(4.16)

6.5 Impulse Losses

A key concept in variable topology systems is that of impulsive losses. The term ‘impulse’ is used in conjunction with two subtly different issues which must be distinguished here. The first is the impulse modes associated with the causally dynamic model and the initial value of the pseudo-state: i.e. the mathematical treatment of ideal switching. The second is the abstraction of the modes of operation themselves: much of the existing work on the subject investigates collisions using restitution, where the contact phase itself (and consequent dissipation) is so short as to be abstracted to a discontinuity.

Considerable work has been dedicated to the question of impulse losses on commutation, including Mosterman’s work on implicit modelling [35] and Zimmer and Cellier’s proposal for an Impulse Bond Graph [65]. Mosterman’s work in particular gave rise to a body of work where state variables are reinitialised after each discontinuous event. These authors use the classical case study of Newton’s Collision Law with restitution. Collision is an example of a subset of hybrid model called the Impulse model [7]. Here, the continuous state changes impulsively on hitting prescribed regions of state space. The ‘jumps’ in state space are not energy conserving: and hence an impulse loss must be accounted for. In the case of collision, the continuous state changes from positive to negative velocity with any energy loss accounted for via the coefficient of restitution.

The use of a Boolean controlled junction in the hybrid bond graph dictates the way a discontinuity is abstracted: a switch must be ON or OFF, contact TRUE or FALSE, etc. In the case of a collision, this means that the short ‘in contact’ phase is modelled (whereas Newton’s collision law neglects this). Any energy dissipation is modelled on the bond graph during this phase: there is no restitution. The hybrid bond graph with structural switching is always a ‘Switching model’ as defined by Branicky et al. [7], i.e. the vector field changes discontinuously when the state hits a boundary, but these changes are not impulsive.

6.6 Impulse Modes

Impulse modes (also referred to as infinite frequency modes) are a feature of hybrid systems. They occur where a storage element switches from integral to derivative causality, giving a step change in the value of the state. When all elements are in integral causality, E is an identity matrix and the model is in the explicit state space form. When a storage element changes to derivative causality with commutation, an algebraic constraint is typically set up and a non-diagonal term manifests in E. This term, which changes instantaneously from zero to a finite factor of a state variable on commutation, is what gives the impulse mode [60]. Recall the implicit equation (4.15), and compare it to the standard implicit equation. There is a time-varying term $\dot{\boldsymbol{X}}_{d}$ in the algebraic equations yielded by the pseudo-states of the storage elements in derivative causality. This is multiplied by zero (by the lower portion of E) to give an algebraic constraint. However, where storage elements in derivative causality are coupled to the states (i.e. S ₁₂, and therefore E ₁₂ in the implicit equation, are nonzero), a $\dot{\boldsymbol{X}}_{d}$ term is present and the pseudo-state is differentiated across the commutation. The pseudo-state is nominally assumed to have a zero initial value, and take a nonzero value on commutation. This means that there is a step increase in the pseudo-state between the initial condition (incrementally before commutation) and the finite value it holds at time t (incrementally after commutation). The first row of (4.15) after commutation therefore gives

$$\displaystyle\begin{array}{rcl} \boldsymbol{\varLambda }_{11}\dot{\boldsymbol{X}}_{i} -\mathbf{S}_{12}\dot{\boldsymbol{X}}_{d} = \mathbf{KF}_{i}\boldsymbol{X}_{i} + \mathbf{KF}\boldsymbol{X}_{d} + (\mathbf{S}_{14} + \mathbf{S}_{13}\mathbf{HS}_{34})\boldsymbol{U}& &{}\end{array}$$

(4.17)

where:

$$\displaystyle\begin{array}{rcl} \dot{\boldsymbol{X}}_{d} = \frac{(\boldsymbol{X}_{d})_{t} - (\boldsymbol{X}_{d})_{0}} {dt} & &{}\end{array}$$

(4.18)

Differentiating this step change over zero time yields a mode of infinite frequency: this is the impulse mode.

$$\displaystyle{ dt \rightarrow 0\quad \therefore \quad \dot{\boldsymbol{X}}_{d} \rightarrow \infty }$$

(4.19)

Commutation does not always result in a step change and subsequent impulse mode. Recall that the states and pseudo-states are intimately connected: each energy-storage element in dynamic causality has both a state variable (active when the element is in integral causality) and a pseudo-state (active when it is in derivative causality). By considering the type of discontinuity, some observations can be made on the relationship between states and pseudo-states.

A type 1 structural discontinuity yields an impulse on initial commutation as two subsystems with different dynamic properties become joined and constrained (setting a storage element to derivative causality). When the system returns to its original state on subsequent commutation, there is no impulsive mode.

For a type 1 structural discontinuity, where bodies are disconnected (OFF) in the reference mode and the commutation connects them, the initial value of the pseudo-state may indeed be zero if that body was at rest. Alternatively, it may have another value if it is controlled by another source or subsystem. There is typically an energy loss as the body changes its behaviour suddenly (for example, a falling rigid body hitting the ground, or a truck clutch being engaged: both of which give an audible loss). In real life—which is continuous—this is a measurable dissipation occurring over a finite time (albeit a small one). The abstraction to a discontinuity with no resistance is responsible for the impulse loss. The equations for an example system are shown in Fig. 4.19.

Fig. 4.19

Equations for modes in isolation, type 1 discontinuity: reference mode (left) and after commutation of the X1-junction (right)

Assume that a commutation occurs at time t during a simulation. Prior to commutation (at time t − 1) the system is in the reference mode and both storage elements are in integral causality. After commutation, Body 2 is in derivative causality. The second row of the implicit equation gives an algebraic term for $\tilde{p}_{2d}$, but there is also a differential $\tilde{\dot{p}}_{2d}$ term in the first row. Looking at the differentiation across the commutation:

$$\displaystyle{ \tilde{\dot{p}}_{2d} \approx \frac{\tilde{p}_{2d_{(t)}} -\tilde{ p}_{2i_{(t-1)}}} {\varDelta t} }$$

(4.20)

where $\tilde{p}_{2i_{(t-1)}}$ is known from the previous time-step’s calculation, and $\tilde{p}_{2d_{(t)}} =\hat{ p}_{1i_{(t)}}$ because the two inertia elements are now rigidly constrained. Note that all values are known, so there is no need to reinitialise the variables using canonical forms. The time step is also nonzero and known, and governed by the integrator parameters used for computation. A large step change (compared to the time step) may cause computational difficulties at this point as the left-hand side of the state equation can become large. In this case it may be advantageous to set $\tilde{\dot{p}}_{2d_{(t)}} = 0$, $\tilde{p}_{2d_{(t)}} =\hat{ p}_{1i_{(t)}}$ and neglect the impulse. This naturally violates conservation of energy but would ease computation considerably.

If the reverse situation is true, i.e. there is a type 2 structural discontinuity where the bodies are connected in the reference mode and the commutation disconnects them, the initial value of the pseudo-state is not zero.

A type 2 structural discontinuity does not yield an impulse on initial commutation. In this case, the state of the storage element which switches to derivative causality is identical to its value immediately before commutation. Hence there is no step change in state variable and no energy loss.

When the system returns to its original state on subsequent commutation, there is a step change in state variable. However, this does not manifest as an impulsive off-diagonal term in the E matrix: it is simply the newly activated $\dot{\mathbf{X}}_{i}$ term. This term is the output calculated from the state variables and inputs at the current time, and there has been no differentiation over a zero time step. Hence there is no impulse.

In this case, the initial value of the pseudo-state is equal to the [usually finite] value of the corresponding state variable immediately before commutation. Furthermore, after commutation the pseudo-state is not sent to zero. The behaviour of the element may be controlled by some other system, or may tend to zero over time (for example, a clutch disconnecting a load which free-wheels until it finally reaches rest). In this case there is no step change in variable and no impulse. However, when commutation occurs again and the disconnected body is reconnected to the system (going from zero to a finite value), a step change in state variable may then occur. Consider a system with one element in dynamic causality, which has just commutated back to the mode in which it is in integral causality. Row 1 of the implicit equation (which is now explicit) gives

$$\displaystyle{ \mathbf{I}\dot{\boldsymbol{X}}_{i} = \mathbf{KF}_{i}\boldsymbol{X}_{i} + (\mathbf{S}_{14} + \mathbf{S}_{13}\mathbf{HS}_{34})\boldsymbol{U} }$$

(4.21)

Although a step change may have occurred, there is no impulsive term in the equation.

Hence each term in E ₁₂ potentially represents an impulse mode, but in reality there is only an impulse loss where there are type 1 discontinuities . Any algorithm for computing impulsive modes must take the variety of possible cases into account.

The use of pseudo-states means that the state variable never needs to be reinitialised. In type 1 systems, the pseudo-state variable arises because there is a kinematic constraint between two elements, and the pseudo-state of one is equal to the state of the other. In type 2 systems, there is no step change on the initial commutation, but a subsequent commutation may result in a step change: this does not result in an impulsive term in the equations because the differential term is explicit.

A mathematical impulse has infinite magnitude and zero width, hence there is no actual energy loss. In reality, there can be dissipation in the form of an audible noise, spark or heat loss. This can be represented on the bond graph via a resistance element, or neglected in which case conservation of energy does not hold true. Mosterman [41] suggests that conservation of state is the important concept in system modelling, and the impulse energy dissipated during discontinuous events is ‘free energy’.

Each mode change is a sliding mode change and the implicit equation can always be used because one side of it is always known. The use of impulse models like Newton’s collision law (i.e. restitution) are a different case. In impulse models there is a jump in state space between modes of operation and an associated energy loss. This type of impulsive loss should not be confused with the impulse modes described above.

6.7 Control Properties

The term ‘control properties’ refers to those properties obtained from the model which can benefit the control engineer. These are typically stability, controllability/observability, solvability and related properties which can aid the engineer in assessing a design and defining instrumentation and stabilising controllers.

Analysis of the state and implicit equations using matrix-rank criteria—with or without transforming the model to various canonical forms—is well established and perhaps the most common form of system analysis. The use of matrix-rank criteria necessitates an input–output model, i.e. they must be applied after causality has been assigned. The validity of this approach has been called into question. A more promising approach, in keeping with the ideals of physical and behavioural modelling, might be a geometric one as proposed by Lewis [26] and Willems [63]. This is recommended as a topic for further study.

It is well established that a controllability matrix can be constructed for an LTI descriptor system , which has rank equal to model order when the system is controllable. This controllability matrix is a function of the A and B matrices, which are in turn comprised from the submatrices of S. Controllability can hence be seen on the bond graph by analysing the causal paths, or established from the junction structure matrix S. Previous work on hybrid bond graphs (using switched sources) has investigated R-controllability and Impulse-controllability , relating to the finite and impulse modes, respectively. The same distinction is made here.

Recall that the order of the model, and hence the number of finite modes of the system, is given by the number of storage elements in integral causality. It therefore follows that the maximum number of finite modes occurs when most storage elements are in integral causality, i.e. the reference mode. The maximum number of finite modes is given by the order of the model in the reference mode. This is the maximum number of storage elements in integral causality: dim[X _i ]. R-controllability of these finite modes is an intuitive concept, fundamentally the same as the structural controllability defined for a continuous LTI system. The model is R-controllable when independent relationships in the equations—corresponding to causal paths on the bond graph which exist both when preferred integral and preferred derivative causality are applied—are present between each storage element and a source element.

When there is a controlled junction in a causal path, that path is severed or ceased to exist when the junction is OFF. It is intuitive that when a controlled junction occurs between the storage element in integral causality and a source element:

• a Boolean term occurs in the underlying equations which sets the relationship to zero when the junction is OFF, and

• the dynamic causality around the junction clearly shows that the causal path is broken when the junction is OFF.

There are two possible outcomes when this happens. The first is that the storage element remains in integral causality, in which case it may be controlled by another source, or it may be uncontrolled, i.e. there is an uncontrolled finite mode. The other outcome is that the storage element changes its causal assignment and the finite mode ceases to exist: in this case the impulse controllability must be assessed.

There may also be instances where a nearby controlled junction(s) results in dynamic causality on a causal path between the storage element in integral causality and a source element. The controlled junction(s) does not physically sever the causal path, but still clearly affects controllability because the relationship between the source and storage elements is nonexistent in some modes of operation.

A hybrid bond graph is structurally R-controllable iff:

• 1. There is a causal path between each storage element in integral causality and a source element in all modes of operation, i.e.:

  • (a) the causal path does not cross a controlled junction or,

  • (b) there is another path between it and a storage element crossing a controlled junction which operates in a mutually exclusive manner with the first, or,

  • (c) the causal path crosses a controlled junction which forces the storage element into derivative causality when it is OFF.

• 2. In the reference mode, the rank of the controllability matrix is equal to the model order: i.e. the number of storage elements in integral causality when preferred integral causality is applied is equal to the number of storage elements in derivative causality when preferred derivative causality is applied (allowing dualisation of source elements).

This is an extension of R-controllability for a static bond graph, acknowledging the observations made for structural switching and dynamic causality, i.e. that relationships in the model can be dependent on commutation.

Impulse controllability has been established by hybrid bond graph practitioners such as Rahmani and Dauphin-Tanguy [46] by inspecting the switching sources, which is clearly not applicable here as there are none. An equivalent criteria of establishing causal paths between controlled junctions and storage elements could be stated. However, the impulse modes in the underlying equations no longer relate to the switching laws present in the hybrid bond graph with switching sources. In this hybrid bond graph, the impulse modes relate solely to storage elements in dynamic causality. Impulse controllability, in the classical sense, is whether these impulse modes can be controlled by a non-impulsive input, verified by the algebraic tests which involve inspecting the ranks of the E, A and B matrices. In the discussion of impulse modes (Sect. 4.6.6) it was noted that an impulse does not always occur in the model: it depends on the type of discontinuity and commutation.

Recall that impulse [infinite] modes occur when a storage element is in dynamic causality, i.e. it switches between integral and derivative causality with commutation. In a well-constructed model there would not normally be any elements in static derivative causality.

The maximum number of impulse modes is given by the number of storage elements in dynamic causality: $\text{dim}\ [\tilde{\mathbf{X}}_{d}]$.

This is an extension of the property for switched bond graphs (using switched sources). The number of impulse modes in any single mode of operation is given by the number of storage elements in derivative causality. It therefore follows that the maximum possible number of impulse modes is given when all possible storage elements are in derivative causality, and this is in turn given by the storage elements in dynamic causality. Note that this is the maximum for the overall model: when some modes are mutually exclusive, there may not be a single mode of operation where all impulse modes occur.

Since the impulsive modes only exist when the respective storage element is in derivative causality, impulse controllability could be established by a causal path (and algebraic relation) between the element and a source (either directly or via another element which is controlled) in that mode of operation. Looking at the hybrid bond graph, since impulse modes relate to storage elements in dynamic causality, this manifests as a causal path (at least part of which will be dashed, i.e. dynamic) between a storage element in derivative [dynamic] causality and a source element. Hence, Rahmani et al.’s criterion for impulse controllability [46] is adapted and reused here.

The model is impulse controllable iff there exists a causal path between an input source and a controlled junction passing through a storage element in derivative causality.

An uncontrolled impulse mode would indicate an element which has been severed from the sources in the system and switched to derivative causality, such as an accumulator or capacitor discharging when the pump/battery is disconnected.

Observability is assessed in much the same way as controllability, as it is the dual property. The difference is that the observability matrix is a function of the C matrix relating the outputs to the model states (as opposed to the B matrix relating the inputs to the model states).

Impulsive terms can occur when storage elements take derivative causality with commutation. Impulse observability is assumed to be the dual property of impulse controllability. Consequently R-observability for finite modes also exists and is assumed to be the dual of R-controllability. The following properties are therefore presented without proof.

A hybrid bond graph is structurally R-observable iff:

• 1. There is a causal path between each storage element in integral causality and a detector element in all modes of operation, i.e.

  • (a) the causal path does not cross a controlled junction or,

  • (b) there is another path between it and a detector element crossing a controlled junction which operates in a mutually exclusive manner with the first, or,

  • (c) the causal path crosses a controlled junction which forces the storage element into derivative causality when it is OFF.

• 2. In the reference mode, the rank of the observability matrix is equal to the model order: i.e. the number of storage elements in integral casuality when preferred integral causality is applied is equal to the number of storage elements in derivative causality when preferred derivative causality is applied (allowing dualisation of detector elements).

The model is impulse observable iff there exists a causal path between an detector and a controlled junction passing through a storage element in derivative causality.

Asymptotic stability is typically established by finding the solutions of the characteristic polynomial. The roots for all possible modes of operation can be obtained and plotted: roots with positive real parts indicate unstable behaviour. This is a numeric approach rather than a structural one, and outside the scope of structural analysis.

Where asymptotic stability does not exist, it indicates the presence of ‘zero modes’ (eigenvectors with vanishing eigenvalues). Recall that ‘structurally null modes’ (i.e. eigenvalues which are zero, or the poles at the origin) are given by the storage elements which are in integral causality when preferred derivative causality is assigned [19].

For the hybrid bond graph this philosophy can be extended to the number of I- and C-elements which have to stay in [static] integral causality plus the number of I- and C-elements in dynamic causality when a preferred derivative causality is assigned to the bond graph model.

The maximum possible number of structurally null modes is given by the number of storage elements which can take integral causality when preferred derivative causality is assigned to the bond graph.

This is the number of storage elements in [static] integral causality, plus the number of storage elements in dynamic causality in the BGD (Bond graph in preferred derivative causality).

$$\displaystyle{ D_{0} = (\mathrm{dim}[\hat{\mathbf{X}}_{i}] +\mathrm{ dim}[\tilde{\mathbf{X}}_{i}])_{\mathrm{BGD}} }$$

(4.22)

This property is a logical extension of the procedure for finding structurally null modes in a static bond graph. Recall that placing the bond graph in preferred derivative causality yields a mathematical model in an alternative form including the inverse of the system matrices. When storage elements remain in integral causality, it means that A is singular and there are no unique solutions to the system of equations. In particular, inspection of the characteristic equation reveals that there are k structurally null modes relating to the rows of A in which the causal constraints (in the BGD) exist, and these in turn relate to the storage elements that remain in integral causality in the BGD. The characteristic polynomial for the hybrid system:

$$\displaystyle\begin{array}{rcl} P(s)& =& \vert s\mathbf{E}(\varLambda ) -\mathbf{A}(\varLambda )\vert {}\end{array}$$

(4.23)

$$\displaystyle\begin{array}{rcl} P(s)& =& s^{k}(s^{q} + a_{ q-1}s^{q-1} + \cdots + a_{ 1}s^{1} + a_{ 0}){}\end{array}$$

(4.24)

The k structurally null modes may not be obvious from the hybrid bond graph in integral causality. Consider a simple example of two rotating bodies connected by a shaft with a clutch fitted. The hybrid bond graph in preferred derivative causality is shown in Fig. 4.20.

Fig. 4.20

Example system in preferred derivative causality, with ideal clutch

In preferred derivative causality, the reference mode (the mode with most elements in derivative causality) occurs with the clutch engaged (ON), in which case body 1 is still in integral causality. When the clutch is OFF, body 2 is also sent to integral causality. Hence there are two possible structurally null modes , with one of them dependent on commutation of the clutch.

7 Conclusion

A causally dynamic hybrid bond graph has been proposed which provides a wealth of engineering insight (through structural analysis and exploiting causal assignment) and is suitable for simulation.

In proposing this method, the authors felt it important to retain the graphical advantages of bond graph modelling and the principles of idealised physical, acausal model construction. This has been achieved by classifying discontinuities so that they can be represented in the most intuitive way, developing a causally dynamic general hybrid bond graph (with a new dynamic causality notation and novel application of pseudo-state variables), and deriving a unique mixed-Boolean implicit system equation which describes the model in all possible modes of operation.

Classifying discontinuities as structural or parametric immediately shows whether the hybrid assumptions will affect the structural analysis of the model or not, and the use of controlled junctions and elements (respectively) is often intuitive.

The use of the controlled junction, with its inherent dynamic causal assignment, clearly shows how structural commutations (dis)connect submodels and form algebraic constraints. This is reflected in the junction structure matrix by the use of Boolean variables, which denote connections between elements dependent on the state of a controlled junction.

The dynamic causality notation is designed to facilitate analysis of the model’s structure, as well as aiding in equation generation (which describes all modes of operation). Elements in dynamic causality reverse inputs and outputs depending on the mode of operation (i.e. they have an effort input and flow output in some modes, and a flow input and effort output in others). Hence elements in dynamic causality are assigned two inputs and two outputs during equation generation. During any single mode of operation, one input/output pair is active and the other is redundant.

If a storage element is in dynamic causality, it only yields a state output in some modes of operation (when it is in integral causality). In other modes it is in derivative causality, in which case it can be assigned a ‘pseudo-state’ variable which generates an algebraic equation.

A model describing all possible modes of operation is generated. The dynamic causality offers engineering insight, for example, when two rigid bodies contact and a kinematic constraint exists indicating that they behave as a single rigid body. This can be preferable to constraining causality through the addition of parasitic elements, which not only overcomplicates the model but can also even mask an issue or give incorrect behaviour.

The dynamic causality notation offers a unique new way of visualising variable causality and variable topology problems: the latter is no longer strictly variable topology because all system elements are described; they are just not necessarily connected. Dynamic causality can be exploited in the same way as static causality notation, showing how system properties vary with commutation and enabling graph-based structural analysis.

Variable topology problems—notably impact—have received much attention with regard to hybrid bond graphs, due to concerns over whether losses are treated correctly. Using the hybrid bond graph developed here, conservation of momentum holds true because the impact is abstracted to capture the short contact phase, and, in addition, the parameters for Newton’s Collision Law can be derived and the model simplified to a classical collision problem.

Likewise, state reinitialisation has received some attention in the context of hybrid bond graphs. The way that discontinuities are abstracted using this method allows the initial value of each state to be logically deduced.

The unique model describing all possible modes of operation is suitable for both equation-based structural analysis (which is well-established for implicit descriptor systems) and simulation. Simulation often requires the use of solvers developed for implicit descriptor systems, or the use of some model simplification or symbolic manipulation to produce an explicit equation for each mode of operation. A simple example is provided in the Appendix.

The derivations and analyses presented in this thesis largely assume a linear time-invariant model, in order to facilitate comparison with existing control literature. However, the same derivations can be followed with nonlinear functions in place of the linear coefficients during equation generation.

Appendix

In this case study, a simple power converter connected to a DC Motor (an example used repeatedly in the literature) [30, 33] was populated with generic data and used to investigate a discontinuous event. A constant input was used, and the simulation was halted at the event time at which point the load was disconnected and then run again. The states are not reinitialised at the event time: they are simply taken to be the same as at the last time step (which is reasonable since they have reached steady state). N.b. it is possible to simplify this code by specifying event times as an integrator option.

% Run simulation until event

tspan1 = [0:1e-3:(5-(1e-3))];

y01 = [20 0 0]’;

yp01 = zeros(1,3)’;

[t1, y1] = ode15i(@hbg, tspan1, y01, yp01);

% Run simulation from event

tspan2 = [5:1e-3:10];

y02 = y1((length(t1)),:)’;

yp02 = ((y1((length(t1)),:) - y1((length(t1)-1),:))/1e-5)’;

[t2, y2] = ode15i(@hbg, tspan2, y02, yp02);

% Concatenate results vectors

t = [t1; t2];

y = [y1; y2];

where the functions are

function  out = hbg(t, y, yp)

if t == [0:0.2],[0.4:0.6];

% Change this statement depending on the problem under investigation

l1=0;

l2=1;

l3=1;

hsm = hss(l1, l2, l3);

else

l1=1;

l2=0;

l3=1;

hsm = hss(l1, l2, l3);

end

d = length(hsm(:,1));

w = length(u(:,1));

A = hsm(:,1:d);

B = hsm(:,d+1:d+w);

E = hsm(:,d+w+1:d+w+d);

u = [12;0];

out = A*y + B*u - E*yp;

end

---------------------------------

function hsm = hss(l1, l2, l3)

% Define coefficients

L1 = 10e-3;

L2 = 2.25e-7 ;

L3 = 1e-5 ;

R1 = 1.73 ;

R2 = 2e-5  ;

a = 0.00902;

% Populate matrices for this mode

A = [-1*xor(l1,l2)/(L1*R1) -a*xor(l1,l2)/L2

0  0 0

a*xor(l1,l2)/L1 -l3/(L2*R2) 0 0 0

0 0 ~l3/(L3*R2) 0 0

0 0 0 ~xor(l1,l2)/L1 0

0 l3/L2 0 0 -l3/L3];

B = [l1 l2

0 0

0 0

0 0

0 0];

E = [xor(l1,l2) 0 0 0 0

0 1 0 0 l3

0 0 ~l3 0 0

0 0 0 0 0

0 0 0 0 0];

% Remove null lines/columns

order = length(A(1,:));

z = zeros(1,order);

i = 1;

for n = (1:order)

if sum(A(n,:)) == 0 % Delete rows of zeros

else

Ared1(i,:) = A(n,:);

Bred1(i,:) = B(n,:);

Ered1(i,:) = E(n,:);

i = i+1;

end;

end;

i = 1;

for n = (1:order) % Delete Columns of zeros

if sum(Ared1(:,n)) == 0

else

Ared2(:,i) = Ared1(:,n);

Bred2 = Bred1;

Ered2(:,i) = Ered1(:,n);

i = i+1;

end;

end;

hsm = [Ared2 Bred2 Ered2];

end

Some results are shown in Figs. 4.21 and 4.22 for illustration. The load is disconnected 5 s into the simulation. The model runs quickly, and shows a ‘spike’ in voltage immediately after the event. The torque on the motor is increased after the event, consistent with the absence of the load.

Fig. 4.21

Voltage on example power converter: constant input, load disconnected during operation

Fig. 4.22

Torque on example power converter: constant input, load disconnected during operation