Abstract
The theory of the elastica is discussed in this chapter. In addition to classical buckling problems, several applications of this theory to rod-like bodies adhering to rigid substrates are discussed.
Access provided by CONRICYT-eBooks. Download chapter PDF
Similar content being viewed by others
1 Introduction
For many problems, the string model we discussed is inadequate. This is particularly the case if the body that the string is intended to model shows an ability to respond to applied moments. In this instance, the next member in the hierarchy of potential models is a rod theory. There are a wide range of rod theories and the simplest possible nonlinear theory is known as the elastica. The elastica originates in a seminal work [106] by Leonhard Euler (1707–1783) in 1744 and a linearized version of this theory produces the well-known Bernoulli-Euler beam model. As we shall see in Chapter 5, Euler’s theory of the elastica was extended to include torsion and nonplanar motions by Kirchhoff and others in the 19th century.
Over the course of three centuries since its initial development, Euler’s theory of the elastica has been extended to include dynamical effects, material momentum, adhesion, and growth, among others. The theory has also been extensively applied to model many important structural mechanics problems such as growth of tree stems, deflection and buckling of columns, and deformation of carbon nanotubes, among many others (cf. Figure 4.1). In this chapter, we can only touch on a small subset of these applications. In addition to discussing some of Euler’s extraordinary analysis of the equations for the elastica, we emphasize adhesion problems as they also illuminate the role of the balance of material momentum and examine Bosi et al.’s ingenious arm scale that they presented in [32]. Prior to solving problems, we first summarize the governing equations for a rod which is subject to terminal loadings, applied forces, and applied moments. Our development of the balance laws will have evident similarities to the corresponding developments for the theory of the string in Chapter 1
A selection of problems that are analyzed using the elastica. (a) Buckling of an initially straight rod under the combined action of a terminal force − P A 2 and its own weight. The deformed configurations shown in this figure correspond to equilibrium configurations of the rod for values of the load P which are successively greater than the buckling load. (b) A simple rod-based model for the spine where the spine is fixed to the sacrum at ξ = 0 and to the head at ξ = ℓ. The intrinsic curvature κ 0 of the elastica in this model mimics the intrinsic curvature of the spine. (c) A terminally loaded rod which has a portion adhered to a flat horizontal surface.
After applying the theory to several problems, we then explore a variational formulation of the equations governing the elastica. This formulation enables us to establish nonlinear stability criteria for equilibrium configurations of the elastica and a short introduction to the calculus of variations needed for the formulation can be found in Chapter 9 While variational methods for rods can be found in Kirchhoff’s seminal paper [185] from 1859, these methods for the elastica were taken to another level by Born in his dissertation [31] from 1906. We can only speculate as to how Born’s work was inspired by the remarkable series of results on calculus of variations that were produced in Berlin and Göttingen at the end of the 19th century.Footnote 1 There has recently been a resurgence of interest (and new results) in stability criteriaFootnote 2 and some of these developments appear in our discussion of stability criteria for buckled rods and adhered rods that occupy the closing sections of this chapter. Our discussion of buckling and adhesional instabilities in this chapter relies heavily on the works by O’Reilly and Peters [268, 269] and Majidi, O’Reilly, and Williams [219, 220].
2 Kinematical Considerations
For the elastica, the rod is modeled with the assistance of a flexible material curve \(\mathcal{L}\) which resists bending. The classical treatment of this theory assumes that the material curve is inextensible, but we relax this assumption in the development of the theory and allow the material curve to stretch. The position vector of a point on the material curve in the present configuration \(\mathcal{C}\) is defined by the vector-valued function
Here, \(\left \{\mathbf{A}_{1},\mathbf{A}_{2},\mathbf{A}_{3} = \mathbf{A}_{1} \times \mathbf{A}_{2}\right \}\) is a right-handed Cartesian basis for \(\mathbb{E}^{3}\). The convected coordinate ξ that is used to denote material points on the material curve is chosen to be the arc-length parameter of this curve in a fixed reference configuration. Thus, the arc-length parameter of the material curve in the present configuration and ξ are related:
where μ is the stretch. We choose the parameterization s such that μ > 0. For many statics problems where the material curve is assumed to be inextensible (i.e., μ = 1), s and ξ are used interchangeably.
Referring to Figure 4.2, the material curve models the centerline of the planar rod-like body, and the rotation of a material curve which is orthogonal to the centerline can be defined using an angle \(\theta =\theta \left (\xi,t\right )\). In this case,
where \(\mathbf{e}_{t} = \frac{\partial \mathbf{r}} {\partial s}\) is the unit tangent vector to the material curve in its present configuration and the prime denotes the partial derivative with respect to ξ.
(a) Schematic of the planar deformation of a three-dimensional body \(\mathcal{B}\). The body is bounded by a lateral surface surrounding a centerline and bounding material lines. (b) The present configuration of the elastica used to model \(\mathcal{B}\). Observe that the representative material lines displayed in \(\mathcal{B}\) are assumed to remain orthogonal to the material curve \(\mathcal{L}\). The latter models the centerline of \(\mathcal{B}\).
Material fibers of the rod that are orthogonal to the centerline are assumed to remain orthogonal to the centerline. Consequently, the curvature κ of the centerline is related to θ:
In a state where neither forces nor moments act on the rod, we allow for the situation where the centerline can have a curvature and refer to this curvature as an intrinsic curvature κ 0 = κ 0(ξ). An example of a rod with nonzero intrinsic curvature can be seen in the model for the spine shown in Figure 4.1(b). We also define an angular velocity vector and a strain vector \(\boldsymbol{\nu }-\boldsymbol{\nu }_{0}\):
In the sequel, κ −κ 0 will be known as the bending strain in the rod.
At a discontinuity, we have the jump conditions at a material point ξ associated with the kinematics of the curve. We assume that the position vector of the centerline is continuous and that the cross sections of the rod can be continuously related to the tangent vector:
We leave it as an exercise for the reader to imagine situations where (4.6) are violated by \(\mathcal{L}\) being severed or a material fiber which is initially normal to \(\mathcal{L}\) being split into two pieces and pulled apart. Continuity of θ is synonymous with continuity of r ′. Thus, the centerline of the rod cannot exhibit kinks. By differentiating \(\mathbf{r}\left (\gamma (t),t\right )\) and \(\theta \left (\gamma (t),t\right )\) with respect to time at a point of discontinuity ξ = γ, we can show that
where the angular velocity ω γ is the sole component of \(\boldsymbol{\omega }_{\gamma } =\omega _{\gamma }\mathbf{A}_{3}\).
The linear momentum G per unit length of ξ of the rod is defined by the expression
where \(\rho =\rho \left (\xi,t\right )\) is the mass density per unit length of ξ, and μ is the stretch. In the sequel μ = 1, but to facilitate comparisons with the string theory we do not impose this condition here. Further, the angular momentum density of the rod relative to O per unit length of ξ is
where y 22 is an inertia coefficient which has units of length squared and is related to the second moment of area I.Footnote 3 For example, for a homogeneous rod whose cross section has a height h and a width b, ρ 0 = ρ 0 ∗ bh, and \(\rho _{0}y^{22} =\rho _{ 0}^{{\ast}}I =\rho _{ 0}^{{\ast}}\left (bh^{3}/12\right )\). Hence, y 22 = h 2∕12. Supplementing this pair of momenta, the material momentum P for the elastica is defined as
We also note that the kinetic energy density T of the elastica is
The evident parallels of this expression to that for the planar motion of a rigid body should be noted.
The theory of the inextensible elastica assumes that the strain energy function depends on the bending strain Δ κ = θ ′ −κ 0 = κ −κ 0. If the rod is nonhomogeneous, then the strain energy function ψ can also depend on the material coordinate ξ:
For the constitutive relation proposed by Euler for the inextensible elastica,
where the product of Young’s modulus E and the second moment of area I, EI, is known as the flexural rigidity. Recently, modest generalizations of this constitutive relation have found application in elastica-based models for soft robot actuators (cf. [286, 372, 373] and references therein). For the extensible case, the strain energy function additionally depends on the stretch μ. One representation for this function is
For the extensible case, we note that θ ′ = μ κ. Alternatively, we could prescribe the functional representation
where \(\hat{\psi }\left (\mu \kappa -\kappa _{0},\mu,\xi \right ) =\tilde{\psi } \left (\kappa -\kappa _{0},\mu,\xi \right )\).
If we consider two motions of the elastica which differ by a rigid body motion, then it is straightforward to use the results from Section 1.4.5 in Chapter 1 to show that
Because the motion of the elastica is planar, the rotation Q has a fixed axis of rotation A 3. As a consequence of the relations (4.16), we can verify that the strain energy functions ψ and \(\hat{\psi }\) that were discussed earlier (cf. Eqns. (4.12) and (4.14)) are invariant under superposed rigid body motions:
The importance of these results lies in our expectation that the strain energy of the elastica should not change if we rigidly move the elastica from one configuration to another.
3 Balance Laws
Preparatory to writing the conservation laws for the rod, we admit the following force fields for the theory of the elastica: a contact force, n = n(ξ, t); a contact material force, C = C(ξ, t),
and a contact moment, m = m(ξ, t). The body forces and surface tractions acting on the lateral surface of the three-dimensional body that the rod is modeling contribute to the assigned force, ρ μ f = ρ μ f(ξ, t), and the assigned moment, m a = m a (ξ, t) = M a A 3, each per unit length ξ of the elastica. For the applications considered here, the prescriptions for f and m a will be in agreement with more detailed treatments that are presented in Chapter 5 (cf. Eqns. (5.70) and (5.71)) and Section 7.6.1 in Chapter 7 Completing the assigned forces, we have the assigned material force b. As with the earlier developments of the theory of an elastic string, we are motivated by the works of Green and Naghdi [132] and Marshall and Naghdi [230], among others, and admit singular supplies of momentum, F γ , material momentum, B γ , angular momentum relative to O, \(\mathbf{M}_{O_{\gamma }}\), and power, \(\varPhi _{\mathrm{E}_{\gamma }}\), at a specific material point ξ = γ(t).Footnote 4 It is useful to note that, in comparison to the string theory, the new quantities introduced here are moments and strains associated with the rotation θ of the tangent vector to \(\mathcal{L}\).
We adopt the following balance laws for any fixed material segment (ξ 1, ξ 2) of the elastica. First, we record the conservations of mass and inertia:
The balance of linear momentum is
The balance of angular (or moment of) momentum relative to O is
As with the string, one has a balance of material momentum,
One also has the balance of energy:
The similarities in structure between these balance laws and those we presented earlier for a string should be recorded. In addition, you should notice the alterations made to the balances of energy, material momentum, and angular momentum to accommodate the moment fields.
As we shall see later in our discussion of the elastica arm scale, (4.22) will lead to a useful conservation law. We also take this opportunity to note that the balance of material momentum for a homogeneous rod, albeit in the absence of assigned forces and moments, has appeared as a conservation law of the form
in the literature (see [66, 182, 183] and references therein). Indeed for the static case, the conservation of C can be found in Love [213, Eqn. (7) in Sect. 262]. However, for the problems of interest in this chapter, we find that we need to allow for a nonzero b and a singular supply of material momentum B γ .
3.1 Local Balance Laws and Constitutive Relations
For the elastica, we assume that the laws (4.19)–(4.23) hold for any material segment. With the help of the procedure used to localize the balance laws, we find the following balance laws should hold at a point ξ ≠ γ for the elastica. First, we have moment of inertia and mass conservations:
Next, we find the balance laws for linear and angular momentum:
We also find local forms of the material momentum balance and energy balance:
and
We have used Eqns. (4.25)–(4.26) to simplify the energy balance (4.28).
To establish a determinate system of governing equations for the elastica, we first need to establish constitutive relations for n and m. The methodology we use to establish these relations has parallels to the ones used earlier for strings in Section 1.6 of Chapter 1 and, in Section 8.6 of Chapter 8, for a three-dimensional continuum. We first consider the inextensible case: μ = 1, \(\frac{\partial \mathbf{v}} {\partial \xi } =\boldsymbol{\omega } \times \frac{\partial \mathbf{r}} {\partial \xi }\), and the energy equation (4.28) simplifies dramatically:
Additionally, it is assumed that
Consequently,
Next, we assume that the local form of the balance of energy (4.29) is identically satisfied by all motions of the elastica. Thus, we seek solutions m and n of Eqn. (4.29). Using a standard procedure, we find the desired constitutive relations:
where \(n_{1} = n_{1}\left (\xi,t\right )\) and \(n_{2} = n_{2}\left (\xi,t\right )\) must be determined from the balance laws. Use of the relations (4.32) implies that the local form of the energy balance is identically satisfied. We note that these relations include as a special case the Bernoulli-Euler relations for m:
where the strain energy function is prescribed as
Observe that in contrast to the theory of the string, n is no longer restricted to being parallel to r ′ and now has a component in the normal direction e n to the material curve \(\mathcal{L}\). This additional component can be interpreted as a shearing force.
The constitutive relations for the extensible elastica follow a similar line of argument with the strain energy function now being assumed to additionally depend on the stretch μ:
With the help of an identity,
the balance of energy (4.28) simplifies to
Whence, we find the constitutive relations
where the (shear) force n n e n must be determined from the balance laws. It is an interesting exercise to compare the constitutive relation for n and its counterpart for an elastic string (cf. Eqn. (1.96)). Another interesting exercise is to compute the constitutive relations for m and n that arise when ψ is assumed to have the functional form \(\rho \mu \tilde{\psi }\left (\kappa -\kappa _{0},\mu,\xi \right )\) that was mentioned earlier.
For both the extensible and inextensible cases, we prescribe the assigned material force b so that the local form of the material momentum balance law (4.27) is identically satisfied:
A similar prescription was used earlier with the theory of an elastic string and shall also be employed in the sequel with more elaborate rod theories.
3.2 Jump Conditions
Five jump conditions are obtained from the balance laws. The procedure is identical to that discussed in Section 1.5.3 in Chapter 1 Before presenting the conditions, we emphasize that they are supplemented by the compatibility conditions (4.6) and (4.7)2, 4:
Turning to the jump conditions from the balance laws at a point ξ = γ, we find that
It is convenient to define a moment M γ relative to the material point ξ = γ:
The moment M γ will also prove to be convenient to use when dealing with boundary conditions.
The singular supplies in these jump conditions can be related by an identity which follows from the jump condition (4.41)6 in a fashion similar to that used to establish (1.88)Footnote 5:
Note that the singular supplies are each associated with their conjugate velocity. Continuing a theme from earlier, we consider (4.43) to be an identity satisfied by the supplies and make no further mention of the jump condition (4.41)6 from the energy balance.
As we have shown previously, the jump conditions are also helpful in establishing boundary conditions. For instance, for the situation shown in Figure 4.3, we can use the jump conditions to infer that \(\mathbf{n}\left (0^{+},t\right ) = -\mathbf{F}_{0}\) and \(\mathbf{m}\left (\ell^{-},t\right ) = \mathbf{M}_{\ell}\). In addition, in the absence of singular supplies and assuming that \(\dot{\gamma }= 0\) (i.e., γ corresponds to a constant material point), the jump conditions yield
so n and m are continuous at such material points.
3.3 Summary of the Governing Equations
In the applications that follow, the material curve shall be assumed to be inextensible and the local forms of the balances of energy and material momentum are considered to be identically satisfied. In addition, the jump condition from the energy balance will be used to determine \(\varPhi _{\mathrm{E}_{\gamma }}\). Thus, the governing equations for the inextensible elastica that are used in the sequel are the differential equations (4.26) supplemented by the Bernoulli-Euler constitutive relations (4.33) and the jump conditions for linear momentum, material momentum, and moment of momentum (4.41)3, 4, 5. We shall also appeal to the compatibility conditions (4.40).
4 A Terminally Loaded Elastica and the Kinetic Analogue
As a first application of the theory of the elastica, we consider the classical problem of a uniform rod of length ℓ which is subject to loadings at its ends. This problem, that of a terminally loaded rod, is the subject of Euler’s celebrated work [106] and we will reproduce several of his results. For such a homogenous rod in the absence of assigned forces and moments, the equation governing the static equilibrium configuration can be found from Eqn. (4.26). The latter equations simplify dramatically to the following pair of results:
where n 0 is a constant. Here, the homogeneous rod is assumed to be subject to the following constant terminal loadings:
and the Bernoulli-Euler constitutive relations, m = EI θ ′ A 3, are assumed. Observe that Eqn. (4.46) implies that n 0 = −P 1 A 1 − P 2 A 2. For the case where P 2 = 0, it should be apparent that if P 1 > 0 (P 1 < 0), then the rod is in compression (tension) if \(\mathbf{r}^{'}\left (0^{+},t\right ) \cdot \mathbf{A}_{1} > 0\).
With some additional manipulations, the ordinary differential equation for θ(ξ) reduces to
Solutions to this equation which pertain to the boundary-value problem of interest must satisfy the boundary conditions:
This pair of conditions follow from Eqn. (4.46) and the jump condition (4.41)5 from the balance of angular momentum.
We can express the differential equation (4.47) in an alternative form by defining a constant angle β:
Whence, Eqn. (4.47) becomes
Equivalently, one can choose A 1 and A 2 so that F 0 and F ℓ have the simple representations F 0 = P A 1 and F ℓ = −P A 1. That is, one rotates A 1 and A 2 through an angle β about A 3 so that F 0 = −F ℓ are parallel to A 1. We choose to make such a selection, and so (4.47) simply becomes
A variety of pairs of suitable boundary conditions for θ(ξ) will be explored in the remainder of this chapter.
Dating to the 1800s, it was realized that the ordinary differential equation (4.51) is analogous to that governing the motion of a planar pendulum shown in Figure 4.4:
where the center of mass of the pendulum is located a distance \(\bar{\ell}\) from the pin-joint at O, and the mass moment of inertia of the pendulum about O is \(I_{O} = m\bar{\ell}^{2}\). That is, the pendulum is analogous to the terminally loaded elastica: a correspondence that is known as the kinetic analogue. The advantage of the correspondence is that it enables the use of known analytical solutions to Eqn. (4.52) to help develop an understanding of the solutions θ(ξ) to the differential equation (4.51) and analytical expressions for the corresponding r(ξ).
To elaborate, consider a given boundary-value problem for a rod so that P 1, P 2, EI, and a length scale ℓ 0 are specified. Then, the correspondence between the pendulum equations of motion and those for the rod are found by first specifying the angle β (using Eqn. (4.49)), the length \(\bar{\ell}\), and the scale T 0 (in seconds):
Then, the solution to the equation of motion for the pendulum (4.52) which satisfies the boundary conditions (cf. Eqn. (4.48))
is analogous to the corresponding solution θ(ξ) to Eqn. (4.45).
As we shall see in several examples in Sections 4.5.3 and 4.6.4, the kinetic analogue enables one to obtain useful quantitative information on θ(ξ). However, in order to determine the equilibrium configuration, this information must then be translated using the identities \(\frac{\partial Y } {\partial \xi } =\sin (\theta )\) and \(\frac{\partial X} {\partial \xi } =\cos (\theta )\) to provide the corresponding equation for the position vectors r(ξ) of points on the centerline of the rod (cf. Eqn. (4.3)2, 3). The most extraordinary examples of such calculations date to Euler [106] in the 18th century and Hess [168] among others in the 19th century.Footnote 6 A discussion of these works can be found in Love’s treatise [213, Sections 262–263] and Truesdell’s epic commentary [350]. In addition to these works, the papers by Batista [17], Bigoni et al. [26], Coleman and Dill [65], and Domokos and Ruina [92] are recommended reading and resources for additional perspectives and references to works on the elastica.
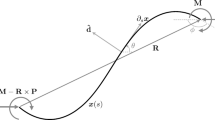
The solutions \(\mathbf{r}\left (\xi \right )\) found by Euler [106] and documented further by Hess [168] and Love [213, Sections 262–263] are presented in Figures 4.5 and 4.6. To discuss the figures, we assume that A 1 has been chosen so that β = 0 and the terminal load at ξ = 0 is simply F 0 = P A 1 with P > 0. We now comment on the solutions shown in the aforementioned figures. First, the equilibria of the equations \(EI\theta ^{''} + P_{1}\sin \left (\theta \right ) = 0\) correspond to straight equilibrium configurations of the rod. The equilibrium \(\left (\theta,\theta ^{'}\right ) = (0,0)\) corresponds to the compressed state, while the equilibrium \(\left (\theta,\theta ^{'}\right ) = (\pi,0)\) corresponds to the rod in tension. The reversal of the rod, which is akin to a reflection, that is evident in Figures 4.5 can be understood by examining the equilibrium configurations shown in this figure and the companion Figure 4.6.
A selection of some classic inflexional solutions \(\theta ^{'}\left (\theta \right )\) and r(ξ) to the boundary-value problem (4.48) and (4.51) for a terminally loaded elastica where the length ℓ is varied and the loading parameter \(\frac{P\ell_{0}^{2}} {EI}\) is held constant. The arrows on the graphs of \(\theta ^{'}\left (\theta \right )\) and r(ξ) correspond to the direction of increasing ξ from 0 to ℓ. The solution labeled a corresponds to the straight compressed elastica (and the equilibrium \(\left (\theta,\theta ^{'}\right ) = (0,0)\)); each one of the solutions labeled b-c correspond to elastic rods with points of inflexion; and the solution labeled d is the solution corresponding to a tensile load (and the equilibrium \(\left (\theta,\theta ^{'}\right ) = (\pi,0)\)). Observe that the rod in a is in compression, while the rod is in a state of tension in d.
An additional selection of some classic solutions \(\theta ^{'}\left (\theta \right )\) and r(ξ) to the boundary-value problem (4.48) and (4.51) for a terminally loaded elastica where the length ℓ is varied and the loading parameter \(\frac{P\ell_{0}^{2}} {EI}\) is held constant. The arrows on the graphs of \(\theta ^{'}\left (\theta \right )\) and r(ξ) correspond to the direction of increasing ξ from 0 to ℓ. The solutions labeled e-h are each examples of inflexional elastica and solutions labeled i-j are each examples of non-inflexional elastica. For the latter, terminal bending moments are always needed for equilibrium.
The solutions highlighted in Figure 4.5 each correspond to configurations of the elastica that are known as inflexional by Love [213]. These solutions, if ℓ is sufficiently large, contain points where the bending moment vanishes. Consequently, if ℓ is chosen appropriately, they can be supported by terminal forces only. This is the case for the solutions r(ξ) shown in Figure 4.5. By way of contrast, a family of inflexional solutions are shown in Figure 4.7 which are intended to further illuminate the correspondence between the trajectories in the phase portrait and the boundary conditions at the two ends of the rod.
A selection of some classic non-inflexional solutions \(\theta ^{'}\left (\theta \right )\) and r(ξ) to the boundary-value problem (4.48) and (4.51) for a terminally loaded elastica where the length ℓ is varied and the loading parameter \(\frac{P\ell_{0}^{2}} {EI}\) is held constant. It should be evident from these examples that, depending on the value of \(\theta ^{'}\left (\xi =\ell\right )\), a terminal moment M ℓ may be required to maintain equilibrium. The arrows on the graphs of \(\theta ^{'}\left (\theta \right )\) and r(ξ) correspond to the direction of increasing ξ from 0 to ℓ.
The solutions labeled g and h in Figure 4.6 can be manifested in infinitely long rods by terminal forces alone. Each of the configurations for r(ξ) have a single loop and the corresponding solution curve \(\theta ^{'}\left (\theta \right )\) in the phase portrait is known as a homoclinic orbit or separatrix. Two other types of solutions are shown in Figure 4.6. First, we find solutions where self-contact occurs. This occurs first for the solution labeled e and as one approaches the separatrix (labeled g and h), the centerline of the elastica passes through itself and the reversal discussed earlier now becomes possible. With this reversal, the straight rod passes from a state of compression to one of tension.
Equilibrium configurations of the elastica that correspond to solutions of the form i and j shown in Figure 4.6 are classified by Love [213] as non-inflexional. Regardless of ℓ, these solutions require terminal moments in addition to terminal forces. If ℓ is sufficiently large, the space curve formed by r(ξ) inevitably involves self-contact of the rod at a discrete number of points. The self-contact phenomenon associated with the loop formation is technically challenging not least because we are assuming planar solutions yet an equilibrium configuration having a loop must be nonplanar. We shall return to this problem in Section 5.15.3 of Chapter 5 where a more sophisticated rod model is used to examine loop formation. Additional examples of the correspondence between solutions of the planar pendulum equation of motion and the shape of r(ξ) can also be found in Figure 5.16 and throughout the remainder of this chapter.
5 The Adhesion of a Rod
For the next set of applications of interest, we consider an elastic rod which is in partial contact with a horizontal surface (see Figure 4.8). Specifically, the portion \(\xi \in \left (\gamma,\ell\right )\) is glued to the surface by a bond whose adhesive strength per unit length of rod is W ad. This positive material constant is the work required to free a unit length of the rod from the horizontal surface.Footnote 7 At the other end of the rod, a terminal force P and a terminal moment M 0 are applied at ξ = 0. The terminal loading can be used to peel the rod from the horizontal surface or maintain a state of adhesion. In addition to the deformed shape of the rod, one of the crucial unknowns in this problem is the value γ of the coordinate ξ where the adhesive bond is broken. The adhesion problem we are considering is sometimes referred to as the peeling problem or the peel test.
Our goal here is to show how to formulate and solve the adhesion problem. The method we present relies heavily on the jump condition from the balance of material momentum. This condition produces a boundary condition at the interface between the adhered and free segments of the rod.Footnote 8 We model the rod as an elastica and note that such a model has received considerable attention in the literatureFootnote 9 in part because of its analytical tractability and in part because the system of interest is a prototype for studies of adhesion in peeling tape, Gecko setae [16], and carbon nanotubes [116, 117, 374].
5.1 General Considerations
We consider the simplest model for the adhesion problem and use the static version of the elastica theory. For convenience, we divide the rod into three sections: \(\mathcal{S}_{\mathrm{I}}\): 0 < ξ < γ, \(\mathcal{S}_{\mathrm{II}}\): ξ = γ, and \(\mathcal{S}_{\mathrm{III}}\): ℓ > ξ > γ. On \(\mathcal{S}_{\mathrm{I}}\), there are no body forces or surface tractions on the lateral surface, thus m a = 0 and f = 0. This is in contrast to the situation on \(\mathcal{S}_{\mathrm{III}}\) where surface tractions are present and \(EI \frac{\partial \theta } {\partial \xi } = 0\). At ξ = γ, we have a discontinuity, a material momentum supply
and unknown momentum supplies F γ and M γ . As the problem is static and the centerline of the rod is inextensible, we will use s and ξ interchangeably. A variational formulation of this problem that is presented in Section 4.7.2.2 yields additional motivation for the prescription B γ = −W ad and also demonstrates that the prescription (4.55) is in accord with other formulations of this adhesion problem.
Referring to Section 4.3, we recall the local form of the balance laws and constitutive relations for this theory:
Here, we have specialized the prescription for C to the static case.
On \(\mathcal{S}_{\mathrm{I}}\), we have the boundary conditions
Correspondingly, on \(\mathcal{S}_{\mathrm{III}}\), we have the boundary conditions and contact conditions
At ξ = γ, r and θ are continuous,Footnote 10 and we have the jump conditions
Note that we used the fact that \(\mathbf{m}\left (\gamma ^{+}\right ) = \mathbf{0}\) in writing the second jump condition.
The governing equations for the boundary-value problem on \(\mathcal{S}_{\mathrm{I}}\) yield the provisional solutions
The differential equation (4.60)2 needs to be solved subject to the boundary conditions
where θ − ′ is presently unknown. For the boundary-value problem on \(\mathcal{S}_{\mathrm{III}}\), we find from the balance laws that
for \(\xi \in \left (\gamma,\ell\right )\).
At the discontinuity, the jump conditions (4.59) can be explored in further detail. Substituting for the fields at γ +, we solve for F γ and M γ and specify \(\frac{\partial \theta } {\partial \xi }\left (\gamma ^{-}\right )\):
These results are also displayed in Figure 4.9.
We remark that the equation (4.63)3 for θ − ′, which is known as the adhesion boundary condition, arises from the material momentum balance law. In treatments of this problem where the material momentum balance law is not used, other assumptions are employed (cf. Majidi [217]). For instance, Glassmaker and Hui [117] postulate an energy balance in order to obtain an expression that is equivalent to (4.63)3. The interested reader is also referred to Section 4.7.2.2 where, as we mentioned previously, a variational formulation of the adhesion boundary condition is presented.
5.2 Summary of the Solution Procedure
To solve the adhesion problem, we need to solve the differential equation (4.60)2 subject to the boundary conditions (4.61) where θ − ′ is determined from the equation
The resulting solution of the boundary-value problem also provides the length γ.
The general solution to the differential equation (4.60)2 can be obtained using classical methods and is aided by a graphical representation of the solutions that can be seen in Figure 4.10. Because there are no assigned forces acting on \(\mathcal{S}_{\mathrm{I}}\) of the rod, b p = 0 and the local form of the balance of material momentum (4.56)3 shows that C is conserved by the solutions to (4.60)2:
To examine the solutions to the boundary-value problem, it is first convenient to non-dimensionalize the differential equation using the variables
With the help of these variables, we find that the first integral −C of (4.60)2 has the dimensionless representation
where e 0 is a constant determined by the boundary conditions.
The solutions of (4.60)2 where f 2 > 0 and f 1 = 0. The equilibrium denoted by a hexagon is the equilibrium \(\theta = \frac{\pi } {2}\), and the second equilibrium which is denoted by a star is the equilibrium \(\theta = -\frac{\pi }{2}\). The arrows indicate the direction of increasing s.
Comparing the boundary condition (4.64) to the conservation (4.67), we find that
Thus the solution to the differential equation (4.60)2 of interest to us is the integral curve corresponding to e 0 = w ad. In addition, we notice that e 0 = w ad on \(\mathcal{S}_{\mathrm{I}}\) is consistent with the result that C = 0 throughout the segment \(\mathcal{S}_{\mathrm{III}}\). At the other end of the rod, we can use the fact that e 0 = w ad along with the boundary condition (4.61)2 for \(\frac{\partial \theta } {\partial \xi }\) to find an equation for \(\theta _{0} =\theta \left (\xi = 0\right )\) from the conservation (4.67):
In addition to using this equation to determine θ 0, the equation is also useful for finding allowable parameter ranges for adhesion (w ad), terminal bending moment (ω 0), and terminal forces (f 1, 2).
We can also use the integral (4.67) to obtain an analytical expression for θ(x):
where x 0 = 0. The integral on the right-hand side of this equation is an elliptic integral of the first kind, and an analytical solution for θ(x) can be developed.Footnote 11 We express this analytical solution symbolically as
The function f has four constants (x 0 = 0, e 0, ω 0, and θ 0) which need to be prescribed or are specified using Eqns. (4.68) and (4.69). A graphical summary of the aforementioned solution procedure can be seen in Figure 4.11 for two cases: one where ω 0 = 0 and the other where ω 0 < 0.
Two representative solutions of (4.60)2 where f 2 > 0 and f 1 = 0. The solution where \(\frac{d\theta } {d\xi }\left (\xi = 0\right ) = 0\) is discussed in Section 4.5.3.1, and the solution where \(\frac{d\theta } {d\xi }\left (\xi = 0\right ) > 0\) is discussed in Section 4.5.3.2. In the interests of clarity, the dimensionless adhesion energy w ad has distinct values for the pair of solutions.
The identity (4.70) along with Eqns. (4.68) and (4.69) can also be used to determine the length of the adhered length ℓ −γ of the rod by setting \(x_{1} = \frac{\gamma }{\ell}\) and \(\theta _{1} =\theta \left (x = g\right ) = 0\):
It is useful to note that the right-hand side of this equation can be evaluated without explicitly determining the shape of the deformed rod.
5.3 Examples
In the examples we now consider, we restrict attention to a rod where the force acting at one of the terminal points is P = P 2 A 2. In the first example, we assume that no moment acts at the point of application of the load. We find that this assumption leads to a very limited range of adhesive solutions. In the second example, we relax the boundary condition and assume that a terminal moment is applied. We then find a much wider range of situations where adhesion is possible. This is to be expected as the moment serves to press the rod onto the adhesive layer.
5.3.1 Pulling up or pushing down on the adhesive layer
To further illustrate the previous developments, consider the situation shown in Figure 4.8 with P = P 2 A 2. That is, n(ξ) = −P 2 A 2 on \(\mathcal{S}_{\mathrm{I}}\). We next use the developments of the previous section. First, we use the boundary condition (4.61)2 along with the conservation (4.67) to conclude that
where \(\theta _{0} =\theta \left (x = x_{0} = 0\right )\). As e 0 = w ad, we can immediately see that the type of contact we are considering requires that the bond strength be less than the applied force: \(w_{\mathrm{ad}} \leq \left \vert f_{2}\right \vert \). That is, in terms of the dimensioned quantities, \(W_{\mathrm{ad}} \leq \left \vert \!\left \vert P_{2}\mathbf{A}_{2}\right \vert \!\right \vert \).
The integral (4.70) reduces to
This integral can be expressed as the sum of two elliptic integrals of a well-known form.Footnote 12 We present our results for the case f 2 > 0, and can infer the results for f 2 < 0 where needed using symmetry arguments. Evaluating the right-hand side of (4.74), we find that
where \(F\left (\phi,k\right )\) is an elliptic integral of the first kind and \(K\left (k\right )\) is a complete elliptic integral of the first kind:
In (4.75), the modulus k and angle ϕ 1 are defined as
where \(\theta _{1} =\theta \left (x = x_{1}\right )\). With the help of our earlier observation that e 0 = w ad on \(\mathcal{S}_{\mathrm{I}}\), we can easily obtain a pair of more illuminating expressions for k:
The solution (4.75) can be used to determine the deformed shape of the rod once θ 0 and γ have been determined from the boundary conditions.
To determine the contact length ℓ −γ, we invoke the boundary condition \(\theta \left (\gamma \right )\) = 0. Thus,
where the angle ϕ g corresponding to \(\theta \left (\gamma \right ) = 0\) is computed using Eqn. (4.77)2:
From Eqns. (4.73) and (4.79), we can determine the initial inclination θ 0 of the rod, and the length of the contact region for a given P 2 and \(\frac{w_{\mathrm{ad}}} {f_{2}} = \frac{W_{\mathrm{ad}}} {P_{2}}\). The results are presented in Figure 4.12 and the corresponding solution curve of the ordinary differential equation can be seen in Figure 4.11.
Referring to Figure 4.12, several results can be concluded from (4.79). First, for the type of solutions we are seeking, the ratio of the adhesive strength W ad to the peeling force P 2 is restricted to lie in the range \(-1 \leq \frac{W_{\mathrm{ad}}} {P_{2}} \leq 1\). Outside of this range, either an adhesive solution is not possible, or the rod is entirely adhered to the surface. When P 2 is within the range needed for an adhesive solution, the precise amount of contact depends on P 2 and there will be a unique value of θ 0 for this solution. Figure 4.12(b) also illustrates that the contact length ℓ −γ increases as \(\frac{W_{\mathrm{ad}}} {\left \vert P_{2}\right \vert } = \frac{w_{\mathrm{ad}}} {\left \vert f_{2}\right \vert }\) decreases. This seems contradictory until one realizes that as \(\frac{w_{\mathrm{ad}}} {\left \vert f_{2}\right \vert } \rightarrow 0\), the angle of inclination θ 0 at the tip of the rod also tends to 0. That is, it is not possible to vary P 2 and θ 0 independently without changing the contact length ℓ −γ.
5.3.2 The Helpful Effects of a Terminal Moment M 0
We again consider the problem of the previous section, but replace the boundary condition \(\frac{d\theta } {d\xi }\left (\xi = 0\right ) = 0\) with the condition that \(\theta \left (\xi = 0\right ) =\theta _{0} = -\frac{\pi }{2}\). For this case, there will be a terminal moment \(\mathbf{M}_{0} = -EI \frac{\partial \theta } {\partial \xi }\left (0^{+}\right )\mathbf{A}_{ 3}\) acting at ξ = 0 and f 2 > 0 (see Figure 4.9). The results for the case \(\theta \left (\xi = 0\right ) =\theta _{0} = \frac{\pi } {2}\) and f 2 < 0 can be inferred using symmetry arguments.
We can use the analysis of the previous section with some slight modifications. As boundary conditions, we now have
The last condition is equivalent to e 0 = w. Applying (4.81)2 to the conservation (4.67), we find that
where \(-\omega _{0} = \frac{d\theta } {dx}\left (x = 0^{+}\right ) > 0\). Thus, we have quickly found an expression for M 0:
You will notice that the moment at ξ = 0 can improve the strength of the bond by increasing the range of allowable forces f 2.
The solution of the governing differential equation we now seek is shown in Figure 4.11. It differs from the solution of the previous subsection in that \(\frac{d\theta } {dx}\left (x = 0\right )\neq 0\). The elliptic integral we now need to solve is
Again, the integral on the right-hand side can be expressed in a canonical formFootnote 13 and we can solve for x 1. Evaluating the result when x 1 = g and θ 1 = 0, the contact point can be determined:
For this case \(\frac{w_{\mathrm{ad}}} {f_{2}}\) ranges from 1 to ∞, and, for a given value of this adhesion parameter, a contact length can be determined with the help of the solution (4.85). As can be inferred from Figure 4.13, for a given value of \(\frac{w_{\mathrm{ad}}} {f_{2}}\), we can determine the corresponding value of \(\frac{\gamma } {\ell}\sqrt{ f_{2}}\), and, based on the value of f 2 compute the contact length ℓ −γ. As \(\frac{w_{\mathrm{ad}}} {f_{2}} \rightarrow \infty \), the contact length tends to ℓ.
The solution \(\frac{\gamma }{\ell}\sqrt{\left \vert f_{2 } \right \vert }\) as a function of \(\frac{w_{\mathrm{ad}}} {\left \vert f_{2}\right \vert }\) for the adhesion problem where the terminal end of the rod is constrained so that \(\theta _{0} = -\frac{\pi }{2}\) when f 2 > 0 and \(\theta _{0} = \frac{\pi } {2}\) when f 2 < 0. For these cases, a moment whose dimensionless form is \(\mathbf{M}_{0} = -\mbox{ sgn}\left (f_{2}\right )\frac{EI} {\ell} \sqrt{w_{\mathrm{ad } } - \left \vert f_{2 } \right \vert }\mathbf{A}_{3}\) acts at ξ = 0.
Results for f 2 < 0 and \(\theta _{0} = \frac{\pi } {2}\) are also shown in Figure 4.13. These results can be easily inferred from the previous analysis using either a symmetry argument or by direct calculation. We note in particular that as \(\omega _{0} = -\frac{d\theta } {dx}\left (x = 0^{+}\right ) > 0\), the terminal moment in this case can be shown to have the representations
These expressions are notably consistent with our earlier results.
5.3.3 Closing Remarks
In conclusion, we have presented an analysis of the adhesion of a rod under terminal loading P = P 2 E 2 with a substrate. When the adhesive is weak, we found that the bond could be supported without the application of a terminal moment. However, for larger values of \(\frac{W_{\mathrm{ad}}} {\left \vert P_{2}\right \vert }\), application of a terminal moment helped to strengthen the bond.
6 The Elastica Arm Scale
In 2014, Bosi et al. [32] presented a novel measuring scale shown in Figure 4.14. The scale uses an elastic rod of length ℓ that is free to move inside a frictionless sleeve which is inclined at an angle α to the vertical. Weights P 1 and P 2 are attached to the respective ends of the lamella and, assuming that one of the weights and the slope of the tangent at the ends of the rod are known, the second weight can be determined from the relation
The device is referred to as an “elastica arm scale” and the inspiration for its design can be traced to the papers by Bigoni et al. [25, 27] on Eshelby-like forces in continua. We also refer the interested reader to Bigoni et al. [26] and Bosi et al. [33, 34] for related works and additional perspectives.
In this section of the book we will demonstrate how the scale operates by deriving the relation (4.87). In the process of the derivation, we find that we are able to extend Eqn. (4.87) to the case where the weight of the rod is considered and terminal moments can be applied to the ends (cf. Eqn. (4.115) on Page 108):
The analysis we employ, which is adapted from our recent paper [266], makes extensive use of the balance law for material momentum, shows that a conserved quantity \(\mathsf{C} -\rho _{0}g\hat{\mathbf{g}} \cdot \mathbf{r}\) can be used to establish the relation (4.87), and includes the effects of terminal moments which were not considered in our earlier work. Our analysis complements the work of Bosi et al. [32]. These authors used a variational formulation to establish Eqn. (4.87) and they also include a nonlinear stability analysis of the equilibrium configurations of the rod.
6.1 Background
The rod in this problem takes on static configurations that are shown schematically in Figure 4.15. The rod is assumed to be inextensible, and so we use the arc-length parameter s in place of ξ in the sequel. To enable easy comparisons with the literature on the arm scale, we define the following representation for the unit tangent to the curve:
We note that for this problem θ represents the angle subtended by r ′ with the A 2 axis. The rod will be assumed to be homogeneous with a uniform mass density ρ 0 per unit length of s and the classic strain energy function \(\rho _{0}\psi = \frac{EI} {2} \left (\theta ^{'}\right )^{2}\).
Schematic representation of the Bosi et al.’s elastica arm scale. While neither the weight of the rod nor the presence of terminal moments is included in the original analysis of Bosi et al. [32], we show how they can be accommodated into their measurement device.
We are now in a position to recall from Section 4.3 the balance laws for forces, material forces, and moments for the elastica:
In these local forms, the force b is such that the material momentum balance law (4.89)1 is identically satisfied and the force C is prescribed as
We thus find from Eqn. (4.39) that the assigned body force for the homogeneous rod is
The assigned body force ρ 0 f is not constant throughout the rod, so we refrain from simplifying this expression further at this stage in the analysis.
At a point of discontinuity s = γ, the following jump conditions hold:
As with many of the problems considered in this book, the latter pair of jump conditions are useful in establishing boundary conditions.
6.2 The Deformable Arm Scale
To analyze the arm scale it is convenient to consider three segments: the left freely hanging section, s ∈ [0, a 1); the right freely hanging section, s ∈ (a 2, ℓ]; and the section inside the smooth guide of length ℓ ∗ where
Thus, in determining the equilibrium configuration of the deformed rod, it suffices to determine either a 1 or a 2. The guide or sleeve is inclined at an angle α to the vertical.
6.2.1 The freely hanging segment s ∈ [0, a 1)
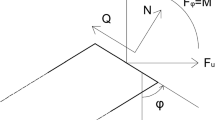
The first section of the rod we consider extends from the free end at s = 0 to the start of the guide at s = a 1. At the free end, we assume that a force \(\mathbf{F}_{0} = P_{1}\hat{\mathbf{g}}\) along with a moment M 0 = M 1 A 3 act. Here, the unit vector \(\hat{\mathbf{g}}\), which points downward, has the representation
With the help of the jump conditions (4.92)2, 3, we find that
With the help of the constitutive equations for m and dropping the+, we conclude that the boundary conditions on this section are
With the help of the balance laws for linear and angular momentum (4.89)2, 3, we find that
From one of these results, expressions for the material force C can be computed from Eqns. (4.90) and (4.96):
In the first of these expressions for C, we used the abbreviation M(s) = m(s) ⋅ A 3. Because the rod is homogeneous, after computing b using Eqn. (4.39), it is straightforward to find the following energy conservation law from the local form of the balance of material momentum (4.89)1:
We note that \(-\rho _{0}g\hat{\mathbf{g}} \cdot \mathbf{r}\) is the gravitational potential energy for the material point located at r on the rod. Thus, in the case where gravity is ignored and the terminal moment M 1 A 3 is absent, the material force C is constant throughout this segment of the rod: \(\mathsf{C}(s) = \mathsf{C}(0) = -P_{1}\hat{\mathbf{g}} \cdot \mathbf{r}^{'}(0)\). This conservation is equivalent to the conservation law presented in Love [213, Eqn. (7) in Sect. 262] and is central to the analysis of the arm scale presented in Bosi et al. [32].
6.2.2 The freely hanging segment s ∈ (a 2, ℓ]
The second segment of the rod of interest is terminally loaded at one end and extends to the sleeve at the other. At the free end, we assume that a force \(\mathbf{F}_{\ell} = P_{2}\hat{\mathbf{g}}\) along with a moment M ℓ = M 2 A 3 act. With the help of the jump conditions (4.92)2, 3, we find that
Dropping the−, we conclude that for this portion of the rod, the boundary conditions are
We parallel the developments in the previous section and compute that
From these results and the balance of material forces, we again find a conservation law:
For this segment of the rod, the material force has the representations
As in the previous section, if gravity and the terminal moment are ignored, then C(s) is conserved along this segment of the rod where \(\mathsf{C}(\ell) = -P_{2}\hat{\mathbf{g}} \cdot \mathbf{r}^{'}(\ell)\).
6.2.3 The segment s ∈ [a 1, a 2] of the rod in the smooth sleeve and the points of discontinuity
It is straightforward to show that the slope of the rod is continuous where the rod enters and exits the sleeve:
However, these results in no way imply that the curvature of the rod is continuous at these points. At s = a 1 and s = a 2, we assume that respective singular forces, \(\mathbf{F}_{a_{1}}\) and \(\mathbf{F}_{a_{2}}\), and respective singular moments, \(\mathbf{M}_{a_{1}}\) and \(\mathbf{M}_{a_{2}}\), act on the rod. In addition, for the segment of the rod in the frictionless guide, the assigned force acting on the rod can be decomposed into a gravitational force and a normal force λ(s)A 1 (cf. Figure 4.16).
Schematic showing the forces \(\mathbf{F}_{a_{1}}\), \(\mathbf{F}_{a_{2}}\), and λ A 1, moments, \(\mathbf{M}_{a_{1}}\) and \(\mathbf{M}_{a_{2}}\), and terminal loadings acting on the elastica arm scale. It is important to observe that there are no singular supplies of material momentum in this system: \(\mathsf{B}_{a_{1}} = 0\) and \(\mathsf{B}_{a_{2}} = 0\).
The balance of linear momentum for the portion of the rod in the sleeve reads
As θ = 0 for this section of the rod, the balance of angular momentum reduces to
That is, n is tangent to the rod. We can now revisit the balance of linear momentum and solve for the normal force acting on the rod:
Furthermore, the contact material force C is simply
In contrast to the other two segments of the rod, C decreases linearly with increasing s and the following material force b needs to be supplied to satisfy the material momentum balance law (4.89)1 (cf. Eqn. (4.39)):
Paralleling the developments in the previous segments of the rod, we again find that the energy \(\mathsf{C} -\rho _{0}g\hat{\mathbf{g}} \cdot \mathbf{r}\) is conserved for this segment of the rod.
At s = a 1, we assume a vanishing singular supply \(\mathsf{B}_{a_{1}} = 0\) along with a singular force \(\mathbf{F}_{a_{1}}\) and singular moment \(\mathbf{M}_{a_{1}}\) acts. Thus, from the jump conditions (4.92),
It is important to observe here that \(\mathbf{F}_{a_{1}}\) is an unknown reaction force while \(\mathbf{M}_{a_{1}}\) is prescribed by the solution to the boundary-value problem for the hanging segment s ∈ [0, a 1). Noting that C is continuous at s = a 1, we use the jump condition (4.111)3 to solve for \(\mathbf{n}\left (a_{1}^{+}\right ) \cdot \mathbf{A}_{2}\):
The analysis at the exit point s = a 2 closely parallels the case for s = a 1. Again, we prescribe \(\mathsf{B}_{a_{2}} = 0\) and assume that a singular force \(\mathbf{F}_{a_{2}}\) and singular moment \(\mathbf{M}_{a_{2}}\) act at s = a 2. The jump condition associated with the material force balance yields continuity of C, and so we find
It should be clear from the relations (4.112) and (4.113) that the axial component of the force n experiences jumps at s = a 1 and s = a 2. However, because we assume that \(\mathsf{B}_{a_{1}} = 0\) and \(\mathsf{B}_{a_{2}} = 0\), C does not and this continuity serves to determine the jump in n. Continuity of C and r implies that the conserved quantity \(\mathsf{C} -\rho _{0}g\hat{\mathbf{g}} \cdot \mathbf{r}\) is continuous at s = a 1 and s = a 2.
6.3 The Operation of the Arm Scale
With the help of Eqns. (4.98), (4.104), and (4.109), we are now in a position to examine the distributions of the material force C and the conserved quantity \(\mathsf{C} -\rho _{0}g\hat{\mathbf{g}} \cdot \mathbf{r}\) along the rod. A summary of the results is presented in Figure 4.17. The conservation of \(\mathsf{C} -\rho _{0}g\hat{\mathbf{g}} \cdot \mathbf{r}\) provides the equation governing the operation of the arm scale. To see this, we use the expressions for C mentioned earlier to find that
On substituting for r ′ from Eqn. (4.88), \(\mathbf{n}(0) = -P_{1}\hat{\mathbf{g}}\), and \(\mathbf{n}(\ell) = P_{2}\hat{\mathbf{g}}\), it is straightforward to show that
This equation is the extension of the relation (4.87) when the weight of the rod is included and terminal moments are allowed. It is the operating principle for the arm scale: Given P 1, M 1, M 2, α, the length of the sleeve, ρ 0 g, the difference in heights between the ends of the rod, and measurements of θ(0) and θ(ℓ), P 2 can be determined.
We can use the jump conditions \(\mathbf{F}_{a_{1}} + \left [\!\left [\mathbf{n}\right ]\!\right ]_{a_{1}} = \mathbf{0}\) and \(\mathbf{F}_{a_{2}} + \left [\!\left [\mathbf{n}\right ]\!\right ]_{a_{2}} = \mathbf{0}\) to determine the reaction forces:
Both of these forces are related to the bending moment (and bending strain) in the rod. In [32], the (underbraced) terms \(\frac{M^{2}(a_{ 2}^{+})} {2EI}\) and \(\frac{M^{2}(a_{ 1}^{-})} {2EI}\), which are the axial components of \(\mathbf{F}_{a_{1}}\) and \(\mathbf{F}_{a_{2}}\), are called Eshelby-like forces. Here, and as displayed in Figure 4.16, we have shown how they manifest in reaction forces and how they can be explicitly attributed to the material force C.
6.4 Insights from a Pair of Pendula
To gain a different appreciation for the dramatic change in strain energy that occurs at s = a 1 and s = a 2 in the elastica arm scale, we ignore the weight of the elastica, set the terminal moments M 0 = M ℓ = 0, and consider a pair of pendula. The dimensionless time variable τ and important instances for the pendula are identified as follows:
Observe that as s ranges from 0 → ℓ, τ ranges from 0 → 1. Here, we are modifying the classic kinetic analogue for a single elastica that we discussed in Section 4.4 to incorporate the unusual boundary conditions at s = a 1, 2.
One of the pendula is analogous to the section s ∈ [0, a 1 −) of the elastica. In the absence of terminal moments and ignoring the weight of the rod, the equation governing this section is (from Eqn. (4.97))
Thus, we can consider the motion of an analogous simple pendulum which oscillates about its downward equilibrium with a dimensionless frequency ω 1:
The equations of motion of this pendulum, which is shown in Figure 4.18, are
The second pendulum models the segment of rod s ∈ (a 2 +, ℓ]. For this segment of the rod we have (from Eqn. (4.102))
Thus, we can consider the motion of an analogous simple pendulum which oscillates about its downward equilibrium with a dimensionless frequency ω 2,
and whose equations of motion are described by
We refer to this pendulum as pendulum II and its counterpart of length ℓ 1 as pendulum I. If the dimensional measure t of time is given by t = β τ where β is a constant, then the lengths of pendulum I and pendulum II are
The pair of pendula and the analogue model for the elastica arm scale. (a) The pendulum analogous to the segment s ∈ (0, a 1 −) and (b) the pendulum analogous to the segment s ∈ (a 2 +, ℓ). The distinct lengths ℓ 1 and ℓ 2 of the pendula are defined in (4.124) and are respectively inversely proportional to the loads P 1 and P 2.
With the help of Figure 4.19, we are now in a position to discuss the analogue model for the elastic arm scale. Consider pendulum I and assume that it is released from rest with \(\phi _{1}(0) =\theta \left (0\right )+\alpha\). The pendulum falls as shown in Figure 4.19(b) and eventually collides with a surface in a perfectly plastic collision (cf. Figure 4.19(c)) wherein it loses all its kinetic energy. After a period \(\frac{a_{2}-a_{1}} {\ell}\) of no motion, pendulum II, which is at rest inclined at an angle ϕ 2 = α to the vertical, is launched with a speed \(\frac{d\phi _{2}} {d\tau } \left (\tau _{2}^{+}\right ) > 0\) (cf. Figure 4.19(d)). The resulting motion of pendulum II persists until τ = 1 where it eventually comes to a state of instantaneous rest (cf. Figure 4.19(e) & (f)). The counterpart of the material force C in this problem is the total energy of the individual pendula:
We assume that the value of the total energies of both pendula are identical when they are in motion. This assumption prescribes \(\frac{d\phi _{2}} {d\tau } \left (\tau _{2}^{+}\right )\):
In addition, the equality of the energies also implies that
This identity is the counterpart to the relation (4.87) for the arm scale.
The kinetic analogue also sheds light on solving the boundary-value problem associated with the elastic arm (whose weight is ignored). For a given loading P 1 and P 2 on the elastica arm scale and a given length a 2 − a 1 of sleeve, ω 1 and ω 2 can be computed, and the phase portraits for both pendula can be constructed (cf. Figure 4.20). Now the solution shown in Figure 4.20(a) starts with a chosen ϕ 1(0). This value of ϕ 1(0) then determines the time of flight \(\tau _{1} = \frac{a_{1}} {\ell}\) to the impact event. This time of flight then prescribes the allowable time of flight \(1 -\frac{a_{2}} {\ell}\) for pendulum II (cf. Figure 4.20(b)). The initial speed \(\frac{d\phi _{2}} {d\tau } \left (\tau _{2}^{+}\right ) > 0\) is prescribed by Eqn. (4.126) and then it remains to verify that ϕ 2 must transition to a state of instantaneous rest in \(1 -\frac{a_{2}} {\ell}\) units of dimensionless time at a value of ϕ 2 given by Eqn. (4.127). Typically, for a given loading P 1 and P 2 on the elastica scale arm and a given length a 1 − a 2 of sleeve, it is necessary to iterate the values of ϕ 1(0) and a 1 so as to find a solution that satisfies Eqns. (4.126) and (4.127) given the time of flight \(1 -\frac{a_{2}} {\ell}\) for pendulum II.
An example of a solution for prescribed values of ω 1, ω 2, and a 2 − a 1 is shown in Figure 4.21(a). The configuration of the elastic rod corresponding to this solution is constructed in Figure 4.21(b) after integrating Eqn. (4.88) to determine the position vector of the centerline r. In computing the solution numerically, we found that
For the impact at \(\tau =\tau _{1} = \frac{a_{1}} {\ell}\), an energy
is lost by pendulum I. However for the launch at \(\tau =\tau _{2} = \frac{a_{2}} {\ell}\), an energy
is transferred to pendulum II. The plots of the total energies of the pendula shown in Figure 4.21(c) confirm conservation of energy during the pendulum motions while the pendula are moving - although the analogy we have presented breaks down when the pendula are stationary during the time interval \(\tau \in \left (\tau _{1},\tau _{2}\right )\).
(a) A solution to the pendulum equations of motion (4.120) and (4.123), (b) the corresponding elastica arm scale, and (c) the energy of the pendula during their motions. Referring to Eqns. (4.120) and (4.123), for the results shown in this figure, α = 60∘, ω 1 2 = 20, ω 2 2 = 40, the sleeve is 36. 44% of the length ℓ of the elastic rod, \(\tau _{1} = \frac{a_{1}} {\ell}\), and \(\tau _{2} = \frac{a_{2}} {\ell}\). The phase plane representation for the solution shown in (a) corresponds to the trajectory labeled E in Figure 4.20.
When one of the terminal loads is zero, then it is possible to use a single pendulum to develop an analogue model for the deformable scale. In this case, say if P 1 = 0, then Eqn. (4.127) implies that θ(ℓ) +α = 90∘. For pendulum II, we have e 2 = 0, \(\phi _{2}\left (1 -\frac{a_{2}} {\ell} \right ) =\alpha\), and ϕ 2(1) = 90∘. Thus, it is possible to quickly arrive at a closed form expression for \(\frac{a_{2}} {\ell}\) from Eqn. (4.125)2 Footnote 14:
K(x) is a complete elliptic integral of the first kind, and F(x, m) is an elliptic integral of the first kind.Footnote 15 The solutions \(\frac{a_{2}} {\ell}\) to Eqn. (4.131) are shown in Figure 4.22. Observe that for \(\frac{P_{2}\ell^{2}} {EI} > K^{2}\left (\frac{1} {2}\right )\), the scale can be operated at all values of \(\alpha \in \left (0,90^{\circ }\right )\). In addition, the more vertical the sleeve (i.e., the smaller the value of α), the more sensitive the measurement \(\frac{a_{2}} {\ell}\) is to changes in \(\omega _{2}^{2} = \frac{P_{2}\ell^{2}} {EI}\). This result is evident from Figure 4.22 or \(\ell \frac{\partial f} {\partial P_{2}}\) that can be calculated from Eqn. (4.131). Finally, we note that the range of values of α for which the scale operates is limited when \(0 < \frac{P_{2}\ell^{2}} {EI} < K^{2}\left (\frac{1} {2}\right )\).
The length \(\frac{a_{2}} {\ell}\) as a function of α when P 1 = 0 for various values of P 2. The results shown in this figure are calculated using Eqn. (4.131) with i, ω 2 2 = 1; ii, \(\omega _{2}^{2} = K^{2}\left (\frac{1} {2}\right ) \approx 3.43759\); iii, ω 2 2 = 5; iv, ω 2 2 = 20; and v, ω 2 2 = 40.
Our analysis of the arm scale assumes that
which in turn lead to a derivation of the relation Eqn. (4.87) for the operation of an arm scale (where the weight of the elastica was neglected). As with the chain problems, such as the chain fountain, discussed in Chapter 2, the prescriptions for the supplies of material momentum must be justified by experiment. To this end, we note that the relation Eqn. (4.87) governing the arm scale has been validated experimentally by Bosi et al. [32]. Their experiments justify the prescriptions we used for \(\mathsf{B}_{a_{1}}\) and \(\mathsf{B}_{a_{2}}\).
7 Potential Energies and a Variational Formulation
For many problems that use the elastica as a model for a rod-like body, it is possible to use a variational principle to establish the equations of motion. A principal advantage of a variational formulation is that it also enables stability criteria to be established for the equilibrium configuration of the rod. Among others, these criteria enable the interpretation of buckling phenomena as instabilities. Central to any variational formulation is a potential energy functional Π and in this section we will be concerned with establishing such a function for a variety of boundary-value problems, a sample of which were shown earlier in Figure 4.1. Additional background on variational methods can be found in Chapter 9 and the references cited therein.
We restrict attention to rods which are terminally loaded with constant forces and constant moments. In the context of planar motions of the elastica, such forces and moments are conservative.Footnote 16 We also assume that the assigned force ρ 0 f is conservative; the prototypical example of such a force is gravitational: ρ 0 f = −ρ 0 g A 2. In a second example, we allow for the fact that a portion of the rod may have adhered to a rigid surface.
7.1 A Terminally Loaded Rod Deforming Under a Conservative Assigned Force
As our first example, consider a rod which is fixed at ξ = 0 and loaded at ξ = ℓ by a terminal force and terminal moment:
Examples of such rods can be seen in Figures 4.1(a) & (b). For these examples, we have the respective specifications:
The example we consider in this section does not encompass the elastica arm scale or the adhered rod because the boundary condition at one end of the rod does not pertain to a fixed material point.
The balance laws (4.26) and jump conditions (4.41)1, 3 imply that
where we have dropped the− ornamenting some of the ℓs in these equations.
The total elastic strain energy Π E of the elastica is
Noting that the potential energy of the terminal load is −P ⋅ r(ℓ) and exploiting the constancy of P, we find that this potential energy, which we denote by Π P , can be represented as
As the end ξ = 0 of the rod is fixed, we can ignore P ⋅ r(0) in much of the sequel. The contribution from the moment M ℓ can be expressed as
We have not found a discussion of \(\varPi _{\mathbf{M}_{\ell}}\) in the literature, but note that it is crucial to assume in the establishment of the final representation that M ℓ is constant and parallel to the constant axis of rotation A 3. If either of these conditions are violated, then the moment will typically be nonconservative.
The potential energy Π f of the assigned force ρ 0 f is simply the integral of −ρ 0 f ⋅ r over the length of the rod. However, to make this expression tractable to later analysis, we need to use the fundamental theorem of calculus and replace r with the integral of r ′ and then change the order of integration in the resulting integral.Footnote 17 These manipulations are summarized in the following identities:
This completes the discussion of representations for the components of Π.
Combining the potential energy functions, we find the total potential energy of the rod:
where the constant C 0 = −∫ 0 ℓ ρ 0(s)f(s)ds ⋅ r(0) −P ⋅ r(0) −M ℓ ⋅ θ(0)A 3. It is important to note that the term inside the curly brackets, which is equivalent to n(ξ = s), is a function of ξ and not r.
After substituting for r ′ = cos(θ)A 1 + sin(θ)A 2, we find that Π is a functional of the form Π = ∫ 0 ℓ f(θ, θ ′, ξ)ds. We seek extremizers of Π using methods from the calculus of variations. To perform the variation, we let
where the variation η(ξ) satisfies the boundary condition
We substitute (4.141) into Π and then assume that \(\lim _{\epsilon \rightarrow 0}\frac{d\varPi } {d\epsilon } = 0\). In other words, θ ∗(ξ) extremizes Π. Using the standard methods from the calculus of variationsFootnote 18 we find a pair of necessary conditions for θ ∗ to extremize Π. The first of these conditions is the Euler-Lagrange necessary condition (cf. Eqn. (9.14)),
where
In addition, the second condition is the natural boundary condition at ξ = ℓ (cf. Eqn. (9.12)):
Upon inspection, we conclude that Eqns. (4.143) and (4.145) are identical to the governing equation (4.135)4 and boundary condition (4.135)2 we discussed earlier. We denote the solution to (4.143) with an asterisk. What is important to note is that the solution θ(ξ) = θ ∗(ξ) to either of these governing equations that satisfies the boundary conditions
satisfies a necessary condition for an extremizer of Π. Whether or not it is a minimizer or a maximizer can be partially ascertained by looking at the second variation of Π, a task we shall shortly examine.
The material we have just presented pertains to a rod where one end is clamped and the other is free. The corresponding developments where both ends are clamped or both ends are free are straightforward to deduce and we leave them as an exercise for the reader.
7.2 Application to an Adhesion Problem
Consider the problem shown in Figure 4.8 of a rod for which a portion ℓ −γ is contacting a rigid surface or the elastica arm scale shown in Figure 4.15. For these problems, additions are needed to our previous developments. The most significant of these amendments involves subdividing the potential energy functional into a set of piecewise potential energy functionals whose limits of integration are variable.
For a rod which is in contact with a rigid substrate, the total potential energy of the rod will be composed of the potential energy of terminal forces and moments, the integral of the strain energy per unit length, and the adhesion energy per unit length − W ad. Many of the details, particularly for the segment of the rod ξ ∈ [0, γ], are similar to those discussed earlier and so we focus on the differences. In particular for this rod, the balance of linear momentum can be used to show that
It is convenient to decompose the potential energy into the sum of the elastic potential energy in the noncontacting and contacting sections. Modulo an additive constant, the resulting expression for the total potential energy Π isFootnote 19
In writing Eqn. (4.148), we noted that r ′ = A 1 and θ = 0 in the contact region and we defined an additive constant to Π:
The adhesion energy W ad is subtracted from the penultimate term in Eqn. (4.148). This subtraction can be explained by the fact that W ad is defined as the work of the adhesive and elastic restoring forces during interfacial detachment.Footnote 20
In the sequel, the behavior of the functional (4.148) with respect to variations in θ and γ will be computed:
In terms of a more classic notation, the respective variations in θ and γ are δ θ = ε η and δ γ = ε μ. In the region where the rod is adhering to the horizontal surface, θ is prescribed and so
It is known that the variations of θ and γ are not independent and must satisfy compatibility conditions.Footnote 21 To find these conditions we compute the first and second derivatives of \(\theta \left (\xi =\gamma ^{{\ast}}+\epsilon \mu,\epsilon \right )\) with respect to ε evaluated at ε = 0. The desired set of compatibility conditions are obtained by taking the first and second derivatives of Eqn. (4.150)1 with respect to ε and then setting ε → 0:
These conditions prove remarkably useful when simplifying expressions for the first and second variations of Π.
7.2.1 Static Balance Laws
By considering variations of the form (4.150)1 and keeping γ fixed, we find that the equation \(\left.\frac{d\varPi } {d\epsilon }\right \vert _{\epsilon =0} = 0\) leads, as anticipated, to a differential equation which is identical to that obtained using the balances of linear and angular momentum:
where \(\xi \in \left (0,\gamma \right )\). This differential equation is often known as the Euler-Lagrange equation because it is intimately related to the Euler-Lagrange necessary condition. We also obtain the boundary conditions at ξ = 0 and ξ = γ ∗−:
In the condition (4.153), we identified the term comprised of P and ρ 0 f with the contact force n (cf. Eqn. (4.147)).
7.2.2 Adhesion Boundary Conditions
To consider the variations of γ, we need to use the Leibniz rule. You may recall that we used this rule earlier in Chapter 1 (cf. Eqn. (1.48)) to obtain jump conditions from the integral form of the balance laws. In the present context, this rule takes the form
The natural boundary condition at the edge of the region of adhesive contact is obtained by applying the variations (4.150). After differentiating the expression for the functional Π with respect to ε, using the Leibniz rule (4.155), taking the limit ε → 0, using Eqns. (4.153) and (4.154), and then setting the resulting expression to 0, we find that
The condition (4.156) must hold for all μ. Whence, we find the adhesion boundary conditionFootnote 22
This boundary condition can be further simplified by noting that (because θ is a continuous function of ξ) \(\left [\!\left [\mathbf{r}^{'}\right ]\!\right ]_{\gamma } = \mathbf{0}\). Thus, we can use Eqn. (4.41)1 to write
In the absence of shear adhesion (i.e., F γ is normal to the surface and so F γ ⋅ E 1 = 0) or when the shear traction is distributed along the interface between the rod and the surface, the boundary condition (4.158) is the same natural boundary condition previously derived in [217] and [318] and corresponds to the jump in material momentum (4.41)2 with B γ = −W ad. When adhesion is absent, as it is in the elastica arm scale, then W ad = 0 and the condition corresponding to Eqn. (4.158) is discussed and exploited in [27, 32].
In addition to a force F γ and material force B γ at the edge of the region of adhesive contact, a moment M γ can also be present. This moment is computed from Eqn. (4.41)3:
An example of M γ can be seen in Figure 4.9. Moments of this type also appear in the elastica arm scale (cf. Eqn. (4.111)) and are similar to the adhesion moment discussed in the literature (cf. [282]).
Where no confusion should arise, in the sequel we will drop the∗ ornamenting the solutions θ ∗(ξ) and γ ∗ of the boundary-value problem.
8 Conditions for Stability from the Second Variation
We now turn to examining stability conditions for the equilibrium configurations discussed in the previous sections. The central idea here is to consider an expansion of Π about ε = 0:
where ε 0 ∈ [0, ε]. Now for an equilibrium configuration the first variation of Π is zero:
and, after assuming that \(\frac{d^{2}\varPi } {d\epsilon ^{2}}\) is continuous in a neighborhood of ε = 0, we can conclude that
The latter term is known as the second variation δ 2 Π of Π:
Thus, if \(\left.\frac{d^{2}\varPi } {d\epsilon ^{2}} \right \vert _{\epsilon =0} \geq 0\), then the potential energy functional is minimized at an equilibrium configuration. This nonnegativity of the second variation enables us to conclude that the configuration satisfies a necessary condition for stability. If the stronger condition \(\left.\frac{d^{2}\varPi } {d\epsilon ^{2}} \right \vert _{\epsilon =0} > 0\) holds, then we can conclude that the configuration satisfies a sufficient condition for stability and we classify the configuration as stable. By way of contrast, if we can show that \(\left.\frac{d^{2}\varPi } {d\epsilon ^{2}} \right \vert _{\epsilon =0} < 0\), then the necessary condition for stability is not satisfied and we conclude that the equilibrium configuration is unstable.
We now explore conditions that can be used to determine the sign of \(\left.\frac{d^{2}\varPi } {d\epsilon ^{2}} \right \vert _{\epsilon =0}\) and use them to establish a necessary condition, which we denote as N1, for stability. For some cases, we are able to establish a pair of sufficiency conditions, which are referred to as B1 and S1, for stability. For the purposes of exposition, it is convenient to first consider the adhesion problem in Section 4.7.2. Our presentation is based on the works of Majidi, O’Reilly, and Williams [219, 220].
8.1 A Representation for the Second Variation
We return to the adhesion problem shown in Figure 4.8 and discussed in Section 4.7.2. For this problem, the potential energy functional to be examined was presented in Eqn. (4.148) and we reproduce it here for convenience:
We consider variations of θ and γ of the form (4.150) and evaluate \(\left.\frac{d^{2}\varPi } {d\epsilon ^{2}} \right \vert _{\epsilon =0}\). After some rearranging, we find that this derivative has a simple additive decomposition:
where
To start to simplify this expression, we first invoke the compatibility conditions (4.152):
This helps to eliminate η ′ and η from the expression (4.165):
We next appeal to the balance laws for the two segments of the rod:
where λ A 2 is the normal force exerted by the horizontal surface on the rod. Omitting details, the end result of the manipulations is that the expression for \(\left.\frac{d^{2}\varPi } {d\epsilon ^{2}} \right \vert _{\epsilon =0}\) reduces to a desirable decoupled form:
The terms associated with μ 2 can be simplified further by appealing to the fact that the segment of the rod in contact with the flat surface has a constant θ ∗ = 0, however we do not pause to do this here. We also note that for many problems with homogeneous rods in the absence of intrinsic curvature and gravitational loading, the simplifications to the right-hand side of Eqn. (4.170) are extensive and reduce the term associated with μ to a single term: \(+\mu ^{2}S\left (\gamma ^{-}\right )\theta ^{{\ast}}\left (\gamma ^{-}\right )\).
It is important to notice that the integral term in Eqn. (4.170) may not be positive because we are uncertain as to the contribution of the term \(P\eta ^{2} = \left (\mathbf{n} \cdot \mathbf{r}^{'}\right )\eta ^{2}\). This is particularly the case when the rod is in compression (and we anticipate that possible buckling instabilities might be present). To proceed, we follow an idea dating to the French mathematician Adrien-Marie Legendre (1752–1833) in 1786 and add the following term to Eqn. (4.170)Footnote 23:
Manipulating the resulting expression for J from Eqn. (4.170), we find that
It is useful to note that
Thus, provided a solution w(ξ) to the following Riccati equation can be found,
we can then express J in its final desired form:
where
Observe that adding the identity (4.171) to J succeeds in making the integrand a positive semi-definite function of η (provided we can find a bounded solution w(ξ) to the Riccati equation). It is also interesting to observe that we have some freedom in choosing the initial conditions for w(ξ) and this freedom will be exploited in the sequel.
8.2 Conjugate Points and the Riccati and Jacobi Equations
For many problems seeking a bounded solution w(ξ) to the Riccati equation is challenging. Part of the challenge is to distinguish parameter regimes where the solution becomes unbounded from their bounded counterparts. Fortunately, a remedy is at hand that is attributed to the German mathematician Carl Jacobi (1804–1851). The solution is to employ a Jacobi transformation which relates the function w(ξ) to another function u(ξ):
Substituting for w(ξ) in the Riccati equation (4.174), one finds that this transformation produces a Jacobi differential equation for u(ξ) from Eqn. (4.174):
We consider solutions \(u(\xi )\,\forall \xi \in [0,\gamma ]\) to Eqn. (4.178) which satisfy the initial conditions
Note that this pair of initial conditions is equivalent to w(0) = 0. If the solution \(u\left (\xi _{c}\right ) = 0\) for some ξ c , then the point ξ c is said to be conjugate to ξ = 0.Footnote 24
To relate unbounded solutions of the Riccati equation to conjugate points, we recall a theorem that can be found in [298]:
Bounded solutions to the Riccati equation (4.174) for w(ξ) on a given interval exist if, and only if, a solution \(u\left (\xi \right )\) for the corresponding Jacobi differential equation (4.178) exists on the same interval with \(u\left (\xi \right )\neq 0\) and w given by (4.177).
We use this theorem to conclude that the solution to the Riccati equation becomes unbounded at a conjugate point: \(\lim _{\xi \rightarrow \xi _{c}}\left \vert w\left (\xi \right )\right \vert = \infty \) (see Figure 4.23(b)). On the other hand, and as demonstrated in Figure 4.23(a), the existence of a bounded solution \(w(\xi )\,\forall \xi \in [\gamma,\ell]\) is equivalent to the nonexistence of conjugate points to ξ = ℓ in the interval [γ, ℓ] for the solution u(ξ) to the Jacobi equation (4.178).
Schematic of solutions u(ξ) to a Jacobi equation (4.178) and the corresponding solutions w(ξ) to a Riccati equation (4.174). In (a) there is no conjugate point to ξ = 0 in the interval \(\left [0,\gamma \right ]\) and in (b) there is a conjugate point ξ c to ξ = 0 in the interval \(\left [\gamma,\ell\right ]\) where \(w\left (\xi \right ) \nearrow \infty \) as ξ ↗ ξ c and \(w\left (\xi \right ) \searrow -\infty \) as ξ ↘ ξ c . For the examples shown in (a), \(\frac{P\ell^{2}} {EI} = -1\) and γ = 0. 8ℓ. Correspondingly for (b), the parameter values are \(\frac{P\ell^{2}} {EI} = -5\) and γ = 0. 8ℓ and, as a result, ξ c ≈ 0. 70248ℓ.
8.3 The Criterion N1
We have now compiled all the needed background to state the necessary condition for stability which we denote by N1. Part of this criterion pertains to the buckling instability of the rod. The second part of the criterion is intimately related to the kinematics at the adhesion point ξ = γ.
CRITERION N1: If a solution \(\left \{\theta ^{{\ast}}(\xi ),\gamma ^{{\ast}}\right \}\) to the boundary-value problem (4.153),(4.154), and (4.158) minimizes Π then the solution \(w(\xi )\,\forall \xi \in \left [0,\gamma ^{{\ast}}\right ]\) to the boundary-value problem
cannot become unbounded in the interval \(\left [0,\gamma ^{{\ast}}\right ]\) and the following inequality must be satisfied:
We sketch a proof of the criterion as follows. First, if a solution w(ξ) to the Riccati equation (4.180) can be found, then we can decompose J into the sum of J 1 and J 2 as shown in (4.175). Further, J 1 will be positive semi-definite (cf. Eqn. (4.176)). Simplifying J 2 using the fact that w(0) = 0, we find that it is sufficient for Eqn. (4.181) to hold in order for J 2 ≥ 0. This completes the proof.
The adhesion boundary condition (4.158) can often be used to express \(\theta ^{{\ast}'}\left (\gamma ^{{\ast}+}\right )\) in terms of W ad. In this instance, the condition (4.181) can then be interpreted as a condition on the relative work of the adhesion to that of loading P 1. On the other hand, the existence of a solution to the Riccati equation (4.180) implies that the rod has not buckled.
8.4 The Criterion B1
Many of the buckling problems of interest involve rods where one end is free and the other is clamped at ξ = ℓ. To examine stability for these cases, it suffices to examine J and ignore the effects of γ. To ignore the effects of changing γ, one simply sets μ = 0 in the expression for J shown in Eqn. (4.175). In this case, we can establish a very useful sufficient condition for stability by choosing the initial condition w(0) = 0 and appealing to some known results from the calculus of variations.Footnote 25 We label the resulting criterion B1.
CRITERION B1: Consider the case of a terminally loaded rod which is clamped at ξ = ℓ and subject to a conservative assigned body force. If a solution \(\left \{\theta ^{{\ast}}(\xi )\right \}\) to the boundary-value problem
results in a solution \(u(\xi )\,\forall \xi \in [0,\ell]\) to Eqns. (4.178) and (4.179) with no conjugate points in ξ ∈ [0,ℓ] then the equilibrium configuration defined by θ ∗ (ξ) is stable.
This stability criterion is classical and equivalent statements can be found in many papers on stability of rods featuring variational methods. The criterion can also be stated in terms of the Riccati differential equation. However, because of the simplicity of J 2 (i.e., J 2 = 0) it is more convenient to state the result using the Jacobi differential equation. We shall explore an application of B1 in Section 4.9.
8.5 The Criterion S1
For some applications featuring adhered rods, the geometry of the adhesive interface as well as the constitutive properties of the rod conspire so that the boundary term J 2 defined in Eqn. (4.176) can be set to zero by simply choosing the initial condition
One example of such a situation arises when the rod is homogeneous, has no intrinsic curvature and \(\theta ^{{\ast}'}\left (\gamma ^{\pm }\right ) = 0\). In this case, we can strengthen N1 to yield a sufficient condition, which we denote by S1, for stability. Because J 2 = 0, the forthcoming criterion only pertains to perturbations in θ: perturbations to γ need not be considered.
Referring to Theorem 3 in [113, Section 26], we can now readily establish a sufficient condition for positive definiteness of J and, hence, a sufficient condition for stability.Footnote 26 In the interests of brevity, we merely state the criterion:
CRITERION S1: Consider the case \(\theta ^{{\ast}}\left (\gamma ^{+}\right ) = 0\) . If a solution \(\left \{\theta ^{{\ast}}(\xi ),\gamma ^{{\ast}}\right \}\) to the boundary-value problem is such that either
-
(i)
a bounded solution \(w(\xi )\,\forall \xi \in [\gamma ^{{\ast}},\ell]\) to Eqn. (4.174) can be found where w(ℓ) = 0, or
-
(ii)
there are no points conjugate to ξ = ℓ in the interval [γ ∗ ,ℓ],
then \(\left \{\theta ^{{\ast}}(\xi ),\gamma ^{{\ast}}\right \}\) is stable.
Clearly, the development of a stability criterion in this case is identical in all but one respect to the case of a rod fixed at one end and subject to a terminal load P at the other.Footnote 27 The distinction from this classical problem is that the length ℓ −γ of the beam is typically a (nonlinear) function of P, EI, and W ad.
9 Simple Examples of Buckling
We now consider a series of examples designed to illustrate the conditions established in the previous section.
9.1 Compressing an Adhered Rod
To illuminate the criteria N1 and S1, consider the rod shown in Figure 4.24.Footnote 28 The rod of length ℓ has a section of length γ which is restrained by friction from moving on a horizontal surface. The contact between the rod and the surface can be maintained with W ad = 0. An applied force F A 1 acts at the material point ξ = 0. Clearly, if the applied force F is too large then the unattached section of the rod will buckle. This buckling instability will be revealed using the criterion S1.
To analyze this problem, we first solve the balance laws with the help of the appropriate boundary conditions and find the trivial solution
This solution is statically admissible for all values of F and all adhesion lengths γ > 0. To examine the possibility of buckling, we establish the appropriate single Riccati and Jacobi equations, from Eqns. (4.174) and (4.178):
The boundary conditions for these differential equations are, respectively,
The solutions of the pair of boundary-value problems are
Using the solutions (4.187), it is straightforward to show that the Riccati equation (4.185)1 has a bounded solution and, equivalently, there are no conjugate points to ξ = 0 in the interval [0, γ) provided F < F crit Footnote 29:
We conclude with the help of S1 that the straight configuration θ ∗ = 0 is stable provided F < F crit and unstable otherwise. Notice that instability occurs when the rod buckles and is independent of the adhesive.
Now suppose that F > F crit. It follows that \(u\left (\xi _{c}\right ) = 0\) for ξ = ξ c . That is, ξ = ξ c is the conjugate point to ξ = 0. We observe from the solutions (4.187) that w(ξ) ↗ ∞ as ξ ↘ ξ c as expected from our earlier discussion in Section 4.8.2. We can thus appeal to the criterion N1 to conclude that the equilibrium configuration in this case is unstable.
9.2 Buckling of a Clamped Rod
We now examine the classic problem of a straight uniform rod which is clamped at ξ = ℓ, subjected to a vertical force − F A 2 at the free end ξ = 0, and must support its own weight (see Figure 4.25). Initially the rod is straight, but as F increases this straight configuration will eventually become unstable, and the rod will then buckle into one of either two configurations (which turn out to be stable). Examples of the buckled states are shown in Figure 4.26. This buckling problem has a celebrated history and we refer the reader to the discussions in Love’s textbook [213], a paper by Maddocks [215], Timoshenko and Gere’s textbook on elastic stability [345, Chapter 2], and a seminal historical review by Truesdell [350]. By way of additional applications, a closely related analysis applied to understanding the stability of the human spine in the sagittal plane can be found in [211].
(a) Schematic of the buckled states of a heavy terminally loaded strut elastica which is subject to a terminal load − F A 2. (b) The solution of the Jacobi equation (4.191)2 for the buckled strut as β increases from β crit. For the examples shown, α = 1. 0, β crit ≈ 2. 16, and the values of \(\beta = \frac{F\ell^{2}} {EI}\) used in (a) and (b) are 2. 2, 5, 10, and 20.
For the problem at hand,
It follows that
The Euler-Lagrange, Jacobi, and Riccati equations for this problem can be deduced from Eqns. (4.153)1, (4.178), and (4.174), respectively:
The solutions to these equations are subject to the following boundary conditions:
In the sequel, we shall fix the dimensionless weight parameter \(\alpha = \frac{\rho _{0}g\ell^{3}} {EI}\) and vary the terminal load parameter \(\beta = \frac{F\ell^{2}} {EI}\).
Examining the solution to the Euler-Lagrange equation (4.191)1, we observe that the straight strut (i.e., θ ∗ = −90∘) is a solution for all F and ρ 0 g. Assuming that α is sufficiently small, we find that the Riccati equation (4.191)3 for the straight strut has a bounded solution provided β is smaller than a critical value β crit.Footnote 30 A representative sample of w for varying β is shown in Figure 4.26(b). When β ≥ β crit, then Eqn. (4.191)3 does not have a solution. We conclude with the help of S1 that the straight strut is stable for β < β crit and, using B1, that the straight strut is unstable for β ≥ β crit. For β > β crit, the Euler-Lagrange equation (4.191)1 admits two nontrivial solutions (or buckled states) which are mirror images of each other. The evolution of these solutions as F is increased beyond its critical value F crit = EI β crit∕ℓ 2 is shown in Figure 4.26(a). We note that, as F is increased, the strut shows considerable deflection from the vertical. It suffices to examine a single Riccati equation (4.191)3 to determine the stability of both buckled solutions. Referring to Figure 4.26(b), we find that the Riccati equation (4.191)3 possess bounded solutions for each one of the pair of buckled states and conclude, with the help of the criterion S1, that the buckled states are stable.
9.3 Stability of Peeling
The third class of problems we examine involves a rod which is partially adhered to a rigid surface. Examples of this class of problem were considered in Section 4.5 and, for the reader’s convenience, we rapidly recall some of these developments here. The example discussed here is adapted from [219].
Referring to Figures 4.8 and 4.27, we assume that the rod is terminally loaded at ξ = 0 by a force F 0 = P = P 1 A 1 + P 2 A 2 and a terminal moment M 0 = M 0 A 3. At ξ = γ, the rod adheres to the flat horizontal surface with the aid of a dry adhesion mechanism. Paralleling our previous developments it can be shown that the ordinary differential equation governing θ(ξ) for ξ ∈ [0, γ) is
where
As part of the solution process, θ − ′, θ(ξ = 0) = θ 0, and γ will be determined. At ξ = γ, the adhesion boundary condition holds:
and owing to the conservation of C on \(\left (0,\gamma \right )\), we can relate the adhesion energy at ξ = γ to the configuration of the rod (cf. Eqn. (4.67)):
At this stage, it is convenient to reintroduce several dimensionless quantities,
and loading parameters,
Note that we have dropped the ∗ ornamenting the solutions θ ∗ and γ ∗ to the boundary-value problem.
Deformed configurations of the terminally loaded rod for various values of f 1: − 2, − 3, − 4, − 5, and − 5. 9. The corresponding values of Γ (which is defined in Eqn. (4.205)) for these solutions are − 1. 03053, 1. 37988, 2. 3106, 1. 76842, and − 0. 000105, respectively. The inset image shows the corresponding solutions v(s) for the Riccati equation (4.204). Unlike the other three solutions shown, the solutions displayed for f 1 = −2 and f 1 = −5. 9, which are labeled u, do not satisfy (4.205) and are unstable. The remaining parameters for the solutions shown are f 2 = −1, ω 0 = −3, and w ad = 6.
Solving the boundary-value problem is greatly facilitated by noting that γ can be determined using the conservation of C and the adhesion boundary condition. To elaborate, at \(x =\bar{ g} =\gamma /\ell\) we find that
Applying the conservation to the other end of the rod (at ξ = 0) permits us to conclude that
where θ 0 = θ(ξ = 0). Thus,
The first of these equations can be used to determine θ 0. It can also be used to show a necessary restriction on some of the parameters of the system:
We observe from this equation that the stronger the dry adhesive, the greater the magnitude of the terminal force needed to ensure an adhered state. Further, for a given terminal force, a terminal moment can be introduced to ensure the necessary condition (4.202) is satisfied.
The second of the conditions (4.201) can be used to solve for γ:
Once γ has been determined using the identity (4.203), it is then straightforward to solve the initial-value problem consisting of the ordinary differential equation (4.193) subject to the boundary conditions \(\theta \left (0\right ) =\theta _{0}\) and θ ′(0) = −M 0∕EI in order to determine θ(ξ) = θ ∗(ξ). With the assistance of Eqn. (4.203), we take this opportunity to note the expected result that, for a given loading f 1 and f 2, the adhered length of the rod (ℓ −γ) increases with increasing w ad.
The solution \(\left \{\theta ^{{\ast}}(\xi ),\gamma ^{{\ast}}\right \}\) to the boundary-value problem is then interrogated using Criterion N1 to determine stability. We recall from Section 4.8.3:
CRITERION N1: If a solution \(\left \{\theta ^{{\ast}}(\xi ),\gamma ^{{\ast}}\right \}\) to the boundary-value problem (4.193) minimizes Π then the solution \(v(x)\,\forall x \in [0,\gamma ^{{\ast}}/\ell]\) to the Riccati equation
cannot become unbounded in the interval [0,γ ∗ ∕ℓ] and the following inequality must be satisfied at the point \(x =\bar{ g} =\gamma ^{{\ast}}/\ell\) :
As discussed in [219, 220], the presence of the bounded solution to the Riccati equation indicates stability of the rod. This existence result is identical to the more familiar use of an equivalent Jacobi equation in studies on buckling that can be found in the literature. The condition (4.205) is intimately related to the work of the adhesion W ad at ξ = γ.
While the solution space of EI θ ″ + P 1sin(θ) − P 2cos(θ) = 0 has a wealth of solutions, most of them are not applicable to the adhesion problem of interest. To elaborate further on this, we define the angle β subtended by P with the horizontal:
The solutions θ(s) of interest are those that satisfy
with
Thus the set of admissible solutions excludes the region in state space from the fixed point at θ = β (where w ad = f) to the level set of \(\theta -\frac{\partial \theta } {\partial s}\) where w ad = 0 (see Figure 4.28).
Phase portrait of the ordinary differential equation (4.207). The shaded region containing the point \(\left (\theta, \frac{\partial \theta } {\partial s}\right ) = (\beta,0)\) is bounded by the level-set corresponding to w ad = 0 and does not contain solutions to the adhesion boundary-value problem. The trajectories labeled with values of f 1 correspond to the solutions shown in the inset image in this figure and in (additional detail in) Figure 4.27.
9.3.1 An Example
We now consider a numerical example to illustrate the previous developments. After a parameter search, we select a rod with a preload in the normal direction and an applied moment on the end:
We now vary the (dimensionless) shear force f 2. Arbitrary values of f 2 are not possible, and our first check is to examine the existence of a physically realistic γ using Eqn. (4.203). Some of the numerical results are shown in Figure 4.29(a). We see from this figure that − 1. 5 > f 2 > ≈ −5. 986 in order for γ to be realizable. That is, γ ∈ (0, ℓ). We also observe that changing ω 0 changes the adhered length of the rod, and, from Figure 4.29(b), how the angle of inclination θ 0 at the free end also changes.
The dimensionless length \(\frac{\gamma }{\ell}\) and angle θ 0 computed using (4.203) and (4.201)1, respectively, as a function of the dimensionless shear force \(f_{1} = \left ( \frac{\ell^{2}} {EI}\right )\mathbf{P} \cdot \mathbf{A}_{1}\) for three values of ω 0: i, ω 0 = −2. 0; ii, ω 0 = −3. 0; and iii, ω 0 = −4. 0. The remaining parameters for the solution shown are f 2 = −1 and w ad = 6.
For each of the solutions computed, we next calculate Γ using Eqn. (4.205). After checking the sign of Γ, we then appeal to Criterion N1 to ascertain instability. As summarized in Figure 4.27, the configurations with f 1 = −2 and f 1 = −5. 9 are unstable. Because a bounded solution to the appropriate Riccati equation (4.204) exists for all the configurations shown, this instability can be attributed entirely to adhesion.
10 Additional Areas of Application of the Elastica
Euler’s elastica, being the simplest nonlinear rod theory, has been applied to a wealth of problems and space precludes us from giving full justice to all these works. Among many others, the areas of application include flexible risers in ocean environments [312, 313], folding of thin sheets [216], soft robot gripping and locomotion mechanisms [372, 373], the buckling of rods in constrained environments [91] and in carbon nanotube bundles [374], and the growth and dynamics of plant stems. The application of the elastica to plant growth has several interesting aspects including an intermediate growth configuration, branching and tree-like structures, a time-evolving intrinsic curvature and constitutive relations that change with time. This area of application was championed by the works by Silk and her coworkers [322–324] and further promoted by Goldstein and Goriely’s work [118] on evolving constitutive relations. We refer the reader to [109, 121, 122, 145, 269, 273, 274, 368] for additional references and perspectives on this interesting area of application and close this chapter with the hope that we have given the reader the relevant background to comprehend, critique, and appreciate the aforementioned works.
11 Exercises
Exercise 4.1:
Suppose a rod (of length ℓ) is subject to terminal forces F 0 = R A 1 and F ℓ = −R A 1. Show that n is constant and that Eqn. (4.26) reduces to an ordinary differential equation for θ:
What are the boundary conditions for \(\theta ^{'}\left (\xi = 0^{+}\right )\) and \(\theta ^{'}\left (\xi =\ell ^{-}\right )\)? Show that Eqn. (4.210) is equivalent to the equation of motion of a simple pendulum in a gravitational field. By non-dimensionalizing this equation, numerically determine its solutions for three values (say − 5, 0, and 5) of the parameter
It is a good idea to plot the solutions on the plane \(\theta -\frac{\partial \theta } {\partial u}\) where \(u = \frac{\xi }{\ell}\). You should also verify that your solutions conserve the energy
Exercise 4.2:
Determine the shape r(ξ) of the elastica corresponding to the trajectories you found in Exercise 4.1. For your solutions, it is convenient to choose \(\mathbf{r}\left (\xi = 0\right ) = \mathbf{0}\).
-
(a)
Determine the terminal moments M 0 and M ℓ needed to support these solutions.
-
(b)
For the case β = 0, give an interpretation for the presence of an infinite number of equilibria of (4.210). In addition, show that the space curve formed by \(\mathbf{r}\left (\xi \right )\) is either a straight line or the arc of a circle.
-
(c)
Discuss the distinction between the cases β > 0 and β < 0.
-
(d)
For the case β > 0, compare your results to Hess’s which date to 1885 and can be found in Love’s book [213, Page 404]. You should comment on the “apparent” change in the boundary conditions between Figures 51–53 and 54 of [213]. In addition, discuss why terminal moments are needed to capture all the solutions shown on [213, Page 404].
Exercise 4.3:
Consider an elastica of length ℓ which is horizontal and subject to terminal forces:
Show that if \(R = R_{c_{n}}\) for some integer n where
then, in addition to the trivial solution θ = 0, another solution is possible. The existence of this other solution is known as a buckling instability and \(R_{c_{n}}\) is known as a buckling load. Give an interpretation of the buckling phenomenon using the phase portrait similar to that shown in Figure 4.10. You should also notice that by fixing R, buckling can also be achieved by varying the length ℓ.Footnote 31
Exercise 4.4:
For the case where β > 0 and assuming that θ is small, show that Eqn. (4.210) reduces to the equation for a Bernoulli-Euler beam subject to a terminal loadingFootnote 32:
What is the analytical solution to this equation and how many boundary conditions are needed to uniquely prescribe a solution?
Exercise 4.5:
Using the non-dimensionalizations (4.66), verify that Eqn. (4.60)2 can be written in the form
Using a change of variables, show that this equation can be simplified to
where
Argue that Eqn. (4.217) can also be obtained by suitably rotating the basis vectors A 1 and A 2 about A 3. Establish a first integral of Eqn. (4.217).
Exercise 4.6:
Consider the adhesion problem discussed in Section 4.5.3.1. Using Eqn. (4.75), establish an expression for θ as a function of \(\frac{\xi }{\ell}\sqrt{-f_{2}}\). With the help of these expressions and Eqn. (4.79), determine r(ξ) using either numerical or analytical techniques.
Exercise 4.7:
Consider the adhesion problem discussed in Section 4.5.3.2. Using elliptic functions, establish an expression for θ as a function of \(\frac{\xi }{\ell}\sqrt{-f_{2}}\). With the help of these expressions and Eqn. (4.85), determine r(ξ) using either numerical or analytical techniques.
Exercise 4.8:
Suppose a variant of the adhesion problems discussed in Sections 4.5.3.1 and 4.5.3.2 is considered where f 1 ≠ 0. Show that by using the results of Exercise 4.5 it is possible to solve the adhesion problem with a small amount of modifications to the analyses presented in these subsections.
Exercise 4.9:
Consider the Johnson-Kendall-Robert’s (JKR) theory of adhesion [175] applied to the adhesion problems discussed in Section 4.5.3. In this theory, one solves the problem by seeking minimizers (γ and \(\theta \left (\xi \right )\)) of the potential energy functional
subject to the condition that \(\theta \left (\xi \right ) = 0\) for \(\xi \in \left [\gamma,\ell\right ]\). Show that the Euler-Lagrange necessary condition for an extremizer yields the differential equation (4.60)2, and the Weierstrass corner condition (9.25) yields the boundary condition (4.64).Footnote 33 From these results, you should be able to conclude that the solution γ found earlier is such that the potential energy of the system is extremized.
Notes
- 1.
These developments are discussed at length in Bolza’s marvelous textbook [30].
- 2.
- 3.
- 4.
As usual, for ease of exposition and without loss of generality, we assume that there is at most one such point.
- 5.
- 6.
- 7.
- 8.
- 9.
- 10.
See Eqn. (4.6).
- 11.
- 12.
See Example 288.50 for the integral \(\int _{\psi }^{ \frac{\pi }{ 2} } \frac{d\theta } {\sqrt{a+b\sin \left (\theta \right )}}\) where \(b > \left \vert a\right \vert > 0\) in [41].
- 13.
See Example 288.00 for the integral \(\int _{\psi }^{ \frac{\pi }{ 2} } \frac{d\theta } {\sqrt{a+b\sin \left (\theta \right )}}\) where a > b > 0 in [41].
- 14.
- 15.
- 16.
- 17.
Our manipulations of Π f are inspired by related work in a recent paper by Farjoun and Neu [108].
- 18.
- 19.
The contribution of ρ 0 f to this expression follows from Eqn. (4.139) with some minor modifications to one of the limits of integration.
- 20.
Alternatively, the adhesion may be represented as a surface potential by also adding W ad ℓ to Π. This is accomplished by eliminating W ad in the second integrand and adding it to the first integrand.
- 21.
Compatibility conditions of the form (4.152) for adhesion problems can be found in [219] and [318] and for problems where the rod passes through a sleeve, as in the elastica arm scale, in [27, 32]. They express the restrictions that variations in \(\theta \left (\gamma ^{\pm }\right )\) and γ are not always independent.
- 22.
- 23.
- 24.
Our definition of the conjugate point differs from the traditional definition as the latter applies to the case where the rod is clamped at both of its ends.
- 25.
- 26.
- 27.
That is, the problem of a terminally loaded fixed-free strut.
- 28.
This example is adopted from [219]. It is the simplest illustrative example of a buckling problem featuring adhesion that we could find.
- 29.
This is equivalent to the classical result for the buckling load of a fixed-free strut.
- 30.
An analytic expression, featuring Airy functions, for w(ξ) can be established for Eqn. (4.191)3 when θ ∗ = −90∘.
- 31.
- 32.
- 33.
References
Alexander, J.C., Antman, S.S.: The ambiguous twist of Love. Quarterly of Applied Mathematics 40 (1), 83–92 (1982/83)
Autumn, K., Sitti, M., Liang, Y.A., Peattie, A.M., Hansen, W.R., Sponberg, S., Kenny, T.W., Fearing, R., Israelachvili, J.N., Full, R.J.: Evidence for van der Waals adhesion in gecko setae. Proceedings of the National Academy of Sciences 99 (19), 12,252–12,256 (2002). URL http://dx.doi.org/10.1073/pnas.192252799
Batista, M.: Analytical treatment of equilibrium configurations of cantilever under terminal loads using Jacobi elliptical functions. International Journal of Solids and Structures 51 (13), 2308–2326 (2014). URL http://dx.doi.org/10.1016/j.ijsolstr.2014.02.036
Bigoni, D., Bosi, F., Corso, F.D., Misseroni, D.: Instability of a penetrating blade. Journal of the Mechanics and Physics of Solids 64, 411 – 425 (2014). URL http://dx.doi.org/10.1016/j.jmps.2013.12.008
Bigoni, D., Bosi, F., Misseroni, D., Dal Corso, F., Noselli, G.: New phenomena in nonlinear elastic structures: from tensile buckling to configurational forces. In: D. Bigoni (ed.) Extremely Deformable Structures, pp. 55–135. Springer-Verlag, Vienna (2015). URL http://dx.doi.org/10.1007/978-3-7091-1877-1_2
Bigoni, D., Corso, F.D., Bosi, F., Misseroni, D.: Eshelby-like forces acting on elastic structures: Theoretical and experimental proof. Mechanics of Materials 80, 368–374 (2015). URL http://dx.doi.org/10.1016/j.mechmat.2013.10.009
Bolza, O.: Lectures on the Calculus of Variations, third edn. Chelsea, New York (1973)
Born, M.: Untersuchungen über die Stabilität der elastischen Linie in Ebene und Raum, unter verschiedenen Grenzbedingungen. Dieterichsche Universitäts-Buchdruckerei, Göttingen (1906)
Bosi, F., Misseroni, D., Dal Corso, F., Bigoni, D.: An elastica arm scale. Proceedings of the Royal Society A: Mathematical, Physical and Engineering Science 470 (2169), 20140,232 (2014). URL http://dx.doi.org/10.1098/rspa.2014.0232
Bosi, F., Misseroni, D., Dal Corso, F., Bigoni, D.: Development of configurational forces during the injection of an elastic rod. Extreme Mechanics Letters 4, 83–88 (2015). URL http://dx.doi.org/10.1016/j.eml.2015.04.007
Bosi, F., Misseroni, D., Dal Corso, F., Bigoni, D.: Self-encapsulation, or the ‘dripping’ of an elastic rod. Proceedings of the Royal Society of London A: Mathematical, Physical and Engineering Sciences 471 (2179), 20150,195 (2015). URL http://dx.doi.org/10.1098/rspa.2015.0195
Byrd, P.F., Friedman, M.D.: Handbook of Elliptic Integrals for Engineers and Scientists, Die Grundlehren der mathematischen Wissenschaften, vol. 67. Springer-Verlag, New York (1971). Second edition, revised
Coleman, B.D., Dill, E.H.: Flexure waves in elastic rods. Journal of the Acoustical Society of America 91 (5), 2663–2673 (1992). URL http://dx.doi.org/10.1121/1.402974
Coleman, B.D., Dill, E.H., Swigon, D.: On the dynamics of flexure and stretch in the theory of elastic rods. Archive for Rational Mechanics and Analysis 129 (2), 147–174 (1995). URL http://dx.doi.org/10.1007/BF00379919
Domokos, G., Holmes, P., Royce, B.: Constrained Euler buckling. Journal of Nonlinear Science 7 (3), 281–314 (1997). URL http://dx.doi.org/10.1007/BF02678090
Domokos, G., Ruina, A.: A circle construction based on elastostatics and hydrodynamics. Mechanics Research Communications 20 (3), 181–185 (1993). URL http://dx.doi.org/10.1016/0093-6413(93)90054-R
Eshelby, J.D.: The continuum theory of lattice defects. In: F. Seitz, D. Turnbull (eds.) Solid State Physics, vol. 3, pp. 79–144. Academic Press (1956). URL http://dx.doi.org/10.1016/S0081-1947(08)60132-0
Euler, L.: Methodus Inveniendi Lineas Curvas Maximi Minimive Proprietate Gaudentes, sive Solutio Problematis Isoperimetrici Lattissimo Sensu Accepti: Additamentum 1 De Curvis Elasticis. Leonhardi Euleri Opera Omnia, Series prima (Opera mathematica), Vol. XXIV, Auctoritate et impensis Societatis Scientiarum Naturalium Helveticae. Orell Füssli, Zürich (1952). An English translation of this work can be found in [254].
Farjoun, Y., Neu, J.: The tallest column: A dynamical system approach using a symmetry solution. Studies in Applied Mathematics 115 (3), 319–337 (2005). URL http://dx.doi.org/10.1111/j.1467-9590.2005.00316.x
Faruk Senan, N.A., O’Reilly, O.M., Tresierras, T.N.: Modeling the growth and branching of plants: A simple rod-based model. J. Mech. Phys. Solids 56 (10), 3021–3036 (2008). URL http://dx.doi.org/10.1016/j.jmps.2008.06.005
Gelfand, I.M., Fomin, S.V.: Calculus of Variations. Prentice-Hall, Englewood Cliffs, N. J. (1964)
Glassmaker, N., Jagota, A., Hui, C., Noderer, W., Chaudhury, M.: Biologically inspired crack trapping for enhanced adhesion. Proceedings of the National Academy of Sciences 104 (26), 10,786–10,791 (2007). URL http://dx.doi.org/10.1073/pnas.0703762104
Glassmaker, N.J., Hui, C.Y.: Elastica solution for a nanotube formed by self-adhesion of a folded thin film. Journal of Applied Physics 96 (6), 3429–3434 (2004). URL http://dx.doi.org/10.1063/1.1779974
Goldstein, R.E., Goriely, A.: Dynamic buckling of morphoelastic filaments. Physical Review E 74, 010,901 (2006). URL http://dx.doi.org/10.1103/PhysRevE.74.010901
Goriely, A.: The Mechanics and Mathematics of Biological Growth. Springer-Verlag, New York (2017)
Goriely, A., Neukirch, S.: The mechanics of attachment in twining plants. Physical Review Letters 97, 184,302 (2006). URL http://dx.doi.org/10.1103/PhysRevLett.97.184302
Green, A.E., Naghdi, P.M.: A derivation of jump condition for entropy in thermomechanics. Journal of Elasticity 8 (2), 119–182 (1978). URL http://dx.doi.org/10.1007/BF00052481
Guillon, T., Dumont, Y., Fourcaud, T.: A new mathematical framework for modelling the biomechanics of growing trees with rod theory. Mathematical and Computer Modelling 55 (9–10), 2061–2077 (2012). URL http://dx.doi.org/10.1016/j.mcm.2011.12.024
van der Heijden, G.H.M., Peletier, M.A., Planqué, R.: On end rotation for open rods undergoing large deformations. Quarterly of Applied Mathematics 65 (2), 385–402 (2007). URL http://dx.doi.org/10.1090/S0033-569X-07-01049-X
Hess, W.: Ueber die Beigung und Drillung eines unendlich dünnen elastischen Stabes mit zwei gleichen Widersänden, auf dessen freies Ende eine Kraft und ein um die Hauptaxe ungleichen Widerstandes drehendes Kräftepaar einwirkt. Mathematische Annalen 25 (1), 1–38 (1885). URL http://dx.doi.org/10.1007/BF01446419
Hoffman, K.A., Manning, R.S., Maddocks, J.H.: Link, twist, energy, and the stability of DNA minicircles. Biopolymers 70 (2), 145–157 (2003). URL http://dx.doi.org/10.1002/bip.10430
Israelachvili, J.R.: Intermolecular and Surface Forces: With Applications to Colloidal and Biological Systems (Colloid Science), second edn. Academic Press, San Diego (1992)
Johnson, K.L., Kendall, K., Roberts, A.D.: Surface energy and the contact of elastic solids. Proceedings of the Royal Society. London. Series A. Mathematical, Physical and Engineering Sciences 324 (1558), 301–313 (1971). URL http://dx.doi.org/10.1098/rspa.1971.0141
Kendall, K.: The adhesion and surface energy of elastic solids. Journal of Physics D: Applied Physics 4 (8), 1186–1195 (1971). URL http://dx.doi.org/10.1088/0022-3727/4/8/320
Kienzler, R., Herrmann, G.: Mechanics in Material Space: With Applications to Defect and Fracture Mechanics. Springer-Verlag, Berlin (2000)
Kienzler, R.R., Herrmann, G.G.: On material forces in elementary beam theory. ASME Journal of Applied Mechanics 53 (3), 561–564 (1986). URL http://dx.doi.org/10.1115/1.3171811
Kirchhoff, G.: Über des gleichgewicht und die Bewegung eines unendlich dünnen elastichen Stabes. Crelles Journal für die reine und angewandte Mathematik 56, 285–313 (1859). URL http://dx.doi.org/10.1515/crll.1859.56.285
Lawden, D.F.: Elliptic Functions and Applications, Applied Mathematical Sciences, vol. 80. Springer-Verlag, New York (1989)
Lotz, J.C., O’Reilly, O.M., Peters, D.M.: Some comments on the absence of buckling of the ligamentous human spine in the sagittal plane. Mechanics Research Communications 40 (1), 11–15 (2012). URL http://dx.doi.org/10.1016/j.mechrescom.2011.11.010
Love, A.E.H.: A Treatise on the Mathematical Theory of Elasticity, fourth edn. Cambridge University Press, Cambridge (1927)
Maddocks, J.H.: Stability of nonlinearly elastic rods. Archive for Rational Mechanics and Analysis 85 (4), 311–354 (1984). URL http://dx.doi.org/10.1007/BF00275737
Mahadevan, L., Keller, J.B.: Periodic folding of thin sheets. SIAM Journal on Applied Mathematics 55 (6), 1609–1624 (1995). URL http://dx.doi.org/10.1137/S0036139994263410
Majidi, C.: Remarks on formulating an adhesion problem using Euler’s elastica. Mechanics Research Communications 34 (1), 85–90 (2007). URL http://dx.doi.org/10.1016/j.mechrescom.2006.06.007
Majidi, C., Adams, G.G.: Adhesion and delamination boundary conditions for elastic plates with arbitrary contact shape. Mechanics Research Communications 37 (2), 214–218 (2010). URL http://dx.doi.org/10.1016/j.mechrescom.2010.01.002
Majidi, C., O’Reilly, O.M., Williams, J.A.: On the stability of a rod adhering to a rigid surface: Shear-induced stable adhesion and the instability of peeling. Journal of the Mechanics and Physics of Solids 60 (5), 827–843 (2012). URL http://dx.doi.org/10.1016/j.jmps.2012.01.015
Majidi, C., O’Reilly, O.M., Williams, J.A.: Bifurcations and instability in the adhesion of intrinsically curved rods. Mechanics Research Communications 49, 13–16 (2013). URL http://dx.doi.org/10.1016/j.mechrescom.2013.01.004
Manning, R.S.: Conjugate points revisited and Neumann-Neumann problems. SIAM Review 51 (1), 193–212 (2009). URL http://dx.doi.org/10.1137/060668547
Manning, R.S., Rogers, K.A., Maddocks, J.H.: Isoperimetric conjugate points with application to the stability of DNA minicircles. Proceedings of the Royal Society of London. Series A: Mathematical, Physical and Engineering Sciences 454 (1980), 3047–3074 (1998). URL http://dx.doi.org/10.1098/rspa.1998.0291
Marshall, J.S., Naghdi, P.M.: A thermodynamical theory of turbulence. I. Basic developments. Philosophical Transactions of the Royal Society of London. Series A. Mathematical and Physical Sciences 327 (1595), 415–448 (1989). URL http://dx.doi.org/10.1098/rsta.1989.0001
Oldfather, W.A., Ellis, C.A., Brown, D.M.: Leonhard Euler’s elastic curves. Isis 20 (1), 72–160 (1933). URL http://www.jstor.org/stable/224885
O’Reilly, O.M.: The energy jump condition for thermomechanical media in the presence of configurational forces. Continuum Mechanics and Thermodynamics 18 (6), 361–365 (2007). URL http://dx.doi.org/10.1007/s00161-006-0036-3
O’Reilly, O.M.: A material momentum balance law for rods. Journal of Elasticity 86 (2), 155–172 (2007). URL http://dx.doi.org/10.1007/s10659-006-9089-6
O’Reilly, O.M.: Intermediate Engineering Dynamics: A Unified Treatment of Newton-Euler and Lagrangian Mechanics. Cambridge University Press, Cambridge (2008)
O’Reilly, O.M.: Some perspectives on Eshelby-like forces in the elastica arm scale. Proceedings of the Royal Society of London. Series A: Mathematical, Physical and Engineering Sciences 471 (2174), 20140,785 (2015). URL http://dx.doi.org/10.1098/rspa.2014.0785
O’Reilly, O.M., Peters, D.M.: On the stability analyses of three classical buckling problems for the elastic strut. Journal of Elasticity 105 (1–2), 117–136 (2011). URL http://dx.doi.org/10.1007/s10659-010-9299-9
O’Reilly, O.M., Peters, D.M.: Nonlinear stability criteria for tree-like structures composed of branched elastic rods. Proceedings of the Royal Society of London. Series A: Mathematical, Physical and Engineering Sciences 468 (2137), 206–226 (2012). URL http://dx.doi.org/10.1098/rspa.2011.0291
O’Reilly, O.M., Tresierras, T.N.: On the evolution of intrinsic curvature in rod-based models of growth in long slender plant stems. International Journal of Solids and Structures 48 (9), 1239–1247 (2011). URL http://dx.doi.org/10.1016/j.ijsolstr.2010.12.006
O’Reilly, O.M., Tresierras, T.N.: On the static equilibria of branched elastic rods. International Journal of Engineering Science 49 (2), 212–227 (2011). URL http://dx.doi.org/10.1016/j.ijengsci.2010.11.008
Pamp, A., Adams, G.G.: Deformation of bowed silicon chips due to adhesion and applied pressure. Journal of Adhesion Science and Technology 21 (11), 1021–1043 (2007). URL http://dx.doi.org/10.1163/156856107782105963
de Payrebrune, K.M., O’Reilly, O.M.: On constitutive relations for a rod-based model of a pneu-net bending actuator. Extreme Mechanics Letters 8 (C), 38–46 (2016). URL http://dx.doi.org/10.1016/j.eml.2016.02.007
Peters, D.M.: Nonlinear stability criteria for elastic rod structures. Ph.D. thesis, University of California at Berkeley (2011). URL https://escholarship.org/uc/item/6km3q6b7
Plaut, R.H., Dalrymple, A.J., Dillard, D.A.: Effect of work on contact of an elastica with a flat surface. Journal of Adhesion Science and Technology 15 (5), 565–581 (2001). URL http://dx.doi.org/10.1163/156856101300189934
Plaut, R.H., Williams, N.H., Dillard, D.A.: Elastica analysis of the loop tack adhesion test for pressure sensitive adhesives. Journal of Adhesion 76 (1), 37–53 (2001). URL http://dx.doi.org/10.1080/00218460108029616
Podio-Guidugli, P.: Peeling tapes. In: P. Steinmann, G.A. Maugin (eds.) Mechanics of Material Forces, Advances in Mechanics and Mathematics, vol. 11, pp. 253–260. Springer-Verlag, New York (2005). URL http://dx.doi.org/10.1007/0-387-26261-X_25
Reid, W.T.: Riccati Differential Equations. Academic Press, New York (1972)
Santillan, S.T., Virgin, L.N.: Numerical and experimental analysis of the static behavior of highly deformed risers. Ocean Engineering 38 (13), 1397–1402 (2011). URL http://dx.doi.org/10.1016/j.oceaneng.2011.06.009
Santillan, S.T., Virgin, L.N., Plaut, R.H.: Static and dynamic behavior of highly deformed risers and pipelines. ASME Journal of Offshore Mechanics and Artic Engineering 132 (2), 021,401 (2010). URL http://dx.doi.org/10.1115/1.4000555
Seifert, U.: Adhesion of vesicles in two dimensions. Physical Review A 43 (12), 6803–6814 (1991). URL http://dx.doi.org/10.1103/PhysRevA.43.6803
Silk, W., Erickson, R.O.: Kinematics of hypocotyl curvature. American Journal of Botany 65 (3), 310–319 (1978). URL http://www.jstor.org/stable/2442271
Silk, W., Wang, L.L., Cleland, R.E.: Mechanical properties of the rice panicle. Plant Physiology 70 (2), 460–464 (1982)
Timoshenko, S.P., Gere, J.M.: Theory of Elastic Stability, second edn. McGraw-Hill, New York (1961)
Truesdell, C.: The Rational Mechanics of Flexible or Elastic Bodies, 1638–1788. Leonhardi Euleri Opera Omnia, Series secunda (Opera mechanica et astronoca), Vol. XI, sectio secunda. Auctoritate et impensis Societatis Scientiarum Naturalium Helveticae. Orell Füssli, Zürich (1960)
Williams, J.A.: Adhesional instabilities and gecko locomotion. Journal of Physics D: Applied Physics 48 (1), 015,401 (2015). URL http://dx.doi.org/10.1088/0022-3727/48/1/015401
Yamamoto, H., Yoshida, M., Okuyama, T.: Growth stress controls negative gravitropism in woody plant stems. Planta 216 (2), 280–292 (2002). URL http://dx.doi.org/10.1007/s00425-002-0846-x
Zhou, X., Majidi, C., O’Reilly, O.M.: Flexing in motion: A locomotion mechanism for soft robots. International Journal of Non-Linear Mechanics 74, 7–17 (2015). URL http://dx.doi.org/10.1016/j.ijnonlinmec.2015.03.001
Zhou, X., Majidi, C., O’Reilly, O.M.: Soft hands: An analysis of some gripping mechanisms in soft robot design. International Journal of Solids and Structures 64–65, 155–165 (2015). URL http://dx.doi.org/10.1016/j.ijsolstr.2015.03.021
Zhou, X., O’Reilly, O.M.: On adhesive and buckling instabilities in the mechanics of carbon nanotubes bundles. ASME Journal of Applied Mechanics 82 (10), 101,007 (2015). URL http://dx.doi.org/10.1115/1.4030976
Ziegler, H.: Principles of Structural Stability, second edn. Birkhaüser, Basel (1977). URL http://dx.doi.org/10.1007/978-3-0348-5912-7
Author information
Authors and Affiliations
Rights and permissions
Copyright information
© 2017 Springer International Publishing AG
About this chapter
Cite this chapter
O’Reilly, O.M. (2017). Theory of the Elastica and a Selection of Its Applications. In: Modeling Nonlinear Problems in the Mechanics of Strings and Rods. Interaction of Mechanics and Mathematics. Springer, Cham. https://doi.org/10.1007/978-3-319-50598-5_4
Download citation
DOI: https://doi.org/10.1007/978-3-319-50598-5_4
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-319-50596-1
Online ISBN: 978-3-319-50598-5
eBook Packages: EngineeringEngineering (R0)