Keywords

1 Introduction

The rapid development of artificial intelligence has attracted researchers’ attention on multi-agent systems. The Distributed Constraint Optimization Problem (DCOP), as an important research direction on multi-agent, has been widely used in various fields in recent years. With the exponential growth of scale for DCOP, supercomputers have become the primary choice to cope with large-scale DCOP due to the storage and computing capacity of traditional computers. Nowadays, the common way to solve DCOP is to calculate the operating parameters by users who masters the domain knowledge and provide them to the supercomputing platform, which time-consuming and labor-intensive. So automatically provided accurate operating parameters for DCOPs can improve the operation speed and enables the rational use of computational resources.

The prediction of DCOP hyper-parameters is difficulty. First, DCOP involves many hyper-parameters, such as the DCOP algorithm and the corresponding parameters, the graph partitioning algorithm. Second, correlation exists between hyper-parameters of DCOP. The performance under a single optimal parameter do not guarantee the overall optimal.

The multiply hyper-parameter prediction of DCOP can be simply considered as a multi-label recognition problem [3, 10]. However, the data of both image [4,5,6,7,8,9] and text problem are [11,12,13,14] regular, while the graph representation of DCOP is irregular data, so it is not possible to directly apply the present multi-label classification methods to the prediction for the hyper-parameter set of DCOP.

This paper addresses the difficulties of DCOP multiply hyper-parameter prediction and proposes a multiply hyper-parameter prediction framework combining graph neural network and recurrent neural network, whose contributions include the following:

(1) As there is no research on multi-parameter prediction for DCOPs, this paper gives the basic definition of the optimal parameter set and turns the DCOP multiply hyper-parameter prediction problem into a multi-label classification problem.

(2) For the multiply hyper-parameter prediction problem, this paper proposes a GRNN (Graph Recurrent Neural Networks) frameworks combining graph neural networks and recurrent neural networks, which considering the correlation of each parameter. The framework learned the features of the DCOP constraint graph by graph neural networks and handled the higher order parameter correlations by recurrent neural network.

(3) The extraction accuracy of graph feature vectors can affect the prediction accuracy of multiply hyper-parameter. This paper explores the influence on the number of layers of the graph neural network.

This paper is organized as follows: Sect. 2 introduces the basic theory of DCOP multiply hyper-parameter prediction and transforms the DCOP multiply hyper-parameter prediction problem into a multi-label classification problem, Sect. 3 introduces the multiply hyper-parameter prediction framework--- GRNN in detail, Sect. 4 analyzes the experimental results and discusses the experimental results and summarizes in Sect. 5.

2 Background

The performance of DCOP on supercomputing platforms are often associated with multiply hyper-parameter, such as graph partitioning algorithm [15], the DCOP algorithm, and the parameters corresponding to that algorithm. Before to predict the optimal hyper-parameter set, the definition of the optimal set of parameters \({OPT}_{para}\) is given.

2.1 Definition of Optimal Set of Parameters

Given an DCOP instant and the overall sets of parameters for the instance \(P_{para} = \{ Para_{1} ,Para_{2} , \ldots ,Para_{N} \}\). For each set of parameters \({Para}_{i}\), which includes the execution method \({E}_{m}\), the algorithm \(A\) and the parameters corresponding to that algorithm \(P_{A} = \{ P_{{A_{1} }} ,P_{{A_{2} }} , \ldots ,P_{{A_{f} }} \}\), the graph partitioning algorithm \({G}_{p}\) and the number of cores \(k\), where \(Para_{i} = [E_{m} ,\left\{ {P_{{A_{1} }} ,P_{{A_{2} }} , \ldots ,P_{{A_{f} }} } \right\},G_{p} ,k]\). The goal for this paper is to search the optimal set of parameters \({Para}_{opt}\) with the minimization completion time.

Firstly, we give a definition for the completion time of any instance under the set of parameters \({Para}_{i}\). If the \({Para}_{i}\) is selected, the instance implement the graph partitioning algorithm \({G}_{p}\) to divide the DCOP's constrained graph into \(k\) parts and call the DCOP algorithm \(A\) and the parameters under the algorithm \(A\) to run the instance (synchronously or asynchronously) on \(k\) processes for a total of \(n\) rounds. Define the effective running time of the \(i\_th\) round under the parameter \({Para}_{i}\) to be \({t}_{{pi}_{j}}\), which is the time for the cost function of DCOP to reach 0. This paper assumes that each instance of DCOP is solvable, i.e., there exists an effective time for the cost function to reach 0.

As the law of large numbers (LLN) in probability theory, where the average obtained from multiple experiments should be close to the expectation when performing the same experiment with multiple times, and the average will be closer to the expectation as the number of experiments increases. So, in this chapter, the completion time of any instance under the set of parameters is defined as the average completion time.

$${t}_{pi}=\frac{\sum_{j=1}^{n}{t}_{{pi}_{j}}}{n}$$
(1)

where \({t}_{pi}\) is the completion time of the \(j\_th\) round of DCOP under the parameter set \({Para}_{i}\) and \(n\) is the total number of rounds run.

when the completion time of any instance under the set of parameters is defined then this paper defines the optimal set of parameters as follows:

$${Para}_{opt}=argmin({t}_{p1},{t}_{p2},\dots ,{t}_{pN})$$
(2)

where N is the total capacity of the parameters \({P}_{para}\).

2.2 Comparison with Different Sets of Parameters

This paper introduces a small example, graph coloring problem, to compute \({Para}_{opt}\), and gives a representation of the completion time under different parameters sets. The example divides the constrained graph of DCOP into 1–4 subgraphs by the Giran-Newman algorithm or the METIS algorithm for graph partitioning. Each subgraph is then placed on the corresponding core to implement using the DCOP algorithm (DSA) either synchronously or asynchronously.

The result under some sets of parameters is showed in Fig. 1, which the example contains a total of 6 cases, and 10 rounds are executed for each set of parameters. The completion time is calculated by Eq. (2) and the optimal parameter for this example is obtained from Eq. (2) which is \({P}_{para}=\{\mathrm{sy},\mathrm{Giran}-\mathrm{Newman},\mathrm{DSA},\mathrm{p}=0.7, 3\}\).

Fig. 1.
figure 1

The completion time under sets of parameters for graph coloring problem

Full size image

As shown in Fig. 1, the results under different sets of parameters are different and irregular, thus it hard to find the optimal parameters according to the traditional statistical methods. With the rapid development of neural networks, the multi-label classification solution problem has matured. In this paper, we will transform the multiply hyper-parameter prediction problem into a multi-label classification problem which using the optimal parameters as labels.

This paper gives the definition of multiply hyper-parameter prediction. For Each DCOP instance \({G}_{i}\in {R}_{m}\), which owns \(L\) subsets \(y\) in the parameter label space \(Y\). The multi-parameter prediction task is to learn a function $h: \({h: R}_{m}\to 2{Y}^{D}=\{({x}_{i},{y}_{i})|1\le \mathrm{i}\le \mathrm{N}\}\), where \(\mathrm{N}\) is the total amount of training data, \({x}_{i}\) is the vector in the input feature \({R}_{m}\) of the \(i\_th\) instance and \({y}_{i}\subset Y\) is a subset of the label space \(Y\). Unlike the multiclassification problem where each instance is assigned only one label, the generalization of the multilabel problem provides multiple label assignments for each instance at the same time.

3 Multiply Hyper-parameter Prediction Model

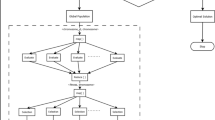
In this section, a neural network framework---GRNN is proposed to predict the multiply hyper-parameters set, as shown in Fig. 2. The framework consists of three modules, the preprocessing module, the graph representations feature extraction module, and the multilabel prediction module. The preprocessing module converts the DCOP into a graph representation and extract the fixed-length feature vectors by the graph representations feature extraction module. Then, according to these feature vectors, the higher-order correlations between parameters are modeled in the multi-parameter prediction module.

Fig. 2.
figure 2

Multiply hyper-parameter Prediction Framework Diagram

Full size image

3.1 Preprocessing Module

The DCOP cannot be solved directly in a graph neural network, [1, 2, 17] it needs to convert the DCOP into a graph representation. Since this paper may involve multiple graph representations, where different algorithms correspond to different graph representations. To ensure consistency, this paper uniformly converts the DCOP into a constraint graph.

3.2 Graph Feature Extraction Module

For the feature vector extraction of the DCOP, the GraphSNN is chosen in this paper. This network maps the local structure into the aggregation, considering not only the features of the neighbors but also the overlapping subgraphs. The feature extraction of DCOP includes node feature extraction as well as graph feature extraction.

3.2.1 Node Feature Extraction

Regarding node feature extraction, to better describe the neighborhood relationship between vertex \(v\) and its neighbors \(u\), GraphSNN defines structural coefficients \(\omega ({S}_{v},{S}_{uv})\) for each vertex \(v\), \(\omega :S\times {S}^{*}\to R\).

$$\omega \left({S}_{v},{S}_{uv}\right)=\frac{|{E}_{vu}|}{{(|V}_{vu}|{|V}_{vu}-1|){{|V}_{vu}|}^{\lambda }}$$
(3)

where \(\omega ({S}_{v},{S}_{uv})\) is the structure coefficient of vertex \(v\) and its neighbors. \({S}_{v}\) is the neighborhood subgraph of vertex \(v\) and \({S}_{uv}\) is the set of overlapping subgraphs of vertex \(v\) with \(\lambda >0\). \(\omega \left({S}_{v},{S}_{uv}\right)\) satisfies the properties of local compactness, local denseness, and isomorphism invariance. Let its adjacency matrix be \(A={({A}_{uv})}_{uv\in V}\), where \({A}_{uv}= \omega \left({S}_{v},{S}_{uv}\right)\).

GraphSNN also defines a weighted adjacency matrix A = \(\stackrel{-}{{({A}_{uv})}_{uv\in V}}\), where \(\overline{{A }_{uv}}\) is the normalized value of \({A}_{uv}\), \(\overline{{A }_{uv}}=\frac{{A}_{uv}}{{\sum }_{u\in N(v)}{A}_{uv}}\). So, the node eigenvectors of \(v\) are updated as

$${m}_{a}^{t}={\mathrm{Aggregate}}^{N}(\{{A}_{vu}{,h}_{u}^{t})|u\in N(v)$$
$${m}_{v}^{t}={\mathrm{Aggregate}}^{I}({A}_{vu}|u\in N\left(v\right)){h}_{v}^{t}$$
(4)
$${h}_{t+1}^{v}=Combine({m}_{v}^{t}{,m}_{a}^{t})$$

\({\mathrm{Aggregate}}^{N}(*)\) and \({\mathrm{Aggregate}}^{I}(*)\) are two different parameterized cumulative functions. Where \({m}_{a}^{t}\) is the information aggregated from the neighbors \(v\) and their structural coefficients, \({m}_{v}^{t}\) after performing the multiplication between the cumulative function \({\mathrm{Aggregate}}^{I}(*)\) and the multiplication between the eigenvectors, the “adjusted” message from \(v\) to account for the structural effects of its neighbors.

Specifically, the update function of GraphSNN for each vertex \(v\in V\), whose node feature vector at \(t+1\) layer is

$${h}_{v}^{t+1}={MLP}_{\theta }{\gamma }^{t}({\sum }_{v\in N\left(u\right)}{A}_{uv}+1){h}_{v}^{t}{\sum }_{u\in N\left(v\right)}{A}_{uv}+1){h}_{u}^{t})$$
(6)

where \({\gamma }^{t}\) is a scalar parameter that can be learned. \(N\left(v\right)\) refers to the one-hop neighbors \(v\), and multiple layers can be stacked to handle more than one-hop neighbors. Note that to ensure the Monolicity of feature aggregation in the presence of structural coefficients, add 1 to the first and second terms of Eq. (6).

3.2.2 Graph Feature Extraction

For the graph classification problem, all node features in the graph need to be transformed into graph features, and the whole graph is represented as \({h}_{G}\).

$${h}_{G}=Readout({h}^{k}|v\in G)$$
(7)

where \({h}_{G}\) is the graph G denotes the vector and Readout denotes the substitution invariant function, which can also be a graph-level pooling function.

The Readout function of the GraphSNN framework is single-shot. To consider all the structural information, the GraphSNN framework utilizes the information from all iterations of the model and uses an architecture similar to Jumping Knowledge Networks. The graphs represent connections in all iterations/layers and the \(Readout\) function sums all node features from the same iteration.

$${h}_{G}=Concat({\sum }_{u\in N\left(v\right)}{h}_{v}^{k}|k=\mathrm{0,1},\dots ,K)$$
(8)

3.3 Hyper-parameter Prediction Module

After graphSNN obtains the representation graph vector of DCOP, the parameter prediction module uses the output graph vector of graphSNN as the initial state input for label prediction. Because there is some correlation before the parameters, for this reason LSTM is chosen in this paper to predict multiple parameters.

Despite the existence of several LSTM variants, this paper selects the standard LSTM, and applies an additional word embedding layer for the labels. The LSTM consists of three gates: an input gate \(i\), an output gate \(o\), and a forgetting gate \(f\). The three gates work in concert to control what is read on the input, what is output, and what is forgotten, allowing some complex long-term relationships to be modeled.

$$\begin{array}{*{20}l} {i = \sigma (W^{\left( i \right)} x_{t} + U^{\left( i \right)} h_{t - 1} + b^{\left( i \right)} )} \hfill \\ {o = \sigma (W^{\left( o \right)} x_{t} + U^{\left( o \right)} h_{t - 1} + b^{\left( o \right)} )} \hfill \\ {f = \sigma (W^{\left( f \right)} x_{t} + U^{\left( f \right)} h_{t - 1} + b^{\left( f \right)} )} \hfill \\ {u = tanh(W^{\left( u \right)} x_{t} + U^{\left( u \right)} h_{t - 1} + b^{\left( u \right)} )} \hfill \\ {c_{t} = i \odot u + f \odot c_{t - 1} } \hfill \\ {h_{t} = o \odot {\text{tanh}}(c_{t} )} \hfill \\ \end{array}$$
(9)

where \(\sigma (*)\) denotes element-by-element multiplication, which is a sigmoid function. \({x}_{t}\in {R}_{d}\) is the input of the lower layer at time step t. If the lower layer is a word embedding of parameters, then d can be the dimension of the labeled word vector or can be the hidden state dimension of the lower layer, if the lower layer is an LSTM. If there are \(q\) LSTM units, then for all types \(\left(i,o,f,u\right),{h}_{t}\in {R}_{q},W\left(*\right)\in {R}_{q}\times d\) and \(b(*)\in {R}_{q}\).The memory cell \({c}_{t}\) is the key in the LSTM, which maintains long-term dependencies while getting rid of the gradient disappearance/explosion problem. The forget gate \(f\) is used to erase some parts of the memory cell, while the input gate \(i\) and the output gate \(o\) control what is read from and written to the memory cell.

LSTM by linear transformation as Eq. (9) in each type \(\left(i,o,f,u\right)\) with additional terms\(W\left(T\right)T\), where \(T\) is the output constraint graph feature from GNN with fixed dimension\(t\), \(W\left(T\right)\in {R}_{q}\times t\), \(q\) is the hidden dimension of LSTM, e.g. input The formula for the gate reads.

$$i=\sigma ({W}^{\left(i\right)}{x}_{t}+{U}^{\left(i\right)}{h}_{t-1}+W\left(T\right)T)$$
(10)

The label sequence prediction always starts with the tag < START >. At each time step, there is a SoftMax layer on top of the LSTM top layer. The probability of each label is calculated by first applying a linear transformation to the hidden state of the top LSTM layer.

Then, the tag with the highest probability is predicted. The prediction of the tag ends with the < END > tag. Therefore, for each input DCOP, a sequence of labels of different lengths is predicted. Ideally, the label sequence for each input DCOP matches exactly with the subset of labels belonging to that input DCOP.

4 Experimental Results and Analysis

4.1 Experimental Data

In the paper, we choose the graph coloring problem, a typical model of DCOP, to generate the corresponding dataset of this experiment. The datasets consist of two main parts, one part is the description of the DCOP and the corresponding constraint graph, and the other part is the label set which correspond to the multiply hyper-parameter. In this chapter, these two parts are introduced separately.

4.1.1 DCOP Problem Description

The graph coloring problem is a typical DCOP that has been widely used in coordination algorithms for sensor networks as well as benchmark, and many DCOP algorithms have also used it for performance comparisons.

In the distributed graph coloring problem, variables are located at the nodes of the constraint graph and choose a color (i.e., \({x}_{i }\in (1,...,\mathrm{c})\) to avoid conflicts (i.e., choosing the same color) with other variables(nodes) connected to themselves through edges. Thus, the cost of each variable is expressed as

$$U_{m} \left( {x_{m} } \right) = \gamma_{m} \left( {x_{m} } \right) - \sum\nolimits_{{i \in \frac{N(m)}{m}}} x_{i} \otimes x_{j}$$
(11)

where, \(x_{i} \otimes x_{j} = \left\{ {\begin{array}{*{20}l} {10} \hfill & {if\,x_{i} = = x_{j} } \hfill \\ 0 \hfill & {otherwise} \hfill \\ \end{array} } \right.\), \({\gamma }_{m}\left({x}_{m}\right)\ll 1\), reflecting the preference of the variable for any color in the absence of conflict. Consistent with the DCOP definition, the goal is to find the state of each variable that minimizes the conflict. In this experiment, this paper sets \({\gamma }_{m}\left({x}_{m}\right)=0\) and sets the edge conflict cost, i.e., two nodes with edges in the constraint graph choose the same color, \(x_{i} \otimes x_{j} = 10\).

4.1.2 Random Graph Generation Based on Graph Coloring DCOP

In this experiment, three kinds of undirected, unweighted and connected random graphs are generated by network further four datasets are selected which cover the basic random graphs, etc.

  1. 1)

    dataset contains 438 random graph instances of 11 colors generated by the Erdős - Rényi model, which 316 instances are generated by the gnm function with 200 nodes and 200–400 edges, and 122 instances are generated by the gnp function with an link probability from 0.1–0.2.

  2. 2)

    The second dataset has 29 instances of 11-color random graph coloring, which consists of instances generated by the Small wolrd model.

  3. 3)

    The third dataset has 100 instances of 11-color random graph coloring. The instances are generated by the Barabasi Albert model. The random graph degree generated by this model has a power-law distribution.

  4. 4)

    The fourth dataset are assembled the above three datasets.

4.1.3 Hyper-parameter Set Generation and Validity

Since the goal of this paper is to find the set of optimal hyper-parameters, and the framework is a supervised learning framework, this section starts by labeling each random graph with the original label. To ensure the accuracy of the prediction, this chapter needs to ensure the validity of the labels and that the initial assignment is robust. To verify the validity of the framework, this paper selected DCOP algorithms such as DSA, MGM, etc., and the Giran- Newman algorithm as well as the METIS graph partitioning algorithm.

To ensure the validity of the labels, this paper conducts 10 trials for each set of hyper-parameters and hopes that the results of each set of hyper-parameters on experiments are stable, i.e., the variance is not large. In this paper, we analyze the results of each set of hyper-parameters as shown in Fig. 3.

From Fig. 3, we finds that the variance of the fitted curve coefficients is low, about 0.26 times the mean. The expected time can be considered as the label of the constrained graph.

Fig. 3.
figure 3

The relationship between expected running time and variance

Full size image

For the label distribution, we run multiple DCOP problems in this paper and find a more uniform parameter distribution, as shown in Fig. 4. The figure shows the optimal parameter distribution of the dataset \({\mathrm{DCOP}}_{\mathrm{BA}}\) after multiple rounds of experiments.

Fig. 4.
figure 4

The distribution for BA parameter

Full size image

4.1.4 Dataset Description

For this purpose, the structural information of the four datasets trained and the labeling information are described in this paper as follows, as shown in the Table 1, Where \({\mathrm{DCOP}}_{\mathrm{ER}}\) is dataset 1, a random graph generated for the Erdős - Rényi model, \({\mathrm{DCOP}}_{\mathrm{BA}}\) is dataset 2, a random graph generated by the Barabasi Albert model, \({\mathrm{DCOP}}_{\mathrm{SW}}\) is dataset 3, a random graph instance generated for the SW model, \({\mathrm{DCOP}}_{\mathrm{ALL}}\) is data set 4, which is the merge of the above four data sets.

Table 1. Dataset description
Full size table

4.2 Experimental Results and Analysis

4.2.1 Evaluation Index

To fairly compare the results of other methods, the average precision (CP) is reported in this section for performance evaluation.

$$CP=\frac{1}{c}{\sum }_{i}\frac{{N}_{i}^{c}}{{N}_{i}^{p}}$$
(12)

4.2.2 Parameter Setting and Running Platform

All experiments were performed on a server with an Intel Xeon CPU 4110 equipped with 20 2.20 GHz cores. The system was Linux 3.10.0 and all DCOPs were implemented in the PyDCOP library. All multiclassification graph neural networks were implemented in pytorch.

This paper uses the Adam optimizer [16] with λ = 1. For all datasets of DCOP, the model was trained for 500 periods with a learning rate of 0.01, a loss rate of 0.5, a hidden layer of 256, and γ = 0.1. This chapter select the random division method, i.e., the graph is randomly divided into 60\%, 20\% and 20\% for training, validation, and testing.

4.2.3 Analysis of Experimental Results

Since this paper is required to calculate the optimal parameters, in order to verify the effectiveness of the algorithm, two common methods are compared: 1) ordinary dichotomous GNN, i.e., GNN is used to generate the graph features of the DCOP constraint graph, for each label, which is treated as a one-by-one dichotomous classification in this chapter. (2) Since this paper does not involve many parameters, the multi-classification method graphSNN is chosen as a comparison experiment. Since the parameters involved in this chapter are less, the method converts the multi-parameter prediction into a multi- classification method and puts it into the graphSNN network. The results are shown in Table 2.

Table 2. The accuracy for the prediction
Full size table

Table 2 lists the accuracy results of multiply hyper-parameters prediction for different datasets. The results show that the accuracy of both the multiclassification algorithm---GraphSNN and the GRNN algorithm on all the datasets is higher than that of the ordinary binary classification algorithm GNN. For the GraphSNN algorithm and GRNN algorithm, the accuracy of the recurrent neural network does not play a larger role when there are few labels, and its accuracy is not as good as that of the GraphSNN, and its ER dataset and WS dataset both perform less well than the GraphSNN when there are only three labels. In the ER dataset, the accuracy of GraphSNN is 10.7% higher than that of GRNN method, and in the SW dataset, the accuracy is 5.8% higher. However, the accuracy of GRNN improves as the number of labels increases, and it improves by 27.54% in the BA dataset and 14% in the total dataset compared to the GraphSNN.

4.2.4 The Effect of Graph Neural Network Depth on Performance

The exaction of graph features is one of the most important factors affecting multi- parameter prediction, and different graph neural network embedding operations have an impact on the performance of experimental results. Specifically, different layers of graph neural networks have different obtained graph features. For this reason, this section explores the effect of different neural network layers on the prediction results, as shown in the Table 3.

Table 3. The accuracy on different neural network layers
Full size table

It finds that the accuracy of the prediction results to decrease to some extent when increasing the number of layers of the convolutional layers. The possible reasons for this are mainly due to the following two points. One is that the number of parameters will also become dramatically larger due to the increase in the number of layers of the convolution of the graph which will cause the overfitting phenomenon to some extent. Second, although the method in this paper greatly alleviates the over-smoothing problem, but it does not avoid the over-smoothing problem, and the deepening of the convolutional layer will add the over-smoothing problem leads to performance degradation.

5 Summary

Multiply hyper-parameter prediction of DCOP is an important subject, and its high accuracy can be an effective guarantee of DCOP. This paper first demonstrates experimentally that DCOP has large differences in its operation results under multiple sets of parameters and that traditional methods cannot effectively predict multiple parameters accurately. Then transforms the multiply hyper-parameter prediction problem of DCOP into a multi-label prediction problem and proposes a novel neural network-based multi-label classification method. Experiments demonstrate the effectiveness of the methods from both qualitative and quantitative perspectives, respectively.

However, the GRNN is a supervised prediction models, which require multiple runs of DCOP to generate the corresponding training data, and the data acquisition cost is relatively expensive. In the future, we will learn new techniques such as semi-supervised graphical neural networks to solve the problem.