Keywords

1 Introduction

Kalman filter algorithm is a common state estimation method. This method has been widely concerned and applied since it was put forward in the 1960s. Its feature is that it can predict the estimated value of the next moment or even the next moment according to the current data through iteration, so as to solve the dynamic target estimation problem with interference [1]. In addition, Kalman filter has also been widely applied in the engineering field, such as integrated navigation [2,3,4], target tracking [5, 6], fault diagnosis and detection [7, 8]. At present, many improved Kalman filtering algorithms emerge in an endless stream. From the initial solution of linear system problems to the present solution of nonlinear system problems, simple classical Kalman filtering at the very beginning, Later, adaptive Kalman filtering with unknown noise statistics or model parameters and other uncertain information [9], self-correcting Kalman filtering [10, 11], robust Kalman filtering theory [12, 13] and so on. In recent years, with the development of fractional-order calculus theory, the filter problem of fractional-order system has gradually attracted people's attention. The state estimation of fractional-order system is a new idea and new direction of the development of the theory of state estimation, and also meets the actual production demand.

Fractional calculus was proposed by Leibniz and L'Hospital in 1965, and then Liouville and Riemann proposed the definition of fractional derivatives. However, it was initially studied only by engineers, and it was not until the late 1960s that fractional calculus was gradually developed, and it was discovered that fractional derivatives would allow more accurate descriptions of systems in simulation modeling or stability analysis. With the passing of time, the control system theory gradually develops, the traditional calculus theory is not enough to meet the needs of production and research. Fractional calculus became more active in the theory of control systems and played an indispensable role. Literature [14] and [15] proposed fractional Kalman filtering algorithm and extended fractional Kalman filtering algorithm, and analyzed specific cases to discuss the possibility of applying these algorithms to fractional system parameters and fractional estimation, and their algorithms have been applied to image processing, signal transmission and other fields [16, 17]. But compared with the traditional Kalman filter, its application is not so wide. At present, generalized fractional systems have been widely used in the fields of circuit [18, 19] and sensor fault estimation [20]. The fusion estimation problem of generalized fractional systems discussed in this paper has certain theoretical significance and potential application value.

In this paper, a typical fractional-order singular system is firstly transformed into two normal fractional-order subsystems by non-singular linear transformation method. Then, a fractional-order Kalman state filter with correlated noise subsystems is derived based on projective theory. For multi-sensor generalized fractional-order systems, the global optimal weighted observation fusion algorithm is applied to derive the optimal information fusion fractional-order Kalman filter, and the simulation results verify the effectiveness of the proposed algorithm.

2 Problem Formulation

Consider the following linear generalized fractional stochastic system

$$ M\Delta^\gamma x(k + 1) = \Phi x(k) + Bw(k) $$
(1)
$$ x(k) = \Delta^\gamma x(k) - \sum_{j = 1}^k {( - 1)^j \gamma_j x(k - j)} \, $$
(2)
$$ y(k) = Hx(k) + v(k) $$
(3)

where \(x(k + 1) \in R^n\) is the state of the system, \(\Phi \in R^{n \times n}\) is the target variance coefficient matrix, \(B \in R^{n \times r}\) is the target noise matrix, \(\Delta^\gamma\) is a fractional operator, \(\gamma\) is fractional order, \(H\) is the observation matrix of the observation equation, \(v(k)\) is the observed noise, \(M,H\) is the constant matrix of corresponding dimension.

Assumption 1:

\(M \in R^{n \times n}\) is a singular square matrix, means \({\text{rank}} M = n_1 < n\), \(\det M = 0\).

Assumption 2:

The system is regular, means \(\exists z \in C\), so \(\det (zM - \Phi ) \ne 0\).

Assumption 3:

\(w(k) \in R^r\) and \(v(k)\) are zero mean uncorrelated white noise:

$$ {\text{E}} \left\{ {\left[ \begin{gathered} w(k) \hfill \\ v(k) \hfill \\ \end{gathered} \right]\left[ {\begin{array}{*{20}c} {w^{\text{T}} (k)} & {v^{\text{T}} (k)} \\ \end{array} } \right]} \right\} = \left[ {\begin{array}{*{20}c} {Q_w } & 0 \\ 0 & {Q_v \delta_{ij} } \\ \end{array} } \right] $$
(4)

where \({\text{E}}\) is the expected value, \({\text{T}}\) is the transpose symbol.

Assumption 4:

The system is fully observable, So there's the matrix \(K\) that makes:

$$ rank\left[ {\begin{array}{*{20}c} {zM - (\Phi - KH)} \\ H \\ \end{array} } \right] = n_1 ,rank\left[ {\begin{array}{*{20}c} M \\ H \\ \end{array} } \right] = n $$
(5)

Assumption 4 leads to the existence of two non-singular square matrices \(R,W\) that make [77]

$$ \, RMW = \left[ {\begin{array}{*{20}c} {I_{n_1 } } & 0 \\ 0 & 0 \\ \end{array} } \right]{ , }R(\Phi - KH)W = \left[ {\begin{array}{*{20}c} {Y_1 } & 0 \\ 0 & {I_{n_2 } } \\ \end{array} } \right] $$
(6)

where \(n_1 + n_2 = n\).Introducing block matrix representation:

$$ RK = \left[ \begin{gathered} K_1 \hfill \\ K_2 \hfill \\ \end{gathered} \right],RB = \left[ \begin{gathered} B_1 \hfill \\ B_2 \hfill \\ \end{gathered} \right],HW = \left[ {H_1 \, H_2 } \right] $$
(7)

and introduce state:

$$ x(k) = W\left[ \begin{gathered} x_1 (k) \hfill \\ x_2 (k) \hfill \\ \end{gathered} \right] $$
(8)

where \(x_1 (k) \in R_{n_1 } ,x_2 (k) \in R_{n_2 }\).

Equation (3) is multiplied by \(K\) and subtracted by Eq. (1)

$$ M\Delta^\gamma x(k + 1) = (W - KH)x(k) + Ky(k) + \overline{w}(k) $$
(9)
$$ \overline{w}(k) = Bw(k) - Kv(k) $$
(10)

\(P\) is left multiplied by formula (9), and formula (6)–(8) is used to derive the observable model as follows:

$$ \left[ {\begin{array}{*{20}c} {I_{n_1 } } & 0 \\ 0 & 0 \\ \end{array} } \right]\left[ \begin{gathered} \Delta^\gamma x_1 (k + 1) \hfill \\ \Delta^\gamma x_2 (k + 1) \hfill \\ \end{gathered} \right] = \left[ {\begin{array}{*{20}c} {Y_1 } & 0 \\ 0 & {I_{n_2 } } \\ \end{array} } \right]\left[ \begin{gathered} x_1 (k) \hfill \\ x_2 (k) \hfill \\ \end{gathered} \right] + \left[ \begin{gathered} \overline{K}_1 \hfill \\ \overline{K}_2 \hfill \\ \end{gathered} \right]y(k) + \left[ \begin{gathered} B_1 \hfill \\ B_2 \hfill \\ \end{gathered} \right]w(k) $$
(11)
$$ y(k) = \left[ {H_1 \, H_2 } \right]\left[ \begin{gathered} x_1 (k) \hfill \\ x_2 (k) \hfill \\ \end{gathered} \right] + v(k) $$
(12)

This leads to two reduced order subsystems:

$$ \Delta^\gamma x_1 (k + 1) = Y_1 x_1 (k) + \overline{K}_1 y(k) + B_1 w(k) $$
(13)
$$ x_2 (k) = - \overline{K}_2 y(k) - B_2 w(k) $$
(14)
$$ y(k) = H_1 x_1 (k) + H_2 x_2 (k) + v(k) $$
(15)

by substituting Eq. (14) into Eq. (15), a subsystem with different local dynamic transformation types and the same local state \(x_1 (k)\) is derived:

$$ \Delta^\gamma x_1 (k + 1) = Y_1 x_1 (k) + \overline{K}_1 y(k) + B_1 w(k) $$
(16)
$$ z(k) = H_1 x_1 (k) + \tau (k) $$
(17)

therein defined:

$$ z(k) = (I_m + K_2 H_2 )y(k) $$
(18)
$$ \tau (k) = v(k) - H_2 B_2 w(k) $$
(19)

from (17), (18)

$$ y(k) = (I_m + \overline{K}_2 H_2 )^{ - 1} \left[ {H_1 x_1 (k) + \tau (k)} \right] $$
(20)

for the transformed conventional subsystem (16), if a non-zero term is added to the right side and substituted into formula (20), it can be obtained:

$$ \begin{aligned} \Delta^\gamma x_1 (k + 1) = & Y_1 x_1 (k) + \overline{K}_1 (I_m + \overline{K}_2 H_2 )^{ - 1} \times \left[ {H_1 x_1 (k) + \tau (k)} \right] + B_1 w(k) + \\ & \quad \quad \quad \;\Lambda \left[ {z(k) - H_1 x_1 (k) - \tau (k)} \right] \\ & \quad = \left[ {Y_1 + \overline{K}_1 (I_m + \overline{K}_2 H_2 )^{ - 1} H_1 - \Lambda H_1 } \right]x_1 (k) + \\ & \Lambda z(k) + \left[ {\overline{K}_1 (I_m + \overline{K}_2 H_2 )^{ - 1} \tau (k) + B_1 w(k) - \Lambda \tau (k)} \right] \\ \end{aligned} $$
(21)

where \(\Lambda\) is the undetermined matrix and can be set:

$$ \Phi_1 = Y_1 + \overline{K}_1 (I_m + \overline{K}_2 H_2 )^{ - 1} H_1 - \Lambda H_1 $$
(22)
$$ \phi (k) = \overline{K}_1 (I_m + \overline{K}_2 H_2 )^{ - 1} \tau (k) + B_1 w(k) - \Lambda \tau (k) $$
(23)

Then equation of state (21) can be reduced to

$$ \Delta^\gamma x_1 (k + 1) = \Phi_1 x_1 (k) + \Lambda z(k) + \phi (k) $$
(24)

However, the observation equation is still Eq. (17). According to assumption 3, we can know:

$$ E\left[ {\phi (k)} \right] = 0 $$

then have

$$ \begin{aligned} & E\left[ {\phi (k)\tau^T (j)} \right] = E[\overline{K}_1 (I_m + \overline{K}_{2} H_{2} )^{ - 1} \tau (k) + B_1 w(k) - \Lambda \tau (k)] \\ & \quad \quad = \overline{K}_1 (I_m + \overline{K}_2 H_2 )^{ - 1} Q_\tau + E\left[ {B_1 w(k)\tau^T (j)} \right] - \Lambda Q_\tau \\ & \quad \quad = \overline{K}_1 (I_m + \overline{K}_2 H_2 )^{ - 1} Q_\tau - B_1 Q_w (H_2 B_2 )^T - \Lambda Q_\tau \\ \end{aligned} $$
(25)

and \(Q_\tau\) is the reciprocal covariance matrix of \(\tau (k)\):

$$ Q_\tau = E\left[ {\tau (k)\tau^T (j)} \right] = Q{\,}_v + H_2 B_2 Q{\,}_w(H_2 B_2 )^T $$
(26)

so you can take the undetermined matrix

$$ \Lambda = \left[ {\overline{K}_1 (I_m + \overline{K}_2 H_2 )^{ - 1} Q_\tau - B_1 Q_w (H_2 B_2 )^T } \right]Q_\tau^{ - 1} $$
(27)

therefore, there is \(E\left[ {\phi (k)\tau^T (j)} \right] = 0\), that is, \(\phi (k)\) is unrelated to \(\tau (j)\), and the auto-covariance matrix of \(\phi (k)\) is easily obtained:

$$ \begin{gathered} E\left[ {\phi (k)\phi_{\,}^{\text{T}} (j)} \right] = \overline{K}_1 (I_m + \overline{K}_2 H_2 )^{ - 1} Q_\tau \times \left[ {\overline{K}_1 (I_m + \overline{K}_2 H_2 )^{ - 1} } \right]^T \hfill \\ \, + B_1 Q_w B_1^{\text{T}} + \Lambda Q_\tau \Lambda^{\text{T}} \hfill \\ \end{gathered} $$
(28)

substitute into Eq. (27) to get

$$ \begin{aligned} & E\left[ {\phi_{\,} (k)\phi_{\,}^T (j)} \right] = \overline{K}_1 (I_m + \overline{K}_2 H_2 )^{ - 1} Q_\tau \times \left[ {\overline{K}_1 (I_m + \overline{K}_2 H_2 )^{ - 1} } \right]^T + B_1 Q_w B_1^{\text{T}} + \\ & \quad \quad \quad \left[ {\overline{K}_1 (I_m + \overline{K}_2 H_2 )^{ - 1} Q_\tau - B_1 Q_w (H_2 B_2 )^T } \right] \\ & \quad \quad \quad \times \left\{ {\left[ {\overline{K}_1 (I_m + \overline{K}_2 H_2 )^{ - 1} Q_\tau - B_1 Q_w (H_2 B_2 )^T } \right]Q_\tau^{ - 1} } \right\}^T \\ \end{aligned} $$
(29)

So \(\phi (k)\) has zero mean white noise, and the variance is

$$ \begin{aligned} & Q_\phi = \overline{K}_1 (I_m + \overline{K}_2 H_2 )^{ - 1} Q_\tau \left[ {\overline{K}_1 (I_m + \overline{K}_2 H_2 )^{ - 1} } \right]^T + B_1 Q_w B_1^{\text{T}} \\ & \quad \quad \quad + [\overline{K}_1 (I_m + \overline{K}_2 H_2 )^{ - 1} Q_\tau - B_1 Q_w (H_2 B_2 )^T ] \times \\ & \quad \left\{ {\left[ {\overline{K}_1 (I_m + \overline{K}_2 H_2 )^{ - 1} Q_\tau - B_1 Q_w (H_2 B_2 )^T } \right]Q_\tau^{ - 1} } \right\}^T \\ \end{aligned} $$
(30)

which is independent of white noise \(\tau (k)\).Generalized fractional filtering problem is to calculate the minimum variance estimation \(\hat{x}(\left. k \right|k)\) of state \(x(k)\) based on the observed value \(y(1), \cdots ,y(k)\) of data obtained by multiple sensors.

3 Kalman Filter for Single Sensor Generalized Fractional Order System

Theorem 1 For the observable singular system (1)–(3), under hypothesis 1-(4), the reduced-order subsystem (17) and (24) has a local recursive fractional Kalman filter of \(x_1 (k)\).

$$ \hat{x}_1 (k|k) = \hat{x}_1 (k|k - 1) + K_1 (k)[z(k) - H_1 \hat{x}_1 (k|k - 1)] $$
(31)
$$ \Delta^\gamma \hat{x}_1 (k|k - 1) = \Phi_1 \hat{x}_1 (k - 1|k - 1) + \Lambda z(k - 1) $$
(32)
$$ \hat{x}_1 (k|k - 1) = \Delta^\gamma \hat{x}_1 (k|k - 1) - \sum_{j = 1}^k {( - 1)^j \gamma_j \hat{x}_1 (k - j|k - j)} $$
(33)
$$ P_1 (k|k - 1) = (\Phi_1 + \gamma_1 )P{\,}_1(k - 1|k - 1) \times (\Phi_1 + \gamma_1 )^{\rm T} + \sum_{j = 2}^k {\gamma_j P_1 (k - j|k - j)\gamma_j^{\rm T} } + Q_\phi $$
(34)
$$ P_1 (k|k) = (I_n - K_1 (k)H_1 )P_1 (k|k - 1) $$
(35)
$$ K_1 (k) = P_1 (k|k - 1)H_1^{\rm T} \times \left[ {H_1 P_1 (k|k - 1)H_1^{\rm T} + Q_\eta } \right]^{ - 1} $$
(36)

put in the initial value \(\hat{x}_1 (0|0) = \rho_{01} ,P_1 (0|0) = P_{01}\).

Proof:

It can be obtained from literature [13] that

$$ \begin{gathered} \hat{x}_1 (k|k - 1) = {\text{proj}} (x_1 (k)|z(1), \cdots ,z(k - 1)) = {\text{proj}} [\Phi_1 x_1 (k - 1) + \Lambda z(k - 1) + \phi (k - 1) - \hfill \\ \sum_{j = 1}^k {( - 1)^j \gamma_j x_1 (k - j)|z(1), \cdots ,z(k - 1)} ] = \Phi_1 {\text{proj}} [x_1 (k - 1)|z(1), \cdots ,z(k - 1)] + \hfill \\ \Lambda {\text{proj}} [z(k - 1)|z(1), \cdots ,z(k - 1)] - \sum_{j = 1}^k {( - 1)^j \gamma_j {\text{proj}} [x_1 (k - j)|z(1), \cdots ,} z(k - 1)] \hfill \\ \end{gathered} $$
(37)

available at this time

$$ \hat{x}_1 (k|k - 1) = \Phi_1 \hat{x}_1 (k - 1|k - 1) + \Lambda z(k - 1) - \sum_{j = 1}^k {( - 1)^j \gamma_j \hat{x}_1 (k - j|k - j)} $$
(38)

So we get (32) and (33) easily.

According to literature [13], the one-step optimal linear prediction \(\hat{z}(\left. k \right|k - 1)\) of \(z(k)\) can be obtained, i.e.

$$ \begin{aligned} \hat{z}(k|k - 1) & \; = {\text{proj}} [z(k)|z(1), \cdots ,z(k - 1)] \\ & = {\text{proj}} [H_1 x_1 (k) + \tau (k)|z(1), \cdots ,z(k - 1)] \\ & = H_1 \hat{x}_1 (k|k - 1) \\ \end{aligned} $$
(39)

thus easy to obtain

$$ \hat{x}_1 (k|k) = \hat{x}_1 (k|k - 1) + K_1 (k)\varepsilon (k) $$
(40)

among them \(\varepsilon (k) = z(k) - \hat{z}(k|k - 1)\), \(K_1 (k) = E[x_1 (k)\varepsilon^{\rm T} (k)][E(\varepsilon (k)\varepsilon^{\rm T} (k)]^{ - 1}\) is called Kalman

filter gain. Define \(\tilde{x}_1 (k|k - 1) = x_1 (k) - \hat{x}_1 (k|k - 1)\), then \(E[x_1 (k)\varepsilon^T (k)] = E[(\hat{x}_1 (k|k - 1) + \tilde{x}_1 (k|k - 1))\).

\(\times (H_1 \tilde{x}_1 (k|k - 1) + \tau (k))^{\rm T} ]\), By projective orthogonality we have \(\hat{x}_1 (k|k - 1) \bot \tilde{x}_1 (k|k - 1)\), \(\tau (k) \bot \hat{x}_1 (k|k - 1)\), \(\tau (k) \bot \tilde{x}_1 (k|k - 1)\), then

$$ E[x_1 (k)\varepsilon^T (k)]{ = }P_1 (k|k - 1)\overline{H}^{\rm T} $$
(41)

In the same way, we can get

$$ E[\varepsilon (k)\varepsilon^T (k)] = E[(z(k) - \hat{z}(k|k - 1)) \times (z(k) - \hat{z}(k|k - 1))^{\rm T} ] = \overline{H}P_1 (k|k - 1)\overline{H}^{\rm T} + Q_\xi $$
(42)

where \(P_1 (k|k - 1) =\) \(E[(x_1 (k) - \hat{x}_1 (k|k - 1))(x_1 (k) -\) \(\hat{x}_1 (k|k - 1))^{\rm T} ]\) is the prediction error variance matrix.It can be obtained from (40) that

$$ \hat{x}_1 (k|k) = \hat{x}_1 (k|k - 1) + P_1 (k|k - 1)H_1^{\rm T} \times \left[ {H_1 P_1 (k|k - 1)H_1^{\rm T} + Q_\eta } \right]^{ - 1} \varepsilon (k) $$
(43)

\(K_1 (k) = P_1 (k|k - 1)H_1^{\rm T} [H_1 P_1 (k|k - 1) \times\)\(H_1^{\rm T} + Q_\eta ]^{ - 1}\) is denoted as the gain matrix of fractional Kalman filter, then formulas (31) and (36) can be obtained.

$$ \begin{gathered} \;\;x_1 (k) - \hat{x}_1 (k|k - 1) = \Phi_1 x_1 (k - 1) + \Lambda z(k - 1) + \phi (k - 1) - \sum_{j = 1}^k {\left[ {( - 1)^j \gamma_j x_1 (k - j)} \right]} \hfill \\ \;\;\;\;\; - \Phi_1 \hat{x}_1 (k - 1|k - 1) - \Lambda z(k - 1) + \sum_{j = 1}^k {\left[ {( - 1)^j \gamma_j \hat{x}_1 (k - j|k - j)} \right]} = (\Phi_1 + \gamma_1 ) \times \hfill \\ [x_1 (k - 1) - \hat{x}_1 (k - 1|k - 1)] - \sum_{j = 2}^k {( - 1)^j \gamma_j (x_1 (k - j) - \hat{x}_1 (k - j|k - j))} + \phi (k - 1) \hfill \\ \end{gathered} $$
(44)

where \(E[(x_{1m} - \hat{x}_{1\left. m \right|m - 1} )(x_{1n} - \hat{x}_{1\left. n \right|n - 1} )^T ] = 0\begin{array}{*{20}c} , & {m \ne n} \\ \end{array}\).It follows that:

$$ \begin{aligned} P_1 (k|k - 1) & = E[(x_1 (k) - \hat{x}_1 (k|k - 1)) \times (x_1 (k) - \hat{x}_1 (k|k - 1))^{\rm T} ] \\ & = (\Phi_1 + \gamma_1 )P_1 (k|k)(\Phi_1 + \gamma_1 )^{\rm T} + \sum_{j = 2}^k {\gamma_j P_1 (k - j|k - j)\gamma_j^{\rm T} } + Q_\phi \\ \end{aligned} $$
(45)

where, \(Q_\phi\) is the autocovariance matrix of \(\phi (k)\), which is given by Eq. (28) and can be proved by Eq. (34).

It can be obtained from Eqs. (17) and (31) that

$$ \begin{aligned} x_1 (k) - \hat{x}_1 (\left. k \right|k) & = x_1 (k) - \{ \hat{x}_1 (\left. k \right|k - 1) + K_1 (k) \times [z(k) - H_1 \hat{x}_1 (\left. k \right|k - 1)]\} \\ & = x_1 (k) - \hat{x}_1 (\left. k \right|k - 1) - K_1 (k) \times [H_1 x_1 (k) + \tau (k) - H_1 \hat{x}_1 (\left. k \right|k - 1)] \\ & = [I_n - K_1 (k)H_1 ](x_1 (k) - \hat{x}_1 (\left. k \right|k - 1)) - K_1 (k)\tau (k) \\ \end{aligned} $$
(46)
$$ \begin{aligned} P_1 (k|k) & = E[(x_1 (k) - \hat{x}_1 (k|k))(x_1 (k) - \hat{x}_1 (k|k))^{\rm T} ] \\ & = [I_n - K_1 (k)H_1 ]P_1 (k|k - 1) \times [I_n - K_1 (k)H_1 ]^{\rm T} + K_1 (k)Q_\tau K_1^{\rm T} (k) \\ & = (I_n - K_1 (k)H_1 )P_1 (k|k - 1) \\ \end{aligned} $$
(47)

Theorem 2:

Fractional subsystem 2 has a local recursive fractional Kalman filter under Eqs. (14) and (15).

$$ \hat{x}_2 (\left. k \right|k) = - (I + \overline{K}_2 H_2 )^{ - 1} \overline{K}_2 H_1 \hat{x}_1 (k|k) $$
(48)

Prove:

Applying theorem 1, it can be proved easily by Eqs. (14) and (15).

4 Observational Fusion Kalman Filter for Generalized Fractional-Order Systems

The observation fusion of generalized fractional order system is carried out for the normalized subsystem, so the normalized subsystem of multi-sensor generalized fractional order system is considered as follows.

$$ \Delta^\gamma x_1 (k + 1) = \Phi_1 x_1 (k) + \Lambda_i z_i (k) + \phi_i (k) $$
(49)
$$ z_i (k) = H_{1i} x_i (k) + \tau_i (k) $$
(50)
$$ z_i (k) = (I_m + \overline{K}_2 H_{2i} )y_i (k) $$
(51)
$$ \tau_i (k) = v_i (k) - H_{2i} B_2 w(k) $$
(52)
$$H_{1i} = G_i \overline{H}i = 1, \cdots ,L $$
(53)

where \(x_i (k) \in R^n\) is the state quantity and \(z_i (k) \in R^m\) is the observation of the ith sensor,\(\tau_i (k) \in R^{m_i }\) is observed noise, \(H_{1i} \in R^r\) is observed white noise,\(\Phi_1\)、\(\overline{K}_2\)、\(\overline{H}\) is a known constant matrix of appropriate dimension, and the observed matrix \(\overline{H}_i\) has the same \(m \times n\) dimensional right factor \(\overline{H}\),and

$$ \Delta^\gamma x_1 (k + 1) = \left[ {\begin{array}{*{20}c} {\Delta^\gamma x_{1i} (k + 1)} \\ \vdots \\ {\Delta^\gamma x_{1n} (k + 1)} \\ \end{array} } \right] $$

Assumption 5:

\(\phi_i (k) \in R^r\) and \(\tau_i (k) \in R^n\) are mutually independent white noises with zero mean and variance matrices \(Q_{\phi i}\) and \(Q_{\tau_i }\), respectively, and

$$ {\text{E}} \left\{ {\left[ \begin{gathered} \phi_i (k) \hfill \\ \tau_i (k) \hfill \\ \end{gathered} \right]\left[ {\phi_i^T (k) \, \tau_j^{\text{T}} (k)} \right]} \right\} = \left[ \begin{gathered} Q_{\phi i} \delta_{ij} { 0} \hfill \\ 0 \, Q_{\tau i} \delta_{ij} \hfill \\ \end{gathered} \right]\delta_{tk} $$
(53)

where \({\text{E}}\) is the mean symbol and \({\text{T}}\) is the transpose symbol,\(\delta_{tt} = 1\), \(\delta_{tk} = 0 \, (t \ne k)\)。

Assumption 6:

\((\Phi_1 \, H_{1i} )\) is a completely observable pair.

Assumption 7:

The matrix \(\sum_{i = 1}^L {[G_i^{\text{T}} R_{\xi i}^{ - 1} G_i ]^{ - 1} }\) is invertible.

The centralized fusion observation equation can be obtained from Eqs. (50)–(54) that

$$ z_0 (k) = H_0 x(k) + \tau_0 (k) $$
(55)
$$ z_0 (k) = [z_1^{\text{T}} (k), \cdots ,z_L^{\text{T}} (k)]^T $$
(56)
$$ H_0 = [H_0^{\text{T}} , \cdots ,H_L^{\text{T}} ]^T $$
(57)
$$ \tau_0 (k) = [\tau_1^{\text{T}} (k), \cdots \tau_L^{\text{T}} (k)]^T $$
(58)

The fused observation noise \(\tau_0 (k)\) has a variance matrix

$$ Q_{\tau_0 } = {\text{diag}} (Q_{\tau_1 } , \cdots ,Q_{\tau_L } ) $$
(59)

Equation (55) can be regarded as an observation model for \(H_1 x_1 (k)\), so the weighted least squares (WLS) method can be applied to estimate \(H_1 x_1 (k)\) as

$$ z(k) = \left[ {G_0^{\text{T}} Q_{\tau 0}^{ - 1} G_0 } \right]^{ - 1} G_0^{\text{T}} Q_{\tau 0}^{ - 1} z_0 (k) $$
(60)

The weighted observation fusion equation can be obtained by substituting Eq. (60) into (55)

$$ z(k) = H_1 x(k) + \tau (k) $$
(61)

And it has fused observation noise

$$ \tau (k) = \left[ {G_0^{ - 1} Q_{\tau_0 }^{ - 1} G_0 } \right]^{ - 1} G_0^{ - 1} Q_{\tau_0 }^{ - 1} \tau_0 (k) $$
(61)

It has the minimum error variance matrix

$$ Q_\tau = \left[ {G_0^{ - 1} Q_{\tau_0 }^{ - 1} G_0 } \right]^{ - 1} $$
(63)

5 Simulation Study

Generalized fractional systems have important applications in circuits[18, 19] and sensor fault estimation[20]. Here, the canonical form of a generalized fractional order circuit system is considered.

$$ \left[ {\begin{array}{*{20}c} 1 & 0 \\ 0 & 0 \\ \end{array} } \right]\left[ \begin{gathered} \Delta^\gamma x_1 (k + 1) \hfill \\ \Delta^\gamma x_2 (k + 1) \hfill \\ \end{gathered} \right] = \left[ {\begin{array}{*{20}c} {0.1} & 0 \\ 0 & 1 \\ \end{array} } \right]\left[ \begin{gathered} x_1 (k) \hfill \\ x_2 (k) \hfill \\ \end{gathered} \right] + \left[ {\begin{array}{*{20}c} 0 \\ 1 \\ \end{array} } \right]y(k) + \left[ {\begin{array}{*{20}c} 1 \\ 0 \\ \end{array} } \right]w(k) $$
(64)
$$ y(k) = \left[ {1{ 0}} \right]\left[ \begin{gathered} x_1 (k) \hfill \\ x_2 (k) \hfill \\ \end{gathered} \right] + v(k) $$
(65)

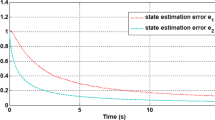
where \(w(k)\) and \(v(k)\) are uncorrelated white noise with zero mean andvariance \(Q = 0.01\) and \(Q_v = 0.02\),respectively,\(n_1 = 0.01\),the problem is to find a generalized fractional Kalman filter \(\hat{x}(k|k) = [\hat{x}_1 (k|k),\hat{x}_2 (k|k)]^{\rm T}\) for state \(x(k)\).The simulation results are shown in Fig. 1.

According to theorem 1, the model given above is simulated and analyzed. Figs. 1 and 2 show the filtering results of state values and estimated values of subsystem 1 and subsystem 2. As can be seen from the figure, the estimated value can almost keep up with its state truth value, which is comparable to the effect of Model II. The error is basically within 0.1, so it can be seen that the generalized fractional-order filtering algorithm is feasible. Of course, the effect can be improved by adjusting the parameters. Then, weighted observation fusion was explored for the above model, and simulation analysis was carried out. Based on (64) and (65), different local observation noise error variances were considered respectively as: \(Q_{v1} = 0.02\), \(Q_{v2} = 0.1\), \(Q_{v3} = 1\), As shown in Fig. 3, observation fusion is carried out on subsystem 1 after normalization, and curves of state truth value and observation estimation are made. By analogy with Fig. 1 of local valuation, there are obvious changes.

Fig. 1.
figure 1

Comparison of true and estimated values for Subsystem 1

Full size image
Fig. 2.
figure 2

Comparison between true value and estimated value of subsystem 2

Full size image
Fig. 3.
figure 3

Comparison of the state truth value of subsystem 1 with the weighted observation fusion estimate

Full size image

In order to further compare and analyze the estimation accuracy of local fusion, on the basis of (63) and (64), different local observation noise error variances are considered as: \(Q_{v1} = 0.02,\)\(Q_{v2} = 0.1,Q_{v3} = 1\),The comparison graph of mean square error obtained by 100-step Monte-Carlo simulation of the three fusion estimates is shown in Fig. 4. MSEm, MSCI123, MSEguance and MSEjizhong represent the mean square error curves of suboptimal weighted state fusion, SCI fusion, weighted observation fusion and centralized fusion, respectively. At \({\text{k = 60}}\),then

$$ \begin{gathered} {\text{MSEm}} = 0.00{73}0{4659} \hfill \\ {\text{MSCI123}} = 0.00{65}0{6}0{6} \hfill \\ {\text{MSEguance}} = 0.00{647497} \hfill \\ {\text{MSEjizhong}} = 0.00{647497} \hfill \\ \end{gathered} $$

As can be seen from the figure, the actual estimation accuracy of SCI fusion is similar to that of distributed suboptimal state fusion, but lower than that of weighted observation fusion. The estimated accuracy of weighted observation fusion is the same as that of centralized fusion, which is a globally optimal weighted fusion algorithm.

Note 1 Based on subsystem 1 after weighted fusion, the corresponding state estimator of subsystem 2 can also be obtained from Theorem 2. According to the optimality of the state fusion estimation of subsystem 1, it is easy to know that the corresponding state estimator of subsystem 2 also has the same optimality.

Fig. 4.
figure 4

Comparison curve of mean square error of three fusion estimates

Full size image

6 Conclusions

A fractional Kalman state filter for fractional descriptor systems is proposed in this paper. For multi-sensor generalized fractional order system, the global optimal weighted observation fusion algorithm is applied to derive the optimal information fusion fractional order Kalman filter. The proposed algorithm has global optimality and equivalent estimation accuracy compared with the centralized fusion algorithm, but the computational complexity is greatly reduced, which is convenient for engineering applications. A simulation example proves the effectiveness and feasibility of the method.