Numerical Investigation of Nonlinear Guided Wave Propagation in a Functionally Graded Material

Abstract

Functionally graded materials (FGM) have recently received extensive attention for their exceptional mechanical properties. This paper presents the nonlinear interaction of the guided waves with micro-crack in an FGM plate. For this purpose, a 2D finite element model of an FGM plate composed of ceramic and metal mixture is developed. The effective gradient of the properties is expressed by a continuous polynomial law as a function of the thickness. The simulation results showed that the generation of higher harmonics provides a sensitive means for micro-crack detection in FGM plates. Moreover, the amplitudes of the harmonics increase with the increase in micro-crack length.

1 Introduction

Bio-inspired composite materials with varying physical characteristics have recently attracted the interest of many engineers and researchers. These materials are also called functionally graded materials (FGM) which can solve the problems associated with stress channelling and stress peeling effects compared to the conventional layered composites [1, 2]. Due to the superior performance of FGM and the continuous development of technology, it has been widely used in biomedical, optics, aerospace, civil engineering, automotive, and various other fields [3].

In recent years, guided waves in FGM structures have received much interest for non-destructive testing. Several numerical and analytical methods have been developed to study guided wave propagation in plate structures made of FGM. Zhu et al. [4] developed a recursive formulation of the reverberation-ray matrix to investigate the dispersion behaviour of waves in the FGM plates. Gravenkamp et al. [5] used the scaled boundary finite element method (SBFEM) to calculate dispersion characteristics in plate structures. The technique applies to homogeneous plates, layered composites, and plates with continuously varying material parameters in the thickness direction. Amor et al. [6] employed the Peano-Series method for solving Lamb wave modes of lowest-order propagating in FGM plates made of aluminium nitride. Kuznetsov [7] studied the propagation of harmonic Lamb waves in plates made of FGM with transverse inhomogeneity using the modified Cauchy six-dimensional formalism. Dispersion curves for FGM isotropic plates with different kinds of exponential inhomogeneity are obtained and compared with those for homogenised isotropic plates. Malik et al. [8] presented a new approach for directly calculating group velocity curves using the wave and finite element (WFE) method. The WFE scheme exploits the periodicity of the structure to extract the group and phase velocity curves.

The guided waves have emerged as an active system capable of exciting the structure in a prescribed manner. Guided waves offer the advantage of large-area inspection with a minimum number of installed sensors [9]. Damage detection based on guided waves can be either linear on nonlinear. In the linear method, the wave characteristics like amplitude, time-of-flight, and dispersion are then analysed from the sensor signal to get information regarding the damage. However, linear methods require baseline data to compare with the existing data. Also, the changing environment and operational conditions affect the damage detection procedures [10]. Recent studies show that the nonlinear ultrasonic methods are advantageous compared to linear methods. This method does not depend on baseline data and is more sensitive to microcracks/fatigue cracks. The nonlinearity can be either due to material nonlinearity or contact nonlinearity [11,12,13].

This work investigates the interaction of primary guided waves with a microcrack in the FGM plate numerically. The nonlinearity considered in this study is due to breathing crack, which generates contact acoustic nonlinearity. The sensitivity of primary Lamb wave modes in detecting microcracks having different lengths is also studied. Numerical modelling of FGM structures is complicated because the mechanical properties of FGM vary throughout the boundary gradient smoothly. Strong mathematical background with knowledge of elasticity, mechanics, and extensive programming/scripting skills is required to develop and solve complex models. This work uses a simplified approach to model FGM using the commercially available software package Abaqus. The modelling aspects are discussed in the subsequent sections.

2 Finite Element Modelling

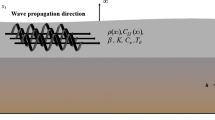
The geometry of the FGM plate considered for the study is shown in Fig. 1. The total length of the plate is 1 m.

Fig. 1

Geometry of the FGM plate

The plate is made of a chrome-ceramic mixture. The lower surface of the plate consists of chrome (cr) alone, whereas the top surface of the plate is composed of only ceramic (cer). The material property is shown in Table 1. The effective material property (${\alpha }^{eff}$) of FGM possesses the following form:

Table 1 Material properties of FGM plate

$${\alpha }^{eff}=\left({\alpha }^{cer}-{\alpha }^{cr}\right){\left(\frac{y+h}{2h}\right)}^{n}+{\alpha }^{cr}$$

(1)

where 2 h (12 mm) is the thickness of the plate, $\alpha$ denotes the material property, and n is the coefficient of the gradient. The typical profiles of the material property (density) that vary with thickness are shown in Fig. 2.

Fig. 2

Profile of density

The FGM plate is assumed to be in plane strain condition. A four-node bilinear plane strain quadrilateral element (CPE4R) is used to mesh the FGM plate. The finite element model is discretised such that there are 15–20 elements per wavelength so that a good spatial resolution of the propagating wave is achieved. The time increment for explicit dynamic analysis is chosen based on the Courant-Friedrich-Levy criteria [14]. The fundamental Lamb wave modes are excited by applying a uniform force at the end of the plate. An 8-count Hanning windowed sinusoidal tone burst is used to excite Lamb wave modes.

To obtain a dimensional dependent property is not directly available in any package. However, it is possible to generate the required distributed property as a function of other values, which is only a function of position. The material properties such as density, Young’s modulus, and Poisson’s ratios are first defined as a function of temperature. The coefficient of thermal expansion is then set to zero to eliminate thermal stresses. The temperature values for each node are defined as a function of position (dimension). This makes material properties depend only on position. The density distribution across the thickness obtained through simulation is shown in Fig. 3.

Fig. 3

Distribution of density across the thickness

3 Results and Discussion

The group velocities obtained by the finite element method (FEM) are compared with the available results. The coefficient n for the FGM plate is taken as 1. Figure 4 shows the comparison of group velocities. The maximum frequency considered for the current study is limited to 200 kHz to cut off higher wave modes. It is observed that the finite element solutions are in good agreement with the group velocity dispersion curves.

Fig. 4

Comparison of group velocities a S₀ mode, b A₀ mode (solid line [15], symbols—FEM)

The displacement distribution of the Lamb wave modes is explored at a given frequency. The displacement profile of longitudinal (U1) and transverse (U2) components across the thickness for A₀ and S₀ wave modes is presented in Fig. 5. The mode shapes are plotted for ceramic, chrome, and FGM (n = 1) plates when the plate is excited with a central frequency of 100 kHz. It is observed that the U1 displacement under A₀ mode and the U2 displacements under S₀ mode are antisymmetric about the central plane of the plate for ceramic and chrome plates. However, FGM plates show a slightly inverse symmetry with respect to a deviated axis away from the geometrical axis of symmetry. Similarly, for ceramic and chrome plates, the U1 displacement in S₀ mode and U2 displacement A₀ is found to be symmetric with respect to the central axis of the plate. Whereas, for the FGM plate, the displacement components are not symmetric with respect to the central axis of the plate.

Fig. 5

Normalised displacement amplitudes of lamb wave modes a A₀ mode—U1, b A₀ mode—U2, c S₀ mode—U1, d S₀ mode—U2

3.1 FGM Plate with a Microcrack

The interaction of primary guided waves with a microcrack in the FGM plate is then investigated numerically. The schematic diagram indicating the location of the microcrack and sensors (S1, S2, …) are shown in Fig. 6. For simulating contact acoustic nonlinearity, the crack in the plate is modelled as a seam crack. The details regarding the modelling aspects can be referred to our previous work [16]. Four different crack length to thickness ratios (a/2h) are considered for the study.

Fig. 6

FGM plate with a microcrack

The displacement (U1) response in the time-domain and frequency-domain for different cases when the FGM plate is excited at a frequency of 100 kHz is shown in Fig. 7. It is observed that the waveform gets slightly distorted due to the presence of a microcrack. The shape of the wave packet changes considerably with increases in crack length. The same is reflected in the frequency domain. From Fig. 7b, it is understood that no harmonics are generated in the case of a healthy plate. However, for damaged plates, higher harmonics are generated in addition to the excitation frequency. It is also seen that the amplitude of harmonic components increases with an increase in crack length.

Fig. 7

Displacement (U1) response in a time-domain and b frequency-domain

The use of the relative acoustic nonlinearity parameter is effective in characterising damage [11, 12]. The parameter is defined as A₂/A₁², where A₁ and A₂ are the amplitudes of the fundamental and second harmonic frequency components, respectively. The variation of this parameter is analysed for the FGM plate with different crack lengths. Figure 8a shows the variation of the relative nonlinearity parameter with respect to a/2h. It is observed that the relative amplitude increases with an increase in crack length for both the wave modes. The variation of the relative amplitude as a function of the propagation distance is plotted in Fig. 8b. Based on the linear fit, the relative amplitude increases with an increase in propagation distance for S₀ mode, whereas for A₀ mode, the relative amplitude decreases.

Fig. 8

Relative acoustic nonlinearity parameter as a function of a crack length to thickness, b propagating distance

4 Conclusion

The nonlinear guided wave technique is investigated to detect microcracks in FGM plates. The interaction of primary Lamb waves with the microcrack of various lengths is performed using finite element simulations. The results indicate that higher harmonic generation provides a sensitive tool for detecting microcracks in FGM plates. Also, the acoustic nonlinearity parameter showed an increasing trend with an increase in the length of the micro-crack. The current study also introduces a simplified approach to modelling the FGM, which does not require deep knowledge of mathematical models and provides high accuracy.