1 Introduction

FGMs are applied widespread in additive manufacturing, aerospace, and medical therapy [1,2,3] due to their remarkable adhesion and plasticity. However, FGM is susceptible to defects such as voids and micro-cracks over long periods of service. Therefore, the accurate detection and evaluation of the internal condition of FGM is a significant challenge. Acoustic waves have emerged as indispensable tools for conveying critical information about materials [4, 5], driving continuous advances in materials inspection. However, the complex operating environments of FGM [6,7,8] coupled with temperature variations have the potential to bias non-destructive testing. To accurately detect internal defects of FGM, a comprehensive understanding of the propagation characteristics of waveguides at different thermal conditions has become essential.

Many researchers have conducted extensive investigations on the propagation of acoustic waves in thermoelastic FGM plate. For example, Fan et al. [9] studied the reflection phenomenon of plane harmonic waves in functionally gradient thermoelastic media using the generalized thermoelasticity theory. Li et al. [10] developed a fractional order control equation to analyze coupled thermoelastic wave propagation, and investigated the effects of micro-structural parameters and fractional order on the propagation and attenuation of thermoelastic waves. Manthena et al. [11] obtained analytical solutions in the heat conduction equations and studied the stress and displacement distributions in a rectangular FGM plate using integral transform technique in detail. Dai et al. [12] carried out a comparative analysis of different volume fraction functions and temperature variations, and investigated the wave transmission and nanofluidic transport through nanotubes in FGM. Sheokand et al. [13] used the positive modal technique to derive comprehensive analytical expressions for displacement components, stress and temperature fields. Their research focused on the study of thermoelastic interactions in FGM under the two-phase hysteresis model. Seyed et al. [14] used strain-gradient elasticity and Green–Naghdi theory to study the effects of length parameters, microlength inertia, and thermal parameters on thermal wave propagation in higher-order materials. Liu et al. [15] investigated the influence of thermal damping velocity coefficients of epoxy functional gradient layers on temperature and longitudinal displacements. Kapil et al. [16] developed a theoretical model for a thermoelastic plane wave and studied the reflection of thermoelastic waves in a fibre-reinforced medium with variable thermal conductivity. It is important to note that the above studies primarily focused on the propagation characteristics of bulk waves in thermoelastic FGM.

In addition, the ultrasonic guided wave has emerged as a novel and efficient non-destructive testing method in recent years. It offers advantages such as extended detection range and precision tomography. This method has found wide applications in defect detection and mechanical property characterization. It has attracted the interest of researchers in the thermoelastic material detection and evaluation. Sharma et al. [17] investigated the effects of anisotropy and temperature on guided wave propagation in composite substrates. Using Kirchhoff theory and Moore-Gibson-Thomson (MGT) theory of thermoelasticity, Kumari et al. [18] investigated the propagation characteristics of bending edge waves in porous FGM plates in a thermal environment. She et al. [19] studied the dispersion relation of thermoelastic waves in porous FGM plates based on the Galyokin method. Wang et al. [20] introduced an advanced Legendre polynomial series approach to analyze circumferential thermoelastic Lamb waves in fractional order orthogonal anisotropic cylindrical plates. They further extended their research to include thermoelastic longitudinal guided waves in non-uniform hollow cylinders [21] and thermoelastic circumferential Lamb waves in nonlocal nano-hollow cylinders composed of FGM [22]. Yu et al. [23, 24] used the Green–Naghdi generalized thermoelasticity theory to study circumferential guided thermoelastic waves in orthotropic anisotropic cylindrical bending plates under stress-free isothermal boundary conditions, as well as the propagation of thermoelastic guided waves in orthogonal anisotropic plates under stress-free isothermal boundary conditions. However, as the cut-off order of the Legendre polynomials increases, the dimension of the eigen-matrix of the conventional Legendre polynomial method also increases. This is accompanied by more complicated integration operations. Additionally, the semi-analytical finite element method (SAFEM) is an effective method for solving dispersion characteristic of complex structures with arbitrary cross sections [25, 26]. Yang et al. [27, 28] utilized acoustoelastic theory in combination with the semi-analytical finite element method (AE-SAFEM) to study the impact of axial stress on the acoustoelastic guided wave propagation characteristic of arbitrary cross-section. Based on this, they proposed a thermo-acoustoelastic theory combined with the semi-analytical finite element method (TAE-SAFEM) to investigate the effects of uniform and non-uniform thermal effects on the acoustoelastic guided wave propagation. However, while SAFEM improves computational efficiency compared to the finite element method (FEM) that discretizes the entire waveguide structure, the numerical accuracy is more affected by finite element mesh accuracy. The theoretical modeling related to the thermo-elastic guided wave propagation problem mainly focuses on elastic plate structures, tube structures and shaped structures. There are fewer related reports on functionally gradient material structures.

In our research, we propose the state vector and Legendre polynomial methods to avoid complex integral calculations. It can solve high-frequency wave propagation problems in complex waveguide structures. We rewritten the wave equations and geometrical equations by using the state vectors, and transform the relevant parameter matrices into upper triangular and symmetric matrices forms. Additionally, the dispersion equation can be solved by utilizing the orthogonal completeness and recursive property of the Legendre polynomial. The proposed approach converts the problem into an eigenvalue problem, which overcomes the issue of calculating the high cut-off term of the conventional Legendre polynomial method. Meanwhile, it can also solve the leaky and missing root problems of the conventional matrix method due to the numerical instability. Using the unique orthogonal completeness and recursive properties of the Legendre polynomial, analytic expressions for different recursive operators can be derived. It greatly improves the computational efficiency under the premise of ensuring the correctness of the operation. An alternative and effective method is provided to extract the dispersion curve of the waveguided structures. Previously, we investigated wave propagation in FGM plates [29] and pipes [30] with varying gradients. Our findings indicate that computational efficiency is significantly improved compared to the global matrix method. In this study, the Green–Naghdi theory [31,32,33] has been incorporated and extended to numerically analyze the propagation characteristics of thermoelastic guided waves in FGM plates versus temperature. Furthermore, the accuracy of the proposed non-hierarchical theoretical solution method has been validated through frequency domain simulations of an FGM plate versus temperature. The meaning of “hierarchical” is to discretize the functionally gradient material plate into multi-layered plates with the same layer thickness. Each layer has independent mechanical parameters. The meaning of “non-hierarchical” is that the functionally gradient material plate is regarded as an independent media. The mechanical parameters vary continuously along the thickness direction and satisfy the specific functional distribution form. In addition, the effect of different Legendre polynomial cut-off orders on the convergence of the dispersion curve solutions was investigated. Finally, the effects of gradient index and temperature on guided wave propagation characteristics in FGM plate are analyzed.

2 Problem Formulation

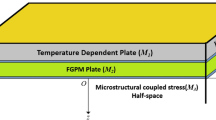
In the global coordinate system (x1, x2, x3), consider an FGM plate with material properties (density ρ and elastic constants CIJ, where I and J range from 1 to 6) varying with the thickness L (0 ≤ x2 ≤ L), which is infinite in the x1 and x3 direction but finite in the x2 direction, as shown in Fig. 1. Also, we assume that the guided wave propagates along the x1 direction.

Fig. 1
figure 1

Geometry of the FGM plate

Full size image

2.1 Wave Equations

In this study, we assume that the top material of the FGM is A, the bottom material is B, and the internal material parameters gradually evolve from A to B according to the corresponding functional relationship. And the material at any thickness position can be expressed as ρ(x2) and CIJ(x2). Subsequently, based on the small deformation assumption, the generalized constitutive relationship, the displacement–strain relationship and the wave equation can be expressed as:

$$ \left\{ {\begin{array}{*{20}l} {\sigma_{ij}^{\,} = c_{ijkl}^{\,} \left( {x_2 } \right)\varepsilon_{kl}^{\,} } \hfill & {i,j,k,l \in \{ 1,2\} } \hfill \\ {\varepsilon_{kl}^{\,} = \frac{1}{2}\left( {u_{k,l}^{\,} + u_{k,l}^{\,} } \right)} \hfill & {k,l \in \{ 1,2\} } \hfill \\ {\sigma_{ij,j}^{\,} = \rho (x_2 )\frac{\partial^2 u_i }{{\partial t^2 }}} \hfill & {i,j \in \{ 1,2\} } \hfill \\ \end{array} } \right. $$
(1)

where σij, εij and ui denote the stress tensor, strain tensor and displacement component in the Cartesian coordinate system, respectively. And cijkl(x2) denotes the elastic constant along the thickness direction. Meanwhile, in order to describe the propagation of ultrasonic guided waves in the FGM plate versus temperature, the control equation can be rewritten using Green–Naghdi (G–N) theory as:

$$ K_i T_{j,j} - T_0 \beta \left( {\ddot{u}_{j,j} + \ddot{U}_{j,j} } \right) = \rho C_{\text{e}} \ddot{T}\;\;\;i,j \in \left\{ {1,2} \right\} $$
(2)

Since the influence of the temperature on the theoretical model is taken into account, the temperature-dependent characteristic parameters include the theoretical material constants, volume expansion coefficients, constant strain specific heats, homogeneous reference temperatures, and the temperature parameters, which are defined as Ki, βi, Ce, T0, and T, respectively.

For a free harmonic propagating in the x1 direction, the stress and displacement solution versus temperature can be expressed as:

$$ \begin{aligned} {{\mathbf{u}}} & = \left[ {\begin{array}{*{20}c} {u_1^{\,} } & {u_2^{\,} } \\ \end{array} } \right]e^{ - j\left[ {\kappa x_1 - \omega t} \right]} \\ {{\varvec{\tau}}}_i^{\,} & = \left[ {\begin{array}{*{20}c} {\sigma_{i1}^{\,} } & {\sigma_{i2}^{\,} } \\ \end{array} } \right]e^{ - j\left[ {\kappa x_1 - \omega t} \right]} \\ {{\varvec{T}}} & = Te^{ - j\left[ {\kappa x_1 - \omega t} \right]} \\ {\varvec{\Upsilon }}_{\,}^{\,} & = \left[ {\begin{array}{*{20}c} {{{\mathbf{u}}}^{\,} } \\ {{{\varvec{T}}}^{\,} } \\ \end{array} } \right]e^{ - j\left[ {\kappa x_1 - \omega t} \right]} \\ {\varvec{\Pi }}_i^{\,} & = \left[ {\begin{array}{*{20}c} {{{\varvec{\tau}}}_i^{\,} } \\ {{{\varvec{T}}}^{\,} } \\ \end{array} } \right]e^{ - j\left[ {\kappa x_1 - \omega t} \right]} \\ \end{aligned} $$
(3)

where κ and ω are the wave number and angular frequency. Subsequently, substituting Eq. (3) into the wave equation in Eq. (1) yields Eq. (4):

$$ \frac{\partial }{\partial x_2 }{\varvec{\Pi }}_2^{\,} = - \rho \left( {x_2 } \right)\omega^2 {\varvec{\Upsilon - }}\frac{\partial }{\partial x_1 }{\varvec{\Pi }}_1^{\,} $$
(4)

Similarly, substituting Eq. (3) into Eq. (1) and simplifying using the auxiliary variables (\({\varvec{\Pi }}\), \({\varvec{\Upsilon }}\)), the constitutive relationships in the FGM plate can be obtained:

$$ \begin{aligned} {\varvec{\Pi }}_1^{\,} & = \left[ {D_{11} } \right]\frac{{\partial {\varvec{\Upsilon }}}}{\partial x_1 } + \left[ {D_{12} } \right]\frac{{\partial {\varvec{\Upsilon }}}}{\partial x_2 } + \left[ {D_{14} } \right]{\varvec{\Upsilon }} \\ {\varvec{\Pi }}_2^{\,} & = \left[ {D_{21} } \right]\frac{{\partial {\varvec{\Upsilon }}}}{\partial x_1 } + \left[ {D_{22} } \right]\frac{{\partial {\varvec{\Upsilon }}}}{\partial x_2 } + \left[ {D_{24} } \right]{\varvec{\Upsilon }} \\ \end{aligned} $$
(5)

where [Dij] is a matrix of coefficients consisting of elastic constants. Clearly Eq. (5) can be further aligned along the x1 direction:

$$\begin{aligned} {\varvec{\Pi }}_1^{\,} &= [D_{11} ]\frac{{\partial {\varvec{\Upsilon }}}}{\partial x_1 } + [D_{12} ][D_{22} ]^{ - 1} \\ &\left( {{\varvec{\Pi }}_2^{\,} - [D_{21} ]\frac{{\partial {\varvec{\Upsilon }}}}{\partial x_1 } - [D_{24} ]{\varvec{\Upsilon }}} \right) + [D_{14} ]{\varvec{\Upsilon }}\end{aligned} $$
(6)

Similarly, Eq. (6) can be written in the corresponding vector form:

$$\begin{aligned} {\varvec{\Pi }}_1^{\,} = &\left[ \left[ {D_{12} } \right]\left[ {D_{22} } \right]^{ - 1} \ - \left[ {D_{12} } \right]\left[ {D_{22} } \right]^{ - 1} \left( {\frac{\partial }{\partial x_1 }\left[ {D_{21} } \right] + \left[ {D_{24} } \right]} \right) \right. \\ & \left.+ \frac{\partial }{\partial x_1 }\left[ {D_{11} } \right] + \left[ {D_{14} } \right] \right]\left( {\begin{array}{*{20}c} {{\varvec{\Pi }}_2^{\,} } \\ {\varvec{\Upsilon }} \\ \end{array} } \right)\end{aligned} $$
(7)

Bringing Eq. (7) into Eq. (4):

$$\frac{\partial }{\partial x_2 }{\varvec{\Pi }}_2^{\,} = \left[ {j\kappa \begin{array}{*{20}c} {\left[ {D_{12} } \right]\left[ {D_{22} } \right]^{ - 1} } -{ \rho \left( {x_2 } \right)\omega^2 [I] - \kappa^2 \left[ {\left[ {D_{12} } \right]\left[ {D_{22} } \right]^{ - 1} \left[ {D_{21} } \right] - \left[ {D_{11} } \right]} \right] + j\kappa \left[ {[D_{14} ] - [D_{12} ][D_{22} ]^{ - 1} [D_{24} ]} \right]} \\ \end{array} } \right]\left( {\begin{array}{*{20}c} {{\varvec{\Pi }}_2^{\,} } \\ {\varvec{\Upsilon }} \\ \end{array} } \right)$$
(8)

The constitutive relationship in Eq. (5) along the thickness direction can also be simplified into vector form:

$$ \frac{\partial }{\partial x_2 }{\varvec{\Upsilon }} = \left[ {\begin{array}{*{20}c} {\left[ {D_{22} } \right]^{ - 1} } & {j\kappa \left[ {D_{22} } \right]^{ - 1} \left[ {D_{21} } \right] - \left[ {D_{22} } \right]^{ - 1} \left[ {D_{24} } \right]} \\ \end{array} } \right]\left( {\begin{array}{*{20}c} {{\varvec{\Pi }}_2^{\,} } \\ {\varvec{\Upsilon }} \\ \end{array} } \right)$$
(9)

The following matrix can be obtained by associating Eqs. (8) and (9):

$$ \frac{\partial }{\partial x_2 }\ \left( {\begin{array}{*{20}c} {{\varvec{\Pi }}_2^{\,} } \\ {\varvec{\Upsilon }} \\ \end{array} } \right)= \left[ {\begin{array}{*{20}c} {j\kappa \left[ {D_{12} } \right]\left[ {D_{22} } \right]^{ - 1} } & { - \rho \left( {x_2 } \right)\omega^2 [I] - \kappa^2 \left[ {\left[ {D_{12} } \right]\left[ {D_{22} } \right]^{ - 1} \left[ {D_{21} } \right] - \left[ {D_{11} } \right]} \right] + j\kappa \left[ {[D_{14} ] - [D_{12} ][D_{22} ]^{ - 1} [D_{24} ]} \right]} \\ {\left[ {D_{22} } \right]^{ - 1} } & {j\kappa \left[ {D_{22} } \right]^{ - 1} \left[ {D_{21} } \right] - \left[ {D_{22} } \right]^{ - 1} \left[ {D_{24} } \right]} \\ \end{array} } \right]\ \left( {\begin{array}{*{20}c} {{\varvec{\Pi }}_2^{\,} } \\ {\varvec{\Upsilon }} \\ \end{array} } \right) $$
(10)

Note that [D2i] contains functional relations in the x2 direction. Subsequently, the simplified dispersion equation can be obtained by substituting the constitutive equation in the x2 direction in Eq. (5) and the rewritten constitutive equation in the x1 direction in Eq. (6) into the wave equation in Eq. (4).

$$ \begin{aligned} & \kappa^2 \left[ {D_{11} } \right]{\varvec{\Upsilon }} + j\kappa \left( {\left[ {D_{12} } \right] + \left[ {D_{21} } \right]} \right)\frac{{\partial {\varvec{\Upsilon }}}}{\partial x_2 }\\ &\quad - \rho \left( {x_2 } \right)\omega^2 {\varvec{\Upsilon }} - \left[ {D_{22} } \right]\frac{{\partial^2 {\varvec{\Upsilon }}}}{\partial x_2^2 } \\ & \quad + j\kappa [D_{14} ]{\varvec{\Upsilon }} - \left[ {D_{24} } \right]\frac{{\partial {\varvec{\Upsilon }}}}{\partial x_2 } + j\kappa \frac{{\partial \left[ {D_{21} } \right]}}{\partial x_2 }{\varvec{\Upsilon }} \\ &\quad- \frac{{\partial \left[ {D_{22} } \right]}}{\partial x_2 }\frac{{\partial {\varvec{\Upsilon }}}}{\partial x_2 } - \frac{{\partial \left[ {D_{24} } \right]}}{\partial x_2 }{\varvec{\Upsilon }} = 0 \\ \end{aligned} $$
(11)

Here, it can be seen that there are two unknown quantities in the dispersion equation, the wave number κ and the displacement component \({\varvec{\Upsilon }}\). In order to improve the computational efficiency and reduce the computational volume, introducing the unit elastic constant C0, the unit density ρ0, and the relative wave number \(\kappa_0 = {{\upomega }}\sqrt {{{{\rho_0 } / {C_0 }}}}\), where \(\chi = \kappa /\kappa_0\). \(\left[ {D_{ij} } \right]^{\prime}\) is the first-order differentiation of the elastic constant along the direction of the thickness, and Eq. (11) can be written after simplification:

$$ \begin{aligned} & \chi^2 \left[ {D_{11} } \right]\frac{{\varvec{\Upsilon }}}{C_0 } + j\chi \frac{{\left( {\left[ {D_{12} } \right] + \left[ {D_{21} } \right]} \right)}}{\chi_0 C_0 }\frac{{\partial {\varvec{\Upsilon }}}}{\partial x_2 }\\ &\quad - \frac{{\rho \left( {x_2 } \right)}}{\rho_0 }{\varvec{\Upsilon }} - \frac{{\left[ {D_{22} } \right]}}{\chi_0^2 C_0 }\frac{{\partial^2 {\varvec{\Upsilon }}}}{\partial x_2^2 } + j\chi \frac{{[D_{14} ]}}{\chi_0 C_0 }{\varvec{\Upsilon }} \\ & \quad - \frac{{\left[ {D_{24} } \right]}}{\chi_0^2 C_0 }\frac{{\partial {\varvec{\Upsilon }}}}{\partial x_2 } + j\chi \frac{{\left( {\left[ {D_{21} } \right]} \right)^{\prime} }}{\chi_0 C_0 }{\varvec{\Upsilon }} \\ &\quad- \frac{{\left( {\left[ {D_{22} } \right]} \right)^{\prime} }}{\chi_0^2 C_0 }\frac{{\partial {\varvec{\Upsilon }}}}{\partial x_2 } - \frac{{\left( {\left[ {D_{24} } \right]} \right)^{\prime} }}{\chi_0^2 C_0 }{\varvec{\Upsilon }} = 0 \\ \end{aligned} $$
(12)

2.2 Legendre Polynomial Expansions

In order to obtain the numerical solution of the dispersion equation \({\varvec{\Upsilon }}\), a superposition of the displacement and the temperature is fitted using Legendre polynomials as shown in Eq. (13):

$$ {\varvec{\Upsilon }} = \sum_{n = 0}^{N - 1} {\Re_n^l P_n (\iota )} $$
(13)

where

$$ \Re_n^l =\left[ {\begin{array}{*{20}c} {\Re_{un}^1 } & {\Re_{un}^2 } & {\Re_{Tn}^3 } \\ \end{array} } \right]^{\prime} $$

Here, \(\Re_n^l\) is the displacement and temperature magnitude matrix. The subscript u represents the displacement magnitude term and T represents the temperature magnitude term. \(P_n (\iota )\) is the nth-order Legendre polynomial on \(\iota \in \left[ { - 1,1} \right]\), l represents the different directions with values in the range [1, 2, 3], and N is the cut-off order of the selected Legendre polynomial. Meanwhile, considering the effective action interval of Legendre polynomial, the coordinate x2 must be converted to coordinate \(\iota\), so the following treatment is carried out:

$$ \iota = \ \ell^{\,} \left( {x_2 - \frac{h}{2}} \right),\quad \ \ell^{\,} = {\raise0.7ex\hbox{$2$} \!\mathord{\left/ {\vphantom {2 h}}\right.\kern-0pt}\!\lower0.7ex\hbox{$h$}} $$
(14)

The new dispersion equation can be obtained by substituting Eqs. (13) and (14) into Eq. (12):

$$ \begin{aligned} & \chi^2 \sum_{n = 0}^{N - 1} {\int_{ - 1}^1 {\frac{{\left[ {D_{11} } \right]}}{C_0 }\Re_n^l P_n (\iota )} } P_m \left( \iota \right)d\iota\\ &\quad + j\chi \ell \sum_{n = 0}^{N - 1} {\int_{ - 1}^1 {\frac{{\left( {\left[ {D_{12} } \right] + \left[ {D_{21} } \right]} \right)}}{\chi_0 C_0 }\Re_n^l \frac{\partial P_n (\iota )}{{\partial \iota }}} } P_m \left( \iota \right)d\iota \\ &\quad - \sum_{n = 0}^{N - 1} {\int_{ - 1}^1 {\frac{{\rho \left( {x_2 } \right)}}{\rho_0 }\Re_n^l P_n (\iota )} } P_m \left( \iota \right)d\iota \\ & \quad - \ell^2 \sum_{n = 0}^{N - 1} {\int_{ - 1}^1 {\frac{{\left[ {D_{22} } \right]}}{\chi_0^2 C_0 }\Re_n^l \frac{\partial^2 P_n (\iota )}{{\partial \iota^2 }}} } P_m \left( \iota \right)d\iota \\ &\quad + j\chi \sum_{n = 0}^{N - 1} {\int_{ - 1}^1 {\frac{{[D_{14} ]}}{\chi_0 C_0 }\Re_n^l P_n (\iota )} } P_m \left( \iota \right)d\iota \\ &\quad - \ell \sum_{n = 0}^{N - 1} {\int_{ - 1}^1 {\frac{{\left[ {D_{24} } \right]}}{\chi_0^2 C_0 }\Re_n^l \frac{\partial P_n (\iota )}{{\partial \iota }}} } P_m \left( \iota \right)d\iota \\ & \quad + j\chi \sum_{n = 0}^{N - 1} {\int_{ - 1}^1 {\frac{{\left( {\left[ {D_{21} } \right]} \right)^{\prime} }}{\chi_0 C_0 }\Re_n^l P_n (\iota )} } P_m \left( \iota \right)d\iota\\ &\quad - \ell \sum_{n = 0}^{N - 1} {\int_{ - 1}^1 {\frac{{\left( {\left[ {D_{22} } \right]} \right)^{\prime} }}{\chi_0^2 C_0 }\Re_n^l \frac{\partial P_n (\iota )}{{\partial \iota }}} } P_m \left( \iota \right)d\iota\\ &\quad - \sum_{n = 0}^{N - 1} {\int_{ - 1}^1 {\frac{{\left( {\left[ {D_{24} } \right]} \right)^{\prime} }}{\chi_0^2 C_0 }\Re_n^l P_n (\iota )} } P_m \left( \iota \right)d\iota = 0 \\ \end{aligned} $$
(15)

The material properties of FGM plates can be described as [34]:

$$ \begin{aligned} C_{IJ} (x_2 ) & = C_{IJ}^2 + (C_{IJ}^1 - C_{IJ}^2 )V_1 (x_2 ) \\ \rho (x_2 ) & = \rho^2 + (\rho^1 - \rho^2 )V_1 (x_2 ) \\ & \quad V_1 (x_2 ) + V_2 (x_2 ) =1 \\ \end{aligned} $$
(16)

where V1(x2) is the gradient volume fraction at the surface of the FGM plate and V2(x2) is the gradient volume fraction at the bottom of the FGM plate, while the gradient exponential function of Eq. (17) was chosen:

$$ V_1 = \left( {1 - \frac{x_2 }{h}} \right)^p \;\;\left( {0 \le x_2 \le h,\;\;0.2 \le p \le 2} \right) $$
(17)

Thus, the corresponding material parameters can be obtained from different gradient volume fractions:

$$ \begin{aligned} C_{IJ} \left( \iota \right) & = C_{IJ}^2 { + }\left( {C_{IJ}^1 - C_{IJ}^2 } \right)\left( {\frac{1}{2} - \frac{\iota }{2}} \right)^p \\ \rho \left( {x_2 } \right) & = \rho^2 { + }\left( {\rho^1 - \rho^2 } \right)\left( {1 - \frac{x_2 }{h}} \right)^p \\ C^{\prime}_{IJ} \left( \iota \right) & = - \frac{p}{h}\left( {C_{IJ}^1 - C_{IJ}^2 } \right)\frac{1}{{2^{p - 1} }}\left( {1 - \iota } \right)^{p - 1} \\ \end{aligned} $$
(18)

The power function in Eq. (18) has a high complexity to be solved by direct substitution, so it can be fitted by univariate nonlinear fitting as [35]:

$$ \begin{aligned} \left( {\frac{1}{2} - \frac{\iota }{2}} \right)^p &= S_1 \iota^8 + S_2 \iota^7 + S_3 \iota^6 + S_4 \iota^5 + S_5 \iota^4 + S_6 \iota^3 \\ &\quad + S_7 \iota^2 + S_8 \iota^1 + S_9 , \\ \left( {\frac{1}{2} - \frac{\iota }{2}} \right)^{p - 1} &= Q_1 \iota^8 + Q_2 \iota^7 + Q_3 \iota^6 + Q_4 \iota^5 + Q_5 \iota^4\\ &\quad + Q_6 \iota^3 + Q_7 \iota^2 + Q_8 \iota^1 + Q_9 ; \\ \end{aligned} $$
(19)

Equation (20) can be obtained by substituting Eqs. (18) and (19) into Eq. (15):

$$\begin{aligned} & \chi ^2 \frac{{\left[ {D_{11}^2 } \right]}}{{C_0 }}\sum_{n = 0}^{N - 1} {\int_{ - 1}^1 {\Re _n^l P_n (\iota )} } P_m \left( \iota \right)d\iota + j\chi \ell \frac{{\left( {\left[ {D_{12}^2 } \right] + \left[ {D_{21}^2 } \right]} \right)}}{{\kappa _0 C_0 }}\\ &\quad\sum_{n = 0}^{N - 1} {\int_{ - 1}^1 {\Re _n^l \frac{{\partial P_n (\iota )}}{{\partial \iota }}} } P_m \left( \iota \right)d\iota - \rho _2 \omega ^2 \sum_{n = 0}^{N - 1} {\int_{ - 1}^1 {\Re _n^l P_n (\iota )} } P_m \left( \iota \right)d\iota \\ & \quad - \frac{{\left[ {D_{22}^2 } \right]}}{{\kappa _0 ^2 C_0 }}\ell ^2 \sum_{n = 0}^{N - 1} {\int_{ - 1}^1 {\Re _n^l \frac{{\partial ^2 P_n (\iota )}}{{\partial \iota ^2 }}} } P_m \left( \iota \right)d\iota + j\chi \frac{{[D_{14}^2 ]}}{{\kappa _0 C_0 }}\sum_{n = 0}^{N - 1} {\int_{ - 1}^1 {\Re _n^l P_n (\iota )} } P_m \left( \iota \right)d\iota - \frac{{\left[ {D_{24}^2 } \right]}}{{\kappa _0 ^2 C_0 }}\ell \sum_{n = 0}^{N - 1} {\int_{ - 1}^1 {\Re _n^l \frac{{\partial P_n (\iota )}}{{\partial \iota }}} } P_m \left( \iota \right)d\iota \\ & \quad + \chi ^2 \frac{{\left( {\left[ {D_{11}^1 } \right] - \left[ {D_{11}^2 } \right]} \right)}}{{C_0 }}\sum_{n = 0}^{N - 1} {\int_{ - 1}^1 {\Re _n^l \left( \begin{gathered} S_1 \iota ^8 + S_2 \iota ^7 + S_3 \iota ^6 + S_4 \iota ^5 + S_5 \iota ^4 \hfill \\ + S_6 \iota ^3 + S_7 \iota ^2 + S_8 \iota ^1 + S_9 \hfill \\ \end{gathered} \right)P_n (\iota )} } P_m \left( \iota \right)d\iota \\ & \quad + j\chi \ell \frac{{\left( {\left( {\left[ {D_{12}^1 } \right] - \left[ {D_{12}^2 } \right]} \right) + \left( {\left[ {D_{21}^1 } \right] - \left[ {D_{21}^2 } \right]} \right)} \right)}}{{\kappa _0 C_0 }}\sum_{n = 0}^{N - 1} {\int_{ - 1}^1 {\Re _n^l \left( \begin{gathered} S_1 \iota ^8 + S_2 \iota ^7 + S_3 \iota ^6 + S_4 \iota ^5 + S_5 \iota ^4 \hfill \\ + S_6 \iota ^3 + S_7 \iota ^2 + S_8 \iota ^1 + S_9 \hfill \\ \end{gathered} \right)\frac{{\partial P_n (\iota )}}{{\partial \iota }}} } P_m \left( \iota \right)d\iota \\ & \quad - \frac{{\rho _1 - \rho _2 }}{{\rho _0 }}\sum_{n = 0}^{N - 1} {\int_{ - 1}^1 {\Re _n^l \left( \begin{gathered} S_1 \iota ^8 + S_2 \iota ^7 + S_3 \iota ^6 + S_4 \iota ^5 + S_5 \iota ^4 \hfill \\ + S_6 \iota ^3 + S_7 \iota ^2 + S_8 \iota ^1 + S_9 \hfill \\ \end{gathered} \right)P_n (\iota )} } P_m \left( \iota \right)d\iota \\ & \quad - \frac{{\left( {\left[ {D_{22}^1 } \right] - \left[ {D_{22}^2 } \right]} \right)}}{{\kappa _0 ^2 C_0 }}\ell ^2 \sum_{n = 0}^{N - 1} {\int_{ - 1}^1 {\Re _n^l \left( \begin{gathered} S_1 \iota ^8 + S_2 \iota ^7 + S_3 \iota ^6 + S_4 \iota ^5 + S_5 \iota ^4 \hfill \\ + S_6 \iota ^3 + S_7 \iota ^2 + S_8 \iota ^1 + S_9 \hfill \\ \end{gathered} \right)\frac{{\partial ^2 P_n (\iota )}}{{\partial \iota ^2 }}} } P_m \left( \iota \right)d\iota \\ & \quad + j\chi \frac{{\left( {\left[ {D_{14}^1 } \right] - \left[ {D_{14}^2 } \right]} \right)}}{{\kappa _0 C_0 }}\sum_{n = 0}^{N - 1} {\int_{ - 1}^1 {\Re _n^l \left( \begin{gathered} S_1 \iota ^8 + S_2 \iota ^7 + S_3 \iota ^6 + S_4 \iota ^5 + S_5 \iota ^4 \hfill \\ + S_6 \iota ^3 + S_7 \iota ^2 + S_8 \iota ^1 + S_9 \hfill \\ \end{gathered} \right)P_n (\iota )} } P_m \left( \iota \right)d\iota \\ & \quad - \frac{{\left( {\left[ {D_{24}^1 } \right] - \left[ {D_{24}^2 } \right]} \right)}}{{\kappa _0 ^2 C_0 }}\ell \sum_{n = 0}^{N - 1} {\int_{ - 1}^1 {\Re _n^l \left( \begin{gathered} S_1 \iota ^8 + S_2 \iota ^7 + S_3 \iota ^6 + S_4 \iota ^5 + S_5 \iota ^4 \hfill \\ + S_6 \iota ^3 + S_7 \iota ^2 + S_8 \iota ^1 + S_9 \hfill \\ \end{gathered} \right)\frac{{\partial P_n (\iota )}}{{\partial \iota }}} } P_m \left( \iota \right)d\iota \\ & \quad - j\chi \frac{{\left( {\left[ {D_{21}^1 } \right] - \left[ {D_{21}^2 } \right]} \right)}}{{\kappa _0 C_0 }}\frac{p}{h}\sum_{n = 0}^{N - 1} {\int_{ - 1}^1 {\Re _n^l \left( \begin{gathered} Q_1 \iota ^8 + Q_2 \iota ^7 + Q_3 \iota ^6 + Q_4 \iota ^5 + Q_5 \iota ^4 \hfill \\ + Q_6 \iota ^3 + Q_7 \iota ^2 + Q_8 \iota ^1 + Q_9 \hfill \\ \end{gathered} \right)P_n (\iota )} } P_m \left( \iota \right)d\iota \\ & \quad + \ell \frac{{\left( {\left[ {D_{22}^1 } \right] - \left[ {D_{22}^2 } \right]} \right)}}{{\kappa _0 ^2 C_0 }}\frac{p}{h}\sum_{n = 0}^{N - 1} {\int_{ - 1}^1 {\Re _n^l \left( \begin{gathered} Q_1 \iota ^8 + Q_2 \iota ^7 + Q_3 \iota ^6 + Q_4 \iota ^5 + Q_5 \iota ^4 \hfill \\ + Q_6 \iota ^3 + Q_7 \iota ^2 + Q_8 \iota ^1 + Q_9 \hfill \\ \end{gathered} \right)\frac{{\partial P_n (\iota )}}{{\partial \iota }}} } P_m \left( \iota \right)d\iota \\ & \quad + \frac{{\left( {\left[ {D_{24}^1 } \right] - \left[ {D_{24}^2 } \right]} \right)}}{{\kappa _0 ^2 C_0 }}\frac{p}{h}\sum_{n = 0}^{N - 1} {\int_{ - 1}^1 {\Re _n^l \left( \begin{gathered} Q_1 \iota ^8 + Q_2 \iota ^7 + Q_3 \iota ^6 + Q_4 \iota ^5 + Q_5 \iota ^4 \hfill \\ + Q_6 \iota ^3 + Q_7 \iota ^2 + Q_8 \iota ^1 + Q_9 \hfill \\ \end{gathered} \right)P_n (\iota )} } P_m \left( \iota \right)d\iota = 0 \\ \end{aligned}$$
(20)

It is important to note that the linear operators for the Legendre polynomials have been given in the literature [29], and it is not difficult to observe that the limitations of the partial differential terms in the dispersion equations make the Legendre polynomials have a minimum effective range of [0, N − 3], and thus provide only 2(N − 2) equations. However, this does not allow for the solution of 2N amplitude and temperature quantities. Therefore, it is necessary to introduce boundary conditions and combine them with dispersion equations to further supplement the unknown covariates that need to be calculated. In this case, the free stress boundary conditions at the upper and lower boundaries can be expressed as:

$$\left\{ \begin{array}{*{20}l} {\sum_{n = 0}^N {\left( {\frac{{\left[ {D_{22}^1 } \right]}}{\kappa_0 }\left( { - 1} \right)^{n + 1} \ell \frac{{n\left( {n + 1} \right)}}{2} + \left( {[D_{24}^1 ] - j\chi \left[ {D_{21}^1 } \right]} \right)\left( { - 1} \right)^n } \right)\Re_n^l } = 0} \hfill & \quad {\left( {lower} \right)} \hfill \\ {\sum_{n = 0}^N {\left( {\frac{{\left[ {D_{22}^2 } \right]}}{\kappa_0 }\ell \frac{{n\left( {n + 1} \right)}}{2} + \left( {[D_{24}^2 ] - j\chi \left[ {D_{21}^2 } \right]} \right)} \right)} \Re_n^l = 0} \hfill & \quad {\left( {upper} \right)} \hfill \\ \end{array} \right.$$
(21)

Subsequently, the coupling Eq. (20) with Eq. (21) can be obtained:

$$ \chi^2 {{\varvec{\Gamma}}}_{3N \times 3N}^{\,} {{\mathbf{E}}}_{3N \times 1}^{\,} + j\chi {{\varvec{\varPsi}}}_{3N \times 3N}^{\,} {\mathbf{D}}_{3N \times 1}^{\,} + {\mathbf{Z}}_{3N \times 3N}^{\,} {\mathbf{D}}_{3N \times 1}^{\,} = 0\ $$
(22)

where \({{\varvec{\Gamma}}}\), \({{\varvec{\varPsi}}}\), \({\mathbf{Z}}\) is the coefficient matrix, and \({{\mathbf{E}}}\) is \([{\varvec{\Upsilon }}_0^i ,{\varvec{\Upsilon }}_1^i ,{\varvec{\Upsilon }}_2^i , \ldots ,{\varvec{\Upsilon }}_{N - 1}^i ]^T\). Meanwhile, in order to transform the quadratic eigenvalue problem into a linear eigenvalue problem, the unit matrix \({{\mathbf{I}}}\) and auxiliary variables \({\mathbf{R}} =j\chi {\varvec{\Gamma E}}\) are introduced Eq. (22) is further rewritten:

$$ \begin{aligned} &\left( {\left[ {\begin{array}{*{20}c} {{{\varvec{\varPsi}}}_{3N \times 3N} } & { - {{\mathbf{I}}}_{3N \times 3N} } \\ { - {{\varvec{\Gamma}}}_{3N \times 3N} } & 0 \\ \end{array} } \right] - \frac{j}{\chi }\left[ {\begin{array}{*{20}c} {{\mathbf{Z}}_{3N \times 3N} } & 0 \\ 0 & {{{\mathbf{I}}}_{3N \times 3N} } \\ \end{array} } \right]} \right)\\ &\qquad\left[ {\begin{array}{*{20}c} {{{\mathbf{E}}}_{3N \times 1} } \\ {{\mathbf{R}}_{3N \times 1} } \\ \end{array} } \right] = 0 \end{aligned}$$
(23)

Finally, the eigenvalues and eigenvectors in Eq. (23) are solved, which can directly realize the accurate plotting of the dispersion curves versus temperature in FGM plates.

3 Numerical Validation

3.1 Frequency Domain Simulation

Based on the theoretical derivation described previously, propagation characteristics of guided waves in an isotropic FGM plate are computed under the influence of temperature. To validate the accuracy of our proposed theoretical approach, we create an acoustic frequency domain simulation model for a multilayer plate subjected to a temperature, as shown in Fig. 2. The goal is to obtain a hierarchical solution for the FGM in solid mechanics module. In this case, the first layer of the isotropic FGM plate consists of copper, while the eleventh layer consists of steel. The performance parameters are shown in Table 1. According to the Eq. (18), the material parameters including density and elastic modulus of the intermediate layers follow a functional distribution. Each layer has a thickness of 0.1 mm, and the temperature is maintained at 293 K.

Fig. 2
figure 2

Schematic diagram of the FGM plate simulation model

Full size image
Table 1 Steel–copper material parameters [36]
Full size table

During the modelling process, the heat transfer in solids module is used to simulate the temperature distribution. Thermal conductivity coefficients and constant pressure heat capacity values are assigned to each material layer. Thermal isolation conditions are implemented at the boundary surfaces, while temperature boundaries are defined at the top and bottom interfaces. In conjunction with the solid mechanics module, mechanical parameters such as elastic modulus, Poisson's ratio, and density are assigned to each layer of the linear elastic material. To account for the reflection and refraction effects of sound waves along the longitudinal direction, Floquet periodic boundaries are introduced on both sides of the model, effectively extending the model infinitely along the longitudinal direction [37]. In addition, triangular fine meshing is used to improve simulation accuracy. Subsequently, the wave numbers in the frequency range can be obtained by parametrically scanning the eigenfrequencies and the guided wave dispersion curves of the FGM plates accurately.

3.2 Comparison

To verify the accuracy of the non-hierarchical numerical calculations for the FGM plate, the dispersion curves of an 11-layer FGM plate are calculated by the proposed simulation model and shown in Fig. 3. It shows theoretical calculation results as red circles, while the black solid line represents guided wave dispersion curve derived from the simulation model. A comparison shows that the results from the hybrid theoretical method (State Vector and Legendre Polynomial-GN hybrid method, SVLP-GN) and the frequency domain simulation model are both reliable and stable for frequency-thickness products below 2 MHz × 1.1 mm.

Fig. 3
figure 3

Comparison of the proposed theoretical results and simulation results at 293 K

Full size image

3.3 Guided Wave Propagation in FGM Plate

The volume fraction of a 1 mm isotropic steel–copper FGM plate was then examined as an illustrative example. The material parameters are shown in Table 1, with different assumed values for the gradient index p = 0.2, 0.5, 1, and 2. It is important to note that changing the gradient index directly affects the mechanical properties of the FGM plates, which leads to significant changes in the wave propagating characteristics. As shown in Fig. 4a, the surface is rich in steel at x2 = 0 and rich in copper at x2 = h. This results in an obvious shift in the trend of the volume fraction distribution along the thickness. In addition, at arbitrary positions along the thickness direction for different gradient indices, the two mechanical parameters elastic modulus and density were calculated. Figure 4b, c clearly show a positive correlation between elastic modulus and volume fraction, while the opposite is true for density.

Fig. 4
figure 4

The FGM plate volume fraction and mechanical parameter curves

Full size image

3.4 Convergence Analysis

While traditional methods obtain dispersion curves by solving transcendental equations [38], in this method the solution of dispersion equations is transformed into an eigenvalue problem. When dealing with guided wave propagation problems versus temperature, it is usually necessary to consider the displacement and temperature in the form of a general solution and approximate the fit by Legendre polynomials within the cut-off term M [39]. To observe the convergence of the proposed method, the phase velocity dispersion curves of steel–copper FGM plates with exponential gradient p = 2 are numerically calculated for different cut-off terms: M = 11, 12, 13 and 14 at a temperature of 293 K. As shown in Fig. 5a, for M ≥ 11, the dispersion curves can be effectively plotted in the range of 0–6 MHz. However, in the frequency range near 8 MHz, the calculation results do not agree well for M = 11. From the zoomed plot in Fig. 5b, it can be observed that numerical instability occurs at M = 11, but as the cut-off term increases, the different dispersion curves approach each other. At M = 13 and 14, the frequency dispersion curves show better agreement. Therefore, it can be concluded that in this case a convergent solution can be obtained with a cut-off term of M > 13. It should be noted that setting a higher cut-off term will result in more stable and accurate calculation results, but will also increase the actual calculation time.

Fig. 5
figure 5

Dispersion curves in steel–copper FGM plate at different cut-off orders M at 293 K

Full size image

4 Numerical Results and Discussion

4.1 Effect of Gradient Index on Guided Wave Propagation

To investigate the influence of the gradient index p on the guided wave propagation characteristics, the SVLP-GN method was used to calculate the phase velocity dispersion curves of isotropic FGM plate at 293 K for different values of p (0.2, 0.5, 1, and 2) based on the volume fraction curves mentioned above. The dispersion curves are shown in Fig. 6. The A0 mode is represented by the red solid line with red solid star triangles, the S0 mode by the blue solid line with blue solid dots, and the higher order modes by the black solid lines. The dispersion curves of thermoelastic guided waves can be plotted in the frequency range of 0–8 MHz, with the phase velocity varying with the gradient index within this frequency range. In particular, the phase velocities of the symmetric and antisymmetric modes decrease as the gradient index p increases at 293 K. At the same time, the number of modes within the same frequency range increases and the cut-off frequency of the higher order modes decreases. In addition, as indicated by the red dashed circle, the weak coupling effect becomes more pronounced in the 0–8 MHz range as adjacent higher order modes gradually approach each other.

Fig. 6
figure 6

Dispersion curves of steel–copper FGM plate with different p at 293 K

Full size image

To fulfill the anisotropy characteristics of FGM in practical applications and extend the scope of the proposed computational approach, a theoretical model for anisotropic FGM plate with different gradient indices p versus temperature was developed. Using the material parameters listed in Table 2, we performed numerical calculations of the phase velocity dispersion curves for a 1 mm Si3N4-Zinc FGM plate with different gradient indices (p = 0.2, 0.5, 1, and 2), and the results are shown in Fig. 7.

Table 2 Si3N4-Zinc material parameters [40]
Full size table
Fig. 7
figure 7

Dispersion curves of Si3N4-Zinc FGM plate with different p at 293 K

Full size image

The red solid lines represent the A0 mode, the blue solid lines represent the S0 mode, and the remaining black solid lines represent the higher order modes. It is evident that in the frequency-thickness product range of 0–8 MHz mm, an increase in the exponential gradient leads to a greater number of modes at the same temperature. Furthermore, similar to the isotropic FGM plate, the phase velocity of the anisotropic FGM plate decreases as the gradient index increases. In addition, the phase velocity of the S0 mode exhibits a more pronounced decay compared to the A0 mode at corresponding frequencies. Interestingly, unlike the steel–copper FGM plate, the Si3N4-Zinc FGM plate does not exhibit a significant weak coupling effect between adjacent branches.

4.2 Effect of Temperature on the Guided Wave Propagation in FGM Plate

Numerical calculations of the dispersion curves at different temperatures, keeping the gradient index constant (p = 2), were performed to study the effect of temperature variations on the propagation characteristics of guided waves in FGM plate. The SVLP-GN method was used for these calculations. Furthermore, to study guided wave behaviour in different types of typical FGM plate, we calculated dispersion curves for 1 mm isotropic steel–copper FGM plate and anisotropic Si3N4-Zinc FGM plate. We paid special attention to the interplay between temperature variations and dispersion characteristics. These modes represent the fundamental modes in the lower frequency range and are preferred for ultrasound detection because of their unique weak dispersion and high resolving power. The results are shown in Fig. 8.

Fig. 8
figure 8

Dispersion curves of isotropic and anisotropic FGM plates at 283–523 K

Full size image

In Fig. 8, the dispersion curves are represented by blue solid lines with blue solid dots, triangles, and crosses for temperatures of 283 K, 323 K, and 373 K, respectively. The red solid lines with red solid diamonds, hexagons, and squares correspond to temperatures of 423 K, 473 K, and 523 K, respectively. In general, the changes in phase velocity caused by temperature variations are relatively small compared to the frequency-thickness product. However, a closer look at the phase velocity dispersion curves near the 0.1 MHz frequency range shows that both the A0 and S0 modes exhibit a decrease in phase velocity with increasing temperature. It is worth noting that the temperature-dependent phase velocity changes are more pronounced for the A0 mode compared to the S0 mode. Furthermore, while the phase velocity evolution pattern with temperature remains relatively consistent in the isotropic FGM plate, some minor fluctuations in the phase velocity of the S0 mode are observed in the anisotropic FGM plate.

In Sect. 2, the eigenvalues and eigenvectors of the linear equation system can be obtained simultaneously by solving Eq. (23). At the same time, by substituting the eigenvectors into the expressions of the displacements, the displacement modal structure of any guided wave mode versus temperature can be reconstructed. Here, the displacement distribution curves of the S0 mode at 1 MHz are plotted for the steel–copper functionally gradient material plate at 293–543 K, as shown in Fig. 9. Among them, the red solid lines indicate the displacement distribution curves along the x1 propagation direction versus temperature, and the blue dashed lines indicate the displacement distribution curves along the x2 direction versus temperature, respectively. From Fig. 9b–e, it can be seen that the changes in the displacement modal structure are affected by temperature effects. Moreover, both the u1 and u2 tend to increase as the temperature rises. In addition, the displacement distribution curves show good continuity along the thickness direction.

Fig. 9
figure 9

S0 mode displacement modal structure for steel–copper FGM plate versus temperature

Full size image

4.3 Temperature Sensitivity Analysis

To study the effect of temperature changes on the phase velocity of fundamental modes at different frequencies, steel–copper and Si3N4-Zinc FGM plates are selected with gradient index p = 0.2, 0.5, 1, and 2 as examples. The phase velocity temperature sensitivity curves of the fundamental modes at various frequencies were derived by comparing the dispersion curves obtained at 283 K and 523 K. The results are shown in Figs. 10 and 11. Figure 10 shows that in the 0–1 MHz frequency range, the phase velocity sensitivity values of the symmetric modes exhibit relatively smooth variations. On the other hand, the phase velocity temperature sensitivity of the antisymmetric modes shows consistently negative values, with significantly larger absolute sensitivities than the symmetric modes, indicating strong dispersion effects. Similarly, the anisotropic FGM plate follows a similar pattern as shown in Fig. 11. Notably, in the isotropic FGM plate, the phase velocity temperature sensitivity of the A0 mode in the 0–0.2 MHz range increases with a higher gradient index. In addition, we observe a pronounced phase velocity temperature sensitivity at the zero frequency of the A0 mode in both isotropic and anisotropic FGM plates. In other words, the effect of temperature on the phase velocity can be better explored by utilizing the A0 modes of low frequency guided waves.

Fig. 10
figure 10

Phase velocity sensitivity curves for isotropic steel–copper FGM plate

Full size image
Fig. 11
figure 11

Phase velocity sensitivity curves for anisotropic Si3N4-zinc FGM plate

Full size image

5 Conclusion

This study is aimed at proposing an analytical method to analyze the wave propagation problem of FGM plates versus temperature. The specific findings of the study are as follows:

  1. 1.

    In the framework of Green–Naghdi theory, guided wave dispersion equations along the thickness direction of FGM plates versus temperature are constructed and solved by state vector and Legendre polynomial hybrid approach.

  2. 2.

    A frequency domain simulation model is constructed to verify the effectiveness of the proposed method by simulating the multi-layered plate versus temperature using the same material parameters.

  3. 3.

    The propagation characteristics of guided waves in both isotropic steel–copper plate and anisotropic Si3N4-Zinc FGM plate under different temperature and gradient distribution states are investigated. Some interesting and important phenomena are discovered:

    1. (a)

      The effect of cut-off order on the convergence of the solution is analyzed for the phase velocity dispersion curve of isotropic steel–copper plate in the frequency range 0–8 MHz. It is found that there is good convergence when the Legendre polynomials have a cut-off order of M > 13.

    2. (b)

      A significant influence of the gradient index variation on the mechanical properties of the functionally gradient material, with an increase in the gradient index leading to a decrease in the phase velocity values of the fundamental modes.

    3. (c)

      The effects of different temperature conditions on the dispersion characteristics are investigated. It is found that for a given frequency-thickness product, the phase velocity of both symmetric and anti-symmetric modes decreases with increasing temperature, with A0 mode having higher phase velocity sensitivity at zero frequency.

    4. (d)

      The changes in the displacement modal structure are affected by temperature effects. Both the u1 and u2 tend to increase as the temperature rises.

When applying ultrasonic guided waves for structural health monitoring of the object under test, the temperature can lead to changes in wave propagation, which will affect the accuracy of the monitoring results. This work establishes a link between temperature, gradient distribution, and guided wave dispersion in the FGM plate, which can be subsequently utilized to realize the compensation of guided wave detection under ambient temperatures. It provides a theoretical basis for improving the accuracy of guided wave structural health monitoring technology in variable temperature environments.