Keywords

Introduction

In a traditional inventory system, researchers find the optimal policy separately for producers and retailers. This individual optimal strategy is no longer much beneficial for the whole supply chain system in today’s global market. It has been confirmed that the integrated method results in a remarkable cost-saving and enhanced profit when it is compared with the individual decision made by the producer and the supplier [1]. Therefore, every organization adopted an integrated policy to achieve the mutual benefit of both producer and retailer. In the last few decades, many researchers developed numerous integrated inventory models based on several assumptions. Goyal [2] was the earliest researcher to establish an integrated vendor–buyer inventory model. He reveals that if we optimize joint economic cost for buyer and vendor instead of independent economic cost for buyer and vendor, then it will be profitable for both, i.e., for the whole supply chain. Benerjee [3] presented the integrated inventory model assuming JELS (joint economic lot size). Lu [4] extended single buyer into multiple buyers and developed single-vendor multi-retailer integrated model. So many researchers such as [5,6,7,8,9,10] have developed integrated inventory models considering deterioration for suppliers and retailers. Manna et al. [11] established a production method in a single production process, which is considered to minimize the production cost. Ghosh et al. [12] developed a single-producer multi-retailer supply chain system using the Stackelberg game method to maximize the profits of supply system participants.

Deterioration of items is the phenomenon of decay, dryness, vaporization, or spoilage of products in such a way that they lose their originality and sometimes become useless. Whitin [13] was first researcher who studied inventory of deteriorating items. Ghare and Schrader [14] also considered the impact of deterioration in inventory and developed a mathematical model for deteriorating products. Numerous researchers consider the effect of deterioration in their study and provide a fruitful optimal strategy for deteriorating items [15,16,17]. In most of the studies, it is assumed that deterioration of products starts from the instant of their arrival, i.e., at a retail stage but in reality, it can be seen easily that deterioration takes place during production as well as in transportation. Lin et al. [18] reveal that due to transport deterioration the amount of product acquired by the buyer is always lesser than the product ordered. Soysal et al. [19], Rong et al. [20] considered in-transit deterioration, and Wu and Sarker [9], Lin and Lin [21] have considered in-transit deterioration into an integrated model. Lin and Lin [21] stated that certain types of chemicals, foods, electronic components, etc. start deteriorating from the production stage. Mallick et al. [22] developed a two-level supply chain system for perishable items to optimize integrated overall profit by optimizing the retailer replenishment level and trade period. As soon as the production is completed these items start deteriorating instantly which affects the producer inventory level, thus the negative effect of deterioration during the production stage cannot be neglected. Since the model is deterministic therefore demand and deterioration rate are assumed to be known and constant. However, based on the above literature review, no researcher has considered the effect of deterioration during the production, transportation, and retail stage together in an integrated model. To fulfill this gap, we have considered a three-stage deterioration incorporated with integrated inventory model, which is more realistic for the inventory system.

Motivation and Research Contribution

As the authors have seen in the literature survey part, numerous researchers have worked on integrated model with the deteriorating nature of items. According to our examination of the literature, no researcher has examined the influence of deterioration during the production, transportation, and retail stages in an integrated model. This has motivated authors to consider three-stage deterioration in an integrated system.

This study examined a single-producer single-retailer integrated inventory model considering the three-stage deterioration nature of items. The goal of this research is to determine the ideal number of deliveries, lot size, and replenishment period to reduce the overall integrated cost of the supply chain. Here, deterioration rates in each stage are considered different. The convexity nature of the integrated cost function is represented graphically. A solution method is developed to determine optimal values of the integrated system. Finally, the developed model has been numerically analyzed by a numerical example.

Assumptions and Notations

To formulate the suggested model, we have assumed the below assumptions and notations:

Assumptions

  1. 1.

    One producer and one retailer are considered.

  2. 2.

    A single item having three-stage deterioration during each phase of the supply chain such as production, in-transit, and retail is considered.

  3. 3.

    The rate of production and demand is constant.

  4. 4.

    Shortages are not considered.

  5. 5.

    Deteriorated items are not repaired or replaced.

  6. 6.

    There is a single production cycle and N deliveries per order.

Notations

Symbol

Description

\(P\)

Production rate

\(D\)

Demand rate

Q

Quantity ordered by retailer’s

\(q\)

Quantity received by retailer’s

\(u\)

Cost of transportation per unit time

\(I_{r1} \left( t \right)\), \(I_{r2} \left( t \right)\)

Retailer’s stock level at t during in-transit period and retail period respectively

\(I_{p1} \left( {t_{1} } \right)\), \(I_{p2} \left( {t_{2} } \right)\)

Stock level of producer in production period and non-production period respectively

\(F\)

Fixed ordering cost of retailer per unit time

\(T\)

Cycle length

\(T_{p1}\), \(T_{p2}\)

Production period and non-production period for producer in each cycle

\(T/N\)

Stock cycle length per delivery for retailer

\(T_{r1}\)

Transportation time per shipment

\(\theta_{r}\)

Rate of deterioration for item during in-transit and retail stage

\(\theta_{p}\)

Rate of deterioration for item during production stage

\(h_{r}\), \({ }h_{p}\)

Retailer’s and producer’s unit holding cost per item per unit time respectively

\(d_{r}\)

Retailer’s unit deteriorated cost

\(d_{p}\)

Producer’s unit deteriorated cost

ITC

Integrated total cost per unit time

Model Formulation

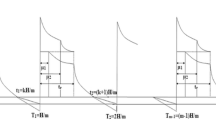
The status of inventory at any time for producer as well as for retailer is depicted in Fig. 7.2. At \(t = 0\), production is started and when one shipment gets ready, it dispatches to the retailer. Therefore, producer’s inventory falls due to demand and raises due to production. After some time, i.e., at \(t = T_{p1}\) the producer stops production and produced items in stores, where inventory level falls due to demand of retailers and deterioration of items. Figure 7.1 shows the inventory status of both the retail and in-transit stages of retailers within one ordering cycle. At time \(t = 0,{ }Q\) unit of the items are shipped to the retailer and \(T_{r1} { }\) is the transportation period per shipment. During in-transit stage \(\left[ {0,T_{r1} } \right]\), items deteriorate with the deterioration rate \(\theta_{r}\) and therefore retailer get \(q{ }\) units of items instead of \(Q\) units. During retail stage \(\left( {T_{r1} , \frac{T}{N} - T_{r1} } \right)\), inventory level falls due to demand of customers and deterioration, and at \(t = T/N\), retailer’s inventory becomes zero and instantly the retailer’s receive next lot dispatched by the producer, and the cycle continues.

Fig. 7.1
figure 1

Retailer’s inventory level during in-transit and retail stage

Full size image
Fig. 7.2
figure 2

Integrated inventory model for producer and retailer

Full size image

Retailer’s Perspective

The inventory differential equation of retailer during retail stage is as follows:

$$ \frac{{{\text{d}}I_{r2} \left( t \right)}}{{{\text{d}}t}} = - \theta_{r} I_{r2} \left( t \right) - D{ },\quad \quad T_{r1} \le t \le \left( {\frac{T}{N} - T_{r1} } \right) $$
(7.1)

With the boundary condition \(I_{r2} \left( {T/N} \right) = 0\), we get

$$ I_{r2} \left( t \right) = \frac{D}{{\theta_{r} }}\left( {e^{{\theta_{r} \left( {\frac{T}{N} - t} \right){ }}} - 1} \right),\quad \quad T_{r1} \le t \le \left( {\frac{T}{N} - T_{r1} } \right) $$
(7.2)
$$ {\text{At}}\,t = T_{r1} ,{ }q = { }\frac{D}{{\theta_{r} }}\left( {e^{{\theta_{r} \left( {\frac{T}{N} - t} \right){ }}} - 1} \right) $$
(7.3)

During in-transit stage, the retailer stock level \(I_{r1} \left( t \right)\) can be represented by the given differential equation

$$ \frac{{{\text{d}}I_{r1} \left( t \right)}}{{{\text{d}}t}} = - \theta_{r} I_{r1} \left( t \right){ },\quad \quad 0 \le t \le T_{r1} $$
(7.4)

With the boundary condition \(I_{r1} \left( {T_{r1} } \right) = q,{ }I_{r1} \left( 0 \right) = Q\), we can get

$$ Q = { }\frac{{De^{{\theta_{r} T_{r1} }} }}{{\theta_{r} }}\left( {e^{{\theta_{r} \left( {\frac{T}{N}{ } - T_{r1} } \right)}} - 1} \right) $$
(7.5)

This is the quantity ordered by the retailer.

The average cost for retailer per unit time:

Retailer’s setup cost \(= \frac{F + uL}{T}\).

Retailer’s holding cost

$$ = \frac{{h_{r} N}}{T}\mathop \int \limits_{{T_{r1} }}^{T/N} I_{r2} \left( t \right){\text{d}}t{ } = \frac{{h_{r} {\text{DN}}}}{{T\theta_{r}^{2} }}\left[ {e^{{\theta_{r} \left( {\frac{T}{N} - T_{r1} } \right)}} - \left( {\frac{T}{N} - T_{r1} } \right) - 1} \right] $$

Deterioration cost for retailer’s

$$ = \frac{{d_{r} N}}{T}\left[ {Q - D\left( {\frac{T}{N} - T_{r1} } \right)} \right] = \frac{{d_{r} {\text{ND}}}}{2T}\theta_{r} \left[ {\left( {\frac{{T^{2} }}{{N^{2} }} - T_{r1}^{2} } \right)} \right] $$

The retailer total average cost is given as:

$$ \begin{gathered} = \frac{{\left( {F + uT_{{r1}} N} \right)}}{T} + \frac{{h_{r} {\text{DN}}}}{{2T}}\left[ {\left( {\frac{T}{N} - T_{{r1}} } \right)^{2} \left( {1 + \frac{{\theta _{r} }}{3}\left( {\frac{T}{N} - T_{{r1}} } \right)} \right)} \right] \hfill \\ + \frac{{d_{r} {\text{ND}}}}{{2T}}\theta _{r} \left[ {\left( {\frac{{T^{2} }}{{N^{2} }} - T_{{r1}} ^{2} } \right)} \right] \hfill \\ \end{gathered} $$
(7.6)

Producer’s Perspective

During production period the producer’s inventory level is given by following differential equations

$$ \frac{{{\text{d}}I_{p1} \left( {t_{1} } \right)}}{{{\text{d}}t_{1} }} = P - D\quad \quad { }0 \le t_{1} \le T_{p1} $$
(7.7)

With boundary condition \(I_{p1} \left( 0 \right) = 0\) and solving Eq. (7.7),

$$ I_{p1} \left( {t_{1} } \right) = \left( {P - D} \right)t_{1} $$
(7.8)

During non-production period the producer’s inventory level is given by

$$ \frac{{{\text{d}}I_{p2} \left( t \right)}}{{{\text{d}}t}} = - \theta_{p} I_{p2} \left( t \right) - D{ },\quad \quad 0 \le t_{2} \le T_{p2} $$
(7.9)

With boundary condition \(I_{p2} \left( {T_{p2} } \right) = 0\) and solving Eq. (7.9),

$$ I_{p2} \left( {t_{2} } \right) = \frac{D}{{\theta_{p} }}\left[ {e^{{\theta_{p} \left( {T_{p2} - t_{2} } \right)}} - 1} \right] $$
(7.10)

At the point \(I_{p1} \left( {T_{1} } \right) = I_{p2} \left( 0 \right),{ }\) we get

$$ T_{p1} = \frac{{{\text{DT}}_{p2} }}{P - D}\left[ {1 + \frac{{\theta_{p} T_{p2} }}{2}} \right] $$
(7.11)

From the relation,

$$ T = T_{p1} + T_{p2} $$
(7.12)
$$ T = \frac{{T_{2} }}{P - D}\left( {p + \frac{1}{2}{\text{d}}\theta T_{2} } \right) $$
(7.13)

Producer’s average cost per unit time.

Set-up cost for producer’s \(= \frac{{S_{p} }}{T}\).

Producer’s holding cost

$$ = \frac{{h_{p} }}{T}\left[ {\mathop \int \limits_{0}^{{T_{p1} }} I_{p1} \left( {t_{1} } \right){\text{d}}t_{1} + \mathop \int \limits_{0}^{{T_{p2} }} I_{p2} \left( {t_{2} } \right){\text{d}}t_{2} - N\mathop \int \limits_{0}^{\frac{T}{N}} I_{r2} \left( {t_{2} } \right){\text{d}}t_{2} } \right] $$
$$ \begin{gathered} = \frac{{h_{p} }}{T}\left[ {\left( {P - D} \right)\frac{{T_{p1}^{2} }}{2} + \frac{{{\text{DT}}_{p2}^{2} }}{2}\left( {1 + \frac{{\theta_{p} T_{p} }}{3}} \right) - \frac{{{\text{NDT}}_{r1}^{2} }}{2}\left( {1 + \frac{{\theta_{r} T_{r1} }}{3}} \right)} \right. \hfill \\ \left. { - \frac{{{\text{ND}}}}{2}\left( {\frac{T}{N} - T_{r1} } \right)^{2} \left( {1 + \frac{{\theta_{r} }}{3}\left( {\frac{T}{N} - T_{r1} } \right)} \right)} \right] \hfill \\ \end{gathered} $$

Deterioration cost for producer’s

$$ = \frac{{d_{{{\text{cp}}}} }}{T}\left[ {\left( {{\text{PT}}_{p1} - {\text{DT}}} \right) - N\left( {Q - D\left( {\frac{T}{N} - T_{r1} } \right)} \right)} \right] $$
$$ = \frac{{d_{{{\text{cp}}}} }}{T}\left[ {\left( {{\text{PT}}_{p1} - {\text{DT}}} \right) - \frac{{{\text{ND}}\theta_{r} }}{2}\left( {\frac{{T^{2} }}{{N^{2} }} - T_{r1}^{2} } \right)} \right] $$

Total cost for the producer is the resultant of setup, holding, and deterioration cost.

$$ \begin{gathered} = \frac{{S_{p} }}{T} + \frac{{h_{p} }}{T}\left[ {\left( {P - D} \right)\frac{{T_{{p1}}^{2} }}{2} + \frac{{DT_{{p2}}^{2} }}{2}\left( {1 + \frac{{\theta _{p} T_{p} }}{3}} \right) - \frac{{{\text{NDT}}_{{r1}}^{2} }}{2}\left( {1 + \frac{{\theta _{r} T_{{r1}} }}{3}} \right)} \right. \hfill \\ \left. { - \frac{{{\text{ND}}}}{2}\left( {\frac{T}{N} - T_{{r1}} } \right)^{2} \left( {1 + \frac{{\theta _{r} }}{3}\left( {\frac{T}{N} - T_{{r1}} } \right)} \right)} \right] + \frac{{d_{{{\text{cp}}}} }}{T}\left[ {\left( {{\text{PT}}_{{p1}} - {\text{DT}}} \right)} \right. \hfill \\ \left. { - \frac{{{\text{ND}}\theta _{r} }}{2}\left( {\frac{{T^{2} }}{{N^{2} }} - T_{{r1}}^{2} } \right)} \right] \hfill \\ \end{gathered} $$
(7.14)

Integrated total cost per unit time

$$ \begin{gathered} = \frac{{\left( {F + uT_{{r1}} N} \right)}}{T} + \frac{{h_{r} {\text{DN}}}}{{2T}}\left[ {\left( {\frac{T}{N} - T_{{r1}} } \right)^{2} \left( {1 + \frac{{\theta _{r} }}{3}\left( {\frac{T}{N} - T_{{r1}} } \right)} \right)} \right] \hfill \\ + \frac{{d_{r} {\text{ND}}}}{{2T}}\theta _{r} \left[ {\left( {\frac{{T^{2} }}{{N^{2} }} - T_{{r1}} ^{2} } \right)} \right] + \frac{{S_{p} }}{T} + \frac{{h_{p} }}{T}\left[ {\left( {P - D} \right)\frac{{T_{{p1}}^{2} }}{2} + \frac{{{\text{DT}}_{{p2}}^{2} }}{2}\left[ {1 + \frac{{\theta _{p} T_{p} }}{3}} \right]} \right. \hfill \\ \left. { - \frac{{{\text{NDT}}_{{r1}}^{2} }}{2}\left[ {1 + \frac{{\theta _{r} T_{{r1}} }}{3}} \right] - \frac{{{\text{ND}}}}{2}\left( {\frac{T}{N} - T_{{r1}} } \right)^{2} \left( {1 + \frac{{\theta _{r} }}{3}\left( {\frac{T}{N} - T_{{r1}} } \right)} \right)} \right] \hfill \\ + \frac{{d_{{{\text{cp}}}} }}{T}\left[ {\left( {{\text{PT}}_{{p1}} - {\text{DT}}} \right) - \frac{{{\text{ND}}\theta _{r} }}{2}\left( {\frac{{T^{2} }}{{N^{2} }} - T_{{r1}}^{2} } \right)} \right] \hfill \\ \end{gathered} $$
(7.15)

Solution Method

The following procedure is followed to find out the optimal solution-

  1. Step 1.

    Place the Eqs. (7.11) and (7.13) in Eq. (7.15).

  2. Step 2.

    Substitute all the values of the parameter.

  3. Step 3.

    Partially Derive ITC w.r.to \(T_{p2}\) and \(T_{r1}\) and put it equal to 0. Point out the resulting minimum value of \(T_{p2}\), for each \(N.\)

  4. Step 4.

    Evaluate the corresponding value of \(T_{p1}\) and \(T\) from Eq. (7.11) and (7.13), for each \(N\).

  5. Step 5.

    Evaluate the optimal number of deliveries \(N^{*}\) s.t. \({\text{ITC}}\left( {N^{*} - 1} \right) \ge {\text{ITC}}\left( {N^{*} } \right) \le {\text{ITC}}\left( {N^{*} + 1} \right)\)

  6. Step 6.

    Evaluate the value of \(Q\), from the Eq. (7.5).

Numerical Example and Sensitivity Analysis

To emphasize the applicability of this model, we assume a numerical example. The data of the numerical example is shown in Table 7.1. On implementing the above solution method, we get the optimal value of N and optimal integrated total cost as \(N = 2,{\text{ ITC}} = \$ 7667.74 \). The corresponding value of production period, non-production period, and other time parameters are presented in Table 7.2. The optimal lot size \(Q^{*} = 16\) units and optimal producer production quantity are 1200 units. The convexity of integrated total cost function (ITC) is graphically depicted in Fig. 7.3.

Table 7.1 Values of parameter for numerical example
Full size table
Table 7.2 Optimal number of delivery (N) and optimal integrated total cost (ITC)
Full size table
Fig. 7.3
figure 3

Convexity of integrated total cost function versus time parameter

Full size image

The output of sensitivity analysis of the major key parameters is shown in Table 7.3. The key parameters of the system are increased and decreased by 20% and the variational sensitivity outcome is depicted in Fig. 7.4. Based on the analysis, we can conclude that the deterioration cost parameters \(\left( {d_{r} ,{ }d_{p} } \right)\) and deterioration rate \(\left( {\theta_{r} ;{ }\theta_{p} } \right)\) are highly sensitive because small increments in \(\left( {d_{r} ,{ }d_{p} } \right)\) and \(\left( {\theta_{r} ;{ }\theta_{p} } \right)\) results high variation in N. Therefore, the manager should give priority to \(\left( {d_{r} ,{ }d_{p} } \right)\) and \(\left( {\theta_{r} ;{ }\theta_{p} } \right)\) parameters.

Table 7.3 Sensitivity analysis of key parameters
Full size table
Fig. 7.4
figure 4

Sensitivity results with respect to key parameters

Full size image

Conclusion

In this study, we introduce an integrated single-producer single-retailer inventory model for three-stage deteriorating items. This paper considers deterioration during each stage like production, transportation, and retail. We have first derived the integrated cost expression and formulated a solution method to obtain optimal lot size, deliveries, replenishment period, and production quantity to minimize the integrated overall cost. Further, a numerical example has been carried out to elaborate the model and conducted the sensitivity analysis to find which key parameters affect the outcome with small change. This model is very realistic for highly volatile items. The convexity of cost expression is exhibited graphically with respect to variable parameters.

This study is limited to single-producer single-retailer which can be extended by considering multi-producer multi-retailer. An interesting extension of this study one can include the carbon emission factor. This paper can also be generalized by assuming price-dependent demand, fuzzy stochastic environment, variable holding cost, and trade credit policies [23, 24].