Keywords

1 Introduction

Numerous authors have investigated the propagation of shock waves in a medium with exponentially changing density [1,2,3,4,5]. Radiation’s repercussions have not been taken into consideration by these authors. Several researchers [6,7,8,9] have developed similar or non-similar solutions for the propagation of a shock wave with radiation heat transfer effects in an exponential medium. The propagation of a strong shock wave through a material whose density changes with distance from the point of the explosion was examined by [10, 11].

In many disciplines of science and engineering, the study of shock waves propagation in a dusty gas is significant due to their vast range of applications(see [12,13,14]). Pai et al. [15] have obtained a similarity solution for the propagation of a shock wave in dusty gas with constant density. Vishwakarma [16] then explored the propagation of shock waves with exponentially varying density in a dusty gas using a non-similarity method. Singh and Vishwakarma [17] explored shock wave propagation with exponentially changing density and radiation heat flux in a dusty gas. The consequences of viscosity have not been considered by these authors.

In the thin transition zone through which the gas travels from its initial state of thermodynamic equilibrium to its final, also equilibrium state, flow variables such as pressure, density, and particle velocity rapidly change. The shock front is the thermodynamic equilibrium inside this region, and it can be significantly affected. As a result, dissipative processes due to viscosity must be considered when analyzing shock wave propagation behind the shock front. Rankine [18], Rayleigh [19], and Taylor [20] explored the dissipative processes caused by viscosity and thermal conduction in the beginning. Henderson et al. [21] investigated the effects of thermal conductivity and viscosity on shock waves in argon. Simeonides [22] investigated the influence of viscousness on hypersonic flow. In a compressible gas, Huang et al. [23] explored viscous shock waves. It’s worth noting that many previous research has remained focused on viscous shocks in a perfect gas. Nevertheless, it is widely recognized that the viscosity in a non-ideal gas, as compared to that in an ideal gas, plays a major role in the characterization of shocks.

To the best of the authors’ knowledge, no research on the effects of viscosity on shock wave propagation has yet been reported. For this purpose, in the current work, we develop a non-similar solution taking viscosity into account for the propagation of a shock wave.

It is believed that the dusty gas is gray and opaque and that the shock is isothermal. Radiation energy and pressure are thought to be insignificant in comparison to material energy and pressure, hence only the radiation flux is taken into account. The non-linear dissipative mechanism due to viscosity q is assumed to be negligibly small, except in the neighborhood of the shock, and is taken as the function of flow variables and their derivatives as in von Neumann and Richtmyer [24]. Small solid particles are treated as a pseudo-fluid to accomplish some fundamental shock propagation properties, with the heat conduction of the mixture considered to be minimal and the flow field preserving the equilibrium flow state (see [25]).

2 Basic Equations and Boundary Conditions

The governing equations incorporating the viscosity term proposed, for the spherically symmetric, one-dimensional unsteady flow with radiation heat flux in a dusty gas, can be written as [9, 16, 24]

$$\begin{aligned}&\dfrac{\partial u}{\partial t}+u \dfrac{\partial u}{\partial r}+\dfrac{1}{\rho } \left( \dfrac{\partial p}{\partial r}+\dfrac{\partial q}{\partial r}\right) =0 \nonumber \\&\dfrac{\partial \rho }{\partial t}+u\dfrac{\partial \rho }{\partial r}+\rho \dfrac{\partial u}{\partial r}+\dfrac{2\rho u}{r}=0\\&\dfrac{\partial e_{m}}{\partial t}+u \dfrac{\partial e_{m}}{\partial r}-\dfrac{p+q}{\rho ^{2}}\left( \dfrac{\partial \rho }{\partial t}+u\dfrac{\partial \rho }{\partial r}\right) +\dfrac{1}{\rho r^{2}}\dfrac{\partial }{\partial r}\left( Fr^{2}\right) =0 \nonumber \end{aligned}$$
(1)

where t and r are the independent time and space coordinates, respectively, p—pressure of the mixture, u—radial direction flow velocity, \(\rho \)—density of the mixture, \(e_{m}\)—internal energy per unit mass of the mixture, F—radiation heat flux, and q—artificial viscosity.

The expression for artificial viscosity q is given by ([26] also see the references within)

$$\begin{aligned} q=\dfrac{1}{2}K^2\rho r^2\dfrac{\partial u}{\partial r}\left( \vert \dfrac{\partial u}{\partial r}\vert -\dfrac{\partial u}{\partial r}\right) \end{aligned}$$
(2)

where K is a constant parameter that can be modified easily in any numerical experiment.

Using Rosseland’s diffusion approximation and assuming local thermodynamic equilibrium, we have

$$\begin{aligned} F=-\dfrac{c\mu }{3}\dfrac{\partial }{\partial r}\left( aT^{4}\right) \end{aligned}$$
(3)

where c—velocity of light, \(\mu \)—mean free path of radiation, and ac/4—Stefan-Boltzmann constant.

The mean free path of radiation \(\mu \) which is a function of absolute temperature T and density \(\rho \) is given by Wang [27] as

$$\begin{aligned} \mu =\mu _{0}\rho ^{\alpha ^{\star }}T^{\beta ^{\star }} \end{aligned}$$
(4)

where \(\alpha ^{\star },\beta ^{\star }\) are constants.

The dusty gas equation of state is as follows: (Pai [28])

$$\begin{aligned} p=\dfrac{1-K_{p}}{1-Z}\rho R^{\star }T \end{aligned}$$
(5)

where \(R^{\star }\)—gas constant, Z—volume fraction of solid particles in the mixture, and \(K_p\)—mass concentration of solid particles.

Z and \(K_p\) are related as

$$\begin{aligned} K_{p}=\dfrac{Z\rho _{sp}}{\rho } \end{aligned}$$
(6)

where \(\rho _{sp}\)—solid particle species density. For an equilibrium flow, \(K_p\) is constant throughout the flow.

The mixture’s internal energy \(e_m\) can be expressed as follows:

$$\begin{aligned} e_{m}=\left[ K_{p}C_{sp}+(1-K_{p})C_{v}\right] T=C_{vm}T \end{aligned}$$
(7)

where \(C_{vm} \)—mixture’s specific heat at constant volume, \(C_v \)—specific heat of a gas at a constant volume, and \(C_{sp} \)—specific heat of solid particles. The specific heat at constant pressure process is

$$\begin{aligned} C_{pm}=K_{p}C_{sp}+(1-K_{p})C_{p} \end{aligned}$$
(8)

where \(C_p \)—specific heat of the gas at constant pressure process.

The ratio of the specific heats of the mixture is given by (see [28])

$$\begin{aligned} \varGamma =\dfrac{\gamma \left( 1+\dfrac{\sigma \beta ^{\prime }}{\gamma }\right) }{1+\sigma \beta ^{\prime }} \end{aligned}$$
(9)

where

$$\begin{aligned} \gamma =\dfrac{C_{p}}{C_{v}} \sigma =\dfrac{K_{p}}{1-K_{p}} \beta ^{\prime }=\dfrac{C_{sp}}{C_{v}}. \end{aligned}$$
(10)

Therefore, the internal energy \(e_m\) is given by

$$\begin{aligned} e_{m}=\dfrac{p(1-Z)}{\rho (\varGamma -1)}. \end{aligned}$$
(11)

The propagation of a spherical shock wave into a resting medium with a small constant counter pressure is investigated. Further, the medium’s initial density is assumed to follow the exponential law

$$\begin{aligned} \rho =A e^{\alpha r} \end{aligned}$$
(12)

where \(A, \alpha \) are the constants which are positive.

The jump conditions across the shock are as follows:

$$\begin{aligned}&u_{2}=\left( 1-\beta \right) V \nonumber \\&\rho _{2}=\frac{\rho _{1}}{\beta } \nonumber \\&p_{2}=(1-Z_{1}-\dfrac{4K^2(1-\beta )^{2}}{\beta e^{\alpha r}})\rho _{1}V^{2} \nonumber \\&F_{2}=(1-\beta )\left[ \dfrac{(1+\varGamma )\beta +(1-\varGamma )-2Z_{1}}{2(\varGamma -1)}-\dfrac{1-Z_{1}}{(\varGamma -1)M_{e}^{2}}+\dfrac{4K^2(1-\beta )(Z_1-\beta )}{\beta e^{\alpha r}(\varGamma -1)}\right] \rho _{1}V^{3} \nonumber \\&z_{2}=\dfrac{z_{1}}{\beta }\nonumber \\&q_2=\dfrac{4K^2(1-\beta )^2 \rho _1 V^2}{\beta e^{\alpha r}} \end{aligned}$$
(13)

where R is the distance between the shock front and the point of symmetry, \(U = \dfrac{dR}{dt} \) is the shock velocity, suffices “1” and “2” are the values just ahead and behind the shock, and \(F_1 = 0\) (see [7]). Also, the expression for \(\beta \) is given by

$$\begin{aligned} \beta =Z_1+\dfrac{1-Z_1}{\varGamma M_e^{2}} \end{aligned}$$
(14)

where

$$\begin{aligned} M_e^{2}=\dfrac{V^{2}}{a_1^{2}} a_1^{2}=\dfrac{\varGamma P_1}{\rho _1(1-Z_1)} \end{aligned}$$
(15)

\(M_e\) stands for the shock-Mach number, which refers to the sound speed \(a_1\) in the dusty gas.

In general, \(Z_1\), the solid particles’ volume fraction at the initial state is not constant. However, because solid particles have a much higher density than gas (Miura and Glass [13]), the volume occupied by solid particles is extremely small, and \(Z_1\) can be assumed to be a small constant. \(Z_1\) is expressed as (Naidu et al. [29])

$$\begin{aligned} Z_1=\dfrac{K_p}{G(1-K_p)+K_p}. \end{aligned}$$
(16)

Here, G is the solid particles density divided by the initial gas density.

Let the solution to Eqs. (1), (2), and (3) be of the form

$$\begin{aligned} u=t^{-1}U(\eta ), \rho =t^{\gamma ^{\star }}D(\eta ), p=t^{\gamma ^{\star }-2}P(\eta ), F=t^{\gamma ^{\star }-3}Q(\eta ), q=t^{\gamma ^{\star }-2}S(\eta ) \end{aligned}$$
(17)

where

$$\begin{aligned} \eta =te^{\delta ^{\star } r} \delta ^{\star }\ne 0 \end{aligned}$$
(18)

and \(\gamma ^{\star }, \delta ^{\star }\) are the constants that will be determined subsequently. The shock surface is chosen to be

$$\begin{aligned} \eta _0=constant \end{aligned}$$
(19)

as a result of which the velocity is given by

$$\begin{aligned} V=-\dfrac{1}{\delta ^{\star } t}. \end{aligned}$$
(20)

As a result, it is self-evident that \(\delta ^{\star }<0\). In the form of (17), the solutions of the equations (1),(2), and (3) are compatible with the shock conditions only if

$$\begin{aligned} \alpha ^{\star } =1, \beta ^{\star }=-\dfrac{5}{2}, \gamma ^{\star }=2, \delta ^{\star }=-\dfrac{\alpha }{2}. \end{aligned}$$
(21)

The Mach number \(M_e\) of the shock is given by

$$\begin{aligned} M_e^2=\dfrac{V^2}{a_1^2}=- \dfrac{4(1-Z_1)A}{\varGamma p_1 \alpha ^2 \eta _0}= constant \end{aligned}$$

For a very strong shock, as \(M_e\) is a constant, and \(p_1\) is of order zero, we assume that the shock holds its enormous strength over a long period of time. As a result, the solutions in the following section are valid whenever \(t>\tau \) until \(Z_1\) stays small, where \(\tau \) is the duration of the initial impulse. It can be obtained from Eqs. (20) and (21) that

$$\begin{aligned} R=\dfrac{2}{\alpha }log\dfrac{t}{\tau }. \end{aligned}$$
(22)

3 Solution

By solving equations (1), (2), and (3), the flow variables in the flow field behind the shock front will be obtained. Equations (17), (20), and (21) provide us

$$\begin{aligned}&\dfrac{\partial u}{\partial t}=u\delta ^{\star } V-V \dfrac{\partial u}{\partial r} \dfrac{\partial \rho }{\partial t}= V \rho \alpha -V \dfrac{\partial \rho }{\partial r} \nonumber \\&\dfrac{\partial p}{\partial t}=-V \dfrac{\partial p}{\partial r} \dfrac{\partial q}{\partial t}=-V \dfrac{\partial q}{\partial r}. \end{aligned}$$
(23)

Using the above Eq. (23) and considering the transformations

$$\begin{aligned}&r^{\prime }=\dfrac{r}{R} u^{\prime }=\dfrac{u}{V} p^{\prime }=\dfrac{p}{p_2} \nonumber \\&\rho ^{\prime }=\dfrac{\rho }{\rho _2} F^{\prime }=\dfrac{F}{F_2} q^{\prime }=\dfrac{q}{q_2} \end{aligned}$$
(24)

in basic equations (1), (2), and (3), we get

$$\begin{aligned}&\dfrac{d\rho ^{\prime }}{dr^{\prime }}=\dfrac{\rho ^{\prime }}{1-u^{\prime }}\left[ 2 log\dfrac{t}{\tau }+\dfrac{du^{\prime }}{dr^{\prime }}+\dfrac{2u^{\prime }}{r^{\prime }}\right] \end{aligned}$$
(25)
$$\begin{aligned}&\dfrac{dp^{\prime }}{dr^{\prime }}=\dfrac{\rho ^{\prime }}{(1-Z_1)\beta }\left[ (1-u^{\prime })\dfrac{du^{\prime }}{dr^{\prime }}+u^{\prime }log\dfrac{t}{\tau }\right] -\dfrac{\Theta }{1-Z_1-\Theta }\dfrac{dq^{\prime }}{dr^{\prime }} \end{aligned}$$
(26)
$$\begin{aligned}&\dfrac{du^{\prime }}{dr^{\prime }}=\dfrac{2(1-\beta )}{r^{\prime }}\sqrt{\dfrac{q^{\prime }}{\rho ^{\prime }\left( t/\tau \right) ^{2r^{\prime }}}} \end{aligned}$$
(27)
$$\begin{aligned} \dfrac{dF^{\prime }}{dr^{\prime }}=&\dfrac{1-Z_1-\Theta }{(1-\beta )\left[ \dfrac{(1+\varGamma )\beta +(1-\varGamma )-2Z_{1}}{2}-\dfrac{1-Z_{1}}{M_{e}^{2}}+\dfrac{\Theta (Z_1-\beta )}{(1-\beta )}\right] } \nonumber \\&\left\{ \left[ \dfrac{(\beta -Z_1 \rho ^{\prime })(1-u^{\prime })^{2}\rho ^{\prime }}{(1-Z_1)\beta ^{2}}-\varGamma p^{\prime }\right] \dfrac{du^{\prime }}{dr^{\prime }}\right. \nonumber \\&\left. +\dfrac{(1-u^{\prime })(\beta -Z_1 \rho ^{\prime })\rho ^{\prime }u^{\prime }log \dfrac{t}{\tau }}{(1-Z_1)\beta ^{2}}-\dfrac{2\varGamma p^{\prime } u^{\prime }}{r^{\prime }}\right. \nonumber \\&\left. -\dfrac{(\beta -Z_1 \rho ^{\prime })(1-u^{\prime })\rho ^{\prime }}{(1-Z_1)\beta ^{2}}\dfrac{\Theta }{1-Z_1-\Theta }\dfrac{dq^{\prime }}{dr^{\prime }}\right. \nonumber \\&\left. -\dfrac{\Theta }{1-Z_1-\Theta }q^{\prime }(\varGamma -1)(1-u^{\prime })\left[ \dfrac{2 log\dfrac{t}{\tau }}{u^{\prime }-1}+\dfrac{1}{\rho ^{\prime }}\dfrac{d\rho ^{\prime }}{dr^{\prime }}\right] \right\} -\dfrac{2F^{\prime }}{r^{\prime }} \end{aligned}$$
(28)
$$\begin{aligned} \dfrac{dq^{\prime }}{dr^{\prime }}=&\dfrac{1-Z_1-\Theta }{\Theta \beta (\beta -Z_1\rho ^{\prime })(1-u^{\prime })(1-Z_1) } \nonumber \\&\left\{ \dfrac{F^{\prime }(1-Z_1)\beta (1-u^{\prime })\sqrt{\rho ^{\prime }} log \dfrac{t}{\tau }}{NL\sqrt{p^{\prime }}\sqrt{\beta -Z_1\rho ^{\prime }}}+(1-u^{\prime })(\beta -Z_1\rho ^{\prime })\rho ^{\prime }u^{\prime }log \dfrac{t}{\tau } \right. \nonumber \\&\left. -2p^{\prime } \beta ^{2}(1-Z_1)log \dfrac{t}{\tau }- \dfrac{2 p^{\prime }u^{\prime }\beta ^{2}(1-Z_1)}{r^{\prime }}\right. \nonumber \\&\left. \left[ p^{\prime } \beta ^{2}(1-Z_1)-(\beta -Z_1\rho ^{\prime })\rho ^{\prime }(1-u^{\prime })^{2}\right] \dfrac{du^{\prime }}{dr^{\prime }} \right\} \end{aligned}$$
(29)

where

$$\begin{aligned} N=\dfrac{4ac\mu _{0} \alpha }{3\sqrt{R^{\star }}^3} \end{aligned}$$

is a non-dimensional radiation parameter and

$$\begin{aligned} L=\dfrac{(\varGamma -1)\sqrt{(1-Z_1-\Theta )^{3}}}{2(1-\beta )\left[ \dfrac{(1+\varGamma )\beta +(1-\varGamma )-2Z_1}{2}-\dfrac{1-Z_1}{M_e^{2}}+\dfrac{\Theta (Z_1-\beta )}{(1-\beta )}\right] \beta \sqrt{(1-K_p)^{3}}} \end{aligned}$$

and

$$\begin{aligned} \Theta =\dfrac{4K^2(1-\beta )^{2}}{\beta (t/\tau )^{2r^{\prime }}}. \end{aligned}$$

The shock conditions get the following form in terms of dimensionless variables

$$\begin{aligned} r^{\prime }=1, p^{\prime }=1, \rho ^{\prime }=1, F^{\prime }=1, q^{\prime }=1, u^{\prime }=1-\beta . \end{aligned}$$
(30)

The solution to our problem is given by Eqs. (25)–(29) along with the boundary conditions (30). Due to the fact that the motion behind the shock can be calculated only when a certain time is supplied, the resulting solution is non-similar.

4 Results and Discussion

From the shock front \(r^{\prime }=1\), we begin the numerical integration of Eqs. (25)–(29) along with boundary conditions (30) and work our way inwards to acquire the solutions. At specified instants when \(t/\tau =2\) or 4, distributions of flow variables \(\rho ^{\prime }=\dfrac{\rho }{\rho _2}, p^{\prime }=\dfrac{p}{p_2}, u^{\prime }=\dfrac{u}{u_2}\) are obtained. For the sake of numerical integration, values of \(K_p, \gamma , G, M_e^{2}, N,\chi \), and K are assumed to be \(K_p=0, 0.2, 0.4; \gamma =1.4; G=10, 50\) (see [15]), \(M_e^{2}=20, N=10\) (see [9]), \(\chi =1\) (see [13]), and \(K=0, 0.0349, 0.349\) (see [26]).

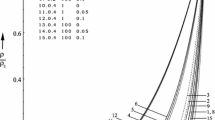
Figures 1, 2, and 3 depict the variation of \(\rho ^{\prime }, p^{\prime }\), and \(u^{\prime }\) with reduced distance \(r^{\prime }\) for varied values of viscosity parameter K at different times \(t/\tau \) for fixed values of \(N,K_p\), and G.

Fig. 1
figure 1

Reduced density \(\rho ^{\prime }\) variation behind the shock front when \(N=10, G=50\), and \(K_p=0.2\)

Full size image
Fig. 2
figure 2

Reduced pressure \(p^{\prime }\) variation behind the shock front when \(N=10, G=50\), and \(K_p=0.2\)

Full size image
Fig. 3
figure 3

Reduced flow velocity \(u^{\prime }\) variation behind the shock front when \(N=10, G=50\), and \(K_p=0.2\)

Full size image

Density \(\rho ^{\prime }\) and pressure \(p^{\prime }\) decline as we travel inwards from the shock front, as seen in Figs. 1 and 2. Further, from Fig. 3, it can be seen that the reduced flow velocity \(u^{\prime }\) increases when \(K=0\) , whereas, it decreases when \(K\ne 0\). In the presence of viscosity, the nature of reduced flow variables(concave upwards) is in contrast with the case of no viscosity \(K=0\)(concave downwards). It can be further observed that when \(K=0\), the values of \(\rho ^{\prime },p^{\prime }\), and \(u^{\prime }\) tend to be the same with the values of Singh and Vishwakarma [17] work.

An increase in the viscosity parameter K causes the density \(\rho ^{\prime }\), the pressure \(p^{\prime }\), and the velocity \(u^{\prime }\) to decrease as well as the slopes of \(\rho ^{\prime }\) and \(p^{\prime }\) to decrease at any point in the flow behind the shock front. An increase in time \(t/\tau \) causes density \(\rho ^{\prime }\), pressure \(p^{\prime }\) to decline, and the flow velocity \(u^{\prime }\) to rise.

Figures 4, 5, and 6 illustrate the reduced flow variables variation with reduced distance for varied values of solid particle mass concentration \(K_p\) and the ratio of solid particle density to initial gas density G for given values of N, K, and \(t/\tau \).

Fig. 4
figure 4

Reduced density \(\rho ^{\prime }\) variation behind the shock front when \(N=10, K=0.349\), and \(t/\tau =2\)

Full size image
Fig. 5
figure 5

Reduced pressure \(p^{\prime }\) variation behind the shock front when \(N=10, K=0.349\), and \(t/\tau =2\)

Full size image
Fig. 6
figure 6

Reduced flow velocity \(u^{\prime }\) variation behind the shock front when \(N=10, K=0.349\), and \(t/\tau =2\)

Full size image

It can be observed from Figs. 4, 5, and 6 that reduced density \(\rho ^{\prime }\), reduced pressure \(p^{\prime }\), and reduced velocity decrease as one moves inside from the shock front. Whereas, the nature of reduced velocity \(u^{\prime }\) (concave downwards) is opposite to those of density \(\rho ^{\prime }\) and pressure \(p^{\prime }\) (concave upwards). When shock travels through a dusty gas, the values of density \(\rho ^{\prime }\), pressure \(p^{\prime }\) increase; however, the shock speed \(u^{\prime }\) drops when compared to a perfect gas (\(K_p=0\)) or a dusty gas with a larger \(K_p\). The existence of solid particles in dusty gas is accountable for this phenomenological behavior.

For given K, N, and G values, increasing the mass concentration of solid particles \(K_p\) increases \(\rho ^{\prime },p^{\prime }\) and decreases \(u^{\prime }\), as well, increases the slopes of density, pressure profiles. Also, an increase in the ratio of solid particle density to initial gas density G for fixed values of N, K, and \(K_p\) results in the decrease of density, pressure and an increase in fluid velocity.