Keywords

1 Introduction

Nowadays, integrated electronics are becoming increasingly important, allowing circuits to be easily inserted into many applications such as telecommunications, transports and domotics. This progress has improved fabrication techniques by producing more efficient components embedded in complex systems [1]. The high integration density of circuits contributes to the increasing problems of electromagnetic compatibility. On the other hand, the increase in the number of functions inside the same chip leads to an increase in parasitic emissions in the form of radiation that can reach the different neighboring circuits. The resolution of electromagnetic interference problems is difficult for systems integrating chips of different types. Let’s take the example of a transmission-reception system, its front end stage corresponds to the analog circuits located between the antenna and the signal processing stage [2]. With the recent development, manufacturers have been able to integrate the transmission, reception, modulation, demodulation and signal processing stages in the same device. This large scale integration means that engineers have to find solutions in the design to avoid time consuming and costly redesign phases [3, 4].

The objective of this paper is to develop and propose mathematical models that represent the electromagnetic field effects, associated with signal and power integrity, in CMOS integrated circuits operating at high frequencies. Indeed, this work is divided as follows: Sect. 2 is dedicated to the state of the art of the existing and electrical interconnections problems in the presence of a parasitic electromagnetic field. The third section discusses examples of electromagnetic coupling between uniform and nonuniform interconnections and with linear and nonlinear loads. Finally, Sect. 4 concludes the paper.

2 Signal Integrity Analytical Study in Deep Sub-micrometer Interconnect Lines

With the development of embedded systems, the modules (analog, digital, microwave, power ...) are more integrated. Therefore, the problems of signal integrity, electromagnetic compatibility (EMC) and reliability in different domain (microelectronics, automotive, aeronautics ...) are increasing [5, 6]. Signal integrity is described as the management behavior of logic signals so as not to disturb the electronic board’s functionality. This will require the study of the influence of passive elements (interconnects, packages and wires) on electronic systems. Electromagnetic emission is generated by electromagnetic disturbances, emitted intentionally or not by the source. This emission can be conducted through power and signal lines, or radiated. In the near field, the mutual coupling mechanism corresponds to inductive and capacitive coupling. The victim is characterized by its electromagnetic susceptibility, which means that it is sensitive to incident electromagnetic interferences. The robustness of the victim to electromagnetic disturbances is quantified by the concept of electromagnetic immunity [7, 8].

2.1 Electromagnetic Coupling Equations of Nonuniform Interconnect Lines

For nonuniform coupled interconnections, to study and analyze the phenomena mentioned above, the quasi transvers electromagnetic model is assumed [9].

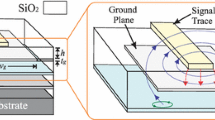
Consider M imperfect interconnect lines immersed in an incident field, as shown in Fig. 1, modeled by the following system of coupled partial differential equations (Telegrapher’s equations) [10, 11]:

$$\begin{aligned} \left\{ \begin{array}{cl} \frac{\partial {\textbf {V}}(x,t)}{ \partial x}+ {\textbf {R}}(x){\textbf {I}}(x,t)+{\textbf {L}}(x)\frac{\partial {\textbf {I}}(x,t)}{ \partial t} = {\textbf {V}}_{{\textbf {s}}} (x,t) \\ \frac{\partial {\textbf {I}}(x,t)}{ \partial x}+ {\textbf {G}}(x){\textbf {I}}(x,t)+{\textbf {C}}(x)\frac{\partial {\textbf {V}}(x,t)}{ \partial t} = {\textbf {I}}_{{\textbf {s}}} (x,t) \end{array} \right. \end{aligned}$$
(1)

where the voltages \({\textbf {V}}\) and currents I are expressed in \(M\times 1\) column vector form, and interconnect parameters R, L, C and G are expressed in \(M\times M\) matrices per unit length distributed voltages and currents, respectively, and are written as follows [11]:

$$\begin{aligned} V_s(x,t)=-\frac{\partial E_T(x,t) }{\partial x}+E_L(x,t) \end{aligned}$$
(2)
$$\begin{aligned} I_s(x,t)=-G(x) E_T(x,t) -C(x)\frac{\partial E_T(x,t)}{\partial x} \end{aligned}$$
(3)

where \({\textbf {V}}_{\textbf {s}}\) and \({\textbf {I}}_{\textbf {s}}\) are expressed in \(M\times 1\) column vector form, \({\textbf {E}}_{\textbf {T}}\) and \({\textbf {E}}_{\textbf {L}}\) are the transverse and longitudinal components of the incident electric field, respectively.

The cross-sectional view of modeled structure is shown in Fig. 1.

Fig. 1
figure 1

Cross-sectional view of multiple interconnects illuminated by an incident field \(\overrightarrow{E}\)

Full size image

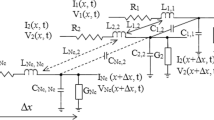
In this work we will present the finite difference method in the time domain (FDTD) to solve the equations system (1). This method is based on the discretization of the spatial domain into Nx cells each of length \(\Delta x\), and the time domain into Nt intervals each of duration \(\Delta t\). This discretization uses an interlaced leap-frog scheme such that the currents are computed at \((t+\Delta t/2)\) steps and \((x+\Delta x)\) positions, whereas the voltages are computed at \((t+\Delta t)\) steps and \((x+\Delta x/2)\) positions.

The recurrence relations of voltage and current along the line interconnects, are given by:

For \(k=2,3, \ldots Nx\)

$$\begin{aligned} V_{k+1/2}^{n}= & {} A_{1} ^{-1}\Big (A_{2} V_{k+1/2}^{n-1}-I_{k}^{n-1/2}+I_{k-1}^{n-1/2}\nonumber \\ {}{} & {} +\Delta x\left( {G_{k} E_{k}^{n}S +\frac{1}{\Delta t}C_{k}({E_{k}^{n+1}-E_{k}^n}}\right) A_{k}\Big ) \end{aligned}$$
(4)

For \(k=1,2,3, \ldots Nx\)

$$\begin{aligned} I_{k}^{n+1/2}=A_3^{-1} \left( {A_4 I_{k}^{n-1/2}-V_{k+1/2}^{n } +V_{k-1/2}^{n } +\frac{\Delta x }{\Delta t} D_k \left( {E_{k}^{n+1}-E_{k}^{n } } \right) }\right) \end{aligned}$$
(5)

With \(A_1, A_2, A_3\) and \(A_4\) are square matrices \(M\times M\) dependent on the line parameters R, L, C and G. The \(M\times 1\) column vectors \(A_k\) and \(D_k\) depend on the position of the interconnections, the characteristics of the incident field and the modal velocities propagated in the structure. So, \(A_1 = \frac{\Delta x}{\Delta t}{} {\textbf {C}}+\frac{\Delta x}{2}{} {\textbf {G}}\); \(A_2 = \frac{\Delta x}{\Delta t}{} {\textbf {C}}-\frac{\Delta x}{2}{} {\textbf {G}}\); \( A_3 = \frac{\Delta x}{\Delta t}{} {\textbf {L}}+\frac{\Delta x}{2}{} {\textbf {R}}\); \(A_4 = \frac{\Delta x}{\Delta t}{} {\textbf {L}}-\frac{\Delta x}{2}{} {\textbf {R}}\), and with \(E_{k}^{n}\) is the incident field at position k and time n.

To determine the voltages and currents at the ends of the structure investigated, the nature of the load circuits must be taken into account. In the following paragraph, nonlinear loads based on CMOS inverters are described in detail.

2.2 Coupled Interconnect Lines with Nonlinear Loads

We consider the structure of Fig. 2. The interconnections are driven by CMOS inverters and are loaded by parallel RC circuits.

Fig. 2
figure 2

a M-interconnects coupled with drivers and loads. b CMOS inverter model

Full size image

In fact, the CMOS inverter can be modeled by several models. The most widely used model in submicron CMOS technology is the alpha power law model. The drain current of the PMOS and NMOS transistors can be given by:

$$\begin{aligned} I_P={\left\{ \begin{array}{ll} {0}, \quad V_g \ge V_{DD}-|V_{TP}| \\ k_lp(V_{DD}-V_g-|V_{TP}|)^{\alpha p/2} (V_{DD}-V_1),\quad V_1 > V_{DD}-V_{SATP} \\ k_sp(V_{DD}-V_g-|V_{TP}|)^{\alpha p},\quad V_1 \le V_{DD}-V_{SATP} \end{array}\right. } \end{aligned}$$
(6a)
$$\begin{aligned} I_{N}={\left\{ \begin{array}{ll} {0},\quad V_g \le V_{TN} \\ k_{ln}(V_g-V_{TN})^{\frac{\alpha n}{2}}V_1,\quad V_1 < V_{SATN} \\ k_{sn}(V_g-V_{TN})^{\alpha n},\quad V_1 \ge V_{SATN} \end{array}\right. } \end{aligned}$$
(6b)

where \(V_{DD}\) and \(V_g\) are the supply voltage and excitation source voltage, respectively. \(k_l\) and \(k_s\) are the parameters in linear and saturation states, respectively, \( \alpha \) is the velocity saturation index and \(V_T\) is the threshold voltage.

The input voltage of the interconnections can be computed by the following recurrence relation:

$$\begin{aligned} V_{1}^{n+1}= & {} Q_{1} V_{1}^{n}+Q_2 \left( {I_{0}^{n}-2I_{1}^{n+1/2}+I_{P}^{n+1}-I_{N}^{n+1}+\frac{1}{\Delta t} C_m \left( V_{g}^{n+1}- V_{g}^{n} \right) }\right) \nonumber \\ {}{} & {} +PW_{1}^{n} \end{aligned}$$
(7)

where

\(Q_1=PA_{1}^{-1}\left( A_{2}+\left( C_m+C_d \right) /\Delta t\right) \), \( Q_{2}=PA_{1}^{-1}\), \(P=\big [ U+A_{1}^{-1} \left( C_{m}+C_d \right) / \Delta t \big ]^{-1}\) and \(W_{1}^{n}=\Delta x A_{1}^{-1}\left( G\left( 1 \right) E_{1}^{n}+\frac{1}{\Delta t} C\left( 1\right) \left( E_{1}^{n+1}-E_{1}^{n} \right) \right) A\left( 1 \right) \),with \(E_{1}^{n}\) is the incident field at position \(k=1\) and time n.

The output voltage is given by the following recurrence relationship:

$$\begin{aligned} V_{Nx+1}^{n+1}=K_1^{-1} \left( K_2 V_{Nx+1}^{n}+I_{Nx}^{n}+K_3 E_{Nx}^{n}+K_4 E_{out}^{n-1}+K_5 E_{Nx}^{n+1} \right) \end{aligned}$$
(8)

Which matrices \(K_{1}, K_{2}, K_{3}, K_{4}\), and \( K_5 \) have the following formulas: \(K_{1}=\frac{\Delta x}{2 \Delta t}C+\frac{ \Delta x}{2} G+\frac{1}{\Delta t}C_L+G_L\); \(K_{2}=\frac{\Delta x}{2 \Delta t}{} {\textbf {C}}+ \frac{1}{\Delta t}C_L\); \(K_3=\frac{\Delta x}{2}GA+\frac{\Delta x}{2\Delta t}CA-\frac{\Delta x^2}{2 \Delta t^2 }CD+ \frac{\Delta x^2}{4\Delta t}GD\); \(K_{4}=-\frac{\Delta x}{2 \Delta t}CA+\frac{\Delta x^2}{4 \Delta t^2}CD-\frac{\Delta x^2}{4 \Delta t}GD\); \(K_5=\frac{\Delta x^2}{4 \Delta t^2}GD\). With \( E_{Nx}^{n}\) is the incident field at position \(k=N_x\) and time n. The relationships of the voltage and current at the input, output and along the line interconnects are implemented in MATLAB. Some examples will be studied in the following section.

3 Examples and Discussion

3.1 Uniform Interconnects Loaded with Nonlinear Circuits and Excited by Incident Field

The example in Fig. 3 considers three coupled interconnects with nonlinear terminations. The three lines are excited by a trapezoidal incident field of amplitude 1 kV/m and rise and fall time \(T_r=T_f=0.1\,\text {ns}\) and pulse width \(T_w=5\,\text {ns}\). In addition, the 2nd interconnect is excited by a trapezoidal voltage source of amplitude 5V with rise and fall time \(T^{\prime }_r=T^{\prime }_f=0.1\,\text {ns}\) and pulse width \( T^{\prime }_w=25\,\text {ns}\).

Fig. 3
figure 3

Example of a three interconnect structure test circuit with nonlinear loads

Full size image

After obtaining the input and output voltage recurrence relations, we implemented them on MATLAB and obtained the following result at the output of the second line (Fig. 4a). We also simulated the structure with the PSPICE tool (Fig. 4b).

Fig. 4
figure 4

Results at the output voltage of the second line, a MATLAB b PSPICE

Full size image

As a conclusion, we found a good agreement between the two results obtained by the MATLAB and PSPICE tools.This proves the accuracy of our model.

3.2 Nonuniform Interconnects Loaded with Nonlinear Circuits and Excited by Incident Field

With the increasing flow of data in telecommunication systems and the increasing demand for faster data processing, there has been a renewed interest in modeling various non-ideal effects of the conductors that interconnect the different subsystems. The example discussed here is frequently found in reality. This example illustrates two nonuniform interconnect lines, the first is excited by a trapezoidal voltage source of delay T = 1 ns and the whole is excited by an external field of delay \(T^{\prime }=3\,\text {ns}\) as shown in Fig. 5.

Fig. 5
figure 5

Schematic of two nonuniform interconnect lines in the presence of an external field \(\overrightarrow{E}\)

Full size image

For this example, we performed simulations with the MATLAB tool. The induced voltage at the input of the 2nd victim line is shown in Fig. 6a. Also, the structure was simulated with the PSPICE tool (Fig. 6a).

Fig. 6
figure 6

Input voltage of the 2nd interconnect nouniform victim line, a MATLAB b PSPICE

Full size image

Comparing both results obtained by MATLAB and PSPICE tools, we observe good agreement between them. Therefore, the proposed models of coupled and nonuniform interconnects are verified.

4 Conclusion

Based on the FDTD method, we have modeled and simulated the electromagnetic coupling between nonuniform interconnect lines loaded by nonlinear circuits, using the telegrapher equations. The signal propagation mode is assumed to be quasi-TEM. Thus we have analyzed the validity of our algorithm implemented on MATLAB using PSPICE in the case of the presence of external conducted and radiated disturbances. The obtained results show a good agreement between the simulations performed with MATLAB and PSPICE. The proposed algorithm has been validated numerically with different examples.