Lncosh-Based Adaptive Control Algorithm for Single-Stage SPV Grid-Interfaced System

Abstract

This work proposes the use of a logarithmic hyperbolic cosine (Lncosh)-based adaptive algorithm for a single-stage solar photovoltaic (SPV) grid-interfaced system. The design incorporates a VSC coupled SPV array to provide active power along with reactive power compensation. It also serves to offer load balancing, reduction of harmonics, and power factor correction. A maximum power point (MPP) extraction method based on the incremental conductance (InC) technique, integrated with the VSC control algorithm, is employed to ensure that the SPV array operates at the MPP under varying levels of irradiation. The Lncosh-based algorithm simultaneously offers benefits of both the least mean squares (LMS) and sign-error LMS algorithms, providing faster convergence without sacrificing the mean-square-error (MSE) performance. The proposed configuration is implemented for simulation in MATLAB with the Simulink environment; the steady-state and the dynamic behavior is observed and verified to be well within recommended limits.

1 Introduction

The last few decades have seen the decay of fossil-fuel-based energy sources as the demand for energy consumption continued to grow. Along with an increasing concern for the global environment, this has motivated the search and development of renewable alternatives. Among these alternatives, there has been widescale adoption of technologies such as SPV systems in the form of distributed energy resources (DERs) [1].

There is a host of difficulties to be tackled when interfacing SPV systems with the utility grid. The majority of these include poor reliability, voltage instability, and degraded power quality [2]. SPV systems may be integrated with the utility grid in either single-stage or double-stage topologies. The double-stage topology performs MPP extraction in the first stage and output power control in the second stage, while the single-stage topology achieves both functions in one stage. Several MPPT techniques have been discussed in [3].

The integration of SPV arrays with the utility grid is done with the help of power electronic converters, mainly VSCs [4]. The converter can be controlled to offer load balancing, reduction of harmonics, power factor correction, and/or zero voltage regulation (ZVR). Numerous algorithms have been reported for the control of VSC coupled SPV systems [5,6,7,8].

The use of algorithms based on adaptive filtering theory, for unfamiliar systems, has confirmed the capability of the theory to track variations in the properties of such systems [2]. The algorithm parameters are self-adjusted in response to changes in the surrounding environment, ensuring that the behavior of the system remains appropriately in order. The least mean squares (LMS) algorithm [9] and sign-error LMS (SELMS) algorithm are two such algorithms that have been used for the control of VSC coupled SPV [10]. The LMS algorithm offers faster convergence compared to the SELMS algorithm [11]; however, the SELMS algorithm offers better mean-square-error (MSE) performance.

Recently a Lncosh-based algorithm, consisting of a cost function employing the natural logarithm of the hyperbolic cosine function, has been proposed in [12]. The Lncosh-based algorithm provides convergence characteristics akin to the LMS algorithm and robustness analogous to the SELMS algorithm [13]. It offers advantages of both the algorithms, performing similar to the LMS algorithm for errors of small magnitude and like the SELMS algorithm for errors of large magnitude [14].

In this work, the proposed Lncosh-based algorithm is implemented for the grid integration of a VSC coupled SPV array. The proposed configuration is implemented for simulation in MATLAB with the Simulink environment for Unity Power Factor (UPF) correction mode of operation as well as load balancing and reduction of harmonics.

1.1 Configuration of Proposed System

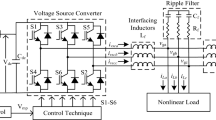
A composite circuit/block diagram representing the proposed configuration is shown in Fig. 1. The procedure for the calculation of the system parameters is given in [15]. The parameters for the proposed configuration are given in the Appendix.

Fig. 1

Configuration of proposed system

2 Control Algorithm

The proposed control algorithm is developed for a single-stage three-phase configuration and consists of two parts: MPP Extraction Control and VSC Control.

The following signals are sensed: SPV array current and voltage (I_spv, V_spv), grid line-voltages at the PCC (v_tab, v_tbc), VSC DC-link voltage (V_dc), three-phase load currents (i_La, i_Lb, i_Lc), and three-phase grid currents (i_ta, i_tb, i_tc).

2.1 MPP Extraction Control

The goal of the MPP Extraction control is to ensure that the SPV array operates at the MPP under varying levels of irradiation, and provide a VSC DC-link reference-voltage ($V_{{{\text{dc}}}}^{r}$) for the sensed VSC DC-link voltage (V_dc) to track.

The output power of the SPV array is proportional to the amount of incident radiation. As a result, peak power extraction is needed to increase performance. An InC-based MPP extraction method is used to acquire the desired power maxima. The method uses incremental changes in V_spv and I_spv to estimate the result of a voltage shift.

In case of the proposed SPV system, the V_dc equals the V_spv. At steady-state, the V_dc equals the SPV array voltage at maximum power (V_MPP). The InC-based MPP extraction method, besides being high-speed and accurate under a variety of environmental conditions, is easy to implement.

2.2 VSC Control

The VSC control algorithm focuses on the generation of a series of trigger signals for the appropriate switching of the converter switches. The algorithm may also offer ancillary services such as load balancing, reduction of harmonics, improved PCC voltage regulation, and power factor correction.

A Lncosh-based converter control algorithm, shown in Fig. 2, is proposed [12].

Fig. 2

Lncosh-based control algorithm for voltage source converter control

The PCC phase voltages (v_ta, v_tb, v_tc) are evaluated from the grid line-voltages (v_tab, v_tbc) sensed at the PCC, using (1).

$$v_\text{ta} = \frac{{2v_\text{tab} + v_\text{tbc} }}{3},v_\text{tb} = \frac{{ - v_\text{tab} + v_\text{tbc} }}{3},v_\text{tc} = \frac{{ - v_\text{tab} - 2v_\text{tbc} }}{3}$$

(1)

From the phase voltage measurements, the unit templates in-phase (x_pa, x_pb, x_pc) with the grid voltage are estimated using (2)

$$x_\text{pa} = \frac{{v_\text{ta} }}{{V_\text{PCC} }},x_\text{pb} = \frac{{v_\text{tb} }}{{V_\text{PCC} }},x_\text{pc} = \frac{{v_\text{tc} }}{{V_\text{PCC} }}$$

(2)

where V_PCC is the magnitude of the PCC terminal voltage, given using (3).

$$V_\text{PCC} = 0.816\sqrt {(v_\text{ta}^{2} \;\; + v_\text{tb}^{2} \; + v_\text{tc}^{2} \;)}$$

(3)

The unit templates in-quadrature (x_qa, x_qb, x_qc) with the grid voltage are derived from x_pa, x_pb, x_pc using (4).

$$x_\text{qa} = \frac{{ - x_\text{pb} + x_\text{pc} }}{\sqrt 3 },x_\text{qb} = \frac{{3x_\text{pa} + x_\text{pb} - x_\text{pc} }}{2\sqrt 3 },x_\text{qc} = \frac{{ - 3x_\text{pa} + x_\text{pb} - x_\text{pc} }}{2\sqrt 3 }$$

(4)

The VSC DC-link voltage (V_dc) is controlled by a P.I. controller in such a way that it tracks the VSC DC-link reference-voltage (V^r_dc). The VSC DC-link voltage error (V_dce) is determined for the ith sampling instant using (5)

$$V_\text{dce} \left( i \right) = V_\text{dc}^{r} \;\left( i \right)\; - V_\text{dc} \left( i \right)$$

(5)

and supplied to the DC-P.I. controller. The DC-P.I. controller provides the in-phase loss component (φ_lp) required to maintain V_dc at V^r_dc. φ_lp is estimated for the ith sampling instant using (6).

$$\varphi_\text{lp} (i + 1) = \varphi_\text{lp} (i) + \lambda_\text{DCp} \left( {V_\text{dce} \left( {i + 1} \right) - V_\text{dce} \left( i \right)} \right) + \lambda_\text{DCi} (i + 1)V_\text{dce} (i + 1)$$

(6)

where λ_DCp and λ_DCi are respectively the values of proportional gain constant and integral gain constant for the DC-P.I. controller.

Similarly, another P.I. controller, termed the AC-P.I. controller, regulates the terminal voltage (V_PCC) so that it tracks the reference terminal voltage ($V_\text{PCC}^{r}$) (set to 0.816 * 415 = 340 V). The terminal voltage error (V_PCCe) is given using (7)

$$V_\text{PCCe} \left( i \right) = V_\text{PCC}^{r} \left( i \right) - V_\text{PCC} \left( i \right)$$

(7)

and acts as input to the AC-P.I. controller. The AC-P.I. controller outputs the quadrature-phase loss component (φ_lq) which is used to regulate V_PCC at $V_\text{PCC}^{r}$. φ_lq is estimated for the ith sampling instant using (8).

$$\varphi_\text{lq} (i + 1) = \varphi_\text{lq} (i) + \lambda_\text{ACp} \left( {V_\text{PCCe} \left( {i + 1} \right) - V_\text{PCCe} \left( i \right)} \right) + \lambda_\text{ACi} (i + 1)V_\text{PCCe} (i + 1)$$

(8)

where λ_ACp and λ_ACi are respectively the values of proportional gain constant and integral gain constant for the AC-P.I. controller.

To improve the performance of the SPV system under dynamic conditions, the control algorithm includes an SPV feed-forward component. The SPV feed-forward component (φ_spv) for the ith sampling instant is given using (9)

$$\varphi_\text{spv} \left( i \right) = 0.66 * \frac{{P_\text{spv} \left( i \right)}}{{V_\text{PCC} }}$$

(9)

where P_spv(i) is the SPV array power output for the ith sampling instant.

The in-phase load component of phase-a (φ_pa), for the ith sampling instant, is evaluated from the proposed Lncosh-based algorithm using (10)

$$\varphi_\text{pa} \left( {i + 1} \right) = \varphi_\text{pa} \left( i \right) + \;\tau_\text{s} \tanh \left[ {\eta_\text{pa} (i)} \right]x_\text{pa} \left( i \right) - \rho \frac{{{\text{sgn}} \left[ {\varphi_\text{pa} \left( i \right)} \right]}}{{1 + \varepsilon \left| {\varphi_\text{pa} \left( i \right)} \right|}}$$

(10)

where τ_s is the step-size, ρ is the zero-attractor coefficient, and ε⁻¹ is the shrinkage coefficient [10, 12]. η_pa(i) is the error of the in-phase current component of phase-a, given for the ith sampling instant using (11)

$$\eta_\text{pa} (i)\; = i_\text{La} (i)\; - x_\text{pa} \left( i \right)\varphi_\text{pa} \left( i \right)$$

(11)

where i_La(i) is the sensed load current in phase-a for the ith sampling instant.

Correspondingly, the in-phase load components of phase-b (φ_pb) and phase-c (φ_pc), for the ith sampling instant, are estimated using (10) for the phases b and c.

The quadrature-phase load component of phase-a (φ_qa), for the ith sampling instant, is evaluated using (12)

$$\varphi_\text{qa} \left( {i\; + 1} \right) = \varphi_\text{qa} \left( i \right) + \tau_\text{s} \tanh \left[ {\eta_\text{qa} \left( i \right)} \right]x_\text{qa} \left( i \right) - \rho \frac{{{\text{sgn}} \left[ {\varphi_\text{qa} \left( i \right)} \right]}}{{1 + \varepsilon \left| {\varphi_\text{qa} \left( i \right)} \right|}}$$

(12)

where τ_s is the step-size, ρ is the zero-attractor coefficient, and ε⁻¹ is the shrinkage coefficient [10, 12]. η_qa(i) is the error of the quadrature-phase current component of phase-a, given for the ith sampling instant using (13).

$$\;\eta_\text{qa} (i)\; = i_\text{La} (i)\; - x_\text{qa} \left( i \right)\varphi_\text{qa} \left( i \right)$$

(13)

Correspondingly, the quadrature-phase load components of phase-b (φ_qb) and phase-c (φ_qc), for the ith sampling instant, are estimated using (12) for the phases b and c.

The total in-phase grid reference-current component (φ_tp) is given using (14)

$$\varphi_\text{tp} = \varphi_\text{Lp} + \varphi_\text{lp} - \varphi_\text{spv}$$

(14)

where the average in-phase load component (φ_Lp) is given using (15).

$$\varphi_\text{Lp} = \frac{{\left( {\varphi_\text{pa} + \varphi_\text{pb} + \varphi_\text{pc} } \right)}}{3}$$

(15)

Similarly, the total quadrature-phase grid reference-current component (φ_tq) is given using (16)

$$\varphi_\text{tq} = \varphi_\text{lq} - \varphi_\text{Lq}$$

(16)

where the average quadrature-phase load component (φ_Lq) is given using (17).

$$\varphi_\text{Lq} = \frac{{\left( {\varphi_\text{qa} + \varphi_\text{qb} + \varphi_\text{qc} } \right)}}{3}$$

(17)

The in-phase reference-currents ($i_{{{\text{tpa}}}}^{*} ,i_{{{\text{tpb}}}}^{*} ,i_{{{\text{tpc}}}}^{*}$) and the quadrature-phase reference-currents ($i_{{{\text{tqa}}}}^{*} ,i_{{{\text{tqb}}}}^{*} ,i_{{{\text{tqc}}}}^{*}$) are estimated using (18) and (19), respectively.

$$i_\text{tpa}^{ * } = \varphi_\text{tp} x_\text{pa} ,i_\text{tpb}^{ * } = \varphi_\text{tp} x_\text{pb} ,i_\text{tpc}^{ * } = \varphi_\text{tp} x_\text{pc}$$

(18)

$$i_\text{tqa}^{ * } = \varphi_\text{sq} x_\text{qa} ,i_\text{tqb}^{ * } = \varphi_\text{sq} x_\text{qb} ,i_\text{tqc}^{ * } = \varphi_\text{sq} x_\text{qc}$$

(19)

The summation of $i_{{{\text{tpa}}}}^{*} ,i_{{{\text{tpb}}}}^{*} ,i_{{{\text{tpc}}}}^{*}$ and $i_{{{\text{tqa}}}}^{*} ,i_{{{\text{tqb}}}}^{*} ,i_{{{\text{tqc}}}}^{*}$ for each phase respectively gives the three-phase total reference-currents ($i_{{{\text{ta}}}}^{*} ,i_{{{\text{tb}}}}^{*} ,i_{{{\text{tc}}}}^{*}$).

$$i_\text{ta}^{ * } = i_\text{tpa}^{ * } + i_\text{tqa}^{ * } ,i_\text{tb}^{ * } = i_\text{tpb}^{ * } + i_\text{tqb}^{ * } ,i_\text{tc}^{ * } = i_\text{tpc}^{ * } + i_\text{tqc}^{ * }$$

(20)

For the generation of VSC trigger signals, a hysteresis current controller (HCC) is brought into use. The HCC takes as input a 3 × 1 vector of error signals generated from calculating the difference between $i_{{{\text{ta}}}}^{*} ,i_{{{\text{tb}}}}^{*} ,i_{{{\text{tc}}}}^{*}$ and i_ta, i_tb, i_tc for each individual phase, respectively and generates the appropriate trigger signals.

3 Simulation Results and Discussion

The proposed configuration is implemented for simulation in MATLAB with the Simulink environment for UPF correction mode of operation, and its steady-state and dynamic behavior is verified under various conditions.

3.1 Steady-State Behavior Under Non-linear Load

The behavior of the proposed configuration, under steady-state, with a non-linear load connected at the PCC is simulated, and the results are shown in Fig. 3. V_dc is sustained at the V_MPP of the SPV array. The active power output (P_t) of the grid is negative as the VSC is supplying some of the active power generated by the SPV array (P_spv) back to the grid. Since the VSC meets the load's reactive power requirements, the grid's reactive power output (Q_t) is zero. The power factor at the grid side is corrected to unity and the grid side total harmonic distortion (THD) values are in agreement with the IEEE-519 standard [16].

Fig. 3

Steady-state behavior under non-linear load

3.2 Dynamic Behavior Under Variable Irradiance

Figure 4 Illustrates the dynamic behavior of the configuration for a simulated change in irradiance G from 1000–600 W/m² at 0.6 s. As G is reduced, the power output P_spv of the SPV array drops; as such P_t rises to a value, less negative than earlier. The output current I_spv of the SPV array and the grid currents i_tabc also decrease. The power factor at the grid side is maintained at unity and the grid side THD values comply with [16].

Fig. 4

Dynamic behavior of the configuration for change in solar irradiance

3.3 Dynamic Behavior Under Imbalanced Load

At 0.35 s, the load connected at phase a is disconnected to simulate an imbalance in load, and the behavior of the configuration is observed. The findings are depicted in Fig. 5. V_dc is maintained as per the MPP extraction control. The further decrease in the value of P_t can be accounted for by the fact that more of the SPV array power P_spv is available to be transferred to the grid side after the loss of load. The voltage and the current waveforms on the grid side are sinusoidal with unity power factor, showing the proper operation of the control algorithm for load balancing. The THD values on the grid side are again observed to be in compliance with the IEEE-519 standard.

Fig. 5

Dynamic behavior of the configuration for imbalance in load

3.4 Comparison with LMS and SELMS Algorithm

In Fig. 6, a comparison of the average in-phase load component (φ_Lp) under a simulated imbalance in load, from 0.25–0.45 s, is shown for the proposed Lncosh-based algorithm, the LMS algorithm, and the SELMS algorithm. The convergence characteristics of the Lncosh-based algorithm are similar to the LMS algorithm and much faster than the SELMS algorithm. The oscillations in φ_Lp for the proposed algorithm are observed to be less than that in the case of LMS and comparable to that for the SELMS algorithms. The THD values for the grid current are 1.60%, 2.87% and 1.53%, respectively, for the proposed Lncosh-based algorithm, the LMS algorithm, and the SELMS algorithm.

Fig. 6

Comparison of the Lncosh-based algorithm against LMS and SELMS algorithms

4 Conclusion

The Lncosh-based adaptive algorithm has been described for the grid interfacing of a single-stage three-phase SPV system. The proposed configuration is implemented for simulation in MATLAB with the Simulink environment. The steady-state behavior and the dynamic behavior of the configuration under conditions of variable irradiance and load imbalance are shown to be reliable. The tracking of the MPP is proper under varying levels of irradiance. Moreover, the response of the proposed control algorithm for a simulated imbalance in load is observed to be better than conventional LMS and SELMS algorithms. The results show correspondence with IEEE-519 standards.

Appendix: System Parameters

Grid voltage, V_LL = 415 V (rms); SPV array parameters: V_MPP = 710 V, I_MPP = 46 A, P_MPP = 32 kW (all parameters at G = 1000 W/m²); VSC DC-link voltage, V_dc = 700 V; interfacing inductance, L_f = 2 * 10^–3 H; DC-link capacitance, C_dc = 8 * 10^–3 F; sampling time, T_s = 1 * 10^–6 s; ripple filter parameters, R_rf = 5Ω, C_rf = 1 * 10^–5 F; AC-P.I. controller parameters, λ_ACp = 0.7 and λ_ACi = 0.5; DC-P.I. controller parameters, λ_DCp = 0.7 and λ_Dci = 0.5; load parameters, 3-phase diode-bridge rectifier feeding a series RL load of 20 Ω and 1 * 10^–1 H; Hysteresis bandwidth = 0.01.