1 Introduction

Recent data suggest the growing importance of renewable energy sources compared to conventional energy sources throughout the world. The degree of penetration of renewable resources in the electric utility grid has also increased substantially in the last decade as policies to incentivize and promote their development are enacted. Among the renewable sources, solar photovoltaic seems to be an appealing energy solution. It provides a wide variety of end-use applications, from commercial utilities to residential rooftops. When effectively harnessed, energy from SPVs has the potential to meet all of the world’s current and projected needs [1,2,3,4,5]. Because of all of its benefits, SPVs are expected to become an essential renewable source during the energy transition to sustainable development in the twenty-first century. Various attempts in the form of improved control strategies have been reported to better integrate SPV generation with the electric utility grid. According to their application, SPV systems may exist in on-grid/off-grid single-stage/double-stage configurations [6]. From the review of various published scientific articles, it can be observed that there are primarily two control objectives that are identified for any of the control algorithms described for the integration of SPV systems: the first being MPPT control and the second being power electronics converter (VSC) control [7,8,9,10,11,12,13,14].

The aim of the MPPT control is to extract the maximum amount of power from SPV array under all situations so that the operational efficiency of the SPV system is improved. Therefore, the selection of a suitable MPPT control is essential. Various MPPT techniques for SPV systems have been discussed and compared in [15]. The traditional perturb and observe (P & O) MPPT technique operates by perturbing the SPV array voltage by a set value and then monitoring the change in power [16]. It is simple to implement but suffers the drawback of occasional deviations from the MPPT under rapidly changing irradiance levels. The implementation of the INC-based algorithm [17] is comparable in complexity to the P and O technique but offers a higher yield under varying levels of irradiance. Several intelligent techniques based on fuzzy control, neural network control and particle swarm optimization have been presented throughout [18,19,20,21,22]. These operate well under the conditions of partial shading and varying atmospheric conditions. The MPPTs based on intelligent techniques do not require an accurate model of the SPV array but may require retuning from time to time.

The type of the load(s) connected at the PCC will determine the amount of reactive power and harmonic drawn from the grid in the absence of any other sources at the PCC. The extensive use of nonlinear loads and occurrence of dynamic disturbances such as unbalanced nonlinear load and variable solar irradiance at PCC lead to various power quality problems reported in [23, 24]. However, the proper operation of the VSC connected at PCC may serve to offer ancillary functions such as harmonics reduction, load balancing, injection of reactive power and hence power factor correction at the point of common coupling (PCC). Thus, there is a need to continually improve VSC control algorithms to achieve [25,26,27,28] flexible and reliable interfacing of SPV systems with the electric utility grid. Different conventional and adaptive control schemes for VSC control have been presented in the literature. Synchronous reference frame theory (SRFT) or d–q control is one of the conventional schemes based on indirect current control technique that employs coordinate transformations (Clarke transformation to convert abc to αβ and Park transformation to convert αβ to dq) to generate DC components of measured parameters for the purpose of VSC control. The control technique maintains the voltage at the PCC along with power factor correction. The SRFT or d–q algorithm when employed with low-pass filter to estimate the direct axis component results in elimination of harmonic components but also degrades the power quality in the distribution grid [29]. Also, SRFT or d–q theory-based control scheme needs to be implemented with PLL (phase-locked loop) to generate unit voltage templates (sine and cosine signals) which results in more computational burden. The instantaneous reactive power theory (IRPT) or p–q-based control algorithm accuracy is largely synchronous frame accuracy dependent. It is based on Clarke transformation to convert rotating frame DC variables into stationary frame AC variables. Then, these components are used to calculate the three-phase active and reactive power. The second harmonic component is mitigated from the estimated powers by employing LPF which makes the system transient response sluggish [30,31,32]. The second-order generalized integrator (SOGI) shows improvement in steady-state performance along with fast dynamic response [33]. However, it is failed to track fundamental load current accurately whenever there is a change in frequency. Hyperbolic tangent function-based least mean square (LMS) control has a very fast dynamic response, but it suffers from large oscillations [34] The adaptive filter theory [35]-based LMS, least mean fourth (LMF), sign-error and normalized LMS control have shown their potential in tracking in varying atmospheric conditions and characteristics. However, while computing weight component corresponding to load current, large steady-state oscillations are associated with LMS and the LMF suffers with slow convergence speed [36,37,38]. A new control algorithm is introduced in [39] obtained by modifying least mean fourth (LMF) so as power quality of SPV system interfaced with distribution grid is improved. Because of fourth-order optimization, the scheme shows good performance in dynamic conditions. However, the scheme is subjected to some shortcomings such as poor steady-state performance and non-capability of DC offset elimination.

The major concern of the proposed work is to maintain power quality for a two-stage SPV gird integrated system in case of dynamic disturbances. The reference grid currents can be obtained by implementation of proposed RA-IHSF algorithm [40] whose main object is extraction of fundamental load current weight components. A robust adaptive technique employing the inverse hyperbolic sine function can provide better steady-state performance and stronger robustness as compared to conventional adaptive filtering algorithms. The performance of the system to implementation of proposed RA-IHSF illustrates that it is more expedient as compared to conventional adaptive filters (for example, LMS and LMF)-based algorithms showing improved dynamic response with less computational burden. Thus, the main aspects of the proposed work are as follows:

  • Utilization of SPV power to feed load.

  • Sinusoidal and balanced grid current in dynamic disturbances such as unbalancing of load and varying solar insolation.

  • Reactive power compensation to load from VSC instead of grid.

  • Power factor correction (PFC) operation.

2 System Description

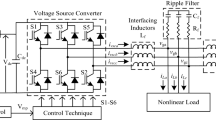
A three-phase, 415 V, 50 Hz grid integrated with a two-stage 44 kW SPV system along with a nonlinear load connected at the PCC is shown in Fig. 1. A DC-link capacitor is required so that SPV array can be interfaced with VSC. The SPV system is incorporated with a DC-to-DC boost converter, and an incremental conductance-based MPPT technique is executed to extract maximum SPV power from the SPV modules. An interfacing inductor is added to the system so as to reduce the ripple in VSC current. The pulses of controlled switching patterns in VSC are generated by the application of proposed RA-IHSF algorithm [40] in grid integrated SPV system. The various components in proposed configuration are estimated in this section.

Fig. 1
figure 1

Proposed system topology

Full size image

The voltage magnitude of DC link \(\left( {V_{{{\text{dc}} - {\text{link}}}} } \right)\) is obtained by the following relation:

$$ V_{{{\text{dc}} - {\text{link}}}} = {{2\sqrt 2 V_{ll} } \mathord{\left/ {\vphantom {{2\sqrt 2 V_{ll} } {\sqrt 3 m}}} \right. \kern-0pt} {\sqrt 3 m}}_{i} $$
(1)

where Vll is line-to-line voltage and mi is the modulation index.

The SPV modules need to be in a single series string (\(N_{S}\)) is obtained as

$$ N_{{\text{s}}} = V_{{{\text{dc}}\_{\text{link}}}} /V_{{{\text{mpp}}}} $$
(2)

where \(V_{{{\text{mpp}}}}\) is rated voltage of SPV array at 1000 W/m2 and 25 °C.

Similarly, the number of series strings connected in parallel \(\left( {N_{{\text{P}}} } \right)\) is estimated as

$$ N_{{\text{P}}} = \left( {P_{{\max }} /V_{{{\text{dc}}\_{\text{link}}}} } \right)/I_{{{\text{mpp}}}} $$
(3)

where \(P_{\max }\) and \(I_{{{\text{mpp}}}}\) is rated power and current of SPV array at 1000 W/m2 and 25 °C, respectively.

The inductor present in DC–DC boost converter is calculated using Eq. (4) [24]

$$ L_{{{\text{boost}}}} = {{V_{{{\text{mpp}}}} \cdot {\text{Duty}}\_Cycle} \mathord{\left/ {\vphantom {{V_{{{\text{mpp}}}} \cdot {\text{Duty}}\_Cycle} {\Delta I_{{\text{a}}} \cdot f_{{{\text{sw}}}} }}} \right. \kern-0pt} {\Delta I_{{\text{a}}} \cdot f_{{{\text{sw}}}} }} $$
(4)

The value of duty cycle can be obtained from MPPT, whereas ∆Ia is the amount of array current’s ripple, while fsw is boost converter switching frequency. The value of interfacing inductor for reducing ripple in VSC current can be calculated using (5) [24]

$$ L_{{{\text{if}}}} = {{\sqrt 3 \cdot m_{{}} \cdot V_{{\text{dc - link}}} } \mathord{\left/ {\vphantom {{\sqrt 3 \cdot m_{{}} \cdot V_{{\text{dc - link}}} } {12 \cdot \lambda \cdot f_{{{\text{vsc}}}} \cdot \Delta I_{{{\text{rip}}}} }}} \right. \kern-0pt} {12 \cdot \lambda \cdot f_{{{\text{vsc}}}} \cdot \Delta I_{{{\text{rip}}}} }} $$
(5)

where m is modulation index, λ is overloading factor, fvsc is switching frequency, and the rated ripple current is denoted by ∆Irip. Here, the value of interfacing inductor is chosen as 2.5 mH. The value of capacitance and resistance of RC filter is set to be 10–5 F and 5 Ω. The capacitance (Cdc) associated with DC link is obtained using (6) [24]

$$ C_{{{\text{dc}}}} = {{P_{{{\text{dc}}}} } \mathord{\left/ {\vphantom {{P_{{{\text{dc}}}} } {2 \cdot \omega \cdot V_{{\text{dc - link}}} \cdot V_{{{\text{dcr}}}} }}} \right. \kern-0pt} {2 \cdot \omega \cdot V_{{\text{dc - link}}} \cdot V_{{{\text{dcr}}}} }} $$
(6)

The parameters of various components shown in Fig. 1 are estimated and tabulated in Table 1.

Table 1 Proposed system parameters
Full size table

3 Control Algorithm

The proposed work is carried out based on two-stage topology of power conversion for integration of SPV with three-phase system. The proposed control scheme is designed to extract maximum SPV power and to maintain power quality at PCC while feeding the extracted solar power to connected loads and grid. Therefore, the overall control consists of two main approaches, namely MPPT control for maximum power extraction and the grid-connected VSC control.

3.1 Control for MPPT

The maximum power can be retrieved from the SPV generation system by implementing a DC-to-DC boost converter with INC-based MPPT control. In INC-based MPPT, the slope of P–V characteristics of SPV system is varied in accordance to the ratio of incremental conductance to instantaneous conductance. Thus, duty cycle of converter is altered as per variation in slope [14].

3.2 Control for Grid-Connected VSC

The grid-connected VSC is operated on the basis of pattern of switching pulses for IGBT-based power electronics switches configured to form VSC as shown in Fig. 2. The proposed control method utilizes a hysteresis current controller (HCC) to produce gating pulses by comparing reference and sensed grid currents. The reference grid currents are estimated by evaluating different weight components. Therefore, the proposed work is about the estimation of active weight component, ψsp, which includes weight component based upon amount of SPV generated power ψpv, weight component corresponding to value of DC-link voltage, ψdc, and active weight component corresponding to load current ψlp. The reactive component, ψsq, comprises weight component corresponding to terminal voltage at PCC, ψtq, and weight component based on reactive component of load current, ψlq.

Fig. 2
figure 2

Proposed control algorithm

Full size image

3.2.1 Robust Adaptive Inverse Hyperbolic Sine Function (RA-IHSF) Algorithm

A robust adaptive technique employing the inverse hyperbolic sine function (IHSF) provides better steady-state performance and stronger robustness when compared to other adaptive filtering algorithms [40].

The cost function of the proposed algorithm is given by:

$$ \begin{aligned} L\left( \theta \right) = & \arg \min J\left[ {L\left( \theta \right)} \right] \\ = & \arg \min \left[ {\sinh^{ - 1} \left( {e^{2} \left( \theta \right)} \right)} \right] \\ \end{aligned} $$
(7)

where e(θ) is estimated error signal of the proposed algorithm.

The calculation of estimated error signal in proposed algorithm is carried out by equation,

$$ e\left( \theta \right) = {\text{d}}\left( \theta \right) - \psi^{{\text{T}}} \left( \theta \right) \cdot x\left( \theta \right) $$
(8)

where x(θ) is input vector. In the modelling of RA-IHSF control for VSC, these vectors are termed as unit in-phase vectors (xpa, xpb, xpc) and unit quadrature vectors (xqa, xqb, xqc), which are required to generate reference active and reactive grid currents. The response d(θ) is modelled as, \({\text{d}}\left( \theta \right) = \psi_{0}^{T} \left( \theta \right) \times x\left( \theta \right) + v(\theta )\), where ψ0 represents the optimal weight vector, while v(θ) represents the source of noise. For given input x(θ) and weight value ψ(θ), the estimated output is represented by term \(\psi^{{\text{T}}} \left( \theta \right) \cdot x\left( \theta \right)\).

The gradient term for the optimization of algorithm is obtained as:

$$ = \frac{{\partial J\left( {\psi \left( \theta \right)} \right)}}{\partial \psi \left( \theta \right)} = \frac{{\partial \left( {\sinh^{ - 1} \left( {e^{2} \left( \theta \right)} \right)} \right)}}{\partial \psi \left( \theta \right)} = \frac{ - 2}{{\sqrt {1 + e^{2} \left( \theta \right)} }}e\left( \theta \right) \cdot x\left( \theta \right) $$
(9)

The iterative scheme is given by:

$$ \psi \left( {\theta + 1} \right) = \psi \left( \theta \right) - \mu \frac{{\partial J\left( {\psi \left( \theta \right)} \right)}}{\partial \psi \left( \theta \right)} $$
(10)
$$ \psi \left( {\theta + 1} \right) = \psi \left( \theta \right) + \frac{2\mu }{{\sqrt {1 + e^{2} \left( \theta \right)} }}e\left( \theta \right) \cdot x\left( \theta \right) $$
(11)

where µ is the step size.

3.2.2 Generation of Reference Grid Currents

The generation of reference grid currents is subdivided into several stages as per the sequence of operations.

3.2.2.1 Estimation of Unit Templates

The line-to-neutral voltages (vga, vgb, vgc) are estimated at PCC using (12) [24]

$$ \left[ {\begin{array}{*{20}c} {v_{ga} } \\ {v_{gb} } \\ {v_{gc} } \\ \end{array} } \right] = \frac{1}{3}\left[ {\begin{array}{*{20}c} {2\quad } \\ { - 1\quad } \\ { - 1\quad } \\ \end{array} \begin{array}{*{20}c} {} \\ {} \\ {} \\ \end{array} \begin{array}{*{20}c} 1 \\ 1 \\ 2 \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {v_{gab} } \\ {v_{gbc} } \\ \end{array} } \right] $$
(12)

where vgab and vgbc are PCC line-to-line voltages.

The magnitude of terminal voltage (Vt) is estimated as:

$$ V_{{\text{t}}} = \sqrt {0.66 \cdot \left( {v_{ga}^{2} + v_{gb}^{2} + v_{gc}^{2} } \right)} $$
(13)

The in-phase unit templates (xpa, xpb, xpc) are determined using (14)

$$ \left[ {\begin{array}{*{20}c} {x_{pa} } \\ {x_{pb} } \\ {x_{pc} } \\ \end{array} } \right] = \frac{1}{{V_{{\text{t}}} }}\left[ {\begin{array}{*{20}c} {v_{ga} } \\ {v_{gb} } \\ {v_{gc} } \\ \end{array} } \right] $$
(14)

The unit templates in-quadrature (xqa, xqb and xqc) can be derived using (15)

$$ \begin{aligned} x_{{qa}} & = \frac{{ - x_{{pb}} + x_{{pc}} }}{{\sqrt 3 }},{\mkern 1mu} \hfill \\ x_{{qb}} &= \frac{{\sqrt 3 x_{{pa}} }}{2} + \frac{{\left( {x_{{pb}} - x_{{pc}} } \right)}}{{2\sqrt 3 }}, \hfill \\ {\mkern 1mu} x_{{qc}} &= - \frac{{\sqrt 3 x_{{pa}} }}{2} + \frac{{\left( {x_{{pb}} - x_{{pc}} } \right)}}{{2\sqrt 3 }} \hfill \\ \end{aligned} $$
(15)
3.2.2.2 Estimation of Weight Component Corresponding to DC-Link Voltage (ψ dc ) and Terminal Voltage at PCC (ψ tq )

The weight component, ψdc, for sustaining DC-link voltage at VSC side is determined using (16) and (17)

$$ V_{{\text{dc - link}}}^{{{\text{err}}}} \left( \theta \right) = V_{{\text{dc - link}}}^{{{\text{refr}}}} \left( \theta \right) - V_{{\text{dc - link}}} \left( \theta \right) $$
(16)

where Vdc-linkerr is the deviation of reference DC-link voltage (Vdc-linkref) from actual DC-link voltage (Vdc-link) at VSC. Vdc-linkerr is utilized for obtaining weight component ψdc in PI controller which can be estimated as,

$$ \begin{aligned} \psi _{{{\text{dc}}}} \left( {\theta + 1} \right)& = \psi _{{{\text{dc}}}} \left( \theta \right) + \xi _{{\text{i}}} V_{{{\text{dc - link}}}}^{{{\text{err}}}} \left( {\theta + 1} \right) \\ & \quad + \xi _{{\text{p}}} \left\{ {V_{{{\text{dc - link}}}}^{{{\text{err}}}} \left( {\theta + 1} \right) - V_{{{\text{dc - link}}}}^{{{\text{err}}}} \left( \theta \right)} \right\} \\ \end{aligned} $$
(17)

where ξi and ξp represent the integral gain and proportional gain, respectively, for the PI controller.

Likewise, another PI controller regulates the magnitude of PCC voltage (Vt) so that it tracks the PCC voltage reference (Vtrefr). The PCC voltage error is given by

$$ V_{{\text{t}}}^{{{\text{err}}}} \left( \theta \right) = V_{{\text{t}}}^{{{\text{refr}}}} \left( \theta \right) - V_{{\text{t}}} \left( \theta \right) $$
(18)

where Vt err is utilized for obtaining quadrature phase loss component ψtq in PI controller which is used to regulate the PCC voltage and can be estimated as,

$$ \begin{aligned}\psi_{{{\text{tq}}}} \left( {\theta + 1} \right) &= \psi_{{{\text{tq}}}} \left( \theta \right) + \xi_{{\text{i}}} V_{{\text{t}}}^{{{\text{err}}}} \left( {\theta + 1} \right)\\ &\quad + \xi_{{\text{p}}} \left\{ {V_{{\text{t}}}^{{{\text{err}}}} \left( {\theta + 1} \right) - V_{{\text{t}}}^{{{\text{err}}}} \left( \theta \right)} \right\} \end{aligned}$$
(19)
3.2.2.3 SPV Feed-Forward Component (ψ pv )

SPV feed-forward component (ψpv) corresponding to extracted SPV power can be estimated as:

$$ \psi_{{{\text{pv}}}} \left( \theta \right) = {{2 \cdot P_{{{\text{PV}}}} \left( \theta \right)} \mathord{\left/ {\vphantom {{2 \cdot P_{{{\text{PV}}}} \left( \theta \right)} {3 \cdot V_{t} }}} \right. \kern-0pt} {3 \cdot V_{t} }} $$
(20)

where PPV is maximum extracted SPV power with the aid of MPPT technique.

3.2.2.4 Active and Reactive Weight Components Corresponding to Load Current

The value of the active weight component corresponding to load current can be found out with the proposed RA-IHSF algorithm. The weight ψlpa corresponding to phase ‘A’ load current, iLa, is estimated as:

$$\begin{aligned} \psi_{lpa} \left( {\theta + 1} \right)& = \psi_{lpa} \left( \theta \right) + 2\mu \cdot \frac{1}{{\sqrt {1 + \varepsilon_{pa}^{2} \left( \theta \right)} }} \\&\quad- \varepsilon_{pa} \left( \theta \right) \cdot x_{pa} \left( \theta \right)\end{aligned} $$
(21)

where µ is step size.

The error ɛpa (θ) is defined using (22).

$$ \varepsilon_{pa} \left( \theta \right) = i_{La} \left( \theta \right) - \psi_{lp} \left( \theta \right) \cdot x_{pa} \left( \theta \right) $$
(22)

Likewise, the active weight components concerned to load currents of phase ‘B’ and ‘C’ are obtained using (23) and (25).

$$ \begin{aligned}\psi_{lpb} \left( {\theta + 1} \right)& = \psi_{lpb} \left( \theta \right) + 2\mu \cdot \frac{1}{{\sqrt {1 + \varepsilon_{pb}^{2} \left( \theta \right)} }} \\&\quad- \varepsilon_{pb} \left( \theta \right) \cdot x_{pb} \left( \theta \right) \end{aligned}$$
(23)

where

$$ \varepsilon_{pb} \left( \theta \right) = i_{Lb} \left( \theta \right) - \psi_{lp} \left( \theta \right) \cdot x_{pb} \left( \theta \right) $$
(24)
$$\begin{aligned} \psi_{lpc} \left( {\theta + 1} \right) &= \psi_{lpc} \left( \theta \right) + 2\mu \cdot \frac{1}{{\sqrt {1 + \varepsilon_{pc}^{2} \left( \theta \right)} }} \\&\quad- \varepsilon_{pc} \left( \theta \right) \cdot x_{pc} \left( \theta \right)\end{aligned} $$
(25)

where

$$ \varepsilon_{pc} \left( \theta \right) = i_{Lc} \left( \theta \right) - \psi_{lp} \left( \theta \right) \cdot x_{pc} \left( \theta \right) $$
(26)

Similarly, the value of reactive weight component of phase ‘A’ load current is determined as:

$$ \begin{aligned}\psi_{lqa} \left( {\theta + 1} \right) &= \psi_{lqa} \left( \theta \right) + 2\mu \cdot \frac{1}{{\sqrt {1 + \varepsilon_{qa}^{2} \left( \theta \right)} }} \\&\quad - \varepsilon_{qa} \left( \theta \right) \cdot x_{qa} \left( \theta \right) \end{aligned}$$
(27)

where µ is step size.

The error ɛqa (θ) is defined using (28)

$$ \varepsilon_{qa} \left( \theta \right) = i_{La} \left( \theta \right) - W_{lq} \left( \theta \right) \cdot x_{qa} \left( \theta \right) $$
(28)

Likewise, the reactive weight components concerned to load currents of phase ‘B’ and ‘C’ are obtained using (29) and (31)

$$ \begin{aligned}\psi_{lqb} \left( {\theta + 1} \right) &= \psi_{lqb} \left( \theta \right) + 2\mu \cdot \frac{1}{{\sqrt {1 + \varepsilon_{qb}^{2} \left( \theta \right)} }} \\&\quad- \varepsilon_{qb} \left( \theta \right) \cdot x_{qb} \left( \theta \right)\end{aligned} $$
(29)

where

$$ \varepsilon_{qb} \left( \theta \right) = i_{Lb} \left( \theta \right) - W_{lq} \left( \theta \right) \cdot x_{qb} \left( \theta \right) $$
(30)
$$ \psi_{lqc} \left( {\theta + 1} \right) = \psi_{lqc} \left( \theta \right) + 2\mu \cdot \frac{1}{{\sqrt {1 + \varepsilon_{qc}^{2} } }} - \varepsilon_{qc} \left( \theta \right) \cdot x_{qc} \left( \theta \right) $$
(31)

where

$$ \varepsilon_{qc} \left( \theta \right) = i_{Lc} \left( \theta \right) - W_{lq} \left( \theta \right) \cdot x_{qc} \left( \theta \right) $$
(32)
3.2.2.5 Calculation of Grid Reference Currents

To calculate the total active grid reference current weight component (ψsp), a sign convention is used. The load and loss components which show power consumption at the PCC are assigned a positive sign, while the SPV feed-forward component which shows power input is assigned a negative sign. The total active grid reference current weight component (ψsp) is calculated by algebraically summing the weight component corresponding to DC-link voltage (ψdc) to the average active load current component (ψlp) and subtracting the SPV feed-forward component (ψpv).

$$ \psi_{sp} = \psi_{lp} + \psi_{dc} - \psi_{pv} $$
(33)

where

$$ \psi_{lp} = {{\left( {\psi_{lpa} + \psi_{lpb} + \psi_{lpc} } \right)} \mathord{\left/ {\vphantom {{\left( {\psi_{lpa} + \psi_{lpb} + \psi_{lpc} } \right)} 3}} \right. \kern-0pt} 3} $$
(34)

Similarly, the total reactive grid reference current component (ψsq) is calculated by subtracting the average reactive load current weight component (ψlq) from the weight component corresponding to terminal voltage at PCC (ψtq),

$$ \psi_{sq} = \psi_{tq} - \psi_{lq} $$
(35)

where

$$ \psi_{lq} = {{\left( {\psi_{lqa} + \psi_{lqb} + \psi_{lqc} } \right)} \mathord{\left/ {\vphantom {{\left( {\psi_{lqa} + \psi_{lqb} + \psi_{lqc} } \right)} 3}} \right. \kern-0pt} 3} $$
(36)

The active reference grid currents are evaluated using (37)

$$ \left[ {\begin{array}{*{20}c} {i_{gpa}^{refr} } \\ {i_{gpb}^{refr} } \\ {i_{gpc}^{refr} } \\ \end{array} } \right] = \psi_{sp} \left[ {\begin{array}{*{20}c} {x_{pa} } \\ {x_{pb} } \\ {x_{pc} } \\ \end{array} } \right] $$
(37)

Similarly, the reactive reference grid currents are evaluated as:

$$ \left[ {\begin{array}{*{20}c} {i_{gqa}^{refr} } \\ {i_{gqb}^{refr} } \\ {i_{gqc}^{refr} } \\ \end{array} } \right] = \psi_{sq} \left[ {\begin{array}{*{20}c} {x_{qa} } \\ {x_{qb} } \\ {x_{qc} } \\ \end{array} } \right] $$
(38)

The total three-phase reference grid currents are calculated by summing up the active and reactive reference grid currents.

$$\begin{aligned} i_{ga}^{refr}& = i_{gpa}^{refr} + i_{gqa}^{refr} ,\,i_{gb}^{refr} = i_{gpb}^{refr} + i_{gqb}^{refr} ,\,i_{gc}^{refr} \\&= i_{gpc}^{refr} + i_{gqc}^{refr} \end{aligned}$$
(39)

The proposed control method with a hysteresis current controller (HCC) is utilized to produce gating pulses for switching of the VSC switching devices. The error signals are computed by comparing actual (iga, igb, igc) and reference grid currents (igarefr, igbrefr, igcrefr). The error signals are then sent through the HCC which generates gating pulses.

4 Results and Discussion

The proposed two-stage SPV gird integrated system with nonlinear load is simulated using RA-IHSF, and the performance of the system is depicted in results. For nonlinear load, the results depict the solar power extraction and reactive power compensation while also providing load balancing at different dynamic conditions such as unbalanced nonlinear load and variable solar irradiance. To illustrate the performance, the waveform of solar irradiance (G), PCC voltages (vg), grid currents (ig), grid real power (PG), grid reactive power (QG), DC-link voltage (VDC), phase ‘a’ load current (iLa), load real power (PL), VSC current (iinv), VSC real power (PC), SPV voltage (VPV), SPV current (IPV), SPV power (PPV) and various calculated weights such as ψlp, ψpv, ψdc and ψsp are shown in Figs 3, 4, 5 and 6 for different conditions. The THD analysis of load current, grid voltage and current is also shown in these figures.

Fig. 3
figure 3

Response for steady-state behaviour proposed system

Full size image
Fig. 4
figure 4

System response for unbalancing of nonlinear load

Full size image
Fig. 5
figure 5

Response of the system for varying irradiance

Full size image
Fig. 6
figure 6

System response for zero solar irradiance

Full size image

4.1 Steady-State Behaviour of Proposed System

The suggested system steady-state performance is obtained by simulating it with a nonlinear load connected at the PCC, and the response is presented in Fig. 3. The phase voltages (vg) and the phase currents (ig) of grid are found to be sinusoidal. The phase angle is 180 degree between phase voltages and currents of grid for each phase indicating grid’s unity power factor operation. The load current waveform for phase ‘A’ (iLa) and the VSC output current waveform for phase ‘A’ (iinv) show their non-sinusoidal nature. Also, the PI controller is firmly maintained the voltage magnitude of VSC-DC link (VDC) to 700 V. The SPV array operates at maximum power point (IPV and VPV) with INC MPPT and so generating maximum power (PPV) at irradiance (G) of 1000 W/m2. The grid active power output (PG) is negative because the VSC is supplying a part of active power generated by the SPV array (PPV) back to the grid after full filling the load active demand (PL). As a result, the grid is absorbing power rather than delivering it. The grid reactive power output (QG) is zero as the VSC supplies the reactive power requirements of the load. The total active grid reference current component (ψsp), weight component corresponding to DC-link voltage (ψdc), the average active load component (ψlp) and SPV feed-forward component (ψpv) are also shown. Also, the total harmonic distortion value for the grid voltage and load current is 0.03% and 23.63%, respectively. The % THD in grid current is found to be 0.28% which is well in agreement with the 5% suggested by the IEEE-519 standard.

4.2 Dynamic Behaviour Under Unbalanced Nonlinear Load

To simulate an unbalanced load, the load connected to phase ‘A’ is removed at 0.3 s and the behaviour of the system is observed and the response is presented in Fig. 4. The phase voltages (vg) and the phase currents (ig) of grid are found to be sinusoidal. Also, the phase angle between phase voltage and current of grid is 180 degree indicating grid’s ability to sustained unity power factor operation during load unbalancing. After 0.3 s, grid current is increased which means more power is transferred to grid as load demand reduces due to phase removal. The load current waveform for phase ‘A’ (iLa) and the VSC output current waveform for phase ‘A’ (iinv) show their non-sinusoidal nature. Also, results shows that the magnitude of phase ‘A’ becomes zero after phase removal at 0.3 s. The SPV array still operates at maximum power point (IPV and VPV) generating maximum power (PPV) as there is no change in irradiance, and only load is unbalanced. The grid active power output (PG) is negative because the VSC is supplying a part of active power from SPV array (PPV) back to the grid after full filling the active load demand (PL). However, the negative magnitude of PG is increased after load unbalancing at 0.3 s, which means more active power is supplied to grid as amount of active load demand is reduced due to phase removal of nonlinear load. The grid reactive power output (QG) is zero as the VSC supplies the reactive power requirements of the load. There is a decrease in ψlp due to load phase removal, while ψpv remains constant as SPV power (PPV) is unchanged due to constant solar insolation in this case, resulting in more negative value of ψsp. The VSC-DC-link voltage (VDC) and magnitude of point of common coupling voltage (Vt) are still well maintained at 700 V and 415 V, respectively. The total harmonic distortion value for the grid voltage and load current is also presented. The % THD in grid current is found to be 0.91% which is well in agreement with the 5% suggested by the IEEE-519 standard.

4.3 Dynamic Behaviour Under Variable Solar Irradiance

Figure 5 illustrates the dynamic behaviour of the system in case of simulated drop in irradiance to 600 W/m2 from 1000 W/m2 at 0.4 s. As the solar irradiance decreases, the extracted SPV power from the SPV (PPV) is reduced; as such the active power output of the VSC is reduced. The output current of the SPV array (IPV) and the grid currents (ig) also decrease. The active power output of the grid (PG) continues to be negative but increases to a value less negative than earlier as a reduced amount of power is available to be supplied back to the grid. The maximum power point operation of the controller is appropriate with the change in the solar irradiance along with VSC-DC-link voltage (VDC) which is well sustained to 700 V. The reactive output power of the grid (QG) is again zero. Three-phase PCC voltage (vg) waveform and three-phase grid current (ig) waveform remain sinusoidal. The load current (iLa) waveform and the VSC output current (iinv) waveform for phase ‘A’ are also shown. The phase angle is 180 degree between each phase voltage and current of grid indicating grid’s unity power factor operation. The grid phase current decreases after the change in irradiance, but the grid phase voltage remains the same. The % THD in grid current found to be 0.60% which is well in agreement with the 5% suggested by the IEEE-519 standard.

Figure 6 illustrates the dynamic behaviour of the system for a simulated drop in solar irradiance from 600 W/m2 to zero at 0.6 s. As the SPV insolation is interrupted, hence, the SPV power drops to zero. The active power of VSC is now zero, and hence, it only supplies the reactive demand of the load. The active power output of the grid (PG) now becomes positive which means that the active power demand of load is now supplied by the grid. This is shown in waveform of grid current (ig) which illustrates the phase reversal of the grid current at zero crossing. The VSC-DC-link voltage (VDC) is still well maintained at 700 V. The reactive power output of the grid (QG) is again zero. The phase grid voltage (vg) waveform and phase grid current (ig) waveform remain sinusoidal. The load current (iLa) waveform and the VSC output current (iinv) waveform for phase ‘A’ are also shown. The voltage and current of each phase of grid are now in-phase and hence indicate grid’s unity power factor operation. The % THD in grid current is found to be 0.58% which is well in agreement with the 5% suggested by the IEEE-519 standard.

4.4 Comparison of RA-IHSF Against Traditional Controls

The proposed RA-IHSF-based control technique is compared with traditional techniques by developing and simulating the Simulink models of conventional LMF and LMS control approach. In dynamic disturbances, oscillations in the active load weight component (ψlp) by the proposed RA-IHSF technique are less than LMS and comparable to LMF technique, while convergence speed of weight computation is more than LMF and comparable to LMS technique as illustrated in Fig. 7a. The proposed RA-IHSF control technique mitigates grid current harmonics more as compared to traditional ones as illustrated in terms of per cent THD in Fig. 7b, c and d. All these comparisons are summarized in Table 2.

Fig. 7
figure 7

Comparison of RA-IHSF with traditional techniques

Full size image
Table 2 Comparison of RA-IHSF with traditional techniques
Full size table

5 Conclusion

The configuration of the grid integrated SPV system with proposed control algorithm is developed and simulated in Simulink environment of MATLAB. The proposed robust adaptive inverse hyperbolic sine function (RA-IHSF)-based control is employed to control the operation of VSC by altering the switching patterns of pulses. Thus, the proposed control approach provides the interfacing of SPV with the grid while maintaining grid current sinusoidal and balanced in dynamic disturbances such as load unbalancing and varying solar insolation. The proposed scheme provides load balancing and reactive power demand and mitigates harmonic content of grid current along with PFC. Maintaining THD values as low as on a system can further assure improved equipment performance and a longer equipment life. Also, reduction in oscillations and better convergence speed are shown in weight computation by implementing RA-IHSF technique. Thus, a much better performance is demonstrated for the developed system when employed with proposed RA-IHSF technique in place of traditional techniques. In the booming era of electric vehicles (EVs), the proposed control approach of VSC can be implemented for operation of charging stations for EVs powered with grid integrated SPV systems.