Keywords

1 Introduction

In present century, fractional calculus has been established as a vibrant field of study in engineering and science, as many researchers are paying interest to it due to its diversified implementation in various fields like heat transfer, signal processing, biology, robotics, electronics, genetic algorithms, control systems, etc. Many mathematical models are governed by fractional order differential equations. These ideas were attributed to Leibniz, Liouville, Riemann, Caputo, etc. The basic literature related to fractional derivatives and integrals is discussed in refs [1, 2].

In examining the physical phenomena, the study of nonlinear FDEs executes a significant role. Various methods have already been implemented to attain exact solutions of FPDEs [3,4,5]. Few distinguished efforts have been noticed by the scientists for analyzing FDEs arising in mathematical physics. In this manuscript, the conformal time fractional CBS equation has been contemplated for the first time.

Consider the conformable time fractional (2+1)-dimensional CBS equation

$$T_t^\alpha u_x - 4u_x u_{xy} - 2u_{xx} u_y + u_{xxxy} = 0$$
(1.1)

where \(\alpha\) denotes the order of conformable derivative. Bogoyavlenskii constructed the CBS equation by utilizing the modified Lax formalism [6, 7]. Later, it was derived by Schiff [8] using self-dual Yang Mills equation. The fundamental interaction of a Riemann wave along the y-axis with a long wave along the x-axis is governed by the CBS equation.

Methods such as Cole Hopf transformation [9], singular manifold method [10, 11], similarity transformations method [12], the Tanh–Coth method [13], the Tanh function method [14], the improved Tanh–Coth method [15], sine–cosine approach [16], the extended homoclinic test approach [17], Hirota’s bilinear method [18], and the Lie transformation method [10, 19] had been employed to acquire solutions of CBS equation. But the extensive study of conformable time fractional CBS equation is just the opening.

The acquired exact solutions for fractional (2+1)-dimensional CBS equation have been documented first time ever in this manuscript.

This paper is systematized as follows. In Sect. 2, introduction to conformable fractional derivative has been provided. The algorithm of generalized Kudryashov and modified Kudryashov technique is provided in Sect. 3. The Kudryashov techniques have been implemented to fractional CBS equation which is discussed in Sect. 4. In Sect. 5, results are furnished, and Sect. 6 concludes the article.

2 Conformable Fractional Derivative

The conformable fractional derivative of a function \(u\left( t \right)\) of order \(\alpha\) is defined by [20,21,22]

$$T_\alpha \left( {u\left( t \right)} \right) = \mathop {\lim }\limits_{\tau \to 0} \frac{{u\left( {t + \tau t^{1 - \alpha } } \right) - u\left( t \right)}}{\tau }\quad {\text{for all}}\,t > 0, \alpha \in \left( {0 ,1} \right)$$
(2.1)

Some properties of conformal fractional derivatives are as follows [22]

  1. (i)

    \(T_\alpha \left( {au + bv} \right) = aT_\alpha \left( u \right) + bT_\alpha \left( v \right)\).

  2. (ii)

    \(T_\alpha \left( {t^\mu } \right) = \mu t^{\mu - \alpha } ,{\text{for all}}\,\mu \in \rm{\mathbb{R}}\).

  3. (iii)

    \(T_\alpha \left( {u*v} \right)\left( t \right) = t^{1 - \alpha } v^{\prime}\left( t \right)u^{\prime}(v(t))\).

3 Algorithm of the Proposed Method

The generalized Kudryashov and modified Kudryashov techniques have been employed to calculate the exact solutions of fractional (2+1)-dimensional CBS equations. A number of researchers have demonstrated the generalization, reliability, and efficacy of this approach [23, 24]. The basic ideas of generalized Kudryashov and modified Kudryashov methods are discussed in Refs. [22, 25, 26].

4 Exact Solution of Time Fractional (2+1)-Dimensional CBS Equation

This segment consists of the solutions of time fractional (2+1)-dimensional CBS equations by utilizing the generalized Kudryashov and modified Kudryashov techniques to calculate the exact solution for the same.

4.1 Application of Generalized Kudryashov Technique

By utilizing the wave transformation [27] \(u\left( {x,y,t} \right) = U\left( \xi \right)\), \(\xi = x + y - \lambda \left( {\frac{t^\alpha }{\alpha }} \right)\), Eq. (1.1) can be reduced as

$$- \lambda U_{\xi \xi } - 6U_\xi U_{\xi \xi } + U_{\xi \xi \xi \xi } = 0$$
(4.1)

where \(\lambda\) is the constant that is to be evaluated later. Now, the value of N is found to be 1 by equating the nonlinear term and highest order derivative term of Eq. (4.1).

Therefore,

$$U\left( \xi \right) = \varphi_0 + \varphi_1 \psi \left( \xi \right)$$
(4.2)

where \(\psi \left( \xi \right) = \frac{1}{1 \pm e^\xi }\).

\(\varphi_0 , \varphi_1\) are constants to be determined.

Next, system of algebraic equations was acquired from Eq. (4.2), substituting the derivatives of \(U\left( \xi \right)\) and considering the ansatz. The same powers of \(\psi^i , \left( {i = 1, 2, 3, \ldots } \right)\) are collected and equate to zero, to acquire the following system of nonlinear equations:

Coefficient of \(\psi^1\):

$$\varphi_1 - \lambda \varphi_1 = 0,$$
(4.3)

Coefficient of \(\psi^2\):

$$- 15\varphi_1 + 6\varphi_1^2 + 3\varphi_1 \lambda = 0,$$
(4.4)

Coefficient of \(\psi^3\):

$$50\varphi_1 - 24\varphi_1^2 - 2\varphi_1 \lambda = 0,$$
(4.5)

Coefficient of \(\psi^4 :\)

$$- 60\varphi_1 + 30\varphi_1^2 = 0,$$
(4.6)

Coefficient of \(\psi^5\):

$$24\varphi_1 - 12\varphi_1^2 = 0,$$
(4.7)

On solving Eqs. (4.3)–(4.7), the following nontrivial solutions can be acquired.

Case I: For \(\varphi_1 = 2, \lambda = 1\) and \(\psi\left( \xi \right) = \frac{1}{1 + e^\xi }\), the new exact solution of the conformable time fractional CBS equation given in Eq. (1.1) can be identified as

$$u_1 \left( {x,y,t} \right) = \frac{{2 + \varphi_0 + \varphi_0 \cos h\left[ { x + y - \frac{ t^\alpha }{\alpha }} \right] + \varphi_0 \sin h\left[ { x + y - \frac{ t^\alpha }{\alpha }} \right]}}{{1 + \cos h\left[ { x + y - \frac{ t^\alpha }{\alpha }} \right] + \sin h\left[ { x + y - \frac{ t^\alpha }{\alpha }} \right]}}$$
(4.8)

Case II: For \(\varphi_1 = 2, \lambda = 1\) and \(\psi \left( \xi \right) = \frac{1}{1 - e^\xi }\), the exact solution of Eq. (1.1) is given by

$$u_{2 } \left( {x,y,t} \right) = \frac{{ - 2 - \varphi_0 + \varphi_0 \cos h\left[ {x + y - \frac{ t^\alpha }{\alpha }} \right] + \varphi_0 \sin h\left[ {x + y - \frac{ t^\alpha }{\alpha }} \right]}}{{ - 1 + \cos h\left[ {x + y - \frac{t^\alpha }{\alpha }} \right] + \sin h\left[ {x + y - \frac{t^\alpha }{\alpha }} \right]}}$$
(4.9)

4.2 Application of Modified Kudryashov Technique

Equation (4.2) can be attained in the aforementioned manner. Next, considering the ansatz \(\psi \left( \xi \right) = \frac{1}{1 \pm a^\xi }\) in Eq. (4.2) and substituting the derivatives of \(U\left( \xi \right)\) in Eq. (4.1), the following equations can be acquired.

Coefficient of \(\psi^1\):

$$- \lambda \varphi_1 \left( {\ln \left( a \right)} \right)^2 + \varphi_1 \left( {\ln \left( a \right)} \right)^4 = 0,$$
(4.10)

Coefficient of \(\psi^2\):

$$3\varphi_1 \lambda \left( {\ln \left( a \right)} \right)^2 + 6\varphi_1^2 \left( {\ln \left( a \right)} \right)^3 - 15\varphi_1 \left( {\ln \left( a \right)} \right)^4 = 0,$$
(4.11)

Coefficient of \(\psi^3\):

$$- 2\varphi_1 \lambda \left( {\ln \left( a \right)} \right)^2 - 24\varphi_1^2 \left( {\ln \left( a \right)} \right)^3 + 50\varphi_1 \left( {\ln \left( a \right)} \right)^4 = 0,$$
(4.12)

Coefficient of \(\psi^4 :\)

$$30\varphi_1^2 \left( {\ln \left( a \right)} \right)^3 - 60\varphi_1 \left( {\ln \left( a \right)} \right)^4 = 0,$$
(4.13)

Coefficient of \(\psi^5\):

$$- 12\varphi_1^2 \left( {\ln \left( a \right)} \right)^3 + 24\varphi_1 \left( {\ln \left( a \right)} \right)^4 = 0,$$
(4.14)

On solving Eqs. (4.10)–(4.14), the following nontrivial solutions can be attained.

Case I: For \(\varphi_1 = 2\ln \left( a \right),\lambda = \left( {{\text{ln}}\left( a \right)} \right)^2\) and \(\psi \left( \xi \right) = \frac{1}{1 + a^\xi }\), the new exact solution of the conformable time fractional CBS equation given in Eq. (1.1) can be identified as

$$u_3 \left( {x,y,t} \right) = \frac{{\varphi_0 a^{x + y} + \varphi_0 a^{\frac{{t^\alpha \left( {\ln \left( a \right)} \right)^2 }}{\alpha }} + 2 a^{\frac{{t^\alpha \left( {\ln \left( a \right)} \right)^2 }}{\alpha } } \ln \left( a \right)}}{{a^{x + y} + a^{\frac{{t^\alpha \left( {\ln \left( a \right)} \right)^2 }}{\alpha }} }}.$$
(4.15)

Case II: For \(\varphi_1 = 2\ln \left( a \right),\lambda = \left( {{\text{ln}}\left( a \right)} \right)^2\) and \(\psi \left( \xi \right) = \frac{1}{1 - a^\xi }\), the exact solution of Eq. (1.1) is given by

$$u_4 \left( {x,y,t} \right) = \frac{{\varphi_0 a^{x + y } - \varphi_0 a^{\frac{{t^\alpha \left( {\ln \left( a \right)} \right)^2 }}{\alpha }} - 2 a^{\frac{{t^{\alpha } \left( {\ln \left( a \right)} \right)^2 }}{\alpha } } \ln \left( a \right)}}{{a^{x + y} - a^{\frac{{t^\alpha \left( {\ln \left( a \right)} \right)^2 }}{\alpha }} }}$$
(4.16)

5 Results

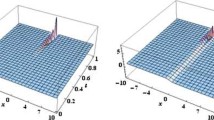
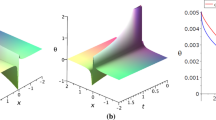
The exact solutions of conformable time fractional (2+1)-dimensional CBS equation have been attained for the first time by employing the generalized Kudryashov and modified Kudryashov techniques with the aid of wave transform. The following 3D graphical models of the obtained solutions \(u\left( {x,y,t} \right)\) have been illustrated in Figs. 1, 2, 3, 4, 5, 6, 7, and 8 for various values \(\alpha\) and by choosing appropriate values to the parameters.

Fig. 1
figure 1

3D plot of \(u_1 \left( {x,y,t} \right)\) for time fractional CBS equation given in Eq. (4.8) when \(\varphi_0 = 1, y = 1,\) at (i) \(\alpha = 0.25\), (ii) \(\alpha = 0.5\)

Full size image
Fig. 2
figure 2

3D plot of \(u_1 \left( {x,y,t} \right)\) for time fractional CBS equation given in Eq. (4.8) when \(\varphi_0 = 1, y = 1,\) at (i) \(\alpha = 0.75\), (ii) \(\alpha = 1\)

Full size image
Fig. 3
figure 3

3D plot of \(u_2 \left( {x,y,t} \right)\) for time fractional CBS equation given in Eq. (4.9) when \(\varphi_0 = 1, y = 1,\) at (i) \(\alpha = 0.25\), (ii) \(\alpha = 0.5\)

Full size image
Fig. 4
figure 4

3D plot of \(u_2 \left( {x,y,t} \right)\) for time fractional CBS equation given in Eq. (4.9) when \(\varphi_0 = 1, y = 1,\) at (i) \(\alpha = 0.75\), (ii) \(\alpha = 1\)

Full size image
Fig. 5
figure 5

3D plot of \(u_3 \left( {x,y,t} \right)\) for time fractional CBS equation given in Eq. (4.15) when \(\varphi_0 = 1, y = 1, a = 2\) at (i) \(\alpha = 0.25\), (ii) \(\alpha = 0.5\)

Full size image
Fig. 6
figure 6

3D plot of \(u_3 \left( {x,y,t} \right)\) for time fractional CBS equation given in Eq. (4.15) when \(\varphi_0 = 1, y = 1, a = 2\) at (i)\(\alpha = 0.75\), (ii) \(\alpha = 1\)

Full size image
Fig. 7
figure 7

3D plot of \(u_4 \left( {x,y,t} \right)\) for time fractional CBS equation given in Eq. (4.16) when \(\varphi_0 = 1, y = 1, a = 2\) at (i)\(\alpha = 0.25\), (ii) \(\alpha = 0.5\)

Full size image
Fig. 8
figure 8

3D plot of \(u_4 \left( {x,y,t} \right)\) for time fractional CBS equation given in Eq. (4.16) when \(\varphi_0 = 1, y = 1, a = 2\) at (i)\(\alpha = 0.75\), (ii) \(\alpha = 1\)

Full size image

6 Conclusion

Here, the solitary wave solutions of conformable time fractional (2+1)-dimensional CBS equations are investigated. The generalized Kudryashov and modified Kudryashov techniques have successfully implemented to formally derive these solutions. To visualize the mechanism of fractional CBS equation, the graphs of the acquired solutions are furnished by selecting suitable values to the parameters. This discourse evident that the focused methods are efficacious for analytical solutions of higher order FDEs. It can also be manifested that the methods are thoroughly dependable and significant to discover new exact solutions.