Introduction

Fractional calculus has been participated a significant role in numerous applications for modeling anonymous diffusion, signal processing, image processing, control theory and various other dynamical system [1,2,3,4]. Fractional differential equations (FDEs) have appealed great consideration because of their implementations in various physical difficulty. The descriptions of properties of physical happenings are aptly described by FDEs. Therefore, an efficient technique is required for solving nonlinear FDEs. Different analytical and numerical techniques have been utilized to derive approximate and exact solutions of FDEs [5,6,7,8].

The analysis of nonlinear equations performs a significant part in examining the physical phenomena. Both mathematicians and physicists made noteworthy development in analysing explicit solutions of nonlinear FDEs. In this present article, the emphasis is on the implementation of the Kudryashov technique for determining the analytical exact solution of time-fractional KDE with a prospect to demonstrate the efficiency of this technique in managing nonlinear equation. This method is comparatively a new approach that provides analytical solutions to both linear and nonlinear problems. It may be deemed as an effective tool for physicists, scientists and applied mathematicians in order to yield analytical exact solutions to the generalized differential equations.

Some noteworthy attempt has been anticipated by the researchers for studying nonlinear equations arising in mathematical physics. Here, the KDE has been considered, that plays an essential part both in applied mathematics and physics. The analysis of nonlinear equations performs a significant part in examining the physical phenomena.

Consider the time-fractional KD equations as follows

$$ \begin{array}{ll} &D_{t}^{\alpha } u - u_{xxx} - 6buu_{x} + \frac{3}{2}au^{2} u_{x} - 3v_{y} + 3au_{x} v = 0,\hfill \\ & \quad u_{y} = v_{x} , \hfill \\ \end{array}$$
(1.1)

where \( \alpha \)\( (0 < \alpha \le 1) \) denotes the order of fractional derivative, a and b are real parameters. The KDE is a new nonlinear integrable evolution equation on two spatial dimensions and one temporal. It was first derived by Konopelchenko and Dubrovsky [9] in 1984. KDE of integer order appears in a great variety of subjects as such in physics, signals processing, dynamics and control theory, and has attracted much attention of more and more scholars.

Numerous methods such as the Exp-function method [11], homogenous balance method [10], the inverse scattering transform method [9], the F-expansion method [12], the improved tanh function method [13, 14], the tanh-sech method, the cosh-sinh method and exponential method [15], Hirota’s method [16], \( \left( {G^{\prime}/G} \right) \)-expansion method [17], rational expansion method [18], and singular manifold method [19] had been utilized to attain exact solutions of KDE.

But the comprehensive analysis of the nonlinear fractional KDE is just the opening. The exact analytical solutions of fractional KDE have been documented first time ever in this manuscript. Hence, the main objective is to establish novel exact solutions of fractional KDE by utilizing the generalized Kudryashov technique.

The manuscript is organized as follows. An introduction to fractional calculus, definitions of Jumarie’s modified Riemann–Liouville (mRL) derivative have been provided in Sect. 2. In Sect. 3, the algorithm to solve FPDEs by utilizing generalized Kudryashov technique via fractional complex transform is proposed. The Kudryashov technique has been employed to establish the new analytical solutions for fractional KDE is discussed in Sect. 4. The numerical simulations are presented in Sects. 5 and 6 completes the manuscript.

Modified Riemann–Liouville Derivative

The Jumarie’s mRL derivative [20, 21] of order \( \alpha \) is stated by

$$ g^{(\alpha )} (t) = \mathop {\lim }\limits_{h \to 0} \left( {\frac{{\sum\limits_{k = 0}^{\infty } {( - 1)^{k} \left( {\begin{array}{*{20}c} \alpha \\ k \\ \end{array} } \right)g\{ t + (\alpha - k)h\} } }}{{h^{\alpha } }}} \right),\quad \alpha \in \Re ,\quad 0 < \alpha \le 1 $$
(2.1)

which can be written as

$$ D_{t}^{\alpha } g(t) = \left\{ {\begin{array}{*{20}l} {\frac{1}{\varGamma ( - \alpha )}\int\limits_{0}^{t} {(t - \xi )^{( - \alpha - 1)} [g(\xi ) - g(0)]d\xi } } \hfill & {\text{if}\quad \alpha < 0} \hfill \\ {\frac{1}{\varGamma ( - \alpha )}\frac{d}{dt}\int\limits_{0}^{t} {(t - \xi )^{ - \alpha } [g(\xi ) - g(0)]d\xi } } \hfill & {\text{if}\quad 0 < \alpha < 1} \hfill \\ {[g^{(\alpha - m)} (t)]^{(n)} } \hfill & {\text{if}\quad m \le \alpha < m + 1,m \ge 1} \hfill \\ \end{array} } \right. $$
(2.2)

Algorithm of Generalized Kudryashov method

The steps involving generalized Kudryashov technique are discussed below:

Step 1 Consider a nonlinear FPDE, comprising two variables \( x \) and \( t \) as

$$ P\left( {u,u_{x} ,u_{xx} ,u_{xxx} , \ldots D_{t}^{\alpha } u, \ldots } \right) = 0,\quad 0 < \alpha \le 1 $$
(3.1)

where \( P \) is a polynomial involving \( u \) and its various partial derivatives and nonlinear terms, u = u(x, t) is an unknown function.

Step 2 Utilizing the FCT [22, 23]:

$$ u\left( {x,t} \right) = U\left( \xi \right),\quad \xi = c_{1} \left( {x - \frac{{kt^{\alpha } }}{\varGamma (\alpha + 1)}} \right) $$
(3.2)

where \( c_{1} \) and \( k \) are constants that are to be evaluated later. Hence the FDE is transformed to the following ODE for \( u(x,t) = U(\xi ) \):

$$ P(U,c_{1} U^{\prime},c_{1}^{2} U^{\prime\prime}, \ldots , - c_{1} kU^{\prime}, \ldots ) = 0. $$
(3.3)

Here, P is function of \( U(\xi ) \) and “׳” denotes \( \frac{d}{d\xi }. \)

Step 3 Suppose that the solution of Eq. (3.3) can be expressed by a polynomial in \( \phi (\xi ) \) as follows:

$$ U(\xi ) = \sum\limits_{n = 0}^{N} {a_{n} } \phi^{n} (\xi ), $$
(3.4)

where \( a_{n} ,n = 0,1,2, \ldots ,N \)\( (a_{N} \ne 0) \) are constant to be evaluated, the integer N is computed by balancing the nonlinear term with the highest order derivative term occurring in Eq. (3.3) and \( \phi (\xi ) \) is the function of the form

$$ \phi (\xi ) = \frac{1}{1 + \exp (\xi )}, $$
(3.5)

that satisfies the ODE

$$ \frac{d}{d\xi }\phi (\xi ) = \phi^{2} (\xi ) - \phi (\xi ). $$
(3.6)

Step 4 Putting Eq. (3.4) in Eq. (3.3) and utilizing Eq. (3.5), collecting all the terms with the same powers of \( \phi^{i} (i = 0,1,2, \ldots ) \) together, the eq. (3.3) is transformed to a new polynomial in \( \varphi \). Equating every coefficient of this polynomial to zero provides a set of algebraic equations for \( a_{i} (i = 0,1,2, \ldots ,n) \).

Step 5 The algebraic equations acquired above can be solved and subsequently substituted in Eq. (3.4), the explicit exact solutions of Eq. (3.1) can be attained immediately.

Analytical solution of time-fractional KDE

This segment consists of the solutions of fractional KDE by using the newly proposed Kudryashov technique to calculate the exact solution of time-fractional KDE (1.1).

By applying the FCT \( \xi = k_{1} x + k_{2} y + \frac{{k_{3} t^{\alpha } }}{\varGamma (\alpha + 1)} \), Eq. (1.1) can be converted to the nonlinear ODEs as:

$$ \begin{aligned} k_{3} U^{\prime} - k_{1}^{3} U^{\prime\prime\prime} - 6bk_{1} UU^{\prime} + \frac{3}{2}ak_{1} U^{2} U^{\prime} - 3k_{2} V^{\prime} + 3ak_{1} U^{\prime}V = 0 \hfill \\ {\text{and}}\;k_{2} U^{\prime} = k_{1} V^{\prime} \hfill \\ \end{aligned} $$
(4.1)

Now, by balancing the nonlinear term with the highest order derivative term of Eq. (4.1), the value of N is 1.

Therefore, from Eq. (3.4)

$$ U(\xi ) = a_{0} + a_{1} \phi (\xi ), $$
(4.2)

where \( \phi (\xi ) = \frac{1}{1 + \exp (\xi )} \) is new variable as given in Eq. (3.5)

Then from Eq. (4.2), putting the derivatives of \( U(\xi ) \) and taking the ansatz into account, a system of algebraic equations were obtained. Collecting the same powers of \( \phi^{i} \) and equating to zero, the following system of nonlinear equations can be acquired:

$$ {\text{Coefficient of}}\quad \varphi^{1}{:} - 3aa_{0} a_{1} k_{1} - \frac{3}{2}aa_{0}^{2} a_{1} k_{1} + 6a_{0} a_{1} bk_{1} + a_{1} k_{1}^{3} + \frac{{3a_{1} k_{2} }}{{k_{1} }} - a_{1} k_{3} = 0, $$
(4.3)
$$ \begin{aligned} & {\text{Coefficient of}}\quad \varphi^{2} {:}3aa_{0} a_{1} k_{1} + \frac{3}{2}aa_{0}^{2} a_{1} k_{1} - 3aa_{1}^{2} k_{1} - 3aa_{0} a_{1}^{2} k_{1} - 6a_{0} a_{1} bk_{1} + 6ba_{1}^{2} k_{1} \\ & \quad - 7a_{1} k_{1}^{3} - \frac{{3a_{1} k_{2}^{2} }}{{k_{1} }} + a_{1} k_{3} = 0, \\ \end{aligned} $$
(4.4)
$$ {\text{Coefficient of}}\quad \varphi^{3} {:}3aa_{1}^{2} k_{1} - 3aa_{0} a_{1}^{2} k_{1} - \frac{3}{2}aa_{1}^{3} k_{1} - 6ba_{1}^{2} k_{1} + 12a_{1} k_{1}^{3} = 0, $$
(4.5)
$$ {\text{Coefficient of}}\quad \varphi^{4} {:}\frac{3}{2}aa_{1}^{3} k_{1} - 6a_{1} k_{1}^{3} = 0. $$
(4.6)

The following family of nontrivial solutions can be acquired by solving the above system of algebraic equations.

Case I

$$ \begin{aligned} a_{0} & = \frac{2b}{a} - \frac{{k_{1} }}{\sqrt a } - \frac{{k_{2} }}{{k_{1} }}, \\ a_{1} & = \frac{{2k_{1} }}{\sqrt a }, \\ k_{3} & = \frac{{12b^{2} k_{1}^{2} - ak_{1}^{4} - 12abk_{1} k_{2} + 6ak_{2}^{2} + 3a^{2} k_{2}^{2} }}{{2ak_{1} }} \\ \end{aligned} $$

and k1 and k2 are arbitrary.

Substituting the values of \( a_{0} ,a_{1} \) and \( k_{3} \), obtained above, we get

$$ \begin{aligned} U(\xi ) & = \left( {\frac{2b}{a} - \frac{{k_{1} }}{\sqrt a } - \frac{{k_{2} }}{{k_{1} }}} \right) + \left( {\frac{{2k_{1} }}{\sqrt a }} \right)\frac{1}{1 + \exp (\xi )} \\ & = \frac{2b}{a} - \frac{{k_{2} }}{{k_{1} }} - \frac{{k_{1} }}{\sqrt a }\tanh \left( {\frac{\xi }{2}} \right) \\ \end{aligned} $$
(4.8)
$$ V(\xi ) = \frac{{k_{1} }}{{k_{3} }}U(\xi ) = - \frac{{ - 2bk_{1} + ak_{2} + k_{1}^{2} \sqrt a \tanh \left( {\frac{\xi }{2}} \right)}}{{ak_{2} }} $$
(4.9)

where \( \xi = k_{1} x + k_{2} y + \frac{{k_{3} t^{\alpha } }}{\varGamma (\alpha + 1)} \).

Case II

$$ \begin{aligned} a_{0} & = \frac{{2bk_{1} + k_{1}^{2} \sqrt a - ak_{2} }}{{ak_{1} }}, \\ a_{1} & = \frac{{ - 2k_{1} }}{\sqrt a }, \\ k_{3} & = \frac{{12b^{2} k_{1}^{2} - ak_{1}^{4} - 12abk_{1} k_{2} + 6ak_{2}^{2} + 3a^{2} k_{2}^{2} }}{{2ak_{1} }} \\ \end{aligned} $$

and k1 and \( k_{2} \) are arbitrary.

Substituting the values of a0, a1 and k3, obtained above, we get

$$ U(\xi ) = \frac{{2bk_{1} - ak_{2} + k_{1}^{2} \sqrt a \tanh \left( {\frac{\xi }{2}} \right)}}{{ak_{1} }} $$
(4.10)
$$ V(\xi ) = \frac{{2bk_{1} - ak_{2} + k_{1}^{2} \sqrt a \tanh \left( {\frac{\xi }{2}} \right)}}{{ak_{2} }} $$
(4.11)

where \( \xi = k_{1} x + k_{2} y + \frac{{k_{3} t^{\alpha } }}{\varGamma (\alpha + 1)} \).

Results

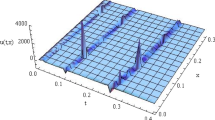
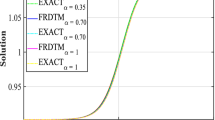
For time fractional KD equation, the exact solutions have been attained for the first time by generalized Kudryashov technique with the aid of fractional complex transform. In case of time fractional KD equation, the following Figs. 1, 2, and 3 show the solitary wave solution of \( u\left( {x,y,t} \right) \), obtained by the proposed Kudryashov technique for different values of α.

Fig. 1
figure 1

The 3-D plot of Solitary wave solution of \( u(x,y,t) \) for KD equation when \( a = b = 1, \) \( y = 1 \) and \( \alpha = 1 \)

Full size image
Fig. 2
figure 2

The 3D plot of Solitary wave solution of \( u(x,y,t) \) for fractional KD equation when \( a = b = 1, \) \( y = 1 \) and \( \alpha = 0.75 \)

Full size image
Fig. 3
figure 3

The 3D plot of Solitary wave solution of \( u(x,y,t) \) for fractional KD equation when \( a = b = 1, \) \( y = 1 \) and \( \alpha = 0.5 \)

Full size image

Conclusion

In this manuscript, the solitary wave solutions of time-fractional (2 + 1) dimensional KDE have been acquired by utilizing the Kudryashov technique. By applying the FCT, a FDE can be transformed into its equivalent ODE form. The novel exact solutions, thus obtained may be suitable for description of physical phenomena accurately. This study signifies that the focused method is efficient for analytical solution of time fractional KD equation. Also it manifests that performance of the technique is substantially influential and absolutely dependable for finding new exact solutions.