Modeling and Control of PV Systems for Maximum Power Point Tracking and Its Performance Analysis Using Advanced Techniques

Abstract

Maximum power point tracking (MPPT) is a necessary and primary concern in modern photovoltaic (PV) energy systems. The nonlinear nature of the output characteristics of PV systems causes it to supply maximum amount of power at a particular point of operation which is known as the maximum power point (MPP). For optimal utilization of the PV modules effective tracking of this particular operating point is necessary for most of the PV energy systems. Over the years, many different approaches have been proposed for maximum power point tracking in PV energy systems. But most of these literatures do not draw a complete picture of the design, control and operation process of the whole system involved in MPPT. To alleviate such difficulties, this chapter discusses the MPPT system in an exhaustive manner using a novel integrated model of the system for designing robust and effective controllers for MPPT. This chapter considers a system where a PV module is connected to a DC-DC converter system for demonstrating the process. Firstly, a novel small-signal model of the system where a PV module is connected to any of the three basic DC to DC converters is obtained by utilizing the perturbation and linearization method on the available large signal models. Then, using these small-signal models, generalized transfer function models of the systems are obtained by application of simple circuit theory. The intrinsic nonlinearities of the system and other inherent factors that create difficulty in controller design are also pointed out. As an effective solution to this problem of nonlinearity, the design and implementation process of a gain-scheduled PID controller for controlling such highly non-linear systems is presented. Moreover, the design and implementation of an MPPT control loop around the voltage control loop are described using some advanced computation-based algorithms, namely, Particle Swarm Optimization (PSO), Differential Evolution Algorithm (DEA) and Binary Coded Genetic Algorithm (BCGA) for MPPT. In addition to that, a comparative analysis of the three metaheuristic algorithms implemented here is also presented in this chapter. All the discussed theoretical aspects were validated through simulation in MATLAB/SIMULUNK implementing various real-world scenarios such as partial shading, load disturbance, etc. The novel modeling approach, the systematic control system design approach, the MPPT algorithm design methods and implementation and their comparative analysis can be of great usefulness to a designer.

12.1 Introduction

In general, a photovoltaic energy conversion system comprises of photovoltaic modules, power electronic converters, controllers, and loads. Figure 12.1 depicts the structure of a typical PV energy conversion system. Such PV systems are classified into different categories depending on the type of loads connected to the system, the number of power electronic conversion stages present in the system, grid connection, etc.

Fig. 12.1

General representation of photovoltaic energy systems

On the basis of interaction with the grid, photovoltaic energy systems are categorized into three categories, namely, grid-tied system, off-grid system and grid-interactive hybrid system. In a typical grid-tied PV energy system the power generated by the PV modules is fed directly into the utility grid with the help of some power electronic interfaces (Malinowski et al. 2017), whereas, in case of an off-grid system the loads are fed from the PV modules which are assisted by energy storage systems/batteries (Malinowski et al. 2017). The structure of a grid-interactive hybrid PV-battery system is a hybrid combination of off-grid and grid-tied PV systems (Khezri et al. 2020). Such systems are made of a typical energy storage systems along with the PV modules and these can be operated in either of the grid-tied of off-grid mode of operation.

The majority of grid-tied and off-grid PV systems are either single-stage (Guo et al. 2020) conversion system where the inverter itself tracks the MPP or double-stage conversion system (Fahad et al. 2019) where a DC-DC converter tracks the MPP and the DC-AC inverter pumps the energy into the grid or load from the DC-DC converter. Even though single-stage conversion is more efficient it is hard to apply in low or medium voltage PV systems (Guo et al. 2020). In this chapter the modeling, control and MPPT in a typical PV system with a DC-DC converter in the first stage, as shown in Fig. 12.2 is discussed. In case of such a system, the representation of the inverter input port as a resistor drastically simplifies the analysis of the system without any significant loss of actual system characteristics (Li et al. 2019).

Fig. 12.2

Schematic of double-stage PV system

Even though, the topology, operation and control system structures are different for the different types of systems mentioned above, the design and implementation of MPPT in those systems are somewhat similar. Many different algorithms and methods have been suggested throughout the years for both single-stage and double-stage conversion of solar energy. There are some conventional techniques, such as, “perturb and observe (P&O) technique” (Haque 2014), “incremental conductance technique (InC)” (Shang et al. 2020), “open circuit voltage method” (Ko et al. 2020), “short circuit current method” (Ko et al. 2020), etc. Even though, these conventional methods are relatively easy to implement, most of the time these methods fail to track the “global MPP” under “partial shading conditions.” To solve the problem of stagnation of the classical methods many new techniques have been proposed. In recent years, with the advent of fast computational systems the MPPT problem is being considered as an optimization problem. Consequently, many optimization algorithms have been suggested in literature. Implementation of“particle swarm optimization (PSO)” in MPPT is discussed by Li et al. (2019). References (Fathy et al. 2018; Lyden et al. 2020; Rezk et al. 2019) and (Allahabadi et al. 2021) shows the application of “teaching and learning based optimization (TLBO),” “simulated annealing (SA),” “fuzzy logic control (FLC),” and “artificial neural network (ANN)” respectively. In terms of speed and tracking of global MPP performance of these methods are satisfactory. But these improvements in tracking performance and efficiency come at a cost of increased complexity, requirement of more costly components and requirement of more numbers of sensors. The target of this chapter is to discuss the various aspects of the advanced computation-based MPPT system. It discusses different aspects of modeling and control system design for MPPT in PV systems. It also analyses some popular advanced computation-based metaheuristic algorithm-based MPPT systems and presents a comparative analysis of the presented algorithms based on their characteristics and tracking performance.

This chapter describes the MPPT system design procedure in a systematic manner. First, the small signal modeling of the PV module and its combination with the canonical model of DC-DC converter is presented. Then the controller design process followed by the implementation and comparison of MPPT algorithms are discussed. The complete design process described in this chapter is summarized in the flowchart of Fig. 12.3.

Fig. 12.3

Flowchart of the described design Process

The rest of the chapter is organized as follows. Section 2 derives the small signal modeling of a PV module based on perturb and observe technique which is then combined with a canonical model of the DC-DC converters in Sect. 3. A gain scheduled PID controller is then designed in Sect. 4 depending on the system model. After that, the simulation results for different advanced algorithm-based MPPT algorithms are presented in Sect. 5. Section 6 presents comparative analysis of these algorithms when applied for MPPT which is followed by the evaluation of system performance subjected to load change in Sect. 7. Finally, the chapter is summarized in Sect. 8. The key contributions of this chapter are:

• Novel Small-signal model of PV module and its combination with existing canonical model of DC-DC converters.

• Design of gain scheduled PID controller using the derived system models.

• Implementation of advanced soft-computing algorithm-based MPPT algorithms and their comparative analysis.

12.2 Small-Signal Model of Photovoltaic Module

Majority of MPPT algorithms are implemented as a high level control algorithm which controls the command signal for an internal control loop. The inner control loop may be implemented to track and regulate the system voltage or current in accordance with the command signal generated by the MPPT algorithm. In order to properly design and implement this necessary control system one requires an accurate small-signal model representation of the actual system at the concerned operating points.

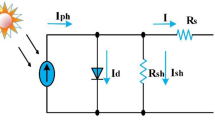
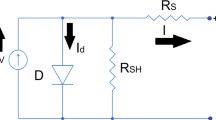
The small-signal model of a PV module can be analytically derived from its large-signal nonlinear model as shown by Rana et al. (2020). In this chapter a single-diode model of the PV cell, as shown by Shang et al. (2020) is used as the large-signal model to be utilized for derivation of the small signal model. Generally, several such PV cells are interconnected in both series–parallel configuration with each other to construct a PV module. Li et al. (2019) stated that the equivalent circuit schematic of such PV module can be drawn as shown in Fig. 12.4a having terminal characteristics as shown in Fig. 12.4b.

Fig. 12.4

a Equivalent circuit representation of a PV module. b Characteristics of a PV module

The relationship between the terminal current and voltage of the PV module in Fig. 12.4a can be written as in Eq. (12.1) as shown by Li et al. (2019). Here, N_s and N_p are number of PV cells connected respectively in series and parallel manner to construct the module, R_sh and R_s are equivalent shunt and series resistances of each cell, η is the quality factor of the material, q denotes the value of the charge of a single electron, I_rs is the diode reverse saturation current, K represents Boltzmann’s constant, and T stands for the absolute temperature in Kelvin.

$$I = N_p I_{ph} - N_p I_{rs} \left[ {\exp \left\{ {\frac{q(V/N_s + IR_s /N_p )}{{\eta KT}}} \right\}} \right] - \left[ {\frac{N_p V/N_s + IR_s }{{R_{sh} }}} \right] \,$$

(12.1)

“The nonlinear large-signal model represented by (1) can be linearized by using analytical methods to derive a small-signal model at a particular operating point of the system. In this chapter the “perturbation and linearization” technique is used to linearize the system around a quiescent operating point and obtain the small-signal model” (Rana et al. 2020). Equation (12.2) is obtained when small perturbations in the PV terminal voltage and current, (v͡_pv, i͡_pv) are applied around the operating point, (V_pv, I_pv) in Eq. (12.1).

$$\begin{aligned} I_{pv} + \mathop{i}\limits^{\frown}_{pv} = N_p I_{ph} & - N_p I_{rs} \left[ {\exp \, \left\{ {\frac{{q(V_{pv} /N_s + I_{pv} R_s /N_p ) + q(\mathop{v}\limits^{\frown}_{pv} /N_s + \mathop{i}\limits^{\frown}_{pv} R_s /N_p )}}{\eta KT}} \right\}} \right] \\ & - \left[ {\frac{{(N_p V_{pv} /N_s + I_{pv} R_s ) + (N_p \mathop{v}\limits^{\frown}_{pv} /N_s + \mathop{i}\limits^{\frown}_{pv} R_s )}}{{R_{sh} }}} \right] \end{aligned}$$

(12.2)

After expanding the exponential term in (2) using Taylor series expansion with respect to the small perturbation terms (3) is obtained.

$$\begin{aligned} I_{{pv}} + \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{i} _{{pv}} & = N_{p} I_{{ph}} - \left[ {\frac{{(N_{p} V_{{pv}} /N_{s} + I_{{pv}} R_{s} )}}{{R_{{sh}} }}} \right] - \left[ {\frac{{(N_{p} \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{v} _{{pv}} /N_{s} + \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{i} _{{pv}} R_{s} )}}{{R_{{sh}} }}} \right] \\ & - N_{p} I_{{rs}} \left[ {\exp {\text{ }}\left\{ {\frac{{q(V_{{pv}} /N_{s} + I_{{pv}} R_{s} /N_{p} )}}{{\eta KT}}} \right\}} \right. \\ & \left\{ {1 + {\text{ }}\frac{{q(\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{v} _{{pv}} /N_{s} + \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{i} _{{pv}} R_{s} /N_{p} )}}{{\eta KT}} + {\text{ }}\frac{1}{{2{\text{ }}!}}\frac{{q^{2} (\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{v} _{{pv}} /N_{s} + \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{i} _{{pv}} R_{s} /N_{p} )^{2} }}{{\left( {\eta KT} \right)^{2} }}} \right. \\ & \left. {\left. { + {\text{ }}\frac{1}{{3{\text{ }}!}}\frac{{q^{3} (\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{v} _{{pv}} /N_{s} + \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{i} _{{pv}} R_{s} /N_{p} )^{3} }}{{\left( {\eta KT} \right)^{3} }}...} \right\} - 1} \right] \\ \end{aligned}$$

(12.3)

Since, the perturbations are assumed to be very small, the higher power of these terms would result in even smaller terms which have very little effect on the system. So, a first order approximation may be used to neglect the terms containing higher powers of the perturbations. After the approximation and some rearrangements (3) results in (4).

$$\begin{gathered} I_{pv} + \mathop{i}\limits^{\frown}_{pv} = N_p I_{ph} - N_p I_{rs} \left[ {\exp \, \left\{ {\frac{{q(V_{pv} /N_s + I_{pv} R_s /N_p )}}{\eta KT}} \right\} - 1} \right] \hfill \\ \, - \left[ {\frac{{(N_p V_{pv} /N_s + I_{pv} R_s )}}{{R_{sh} }}} \right] \hfill \\ \, - N_p I_{rs} \left[ {\exp \, \left\{ {\frac{{q(V_{pv} /N_s + I_{pv} R_s /N_p )}}{\eta KT}} \right\}\left\{ { \, \frac{{q(\mathop{v}\limits^{\frown}_{pv} /N_s + \mathop{i}\limits^{\frown}_{pv} R_s /N_p )}}{\eta KT}} \right\}} \right] \hfill \\ \, - \left[ {\frac{{(N_p \mathop{v}\limits^{\frown}_{pv} /N_s + \mathop{i}\limits^{\frown}_{pv} R_s )}}{{R_{sh} }}} \right] \hfill \\ \, \hfill \\ \, \hfill \\ \, \hfill \\ \end{gathered}$$

(12.4)

It can be observed that the first term on LHS and the first three terms on the RHS of (4) represent the DC relationship between PV current and voltage, whereas, the other terms in the equation represent the small-signal relationship. After equating the small-signal terms on both sides of (4) one can derive (5).

$$\mathop{i}\limits^{\frown}_{pv} = - \alpha (\mathop{v}\limits^{\frown}_{pv} /N_s + \mathop{i}\limits^{\frown}_{pv} R_s /N_p ) - (N_p \mathop{v}\limits^{\frown}_{pv} /N_s R_{sh} ) - (\mathop{i}\limits^{\frown}_{pv} R_s /R_{sh} )$$

(12.5)

$${\text{where}},\alpha = {{\left[ {qN_p I_{rs} \exp \left\{ {\frac{{q(V_{pv} /N_s + I_{pv} R_s /N_p )}}{\eta KT}} \right\}} \right] \, } / {\eta KT}}$$

(12.6)

Some rearrangements of (5) result in the required linear model representation of the PV module as shown in (7). Here, σ is the small-signal conductance of the PV module, mathematically its value is equal to the negative value of the slope of the I-V curve of the module.

$$\mathop{i}\limits^{\frown}_{pv} = - \sigma {.}\mathop{v}\limits^{\frown}_{pv}$$

(12.7)

$${\text{where}},\sigma = \frac{{(\alpha /N_s ) + (N_p /N_s R_{sh} )}}{{1 + (\alpha R_s /N_p ) + (R_s /R_{sh} )}}$$

(12.8)

Using the relationship in (7) the small-signal model of the PV module can be interpreted as a variable resistor as in Fig. 12.5a whose value depends on the operating point of the system. If the relative directional representation between the voltage and current is reversed then the model can be drawn with a resistor having positive value as in Fig. 12.5b.

Fig. 12.5

Small signal model of PV module a equivalent model from Eq. (12.7). b With reversed current direction

12.3 The Integrated Small-Signal Model

In a typical double-stage PV system the MPPT operation is performed in the DC-DC conversion stage. Different types of converters can be used to serve this purpose. Figure 12.6 shows the circuit configuration of such systems with the three well-known basic DC to DC converters, namely, Buck, Boost and Buck-boost converter. Here, the load, which might be an inverter or any other kind of load is modelled as a resistor R₀.

Fig. 12.6

DC-DC conversion stage of PV systems incorporating (a) Buck converter (b) Boost converter (c) Buck-boost converter

The liner small-signal model of PV system derived in the previous section can be used for system modeling purpose. In this chapter, the linear resistive model is integrated with a general canonical model of the DC-DC converters operating in continuous conduction mode (CCM) to obtain the complete small-signal model representation of the system. “The canonical model of DC-DC converter is a generalized representation of the converters where the basic structure of the equivalent circuit remains same for all the converters” (Cuk 1977). The schematic of the system can be seen in Fig. 12.7, where, the small-signal resistance of the PV module is represented by r.

Fig. 12.7

Complete Linear Small-Signal Model Representation of the System

The expression of the values of the different passive circuit components in the canonical converter model is different for the different converters. These expressions for the aforementioned DC-DC converters used in this chapter are given in Cuk (1977), a modified version of which are reproduced in Table 12.1.

Table. 12.1 Parameters of canonical model for basic DC-DC Converters

With the help of Fig. 12.7 and Table 12.1, one can obtain various transfer functions of the system. In this chapter, the voltage across the terminals of the PV module is taken as the parameter to be controlled for MPPT applications. Which necessitates the derivation of the control to output transfer function, where the duty cycle of the PWM converter switch is the control signal and the voltage across the terminals of the PV module is considered as the output signal.

Applying conventional circuit theories, such as KVL and KCL, the necessary transfer function can be derived in the form shown in (9).

$$G_{vd} (s) = \frac{{\mathop{v}\limits^{\frown}_{pv} (s)}}{{\mathop{d}\limits^{\frown} (s)}} = \frac{b_2 s^2 + b_1 s + b_0 }{{a_3 s^3 + a_2 s^2 + a_1 s + a_0 }}$$

(12.9)

$${\text{Here}},a_0 = \frac{R_0 }{{M^{2 } }} + r$$

(12.10)

$$a_1 = \frac{L_e }{{M^2 }} + \frac{rC_1 R_0 }{{M^2 }} + rC_2 R_0$$

(12.11)

$$a_2 = \frac{rC_1 L_e }{{M^2 }} + \frac{L_e C_2 R_0 }{{M^2 }}$$

(12.12)

$$a_3 = \frac{rL_e C_1 C_2 R_0 }{{M^2 }}$$

(12.13)

$$b_0 = - r\left\{ {e(s) + \frac{j(s)R_0 }{{M^2 }}} \right\}$$

(12.14)

$$b_1 = - r\left\{ {e(s)R_0 C_2 + \frac{j(s)L_e }{{M^2 }}} \right\}$$

(12.15)

$$b_2 = - \frac{j(s)rR_0 L_e C_2 }{{M^2 }}$$

(12.16)

The expression of the different elements of the polynomials in numerator and denominator of (9) for different DC-DC converters can be derived using the parameter values from Table 12.1. The derived coefficients are tabulated in Table 12.2. It needs to be mentioned that, since some of the canonical model parameters are complex frequency dependent, the expression of the different coefficients need to be reorganized to obtain the final form in Table 12.2.

Table 12.2 Coefficients of transfer function polynomials

The transfer function model in (9) along with Table 12.2 can be used for analysing the system behaviour and design a suitable controller to control the terminal voltage of the PV modules.

12.4 System Analysis and Controller Design

The transfer functions that have been derived so far can be used to analyse the system before designing the control system for the system. In this chapter, a typical PV system with a Boost converter as in Fig. 12.6b having parameter values as depicted in Table 12.3 is considered for the system analysis purpose. The bode plots of the transfer functions at different operating points, i.e. at different values of converter’s duty cycle are illustrated in Fig. 12.8.

Table 12.3 Parameter values of PV module and converter

Fig. 12.8

Bode plots of the transfer functions for boost converter at different operating points

From Fig. 12.8 one can interpret that as the operating point varies, the dynamic response of the open-loop system also change. The frequency responses presented here are similar to a typical three pole system response with a high frequency pole at relatively lower duty cycles. It can be observed that the bandwidth of the open loop system increases with the PWM duty cycle up to a certain limit then it decreases again, and the phase margin of the system keeps decreasing as the duty cycle increases. Moreover, the natural damping of the system is not same at all the operating points; the system is well damped around the MPP which happens to occur at 70% duty cycle but the damping is not good enough for relatively smaller and larger duty cycle than this. During the design process of a controller for the system one should consider these key features of the frequency response of the system.

Even though the dynamic response of the system changes with operating point, it is still possible to implement conventional control approaches, such as PI or PID control for the system with the help of “quasi-static approximation” (Kocher and Steigerwald 1982). But in such cases, the performance of the system will be suboptimal because of the non-adaptability of the controller. But the overall response of the MPPT system depends largely on the performance of the control system, which is why the control system has to be robust and optimal. Consequently, different kinds of adaptive control approaches are proposed in literature. Such as sliding mode control (Meng et al. 2018), fuzzy logic control (Chamanpira et al. 2019), etc. In this chapter, a gain scheduled PID controller (Shao et al. 2019) is considered for controlling the system and ensuring satisfactory response. The structure of the inner control system is depicted in Fig. 12.9. The gain scheduling could be done on the basis of different system variable. The PV module voltage varies linearly with irradiance but current varies logarithmically with the irradiance the variation in the voltage is smaller than current. That is why the voltage of the PV module is taken as the variable depending on which the gain scheduling is implemented. Using the transfer functions of the system the PID controllers were tuned at the different operating points and using these tuning data the look-up tables (LUTs) were implemented. The differential gain was filtered using a first order filter and a clamping algorithm was implemented to avoid windup problem of the integrator.

Fig. 12.9

Detailed schematic with inner control loop of the system with gain scheduled PID control

12.5 Advanced Soft-Computing Algorithms for MPPT

Soft computing algorithms are generally algorithms that are based on some form of artificial intelligence or are inspired by some natural phenomena. In recent days, these algorithms have found an overwhelmingly rising application in the field of MPPT in various systems. Some of these instances include application of “artificial neural network (ANN)” (Allahabadi et al. 2021), “simulated annealing (SA)” (Lyden et al. 2020), “teaching and learning based optimization (TLBO)” (Fathy et al. 2018), etc. In this chapter the application and performance analysis of “particle swarm optimization (PSO)” based MPPT (Rana et al. 2020), “differential evolution algorithm (DEA)” (Rana et al. 2020) and “binary coded genetic algorithm (BCGA)” (Nagarani and Nesamony 2019) is discussed. This chapter also compares these algorithms based on their tracking performance and convergence characteristics.

The system performance for the different aforementioned MPPT algorithms is examined by simulating them in Matlab/Simulink. The schematic of the simulations model is shown in Fig. 12.9. As discussed earlier the MPPT algorithm is implemented as a higher level control algorithm which generates the reference or command signal for the internal control loop. For a system with structure like this, the designer has to ensure that the internal control loop is significantly faster than the external control loop. For demonstration purpose the outer control or the MPPT control algorithms are implemented in such a way that the fastest change that they can make to the command signal has an interval of at least 15 ms between them whereas, the settling time of the inner control loop is maintained at around 5 ms. The simulations are performed for two different shading conditions with the power-voltage curve as shown in Fig. 12.10. It can be inferred that one of the conditions are uniform irradiation condition which is applied to the system for the first half of the simulations while the other one is a typical partial shading condition which is applied to the system during the second half of the simulations. The irradiance condition on the different PV modules and the power and voltage at the MPP for those conditions are given in Table 12.4. Using this format of simulation the different algorithms are evaluated.

Fig. 12.10

Output power versus output voltage curve of PV array for different shading conditions

Table 12.4 Parameters of a single PV module

12.5.1 Particle Swarm Optimization (PSO) for MPPT

The “particle swarm optimization algorithm (PSO),” first introduced by Kennedy and Eberhart (Kennedy and Eberhart 1995), is inspired by two natural phenomena known as “Bird-Flocking and Fish-Schooling” (Khan et al. 2021), where each particle use the collective intelligence and experience of all the agents or particles to move towards an optimal point in the search space. The application of PSO for MPPT in PV system is described in Li et al. Jan. (2019). The flowchart of MPPT algorithm based on PSO is presented in Fig. 12.11. The mathematical process for performing the various steps of the PSO algorithm is summarized in (17), (18) and (19) (Li et al. 2019). Here, p_iⁿ and v_iⁿ are the position and the velocity of the ith particle in nth iteration respectively, C₁ and C₂ are tuning parameters, r₁ and r₂ are random numbers between 0 and 1, w is the dynamic inertia weight factor with maximum and minimum values w_max and w_min, respectively, m is the number of maximum iteration, and P_best and G_best are personal best and global best solution. It is worth mentioning that the weight factor w reduces gradually as the search process progresses; this is implemented to let the particles explore the search space more at the beginning and make them converge and move less near the ending of the search process.

$$w = w_{\max } - [\{ (w_{\max } - w_{\min } )n\} /m]$$

(12.17)

$$v_i^{n + 1} = wv_i^n + C_1 r_1 (P_{best_i } - p_i^n ) + C{}_2r_2 (G_{best_i } - p_i^n )$$

(12.18)

$$p_i^{ \, n + 1} = p_i^{ \, n} + v_i^{ \, n + 1}$$

(12.19)

Fig. 12.11

Flowchart of PSO for MPPT

The shading detection algorithm as shown in Fig. 12.11 is a simple algorithm for PSC detection (Wellawatta and Choi 2018). It keeps track of the power available at a certain set point and whenever the power changes more than a certain percentage of the previous power it triggers a new search for MPP. The Maximum number of iteration that are allowed is used as the stopping criteria for the PSO algorithm.

The variation in power and voltage levels of the PV array with time which are obtained from the simulation model with the simulation setup as discussed earlier is illustrated in Fig. 12.12. It can be observed that the MPPT algorithm based on PSO tracks the MPP with fair accuracy. The system parameters converge to the MPP with gradually reducing oscillations. Since, the MPPT based on PSO algorithm is bursty in nature, i.e. the search process is carried out in intervals or only when necessary, the oscillations after a complete search process are very less or negligible. Moreover, the performance of the inner control loop with the gain scheduled PID controller can also be said to be satisfactory. The gain scheduled controller makes the system voltage to settle down at the reference voltage commanded by the PSO algorithm within 5 ms with no or very less overshoots and undershoots.

Fig. 12.12

Power and voltage of PV array for MPPT based on PSO

12.5.2 Differential Evolution Algorithm (DEA) for MPPT

“Differential evolution algorithm (DEA)” was invented by Storn and Price (1997). DEA is a nature-inspired evolutionary algorithm where each element in the population (chromosome) undergoes a process called mutation followed by a process called crossover to obtain the optimal solution in the search space. Figure 12.13 captures the flowchart of the MPPT based on DEA algorithm implemented in this study (Zhang and Sui 2020). In this case, also the partial shading detection algorithm is similar to the algorithm in case of the PSO-based MPPT mentioned in the previous discussion. Equations (12.20)–(12.24) represents the mathematical process of mutation, crossover, population update and parameter update which are undergone in course of the run of this algorithm. Instead of a static parameter-based DE algorithm a dynamic parameter-based algorithm as shown by Brest et al. (2006) is implemented here for better tracking performance and smoother convergence.

Fig. 12.13

Flowchart of DEA for MPPT

$$v_i^{n + 1} = x_{r1}^n + F^{n + 1} (x_{r2}^n - x_{r3}^n )$$

(12.20)

$$u_i^{n + 1} = \left\{ {\begin{array}{*{20}c} {v_i^{n + 1} ,{\text{ if }}r \le CR^{n + 1} {\text{ or }}i = I_{rand} } \\ {x_i^n ,{\text{ if }}r > CR^{n + 1} {\text{ and }}i \ne I_{rand} } \\ \end{array} } \right.$$

(12.21)

$$x_i^{n + 1} = \left\{ {\begin{array}{*{20}c} {u_i^{n + 1} ,{\text{ if }}f(u_i^{n + 1} ) \ge f(x_i^n )} \\ {x_i^n ,{\text{ Otherwise}}} \\ \end{array} } \right.$$

(12.22)

$$CR^{n + 1} = CR^n - [(CR^1 - CR_{\min } )/m]$$

(12.23)

$$F^{n + 1} = F^n - [(F_{\max } - F^1 )/m]$$

(12.24)

Here, v_iⁿ, u_iⁿ and x_iⁿ are the ith element of the mutated-vector, trial-vector and target-vector respectively in the nth iteration, CRⁿ and Fⁿ are the crossover rate and the scaling factor in nth iteration, the variables I_rand, r1, r2 and r3 are randomly generated integers. I_rand ranges from 1 to the dimension of the elements, and the others are with values in between 1 and population size which are used to select the elements from the population to undergo mutation, r is also a randomly generated number that ranges from 0 to 1, The fitness value of the element x is represented by f(x). CR_min is the lowest limit of crossover rate and ${F}_{\mathrm{max}}$ is upper limit of the scaling factor.

The variation in power and voltage levels of the PV array with time for the MPPT based on DEA algorithm is visualized in Fig. 12.14. It can be perceived that the oscillations in the power and voltage waveforms are much more chaotic than that PSO-based MPPT algorithm. But as the search progress, the oscillation gradually reduces and finally, the MPP is tracked down with good accuracy. Apart from that, it can also be observed that the inner control loop’s performance is also satisfactory. It makes the voltage of the PV module track the set point with fast response (settles within 5 ms) and with less number of overshoots and undershoots.

Fig. 12.14

Power and voltage of PV array for MPPT based on DEA

12.5.3 Binary Coded Genetic Algorithm (BCGA) for MPPT

“The binary coded genetic algorithm (BCGA) also known as genetic algorithm (GA) is a metaheuristic algorithm that employs the principle of natural evolution by employing a systematic process of selection, crossover, mutation, etc., to find the best-fit solution of a problem in the search space” (Chaturvedi 2008). Reference (Garud et al. 2021) presents the implementation of GA for modeling PV system. The flowchart of the BCGA based MPPT algorithm implemented in this study is presented in Fig. 12.15. Similar to the previous cases, in this case also the PSC detection algorithm is a simple power monitoring-based algorithm. For the purpose of selection of the parents before they go into the mating pool, Roulette Wheel selection technique (Katoch et al. 2021) is used and for cross-over, single point crossover is implemented (Chaturvedi 2008).

Fig. 12.15

Flowchart of BCGA for MPPT

Figure 12.16 captures the variation of the output power and the output voltage of the PV array obtained from the simulation model for BCGA based MPPT. It can be noticed that the BCGA based MPPT control system tracks the global MPP for both uniformly irradiated as well as partially shaded condition with fair degree of accuracy. In this case, it can be seen that the oscillations during the search are lesser compared to the previous algorithms and the oscillations become negligible after the convergence of the algorithm. Moreover, the convergence time is significantly lesser than the other algorithms in this case. The inner gain scheduled controller also performs satisfactorily. The setpoint tracking is performed with very good accuracy, fast response and less number of overshoot and undershoot in the voltage waveform of the PV module.

Fig. 12.16

Power and voltage of PV array for MPPT based on BCGA

12.6 Comparative Analysis

The MPPT algorithms described in the previous section are all based on some metaheuristic algorithm. But at this point of discussion, it is still somewhat unclear which one of them performs better than the others or what are the criteria that sets them apart from each other. The following comparative study ponders on some of these questions. The comparison of the different algorithms are done on the basis of their convergence characteristic (Lolla et al. 2021) and tracking performance.

12.6.1 Convergence Characteristics

The convergence characteristic of an algorithm reveals many useful information about the performance of the algorithm. The characteristic typically shows how the error value changes with respect to the progression of the algorithm. In this chapter, the root mean squared error is plotted with respect to the iteration number of the algorithm. The formula for calculating the root mean squared (RMSE) error is shown in Eq. (12.25). Here, x_mpp represents the MPP voltage (V_mpp) and power (P_mpp), x_i is the ith element in the population in a particular iteration, and N is the aggregate number of elements in that set of population.

$$RMSE = \sqrt {\left[ {{{\left\{ {\sum_{i = 1}^N {(x_{mpp} - x_i )^2 } } \right\}} / N}} \right]}$$

(12.25)

Figure 12.17 portrays the convergence characteristics of the power and voltage obtained for the both uniform and partial shading case studies for the three algorithms used for MPPT in this chapter. From Fig. 12.17a and b, it can be observed that the PSO and DEA converges to the MPP with a monotonically decreasing error characteristic, whereas, the BCGA tends to diverge at the beginning but converges hastily at the ending part of the search. Fig. 12.17c and d show similar kind of behaviour for the DEA. Since, the DEA and the BCGA algorithms are inspired by the natural evolution process where the fate of the future population depends greatly on their predecessor, the performance of these algorithms is greatly dependent on the fitness and quality of the initial population. As a result, when the randomly generated initial population is of poor quality the performance of the algorithms degrades. So, for these two algorithms the initial population has to be generated carefully. On the other hand, the PSO algorithm is not that much dependent on the initial population. Its performance depends on the velocity of the particles, and diversity of the population. This is why, the PSO algorithms converge to the MPP in both the cases with a smoother characteristics.

Fig. 12.17

Convergence characteristics of the algorithms. a Voltage convergence for uniform irradiation b Power convergence for uniform irradiation c Voltage convergence for PSC d Power convergence for PSC

Apart from that, it should be noted that the BCGA shows a snappy characteristics, i.e. the algorithm has a tendency to converge faster to the best solution found in a particular iteration in the search space. Which results in less exploration in the search space. In some cases, this might cause the algorithm to obtain a suboptimal solution (local MPP) and miss the optimal solution (global MPP).

12.6.2 Tracking Efficiency

It was previously discussed that the oscillations during the search process are largest for the DEA algorithm, least for the BCGA and moderate for the PSO algorithm-based MPPT. It was also shown in the previous section that the BCGA converges fastest and the DEA converges slowest. So, assuming that the runtime for all the algorithms are same and they all successfully track the global MPP, the energy lost during the search process will be most for the DEA, least for the BCGA, and moderate for the PSO based MPPT. This means that the BCGA will be most efficient and then there will be PSO and DEA in subsequent order.

But it has to be noted that all the algorithms do not track the exact same operating point. Consequently, their tracking efficiency changes. To obtain their steady state efficiency the power loss during the search process are neglected and the tracking efficiency is calculated on the basis of the expression in (26) as given by Islam et al. (2018). The efficiencies calculated for the case studies presented in this chapter are shown in Table 12.5. It can be seen that the efficiencies are more or less same. So, it can be said that only the performance during search process sets them apart.

$$\eta = \frac{{Power{\text{ Tarcked}}}}{{P_{mpp} }} \times 100\%$$

(12.26)

Table 12.5 Tracking efficiency of the MPPT algorithms

12.7 Effect of Load Variation

In a PV system, the performance of the whole control system depends largely on the inner control loop, i.e. the gain scheduled PID controller in this chapter. The controller must be immune to the various disturbances that are present in the system. Otherwise, the system will have to frequently search for the MPP whenever a disturbance occurs. One of the major disturbances that occur in such systems is load disturbance. The performance of the system for changing load conditions is shown in Fig. 12.18. The load change is realized as a step change in the load resistance (R₀) at 0.2 s and ramp change between 0.6 s and 1 s of simulation. It can be observed that the system performs very satisfactorily. The voltage regulation is very accurate and the system successfully maintains the MPP rejecting the effects of these disturbances.

Fig. 12.18

System performance under load disturbances

12.8 Summary

Advanced computation-based metaheuristic algorithms are increasingly being applied in the case of MPPT applications in PV systems. These algorithms ensure better performance under both uniform irradiation and partial shading condition. To design an effective MPPT system implementing these advanced algorithms involves complex tasks such as proper system modeling, robust controller design. etc. This chapter discussed some of these aspects in detail. An analytical method-based generalized modeling approach for PV system with DC to DC converters that operate in CCM is presented and then based on this model the controller design process is presented. The performance of the system is shown to be satisfactory when different soft-computing algorithms. The comparative analysis revealed the strength and weaknesses of the algorithms. It was shown that the soft-computing algorithm-based MPPT system tracks the MPP with good accuracy and fast response, but it has to be noted that since these algorithms are not gradient-based continuous running algorithm but rather bursty in nature, they may not be the most effective choice to track MPP under slowly varying irradiance condition. Especially, when the rate of change of irradiance is close to the convergence time of the algorithms. To solve such problems, hybrid algorithms can be used, where the metaheuristic algorithm first finds the MPP and then a gradient-based traditional MPP algorithm is used to maintain the MPP.

So, the key takeaways and inferences from this chapter are:

• The small-signal model of the PV system with DC-DC converters are not the same at all operating points. Rather, they vary with the operating points. But quasi-static approximation can be used to design the controllers at different strategic operating points and they can be combined to control the system properly. A gain-scheduled PID controller is such a controller.

• The soft-computing algorithms perform satisfactorily under fast changing shading conditions but they reduce the system efficiency when subjected to slowly varying shading condition.

• Even though, the tracking efficiency of all the MPPT algorithms presented in this chapter are more or less similar, they have different convergence characteristics and different computational complexity. As a result, they should be chosen based on the type of application.