Flow and Thermal Characteristics of Jet Impingement on a Dimple Plate Using Large Eddy Simulation

Abstract

A round turbulent air jet is impinging on heated plate and is numerically analyzed by large eddy simulation (LES) at the plate to nozzle spacing, h/D_j = 2(where D_j is jet diameter), Reynolds number (Re_j) = 5000, and diameter ratio (D/D_j) = 0.318 (where D is dimple print diameter), and relative depth (δ/D_j = 0.3) (where δ is dimple depth) for concave and convex dimples and is used in the present study, LES, consider sub-grid scale (SGS) model, i.e., Wall Adaptive Local Eddy viscosity (WALE). Averaging in space and time is performed to give information of mean velocity in stagnation and wall jet regions. Various important dynamical stream structures have been visualized from the instantaneous data obtained from LES. The local Nusselt number, mean velocity, and coefficient of pressure are calculated for both configration of dimples. Various flow phenomena such as flow separation and reattachment are represented and their effect on heat transfer phenomenon are explained. Vorticity contours were in good resemblance with experimental results (Terekhov et al., Impingement of an impact jet onto a spherical cavity. Flow structure and heat transfer. Int J Heat Mass Transfer 52:2498–2506, 2009; Kanokjaruvijit and Martinez-botas, Int J Heat Mass Transfer 48:161–170, 2005). Results obtained from WALE sub-grid scale model are in good accordance with experimental results.

1 Introduction

Impinging jet has wide industrial applications because of its high rates of convective heat transfer in the target area. The use of impinging jet in industries includes the cooling of gas turbine blades, combustion chamber, dicing on aircraft, tempering of metal and glass, the printing of circuit boards, cooling of microelectronic components, and drying of papers and textiles. There have been attempts to increase the heat transfer of the precarious components located in the heated sections, such as temperatures reaches 2000 ℃, for example, in the internal region of blades and the wall of the combustor. For local heat transfer enhancement, jet impingement is among the most potent methods of heat transfer developed by forming different scales of vortex pairs. Jet impingement cooling with slot nozzle has very exhaustive research during the past year both experimentally and numerically.

Extensive amount of experimental and numerical study focuses on smooth target flat surface of impinging jet. However, few researchers have worked on target convex and concave surfaces. Gau and Chung (1991) experimentally examine slot jet impinging on the concave and convex surfaces, and an observed bunch of counter-rotating vortices was produced near the wall on the stagnation point in convex surface, which amplifies the momentum transit in the flow and enhances the heat transfer process on the impinging wall. The increase of surface curvature can increase the size of the counter-rotating vortices, and in this case study of the concave surface, absence of three-dimensional vortices in the stagnation point were observed. The heat exchanger surface geometry modification is supposed to be an implicit means to control heat transfer and cooling of surfaces; hence, concave and convex dimpled on flat plate altered the flow phenomena and in turn cause augmentation in heat transfer characteristic. A complex unstable flow structure can evolve as a result of vortex formation processes in local flow detachment zones around barriers in the form of cavities/trenches, exhibiting large-scale low-frequency flow pulsations (Dyban et al. 1971), and in such a situation, prediction of heat transfer characteristic is a bit difficult. Effect of Reynolds number significantly affects the pressure distribution and shear stress variation. Kawale and chndermohan (Kawale and Chandermohan 2017) studied the effect of Reynolds number on static pressure and shear stress for cleaning flat soiled surface.

Terekhov et al. (2009) conducted the experimental study with the round jet flowing around the obstacle in the form of single spherical cavity for Re = (1.2–5.8 × 10⁴), D_c/d_j = 5.2, H/d_j = 0–10, D/D_c = 0–0.5. At D/D_c < 0.13, flow over dimples is comparative similar to a flat plate's flow. In case D/D_c > 0.26, formation of large-scale pulsing toroidal vortex in cavity is observed. This vortex results in the formation of a returnable flow of the gas heated up in a cavity and produces hindrance in the heat exchange phenomenon. Kanokjaruvijit and Martinez-Botas (2005), the effect of the crossflow scheme on heat transfer was investigated, and they found that impingement onto dimples is good with the maximum crossflow scheme and larger jet to plate spacing due to the coupled effect of impingement and channel flow.

Xie et al. (2013) experimentally and numerically studied the fluid flow and heat transfer characteristics of a round jet impinging on the single concave dimple on a flat plate for different Reynolds numbers 5000–23,000. The distance between jet nozzle and the plate was fixed and equal to H/D = 2 with jet to dimple diameter Dj/D = 0.318, 0.5, 1.045 and non-dimensional depth of dimple of δ/D = 0.1, 0.2, 0.3 with the help of combined particle image velocimetry (PIV). Correlative expressions of the local Nusselt number, the Nusselt number at stagnation points, and the average Nusselt number were shown. It can be observed that the depth of dimple significantly affects pressure distribution and local Nusselt number. At δ/D = 0.1, results obtained are similar to that of flat plate, and as depth increases, local Nusselt number reduces, but the average Nusselt number is more than that of a flat plate. However, in the case of convex dimple, the local Nusselt number is higher in the comparison with a smooth surface on the whole, and the local Nusselt number increases with the protrusion relative depth (Zhang et al. 2013). Azad et al. (2000) conducted studies on variation of heat transfer by impinging jet with array of cylindrical dimpled surface experimentally (Re_j = 4850–18,300 and d/D = 0.5). The experimental results suggest that the local Nusselt number for the dimpled target surface and the corresponding smooth target surface is about the same. When compared to a smooth surface, the dimpled surface enables better heat to transfer due to the larger surface area.

Van Hout et al. (2018) performed PIV investigation on dimple geometries with spherical, cubic, conical, and triangular-shaped dimples. Majorly, the study investigates the development of secondary vortices and their interaction with the primary vortices that originated in the free jet, as well as the outer shear layer similarities in the wall jet. Experiments were performed at a nozzle to target distance of about 5D for three Reynolds numbers, Re = 1473, 6322, and 12,438. It can be observed that none of the dimpled surfaces immensely altered the generation of the secondary vortices by the primary vortices and their successive interaction. Ligrani et al. (2001) observes an flow structure due to dimple depressions on a channel surface with help of smoke wires to visualize the flow and investigated a primary vortex pair which are periodically and continuously sheding from the central portion of each dimple. It was observed that as the distance between nozzle and target surface decreases, the strength of the primary vortex pair is amplified and gives rise to two additional secondary vortex pairs.

Numerical simulations were mostly carried by RANS modeling which foresees the dispersion of mean stream and temperature around dimple due to impinging jet, making it difficult to capture flow structure and eddies and its dissipation around dimple. The capturing of coherent structures can be settled utilizing either direct numerical simulations (DNS) or large eddy simulations (LES). A direct numerical simulations (DNS) gives a lot of data about the tempestuous idea of the flow, and the DNS model additionally turns out to be a significant expensive methodology for higher Reynolds number and complex geometry. As to the best of the authors’ knowledge, no study is available in the literature in concern with using LES for simulating jet impingement cooling on dimple plate. Mostly, studies on large eddy simulation for jet impingement are done on flat plate. Shukla and Dewan (2019) performed sub-grid scale LES on a flat plate with a low nozzle to plate spacing and Reynolds number of 20,000 and captured the occurrence of the secondary peak in Nusselt number. They found that LES model predicts well the Nusselt number and overcomes the problems faced by RANS model for over-predicting the Nusselt number especially at the stagnation point.

As previously stated, literature evaluations show that when applied to jet impingement heat transfer, LES is accurate. Furthermore, just a few researches on LES of slot jet impingement heat transfer on a flat plate have been documented, and to the best of the authors’ knowledge, no study on jet impingement on a dimpled plate with LES has been undertaken. WALE, LES, sub-grid model was used in present investigation.

2 Problem Statement

The three-dimensional cylindrical computing domain is depicted in Fig. 1. The inflow at the nozzle inlet is obtained from non-uniform fields derived from RANS simulation of the nozzle channel,which is mapped on the inlet of domain, where nozzle velocity (V) was specified at the inlet based on the value of Reynolds number, Re_j = V(D_j)/ν (where D_j denotes jet diameter and ν is the kinematic viscosity).

Fig. 1

Pictorial representation of computational domain. a Concave. b Convex

A turbulent intensity of 4% is taken as taken in the experiment of Xie et al. (2009). At the outlet, the outflow conditions were applied. And, outlet was kept at a sufficiently large distance from the nozzle center line (X/D_j = 13) to avoid backflow. Reynolds number (Re_j) 5000, nozzle to plate spacing of h/D_j = 2, diameter ratio (D/D_j) = 0.318, and relative depth (δ/D_j = 0.3), for both concave and convex dimples, are utilized in present study.

3 Governing Equation

The large eddy simulation (LES) method is premised on the theory that larger length scales are sensitive to initial and boundary conditions, whereas smaller length scales are isotropic. The large-scale eddies are resolved, whereas smaller scale eddies are modeled. As a result, unlike DNS, LES requires a coarser grid. A filtering process is being used to distinguish the larger scale from the smaller scale depending on the given reference scale. It filters out eddies with length scales that are smaller than the filtering grid spacing or width employed in the computations.

Filtering can be thought of as the convolution of a function with a filtering kernel G.

$$\overline{{u_{i} }} (\vec{x}) = \int {G\left( {\vec{x} - \vec{\xi }} \right)u} \left( {\vec{\xi }} \right)d\vec{\xi }$$

(1)

resulting in

$$u_{i} = \overline{{u_{i} }} + u^{\prime}_{i}$$

(2)

where $\overline{{u_{i} }}$ is the resolvable scale part and $u^{\prime}_{j}$ is the sub-grid scale part; then, filtering the resulting equation gives the equations of motion for the resolved field:

$$\frac{{\partial \overline{{u_{i} }} }}{\partial t} + \overline{{u_{j} }} \frac{{\partial \overline{{u_{i} }} }}{{\partial x_{j} }} = - {\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 \rho }}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$\rho $}}\frac{{\partial \overline{p}}}{{\partial x_{i} }} + \frac{\partial }{{\partial x_{j} }}\left( {v\frac{{\partial \overline{{u_{i} }} }}{{\partial x_{j} }}} \right) + {\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 \rho }}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$\rho $}}\frac{{\partial T_{ij} }}{{\partial x_{j} }}$$

(3)

$$\frac{{\partial u_{i} }}{\partial t} + u\frac{{\partial u_{i} }}{{\partial x_{j} }} = - {\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 \rho }}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$\rho $}}\frac{\partial p}{{\partial x_{i} }} + \frac{\partial }{{\partial x_{j} }}\left( {v\frac{{\partial u_{i} }}{{\partial x_{j} }}} \right)$$

(4)

The extra term $\frac{{\partial T_{ij} }}{{\partial x_{j} }}$ arises from the nonlinear advection terms, because of fact that

$$\overline{{u_{j} \frac{{\partial u_{i} }}{{\partial x_{j} }}}} \ne \overline{{u_{j} }} \frac{{\partial \overline{{u_{i} }} }}{{\partial x_{j} }}$$

(5)

$$T_{ij} = \overline{{u_{i} }} \overline{{u_{j} }} - \overline{{u_{i} u_{j} }}$$

(6)

the Boussinesq hypothesis, and seeks to calculate (the deviatoric part of) the SGS stress using:

$$T_{ij} - {\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 3}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$3$}}T_{kk} \delta_{ij} = - 2\mu_{t} \overline{{S_{ij} }}$$

(7)

where $\overline{{s_{ij} }}$ is the rate of strain tensor for the resolved scale defined by

$$\overline{{s_{ij} }} = {\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 2}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$2$}}\left( {\frac{{\partial \overline{{u_{i} }} }}{{\partial x_{j} }} + \frac{{\partial \overline{{u_{j} }} }}{{\partial x_{i} }}} \right)$$

(8)

and v_t is the sub-grid scale turbulent viscosity. Replacing into the filtered Naiver-Stokes equations, we then have

$$\frac{{\partial \overline{{u_{i} }} }}{\partial t} + \overline{{u_{j} }} \frac{{\partial \overline{{u_{i} }} }}{{\partial x_{j} }} = - {\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 \rho }}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$\rho $}}\frac{{\partial \overline{p} }}{{\partial x_{i} }} + \frac{\partial }{{\partial x_{j} }}\left[ {\nu + \nu_{t} } \right]\frac{{\partial \overline{{u_{i} }} }}{{\partial x_{j} }}$$

(9)

$$T_{ij} - {\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 3}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$3$}}T_{kk} \delta_{ij} = - 2(C_{s} \Delta )^{2} \left| {\left. {\overline{S} } \right|} \right.S_{ij}$$

(10)

The eddy viscosity is modeled as

$$\mu_{sgs} = \rho (c_{s} \Delta )^{2} \left. {\left| {\overline{S} } \right.} \right|$$

(11)

where the box width is usually taken to be

$$\Delta = ({\text{Volume}})^{\frac{1}{3}} \quad {\text{and}}\quad \overline{S} = \sqrt {2S_{ij} S_{ij} }$$

3.1 Wall Adaptive Local Eddy Viscosity (WALE)

The Wall Adaptive Local Eddy viscosity (WALE) model is an algebraic eddy viscosity model similar to the Smogorinski SGS model, but it has some peculiar features not present in the Smogorinski model, such as taking the rotation rate into account while calculating VSGS. Transitions can be controlled by the WALE model (Nicoud and Ducros 1999). WALE model also returns a zero turbulent viscosity for laminar shear flow, allowing for the proper treatment of laminar zones in domain; i.e., damping is not required for VSGS near the wall

$$\mu_{t} = \rho \Delta_{s}^{2} \frac{{(S_{ij}^{d} S_{ij}^{d} )^{3/2} }}{{(\overline{{S_{ij} }} \overline{{S_{ij} }} )^{5/2} + (S_{ij}^{d} S_{ij}^{d} )^{5/4} }}$$

(12)

where

$$\Delta_{s} = C_{w} V^{1/3}$$

$$S_{ij}^{d} = 1/2(\overline{g}^{2}_{ij} + \overline{g}^{2}_{ji} ) - 1/3\delta_{ij} \overline{g}^{2}_{kk}$$

(13)

$$\overline{g}_{ij} = \frac{{\partial \overline{{u_{i} }} }}{{\partial x_{j} }}$$

$$\overline{g}^{2}_{ij} = \overline{{g_{ik} }} \overline{{g_{kj} }}$$

where $\overline{{S_{ij} }}$ is the rate of strain tensor for the resolved scale defined by where the constant $C_{w} = 0.325$.

4 Numerical Strategy

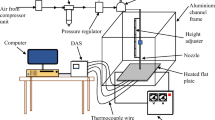
The numerical investigation was conducted using OpenFOAM, an open-source finite volume technique (FVM)-based CFD software. By maintaining density constant, bouyantPimpleFoam, an FVM-based transient solver, was used. The pressure–velocity coupling is controlled by the PIMPLE algorithm, with a collocated grid arrangement. Backward scheme and adjustable time step were used to discretize the temporal derivative. The courant number is kept less than unity to maintain precision. The Gauss linear scheme is used to discretize the gradient and divergence, whereas the Gauss linear corrected method is used to discretize the Laplacian term. For pressure, preconditioned conjugate gradient (PGC) solver is utilized, and for velocity and other properties, smoothSolver is used. Averaging is performed after a steady state is reached. Table 1 shows the thermal fluid properties of air used in the present study. The compressibility effect and temperature dependence on air were disregarded in the present study.

Table 1 Properties of air

4.1 Boundary Conditions

Nozzle inlet: The inlet is mapped with a fixed velocity inlet condition of non-uniform fields produced from a RANS simulation of the nozzle channel.

TOP: Pressure inlet boundary condition is maintained at the top.

Flat plate (consisting dimple): No-slip boundary condition with a constant heat flux is assumed at the flat plate. And for pressure, Von Neumann bc with value atmospheric is used,and sub-grid scale kinetic energy is zero.

Outlet: The pressure inlet–outlet conditions were applied at the outlet.

4.2 Grid Resolution

Detail of grid size for flat, concave, and convex dimple domains is depicted in Table 2. Near the wall region, y ⁺  ~ 1 at the first grid points and minimum values of wall distance Δx⁺  = 35 and Δz⁺  = 55 were maintained. A non-uniform mesh was used in the present study, and O-grids were used in order to capture curved surfaces of dimple which can be seen in Fig. 2, and at important locations where flow mechanics were predicted to be complex, the mesh was finer, such as near the wall region, stagnation region, and wall jet regions. The quality of LES mesh was examined with the help of function IQ_v which depends on sub-grid scale viscosity and dynamic viscosity, and its value should lie between 0.8 and 0.99. As shown in Fig. 3, it can be observed that value of IQ_v is within appropriate range. Grid independence study recommends utilization of higher number of grids; i.e., G-2 is used for further studies

Table 2 Detail description of grid and grid independence study

.

Fig. 2

Representation of computational grid concave (left) and convex (right)

Fig. 3

IQ_v representation of grid concave (left) and convex (right)

5 Results and Discussion

5.1 Numerical Model Validation

Validation study of WALE, LES, sub-grid models for thermal and fluid flow by experimental data (Ashforth-Frost et al. 1997) is performed at Re_j = 20,000, h/D_j = 4 as shown in Figs. 4 and 5. Figure 6a depicts WALE, LES, sub-grid models performed better in capturing Nusselt number variation when compared with experimental result (Ashforth-Frost et al. 1997). It is observed in Fig. 6a that WALE sub-grid model shows the lowest percentage deviation in stagnation point Nusselt number of about 2% with the experimental results (Shukla and Dewan 2019). Similar trends can be observed in fluid flow characteristics depicted with help of mean velocity variation in Fig.  6b. Figure 6b shows that mean velocity is captured better by WALE, LES, sub-grid models with experimental results of mean velocity at (span-wise) X/D_j = 1. However, ability of WALE, LES, sub-grid model is to predict laminar to turbulent transition, flow separation, and near-wall phenomenon. The above validations and advantages lead to the study of dimple in present study with the help of WALE, LES, sub-grid model.

5.2 Flow Field Predictions

Figure 5 represents instantaneous velocity vector at Re_j = 5,000 for both convex and concave dimple target surfaces. As the jet enters the quiescent domain, the shear region is formed due to the interaction of jet and quiescent domain which can be seen in Figs. 5a and b. After the jet strike, the curved surface deflection of the jet is depicted with the aid of vector contours. In Fig. 5a rotation of vectors just above the concave surface, a large toroidal vortex is present which mainly affects the mainstream jet and altered many flow and thermal characteristics. As the jet exits the concave surface downstream, i.e., X > 0.23, flow separation can be depicted with reversed velocity vectors. Similarly, in Fig. 5b, on the convex surface at X = 0.014, the region of flow separation can be seen which is due to adverse pressure gradient, and this phenomena affect the thermal phenomenon at that region. At the edge of the concave surface, i.e., at X = 0.023, a recirculation region is formed, which creates a low-pressure region.

Fig. 4

a Comparison of various LES sub-grid models for experimental results (Shukla and Dewan 2019). b Comparison of present LES sub-grid model results of mean velocity with experimental data (Shukla and Dewan 2019)

Fig. 5

Instantaneous velocity vector representing various flow regimes in a Concave surface. b Convex surface

Fig. 6

Distribution of coefficient of pressure (C_p) along radial position (X/D), concave dimple, convex dimple, and flat surface for Re_j = 5000, D/D_j = 0.381, and δ/D_j = 0.3

Figure 6 represents the variation of coefficient of pressure C_p for various concave, convex, and flat surfaces along with the radial positions (X/D), where $C_{P} = {\raise0.7ex\hbox{${2(P_{i} - P_{0} )}$} \!\mathord{\left/ {\vphantom {{2(P_{i} - P_{0} )} {\rho_{o} U_{0}^{2} }}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${\rho_{o} U_{0}^{2} }$}}$ (U_o and $\rho_{o}$ are velocity and density at the jet inlet). Parabolic distribution of C_p is observed for all three surfaces, that is, per the observation of Xie et al. (Xíe et al. 2013). As a single jet impinges on a concave surface, flow undergoes acceleration in the radial direction according to the surface profile of dimple. At X/D > 0.4–0.6, acceleration of flow is reduced due to reduction in favorable pressure gradient. Due to the high depth of concave dimple, adverse pressure gradient is formed at the edge of the dimple which leads to the turning of the stream which leads to a formation of large toroidal vortices. In context to concave dimple, convex dimple also follows the parabolic distribution of coefficient of pressure. Similar to convex dimple, due to curved surface, there is the intense acceleration of jet, but in region X/D = 0.4–0.6, due to adverse pressure gradient, deceleration of stream takes place which leads to flow separation after the reattachment flow again starts accelerating slowly. Majorly, δ/Dj ratio governs the extent of adverse pressure gradient in both concave and convex surfaces. In contrast to a curved surface, flat surface shows the lesser acceleration of flow and less adverse pressure gradient and generally follows bell-shaped profile for pressure distribution.

Figure 7 shows a comparison of vorticity obtained from PIV (Xie et al.) and LES performed in the present study obtained by attaining a steady state, for both concave and convex surfaces. In the shear region where the jet interacts with quiescent air, high mixing and high-velocity gradient occurs which leads to higher vorticity. According to Xie et al., PIV is problematic at smaller separation point due to less availability of PIV particles; however, LES does not have any such shortcoming, and higher vorticity can be observed on dimple surface as shown in Fig. 7b. Deflection of jet after striking dimple and exiting dimple can be observed accurately in LES as per results obtained from PIV results. From Fig. 7d, one can observe accurate prediction of large toroidal vortices.

Fig. 7

Vorticity contour on curved surfaces for Re_j  = 5000, D/D_j  = 0.381, and δ/D_j  = 0.3. a Convex (PIV). b Convex (LES). c Concave (PIV). d Concave (LES)

5.3 Thermal Field Prediction

Figure 8 represents stream-wise mean temperature variation on curved surface at different position (X/D) for Rej = 5000, D/Dj = 0.381, and δ/Dj = 0.3. It can be observed that non-dimensional temperature is higher at edge of dimple (X/D = 0.52); in case of both concave and convex surfaces, this is mainly due to flow separation at this region. It can be noticed from Figs. 8a and b that thermal boundary layer thickness is higher at edge of dimple surface (X/D = 0.52) which causes reduction in heat transfer. Thickness of thermal boundary layer increases as we move toward the edge of dimple from the stagnation point, i.e., (X/D = 0–0.45), which can be observed from Figs. 8a and b.

Fig. 8

Stream-wise mean temperature variation on curved surface at different position (r/D) for Re_j = 5000, D/D_j  = 0.381, and δ/D_j = 0.3. a Concave. b Convex

Figure 9 shows variation of time averaged local Nusselt number (Nu) along radial position (X/D), concave dimple, convex dimple, and flat surface for Re_j = 5000, D/D_j = 0.381, and δ/D_j = 0.3. The value of Nusselt number is maximum at stagnation point, and it reduces as X/D increases, but a sudden drop in local Nusselt number at X/D = 0.52 in convex dimple is observed which is due to separation of the boundary layer at that location due to adverse pressure gradient. However, after reattachment of the boundary layer, the boundary layer becomes thin which causes an increase in Nusselt number after boundary layer separation. In the case of concave dimple, drop in Nusselt number is higher than that of convex dimple due to formation of recirculation region formed because of a large toroidal vortex. And further along, the X/D Nusselt number reduces. For flat plate, peak in Nusselt number is captured near the stagnation point and decreases by following bell-curve nature. Convex surface has the highest Nusselt number followed by flat plate and the least in case of the concave surface. But due to increased surface area, overall heat transfer increases in both concave and convex surfaces, diminishing the effect of large toroidal vortices and flow separation.

Fig. 9

Distribution of time averaged local Nusselt number (Nu) (obtained from LES) along radial position (X/D), concave dimple, convex dimple, and flat surface for Re_j = 5000, D/D_j = 0.381, and δ/D_j  = 0.3

6 Conclusion

WALE sub-grid scale models were utilized for studying jet impingement on a concave and convex target surfaces at h/D_j = 2, Reynolds number (Re_j) 5000, and diameter ratio (D/D_j) = 0.318, and relative depth (δ/D_j = 0.3). The conclusions are as follows:

• 1. The results obtained from LES of the flow characteristics (vorticity) are close with experimental results obtained from PIV. The flow separation and reattachment are observed in present results.

• 2. Flow separation and presence of large toroidal vortices are well-explained with the help of the coefficient of pressure (C_p) and its effect on heat transfer.

• 3. Time averaged Nusselt number for convex dimple is the highest than flat plate and concave dimple except at the edge of dimple surface where flow separation occurs and drop in Nusselt number is observed.

• 4. At the stagnation point, convex dimple has 25 and 32.5% increment in Nusselt number compared to flat and concave dimpled plates, respectively.