Numerical Investigation of Impinging Jets Flow Using a Multiscale Turbulence Model

Abstract

Impinging jets flow is a complex turbulence flow and has strong heat transport capacity, which was generally used in civil aviation area such like wing anti-ice, turbine blade cooling, etc. In this paper impinging jets flow was simulated using the multiscale turbulence model based on the variable interval time average method. The numerical method used in this simulation is a structured staggered mesh scheme. The computational result shows that the multiscale turbulence model can successfully simulate flow and heat transfer characteristics of impinging jets from wall surface to potential core area. The Nusselt number also agree better with experiments than that of the standard k-ω model.

1 Introduction

Impinging jets flow question is a complex turbulence system, in which the flow eject from hole or slit, and rush to wall. Impinging jets has complicated flow characteristics, including jet flow, backflow, stagnation, wall shear, streamline curvature, etc. The mechanism of turbulence strength and dimension is diversity and hard to capture physical nature. At the same time, mutual effect of all kinds of turbulence vortex extremely influence heat transfer characteristics of flow filed, which leading impinging jets flow an important and difficult question on flow and heat transfer research area.

Although impinging jets flow has complex flow forms, existing mutual interference of turbulence features, it has simple flow geometry structure, becoming an ideal model on flow simulation. Many experimental and numerical investigations of impinging jets flow have been performed so far. Behnia [1], Heyerichs [2], Chen [3], Jaramillo [4] performed numerical simulation of this type of flow to assess predictive ability of k-ε model and k-ω model respectively, however all these simulation based on Reynolds average turbulence model were unsatisfactory. Kubacki [5] believed that the reason is Reynolds average turbulence model weaken the effect of mixing of turbulence energy on jet shearing boundary layer. By contrast, DNS can achieve a simulation result matching with experiment result.

In this paper, a new multiscale turbulence model [6] based on the variable interval time average method was used to simulate impinging jet, and result shows the multiscale model can provide more accurate results than the standard k-ε model, k-ω model and Reynolds stress model. This paper focuses on the application of the multiscale model in numerical simulation of impinging jets flow.

2 Turbulence Model

Multiscale turbulence model is based on variable interval time average method. The equations of turbulence model are as follow.

The continuity equation by Reynolds average method

$$ \left\langle {\frac{{\partial u_{i} }}{{\partial x_{i} }}} \right\rangle = 0 $$

(2.1)

The momentum equation by Reynolds average method

$$ \frac{{\partial \left\langle {u_{i} } \right\rangle }}{\partial t} + \left\langle {u_{j} } \right\rangle \frac{{\partial \left\langle {u_{i} } \right\rangle }}{{\partial x_{j} }} = - \frac{1}{\rho }\frac{\partial \left\langle p \right\rangle }{{\partial x_{i} }} + \nu \frac{{\partial^{2} \left\langle {u_{i} } \right\rangle }}{{\partial x_{j} \partial x_{j} }} - \frac{{\partial \left\langle {u_{i}^{\prime } u_{j}^{\prime } } \right\rangle }}{{\partial x_{j} }} + \left\langle {f_{i} } \right\rangle $$

(2.2)

The zero-order continuity equation by multiscale average method

$$ \frac{{\partial \left\langle {u_{i} } \right\rangle_{{0}} }}{{\partial x_{i} }} = 0 $$

(2.3)

The zero-order momentum equation by multiscale average method

$$ \frac{{\partial \left\langle {u_{i} } \right\rangle_{{0}} }}{\partial t} + \left\langle {u_{j} } \right\rangle_{{0}} \frac{{\partial \left\langle {u_{i} } \right\rangle_{{0}} }}{{\partial x_{j} }} = - \frac{1}{\rho }\frac{{\partial \left\langle p \right\rangle_{{0}} }}{{\partial x_{i} }} + \nu \frac{{\partial^{2} \left\langle {u_{i} } \right\rangle_{{0}} }}{{\partial x_{j} \partial x_{j} }} - \frac{\partial }{{\partial x_{j} }}\left\langle {\left( {\sum\limits_{{\text{I = J + 1}}}^{\infty } {u_{i}^{{\left( {\text{I}} \right)}} } } \right)\left( {\sum\limits_{{{\text{I = J + }}1}}^{\infty } {u_{j}^{{\left( {\text{I}} \right)}} } } \right)} \right\rangle_{{0}} $$

(2.4)

In Eq. (2.2) and (2.4), turbulent stress terms $- \left\langle {u^{\prime}_{i} u^{\prime}_{j} } \right\rangle$ and $- \sum\limits_{{{\text{I = }}1}}^{\infty } {\left\langle {u_{i}^{{\left( {\text{I}} \right)}} u_{j}^{{\left( {\text{I}} \right)}} } \right\rangle_{0} }$ both are calculated as

$$ { - }\left\langle {u^{\prime}_{i} u^{\prime}_{j} } \right\rangle { = }2\nu_{t}^{{}} \left\langle {S_{ij} } \right\rangle - \frac{2}{3}k\delta_{ij} $$

(2.5)

$$ - \sum\limits_{{{\text{I = }}1}}^{\infty } {\left\langle {u_{i}^{{\left( {\text{I}} \right)}} u_{j}^{{\left( {\text{I}} \right)}} } \right\rangle_{0} } = 2\sum\limits_{{{\text{I = }}1}}^{\infty } {\nu_{t}^{{\left( {\text{I}} \right)}} } \left\langle {S_{ij} } \right\rangle_{0} - \frac{2}{3}\sum\limits_{{\text{I = 1}}}^{\infty } {k^{{\left( {\text{I}} \right)}} } \delta_{ij} $$

(2.6)

$\nu_{t}^{{\left( {\text{I}} \right)}}$ as Ith-order viscosity, is calculated as

$$ \nu_{t}^{{\left( {\text{I}} \right)}} = C_{\mu }^{{\left( {\text{I}} \right)}} \frac{{\left[ {k^{{\left( {\text{I}} \right)}} } \right]^{2} }}{{\varepsilon^{{\left( {\text{I}} \right)}} }} $$

(2.7)

All superscript (I) and (J) in equation represent the Ith-order and Jth-order average respectively.

The energy equation by multiscale average method

$$ \frac{{\partial (\overline{E} )}}{\partial t} + \frac{\partial }{{\partial x_{j} }}\left[ {\left( {\,\overline{E} + \frac{{\overline{p} }}{{\overline{\rho } }}} \right)\,\overline{{\,u_{j} }} } \right] = \frac{\partial }{{\partial x_{j} }}\left\{ {\frac{1}{{\overline{\rho } }}\left[ {\overline{{u_{i} }} \left( {\overline{{\sigma_{ij} }} + \overline{{\sigma_{ij}^{T} }} } \right) - \left( {\overline{{q_{j} }} + \overline{{q_{j}^{T} }} } \right)} \right] - \left( {\mu + \frac{{\mu_{T} }}{{Pr_{T} }}} \right)\frac{\partial k}{{\partial x_{j} }}} \right\} $$

(2.8)

In Eq. (2.8), $q_{j}^{T}$ express turbulence heat flux, $Pr_{T}$ express turbulence Prandtl.

3 Geometry Model and Numerical Method

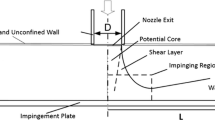
The impingingjet example this paper simulate to verify accuracy of multiscale turbulence model is Ashforth-Frost [7] semiconfined orthogonally impinging slot jet experiment, as shown in Fig. 1.

Fig.1.

Diagram of impinging jet

The simulation condition is totally same as experiment. Jet height H/B=4 and 9.2 were simulated, incoming flow Reynolds number Re=2*10⁴. Simulation use inlet width as characteristic length. The inlet was set to constant velocity. The outlet was set to rated environment pressure. Figure 2 shows the partial calculation grids of impinging jet flow field for H/B=9.2.

Fig. 2.

Partial calculation grids of impinging jet flow field for H/B = 9.2

4 Simulation Results and Analysis

Figure 3–4 shows the two different H/B flow field. At H/B = 4, jet flow hasn’t fully developed when rush to plate. The impinging plate is still within the potential core of the jet. At H/B = 9.2, jet flow has fully developed and potential core can smooth transit to central symmetric line, and was unaffected by impinging plate. The length of potential core are 4 and 7.5 jet inlet width for H/B = 4 and 9.2 each, both match up with experiment data accurately.

Fig. 3.

Velocity vector plot H/B = 4

Fig. 4.

Velocity vector plot H/B = 9.2

Figure 5–6 shows the two different H/B velocity profile nearby impinging plate wall surface, which has a high precision simulation result.

Fig. 5.

Velocity profile nearby impinging plate wall surface H/B = 4

Fig. 6.

Velocity profile nearby impinging plate wall surface H/B = 9.2

Figure 7 shows the plate Nusselt number distribution for impinging jet H/B = 4, and using DNS and standard k-ω model WX (Wilcox Stanard model)^[4] as a contrast. It can be seen that multiscale model and DNS simulation result are consistence with experiment. The multiscale model successfully simulate two peek distribution structure of Nusselt number. The second peek means the reflection of bounce of flow rushing to plate, which enhance the heat transfer efficiency. This two Nusselt number peek phenomenon wasn’t captured by k-ω model.

Fig. 7.

Distribution of nusselt number H/B = 4

5 Result

Impinging jets flow are common in engineering. This paper presented multi-scale turbulence model is applied to the complex impinging jets turbulent flow and heat transfer problems. The calculated results show that the multi-scale system can not only correctly predict the complex flow characteristics, but also be able to accurately reflect the heat transfer characteristics. The example has fully confirmed the multi-scale model for simulating complex flow and heat transfer problems.